Introduction

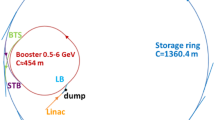
The High Energy Photon Source (HEPS) [1, 2], which is under construction in Beijing, is the first fourth-generation synchrotron light source in China. The goal of the HEPS project [2] is to build a high-performance high-energy synchrotron light source with 6 GeV beam energy, 200 mA beam current, and the horizontal natural emittance lower than 60 pm\(\cdot \)rad, promising radiation brightness of up to \(1\times 10^{22}\) [\(\mathrm photons\cdot s^{-1}\cdot mm^{-2}\cdot mrad^{-2} \cdot (0.1\% \,bw)^{-1}\)] at typical hard X-ray regime. After several years of iterations, the physics design of the HEPS accelerator, which consists of a 500 MeV LINAC, a booster synchrotron to ramp the beam energy to 6 GeV, a 6 GeV storage ring, and three beam transfer lines, was basically finished. The basic layout of HEPS accelerator is shown in Fig. 1 [1]. The three beam transfer lines shown in Fig. 1, named “LTB,” “BTS,” and “STB,” are used to deliver electron beams from LINAC to booster, from booster to storage ring, and from storage ring to booster, respectively. The main reason to have the high-energy beam transfer line “STB” is to use the booster as a high-energy accumulator [3], which will be discussed in detail later in this manuscript.

Fig. 1
figure 1

Layout of the HEPS accelerator

Full size image

The latest baseline designs (labeled as V3.0) of the LINAC [4], the booster [5], the beam transfer lines [6], and the storage ring [7] were given in 2020. Based on these baseline lattices, the designs and optimizations of many types of hardware (see, e.g., [8,9,10,11,12]) and detailed physics studies [3, 13,14,15,16,17,18,19,20] were carried out and basically finished.

It is widely known that the synchrotron light to be delivered to the users is mainly generated when the electron beam passing through the insertion devices (IDs) or bending magnets in the storage ring. Therefore, it is necessary to compute the equilibrium parameters of the electron beam in the storage ring for the purpose of precisely estimating the actual performance of the synchrotron light. Both the single-particle dynamics and the current-dependent collective effects [21] need to be considered to compute the full-current, equilibrium parameters of the electron beam.

It is important to point out that the design and operation status of the IDs also strongly affect the electron beam parameters, mainly in the following manners. Firstly, the IDs increase the energy loss per turn and reduce the radiation damping time, indicating that the RF parameters and the corresponding equilibrium bunch length would change. Secondly, the IDs introduce remarkable impedance, contributing to the collective effects. The baseline designs of all the 14 IDs in Phase I of HEPS have been given in reference [8]. However, there are too many different operation status of the IDs to enumerate all possibilities, mainly because the settings of each ID will vary individually according to the requirements of the users’ experiments. We therefore consider two typical settings of the IDs in the following computations, which are without ID (named “bare lattice,” indicating all the IDs are at the maximum gaps) and with all the IDs adjusted to the nominal operation status (named “14-ID lattice”), respectively. In other status of the IDs, the electron beam parameters are in between the values corresponding to these two typical settings.

RF cavities are used to compensate the energy loss and to provide longitudinal stable bucket. Different operation status of IDs would result in different radiation energy losses, indicating that the RF voltage needs to be different. Furthermore, the RF parameters also affect the full-current, equilibrium parameters of the electron beam significantly. In HEPS storage ring, the main RF frequency is 166.6 MHz [22]. The active third harmonic cavities are planned to be used for lengthening the bunches. A bucket height of 4% is expected to be provided by RF cavities.

As mentioned above, the designed total beam current in HEPS storage ring is 200 mA. The so-called high-brightness mode and high-bunch-charge mode are proposed as the two baseline operation modes of HEPS storage ring. The main difference between these two operation modes is the number of bunches and therefore the single-bunch charge. In the “high-brightness mode,” 680 bunches out of 756 buckets will be filled in the storage ring with approximately 1.33 nC per bunch. And 63 bunches are planned to be distributed evenly in the storage ring in the “high-bunch-charge mode,” with approximately 14.41 nC per bunch.

To compute the full-current, equilibrium parameters of the electron beam corresponding to the aforementioned two operation modes, the collective effects, such as the impedance-induced collective effects and intra-beam scattering (IBS), need to be considered. The detailed impedance model was developed by careful impedance computations of all the vacuum components. The needed basic lattice parameters and the frequencies of the RF system of the storage ring are listed in Table 1.

Table 1 Main lattice parameters of HEPS storage ring
Full size table

The parameters given in Table 1 correspond to the lattice without any imperfection. Actually, comprehensive error correction simulation studies were carried out, and the corrections of imperfections were studied in detail [14, 23,24,25,26]. The error analyses indicated that the lattice parameters can be basically restored after careful correction. And, studies [27] indicated that the errors do not show a significant influence on the equilibrium beam parameters; it should be reasonable to use these parameters (as nominal values) without consideration of errors. On the other hand, the lattice parameters and electron beam parameters will be slightly different when different error seeds were used. It would be hard (and not very meaningful) to enumerate the results corresponding to all the error seeds. Therefore, the parameters presented in this paper can only give some typical values (obtained without considering errors) for the discussions.

The two operation modes of the storage ring require bunches with different charges, causing different beam parameters in the injector. We hereby compute the typical beam parameters in the booster before extraction and the beam parameters at the end of the LINAC corresponding to the two operation modes. The needed basic parameters of the latest baseline lattices and the main RF parameters [28] of the HEPS booster are listed in Table 2.

Table 2 Main lattice parameters of HEPS booster (at 6 GeV)
Full size table

The rest of this paper is organized as follows. In “Electron beam parameters in storage ring” section, the computation process and results of the equilibrium beam parameters in the storage ring, corresponding to the two proposed operation modes, are described. Then, the beam parameters in the booster and the LINAC are given accordingly in “Electron beam parameters in HEPS injector” section. The conclusions and discussion are given in “Conclusions and discussions” section.

Electron beam parameters in storage ring

In this section, we would present the computations of the electron beam parameters in the HEPS storage ring in detail. First of all, the RF parameters need to be determined. In the double-frequency RF system, the total RF voltage (see, e.g., Eq. (1)) is determined by the summation of the fundamental RF and harmonic RF, marked by the subscripts 1 and 2, respectively.

$$\begin{aligned} V_{\textrm{total}}=V_1\sin \phi _1+V_2\sin \phi _2. \end{aligned}$$
(1)

Note that there are non-unique settings of the harmonic cavities which can provide bunch lengthening [29, 30]. For simplicity, we chose the so-called ideal HC setting, which can provide the ideally flat RF potential together with the main RF, in the computations. The main reason of this choice was that the longitudinal bunch distribution was expected to have a long-flat top, and significant bunch lengthening can be achieved, by applying the “ideal HC” setting. The “ideal HC” condition can be achieved by setting both the first and the second derivatives of the total RF voltage at the synchronous phase of the fundamental RF (\(\phi _{1s})\) to zero:

$$\begin{aligned} \begin{aligned} \frac{\partial V_{\textrm{total}}}{\partial \phi _1}\Bigg \vert _{\phi _1=\phi _{1s}}=0 \\ \frac{\partial ^2 V_{\textrm{total}}}{\partial \phi _1^2}\Bigg \vert _{\phi _1=\phi _{1s}}=0. \end{aligned} \end{aligned}$$
(2)

Nevertheless, using only the main RF cavities (called “w/o HC” setting) was also considered in the following computations, mainly for completeness.

As mentioned above, the RF cavities need to provide 4% bucket height. The resulting RF voltages and phases at the aforementioned two settings (“w/o HC” and “ideal HC”), for both the “bare lattice” and “14-ID lattice,” are listed in Table 3.

Table 3 Main RF parameters
Full size table

With the RF parameters given in Table 3 and the basic lattice parameters given in Table 1, a set of “equilibrium” parameters of electron beams without considering any collective effect can already be obtained. However, these beam parameters are valid only at the “zero-current” limit.

Many different collective effects needed to be considered in the computations of the equilibrium beam parameters in the proposed operation modes. The main collective beam effects [21] can be divided into two categories, namely the impedance-induced effects (such as the microwave instability (MWI) and transverse mode coupling instability (TMCI)) and non-impedance-induced collective effects (e.g., intra-beam scattering (IBS)). The coupling impedance of the whole ring (shown in Fig. 2) [27, 31,32,33], which is the basis for the studies of the impedance-induced collective effects, was developed based on element-by-element computations with either analytic formulae or numerical simulation codes. The transverse impedance for each element has been normalized by the local betatron functions. Considering a natural bunch length of around 5 mm without HC, a driving bunch of 3 mm was used in the numerical simulations of impedance. The resulting frequency range of impedance should be wide enough in predicting the collective instabilities. More details regarding impedance modeling and optimization will be presented in a forthcoming paper.

Fig. 2
figure 2

Impedance model of the HEPS storage ring. The left and right plots are the longitudinal and vertical impedance spectrum, respectively. The red and green curves are the real and imaginary parts of impedance without including any insertion device, respectively. The blue and black dotted curves are the real and imaginary parts of impedance with the consideration of all the 14 IDs in Phase I of HEPS project, respectively

Full size image

To compute the equilibrium beam parameters, both the aforementioned impedance-induced collective effects and IBS needed to be considered. Our computations showed that the longitudinal bunch parameters were dominated by the longitudinal impedance in the two nominal operation modes in HEPS storage ring. Furthermore, we did not observe any degradation of transverse bunch parameters when considering impedance only in the two nominal operation modes in HEPS storage ring. Therefore, we first carried out multi-particle tracking simulations using the elegant [34] code and its parallel version Pelegant [35] with the consideration of only the longitudinal impedance in the two nominal operation modes. Then, the IBS effect was computed, starting from the obtained “equilibrium” beam parameters, via the analytic formulae developed by Bjorken and Mtingwa [36]. The resulting bunch length, energy spread, and the transverse emittances are listed in Table 4.

Table 4 Main equilibrium beam parameters (10% coupling)\(^1\)
Full size table

Furthermore, the Touschek lifetime \(\left( T_l\right) \) can be computed using the equilibrium beam parameters, by A. Piwinski’s method [37]:

$$\begin{aligned} \frac{1}{T_l} = \left<\frac{r_p^2 c N_p}{8\pi \gamma ^2\sigma _s\sqrt{\sigma _x^2\sigma _z^2-\sigma _p^4D_x^2D_z^2}\tau _m}F\left( \tau _m,B_1,B_2\right) \right> \end{aligned}$$
(3)

with

$$\begin{aligned}{} & {} F\left( \tau _m,B_1,B_2\right) = \sqrt{\pi \left( B_1^2-B_2^2\right) }\tau _m\int _{\tau _m}^\infty \left( \left( 2 + \frac{1}{\tau }\right) ^2\right. \nonumber \\{} & {} \quad \left. \left( \frac{\tau /\tau _m}{1+\tau }-1\right) +1 \right. \nonumber \\{} & {} \left. -\frac{\sqrt{1+\tau }}{\sqrt{\tau /\tau _m}}-\frac{1}{2\tau }\left( 4+\frac{1}{\tau }\right) \ln \frac{\tau /\tau _m}{1+\tau }\right) e^{-B_1\tau }I_o\left( B_2\tau \right) \frac{\sqrt{\tau }d\tau }{\sqrt{1+\tau }}\nonumber \\ \end{aligned}$$
(4)

where \(r_p\) is the classical particle radius. c is the speed of light in vacuum. \(N_p\) is the number of particles in one bunch. \(\sigma _x\) and \(\sigma _z\) are the horizontal and vertical bunch sizes, respectively. \(\sigma _s\) is the RMS bunch length. \(D_x\) and \(D_z\) are the horizontal and vertical dispersion function, respectively. \(B_1\) and \(B_2\) are two factors given in [37]. \(\tau _m=\beta ^2\delta _m^2\), with \(\delta _m\) is the local momentum aperture (LMA).

To compute the local momentum aperture (LMA), six-dimensional tracking with the considerations of RF cavities, synchrotron radiation damping, and quantum excitation was carried out. The physical aperture was set as ± 11 mm along the whole ring in the tracking. More realistic physical aperture was also tested in several 7BA cells, and the difference between the two settings was negligible. The obtained LMA values in one superperiod (two 7BA cells) for the both the “bare lattice” and the “14-ID lattice” are shown in Fig. 3. The corresponding Touschek lifetime is also given in Table 4.

Fig. 3
figure 3

LMA in two continuous 7BA cells for the “bare lattice” and the “14-ID lattice”

Full size image

Note that the errors affect both the linear and the nonlinear dynamics, leading to the distortion of linear optics, the shrink of dynamic aperture (DA), the reduction in LMA, etc. Fortunately, the distortion of linear optics can be basically recovered after the careful correction of errors. Studies [14] indicate that the DA can become sufficiently large for injection after the correction of errors. Furthermore, the reduction in Touschek lifetime after the correction of errors is expected to be not severe [38]. Taking the Touschek lifetime of the electron beam in the “high-brightness mode” of the 14-ID lattice (with the “ideal HC” setting) as an example, the Touschek lifetime is about 7.39 h without consideration of any error, as shown in Table 4. But, studies using several error lattices indicate that the Touschek lifetime is all reduced but still longer than 5 h under the same conditions except including errors.

Electron beam parameters in HEPS injector

The essential purpose of the injector is to provide the needed electron bunches to the storage ring. Therefore, the requirements of the bunch charge and number of bunches per ramping cycle are mainly determined by the operation modes, the desired beam current stability, and the Touschek lifetime of the storage ring. Based on the discussions with the beamline experts, the current stability of the electron beams in storage ring is targeting 0.3% when the total beam current is approximately 200 mA in our design. And the two operation modes in the “14-ID lattice” with “ideal HC” (corresponding to the beam parameters in the last column in Table 4) were chosen as the nominal cases which were used to give requirements to the booster. Furthermore, it is worth to point out that the required bunch charge in the booster is a little bit different when filling the storage ring from zero current and refilling the storage ring in “top-up” operation. For both cases, the main beam parameters are shown in Table 5. We hereby take the “top-up” operation case as an example to present the detailed computation process of the electron beam parameters in the booster before extraction.

HEPS employs the “high-energy accumulation” scheme [3]. The process can be described as follows: When the electron beam in the storage ring needs to be refilled, the bunch with the lowest charge will be extracted first from the storage ring, be injected into the booster, merging with the existing 6 GeV bunch in the booster to increase the single-bunch charge, and then be injected back to the storage ring. There are two high-energy transfer lines connecting the storage ring and the booster [6]. Ninety percent transfer efficiency was assumed when the electron bunch passing through each high-energy transfer line.

When refilling the storage ring operated in the “high-brightness mode,” the required single-bunch charge in the booster before merging with the bunch coming from the storage ring is approximately 0.59 nC. The bunch charge after merging is approximately 1.79 nC. And, when the storage ring operates in the “high-bunch-charge mode,” the required charge of the electron bunch, which is going to be merged with the high-charge bunch coming from the storage ring, needs to be approximately 4.54 nC. The highest single-bunch charge in the booster after merging is about 17.46 nC.

Similar to the impedance model developed for the storage ring, the impedance for each vacuum component of the booster was calculated individually with a driving bunch of 3 mm, and the transverse impedance was normalized by the local beta function. The longitudinal and vertical impedance models of the booster [39] are shown in the left and right plots of Fig. 4, respectively. To obtain more realistic bunch parameters in the booster before extraction, the lattice parameters and RF parameters of the booster listed in Table 2 were used. The simulations were carried out in the following two steps. First, we simulated the ramping process of a bunch with the required charge from 500 MeV to 6 GeV in the booster. Second, the ramped bunch was merged with the re-injected bunch from the storage ring, and the merged bunch was tracked for 10,576 turns, corresponding to approximately 16 ms (~7 times of transverse damping time, ~3.4 times of longitudinal damping time) determined by the previous study. The obtained bunch parameters right before the extraction are listed in Table 5.

Fig. 4
figure 4

The longitudinal and vertical impedance of the HEPS booster

Full size image
Table 5 Main beam parameters in booster before extraction (1% coupling)
Full size table

As the first-stage of HEPS injector, the main design goal of the LINAC is to fulfill the requirements of the booster. According to the aforementioned bunch charge in the booster before extraction and the assumption of 80% transfer efficiency in the ramping process, the needed single-bunch charge at the exit of the LINAC is approximately in the range of 0.75 nC and 5.7 nC. Furthermore, considering to fulfill the special requirement to the LINAC in the commissioning stage [4] and to reserve more safety margins, the optimization of the LINAC was at 7.0 nC per bunch. Space charge and the short-range wakefield in the accelerating structures were both included in the computations of the electron beam parameters in the LINAC. Tracking simulations were carried out to obtain the beam parameters at the exit of the LINAC, which are shown in Table 6. When the bunch charge is 0.75 nC and 7.0 nC, the accelerating phase of accelerating structure is 90 degree and 83 degree.

Table 6 Main beam parameters in HEPS LINAC\(^1\)
Full size table

Conclusions and discussion

After many years’ iterations and comprehensive studies, the physics designs of HEPS accelerators were finished. In this paper, we presented the main electron beam parameters in the storage ring, the booster (before extraction), and the LINAC, for the full-current operation of the storage ring.

The given equilibrium parameters of electron beam in the storage ring correspond to the two baseline operation modes, namely the “high-brightness mode” and the “high-bunch-charge mode.” To compute the equilibrium parameters, the impedance-induced collective effects were first considered. Then, the IBS effect was included analytically. Using the obtained electron beam parameters and the LMA of the storage ring, Touschek lifetime was then computed.

By considering the requirements of the storage ring to the booster, together with the impedance model of the booster itself, the beam parameters in the booster before extraction were given. According to these parameters, the optimization point of the LINAC was determined to be 7.0 nC bunch charge. Taking the space charge effect and short-range wakefield in the LINAC into considerations, the main beam parameters in HEPS LINAC were also given.

In a word, the electron beam parameters of HEPS accelerators were given in detail in this paper, which can provide an important reference for the precise evaluation of the radiation performance, and the upcoming commissioning and operation of HEPS.