Introduction

AstroBio Cube Sat (ABCS) is a 3U CubeSat [1] designed and developed in partnership between INAF, Italian National Institute of Astrophysics, Sapienza University of Rome, and Alma Mater Studiorum University of Bologna, on the Vega C Maiden Flight launch opportunity offered by European Space Agency (ESA) with the support of the Italian Space Agency (ASI) [2]. The project aims to test an automated onboard laboratory in space environments based on Lab-on-Chip (LoC) technology [3] to provide a highly integrated in-situ multiparameter platform that uses immunoassay tests to exploit chemiluminescence detection.

In-orbit validation of the proposed technology would represent a significant breakthrough for autonomous execution of bio-analytical experiments in space with potential application in planetary exploration for biomarkers detection, astronauts’ healthcare, space stations’ environmental monitoring and more (see for example [4]).

The ABCS will be deployed within the inner Van Allen belt (5830 km altitude). At this altitude, ABCS will experience radiation doses orders of magnitude greater than in Low Earth Orbit, where CubeSats usually operate. According to the calculation carried out with SPENVIS [5], the total flux intensity in the mission orbit is 1.41E + 07 particles/cm2/s. Trapped particles (electron and proton) are the main component of the total flux. Solar Energetic Particles (SEP) and Galactic Cosmic Ray (GCR) are ions with atomic numbers Z from 1 to 92. The former originated from Solar activity has a higher flux (but lower energies) than the latter, which, being of galactic origin, has a peak kinetic energy of 100 GeV/nucleon. The interaction of each kind of source particle with the satellite structure generates a cascade of secondary particles with lower kinetic energy and a higher probability of interacting further within the satellite interior, releasing dose, causing damages to the material, and altering the subsystem’s functionality.

Our activity aims to exploit nuclear methodology to support the design of future aerospace missions evaluating shielding materials, foreseeing detectors readout and damage level in the electronic component. We also evaluate the representativity of the radiation damage tests carried out in ground facilities.

This work reports the preliminary modelling activity performed with the FLUKA (Fluktuierende Kaskade) [6] Monte Carlo code to estimate the Total Ionising Dose (TID) and the 1 MeV neutron Silicon equivalent damages (SI1MEVNE) fluence on some components of the ABCS payload and the external Solar Panels (SPs) delivered by the mission orbital source terms. We also estimate the effectiveness of a shielding solution for the payload designed within the mass mission budget.

Finally, we started a preliminary comparison of the orbital simulation results with the one obtained from a full-scale simulation of an ABCS neutron irradiation within the Thermal Column Cavity (TCC) of the TAPIRO nuclear reactor facility at ENEA-CASACCIA Research Centre that is included in the ASIF initiative between ASI, ENEA, and INFN [7,8,9] for the qualification of electronics components and system for aerospace application.

These results will constitute the basis for defining an experimental setup within the TCC of the TAPIRO to test some LoC functionality during neutron irradiation. Also, comparing the simulation results with the data collected during the ABCS mission will allow a quantitative tuning of the modelling tools.

Calculation assumption and model definitions

Implementation of the ABCS layout’s relevant features in the FLUKA and MCNP models

As reported in the exploded view of Fig. 1, we can distinguish the satellite skeleton made in aluminium Al5046 alloy constituted by four side panels, a top and bottom lids, all mounted on four rails. On the external surface of each side, there is a solar panel.

Fig. 1
figure 1

Comparison of the satellite’s exploded view (1) with the layout’s sections obtained by FLAIR (FLUKA Advanced Interface) in the FLUKA model. The model layout retains only the geometrical features and the materials necessary for particles transport and shielding considerations. In particular, Sect. 2 shows the pressurized primary payload, the ancillary radiation dose sensors box, the upper and lower support plate. Section 3 shows the position of the Attitude Control System (ACS) magnetic cylinders

Full size image

The pressurized primary payload (the ABCS payload in the following) is contained in an Al5046 box, in which are located:

  • An LoC with its readout board;

  • An interface board with pumps and drivers for fluid injection;

  • RADFETs (Radiation Field-Effect transistors) for radiation dose measurements;

  • A pack of rechargeable batteries;

  • A heater coupled with a passive multi-layer insulation system ensures payload temperature control.

The goal of the primary payload is to perform immunoassays using light detection of immobilized target molecules within the chip, exploiting chemiluminescence reaction at controlled temperature and pressure.

As a secondary payload, the satellite interior hosts an AL5046 aluminium alloy box containing the ancillary radiation sensor system to monitor the orbital radiation doses levels.

Due to the mass budget restriction, the implemented Attitude Controller System (ACS) is based on hysteresis rods and permanent magnets passive system that should ensure an orthogonal orientation relative to the Earth’s magnetic field lines after the satellite deployment. The magnetic cylinders are located between the bottom lid and the support plate (see section AA′ in Fig. 1). In contrast, the hysteresis rods are inserted in each side panel of the satellite structure.

Our simulation goals are preliminarily limited to estimating shielding solution effectiveness into the ABCS payload and the design of irradiation experiments with fission neutrons, so we simplify the layout as reported limiting the number of components to the elements that act as primary shielding materials for the ABCS payload, also simplifying the interpretation of the secondary particles showers generated during the simulations. Furthermore, the design of the neutron irradiation requires a future study of the level of activation of the materials to avoid long cooling periods that prejudicated the execution of post-irradiation tests in external laboratories.

Figure 2 shows plant and side cross sections as obtained by FLAIR (FLUKA Advanced Interface) [10] on the model implemented for the particle transport simulation. The components implemented in the FLUKA model are the skeleton structure of the satellite, the solar panels, the ABCS and secondary payload boxes, the support plates, the magnetic cylinders, the connector plugs on the top of the ABCS payloads and four Print Circuit Board (PCB) and the air volume contained within it. Comparing the model layout with the exploded view of Fig. 1, we realize that the estimation of the dose rates or the equivalent damages, due to the absence of the excluded components shielding contribute, overestimates the quantities experimented in the complete satellite layout. In the future, we will model the complete ABCS layout to compare the estimated dose–response with the data obtained from the mission telemetry. Finally, we will perform a complete radiometric study.

Fig. 2
figure 2

On the left, the image reports the magnification of the external layers structure of the solar panel and the shielding solution, corresponding to the ones illustrated in Table 1. The central cross section, from which the magnification belongs, is taken along the B-B’ direction located at the height of the ABCS payload, as shown in the rightmost part of the figure. The two sections help to clarify further the simplified mass distribution assumed in the FLUKA model

Full size image

Figure 2 also shows a magnification of the structure of one of the ABCS long sides constituted by a sequence of layers, from out to in, representing the materials of the solar cell, the PCB Stack-Up, and the aluminium panel constituting the innermost boundary.

Due to the satellite mass budget limit, we limit the shielding to an area (6.7 cm × 15.05 cm) to protect further the ABCS payload around the four side panels borders. In such an area, we remove from the external the aluminium for a total thickness of 0.2 cm, substituting it with a first tungsten layer (thickness = 0.06 cm) to stop charged particles, followed by a second layer of epoxy resin (thickness = 0.1 cm) that stops secondary charged particles, maintaining a residual aluminium thickness of 0.04 cm. This solution, whose materials layer sequence has been optimized in preliminary simulations of a simple slabs model, increases the total ABCS total mass of 300 g remaining within the mass mission budget. Table 1 resumes the layers sequence and the material compositions for the solar cell and the adopted shielding solution.

Table 1 Materials used for each FLUKA region constituting Solar cell and further shielding layers
Full size table

To simulate the ABCS’s neutron irradiation in the TCC position of the TAPIRO, we export the ABCS geometry definition contained in the FLUKA input to the MCNP formalism using a utility contained in the FLAIR package. As reported in Fig. 3, we insert the ABCS geometry into the TAPIRO’s MCNP input deck, locating it inside the TCC irradiation position.

Fig. 3
figure 3

Geometric cross section obtained with the MCNP plotter shows the ABCS geometry’s integration into the TAPIRO’s MCNP model. The TCC hosts the whole satellite in the proximity of the outermost reflector surface. The RC1 (Radial Channel 1) irradiation position is also visible on the opposite side of the core. The iconic representations of the ABCS on the left side of the image describe two alternative static orientations considered for irradiation in the preliminary calculations (see text)

Full size image

In some preliminary simulations, we consider three different irradiation layouts to evaluate the differences in the responses due to the ABCS orientations within the TCC (see Fig. 3) in the MCNP simulations. First, we locate one of the ABCS sides in the proximity of the external reflector (side irradiation). In the second, we place the ABCS to position the bottom lid near the reflector (bottom lid irradiation). Finally, we locate the top lid near the reflector (top lid irradiation). Comparing the intensities of the SI1MEVNE fluxes (see paragraph 2.5) into card four in preliminary MCNP simulations, we find that the side irradiation maximizes the equivalent flux. In contrast, the equivalent fluxes of the bottom and top lid irradiation positions have 63% and 30% of the side positions. Having this figure in mind, we decided to perform the simulations using the side irradiation position, reserving, for future study, the search of an optimized irradiation geometry.

Orbital source term definitions

The Van Allen’s Belt radiative environment takes its origins, far from the Earth, in the mutual interaction of the Solar Wind (SW) ions, emitted during the Sun periodic activity, and the GCR ions. Thus, the intensity of the GCR ions is anticorrelated to the SW intensity decreasing during solar maximum and increasing during the solar minimum. Sometimes, there is a superimposition to the usual solar cycle of a Solar Event Flares (SEF) for a relatively short period, causing a high-intensity plasma emission in the form of Solar Energetic Particles (SEP). Near the Earth, the shielding influence of the geomagnetic field allows the deflection of the less energetic fraction of both GCR and SEP that slow down along the geomagnetic field’s lines, remaining trapped for a long time in complex trajectories. Only the fraction of the ions having sufficiently high kinetic energy penetrate beyond the Belt, interacting with the atmosphere and generating the well-known atmospheric particles’ shower, whose secondary partially reach the ground [11].

In conclusion, the Van Allen radiation source includes trapped particles (protons and electrons), GCR ions and SEP ions. The SW cyclic emission has, on average, an energy distribution less energetic than the GCR’one that reaches ultra-relativistic kinetic energies. Therefore, to define the whole orbital radiation source, we implement in SPENVIS the ABCS mission at the altitude of 5830 km on a circular orbit.

The quantification of the trapped particles’ source term deserves some clarification based on the information reported on the online manual of the SPENVIS code.

For example, in SPENVIS, the standard package to evaluate the trapped protons and electrons source terms use the A8 model based on the data collected from a series of satellites up to 1970. SPENVIS software is black-boxed, as often happens for engineered codes, and the A8 system is called requesting an alternative evaluation at maximum or minimum generic solar activity.

Despite the modification of the geomagnetic field and the new data collected during recent years assigning the AP8/AE8 estimation a factor two of uncertainty, it remains the reference for the satellite design.

For this reason, the AP9/AE9 models have been introduced into a separate module that the users can invoke for the sole evaluation purpose. Based on statistical foundation, the A9 infers the trapped particles source terms from more recent data and updates geomagnetic field models considering the solar activity of the specific mission period.

In order to quantify the possible response differences in the simulation due to the trapped particle source terms, we calculate the intensity and the energy spectra of the trapped particles using the AP8/AE8 models at both solar minimum and maximum and also using the AP9/AE9 models.

Figure 4 reports the considered ABCS’ s orbital trajectory and the trapped proton’s total flux intensity along the track, comparing the AP8 maximum and minimum responses. According to SPENVIS AP8 calculation, trapped protons are the most effective radiative component, and the ABCS is subjected to maximum irradiation for a significant part of its orbit. This situation can be worst if a SEF takes place during the mission. It is also apparent that the flux intensity level reported in the chromatic scale for solar minimum and maximum are very close. Therefore, to remain conservative, we always rescale all the presented simulation results to the total intensity averaged on the mission time using A8 for the trapped particles and the condition of solar minimum for GCR. Finally, we considered the averaged flux intensity during the week of maximum activity within the mission period concerning SEP emissions.

Fig. 4
figure 4

ABCS ground track on a world map: The proton flux intensity along the ABCS orbit, estimated by the AP8 models, is reported for solar minimum (a) and maximum (b) on the side logarithm chromatic scales. In both cases, ABCS is subjected to the maximum flux intensity for a significant part of its orbit

Full size image

Figure 5a compares the trapped electron energy distribution for the averaged mission fluxes obtained with the AE8 and AE9 models. The AE8 results yield identical spectra and almost the same total flux intensity at solar minimum and maximum (see Table 2). In contrast, the AE9 model foresees a lowering of the electron population in the energy range from 0.001 to 0.005 GeV and a higher total flux intensity (Table 2).

Fig. 5
figure 5

Comparison of the energy distributions of the trapped electron (a) and proton (b) fluxes at the ABCS orbit according to AE8/AP8 (at solar maximum and minimum) and the AP9/AE9

Full size image
Table 2 Total flux intensities of the orbital
Full size table

Figure 5b and Table 2 report the same comparisons for trapped protons. The AP8 energy spectra are coincident for solar maximum (total flux intensity 5.08E + 06 cm−2 s−1) and minimum (total flux intensity 5.02e + 06 cm−2 s−1). The AP9 model shows a more marked spectral difference for trapped protons relative to AP8: the flux intensity from 1E − 04 to 1E − 03 GeV is higher than in AP8. Conversely, for energy greater than 1e − 03 GeV, up 0.2 GeV, the AP9 flux intensity is systematically lower than AP8 one. The AP9 total flux intensity is 7.95E6 cm−2 s−1).

Although it goes beyond the scope of the present work, a possible explanation of the closeness of the spectral properties of trapped particles at solar minimum and maximum could be attributed to the altitude of the ABCS, where, according to the SPENVIS manual, the model becomes inaccurate.

In light of the data outcomes, we decided to carry out the FLUKA simulations using trapped particles source terms obtained from AP9/AE9 and AP8/AE8 models and discuss the differences in the simulations results.

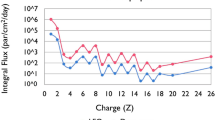
The complete SPENVIS output generates information for the emission of GCR and SEP ions with atomic numbers between hydrogen and uranium (Z = 1−92). We use pre-processing software to separate the SPENVIS ion data in individual files with a format accepted by FLUKA. Figure 6 compares the total emission intensities for GCR and SEP ions in a limited range of the atomic number Z from 1 to 30 (from hydrogen to zinc) foreseen by SPENVIS in the ABCS orbit.

Fig. 6
figure 6

Comparison of the flux intensity (logarithm scale) for ions emission from GCR and SEP (Ions Atomic Number range Z = 1 − 30)

Full size image

Table 2 shows the selected particle contributions based on their intensity and transport characteristics: trapped electrons and protons, protons, helium from GCR and SEP. We also selected GCR iron and SEP oxygen, despite their weak intensity, because their transport involves high energy nucleus-nucleus collisions between nuclei heavier than helium and yield in peculiar particle shower patterns that we want to investigate. Trapped proton and electron worth 99.99% of the total flux. The GCR accounts for only 0.001–0.003%, and the SEP ions represent 0.0033–0.0016% of the total emission.

Figure 7 compares the energy spectra used in the FLUKA simulation for electrons and ions reported in Table 2. The most intense emission is for the trapped electron, showing the lowest maximum kinetic energy compared with the other components. Trapped proton and SEP emissions show their maximum energy emission at 0.1 GeV/nucleon. In contrast, GCR emissions reach the 100 GeV/nucleon that, for example, set the maximum total kinetic energy of 56Fe to 5.6 TeV. Consequently, we used the FLUKA version that includes the DPMJet (multipurpose event generator based on the Dual Parton Model DPM) [12] module to simulate the nucleus-nucleus collision in this energy regime.

Fig. 7
figure 7

source terms used in the FLUKA simulations

Comparison of the energy differential fluxes of the

Full size image

The data furnished by SPENVIS belongs from the solution of the dynamic interaction of the geomagnetic field with the plasma of charged particles distribution on a large spatial scale. The ACS control allows pointing the Z axes (i.e. the axis normal to the bottom and the top lids—see Fig. 1) of the ABCS parallel to the Earth magnetic vector after a short period of rotational kinetic be dissipated thermal energy. Several ACS analysis was performed to assess ABCS pointing performance assuming different starting angular velocities after the deployment. Regardless of the initial condition, the results indicate that ABCS reached the desired attitude within one day from the deployment reported in Table 3.

Table 3 ABCS target orbit
Full size table

To define the emission source to be used for the FLUKA simulations on the ABCS space scale, we consider the following:

  1. 1.

    From some preliminary FLUKA simulations tests carried out with protons on the ABCS geometry, we test several irradiation geometries, similar to the ones reported in Fig. 3 for the neutron irradiation in TAPIRO, realizing doses rate into the ABCS payload ranging from 4 to 50% of the doses imparted from isotropic particles emission on a spherical surface having the satellite in its centre that is very similar to assume a random satellite rotation. Consequently, the most severe irradiation geometry encountered by the satellite should be in the period in which the ACS control has not yet stabilized the satellite in the target orbit.

  2. 2.

    On the local satellite scale, ions and electrons have a negligible probability of mutual interaction, allowing the source’s decomposition in additive non-interacting terms.

  3. 3.

    The GCR and SEP radiation terms have weaker intensity than trapped particles. Light ions (proton and α) are predominant to the other heavier ions.

Consequently, we defined a spherical surface (radius 20 cm) with the satellite in its centre. The emission points are randomly sampled on the sphere surfaces and inward-directed with a uniform distribution within the admitted angular range. This spatial distribution ensures an isotropic particles flux in the interior sphere space that maximizes the fraction of the particles impinging the satellite body and corresponds to a conservative irradiation geometry against which evaluates the shielding solution. As stated at point 2, we split the whole source into many sources, one for each kind of particle, to run in separate simulations. To obtain the overall values of each estimated quantity, we sum up the individual source contributions. Finally, we simplify the GCR and SEP radiation terms, considering the proton and alpha primary emission and neglecting, according to point 3, the contribution of all the heavy ions except 56Fe for GCR and 16O for SEP.

The source term for simulation with MCNP in the TAPIRO reactor

The TAPIRO reactor, located in the ENEA-Casaccia Research Centre of Rome-Italy, is a fast neutron spectrum irradiation facility. Since 1971, TAPIRO has been used to design shielding solutions for fast nuclear reactors, test radiation damage for electronic components, and do dosimetry studies. TAPIRO nominal power is 5 kW. The Helium-cooled core is a cylinder of Uranium–Molybdenum alloy surrounded by a Copper reflector. The control rod system, housed in the copper reflector, is constituted by five movable cylindrical sectors that regulate the reactor power by increasing or reducing the neutrons’ escape from the core. A complete MCNP [13] model of the facility has been developed and validated during the years (see for example [14]) and continuously upgraded to perform the design of neutron irradiation experiments.

Figure 8 shows the irradiation position selected for the comparative simulation tests. The Radial Channel 1 (RC1) irradiates a relatively small sample, and its energy neutron spectrum is stable, and it has been experimentally measured [15].

Fig. 8
figure 8

Geometric cross section of TAPIRO reactor MCNP model showing the TCC and the Radial Channel 1 irradiation position: the area near the external reflector is the region in which ABCS will be located (see also Fig. 3)

Full size image

As confirmation of the goodness of the TAPIRO model, a comparison of the measured and simulated neutron spectra in the RC1 channel is reported in Fig. 9 (blue and black curve, respectively), showing a good agreement between the two curves. The simulated spectrum has the maximum relative error of 1% in the energy range from 0.1 eV to 20 MeV. The experimental spectrum has been measured using the unfolding method based on the activation of metallic foils and the measurements of the activation rate by γ-spectrometry: in this case, the error is 4%.

Fig. 9
figure 9

Comparisons of the neutron energy distribution obtained in RC1. The black curve is obtained from experimental measurements and the red from the TAPIRO MCNP model: the two curves are in good agreement. An MCNP estimate of the neutron flux in the TCC is also reported (blue curve) for the discussion on the design of the ABCS irradiation experiment

Full size image

Due to its significant volume, which can host the whole ABCS satellite, the thermal column has a neutron flux and energetic distribution that could change according to the experiment layout, and it needs, each time, a dedicated qualification. For this reason, Fig. 9 also reports the simulated spectrum in an air-filled volume of the TCC that will host the ABCS layout (blue curve).

As expected, RC1 has a more intense neutron flux because it is closer to the core, and its energy distribution retains the characteristics of a pure fission spectrum. Conversely, the neutrons arriving in TCC from the core must escape from the reflector and slow down in the reactor structure. Consequently, they show a lower flux intensity and a low-energy distribution with a broad maximum in the epithermal neutron energy range (1–100 keV). However, since those features are entirely congruent with the expected neutron transport pattern for the TAPIRO and considering the agreement between experimental and simulated results in RC1, the model appears adequate to simulate the ABCS neutron irradiation in the TCC.

Consequently, we run an MCNP simulation in the KCODE [13] modality that generates the fission distributions of the reactor core using an iterative fission scheme and transports the generated fission neutrons through the system. The MCNP iteration scheme refines the fission distributions until it becomes compatible with the reactor configuration and the fission chain reaction’s self-sustain condition. Thus, the model approaches a steady-state that could be rescaled to a user’s defined fission power. In a previous work [14], the MCNP model reproduces the experimental TAPIRO critical configuration.

Description of the MCNP and FLUKA simulation sets

To investigate the shielding solution effectiveness, we need to run two simulations for each source term, respectively, with the unshielded and shielded layout, for a total of sixteen simulations.

The precision of the Monte Carlo results depends on the number of primary source particles used for the simulation [16]. Higher precision is generally obtained by increasing the number of primary particles at the cost of higher calculation time. We implement FLUKA on the high-performance computing system CRESCO (Computational Research Centre on COmplex systems) [17] to shorten calculation time, executing the simulation in the “embarrassing parallel” [18] modality, resulting from several replicas of the same problem having different seeds for the pseudo-random number generator are obtained. The results from each replica are like independent measurements of experimental quantities, and their mean μ and standard deviations σ are the final simulation results. We quantify the attained precision level using the relative error Er = σ/µ. In an embarrassing parallelism scheme, the overall number of primary particles P, connected with the simulation precision, is

$$P = N p;$$
(1)

with N = number of CPU, p = number of particles per CPU (on which run a simulation replica), P = overall number of particles in the simulation.

This calculation methodology also allows the individual analysis of each source term, optimizing precision and simulation time by changing the number of particles and CPUs. Table 4 reports the parameters adopted to minimize the relative error, within a sustainable simulation time, for each source term used on the configurations with the shielding protection of the satellite structure (“No Further Shielding”—NFS) and the one with further shielding (“Further Shielding”—FS) due to the layered shield solution (see paragraph 2.5). A detailed analysis of the optimization of the estimator’s relative error goes beyond the scope of the present paper. For example, the relative errors reported in the last columns of Table 4 deal with the absorbed doses in the ABCS payload. Their values are below the 2% of relative error except for trapped electrons that, due to their low mean emission energy, were severely attenuated by the satellite structure and the shielding materials yielding in more dispersed values of the mean TID rate with a relative error ranging from 6 to 10% that is still acceptable for this type of simulation.

Table 4 Resumes of the simulations executed in the present work and performance on CRESCO
Full size table

Also, in the case of the TAPIRO MCNP model, we performed the first simulation test with both the NFS and FS layouts. Next, we use an MCNP 6.2 parallel version compiled and linked with the OPENMPI library (Open Message Passing Interface) on the CRESCO computational facility. The simulations run on 288 CPUs for five hours, obtaining a relative error Er of approximatively 1% for all the estimators.

Estimation of the TID and SI1MEVNE in selected satellite components

It is convenient to recall that a user-defined region is a space volume filled with a single homogeneous material in the Monte Carlo transport jargon. During the implementation of the geometry, we define the components of the satellite as regions on which we requested the estimation of the quantities of interest that for ABCS are:

  1. 1.

    All the regions define the SP components (see Table 1);

  2. 2.

    All the regions define the four cards and the filling air of the ABCS payload interior (see Fig. 2).

We refer to those components as “target components” in the following.

Table 5 reports the list of estimators used in the present work with a brief explanation of their main characteristics and scope. The 3rd column of Table 5 specifies which satellite components we choose to apply the estimators. For example, a track-length-based estimator [19] evaluates particles flux or flux derived quantities (nuclear reaction rates, equivalent damages) averaged on one region volume. We also use a variant of the track length estimator to estimate the same quantity in a user-defined spatial mesh (see, for example, Fig. 9) or in a matrix of user-defined geometrical regions.

Table 5 List of the estimators used in the FLUKA simulations related to the present work
Full size table

The SI1MEVNE fluence uses the proportionality of neutron damage to the non-ionizing energy deposition of the Primary Knock-on Atom (and its damage cascade) in the widely validated silicon-based components [20]. Consequently, using the displacement kerma as a function of energy as a damage function

$$\overline{F}_{D} = \frac{{\mathop \int \nolimits_{0}^{\infty } \phi \left( E \right)F_{D} \left( E \right)dE}}{{\mathop \int \nolimits_{0}^{\infty } \phi \left( E \right)dE}}$$
(2)

where \(\overline{F}_{D}\) = average damage produced per neutron (damage constant). \(\mathop \int \limits_{0}^{\infty } \phi \left( E \right)dE\) is the total neutron fluence. \(\phi \left( E \right)\) and \(F_{D} \left( E \right)\) are the fluence energy distribution and the damage production energy distribution. Since \(\overline{F}_{D} * \phi \left( E \right)\) is the total amount of displacement damage, a fluence that would produce an equivalent amount of displacement damage is

$$\overline{F}_{{DE_{{{\text{Ref}}}} }} * \phi_{{E_{{{\text{Ref}}}} }} = \overline{F}_{D} * \phi \left( E \right);$$
(3)

where \(E_{{{\text{Ref}}}}\) = 1 MeV is reference energy and \(\overline{F}_{{DE_{{{\text{Ref}}}} }} = \overline{F}_{{D,1\,{\text{MeV}}}}\) = 95 MeV * mb for Silicon.

Consequently, the 1 MeV Silicon damage equivalent fluence is

$$\phi = \frac{1}{{\overline{F}_{{D,1\;{\text{MeV}}}} }} \mathop \int \limits_{0}^{\infty } \phi \left( E \right)F_{D} \left( E \right)dE;$$
(4)

It is worthy of notice that, as reported in column two Table 5, the SI1MEVNE fluence and TID estimates have the units of particles/cm2 and Gy per primary source particles, respectively. Consequently, we must rescale each response to its source’s intensities reported in Table 2, obtaining a dose rate (Gy/s) for TID and flux (particles/cm2/s) for SI1MEVNE. The overall estimated response R was finally obtained, summing up all the individual source term responses (\(R = \sum\nolimits_{i} {R_{i} }\)) of the selected estimator.

We use TID and SI1MEVNE fluence estimates to evaluate the relative effectiveness of the shielding solution. Defining the shielding effectiveness \(\eta\) as

$$\eta = \frac{{\left( {R_{2} - R_{1} } \right)}}{{R_{1} }}*100;$$
(5)

R2 is the overall estimator’s response after adopting the additive shielding solution, and R1 is the overall estimator’s response to the configuration without such a shielding solution. Therefore, \(\eta\) quantifies the shielding effectiveness of configuration 2 relative to configuration 1. Negative values of the \(\eta\) indicate an increase in the shielding effectiveness; conversely, positive values indicate a decrease in the shielding effectiveness. Table 6 reports some TID rate estimations from FLUKA simulations with a trapped proton source term to clarify this point. Figure 10 can also help visualize the spatial distribution of the TID rates of the three considered configurations.

Table 6 Estimated TID rate for card 4 in the progressive construction of the ABCS layout around the target components
Full size table
Fig. 10
figure 10

The comparison of the trapped proton dose rate as obtained using AP8 data integrated along the Z-axis of the FLUKA reference system and reported on an X–Y cross section of the satellite geometry: a making void all the satellite components except the cards and the air in the payload; b in the absence of the shielding; c in the presence of the shielding. In adding the shielding (cases b to c), the TID rate decrease agrees with the target components’ shielding effectiveness (η = − 19.52%)

Full size image

The “Void” configuration is obtained setting to vacuum all the materials in the satellite model except for the ABCS payload air volume and the four cards. The “No-Further Shield” (NFS) configuration refers to the satellite layout without the additive shielding solution adopted to protect the primary payload further. Finally, the “Further Shield” (FS) configuration comprises the additive protection for the primary payload.

The TID rate data reported in the second row of Table 6 show a significant decrease passing from the VOID to the NFS configuration. In contrast, the transition from NFS to the FS configuration decreases the TID rate slightly.

According to Eq. (5), the third row of Table 6 reports the values of η for the NFS and FS configurations relative to the Void configuration: the satellite’s structure (NFS configuration) is responsible for the decreases of the TID rate of η = − 99.86%, whereas the FS configuration adds just a 0.03% of the TID rate decrease.

Since we are focused on the shielding effectiveness of the FS configuration, we decided to calculate its η relative to the NFS configuration, obtaining η = − 21.50%. Consequently, we adopt the NFS as a reference configuration for the calculation of η, having the advantage to start from a more realistic configuration than the Void.

In the following, we compare the contributions to the overall TID and SI1MEVNE responses from the different source terms (see Tables 8, 10, 12). To avoid confusion, we use for the shielding effectiveness a different relation

$$\eta^{*} = \frac{{\left( {R_{{{\text{FSi}}}} - R_{{{\text{NFSi}}}} } \right)}}{{R_{{{\text{NFS}}}} }}*100;$$
(6)

where \(R_{{{\text{NFS}}}} = \sum\nolimits_{i} {R_{{{\text{NFSi}}}} }\) is the overall response of the estimator obtained as the sum of each considered source term for the NFS configuration and \(\eta^{*}\) is the shielding effectiveness due to the single source term relative to an overall response.

Table 7 Comparison of TID rates deposited in Air and PCB cards into the ABCS payload
Full size table
Table 8 Comparison of the contribution to the TID rate in PCB Card 4
Full size table
Table 9 TID rate deposited into the solar cell components
Full size table

Results and discussion

TID rate estimation in ABCS payload

Table 7 compares the overall TID rate and the shielding effectiveness \(\eta\) (see Eq. 5) in the target components of the ABCS payload. Due to the source isotropy, both in the absence and in the presence of further shielding, the four Cards show very close dose rates. The lower TID rates of the innermost Cards (2 and 3) are due to the shielding effects of Cards (1 and 4) in outermost positions. In all the considered cases, the η value is from − 18 to − 19.9% with AP8/AE8 dataset, and it decreases for the AP9/AE9 dataset in a range of values from − 14.6 to 18.7%. In terms of absolute values, we observe that, on average, the AP9/AE9 dataset lead to a decrease of factor 3.4 in the dose rate.

Table 8 shows how the different evaluations of the trapped proton source term obtained from the AP8 and AP9 models change the repartition of the contribution to the overall TID rate of card 4. According to Fig. 5b, AP8 foresee a more energetic spectrum than AP9 with total flux intensities of the same order of magnitude, resulting in a TID rate that is a factor 24–25 higher than one obtained from AP9. Consequently, the trapped proton delivers the most significant dose fraction when AP8 data were used in the simulation, followed by the SEP protons. Conversely, SEP protons are the dominant source term in the AP9 simulation. Concerning the trapped electron, examining the energetic spectra reported in Fig. 5a, we found that the AE8 and AE9 differences are less than in the case of the trapped proton. Consequently, the higher TID rate observed with AP9 depends on higher total flux intensity than the spectral changes.

GCR Hydrogen and Helium are the sole ions in Table 8 that cause an increase in their dose rate contributions in the presence of shielding. A possible explanation is the interaction of the high energy tails of the GCR ions with the shielding layers generating less energetic secondary particles having a higher probability of depositing energy into the payload target components. However, their contributions are too little to revert the overall shielding effectiveness in absolute terms.

Conversely, the 56Fe ion contribution to the TID rate decreases when the shielding is present, suggesting that the secondaries born from the interactions with the shielding layers could have an asymmetric kinetic energy distribution: some still has enough energy to pass through the ABCS payload without interacting within its boundary, other exits from the fragmentation reaction with kinetic energy sufficiently lower to stop into the shielding layer. This mechanism will be clarified, addressing further work to simulations with higher statistics and event by event analysis.

SEP ions were shielded more efficiently than GCR because of their lower energy distributions. As in the case of GCR ions, SW ions of increasing Z were progressively shielded better: 16O, the SEP heaviest ion considered in the simulation, has the more significant TID rate decrease in Card 4.

The examination of the bi-dimensional mapping of the dose rate spatial distribution obtained, superimposing their meshed responses to an x – y cross section of the satellite’s geometry (see Table 3, 2nd row), confirms the dose decreases quantified using the parameter \(\eta\). Figure 10 shows that the dose decreases (\(\eta\) = − 19.52%) for trapped protons is apparent also comparing the reported images.

Figure 11 compares the dose rate spatial distribution for the GCR proton (η = + 4.88%) with and without shielding. The images confirm the dose increase when the shielding is present.

Fig. 11
figure 11

The comparison of the GCR proton dose rate integrated along the Z-axis of the FLUKA reference system and reported on an X–Y cross section of the satellite geometry: a in the absence of the shielding; b in the presence of the shielding. The TID rate increase agrees with the target components’ shielding effectiveness (η =  + 4.88%)

Full size image

The dose rate decreases for the 56Fe ions contribution (η = − 1.30%) is confirmed by the dose rate mapping comparisons reported in Fig. 12.

Fig. 12
figure 12

The comparison of the GCR 56Fe dose rate integrated along the Z-axis of the FLUKA reference system and reported on an X–Y cross section of the satellite geometry: a in the absence of the shielding; b in the presence of the shielding. The TID rate decrease agrees with the target components’ shielding effectiveness (η = − 1.30%)

Full size image

Also, Fig. 13, which compares the simulated dose rate spatial distributions for SEP protons, agrees to the decrease quantified by η = − 11.15%. The images also show anisotropies in the dose distribution induced by the four cards whose mutual shielding breaks the irradiation spherical symmetry, causing localized dose increases to each image’s “left” and “right” sides.

Fig. 13
figure 13

The comparison of the SEP proton dose rate integrated along the Z-axis of the FLUKA reference system and reported on an X–Y cross section of the satellite geometry: a in the absence of the shielding; b in the presence of the shielding. The dose rate decrease agrees with the target components’ shielding effectiveness (η = − 11.15%)

Full size image

TID rate and shielding effectiveness estimations in the solar panels

It is apparent that being the SPs the outermost components of the satellite, they have a direct and unshielded exposition to the orbital radiation source. As expected, the data reported in Table 9 show that the FS configuration has no impact on the TID rate on SP components. As a consequence of the progressively increasing shielding offered by the outer layers to the inner ones, a monotonic TID rate decrease is always present in NFS and FS configurations. We observe that in agreement with the null values of η reported in Table 9, the dose rate distribution in SPs (Figs. 10, 11, 12 and 13) remains unaltered.

Table 10 Comparison of the contribution of each
Full size table

Table 10 shows the contribution of each source term to the TID rate in the SP’s Middle Cell. The FS solution does not affect the trapped particles (η = 0.00%), increases dose rate from SEP 16O (η = 0.57%), GCR He (η = 2.80%), and GCR H (η = 4.88%) also, it causes minor dose rate decreases inthe other SEP and GCR ions. Again, those dose rate contributions are negligible compared to one of the trapped particles, leaving the TID rate unaltered. Furthermore, the limited shielding offered from the outermost layers of the SP to the Middle cell does not enhance the spectral differences between the A8 and A9 models for the trapped particles maintaining their contributions to the overall TID rate dominant on the other ions.

The silicon 1 MeV neutron equivalent fluxes in the ABCS target components

The SI1MEVNE flux is a quantity that allows the comparison of the damages induced during irradiation by different kinds of particles. In the present paper, we use this quantity to estimate the damage level in the ABCS target component in the irradiation orbital condition and compare the responses from simulated neutron irradiation of the whole satellite within the TCC of the TAPIRO reactor. In the following discussion, we refer to the simulations carried out with the orbital source as ABCS simulation and name the others as TAPIRO simulations.

Table 11 compares the SI1MEVNE fluxes estimations of Card 4 in the ABCS simulation with those obtained in the TAPIRO’s simulations. Using the A8 data for trapped particles leads to equivalent flux damage higher of factor 2.8–3.1 than the one obtained with A9 with a decrease of the shielding effectiveness − 15.66% to − 6.86%. This finding is aligned with the already discussed spectral change for the trapped particles introduced by the A8/A9 models. Because of the poor shielding effectiveness against neutrons (\(\eta\) = − 3.36%) that penetrate more the shielding designed for the charged particles, the predicted TAPIRO SI1MEVNE flux outperforms the flux of the orbital ABCS simulations. We observe that, according to the AP8/AE8 models, the equivalent fluence received by Card 4 in a two-year exposition to the orbital source is realized in a 47 min neutron irradiation in the TCC using a nuclear power of just 50 W (the 1% of the 5 kW maximum nuclear power of TAPIRO).

Table 11 Comparison of the SI1MEVNE fluxes in Card 4
Full size table

Table 12 reports the contribution of each orbital source term to the overall SI1MEVNE flux, showing a trend like the one obtained for the TID rate (See Table 8). With AP8, the trapped protons are responsible for the more significant fraction of silicon equivalent damages, followed by SEP and GCR proton. The use of the A9 shows that the more significant contribution is from the SEP proton followed by trapped and GCR proton. The shielding effectiveness is higher for trapped particles causing a decrease of their equivalent damages, whereas GCR ions show a positive shielding effective increasing their contribution. The trend is more marked for the A9 data, where the contribution of the trapped proton to the equivalent damage is reduced.

Table 12 Contribution of each
Full size table

Table 13 reports the SI1MEVNE fluxes in SP’s regions for both ABCS and TAPIRO simulations. In the orbital irradiation condition, being SPs located in the outermost positions outside the shielding protection, the SI1MEVNE fluxes remain practically unchanged with and without shielding. In addition, we observe a progressive decrease in flux intensity from the outermost to the innermost solar panel regions three orders of magnitude. Both A8 and A9 data confirm this trend. However, according to their spectral and intensity differences, the starting equivalent flux in the Anti-Reflex layer for the A9 is a factor 1.5 higher than in the A8. Accordingly, the A9 equivalent fluxes in the subsequent layers decrease more rapidly than in the A8 series. Conversely, the SI1MEVNE fluxes estimates for the TAPIRO simulations show an almost constant damage flux that can be ascribed to the different mechanisms of transport and interaction of neutrons in the matter to one of the charged particles.

Table 13 Comparison of the SI1MEVNE fluxes in Solar Panel obtained with the orbital
Full size table

From Table 13, a TAPIRO irradiation of 1.5 h in TCC at the power of 5 kW correspond to 30 h of exposure of the anti-reflex layer (the outermost SPs component) to the orbital source. In the same condition, the SP contact layer (the innermost SP component) receives a fluence equivalent to 8429 h of exposure to the orbital source.

Final remarks and conclusion

Using the SPENVIS and FLUKA codes is possible to model the satellite’s layout and estimate the quantities relevant for the analysis of the radiometric behaviour of the various satellite components with acceptable computational time, encouraging us to develop a modelling methodology that can be included in the concurrent design of future missions.

The separation strategy in different source terms of the Van Allen radiation environment adopted in the present work simplifies the TID and SI1MEVNE estimations. According to the A8 model, the subsequent analysis of each source term shows the trapped particles’ prominent role in delivering dose and damages. In contrast, the data from the A9 mitigate the effect of the trapped particles, reducing the overall radiometric impact and increasing the relative role of SEP and GCR. However, to remain conservative, we decided to adopt the worst scenario furnished by the A8 model for our critical mission review.

Considering the mission’s mass budget, a shielding solution of the weight of 300 g constituted by subsequent layers of tungsten, resins, and aluminium located in an area to protect the primary payload (FS configuration) decreases the 20% overall dose rate to the target components in relative to the NFS configuration. Therefore, we renounce the search for a more effective shielding layout because preliminary simulations show us that a decrease of 50–60% of the dose rate could be attained only by increasing the shield weight to 1 kg, which is entirely unacceptable.

The FS solution is effective for trapped and SEP particles but not for GCR particles whose higher emission energy could still induce Single Event Effects (SEE) to the onboard electronics.

Due to their external position, the SPs are exposed to irradiation without any possibility of shield receiving an overall dose rate of 2 to 5 orders of magnitude higher than those experimented in the ABCS payload.

The calculation methodology could be easily extended in the future to other quantities, such as Displacement Per Atoms (DPA), Non-Ionizing Energy Losses (NIEL), and SEE [21], allowing, on a more specific implementation of the onboard electronic components, the correlation between irradiation and components availability during missions.

The roadmap to validate the methodology requires a comparison of the simulation outcomes with new experiments carried out at least with protons of relatively high energy (30–70 MeV) and electrons from accelerator’s beams.

The comparisons of the simulations results between the TAPIRO-TCC and orbital irradiations show that TAPIRO outperforms the orbital source in the Silicon 1 MeV equivalent damage flux. This finding is supported by the agreement between the measured neutron energy spectrum in TAPIRO’s RC1 and the simulated one. Future work will be addressed in designing an experimental campaign conducted in the TAPIRO’s TCC, where it is possible to irradiate CubeSat units while in operation. Obviously, to ascertain the goodness of the simulation results and the facility representativeness limits, careful comparison with the radiometric data obtained during the mission will be mandatory.