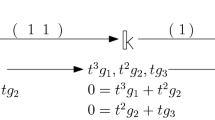Persistence Steenrod modules

Abstract

It has long been envisioned that the strength of the barcode invariant of filtered cellular complexes could be increased using cohomology operations. Leveraging recent advances in the computation of Steenrod squares, we introduce a new family of computable invariants on mod 2 persistent cohomology termed $Sq^k$-barcodes. We present a complete algorithmic pipeline for their computation and illustrate their real-world applicability using the space of conformations of the cyclo-octane molecule.

1 Introduction

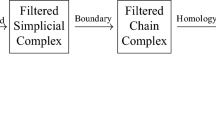
Persistent homology is one of the primary tools in the rapidly developing field of topological data analysis. A motivating example for this technique is the study of a finite point cloud of data embedded in Euclidean space. From it, we can produce a collection of nested simplicial complexes

$$\begin{aligned} X_0 \rightarrow X_1 \rightarrow \cdots \rightarrow X_n. \end{aligned}$$

For example, by taking the nerve of balls of uniformly increasing diameter whose centers are the given points. The homology construction provides us with a collection of linear maps

(1)

This is an example of a (graded) persistence module and its barcode, a summary of the way Betti numbers are shared by consecutive simplicial complexes, serves as a principled and robust feature of the data. This invariant is effectively computable and some of the open source software developed for this end can be found in Pérez et al. (2021), (Tauzin et al. 2021; The GUDHI Project 2020; Bauer 2021). For an expository treatment of persistent homology, we refer the reader to Carlsson (2009) or Edelsbrunner and Harer (2010).

Assuming $\Bbbk$ is a field, a straightforward duality argument shows that the barcode of (1) is equivalent to the barcode of its persistent cohomology

(2)

When $\Bbbk$ is the field ${\mathbb {F}}_p$ with p elements, we can define for each $k \ge 1$ an additional barcode naturally associated to (2) by consistently recording the ranks of Steenrod’s cohomology operation $P^k$ in the commutative diagram

In this work we focus on the case $p=2$ where Steenrod operations are denoted $Sq^k$ and referred to as Steenrod squares, a term that comes from the fact that $Sq^k([\alpha ]) = [\alpha ] \smallsmile [\alpha ]$ where k is the cohomological degree of $\alpha$ and $\smallsmile$ denotes the cup product on cohomology. The ranks of Steenrod operations and in particular of Steenrod squares are able to detect finer information beyond the Betti numbers of a space. For example:

• (1) The real projective plane and the wedge of a circle and a sphere have, with $\mathbb {F}_2$-coefficients, the same Betti numbers, yet the rank of $Sq^1$ tells them apart.

• (2) Similarly, the complex projective plane and the wedge of a 2-sphere and a 4-sphere have the same Betti numbers with any coefficients, yet the rank of $Sq^2$ distinguishes them.

• (3) The suspensions of the two spaces above have the same Betti numbers and also isomorphic cohomology rings, yet the rank of $Sq^2$ tells them apart.

The main contribution of this work is the theoretical and algorithmic developments needed to use the finer discriminatory power of Steenrod squares in persistent cohomology. Specifically, we define $Sq^k$-barcodes and introduce a method for their computation. Using a performance oriented implementation of our methods, we present examples showing that the finer information they reveal is non-trivially present in the point cloud of conformations of the cyclo-octane molecule $\text {C}_{8}\text {H}_{16}$.

1.1 Outline

We begin in Sect. 2 with an overview of the basic notions used in the rest of this article. They concern homological algebra, simplicial topology, and persistence theory. In Sect. 3 we introduce the Steenrod squares $Sq^k$ through explicit formulas at the cochain level and discuss their relevance. In Sect. 4 we introduce persistence Steenrod modules and their $Sq^k$-barcodes, and show how to computationally incorporate these invariants into the persistent cohomology pipeline. We present three examples in Sect. 5, including one obtained from data sampled from the space of conformations of $\text {C}_{8}\text {H}_{16}$. We close by providing conclusions in Sect. 6.

2 Conventions and preliminaries

We assume familiarity with the notions of chain complex over a ring $\Bbbk$ and of its associated homology graded $\Bbbk$-module.

2.1 Tensor and hom complexes

In this subsection we review two natural chain complexes associated to any pair of chain complexes C and $C^\prime$.

The tensor product $C \otimes C^\prime$ is the chain complex whose degree-n part is

$$\begin{aligned} \left( C \otimes C^\prime \right) _n = \bigoplus _{i+j=n} C_i \otimes C^\prime _j, \end{aligned}$$

where $C_i \otimes C^\prime _j$ is the tensor product of $\Bbbk$-modules, and whose boundary map is defined by

$$\begin{aligned} \partial (v \otimes w) = \partial v \otimes w + (-1)^{|v|} v \otimes \partial w. \end{aligned}$$

The hom complex $\mathrm {Hom}(C, C^\prime )$ is the chain complex whose degree-n part is the subset of linear maps between them that increase degree by n, i.e.,

$$\begin{aligned} \mathrm {Hom}(C, C^\prime )_n = \{f :C \rightarrow C^\prime \ |\ \forall k \in \mathbb {Z}, \ f(C_k) \subset C^\prime _{k+n}\}, \end{aligned}$$

and boundary map defined by

$$\begin{aligned} \partial f = \partial _{C^\prime } \circ f - (-1)^{n} f \circ \partial _C. \end{aligned}$$

A chain map is a 0-cycle in this chain complex, and two chain maps are chain homotopy equivalent if they are homologous cycles. We extend this terminology and say that two maps $f, g \in \mathrm {Hom}(C, C^\prime )$ are homotopic if their difference is nullhomologous, referring to a map $h \in \mathrm {Hom}(C, C^\prime )$ such that $\partial h = f - g$ as a homotopy between them.

Regarding $\Bbbk$ as a chain complex with 0-part equal to $\Bbbk$ and all other parts equal to 0 the linear dual of a chain complex C is the chain complex $\mathrm {Hom}(C, \Bbbk )$. For historical reasons we will use cohomological grading for the dual of a chain complex, placing the dual of a chain in degree n also in degree n instead of $-n$ as would be more appropriate.

For any three chain complexes, there is a natural adjunction isomorphism:

$$\begin{aligned} \mathrm {Hom}(C \otimes C^\prime , C^{\prime \prime }) \cong \mathrm {Hom}(C, \mathrm {Hom}(C^\prime , C^{\prime \prime })). \end{aligned}$$

(3)

2.2 Invariants and coinvariants

Symmetries on chain complexes play an important role in this work. Let G be a finite group. We will later focus solely on the symmetric group $\mathbb {S}_2$. We denote by $\Bbbk [G]$ the group ring of G, i.e., the free $\Bbbk$-module generated by G together with the ring product defined by linearly extending the group structure on G. We refer to a chain complex of $\Bbbk [G]$-modules as a chain complex with a G-action.

To any chain complex C with a G-action we naturally associate the following two chain complexes. The subcomplex of invariant chains of C, denoted by $C^G$, contains all elements $c \in C$ satisfying $g \cdot c = c$ for every $g \in G$. The quotient complex of coinvariant chains of C, denoted by $C_G$, is the chain complex obtained by identifying elements $c, c^\prime \in C$ if there exists $g \in G$ such that $c^\prime = g \cdot c$.

Let C and $C^\prime$ be chain complexes and assume C has a G-action. The chain complex $\mathrm {Hom}(C, C^\prime )$ has a G-action induced from $(g \cdot f)(c) = f(g^{-1} \cdot c)$ and there is an isomorphism:

$$\begin{aligned} \mathrm {Hom}(C, C^\prime )^G \cong \mathrm {Hom}(C_G, C^\prime ). \end{aligned}$$

(4)

2.3 Simplicial complexes

Simplicial complexes are used to combinatorially encode the topology of spaces and occur naturally on real-world data.

An abstract and ordered simplicial complex, or a simplicial complex for short, is a pair of sets (V, X) where V is a poset and the elements of X are non-empty finite subsets of V, such that:

• (1) The restriction of the partial order of V to any element in X defines a total order on it.

• (2) For every v in V, the singleton $\{v\}$ is in X.

• (3) If x is in X and y is a subset of x, then y is in X.

We abuse notation and denote the pair (V, X) simply by X.

The elements of X are called simplices and the dimension of a simplex is defined by subtracting 1 from its cardinality. Simplices of dimension d are called d-simplices. We abuse terminology and refer to the elements of V and to their associated 0-simplices both as vertices.

A simplicial complex Y is a subcomplex of a simplicial complex X if every simplex of Y is a simplex of X. In this case we say that (X, Y) is a simplicial complex pair and write $(X, Y) \subseteq (X^\prime , Y^\prime )$ if $X \subseteq X^\prime$ and $Y^\prime \subseteq Y$.

A filtered simplicial complex is a simplicial complex X together with subcomplexes

$$\begin{aligned} \emptyset = X_{-\infty } \subseteq \cdots \subseteq X_i \subseteq X_{i+1} \subseteq \cdots \subseteq X_{+\infty } = X. \end{aligned}$$

2.4 Simplicial cohomology

Let (X, Y) be a simplicial complex pair. Denoting the subsets of n-dimensional simplices by $X_n \subset X$ and $Y_n \subset Y$, the chain complex $C_\bullet (X, Y; \Bbbk )$ of relative chains of the pair (X, Y) is defined as follows: Its degree-n part is

$$\begin{aligned} C_n(X, Y; \Bbbk ) = \frac{\Bbbk \big \{ X_n \big \}}{\Bbbk \big \{ Y_n \big \}} \end{aligned}$$

i.e., the $\Bbbk$-module freely generated by the n-dimensional simplices in X modulo those in Y, and its differential, referred to as boundary map, is defined on basis elements by

where $d_i$ is the operator that removes the $i^\mathrm {th}$ element in x with respect to the induced total order. We refer to $C_\bullet (X, \emptyset ; \Bbbk )$ simply as the absolute chains of X and simplify its notation to $C_\bullet (X; \Bbbk )$.

The relative cochains of the pair (X, Y) is the cochain complex $C^\bullet (X, Y; \Bbbk )$ defined explicitly by

$$\begin{aligned} C^{n}(X, Y; \Bbbk ) = \mathrm {Hom}_{\Bbbk }(C_n(X, Y; \Bbbk ),\ \Bbbk ) \end{aligned}$$

with

$$\begin{aligned} \delta _{n}(\alpha )(c) = (-1)^n\alpha (\partial _n c). \end{aligned}$$

We refer to $C^\bullet (X, \emptyset ; \Bbbk )$ as the absolute cochains of X and use the notation $C^\bullet (X; \Bbbk )$ for it. Notice that $C^{n}(X, Y; \Bbbk )$ is isomorphic to the subspace of $C^{n}(X; \Bbbk )$ that vanish on $C_n(Y; \Bbbk )$. The cohomology of this pair, denoted by $H^{\bullet }(X, Y; \Bbbk )$, is defines as the cohomology of $C^{\bullet }(X, Y; \Bbbk )$.

Given pairs $(X_1, Y_1) \subseteq (X_2, Y_2)$ there are natural maps:

$$\begin{aligned} C^{\bullet }(X_1, Y_1; \Bbbk )&\leftarrow C^{\bullet }(X_2, Y_2; \Bbbk ),\\ H^{\bullet }(X_1, Y_1; \Bbbk )&\leftarrow H^{\bullet }(X_2, Y_2; \Bbbk ), \end{aligned}$$

respectively defined and induced by restriction.

Relative and absolute homology in the simplicial context is defined similarly but we do not use them in this work.

2.5 Persistence theory

In this subsection $\Bbbk$ is assumed to be a field. We will now review the basic concepts of the theory of persistence over $\Bbbk$ from a point of view that prioritizes persistent cohomology. We refer to Zomorodian and Carlsson (2005) or de Silva et al. (2011) for a more detailed exposition.

The totally ordered set $\overline{\mathbb {Z}}$, known as extended integers, is the union of $\mathbb {Z}$ with two elements $-\infty$ and $+\infty$ such that

$$\begin{aligned} -\infty< i < +\infty \end{aligned}$$

for any integer i.

A persistence module ${\mathcal {M}}$ (over $\Bbbk$) is a diagram of $\Bbbk$ vector spaces and linear maps

For $i \le j$ in $\overline{\mathbb {Z}}$ we denote by ${\mathcal {M}}_{i,j}$ the unique composition $\mathcal {M}(i) \leftarrow \mathcal {M}(j)$ in the diagram. We say that $\mathcal {M}$ is pointwise finite-dimensional (p.f.d.) if the dimension of $\mathcal {M}(i)$ is finite for each $i \in \overline{\mathbb {Z}}$.

A graded persistence module $\mathcal {M}^\bullet = \{\mathcal {M}^d\}_{d \in \mathbb {Z}}$ is a collection of persistence modules indexed by the integers. We say $\mathcal {M}^\bullet$ is p.f.d. if each $\mathcal {M}^d$ is.

A morphism of persistence modules is a diagram of vector spaces and linear maps

To any morphism $\phi$ of persistence modules we can naturally associate persistence modules corresponding to its kernel $\ker \phi$ and image ${{\,\mathrm{\mathrm {img}}\,}}\phi$.

A multiset is a pair $(M, \mu )$ where M is a set and $\mu :M \rightarrow {\overline{\mathbb {Z}}}$ is a function attaining only values greater than 0. We refer to $\mu (m)$ as the multiplicity of m and define the cardinality of a multiset $(M, \mu )$ as

$$\begin{aligned} {{\,\mathrm{card}\,}}M = \sum _{m \in M} \mu (m) \end{aligned}$$

if this sum is defined and $+\infty$ otherwise. We sometimes regard sets as multisets with multiplicity function constant and equal to 1.

Let $\mathcal {M}$ be a p.f.d. persistence module, its barcode is the multiset $Bar_\mathcal {M}$ of pairs $[p.q] \in \overline{\mathbb {Z}} \times \overline{\mathbb {Z}}$ such that for any two extended integers $i \le j$

$$\begin{aligned} {{\,\mathrm{rank}\,}}\mathcal {M}_{i,j} = {{\,\mathrm{card}\,}}\big \{[p.q] \in Bar_{\mathcal {M}} \mid p \le i \le j \le q \big \}. \end{aligned}$$

The barcode is a complete invariant of p.f.d. persistence modules. We will sometimes use the notation $(p-1, q] {\mathop {=}\limits ^{\mathrm {def}}}[p,q]$. The finite and infinite parts of the barcode are defined by

$$\begin{aligned} Bar^{\, \mathrm {fin}}_{\mathcal {M}}&= \big \{[p.q] \in Bar_{\mathcal {M}} \mid p,q \in \mathbb {Z}\big \}, \\ Bar^{\, \mathrm {inf}}_{\mathcal {M}}&= Bar_{\mathcal {M}} \setminus Bar^{\, \mathrm {fin}}_{\mathcal {M}}. \end{aligned}$$

The barcode of a graded persistence module $\mathcal {M}^\bullet$ is the collection

$$\begin{aligned} Bar_{\mathcal {M}^\bullet } = \big \{ Bar_{\mathcal {M}^d} \big \}_{d \in \mathbb {Z}}\ . \end{aligned}$$

Given a filtered simplicial complex X, define respectively its persistent relative and absolute cohomology by

$$\begin{aligned} {\mathcal {H}}_R^\bullet (X; \Bbbk )(i)&= H^\bullet (X, X_{i}; \Bbbk ),&{\mathcal {H}}_A^\bullet (X; \Bbbk )(i)&= H^\bullet (X_{i}; \Bbbk ), \end{aligned}$$

with linear maps induced by restriction. When X and $\Bbbk$ are clear from the context we omit them from the notation. We say X is p.f.d. if either, and therefore both, of these are.

The barcodes of these persistence modules contain equivalent information. More precisely, as shown in de Silva et al. (2011) or more categorically in Bauer and Schmahl (2020), the finite parts of these are equal as graded multisets after a degree shift and there is a bijection of multisets between their infinite parts. Explicitly,

(5)

Although we do not use them in this work, persistent relative and absolute homology can be defined similarly and shown to have barcodes containing the same information encoded by those above.

3 Steenrod squares

In this section we introduce the cohomology operations

$$\begin{aligned} Sq^k :H^\bullet (X, Y; \mathbb {F}_2) \rightarrow H^{\bullet }(X, Y; \mathbb {F}_2) \end{aligned}$$

defined for any simplicial complexes pair (X, Y) and every integer k. These operations are natural. In particular, for $(X_1, Y_1) \subseteq (X_2, Y_2)$ the diagram

(6)

commutes. Therefore, as will be developed in Sect. 4, any $Sq^k$ defines an endomorphism of the persistent (absolute and relative) cohomology of a filtered complex.

3.1 History and definition

The diagonal map of spaces

induces a product in cohomology with field coefficients

$$\begin{aligned} \smallsmile :H^\bullet (X) \otimes H^\bullet (X) \xrightarrow {\cong } H^\bullet (X \times X) \xrightarrow {H^\bullet (D)} H^\bullet (X), \end{aligned}$$

which is (graded) commutative, since the diagonal is invariant under the transposition

One can then ask if this product can be defined with integer coefficients. During the mid 1930’s Alexander, Kolmogorov, Čech and Whitney defined the cup product dualizing a simplicial chain approximation to D given by

Please consult Whitney (1988) for further historical notes. The chain map $\Delta$ is not invariant under the transposition map

that is to say, $\Delta - T \Delta \ne 0$.

In 1947, Steenrod published his seminal paper (Steenrod 1947) introducing the square operations through an effective construction of “coherent homotopies” correcting the broken symmetry of $\Delta$ (denoted by $\Delta _0$ from now on). To explain this, let us consider the map $(1 - T) \Delta _0$ as a 0-cycle in $\mathrm {Hom}\left( C_\bullet , C_\bullet ^{\otimes 2} \right)$, a chain complex with an $\mathbb {S}_2$-action induced from T. The cup-1 coproduct, defined explicitly by

$$\begin{aligned} \Delta _1 [0, \dots , n] = \sum _{i<j} \pm \, [0, \dots , i, j, \dots , n] \otimes [i, \dots , j], \end{aligned}$$

is a boundary for this cycle ($\partial \Delta _1 = (1 - T) \Delta _0$). The cup-1 coproduct $\Delta _1$ corrects the lack of symmetry of $\Delta _0$ homologically, but it is itself not symmetric. Steenrod gave formulae for higher corrections, the cup-i coproducts $\Delta _i$, satisfying

$$\begin{aligned} \partial (\Delta _{i+1}) = \Delta _i - (-1)^i T \Delta _i. \end{aligned}$$

More abstractly, if W is the minimal resolution of $\mathbb {Z}$ by free $\mathbb {Z}[\mathbb {S}_2]$-modules

$$\begin{aligned} \mathbb {Z}[\mathbb {S}_r]\{e_0\} \xleftarrow {1-T} \mathbb {Z}[\mathbb {S}_r]\{e_1\} \xleftarrow {1+T} \mathbb {Z}[\mathbb {S}_r]\{e_2\} \xleftarrow {1-T} \cdots , \end{aligned}$$

he effectively constructed a natural equivariant chain map

$$\begin{aligned} W \otimes C_\bullet \rightarrow C_\bullet ^{\otimes 2}, \end{aligned}$$

(7)

where $C_\bullet$ denotes the chains of a simplicial complex. Passing to mod 2 coefficients, Steenrod extracted from this construction finer invariants on the cohomology of spaces which we now review.

Using the linear duality functor on the map (7) and passing to invariant chains we have a chain map

$$\begin{aligned} \mathrm {Hom}\left( C_\bullet \otimes C_\bullet , \mathbb {F}_2\right) ^{\mathbb {S}_2} \longrightarrow \mathrm {Hom}\left( W \otimes C_\bullet , \mathbb {F}_2\right) ^{\mathbb {S}_2}, \end{aligned}$$

which we can complete, using the isomorphisms (3) and (4) of Sect. 2, to a commutative diagram

where the choice of coefficients ensures the doubling map $\alpha \mapsto \alpha \otimes \alpha$ is linear. Using the adjunction isomorphism (3), the dashed arrow defines a linear map

descending to mod 2 homology, and the Steenrod square operations are defined by reindexing this map. Explicitly,

The importance of Steenrod operations in stable homotopy theory is hard to overstate, see for example Adams (1974). For a more leisure exposition of the construction and properties of Steenrod squares we refer to, for example, Mosher and Tangora (1968).

Remark

The name of these operations comes from the fact that $Sq^k([\alpha ]) = [\alpha ] \smallsmile [\alpha ]$ where k is the cohomological degree of $\alpha$ and $\smallsmile$ denotes the cup product on cohomology. The non-triviality of Steenrod squares is an obstruction to the existence of a commutative product of cocycles lifting $\smallsmile$.

Remark

The operation $Sq^1$ agrees with the Bockstein homomorphism. Namely, the connecting homomorphism induced from the following exact sequence of coefficient

$$\begin{aligned} 0 \rightarrow \mathbb {Z}/2\mathbb {Z}\xrightarrow {2} \mathbb {Z}/4\mathbb {Z}\rightarrow \mathbb {Z}/2\mathbb {Z}\rightarrow 0. \end{aligned}$$

Remark

Steenrod square operations are parameterized by classes on the mod 2 homology of $\mathbb {S}_2$. From this viewpoint, Steenrod defined operations at odd primes non- constructively using the mod p homology of $\mathbb {S}_p$. For his construction please consult Steenrod and Epstein (1962). We do not treat these operations in the present paper.

3.2 Cup-i formulas

Throughout the rest of this article we set the ground ring $\Bbbk$ to be the field with two elements $\mathbb {F}_2$. We will describe explicitly a natural equivariant chain map

$$\begin{aligned} W \otimes C_\bullet \rightarrow C_\bullet \otimes C_\bullet \end{aligned}$$

or, equivalently, an equivariant chain map

Let X be a simplicial complex and $x \in X_n$. For a set

$$\begin{aligned} U = \{u_1< \dots < u_r\} \subseteq \{0, \dots , n\} \end{aligned}$$

we use the notation $d_U(x) = d_{u_1} \ldots \, d_{u_r}(x)$.

Definition 1

(Medina-Mardones 2021c) The simplicial cup-i coproduct

$$\begin{aligned} \Delta _i:C_\bullet (X; \mathbb {F}_2) \rightarrow C(X; \mathbb {F}_2)^{\otimes 2}_\bullet \end{aligned}$$

is the linear map defined on a basis element x in dimension n by

$$\begin{aligned} \Delta _i(x) = \sum _U d_{U^0}(x) \otimes d_{U^1}(x), \end{aligned}$$

where the sum is taken over all sets $U = \{u_1< \dots < u_{n-i}\}$ with $u_j \in \{0, \dots , n\}$ and

$$\begin{aligned} U^0 = \{u_j\ |\ u_j + j \equiv 0 \text { mod } 2\}, \qquad U^1 = \{u_j\ |\ u_j + j \equiv 1 \text { mod } 2\}. \end{aligned}$$

These formulas are in a sense dual to Steenrod’s original in Steenrod (1947) but, as shown in Medina-Mardones (2022), they are equivalent. We have the homological relation

$$\begin{aligned} \partial (\Delta _{i+1}) = (1+T) \Delta _i \end{aligned}$$

for any integer i, and naturality for pairs $(X_1, Y_1) \subseteq (X_2, Y_2)$ making the diagram

(8)

commute.

Definition 2

Let (X, Y) be a pair of complexes. The k-th Steenrod square

$$\begin{aligned} Sq^k:H^\bullet (X,Y;\mathbb {F}_2) \rightarrow H^{\bullet }(X,Y;\mathbb {F}_2) \end{aligned}$$

is the linear map sending a class $[\alpha ]$ represented by a cocycle $\alpha \in C^{n}(X,Y;\mathbb {F}_2)$ to the class represented by the cocycle whose value on $c \in C_{n+k}(X,Y;\mathbb {F}_2)$ is

$$\begin{aligned} (\alpha \otimes \alpha ) \Delta _{n-k} (c). \end{aligned}$$

We notice that thanks to (8), the Steenrod square operations are natural for pairs $(X_1, Y_1) \subseteq (X_2, Y_2)$, i.e., diagram (6) commutes.

Example 1

Let us consider the model of the real projective plane $\mathbb {R}\mathrm {P}^2$ presented in Fig. 1 together with the cocycle $\alpha$, dual to

$$\begin{aligned} a = [2,4]+[2,3]+[3,5]+[1,5]+[1,4], \end{aligned}$$

representing the generator of $H^1(\mathbb {R}\mathrm {P}^2; \mathbb {F}_2) \cong \mathbb {F}_2$. According to Definition 2, the cocycle $(\alpha \otimes \alpha ) \Delta _0(-)$ represents the class $Sq^1\big ( [\alpha ] \big ) \in H^2(\mathbb {R}\mathrm {P}^2)$. Using Definition 1 and bilinearity, we are looking for basis elements $[i, j] \otimes [i', j']$ appearing in $a \otimes a$ with $j = i'$ and such that $[i,j,j'] \in \mathbb {R}\mathrm {P}^2$. The cocycle $(\alpha \otimes \alpha ) \Delta _0(-)$ is given by adding together $[i, j, j']$ for each such basis element. In our case, out of 25 basis elements appearing in $a \otimes a$ only $[2, 3] \otimes [3, 5]$ contributes a non-zero term and, therefore, $Sq^1\big ([\alpha ]\big )$ is represented by the cocycle dual to [2, 3, 5], and

$$\begin{aligned} {{\,\mathrm{rank}\,}}\big (Sq^1:H^1(\mathrm {\mathbb {R}\mathrm {P}}^2;\mathbb {F}_2) \rightarrow H^2(\mathrm {\mathbb {R}\mathrm {P}}^2;\mathbb {F}_2) \big ) = 1. \end{aligned}$$

Fig. 1

Real projective plane $\mathbb {R}\mathrm {P}^2$ together with a chosen representative of the non-zero class in $H^1(\mathbb {R}\mathrm {P}2; {\mathbb {F}}_2)$

Remark

The $\Delta _i$ maps are deeply rooted in the combinatorics of simplices. To illustrate their primitive nature we mentioned that another fundamental construction can be derived from them: the nerve of n-categories (Street 1987; Medina-Mardones 2020b). This is a reflection of a profound connection between convex geometry, higher category theory and Steenrod higher diagonals (Kapranov and Voevodsky 1991; Laplante-Anfossi et al. 2022).

Remark

We have focused on simplicial complexes since they are better known and lead to faster computations, but there are also effective constructions of Steenrod cup-i coproducts for cubical complexes (Kadeishvili 2003; Krčál and Pilarczyk 2016; Kaufmann and Medina-Mardones 2021a). Our algorithms, presented in Sect. 4.4, can be adapted using these to compute Steenrod barcodes of cubical complexes.

Remark

To define Steenrod operations effectively at any prime p, the cup-i coproducts where generalized in Kaufmann and Medina-Mardones (2021b) to cup-(p, i) coproducts for simplicial and cubical chains using the operadic methods of P. May (1970) and the model of the $E_\infty$-operad introduced by the second named author (Medina-Mardones 2020a, 2021b). These have been implemented in the computer algebra system ComCH (Medina-Mardones 2021a). The incorporation into the persistence pipeline of Steenrod operations at odd primes is left to future work.

3.3 Self-intersections

Fig. 2

The torus is obtained by gluing together horizontal and vertical boundary components with no twists. The self-intersection for any 1-cycle is always even. The Klein bottle is obtained by gluing horizontal and vertical boundary components with a twist. The self-intersection of the depicted 1-cycle is odd

From a geometric viewpoint, the cup product can be interpreted in terms of intersections of cycles in certain cases. For any space, Thom showed that every mod 2 homology class is represented by the push-forward of the fundamental class of a closed manifold W along some map to the space. Furthermore, if the target M is a closed n-manifold and therefore satisfies Poincaré duality

$$\begin{aligned} H^k(M; \mathbb {F}_2) \xrightarrow {\cong } H_{n-k}(M; \mathbb {F}_2), \end{aligned}$$

the cohomology class dual to the homology class represented by the intersection of two transverse maps $V \rightarrow M$ and $W \rightarrow M$, or more precisely their pull-back $W \times _M V \rightarrow M$, is the cohomology class $[\alpha ] \smallsmile [\beta ]$ where $[\alpha ]$ and $[\beta ]$ are respectively dual to the homology classes represented by $W \rightarrow M$ and $V \rightarrow M$.

By taking $[\alpha ] = [\beta ]$ of cohomological degree k, we have that $Sq^k \big ( [\alpha ] \big ) = [\alpha ] \smile [\alpha ]$ is represented by the transverse self-intersection of $W \rightarrow M$, that is, the intersection of this map and a generic perturbation of itself.

For example, let us consider the Torus $\mathrm {T}$ and the Klein bottle $\mathrm {K}$. Two manifolds with the same mod 2 Betti numbers. These surfaces are distinguished by the fact that

$$\begin{aligned}&{{\,\mathrm{rank}\,}}\big ( Sq^1:H^1(\mathrm {T}; \mathbb {F}_2) \rightarrow H^2(\mathrm {T}; \mathbb {F}_2) \big ) = 0, \\&{{\,\mathrm{rank}\,}}\big ( Sq^1:H^1(\mathrm {K}; \mathbb {F}_2) \rightarrow H^2(\mathrm {K}; \mathbb {F}_2) \big ) = 1, \end{aligned}$$

which we can verify geometrically, as depicted in Fig. 2, by noticing that the transverse self-intersection of a map $S^1 \rightarrow \mathrm {T}$ parallel to any boundary component is always an even number of disjoint points, whereas that of a map $S^1 \rightarrow \mathrm {K}$ parallel to the untwisted boundary component is always an odd number.

In manifold topology, the relationship at the (co)homology level between cup product and intersection is classical. For a comparison between these at the level of (co)chain see Friedman et al. (2021).

3.4 Relations and further structure

The cup-i coproducts or, equivalently, their linear dual products, arise from effectively constructing coboundaries that coherently enforce the commutativity relation of the cup product in cohomology. This is an example of a general principle: constructing cochains enforcing cohomological relations lead to further cohomological structures. In our case, the commutativity relation of cup product gives rise to Steenrod operations.

There are two notable relations satisfied by the Steenrod square operations. The first one, known as the Cartan relation, expresses the interaction between these operations and the cup product:

$$\begin{aligned} Sq^k \big ( [\alpha ] [\beta ] \big ) = \sum _{i+j=k} Sq^i \big ( [\alpha ] \big )\, Sq^j \big ( [\beta ] \big ), \end{aligned}$$

whereas the second, the Adem relation (Adem 1952), expresses dependencies appearing among the iteration of operations:

$$\begin{aligned} Sq^i Sq^j = \sum _{k=0}^{\lfloor i/2 \rfloor } \left( {\begin{array}{c}j-k-1\\ i-2k\end{array}}\right) Sq^{i+j-k} Sq^k \end{aligned}$$

(9)

where $\lfloor - \rfloor$ denotes the integer part function and the binomial coefficient is reduced mod 2.

To tap into the secondary structure associated with these relations, one needs to provide effective proofs for them, that is to say, construct explicit cochains that enforce the relations when passing to cohomology. Such effective proofs were recently given respectively in Medina-Mardones (2020c) and Brumfiel et al. (2021), and we expect that the additional structure they unlock will also play a role in applied topology.

4 Persistence Steenrod modules

In this section we define persistence Steenrod modules and their associated barcodes. We also introduce, for finite filtered simplicial complexes, a complete algorithmic pipeline for their computation.

Definition 3

A persistence Steenrod module (over ${\mathbb {F}_2}$) is a graded persistence module $\mathcal {M}^\bullet$ of $\mathbb {F}_2$ vector spaces together with a degree-k endomorphism

$$\begin{aligned} Sq^k :\mathcal {M}^{\bullet } \rightarrow \mathcal {M}^{\bullet } \end{aligned}$$

for each integer k, such that $Sq^k(i)$ satisfies the Adem relations (9) for every $i \in \overline{\mathbb {Z}}$.

Similar to how persistence modules can be thought of as modules over the polynomial algebra $\mathbb {F}_2[x]$, persistence Steenrod modules correspond to modules over the algebra $\mathcal {A}[x]$ where $\mathcal {A}$ is the Steenrod algebra, the free algebra generated by symbols $Sq^k$ modulo the ideal generated by the Adem relations.

4.1 Steenrod barcode

The following computable invariant of persistence Steenrod modules is central to applications.

Definition 4

For any integer k, the $Sq^k$-barcode of a persistence Steenrod module $\mathcal {M}^\bullet$, denoted by $Sq^kBar_{\mathcal {M}^\bullet }$, is the barcode of the image persistence module ${{\,\mathrm{\mathrm {img}}\,}}Sq^k$. We refer to the collection of all of these as the Steenrod barcode of $\mathcal {M}^\bullet$.

The following example illustrates that, unlike barcodes of regular persistence modules, Steenrod barcodes of persistence Steenrod modules are not a complete invariant. Let $M^\bullet$ be the graded vector space given by

$$\begin{aligned} M^0 = \mathbb {F}_2\{x_0\}, \qquad M^1 = \mathbb {F}_2\{x_1\}, \qquad M^2 = \mathbb {F}_2\{x_2, y_2\}, \end{aligned}$$

and equal to 0 in all other degrees. Let $\mathcal {M}$ be the graded persistence module

$$\begin{aligned} \mathcal {M}^\bullet (i) ={\left\{ \begin{array}{ll} M^\bullet &{} i = 0, \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

We make $\mathcal {M}^\bullet$ into a persistence Steenrod module in two non-isomorphic ways, but with the same Steenrod barcodes, by defining

$$\begin{aligned} Sq^2(x_0) = x_2, \qquad Sq^1(x_1) = x_2, \qquad Sq^0 = \mathsf {id}, \end{aligned}$$

and

$$\begin{aligned} Sq^2(x_0) = x_2, \qquad Sq^1(x_1) = y_2, \qquad Sq^0 = \mathsf {id}. \end{aligned}$$

We thank Prasit Bhattacharya for suggesting this example.

The most prominent examples of persistence Steenrod modules are given by persistent relative and absolute cohomology of a filtered complex X. In this case, denoting both ${\mathcal {H}}^\bullet _R$ and ${\mathcal {H}}^\bullet _A$ by ${\mathcal {H}}^\bullet$, we have

$$\begin{aligned} Sq^0 Bar_{{\mathcal {H}}^\bullet (X;\, \mathbb {F}_2)} \cong Bar_{{\mathcal {H}}^\bullet (X;\, \mathbb {F}_2)} \end{aligned}$$

since $Sq^0$ is the identity.

4.2 Duality

The following example illustrates that, unlike the case of regular barcodes discussed in (5), the Steenrod barcode of persistent relative and absolute cohomology need not completely determine each other. Let $\mathrm {M}$ be the Möbius band and consider the filtration $S^1 \rightarrow \mathrm {M}$ where the circle is included as the boundary of $\mathrm {M}$. Given that $H^\bullet (\mathrm {M}, S^1)$ is isomorphic to the reduced absolute cohomology of the real projective plane $\mathrm {M}/S^1 \cong \mathbb {R}\mathrm {P}^2$, and that $\mathrm {M}$ is homotopy equivalent to its central circle, one can verify that the Steenrod barcode of absolute cohomology is empty but that of relative cohomology is not.

An important case where the Steenrod barcodes of persistent relative and absolute cohomology determine each other is when there are only finite bars in their regular barcodes. More precisely, let X be a p.f.d. filtered complex such that for some integer n either

$$\begin{aligned} Bar_{{\mathcal {H}}^n_R(X;\, \mathbb {F}_2)} = Bar_{{\mathcal {H}}^n_R(X;\, \mathbb {F}_2)}^{\mathrm {fin}} \end{aligned}$$

or, equivalently,

$$\begin{aligned} Bar_{{\mathcal {H}}^{n-1}_A(X;\, \mathbb {F}_2)} = Bar_{{\mathcal {H}}^{n-1}_A(X;\, \mathbb {F}_2)}^{\mathrm {fin}} \,. \end{aligned}$$

Then, for every integer k there is a bijection of multisets

(10)

We illustrate the argument in an example that contains all the ideas of the proof. For complete details we refer to the study of dualities in the categorical framework presented in Bauer and Schmahl (2020). Consider $Sq^1$ and a two stage filtration $X_1 \rightarrow X_2$ or, more explicitly,

$$\begin{aligned} X_n = {\left\{ \begin{array}{ll} \emptyset &{} n < 1, \\ X_1 &{} n = 1, \\ X_2 &{} n > 1, \end{array}\right. } \end{aligned}$$

and the diagram

where the horizontal maps are part of the long exact sequence of the pair $(X_2, X_1)$. Consider $\beta \in H^n(X_2,X_1)$ with $Sq^1 \beta \ne 0$. Since all regular bars are finite $j^*_n \, \beta = 0$ so $j^*_{n+1} Sq^1 \beta = 0$ and we have an $Sq^1$-bar $(0, 1]_R^{n}$. By exactness, $\delta _{n-1} \alpha = \beta$ for some $\alpha \in H^{n-1}(X_1)$ where $\delta _{n-1}$ is the $(n-1)^\mathrm {th}$ connecting homomorphism. Since these commute with Steenrod squares, we have $Sq^1 \alpha \ne 0$. Furthermore, $Sq^1 \alpha$ is not in the image of $i_n^*$ since otherwise $Sq^1 \beta$ would be 0. Therefore, there is a $Sq^1$-bar $(0,1]_A^{n-1}$.

Conversely, given $\alpha \in H^{n-1}(X_1)$ with $Sq^1 \alpha \ne 0$ the finiteness assumption implies that $\delta _n \, Sq^1 \alpha \ne 0$ so we have a $Sq^1$-bar $(0,1]_A^{n-1}$. Denote by $\beta$ the element $\delta _{n-1} \alpha$ and notice that $Sq^1 \beta \ne 0$ with exactness implying $j_n^*Sq^1 \beta = 0$, so we have a $Sq^1$-bar $(0,1]_R^{n}$.

4.3 Truncations

Given a filtered complex X and an integer n there are two naturally associated filtered complexes $X_{\ge n}$ and $X_{\le n}$ defined respectively by

$$\begin{aligned} (X_{\ge n})_k = {\left\{ \begin{array}{ll} X_n &{} k < n, \\ X_k &{} k \ge n, \end{array}\right. } \qquad (X_{\le n})_k = {\left\{ \begin{array}{ll} X_k &{} k \le n, \\ X_n &{} k > n, \end{array}\right. } \end{aligned}$$

and referred to as the above and below truncations at $X_n$. Persistent relative (resp. absolute) cohomology behaves well with respect to above (resp. below) truncations. Explicitly, there exist canonical inclusions

$$\begin{aligned} \begin{aligned} Bar_{\mathcal {H}^\bullet _R(X_{\ge n})} \rightarrow Bar_{\mathcal {H}^\bullet _R(X)}, \\ Bar_{\mathcal {H}^\bullet _A(X_{\le n})} \rightarrow Bar_{\mathcal {H}^\bullet _A(X)}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} Sq^\bullet Bar_{\mathcal {H}^\bullet _R(X_{\ge n})} \rightarrow Sq^\bullet Bar_{\mathcal {H}^\bullet _R(X)}, \\ Sq^\bullet Bar_{\mathcal {H}^\bullet _A(X_{\le n})} \rightarrow Sq^\bullet Bar_{\mathcal {H}^\bullet _A(X)}. \end{aligned} \end{aligned}$$

We remark that this form of “stability” of Steenrod barcodes may fail when considering persistent relative (resp. absolute) cohomology and below (resp. above) truncations. For example, consider the filtration $S^1 \rightarrow \mathrm {M}\rightarrow \mathrm {C}\mathrm {M}$, where $\mathrm {C}\mathrm {M}$ is the cone on the Möbius band. The Steenrod barcode of the relative absolute cohomology of this filtration is empty whereas, as discussed at the beginning of Sect. 4.2, its below truncation at $\mathrm {M}$ is not.

4.4 Computing the Steenrod barcode

In this subsection we provide algorithms to compute the Steenrod barcode of the persistent relative cohomology of a finite filtered simplicial complex X

$$\begin{aligned} \emptyset = X_{-1} \subset X_0 \subset X_1 \subset \cdots \subset X_m = X, \end{aligned}$$

together with a total order of its elements

$$\begin{aligned} a_0< a_1< \cdots < a_m \end{aligned}$$

such that for all $j \in \{0, \dots , m\}$ we have

$$\begin{aligned} X_j = \{a_i \in X\ |\ i \le j\}. \end{aligned}$$

Most of this pipeline is applicable to other filtered cellular complexes, with the exception of Algorithm 2.

4.4.1 Regular barcode

Let us begin by reviewing an effective construction of the barcode of the persistent relative cohomology of X. Let D be the matrix representing

$$\begin{aligned} \partial :C_\bullet (X; \mathbb {F}_2) \rightarrow C_\bullet (X; \mathbb {F}_2) \end{aligned}$$

in the canonical ordered basis $\{a_0< \cdots < a_m\}$. We index columns and rows in this matrix starting at 0, and denote ${\overline{j}} = m-j$ for all $j \in \{0, \dots , m\}$. Consider $D^\perp$ defined by

$$\begin{aligned} D^\perp _{p,\, q} = D_{{\overline{q}},\, {\overline{p}}}. \end{aligned}$$

Notice that $D^\perp _{\le j, \le j}$ represents the coboundary of $C^\bullet (X, X_{{\overline{j}}-1}; \mathbb {F}_2)$.

Fig. 3

Column reduction algorithm

Applying to $D^\perp$ a version of Algorithm 1 in Fig. 3 that remembers the performed operations we produce a reduced matrix R and an upper triangular invertible matrix V satisfying

$$\begin{aligned} R = D^\perp V. \end{aligned}$$

Denoting the j-th column of R by $R_j$, let

$$\begin{aligned} P = \{j \mid R_j = 0\}, \qquad N = \{j \mid R_j \ne 0\} \qquad E = P \setminus \{\text {pivots of } R\}. \end{aligned}$$

There exists a canonical bijection between the union of N and E, and the barcode of persistent relative cohomology given by

$$\begin{aligned} N \ni j&\mapsto \big [\, {\overline{j}}, \overline{\mathrm {pivot}\,R_j} \, \big ] \in Bar_{\mathcal {H}^{\dim (a_j)+1}_R}^{\mathrm {fin}} \\ E \ni j&\mapsto \big [\! -1, {\overline{j}} \, \big ] \in Bar_{\mathcal {H}^{\dim (a_j)}_R}^{\mathrm {inf}} \end{aligned}$$

that provides a preferred cocycle representative for each of these bars:

$$\begin{aligned}{}[i,j] \mapsto {\left\{ \begin{array}{ll} V_{{\overline{j}}}, &{} i = -1, \\ R_{{\overline{i}}}, &{} i \ne -1. \end{array}\right. } \end{aligned}$$

More specifically, a basis for $H^\bullet (X, X_{{\overline{j}}-1})$ thought of as a subspace in the direct sum

$$\begin{aligned} \ker \delta = {{\,\mathrm{\mathrm {img}}\,}}\delta \oplus H^\bullet (X, X_{{\overline{j}}-1}; \Bbbk ), \end{aligned}$$

is given by the set of cochains corresponding to the vectors in the union of

$$\begin{aligned} \big \{R_k \mid k \in N,\, j < \mathrm {pivot}(R_k)\big \} \quad \text {and} \quad \{V_i \mid i \in E,\, i \le j\}, \end{aligned}$$

and a basis for ${{\,\mathrm{\mathrm {img}}\,}}\delta$ is given by

$$\begin{aligned} \{R_i \mid i \in N,\, i \le j\}. \end{aligned}$$

4.4.2 Steenrod barcode

We now describe an effective construction of the Steenrod barcode of the persistent relative cohomology of X. For any integer $k \ge 0$, let $\mathtt {sq^k}$ be an algorithm taking as input a vector corresponding to a cochain $\alpha \in C^n(X, X_i)$ and producing the vector corresponding to the cochain

$$\begin{aligned} (\alpha \otimes \alpha ) \Delta _{n-k}(-). \end{aligned}$$

Such an algorithm, based on the explicit formulas of Sect. 3, is presented as Algorithm 2 in Fig. 4. Let $Q^k$ be the square matrix with columns given by

$$\begin{aligned} Q^k_i = {\left\{ \begin{array}{ll} \mathtt {sq^k}(V_i) &{} i \in E, \\ \mathtt {sq^k}(R_j) &{} i = \mathrm {pivot}(R_j), \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Fig. 4

Algorithm producing for a simplicial complex X, non-negative integer n, integer k between 1 and n, and cocycle $\alpha$, presented as a set $A \subseteq X_n$, a cocycle representing $Sq^k([\alpha ])$ identified with a set $B \subseteq X_{n+k}$. We use the notation $S {{\,\mathrm{\triangle }\,}}S^\prime = S \cup S^\prime \setminus (S \cap S^\prime )$ and $index(S) = \{index(s) \mid s \in S\}$

For matrices M and N of dimensions $m \times p$ and $m \times q$ we define the $m \times (p+q)$ matrix $M \mid N$ by

$$\begin{aligned} (M \mid N)_i = {\left\{ \begin{array}{ll} M_i, &{} i \le p, \\ N_{i-p}, &{} i > p. \end{array}\right. } \end{aligned}$$

We now have all the elements needed to introduce Algorithm 3 in Fig. 5 whose output is the $Sq^k$-barcode of the persistent relative cohomology of X. Intuitively, the step from $j-1$ to j either adds a new non-zero coboundary $R_j$ (which implies $Q^k_j = 0$) or the image $Q^k_j$ of a persistent cocycle generator (which implies $R_j=0$). In either case, we need to reduce with respect to the subspace of coboundaries, generated by $R_{\le j}$, the image of $Sq^k$, which is generated by $Q^k_{\le j}$. This process is done keeping track of when columns in $Q^k$ become zero and extracting from this information the $Sq^k$-barcode of the filtration.

Fig. 5

Algorithm producing the $Sq^k$-barcode of a filtered simplicial complex given its reduced anti-transposed boundary matrix R and a matrix $Q^k$ containing as a columns the images under $Sq^k$ of cocycles representing the barcode of its persistent relative cohomology

We leave the development of a pipeline for persistent absolute cohomology to future work, remarking that, as described in (10), its associated Steenrod barcode is equal to that of persistent relative cohomology if all regular bars are finite, a situation often countered in practice.

5 Examples

To demonstrate the feasibility of extracting Steenrod barcodes from realistic datasets using the computational pipeline described in Sect. 4, we have produced two open-source software implementations: one¹ is a Python package optimized by means of the Numba library (Lam et al. 2015), and the other² is a performance-oriented C+ + package inspired by the PHAT library (Bauer et al. 2014).

While detailed performance benchmarking is beyond the scope of this paper, some remarks are in order. First, we note that both our implementations apply the clearing optimization (Chen and Kerber 2011) to Algorithm 1. It is well-known (see e.g. the discussion in Bauer (2021)) that clearing is particularly effective when computing relative persistent cohomology – and even more so when the filtration is constructed via a Vietoris–Rips process. Second, although the computation of matrix $Q^{k}$ (input to Algorithm 3) is in principle embarrassingly parallelizable by tasking fully independent threads with the calculation of different columns, we have not yet pursued this path in our code.

Third, we expect (and observe experimentally) that “sparsifying” our filtrations via simplicial collapses (Pritam 2020; Boissonnat and Pritam 2020), operations that preserve the homotopy type of each complex, can lead to a cascade of space and time improvements across our computational pipeline. This is presumably because:

• (1) the run-time and memory usage in Algorithm 1 is reduced, yielding sparser R and V matrices and hence cocycle representatives with smaller sizes on average;

• (2) the outer forall loop in Algorithm 2 becomes faster for smaller cocycles;

• (3) the leaner R matrix reduces the computational run-time and memory usage once again in the final Steenrod barcode computation, Algorithm 3.

(2) above deserves more emphasis: our experiments suggest that, in typical datasets, the main bottleneck in the entire pipeline is the computation of $\mathtt {sq}^k$ for a few exceptionally sizable cocycle representatives. This is due to the quadratic complexity of the forall loop in Algorithm 2. By replacing the largest cocycle representatives returned by (any implementation of) Algorithm 1 with cohomologous ones with a smaller size, one could presumably alleviate this problem. Our preliminary attempts using right-to-left reductions on the matrix R output by Algorithm 1 have yielded promising results; in the future, we hope to further improve our implementations in this direction, as well as making it easily accessible through its incorporation into giotto-tda (Tauzin et al. 2021).

We now report the results of computing $Sq^1$-barcodes in a synthetic and a natural dataset. In both cases we start from a point cloud and construct an associated filtered simplicial complexes through the Vietoris–Rips process with a fixed simplex dimension threshold of 3 (simplices with 4 or less vertices) and some distance threshold. We close this section with a comparison of the $Sq^2$-barcode of two filtered complex models of the cone on the suspension of, respectively, $\mathbb {C}\mathrm {P}^2$ and $S^2 \vee S^4$. Our experiments are fully reproducible as Jupyter notebooks.$^{1}$

5.1 Flat Klein bottle

Our first example is constructed from a matrix of geodesic distances among N points in a metrically flat Klein bottle. This is the Riemannian manifold $\mathcal {M} = (\mathbb {R}^2 / {\sim }, g)$ obtained from $\mathbb {R}^2$ with its usual metric via the equivalence relation $(x, y) \sim (x + n, 1 - y + m) \ \forall \ m, n \in \mathbb {Z}$. To define this point cloud we selected $N = 100$ points corresponding to the vertices of a square grid inside the unit square $[0, 1]^2$.

5.1.1 Persistent relative cohomology

Let X be the Vietoris–Rips filtered complex associated to this point cloud with distance threshold $R = 0.3$. We apply our pipeline to compute the regular barcode of ${\mathcal {H}}^i_R(X;\, \mathbb {F}_2)$ for $i = 1,2$ and their associated $Sq^1$-barcode. The results are presented in Fig. 6. There are three infinite bars: two in degree 1 – which happen to have identical birth and death due to the symmetry in our construction – and one in degree 2. Our implementation detects an infinite bar in ${{\,\mathrm{\mathrm {img}}\,}}(Sq^1) \cap \mathcal {H}^2_R$. This cohomological profile agrees with that expected from a filtered Klein bottle.

Fig. 6

Regular barcode of ${\mathcal {H}}^i_R(X;\, \mathbb {F}_2)$ for $i = 1,2$ and associated $Sq^1$-barcode. Here X is the Vietoris–Rips filtered complex associated to $N = 100$ points in a metrically flat Klein bottle and distance threshold $R = 0.3$. Arrowheads indicate infinite bars and integers over a bar denote its multiplicity (otherwise, the multiplicity is 1). Vietoris–Rips filtration values are shown on the horizontal axis

5.1.2 Persistent absolute cohomology

Let X be the Vietoris–Rips complex obtained from the same point cloud with no distance threshold. In Fig. 7 we present the regular barcode of ${\mathcal {H}}^i_A(X;\, \mathbb {F}_2)$ for $i = 1,2$ and associated $Sq^1$-barcode, obtained using our pipeline and the duality of Steenrod persistent cohomology (Sect. 4.2). Our implementation detects a single Steenrod bar in ${{\,\mathrm{\mathrm {img}}\,}}(Sq^1) \cap \mathcal {H}^2_A$, which is born with the $\mathcal {H}^1_A$ bars and dies with the $\mathcal {H}^2_A$ bar. Once again, this cohomological profile is consistent with that of a filtered Klein bottle.

Fig. 7

Regular barcode of ${\mathcal {H}}^i_A(X;\, \mathbb {F}_2)$ for $i = 1,2$ and associated $Sq^1$-barcode. Here X is the Vietoris–Rips filtered complex associated to $N = 100$ points in a metrically flat Klein bottle and no distance threshold

5.2 Conformational space of cyclo-octane

Our second example involves a sampling of the conformational space of the cyclo-octane molecule $\text {C}_{8} \text {H}_{16}$. We started with a dataset, originally from Martin et al. (2010), which consists of 6040 vectors in $\mathbb {R}^{24}$. Each of these vectors collects the 3D coordinates of all 8 carbon atoms in a given cyclo-octane conformation after alignment to a reference one. In Martin et al. (2010), this dataset was used to argue that the full conformational space of cyclo-octane is not a manifold, being in fact the union of a 2-sphere with a Klein bottle glued together along two circles of singularities. The reader can consult the papers Membrillo-Solis et al. (2019), Adams and Moy (2021) for further details and references.

Candidate singular points in this dataset can be identified in a variety of ways; we used a set of 627 singular points isolated in Stolz et al. (2020) via local persistent cohomology.³ We removed these points from the dataset, and clustered the remaining 5413 points using the HDBSCAN algorithm of Ricardo et al. (2013) to obtain (samplings of) four 2-strata – presumably corresponding to a dense open subset of the Klein bottle, and three open connected subsets of the 2-sphere.

As computed in Membrillo-Solis et al. (2019), the persistent absolute homology ${\mathcal {H}}_\bullet$ of the Vietoris–Rips filtered complex associated to the point cloud with $N = 3547$ elements supported on the presumed Klein bottle has, excluding the basic bar from ${\mathcal {H}}_0$, three prominent bars in its barcode. Their birth and death values occur respectively before and after the value $R = 1.2$ and two come from ${\mathcal {H}}_1$ while the other from ${\mathcal {H}}_2$.

5.2.1 Persistent relative cohomology

Fig. 8

Regular barcode of ${\mathcal {H}}^i_R(X;\, \mathbb {F}_2)$ for $i = 1,2$ and associated $Sq^1$-barcode Here X is the $R = 1.2$ Vietoris–Rips filtered complex associated to the $N = 3547$ “Klein bottle component” of the sampled conformational space of $\text {C}_{8} \text {H}_{16}$. Bars in the persistent relative cohomology barcode with lifetime shorter than 0.2 are not shown to reduce clutter

We study the persistent relative cohomology of X, the Vietoris–Rips filtered complex associated to this point cloud with distance thresholds $R = 1.2$. In Fig. 8 we show, discarding short-lived bars ($< 0.2$) for ease of visualization, the regular barcode of ${\mathcal {H}}^i_R(X;\, \mathbb {F}_2)$ for $i = 1,2$ and their associated $Sq^1$-barcode. Our implementation detects two $Sq^1$-bars. One is infinite and born with one of the two infinite ${\mathcal {H}}^1_R$ bars, while the other is born with the other ${\mathcal {H}}^1_R$ bar and dies with the most prominent finite ${\mathcal {H}}^2_R$ bar. The infinite parts of these barcodes are consistent with a filtered Klein bottle, where one of the infinite degree 1 bars interacts non-trivially with the degree 2 one. The finite Steenrod bar adds extra information revealing a non-trivial interaction between the other infinite degree 1 bar and a finite degree 2 bar. Refinements to the model for the conformation space of the cyclo-octane molecule resulting from the incorporation of this finer feature go beyond the scope of this example and are left unexplored.

5.2.2 Persistent absolute cohomology

Fig. 9

Regular barcode of ${\mathcal {H}}^i_A(X;\, \mathbb {F}_2)$ for $i = 1,2$ and associated $Sq^1$-barcode. Here X denotes the $R = 1.5$ Vietoris–Rips filtered complex associated to an $N = 800$ random subsample of the “Klein bottle component” of the conformational space of $\text {C}_{8} \text {H}_{16}$

For this data set we will also compute a Steenrod barcode for absolute persistent cohomology. We will use a distance threshold chosen to be larger than the death value of all prominent features. To do so we consider a subsample consisting of $N = 800$ randomly selected points. The persistent homology barcode of the associated Vietoris–Rips filtered complex with no distance threshold contains three prominent bars, and their death values are all less than $R = 1.5$. As expected, two of these are associated to ${\mathcal {H}}_1$ and the other to ${\mathcal {H}}_2$. Let X be the the Vietoris–Rips filtered complex with distance thresholds $R = 1.5$ obtained from this subsample. We remark that the threshold chosen ensures a correspondence between persistent relative and absolute cohomology of the Steenrod bars associated to their prominent features (Sect. 4.2). In Fig. 9 we show, discarding no bars, the regular barcode of ${\mathcal {H}}^i_A(X;\, \mathbb {F}_2)$ for $i = 1,2$ and associated $Sq^1$-barcode. As expected, the interaction between the more prominent bars witnessed by the Steenrod barcode is consistent with a filtered Klein Bottle.

5.3 Complex projective space and a wedge of spheres

We conclude this section comparing the $Sq^2$-barcodes of the persistent absolute cohomology of two filtered simplicial complexes. On one hand, we have a filtration of the cone on the suspension of the complex projective space $\mathrm C \, \Sigma \, {\mathbb {C}}\mathrm P^2$, and, on the other, one of $\mathrm C \, \Sigma \, (S^2 \vee S^4)$, where, as usual, $S^n$ denotes the n-dimensional sphere. As mentioned in the introduction, $\Sigma \, (S^2 \vee S^4)$ and $\Sigma \, {\mathbb {C}}\mathrm P^2$ have isomorphic cohomology rings over any coefficients, but they can be distinguished by the action of $Sq^2$ on their mod 2 cohomology.

Interpreting bars as points in the plane, we plot in Fig. 10 the regular and $Sq^2$-barcodes of the persistent absolute cohomology of these filtrations. After rescaling by the number of simplices, we can see that the regular barcodes, symbolized by colored circles, are very similar; yet there is a $Sq^2$-bar, represented by a brown diamond, present in the second figure only.

Fig. 10

Persistence diagram representations of the regular and $Sq^2$-barcodes of the persistent absolute cohomology of (a) a filtered complex modeling the cone on the suspension of $S^2 \vee S^4$, and (b) a filtered complex modeling the cone on the suspension of $\mathbb {C}\mathrm {P}^2$

6 Conclusion

Steenrod barcodes increase the discriminatory power of traditional barcodes, providing finer computable topological invariants of filtered spaces. Furthermore, as we showed using the conformation space of $\text {C}_8\text {H}_{16}$, the additional information these invariants reveal is non-trivially present in real-world examples.