Advertisement

Cognitive Aging and Long-Term Maintenance of Attentional Improvements Following Meditation Training

  • Anthony P. Zanesco
  • Brandon G. King
  • Katherine A. MacLean
  • Clifford D. Saron
Open Access
Original Article
First Online:
Received:
Accepted:

Abstract

Sustained attention is effortful, demanding, and subject to limitations associated with age-related cognitive decline. Researchers have sought to examine whether attentional capacities can be enhanced through directed mental training, with a number of studies now offering evidence that meditation practice may facilitate generalized improvements in this domain. However, the extent to which attentional gains are maintained following periods of dedicated meditation training and how such improvements are moderated by processes of aging have yet to be characterized. In a prior report (Sahdra et al., Emotion 11, 299–312, 2011), we examined attentional performance on a sustained response inhibition task before, during, and after 3-months of full-time meditation. We now extend this prior investigation across additional follow-up assessments occurring up to 7 years after the conclusion of training. Performance improvements observed during periods of intensive practice were partially maintained several years later. Importantly, aging-related decrements in measures of response inhibition accuracy and reaction time variability were moderated by levels of continued meditation practice across the follow-up period. The present study is the first to offer evidence that intensive and continued meditation practice is associated with enduring improvements in sustained attention and response inhibition, with the potential to alter longitudinal trajectories of cognitive change across the lifespan.

Keywords

Aging Meditation Response Inhibition Sustained Attention Vigilance 

The human capacity to sustain attention over time is limited and effortful, and is prone to fatigue, lapses, and fluctuations with prolonged engagement (Fortenbaugh et al. 2017; Langner and Eickhoff 2013; Warm et al. 2008). These limitations are exacerbated by age-related cognitive decline (Fortenbaugh et al. 2015; Lustig and Jantz 2015; Smittenaar et al. 2015), and there is now considerable interest in identifying training interventions that can offer effective remediation in aging populations and promote cognitive improvements in healthy individuals at large (e.g., Anguera et al. 2013; Bavelier and Davidson 2013). Increasingly, researchers have emphasized meditation- and mindfulness-based approaches for the training of attention. Meditation-based trainings have been shown to temper transient lapses in attention that disrupt ongoing task performance (Jha et al. 2015; Lutz et al. 2009; Morrison et al. 2014; Mrazek et al. 2013; van Vugt and Jha 2011; Zanesco et al. 2013, 2016), and improve individuals’ ability to sustain attention over time (MacLean et al. 2010; Sahdra et al. 2011; Zanesco et al. 2013). However, the extent to which attentional improvements endure after periods of dedicated training, and how continued meditation practice is associated with cognitive change across the lifespan remains unclear and understudied.

The limited, fluctuating, and effortful nature of attention historically forms a central motivation for improving attentional abilities through meditation among diverse Buddhist contemplative traditions (e.g., Gunaratana 2011; Wallace 1999). From this perspective, meditation is conceptualized as a detailed, formalized system of mental training through which practitioners cultivate specific cognitive capacities over time, including increased clarity, stability, and duration of attentional focus (Wallace 1999). While acknowledging that these traditions are shaped by a multitude of sociohistorical and soteriological factors, contemporary neurocognitive frameworks of mindfulness and meditation have endeavored to characterize families of meditation practice in terms of known features of attention and cognitive control (Dahl et al. 2015; Lippelt et al. 2014; Lutz et al. 2008, 2015; Vago and Silbersweig 2012), and theories of skill learning and plasticity (Slagter et al. 2011). Yet, the enduring consequences of continued meditation training have received sparse consideration in this emerging literature. Longitudinal investigations that track practitioners across periods of training and years of practice are critical for understanding the durability of trait-level cognitive changes associated with meditation, and for broadly characterizing the influence of attentional training on cognitive development across the lifespan.

Meditation techniques are commonly understood and disseminated by contemplative practitioners, teachers, and mindfulness-based clinicians as exercises for use in long-term or life-long personal development. Nevertheless, few studies have attempted to characterize how meditation-related cognitive improvements develop over years of practice, or whether such improvements are maintained following periods of formal training. Investigations detailing the developmental trajectory and maintenance of training-related improvements are vital to understanding the benefits and limitations of mindfulness-based interventions as traditionally conceptualized. Ideally, such studies would implement repeated assessments spread across extended time intervals; attempt to distinguish periods of intensive training from less-intensive durations of practice; and track both the quality and amount of time that practitioners dedicate to continued practice over these extended intervals. It is plausible, for example, that the benefits of acute periods of training are difficult to maintain absent an ongoing commitment to meditation or other lifestyle or behavioral changes that support continued engagement with contemplative practice. There is a need to examine how meditation-related improvements manifest in concert with developmental changes in cognition, and whether meditation practice can moderate the effects of aging-related cognitive decline.

Studies of cognitive aging offer compelling evidence that the ability to sustain attention and inhibit prepotent response tendencies is diminished in later life (e.g., Fortenbaugh et al. 2015; Smittenaar et al. 2015), and greater reaction time variability during task performance has been proposed as an important marker of age-related impairment in executive control (MacDonald et al. 2006; Vasquez et al. 2014; West et al. 2002). Age-related deficits in these domains have spurred the development of targeted intervention strategies for improving cognitive performance in older adults, including computer-based cognitive training programs (e.g., Anguera et al. 2013; Toril et al. 2014), general lifestyle interventions (e.g., Park et al. 2014), and mindfulness-based approaches (for reviews, see Gard et al. 2014; Malinowski and Shalamanova 2017; Kurth et al. 2017). Although several studies have reported cross-sectional differences between meditation practitioners and meditation-naïve controls in older adult samples (e.g., Laneri et al. 2016; Sperduti et al. 2016; van Leeuwen et al. 2009), relatively few studies have investigated meditation training as a directed intervention for older populations (e.g., Malinowski et al. 2017). Overall, research tentatively supports the claim that meditation practice can protect against age-related deficits in attention and executive function. Notably, however, no studies have longitudinally tracked meditation practitioners over years of continued practice to examine the moderation of age-related decline.

In our ongoing work, we have employed resource-demanding vigilance tasks—such as our sustained response inhibition task (RIT)—to assess skilled attentional performance in cognitively healthy adults (MacLean et al. 2009; Sahdra et al. 2011). In the RIT, participants are asked to discriminate between rare target and frequent non-target stimuli (small vertical lines) while inhibiting behavioral responses to targets over the course of performance. Using this task, we have demonstrated increases in response inhibition accuracy and attenuation of the vigilance decrement across a 3-month period of intensive training in focused attention meditation (Sahdra et al. 2011), and replicated these results in an independent 1-month training study incorporating a related style of practice (Zanesco et al. 2013). In addition to measures of performance accuracy, reductions in reaction time variability were also observed in this latter study. We now revisit our previous data (Sahdra et al. 2011) in light of an extensive long-term follow-up investigation. Our goal is to characterize the maintenance of training-related improvements across an extended post-training interval, and to examine the influence of continued meditation practice on age-related cognitive decline and longitudinal training trajectories.

In our prior report, training and wait-list control participants were assessed on the RIT at the beginning, middle, and end of a 3-month intensive meditation training (Sahdra et al. 2011). Follow-up assessments were conducted approximately 6 months, 1.5 years, and 7 years following the intervention. During training, practitioners engaged in shamatha meditation practices (Wallace 2006) that are thought to increase the clarity, stability, and duration of an individual’s concentration and to reduce the felt cognitive effort required to maintain attention in a sustained manner (Lutz et al. 2015). From a neurocognitive perspective, the features of concentration targeted by shamatha practice share considerable conceptual overlap with measures of attention derived from vigilance tasks such as our RIT. These tasks place substantial demand on supporting cognitive systems, leading to a monotonic decline in one’s capacity to detect and appropriately respond to target stimuli over time (i.e., vigilance decrement; Mackworth 1948). Studies of vigilance, moreover, have demonstrated that increased task discrimination difficulty can lead to a corresponding increase in the magnitude of this performance decrement and in the amount of subjective effort, distress, and demand reported by an individual (see for review, Langner and Eickhoff 2013; See et al. 1995; Warm et al. 2008). In order to minimize the potential influence of individual differences in discrimination capacity on observed training effects, we implemented a visual thresholding procedure designed to control levels of task difficulty across participants and assessments.

Lapses in attentional performance may also result from graded variation in attentional control on a moment-to-moment basis (e.g., Adam et al. 2015), or from shifts in attention to task-unrelated thought (e.g., mind wandering; Smallwood and Schooler 2015). Indeed, increased research on mind wandering and related phenomena (e.g., Cheyne et al. 2009; Seli et al. 2013; Smallwood and Schooler 2015), and the behavioral consequences of variability in attention and associated functional brain networks (e.g., Adam et al. 2015; Bellgrove et al. 2004; Weissman et al. 2006), has motivated attempts to reconcile accounts of the vigilance decrement with these more transient attentional lapses and fluctuations that occur during ongoing task performance (Langner and Eickhoff 2013; Thomson et al. 2015). This work suggests that variability of response times may partly reflect graded fluctuations in attention or episodes of task-unrelated thought. We therefore examined response time variability over the course of performance to characterize how ongoing fluctuations in attentional stability are influenced by longitudinal processes of aging and continued practice.

The primary study aims were to investigate the maintenance of training-related changes in response inhibition, reaction time variability, and vigilance over a 7-year period, and to assess the moderating influences of aging-related declines in performance and individual differences in continued meditation practice. We hypothesized that practitioners would maintain some attentional benefits of training, and that continued practice of meditation following training would be associated with this maintenance. We also predicted an interaction between the amount of continued practice and age-related declines in sustained attention and response inhibition. Older practitioners who devoted greater time to meditation practice in the years following training were expected to show reduced effects of age-related decline, in contrast to individuals who engaged in comparatively less continued practice.

Method

Participants

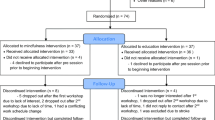
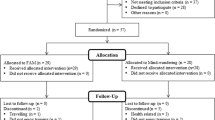
Sixty experienced meditation practitioners were assigned to either an initial training (N = 30) or wait-list control (N = 30) group through stratified random assignment; groups were matched on age (M = 48.96 years at study assignment, range = 22–69), gender, prior meditation experience, and baseline personality variables (see MacLean et al. 2010; Sahdra et al. 2011, for full recruitment and matching criteria). During an initial 3-month retreat (retreat 1), training participants resided and practiced meditation at Shambhala Mountain Center (SMC) in Red Feather Lakes, Colorado. During retreat 1, wait-list control participants traveled to SMC for week-long assessment periods but otherwise maintained their daily routines at home between assessments. Approximately 3 months after retreat 1, these same wait-list control participants received formally identical training during a second 3-month residential retreat at SMC (retreat 2; n = 29).1 All participants were invited to participate in three follow-up assessments conducted approximately 6 months (M = 6.6 months, range = 4.7–11.9), 1.5 years (M = 17.9 months, range = 15.6–20.2), and 7 years (M = 81.9 months, range = 73.3–93.9) following the conclusion of their respective training periods. Follow-up attrition was generally low (> 70% retention at each assessment; see Table 1 for sample size at each assessment). All participants were compensated $20 per hour of data collection.
Table 1

Task parameters and descriptive statistics for RIT-dependent measures

Measure

Training

Follow-up

Pre

Mid

Post

6-Month

1.5-Year

7-Year

R1 Training group

 N

30

30

30

28

22

21

 Age

50.25 (12.6)

50.34 (12.6)

50.44 (12.6)

50.35 (12.5)

50.69 (11.9)

56.19 (12.2)

 Re-parameterized

Yes

Yes

Yes

Yes

Yes

Yes

 Discrimination

3.77 (.39)

4.11 (.18)

4.14 (.27)

3.89 (.23)

4.10 (.44)

3.90 (.55)

 Accuracy (A)

0.80 (.05)

0.88 (.06)

0.88 (.06)

0.88 (.07)

 

0.90 (.07)

 RTCV

0.25 (.07)

0.24 (.06)

0.24 (.06)

0.26 (.06)

 

0.26 (.06)

R2 Training group

 N

29

29

29

27

22

23

 Age

47.51 (15.5)

47.60 (15.5)

47.70 (15.5)

48.46 (14.9)

51.38 (14.9)

54.79 (15.4)

 Re-parameterized

Yes

No

No

No

No

Yes

 Discrimination

4.03 (.31)

4.08 (.22)

4.11 (.23)

4.15 (.24)

4.11 (.28)

3.96 (.43)

 Accuracy (A)

0.88 (.05)

0.91 (.05)

0.92 (.05)

0.91 (.05)

0.92 (.05)

0.89 (.07)

 RTCV

0.26 (.08)

0.22 (.06)

0.20 (.07)

0.25 (.06)

0.26 (.06)

0.27 (.07)

Note: means and standard deviations (in parentheses) are provided for participant age and RIT performance measures. The number (N) and mean age of participants with complete data at each assessment are indicated for each group. Re-parameterized indicates whether the RIT target was pre-set (No) or re-thresholded (Yes) at a given assessment. Discrimination is the achieved mean visual angle of the PEST procedure. Accuracy (perceptual sensitivity, A) and RTCV (reaction time coefficient of variation) are computed across the full 32-min RIT

Meditation Training

Meditation training occurred under guidance of B. Alan Wallace, a Buddhist teacher and contemplative scholar. Training included shamatha techniques designed to foster calm sustained attention on a chosen object, and complementary techniques, known as the Four Immeasurables (compassion, loving-kindness, empathetic joy, and equanimity), aimed at generating benevolent aspirations for the well-being of oneself and others (Wallace 2006, 2011). Primary practice involved mindfulness of breathing, in which attention is drawn to the tactile sensations of the breath. Participants also practiced attending to the arising of mental content (e.g., thoughts, perceptions, sensations), a technique known as settling the mind into its natural state, and focusing attention on the sense of awareness itself, known as shamatha without a sign (Wallace 2006, 2011). Participants met twice daily for group practice and discussion, devoted about 6 h of their remaining day to solitary shamatha meditation, and about 45 min to Four Immeasurables meditation. In addition to these formal practice sessions, participants were encouraged to maintain mindful, present-centered awareness throughout their day, and met with Dr. Wallace privately once a week for guidance and advice. Full details regarding the techniques employed and training time dedicated to each practice can be found in Sahdra et al. (2011) and Rosenberg et al. (2015).

At the 7-year follow-up assessment, participants were asked to estimate the amount of time they spent meditating outside of formal retreat settings (i.e., daily, non-intensive practice) across the follow-up period. Participants estimated their current weekly practice time, then adjusted these values to estimate their total practice hours for the previous year, before finally providing adjusted estimates for each preceding year. Practice estimates were then summed over the entire follow-up period (M = 3127.95 h, median = 1896, range = 249–14,900). In addition, participants were asked to estimate the total number of days they spent in formal retreat (i.e., intensive) practice across this period (M = 293.19 days on retreat, range = 0–2125). Among participants with available data (n = 40), all reported some form of continued meditation practice across this follow-up interval; 85% attended at least one meditation retreat; 55% reported that Dr. Wallace remained one of their primary meditation teachers; and 60% directly identified shamatha meditation or mindfulness of breathing as one of their primary meditation practices.

Procedure

Retreat 1 training participants were tested at the beginning (preassessment), middle (midassessment), and end (postassessment) of retreat 1. Wait-list control participants were assessed at the beginning, middle, and end of both meditation retreats, first serving as control participants for retreat 1, then as active training participants for retreat 2. Finally, participants in both groups were tested at each of the three follow-up assessments (6-month, 1.5-year, and 7-year). See Table 1 for an overview of the assessment schedule and RIT task parameters.

At each assessment, participants completed an initial discrimination threshold procedure followed by the 32-min continuous RIT.2 Participants responded to commonly occurring non-target (long line) stimuli while withholding behavioral responses to rare target (short line) stimuli. All procedures were approved by the institutional review board of the University of California, Davis, and all participants gave full informed consent.

Threshold

The discrimination threshold procedure (~ 10 min) was designed to equate task demand across participants and to calibrate individual task difficulty (see MacLean et al. 2009). Participants maintained fixation on a small dot at the center of the screen while single gray vertical lines appeared one at a time against a black background. Each line stimulus was presented for 150 ms. A visual mask pattern was presented before and after the line stimulus for 100 ms. The mask was comprised of small lines (0.07° wide and 0.28° to 0.45° long) positioned throughout a 5.0° × 1.0° space surrounding the fixation point. The mask pattern varied randomly on each trial and was not presented concurrently with line stimulus presentation. The inter-stimulus interval varied randomly but was constrained to a mean of 1850 ms and a range (rectangular distribution) of 1550–2150 ms. Participants were asked to respond as quickly and accurately as possible with the left mouse button (right index finger) to frequent long lines (70% of stimuli) and to withhold responses to rare short lines (30% of stimuli). Sound feedback was provided for correct and incorrect responses.

The length of the short-line target was adjusted according to parameter estimation through sequential testing (PEST; Taylor and Creelman 1967). This procedure was used to establish the target line length that can be correctly discriminated at a pre-determined accuracy rate for a given participant, which defined an individual’s discrimination threshold in units of visual angle. A larger threshold value indicates a longer short-line target, and thus better discrimination. PEST accuracy was set to 85% at the retreat 1 preassessment; at all other assessments, accuracy was set at 75%. This change in procedure was implemented to ensure high task demand for the remainder of assessments, after we failed to observe reliable vigilance decrements at 85% difficulty (Sahdra et al. 2011).

RIT

Participants completed the 32-min RIT immediately following the PEST threshold procedure (960 trials in total). Stimulus and response parameters were identical to the threshold procedure except that (1) the length of the target line remained constant throughout the task, (2) targets occurred less frequently (10% of all stimuli totaling 96 target lines), and (3) sound feedback was not present.

For each group and assessment, the short-line target was individually determined based on a participant’s PEST discrimination threshold using one of two target-setting manipulations: either (1) difficulty was adjusted by re-parameterizing the target stimulus to a participant’s current PEST discrimination threshold, or (2) difficulty was pre-set to a participant’s previously measured discrimination threshold. When re-parameterized, the RIT target length was determined from the PEST immediately preceding the RIT at that same assessment point. This manipulation of target length across assessments was informed by our observation (described in MacLean et al. 2010) that systematic improvements in discrimination thresholds may have limited our ability to observe training-related performance improvements in performance accuracy.

Response inhibition accuracy was quantified using the non-parametric index of perceptual sensitivity, A (Zhang and Mueller 2005). Hits were defined as correct inhibitions to targets and false alarms as incorrect inhibitions to non-targets. A ranges from 0 to 1, with 0.5 indicating chance performance and 1 perfect performance. To compare accuracy from retreat 1 preassessment (set at 85% threshold level) to all remaining assessments (set at 75% threshold level), levels of A at the initial assessment were adjusted to estimate performance at 75% [adjusted A = (original A × .75) / .85], an approach consistent with the methods of our prior report (Sahdra et al. 2011). Reaction time variability was quantified as the reaction time coefficient of variability (RTCV = standard deviation RT / mean RT) for non-target trials (864 trials), where lower RTCV values indicate lower reaction time variability. For each participant, perceptual sensitivity (A) and RTCV were calculated for the overall task and for each of eight 4-min contiguous trial blocks (120 trials per block).

Training Assessments

Retreat assessments were conducted in darkened, sound-attenuated testing chambers located in the dormitory where participants resided and practiced meditation. Stimuli were delivered on an LCD monitor (Viewsonic VX-922) while participants maintained a viewing distance of 57 cm from the screen. In retreat 1, the target stimulus was re-parameterized at each assessment; in retreat 2, the target was pre-set to each individual’s retreat 2 preassessment PEST threshold. Thus, target length was not re-parameterized at the retreat 2 mid- or postassessments, but was instead held constant to equate stimulus parameters across the second retreat.

Follow-up Assessments

Each participant was provided a 14′′ IBM T-40 ThinkPad laptop, with detailed instructions for assembling an in-home testing environment, setting dim ambient lighting, and maintaining a viewing distance of 57 cm. For retreat 1 training participants, target length was again re-parameterized at the 6-month and 7-year follow-up assessments; these participants did not complete the RIT at the 1.5-year follow-up assessment, instead completing only the threshold procedure (see Table 1). For retreat 2 participants, target length was again pre-set to each individual’s retreat 2 preassessment threshold for the 6-month and 1.5-year follow-up assessments; at the 7-year assessment, however, target length was re-parameterized. The decision to re-parameterize the target length for both participant groups at the final follow-up was based on the supposition that visual acuity or executive function may have changed substantially since the retreat 2 preassessment, thus making participants’ previous target line length inordinately challenging.3 For follow-up assessments where targets were pre-set, stimuli sizes were scaled to maintain the same visual angle for both laptop and laboratory versions of the task.

Analysis

Multi-level models implemented with SAS PROC MIXED version 9.4 were used to analyze longitudinal changes in discrimination, accuracy (perceptual sensitivity, A), and RTCV. Significance of random effects was evaluated using log-likelihood tests of change in model fit (− 2ΔLL), estimated using restricted maximum likelihood. Reported models were estimated using full maximum likelihood, and fixed effects were evaluated using Satterthwaite approximated degrees of freedom (reported to the nearest integer).

Growth curve models describe the mean trajectory of change in terms of an intercept (i.e., starting point) and slope (i.e., rate of change), with random effects representing between-person variability in these parameters (Ferrer and McArdle 2010; Hoffman 2015). Retreat measurements were spaced at equal intervals, whereas the timing of follow-up assessments varied both within and between individuals. To characterize change during retreat, we modeled a slope across fixed training assessments (pre- = 0, mid- = 1, and postassessment = 2), with a statistically significant slope indicating group-level change. To characterize change across follow-up, we modeled a slope over years since retreat (YSR; scaled in years), where YSR reflects the yearly change in performance since end of retreat (postassessment = 0 years). A statistically significant YSR slope indicates group-level change (e.g., improvement or decline) across follow-up assessments. For models including both retreat and follow-up assessments, these parameters were included as piecewise slopes representing separable components of change attributable to training and YSR respectively (Hoffman 2015).

Random effects were included when significant to allow for individual differences in the intercept, or slope of performance across blocks, training, or YSR. The effect of block (block 1 = 0) represents the linear rate of change (magnitude of the vigilance decrement) across the eight 4-min segments of the RIT. Age was centered such that 0 indicates a participant who was 65 years old at the end of training (age at postassessment=65 years). When included in models with follow-up assessments, the effect of age represents between-person effects of participant age, whereas YSR reflects within-person change across years of follow-up (Hoffman 2015). Visual inspection of age trends suggested quadratic trajectories in performance as participants aged. Quadratic effects are reported where significant.

Results

Summary statistics for perceptual discrimination, accuracy (perceptual sensitivity, A), and reaction time variability across all assessments are reported in Table 1.

Longitudinal Training and Maintenance in Retreat 1

We first analyzed longitudinal change across training (pre-, mid-, and postassessment) and years of follow-up (6 month, 1.5 year, 7 year) for retreat 1 training participants. For each measure, we fit an initial model describing change across block, retreat, and YSR (reported in Table 2). For accuracy and RTCV, we then examined interactions between block and training, and block and YSR. Finally, we examined age as a predictor of performance. Figure 1 depicts mean A and RTCV for the retreat 1 training group across RIT blocks at each assessment. Figure 2 depicts observed changes in discrimination, A, and RTCV across YSR for each individual, with the intercept indicating performance at postassessment (YSR = 0) and the trajectory representing performance over YSR.
Table 2

Growth models of longitudinal training and maintenance in retreat 1 training participants

Model effects

Parameter estimate (SE)

Discrimination

Accuracy

RTCV

Fixed effects

 Intercept

3.766 (.056)**

0.829 (.008)**

0.233 (.011)**

 Linear block

 

− 0.008 (.001)**

0.006 (.001)**

 Linear training

0.545 (.115)**

0.126 (.017)**

− 0.0125 (.004)**

 Quadratic training2

− 0.201 (.053)**

− 0.045 (.008)**

 

 Linear YSR

− 0.019 (.014)

0.004 (.003)

0.056 (.018)**

 Quadratic YSR2

  

− 0.007 (.003)**

Random effects

 Intercept variance

0.032 (.013)**

0.001 (.001)**

0.003 (.001)**

 Block variance

 

0.00002 (.00001)*

0.00003 (.00001)**

 Training variance

 

0.006 (.002)**

0.0003 (.0001)*

 YSR variance

0.002 (.001)*

0.0001 (.0001)**

0.007 (.003)**

 Training2 variance

 

0.002 (.001)**

 

 YSR2 variance

  

0.0001 (.0001)**

 Intercept-block covariance

 

0.0001 (.0001)*

0.0001 (.0001)

 Intercept-training covariance

 

− 0.0003 (.0008)

− 0.0006 (.0003)

 Intercept-YSR covariance

0.005 (.003)

− 0.00002 (.0001)

0.002 (.001)

 Intercept-training2 covariance

 

− 0.00005 (.0004)

 

 Intercept-YSR2 covariance

  

− 0.0002 (.0002)

 Block-training covariance

 

− 0.0002 (.0001)

0.0000004 (.00003)

 Block-YSR covariance

 

− 0.00002 (.00002)

− 0.0002 (.0001)

 Block-training2 covariance

 

0.0001 (.0001)*

 

 Block-YSR2 covariance

  

0.00002 (.00002)

 Training-YSR covariance

 

− 0.0001 (.0002)

− 0.0008 (.001)

 Training-training2 covariance

 

−0.003 (.001)*

 

 Training-YSR2 covariance

  

0.0001 (.0001)

 YSR-training2 covariance

 

− 0.00004 (.0001)

 

 YSR-YSR2 covariance

  

− 0.001 (.0004)**

 Residual variance

0.062 (.008)**

0.004 (.0002)**

0.002 (.0001)**

Fit statistics

   

 − 2 Log-likelihood

− 69.5

− 2831.4

− 3522.6

Note: maximum likelihood estimates are reported for piecewise longitudinal analyses of RIT measures across retreat and years since retreat (YSR). Standard errors are reported in parentheses

2denotes a quadratic parameter

*p < .05; **p < .01

Fig. 1

Mean performance trajectories for accuracy (A) and reaction time variability (RTCV) across the eight contiguous 4-min blocks of the RIT. Retreat 1 and retreat 2 training participants are shown across training (black) and follow-up (red) assessments

Fig. 2

Observed individual performance trajectories for discrimination threshold (in units of visual angle), accuracy (perceptual sensitivity, A), and reaction time variability (RTCV) across years since retreat (YSR). The intercept represents performance at retreat postassessment (YSR = 0) and the model-estimated group trajectory is indicated in red

Discrimination

The inclusion of a random slope for YSR (− 2ΔLL(3) = 21.9, p < .001) significantly improved model fit. There were significant linear, β = 0.545, p < .001, and quadratic, β = − 0.201, p < .001, trajectories across retreat, but no significant linear yearly change over YSR, β = − 0.019, p = .184 (see Fig. 2a). Training participants’ discrimination threshold was estimated to increase (p < .001) by .344° of visual angle from pre- to midassessment. This rate then slowed over time such that participants increased (p < .001) a total of .286° of visual angle from pre- to postassessment. Finally, we included age as a model predictor. Age did not significantly predict discrimination, β = − 0.0013, p = .689, and there were no higher-order interactions of age with training or YSR.

Accuracy

The inclusion of random slopes for block (− 2ΔLL(2) = 20.8, p < .001), training (− 2ΔLL(3) = 34.8, p < .001), YSR (− 2ΔLL(4) = 112.7, p < .001), and quadratic training (− 2ΔLL(5) = 39.4, p < .001) significantly improved model fit. We observed a significant vigilance decrement (i.e., effect of block) with an estimated decline (p < .001) of − .0084 units of A at each RIT block. Random effects confidence intervals (CI) suggested that 95% of participants showed a decrement between − .017 and .0004 units of A for each block. In addition, we observed significant linear, β = 0.126, p < .001, and quadratic, β = − 0.045, p < .001, slopes across training assessments, indicating significant increases in accuracy over retreat. Compared to preassessment, participants increased (p < .001) an estimated total of .081 units of A by midassessment, and an estimated total (p < .001) of .071 units by postassessment.

There were, however, no significant linear changes in A across YSR, β = 0.004, p = .119, 95% CI [− .0012, .0097] (see Fig. 2b). This non-significant change across YSR offers no affirmative statistical evidence in support of maintenance. We therefore further evaluated the estimated change across YSR using TOST equivalence procedures (Lakens 2017). Specifically, we examined the years for which the total accumulated change was significantly smaller than a minimally meaningful effect, defined as half the total increase in accuracy over retreat (ΔL = − 0.035, ΔU = 0.035). The accumulated change across follow-up was practically equivalent to zero from the end of retreat to at least year 4, after which the 90% CI of the remaining years’ estimates overlapped with the upper equivalence bound (see Fig. 3). Maintenance over years 5 to 7 was thus statistically undetermined.
Fig. 3

Model estimated change in accuracy (perceptual sensitivity, A) based on the linear slope across years since retreat (YSR) for a retreat 1 and b retreat 2. Ninety and 95% confidence intervals are displayed around each yearly estimate with a thick line and thin line respectively. Horizontal black dotted lines indicate the lower (ΔL) and upper (ΔU) equivalence bounds for a meaningful effect, defined as half the total increase in accuracy accrued during training for retreat 1 (ΔL = − 0.035, ΔU = 0.035) and retreat 2 (ΔL = − 0.022, ΔU = 0.022)

We next examined whether the within-task performance decrement changed across retreat assessments or YSR. There was no significant interaction between block and linear, β = − 0.004, p = .390, or quadratic training, β = 0.002, p = .439, suggesting that the vigilance decrement was unaffected by training in retreat 1. The effect of block, however, was significantly attenuated across YSR, β = 0.0007, p = .037. Finally, we examined the effects of aging on response inhibition accuracy. Age did not significantly predict A, β = − 0.0003, p = .611, and there were no higher-order interactions between age, block, training, and YSR.

Reaction Time Variability

Random slopes for block (− 2ΔLL(2) = 42.9, p < .001), training (− 2ΔLL(3) = 53.4, p < .001), linear YSR (− 2ΔLL(4) = 54.6, p < .001), and quadratic YSR (− 2ΔLL(5) = 64.6, p < .001) all significantly improved model fit. We observed a significant linear effect of block, indicating an average increase (p < .001) of .006 units of RTCV per block. Random effects CI suggested that 95% of participants showed a per-block change in RTCV between − .005 and .017 units. We also observed a significant linear effect of training, β = − 0.013, p = .003, indicating significant reductions in RTCV. Ninety-five percent of individuals had a slope between − 0.044 and .019 units of RTCV across retreat assessments. Finally, we observed significant linear, β = 0.056, p = .006, and quadratic, β = − 0.007, p = .008, slopes across YSR (see Fig. 2c), indicating that participants lost the benefits of training in the years following retreat, but that this rate of loss slowed and then reversed over time. One year after postassessment (YSR = 1), participants were estimated to have increased (p = .005) .048 units of RTCV, whereas 7 years later, the estimated total increase (p = .031) was .031 units.

No significant interaction between block and training, β = 0.0012, p = .202, was observed when included in the model. There were significant interactions between block and both the linear, β = − 0.009, p = .001, and quadratic, β = 0.0012, p = .001, YSR trends, however, indicating that the within-task increase in RTCV was significantly reduced in the years following training. Finally, age did not significantly predict RTCV, β = − 0.0004, p = .556, in retreat 1 participants. There were no higher-order interactions between age, block, training, or YSR.

Summary

Significant increases in accuracy were observed across retreat 1 training assessments, which were then definitively maintained for at least 4 years following retreat. Improvements (i.e., reductions) in reaction time variability were also observed across retreat, but were lost over the course of follow-up. Interestingly, within-task decrements in performance accuracy and RTCV were attenuated across years of follow-up, but not during retreat, suggesting possible benefits of long-term continued practice. No significant effects of aging were observed.

Longitudinal Training and Maintenance in Retreat 2

We next examined longitudinal change across blocks, training, and YSR in retreat 2 training participants. Parameter estimates are reported in Table 3, and Fig. 1 depicts mean A and RTCV across blocks at each assessment. In retreat 2, the RIT target was pre-set to each participant’s preassessment discrimination threshold for all remaining assessments, excluding the 7-year follow up assessment, for which target length was re-parameterized (see Table 1).
Table 3

Growth models of longitudinal training and maintenance in retreat 2 training participants

Model effects

Parameter estimate (SE)

Discrimination

Accuracy

RTCV

Fixed effects

 Intercept

4.023 (.045)**

0.900 (.007)**

0.248 (.013)**

 Block

 

− 0.008 (.001)**

0.004 (.001)**

 Linear training

0.060 (.019)**

0.045 (.010)**

− 0.067 (.011)**

 Quadratic training2

 

− 0.012 (.005)*

0.019 (.005)**

 Linear YSR

− 0.027 (.012)*

− 0.004 (.003)

0.045 (.009)**

 Quadratic YSR2

  

− 0.006 (.001)**

Random effects

 Intercept variance

0.035 (.011)**

0.001 (.0003)**

0.004 (.001)**

 Block variance

 

0.00002 (.00001)*

 

 Training variance

  

0.0006 (.0002)**

 YSR variance

0.002 (.001)**

0.0002 (.0001)**

0.002 (.001)**

 YSR2 variance

  

0.00004 (.00001)**

 Intercept-block covariance

 

0.0001 (.00004)**

 

 Intercept-training covariance

  

− 0.001 (.0004)*

 Intercept-YSR covariance

0.0008 (.002)

− 0.0002 (.0001)

− 0.0001 (.001)

 Intercept-YSR2 covariance

  

0.00003 (.0001)

 Block-YSR covariance

 

0.00001 (.00001)

 

 Training-YSR covariance

  

− 0.0004 (.0003)

 Training-YSR2 covariance

  

0.00005 (.00004)

 YSR-YSR2 covariance

  

− 0.0002 (.0001)**

 Residual variance

0.027 (.004)**

0.004 (.0002)**

0.003 (.0001)**

Fit statistics

 − 2 Log-likelihood

− 29.6

− 3403.4

− 3473.5

Note: maximum likelihood estimates are reported for piecewise longitudinal analyses of RIT measures across retreat and years since retreat (YSR). Standard errors are reported in parentheses

2denotes a quadratic parameter

*p < .05; **p < .01

Discrimination

Model fit was significantly improved by inclusion of a random slope for YSR (− 2ΔLL(3) = 31.8, p < .001) only. We observed a significant linear increase in discrimination across training, β = 0.060, p = .002, and a significant yearly decrease over YSR, β = − 0.027, p = .029 (see Fig. 2d), suggesting training-related improvements in discrimination capacity that were then lost over years of follow-up. There were no significant effects of age on discrimination threshold, β = − 0.004, p = .101.

Accuracy

Inclusion of random slopes for block (− 2ΔLL(2) = 23.9, p < .001), and YSR (− 2ΔLL(4) = 139.5, p < .001), significantly improved model fit; the random effect of training (− 2ΔLL(3) = 5.1, p = 0.139), however, did not improve fit, suggesting minimal influence of individual differences on change in accuracy across training. The fixed effect of block was significant, β = − 0.008, p < .001, indicating an average per-block reduction of − .008 units of A. The random effects CI suggested that 95% of participants had a vigilance decrement between − .016 and − .0005 units of A. In addition, we observed significant linear, β = 0.045, p < .001, and quadratic, β = − 0.012, p = .012, trends across training, such that participants improved in accuracy during retreat, but that the rate of improvement slowed across assessments. Compared to preassessment, participants increased (p < .001) an estimated total of .033 units of A by midassessment, and an estimated total (p < .001) of .043 units by postassessment.

Although no overall significant yearly changes in A were observed following retreat, β = − 0.004, p = .128, 95% CI [− 0.0094, 0.0013] (see Fig. 2e), we observed significant individual differences in rates of yearly change: 95% of individuals demonstrated changes ranging from − 0.028 to .020 units of A per each year of follow-up. To formally evaluate maintenance, TOST equivalence procedures were used to examine the years for which the total accumulated change in accuracy over YSR was significantly smaller than half the total increase accrued over retreat (ΔL = − 0.022, ΔU = 0.022). Accumulated change was equivalent to zero until at least the second year following retreat, after which maintenance was statistically undetermined (see Fig. 3).

We next investigated whether within-task decrements in A changed across retreat assessments or YSR. There was a significant interaction between block and the linear effect of training, β = 0.0022, p = .030, suggesting that the magnitude of the vigilance decrement was attenuated across training. Specifically, the performance decrement over blocks (β = − 0.008) was estimated to diminish by .002 units at each assessment. The interaction between block and the quadratic effect of training was not significant, β = 0.0009, p = .644, and there was no change in the vigilance decrement over YSR, β = − 0.0006, p = .118, 95% CI [− 0.0013, 0.00015]. These patterns suggest that meditation training improved performance and moderated the vigilance decrement, and that these benefits did not change over years of the follow-up.

Finally, we examined age as a predictor of response inhibition accuracy. There was a significant main effect of age on A, β = 0.0007, p = .048. We next explored interactions between age and other model effects. Age was unrelated to block or to the rate of improvement across training, but was a significant moderator of change after retreat, β = − .0004, p = .026. Specifically, older participants declined at a greater rate across years of follow-up than did younger participants. Moreover, although retreat 2 participants retained training improvements across the follow-up on average, yearly losses were estimated to occur specifically in older (i.e., age = 65) participants, β = − 0.009, p = .036. Figure 4a depicts individual subject trajectories of A at each follow-up assessment as a function of age.
Fig. 4

Observed individual performance trajectories for accuracy (A) and reaction time variability (RTCV) as a function of age for retreat 2 follow-up assessments. The model-estimated aging slope of best fit is indicated in red

Reaction Time Variability

Random effects for the linear slope of training (− 2ΔLL(3) = 55.2, p < .001), and both linear (− 2ΔLL(4) = 78.5, p < .001) and quadratic slopes of YSR (− 2ΔLL(6) = 50.5, p < .001), significantly improved model fit. We observed a significant within-task increase of .004 RTCV units across blocks, β = 0.004, p < .001. There were also significant linear, β = −0.067, p < .001, and quadratic, β = 0.019, p < .001, decreases in RTCV across retreat assessments. The quadratic trend indicates that RTCV was reduced across training, but that the rate of decrease slowed across assessments. At midassessment, participants showed an estimated − .048 (p < .001) unit reduction in RTCV compared to preassessment, while the estimated reduction (p < .001) from pre- to postassessment was − .058 units. Significant linear, β = 0.045, p < .001, and quadratic, β = − 0.006, p < .001, trends in YSR (see Fig. 2f) were also observed. Although participants gradually lost the benefits of training over follow-up, the rate of loss slowed over time: 1 year after postassessment, participants showed an estimated increase (p < .001) of .039 units of RTCV, whereas 7 years later the estimated increase (p = .025) was .044 units.

We observed no significant interactions between block and any other linear or quadratic trajectories, indicating that the per-block increase in RTCV was unaffected by training or YSR. Finally, although there was no significant linear effect of age, β = 0.003, p = .145, we observed a significant quadratic, β = 0.00012, p = .026, effect of age on RTCV. The relationship between RTCV and age was ∪-shaped, such that RTCV was reduced in middle age and increased in older age. Figure 4b depicts individual subject trajectories of RTCV at each follow-up assessment as a function of age.

Summary

Training participants demonstrated overall improvements in discrimination and performance accuracy during retreat 2, and significant attenuation of the vigilance decrement. No statistically significant changes in overall accuracy and vigilance were observed over years of follow-up, with equivalence testing suggesting that changes in accuracy were maintained below half the level of total retreat gains for approximately 2 years. However, when pooled across both retreats, total change in accuracy across YSR was closer to zero, such that the weighted estimate (β = 0.0004, 90% CI [− 0.021,0.021]) remained within the equivalence bounds up to 7 years following retreat. Thus, the true degree of maintenance was likely underestimated across individual retreats. As in retreat 1, RTCV was reduced during training in retreat 2, but improvements were then lost following retreat. Age was a significant predictor of RTCV, and interacted with rate of change over YSR such that losses in performance accuracy were estimated to occur specifically in older participants.

Meditation Practice Moderates Age-Related Decline in Performance

In a final set of analyses, we examined whether the observed age-related declines in performance among retreat 2 participants were moderated by meditation practice across the follow-up period. Estimates of continued practice (M = 2834.2 h, range = 406–11,900) and intensive retreat participation (M = 176.7 days on retreat, range = 0–1460) were available for 19 participants. These variables were entered separately into models for A and RTCV across YSR, after removing participants for whom no practice estimates were available. Hours of practice were rescaled to aid interpretation of model parameters (1 unit represents 100 h).

We first included estimates of continued practice (in hours) over follow-up as a predictor of performance accuracy. Parameter estimates from this model are reported in Table 4. We observed a significant interaction between hours and YSR, β = 0.001, p = .029, and a significant three-way interaction between age, hours, and YSR, β = 0.00004, p = .018. Figure 5 depicts model-estimated simple slopes across YSR at low (1250 h), medium (2000 h), and high (2750 h) values of continued practice for middle-aged (45 years) and older individuals (65 years). As can be seen in Fig. 5, older individuals who engaged in a relatively smaller amount of continued practice over YSR were predicted to experience greater losses of training-related benefits in A. Middle-aged individuals did not experience training losses over YSR, irrespective of their continued practice across this interval. For older individuals, however, there was a marginally significant slope across YSR at lower practice estimates (1250 h), β = − 0.052, p = .099, that reached statistical significance at approximately 750 h of estimated practice.
Table 4

Effects of aging and practice hours across follow-up on retreat 2 performance accuracy

Model effects

Parameter estimate (SE)

Fixed effects

 Intercept

0.999 (.047)**

 Linear block

− 0.010 (.002)**

 Linear YSR

− 0.033 (.011)*

 Age

0.002 (.002)

 Hours of practice

− 0.003 (.002)

 Age-YSR interaction

− 0.001 (.0004)*

 Age-hours interaction

− 0.0001 (.0001)

 YSR-hours interaction

0.001 (.001)*

 YSR-age-hours interaction

0.00004 (.00002)*

Random effects

 Intercept variance

0.001 (.001)

 Block variance

0.00003 (.00002)

 YSR variance

0.0001 (.00004)*

 Intercept-block covariance

0.0002 (.0001)

 Intercept-YSR covariance

− 0.0003 (.0001)

 Block-YSR covariance

0.00002 (.00002)

 Residual variance

0.004 (.0003)**

Fit statistics

 

 − 2 Log-likelihood

− 1014.5

Note: maximum likelihood estimates are reported for RIT accuracy (A) across years since retreat (YSR) in retreat 2 training (n = 19) participants. Age is centered to postassessment and 65 years. Hours of practice are scaled to 100 h per unit. Standard errors are reported in parentheses

*p < .05; **p < .01

Fig. 5

Model estimates of linear change in accuracy (A) across years since retreat for retreat 2 training participants at low (1250 h), medium (2000 h), and high (2750 h) levels of practice hours for middle-aged (45 years) and older individuals (65 years)

We next examined whether continued practice moderated the effects of aging on RTCV (see Table 5 for parameter estimates). We observed significant linear, β = 0.017, p < .001, and quadratic, β = 0.0004, p < .001, trends across age, a significant effect of total practice hours, β = − 0.008, p < .001, and a significant interaction between hours and the linear, β = − 0.0004, p = .004, and quadratic age parameters, β = − .000007, p = .019, for RTCV. Thus, in contrast to performance accuracy, continued meditation practice appeared to directly moderate age-related declines in reaction time variability. Figure 6 illustrates model-estimated simple slopes for low (1250 h), medium (2000 h), and high (2750 h) values of practice across continuous age. As shown in Fig. 6, individuals who engaged in relatively fewer hours of practice over YSR demonstrated greater age-related impairments in RTCV.
Table 5

Effects of aging and practice hours across follow-up on retreat 2 RTCV

Model effects

Parameter estimate (SE)

Fixed effects

 Intercept

0.401 (.029)**

 Linear block

0.004 (.002)**

 Linear YSR

0.003 (.003)

 Linear age

0.017 (.003)**

 Quadratic age2

0.0004 (.0001)**

 Hours of practice

− 0.008 (.001)**

 Age-hours interaction

− 0.0004 (.0001)**

 Age2-hours interaction

− 0.000007 (.000003)*

Random effects

 Intercept variance

0.003 (.001)**

 YSR variance

0.0001 (.0001)**

 Intercept-YSR covariance

− 0.0006 (.0003)*

 Residual variance

0.005 (.0003)**

Fit statistics

 − 2 Log-likelihood

− 1004.6

Note: maximum likelihood estimates are reported for RIT RTCV across years since retreat (YSR) in retreat 2 training (n = 19) participants. Age is centered to postassessment and 65 years. Hours of practice are scaled to 100 h per unit. Standard errors are reported in parentheses

2denotes a quadratic parameter

*p < .05; **p < .01

Fig. 6

Model estimates of reaction time variability (RTCV) at low (1250 h), medium (2000 h), and high (2750 h) levels of practice hours as a function of age for retreat 2 training group participants

Finally, intensive retreat practice (in days) over the follow-up period was examined as a predictor of A and RTCV. Although there were no significant effects on performance accuracy, more reported days on retreat over follow-up was a marginally significant predictor of lower overall RTCV, β = − .00007, p = .058. There were no significant interactions.

Discussion

The present study represents the most extensive longitudinal examination of meditation training-related improvements in sustained attention to date. Using a sustained response inhibition task, performance was examined across six assessment waves over more than a 7-year training and follow-up interval. We observed robust improvements in perceptual discrimination, response inhibition, vigilance, and RTCV across meditation retreat assessments, and extended our prior investigation (Sahdra et al. 2011) to examine the long-term maintenance of training-related improvements. We observed no significant changes in response inhibition accuracy across the 7-year follow-up interval, and improvements were maintained above half the level of overall training gains for several years following the end of retreat. Furthermore, aging-related performance deficits were moderated by continued meditation practice: older participants who reported engaging in more meditation practice following formal training demonstrated attenuated aging-related performance deficits.

Our previous report (Sahdra et al. 2011) detailed relations between increases in performance accuracy on retreat and growth in self-reported adaptive psychological functioning. In the present study, we incorporated reaction time variability as an additional outcome of training, reporting significant reductions in RTCV across both intensive retreat interventions. These findings appear to generalize to other training styles and periods of intensive training (i.e., 1-month training; Zanesco et al. 2013), and provide additional support to the growing body of evidence that meditation training influences the stability of goal-directed attention. Increased stability of attention is a central organizing feature of the benefits of many meditation training regimens (Lutz et al. 2015). Measures of attentional stability, including reaction time variability, therefore hold promise for informing emerging models of the distinctive phenomenological qualities and neurocognitive processes that characterize meditation-related development of cognitive capacities.

Attempts to sustain attention over time can impose system-wide cognitive consequences on processes underlying performance on tasks like the RIT, including discrimination of perceptually challenging stimuli, inhibition of competing response tendencies, and maintenance of attention in an ongoing and stable manner. Consistent with theories of resource depletion (Langner and Eickhoff 2013), our findings support the well-characterized decline in perceptual sensitivity (i.e., performance accuracy) observed in tasks of sustained attention, and further suggest that increases in reaction time variability across task duration are a measurable behavioral consequence of sustaining attention (Wang et al. 2014; Zanesco et al. 2013). This increased variability may reflect graded variation in participants’ ability to maintain attention and regulate behavior over time, or increases in the frequency or disruptiveness of task-unrelated thought (Seli et al. 2013). Importantly, however, training was associated with attenuated within-task performance decrements for accuracy only.

Data characterizing the long-term maintenance of meditation-related improvements are critical for understanding the generalized benefits of contemplative or mindfulness-based approaches to cognitive training. We employed growth curve models to examine separable sources of change across an extensive longitudinal duration: changes over the course of retreat, changes over years since retreat, and changes associated with aging. Using this approach, we observed distinct patterns of maintenance across dependent measures. No significant changes in response inhibition accuracy were observed over the 7-year follow-up period for either retreat intervention. Moreover, equivalence tests supported the assertion that performance accuracy was definitively maintained for several years following retreat; the accumulated change in accuracy was significantly smaller than any meaningful amount (or half the total improvement accrued during retreat) up to 5 years later, demonstrating the durability of training effects well beyond the intervention itself.

The vigilance decrement and the within-task increase in RTCV were attenuated across years of follow-up for retreat 1, whereas we observed no significant changes in vigilance across follow-up for retreat 2. Improvements in perceptual discrimination, however, were lost at a gradual rate over years of follow-up, while improvements in RTCV observed in both retreats were lost shortly following the end of training. It is possible that measures of accuracy and vigilance reflect components of sustained attention that are more robust to long-term maintenance than reaction time variability. Once improved through training, cognitive capacities relating to the global control of attention, target detection, stimulus processing, and response execution may endure to a greater degree than those supporting reductions in ongoing attentional and behavioral fluctuations. It is also presently unclear how factors relating to the training intervention itself, such as individual differences in duration and intensity of practice during the retreat, may have supported long-term maintenance. Clearly, more research is needed to better clarify the relative susceptibility of attentional markers to training interventions.

Growth curve models are characterized by higher levels of statistical power than more traditional analyses (e.g., mean comparisons between assessment waves; Muthén and Curran 1997), and offer analytic advantages when measurement intervals vary between assessments or individuals, or when individuals lack complete data across measurement occasions. Nevertheless, limited sample variability may have reduced our ability to detect significant changes in some parameters over the course of the 7-year follow-up, or to observe direct associations between maintenance of training improvements and continued meditation practice. For example, it is possible that additional assessment waves or greater sampling density may have increased our ability to statistically detect longitudinal changes in accuracy over the follow-up. Moreover, our sample was comprised of experienced meditators who all engaged in considerable amounts of ongoing practice. Future studies should therefore investigate associations between performance and practice hours using samples with greater variability in practice times, or with designs that encourage practitioners to engage in different amounts or styles of practice after periods of formal training to better explore the association between continued practice and maintenance. Finally, procedurally altering the stimulus parameterization at the 7-year follow-up for the retreat 2 group may have partially confounded longitudinal estimates. However, while there was a noticeable drop in performance accuracy between the 1.5- and 7-year assessments, levels of accuracy at 1.5 years were nearly identical to those at the conclusion of retreat.

Consistent with prior research (e.g., Fortenbaugh et al. 2015), we observed curvilinear age-related deficits in RTCV, such that reaction time variability improved through middle-age then declined in later life. In contrast, no age-related declines were found for performance accuracy overall. These findings are in line with cross-sectional evidence noting a relative lack of negative association between age and cognition in meditation practitioners (Gard et al. 2014). Indeed, continued meditation practice appeared to moderate aging effects in performance accuracy and RTCV in our sample. Although older individuals failed to maintain training-related accuracy improvements on average, older practitioners reporting larger amounts of continued practice maintained improvements over the follow-up. These findings provide initial, yet provocative, evidence that continued meditation practice may be associated with a moderation of age-related decline in attentional components known to be sensitive to aging (Fortenbaugh et al. 2015; MacDonald et al. 2006; Smittenaar et al. 2015).

Taken together, the procedural differences in threshold parameterization across our interventions highlight an interesting dichotomy between corrective approaches for ameliorating aging-related cognitive deficits. One approach is to tailor demanding tasks to match individuals’ cognitive capabilities, thereby countering or offsetting losses attributable to age-related decline; an alternative approach might attempt targeted improvement of cognitive deficits through cognitive training, meditation, or related interventions. The present findings offer tentative evidence that age-related influences on response inhibition accuracy and reaction time variability may be buffered through both of these mechanisms, at least among experienced practitioners: in retreat 1, we observed no age-related decline in training participants when the resource demands of the task were adaptively adjusted across assessments to an individual’s performance threshold; in retreat 2—when external demands were held constant—we observed a typical pattern of age-related decline, which was moderated by levels of continued meditation practice.

It is possible that other aspects of participants’ lifestyle or personality might have contributed to the observed moderation of age-related deficits by continued meditation practice. Although groups were matched on multiple demographic and personality factors prior to study onset (see MacLean et al. 2010), our sample presumably differed from the general population on various attributes relevant to ongoing cognitive health. Indeed, socio-economic status and other lifestyle factors have long been thought to influence the rate of cognitive decline across the lifespan, motivating researchers to investigate these factors as potential targets for intervention. Yet recent work has suggested otherwise (e.g., Early et al. 2013; Salthouse 2014), in that lifestyle factors may primarily influence individuals’ baseline scores, rather than rates of cognitive decline. Nevertheless, causation cannot be attributed to the moderation of aging-related decline with continued meditation practice in our sample. It is therefore critical that more research is conducted before advocating meditation practice as an intervention for cognitive aging.

Indirectly, our findings also present a sobering appraisal of the viability of short-term or non-intensive mindfulness interventions for improving sustained attention in a lasting manner. The participants in our sample were experienced practitioners who engaged in amounts of practice across the 7-year follow-up far in excess of standardized mindfulness-based interventions (Creswell 2017), which are clearly not feasible for the wide application of interventions targeting cognitive aging. Although participants reported engaging in periods of intensive retreat practice—as well as non-intensive daily practice—across the 7-year follow-up interval, systematic group-level improvements were largely constrained to the targeted 3-month intervention. These findings support the principle that continued practice over long-term intervals (even large amounts of regular practice across 7 years’ time as in our sample) may not be sufficient to improve sustained attention in experienced practitioners. Instead, periods of intensive training, coupled with well-timed assessments, may be necessary to produce and reveal robust and lasting cognitive improvements. In contrast to these group-wide patterns, we observed significant individual differences in the rates of change across the 7-year follow-up, indicating that performance improved over time for some individuals. Future research should continue to investigate the factors that underlie long-term maintenance and cognitive change.

In conclusion, the present study suggests that intensive and continued meditation is associated with enduring improvements in sustained attention, supporting the notion that the cognitive benefits of dedicated mental training may persist over the long-term when promoted by a regimen of continued practice. Although participants did not generally improve over years of daily meditation practice, continued meditation appears to benefit practitioners by preserving gains accrued during periods of intensive formal training and by altering trajectories of age-related cognitive decline. Continued meditation practice seems to be associated with substantial experiential and developmental influences on practitioners’ attentional capacities over the lifespan. These findings have broad implications for meditation and mindfulness-based approaches to cognitive training and raise important questions regarding the limits of meditation practice on the plasticity of human cognition.

Footnotes

  1. 1.

    One wait-list control participant withdrew prior to retreat 2 for reasons unrelated to the intervention.

  2. 2.

    The full RIT was administered at all assessments, excluding the 2-year follow-up assessment for retreat 1 training participants (see Table 1 and “Follow-up Assessments” section in Method).

  3. 3.

    Target length at the 7-year assessment did not significantly differ from the pre-set threshold used at all other assessments for retreat 2 participants, t(22) = 0.45, p = .658.

Notes

Acknowledgements

We thank Jennifer Pokorny, Stephen Aichele, Tonya Jacobs, David Bridwell, Quinn Conklin, and Sarah Huffman for their help in collecting a portion of these follow-up data. Major support for original data collection and follow-up analyses were provided by Fetzer Institute Grant #2191 and John Templeton Foundation Grant #39970 to C.D.S., gifts from the Hershey Family, Baumann, Tan Teo, Yoga Science, and Mental Insight Foundations, anonymous and other donors all to C.D.S., and the Santa Barbara Institute for Consciousness Studies.

Compliance with Ethical Standards

Conflict of Interest

The authors declare that they have no conflict of interest.

References

  1. Adam, K. C. S., Mance, I., Fukuda, K., & Vogel, E. (2015). The contribution of attentional lapses to individual differences in visual working memory capacity. Journal of Cognitive Neuroscience, 27, 1601–1616.  https://doi.org/10.1162/jocn_a_00811.CrossRefPubMedCentralPubMedGoogle Scholar
  2. Anguera, J. A., Boccanfuso, J., Rintoul, J. L., Al-Hashimi, O., Faraji, F., Janowich, J., ... Gazzaley, A. (2013). Video game training enhances cognitive control in older adults. Nature, 501, 97-101.  https://doi.org/10.1038/nature12486.CrossRefPubMedCentralPubMedGoogle Scholar
  3. Bavelier, D., & Davidson, R. J. (2013). Brain training: games to do you good. Nature, 494, 425–426.  https://doi.org/10.1038/494425a.CrossRefPubMedGoogle Scholar
  4. Bellgrove, M. A., Hester, R., & Garavan, H. (2004). The functional neuroanatomical correlates of response variability: evidence from a response inhibition task. Neuropsychologia, 42, 1910–1916.CrossRefPubMedGoogle Scholar
  5. Cheyne, J. A., Solman, G. J. F., Carriere, J. S. A., & Smilek, D. (2009). Anatomy of an error: a bidirectional state model of task engagement/disengagement and attention-related errors. Cognition, 111, 98–113.  https://doi.org/10.1016/j.cognition.2008.12.009.CrossRefGoogle Scholar
  6. Creswell, J. D. (2017). Mindfulness interventions. Annual Review of Psychology, 68, 491–516.CrossRefPubMedGoogle Scholar
  7. Dahl, C. J., Lutz, A., & Davidson, R. J. (2015). Reconstructing and deconstructing the self: cognitive mechanisms in meditation practice. Trends in Cognitive Science, 19, 515–523.CrossRefGoogle Scholar
  8. Early, D. R., Widaman, K. F., Harvey, D., Beckett, L., Park, L. Q., Farias, ... Mungas, D. (2013). Demographic predictors of cognitive change in ethnically diverse older persons. Psychology and Aging, 28, 633-645.Google Scholar
  9. Ferrer, E., & McArdle, J. J. (2010). Longitudinal modeling of developmental changes in psychological research. Current Directions in Psychological Science, 19, 149–154.CrossRefGoogle Scholar
  10. Fortenbaugh, F. C., DeGutis, J., Germine, L., Wilmer, J. B., Grosso, M., Russo, K., & Esterman, M. (2015). Sustained attention across the life span in a sample of 10,000: dissociating ability and strategy. Psychological Science, 26, 1497–1510.  https://doi.org/10.1177/0956797615594896.CrossRefPubMedCentralPubMedGoogle Scholar
  11. Fortenbaugh, F. C., DeGutis, J., & Esterman, M. (2017). Recent theoretical, neural, and clinical advances in sustained attention research. Annals of the New York Academy of Sciences.  https://doi.org/10.1111/nyas.13318.
  12. Gard, T., Hölzel, B. K., & Lazar, S. W. (2014). The potential effects of meditation on age-related cognitive decline: a systematic review. Annals of the New York Academy of Sciences, 130, 89–103.  https://doi.org/10.1111/nyas.12348.CrossRefGoogle Scholar
  13. Gunaratana, B. H. (2011). Mindfulness in plain English. Somerville: Wisdom Publications.Google Scholar
  14. Hoffman, L. (2015). Longitudinal analysis: modeling within-person fluctuation and change. New York: Routledge.Google Scholar
  15. Jha, A. P., Morrison, A. B., Dainer-Best, J., Parker, S., Rostrup, N., & Stanley, E. (2015). Minds “at attention”: mindfulness training curbs attentional lapses in military cohorts. PLoS One, 10, 1–19.  https://doi.org/10.1371/journal.pone.0116889.Google Scholar
  16. Kurth, F., Cherbuin, N., & Luders, E. (2017). Aging mindfully to minimize cognitive decline. Journal of Cognitive Enhancement, 1, 108–114.  https://doi.org/10.1007/s41465-017-0027-2.CrossRefGoogle Scholar
  17. Lakens, D. (2017). Equivalence tests: a practical primer for t tests, correlations, and meta-analyses. Social Psychological and Personality Science, 8, 355–362.CrossRefPubMedCentralPubMedGoogle Scholar
  18. Laneri, D., Schuster, V., Dietsche, B., Jansen, A., Ott, U., & Sommer, J. (2016). Effects of longterm mindfulness meditation on brain's white matter microstructure and its aging. Frontiers in Aging Neuroscience, 7, 254.  https://doi.org/10.3389/fnagi.2015.00254.
  19. Langner, R., & Eickhoff, S. B. (2013). Sustaining attention to simple tasks: a meta-analytic review of the neural mechanisms of vigilant attention. Psychological Bulletin, 139, 870–900.  https://doi.org/10.1037/a0030694.CrossRefPubMedGoogle Scholar
  20. Lippelt, D. P., Hommel, B., & Colzato, L. S. (2014). Focused attention, open-monitoring and loving kindness meditation: effects on attention, conflict monitoring, and creativity—a review. Frontiers in Human Neuroscience, 5, 1083.  https://doi.org/10.3389/fpsyg.2014.01083.Google Scholar
  21. Lustig, C., & Jantz, T. (2015). Questions of age differences in interference control: when and how, not if? Brain Research, 1612, 59–69.CrossRefPubMedGoogle Scholar
  22. Lutz, A., Slagter, H. A., Dunne, J. D., & Davidson, R. J. (2008). Attention regulation and monitoring in meditation. Trends in Cognitive Sciences, 12, 163–169.  https://doi.org/10.1016/j.tics.2008.01.005.CrossRefPubMedCentralPubMedGoogle Scholar
  23. Lutz, A., Slagter, H. A., Rawlings, N. B., Francis, A. D., Greischar, L. L., & Davidson, R. J. (2009). Mental training enhances attentional stability: neural and behavioral evidence. The Journal of Neuroscience, 29, 13418–13427.  https://doi.org/10.1523/JNEUROSCI.1614-09.2009.CrossRefPubMedCentralPubMedGoogle Scholar
  24. Lutz, A., Jha, A. P., Dunne, J. D., & Saron, C. D. (2015). Investigating the phenomenological matrix of mindfulness-related practices from a neurocognitive perspective. American Psychologist, 70, 632–658.  https://doi.org/10.1037/a0039585.CrossRefPubMedCentralPubMedGoogle Scholar
  25. MacDonald, S. W., Nyberg, L., & Backman, L. (2006). Intra-individual variability in behavior: links to brain structure, neurotransmission and neuronal activity. Trends in Neuroscience, 29, 474–480.CrossRefGoogle Scholar
  26. Mackworth, N. H. (1948). The breakdown of vigilance during prolonged visual search. Quarterly Journal of Experimental Psychology, 1, 6–21.CrossRefGoogle Scholar
  27. MacLean, K. A., Aichele, S. R., Bridwell, D. A., Mangun, G. R., Wojciulik, E., & Saron, C. D. (2009). Interactions between endogenous and exogenous attention during vigilance. Attention, Perception, & Psychophysics, 71, 1042–1058.  https://doi.org/10.3758/APP.71.5.1042.CrossRefGoogle Scholar
  28. MacLean, K. A., Ferrer, E., Aichele, S. R., Bridwell, D. A., Zanesco, A. P., Jacobs, T. L., ... Saron, C. D. (2010). Intensive meditation training improves perceptual discrimination and sustained attention. Psychological Science, 21, 829-839.  https://doi.org/10.1177/0956797610371339.CrossRefPubMedCentralPubMedGoogle Scholar
  29. Malinowski, P., & Shalamanova, L. (2017). Meditation and cognitive ageing: the role of mindfulness meditation in building cognitive reserve. Journal of Cognitive Enhancement, 1, 96–106.  https://doi.org/10.1007/s41465-017-0022-7.CrossRefGoogle Scholar
  30. Malinowski, P., Moore, A. W., Mead, B. R., & Gruber, T. (2017). Mindful aging: the effects of regular brief mindfulness practice on electrophysiological markers of cognitive and affective processing in older adults. Mindfulness.  https://doi.org/10.1007/s12671-015-0482-8.
  31. Morrison, A. B., Goolsarran, M., Rogers, S. L., & Jha, A. P. (2014). Taming a wandering attention: short-form mindfulness training in student cohorts. Frontiers in Human Neuroscience, 7, 897.  https://doi.org/10.3389/fnhum.2013.00897.CrossRefPubMedCentralPubMedGoogle Scholar
  32. Mrazek, M. D., Franklin, M. S., Phillips, D. T., Baird, B., & Schooler, J. W. (2013). Mindfulness training improves working memory capacity and GRE performance while reducing mind wandering. Psychological Science, 24, 776–781.  https://doi.org/10.1177/0956797612459659.CrossRefPubMedGoogle Scholar
  33. Muthén, B. O., & Curran, P. (1997). General longitudinal modeling of individual differences in experimental designs: a latent variable framework for analysis and power estimation. Psychological Methods, 2, 371–402.CrossRefGoogle Scholar
  34. Park, D. C., Lodi-Smith, J., Drew, L., Haber, S., Hebrank, A., Bischof, G. N., & Aamodt, W. (2014). The impact of sustained engagement on cognitive function in older adults: the synapse project. Psychological Science, 25, 103–112.  https://doi.org/10.1177/0956797613499592.CrossRefPubMedGoogle Scholar
  35. Rosenberg, E. L., Zanesco, A. P., King, B. G., Aichele, S. R., Jacobs, T. L., Bridwell, D. A., … Saron, C. D. (2015). Intensive meditation training influences emotional responses to suffering. Emotion, 15, 775-790.  https://doi.org/10.1037/emo0000080.
  36. Sahdra, B. K., MacLean, K. A., Ferrer, E., Shaver, P. R., Rosenberg, E. L., Jacobs, T. L., ... Saron, C. D. (2011). Enhanced response inhibition during intensive meditation training predicts improvements in self-reported adaptive socioemotional functioning. Emotion, 11, 299-312.  https://doi.org/10.1037/a0022764.CrossRefPubMedGoogle Scholar
  37. Salthouse, T. A. (2014). Correlates of cognitive change. Journal of Experimental Psychology: General, 143, 1026–1048.CrossRefGoogle Scholar
  38. See, J. E., Howe, S. R., Warm, J. S., & Dember, W. N. (1995). Meta-analysis of the sensitivity decrement in vigilance. Psychological Bulletin, 117, 230–249.CrossRefGoogle Scholar
  39. Seli, P., Cheyne, J. A., & Smilek, D. (2013). Wandering minds and wavering rhythms: linking mind wandering and behavioral variability. Journal of Experimental Psychology: Human Perception and Performance, 39, 1–5.  https://doi.org/10.1037/a0030954.PubMedGoogle Scholar
  40. Slagter, H. A., Davidson, R. J., & Lutz, A. (2011). Mental training as a tool in the neuroscientific study of brain and cognitive plasticity. Frontiers in Human Neuroscience, 5, 17.  https://doi.org/10.3389/fnhum.2011.00017.CrossRefPubMedCentralPubMedGoogle Scholar
  41. Smallwood, J., & Schooler, J. W. (2015). The science of mind wandering: empirically navigating the stream of consciousness. Annual Review of Psychology, 66, 487–518.  https://doi.org/10.1146/annurev-psych-010814-015331.CrossRefPubMedGoogle Scholar
  42. Smittenaar, P., Rutledge, R. B., Zeidman, P., Adams, R. A., Brown, H., Lewis, G., & Dolan, R. (2015). Proactive and reactive response inhibition across the lifespan. PLoS One, 10.  https://doi.org/10.1371/journal.pone.0140383.
  43. Sperduti, M., Makowski, D., & Piolino, P. (2016). The protective role of long-term meditation on the decline of the executive component of attention in aging: a preliminary cross-sectional study. Aging, Neuropsychology, and Cognition, 23, 691–702.  https://doi.org/10.1080/13825585.2016.1159652.CrossRefGoogle Scholar
  44. Taylor, M. M., & Creelman, C. D. (1967). PEST: efficient estimates on probability functions. The Journal of the Acoustical Society of America, 41, 782–787.CrossRefGoogle Scholar
  45. Thomson, D. R., Besner, D., & Smilek, D. (2015). A resource-control account of sustained attention: evidence from mind-wandering and vigilance paradigms. Perspectives on Psychological Science, 10, 82–96.  https://doi.org/10.1177/1745691614556681.CrossRefPubMedGoogle Scholar
  46. Toril, P., Reales, J. M., & Ballesteros, S. (2014). Video game training enhances cognition of older adults: a meta-analytic study. Psychology and Aging, 29, 706–716.CrossRefPubMedGoogle Scholar
  47. Vago, D. R., & Silbersweig, D. A. (2012). Self-awareness, self-regulation, and self-transcendence (S-ART): a framework for understanding the neurobiological mechanisms of mindfulness. Frontiers in Human Neuroscience, 6, 296.  https://doi.org/10.3389/fnhum.2012.00296.CrossRefPubMedCentralPubMedGoogle Scholar
  48. van Leeuwen, S., Müller, N. G., & Melloni, L. (2009). Age effects on attentional blink performance in meditation. Consciousness and Cognition, 18, 593–599.CrossRefPubMedGoogle Scholar
  49. van Vugt, M. K., & Jha, A. P. (2011). Investigating the impact of mindfulness meditation training on working memory: a mathematical modeling approach. Cognitive Affective Behavioral Neuroscience, 11, 344–353.  https://doi.org/10.3758/s13415-011-0048-8.CrossRefGoogle Scholar
  50. Vasquez, B. P., Binns, M. A., & Anderson, N. D. (2014). Staying on task: age-related changes in the relationship between executive functioning and response time consistency. Journals of Gerontology: Psychological Sciences, 71, 189–200.  https://doi.org/10.1093/geronb/gbu140.CrossRefGoogle Scholar
  51. Wallace, B. A. (1999). The Buddhist tradition of Samatha: methods for refining and examining consciousness. Journal of Consciousness Studies, 6, 175–187.Google Scholar
  52. Wallace, B. A. (2006). The attention revolution. Boston: Wisdom Publications.Google Scholar
  53. Wallace, B. A. (2011). Stilling the mind: Shamatha teachings from Dudjom Lingpa’s Vajra essence. Boston: Wisdom Publications.Google Scholar
  54. Wang, C., Ding, M., & Kluger, B. M. (2014). Change in intraindividual variability over time as a key metric for defining performance-based cognitive fatigability. Brain and Cognition, 85, 251–258.CrossRefPubMedCentralPubMedGoogle Scholar
  55. Warm, J. S., Parasuraman, R., & Matthews, G. (2008). Vigilance requires hard mental work and is stressful. Human Factors, 50, 433–441.  https://doi.org/10.1518/001872008X312152.CrossRefPubMedGoogle Scholar
  56. Weissman, D. H., Roberts, K. C., Visscher, K. M., & Woldorff, M. G. (2006). The neural bases of momentary lapses in attention. Nature Neuroscience, 9, 971–978.  https://doi.org/10.1038/nn1727.CrossRefPubMedGoogle Scholar
  57. West, R., Murphy, K. J., Armilio, M. L., Craik, F. I. M., & Stuss, D. T. (2002). Lapses of intention and performance variability reveal age-related increases in fluctuations of executive control. Brain and Cognition, 49, 402–419.  https://doi.org/10.1006/brcg.2001.1507.CrossRefPubMedGoogle Scholar
  58. Zanesco, A. P., King, B. G., MacLean, K. A., & Saron, C. D. (2013). Executive control and felt concentrative engagement following intensive meditation training. Frontiers in Human Neuroscience, 7, 566.  https://doi.org/10.3389/fnhum.2013.00566.CrossRefPubMedCentralPubMedGoogle Scholar
  59. Zanesco, A. P., King, B. G., MacLean, K. A., Jacobs, T. L., Aichele, S. R., Wallace, B. A., ... Saron, C. D. (2016). Meditation training influences mind wandering and mindless reading. Psychology of Consciousness: Theory, Research, and Practice, 3, 12-33.  https://doi.org/10.1037/cns0000082.Google Scholar
  60. Zhang, J., & Mueller, S. T. (2005). A note on ROC analysis and non-parametric estimate of sensitivity. Psychometrika, 70(1), 145–154.CrossRefGoogle Scholar

Copyright information

© The Author(s) 2018

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  • Anthony P. Zanesco
    • 1
  • Brandon G. King
    • 2
    • 3
  • Katherine A. MacLean
    • 3
  • Clifford D. Saron
    • 3
    • 4
  1. 1.Department of PsychologyUniversity of MiamiCoral GablesUSA
  2. 2.Department of PsychologyUniversity of California, DavisDavisUSA
  3. 3.Center for Mind and BrainUniversity of California, DavisDavisUSA
  4. 4.The MIND InstituteUniversity of California, DavisDavisUSA

Personalised recommendations