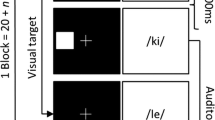
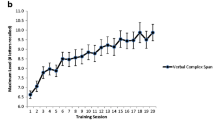
Abstract
Working memory (WM) is the ability to maintain and manipulate task-relevant information in the absence of sensory input. While its improvement through training is of great interest, the degree to which WM training transfers to untrained WM tasks (near transfer) and other untrained cognitive skills (far transfer) remains debated and the mechanism(s) underlying transfer are unclear. Here we hypothesized that a critical feature of dual n-back training is its reliance on maintaining relational information in WM. In experiment 1, using an individual differences approach, we found evidence that performance on an n-back task was predicted by performance on a measure of relational WM (i.e., WM for vertical spatial relationships independent of absolute spatial locations), whereas the same was not true for a complex span WM task. In experiment 2, we tested the idea that reliance on relational WM is critical to produce transfer from n-back but not complex span task training. Participants completed adaptive training on either a dual n-back task, a symmetry span task, or on a non-WM active control task. We found evidence of near transfer for the dual n-back group; however, far transfer to a measure of fluid intelligence did not emerge. Recording EEG during a separate WM transfer task, we examined group-specific, training-related changes in alpha power, which are proposed to be sensitive to WM demands and top-down modulation of WM. Results indicated that the dual n-back group showed significantly greater frontal alpha power after training compared to before training, more so than both other groups. However, we found no evidence of improvement on measures of relational WM for the dual n-back group, suggesting that near transfer may not be dependent on relational WM. These results suggest that dual n-back and complex span task training may differ in their effectiveness to elicit near transfer as well as in the underlying neural changes they facilitate.











Similar content being viewed by others
Notes
The Symmetry Span task traditionally yields two scores: “partial” and “absolute.” Here we focused on partial scores as these have been shown to have higher internal consistency than absolute scores (e.g., Conway et al. 2005).
Variation in payment arose from participants receiving a completion bonus of $15 upon completing all study sessions and maintaining above chance level performance during training (e.g., two consecutive sessions of average performance below chance for each training task resulted in the participant not receiving the bonus). Participants were aware of the contingencies of this bonus.
Our adaptivity criteria for the DNBT is a departure from that used by Jaeggi et al. (2008) and many subsequent studies using this paradigm for training. In Jaeggi et al. (2008), with 12 targets per block (same as used here), if participants made fewer than three mistakes per modality they advanced to the next n-level. Thus, accuracy was considered separately for each modality. Here, we considered accuracy across both modalities for our cutoff values. In the present study, participants had to perform above 85% on both modalities considered together to move up an n-level. This more stringent criteria likely explains why our participants on average did not advance as far up the n-levels as some previous studies (see Fig. 8) as it would have been more difficult to advance up a level and easier to fall back down a level with this criteria.
The direction of the effects and significance remain unchanged when the analyses are tested on all 72 participants that completed both pre- and post-training EEG sessions.
References
Ackerman, C. M., & Courtney, S. M. (2012). Spatial relations and spatial locations are dissociated within prefrontal and parietal cortex. Journal of Neurophysiology, 108(9), 2419–2429. https://doi.org/10.1152/jn.01024.2011.
Au, J., Sheehan, E., Tsai, N., Duncan, G. J., Buschkuehl, M., & Jaeggi, S. M. (2015). Improving fluid intelligence with training on working memory: A meta-analysis. Psychonomic Bulletin & Review, 22(2), 366–377. https://doi.org/10.3758/s13423-014-0699-x.
Badre, D. (2008). Cognitive control, hierarchy, and the rostro-caudal organization of the frontal lobes. Trends in Cognitive Sciences, 12(5), 193–200. https://doi.org/10.1016/J.Tics.2008.02.004.
Bahlmann, J., Blumenfeld, R. S., & D'Esposito, M. (2014). The rostro-caudal axis of frontal cortex is sensitive to the domain of stimulus information. Cerebral Cortex. https://doi.org/10.1093/cercor/bht419.
Bastiaansen, M., Mazaheri, A., & Jensen, O. (2012). Beyond ERP’s: Oscillatory neuronal dynamics. In S. J. Luck & E. S. Kappenman (Eds.), The Oxford handbook of event-related potential components. USA: Oxford University Press.
Beatty, E. L., Jobidon, M. E., Bouak, F., Nakashima, A., Smith, I., Lam, Q., et al. (2015). Transfer of training from one working memory task to another: Behavioural and neural evidence. Frontiers in Systems Neuroscience, 9, 86. https://doi.org/10.3389/fnsys.2015.00086.
Berryhill, M. E., Peterson, D. J., Jones, K. T., & Stephens, J. A. (2014). Hits and misses: Leveraging tDCS to advance cognitive research. Frontiers in Psychology, 5, 800. https://doi.org/10.3389/fpsyg.2014.00800.
Blacker, K. J., & Courtney, S. M. (2016). Distinct neural substrates for maintaining spatial locations and relations in working memory. Frontiers in Human Neuroscience, 10, 594. https://doi.org/10.3389/fnhum.2016.00594.
Blacker, K. J., Ikkai, A., Lakshmanan, B. M., Ewen, J. B., & Courtney, S. M. (2016). The role of alpha oscillations in deriving and maintaining spatial relations in working memory. Cognitive Affective & Behavioral Neuroscience, 16(5), 888–901. https://doi.org/10.3758/s13415-016-0439-y.
Blacker, K. J., Weisberg, S. M., Newcombe, N. S., & Courtney, S. M. (2017). Keeping track of where we are: Spatial working memory in navigation. Visual Cognition, 1–12. https://doi.org/10.1080/13506285.2017.1322652.
Bonnefond, M., & Jensen, O. (2012). Alpha oscillations serve to protect working memory maintenance against anticipated distracters. Current Biology, 22(20), 1969–1974. https://doi.org/10.1016/j.cub.2012.08.029.
Boot, W. R., Blakely, D. P., & Simons, D. J. (2011). Do action video games improve perception and cognition? Frontiers in Psychology, 2(226), 1–6. https://doi.org/10.3389/fpsyg.2011.00226.
Boot, W. R., Simons, D. J., Stothart, C., & Stutts, C. (2013). The pervasive problem of placebos in psychology: Why active control groups are not sufficient to rule out placebo effects. Perspectives on Psychological Science, 8(4), 445–454. https://doi.org/10.1177/1745691613491271.
Brainard, D. H. (1997). The psychophysics toolbox. Spatial Vision, 10(4), 433–436.
Buschkuehl, M., Hernandez-Garcia, L., Jaeggi, S. M., Bernard, J. A., & Jonides, J. (2014). Neural effects of short-term training on working memory. Cognitive, Affective, & Behavioral Neuroscience, 14(1), 147–160. https://doi.org/10.3758/s13415-013-0244-9.
Carpenter, P. A., Just, M. A., & Shell, P. (1990). What one intelligence test measures: A theoretical account of the processing in the raven progressive matrices test. Psychological Review, 97(3), 404–431.
Chein, J. M., & Morrison, A. B. (2010). Expanding the mind's workspace: Training and transfer effects with a complex working memory span task. Psychonomic Bulletin & Review, 17(2), 193–199. https://doi.org/10.3758/PBR.17.2.193.
Chiesa, A., Calati, R., & Serretti, A. (2011). Does mindfulness training improve cognitive abilities? A systematic review of neuropsychological findings. Clinical Psychology Review, 31(3), 449–464. https://doi.org/10.1016/j.cpr.2010.11.003.
Chooi, W. T., & Thompson, L. A. (2012). Working memory training does not improve intelligence in healthy young adults. Intelligence, 40(6), 531–542. https://doi.org/10.1016/J.Intell.2012.07.004.
Cole, M. W., Bagic, A., Kass, R., & Schneider, W. (2010). Prefrontal dynamics underlying rapid instructed task learning reverse with practice. Journal of Neuroscience, 30(42), 14245–14254. https://doi.org/10.1523/Jneurosci.1662-10.2010.
Colom, R., Roman, F. J., Abad, F. J., Shih, P. C., Privado, J., Froufe, M., et al. (2013). Adaptive n-back training does not improve fluid intelligence at the construct level: Gains on individual tests suggest that training may enhance visuospatial processing. Intelligence, 41(5), 712–727. https://doi.org/10.1016/J.Intell.2013.09.002.
Conway, A. R., Kane, M. J., Bunting, M. F., Hambrick, D. Z., Wilhelm, O., & Engle, R. W. (2005). Working memory span tasks: A methodological review and user’s guide. Psychonomic Bulletin & Review, 12(5), 769–786.
Cusack, R., Lehmann, M., Veldsman, M., & Mitchell, D. J. (2009). Encoding strategy and not visual working memory capacity correlates with intelligence. Psychonomic Bulletin & Review, 16(4), 641–647. https://doi.org/10.3758/PBR.16.4.641.
Engle, R. W., Tuholski, S. W., Laughlin, J. E., & Conway, A. R. A. (1999). Working memory, short-term memory, and general fluid intelligence. Journal of Experimental Psychology: General, 128(3), 309–331.
Fan, J., McCandliss, B. D., Sommer, T., Raz, A., & Posner, M. I. (2002). Testing the efficiency and independence of attentional networks. Journal of Cognitive Neuroscience, 14(3), 340–347. https://doi.org/10.1162/089892902317361886.
Foster, J. J., Sutterer, D. W., Serences, J. T., Vogel, E. K., & Awh, E. (2016). The topography of alpha-band activity tracks the content of spatial working memory. Journal of Neurophysiology, 115(1), 168–177. https://doi.org/10.1152/jn.00860.2015.
Green, C. S., Gorman, T., & Bavelier, D. (2016). Action video-game training and its effects on perception and attentional control. In T. Strobach & J. Karbach (Eds.), Cognitive training (pp. 107–116). Switzerland: Springer International Publishing.
Haatveit, B. C., Sundet, K., Hugdahl, K., Ueland, T., Melle, I., & Andreassen, O. A. (2010). The validity of d prime as a working memory index: Results from the “Bergen n-back task”. Journal of Clinical and Experimental Neuropsychology, 32(8), 871–880. https://doi.org/10.1080/13803391003596421.
Haegens, S., Osipova, D., Oostenveld, R., & Jensen, O. (2010). Somatosensory working memory performance in humans depends on both engagement and disengagement of regions in a distributed network. Human Brain Mapping, 31(1), 26–35. https://doi.org/10.1002/hbm.20842.
Herrmann, C. S., Senkowski, D., & Rottger, S. (2004). Phase-locking and amplitude modulations of EEG alpha: Two measures reflect different cognitive processes in a working memory task. Experimental Psychology, 51(4), 311–318. https://doi.org/10.1027/1618-3169.51.4.311.
Hillman, C. H., Erickson, K. I., & Kramer, A. F. (2008). Be smart, exercise your heart: Exercise effects on brain and cognition. Nature Reviews Neuroscience, 9(1), 58–65. https://doi.org/10.1038/nrn2298.
Holmes, J., Gathercole, S. E., & Dunning, D. L. (2009). Adaptive training leads to sustained enhancement of poor working memory in children. Developmental Science, 12(4), F9–F15. https://doi.org/10.1111/j.1467-7687.2009.00848.x.
Hossiep, R., Turck, D., & Hasella, M. (1999). Bochumer Matrizentest (BOMAT) advanced-short version. Gottingen: Hogrefe.
Ikkai, A., Blacker, K. J., Lakshmanan, B. M., Ewen, J. B., & Courtney, S. M. (2014). Maintenance of relational information in working leads to suppression of the sensory cortex. Journal of Neurophysiology, 112(8), 1903–1915. https://doi.org/10.1152/jn.00134.2014.
Jaeggi, S. M., Seewer, R., Nirkko, A. C., Eckstein, D., Schroth, G., Groner, R., & Gutbrod, K. (2003). Does excessive memory load attenuate activation in the prefrontal cortex? Load-dependent processing in single and dual tasks: Functional magnetic resonance imaging study. NeuroImage, 19(2 Pt 1), 210–225.
Jaeggi, S. M., Buschkuehl, M., Jonides, J., & Perrig, W. J. (2008). Improving fluid intelligence with training on working memory. Proceedings of the National Academy of Science, 105(19), 6829–6833. https://doi.org/10.1073/pnas.0801268105.
Jaeggi, S. M., Studer-Luethi, B., Buschkuehl, M., Su, Y. F., Jonides, J., & Perrig, W. J. (2010a). The relationship between n-back performance and matrix reasoning—implications for training and transfer. Intelligence, 38(6), 625–635. https://doi.org/10.1016/J.Intell.2010.09.001.
Jaeggi, S. M., Buschkuehl, M., Perrig, W. J., & Meier, B. (2010b). The concurrent validity of the N-back task as a working memory measure. Memory, 18(4), 394–412. https://doi.org/10.1080/09658211003702171.
Jaeggi, S. M., Buschkuehl, M., Shah, P., & Jonides, J. (2014). The role of individual differences in cognitive training and transfer. Memory & Cognition, 42(3), 464–480. https://doi.org/10.3758/s13421-013-0364-z.
Jausovec, N., & Jausovec, K. (2012). Working memory training: Improving intelligence—changing brain activity. Brain and Cognition, 79(2), 96–106. https://doi.org/10.1016/j.bandc.2012.02.007.
Jensen, O., Gelfand, J., Kounios, J., & Lisman, J. E. (2002). Oscillations in the alpha band (9–12 Hz) increase with memory load during retention in a short-term memory task. Cerebral Cortex, 12(8), 877–882.
Jokisch, D., & Jensen, O. (2007). Modulation of gamma and alpha activity during a working memory task engaging the dorsal or ventral stream. The Journal of Neuroscience, 27(12), 3244–3251. https://doi.org/10.1523/JNEUROSCI.5399-06.2007.
Jonides, J., Schumacher, E. H., Smith, E. E., Lauber, E. J., Awh, E., Minoshima, S., & Koeppe, R. A. (1997). Verbal working memory load affects regional brain activation as measured by PET. Journal of Cognitive Neuroscience, 9(4), 462–475. https://doi.org/10.1162/Jocn.1997.9.4.462.
Kaiser, J., Heidegger, T., Wibral, M., Altmann, C. F., & Lutzenberger, W. (2007). Alpha synchronization during auditory spatial short-term memory. Neuroreport, 18(11), 1129–1132. https://doi.org/10.1097/WNR.0b013e32821c553b.
Kane, M. J., Hambrick, D. Z., Tuholski, S. W., Wilhelm, O., Payne, T. W., & Engle, R. W. (2004). The generality of working memory capacity: A latent-variable approach to verbal and visuospatial memory span and reasoning. Journal of Experimental Psychology: General, 133(2), 189–217. https://doi.org/10.1037/0096-3445.133.2.189.
Kelly, S. P., Lalor, E. C., Reilly, R. B., & Foxe, J. J. (2006). Increases in alpha oscillatory power reflect an active retinotopic mechanism for distracter suppression during sustained visuospatial attention. Journal of Neurophysiology, 95(6), 3844–3851. https://doi.org/10.1152/jn.01234.2005.
Klimesch, W., Sauseng, P., & Hanslmayr, S. (2007). EEG alpha oscillations: The inhibition-timing hypothesis. Brain Research Reviews, 53(1), 63–88. https://doi.org/10.1016/j.brainresrev.2006.06.003.
Klingberg, T., Fernell, E., Olesen, P. J., Johnson, M., Gustafsson, P., Dahlstrom, K., et al. (2005). Computerized training of working memory in children with ADHD—a randomized, controlled trial. Journal of the American Academy of Child and Adolescent Psychiatry, 44(2), 177–186. https://doi.org/10.1097/00004583-200502000-00010.
Kundu, B., Sutterer, D. W., Emrich, S. M., & Postle, B. R. (2013). Strengthened effective connectivity underlies transfer of working memory training to tests of short-term memory and attention. The Journal of Neuroscience, 33(20), 8705–8715. https://doi.org/10.1523/JNEUROSCI.5565-12.2013.
Leung, H. C., Seelig, D., & Gore, J. C. (2004). The effect of memory load on cortical activity in the spatial working memory circuit. Cognitive, Affective, & Behavioral Neuroscience, 4(4), 553–563.
Li, S. C., Schmiedek, F., Huxhold, O., Rocke, C., Smith, J., & Lindenberger, U. (2008). Working memory plasticity in old age: Practice gain, transfer, and maintenance. Psychology and Aging, 23(4), 731–742. https://doi.org/10.1037/a0014343.
Li, C. H., He, X., Wang, Y. J., Hu, Z., & Guo, C. Y. (2017). Visual working memory capacity can be increased by training on distractor filtering efficiency. Frontiers in psychology, 8.
Libby, L. A., Hannula, D. E., & Ranganath, C. (2014). Medial temporal lobe coding of item and spatial information during relational binding in working memory. The Journal of Neuroscience, 34(43), 14233–14242. https://doi.org/10.1523/JNEUROSCI.0655-14.2014.
Linke, A. C., Vincente-Grabovetsy, A., Mitchell, D. J., & Cusack, R. (2011). Encoding strategy accounts for individual differences in change detection measures of VSTM. Neuropsychologia, 49(6), 1476–1486. https://doi.org/10.1016/j.neuropsychologia.2010.11.034.
Lövdén, M., Bäckman, L., Lindenberger, U., Schaefer, S., & Schmiedek, F. (2010). A theoretical framework for the study of adult cognitive plasticity. Psychological Bulletin, 136(4), 659. https://doi.org/10.1037/a0020080.
Luck, S. J., & Vogel, E. K. (1997). The capacity of visual working memory for features and conjunctions. Nature, 390(6657), 279–281. https://doi.org/10.1038/36846.
Lutz, A., Slagter, H. A., Dunne, J. D., & Davidson, R. J. (2008). Attention regulation and monitoring in meditation. Trends in Cognitive Sciences, 12(4), 163–169. https://doi.org/10.1016/j.tics.2008.01.005.
Maris, E., & Oostenveld, R. (2007). Nonparametric statistical testing of EEG- and MEG-data. Journal of Neuroscience Methods, 164(1), 177–190. https://doi.org/10.1016/j.jneumeth.2007.03.024.
McKendrick, R., Ayaz, H., Olmstead, R., & Parasuraman, R. (2014). Enhancing dual-task performance with verbal and spatial working memory training: Continuous monitoring of cerebral hemodynamics with NIRS. NeuroImage, 85(Pt 3), 1014–1026. https://doi.org/10.1016/j.neuroimage.2013.05.103.
Miyake, A., Friedman, N. P., Emerson, M. J., Witzki, A. H., Howerter, A., & Wager, T. D. (2000). The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: A latent variable analysis. Cognitive Psychology, 41(1), 49–100. https://doi.org/10.1006/cogp.1999.0734.
Morrison, A. B., & Chein, J. M. (2011). Does working memory training work? The promise and challenges of enhancing cognition by training working memory. Psychonomic Bulletin and Review, 18, 46–60. https://doi.org/10.3758/s13423-010-0034.
Nichols, T. E., & Holmes, A. P. (2002). Nonparametric permutation tests for functional neuroimaging: A primer with examples. Human Brain Mapping, 15(1), 1–25.
Oostenveld, R., Fries, P., Maris, E., & Schoffelen, J. M. (2011). FieldTrip: open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Computational Intelligence and Neuroscience, 2011, 1.
Parkin, B. L., Ekhtiari, H., & Walsh, V. F. (2015). Non-invasive human brain stimulation in cognitive neuroscience: A primer. Neuron, 87(5), 932–945. https://doi.org/10.1016/j.neuron.2015.07.032.
Pelli, D. G. (1997). The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision, 10(4), 437–442.
Percival, D., & Walden, A. (1993). Spectral analysis for physical applications. Cambridge: Cambridge University Press.
Powers, K. L., Brooks, P. J., Aldrich, N. J., Palladino, M. A., & Alfieri, L. (2013). Effects of video-game play on information processing: A meta-analytic investigation. Psychonomic Bulletin & Review, 20(6), 1055–1079. https://doi.org/10.3758/s13423-013-0418-z.
Redick, T. S., & Lindsey, D. R. (2013). Complex span and n-back measures of working memory: A meta-analysis. Psychonomic Bulletin & Review, 20(6), 1102–1113. https://doi.org/10.3758/s13423-013-0453-9.
Redick, T. S., Broadway, J. M., Meier, M. E., Kuriakose, P. S., Unsworth, N., Kane, M. J., & Engle, R. W. (2012). Measuring working memory capacity with automated complex span tasks. European Journal of Psychological Assessment, 28(3), 164–171. https://doi.org/10.1027/1015-5759/a000123.
Redick, T. S., Shipstead, Z., Harrison, T. L., Hicks, K. L., Fried, D. E., Hambrick, D. Z., et al. (2013). No evidence of intelligence improvement after working memory training: A randomized, placebo-controlled study. Journal of Experimental Psychology-General, 142(2), 359–379. https://doi.org/10.1037/a0029082.
Richmond, L. L., Morrison, A. B., Chein, J. M., & Olson, I. R. (2011). Working memory training and transfer in older adults. Psychology and Aging, 26(4), 813–822. https://doi.org/10.1037/a0023631.
Rogers, R. D., & Monsell, S. (1995). Costs of a predictable switch between simple cognitive tasks. Journal of Experimental Psychology-General, 124(2), 207–231. https://doi.org/10.1037//0096-3445.124.2.207.
Roux, F., & Uhlhaas, P. J. (2013). Working memory and neural oscillations: Alpha-gamma versus theta-gamma codes for distinct WM information? Trends in Cognitive Sciences. https://doi.org/10.1016/j.tics.2013.10.010.
Rudebeck, S. R., Bor, D., Ormond, A., O’Reilly, J. X., & Lee, A. C. H. (2012). A potential spatial working memory training task to improve both episodic memory and fluid intelligence. PLoS One, 7(11). https://doi.org/10.1371/journal.pone.0050431.
Sadaghiani, S., Scheeringa, R., Lehongre, K., Morillon, B., Giraud, A. L., D'Esposito, M., & Kleinschmidt, A. (2012). Alpha-band phase synchrony is related to activity in the fronto-parietal adaptive control network. The Journal of Neuroscience, 32(41), 14305–14310. https://doi.org/10.1523/JNEUROSCI.1358-12.2012.
Salminen, T., Kuhn, S., Frensch, P. A., & Schubert, T. (2016). Transfer after dual n-back training depends on striatal activation change. The Journal of Neuroscience, 36(39), 10198–10213. https://doi.org/10.1523/JNEUROSCI.2305-15.2016.
Sauseng, P., Klimesch, W., Stadler, W., Schabus, M., Doppelmayr, M., Hanslmayr, S., et al. (2005a). A shift of visual spatial attention is selectively associated with human EEG alpha activity. The European Journal of Neuroscience, 22(11), 2917–2926. https://doi.org/10.1111/j.1460-9568.2005.04482.x.
Sauseng, P., Klimesch, W., Schabus, M., & Doppelmayr, M. (2005b). Fronto-parietal EEG coherence in theta and upper alpha reflect central executive functions of working memory. International Journal of Psychophysiology, 57(2), 97–103. https://doi.org/10.1016/j.ijpsycho.2005.03.018.
Schneiders, J. A., Opitz, B., Krick, C. M., & Mecklinger, A. (2011). Separating intra-modal and across-modal training effects in visual working memory: An fMRI investigation. Cerebral Cortex, 21(11), 2555–2564. https://doi.org/10.1093/cercor/bhr037.
Shipstead, Z., Redick, T. S., & Engle, R. W. (2012). Is working memory training effective? Psychological Bulletin, 138(4), 628–654. https://doi.org/10.1037/A0027473.
Simons, D. J., Boot, W. R., Charness, N., Gathercole, S. E., Chabris, C. F., Hambrick, D. Z., & Stine-Morrow, E. A. (2016). Do "brain-training" programs work? Psychological Science in the Public Interest, 17(3), 103–186. https://doi.org/10.1177/1529100616661983.
Stephenson, C. L., & Halpern, D. F. (2013). Improved matrix reasoning is limited to training on tasks with a visuospatial component. Intelligence, 41, 341–357. https://doi.org/10.1016/j.intell.2013.05.006.
Tang, Y. Y., Holzel, B. K., & Posner, M. I. (2015). The neuroscience of mindfulness meditation. Nature Reviews Neuroscience, 16(4), 213–225. https://doi.org/10.1038/nrn3916.
Thompson, T. W., Waskom, M. L., Garel, K. L., Cardenas-Iniguez, C., Reynolds, G. O., Winter, R., et al. (2013). Failure of working memory training to enhance cognition or intelligence. PLoS One, 8(5), e63614. https://doi.org/10.1371/journal.pone.0063614.
Thompson, T. W., Waskom, M. L., & Gabrieli, J. D. (2016). Intensive working memory training produces functional changes in large-scale frontoparietal networks. J Cogn Neurosci, 1–14. doi:https://doi.org/10.1162/jocn_a_00916
Todd, J. J., & Marois, R. (2004). Capacity limit of visual short-term memory in human posterior parietal cortex. Nature, 428(6984), 751–754. https://doi.org/10.1038/nature02466.
Vanderplas, J. M., & Garvin, E. A. (1959). The association value of random shapes. Journal of Experimental Psychology, 57(3), 147–154.
van Gerven, M., Bahramisharif, A., Heskes, T., & Jensen, O. (2009). Selecting features for BCI control based on a covert spatial attention paradigm. Neural Networks, 22(9), 1271–1277.
Vartanian, O., Jobidon, M. E., Bouak, F., Nakashima, A., Smith, I., Lam, Q., & Cheung, B. (2013). Working memory training is associated with lower prefrontal cortex activation in a divergent thinking task. Neuroscience, 236, 186–194. https://doi.org/10.1016/j.neuroscience.2012.12.060.
Zanto, T. P., Rubens, M. T., Thangavel, A., & Gazzaley, A. (2011). Causal role of the prefrontal cortex in top-down modulation of visual processing and working memory. Nature Neuroscience, 14(5), 656–661. https://doi.org/10.1038/nn.2773.
Acknowledgements
We wish to thank Cody Elias, Antonio Vergara, Samantha Dunnum, Myranda Gormley, Leon Li, and Carolyn Xue for help with data collection.
Funding
This project was supported by a Johns Hopkins University Science of Learning Institute Fellowship to KJB, NIH grant R01 MH082957 to SMC, and grant K23 NS073626 to JBE.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
ESM 1
(DOCX 770 kb)
Rights and permissions
About this article
Cite this article
Blacker, K.J., Negoita, S., Ewen, J.B. et al. N-back Versus Complex Span Working Memory Training. J Cogn Enhanc 1, 434–454 (2017). https://doi.org/10.1007/s41465-017-0044-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41465-017-0044-1