The Nash Solution as a von Neumann–Morgenstern Utility Function on Bargaining Games

Abstract

In this paper we prove that the symmetric Nash solution is a risk neutral von Neumann–Morgenstern utility function on the class of pure bargaining games. Our result corrects an error in Roth (Econometrica 46:587–594, 983, 1978) and generalizes Roth’s result to bargaining games with arbitrary status quo.

1 Introduction

In economic theory it is generally assumed that individuals can compare alternatives according to their desirability by some ordinal preference relation. These alternatives can be commodity bundles, resource allocations, income distributions etc. Under well known axioms (von Neumann and Morgenstern 1944; Herstein and Milnor 1953) this ordinal preference relation is representable by a cardinal (expected) utility function, commonly called von Neumann–Morgenstern utility function.

In our social and economic life we often face more complex prospects resulting from the interaction with others. Examples include starting a business, choosing an employer, collaborating in a research project and joining a political party, a sports club or a social network. In order to decide with whom to cooperate we have to evaluate these complex prospects and it is therefore natural to ask whether there exists an extension of the cardinal utility function on simple prospects to positions in games which are commonly used to model the interaction among individuals.

The focus of this paper is on bargaining games as introduced by Nash (1950).¹ A bargaining game is given by a set of feasible utility allocations available to some group of players and a status quo which is an element of the feasible set.² The players can either agree on some point in this set or else receive their status quo utilities. Roth (1978a, b) claims that the Nash solution (Nash 1950) is a von Neumann–Morgenstern utility function on positions in bargaining games, where the weight assigned to a position in a bargaining game is determined by the individual’s attitude towards strategic risk. However, as shown in Gerber (1999), if there are more than two players, then the Nash solution violates one of the axioms that Roth imposes upon the preference relation over positions in bargaining games. This axiom is a considerably stronger version of Nash’s Independence of Irrelevant Alternatives. We will show that under a modified condition one can recover Roth’s result for the special case of a preference relation that reflects risk neutrality. It is an open question if a similar result holds for the case of a risk averse or risk loving individual since the asymmetric Nash solution with appropriately chosen weights does not satisfy the modified condition. A characterization of asymmetric Nash solutions as expected utility functions can only be given on the class of two-person games and on the class of hyperplane games.

Apart from correcting Roth (1978a, b) the purpose of this paper is to extend the characterization of the Nash solution as a von Neumann–Morgenstern utility function on positions in bargaining games to games with arbitrary status quo. To this end we have to impose some additional assumptions upon the preference relation. For example, we will require the preference relation to be translation invariant.

The outline of the paper is the following. Section 2 provides the basic notation and definitions and presents a characterization of symmetric and asymmetric Nash solutions. In Sect. 3 we introduce a preference relation on bargaining positions and present the axioms we impose upon this relation. A counterexample shows that the Nash solution violates one of the axioms in Roth (1978a). In Sect. 4 we state and prove our characterization results for symmetric and asymmetric Nash solutions as von Neumann–Morgenstern utility functions. We conclude with a discussion of our result in Sect. 5.

2 The Nash Solution

We first introduce some notation. In the following ${\mathbb {N}}$ will denote the set of positive integers and ${\mathbb{R}}$ will denote the set of real numbers. By |A| we denote the cardinality of a set A. The set $N=\{1,\ldots ,n\},\,n\in {\mathbb {N}},\,n\ge 2$, will denote the player set. Let R be a nonempty subset of N. Later R will be the set of strategic positions, i.e. the set of relevant players in a bargaining game. ${\mathbb {R}}^R$ denotes the cartesian product of |R| copies of ${\mathbb {R}}$, indexed by the elements of R and by ${\mathbb {R}}^R_+$ and ${\mathbb {R}}^R_{++}$ we denote the set of nonnegative and strictly positive vectors in ${\mathbb {R}}^R$, respectively, i.e. ${\mathbb {R}}^R_+=\{x\in {\mathbb {R}}^R\,\,|\,x\ge 0\}$ and ${\mathbb {R}}^R_{++}=\{x\in {\mathbb {R}}^R\,|\,x\gg 0\}$.³ Throughout the paper we will use the notation ${\mathbb {R}}^n,\,{\mathbb {R}}^n_+,\,{\mathbb {R}}^n_{++}$, instead of ${\mathbb {R}}^N,\,{\mathbb {R}}^N_+,\,{\mathbb {R}}^N_{++}$, respectively. For $x\in {\mathbb {R}}^n$ and $\emptyset \ne R\subseteq N$ let $x_R$ be the projection of x onto ${\mathbb {R}}^R$.

For $A\subseteq {\mathbb {R}}^n$ let $\text {ch}(A)=\{x\in {\mathbb {R}}^n\,|\,\exists y\in A,\, y\ge x\}$ denote the comprehensive hull of A. The set $A\subseteq {\mathbb {R}}^n$ is comprehensive if $\text {ch}(A)=A$. By $\text {cch}\{y^1,\ldots ,y^k\}$ we denote the comprehensive and convex hull of the vectors $y^1,\ldots ,y^k\in {\mathbb {R}}^n$, i.e. $x\in \text {cch}\{y^1,\ldots ,y^k\}$ if there exist $\lambda _1,\ldots ,\lambda _k,\,0\le \lambda _i\le 1\ (i=1,\ldots ,k),\,\sum _{i=1}^k\lambda _i=1$, such that $0\le x\le \sum _{i=1}^k\lambda _iy^i$. A vector x is Pareto optimal in $A\subseteq {\mathbb {R}}^n$ if $x\in A$ and if there exists no vector $y\in A$ such that $y>x$. By $\text {PO}(A)$ we denote the set of Pareto optimal vectors in $A\subseteq {\mathbb {R}}^n$.

Let $\pi :N\rightarrow N$ be a permutation. Then $\pi$ induces a mapping $\pi ^{\star }:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ given by

$$\begin{aligned} (\pi ^{\star }(x))_i=x_{\pi ^{-1}(i)}\ \hbox {for}\ i\in N\ \hbox {and}\ x\in {\mathbb {R}}^n. \end{aligned}$$

For $A\subseteq {\mathbb {R}}^n$ let $\pi ^{\star }(A)=\{\pi ^{\star }(x)\,|\ x\in A\}$.

Let $*:{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ denote the element-wise multiplication of vectors in ${\mathbb {R}}^n$ defined by

$$\begin{aligned} x *y=(x_1y_1,\ldots ,x_ny_n)\ \hbox {for}\ (x,y)\in {\mathbb {R}}^n\times {\mathbb {R}}^n. \end{aligned}$$

$({\mathbb {R}}^n_{++},*)$ is a group in the algebraic sense. For $x\in {\mathbb {R}}^n_{++}$ we denote the inverse element with respect to $*$ by $x^{-1}$, i.e. $x^{-1}=\left( \frac{1}{x_1},\ldots ,\frac{1}{x_n}\right)$. For $A\subseteq {\mathbb {R}}^n$ and $x\in {\mathbb {R}}^n$ let $x*A=\{x*y\,|\ y\in A\}$. Let $a,\,b\in {\mathbb {R}}^n,\,a\gg 0$. The mapping $L^{a,b}:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ with $L^{a,b}(x)=a*x+b$ for all $x\in {\mathbb {R}}^n$ is called a positive affine transformation. For $A\subseteq {\mathbb {R}}^n$ let $L^{a,b}(A)=\{L^{a,b}(x)\,|\,x\in A\}$.

A bargaining game consist of a feasible set of utility allocations S measured in von Neumann–Morgenstern utility scales, and a status quo $d\in S$ which is the outcome of the game if the players do not agree on a utility allocation in S.⁴ The following formal definition makes some additional assumptions on S and d.

Definition 2.1

An n-person (pure) bargaining game is a tuple (S, d), where

• 1. $S\subseteq {\mathbb {R}}^n$ is convex, closed and comprehensive.

• 2. $d\in S$.

• 3. $\{x\in S\,|\ x\ge d\}$ is bounded.

Thus, in contrast to Roth (1978a) we assume free disposability of utility (S is comprehensive) and consider bargaining games with arbitrary status quo.

Let

$$\begin{aligned} \mathbf {\Sigma }=\{(S,d)\,|\ (S,d)\ \hbox {is an }n\hbox {-person bargaining game}\}. \end{aligned}$$

Definition 2.2

For $(S,d)\in \mathbf {\Sigma }$ the set of strategic positions is given by

$$\begin{aligned} R_{(S,d)}=\{i\in N\,|\ \exists x\in S,\,x\ge d,\ \hbox {such that}\ x_i>d_i\}. \end{aligned}$$

Player $i\in N$ is called a dummy for $(S,d)\in \mathbf {\Sigma }$ if $i\not \in R_{(S,d)}.$

$R_{(S,d)}$ is the set of relevant players in the bargaining game. These are those players who can achieve more than their status quo utility without making anyone worse off than in the status quo. Hence, these players are interested in getting an agreement with the other players. By contrast, for a dummy player it does not matter whether there is an agreement or not as long as the agreement does not leave her with less than the status quo utility. It is straightforward to see that if $(S,d)\in \mathbf {\Sigma }$ and $R_{(S,d)}\ne \emptyset$, then there exists $x\in S,\,x\ge d$, such that $x_i>d_i$ for all $i\in R_{(S,d)}$. That is, there exists an agreement that is acceptable for everyone ($x\ge d$) and that is strictly better than the status quo for all relevant players. This follows from convexity of S and the fact that for each strategic position $i\in R_{(S,d)}$ there exists a feasible utility allocation $x\ge d$ with $x_i>d_i$.

The following games will play an important role in the analysis. For $\emptyset \ne R\subseteq N$ let

$$\begin{aligned} D^R=\left\{ x\in {\mathbb {R}}^n\,\left| \, \sum _{i\in R}x_i\le 1\ \hbox {and}\ x_j\le 0\ \hbox {for all}\ j\not \in R\right. \right\} \end{aligned}$$

and note that $(D^R,0)\in \mathbf {\Sigma }$. In any such game $(D^R,0)$ the players in R are in strategic positions. They can achieve more than their status quo utility by distributing one unit among themselves. The remaining players are dummies who can achieve at most their status quo utility. For $x\in {\mathbb {R}}^n$ let

$$\begin{aligned} D_x=\text {ch}(\{x\}) \end{aligned}$$

and note that $(D_x,d)\in \mathbf {\Sigma }$ for all $x,d\in {\mathbb {R}}^n$ with $x\ge d$. For any such game $(D_x,d)$ we would expect the players to agree on x, where each player gets the maximum possible payoff in the game.

A solution assigns a feasible utility allocation to any bargaining game:

Definition 2.3

$\varphi :\mathbf {\Sigma }\rightarrow {\mathbb {R}}^n$ is called a solution if

$$\begin{aligned} \varphi (S,d)\in S\ \hbox {for all}\ (S,d)\in \mathbf {\Sigma }. \end{aligned}$$

We now introduce specific Nash-type solutions that will be characterized in the following. To this end let $p=\left( (p^R)_{\emptyset \ne R\subseteq N}\right)$ be a collection of strictly positive vectors with $p^R\in {\mathbb {R}}^R_{++}$ and $\sum _{i\in R}p^R_i=1$ for all $\emptyset \ne R\subseteq N$. The solution $N^{(p)}:\mathbf {\Sigma }\rightarrow {\mathbb {R}}^n$ is then defined as follows. Let $(S,d)\in \mathbf {\Sigma }$ and let $R=R_{(S,d)}$ be the set of strategic positions. Then

$$N^{{(p)}} (S,d) = \left\{ {\begin{array}{*{20}l} {{\text{argmax}}\left\{ {\prod\limits_{{i \in R}} {(x_{i} - d_{i} )^{{p_{i}^{R} }} } {\mkern 1mu} |\;x \in S,{\mkern 1mu} x \ge d} \right\}} &\quad {{\text{if}}\;R \ne \emptyset } \\ d & \quad {{\text{if}}\;R = \emptyset } \\ \end{array} } \right..$$

For $q\in {\mathbb {R}}^n_{++}$ the weighted Nash solution with weights $q,\,\nu ^q$, is given by $\nu ^q=N^{(p)}$, where $p=\left( p^R)_{\emptyset \ne R\subseteq N}\right)$ is such that $p^R_i=q_i/(\sum _{i\in R}q_i)$ for all $i\in R,\,\emptyset \ne R\subseteq N$. Note that the difference between the solutions $N^{(p)}$ and $\nu ^q$ is that in the latter the relative weight of two players i and j is $p^R_i/p^R_j=q_i/q_j$ independent of the bargaining game where both players have strategic positions. In contrast, for the solution $N^{(p)}$ the relative weight of two players may vary with the bargaining game.

If $q_i=q_j$ for all $i,j\in N$, then $\nu =\nu ^q$ is independent of the particular choice of q and we call $\nu$ symmetric Nash solution. The symmetric and asymmetric Nash solutions were introduced by Nash (1950) and Harsanyi and Selten (1972), respectively. Consider the following axioms on a solution $\varphi$.

(SIR):

Strong individual rationality: For all $(S,d)\in \mathbf {\Sigma }$ and all $i\in N, \varphi _i(S,d)\ge d_i$, with strict inequality whenever $i\in R_{(S,d)}$.

(COV):

Covariance with respect to positive affine transformations: For all $(S,d)\in \mathbf {\Sigma }$, if $L^{a,b}:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ is a positive affine transformation, then

$$\begin{aligned} \varphi \bigg (L^{a,b}(S),L^{a,b}(d)\bigg ) = L^{a,b}\left( \varphi (S,d)\right) . \end{aligned}$$

(IIA):

Independence of irrelevant alternatives: If $(S,d),\,(S',d)\in \mathbf {\Sigma }$ with $S\subseteq S'$ and $\varphi (S',d)\in S$, then $\varphi (S,d)=\varphi (S',d)$.

(SY):

Symmetry: If $(S,d)\in \mathbf {\Sigma }$ is such that $\pi ^{\star }(S)=S$ and $\pi ^{\star }(d)=d$ for all permutations $\pi :N\rightarrow N$ with $\pi \left( R_{(S,d)}\right) =R_{(S,d)}$ and $\pi (i)=i$ for all $i\notin R_{(S,d)}$, then $\varphi _i(S,d)=\varphi _j(S,d)$ for all $i,j\in R_{(S,d)}$.

(DCONT):

Disagreement point continuity: For any sequence $\left( (S,d^m)\right) _m\subset \mathbf {\Sigma }$ such that $\lim _{m\rightarrow \infty }d^m=d\in S$ we have $\lim _{m\rightarrow \infty }\varphi (S,d^m)=\varphi (S,d)$.

SIR is a natural requirement since no player would accept an outcome that gives her less utility than the status quo and no player in a strategic position will find it acceptable to receive only the status quo utility. COV requires that a positive affine transformation of all feasible utility allocations implies that the solution changes accordingly. Note that a positive affine transformation of the utility allocations corresponds to an equivalent representation of the players’ von Neumann–Morgenstern (expected) utility functions. IIA demands that the solution is invariant with respect to the deletion of “irrelevant” utility allocations which are different from the allocation that is chosen by the solution. SY requires the solution to treat all strategic players the same if they are symmetric. Finally, DCONT is a technical property requiring the solution to be continuous in the disagreement point.

Since we were not able to give a reference for the following characterization results on the domain $\mathbf {\Sigma }$ we present the theorem with a proof. The main ideas, of course, are due to Nash (1950) and Roth (1977a).

Theorem 2.4

• 1. A solution $\varphi :\mathbf {\Sigma }\rightarrow {\mathbb {R}}^n$ satisfies SIR,  COV and IIA if and only if there exists $p=\left( (p^R)_{\emptyset \ne R\subseteq N}\right)$ with $p^R\in {\mathbb {R}}^R_{++}$ and $\sum _{i\in R}p^R_i=1$ for all $\emptyset \ne R\subseteq N$, such that $\varphi =N^{(p)}$.

• 2. A solution $\varphi :\mathbf {\Sigma }\rightarrow {\mathbb {R}}^n$ satisfies SIR,  COV, IIA and DCONT if and only if there exists $q\in {\mathbb {R}}^n_{++}$ such that $\varphi =\nu ^q$.

• 3. A solution $\varphi :\mathbf {\Sigma }\rightarrow {\mathbb {R}}^n$ satisfies SIR, COV, IIA and SY if and only if $\varphi =\nu$.

The proof is in the appendix, but let us provide some discussion and the basic ideas of the proof. First, the reader may wonder why we do not require the solution to satisfy Pareto optimality, i.e. $\varphi (S,d)\in \text {PO}(S)$ for all $(S,d)\in \mathbf {\Sigma }$. The reason is that Pareto optimality is implied by SIR,  COV and IIA as we show in the proof of the first claim in Theorem 2.4. The basic idea is as follows (see also Roth 1977a). Suppose there is a bargaining game (S, d) whose solution $\varphi (S,d)$ is not Pareto optimal. Then one could shrink the feasible set by means of a positive affine transformation such that the utility allocation $\varphi (S,d)$ is still feasible and by IIA the solution of the new bargaining game must still be $\varphi (S,d)$. However, by COV the solution is a positive affine transformation of $\varphi (S,d)$ which is a contradiction. The remainder of the proof of part one follows the line of argument in Nash (1950) applied to bargaining games with strategic positions R.

The second part of the theorem provides a characterization of the weighted Nash solution $\nu ^q$. From part 1 we know that a solution that satisfies SIR,  COV and IIA must be equal to $N^{(p)}$ for some p. If the solution in addition satisfies DCONT, then it must be given by $\nu ^q$ for some q. The idea is that any bargaining problem (S, d) can be approximated by a sequence of bargaining games $\left( (S,d^m)\right) _m$ which have no dummy players so that $N^{(p)}(S,d^m)=\nu ^q(S,d^m)$ for all m, where $q=p^N$. Taking limits and using DCONT we then conclude that $N^{(p)}(S,d)=\nu ^q(S,d)$.

Finally, the third part of the theorem easily follows from part one because SY requires the solution to assign the same payoff to two players who are in symmetric strategic positions in a bargaining game. In particular, in any bargaining game $(D^R,0)$ for $\emptyset \ne R\subseteq N$ all players in R must get the same payoff. For $N^{(p)}$ this is only possible if $p^R_i=p^R_j$ for all $i,j\in R$ and hence $N^{(p)}=\nu$.

For later usage we briefly review a result due to Herstein and Milnor (1953) concerning the representation of preferences over lotteries in the expected utility form.⁵

Definition 2.5

A set M is a mixture set if for any $a,b\in M$ and any $0\le p\le 1$ we can associate an element of M denoted by $[pa;(1-p)b]$ which is called a lottery over a and b such that the following conditions are fulfilled:

• 1. $[1a;0b]=a$ for all $a,b\in M$.

• 2. $[pa;(1-p)b]=[(1-p)b;pa]$ for all $a,b\in M,\ 0\le p\le 1.$

• 3. $\left[ q[pa;(1-p)b];(1-q)b\right] =[pqa;(1-pq)b]$ for all $a,b\in M,\ 0\le p,q\le 1.$

Let $\succsim$ be a preference relation on M, i.e. a complete and transitive binary relation on M. The corresponding strict preference relation and indifference relation are defined as usual and are denoted by $\succ$ and $\sim$, respectively. The following axioms guarantee the existence of an expected utility function that represents $\succsim$.

(A1):

(Continuity) Let $a,b,c\in M$. Then the following sets are closed: $\{p\,|\,[p a;(1-p)b]\succsim c\}$ and $\{p\,|\, c\succsim [p a;(1-p)b]\}$.

(A2):

(Independence) Let $a,a',b\in M$ with $a\sim a'.$ Then

$$\begin{aligned} \left[ \frac{1}{2}a;\frac{1}{2}b\right] \sim \left[ \frac{1}{2}a';\frac{1}{2}b\right] . \end{aligned}$$

Theorem 2.6

(Herstein and Milnor 1953) Let $\succsim$ be a preference relation on M that fulfills A1 and A2. Then there exists a utility function $u:M\rightarrow {\mathbb {R}}$ which represents $\succsim$ (i.e. $a\succsim b\iff u(a)\ge u(b)$ for all $a,b\in M$) and which has the property that

$$\begin{aligned} u([pa;(1-p)b])=pu(a)+(1-p)u(b) \end{aligned}$$

for all $a,b\in M,\,0\le p\le 1$. The utility function u is unique up to a positive affine transformation, i.e. if $v:M\rightarrow {\mathbb {R}}$ also represents $\succsim$, then there exist $\alpha ,\,\beta \in {\mathbb {R}},\,\alpha >0,$ such that $v(a)=\alpha u(a)+\beta$ for all $a\in M$.

The expected utility function u is also called von Neumann–Morgenstern utility function.

3 A Preference Relation over Bargaining Positions

Consider an individual (an “outside observer”) who has a preference relation over the set of positions in bargaining games $N\times \mathbf {\Sigma }$. That is, the individual can evaluate the prospect of being player i in game (S, d) versus the prospect of being player j in game $(S',d')$. This includes the case where the individual evaluates the prospect of being in different positions i and $j\ne i$ in the same game (S, d). Hence, we implicitly assume that the utilities that define the bargaining games are derived from the von Neumann–Morgenstern utility function of the individual.

We also assume that the individual can evaluate the prospects of different lotteries over the set of positions in bargaining games. Formally, let $M_{N\times \mathbf {\Sigma }}$ be the mixture set generated by $N\times \mathbf {\Sigma }$ and let $\succsim$ be a preference relation on $M_{N\times \mathbf {\Sigma }}$ which satisfies A1 and A2. In addition we assume that $\succsim$ satisfies the following axioms.

(A3):

For all permutations $\pi :N\rightarrow N$ and all $i\in N$,

$$\begin{aligned} (i,(S,d))\sim \left(\pi (i), \bigg (\pi ^{\star }(S),\pi ^{\star }(d)\bigg )\right). \end{aligned}$$

(A4):

Let $(S,d),\,(S',d')\in \mathbf {\Sigma },\,i\in N$, and $\left( i,(S,d)\right) \sim \left( i,(S',d')\right) .$ Let $e=(1,\ldots ,1)\in {\mathbb {R}}^n$. Then, for all $b\in {\mathbb {R}}^n$

$$\begin{aligned} \left( i,L^{e,b}(S,d)\right) \sim \Big (i,\bigg (L^{e,b}(S'),L^{e,b}(d')\bigg )\Big ). \end{aligned}$$

(A5):

Let $x,\,y,\,z\in {\mathbb {R}}^n,\,i\in N,$ and $0\le p\le 1$, be such that $x_i=p y_i+(1-p) z_i$. Then

$$\begin{aligned} (i,(D_x,x))\sim \left[ p\left( i,(D_y,y)\right) ;(1-p)\left( i,(D_z,z)\right) \right] . \end{aligned}$$

(A6):

Let $(S,d)\in \mathbf {\Sigma },\, i\in N,\, a\in {\mathbb {R}}^n_{++},\, a_i\ge 1,$ and let $S'=a *S ,\,d'=a *d.$ Then

$$\begin{aligned} (i,(S,d))\sim \left[ \frac{1}{a_i}\left( i,(S',d')\right) ;\left( 1-\frac{1}{a_i}\right) \left( i,(D_0,0)\right) \right] . \end{aligned}$$

(A7):

(a) Let $i\in N$ be a dummy in $(S,0)\in \mathbf {\Sigma }$. Then

$$\begin{aligned} (i,(S,0))\sim (i,(D_0,0)). \end{aligned}$$

(b) If $i\in N$ is not a dummy in $(S,0)\in \mathbf {\Sigma }$ then

$$\begin{aligned} (i,(S,0))\succ (i,(D_0,0)). \end{aligned}$$

(c) Let $x,\,d,\,d'\in {\mathbb {R}}^n,$ be such that $x\ge d,\, x\ge d'$, and let $i\in N.$ Then

$$\begin{aligned} (i,(D_x,d))\sim (i,(D_x,d')). \end{aligned}$$

(d) Let $i\in N$ and $\emptyset \ne R\subseteq N, R\ne \{i\}.$ Then

$$\begin{aligned} \left( i,\left( D^{\{i\}},0\right) \right) \succ \left( i,\left( D^R,0\right) \right) . \end{aligned}$$

(A8):

Let $x\in {\mathbb {R}}^n_+$ and let $(S,0),\,(T,0)\in \mathbf {\Sigma }$ be such that $D_x\subseteq S\subseteq T$, and $\left( i,(D_x,0)\right) \sim \left( i,(T,0)\right)$ for all $i\in N$. Then, for all $i\in N$,

$$\begin{aligned} \left( i,(D_x,0)\right) \sim \left( i,(S,0)\right) . \end{aligned}$$

Let us give a short interpretation of the conditions keeping in mind that the desirability of a bargaining position will naturally be correlated with the individual’s expectation about the outcome of the bargaining game. A3 reflects the fact that the name of a bargaining position is irrelevant for its desirability. That is, the individual expects her utility payoff in a specific position to depend only on the structural properties of the game and not the names (numbers) of the players. Axiom A4 might be called translation invariance. Our individual remains indifferent between two bargaining positions if the feasible utility allocations are translated in the same way. Observe that in our framework the utilities that define the bargaining games are derived from the same von Neumann–Morgenstern utility function, namely from the outside observer’s one whose preference relation $\succsim$ is analysed here. Thus, a change in the origin of the utilities cannot be done independently across the different positions and therefore axiom A4 does not follow from the fact that a von Neumann–Morgenstern utility function is unique only up to a positive affine transformation.

A5 and A6 are two different forms of neutrality towards ordinary risk (in contrast to the strategic risk of playing a certain position in a bargaining game). A5 requires the individual to be indifferent between a sure bargaining position and a specific lottery over two bargaining positions. Here all bargaining games are such that the status quo is the unique individually rational allocation in the feasible set and hence the status quo can reasonably be expected to be the outcome of the game. In that case A5 simply follows from the fact that the individual has an expected utility function that defines the feasible sets in the bargaining games. A6 is similar, but now the bargaining games can be more general. If the individual expects that a rescaling of the utility values in a bargaining game only rescales her payoff accordingly, then A6 again follows from the assumption that the individual has an expected utility function on simple prospects.

A7 is self explaining and the assumptions are very natural. The only objection against A7c might be that in a situation where $d_i>d'_i$ the higher status quo outcome for i in $(D_x,d)$ should make the latter more desirable than $(D_x,d')$, even when the maximum payoff that can be achieved by i ($x_i$) is the same. In general this is clearly true. In the situation of A7c, however, the final outcome x seems sure both for $(D_x,d)$ and for $(D_x,d')$ since no rational player will demand a different outcome (there is no “strategic risk”).

A8 is reminiscent of the axiom IIA and its rationale is as follows. If for all player positions the individual is indifferent between the game $(D_x,0)$, where x is the only reasonable outcome, and the game (T, 0), which has a larger feasible set, then the individual reveals that she expects x to be the outcome in (T, 0). In other words, the individual considers all utility allocations in T different from x as irrelevant. In this case the individual should also consider all utility allocations different from x in any subset S of T as irrelevant and hence be indifferent between $(D_x,0)$ and (S, 0) for all player positions whenever $x\in S$.

Assumptions A3, A6 and A7 are mainly borrowed from Roth (1978a) and adopted to our domain $\mathbf {\Sigma }$. Roth does not formulate a condition that is equivalent to A7b. However, this condition is crucial for establishing that the certainty equivalent of playing a bargaining game is strictly positive which we will show later.⁶ Instead of A8 Roth imposed the following assumption on $\succsim$.

(A8$'$):

Let $x\in {\mathbb {R}}^n_+$ and let $(S,0),\,(T,0)\in \mathbf {\Sigma }$ be such that $D_x\subseteq S\subseteq T$, and x is Pareto optimal in T. If $\left( i,(D_x,0)\right) \sim \left( i,(T,0)\right)$ for some $i\in N$, then

$$\begin{aligned} \left( i,(D_x,0)\right) \sim \left( i,(S,0)\right) . \end{aligned}$$

Assumption A8$'$ is considerably stronger than A8, even though A8’ does not imply A8. Roth (1978a) claims that a preference relation which is represented by some Nash solution with weights $q,\,\nu ^q$, satisfies A8$'$. The following example taken from Gerber (1999) shows that this statement and therefore Roth’s characterization result is wrong if $n>2$ (we come back to the case $n=2$ in Sect. 4). Our example refers to the case of the symmetric Nash solution $\nu$, i.e. let ${\widetilde{\theta }}$ be an expected utility function on $M_{N\times \mathbf {\Sigma }}$ defined by ${\widetilde{\theta }}(i,(S,d))=\nu _i(S,d)$ for all $(i,(S,d))\in N\times \mathbf {\Sigma }$. Of course, a similar example can be found for any $\nu ^q$.

Example: Let $N=\{1,2,3\},\,T=D_N,\,x=(0,2/3,1/3)$ and let $S=\text {cch}\{(0,2/3,1/3),(1,0,0)\}$. Then $D_x\subseteq S\subseteq T,\,x$ is Pareto optimal in T, $\nu (T,0)=(1/3,1/3,1/3)$ and $\nu (S,0)=(1/3,4/9,2/9)$. Thus, ${\widetilde{\theta }}(3,(T,0))=\nu _3(T,0)=x_3=\nu _3(D_x,0)={\widetilde{\theta }}(3,(D_x,0))$ but ${\widetilde{\theta }}(3,(S,0))=\nu _3(S,0)\ne x_3$. Therefore, ${\widetilde{\theta }}$ violates condition A8$'$.

We will now show that under our set of assumptions we can partly recover Roth’s characterization result and extend it to the domain $N\times \mathbf {\Sigma }$. To this end let $\succsim$ be a preference relation on $M_{N\times \mathbf {\Sigma }}$ that satisfies assumptions A1–A8. Then, by Theorem 2.6, there exists an expected utility function $\theta$ that represents $\succsim$. Moreover, $\theta$ is unique up to a positive affine transformation. We choose the following normalization which is admissible because of conditions A7b and A7c. Recall that $e=(1,\ldots ,1)\in {\mathbb {R}}^n$. Let $i_0\in N$ be arbitrary. Then

$$\begin{aligned} \theta \left( i_0,(D_e,e)\right)= & \, 1\quad \hbox {and}\\ \theta \left( i_0,(D_0,0)\right)= & \, 0. \end{aligned}$$

Axiom A3 directly implies that $\theta \left( i,(D_e,e)\right) =1$ and $\theta \left( i,(D_0,0)\right) =0$ for all $i\in N$.

The following lemmas are useful steps for proving the main characterization result. The first lemma deals with the game $(D_x,d)$, where x is the only reasonable outcome. It shows that the utility of being player i in this game is $x_i$.

Lemma 3.1

Let $x,\,d\in {\mathbb {R}}^n,\, x\ge d,\, i\in N$. Then

$$\begin{aligned} \theta (i,(D_x,d))=x_i. \end{aligned}$$

Proof

From axiom A7c we get $\theta (i,(D_x,d))=\theta (i,(D_x,x)).$ Therefore, it suffices to prove the claim for the case $d=x$.

Case 1: $0\le x_i\le 1$.

Let $p=x_i$. Then $x_i=p\cdot 1+(1-p)\cdot 0$ and axiom A5 implies

$$\begin{aligned} \theta (i,(D_x,x))= & \, p\,\theta (i,(D_e,e))+(1-p)\,\theta (i,(D_0,0))\\= & \, p\cdot 1+(1-p)\cdot 0\\= & \, p\\= & \, x_i. \end{aligned}$$

Case 2: $x_i>1.$

Let $p=\frac{1}{x_i}.$ Then $1=p\cdot x_i+(1-p)\cdot 0$ and axiom A5 implies

$$\begin{aligned} \theta (i,(D_e,e))= & \, p\,\theta (i,(D_x,x))+(1-p)\,\theta (i,(D_0,0))\\ \iff 1= & \, p\,\theta (i,(D_x,x))+(1-p)\cdot 0\\ \Rightarrow \theta (i,(D_x,x))= & \, \frac{1}{p}=x_i. \end{aligned}$$

Case 3: $x_i<0.$

Let $p=\frac{1}{1-x_i}.$ Then $0=p\cdot x_i+(1-p)\cdot 1$ and axiom A5 implies

$$\begin{aligned} \theta (i,(D_0,0))= & \, p\,\theta \,(i,(D_x,x))+(1-p)\,\theta (i,(D_e,e))\\ \iff 0= & \, p\,\theta \,(i,(D_x,x))+1-p\\ \Rightarrow \theta (i,(D_x,x))= & \, \frac{p-1}{p}=x_i. \end{aligned}$$

$\square$

Since any prospect which gives rise to the utility allocation $x\in {\mathbb {R}}^n$ can be identified with the bargaining game $(D_x,d)\in \mathbf {\Sigma }$ for any $d\in {\mathbb {R}}^n,\,x\ge d$, Lemma 3.1 shows that $\theta$ is indeed an extension of the observer’s utility function that defines the bargaining games.

The following lemma shows that the utility of a dummy player position in any bargaining game is equal to the status quo utility.

Lemma 3.2

Let $i\in N$ be a dummy in $(S,d)\in \mathbf {\Sigma }$. Then

$$\begin{aligned} \theta (i,(S,d))=d_i. \end{aligned}$$

Proof

For $d=0$ the claim is true by virtue of axiom A7a. For $d\ne 0$ player i is a dummy in $\bigg (L^{e,-d}(S),L^{e,-d}(d)\bigg )=\bigg (L^{e,-d}(S),0\bigg )$ as well. Therefore, $\theta \Big (i,\bigg (L^{e,-d}(S),L^{e,-d}(d)\bigg )\Big ) =0=\theta (i,(D_0,0))$. Finally, axiom A4 and Lemma 3.1 imply that $\theta (i,(S,d)) =\theta (i,(D_d,d))=d_i.$ $\square$

Next we show that the utility function $\theta$ is covariant with respect to positive affine transformations of the utility allocations in a bargaining game.

Lemma 3.3

Let $(S,d)\in \mathbf {\Sigma }$ and let $L^{a,b}:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ be a positive affine transformation. Then, for $S'=L^{a,b}(S), d'=L^{a,b}(d)$ and all $i\in N$,

$$\begin{aligned} \theta (i,(S',d'))=a_i\theta (i,(S,d))+b_i. \end{aligned}$$

Proof

Case 1: $b=0$.

Let $i\in N$. If $a_i\ge 1$, then axiom A6 implies

$$\begin{aligned} \theta (i,(S,d))=\frac{1}{a_i}\theta (i,(S',d'))+\left( 1-\frac{1}{a_i}\right) \underbrace{\theta (i,(D_0,0))}_{=0}. \end{aligned}$$

If $a_i < 1$, then $1/a_i >1$ and by the above we conclude that

$$\begin{aligned} \theta (i,(S',d'))=a_i\theta (i,(S,d)). \end{aligned}$$

Case 2: $b\ne 0$.

Define $x\in {\mathbb {R}}^n$ by $x_i=\theta (i,(S,d))$ for all $i\in N$. By Case 1, $\theta \Big (i,\bigg (L^{a,0}(S),L^{a,0}(d)\bigg )\Big ) =a_ix_i$, i.e. $\Big (i,\bigg (L^{a,0}(S),L^{a,0}(d)\bigg )\Big )\sim (i,(D_{a*x},a*x))$ for all $i\in N$ by Lemma 3.1. Then, axiom A4 implies that $(i,(S',d'))\sim (i,(D_{L^{a,b}(x)},L^{a,b}(x))$ and therefore, by Lemma 3.1$\theta (i,(S',d'))=a_ix_i+b_i$ for all $i\in N$. $\square$

For $r=1\ldots ,n$, define the certainty equivalent f(r) for a strategic position in the game $(D^R,0),\, \emptyset \ne R\subseteq N, \,| R\,|=r$, by

$$\begin{aligned} \left( i,\left( D^R,0\right) \right) \sim \left( i,\left( \text {ch}\left( f(r)D^{\{i\}}\right) ,0\right) \right) \ \hbox {for}\ i\in R. \end{aligned}$$

f(r) is well defined because of the continuity axiom A1 and axioms A3,  A7b and A7d. In particular, note that A3 implies that the certainty equivalent only depends on the number of strategic positions, r, in the game $(D^R,0)$ and not on the identity of the players $j\in R, j\ne i$. Also, by A3 the certainty equivalent is the same for all $i\in R$. From A7b we get that $f(r)>0$ for all r and from axiom A7d it follows that $f(r)<1$ for $r>1$. $f(1)=1$ is trivial. The preference relation $\succsim$ reflects neutrality towards strategic risk if $f(r)=1/r$, it reflects risk aversion if $f(r)<1/r$ and risk preference if $f(r)>1/r$ for all $r=1,\ldots ,n$.

Let $e_i\in {\mathbb {R}}^n$ denote the ith unit vector. Then $\theta \left( i,\left( D^R,0\right) \right) =f(r)$ since $D^{\{i\}}=D_{e_i},\, \text {ch}\left( f(r)D^{\{i\}}\right) =f(r)D^{\{i\}}$ for $f(r)>0$ and Lemmas 3.1 and 3.3 apply.

We first derive the utility function $\theta$ on the domain of transferable utility bargaining games which have a Pareto frontier that is given by a hyperplane. We call these games hyperplane games.

Definition 3.4

Let $(S,d)\in \mathbf {\Sigma }$ and let $R=R_{(S,d)}$ be the set of strategic positions. Then (S, d) is called hyperplane game if there exist $c\in {\mathbb {R}}^R_{++}$ and $k\in {\mathbb {R}}$ such that

$$\begin{aligned} S=\left\{ x\in {\mathbb {R}}^n\,\left| \,\sum _{i\in R}c_ix_i\le k \ \hbox {and}\ x_j\le d_j\ \hbox {for all}\ j\notin R\right. \right\} . \end{aligned}$$

Let $\mathbf {\Sigma }^H$ be the set of hyperplane games.

Lemma 3.5

Let $(S,d)\in \mathbf {\Sigma }^H$ be given by

$$\begin{aligned} S=\left\{ x\in {\mathbb {R}}^n\,\left| \,\sum _{i\in R}c_ix_i\le k \ \hbox {and}\ x_j\le d_j\ \hbox {for all}\ j\notin R\right. \right\} , \end{aligned}$$

where $c\in {\mathbb {R}}^R_{++},\,k\in {\mathbb {R}},\,k>\sum _{i\in R}c_id_i$. Then, for all $i\in R$,

$$\begin{aligned} \theta \left( i,(S,d)\right) =\frac{k-\sum _{i\in R}c_id_i}{c_i}f(r)+d_i. \end{aligned}$$

Proof

Let $(S,d)\in \mathbf {\Sigma }^H$ be given as in the statement of the lemma. Define $a\in {\mathbb {R}}^n_{++}$ by

$$a_{i} = \left\{ {\begin{array}{*{20}l} {\frac{{k - \sum\nolimits_{{i \in R}} {c_{i} } d_{i} }}{{c_{i} }}} & \quad {{\text{if}}\;\;i \in R} \\ 1 & \quad {{\text{if}}\;\,i \notin R} \\ \end{array} } \right..$$

Then $(S,d)=\Big (L^{a,d}(D^R),L^{a,d}(0)\Big )$ and Lemma 3.3 implies that for all $i\in R$,

$$\begin{aligned} \theta (i,(S,d))=a_i\theta (i,(D^R,0))+d_i=\frac{k-\sum _{i\in R}c_id_i}{c_i}f(r)+d_i \end{aligned}$$

by definition of f(r). $\square$

4 The Main Result

We are now ready to prove our main result that the Nash solution $\nu$ is a risk neutral von Neumann–Morgenstern utility function on positions in bargaining games.

Theorem 4.1

Let $\succsim$ be a preference relation on $M_{N\times \mathbf {\Sigma }}$ that satisfies A1–A8. Let $\theta$ be the expected utility function which represents $\succsim$ and fulfills $\theta (i,(D_e,e))=1$ and $\theta (i,(D_0,0))=0$ for all $i\in N$. If $f(r)=1/r$ for all $r=1\ldots ,n$, then for all $(S,d)\in \mathbf {\Sigma }$ and all $i\in N, \theta (i,(S,d))=\nu _i(S,d)$.

Proof

It is clear that the expected utility function ${\widetilde{\theta }}$ defined by ${\widetilde{\theta }}(i,(S,d))=\nu _i(S,d)$ for all $(i,(S,d))\in N\times \mathbf {\Sigma }$ satisfies conditions A1–A8. It remains to be shown that $\theta ={\widetilde{\theta }}$. To this end let $(S,d)\in \mathbf {\Sigma }$ and let $R=R_{(S,d)}$ be the set of strategic positions. If $R=\emptyset$ we are done by Lemma 3.2. Thus, let $R\ne \emptyset$ and $r=|R|$.

Case 1: $d=0.$

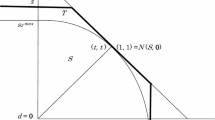
Let $x=\nu (S,0)$, i.e. $c=\prod _{i\in R}x_i^{\frac{1}{r}}>\prod _{i\in R}y_i^{\frac{1}{r}}\ge 0$ for all $y\in S, y\ge 0, y\ne x$, and let $E=\{y\in {\mathbb {R}}^n_+\,|\prod _{i\in R}y_i^{\frac{1}{r}}\ge c\}= \{y\in {\mathbb {R}}^n_+\,|\sum _{i\in R}\frac{1}{r} \log y_i\ge \log c\}.$ The sets E and S are convex with intersection x. Therefore, there exists a plane H that separates E and S. As H is tangent to E in $x,\ H$ is given by

$$\begin{aligned} H=\left\{ z\in {\mathbb {R}}^n\,\left| \, \sum _{i\in R}\frac{1}{r x_i}z_i=1\right. \right\} . \end{aligned}$$

Let

$$\begin{aligned} T=\left\{ z\in {\mathbb {R}}^n\,\left| \,\sum _{i\in R}\frac{1}{r x_i}z_i\le 1, z_j\le 0\ (j\not \in R)\right. \right\} . \end{aligned}$$

Then clearly $S\subseteq T$ since H separates E and S and

$$\begin{aligned} \theta (i,(T,0))=f(r)r x_i=x_i=\theta \left( i,\left( D_x,0\right) \right) \end{aligned}$$

for all $i\in R$ by Lemmas 3.1 and 3.5. If $j\notin R$ then $\theta _j(T,0)=0=x_j$ by Lemma 3.2. Therefore, $(i,(T,0))\sim \left( i,\left( D_x,0\right) \right)$ for all $i\in N$ and by condition A8 we conclude that $\left( i,\left( D_x,0\right) \right) \sim (i,(S,0))$ for all $i\in N$, i.e. $\theta (i,(S,0))=x_i=\nu _i(S,0)$ for all $i\in N$.

Case 2: $d\ne 0.$

Let $x=\nu (S,d)$. Then $x-d=\nu (L^{e,-d}(S),0)$ and Case 1 implies

$$\begin{aligned} \theta \left( i,\left( L^{e,-d}(S),0\right) \right) =x_i-d_i, \end{aligned}$$

i.e. $\Big (i,\bigg (L^{e,-d}(S),L^{e,-d}(d)\bigg )\Big )\sim \left( i,\left( D_{x-d},0\right) \right)$ for all $i\in N$. By axiom A4 this implies

$$\begin{aligned} \left( i,(S,d)\right) \sim \left( i,(D_x,0)\right) , \end{aligned}$$

and from Lemma 3.1 we conclude that

$$\begin{aligned} \theta \left( i,(S,d)\right) =\theta \left( i,\left( D_x,d\right) \right) =x_i \end{aligned}$$

for all $i\in N$. This proves the theorem. $\square$

It is not straightforward to see whether there exists an equivalent to Theorem 4.1 for the case of a preference relation $\succsim$ reflecting risk aversion or risk preference. In view of the definition of the certainty equivalent f(r) and Lemma 3.5 a natural candidate for a cardinal utility function ${\widetilde{\theta }}$ representing $\succsim$ would be defined by asymmetric Nash solutions $\nu ^q$ in the following way (see Roth 1978a, b). Let $(i,(S,d))\in N\times \mathbf {\Sigma }$ and let $R=R_{(S,d)}$ be the set of strategic positions. If $i\notin R$ define

$$\begin{aligned} {\widetilde{\theta }}(i,(S,d))=d_i. \end{aligned}$$

Otherwise, let $q\in {\mathbb {R}}^n_{++}$ be such that $q_i=f(r),\,\sum _{j\in R}q_j=1$ and $q_j=q_k$ for all $j,\,k\in R\setminus \{i\}$. Then, let

$$\begin{aligned} {\widetilde{\theta }}(i,(S,d))=\nu ^q_i(S,d). \end{aligned}$$

Thus, each coordinate ${\widetilde{\theta }}(i,(S,d))$ of ${\widetilde{\theta }},\,i\in R$, belongs to a different asymmetric Nash solution $\nu ^q$ unless $f(r)=1/r$. The utility function ${\widetilde{\theta }}$ fulfills assumptions A1–A7 but it only satisfies A8 if $f(r)=1/r$ for all $r=1,\ldots ,n$, in which case A8 directly follows from IIA. However, ${\widetilde{\theta }}$ as defined above represents $\succsim$ on the set of hyperplane games. The following theorem directly follows from Lemma 3.5.

Theorem 4.2

Let $\succsim$ be a preference relation on $M_{N\times \mathbf {\Sigma }}$ that satisfies A1–A8. Let $\theta$ be the expected utility function which represents $\succsim$ and fulfills $\theta (i,(D_e,e))=1$ and $\theta (i,(D_0,0))=0$ for all $i\in N$. Then, for all $(S,d)\in \mathbf {\Sigma }^H$ and for all $i\in N,\,\theta (i,(S,d))={\widetilde{\theta }}(i,(S,d))$.

Since there are several utility functions on $\mathbf {\Sigma }$ that coincide with ${\widetilde{\theta }}$ on $\mathbf {\Sigma }^H$ Theorem 4.2 is only of limited significance. In order to determine the utility for a position in a bargaining game without side payments given the utility function on hyperplane games we cannot dispense with a condition like A8. Thus, we have to restrict ourselves to the case of $n=2$ if we want to get a characterization result also for the case of a risk loving or risk averse player. Since many real life bargaining situations and also Nash’s original work involve only two parties the following theorem is still a remarkable result.

Theorem 4.3

Let $n=2$ and let $\succsim$ be a preference relation on $M_{N\times \mathbf {\Sigma }}$ that satisfies A1–A7 and A8’. Let $\theta$ be the expected utility function which represents $\succsim$ and fulfills $\theta (i,(D_e,e))=1$ and $\theta (i,(D_0,0))=0$ for all $i\in N$. Then $\theta ={\widetilde{\theta }}$.

Proof

It is clear that the expected utility function ${\widetilde{\theta }}$ satisfies conditions A1–A7. Since $n=2$ it also satisfies A8’. To see this observe that for $x\in {\mathbb {R}}^2_+,\,(S,0),\,(T,0)\in \mathbf {\Sigma }$ and $D_x\subseteq S\subseteq T$, the fact that x is Pareto optimal in T and $x_i={\widetilde{\theta }}(i,(T,0))=\nu ^q_i(T,0)$ for some $i\in N$ imply that $x=\nu ^q(T,0)$. It remains to be shown that $\theta ={\widetilde{\theta }}$. We follow the line of arguments in the proof of Theorem 4.1.⁷ Let $(i,(S,d))\in N\times \mathbf {\Sigma }$ and $R=R_{(S,d)}$ be the set of strategic positions. If $i\notin R$ we are done by Lemma 3.2. Thus, let $i\in R$ and $r=|R|$. Let $q\in {\mathbb {R}}^2_{++}$ be given by $q_i=f(r)$ and $q_j=1-f(r)$ for $j\ne i$. Observe that with this definition $\sum _{j\in R}q_j=1$ also in the case where $r=1$ since $f(1)=1$.

Case 1: $d=0.$

By definition ${\widetilde{\theta }}(i,(S,0))=\nu ^q_i(S,0)$. Let $x=\nu ^q(S,0)$, i.e. $c=\prod _{j\in R}x_j^{q_j}>\prod _{j\in R}y_j^{q_j}\ge 0$ for all $y\in S, y\ge 0, y\ne x$, and let $E=\{y\in {\mathbb {R}}^n_+\,|\prod _{j\in R}y_j^{q_j}\ge c\}= \{y\in {\mathbb {R}}^n_+\,|\sum _{j\in R}q_j \log y_j\ge \log c\}.$ The sets E and S are convex with intersection x. Therefore, there exists a plane H that separates E and S. As H is tangent to E in $x,\ H$ is given by

$$\begin{aligned} H=\left\{ z\in {\mathbb {R}}^n\,\left| \, \sum _{j\in R}\frac{q_j}{x_j}z_j=1\right. \right\} . \end{aligned}$$

Let

$$\begin{aligned} T=\left\{ z\in {\mathbb {R}}^n\,\left| \,\sum _{j\in R}\frac{q_j}{x_j}z_j\le 1, z_k\le 0\ (k\not \in R)\right. \right\} . \end{aligned}$$

Then clearly $S\subseteq T$ since H separates E and S and

$$\begin{aligned} \theta (i,(T,0))=\frac{x_i}{q_i}f(r)=x_i=\theta \left( i,\left( D_x,0\right) \right) \end{aligned}$$

by Lemmas 3.1 and 3.5. By condition A8’ we conclude that $\left( i,\left( D_x,0\right) \right) \sim (i,(S,0))$ which implies $\theta _i(S,0)=x_i={\widetilde{\theta }}(i,(S,0))$.

The proof for Case 2 ($d\ne 0$) proceeds exactly as in Theorem 4.1. $\square$

5 Discussion

It has been shown that under fairly natural assumptions it is possible to deduce a cardinal utility function that represents an individual’s preference relation on the class of positions in bargaining games. If the individual is risk neutral in the sense that she believes in getting a fair share whenever one dollar is to be distributed among some players, then the utility function is given by the symmetric Nash solution. For the case of a risk loving or risk averse player we only succeeded in characterizing the expected utility function if either $n=2$ or if we restrict ourselves to the class of positions in hyperplane games. In both cases the individual’s utility for position i is determined by some asymmetric Nash solution, where the weight for position i equals the player’s risk attitude as expressed by the certainty equivalent f(r), where r is the number of strategic positions in the underlying game. Thus, only for the case of a risk neutral player we were able to fully recover and generalize Roth’s (1978a, b) result that was based on a serious flaw.

Based on an idea of Roth (1978a) we have offered a new interpretation of the symmetric Nash solution as the outcome of the game expected by an individual with risk neutral preferences over bargaining positions. Thus, our paper fits into the line of research that seeks to find justifications for bargaining solutions beyond those given by axiomatizations of solution concepts. At the same time our paper seems to reveal a structural difference between symmetric and asymmetric Nash solutions. While the symmetric Nash solution turns out to be a utility function on positions in bargaining games, it is an open question whether we can characterize asymmetric solutions in the same way if the number of players exceeds two.

Appendix

Proof of Theorem 2.4

• 1. It is straightforward to see that $N^{(p)}$ satisfies SIR, COV and IIA if $p=\left( (p^R)_{\emptyset \ne R\subseteq N}\right)$ with $p^R\in {\mathbb {R}}^R_{++}$ and $\sum _{i\in R}p^R_i=1$ for all $\emptyset \ne R\subseteq N$. Let $\varphi :\mathbf {\Sigma }\rightarrow {\mathbb {R}}^n$ be a solution that satisfies the axioms. We will show that $\varphi (S,d)\in \text {PO}(S)$ for all $(S,d)\in \mathbf {\Sigma }$. Let $(S,d)\in \mathbf {\Sigma }$. By COV w.l.o.g. we can assume that $d=0$. Suppose there exists $x\in S$ such that $x>\varphi (S,0)$. W.l.o.g. assume that there exists some $k\in N$ such that $x_i>\varphi _i(S,0)$ if and only if $i\in \{1,\ldots ,k\}$.⁸ This implies $\{1,\ldots ,k\}\subseteq R_{(S,0)}$ and therefore, by SIR, $\varphi _i(S,0)>0$ for all $i=1,\ldots , k$. Define $a\in {\mathbb {R}}^n_{++}$ by $a_i=\varphi _i(S,0)/x_i$ for $i=1,\ldots ,k$, and $a_j=1$ for $j=k+1,\ldots , n$. Then $a*S\subset S$ and $\varphi (S,0)=a*x\in a*S$. (Observe that $x_i=\varphi _i(S,0)$ for $i=k+1,\ldots , n$.) By IIA this implies $\varphi (a*S,0)=\varphi (S,0)$, but by COV $\varphi (a*S,0)=a*\varphi (S,0)\ne \varphi (S,0)$. This contradiction proves that $\varphi (S,d)\in \text {PO}(S)$ for all $(S,d)\in \mathbf {\Sigma }$.

  Define $p=\left( (p^R)_{\emptyset \ne R\subseteq N}\right)$ by $p^R_i=\varphi _i(D^R,0)$ for all $i\in R,\,\emptyset \ne R\subseteq N$. By SIR we know that $p^R\in {\mathbb {R}}^R_{++}$ and since $\varphi (D^R,0)\in \text {PO}(D^R)$ we conclude that $\sum _{i\in R}p^R_i=1$ for all $\emptyset \ne R\subseteq N$. We will show that $\varphi =N^{(p)}$. Let $(S,d)\in \mathbf {\Sigma }$. If $R_{(S,d)}=\emptyset$, then $\varphi (S,d)=d=N^{(p)}(S,d)$ by SIR. Thus, suppose $R=R_{(S,d)}\ne \emptyset$. By COV w.l.o.g. we can assume that $d=0$ and $N^{(p)}_i(S,0)=p^R_i$ for all $i\in R$. (Observe that $N^{(p)}_i(S,0)>0$ for all $i\in R$.) Then $S\subseteq D^R$ and $\varphi (D^R,0)=\left( (p^R_i)_{i\in R},0_{N\setminus R}\right) \in S$. By IIA we conclude that $\varphi (S,0)=\varphi (D^R,0)=N^{(p)}(S,0)$.

• 2. It is straightforward to see that $\nu ^q$ satisfies SIR, COV, IIA and DCONT for all $q\in {\mathbb {R}}^n_{++}$. Let $\varphi :\mathbf {\Sigma }\rightarrow {\mathbb {R}}^n$ be a solution that satisfies the axioms. By part 1 of the theorem we know that $\varphi =N^{(p)}$ for some $p=\left( (p^R)_{\emptyset \ne R\subseteq N}\right)$ with $p^R\in {\mathbb {R}}^R_{++}$ and $\sum _{i\in R}p^R_i=1$ for all $\emptyset \ne R\subseteq N$. Let $q=p^N\in {\mathbb {R}}^n_{++}$. If $(S,d)\in \mathbf {\Sigma }$ with $R_{(S,d)}=N$, then, by definition, $\nu ^q(S,d)=N^{(p)}(S,d)$. For any $(S,d)\in \mathbf {\Sigma }$ with $R_{(S,d)}\subsetneqq N$ there exists a sequence $\left( (S,d^m)\right) _m\subset \mathbf {\Sigma }$ such that $R_{(S,d^m)}=N$ for all $m\in {\mathbb {N}}$ and $\lim _{m\rightarrow \infty }d^m=d$. Thus, $\nu ^q(S,d^m)=N^{(p)}(S,d^m)=\varphi (S,d^m)$ for all $m\in {\mathbb {N}}$, and by DCONT we conclude that $\nu ^q(S,d)=\varphi (S,d)$.

• 3. Obviously, $\nu$ satisfies SIR, COV, IIA and SY. Let $\varphi :\mathbf {\Sigma }\rightarrow {\mathbb {R}}^n$ be a solution that satisfies the axioms. By part 1 of the theorem we know that $\varphi =N^{(p)}$ for some $p=\left( (p^R)_{\emptyset \ne R\subseteq N}\right)$ with $p^R\in {\mathbb {R}}^R_{++}$ and $\sum _{i\in R}p^R_i=1$ for all $\emptyset \ne R\subseteq N$. By SY and since $N^{(p)}(D^R,0)=\left( (p^R_i)_{i\in R},0_{N\setminus R}\right)$ it follows that $p^R_i=p^R_j$ for all $i,j\in R,\,\emptyset \ne R\subseteq N$, and therefore $\varphi =N^{(p)}=\nu$.

$\square$