1 Introduction

This article concerns the sensitivity of the experimental determination of reactivity to its changes in a subcritical reactor. Such reactors have been proposed for the transmutation of higher actinides, removed from spent nuclear fuel [1,2,3,4,5], with the help of fast neutrons. Subcriticality provides a higher level of criticality safety than the critical fast reactors used for this purpose. This is because the higher actinides to be transmuted provide fewer delayed neutrons in fissions than the main fission nuclides 235U, 239Pu, and fissionable 238U. There is a great need to determine the reactivity of subcritical systems for detailed testing of different known methods such as the slope, Feynman, and area. One of the problems with determining negative reactivity is the so-called spatial effect [6,7,8]. The measured reactivity in subcritical reactors depends on the detector location in the reactor. This is mainly owing to the different energy spectra of the neutrons in the detectors surrounding. Numerically calculated correction factors help to correct the effects when observed in experimental zero-power subcritical systems.

To minimize the spatial effect, we previously proposed the use of various monoisotopic, fissile, and fissionable nuclides as sensitive detector materials [9]. The Sjöstrand method (also known as the “area” method) [10] is one of the basic experimental methods used to determine the reactivity of the core in subcritical systems. It is convenient because of the small statistical uncertainty; therefore, it was proposed to verify it using general transport equations [11]. As a result, it was shown that the information used to calculate the reactivity should come from the entire system and include the entire neutron spectrum, which requires more detectors. The exact value of the reactivity can then be obtained by calculating the weighted average of the results from all detectors. It will be representative of the entire system. The paper presents the possibility of preparing fission chambers for the experimental determination of subcriticality without the need for time-consuming determination of corrections [9]. The proposed set of reactor detectors consists of mono isotopic chambers. Each chamber is dedicated to a specific place in the system. Individual weights, determined a priori for all detectors and their positions, allow for a quick calculation of the resultant subcriticality of the entire system. Once established, the correction factor could change, mainly due to changes in the core configuration. However, the detector indications and their uncertainty also depend on other changes in the core parameters (e.g., temperature or the degree of submersion of the control rods).

It is required that the chosen method should have a wide range of applications, be simple, and not dependent on many factors, so that it can always be used. In our research, we identified the best detector material used for the detector position to obtain the lowest possible variability of the obtained reactivity values and their sensitivity to changes in basic parameters. We present here the results of the relevant calculations for changes in reactivity, small (variable: submersion of control rods and temperature), and larger (modification of fuel composition). All analyses of monoisotopic detectors are presented in the “Results—Sensitivity” section below. The proposed approach is presented in the paragraph “Mono isotopic chambers” In addition to single isotopic materials, 232Th, 235U, 238U, 237Np, and 239Pu and natural U in fission chambers, we also tested boron enriched to 96% 10B in a detector based on neutron absorption. The final results indicate a very low sensitivity of the results owing to changes in the position of the control rods (between − 10 and 10 pcm). For large changes in fuel enrichment at 235U, the uncertainty range is similar (from − 15 to 5 pcm).

2 Experimental section

2.1 System parameters

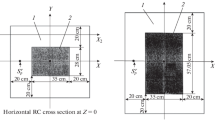
The first condition for obtaining reliable results was a precise evaluation of the eigenvalues of the subcritical system (kkcode) and the delayed neutron fraction (β) for different values of fuel enrichment and temperature. In this study, kkcode is treated as the true value of the neutron multiplier of the system, while karea is the result of the simulation of the experimental determination of this coefficient. We assumed that the satisfactory precision (standard deviation, SD) for kkcode and β should not be greater than ~ 2 pcm. To achieve this precision, we used two calculation methods: one long-term run (1.1 × 109 neutrons) and 60 independent short runs (5 × 104 neutrons). For these calculations, we used MCNP KCODE with the JEFF-3.1 cross-section library and the fast neutron core model VENUS-SC8-3 (F02/05/16) [7], with control rods inserted at a depth of 27.44 cm. In our calculations, the core model contains all 11 detectors (positions shown in Fig. 1).

Fig. 1
figure 1

(Color online) Layout of VENUS SC8-3 (F02/05/16) reactor core configuration [12] with marked detectors [X1–X8 and X13, X14, and X15, last in the cassette (–3,1)], control rods CR1 and CR2, and POAR- powder absorber rod. Assemblies are marked in dark green—safety rods, violet—fuel, light green—lead, gray—graphite and orange—polyethylene blocks with mock-up targets

Full size image

The VENUS system is an experimental subcritical core powered by a GENEPI-3C fast neutron generator based on the (d, t) reaction. The core consisted of fuel assemblies containing uranium metal enriched to 30% by weight of uranium 235,Footnote 1 lead assemblies simulating a coolant, and a lead reflector around the core.

The results of the calculations for the different enrichments are shown in Figs. 2 and 3. In further calculations, the average of two kkcode values was used, one for the long period and the other, with an average of 60 short runs. It turned out, however, that for β more precise values were obtained from the equation resulting from the linear fitting of the dependence of β on enrichment, as illustrated in Fig. 3.

Fig. 2
figure 2

MCNP KCODE computed values of kkcode for 27.44 cm control rod position and different enrichment of uranium fuel. Assumed precision of 1–2 pcm required fit of logarithmic function

Full size image
Fig. 3
figure 3

(Color online) Values of β computed for 27.44 cm CR insertion and different enrichments of U using following methods: MCNP KOPTS (long run) and formula β = 1−ktotnuno/ktotnu (60 short runs)

Full size image

The resulting equation was β [pcm] =  − 2.4535 × Uen + 806.687, where Uen is the mass percentage of 235U in the reactor fuel. The respective standard deviations of kkcode and β were 1.7 pcm and 2.3 pcm.

2.2 Mono isotopic chambers

Because of the difficulties observed in the application of mixtures of fissile and fissionable sensitive detector materials presented earlier [13], we proposed the idea of fission chambers, or other types of neutron detectors, with a single isotope, to be used for subcriticality determination [9]. For each detector, the material optimized for the given detector position in the reactor was selected from a set of nuclides. Computer simulations of the Sjöstrand method experiments should be used to determine the detector response for each material and for all detectors and their positions in the reactor. Numerical simulations were carried out as described in [14] and [9], assuming the detector positions shown in Fig. 1. For each detector position, the neutron flux and its spectrum were calculated using the MCNP code. This, in turn, made it possible to obtain detector responses for various detector nuclides.

Based on the results of the simulation, the weight for every detector, to be used in the final determination of the reactor neutron multiplication factor, is defined as Eq. 1.

$${k}_{\mathrm{area}}={k}_{\mathrm{kcode}} \,\mathrm{for}\, \sum_{i=1}^{n}{\Delta }_{i}{w}_{i}/\sum_{i=1}^{n}{w}_{i}=0\, \mathrm{and}\, {\Delta }_{i}={k}_{\mathrm{kcode}}-{k}_{\mathrm{area},i}; \sum_{i=1}^{n}{w}_{i}=1$$
(1)

where n is the number of detectors, and wi is the weight of the i-th detector with the selected material.

Below, an example of the procedure for selecting nuclides for detector positions is presented for the abovementioned model of reactor VENUS and for all 11 detectors and for standard conditions: control rod (CR) insertion to 27.44 cm, 30% enrichment (235U), and 300 K temperature of the reactor fuel. The following nuclides were assumed as possible detector materials: 235U, 238U, 232Th, 237Np, 239Pu, U-nat, and 10B (96%). For each detector position, for all of the nuclides, simulation of the area method experiment yielded the value of ρ/β and consequently karea. The resulting differences Δ = kkcode−karea are presented in Table 1.

Table 1 Example of results of neutron multiplication factor difference: MCNP kkcode minus karea for selected materials in single simulation of area method (marked values of minimum Δ)
Full size table

Such computations were repeated 11 times, and the set of selected nuclides, optimally suited (with the lowest absolute value of Δ) for all positions, is presented in Table 2.

Table 2 Set of nuclides from 11 repeated simulations for each detector and all materials*
Full size table

Based on the results of the calculations, a set of nuclides was selected with a material with minimum sensitivity for nine detectors and an arbitrarily selected sensitivity for the other two (D3 and D11). These were the following: D1/235U, D2/232Th, D3/239Pu, D4/237Np, D5/237Np, D6/232Th, D7/U-nat, D8/237Np, D9/232Th, D10/239Pu, and D11/U-nat. For each simulation of the experiment, a set of weights for all detectors was determined using the Simplex algorithm. The weight values for the previous results [9] obtained from the 11 simulations are presented in Table 3. In these calculations, the Simplex algorithm started with the same weights for all detectors. In the current sensitivity calculations, the algorithm was repeated four times. After the first, the weights obtained served as initial values in subsequent Simplex applications. Thus, the repeatability of the weight values and their standard deviations improved.

Table 3 Weights of Δ for calculation of weighted average karea from 11 simulations of area method experiment
Full size table

3 Results—sensitivity

Further investigations are another important point when introducing a new experimental method of subcriticality determination, that is, the method’s sensitivity to changing parameters of the core. To determine this in simulations, we selected three possible ways of a parameter change: CR insertion depth in the core, enrichment of uranium fuel, and fuel temperature. The sensitivity of the difference Δ = kkcode−karea to small changes in system reactivity, realized by CR insertion, was tested earlier for some detectors containing mixtures of two isotopes, as reported in [13]. This procedure was repeated for the “monoisotope” detectors, as shown below.

3.1 Control rod insertion depth

Tenfold independent simulations for each of the seven insertion depths and 11 detectors yielded the best nuclides for each detector. All nuclides were considered. In some cases, this was 10 times the same nuclide, but sometimes there were even three choices. In the first approximation, only the results of the best selected material, that is, the most frequently indicated one, were taken into account. Examples are presented in Figs. 4 and 5, respectively.

Fig. 4
figure 4

Results of first approximation of sensitivity to control rod insertion depth for D4. Two nuclides are indicated. Selected is 237Np

Full size image
Fig. 5
figure 5

Results of first approximation of sensitivity to control rod insertion depth for D9. One nuclide is indicated. Selected is 232Th

Full size image

However, we considered that comparing nuclides with different numbers of indications was not representative. Therefore, we repeated evaluations for the detectors with doublets or triplets of nuclides to compare equally representative tenfold results, as presented in Figs. 6 and 7. In this case, it is possible to calculate standard deviations of equal importance. A comparison of the results for all detectors is given in Table 4. One can notice the new average values of each detector weight obtained with the recurrence method, as well as the weighted mean values of Δ for all CR insertions, based on independent simulations of the area method.

Fig. 6
figure 6

Results of final approximation of sensitivity to control rod insertion depth for D3. Three nuclides are indicated. Selected is 239Pu

Full size image
Fig. 7
figure 7

Results of final approximation of sensitivity to control rod insertion depth for D7. Three nuclides are indicated. Selected is U-nat

Full size image
Table 4 Results of Δ from 10 independent simulations of nuclides for all detectors (in pcm)
Full size table

The linear fitting of the calculation results, shown in Figs. 4–7, highlights the trend of changes and its quantitative evaluation, as well as the size of the scatter of the results. The value of the slope of the fitted line is also used in making decisions when choosing the optimal detection material (nuclide) from two or three nuclides with similar other indices.

For detectors D7 and D10, the choice of nuclide with the lowest Δ value was abandoned. Nuclides with slightly higher Δ values were selected using other indicators, that is, the magnitude of the slope of the trend line Δ with respect to the CR immersion depth and whether the Δ values are negative or positive. In the case of detector D7 (Fig. 7), the latter was chosen from the two best nuclides (U-nat and 239Pu) for no good reason. Similarly, for D10, 235U was selected instead of 239Pu.

The resulting weighted mean values of Δ from all detectors for each CR insertion are presented in Fig. 8. A little increase of Δ as the depth of the CR increases (and decreases in kkcode) is visible. The slope value equals 0.26 pcm/cm, while the entire results range from –5 to + 8 pcm. There is also an attempt to introduce a correction to the values, driving an equalization of the results for all insertions. A linear correction is possible and shown in the figure, but only to present how small the differences are.

Fig. 8
figure 8

(Color online) CR insertion depth-related weighted mean of Δ (red) and same after linear correction (blue). Correction according to equation y´ = y–(x•a´–b´), where a´ = a and b´ = –b + mean. Values of a and b from equation of trend (red). Before and after correction, the mean values of Δ for all CR insertions are equal

Full size image

3.2 Fuel enrichment

Larger reactivity changes were realized in the simulations by varying the fuel enrichment. The computed results of the sensitivity of the area method experiment with the use of monoisotopic fission chambers are presented in Table 5. The values of “mean” for detectors are calculated from values of Δ for all enrichments, while that for “weighted mean” are for particular enrichment and for all detectors.

Table 5 Mean values of Δ (from 10 or 20 simulations*) for different fuel enrichments
Full size table

In this step, and with regard to the temperature effect, we used the same detector weights obtained in simulations with different insertion depths CR (Table 4). It is important to check whether the effect of different values of reactivity change on the weights is visible and how large it is. The distributions of delta for the detectors and the resultant values from all detectors are presented in Figs. 9 and 10. It can be observed that for higher enrichment values, the uncertainties of Δ are significantly smaller. The closer to criticality, the smaller the differences between the detectors, and all delta values tend to be zero. This can be explained on the one hand by smaller differences in local neutron spectra, and on the other hand, by better experimental simulation statistics for more efficient multiplication of neutrons when the system is closer to criticality. However, the weighted means of Δ for much smaller enrichments were also quite low (< 15 pcm). It was achieved by optimized values of weights; thus, the most important detector has a 48.5% share in the weighted mean, while the five detectors of smallest importance had only ≤ 2%.

Fig. 9
figure 9

(Color online) Distributions of Δ = kkcode–karea for all detectors and values of fuel enrichment (%235U). For better visibility, axis of Δ is reversed

Full size image
Fig. 10
figure 10

Values of weighted average of Δ from 11 detectors

Full size image

3.3 Fuel temperature effect

Another reason for the change in reactivity during system operation is temperature variation. To account for this effect, we chose the following fuel temperature values in K: 300, 400, 500, and 1000. The values of kkcode and β calculated for these temperatures are given in Table 6 along with the corresponding values of Δ from 11 detectors and their standard deviations. The latter is shown in Fig. 11. It should be emphasized that the JEFF-3.2 cross-section library was used to evaluate the influence of temperature, while JEFF-3.1 was sufficient for all other calculations. Therefore, for the reference conditions (27.44 cm CR insertion, 300 K, and 30% enrichment), the results for Δ differ by approximately 50 pcm. Thus, the influence of the cross-section library was also determined for these two libraries. We believe that this is quite small.

Table 6 Dependence of Δ on fuel temperature from 10 independent simulations of karea experiment
Full size table
Fig. 11
figure 11

Fuel temperature effect to weighted average of Δ from 10 independent experiment simulations for all detectors

Full size image

4 Discussion and conclusions

The proposed new method of designing a set of quasi-mono isotopic detectors for any new subcritical reactor is based on the idea of selecting the detector material that best matches the characteristics of the neutron flux at a given location in the system for all selected detector positions. Of course, each position in the core can be numerically tested at an earlier time, but the core designer, when selecting the detector position, must be free to choose the most desirable ones with respect to the expected applications. The path for obtaining such detector materials is as follows:

  1. 1.

    Precise computer calculations of the eigenvalue of the reactor—kkcode and fraction of delayed neutrons -β (using MCNP KCODE) and

  2. 2.

    Multiple simulations of the Sjöstrand experiment for all planned detector positions and for many possible sensitive detector materials (using the methodology of Talamo et al. [6]).

As a result, for each detector position, the sensitive material is selected with the lowest absolute value of the difference Δ = kkcode–karea. Sometimes, repeated assessments point to different materials. Thus, among all the tested materials, the one that most often showed the minimum Δ value for a given detector position was selected. Rarely, for only positions where two or three materials achieved minimum Δ values, we arbitrarily assumed one of them as potentially more appropriate. Based on the same simulations, a statistical weight was determined for each detector to calculate the common endpoint Δ. The statistical weights, obtained for the entire range of change in reactivity with the control rod insertion depth and where a rather small effect on the weighted mean Δ of all detectors was observed, were also applied to all other factors of reactivity change such as large fluctuations due to varying fuel composition and/or reactor fuel temperature.

The results for the weighted mean from all detectors shown in Fig. 8 present changes in the full range of control rod insertion (between − 10 and 10 pcm). For changes in reactivity owing to different enrichments in 235U between 25.6% and 32.2% (Table 5 and Fig. 10), the corresponding values of Δ are similar (from − 15 to 5 pcm). One can observe a systematic decrease in both Δ and its standard deviation with increasing enrichment. The values of Δ approach zero, and SD approaches ~ 1 pcm. This means that for subriticalities ≥ 0.95, that is, enrichments ≥ 29%, the experimentally determined values of karea have an accuracy better than ± 5 pcm with SD decreasing from 5 to 1 pcm. It can be expected that in real experiments, the statistics of neutron counting will be much better than those in simulations, and the values of SD can decrease from 5 to 1 pcm.

The area method discussed in the article with the use of many selected detectors meets the high stability requirements owing to the variability of the studied factors. Its most important feature is the correct determination of reactivity with variable immersion of control rods, variable temperature, and even variable enrichment. Very good parameters are obtained by introducing many detectors arranged in the system and when we work out a combined response from all detectors.

Our calculations are based on an experimental zero-power reactor, but the main target is to consider high-power cores. The case of detectors for high-temperature subcritical reactors is poorly understood and is almost absent in the available literature [15, 16, 18]. Nevertheless, some detectors in such reactors will be necessary, among other things, to check the value of negative reactivity. The proposed methodology for designing mono isotopic fission chambers should be all the more useful for the optimal operation of these detectors. In addition, other detectors were considered. These can be high-temperature fission chambers working up to 650 °C [15], self-powered detectors [15], and semiconductor SiC [17].

One of the problems related to the determination of negative reactivity is the not-yet-resolved so-called spatial effect [6,7,8]. The measured reactivity in subcritical reactors depends on the location of the detector in the reactor. Numerically calculated correction factors help correct the effects observed in experimental zero-power subcritical systems. The main novelty and significance of this paper is the presentation of the possibility of preparing fission chambers for the experimental determination of subcriticality without the need for time-consuming calculations of corrections after measurement. Individual weights, determined a priori for all detectors and their positions, allow for a quick calculation of the resultant subcriticality of the entire system. We found a very important result, namely, a low sensitivity of the method to changes in reactivity for both small and large variations of control rod submersion, fuel temperature, and fuel composition.