Local determinants of household gas and electricity consumption in Randstad region, Netherlands: application of geographically weighted regression

Abstract

The previous studies on household energy consumption (HEC) are based on an implicit assumption: the impact of geographic determinants on HEC is uniform across a given region, and such impacts could be unveiled regardless of geographic location of households in question. Consequently, these studies have searched for global determinants which explain HEC of all areas. This study aim at examining validity of this assumption in Randstad region by putting forward a question regarding households’ gas and electricity consumption: are the determinants global, stationary across all the areas of the region, or local, varying from one location to another? By application of geographically weighted regression, impact of socioeconomic, housing, land cover and morphological indicators on HEC is studied. It is established that the determinants of HEC are local. This result led to second question: what are the main determinants of gas and electricity consumption in different neighborhoods of Randstad? The results show that variety of factors could be the most effective determinant of gas consumption in different neighborhoods: building age, household size and inhabitants’ age, inhabitants’ income and private housing tenure, building compactness. Whereas, in case of electricity consumption the picture is more deterministic: in most of the neighborhoods the most effective factors are inhabitants’ income and private tenure.

Introduction

The level of household energy consumption (HEC) in Netherlands is high and unsustainable: calculated per capita and adjusted for climate, in 2013 HEC in Netherlands was about 8% higher than average EU-28 [1, 2]; Dutch households’ greenhouse gas emission per capita was 37% higher than the EU-28 average [3]; and sales of gas in the residential and commercial sectors per capita was 202% higher than EU average [2, 4]. Three geographical factors could be accounted for high level of HEC in Netherlands. First, the substantial dependency of HEC on natural gas largely due to the existence of the large amount of natural gas in the northern parts of the Netherlands, in particular the so-called ‘Groningen’ or ‘Slochteren’ gas field which, on its discovery in 1959, seemed abundant enough to satisfy Dutch (and other European countries’) needs for natural gas. This assumption led to a nationwide implementation of natural gas infrastructure; all the households of the country has access to gas and electricity grid. Additionally, given the highly liberalized and competitive energy retail market, the price of energy for household, gas and electricity, is relatively low in Netherlands. In 2012 energy prices for households was 5% lower than the European average [5], whereas GDP per capita was more than 30% higher [6]. In this respect, given the substantial share of HEC from total emission, 16% of total in 2015 [7], policies of Netherlands targeted reduction of HEC by introduction of in Third National Energy Efficiency Action Plan for the Netherlands [8]. The policy document introduces variety of incentives and regulation for curbing HEC which are applicable for all the locations of the Netherlands. The main focus of the introduced measures is improvement of dwellings’ energy efficiency e.g. low interest loans for building insolation, tighter standards for new constructions, restrict measures for efficiency of heating and ventilation systems.

The necessity of reduction of HEC is also reflected between scholars. The existing body of literature on HEC is rich as plenty of previous studies have established links between HEC and variety of determinants among them socioeconomic characteristics, urban form, urban microclimate, housing. However, these studies are limited in scale. Most of the previous studies on HEC use surveys conducted at scale of individual dwellings. Therefore, the larger geographic pattern of HEC, and its geographic drivers, is barely studied. In this respect, missing the larger geographic patterns, all the previous studies are conducted based on an implicit assumption: determinants of HEC are identical in every and each dwelling regardless of its geographic location. In other words, it is assumed that the impact of geographic determinants on HEC is uniform across a given study area, and such impacts could be unveiled by application of aspatial methods. In this respect, vast majority of previous studies have ignored the fact that impact of a given determinant could vary from one location to another. Consequently, these studies bring forward one-size-fits-all type of recommendation for all the areas in question instead of location-specific ones.

The core objective of this study is to bridge this knowledge gap by putting forward two research questions: (a) are the effects of geographic determinant on households’ gas and electricity consumption vary across the neighborhoods of Randstad region? In other words, are the determinants global, stationary across all the areas of the region, or local, varying from one location to another? (b) if the determinants are local, what are the main determinant of gas and electricity use in different neighborhoods of the region? To chase answers to these questions, this study apply geographically weighted regression (GWR) to examine the effect of a variety of socioeconomic, housing, land cover and morphological properties on household’s gas and electricity consumption. In the next parts, first the previous studies on HEC are briefly reviewed. Then after, the methodology, case study and data of this research are described. Subsequently, results are presented and discussed. The paper ends up with a brief conclusions regarding scientific studies and policies on HEC.

Previous studies on HEC

Most of the previous studies on HEC are conducted at the scale of individual dwellings i.e. using household survey regardless of larger geographic pattern of HEC. At this scale, previous studies have shown that variety of factors can affect level of HEC: Inhabitants with higher income have a higher consumption [9, 10]; due to economies of scale, larger household size is associated with lower HEC [11, 12]; age of the inhabitants, particularly presence of senior residents and children, affect HEC [9, 13]; presence of retired or disable inhabitants boost level of HEC [11]; HEC in different housing tenure, due to various systems of paying for energy bills as well as different level of investment in buildings, is significantly different [10, 14]; HEC soar in the building with higher age [9, 10]; land-cover of the neighborhoods can affect land surface temperature and consequently HEC [15, 16]; Wind intensity affect air infiltration and exfiltration of buildings and thus HEC [17, 18]; building density alter HEC by its effect on compactness of dwellings [19, 20]; Rugosity affect effective wind speed and HEC in the neighborhoods [21]; buildings’ surface-to-volume ratio impact HEC by affecting thermal exchange between dwellings [22, 23]; Population density affect HEC via altering level of urbanity and behavior of residents [13, 24]; and solar radiation affect HEC via impacting indoor temperature [25, 26].

Studies on geographic determinates of HEC (conducted on aggregated HEC in neighborhoods, cities, regions, etc.) are few in numbers, however plentiful in amount of information. These studies enhance a geographic understanding of HEC: the locations-specific determinants of HEC at different locations. For instance, a study on rural Chinese areas show that energy price and energy transportation (i.e. distance from coal sources) are among the main determinants of HEC. Furthermore, the study show these effect of vary in different geographies: energy transportation is significant only if the distances is greater than 20 km; impact of energy price soar in high mountains [27]. A study on determinants of HEC in 64 European regions, so-called NUTS2 regions concluded that socioeconomic (income, education, unemployment, poverty) and contextual (e.g. climate) variables significantly affect HEC. The study show that impact of some determinates, e.g. disposable income, is common for all the regions. However that of some determinates vary due to regional development. For example, GDP has a positive effect on HEC of less developed region, due to achieving higher living standard, whereas it has a negative impact on HEC of more developed region, due to achieving higher energy efficiency [28]. A regional study on household’s final energy use in the Netherlands show that quality of buildings and income has a greater impact on HEC of rural areas than urbanized areas. The study conclude that in the suburban areas population density is a significant determinant of HEC, whereas in highly urbanized areas household size or building density are the prominent determinants [29].

Methodology

Prior to application of GWR models, in order to examine the generalizable effects of the geographic determinants on HEC, two conventional linear regression models (OLS) are developed:

$$y_{i} = \beta_{0} + \mathop \sum \limits_{k} \beta_{k} x_{ik} + \varepsilon_{i}$$

(1)

where $y_{i}$ represents the estimated value of HEC (gas or electricity consumption) in the location i, $\beta_{0}$ shows the intercept, $\beta_{k}$ denotes the coefficient slope of the independent variable k, $x_{ik}$ represents the value of independent variable k in location i. $\varepsilon_{i}$ accounts for the random error term in location i. Subsequently, in order to examine the location-specific effects, two GWR models [Eq. (2)] are applied.

$$y_{i} = \beta_{0} \left( {\mu_{i} ,\vartheta_{i} } \right) + \mathop \sum \limits_{k} \beta_{k} (\mu_{i} ,\vartheta_{i} )x_{ik} + \varepsilon_{i}$$

(2)

where $\left( {\mu_{i} ,\vartheta_{i} } \right)$ represents the geographic coordination of location i, $\beta_{k} \left( {\mu_{i} ,\vartheta_{i} } \right)$ and $\beta_{0} \left( {\mu_{i} ,\vartheta_{i} } \right)$ are the local coefficient and intercept of independent variable k estimated specific to location i. The local coefficients at location i is calculated by [Eq. (3)]:

$$\hat{\beta }\left( {\mu ,\vartheta } \right) = \left( {X^{T} W\left( {\mu ,\vartheta } \right)X} \right)^{ - 1} X^{T} W\left( {\mu ,\vartheta } \right)y$$

(3)

where $W\left( {\mu ,\vartheta } \right)$ is the spatial weighting matrix which conceptualize the importance of adjacent neighborhoods of location i:

$$W_{{ij}} = \left\{ {\begin{array}{ll} {e^{{( - d_{{ij}}^{2} /\theta _{{i\left( k \right)}}^{2} )}} ,} & \quad {{\text{if}} \quad d_{{ij}} < \theta _{{i\left( k \right)}} } \\ {0,~} & \quad {\text{otherwise}} \\ \end{array} } \right.$$

(4)

where $W_{ij}$ denotes the weight of location j for the estimation of the location i coefficients, $d_{ij}$ is the geodesic distance between location i and j. $\theta_{i\left( k \right)}$ is an adaptive bandwidth denoting distance from the kth nearest neighbor. Using ArcGIS (version 10.2), the bandwidths of the models are specified so as to minimize the Akaike Information Criterion (AIC) of the GWR models.

The performance of GWR and OLS models are compared by means of five tests. First, adjusted R² of the two models are compared. Second, by comparison between the AICc (corrected Akaike’s Information Criterion) of the models. Typically, at least three points decrease in AICc is seen as a significant improvement (e.g. [30, 31]). Third, comparison of randomness of the distribution of the residuals of the models—validated by Moran’s I Index. The index is a measure of spatial autocorrelation ranged between − 1 and + 1; value closer to zero shows more random distribution. Fourth, in order to examine whether the effect of the determinants on HEC vary across the study areas, stationary indices—proposed by Charlton et al. [32]—of independent variables are calculated. To do so, interquartile ranges of the standard error of coefficients in the GWR model are divided by twice the standard error of coefficients in the OLS model. If value of the stationary index is equal to or greater than one, it indicates that the effect of the given independent variable on HEC is spatially non-stationary. Fifth, ANOVA tests, to compare residuals of GWR and OLS models, are applied.

Case study and data

Case study area and analysis area

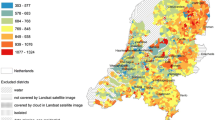
The spatial element used in this study are the buurten, spatial divisions defined by the Dutch central bureau of statistics (CBS)—what we call as neighborhood. The case study of this research—what we call as “study area”—is consisted of neighborhoods of the Randstad region. The Randstad is a highly urbanized metropolitan area located in the south west of the Netherlands consist of the four major cities of Amsterdam, Rotterdam, the Hague and Utrecht, and the areas between them—the so-called “green heart”. In order to avoid the boundary-effect problem in GWR models, all the calculations are carried out on the “study area” plus a 20 km buffer—what we call as “analysis area”. Although all calculations are carried out on the analysis area, ultimately merely the results obtained for “study areas” are taken into consideration (Fig. 1).

Fig. 1

Location map of study area and analysis area

Dependent variables

The dependent variables of the study are gas and electricity consumption per capita within dwellings [33]. As the available data does not show the areas equipped with solar energy supply or district heating, the abnormal values of gas and electricity use needed to be filtered out (incidents with z-value ≤ − 2.5 or z-value ≥ + 2.5) Ultimately, the “analysis area” consists of 3514 neighborhoods and the “study area” of 2413 (Fig. 2a, b). The Moran’s Index test show that high values of gas and electricity consumption (both in study and analysis area) are spatially clustered across the region. The respective Moran’s I z-score is well beyond the threshold of 2.58 (which indicate spatially clustered pattern): 36.8 (in case of gas use in study area), 49.7 (in case of gas use in analysis area), 42.3 (in case of electricity use in study area), 57.6 (in case of electricity use in analysis area). Thus, as spatial variation is significant, application of GWR is essential for enhancing better understanding of such geographic pattern.

Fig. 2

Dependent variables of study: a annual gas consumption per capita 2013 (Mega Joule), b annual electricity consumption per capita 2013 (Mega Joule)

Independent variables

This study use five dependent variables. The variables compress the effect of 21 indicators by means of factor analysis. By choice of the 21 indicators, we tried to include all the potential effective factors without a priori selection (see Table 1). Socioeconomic and housing variables are taken from CBS, 2013 [25]. Land cover variables are extracted from a Bodemgebruik database, 2012 [34]. Building height database in the Netherlands, 3D BAG [35], is used to prepare a digital elevation model (DEM). Cell size of DEM is 10 m. The latter in utilized to prepare urban form indicators. In the next part, a more detailed explanation of some of the variables is presented.

Table 1 The five Independent variables of the study compress the effect of 21 indicators

According to Adolphe [21], the variation of building height, or what he calls as rugosity, could have a significant effect on the urban microclimate. We calculated rugosity as the standard deviation of height values (including those with zero height) of DEM. The frontal area index (λ_f) is the ratio of the total area of external building walls to the total area of the neighborhood. In order to calculate λ_f, firstly external walls need to be identified. To do so, using ArcGIS 10.2 Focal Flow tool, 3 × 3 immediate neighbors of each DEM cell is studied. It is determined that which sides of each DEM cell are external wall (i.e. are not occupied with a building cell or are occupied with a shorter building). The obtained information is used for calculation of total amount of external walls at each DEM cell. This has been instrumented for calculation of λ_f and subsequently aerodynamic roughness length (ARL). ARL is the height in which the effective wind speed is theoretically zero. Higher values of ARL correspond with lower wind intensity [36]. The morphometric model introduced by Macdonald et al. [37], one of the most comprehensive models according to a review by Grimmond and Oke [38], is used:

$$\frac{{Z_{d} }}{{Z_{H} }} = 1 + \alpha^{ - BCR} \left( {BCR - 1} \right)$$

(5)

$$\frac{{Z_{0} }}{{Z_{H} }} = \left( {1 - \frac{{Z_{d} }}{{Z_{H} }}} \right){ \exp }\left( { - \left( {\frac{{0.5\beta C_{D} \lambda_{f} }}{{k^{2} }}\left( {1 - \frac{{Z_{d} }}{{Z_{H} }}} \right)} \right)^{ - 0.5} } \right)$$

(6)

where Z₀ is aerodynamic roughness length for momentum, Z_d is zero-plane displacement height, Z_H is height of roughness element (m), BCR is building coverage ratio, λ_f frontal area index, α = 4.43, β = 1.0, k = 0.4, and C_D ≅ 1.

Deploying the Arcgis 10.2 solar radiation toolbox, the DEM model is used to calculate solar radiation (SLR) on summer (21 June) and winter (21 December) solstice of 2013. The average value of the 2 days is used to calculate two variables: solar radiation per square meters of neighborhoods’ surface [solar radiation on neighborhood (WH/m²)] and per cubic meters of the buildings [solar radiation per building volume (WH/m³)].

To address the potential multicollinearity between the 21 indicators, factor analysis, with extraction method of principal component analysis and rotation method of Oblimin with Kaiser Normalization, is deployed. As result, the effect of the indicators is compressed in five factors (Table 1). As the extraction method is principal component analysis, a small level of independence between the obtained factors is tolerated. Consequently, one of the initial variables, floor area ratio (FAR), has made contribution to two of the factors. Whereas the rest of 20 variables have merely contributed to one factor. The factors explain almost 75% of the total variance of the 21 variables. The first factor, FAC1 Population density and built-up areas, is positively loaded onto built up coverage (%), BCR, λ_f, population density and FAR, and negatively on green-coverage (%). FAC2 Income and private tenure, is positively loaded onto income per capita and property value, and negatively loaded onto disability (%), unemployment (%) and public rental (%). FAC3 Household size and population younger than 14 years old, is positively loaded onto population ages 0–14 (%) and household-size, and negatively loaded onto population ages 65 + (%). FAC4 Building age, is positively loaded onto building median age, and negatively onto floor area after introduction of 1988 building standards (%). FAC5 Building compactness, is and positively onto FAR, rugosity and ARL and negatively onto solar radiation per building volume (WH/m³) and solar radiation on neighborhood (WH/m²).

Results

Comparison between performance of GWR and OLS models

A comparison between adjusted R² of the two OLS and GWR models, shows that all three of the GWR models have a better goodness-of-fit (Table 2). The adjusted R² of the GWR model of gas consumption is some 15% higher than that of OLS. The corresponding number for the electricity consumption models is about 17%. The local R² of the GWR models (Fig. 3) show that in more than 76% of the areas estimation of gas and electricity consumption produced a better R² than OLS model.

Table 2 Diagnostic statistics in GWR and OLS models

Fig. 3

Local adjusted R-squared of GWR estimation of: a gas consumption, b electricity consumption

The comparison between the AICc (corrected Akaike’s Information Criterion) of the GWR and OLS models shows a remarkable improvement in the case of GWR models. The results show that the residuals of GWR models are more randomly distributed rather than those of OLS models; the Moran’s Indices of the GWR models are substantially closer to zero than those of OLS models. The stationary indices of all the independent variables of the GWR models are greater than 1. This indicates that the effect of the variables on HEC is spatially non-stationary (Table 2).

ANOVA test of the residuals in GWR and OLS models indicate a significant improvement in case of GWR models (Table 3).

Table 3 ANOVA test of residuals of GWR and OLS models

Local determinants of HEC

Figure 3 shows the estimated local standardized coefficients of the independent variables in the two GWR models. According to the results of the GWR models, the percentage of the areas with a significant coefficient of FAC1 Population density and built-up areas is rather small (Fig. 4a, f). In the case of the gas consumption model the impact of the factor is significant—at p value < 0.1 level—in 63% of the areas. In case of electricity consumption the percentages is 45%. However, the magnitude of the significant coefficients is considerable in a substantial portion of the areas. The significant coefficients are negatively signed. The magnitude of the coefficient is almost similar in case of the two models.

Fig. 4

Local standardized coefficients: a–d gas consumption model, f–j electricity consumption model

The results of the GWR models of gas and electricity consumption show that in almost all of the areas, the coefficients of FAC2 Income and private tenure are significant (Fig. 4b, g). Roughly speaking, signs of all the significant coefficients are positive. The largest effect of the factor is observed in the case of electricity consumption model (according to the mean standardized coefficient of the GWR model).

The results of GWR models of gas and electricity consumption show that in more than 97% of the areas, the coefficients of FAC3 Household size and population younger than 14 years old are significant (Fig. 4c, h). The sign of all the significant coefficients is negative. The magnitude of the coefficients is almost similar in the two models.

The results show FAC4 Building age has significant effect on a gas consumption in more than 95% of the areas (Fig. 4d, i). However, In case of electricity consumption the factor is not effective in almost 70% of the areas. The magnitude of the coefficients (assessed by the mean value of the GWR models) is remarkably high in the case of gas consumption model. The sign of all the coefficients is positive. In the electricity consumption model, though positive, the magnitude of the coefficients is close to zero.

According to the results of the GWR models, in the case of the gas consumption model, the impact of FAC5 Building compactness is significant in 70% of the areas (Fig. 4e, j). In the case of electricity consumption, the corresponding number is 44%. The coefficients, except in the case of 5% of the areas in electricity consumption model, are negative. The largest magnitude of the effect is observed in the case of the gas consumption model.

Figure 4 illustrates the largest local standardized coefficients (in absolute value)—what we call as the most effective local determinant—in different neighborhoods of the study area. The results show that, variety of factors could be the most effective determinant of gas consumption in different neighborhoods: FAC4 Building age in 37% of the neighborhoods, FAC3 Household size and population younger than 14 years old in 29% of the neighborhoods, FAC2 Income and private tenure in 23% of the neighborhoods, FAC5 Building compactness in 11% of the neighborhoods (Fig. 5a). In case of electricity use model, the picture is more deterministic: in 84% of the neighborhoods FAC2 Income and private tenure is the most effective factors. In the rest of the areas FAC3 Household size and population younger than 14 years old is found to be the most effective (Fig. 5b).

Fig. 5

The most effective local determinants—largest local standardized coefficients (in absolute value)—of: a gas consumption, b electricity consumption

Discussion

The results of GWR models of gas and electricity consumption show that, in almost all the neighborhoods, sign of the coefficients is similar. However, the magnitude of the coefficients remarkably vary across the neighborhoods. The coefficients of FAC1 Population density and built-up areas are negative in almost all the areas. This could be due to higher air temperature, consequent to higher surface temperature, in the neighborhoods with higher percentage of built-up areas (similar to what is suggested by [20]). Also the residents of areas with higher population density, say more urbanized, could be more engaged with outdoor activities and spend less time within their dwellings. This could significantly reduce HEC (similar to the conclusion drawn by [39, 40]). The coefficients of FAC2 Income and private tenure are positive in all of the neighborhoods. Presumably, high-income residents live in larger dwellings and possess more appliances at their homes (similar to conclusion drawn by [41]). All the local coefficients of FAC3 Household size and population younger than 14 years old are negative. This could be due to economies of scale—as suggested by variety of previous studies (e.g. [42]).

Increase in FAC4 Building age has a large impact on increasing gas consumption. This is presumably due to lower energy efficiency of buildings (as concluded by variety of previous studies e.g. [23]). The effect of the factor on electricity consumption is not significant in most of the neighborhoods. However, if significant, the sign of coefficients are positive. Almost all of the local coefficients of FAC5 Building compactness are negative. This could be due to compactness of buildings and higher heat exchange between the dwellings in the neighborhoods with higher FAR (as concluded by variety of authors among them [10]). It also could be due to lower wind intensity (associated with high ARL) which reduce air infiltration/exfiltration and therefore buildings’ thermal loss [18]. Additionally, lower solar radiation in the neighborhoods with higher FAC5 Building compactness, could reduce electricity consumption for cooling and ventilating [43].

The results show that variety of factors could be the most effective determinant of gas consumption in different neighborhoods. Whereas, in case of electricity consumption FAC2 Income and private tenure is the most effective determinant in vast majority of the neighborhoods. This could be explained by different final end-uses of gas and electricity in residential sector.

Eurostat data on final energy consumption of Dutch households in in 2015 [44], show that gas was the main source for space heating (87%) and warm water (90%). In this respect, the results of this study is in line with those of previous studies which show space and water heating could be affected by variety of determines among them occupant characteristics(e.g. [45]), building characteristics (e.g. [46]), housing tenure (e.g. [47]), urbanization rate (e.g. [48]), and number of dwellings per buildings (e.g. [49]). When it comes to electricity consumption, more than 50% of households’ consumption is for lightening and appliances [44]. In this respect the results of this study is in line with previous studies which suggest that households with higher income consume more electricity for lightening—due to owing larger dwellings—and appliances—due to possession of greater number of devices (e.g. [41]).

Conclusion

HEC has been of interest of many researchers and policy makers in the last decades. However, there is an eminent knowledge gap in the existing body of literature on HEC: all the previous studies have implicitly presumed that HEC could be explained by set of spatial stationary reasons and therefore has tried to unveil such everywhere-true reasons. The results of this study show that such presumption is questionable. It is obtained that, in the Randstad region, the of effects of socioeconomic, housing, land cover and morphological indicators on HEC vary from one location to another. In this respect, the main conclusion of this research is: in order to provide a better understanding of HEC, studies in this field need to search for the location specific factors which affect HEC in a given neighborhood.

It is also obtained that GWR models provide a better estimation of HEC rather than the OLS models. Previous studies on HEC have applied a wide range of aspatial techniques e.g. machine learning, linear regression, structural equation models, simulation models (see the review [50]). However, HEC studies lag behind in application of spatial econometrics methods. This studies concludes that HEC studies need to be enriched by further application of spatial statistics.

The results of this study also has a policy implication. By application of GWR, It is established that variety of factors could be the main determinants of level of gas and electricity consumption in different neighborhoods. This suggests that policy making regarding HEC needs a shift in perspective: one-size-fits-all type policies need to be enriched by introduction of location-specific strategies. By proposing such strategies, policy makers could optimally prioritize different incentives and obligations in different neighborhoods. Additionally, the policies as like Third National Energy Efficiency Action Plan [8] need to break through the narrow perspective of building energy efficiency, and take socioeconomic and morphological aspects into their consideration. Another policy implication regards the effect of FAR on household energy consumption, particularly gas use, within dwellings. It is obtained that FAR has a dual impact on consumption: On one hand FAR is associated with level of urbanity (i.e. more population density and built up surfaces), on the other hand FAR affect level of compactness (i.e. lower wind speed and solar radiation). Considering construction of 500,000 new dwellings in Randstad region according to 2014 vision [51], further studies need to assess the impact of this extra FAR on energy household energy consumption.

Further studies need to adopt the existing methods for studying microclimate factors –i.e. air and surface temperature, humidity—to enrich the estimates of HEC (similar to what is applied by [52,53,54]). Additionally, the effect of ever growing urbanization patterns (similar to that of [55, 56]) on HEC need to be further studied. Further research could also seek for a comprehensive framework which combine HEC with potential locations for energy production (similar to the study by [57]). The last, in this study the determinant of gas and electricity consumption have been independently studied, the further studies could investigate the spatial autocorrelation between the two (similar to the methodology used by [58]).