Bayesian adaptive testing with polytomous items

Abstract

An extremely efficient MCMC method for Bayesian adaptive testing with polytomous items is explained both conceptually and in mathematical detail. Results from extensive simulation studies with different item pools, polytomous response models, calibration sample sizes, and test lengths are presented. In addition, the case of adaptive testing from pools with a mixture of dichotomous and polytomous items is addressed.

1 Introduction

The number of applications of computerized adaptive testing (CAT) has increased substantially over the past decade or so. For instance, it has now entered K-12 assessment programs in the U.S. to offer individualized adaptive assessments to millions of students per annum. It has also gained popularity in the patient-reported health outcomes measurement arena, where it has reduced the response burden to patients due to the typical repeated measures designs used in clinical studies. These changes, along with the general trend toward more frequent, on-demand testing (e.g., formative assessment and ecological momentary assessment) have led to the need of continuous item field testing and calibration, and consequently to pressure to reduce sample sizes. Hence, the renewed interest in the problem of how to deal with remaining parameter uncertainty in adaptive testing.

van der Linden and Glas (2000) evaluated the impact of item calibration error in adaptive testing. Due to the nature of its commonly used maximum-information (MI) item-selection criterion, items with large positive error in their discrimination parameters are favored, which tends to result in underestimation of the standard errors of the final ability estimates in fixed-length and premature termination of the test in variable-length adaptive testing. The consequences of this capitalization on chance are mitigated to some degree by the presence of item-selection constraints and the use of item-exposure control methods. But, rather than waiting to see how these factors will actually play out in real-world testing programs, a more practical approach seems to directly account for the parameter uncertainty during ability estimation and item selection. A proper way of doing so is through a Bayesian treatment of the problem based on the information in the full joint posterior distribution of all relevant parameters. Though the approach has already been studied for the case of uncertainty about the ability parameter using empirical Bayes methods (Choi and Swartz 2009; van der Linden 1998; van der Linden and Pashley 2000), the necessity to account for the uncertainty about the item parameters during adaptive testing as well is still rather unrecognized.

As a Bayesian approach to any model uncertainty involves integration of the joint posterior density over its nuisance parameters, it may appear to be too time intensive for real-time application in adaptive testing. However, recently, for the case of the 3PL model, first for use in online continuous item calibration (van der Linden and Ren 2015) and then for item selection in adaptive testing (van der Linden 2018; van der Linden and Ren 2020), an optimized Markov chain Monte Carlo (MCMC) algorithm has been presented. The algorithm is based on Gibbs sampling with a Metropolis–Hastings (MH) step for the conditional posterior distribution of the intentional parameters while resampling the most recent updates of the distributions of all nuisance parameters. Because of rapid mixing of the Markov chain and simple posterior calculations, it was shown to be extremely efficient with running times for the 3PL model entirely comparable with those for the MI algorithms currently in use for adaptive testing.

As already noted, interest in adaptive testing with polytomous items has grown considerably, initially outside the educational testing arena (e.g., patient-reported outcomes measurement) but now also in educational testing (e.g., use of technology-enhanced items). In principle, application of the algorithm to the case of one of the common polytomous models may seem to require the replacement of a few key mathematical expressions only. However, there are critical factors that may affect its performance for these models as well, among them the facts that their information functions are multi-modal and typically span a much wider ability range than for the 3PL model. Consequently, the algorithm may behave differently as a function of the calibration sample size, item-pool composition, and the test length, for instance. The goal of the research reported in the current paper was to find the modifications necessary to implement the algorithm for polytomous items and evaluate their consequences. More specifically, this paper presents the derivation of all necessary mathematical expressions for ability estimation and item selection for the main polytomous response models, as well as the outcomes of extensive simulation studies to assess the performance of the algorithm relative to those for conventional adaptive testing with all item parameters treated as if they were known.

As for the impact of a fully Bayesian approach on the statistical properties of the ability estimates, two opposite effects should be expected. On one hand, as already noted, ignoring the remaining error in the item parameters implies overestimation of our certainty about them and consequently the report of too optimistic estimates of the accuracy of the final ability estimates. Use of this approach to adaptive testing is, therefore, expected to result in more realistic, larger estimates of their inaccuracies. On the other hand, due to its honesty, the earlier problem of capitalization on error in the item parameters is avoided and we should profit from an improved design of the adaptive test. Ideally, the latter should compensate for the former, which indeed was observed in the earlier study for the 3PL model (van der Linden and Ren 2020). As both effects depend on the nature of the response model, it is yet unknown whether the same kind of tradeoff would hold for adaptive testing with polytomous items.

Two different real-world measurement settings involving polytomous items with contrasting objectives and constraints were used. The first was a health-related quality of life (HRQOL) measurement setting where self-reported outcomes such as anxiety, depression, fatigue, pain, and physical functioning were measured through items with Likert-type response categories (e.g., Never, Rarely, ..., Always). The second was an educational setting with ability measured through short partial-credit scoring of constructed-response items and technology-enhanced items. HRQOL measures commonly tap into one highly specialized (and often narrowly-defined) domain at a time, with a high-level of homogeneity of items within each domain. As a result, its items tend to carry a substantial amount of information, supporting extremely short adaptive tests (e.g., less than five items). Contrastingly, educational tests usually need to encompass different content categories, item types, and response formats. Though their items are still amenable to unidimensional scaling, their level of homogeneity is often less compared to HRQOL and may require longer test lengths. Furthermore, it would be unusual for educational testing to be based solely on polytomously scored items; a more common scenario would be testing with a mixture of both dichotomous and polytomous items. The two entirely different measurement settings in this study were chosen, because together they give a robust impression of the results of Bayesian adaptive testing with polytomous items.

2 Models

Two models commonly fitted to ordered polytomous responses are the graded response model (GRM; Samejima 1969) and the generalized partial credit model (GPCM; Muraki 1992). The GRM defines the probability of selecting the ordered response categories $c=0,1,\ldots ,m_{i}-1$ of item i as

$$\begin{aligned} P_{ic}(\theta )\equiv P_{ic}^{*}(\theta )-P_{i(c+1)}^{*}(\theta ), \end{aligned}$$

(1)

where $m_{i}$ is the number of response categories, $\theta$ is the examinee ability or trait parameter, and $P_{ic}^{*}(\theta )$ is defined as

$$\begin{aligned} P_{ic}^{*}(\theta )\equiv {\left\{ \begin{array}{ll} \begin{array}{l} 1\\ \frac{\exp [a_{i}(\theta -b_{ic})]}{1+\exp [a_{i}(\theta -b_{ic})]}\\ 0 \end{array} & \begin{array}{l} c=0\\ 0<c<m_{i}\\ c=m_{i}, \end{array}\end{array}\right. } \end{aligned}$$

(2)

with $a_{i}$ and $b_{ic}$ denoting discrimination and category-boundary parameters, respectively.

The GPCM defines the probability of receiving a score on item i in category c as

$$\begin{aligned} P_{ic}(\theta )\equiv \frac{\mathrm {e}\mathrm {x}\mathrm {p}\left[ \sum _{\nu =0}^{c}Z_{i\nu }(\theta )\right] }{\sum _{c=0}^{m_{i}-1}\mathrm {e}\mathrm {x}\mathrm {p}\left[ \sum _{\nu =0}^{c}Z_{i\nu }(\theta )\right] } \end{aligned}$$

(3)

with

$$\begin{aligned} Z_{i\nu }\equiv a_{i}(\theta -b_{i\nu }), \end{aligned}$$

(4)

where c, $m_{i}$ and $a_{i}$ are defined as before but $b_{i\nu }$ now is a step difficulty parameter and $b_{i0}=0$. Though the two models are equivalent for $m_{i}$ $=$ 2, their item parameters are not directly comparable when $m_{i}$ > 2.

For convenience, for both models, we use ${\varvec{\eta }}_{i}\equiv \left( a_{i},b_{i1},\dots ,b_{i(m_{i}-1)}\right)$ to represent the parameters of item $i$. Generally, the GRM has been favored for fitting rating scale responses (e.g., Likert-type data) whereas the GPCM has been used to score responses to items in cognitive tests. However, for most practical applications, the choice between the two models has been shown to be rather inconsequential.

3 Methods

3.1 MCMC algorithm

The proposed MCMC algorithm is a special Gibbs sampler alternating in real-time between the sampling of the conditional posterior distributions of $\theta$ and the item parameters. However, the latter are just the marginal posterior distributions obtained during their calibration. Therefore, an efficient approach is to save short vectors of draws from these distributions during item calibration and randomly resample them during operational testing. The only remaining part is sampling of the posterior distribution of a single ability parameter for which, because of the sequential nature of adaptive testing, an efficient Metropolis–Hastings (MH) step is possible. The following two sections describe the algorithm more formally.

3.2 Sampling the conditional posterior distribution of ${\eta }_{i}$

Let ${\varvec{\eta }}_{i}^{(s)}=\left( \varvec{\eta }_{i}^{(1)},\dots ,\varvec{\eta }_{i}^{(S)}\right)$ be the vector with S draws for the parameters of item i saved from its calibration for use during operational testing. Random resampling of the vector during the Gibbs iterations amounts to the use of an independence sampler, that is, an MH step with a proposal distribution that does not depend on the previous draw (Gilks et al. 1996, sect. 1.4.1). Choice of this independence sampler has two extremely efficient features: (i) its proposal distribution already matches the stationary distributions for the item parameters and (ii) the acceptance probabilities for each of these parameters are equal to one. A formal proof of these claims was provided by van der Linden and Ren (2015).

3.3 Sampling the conditional posterior distribution of $\theta$

A regular MH step is used to sample the only remaining conditional posterior distribution, the one for the test taker’s ability parameter, $\theta$. Under mild conditions, the distribution is known to converge to a normal centered at its true value (Chang and Ying 2009). Practical experience has shown the convergence to be fast.

The focus is on the update of the posterior distribution of $\theta$ upon item i in the pool administered as the kth item to the examinee. Suppose the examinee’s response to the item was in category c. Let $\varvec{\theta }_{k-1}^{(s)}\equiv (\theta _{k-1}^{(1)},...,\theta _{k-1}^{(S)})$ be the draws saved from the stationary part of the Markov chain during the previous update, where $\varvec{\eta }_{i}^{(s)}$ and $\varvec{\theta }_{k-1}^{(s)}$ are taken to be of equal length for notational convenience only (for the case of unequal length, the shorter vectors are assumed to be recycled against the longer). An obvious choice is to use a prior distribution with mean and variance equal to those of the last posterior distribution. More formally, the prior distribution is N($\mu _{k-1},\sigma _{k-1}^{2})$ with

$$\begin{aligned} \mu _{k-1}\equiv S^{-1}\sum _{s=1}^{S}\theta _{k-1}^{(s)} \end{aligned}$$

(5)

and

$$\begin{aligned} \sigma _{k-1}^{2}\equiv S^{-1}\sum _{s=1}^{S}\left( \theta _{k-1}^{(s)}-\mu _{k-1}\right) ^{2}. \end{aligned}$$

(6)

During iterations $r = 1,\ldots , R$ of the MH step, the proposal density $q_{k}^{(r)}$ is

$$\begin{aligned} q_{k}\left( \theta |\theta ^{(r-1)}\right) \equiv N\left( \theta ^{(r-1)},\sigma _{k-1}^{2}\right) , \end{aligned}$$

(7)

where $\theta ^{(r-1)}$ is the immediately preceding draw and $\sigma _{k-1}^{2}$ is the previous posterior variance in (6). It follows that the probability of accepting the candidate value $\theta ^{*}$ as the rth draw of $\theta$ is equal to

$$\begin{aligned} \text {min}\left\{ \frac{N(\theta ^{*};\mu_{k-1},\sigma _{k-1}^{2})P_{i_{k}c}(\theta ^{*};\varvec{\eta }_{i_{k}}^{(r)})}{N(\theta ^{(r-1)};\mu_{k-1},\sigma _{k-1}^{2})P_{i_{k}c}(\theta ^{(r-1)};\varvec{\eta }_{i_{k}}^{(r-1)})},1\right\} , \end{aligned}$$

where $\varvec{\eta }_{i_{k}}^{(r)}$ is the rth value sampled from the vector of draws $\varvec{\eta }_{i_{k}}^{(s)}$ stored in the system for item $i_{k}$. Observe that the only thing required to calculate the numerator is the simple product of a normal density with the probability of the observed response. The denominator was already calculated in the preceding iteration step.

Of course, both the prior and proposal distributions are always a little wider than the posterior distributions at the current update. But this is exactly what we want these distributions to be in an MH step for a low-dimensional parameter (Gelman et al. 2014, sect. 12.2).

3.4 Item-selection criteria

The (expected) Fisher information for a response to item i is defined as

$$\begin{aligned} I(\theta )&\equiv \mathcal {E}\left[ \left( \frac{\partial }{\partial \theta }\log P_{ic}(\theta ) \right) ^{2}\mid \theta \right] \nonumber \\&=\sum _{c=0}^{m_{i}-1}\left( \frac{\partial }{\partial \theta }\log P_{ic}(\theta ) \right) ^{2}P_{ic}(\theta )\nonumber \\&= \sum _{c=0}^{m_{i}-1}\frac{1}{P_{ic}(\theta )}\left( \frac{\partial }{\partial \theta }P_{ic}(\theta )\right) ^{2}. \end{aligned}$$

(8)

The conventional MI criterion uses the information measure with point estimates substituted for all of its parameters. That is, it selects the next item as

$$\begin{aligned} i_{k+1}=\arg \max _{j}\left\{ I_{j}\left( \hat{\theta _{k}}; \hat{{\varvec{\eta }}}_{j}\right) :j\in R_{k+1}\right\} , \end{aligned}$$

(9)

where $R_{k+1}$ is the set of items available in the item pool to select the (k+1)th item and $\hat{\varvec{\eta }}_{j}$ and $\hat{\theta }_{k}$ are point estimates of the parameters of item j and the examinee’s ability parameter after the response to the kth item in the test, respectively.

The fully Bayesian (FB) version of the criterion uses the posterior expected information of (8) defined as

$$\begin{aligned} I_{i}^{B}\equiv \int \int I\left( \theta ; \varvec{\eta }_{i_{k}}\right) f\left( \theta |\varvec{u}_{k}\right) f \left( \varvec{\eta }_{i_{k}}\right) d\theta d\varvec{\eta }_{i_{k}}, \end{aligned}$$

(10)

where $f\left( \theta |\varvec{u_{k}}\right)$ is the posterior density of ability parameter $\theta$ given the examinee’s response vector $\varvec{u}_{k}$ for the first k items and $f\left( \varvec{\eta }_{i_{k}}\right)$ is the posterior density of item parameter vector $\varvec{\eta }_{i_{k}}$. The next item selected is

$$\begin{aligned} i_{k+1}=\arg \max _{j}\left\{ I_{j}^{B}:j\in R_{k+1}\right\} . \end{aligned}$$

(11)

For the GRM, the partial derivative in (8) is equal to

$$\begin{aligned} \frac{\partial P_{ic}(\theta )}{\partial \theta }=\frac{\partial P_{ic}^{*}(\theta )}{\partial \theta }-\frac{\partial P_{i(c+1)}^{*}(\theta )}{\partial \theta } \end{aligned}$$

(12)

with

$$\begin{aligned} \frac{\partial P_{ic}^{*}(\theta )}{\partial \theta }=a_{i}P_{ic}^{*}(\theta ) (1-P_{ic}^{*}(\theta )) \quad \text { for }\; c=0,\dots ,m_{i}. \end{aligned}$$

(13)

Thus, for this model, the Fisher information can be written as

$$\begin{aligned} I(\theta )&=\sum _{c=0}^{m_{i}-1}\frac{a_{i}^{2}}{P_{ic}(\theta )}\left( P_{ic}^{*} (\theta )(1-P_{ic}^{*}(\theta ))-P_{i(c+1)}^{*}(\theta )(1-P_{i(c+1)}^{*}(\theta )) \right) ^{2}\nonumber \\&= \sum _{c=0}^{m_{i}-1}\frac{a_{i}^{2}}{P_{ic}(\theta )}\left[ \left( P_{ic}^{*} (\theta )-P_{i(c+1)}^{*}(\theta )\right) \left( 1-P_{ic}^{*}(\theta )-P_{i(c+1)}^{*} (\theta )\right) \right] ^{2}\nonumber \\&= \sum _{c=0}^{m_{i}-1}a_{i}^{2}P_{ic}(\theta )\left( 1-P_{ic}^{*}(\theta ) -P_{i(c+1)}^{*}(\theta )\right) ^{2}. \end{aligned}$$

(14)

Again, rather than plugging point estimates of all parameters into the expression, the FB criterion is calculated averaging over the current posterior samples; that is, as

$$\begin{aligned} I_{i}^{B}& \equiv S^{-1}\sum _{s=1}^{S}\sum _{c=0}^{m_{i}-1}\left( a_{i}^{(s)}\right) ^{2} P_{ic}(\theta ^{(s)};a_{i}^{(s)},b_{ic}^{(s)})\nonumber \\& \quad \times \left( 1-P_{ic}^{*}(\theta ^{(s)};a_{i}^{(s)},b_{ic}^{(s)})-P_{i(c+1)}^{*}(\theta ^{(s)};a_{i}^{(s)},b_{ic}^{(s)})\right) ^{2}. \end{aligned}$$

(15)

For the GPCM, the partial derivative in (8) is equal to

$$\begin{aligned} \frac{\partial P_{ic}({{{\theta }}})}{\partial \theta }&=\frac{\mathrm {e}\mathrm {x}\mathrm {p}\left[ \sum _{\nu =0}^{c}Z_{i\nu }(\theta )\right] \times \sum _{v=0}^{c}a_{i}}{\sum _{c=0}^{m_{i}-1}\mathrm {e}\mathrm {x}\mathrm {p} \left[ \sum _{\nu =0}^{c}Z_{i\nu }(\theta )\right] }-\frac{\mathrm {e}\mathrm {x}\mathrm {p}\left[ \sum _{\nu =0}^{c}Z_{i\nu }(\theta )\right] }{\left( \sum _{c=0}^{m_{i}-1}\mathrm {e}\mathrm {x}\mathrm {p}\left[ \sum _{\nu =0}^{c}Z_{i\nu }(\theta )\right] \right) ^{2}}\nonumber \\&\quad \times \sum _{c=0}^{m_{i}-1}\left\{ \left( \sum _{v=0}^{c}a_{i}\right) \mathrm {e}\mathrm {x} \mathrm {p}\left[ \sum _{\nu =0}^{c}Z_{i\nu }(\theta )\right] \right\} \end{aligned}$$

(16)

$$\begin{aligned}&= (c+1)a_{i}P_{ic}(\theta )-a_{i}P_{ic}(\theta )\cdot \sum _{c=0}^{m_{i}-1}(c+1)P_{ic} (\theta )\nonumber \\&= a_{i}P_{ic}(\theta )\left( c+1-\sum _{c=0}^{m_{i}-1}(c+1)P_{ic}(\theta )\right) \nonumber \\&= a_{i}P_{ic}(\theta )\left( c-\sum _{c=0}^{m_{i}-1}cP_{ic}(\theta )\right) . \end{aligned}$$

(17)

Thus,

$$\begin{aligned} I(\theta )&=\sum _{c=0}^{m_{i}-1}\frac{1}{P_{ic}(\theta )}\left( a_{i}P_{ic}(\theta ) \left( c-\sum _{c=0}^{m_{i}-1}cP_{ic}(\theta )\right) \right) ^{2}\nonumber \\&= \sum _{c=0}^{m_{i}-1}a_{i}^{2}P_{ic}(\theta )\left( c-\sum _{c=0}^{m_{i}-1}cP_{ic} (\theta )\right) ^{2}. \end{aligned}$$

(18)

Similarly, averaging over the sampled values of all parameters, the criterion value for item $i$ is calculated as

$$\begin{aligned} I_{i}^{B}\equiv S^{-1}\sum _{s=1}^{S}\sum _{k=0}^{m_{i}-1}\left( a_{i}^{(s)} \right) ^{2}P_{ic}(\theta ^{(s)};a_{i}^{(s)},b_{ic}^{(s)})\left( c-\sum _{c=0}^{m_{i}-1} cP_{ic}(\theta ^{(s)};a_{i}^{(s)},b_{ic}^{(s)})\right) ^{2} \end{aligned}$$

(19)

Observe that, as $\sum _{c=0}^{m_{i}-1}cP_{ic}({{\theta }})$ is the examinee’s expected score on item i, the information in (18) is equal to $a_{i}^{2}$ times the variance of the item score. This property holds for any exponential-family model. The GRM does not belong to this family and fails to have the property.

4 Simulation studies

4.1 Item pools

Two item pools were included in this study, one for each model. The item pool for the GPCM had 95 items. The items were extracted from multiple years of the National Assessment of Educational Progress (NAEP) Reading tests. Their number of score points varied from two to four. The item pool for the GRM was from an HRQOL questionnaire. It also consisted of 95 polytomous items, but each of the items had five response categories. As the two pools differed substantially in item difficulty and we did not want our comparisons to be confounded by this difference, the values of the b parameters in the GRM item pool were shifted to give them the same mean as for the GPCM pool. Summary statistics of the item parameters for both pools are given in Table 1.

Table 1 Summary statistics for the GRM and GPCM item pools

4.2 Setup

The simulation studies started with the calibration of the two item pools using Gibbs sampling with regular MH steps for all parameters for samples of 250, 500 and 1000 simulated test takers with their true ability parameter values randomly drawn from the standard normal distribution. The different sample sizes were chosen to evaluate the impact of item parameter error. The algorithm was run with a burn-in of 5000 and post-burn-in of 15,000 iterations. The test takers’ responses were generated using the values for the item parameter reported in Table 1 as their true values. During all adaptive testing simulations, $N(0,1.5^{2})$ was used as the initial prior distribution for ability estimation, a choice amounting to a mildly informative prior. The items were selected either according to the earlier FB or the MI criterion. After each item, the posterior distribution of the ability parameter was updated using the algorithm described above. After 5, 10 or 15 items, the results were recorded to evaluate the impact of the item parameter uncertainty on ability estimation for different test lengths.

The adaptive testing simulations were thus run for two different item-selection criteria (FB and MI), three calibration sample sizes (250, 500, and 1000), and three test lengths (5, 10, and 15) and two item pools (NAEP and HRQOL). The two item pools were not crossed with the two IRT models; both were calibrated only according to the model that generated the original item parameters reported in Table 1. Hence, the result was a $2\times 3\times 3$ design with a total of 18 different conditions.

4.3 Results

4.3.1 Item pool calibration

The posterior means (EAP estimates) for the items in the pool for the GPCM in (3) are shown in Fig. 1. Obviously, the accuracy of all estimates increased with the calibration sample size. In agreement with common findings, the results for the $b_{i}$ parameters were generally better than for the $a_{i}$ parameters. For the sample size of $N=500$, the estimates of the $b_{i}$ parameters were already quite close to their true values. The same held for most of the estimates of the $a_{i}$ parameters. In fact, the step to the sample size of $N=1000$ was necessary only to bring the results for some of the $a_{i}$ parameters with the higher true values in line with the others.

Fig. 1

Calibration results for the GPCM item pool. The x-axis is for the true parameter values and the y-axis for their EAP estimates. The calibration sizes are $N=250$, 500, 1000. The top row is for discrimination parameters $a_{i}$, the bottom row for step difficulty parameters $b_{i}$ for the items

The calibration results of the pool for the GRM in (1) are given in Fig. 2. Just as for the GPCM item pool, the accuracy of the estimates of the $b_{i}$ parameters was already excellent for the calibration sample size of $N=250$. However, for the $a_{i}$ parameters, the sample size had to increase to $N=1000$ to reach acceptable accuracy. The slightly negative bias associated with the $a_{i}$ parameters for the sample size of $N=250$ can be attributed to the employment of its common prior distribution (truncated normal with mean = 1.0 and SD = 2.5).

Fig. 2

Calibration results for the GRM item pool. The x-axis is for the true parameter values and y-axis for their EAP estimates. The calibration sizes are $N=$ 250, 500, 1000. The top row is for discrimination parameters $a_{i}$, the bottom row the step difficulty parameter $b_{i}$ for the items

To determine the size of the vectors of post-burn-in draws from the calibration to be saved for use in the simulations of operational adaptive testing, autocorrelation plots for the item parameters as a function of the lag size were prepared. The results are shown in Fig. 3. The autocorrelation in the Markov chains for the $a_{i}$ parameter decreased quickly and was less than 0.1 after a lag size greater than 10. However, the autocorrelation for the $b_{i}$ parameters was generally much greater and the criterion of 0.1 was reached uniformly only for lag sizes greater than 30. We, therefore, thinned the post-burn-in part of the chains by a factor of 30 and kept vectors of $S=500$ independent draws for each item parameter for use in the adaptive testing simulations. The means of these vectors were used as point estimates (EAP estimates) of the item parameters when adaptive testing with current MI item selection was simulated.

Fig. 3

Autocorrelation $\rho _{l}$ in the Markov chains for the items parameters as a function of lag size l for each of the calibration sample size of $N=250$, 500, and 1000

4.3.2 Lenght of the Markov chains

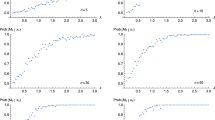
The algorithm was run for 100 replications for each of the simulated conditions to decide on the number of burn-in iterations for the algorithm. The proportions of the number of replications that failed to meet the Gelman and Rubin (1992) convergence criterion of $\sqrt{\hat{R}}<1.1$ as a function of the number of iterations are given in Fig. 4. After $k=1$ item, at the true abilities $\theta =-2$ and $-1$, the speed of convergence for the GPCM item pool was generally faster. But for all other numbers of items and ability levels, there were hardly any differences. Based on these results, a burn-in period for the Markov chains of 350 iterations was used in our main simulations of adaptive testing.

Fig. 4

Proportions of replications that failed the convergence criterion of $\sqrt{\hat{R}}<1.1$ as a function of the number of iterations of the algorithm after $k=1$, 3, 5, 8, 10, 13, and 15 items for examinees simulated at $\theta =-2(1)2$ (sample sizes: solid curves = 250, dashed = 500, dotted = 1000; models: without cross = GPCM, with cross = GRM)

To determine the post-burn-in length of the Markov chains for the ability parameters, it is important to know their autocorrelation structure. Knowledge of the structure enables us to choose the thinning factor necessary to obtain draws that are independent. Figure 5 gives the autocorrelation $\rho _{l}$ as function of lag size l. Again, except for the update of the posterior distribution after one item at the lower ability levels, where the autocorrelation tended to be smaller for the GRM item pool, all functions were quite similar for all test lengths and ability levels. Using the criterion of $\rho _{l}<0.1$, the lag size of 10 was chosen to thin the Markov chains in our main simulations.

Fig. 5

Autocorrelation $\rho _{l}$ in the Markov chains for the ability parameter as a function of lag size l after $k=1$, 3, 5, 8, 10, 13, and 15 items for examinees simulated at $\theta =-2(1)2$ (sample sizes: solid curves = 250, dashed = 500, dotted = 1000; models: without cross = GPCM, with cross = GRM)

Three candidate size of $S=100$, 200 and 500 for the vectors of independent draws from the posterior distributions of $\theta$ were evaluated using 15-item adaptive testing. Each simulated test was replicated 100 times at $\theta =-2(1)2$ both for the GPCM and GRM item pool. Figures 6 and 7 show the average bias and standard error functions for the EAP estimates of the ability parameter for the GPCM and GRM item pool. The differences between these functions were completely negligible. A vector size of $S=100$ would, therefore, have sufficed. However, just to remain on the conservative side, the size of $S=500$ was used in our main simulations of adaptive testing, implying the need to continue the Markov chains for 5000 iterations after burn-in.

Fig. 6

Bias and SE functions for the final ability estimates in adaptive testing simulations from the GPCM item pool. The curves are for the three candidate vector sizes of 100 (dotted curve), 200 (dashed curve), and 500 (solid curve) independent draws from the posterior distributions of the ability parameter

Fig. 7

Bias and SE functions for the final ability estimates in the adaptive testing simulations from the GRM item pool. The curves are for the three candidate vector sizes of 100 (dotted curve), 200 (dashed curve), and 500 (solid curve) independent draws from the posterior distributions of the ability parameter

As an introduction to the performance of the algorithm with these settings, examples of the initial segments of the trace plots for its Markov chains are given in Fig. 8 for the GPCM item pool and Fig. 9 for the GRM item pool. The examples are for the case of fully Bayesian adaptive testing, items calibrated with a sample size of $N=1000$, and true abilities equal to $\theta =-2(1)2$. The plots show immediate stationarity for all simulated ability levels at any stage of testing, a result due to the stability provided by the resampling of the already converged posterior distributions of the item parameters. Also, as expected, the posterior variance of these $\theta$ parameters did decrease quickly with the length of the test.

Fig. 8

Examples of the trace plots of the Markov chains for the posterior distributions of the ability parameters for test takers with true abilities at $\theta =-2, -1, 0, 1, 2$ after $k=1$, 3, 5, 8, 10, 13, 15 items on adaptive tests from the GPCM item pool

Fig. 9

Examples of the trace plots of the Markov chains for the posterior distributions of the ability parameters for test takers with true abilities at $\theta =-2, -1, 0, 1, 2$ after $k=1$, 3, 5, 8, 10, 13, 15 items on adaptive tests from the GRM item pool

4.3.3 Adaptive testing simulations

The results from our main simulation study of adaptive testing with the FB and MI approaches are presented in Fig. 10 for the case of the item pool calibrated with a sample size of $N=500$ (the results for $N=250$ and 1000 did not differ systematically and are not shown here to avoid redundancy). Clearly, the results improved with the length of the test for both approaches and models. For the GRM, the bias, standard error (SE), and root mean-square error (RMSE) functions for the two approaches were nearly identical no matter the length of the test. It seems safe to declare that the two opposite effects for the FB approach of a more realistic accuracy for the ability estimates and better accuracy due to improved test design did compensate each other completely. For the GPCM, all observed differences tended to be at the lowest end of the ability scale, otherwise the three functions were close for all practical purposes. More specifically, the FB approach showed a larger positive bias at $\theta =-2$ for $k=5$ items. Obviously, it took the approach more than five items to overcome the biasing impact of the mildly informative prior distribution for the ability parameter. However, at the same ability level, the approach yielded a smaller SE. And, as shown in the last panel of Fig. 10, the tradeoff between this larger bias and smaller SE resulted in a smaller RMSE for the FB approach. For the longer test length of $k=10$, the difference between the bias at $\theta =-2$ for the two approaches did change sign. This time, the FB approach resulted in a somewhat smaller bias, without having to give up its relatively smaller SE though.

Fig. 10

Bias, SE, and RMSE functions of the final ability estimates in the main adaptive testing simulations from the GPCM and GRM pools with burn-in length of the algorithm of 350 iterations and vectors of 500 independent posterior draws saved for the item and ability parameters. The curves are for two item selection criteria (FB: solid curves; MI: dashed curves) and test lengths of $k=5$ (plain curves), $k=10$ (curves with triangles) and $k=15$ items (curves with crosses)

4.4 Extended simulations for the GPCM pool

The adaptive testing simulations in the previous sections revealed clear differences between the results for the two item pools and their respective models, with generally much better results for the pool with the GRM. For each of the simulated conditions, nearly all of the RMSE and SE functions for this pool were superior.

As revealed by Table 1, the values for the $a_{i}$ parameters for the GPCM pool were much lower than for the GRM pool, a result the authors expect to hold more generally for the domains of educational and health outcomes measurement due to the more homogenous types of items typically used in the latter. As discrimination parameters are the main determinants of the Fisher information, additional simulations were conducted for the GPCM item pool to determine whether this explanation explained the observed differences. In one set of the simulations, the size of the $a_{i}$ parameters for the GPMC pool was just increased; in another the length of the adaptive testing was increased.

4.4.1 Adjusted $a_{i}$ parameters

The $a_{i}$ parameters for the GPCM item pool were adjusted by a factor equal to the ratio of the means of these parameters for the GRM and GPCM item pools. Plots of sums of the item response functions and information functions for the original and adjusted GPCM pools are shown in Fig. 11 along with the same plots for the GRM pool as a reference. Clearly, the curves for the adjusted pool are much closer to the curves for the GRM pool than those for its original version. The remaining differences between the two pools can be attributed to the differences between the number of response categories between the items in the two pools. All GRM items had five response categories whereas the number of categories for the GPCM items varied from two to four.

Fig. 11

Plots of sums of the response functions (upper row) and information functions (lower row) for the items in the pools without (left-hand column) and with (right-hand column) the adjusted $a_{i}$ parameters (GPCM: solid curves; GRM: dashed curves)

The adaptive testing simulations were repeated for the adjusted GPCM item pool. The results are shown in Fig. 12. All curves are now more comparable with those for the GRM pool in Fig. 10. Also, the difference in bias for the two approaches at $\theta =-2$ for the shortest test length disappeared. For a pool of more informative items, it takes the FB approach fewer items to overcome a bias due to the initial prior distribution for the ability parameter.

Fig. 12

Bias, SE, and RMSE functions of the final ability estimates in the main adaptive testing simulations from the GPCM item pool with adjusted $a_{i}$ parameters and a burn-in length of the algorithm of 350 iterations and vectors of 500 independent posterior draws saved for the item and ability parameters. The curves are for two item selection criteria (FB: solid curves; MI: dashed curves) and test lengths of $k=5$ (plain curves), $k=10$ (curves with triangles) and $k=15$ items (curves with crosses)

4.4.2 Increased test lengths

In real-world educational testing, it may be impossible to produce pool of items with discrimination parameters as large as those typical of health outcomes measurement. Therefore, as a more practical alternative, the test length for the GPCM pool was increased to $k=20$, 25, and 30 items. Figure 13 shows the results for these increased test lengths. Though the result are generally much better, a test length of more than 30 items might be needed for the GPCM to obtain obtain RMSE and the SE functions comparable to a test length of $k=15$ items for the GRM pool.

Fig. 13

Bias, SE, and RMSE functions of the final ability estimates in the main adaptive testing simulations from the GPCM item pool with the extended test lengths and a burn-in length of the algorithm of 350 iterations and vectors of 500 independent posterior draws saved for the item and ability parameters. The curves are for two item selection criteria (FB: solid curves; MI: dashed curves) and test lengths of $k=20$ (plain curves), $k=25$ (curves with triangles) and $k=30$ items (curves with crosses)

4.5 Alternative model parameterization

The parameterization in Eqs. 2 and 4 is frequently used to model the response probabilities on polytomous items. However, it is not uncommon to find a regression-type parameterization as an alternative, with

$$\begin{aligned} P_{ik}^{*}(\theta )\equiv {\left\{ \begin{array}{ll} \begin{array}{l} 1\\ \frac{\exp [\alpha _{i}\theta +\gamma _{ik})]}{1+\exp [\alpha _{i}\theta +\gamma _{ik})]}\\ 0 \end{array} &{} \begin{array}{l} k=0\\ 0<k<m_{i}\\ k=m_{i} \end{array}\end{array}\right. } \end{aligned}$$

(20)

for the GRM in (1) and

$$\begin{aligned} Z_{i\nu }\equiv \alpha _{i}\theta +\gamma _{i\nu } \end{aligned}$$

(21)

for the GPCM in (3). All our simulations above were repeated to evaluate the robustness of the proposed algorithm with respect to differences between these two alternative parameterizations. Basically, our results showed no systematic impact of the choice of parameterization on any of the properties of the final ability estimates for both models and adaptive testing approaches. Because of space limitation, more detailed results from these simulations are omitted here.

5 Running times

All simulation were run on a MacPro laptop with 2.5 GHz Intel Core i7 processor and 16 GB memory. The average running time was 0.027 s per item to update the posterior distribution of $\theta$ and select the next item from the GPCM item pool. For the GRM pool, the average running time was 0.020 s per item.

6 Concluding comments

The results from this study illustrate the practical feasibility of the proposed MCMC implementation for polytomously scored test items. Running times in the range of 0.02–0.03 s to update the posterior distribution of the ability parameter and select the next item under the realistic conditions simulated in the study are entirely comparable with those for the currently popular case of maximum-information selection which ignores remaining error in the item parameters. As for the accuracy of the final ability estimates, just as for the case of dichotomous items, it appears to be possible again to give up the current practice of underreporting their standard errors. A fully Bayesian approach to adaptive testing does so while paying for itself in the form of better item selection and, therefore, better designed tests. Another practical advantage, not yet highlighted in this paper, is a possible substantial reduction of the size of the calibration samples required to prepare item pools for adaptive testing. Sample sizes of $N=250$ or 500 showed to perform already remarkably well in our study. The question of how low we actually could go under precisely what conditions certainly deserves further study.