Introduction

A jet of air bubbles introduced in an initially stagnant body of water, aiming for the mobilization of the water mass, its aeration, and the control of its quality and other technical targets, is a common procedure at various scales. It is used at lab scale, at the scale of algae or fish farming (for their protection), at the scale of wastewater treatment plants (aeration of wastewater at the secondary or biological treatment), and at the scale of maritime works (use of air-bubble curtains in underwater explosions and in maintaining harbor water quality). Jets opposing turbidity currents in reservoirs, when transfer tunnels feed water into the reservoir at a higher elevation near a dam, or hydraulic jumps at the tail end of spillways, are similar applications (Bühler et al. 2013). Würsig et al. (2000) performed an experiment in the waters of western Hong Kong; a perforated rubber hose was used to produce a bubble curtain around pile-driving activity, to protect resident or migrating sound-sensitive animals. Peng et al. (2021) examine the effectiveness of an air-bubble curtain system in noise reduction for offshore pile driving. Hilo et al. (2022) investigate the characteristics of air-bubble injection into freestream flow using three different injector models and the effects of the bubble curtain on the sound wave attention (Fig. 1).

Fig. 1
figure 1

A bubble curtain that controls floating waste (https://searial-cleaners.com/our-cleaners/invisibubble-bubble-barrier/)

Full size image

In all the above applications the profound understanding of the physical processes of transfer of energy from the air-bubble stream to the water masses is of utmost importance. From a fluid mechanics point of view, this phenomenon is classified in the class of two-phase flows. The fluids (air and water) are immiscible, but their motion is not as simple as in the case of masses flowing separately interconnected by, and interacting through, a smooth interface. The air phase has the form of a huge number of almost spherical bubbles that cannot be observed or theoretically analyzed individually. Such flows must be simulated properly, and this has been done in previous publications using various methodologies (Lee 1986; Michaelidis 1997; Chen and Marshall 1999; Bothe and Warnecke 2005; Papakonstantis et al. 2011a, b). In Yapa and Dissanayake (2012) the Runge–Kutta method was used to simulate the behavior of gas plumes in shallow to intermediate water depths. The most common approach refers to the Eulerian description of both phases, while the air phase was quantitatively described by the bubbles’ concentration and the resulting difference in local fluid density (Bernard et al. 2000). In Studley (2010), the Eulerian–Eulerian approach was used to model air as the dispersed phase within a continuous phase of water using the commercial software FLUENT, to better understand the hydrodynamics and analyze the mixing characteristics for each configuration for the bubble columns and airlift reactors. Detailed Computational Fluid Dynamics (CFD) modeling of the rising bubbles in the case of few mega-bubbles was also done for the sake of describing the hydrodynamic results on the surrounding water masses (Boegman and Sleep 2012). Beelen et al. (2023) present an excellent review of all recent bibliography on air-bubble systems, and present the development, calibration, and validation of a novel measurement device that can be operated in situ to characterize the bubble curtain alongside acoustic tests.

In this paper a new modeling procedure is presented, extending a relevant past publication (Koutitas and Gousidou 2004) followed by detailed laboratory experiments (Kourafalou et al. 2004; Fyrillas and Nomura 2007; Guo 2014). Its aim is to test the calibration procedure and the final operational validity of the presented model.

Materials and methods

The air-bubble-induced water flow model

This is a special case of two-phase flow. The water is the hosting fluid phase. The hosted phase is air, but not in a simply connected form, with a smooth interface between the two phases. In this case the air is co-flowing in the form of a very large number of bubbles continuously introduced in the water column and operating as the flow generation forcing. The classical formulations of two-phase flows are impossible. The tracking of each bubble is also computationally unfeasible.

The selected modeling approach is the following. The water phase is the phase treated as a continuous medium described by the Navier–Stokes equations in a Eulerian frame, and the air phase is treated as a swarm of “active Lagrangian particles,” tracked in a Lagrangian frame of reference. “Active particles” refers to that they are not passively transported by the hosting water but are generating themselves the water flow by friction (the negative drag), which they exercise in the initially stagnant water, as they move upward from the source location to the free surface, due to their buoyancy. The classical Navier–Stokes solver, in Lucic et al. (2000), is combined in a feed-backing way with the “tracer technique” used for the description of the motion of Lagrangian particles in a moving fluid. The water motion is described in a Eulerian frame of reference while the particles in a Lagrangian frame. The water motion is induced by the volume (distributed) force exercised by the air bubbles. In Mazzitelli et al. (2003) the motion and the action of microbubbles in homogeneous and isotropic turbulence are investigated through three-dimensional direct numerical simulations of the Navier–Stokes equations and applying the Lagrangian approach to track the bubble trajectories. The combined forces acting on the bubbles are mass, drag, lift, and gravity. The numerical simulation of a violent bubble motion is presented in Xi (2004) by a robust mixed-Eulerian–Lagrangian modeling.

It is obvious that the number of “particles” simulating the air bubbles is big, to maintain statistical adequacy, but not equal to the number of the air bubbles themselves. The kinetic and dynamic correlation of a particle with the group of real bubbles, which it represents, it facilitates the procedure.

The tracer technique with active particles

In the case of two-phase flow of water and air bubbles (Fig. 2), the basic parameters are the introduced gas discharge qg and the bubble diameter Db (or radius Rb). It is assumed that the air bubbles reach immediately an equilibrium (buoyancy force = drag force) and maintain vertically a relative-to-the-fluid velocity Ub dominated by their diameter. The flow is generated by the volume (distributed) force of the drag reaction force exercised by the ensemble of the bubbles in a unit volume of the fluid. This is an upward force, which, combined with the diffusion process and the generated pressure gradients, results in the mobilization of the surrounding fluid mass (Sridhar and Katz 1995).

Fig. 2
figure 2

The flow domain configuration, also showing section A-A

Full size image

If the per-unit-mass force exercised by the buoyant bubbles to the water is Fdr, then the flow equations in a two-dimensional vertical (2DV) domain can be written as:

$$\frac{\partial p}{{\partial t}} + \frac{\partial U}{{\partial x}} + \frac{\partial V}{{\partial y}} = {\rm VOL}\frac{\partial c}{{\partial t}}\frac{1}{{dx^{2} }}.$$
(1)

This is the pressure (or continuity) equation, where U and V are the local fluid velocity components along the horizontal and vertical directions, respectively, VOL is the volume of air corresponding to a particle, c is the particles’ concentration (number of particles in a cell of area dx2). There are two important novel features: the use of the notion of fluid pseudo-compressibility, and the consideration of the effect of the almost incompressible air moving with the water:

$$\frac{Du}{{Dt}} = - c_{p}^{2} \frac{\partial p}{{\partial x}} + N\left(\frac{{\partial^{2} U}}{{\partial x^{2} }} + \frac{{\partial^{2} U}}{{\partial y^{2} }}\right) - \frac{{fU(U^{2} + V^{2} )^{1/2} }}{h},$$
(2)
$$\frac{Dv}{{Dt}} = - c_{p}^{2} \frac{\partial p}{{\partial y}} + N\left(\frac{{\partial^{2} V}}{{\partial x^{2} }} + \frac{{\partial^{2} V}}{{\partial y^{2} }}\right) + \frac{{F_{\rm dr} }}{\rho } - \frac{{fV(U^{2} + V^{2} )^{1/2} }}{h}.$$
(3)

In the forces equilibrium equations in Ox, Oy directions, p is the nondimensional pressure, U and V are the local fluid velocity components along the horizontal and vertical directions, respectively, cp is related to the pressure (elastic) wave celerity, N is the eddy viscosity, Fdr is the distributed volume force, or else per-unit-mass vertical drag force exercised by the air bubbles to the surrounding water, ρ is the water density, and h is the flow width (distance between the two plates confining the flow area). A term of wall friction appears in the model to conform to the experimental setup of flow between two transparent walls. The linearized form will be used in the presented applications, as it will be explained, due to the low flow Reynolds numbers, with a derivative λ friction coefficient. This approach incorporating the notion of fluid pseudo-compressibility leads to an easy solution algorithm, as the transient flow state, before reaching the final steady flow conditions, can be tackled in a way similar to free surface flows.

The swarm of air bubbles is treated by the classical “tracer technique.” They are represented by a large number of Lagrangian particles (IP, total number of particles during the simulation period), advected with the local fluid velocities U and V, diffused by the local N values, and keeping in the vertical a velocity in excess of the fluid velocity. Their absolute vertical velocity is V + Ub, where Ub is the particle (bubble) buoyancy velocity, given in Eq. (6).

There are three deriving problems:

  • To estimate the drag on each bubble and the steady vertical buoyancy velocity.

  • To correlate a particle with a number of air bubbles (gas volume).

  • To correlate the drag force on each bubble with the force exercised by the “particles” used in the simulation procedure to represent a number of air bubbles.

The drag on a bubble is given by:

$$F_{\rm d} = c_{\rm d} \frac{\rho }{2}U_{\rm b}^{2} \pi R_{\rm b}^{2},$$
(4)

where cd is the drag coefficient related to the local Reynolds number, Re = (UbDb/ν) by the relation:

$${c}_{\mathrm{d}}=0.4+\frac{24}{\mathrm{Re}}\frac{6}{1+\sqrt{\mathrm{Re}}},$$
(5)

where Db is the bubble diameter, and Rb the bubble radius. From the equilibrium of buoyancy force and the drag force on the bubble the final particle (bubble) buoyancy velocity Ub is given by:

$$U_{\rm b} = \sqrt {\frac{{8gR_{\rm b} }}{{3c{}_{\rm d}}}}.$$
(6)

These equations are solved together by successive approximations. If the air discharge is qo and IP is the number of particles introduced in NM time steps (with time step Dt), then the particles introduced every second are:

$${\rm IPP} = \frac{{\rm IP}}{{{\rm NM} * Dt}},$$
(7)

while the bubbles introduced every second are:

$$N = \frac{{q_{\rm o} }}{{\frac{4}{3}\pi R_{\rm b}^{3} }}.$$
(8)

From the above values it can be concluded that the force on each particle divided by the water density, ρ, is:

$${\rm SHR} = \frac{{N*F_{\rm dr} }}{{\rm IPP}*\rho }.$$
(9)

The volume of air corresponding to each particle is equal to:

$${\rm VOL} = \frac{{q_{\rm O} }}{\rm IPP}.$$
(10)

The Fdr/ρ term in the equilibrium equation along Oy is equal to SHR × c, where c(x, y, t) is the concentration of particles in a mesh of size dx, quantified by the number of particles contained in each cell of the grid.

The boundary conditions applied in the case of bubble-generated flow are:

  1. 1.

    On the bubble-source point, a number IPP of particles is introduced each time step at the “origin.”

  2. 2.

    On the lateral boundaries, the U velocity is suppressed, in the case of confined flow space, or related to the excess pressure head (Δp) U = ±Δpcp (unconfined domain).

  3. 3.

    On the upper and lower boundaries, no normal flow is permitted V = 0.

  4. 4.

    The particles, reaching the boundaries of the flow domain, stay out of it and are not included in the subsequent dynamic computations.

The particles are traced in a Lagrangian frame of reference, and the coordinates of a particle p, Xp and Yp are controlled by the following kinematic conditions:

$$X_{p}^{n + 1} = X_{p}^{n} + Dt * (U_{p} + U_{\rm r} * (2 * {\rm Rnd} - 1)),$$
(11)
$$Y_{p}^{n + 1} = Y_{p}^{n} + Dt * (V_{p} + U_{\rm b} + U_{r} * (2 * {\rm Rnd} - 1)),$$
(12)

where Up, Vp are the water velocity components at the particle p position, found by linear interpolation of the nearest U and V values, Ub is the particle (bubble) buoyancy velocity, Ur is the range of the random velocity of the random walk that a particle executes, simulating the diffusion process, and Rnd are random numbers between 0 and 1, with uniform distribution, internally produced by the computer. According to Einstein (Koutitas and Scarlatos 2016), the range of the random velocity of the random walk that a particle executes is related to the diffusion coefficient N:

$$U_{\rm r} = \left( {6 * \frac{N}{Dt}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} .$$
(13)

Numerical solution algorithm

The numerical solution of both the PDEs describing the water flow and the ODEs describing the air bubbles’ (particles) kinematics, are solved explicitly using first-order FD approximations for the time derivatives and centered FD for the space derivatives. For the solution of the PDEs referring to the water flow, the flow domain is discretized using the well-known staggered Arakawa C grid (Koutitas 1985), where the U and V velocity components are calculated on the sides of the discretization cell and the pressure p, the particle distributed drag SHR, and the particle concentration c are calculated at the center of the cell (Fig. 3).

Fig. 3
figure 3

Air particle and water flow variables on a typical solution cell (Koutitas 1985)

Full size image

The noticeable issues in the numerical solution algorithm are:

  1. 1.

    The initial conditions assumed are of a “cold start.” Zero velocities and pressures are assumed.

  2. 2.

    The particles are introduced from a fixed point (the location of air-bubble sparger) in the flow domain at a rate dominated by the IP and NM values (for example, if IP = 200,000 and NM = 10,000 time steps, then IPP = 20 particles are introduced at each time step).

  3. 3.

    The calculation of SHR values for each cell leads to the development of pressure gradients and fluid acceleration (generation of nonzero U and V values).

  4. 4.

    These U and V values are used in interpolated form Up, Vp for particle p to advect (deterministically transport) the particles (Fig. 3).

  5. 5.

    From the particles’ distribution, the c(x, y, t) values are calculated leading to new SHR values.

  6. 6.

    The solution progresses to the point of kinetic energy stabilization, i.e., to reach steady flow conditions (when the time derivatives approach to zero).

Experimental and modeling setup

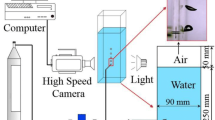
The ultimate aim of the study was the comparison of the modeled results with the experimental measurements, to conclude on the potential of the model for operational applications, like the design of wastewater treatment plants and the water quality control in small harbor basins. Therefore, a series of experiments were conducted at the laboratory of Hydraulic Works and Environmental Engineering, in the Department of Civil Engineering of the Alexander Technological Institute of Thessaloniki, Greece, using the particle image velocimetry (PIV) technique.

Similar experiments have been conducted; high-speed cameras and an image processing technique are used to visualize and quantify the projected void fraction (PVF) of air bubbles by Hilo et al. (2022), and Bohnea et al. (2019) developed a model of the local distribution of the effective wavenumber, where the air fraction was determined by means of an integral method and the bubble size distribution was derived from tank measurements. There are many different approaches to measure bubble properties. According to Beelen et al. (2023), they can be classified into intrusive and non-intrusive measurement techniques. Non-intrusive measurement techniques, based on image analysis, are typically used in configurations where the camera can be placed outside the flow domain and require sophisticated algorithms to deal with overlapping bubbles. Alternatively, a small camera unit can be placed within the bubble curtain, and image analysis can be used locally and semi-intrusively. Our method is using a non-intrusive measurement technique, with a camera outside the flow domain, and PIV analysis software.

The experimental setup comprised a vertical tank of size 50 × 30 × 4 cm made of Plexiglass filled with water. A sparger was installed in the middle of the base of the tank. The airflow produced by the sparger was 2 and 3 L/min. The introduced air generated bubbles of mean diameter 2.5 mm. The bubbles moved vertically, as a jet and buoyant plume, and they were dispersed in the atmosphere as soon as they reached the free surface. Their impact on the water mass was to generate a vertical mass flow due to the negative drag force exercised on the water. Due to the confined flow domain, the upward water flow was symmetrically bifurcated in the horizontal direction, and then moved downward forming two symmetrical gyres. The flow was assumed two-dimensional, confined between the two parallel plates. The velocity distribution in the flow domain was measured by the PIV method, using a laser beam in the middle of the flow domain (2 cm from each wall). The PIV system was two-dimensional, consisting of a twin pulsed Nd: Yag lasers (532 nm wavelength, 300 mJ/pulse at 10 Hz), a cross correlation 8-bit 1 × 1 K CCD camera (Kodak, MEGAPLUS ES 1.0), a synchronizer, a computer, an image acquisition system, and PIV analysis software (Insight 3G). The laser beams were combined and formed a 1-mm-wide sheet by using semi-cylindrical optics. The camera image size had a 1600 × 1192 pixel array and the dimensions of the velocity field were kept at 291 × 214 mm for all the experiments. This means that the resolution of the captured images was typically 5.5 pixel/mm, or that the pixel length was 0.1818 mm. The laser was installed above the tank at a distance of 50 cm from the illuminated water free surface, while the camera viewed from an orthogonal direction. Twin images were recorded with a time separation of 2 ms, while 50 pairs of images were captured in each experiment. The plane photographs were divided into interrogation spots measuring 32 × 32 pixels (5.79 × 5.79 mm).

The cross-correlation between the interrogation spots determined the mean displacement of the particles and thereof the velocity vector. The cross-correlation operation was based on the correlation theorem, stating that the correlation on the spatial domain becomes multiplication on the frequency domain. Correlation made use of the Fast Fourier Transform (FFT). Adjacent interrogation spots were overlapped by 50%, providing a resolution of about 3 mm. After these calculations, the velocity data were filtered with a signal-to-noise filter, a peak height filter, and global and local filters, to remove error vectors. The fluid was seeded with tracer particles, which, for the purposes of PIV, were generally assumed to follow the flow dynamics (Fig. 4) (Wereley and Meinhart 2010; Papakonstantis et al 2011a, b). These particles had a size of about 10 μm in clean water. The motion of the seeding particles was used to calculate the velocities in magnitude and phase. The distance between two neighboring velocity vectors was 3 mm. The experimental uncertainty of the measured velocity with this technique was approximately ±2%. In Wu and Grahib (2002) experiments were conducted for air bubbles of diameter ranging between 0.1 and 0.2 cm. In Zhang and Zhu (2014) large eddy simulations and experimental results of buoyant jets in cross-flow are studied, concluding that the shape, size, and vertical location of simulated jet concentration cross-sections compare well to measured ones.

Fig. 4
figure 4

The measuring system used in the lab (light gray is the photographed area of 291 × 214 mm, and dark gray is the light sheet)

Full size image

The observed magnitude of the water velocity in the tank was in the order of 5 cm/s, which, combined with the flow width of 4 cm, led to overall Reynolds numbers of the flow in the order of 2000, indicating that the flow is not fully turbulent. The water depth was 20, 22, and 24 cm. The velocity field measured by the PIV in the area of the downward flow is not infected by the presence of air bubbles, contrary to the central upward flow zone, where the air bubbles make their presence dominating over the suspended particles used for the water velocity estimation, according to the PIV technique. In that area, the velocity values measured by the PIV were not the water velocities, as the bubbles were incorporated in the PIV analysis. They were the resultant velocities of water heavily laden with air bubbles. The comparison with the velocities produced by the model is therefore possible only in the zone outside the bubble plume. Actually, the comparison between the model and the experiment refers to:

  1. 1.

    The form of the gyres, produced by the model and detected by the PIV in the experiment.

  2. 2.

    The horizontal velocity (U) profile, along the water column in a transect placed in the center of the gyres, with positive and negative values in the upper and lower halves of the flow domain, respectively.

  3. 3.

    The order of magnitude of the water discharge moving outward (from the uprising masses to the tank walls) produced by the model and measured in the experiment.

The discretization step used in the model was dx = 1 cm, and for numerical stability reasons the time step was Dt = 0.005 s. The selected order of magnitude of N (the eddy viscosity coefficient) is 0.0001 m2/s. Sensitivity analysis of that magnitude led to this value, on the basis of the induced size of the air-bubble plume (the horizontal dimension of the plume measured and calculated; Fig. 5).

Fig. 5
figure 5

Influence of the eddy diffusivity parameter N on the bubble plume configuration, for h = 24 cm and Qair = 3 L/min (above: N = 0.0001 m2/s, below: N = 0.001 m2/s)

Full size image

Due to the magnitude of the Reynolds numbers, the smooth walls, and the not fully turbulent flow, the wall friction coefficient was assumed to be in the order of f = 64/Re, justifying the linear friction assumed in the model. Replacement of h and (U2 + V2)1/2 values in the Re number leads to a derivative friction coefficient for the linearized friction terms, − λU and − λV:

$$\lambda = 120\,\nu /h^{2} = 0.0{75}/{\text{s}},$$
(14)

or

$$O\left( \lambda \right) = 0.{1 }({\text{ for}}\;\nu = {1}0^{{ - {6}}} \,{\text{m}}^{{2}} /{\text{s}},\;{\text{and}}\;h = {4}\,{\text{cm}}).$$
(15)

Results and discussion

The form of the produced flow configuration by the model and the experimentally measured for a number of flow conditions is depicted in Figs. 6, 7, 8, 9, and 10. More specifically, the graphical results correspond to water depth h = 20, 22, and 24 cm, and air inflow Qair = 2 or 3 L/min. On the left are the experimental results, which show only half of the experimental unit, whereas on the right the model produced graphical results depict the entire water entity.

Fig. 6
figure 6

Comparison of measured and computed water velocity fields for h = 20 cm and Qair = 2 L/min

Full size image
Fig. 7
figure 7

Comparison of measured and computed water velocity fields for h = 22 cm and Qair = 2 L/min

Full size image
Fig. 8
figure 8

Comparison of measured and computed water velocity fields for h = 22 cm and Qair = 3 L/min

Full size image
Fig. 9
figure 9

Comparison of measured and computed velocity fields for h = 24 cm and Qair = 2 L/min

Full size image
Fig. 10
figure 10

Comparison of measured and computed water velocity fields for h = 24 cm and Qair = 3 L/min

Full size image

Some preliminary conclusions from the simulations are summarized here. The inflow of air bubbles in the water causes the generation of two counter-current channels. The particles of the liquid that are at the centers of the vortices tend to be immobile, while those at the boundaries of the vortices are moving significantly faster. In general, the higher velocity values are found in the center of the plume, while both the surface and the bottom currents are extremely strong. Moreover, the diffusion of air particles into the surrounding fluid is enhanced by increasing the air supply, while the width of the plume increases. The reduction of the amount of air discharged combined with the reduction in the value of turbulence viscosity coefficient delays the achievement of steady flow conditions. Increasing the value of the turbulence viscosity coefficient while keeping constant the quantity of drained air implies the weakening of the velocity vector field.

The U velocity profiles along the vertical sections A-A through the right gyre centers (as shown in Fig. 2), produced by the model and the experiment, are depicted in Figs. 11 and 12, showing that the results are comparable.

Fig. 11
figure 11

Comparison of measured and computed U water velocities distribution along a vertical section for Qair = 2 L/min

Full size image
Fig. 12
figure 12

Comparison of measured and computed U water velocities distribution along a vertical for Qair = 3 L/min

Full size image

The calculated water discharges (integral of positive U values on the upper half of the right gyre) produced by the model and the experiments for various flow configurations are depicted in Table 1, showing also good agreement between the model and the experiment.

Table 1 Water discharge produced by the bubbles
Full size table

Similar studies (Wit et al. 2014) show that the larger the crossflow velocity is, the narrower the width and the smaller the spreading rate of air-bubble plume becomes.

Conclusions

A fluid is described as a substance that continually flows and is categorized into two main subcategories: liquids and gases. The mixture of these two phases is being referred to as a two-phase flow. A vertically injected air amount, into a water body, can result in the generation of such a flow. In this study, a mixture of water and “trapped” air bubbles, is being morphed, which is known as an “air bubble curtain.” In this case the air phase is composed by billions of almost spherical bubbles of infinitesimal size, hence the lack of a continuous interface, which could be easily described by a smooth mathematical function. Despite this fact, analysis of this phenomenon is of critical importance, as it can result in understanding and subsequently optimizing these functions and features that make the generated bubble barrier useful. In this paper a new modeling procedure is presented, extending a relevant past publication (Koutitas and Gousidou 2004) followed by detailed laboratory experiments. Its aim is to test the calibration procedure and the final operational validity of the presented model.

A theoretical analysis of the air-bubble-stream-induced water circulation is presented, using a computer code created by C. Koutitas, of the Aristotle University of Thessaloniki. Based on the interactive application of a typical Navier–Stokes solver for the water phase, and the “active Lagrangian particles” tracer technique, for the air-bubble phase, a dynamic computational model is formulated and solved. The calibration of the model is done by the determination of the eddy viscosity values and the wall friction coefficient. The model has a simple form and low computational resources demands.

Following that, a series of experiments were conducted by G. Pechlivanidis, at the Alexander Technological Institute of Thessaloniki, using the particle image velocimetry (PIV) technique. A systematic set of laboratory experiments led to the model and experiment intercomparison and the deduction of decisive conclusions on the model operability and applicability for important technological applications related to civil engineering works. Marine structures, maritime transport, environmental protection, and improving quality of life are just a few of the sectors in which the suggested technology could be utilized. Its usefulness lies in the fact that an air-bubble curtain has the ability to attenuate wave propagation, control seawater intrusion through locks and river estuaries, oil spills, biofouling, and rivers’ morphological development, aerate, and protect, at the same time, aquifers against water pollution and ice formation.

Further research on model scaling is envisaged at larger scales, to detect the model validity. Some suggestions regarding possible future improvements of the mechanism and further investigation are to run the experiment with different air-bubble diameter, with more than one air injection sources, with inclined container bottom, or with the use of seawater. Of course, a sensitivity analysis on various parameters will complement this research nicely.