Magnetic fields in the solar convection zone

Abstract

It has been a prevailing picture that active regions on the solar surface originate from a strong toroidal magnetic field stored in the overshoot region at the base of the solar convection zone, generated by a deep seated solar dynamo mechanism. This article reviews the studies in regard to how the toroidal magnetic field can destabilize and rise through the convection zone to form the observed solar active regions at the surface. Furthermore, new results from the global simulations of the convective dynamos, and from the near-surface layer simulations of active region formation, together with helioseismic investigations of the pre-emergence active regions, are calling into question the picture of active regions as buoyantly rising flux tubes originating from the bottom of the convection zone. This article also gives a review on these new developments.

Introduction

Looking at a full disk magnetogram (a map showing spatially the line of sight flux density of the magnetic field) of the solar photosphere one sees that the most prominent large scale pattern of magnetic flux concentrations on the solar surface are the bipolar active regions (see Fig. 1). When observed in white light (see Fig. 2), an active region usually contains sunspots and is sometimes called a sunspot group. Active regions are so named because they are centers of various forms of solar activity (such as solar flares) and sites of X-ray emitting coronal loops (see Fig. 3).

Fig. 1

A full disk magnetogram from the Helioseismic and Magnetic Imager (HMI) on board the Solar Dynamic Observatory (SDO) showing the line of sight magnetic flux density on the photosphere of the Sun on June 14, 2014. White (Black) color indicates a field of positive (negative) polarity

Fig. 2

A continuum intensity image of the Sun taken by the HMI on board the SDO on the same day as Fig. 1. It shows the sunspots that are in some of the active regions in Fig. 1

Fig. 3

A full disk soft X-ray image of the solar coronal taken on the same day as Fig. 1 from the X-ray telescope (XRT) on board the Hinode satellite. Active regions appear as sites of bright X-ray emitting loops

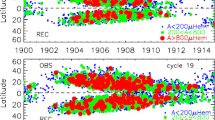
Despite the turbulent nature of solar convection which is visible from the granulation pattern on the photosphere, the large scale bipolar active regions show remarkable order and organization as can be seen in Fig. 1. The active regions are roughly confined into two latitudinal belts which are located nearly symmetrically on the two hemispheres. Over the course of each 11-year solar cycle, the active region belts march progressively from mid-latitude of roughly $35^{\circ }$ toward the equator on both hemispheres (Maunder 1922). The polarity orientations of the bipolar active regions are found to obey the well-known Hale polarity law (Hale et al. 1919; Hale and Nicholson 1925) outlined as follows. The line connecting the centers of the two magnetic polarity areas of each bipolar active region is usually nearly east-west oriented. Within each 11-year solar cycle, the leading polarities (leading in the direction of solar rotation) of nearly all active regions on one hemisphere are the same and are opposite to those on the other hemisphere (see Fig. 1), and the polarity order reverses on both hemispheres with the beginning of the next cycle. The magnetic fields at the solar north and south poles are also found to reverse sign every 11 years near sunspot maximum (i.e., near the middle of a solar cycle). Therefore, the complete magnetic cycle, which corresponds to the interval between successive appearances at mid-latitudes of active regions with the same polarity arrangement, is in fact 22 years.

Besides their highly organized behavior during each solar cycle, active regions are found to possess some interesting asymmetries between their leading and following polarities. Observations show that the axis connecting the leading and the following polarities of each active region is nearly east-west oriented (or toroidal) but on average shows a small tilt relative to the east-west direction with the leading polarity of the region being slightly closer to the equator than the following (see Fig. 1). This small mean tilt angle is found to increase approximately linearly with the latitude of the active region (Wang and Sheeley Jr 1989, 1991; Howard 1991b, a; Fisher et al. 1995; Kosovichev and Stenflo 2008; Stenflo and Kosovichev 2012). This observation of active region tilts is originally summarized in Hale et al. (1919) and is generally referred to as Joy’s law. Note that Joy’s law describes the statistical mean behavior of the active region tilts. The tilt angles of individual active regions in fact show a large scatter about the mean (Wang and Sheeley Jr 1989, 1991; Howard 1991b, a; Fisher et al. 1995; Kosovichev and Stenflo 2008; Stenflo and Kosovichev 2012). Another intriguing asymmetry is found in the morphology of the leading and the following polarities of an active region. The flux of the leading polarity tends to be concentrated in large well-formed sunspots, whereas the flux of the following polarity tends to be more dispersed and to have a fragmented appearance (see Bray and Loughhead 1979). Moreover, the leading polarity spots often form earlier and have a longer lifetime than the following (e.g., McIntosh 1981). Observations also show that the magnetic inversion lines (the neutral lines separating the fluxes of the two opposite polarities) in bipolar active regions are statistically nearer to the main following polarity spot than to the main leading spot (van Driel-Gesztelyi and Petrovay 1990; Petrovay et al. 1990). Furthermore for young growing active regions, there is an asymmetry in the east-west proper motions of the two polarities, with the leading polarity spots moving prograde more rapidly than the retrograde motion of the following polarity spots (see Chou and Wang 1987; van Driel-Gesztelyi and Petrovay 1990; Petrovay et al. 1990).

More recently, vector magnetic field observations of active regions on the photosphere have shown that active region magnetic fields have a small but statistically significant mean twist that is left-handed in the northern hemisphere and right-handed in the southern hemisphere (see Pevtsov et al. 1995, 2001, 2014). The twist is measured in terms of the quantity $\alpha \equiv \langle J_z/B_z \rangle$, the ratio of the vertical electric current over the vertical magnetic field averaged over an active region. The measured $\alpha$ for individual solar active regions show considerable scatter, but there is clearly a statistically significant trend for negative $\alpha$ (left-handed field line twist) in the northern hemisphere and positive $\alpha$ (right-handed field line twist) in the southern hemisphere. In addition, soft X-ray observations of solar active regions sometimes show hot plasma of S or inverse-S shapes called “sigmoids” with the northern hemisphere preferentially showing inverse-S shapes and the southern hemisphere forward-S shapes (Rust and Kumar 1996; Pevtsov et al. 2001, 2014, see Fig. 4 for an example).

Fig. 4

A soft X-ray image of the solar corona on May 27, 1999, taken by the Yohkoh soft X-ray telescope. The arrows point to two “sigmoids” at similar longitudes north and south of the equator showing an inverse-S and a forward-S shape respectively

This hemispheric preference of the sign of the active region field line twist and the direction of X-ray sigmoids do not change with the solar cycle (see Pevtsov et al. 2001, 2014). New high resolution vector magnetic field observations from the Hinode space mission show further evidence for the emergence of twisted active region magnetic flux in association with the formation of active region filaments (see review by Lites 2009).

The cyclic large scale magnetic field of the Sun with a period of 22 years is believed to be sustained by a dynamo mechanism (see e.g. review by Charbonneau 2020). The Hale polarity law of solar active regions indicates the presence of a large scale subsurface toroidal magnetic field generated by the solar cycle dynamo mechanism. The picture of how and where the large scale solar dynamo operates underwent substantial revision due in part to new knowledge from helioseismology regarding the solar internal rotation profile (see DeLuca and Gilman 1991; Gilman 2000). Many mean-field dynamo models utilizing the observed solar differential rotation profile (see e.g. Charbonneau and MacGregor 1997; Dikpati and Charbonneau 1999; Dikpati and Gilman 2001; Rempel 2006) have found the generation and concentration of the large-scale toroidal magnetic field that exhibits the solar-cycle equatorward migration at or near the solar tachocline, the thin shear layer at the base of the solar convection zone, where solar rotation changes from the latitudinal differential rotation of the solar convective envelope to the nearly solid-body rotation of the radiative interior. Furthermore, with its stable (weakly) subadiabatic stratification, the thin overshoot region in the upper part of the tachocline layer (Gilman 2000) allows storage of strong toroidal magnetic fields against their magnetic buoyancy for time scales comparable to the solar cycle period (Parker 1975, 1979; van Ballegooijen 1982; Moreno-Insertis et al. 1992; Fan and Fisher 1996; Moreno-Insertis et al. 2002; Rempel 2003). Given the above reasons, it had become a prevailing picture that solar active regions originate from a strong toroidal magnetic field generated and stored in the overshoot layer at the base of the solar convection zone. Thus many studies have been devoted to addressing the processes of how the toroidal flux is destabilized and rise through the convection zone to form the observed solar active regions. This article focuses on a review (albeit incomplete) of these studies.

However, the need to put the site for the generation and storage of the strong toroidal magnetic field, responsible for the formation of solar active regions, to the overshoot layer at the bottom of the solar convection zone has been questioned (e.g., Brandenburg 2005; Charbonneau 2020). New results from the global 3D MHD simulations of convective dynamos have suggested a new scenario for the active region flux generation in the bulk of the solar convection zone (e.g., Nelson et al. 2011, 2013, 2014; Fan and Fang 2014). Recent advances in realistic near-surface layer radiation MHD simulations of active region/sunspot formation (see, e.g., Cheung et al. 2010; Stein and Nordlund 2012; Rempel and Cheung 2014; Chen et al. 2017), together with new observational constraints obtained from helioseismic investigations of pre-emergence solar active regions (e.g., Birch et al. 2013, 2016) have also raised difficulties for explaining active regions as buoyantly rising flux tubes originating from the bottom of the convection zone. This article also discusses these new developments.

It should be noted that bipolar magnetic regions emerge on the photosphere with a wide range of size scales that span at least 5 orders of magnitude (from below $10^{18}{\mathrm {\ Mx}}$ to $10^{23}{\mathrm {\ Mx}}$) in absolute flux content, ranging from the large, sunspot-containing active regions to small, ephemeral regions (ERs) that appear in the quiet Sun (e.g., Harvey 1993; Hagenaar et al. 2008). The well organized pattern and cycle dependence as described by the butterfly diagram, the Hale polarity rule, and Joy’s law exhibited by active regions are progressively less well obeyed by the smaller bipoles. Small ERs emerge in both the closed-field, mixed polarity quite-sun regions as well as the more unipolar coronal hole regions (e.g., Hagenaar et al. 2008). The nature and origin of ERs are not certain. The ER flux may originate close to the surface, produced by a “local dynamo” due to small-scale convective motions near the surface (e.g., Cattaneo et al. 2003; Bercik et al. 2005; Rempel 2014). Alternatively, ERs may correspond to flux sheared off from emerging or decaying active region flux tubes. The study by Hagenaar et al. (2008) using MDI magnetogram sequences have shown an interesting dependence of the ER emergence rate on the local flux imbalance, with lower emergence rate in regions of larger flux imbalance. This functional dependence is found to be the same for both the closed-field quiet-sun regions and the more unipolar coronal holes. Such a dependence of the ER emergence rate may, however, result from either of the above two scenarios for the origin of ERs (Hagenaar et al. 2008).

High resolution vector magnetic field observations from the Hinode satellite have also revealed new, unprecedented details of the photospheric magnetic field at the solar polar region (Tsuneta et al. 2008). It is found that the polar magnetic field is characterized by unipolar vertical kilogauss patches with super-equipartition field strength, and ubiquitous weaker transient horizontal fields. The origin of these unipolar strong flux tubes is not clear but they may simply be the surviving fragments of the following polarity of the decaying active regions being transported to the polar region through the combined actions of diffusion by supergranular motion and advection by meridional flows (see, e.g., Wang et al. 1989).

Although magnetic fields are generated on all scales in the solar convection zone (e.g Schüssler 2002), in this review, we only focus on the emergence process of active region scale flux tubes, whose generation and dynamic evolution involve the large-scale solar convective envelope and are significantly affected by the solar rotation. The remainder of the review will be organized as follows.

• Section 2 gives a brief overview of some of the simplifying models and computational approaches that have been applied to studying the very subsonic dynamic evolution of magnetic flux tubes in the deep solar convection zone. In particular, the thin flux tube model has been extensively used for understanding the global dynamics of emerging active region flux tubes in the solar convective envelope and (as discussed in the later sections) has produced results that explain the origin of several basic observed properties of solar active regions.

• Section 3 discusses the storage and equilibrium properties of the large scale toroidal magnetic fields in the stable overshoot region below the solar convection zone.

• Section 4 focuses on the magnetic buoyancy instabilities associated with the equilibrium toroidal magnetic fields and the formation of buoyant flux tubes from the base of the solar convection zone.

• Section 5 reviews results on the dynamic rise of emerging flux tubes in the solar convection zone.

  • Section 5.1 discusses major findings from the various thin flux tube simulations of emerging flux loops.

  • Section 5.2 discusses the observed hemispheric trend of the twist of the magnetic field in solar active regions and the models based on rising flux tubes that explain its origin.

  • Section 5.3 reviews results from multi-dimensional MHD simulations with regard to the minimum twist necessary for maintaining cohesion of the buoyantly rising flux tubes.

  • Section 5.4 discusses a further constraint on the twist of the rising flux tubes due to Joy’s law of active region tilts, based on results from 3D spherical-shell anelastic MHD simulations.

  • Section 5.5 discusses the kink evolution of highly twisted rising flux tubes.

  • Section 5.6 reviews the influence of 3D stratified convection on the evolution of buoyant flux tubes.

• Section 6 discusses results from 3D MHD simulations on the asymmetric transport of magnetic flux (or turbulent pumping of magnetic fields) by stratified convection penetrating into a stable overshoot layer.

• Section 7 discusses an alternative mechanism of magnetic flux amplification by converting the potential energy associated with the stratification of the convection zone into magnetic energy.

• Section 8 discusses new results from the global 3D MHD simulations of convective dynamos, which have suggested a new scenario for the active region flux generation in the bulk of the solar convection zone.

• Section 9 reviews new results from realistic, near-surface layer radiation MHD simulations of active region formation, and helioseismic investigations of pre-emergence solar active regions, and discusses their implications on the properties of the subsurface active region emerging flux.

• Section 10 discusses further improved radiation MHD simulations of active region formation that encompass the entire convection zone, avoiding the artificial effects of an imposed lower boundary condition for the near-surface layer simulations.

• Section 11 gives a summary and discussion of the results.

Computational approaches

A simplified model: the thin flux tube model

If the observed solar active regions correspond to flux tubes originating from the base of the solar convection zone, then in order for them to rise through the convection zone and avoid complete disruption by convection, it is reasonable to expect that the flux tubes’ field strength should be at least $B_{\mathrm {eq}}$, where $B_{\mathrm {eq}}$ is the field strength that is in equipartition with the kinetic energy density of the convective motions: $B_{\mathrm {eq}}^2 / 8 \pi = \rho v_{\mathrm {c}}^2 /2$. If we use the results from the mixing length models of the solar convection zone for the convective flow speed $v_{\mathrm {c}}$, then we find that in the deep convection zone $B_{\mathrm {eq}}$ is on the order of $10^4 {\mathrm {\ G}}$. Direct 3D numerical simulations have led to a new picture for solar convection that is non-local, driven by the concentrated downflow plumes formed by radiative cooling at the surface layer, and with extreme asymmetry between the upward and downward flows (see reviews by Spruit et al. 1990; Spruit 1997). Hence it should be noted that the $B_{\mathrm {eq}}$ derived based on the local mixing length description of solar convection may not really reflect the intensity of the convective flows in the deep solar convection zone. With this caution in mind, we nevertheless refer to $B_{\mathrm {eq}}\sim 10^4 {\mathrm {\ G}}$ as the field strength in equipartition with convection in this review.

Assuming that in the deep solar convection zone the magnetic field strength for flux tubes responsible for active region formation is at least $10^4 {\mathrm {\ G}}$, and given that the amount of flux observed in solar active regions ranges from $\sim 10^{20}{\mathrm {\ Mx}}$ to $10^{22}{\mathrm {\ Mx}}$ (see Zwaan 1987), one then finds that the cross-sectional radius of the flux tubes are below about 6 Mm, small in comparison to other spatial scales of variation, e.g., the pressure scale height. Such tubes at the bottom of the convection zone cannot be adequately resolved by the typical grid resolution of present 3D global-scale MHD simulations of the solar convective envelope, and thus the evolution of their magnetic buoyancy instability cannot be well modeled in such 3D MHD simulations. Thus a large body of work on studying the buoyant instability and buoyant rise of the active region scale flux tubes have been carried out using a 1D thin flux tube dynamic model initially derived by Spruit (1981).

Below we first give a description of the thin flux tube formulation, and later in the review we discuss results from both studies using the thin flux tube model, as well as studies using more sophisticated multi-dimensional MHD models.

For an isolated magnetic flux tube that is thin in the sense that its cross-sectional radius a is negligible compared to both the scale height of the ambient unmagnetized fluid and any scales of variation along the tube, the dynamics of the flux tube may be simplified with the thin flux tube approximation (see Spruit 1981; Longcope and Klapper 1997) which corresponds to the lowest order in an expansion of MHD in powers of a/L, where L represents any of the large length scales of variation. Under the thin flux tube approximation, all physical quantities of the tube, such as position, velocity, field strength, pressure, density, etc. are assumed to be averages over the tube cross-section and they vary spatially only along the tube. Thus it is a 1D model that describes the Lagrangian evolution of each tube segment on a space curve. Furthermore, because of the much shorter sound crossing time over the tube diameter compared to the other relevant dynamic time scales, an instantaneous pressure balance is assumed between the tube and the ambient unmagnetized fluid:

$$\begin{aligned} p + \frac{B^2}{8 \pi } = p_{\mathrm {e}} \end{aligned}$$

(1)

where p is the tube internal gas pressure, B is the tube field strength, and $p_{\mathrm {e}}$ is the pressure of the external fluid. Applying the above assumptions to the ideal MHD momentum equation, Spruit (1981) derived the equation of motion of a thin untwisted magnetic flux tube embedded in a field-free fluid. Taking into account the differential rotation of the Sun, ${{\varvec{\Omega }}}_{\mathrm {e}} ({\mathbf {r}}) = \varOmega _{\mathrm {e}} ({\mathbf {r}}) {{\hat{{\mathbf {z}}}}}$, the equation of motion for the thin flux tube in a rotating reference frame of angular velocity ${{{\varvec{\Omega }}}} = \varOmega {{\hat{{\mathbf {z}}}}}$ is (Ferriz-Mas and Schüssler 1993; Caligari et al. 1995)

$$\begin{aligned} \begin{aligned} \rho \frac{d {\mathbf {v}}}{d t} =\,&2 \rho ({\mathbf {v}}\times {{\varvec{\Omega }}}) + \rho ( \varOmega ^2 - \varOmega _{\mathrm {e}}^2) \varpi {\hat{{{\varvec{\varpi }}}}} + (\rho - \rho _{\mathrm {e}}) {\mathbf {g}}_{\mathrm {eff}}\\&{} + {\hat{{\mathbf {l}}}} \frac{\partial }{\partial s} \left( \frac{B^2}{8 \pi } \right) + \frac{B^2}{4 \pi } {\mathbf {k}}- C_{\mathrm {D}}\frac{\rho _{\mathrm {e}}|({\mathbf {v}}_{\mathrm {rel}})_{\perp }|({\mathbf {v}}_{\mathrm {rel}})_{\perp }}{\pi (\varPhi / B)^{1/2} }, \end{aligned} \end{aligned}$$

(2)

where

$$\begin{aligned} {\mathbf {g}}_{\mathrm {eff}}= & {} {\mathbf {g}}+ \varOmega _{\mathrm {e}}^2 \varpi {\hat{{{\varvec{\varpi }}}}}, \end{aligned}$$

(3)

$$\begin{aligned} ({\mathbf {v}}_{\mathrm {rel}})_{\perp }= & {} [{\mathbf {v}}- ({{\varvec{\Omega }}}_{\mathrm {e}} - {{\varvec{\Omega }}}) \times {\mathbf {r}}]_{\perp }. \end{aligned}$$

(4)

In the above, ${\mathbf {r}}$, ${\mathbf {v}}$, B, p, $\rho$, denote the position vector, velocity, magnetic field strength, plasma pressure and density of a Lagrangian tube element respectively, each of which is a function of time t and the arc-length s measured along the tube, $\rho _{\mathrm {e}}({\mathbf {r}})$ denotes the external density at the position ${\mathbf {r}}$ of the tube element, ${{\hat{{\mathbf {z}}}}}$ is the unit vector pointing in the direction of the solar rotation axis, ${\hat{{{\varvec{\varpi }}}}}$ denotes the unit vector perpendicular to and pointing away from the rotation axis at the location of the tube element and $\varpi$ denotes the distance to the rotation axis, ${\hat{{\mathbf {l}}}} \equiv \partial {\mathbf {r}}/ \partial s$ is the unit vector tangential to the flux tube, ${\mathbf {k}}\equiv \partial ^2 {\mathbf {r}}/ \partial s^2$ is the tube’s curvature vector, the subscript $\perp$ denotes the vector component perpendicular to the local tube axis, ${\mathbf {g}}$ is the gravitational acceleration, and $C_{\mathrm {D}}$ is the aerodynamic drag coefficient which is believed to be of order unity. The drag term (the last term on the right-hand side of the equation of motion (2)) is added to approximate the opposing force experienced by the flux tube as it moves relative to the ambient fluid. The term is derived based on the case of incompressible flows past a rigid cylinder under high Reynolds number conditions, in which a turbulent wake develops behind the cylinder, creating a pressure difference between the up- and down-stream sides and hence a drag force on the cylinder (see Batchelor 1967).

If one considered solid body rotation of the Sun, then the Eqs. (2), (3), and (4) can be simplified by letting ${{\varvec{\Omega }}}_{\mathrm {e}} = {{\varvec{\Omega }}}$. Weber et al. (2011) have incorporated the influence of the giant-cell convection and the mean flows in the solar convection envelope on the motion of the thin flux tube through the drag force term in the thin flux tube equation of motion (eq. 2) by letting:

$$\begin{aligned} ({\mathbf {v}}_{\mathrm {rel}})_{\perp } = ({\mathbf {v}}- {\mathbf {v}}_e)_{\perp } \end{aligned}$$

(5)

where ${\mathbf {v}}_e$ is a time dependent velocity field computed separatedly by a global convection simulation (Miesch et al. 2006), which contains the giant-cell convection and a solar like differential rotation. Calculations using the thin flux tube model (see Sect. 5.1) have shown that the effect of the Coriolis force $2 \rho ({\mathbf {v}}\times {{\varvec{\Omega }}})$ and helical convection acting on emerging flux loops can lead to east-west asymmetries in the loops that explain several well-known properties of solar active regions.

Note that in the equation of motion (2), the effect of the “enhanced inertia” caused by the back-reaction of the fluid to the relative motion of the flux tube is completely ignored. This effect has sometimes been incorporated by treating the inertia for the different components of Eq. (2) differently, with the term $\rho (d {\mathbf {v}}/ dt)_{\perp }$ on the left-hand-side of the perpendicular component of the equation being replaced by $(\rho + \rho _{\mathrm {e}}) (d {\mathbf {v}}/ dt)_{\perp }$ (see Spruit 1981). This simple treatment is problematic for curved tubes and the proper ways to treat the back-reaction of the fluid are controversial in the literature (Cheng 1992; Fan et al. 1994; Moreno-Insertis et al. 1996; Osin et al. 1999). Since the enhanced inertial effect is only significant during the impulsive acceleration phases of the tube motion, which occur rarely in the thin flux tube calculations of emerging flux tubes, and the results obtained do not depend significantly on this effect, many later calculations have taken the approach of simply ignoring it (see e.g. Caligari et al. 1995, 1998; Fan and Fisher 1996).

Equations (1) and (2) are to be complemented by the following equations to completely describe the dynamic evolution of a thin untwisted magnetic flux tube:

$$\begin{aligned} \frac{d }{d t} \left( \frac{B}{\rho } \right)= & {} \frac{B}{\rho }\left[ \frac{\partial ({\mathbf {v}}\cdot {{\hat{{\mathbf {l}}}}})}{\partial s} - {\mathbf {v}}\cdot {\mathbf {k}}\right] , \end{aligned}$$

(6)

$$\begin{aligned} \frac{1}{\rho } \frac{d \rho }{d t}= & {} \frac{1}{\gamma p} \frac{d p}{d t} - \frac{\nabla _{\mathrm {ad}}}{p} \frac{d Q}{d t}, \end{aligned}$$

(7)

$$\begin{aligned} p= & {} \frac{\rho R T}{\mu }, \end{aligned}$$

(8)

where $\nabla _{\mathrm {ad}}\equiv (\partial \ln T / \partial \ln p )_s$. Equation (6) describes the evolution of the tube magnetic field and is derived from the ideal MHD induction equation (Spruit 1981). Equation (7) is the energy equation for the thin flux tube (Fan and Fisher 1996), in which dQ/dt corresponds to the volumetric heating rate of the flux tube by non-adiabatic effects, e.g., by radiative diffusion (Sect. 3.2). Equation (8) is simply the equation of state for an ideal gas. Thus the five Eqs. (1), (2), (6), (7), and (8) completely determine the evolution of the five dependent variables ${\mathbf {v}}\,(t,s)$, $B\,(t,s)$, $p\,(t,s)$, $\rho \,(t,s)$, and $T\,(t,s)$ for each Lagrangian tube element of the thin flux tube.

Spruit’s original formulation for the dynamics of a thin isolated magnetic flux tube as described above assumes that the tube consists of untwisted flux ${\mathbf {B}}= B\,{\hat{{\mathbf {l}}}}$. Longcope and Klapper (1997) extend the above model to include the description of a weak twist of the flux tube, assuming that the field lines twist about the axis at a rate q whose magnitude is $2 \pi / L_{\mathrm {w}}$, where $L_{\mathrm {w}}$ is the distance along the tube axis over which the field lines wind by one full rotation and $|qa| \ll 1$. Thus in addition to the axial component of the field B, there is also an azimuthal field component in each tube cross-section, which to lowest order in qa is given by $B_{\theta } = q r_{\perp } B$, where $r_{\perp }$ denotes the distance to the tube axis. An extra degree of freedom for the motion of the tube element—the spin of the tube cross-section about the axis—is also introduced, whose rate is denoted by $\omega$ (angle per unit time). By considering the kinematics of a twisted ribbon with one edge corresponding to the tube axis and the other edge corresponding to a twisted field line of the tube, Longcope and Klapper (1997) derived an equation that describes the evolution of the twist q in response to the motion of the tube:

$$\begin{aligned} \frac{d q}{d t} = - \frac{d \ln \delta s}{d t} \, q + \frac{\partial \omega }{\partial s} + ({\hat{{\mathbf {l}}}} \times {\mathbf {k}}) \cdot \frac{d \,{\hat{{\mathbf {l}}}}}{d t}, \end{aligned}$$

(9)

where $\delta s$ denotes the length of a Lagrangian tube element. The first term on the right-hand-side describes the effect of stretching on q: Stretching the tube reduces the rate of twist q. The second term is simply the change of q resulting from the gradient of the spin along the tube. The last term is related to the conservation of total magnetic helicity which, for the thin flux tube structure, can be decomposed into a twist component corresponding to the twist of the field lines about the axis, and a writhe component corresponding to the “helicalness” of the axis (see discussion in Longcope and Klapper 1997). It describes how the writhing motion of the tube axis can induce twist of the opposite sense in the tube.

Furthermore, by integrating the stresses over the surface of a tube segment, Longcope and Klapper (1997) evaluated the forces experienced by the tube segment. They found that for a weakly twisted ($|qa| \ll 1$) thin tube ($|a \partial _s| \ll 1$, where $\partial _s$ denotes the inverse of the length scale of variation along the tube), the equation of motion of the tube axis differs very little from that for an untwisted tube—the leading order term in the difference is $O[qa^2 \partial _s]$ (see also Ferriz-Mas and Schüssler 1990). Thus the equation of motion (2) applies also to a weakly twisted thin flux tube. By further evaluating the torques exerted on a tube segment, Longcope and Klapper (1997) also derived an equation for the evolution of the spin $\omega$:

$$\begin{aligned} \frac{d \omega }{d t} = - \frac{2}{a} \frac{d a}{d t} \, \omega + v_{\mathrm {a}}^2 \frac{\partial q}{\partial s} , \end{aligned}$$

(10)

where $v_{\mathrm {a}}= B/\sqrt{4\pi \rho }$ is the Alfvén speed. The first term on the right hand side simply describes the decrease of spin due to the expansion of the tube cross-section as a result of the tendency to conserve angular momentum. The second term, in combination with the second term on the right hand side of Eq. (9), describes the propagation of torsional Alfvén waves along the tube.

The two new Eqs. (9) and (10)—derived by Longcope and Klapper (1997)—together with the earlier Eqs. (1), (2), (6), (7), and (8) provide a description for the dynamics of a weakly twisted thin flux tube. Note that the two new equations are decoupled from and do not have any feedback on the solutions for the dependent variables described by the earlier equations. One can first solve for the motion of the tube axis using Eqs. (1), (2), (6), (7), and (8), and then apply the resulting motion of the tube axis to Eqs. (9) and (10) to determine the evolution of the twist of the tube. If the tube is initially twisted, then the twist q can propagate and re-distribute along the tube as a result of stretching (1st term on the right-hand-side of Eq. (9)) and the torsional Alfvén waves (2nd term on the right-hand-side of Eq. (9)). Twist can also be generated due to writhing motion of the tube axis (last term on the right-hand-side of Eq. (9)), as required by the conservation of total helicity.

The thin flux tube (TFT) model described above is physically intuitive and computationally tractable. It provides a description of the dynamic motion of the tube axis in a three-dimensional space, taking into account large scale effects such as the curvature of the convective envelope and the Coriolis force due to solar rotation. The Lagrangian treatment of each tube segment in the TFT model allows for preserving perfectly the frozen-in condition of the tube plasma. Thus there is no magnetic diffusion in the TFT model. However, the TFT model ignores variations within each tube cross-section. It is only applicable when the flux tube radius is thin (Sect. 2.1) and the tube remains a cohesive object (Sect. 5.3). Clearly, the TFT model is very limited and direct MHD calculations that resolve the tube cross-section and its interaction with the surrounding fluid are needed to truly solve the problem. On the other hand, direct MHD simulations that discretize the spatial domain are subject to numerical diffusion. The need to adequately resolve the flux tube—so that numerical diffusion does not have a significant impact on the dynamical processes of interest (e.g., the variation of magnetic buoyancy)—severely limits the spatial extent of the domain that can be modeled. Thus the TFT model has served as an initial step to study the kinds of large scale dynamical effects of a buoyantly rising active region flux tube (assuming it maintains cohesion) in the global convective envelope (Sect. 5.1). With the recent advances in the 3D computational MHD models of the solar convection zone (e.g., Hotta and Iijima 2020), global-scale simulations of the solar convective envelope with an adequate resolution to resolve active region scale flux tubes at the bottom of the solar convection zone are becoming feasible.

The anelastic approximation:

For the bulk of the solar convection zone, the fluid stratification is very close to being adiabatic with $0 < \delta \ll 1$, where $\delta \equiv \nabla - \nabla _{\mathrm {ad}}$ is the non-dimensional superadiabaticity with $\nabla = \partial \ln T / \partial \ln p$ and $\nabla _{\mathrm {ad}}= ( \partial \ln T / \partial \ln p )_{\mathrm {ad}}$ denoting the actual and the adiabatic logarithmic temperature gradient of the fluid respectively, and the convective flow speed $v_{\mathrm {c}}$ is expected to be much smaller than the sound speed $c_{\mathrm {s}}$: $v_{\mathrm {c}}/ c_{\mathrm {s}}\sim \delta ^{1/2} \ll 1$ (see Schwarzschild 1958; Lantz 1991). Furthermore, the plasma $\beta$ defined as the ratio of the thermal pressure to the magnetic pressure ($\beta \equiv p / (B^2/8 \pi )$) is expected to be very high ($\beta \gg 1$) in the deep convection zone. For example for flux tubes with field strengths of order $10^5 {\mathrm {\ G}}$, which is significantly super-equipartition compared to the kinetic energy density of convection, the plasma $\beta$ is of order $10^5$. Under these conditions, a very useful computational approach for modeling subsonic magnetohydrodynamic processes in a pressure dominated plasma is the well-known anelastic approximation (see Gough 1969; Gilman and Glatzmaier 1981; Glatzmaier 1984; Lantz and Fan 1999). The main feature of the anelastic approximation is that it filters out the sound waves so that the time step of numerical integration is not limited by the stringent acoustic time scale which is much smaller than the relevant dynamic time scales of interest as determined by the flow velocity and the Alfvén speed.

Listed below is the set of anelastic MHD equations (see Gilman and Glatzmaier 1981; Lantz and Fan 1999, for details of the derivations):

$$\begin{aligned} \nabla \cdot ( \rho _0 {\mathbf {v}})= & {} 0 , \end{aligned}$$

(11)

$$\begin{aligned} \rho _0 \left[ \frac{\partial {\mathbf {v}}}{\partial t} + ({\mathbf {v}}\cdot \nabla ) {\mathbf {v}}\right]= & {} - \nabla p_1 + \rho _1 {\mathbf {g}}+ \frac{1}{4 \pi } ( \nabla \times {\mathbf {B}}) \times {\mathbf {B}}\nonumber \\&+ \nabla \cdot {{\varvec{\Pi }}}, \end{aligned}$$

(12)

$$\begin{aligned} \rho _0 T_0 \left[ \frac{\partial s_1}{\partial t} + ({\mathbf {v}}\cdot \nabla )(s_0 + s_1 ) \right]= & {} \nabla \cdot ( K \rho _0 T_0 \nabla s_1) + \frac{1}{4 \pi } \eta | \nabla \times {\mathbf {B}}|^2 \nonumber \\&+ ( {{\varvec{\Pi }}}\cdot \nabla ) \cdot {\mathbf {v}}, \end{aligned}$$

(13)

$$\begin{aligned} \nabla \cdot {\mathbf {B}}= & {} 0 , \end{aligned}$$

(14)

$$\begin{aligned} \frac{\partial {\mathbf {B}}}{\partial t}= & {} \nabla \times ( {\mathbf {v}}\times {\mathbf {B}}) - \nabla \times ( \eta \nabla \times {\mathbf {B}}) , \end{aligned}$$

(15)

$$\begin{aligned} \frac{\rho _1}{\rho _0}= & {} \frac{p_1}{p_0} - \frac{T_1}{T_0} , \end{aligned}$$

(16)

$$\begin{aligned} \frac{s_1}{c_p}= & {} \frac{T_1}{T_0} - \frac{\gamma -1}{\gamma } \frac{p_1}{p_0} , \end{aligned}$$

(17)

where $s_0(z)$, $p_0 (z)$, $\rho _0 (z)$, and $T_0 (z)$ correspond to a time-independent, background reference state of hydrostatic equilibrium and nearly adiabatic stratification, and velocity ${\mathbf {v}}$, magnetic field ${\mathbf {B}}$, thermodynamic fluctuations $s_1$, $p_1$, $\rho _1$, and $T_1$ are the dependent variables to be solved that describe the changes from the reference state. The quantity ${{\varvec{\Pi }}}$ is the viscous stress tensor given by

$$\begin{aligned} \varPi _{ij} \equiv \mu \left( \frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i} - \frac{2}{3}(\nabla \cdot {\mathbf {v}})\delta _{ij} \right) , \end{aligned}$$

and $\mu$, K and $\eta$ denote the dynamic viscosity, and thermal and magnetic diffusivity, respectively. The anelastic MHD equations (11)–(17) are derived based on a scaled-variable expansion of the fully compressible MHD equations in powers of $\delta$ and $\beta ^{-1}$, which are both assumed to be quantities $\ll 1$. To first order in $\delta$, the continuity equation (11) reduces to the statement that the divergence of the mass flux equals to zero. As a result sound waves are filtered out, and pressure is assumed to adjust instantaneously in the fluid as if the sound speed was infinite. Although the time derivative of density no longer appears in the continuity equation, density $\rho _1$ does vary in space and time and the fluid is compressible but on the dynamic time scales (as determined by the flow speed and the Alfvén speed) not on the acoustic time scale, thus allowing convection and magnetic buoyancy to be modeled in the highly stratified solar convection zone. Fan (2001) has shown that the anelastic formulation gives an accurate description of the magnetic buoyancy instabilities under the conditions of high plasma $\beta$ and nearly adiabatic stratification.

Because of the divergence free condition of $\rho _0 {\mathbf {v}}$ given in equation (11), one can take the divergence of the momentum equation, where the divergence of the $\rho _0 (\partial {\mathbf {v}}/ \partial t)$ term vanishes, to obtain an elliptic equation for $p_1$ of the form: $\nabla ^2 p_1 = ...$. One way to numerically maintain equation (11) is to solve this elliptic equation for $p_1$ at every time step before substituting it into the momentum equation for advancing the velocity (e.g. Fan 2008). Another well-known method to ensure equation (11) in anelastic MHD codes that use the spectral method is to express $\rho _0 {\mathbf {v}}$ in terms of the curls of vector potentials and numerically advance the equations for the vector potentials (e.g. Glatzmaier 1984; Fan et al. 1999; Featherstone and Hindman 2016).

Fully compressible MHD simulations have also been applied to study the dynamic evolution of a magnetic field in the deep solar convection zone using non-solar but reasonably large $\beta$ values such as $\beta \sim 10$ to 1000 (e.g., Emonet and Moreno-Insertis 1998; Manek et al. 2018). Near the top of the solar convection zone, neither the TFT model nor the anelastic approximation are applicable because the active region flux tubes are no longer thin (Moreno-Insertis 1992) and the velocity field is no longer subsonic. Fully compressible MHD simulations are necessary for modeling flux emergence through the near-surface layer (Sect. 9).

The reduced speed of sound technique (RSST)

Another numerical approach that has been developed for simulating both the substantially subsonic dynamic evolution in the deep convection zone and the highly compressible evolution in the near-surface layer in a single model is the reduced speed of sound technique (RSST) (Hotta et al. 2012b, 2015; Hotta and Iijima 2020). The RSST solves the fully compressible MHD equations, but with the continuity equation modified to be:

$$\begin{aligned} \frac{\partial \rho }{\partial t} = \frac{1}{\xi ^2} \nabla \cdot ( \rho \mathbf{v} ) , \end{aligned}$$

(18)

which effectively reduces the characteristic sound speed to be $c_s / \xi$, where $c_s = \sqrt{(\partial p / \partial \rho )_s}$ is the local adiabatic sound speed. Thus the CFL timestep for numerical integration is constrained by the reduced characteristic sound speed $c_s / \xi$ and can be much less stringent than that constrained by the actual $c_s$ in the deep solar convection zone. Hydrodynamic simulations of stratified convection by Hotta et al. (2012b) showed that the statistical properties of the convective flows remain in good agreement with the results from the simulations without RSST (i.e., with $\xi = 1$) as long as the Mach number of the convective flows remains below 0.7.

With the RSST continuity equation (18) above, mass conservation is no longer maintained instantaneously. However, when a statistical steady state is reached, the divergence free condition of mass flux as in the anelastic approximation is maintained (on average), i.e.,

$$\begin{aligned} 0 = \nabla \cdot \langle \rho \mathbf{v} \rangle \,, \end{aligned}$$

(19)

where, “$\langle \rangle$” represents averaging over a convective turn-over timescale. Applications of the RSST have used a depth dependent $\xi$ in the convection zone, so that either the characteristic sound speed is close to being uniform (e.g., Hotta et al. 2015, 2016) or the Mach number is close to being uniform (e.g., Hotta and Iijima 2020), while also requiring that the Mach number remains significantly below 0.7. In particular, the high resolution global convective dynamo simulations using the RSST by Hotta et al. (2016) have shown that the resulting mean flows (such as the differential rotation) and the cycling mean field in the solar convective envelope are consistent with the results produced by the simulation using the anelastic approximation (Fan and Fang 2014), when the same physical conditions (i.e., the rotation rate, the radiative heat flux, the thermal conductivity, viscosity and magnetic diffusivity) for the model convective envelope are used.

Compared to the anelastic approximation, the RSST has several advantages (Hotta et al. 2012b). For RSST the numerical schemes remain explicit, without having to solve an elliptic equation as in the case of the anelastic approximation, which requires global communication in parallel computing, and thus can more easily scale up for massively parallel computations. The highly compressible dynamics in the near-surface layer where the anelastic approximation becomes invalid can be modeled together with the extremely subsonic dynamics in the deep convection zone in a single domain in the RSST simulations by using a spatially varying $\xi$.

Equilibrium conditions of toroidal magnetic fields stored at the base of the solar convection zone

The mechanical equilibria for an isolated toroidal flux tube or an extended magnetic layer

The Hale’s polarity rule of solar active regions indicates a subsurface magnetic field that is highly organized, of predominantly toroidal direction, and with sufficiently strong field strength (super-equipartition compared to the kinetic energy density of convection) such that it is not subjected to strong deformation by convective motions. In one solar dynamo paradigm, it has been argued that the weakly subadiabatically stratified overshoot layer at the base of the solar convection zone is likely the site for the storage of such a strong coherent toroidal magnetic field against buoyant loss for time scales comparable to the solar cycle period (e.g. Parker 1979; Spiegel and Weiss 1980; Galloway and Weiss 1981; van Ballegooijen 1982).

It is not clear if the toroidal magnetic field is in the state of isolated flux tubes or stored in the form of a more diffuse magnetic layer. Moreno-Insertis et al. (1992) have considered the mechanical equilibrium of isolated toroidal magnetic flux tubes (flux rings) in a subadiabatic layer using the thin flux tube approximation (Sect. 2.1). The forces experienced by an isolated toroidal flux ring at the base of the convection zone is illustrated in Fig. 5a.

Fig. 5

Schematic illustrations based on Schüssler and Rempel (2002) of the various forces involved with the mechanical equilibria of an isolated toroidal flux ring (a) and a magnetic layer (b) at the base of the solar convection zone. In the case of an isolated toroidal ring (see the black dot in (a) indicating the location of the tube cross-section), the buoyancy force has a component parallel to the rotation axis, which cannot be balanced by any other forces. Thus mechanical equilibrium requires that the buoyancy force vanishes and the magnetic curvature force is balanced by the Coriolis force resulting from a prograde toroidal flow in the flux ring. For a magnetic layer (as indicated by the shaded region in (b)), on the other hand, a latitudinal pressure gradient can be built up, so that an equilibrium may also exist where a non-vanishing buoyancy force, the magnetic curvature force and the pressure gradient are in balance with vanishing Coriolis force (vanishing longitudinal flow)

The condition of total pressure balance (1) and the presence of a magnetic pressure inside the flux tube require a lower gas pressure inside the flux tube compared to the outside. Thus either a lower density or a lower temperature (or a combination of the two) inside the flux tube is needed to achieve the lower gas pressure required for pressure balance. If the flux tube is in thermal equilibrium with the surrounding, then the density inside needs to be lower and the flux tube is buoyant. The buoyancy force associated with a magnetic flux tube in thermal equilibrium with its surrounding is often called the magnetic buoyancy (Parker 1975). It can be seen in Fig. 5a that a radially directed buoyancy force has a component that is parallel to the rotation axis, which cannot be balanced by any other forces associated with the toroidal flux ring. Thus for the toroidal flux ring to be in mechanical equilibrium, the tube needs to be in a neutrally buoyant state with vanishing buoyancy force, and with the magnetic curvature force pointing towards the rotation axis being balanced by a Coriolis force produced by a faster rotational speed of the flux ring (see Fig. 5a). Such a neutrally buoyant flux ring (with equal density between inside and outside) then requires a lower internal temperature than the surrounding plasma to satisfy the total pressure balance. If one starts with a toroidal flux ring that is initially in thermal equilibrium with the surrounding and rotates at the same ambient angular velocity, then the flux ring will move radially outward due to its buoyancy and latitudinally poleward due to the unbalanced poleward component of the tension force. As a result of its motion, the flux ring will lose buoyancy due to the subadiabatic stratification and attain a larger internal rotation rate with respect to the ambient field-free plasma due to the conservation of angular momentum, evolving towards a mechanical equilibrium configuration. The flux ring will undergo superposed buoyancy and inertial oscillations around this mechanical equilibrium state. It is found that the oscillations can be contained within the stably stratified overshoot layer and also within a latitudinal range of $\varDelta \theta \lesssim 20^\circ$ to be consistent with the active region belt, if the field strength of the toroidal flux ring $B \lesssim 10^5 {\mathrm {\ G}}$ and the subadiabaticity of the overshoot layer is sufficiently strong with $\delta \equiv \nabla - \nabla _{\mathrm {ad}}\lesssim -10^{-5}$. Flux rings with significantly larger field strength cannot be kept within the low latitude zones of the overshoot region.

Rempel et al. (2000) considered the mechanical equilibrium of a layer of an axisymmetric toroidal magnetic field of $10^5 {\mathrm {\ G}}$ in a subadiabatically stratified region near the bottom of the solar convection zone in full spherical geometry. A field strength of $10^5 {\mathrm {\ G}}$ is considered because earlier thin flux tube models suggest that toroidal magnetic fields in the overshoot layer with field strengths of order $10^5 {\mathrm {\ G}}$ are needed for the magnetic buoyancy instability to develop with reasonably short growth times and form emerging tubes with properties consistent with solar active regions (e.g. Caligari et al. 1995, see also Sect. 4.1). In this case, as illustrated in Fig. 5b, a latitudinal pressure gradient can be built up, allowing for force balance between a non-vanishing buoyancy force, the magnetic curvature force, and the pressure gradient without requiring a prograde toroidal flow. Thus a wider range of equilibria can exist. Rempel et al. (2000) found that under the condition of a strong subadiabatic stratification such as the radiative interior with $\delta \sim -0.1$, the magnetic layer tends to establish a mechanical equilibrium where a latitudinal pressure gradient is built up to balance the poleward component of the magnetic tension, and where the net radial component of the buoyancy and magnetic tension forces is efficiently balanced by the strong subadiabaticity. The magnetic layer reaches this equilibrium solution in a time scale short compared to the time required for a prograde toroidal flow to set up for the Coriolis force to be significant. For this type of equilibrium where a latitudinal pressure gradient is playing a dominant role in balancing the poleward component of the magnetic curvature force, there is significant relative density perturbation ($\gg 1/\beta$) in the magnetic layer compared to the background stratification. On the other hand, under the condition of a very weak subadiabatic stratification such as that in the overshoot layer near the bottom of the convection zone with $\delta \sim -10^{-5}$, the magnetic layer tends to evolve towards a mechanical equilibrium which resembles that of an isolated toroidal flux ring, where the relative density perturbation is small ($\ll 1/\beta$), and the magnetic curvature force is balanced by the Coriolis force induced by a prograde toroidal flow in the magnetic layer. Thus regardless of whether the field is in the state of an extended magnetic layer or isolated flux tubes, a $10^5 {\mathrm {\ G}}$ toroidal magnetic field stored in the weakly subadiabatically stratified overshoot region is preferably in a mechanical equilibrium with small relative density perturbation and with a prograde toroidal flow whose Coriolis force balances the magnetic tension. The prograde toroidal flow necessary for the equilibrium of the $10^5 {\mathrm {\ G}}$ toroidal field is about $200 \mathrm {\ m s}^{-1}$, which is approximately 10% of the mean rotation rate of the Sun. Thus, if the dynamo operated in the overshoot region at the base of the convection zone, then one could expect significant changes in the differential rotation in the overshoot region during the solar cycle as the toroidal field is being amplified (Rempel et al. 2000). Detecting these toroidal flows and their temporal variation in the overshoot layer via helioseismic techniques would be a means by which we can probe and measure the toroidal magnetic field generated by the solar cycle dynamo.

Effect of radiative heating

If a strong super-equipartition field of $10^5 {\mathrm {\ G}}$ is stored at the base of the solar convection zone as suggested by the earlier thin flux tube models (e.g. Caligari et al. 1995, see also Sect. 4.1), then it should be in a state of mechanical equilibrium since convective motion is not strong enough to counteract the magnetic stress (Sect. 5.6). For isolated flux tubes stored in the weakly subadiabatic overshoot layer, the mechanical equilibrium corresponds to a neutrally buoyant state with a lower internal temperature (Sect. 3.1). Therefore flux tubes will be heated by radiative diffusion due to the mean temperature difference between the tube and the surrounding field-free plasma (see Parker 1979; van Ballegooijen 1982). Moreover, it is not adequate to just consider this zeroth order contribution due to the mean temperature difference in evaluating the radiative heat exchange between the flux tube and its surroundings. Due to the convective heat transport, the temperature gradient in the overshoot region and the lower convection zone is very close to being adiabatic, deviating significantly from that of a radiative equilibrium, and hence there is a non-zero divergence of radiative heat flux (see Spruit 1974; van Ballegooijen 1982). Thus an isolated magnetic flux tube with internally suppressed convective transport should also experience a net heating due to this non-zero divergence of radiative heat flux, provided that the radiative diffusion is approximately unaffected within the flux tube (Fan and Fisher 1996; Moreno-Insertis et al. 2002; Rempel 2003). In the limit of a thin flux tube, the rate of radiative heating (per unit volume) experienced by the tube is estimated to be (Fan and Fisher 1996)

$$\begin{aligned} \frac{d Q}{d t} = - \nabla \cdot ({\mathbf {F}}_{\mathrm {rad}}) - \kappa \,( x_1^2 / a^2 ) \, ( {\overline{T}} - {\overline{T}}_{\mathrm {e}} ), \end{aligned}$$

(20)

where ${\mathbf {F}}_{\mathrm {rad}}$ is the unperturbed radiative energy flux, $\kappa$ is the unperturbed radiative conductivity, $x_1$ is the first zero of the Bessel function $J_0 (x)$, a is the tube radius, ${\overline{T}}$ is the mean temperature of the flux tube, and ${\overline{T}}_{\mathrm {e}}$ is the corresponding unperturbed temperature at the location of the tube. The first term on the right hand side of equation (20) corresponds to the radiative heating by the convergence of the radiative heat flux in the background plasma. The second term approximates the perturbation to the radiative diffusion due to the temperature difference inside the flux tube relative to the background plasma (see the detailed derivation of the second term in Fan and Fisher 1996). Under the conditions prevailing near the base of the solar convection zone and for flux tubes that are responsible for active region formation, the first term due to the non-vanishing divergence of the radiative heat flux is found in general to dominate the second term. In the overshoot region, it can be shown that for these flux tubes the time scale for the heating to significantly increase their buoyancy from an initial neutrally buoyant state is long compared to the dynamic time scale characterized by the Brunt–Väisälä frequency. Thus the radiative heating is found to cause a quasi-static rise of the toroidal flux tubes, during which the tubes remain close to being neutrally buoyant. The upward drift velocity is estimated to be $\sim 10^{-3} | \delta |^ {-1} {\mathrm {\ cm\ s}}^{-1}$ which does not depend sensitively on the field strength of the flux tube (Fan and Fisher 1996; Rempel 2003). This implies that maintaining toroidal flux tubes in the overshoot region for a period comparable to the solar cycle time scale requires a strong subadiabaticity of $\delta < - 10^{-4}$, which is significantly more subadiabatic than the values obtained by most of the overshoot models based on the non-local mixing length theory (see van Ballegooijen 1982; Schmitt et al. 1984; Skaley and Stix 1991).

On the other hand if the spatial filling factor of the toroidal flux tubes is large, or if the toroidal magnetic field is stored in the form of an extended magnetic layer, then the suppression of convective motion by the magnetic field is expected to alter the overall temperature stratification in the overshoot region. Rempel (2003) performed a 1D thermal diffusion calculation to model the change of the mean temperature stratification in the overshoot region when convective heat transport is being significantly suppressed. It is found that a reduction of the convective heat conductivity by a factor of 100 leads to the establishment of a new thermal equilibrium of significantly more stable temperature stratification with $\delta \sim -10^{-4}$ in a time scale of a few months. Thus as the toroidal magnetic field is being amplified by the solar dynamo process, it may improve the conditions for its own storage by reducing the convective energy transport and increasing the subadiabaticity in the overshoot region.

Destabilization of a toroidal magnetic field and formation of buoyant flux tubes

In the previous section, we have reviewed the equilibrium properties of a strong ($\sim 10^5 {\mathrm {\ G}}$) toroidal magnetic field stored at the base of the solar convection zone. In this section we focus on the stability of the equilibria and the mechanisms by which the magnetic field can escape in the form of discrete buoyant flux tubes.

The buoyancy instability of isolated toroidal magnetic flux tubes

By linearizing the thin flux tube dynamic equations (1), (2), (6), (7), and (8), the stability of neutrally buoyant toroidal magnetic flux tubes to isentropic perturbations have been studied (see Spruit and van Ballegooijen 1982b, a; Ferriz-Mas and Schüssler 1993, 1995).

In the simplified case of a horizontal neutrally buoyant flux tube in a plane parallel atmosphere, ignoring the effects of curvature and solar rotation, the necessary and sufficient condition for instability is (Spruit and van Ballegooijen 1982b, a)

$$\begin{aligned} k^2 H_p^2< \frac{\beta / 2}{1 + \beta } (1/\gamma + \beta \delta ) , \end{aligned}$$

(21)

where k is the wavenumber along the tube of the undulatory perturbation, $H_p$ is the local pressure scale height, $\beta \equiv p / (B^2/8 \pi )$ is the ratio of the plasma pressure divided by the magnetic pressure of the flux tube, $\delta = \nabla - \nabla _{\mathrm {ad}}$ is the superadiabaticity, and $\gamma$ is the ratio of the specific heats. If all values of k are allowed, then the condition for the presence of instability is

$$\begin{aligned} \beta \delta > -1 / \gamma . \end{aligned}$$

(22)

Note that $k \rightarrow 0$ is a singular limit. For perturbations with $k=0$ which do not involve bending the field lines, the condition for instability becomes (Spruit and van Ballegooijen 1982b)

$$\begin{aligned} \beta \delta > \frac{2}{\gamma } \left( \frac{1}{\gamma } - \frac{1}{2}\right) \sim 0.12 \end{aligned}$$

(23)

which is a significantly more stringent condition than (22), even more stringent than the convective instability for a field-free fluid ($\delta > 0$). Thus the undulatory instability (with $k \ne 0$) is of a very different nature and is easier to develop than the instability associated with uniform up-and-down motions of the entire flux tube. The undulatory instability can develop even in a convectively stable stratification with $\delta < 0$ as long as the field strength of the flux tube is sufficiently strong (i.e., $\beta$ is of sufficiently small amplitude) such that $|\beta \delta |$ is smaller than $1/\gamma$. In the regime of $-1/\gamma< \beta \delta < (2/\gamma )(1/\gamma - 1/2)$ where only the undulatory modes with $k \ne 0$ are unstable, a longitudinal flow from the crests to the troughs of the undulation is essential for driving the instability. Since the flux tube has a lower internal temperature and hence a smaller pressure scale height inside, upon bending the tube, matter will flow from the crests to the troughs to establish hydrostatic equilibrium along the field. This increases the buoyancy of the crests and destabilizes the tube (Spruit and van Ballegooijen 1982b).

Including the curvature effect of spherical geometry, but still ignoring solar rotation, Spruit and van Ballegooijen (1982b, 1982a) have also studied the special case of a toroidal flux ring in mechanical equilibrium within the equatorial plane. Since the Coriolis force due to solar rotation is ignored, the flux ring in the equatorial plane needs to be slightly buoyant to balance the inward tension force. For latitudinal motions out of the equatorial plane, the axisymmetric component is unstable, which corresponds to the poleward slip of the tube as a whole. But this instability can be suppressed when the Coriolis force is included (Ferriz-Mas and Schüssler 1993). For motions within the equatorial plane, the conditions for instabilities are (Spruit and van Ballegooijen 1982b, a)

$$\begin{aligned} \begin{aligned} \frac{1}{2} \beta \delta> (m^2 - 3 - s) f^2 + 2f / \gamma - 1/(2 \gamma )&\quad (m \ge 1),\\ \frac{1}{2} \beta \delta > f^2 (1-s) -2f/\gamma + \frac{1}{\gamma }\left( \frac{1}{\gamma } - \frac{1}{2} \right)&\quad (m = 0) \end{aligned} \end{aligned}$$

(24)

where $f \equiv H_p / r_0$ is the ratio of the pressure scale height over the radius of the bottom of the solar convection zone, m (having integer values $0,1,\dots$) denotes the azimuthal order of the undulatory mode of the closed toroidal flux ring, i.e., the wavenumber $k = m/r_0$, s is a parameter that describes the variation of the gravitational acceleration: $g \propto r^s$. Near the base of the solar convection zone, $f \sim 0.1$, $s \sim -2$. Thus conditions (24) show that it is possible for $m=0,1,2,3,4$ modes to become unstable in the weakly subadiabatic overshoot region, and that the instabilities of the $m=1,2,3$ modes require less stringent conditions than the instability of the $m=0$ mode. Since Eq. (24) is derived for the singular case of an equilibrium toroidal ring in the equatorial plane, its applicability is very limited.

The general problem of the linear stability of a thin toroidal flux ring in mechanical equilibrium in a differentially rotating spherical convection zone at arbitrary latitudes has been studied in detail by Ferriz-Mas and Schüssler (1993, 1995). For general non-axisymmetric perturbations, a sixth-order dispersion relation is obtained from the linearized thin flux tube equations. It is not possible to obtain analytical stability criteria. The dispersion relation is solved numerically to find instability and the growth rates of the unstable modes. The regions of instability in the $(B_0, \lambda _0)$ plane (with $B_0$ being the magnetic field strength of the flux ring and $\lambda _0$ being the equilibrium latitude), under the conditions representative of the overshoot layer at the base of the solar convection zone are shown in Fig. 6 (from Caligari et al. 1995).

Fig. 6

Image reproduced with permission from Caligari et al. (1995), copyright by AAS

Upper panel: Regions of unstable toroidal flux tubes in the $(B_0, \lambda _0)$-plane (with $B_0$ being the magnetic field strength of the flux tubes and $\lambda _0$ being the equilibrium latitude). The subadiabaticity at the location of the toroidal flux tubes is assumed to be $\delta \equiv \nabla - \nabla _{\mathrm {ad}}= -2.6 \times 10^{-6}$. The white area corresponds to a stable region while the shaded regions indicate instability. The degree of shading signifies the azimuthal wavenumber of the most unstable mode. The contours correspond to lines of constant growth time of the instability. Thicker lines are drawn for growth times of 100 days and 300 days. Lower panel: Same as the upper panel except that the subadiabaticity at the location of the toroidal tubes is $\delta \equiv \nabla - \nabla _{\mathrm {ad}}= -1.9 \times 10^{-7}$.

The basic parameters that determine the stability of an equilibrium toroidal flux ring are its field strength and the subadiabaticity of the external stratification. In the case $\delta \equiv \nabla - \nabla _{\mathrm {ad}}= -2.6 \times 10^{-6}$ (upper panel of Fig. 6), unstable modes with reasonably short growth times (less than about a year) only begin to appear at sunspot latitudes for $B_0 \gtrsim 1.2 \times 10^5 {\mathrm {\ G}}$. These unstable modes are of $m=1$ and 2. In case of a weaker subadiabaticity, $\delta \equiv \nabla - \nabla _{\mathrm {ad}}= -1.9 \times 10^{-7}$ (lower panel of Fig. 6), reasonably fast growing modes (growth time less than a year) begin to appear at sunspot latitudes for $B_0 \gtrsim 5 \times 10^4 {\mathrm {\ G}}$, and the most unstable modes are of $m=1$ and 2. These results suggest that toroidal magnetic fields stored in the overshoot layer at the base of the solar convection zone do not become unstable until their field strength becomes significantly greater than the equipartition value of $10^4 {\mathrm {\ G}}$.

Thin flux tube simulations of the non-linear growth of the non-axisymmetric instabilities of initially toroidal flux tubes and the emergence of $\varOmega$-shaped flux loops through the solar convective envelope will be discussed in Sect. 5.1.

Breakup of an equilibrium magnetic layer and formation of buoyant flux tubes

If the toroidal magnetic field responsible for the formation of solar active regions is stored at the base of the convection zone (as suggested by one solar dynamo paradigm), it is possible that the stored magnetic field is in the form of an extended magnetic layer, instead of individual magnetic flux tubes for which the thin flux tube approximation can be applied. The classic problem of the buoyancy instability of a horizontal magnetic field ${\mathbf {B}}= B\,(z) {{\hat{{\mathbf {x}}}}}$ in a plane-parallel, gravitationally stratified atmosphere with a constant gravity $-g {{\hat{{\mathbf {z}}}}}$, pressure $p\,(z)$, and density $\rho \,(z)$, in hydrostatic equilibrium,

$$\begin{aligned} \frac{d }{d z} \left( p + \frac{B^2}{8 \pi } \right) = - \rho g , \end{aligned}$$

(25)

has been studied by many authors in a broad range of astrophysics contexts including

• magnetic fields in stellar convection zones (see Newcomb 1961; Parker 1979; Hughes and Cattaneo 1987),

• magnetic flux emergence into the solar atmosphere (see Shibata et al. 1989),

• stability of prominence support by a magnetic field (see Zweibel and Bruhwiler 1992),

• and the instability of the interstellar gas and magnetic field (see Parker 1966).

The linear stability analysis of the above equilibrium horizontal magnetic layer (Newcomb 1961) showed that the necessary and sufficient condition for the onset of the general 3D instability with non-zero wavenumbers ($k_x \ne 0$, $k_y \ne 0$) in both horizontal directions parallel and perpendicular to the magnetic field is that

$$\begin{aligned} \frac{d \rho }{d z} > - \frac{\rho ^2 g}{\gamma p}, \end{aligned}$$

(26)

is satisfied somewhere in the stratified fluid. On the other hand the necessary and sufficient condition for instability of the purely interchange modes (with $k_x = 0$ and $k_y \ne 0$) is that

$$\begin{aligned} \frac{d \rho }{d z} > - \frac{\rho ^2 g}{\gamma p + B^2/4 \pi }. \end{aligned}$$

(27)

is satisfied somewhere in the fluid—a more stringent condition than (26). Note in Eqs. (26) and (27), p and $\rho$ are the plasma pressure and density in the presence of the magnetic field. Hence the effect of the magnetic field on the instability criteria is implicitly included. As shown by Thomas and Nye (1975) and Acheson (1979), the instability conditions (26) and (27) can be alternatively written as

$$\begin{aligned} \frac{v_{\mathrm {a}}^2}{c_{\mathrm {s}}^2} \frac{d \ln B}{d z} < - \frac{1}{c_p} \frac{d s}{d z} \end{aligned}$$

(28)

for instability of general 3D undulatory modes and

$$\begin{aligned} \frac{v_{\mathrm {a}}^2}{c_{\mathrm {s}}^2} \frac{d }{d z} \left[ \ln \left( \frac{B}{\rho } \right) \right] < - \frac{1}{c_p} \frac{d s}{d z} \end{aligned}$$

(29)

for instability of purely 2D interchange modes, where $v_{\mathrm {a}}$ is the Alfvén speed, $c_{\mathrm {s}}$ is the sound speed, $c_p$ is the specific heat under constant pressure, and ds/dz is the actual entropy gradient in the presence of the magnetic field. The development of these buoyancy instabilities is driven by the gravitational potential energy that is made available by the magnetic pressure support. For example, the magnetic pressure gradient can “puff-up” the density stratification in the atmosphere, making it decrease less steeply with height (causing condition (26) to be met), or even making it top heavy. This raises the gravitational potential energy and makes the atmosphere unstable. In another situation, the presence of the magnetic pressure can support a layer of cooler plasma with locally reduced temperature embedded in an otherwise stably stratified fluid. This can also cause the instability condition (26) to be met locally in the magnetic layer. In this case the pressure scale height within the cooler magnetic layer is smaller, and upon bending the field lines, plasma will flow from the crests to the troughs to establish hydrostatic equilibrium, thereby releasing gravitational potential energy and driving the instability. This situation is very similar to the buoyancy instability associated with the neutrally buoyant magnetic flux tubes discussed in Sect. 4.1.

The above discussion on the buoyancy instabilities considers ideal adiabatic perturbations. It should be noted that the role of finite diffusion is not always stabilizing. In the solar interior, it is expected that $\eta \ll K$ and $\nu \ll K$, where $\eta$, $\nu$, and K denote the magnetic diffusivity, the kinematic viscosity, and the thermal diffusivity respectively. Under these circumstances, it is shown that thermal diffusion can be destabilizing (see Gilman 1970; Acheson 1979; Schmitt and Rosner 1983). The diffusive effects are shown to alter the stability criteria of Eqs. (28) and (29) by reducing the term ds/dz by a factor of $\eta / K$ (see Acheson 1979). In other words, efficient heat exchange can significantly “erode away” the stabilizing effect of a subadiabatic stratification. This process is an example of the double-diffusive instabilities.

Direct multi-dimensional MHD simulations have been carried out to study the break-up of a horizontal magnetic layer by the non-linear evolution of the buoyancy instabilities and the formation of buoyant magnetic flux tubes (see Cattaneo and Hughes 1988; Cattaneo et al. 1990; Matthews et al. 1995; Wissink et al. 2000; Fan 2001).

Cattaneo and Hughes (1988), Matthews et al. (1995), and Wissink et al. (2000) have carried out a series of 2D and 3D compressible MHD simulations where they considered an initial horizontal magnetic layer that supports a top-heavy density gradient, i.e., an equilibrium with a lower density magnetic layer supporting a denser plasma on top of it. It is found that for this equilibrium configuration, the most unstable modes are the Rayleigh–Taylor type 2D interchange modes. Two-dimensional simulations of the non-linear growth of the interchange modes (Cattaneo and Hughes 1988) found that the formation of buoyant flux tubes is accompanied by the development of strong vortices whose interactions rapidly destroy the coherence of the flux tubes. In the non-linear regime, the evolution is dominated by vortex interactions which act to prevent the rise of the buoyant magnetic field. Matthews et al. (1995) and Wissink et al. (2000) extend the simulations of Cattaneo and Hughes (1988) to 3D allowing variations in the direction of the initial magnetic field. They discovered that the flux tubes formed by the initial growth of the 2D interchange modes subsequently become unstable to a 3D undulatory motion in the non-linear regime due to the interaction between neighboring counter-rotating vortex tubes, and consequently the flux tubes become arched. Matthews et al. (1995) and Wissink et al. (2000) pointed out that this secondary undulatory instability found in the simulations is of similar nature as the undulatory instability of a pair of counter-rotating (non-magnetic) line vortices investigated by Crow (1970). Wissink et al. (2000) further considered the effect of the Coriolis force due to solar rotation using a local f-plane approximation, and found that the principal effect of the Coriolis force is to suppress the instability. Further 2D simulations have also been carried out by Cattaneo et al. (1990) where they introduced a variation of the magnetic field direction with height into the previously unidirectional magnetic layer of Cattaneo and Hughes (1988). The growth of the interchange instability of such a sheared magnetic layer results in the formation of twisted, buoyant flux tubes which are able to inhibit the development of vortex tubes and rise cohesively.

On the other hand, Fan (2001) has considered a different initial equilibrium state for a horizontal unidirectional magnetic layer, where the density stratification remains unchanged from that of an adiabatically stratified polytrope, but the temperature and the gas pressure are lowered in the magnetic layer to satisfy the hydrostatic condition. For such a neutrally buoyant state with no density change inside the magnetic layer, the 2D interchange instability is completely suppressed and only 3D undulatory modes (with non-zero wavenumbers in the field direction) are unstable. A strong toroidal magnetic field that may be stored in the weakly subadiabatic overshoot region below the bottom of the convection zone would likely be close to such a neutrally buoyant mechanical equilibrium state (see Sect. 3.1). Anelastic MHD simulations (Fan 2001) of the growth of the 3D undulatory instability of this horizontal magnetic layer show formation of significantly arched magnetic flux tubes (see Fig. 7) whose apices become increasingly buoyant as a result of the diverging flow of plasma from the apices to the troughs.

Fig. 7

Image reproduced with permission from Fan (2001), copyright by AAS

The formation of arched flux tubes as a result of the non-linear growth of the undulatory buoyancy instability of a neutrally buoyant equilibrium magnetic layer perturbed by a localized velocity field. The images show the volume rendering of the absolute magnetic field strength |B|. Only one half of the wave length of the undulating flux tubes is shown, and the left and right columns of images show, respectively, the 3D evolution as viewed from two different angles. A movie corresponding to this figure is available as a supplement.

The decrease of the field strength B at the apex of the arched flux tube as a function of height is found to follow approximately the relation $B / \sqrt{\rho } = {\mathrm {constant}}$, i.e., constant Alf$\acute{\mathrm{v}}$en speed, which is a significantly slower decrease of B with height compared to that for the rise of a horizontal flux tube without any field line stretching, for which case $B/\rho$ should remain constant. The variation of the apex field strength with height following $B/ \sqrt{\rho } = {\mathrm {constant}}$ found in the 3D MHD simulations of the arched flux tubes is in good agreement with the results of the thin flux tube models of emerging $\varOmega$-loops (see Moreno-Insertis 1992) during their rise through the lower half of the solar convective envelope where the stratification is very close to being adiabatic as is assumed in the 3D simulations.

Kersalé et al. (2007) studied the nonlinear 3D evolution of the magnetic buoyancy instability resulting from a smoothly stratified horizontal magnetic field, and with the instability continually driven via the boundary conditions. They considered the case where the prescribed magnetic pressure gradient is such that the equilibrium is unstable to the 3D modes but stable to 2D interchange modes. One important distinction of this work compared to many of the previous studies is that the instability is continually driven through imposing a fixed magnetic pressure gradient at the top and bottom boundaries (Fig. 8) which are stress-free and impermeable.

Fig. 8

Image reproduced with permission from Kersalé et al. (2007), copyright by AAS

Horizontal average of the magnetic field $B_x$ as a function of depth for the initial state (dotted line), at a later time when the instability saturates (dashed line), and in the final steady state (solid line). The magnetic pressure gradient is maintained at the top and bottom boundaries during the non-linear evolution of the magnetic buoyancy instability.

The initial growth of the instabilities from a random perturbation results in the formation of arched flux tubes. In the non-linear stage, the system is found to establish a modulated periodic state where discrete flux tube concentrations with field strength significantly stronger than the initial mean field form periodically as modulated traveling waves (see Figs. 9 and 10). The development of isolated flux tube concentrations results from convergent downflows continually driven by the instability (Fig. 10). This result provides an interesting mechanism for the formation of strong active region flux tubes from dynamo generated large scale field at the base of the convection zone.

Fig. 9

Image reproduced with permission from Kersalé et al. (2007), copyright by AAS

Evolution of the kinetic energy density. The system eventually establishes a modulated periodic state with two disparate time scales.

Fig. 10

Image reproduced with permission from Kersalé et al. (2007), copyright by AAS

Space-time plots for fixed values of x and z of the magnetic energy density (left), the transverse horizontal (y) velocity (middle), and the vertical velocity (right), with the horizontal axis being the y-axis and vertical axis denoting the time.

Buoyancy breakup of a shear-generated magnetic layer

Instead of prescribing an unstable equilibrium of an initial magnetic flux tube or layer, Vasil and Brummell (2008) carried out a series of 3D MHD simulations of the generation of a strong layer of horizontal magnetic field by the action of a vertical shear on a weak vertical field in a subadiabatically stratified atmosphere, and examine the subsequent breakup of the resulting magnetic configuration via magnetic buoyancy instabilities (see Fig. 11).

Fig. 11

Image reproduced with permission from Vasil and Brummell (2008), copyright by AAS

A 3D MHD simulation of the build up and subsequent buoyancy break up of a layer of horizontal magnetic field forced by a vertical shear on an initially weak vertical field in a subadiabatically stratified atmosphere. The sequence of images show the volume renderings of the magnetic field strength.

The aim of these simulations is to examine under what conditions the radial shear of differential rotation operating in the thin solar tachocline layer can amplify a strong enough large scale toroidal magnetic field that undergoes magnetic buoyancy instabilities and develops buoyantly rising structures. The numerical simulations together with a subsequent analytical study (Vasil and Brummell 2009) show that magnetic buoyancy instabilities can indeed develop in the shear-generated magnetic layer (Fig. 11) if the forcing that drives the shear flow is sufficiently large. The needed forcing is such that, in the absence of the magnetic field, it imposes a hydrodynamically unstable shear. It is found that the imposed shear needs to have a Richardson number $R_i$ being less than 1, where $R_i$ measures the relative importance of the stabilizing effect of the stratification over the strength of the shear to overturn the fluid (Vasil and Brummell 2009; Silvers et al. 2009). This result is not surprising because in order for the magnetic layer to be buoyantly unstable, the imposed shear flow needs to transfer enough energy to the magnetic field for it to overcome the stable background stratification (Silvers et al. 2009). It is not clear whether such strong forcing of the shear exists in the solar tachocline. For the observed shear in the solar tachocline, the Richardson number is estimated to be much greater than 1, $R_i \sim 10^3\,\text{-- }\,10^5$ (Gough 2007). However, the observed shear in the tachocline may not correspond to the forcing shear, but is the end steady-state reached when the forcing is balanced by the built-up magnetic stress and turbulent transport.

Silvers et al. (2009) further extend the studies of Vasil and Brummell (2008) and Vasil and Brummell (2009) by considering the fact that the ratio of the magnetic diffusivity ($\eta$) over the thermal diffusivity ($\kappa$) due to the optically thick radiative diffusion in the solar tachocline is very small: $\xi = \eta / \kappa \ll 1$. Under such conditions the double-diffusive magnetic buoyancy instabilities can develop at a much less steep magnetic pressure gradient for the magnetic layer compared to that required for magnetic buoyancy instabilities under the assumption of adiabatic evolution (see Sect. 4.2). The stabilizing effect of the subadiabatic stratification is significantly reduced by the thermal diffusion. Simulations by Silvers et al. (2009) verify that double-diffusive magnetic buoyancy instabilities indeed can develop for a magnetic layer generated by a weak forcing shear that is hydrodynamically stable (with $R_i > 2.96$).

The rise of active region flux tubes from the bottom of the solar convection zone

In this section we review the body of work that assumes that a deep seated solar cycle dynamo generates a strong toroidal magnetic field at the base of the convection zone and studies the rise of active region scale magnetic flux tubes from the bottom of the convection zone to the surface to form the observed solar active regions.

Results from the thin flux tube simulations

Beginning with the seminal work of Moreno-Insertis (1986) and Choudhuri and Gilman (1987), a large body of numerical simulations solving the thin flux tube dynamic equations (1), (2), (6), (7), and (8)—or various simplified versions of them—have been carried out to model the evolution of emerging magnetic flux tubes in the solar convective envelope (see Choudhuri 1989; D’Silva and Choudhuri 1993; Fan et al. 1993, 1994; Schüssler et al. 1994; Caligari et al. 1995; Fan and Fisher 1996; Caligari et al. 1998; Fan and Gong 2000; Weber et al. 2011, 2013). The results of these numerical calculations have provided possible explanations for some of the basic observed properties of solar active regions and put constraints on the field strength of the toroidal magnetic fields if they originate from the base of the solar convection zone.

A set of the earlier calculations (see Choudhuri and Gilman 1987; Choudhuri 1989; D’Silva and Choudhuri 1993; Fan et al. 1993, 1994) considered initially buoyant toroidal flux tubes by assuming that they are in temperature equilibrium with the external plasma. Various types of initial undulatory displacements are imposed on the buoyant tube so that portions of the tube will remain anchored within the stably stratified overshoot layer and other portions of the tube are displaced into the unstable convection zone which subsequently develop into emerging $\varOmega$-shaped loops.

Later calculations (see Schüssler et al. 1994; Caligari et al. 1995, 1998; Fan and Gong 2000) considered more physically self-consistent initial conditions where the initial toroidal flux ring is in the state of mechanical equilibrium. In this state the buoyancy force is zero (neutrally buoyant) and the magnetic curvature force is balanced by the Coriolis force resulting from a prograde toroidal motion of the tube plasma. It is argued that this mechanical equilibrium state is the preferred state for the long-term storage of a toroidal magnetic field in the stably stratified overshoot region (Sect. 3.1). In these simulations, the development of the emerging $\varOmega$-loops is obtained naturally by the non-linear, adiabatic growth of the undulatory buoyancy instability associated with the initial equilibrium toroidal flux rings (Sect. 4.1). As a result there is far less degree of freedom in specifying the initial perturbations. The eruption pattern needs not be prescribed in an ad hoc fashion but is self-consistently determined by the growth of the instability once the initial field strength, latitude, and the subadiabaticity at the depth of the tube are given. For example Caligari et al. (1995) modeled emerging loops developed due to the undulatory buoyancy instability of initial toroidal flux tubes located at different depths near the base of their model solar convection zone which includes a consistently calculated overshoot layer according to the non-local mixing-length treatment. They choose values of initial field strengths and latitudes that lie along the contours of constant instability growth times of 100 days and 300 days in the instability diagrams (see Fig. 6), given the subadiabaticity at the depth of the initial tubes. The tubes are then perturbed with a small undulatory displacement which consists of a random superposition of Fourier modes with azimuthal order ranging from $m=1$ through $m=5$, and the resulting eruption pattern is determined naturally by the growth of the instability.

On the other hand, non-adiabatic effects may also be important in the destabilization process. It has been discussed in Sect. 3.2 that isolated magnetic flux tubes with internally suppressed convective transport experience a net heating due to the non-zero divergence of radiative heat flux in the weakly subadiabatically stratified overshoot region and also in the lower solar convection zone. The radiative heating causes a quasi-static upward drift of the toroidal flux tube with a drift velocity $\sim 10^{-3} |\delta |^{-1} \mathrm {\ cm\ s}^{-1}$. Thus the time scale for a toroidal flux tube to drift out of the stable overshoot region may not be long compared to the growth time of its undulatory buoyancy instability. For example if the subadiabaticity $\delta$ is $\sim - 10^{-6}$, the time scale for the flux tube to drift across the depth of the overshoot region is about 20 days, smaller than the growth times ($\sim$ 100–300 days) of the most unstable modes for tubes of a $\sim 10^5 {\mathrm {\ G}}$ field as shown in Fig. 6. Therefore radiative heating may play an important role in destabilizing the toroidal flux tubes. The quasi-static upward drift due to radiative heating can speed-up the development of emerging $\varOmega$-loops (especially for weaker flux tubes) by bringing the tube out of the inner part of the overshoot region of stronger subadiabaticity, where the tube is stable or the instability growth is very slow, to the outer overshoot region of weaker subadiabaticity or even into the convection zone, where the growth of the undulatory buoyancy instability occurs at a much shorter time scale.

A possible scenario in which the effect of radiative heating helps to induce the formation of $\varOmega$-shaped emerging loops has been investigated by Fan and Fisher (1996). In this scenario, the initial neutrally buoyant toroidal flux tube is not exactly uniform, and lies at non-uniform depths with some portions of the tube lying at slightly shallower depths in the overshoot region. Radiative heating and quasi-static upward drift of this non-uniform flux tube bring the upward protruding portions of the tube first into the unstably stratified convection zone. These portions can become buoyantly unstable (if the growth of buoyancy overcomes the growth of tension) and rise dynamically as emerging loops. In this case the non-uniform flux tube remains close to a mechanical equilibrium state during the initial quasi-static rise through the overshoot region. The emerging loop develops gradually as a result of radiative heating and the subsequent buoyancy instability of the outer portion of the tube entering the convection zone.

All of the aforementioned thin flux tube simulations have ignored the influence of the convective flows on the rising flux tube. The latest calculations by Weber et al. (2011, 2013) have incorporated the influence of the giant-cell convection and the mean flows on the motion of the thin flux tube by using a time-dependent external velocity field, computed separately by a 3D global convection simulation of the rotating solar convective envelope, for the drag force term of the thin flux tube equation of motion. Specifically, this time-dependent external velocity field is computed from the 3D global convection simulation using the anelastic spherical harmonic (ASH) code, as described in Miesch et al. (2006). It captures giant-cell convection and the associated mean flows with a solar-like differential rotation, and has a moderate Reynolds number of about 100 in the middle of the convection zone (Miesch et al. 2006).

In the following subsections we review the major findings and conclusions that have been drawn from the various thin flux tube simulations of emerging flux loops.

Latitude of flux emergence and rise time

As a buoyant flux tube rises, the Coriolis force acting on the radial outward motion of the flux tube (or the tendency for the rising tube to conserve angular momentum) drives a retrograde motion of the tube plasma. This retrograde motion then induces a Coriolis force directed towards the Sun’s rotation axis which acts to deflect the trajectory of the rising tube poleward. The amount of poleward deflection by the Coriolis force depends on the initial field strength of the emerging tube, being larger for flux tubes with weaker initial field as was first found by Choudhuri and Gilman (1987). Simulations by Caligari et al. (1995) of the $\varOmega$-shaped emerging loops that develop due to the undulatory buoyancy instability of the initial toroidal flux tubes at the bottom of the convection zone show that, for tubes with initial field strength $\gtrsim 10^5 {\mathrm {\ G}}$, the trajectories of the emerging loops are primarily radial with poleward deflection no greater than $3^{\circ }$. For tubes with initial field strength exceeding $4 \times 10^4 {\mathrm {\ G}}$, the poleward deflection of the emerging loops remain reasonably small (no greater than about $6^\circ$). However, for a tube with equipartition field strength of $10^4 {\mathrm {\ G}}$, the rising trajectory of the emerging loop is deflected poleward by about $20^\circ$. Such an amount of poleward deflection is too great to explain the observed low latitudes of active region emergence. Furthermore, it is found that with such a weak initial field the field strength of the emerging loop falls below equipartition with convection throughout most of the convection zone. Such emerging loops are expected to be subjected to strong deformation by turbulent convection and may not be consistent with the observed well defined order of solar active regions.

Simulations that incorporate the effect of giant-cell convection on the emerging loops developed due to the undulatory buoyancy instability of the initial toroidal flux tubes at the bottom of the convection zone (Weber et al. 2013) show that including convection produces a scatter in the emerging latitude but also systematically reduces the poleward deflection of the mean latitude of emergence. It is also found that including convection significantly reduces the rise time of the emerging loops, especially for weaker initial tube field strengths. Without convection, the rise time increases with decreasing initial field strength of the toroidal flux tube at the bottom of the convection zone, ranging from about 3 month for $10^5$ G flux tubes to more than 3 years for $1.5 \times 10^4$ G flux tubes. The large rise time for the weak initial field strength is due to the slow growth of the undulatory buoyancy instability at that field strength. With the inclusion of convection, the evolution of the emerging loops becomes dominated by the drag force from the convective motion compared to the magnetic buoyancy for flux tubes with initial field strength below about $3 \times 10^4$ G (Weber et al. 2013, see also Sect. 5.6.1), and as a result the mean rise times of the emerging loops are significantly reduced. It is found that with convection (Weber et al. 2013), the mean rise times of emerging loops with initial field strengths ranging from $1.5 \times 10^4$ G to $10^5$ G are all below 0.7 years, with the mid-field strength (about $4 \times 10^4$ G) flux tubes having the longest rise time, and with the weakest and the strongest field strengths resulting in the lowest rise times (about 1 to 3 months).

Active region tilts

A well-known property of the solar active regions is the so called Joy’s law of active region tilts. The averaged orientation of bipolar active regions on the solar surface is not exactly toroidal but is slightly tilted away from the east-west direction, with the leading polarity (the polarity leading in the direction of rotation) being slightly closer to the equator than the following polarity. The mean tilt angle is a function of latitude, being approximately $\propto \sin (\mathrm {latitude})$ (Wang and Sheeley Jr 1989, 1991; Howard 1991b, a; Fisher et al. 1995; Kosovichev and Stenflo 2008; Stenflo and Kosovichev 2012).

Using thin flux tube simulations of the rise of buoyant $\varOmega$-loops in a rotating solar convective envelope, D’Silva and Choudhuri (1993) were the first to show that the active region tilts as described by Joy’s law can be explained by the Coriolis force acting on the flux loops. As the emerging loop rises, there is a relative expanding motion of the mass elements at the summit of the loop. The Coriolis force induced by this diverging, expanding motion at the summit is to tilt the summit clockwise (counter-clockwise) for loops in the northern (southern) hemisphere as viewed from the top, so that the leading side from the summit is tilted equatorward relative to the following side. Since the component of the Coriolis force that drives this tilting has a $\sin (\mathrm {latitude})$ dependence, the resulting tilt angle at the apex is approximately $\propto \sin (\mathrm {latitude})$.

Caligari et al. (1995) studied tilt angles of emerging loops developed self-consistently due to the undulatory buoyancy instability of toroidal flux tubes located at the bottom as well as just above the top of their model overshoot region, with selected values of initial field strengths and latitudes lying along contours of constant instability growth times (100 days and 300 days). The resulting tilt angles at the apex of the emerging loops (see Fig. 12) produced by these sets of unstable tubes (whose field strengths are within the range of $4 \times 10^4 {\mathrm {\ G}}$ to $1.5 \times 10^5 {\mathrm {\ G}}$) show good agreement with the observed tilt angles for sunspot groups measured by Howard (1991a).

Fig. 12

Image reproduced with permission from Caligari et al. (1995), copyright by AAS

Tilt angles at the apex of the emerging flux loops as a function of the emergence latitudes. The squares and the asterisks denote loops originating from initial toroidal tubes located at different depths with different local subadiabaticity (squares: $\delta \equiv \nabla - \nabla _{\mathrm {ad}}= - 2.6 \times 10^{-6}$ and field strength ranges between $10^5 {\mathrm {\ G}}$ and $1.5 \times 10^5 {\mathrm {\ G}}$; asterisks: $\delta \equiv \nabla - \nabla _{\mathrm {ad}}= - 1.9 \times 10^{-7}$ and field strength ranges between $4 \times 10^4 {\mathrm {\ G}}$ and $6 \times 10^4 {\mathrm {\ G}}$). The shaded region indicates the range of the observed tilt angles of sunspot groups measured by Howard (1991a).

They also found that loops formed from toroidal flux tubes with an equipartition field strength of $10^4 {\mathrm {\ G}}$ develop a tilt angle of the wrong sign at the loop apex.

Later simulations by Weber et al. (2011, 2013) incorporated the influence of the giant-cell convection on the rise of buoyantly unstable thin flux tubes from the bottom of the solar convection zone, and studied the resulting tilt angles at the apex of the emerging loops. For each initial field strength and flux for the toroidal flux tube, a large ensemble of simulations are carried out where the emerging loops are buffeted by the different spatial parts and temporal ranges of the convective flow. The resulting tilt angles vs. emerging latitudes from the simulations are shown in Fig. 13, where the different panels show the results for different ranges of fluxes and initial field strengths, with panel (c) showing the results for all of the field strengths ranging from 15 kG to 100 kG and all of the fluxes ($10^{20}$ Mx, $10^{21}$ Mx, and $10^{22}$ Mx). Linear least-squares fits of the form $\alpha = A \lambda$ (the red line) and $\alpha = B \sin (\lambda )$ (the cyan line), to the simulated tilt angles ($\alpha$) as a function of emerging latitudes ($\lambda$) of the emerging loops, are done for the various flux and magnetic field combinations shown in the different panels.

Fig. 13

Image reproduced with permission from Weber et al. (2013), copyright by authors

Tilt angles versus emerging latitudes at the apex of the emerging loops resulting from the thin flux tube simulations of Weber et al. (2013). The different panels show the results for tubes with various fluxes and initial magnetic field strengths: c includes the results for tubes of all magnetic field strengths ranging from 15 kG–100 kG and all fluxes of $10^{20}$ Mx, $10^{21}$ Mx, and $10^{22}$ Mx, while a shows the results of all magnetic field strengths but $10^{20}$ Mx flux only, b of all magnetic field strengths and fluxes of $10^{21}$ Mx and $10^{22}$ Mx, and d of all fluxes but field strengths of the range 40–50 kG. Linear least-squares fits to the simulated tilt angles as a function of emerging latitudes, of the form $\alpha = A \lambda$ (the red line) and $\alpha = B \sin (\lambda )$ (the cyan line), are over plotted in each panel, where $\alpha$ denotes the tilt angle, $\lambda$ denotes the latitude, and A and B are the slopes whose best fit values and uncertainties are given in the panels. Also for comparison the observed Joy’s law of the active region mean tilt as a function of latitude in the form of $\alpha = A \lambda$ from Dasi-Espuig et al. (2010) based on the sunspot group data (the blue line), and in the form of $\alpha = B \sin (\lambda )$ from Stenflo and Kosovichev (2012) based on the MDI full-disk magnetogram data (the green line) are plotted in each panel.

It is found that buffeting by the giant-cell convection systematically increases the mean tilt angle of the emerging loops in the Joy’s law direction due to the mean kinetic helicity of the upflows of the convection. As a result, emerging loops with weaker initial field strengths ($\lesssim 30$ kG) that exhibit tilts of the wrong sign without the influence of convection, now also show a mean tilt consistent with the Joy’s law sign with convection. Generally for all values of the magnetic flux and magnetic field strength, the slopes of the linear fits (the red and cyan lines) are systematically greater than the corresponding observed Joy’s law slope obtained from the sunspot group data by Dasi-Espuig et al. (2010) (the blue line) and significantly smaller than that obtained from the magnetogram data by Stenflo and Kosovichev (2012) (the green line). Mid-field strengths of 40 kG–50 kG produce the largest best-fit slopes (A and B in Fig. 13d), but the value of slope $B = 26^{\circ } \pm 2^{\circ }$ still falls short of the $32.1^{\circ } \pm 0.7$ value found by Stenflo and Kosovichev (2012) from MDI magnetogram data (the green line).

The influence of convection also produces a scatter of the tilt angles about the mean tilt behavior described by the Joy’s law linear-fit. The root-mean-square (rms) scatter tends to increase with decreasing field strength and decreasing flux (see Table 3 in Weber et al. 2013). Using Mount Wilson sunspot group data, Fisher et al. (1995) found that the rms scatter of the sunspot group tilts from the Joy’s law is $< 40^{\circ }$. Weber et al. (2013) found that emerging loops with field strengths less than about 40 kG produce a scatter that is too large to be consistent with the above observation result. Overall, Weber et al. (2013) suggest that the initial field strength of active region progenitor flux tubes needs to be sufficiently large, probably $\gtrsim 40$ kG, in order for them to satisfy the Joy’s Law trend for the mean tilt angle as well as the observed amount of scatter of the tilt angles about the mean Joy’s Law behavior.

Using a series of 96 minute cadence magnetograms from SOHO MDI and analyzing 715 bipolar magnetic regions which emerged within $30^{\circ }$ from the central meridian and outside already existing active regions, Kosovichev and Stenflo (2008) investigated how the active region tilt angle evolves during flux emergence and how it correlates with other properties of the emerging region. The study shows that at the beginning of emergence the tilt angles are random, and the mean tilt angle is about zero (see Fig. 14a). However by the middle of the emergence period (flux growth period), the tilt angles clearly show a systematic mean as a function of latitude that follows Joy’s law (Fig. 14b). At the end of the emergence period, the Joy’s law dependence has become more pronounced as the scatter from the systematic mean tilt decreases (Fig. 14c). The above result that the systematic mean tilt following Joy’s law is established during the flux emergence period (flux growth period) suggests that the tilt of the emerging flux tube has developed in the interior before reaching the surface. This is consistent with the above model of rising flux tubes where the tilt angle is caused by the effect of the Coriolis force during the rise.

Fig. 14

Image reproduced with permission from Kosovichev and Stenflo (2008), copyright by AAS

The distribution of the tilt angle as a function of sine latitude: a at the beginning of flux emergence, b at the middle of the emergence period, and c at the end of emergence.

Kosovichev and Stenflo (2008) found that the mean tilt angle does not show a systematic dependence on the flux of the active region in contradiction to the result from the thin flux tube calculation of rising flux tubes in the absence of convection (e.g., Fisher et al. 1995). However with the influence of convection included in the thin flux tube simulations, the best-fit slopes for the mean tilt no longer show a significant systematic variation with the flux above the uncertainties, changing from the conclusion without convection (compare Table 1 and Table 2 in Weber et al. 2013).

Furthermore, Kosovichev and Stenflo (2008) found that there is no tendency for the active region mean tilt to relax towards the east-west direction after the emergence has ceased and the driving Coriolis force has vanished, at which time the tension of the flux tube is expected to act to restore the original toroidal orientation of the tube at the base of the solar convection zone. The latter result may be understood if the active region magnetic fields on the photosphere become dynamically disconnected from the interior flux tubes soon after emergence (e.g Fan et al. 1994; Schüssler and Rempel 2005). On the other hand, as suggested in Kosovichev and Stenflo (2008), it may be that Joy’s law of solar active regions reflects not the Coriolis effect of the rising flux tubes but the spiral orientation of the nearly toroidal magnetic field lines in the interior generated by the latitudinal differential rotation (Babcock 1961).

Non-linear simulations of the two-dimensional MHD tachocline (Cally et al. 2003) show that bands of toroidal magnetic fields in the solar tachocline may become tipped relative to the azimuthal direction by an amount that is within $+/- 10^\circ$ at sunspot latitudes due to the non-linear evolution of the 2D global joint instability of differential rotation and toroidal magnetic fields. This tipping may either enhance or reduce the observed tilt in bipolar active regions depending on from which part of the tipped band the emerging loops develop. Thus the basic consequence of the possible tipping of the toroidal magnetic fields in the tachocline is to contribute to the spread of the tilts of bipolar active regions.

Using the line-of-sight magnetograms from the Helioseismic and Magnetic Imager (HMI) on the Solar Dynamic Observatory (SDO), Schunker et al. (2020) have measured the evolution of the tilt angles of 153 emerging active regions. It is found that for the beginning phase (Phase 1) of the flux emergence (during which the polarity separation speed is increasing, lasting about 0.5 days after the time of emergence), the active region polarities are on average east-west aligned with a zero mean tilt angle. The systematic mean tilt of the active regions following Joy’s law is established during the Phase 2 of the emergence when the polarity separation speed is decreasing. These observation results are in general agreement with those of Kosovichev and Stenflo (2008). However, Schunker et al. (2020) found it is still surprising that the active regions emerge with an east-west alignment since the thin flux tube model predicts a systematic tilt angle has developed at the apex of the emerging loop. With a simple model calculation (Apendix C Schunker et al. 2020), they found that the observed average north-south separation motion of the polarities during the emergence is not consistent with an emerging loop with an initial constant tilt at the apex. They concluded that Joy’s law is caused by an inherent north-south separation speed present when the flux first reaches the surface and the polarities move to lie over their foot points anchored at some depth below the surface. Progress to understanding the observed tilt angle evolution during active region flux emergence can be obtained by analyzing the resultant surface flux evolution from the sophisticated radiation MHD simulations of near surface layer active region flux emergence (such as Stein and Nordlund 2012; Birch et al. 2016; Chen et al. 2017), considering different rising structures from the deep interior.

Morphological asymmetries of active regions

An intriguing property of solar active regions is the asymmetry in morphology between the leading and following polarities. The leading polarity of an active region tends to be in the form of large sunspots, whereas the following polarity tends to appear more dispersed and fragmented; moreover, the leading spots often form earlier and tend to be longer lived than the following. Fan et al. (1993) offered an explanation for the origin of this asymmetry. In their thin flux tube simulations of the non-axisymmetric eruption of buoyant $\varOmega$-loops through a rotating model solar convective envelope, they found that an asymmetry in the magnetic field strength develops between the leading and following legs of an emerging loop, with the field strength of the leading leg being about 2 times that of the following leg. The field strength asymmetry develops because the Coriolis force, or the tendency for the tube plasma to conserve angular momentum, drives a counter-rotating flow of plasma along the emerging loop, which, in conjunction with the diverging flow of plasma from the apex to the troughs, gives rise to an effective asymmetric stretching of the two legs of the loop with a greater stretching and hence a stronger field strength in the leading leg. Fan et al. (1993) argued that the stronger field along the leading leg of the emerging loop makes it less subject to deformation by the turbulent convection and therefore explains the more coherent and less fragmented appearance of the leading polarity of an active region.

However, subsequent simulations using the more physical mechanical equilibrium initial state (e.g., Caligari et al. 1995, 1998; Fan and Fisher 1996) show that the field strength asymmetry between the leading and following legs of the emerging loop depends on the initial field strength of the toroidal flux tube. Fan and Fisher (1996) (see Fig. 15) found consistently stronger fields along the leading leg compared to the following for tubes with weaker initial fields ($B < 60$ kG), but nearly equal field strengths of the two legs or even the reverse in the upper convection zone for stronger initial fields. The result is similar when buffeting by giant-cell convection is included in the thin flux tube model (Weber et al. 2011, 2013). Weber et al. (2011) computed dB/ds, the derivative of the field strength along the arc-length s in the direction of solar rotation, at the apex of the emerging loop. It is found that dB/ds tends to be systematically greater (less) than zero, i.e. the leading (following) side having a stronger field, for loops with an initial field strength $\le 50$ kG. But the systematic trend is reversed for greater initial field strengths (60 kG to 100 kG).

Fig. 15

Plots of the magnetic field strength as a function of depth along the emerging loops calculated from the thin flux tube model of Fan and Fisher (1996) showing the asymmetry in field strength between the leading leg (solid curve) and the following leg (dash-dotted curve) of each loop. Panels a, b, and c correspond to the cases with initial toroidal field strengths of 30 kG, 60 kG, and 100 kG respectively. The flux $\varPhi = 10^{22} {\mathrm {\ Mx}}$ and the initial latitude $\theta = 5^\circ$ are the same for the three cases shown

On the other hand, later 3D MHD simulations of emerging flux produced by the convective dynamo coupled to near-surface layer 3D MHD simulations of active region formation (Chen et al. 2017) show that the effect of the giant-cell convective flow can produce the observed earlier formation and the more coherent leading polarity sunspots of solar active regions (see Sect. 9).

Geometrical asymmetry of emerging loops and the asymmetric proper motions of active regions

Another asymmetry in the emerging loop generated by the effect of the Coriolis force is the asymmetry in the east-west inclinations of the two sides of the loop. This asymmetry is first shown in the thin flux tube calculations of Moreno-Insertis et al. (1994) and Caligari et al. (1995) who modeled emerging loops that develop self-consistently as a result of the buoyancy instability of toroidal magnetic flux tubes initially in mechanical equilibrium. Moreno-Insertis et al. (1994) and Caligari et al. (1995) found that as the emerging loop rises, the Coriolis force, or the tendency for the tube to conserve angular momentum, drives a counter-rotating motion of the tube plasma, which causes the summit of the loop to move retrograde relative to the valleys, resulting in an asymmetry in the inclinations of the two legs of the loop with the leading leg being inclined more horizontally with respect to the surface than the following leg. This asymmetry in inclination can be clearly seen in Fig. 16, which shows a view from the north pole of an asymmetric emerging loop obtained from a simulation by Caligari et al. (1995).

Fig. 16

Image reproduced with permission from Caligari et al. (1995), copyright by AAS

A view from the north pole of the configuration of an emerging loop obtained from a thin flux tube simulation of a buoyantly unstable initial toroidal flux tube. The initial field strength is $1.2 \times 10^5 {\mathrm {\ G}}$, and the initial latitude is $15^\circ$. Note the strong asymmetry in the east-west inclination of the two sides of the emerging loop.

When buffeting by giant-cell convection is included in the thin flux tube model (Weber et al. 2011), the systemmatic trend of the geometrical asymmetry remains a robust result for emerging loops that originate from initial flux tubes in mechanical equilibrium. Emerging loops with initial field strength ranging from 15 kG to 100 kG all show this asymmetry.

The observational consequences of this geometric asymmetry are discussed in Moreno-Insertis et al. (1994) and Caligari et al. (1995). The emergence of such an eastward inclined loop is expected to produce apparent asymmetric east-west proper motions of the two polarities of the emerging region, with a more rapid motion of the leading polarity spots away from the emerging region compared to the motion of the following polarity spots. Such asymmetric proper motions are observed in young active regions and sunspot groups (see Chou and Wang 1987; van Driel-Gesztelyi and Petrovay 1990; Petrovay et al. 1990). Furthermore, the asymmetry in the inclination of the emerging loop may also explain the observation that the magnetic inversion line in bipolar regions is statistically nearer to the main following spot than to the main proceeding one (van Driel-Gesztelyi and Petrovay 1990; Petrovay et al. 1990).

Weber et al. (2013) computed an apparent rotation rate of an emerging active region by evaluating the apparent zonal motion of the center point between the leading and the following intersections of the emerging loop with the constant-r surface of 0.95 $R_{\odot }$, when the emerging loop approaches the top boundary of the thin flux tube simulation. It is found that only for emerging loops with initial field strengths $\ge 60$ kG, do the apparent rotation rates approach the local rotation rate at $r = 0.95 \, R_{\odot }$, being faster than the solar surface plasma rotation rate, consistent with the observed sunspot rotation rate (e.g., Gilman and Howard 1985). Although the above geometrically determined apparent rotation speed can approach the local rotation rate at 0.95 $R_{\odot }$, the velocity of the tube plasma near the apex is retrograde with respect to the local rotation rate because of the conservation of angular momentum of the rising tube as it moves away from the rotation axis (e.g., Weber et al. 2011). This retrograde motion of the tube plasma with respect to the local rotation rate is not detected in helioseismic studies of emerging active regions (see Sect. 9.2), and therefore argues against active region and sunspot fields as buoyantly rising flux tubes from the bottom of the solar convection zone.

Hemisphere trend of the twist in solar active regions

Vector magnetic field observations of active regions on the photosphere have revealed that on average the solar active regions have a small but statistically significant mean twist that is left-handed in the northern hemisphere and right-handed in the southern hemisphere (see Pevtsov et al. 1995, 2001, 2003). What is being measured is the quantity $\alpha \equiv \langle J_z/B_z \rangle$, the ratio of the vertical electric current over the vertical magnetic field averaged over the active region. When plotted as a function of latitude, the measured $\alpha$ for individual solar active regions show considerable scatter, but there is clearly a statistically significant trend for negative (positive) $\alpha$ in the northern (southern) hemisphere (see Fig. 17).

Fig. 17

Image reproduced with permission from Pevtsov et al. (2001), copyright by AAS

The figure shows the latitudinal profile of $\alpha _{\mathrm {best}}$ (see Pevtsov et al. 1995, for the exact way of determining $\alpha _{\mathrm {best}}$) for a 203 active regions in cycle 22 (Longcope et al. 1998), and b 263 active regions in cycle 23. Error bars (when present) correspond to 1 standard deviation of the mean $\alpha _{\mathrm {best}}$ from multiple magnetograms of the same active region. Points without error bars correspond to active regions represented by a single magnetogram. The solid line shows a least-squares best-fit linear function.

A linear least squares fit to the data of $\alpha$ as a function of latitude (Fig. 17a) found that $\alpha = -2.7 \times 10^{-10} \, \theta _{\mathrm {deg}}\mathrm {\ m}^{-1}$, where $\theta _{\mathrm {deg}}$ is latitude in degrees, and that the r.m.s. scatter of $\alpha$ from the linear fit is $\varDelta \alpha = 1.28 \times 10^{-8} \mathrm {\ m}^{-1}$ (Longcope et al. 1998). The observed systematic $\alpha$ in solar active regions may reflect a systematic field line twist in the subsurface emerging flux tubes.

If the measured $\alpha$ values are a direct consequence of the emergence of twisted magnetic flux tubes from the interior, then it would imply subsurface emerging tubes with a field line twist of $q = \alpha /2$ (Longcope and Klapper 1997), where q denotes the angular rate of field line rotation about the axis over a unit axial distance along the tube. Several subsurface mechanisms for producing twist in emerging flux tubes have been proposed (see, e.g., the review by Petrovay et al. 2006). The twist may be due to the current helicity in the dynamo generated toroidal magnetic field, from which buoyant flux tubes form at the base of the convection zone (Gilman and Charbonneau 1999), or it may be acquired during the rise of the flux tubes through the solar convection zone (Longcope et al. 1998; Choudhuri 2003; Choudhuri et al. 2004; Chatterjee et al. 2006).

Longcope et al. (1998) explain the origin of the observed twist in emerging active region flux tubes as a result of buffeting by the helical turbulence in the solar convection zone during the rise of the tubes. Applying the dynamic model of a weakly twisted thin flux tube (Sect. 2.1), Longcope et al. (1998) modeled the rise of a nearly straight, initially untwisted tube, buffeted by a random velocity field representative of the turbulent convection in the solar convection zone, which has a nonzero kinetic helicity due to the effect of solar rotation. The kinetic helicity causes helical distortion of the tube axis, which in turn leads to a net twist of the field lines about the axis in the opposite sense within the tube as a consequence of the conservation of magnetic helicity. This process is termed the $\varSigma$-effect by Longcope et al. (1998). Quantitative model calculations of Longcope et al. (1998) show that the $\varSigma$-effect can explain the hemispheric sign, magnitude, latitude variation, and the r.m.s. dispersion of the observed $\alpha$ of solar active regions. Furthermore, the model predicts that the mean twist scales inversely with the flux $\varPhi$ of the active region as: $\sim \varPhi ^{-0.69}$. This is roughly because larger flux tubes rise more rapidly, providing less time for actions of the turbulence.

As discussed in Sect. 5.1.2, $\varOmega$-shaped emerging loops are themselves acted upon by the Coriolis force, developing a “tilt” of the loop. This helical deformation of the tube axis will then also induce a twist of the field lines of the opposite sense within the tube as a consequence of conservation of magnetic helicity. Calculations have been done based on the weakly twisted thin flux tube model (see Eqs. 9 and 10), which describes the evolution of the twist in response to the motion of the tube, taking into account helicity conservation. It is found that this twist generated by the large scale tilting (writhing) of the emerging $\varOmega$-loop resulting from the Coriolis force has the right hemispheric sign and latitude dependence, but is of too small a magnitude to account for the observed twist in solar active regions (Longcope and Klapper 1997; Fan and Gong 2000).

Another interesting and natural explanation for the origin of twist in emerging flux tubes is the accretion of the background mean poloidal field onto the rising flux tube as it traverse through the solar convection zone (Choudhuri 2003; Choudhuri et al. 2004; Chatterjee et al. 2006). In a Babcock–Leighton type dynamo (e.g. section 5 in Charbonneau 2020), the dispersal of solar active regions with a slight mean tilt angle at the surface generates a mean poloidal magnetic field. The mean tilt angle of solar active regions is produced by the Coriolis force acting on the rising flux tubes (see Sect. 5.1.2). In the northern hemisphere, when a toroidal flux tube rises into a poloidal field that has been created due to the tilt of the same type of flux tubes emerged earlier, the poloidal field that gets wrapped around the flux tube by that mechanism will produce a left-handed twist for the tube. This is illustrated in Fig. 18.

Fig. 18

Image reproduced with permission from Choudhuri (2003), copyright by AAS

This figure illustrates that in the northern hemisphere, when a toroidal flux tube (whose cross-section is the hashed area with a magnetic field going into the paper) rising into a region of poloidal magnetic field (in the clockwise direction) generated by the Babcock–Leighton type $\alpha$-effect of earlier emerging flux tubes of the same type, the poloidal field gets wrapped around the cross-section of the toroidal tube and reconnects behind it, creating an emerging flux tube with left-handed twist. In this figure, the north-pole is to the left, equator to the right, and the dashed line indicating the solar surface. Note the $\alpha$-effect for the Babcock–Leighton type solar dynamo model mentioned above is not to be confused with the $\alpha$ value measured in solar active region discussed in this section.

Using a circulation-dominated (or flux-transport) Babcock–Leighton type mean-field dynamo model, Choudhuri et al. (2004) did a rough estimate of the twist acquired by an emerging flux tube rising through the solar convection zone. Fig. 19 shows the resulting butterfly diagram indicating the sign of $\alpha$ of the emerging regions as a function of latitude and time. It is found that at the beginning of a solar cycle, there is a short duration where the sign of $\alpha$ is opposite to the preferred sign for the hemisphere. This is because of the phase relation between the toroidal and poloidal magnetic fields produced by this types of solar dynamo models. At the beginning of a cycle, the mean poloidal magnetic field in the convection zone is still dominated by that generated by the emerging flux tubes of the previous cycle, and toroidal flux tubes of the new cycle emerging into this poloidal field gives rise to a right-handed (left-handed) twist of the tube in the northern (southern) hemisphere. However, for the rest of the cycle starting from the solar maximum, the poloidal magnetic field changes sign and the twist for the emerging tubes becomes consistent with the hemispheric preference. For the whole cycle, it is found that about 67% of the emerging regions have a sign of $\alpha$ consistent with the hemispheric rule. The rough estimate also shows that the magnitude of the $\alpha$ values produced by poloidal flux accretion is consistent with the observed values, and that there is an $a^{-2}$ dependence on the radius a of the emerging tube, i.e., smaller sunspots should have greater $\alpha$ values. This prediction is also made by the $\varSigma$-effect mechanism.

Fig. 19

Image reproduced with permission from Choudhuri (2003), copyright by AAS

Simulated butterfly diagram of active region emergence based on a circulation-dominated mean-field dynamo model with Babcock–Leighton $\alpha$-effect. The sign of the twist of the emerging active region flux tube is determined by considering poloidal flux accretion during its rise through the convection zone. Right handed twist (left handed twist) is indicated by plus signs (circles).

Given the frozen-in condition of the magnetic field, it is expected that the accreted poloidal flux would be confined in a sheath at the outer periphery of the rising tube, and that in order to produce a twist within the tube, some form of turbulent diffusion needs to be invoked (Chatterjee et al. 2006). By solving the induction equation in a co-moving Lagrangian frame following the rising flux tube and using several simplifying assumptions, Chatterjee et al. (2006) modeled the evolution of the magnetic field in the rising tube cross-section as a result of poloidal flux accretion and penetration due to a field strength dependent turbulent diffusivity. They found that with plausible choices of assumptions and parameter values an $\alpha$ value comparable to the observations is obtained.

When a buoyant magnetic flux tube is formed at the base of the solar convection zone from the dynamo generated (predominantly) toroidal magnetic field, it should already obtain an initial twist due to the weak poloidal mean field contained in the magnetic layer. This initial twist will then be further augmented or altered due to poloidal flux accretion and also due to the $\varSigma$-effect as the tube rises through the solar convection zone. MHD simulations of the formation and rise of buoyant magnetic flux tubes directly incorporating the mean field profiles from dynamo models (for both the fields at the base and in the bulk of the convection zone) as the initial state are necessary to quantify the initial twist and contribution from poloidal field accretion. Such simulations should be done for dynamo mean fields at different phases of the cycle to access the cycle variation of the twist in the emerging flux tubes.

In a set of 2D MHD simulations of the buoyant rise of a twisted horizontal magnetic flux tube, Manek et al. (2018) show that the presence of a weak background horizontal field can severely affect the dynamic rise of the tube. It is found that tubes with a twist where the local tube azimuthal field at the bottom of the tube aligns with the background field are more likely to rise than those with the opposite twist, because the rise of tubes with the latter alignment is suppressed by a relatively weaker background field. Manek et al. (2018) therefore suggest that given the orientation of the poloidal field that produces the cycle’s toroidal field via the latitudinal differential rotation, a left-hand (right-hand) twisted toroidal flux tube would more likely survive the rise in the northern (southern) hemisphere, consistent with the observed hermisphere preference of the twist of solar active regions. However, this model assumes that the poloidal and toroidal fields switch polarity exactly in phase, and does not take into account the solar cycle large-scale mean field phase relation (between the poloidal and the toroidal field) from observation and the flux transport dynamo models (e.g., Choudhuri et al. 2004).

Observationally, looking for any systematic variations of the $\alpha$ value (or twist) in solar active regions with the solar cycle phase is helpful for identifying the main mechanisms for the origin of the twist. Using high-quality vector magnetograms taken with the Spectro-polarimeter (SP) on board the Hinode satellite, Hao and Zhang (2011) have examined the hemisphere twist sign rule for active regions (ARs) in the descending phase of solar cycle 23 and the ascending phase of solar cycle 24. They found that the ARs in the ascending phase of solar cycle 24 follow the usual hermisphere trend for the sign of twist, while the ARs in the descending phase of solar cycle 23 do not show the trend. This result appears opposite to the cycle variation predicted by the model of Choudhuri et al. (2004). On the other hand, Hao and Zhang (2011) also found that on average the sunspot umbra and penumbra show opposite signs of the $\alpha$ value (or the current helicity), with the whole AR dominated by the sign in the penumbra, which tends to conform to the hemisphere preferred sign of the twist. This result seems consistent with the model prediction by Chatterjee et al. (2006), which considered the development of the twist of an emerging flux tube by poloidal field accretion and turbulent diffusion, and predicted the existence of a ring of reverse current helicity on the periphery of active regions. The above observational result that weak and inclined fields tend to conform to the hermisphere sign rule of twist and strong and vertical fields tend to violate it has also been found in the study by Otsuji et al. (2015), who also used observations of solar active regions by the Hinode/SP.

Furthermore, observational studies of the correlation between active region twist (as measured by $\alpha$) and tilt angles have revealed interesting results (Holder et al. 2004; Tian et al. 2005; Nandy 2006). The $\varSigma$-effect predicts that the twist being generated in the tube is uncorrelated to the local tilt of the tube at the apex (Longcope et al. 1998). However, due to the Coriolis force, active region $\varOmega$-tubes acquire a mean tilt that has a well defined latitudinal dependence as described by the Joy’s law. The mean twist generated by the $\varSigma$-effect also has a latitudinal dependence that is consistent with the observed hemispheric rule. Thus, due to the mutual dependence of their mean values on latitude there should be a correlation between the tilt angle and twist of solar active regions and the correlation is expected to be positive if one assigns negative (positive) sign to a clockwise (counter-clockwise) tilt. However, Holder et al. (2004) found a statistically significant negative correlation between the twist and tilt for the 368 bipolar active regions studied, opposite to that expected from the mutual dependence on latitude of mean twist and mean tilt of active regions. Removing the effect of the mutual dependence of the mean tilt and mean twist on latitude (by either determining the correlation at a fixed latitude, or by subtracting off the fitted mean tilt and mean twist at the corresponding latitude), they found that the negative correlation is enhanced. Furthermore, it is found that the negative correlation is mainly contributed by those active regions (174 out of 368 regions) that deviate significantly from Joy’s law (by $> 6 \sigma$), while regions that obey Joy’s law to within $6 \sigma$ show no significant correlation between their twist and tilt. A separate study by Tian et al. (2005) found that a sample of 104 complex $\delta$-configuration active regions, more than half of which have tilts that are opposite to the direction prescribed by Joy’s law, show a significant negative correlation between their twist and tilt [after correcting for their definition of the sign of tilt which is opposite to the definition used in Holder et al. (2004)]. The results of Holder et al. (2004) and Tian et al. (2005) both indicate that there is a significant population (about one half in the case of Holder et al. (2004)) of solar active regions whose twist/tilt properties cannot be explained by the $\varSigma$-effect together with the effect of the Coriolis force alone. These active regions are consistent with the situation where the buoyant flux tube that forms at the base of the solar convection zone has acquired an initial twist, such that as it rises upward due to buoyancy into an $\varOmega$-tube, it develops a writhe that is of the same sense as the initial twist of the tube (see Sect. 5.4). In the extreme case, the twist can be so large that the flux tube becomes kink unstable (see Sect. 5.5). The resulting tilt at the apex due to the writhe has the negative correlation with the twist as described in the above observations.

On the minimum twist needed for maintaining cohesion of rising flux tubes in the solar convection zone

As described in Sect. 5.1, simulations based on the thin flux tube approximation have revealed many interesting results with regard to the global-scale dynamics of active region emerging flux loops in the solar convective envelope, which provide explanations for several basic observed properties of solar active regions. However, one major question ignored by the thin flux tube model is how a flux tube remains a discrete and cohesive object as it moves in the solar convection zone. The manner in which solar active regions emerge on the photosphere suggests that they are coherent flux bundles rising through the solar convection zone and reaching the photosphere in a reasonably cohesive fashion. To address this question, 3D MHD models that fully resolve the rising flux tubes are needed.

As a natural first step, 2D MHD simulations were carried out to model buoyantly rising, infinitely long horizontal magnetic flux tubes in a stratified layer representing the solar convection zone, focusing on the dynamic evolution of the tube cross-section. The first of such calculations was done in fact much earlier by Schüssler (1979) and later, simulations of higher numerical resolutions have been performed (Moreno-Insertis and Emonet 1996; Longcope et al. 1996; Fan et al. 1998a; Emonet and Moreno-Insertis 1998). The basic result from these 2D models of buoyant horizontal flux tubes is that due to the vorticity generation by the buoyancy gradient across the flux tube cross-section, if the tube is untwisted, it quickly splits into a pair of vortex tubes of opposite circulations, which move apart horizontally and cease to rise. If on the other hand, the flux tube is sufficiently twisted such that the magnetic tension of the azimuthal field can effectively suppress the vorticity generation by the buoyancy force, then most of the flux in the initial tube is found to rise in the form of a rigid body whose rise velocity follows the prediction by the thin flux tube approximation. The result described above is illustrated in Fig. 20 which shows a comparison of the evolution of the tube cross-section between the case where the buoyant horizontal tube is untwisted (upper panels) and a case where the twist of the tube is just above the minimum value needed for the tube to rise cohesively (lower panels).

Fig. 20

Image reproduced with permission from Fan et al. (1998a), copyright by AAS

Upper panel: Evolution of a buoyant horizontal flux tube with purely longitudinal magnetic field. Lower panel: Buoyant rise of a twisted horizontal flux tube with twist that is just above the minimum value given by Eq. (30). The color indicates the longitudinal field strength and the arrows describe the velocity field. A corresponding movie showing the evolution of the tube for the untwisted and the twisted cases is available as a supplement.

This minimum twist needed for tube cohesion can be estimated by considering a balance between the magnetic tension force from the azimuthal field and the magnetic buoyancy force. For a flux tube near thermal equilibrium whose buoyancy $| \varDelta \rho / \rho | \sim 1/\beta$, where $\varDelta \rho \equiv \rho - \rho _{\mathrm {e}}$ denotes the density difference between the inside and the outside of the tube and $\beta \equiv p / (B^2/ 8 \pi )$ denotes the ratio of the gas pressure over the magnetic pressure, such an estimate (Moreno-Insertis and Emonet 1996) yields the condition that the pitch angle $\varPsi$ of the tube field lines on average needs to reach a value of order

$$\begin{aligned} \tan {\varPsi } \equiv \frac{B_{\phi }}{B_{z}} \gtrsim \left( \frac{a}{H_p}\right) ^{1/2}. \end{aligned}$$

(30)

In Eq. (30), $B_z$ and $B_{\phi }$ denote the axial and azimuthal field of the horizontal tube respectively, a is the characteristic radius of the tube, and $H_p$ is the local pressure scale height. The above result on the minimum twist can also be expressed in terms of the rate of field line rotation about the axis per unit length along the tube q. For a uniformly twisted flux tube, $B_{\phi } = q r B_z$, where r is the radial distance to the tube axis. Then q needs to reach a value of order (Longcope et al. 1999)

$$\begin{aligned} q \gtrsim \left( \frac{1}{H_p a}\right) ^{1/2} \end{aligned}$$

(31)

for the flux tube to maintain cohesion during its rise. Note that the conditions given by Eqs. (30) and (31) and also the 2D simulations described in this section all assume buoyant flux tubes with initial buoyancy $| \varDelta \rho / \rho | \sim 1/\beta$. For tubes with lower level of buoyancy, the necessary twist is smaller with $\tan \varPsi$ and q both $\propto |\varDelta \rho / \rho |^{1/2}$ (see Emonet and Moreno-Insertis 1998).

Longcope et al. (1999) pointed out that the amount of twist given by Eq. (31) is about an order of magnitude too big compared to the twist deduced from vector magnetic field observations of solar active regions on the photosphere. They assumed that the averaged $\alpha \equiv J_z / B_z$ (the ratio of the vertical electric current over the vertical magnetic field) measured in an active region on the photosphere directly reflects the twist in the subsurface emerging tube, i.e., $q = \alpha / 2$ (Longcope and Klapper 1997; Longcope et al. 1998). If this is true then it seems that the measured twists in solar active regions directly contradict the condition for the cohesive rise of a horizontal flux tube with buoyancy as large as $| \varDelta \rho / \rho | \sim 1/\beta$. However it should be noted that the above estimate by Longcope et al. (1999) is largely based on the weakly twisted thin flux tube model. In reality the fragmentation of the emerging flux tube by 3D convection, especially in the top layer of the convection zone where the active region flux tubes clearly can no longer be considered thin, makes the connection of the observed $\alpha$ in solar active regions to the twist q of the rising flux tubes in the deep solar convection zone very uncertain.

Later, 3D simulations of $\varOmega$-shaped arched flux tubes have been carried out (Abbett et al. 2000, 2001; Fan 2001). Fan (2001) performed 3D simulations of arched flux tubes which form from an initially neutrally buoyant horizontal magnetic layer as a result of its undulatory buoyancy instability (see Sect. 4.2 and Fig. 7). It is found that without any initial twist the flux tubes that form rise through a distance of about one density scale height included in the simulation domain without breaking up. This significantly improved cohesion of the 3D arched flux tubes compared to the previous 2D models of buoyant horizontal tubes is not only due to the additional tension force made available by the 3D nature of the arched flux tubes, but also due largely to the absence of an initial buoyancy and a slower initial rise (Fan 2001). With a neutrally buoyant initial state, both the buoyancy force and the magnetic tension force grow self-consistently from zero as the flux tube arches. The vorticity source term produced by the growing magnetic tension as a result of bending and braiding the field lines is found to be able to effectively counteract the vorticity generation by the growing buoyancy force in the apex cross-section, preventing it from breaking up into two vortex rolls. The 2D models (Moreno-Insertis and Emonet 1996; Longcope et al. 1996; Fan et al. 1998a; Emonet and Moreno-Insertis 1998) on the other hand considered an initially buoyant flux tube for which there is an impulsive initial generation of vorticity by the buoyancy force. A significant initial twist is thus required to suppress this initial vorticity generation. Therefore the absence of an initial vorticity generation by buoyancy, and the subsequent magnetic tension force resulting from bending and braiding the field lines allow the arched tube with no net twist in Fan (2001) to rise over a significantly greater distance without disruption.

Abbett et al. (2000) performed 3D simulations where an initial horizontal flux tube is prescribed with a non-uniform buoyancy distribution along the tube such that it rises into an $\varOmega$-shaped loop. As discussed above, due to the prescribed buoyancy in the initial horizontal tube, there is an impulsive initial generation of vorticity by the buoyancy force which breaks up the apex of the rising $\varOmega$-loop if there is no initial twist. However the separation of the two vortex fragments at the apex is reduced due to the three-dimensional effect (Abbett et al. 2000). By further including the effect of solar rotation using a local f-plane approximation, Abbett et al. (2001) found that the influence of the Coriolis force significantly suppresses the degree of fragmentation at the apex of the $\varOmega$-loop (Fig. 21).

Fig. 21

Image reproduced with permission from Abbett et al. (2001), copyright by AAS

The rise of a buoyant $\varOmega$-loop with an initial field strength $B = 10^5 {\mathrm {\ G}}$ in a rotating model solar convection zone at a local latitude of $15^{\circ }$). The $\varOmega$-loop rises cohesively even though it is untwisted. The loop develops an asymmetric shape with the leading side (leading in the direction of rotation) having a shallower angle relative to the horizontal direction compared to the following side.

They also found that the Coriolis force causes the emerging loop to become asymmetric about the apex, with the leading side (leading in the direction of rotation) having a shallower angle with respect to the horizontal direction compared to the following (Fig. 21), consistent with the geometric asymmetry found in the thin flux tube calculations (Sect. 5.1.4).

Another interesting possibility is suggested by the 3D simulations of Dorch and Nordlund (1998), who showed that a random or chaotic twist with an amplitude similar to that given by Eqs. (30) or (31) in the flux tube can ensure that the tube rises cohesively. Such a random twist may not be detected in the photosphere measurement of active region twists which is determined by taking some forms of average of the quantity $\alpha = J_z / B_z$ over the active region.

Martínez-Sykora et al. (2015) carried out a comprehensive multi-parametric study of the buoyant rise of $\varOmega$-shaped magnetic flux tubes in an adiabatically stratified layer with 3D MHD simulations that achieved a hitherto significantly higher spatial resolution and hence significantly higher Reynolds numbers through the use of Adaptive Mesh Refinement (AMR) of the numerical code. They examined the dependence of the tube evolution on the field line twist and on the curvature of the tube axis. They found that the results are quite different for the low-diffusion regime with the Reynolds number for the rising flux tube $R_e \sim O(100)$ compared to those in the high-diffusion regime with $R_e \lesssim O(10)$, which characterized the earlier 3D simulations. In the high-diffusion regime, the amount of longitudinal flux retained in the rising head of the flux tube increases with the curvature of the flux tube axis (see Fig. 22), consistent with the earlier 3D simulations of Abbett et al. (2000). But when the low-diffusion regime is reached (with the use of AMR), a smaller magnetic twist (below the critical value given in equation 31) is able to prevent the splitting of the flux tube into two vortex tubes, and the loop curvature does not play a significant role in the cohesion of the rising tube (see Fig. 23).

Fig. 22

Image reproduced with permission from Martínez-Sykora et al. (2015), copyright by AAS

The cross-sectional structure of the rising flux tube resulting from the simulations in the high-diffusion regime without the AMR as described in Martínez-Sykora et al. (2015). The panels from left to right and top to bottom correspond to cases with the same moderate twist, but significantly decreasing curvature parameter for the tube axis, with the bottom right showing the case with zero curvature.

Fig. 23

Image reproduced with permission from Martínez-Sykora et al. (2015), copyright by AAS

Same as Fig. 22 but resulting from the simulations in the low-diffusion regime with the high level of AMR as described in Martínez-Sykora et al. (2015). The cohesion of the rising tube is significantly improved compared to the corresponding cases shown in Fig. 22, and the total longitudinal flux retained in the head of the rising tube no longer depend significantly on the curvature of the tube axis.

Results from rotating spherical-shell simulations

Fan (2008) has carried out a set of 3D anelastic MHD simulations of the buoyant rise of twisted magnetic flux tubes in an adiabatically stratified model solar convection zone in a rotating spherical shell geometry but without the presence of convection (see Fig. 24 and the associated video for one example simulation). These simulations have considered twisted, buoyant toroidal flux tubes at the base of the solar convection zone with an initial field strength of $10^5 {\mathrm {\ G}}$, being $\sim$ 10 times the equipartition field strength, and thus have neglected the effect of convection. Although it should be noted that the thin flux tube simulations incorporating the influence of the giant-cell convection (Weber et al. 2011, 2013) show that even with such high field strengths, the evolution of the rising flux tube is still significantly impacted in the regions of the strongest downflows. The main finding from the 3D simulations of Fan (2008) is that the twist of the tube induces a tilt at the apex of the rising $\varOmega$-tube that is opposite to the direction of the observed mean tilt of solar active regions, if the sign of the twist follows the observed hemispheric preference. It is found that in order for the tilt driven by the Coriolis force to dominate, such that the emerging $\varOmega$-tube shows a tilt consistent with Joy’s law of active region mean tilt, the initial twist rate of the flux tube needs to be smaller than about a half of that required for the tube to rise cohesively. Under such conditions, the buoyant flux tube is found to undergo severe flux loss during its rise, with less than 50% of the initial flux remaining in the final $\varOmega$-tube that rises to the surface (see Fig. 24). However the severe flux loss may be a result of the high level of diffusion due to the limited spatial resolution of the simulations as shown in Martínez-Sykora et al. (2015). By carrying out 3D MHD simulations with AMR in a local Cartesian domain that achieved a significantly higher spatial resolution and hence significantly higher Reynolds numbers, Martínez-Sykora et al. (2015) found that the tube cohesion for a moderately twisted buoyant flux tube can be significantly improved when the high Reynolds number regime is reached through the use of AMR (see end of Sect. 5.3). Thus simulations in a global rotating spherical shell geometry as Fan (2008) but reaching a significantly higher spatial resolution as that in Martínez-Sykora et al. (2015) are needed.

Fig. 24

Image reproduced with permission from Fan (2008), copyright by AAS

The evolution of a weakly twisted, buoyantly rising $\varOmega$-tube, resulting from a simulation described in Fan (2008, see the LNT run in that paper). A corresponding movie showing the evolution is available as a supplement.

Fig. 25

a 3D volume rendering of the magnetic field strength of a weakly twisted, rising $\varOmega$-tube, whose apex is approaching the top boundary, resulting from a simulation described in Fan (2008, see the LNT run in that paper). (For a corresponding movie see Fig. 24.) b A cross section of B near the top boundary at $r=0.937 R_{\odot }$; c selected field lines threading through the coherent apex cross-section of the $\varOmega$-tube

Furthermore, Fan (2008) found that the Coriolis force drives a retrograde flow along the apex portion of the rising tube, resulting in a relatively greater stretching of the field lines and hence stronger field strength in the leading leg of the tube. With a greater field strength, the leading leg is more buoyant with a greater rise velocity, and remains more cohesive compared to the following leg (see Figs. 25a,b). Figure 25c shows selected field lines threading through the coherent apex cross-section of the final $\varOmega$-tube, resulting from the simulation of a weakly twisted buoyant tube described in Fan (2008, see the LNT run in that paper). It can be seen that the field lines in the leading side are winding about each other smoothly in a coherent fashion, while the field lines in the following side are significantly more frayed.

The 3D simulation of Fan (2008) found a retrograde flow of $\sim 100$ m/s for the tube plasma at the apex of the emerging tube as it reaches about 30 Mm below the surface. This is consistent with the result from the thin flux tube simulations (e.g., Caligari et al. 1995; Weber et al. 2011) and it is due to the tendency for the rising flux tube to conserve the angular momentum as it rises from the bottom of the solar convection zone. This retrograde flow at the rising flux tube’s apex was examined by Birch et al. (2010) for its detectability by the time-distance helioseismology, as a possible subsurface pre-emergence signature for emerging active regions. It was found that a statistical approach of averaging over a large number (about 150) of emerging active regions is needed to reach the sufficient signal to noise ratio for detecting the travel time perturbation signature produced by the flow. Such a statistical study of a large sample of emerging active regions was conducted by Birch et al. (2013), and it puts strong constraints on models of active region flux emergence (Sect. 9.2).

Jouve and Brun (2007) have also carried out anelastic MHD simulations in a rotating spherical shell geometry to study the buoyant rise of an axisymmetric toroidal flux ring in an isentropically stratified (non-convecting) envelope. They have considered a even greater initial field strength of $1.8 \times 10^5 {\mathrm {\ G}}$ for the initial toroidal flux ring. As was discussed in Fan (2008), the poleward deflection of the rise trajectory of the tube due to the Coriolis force is far more severe for an axisymmetric toroidal ring (where the whole ring is moving away from the rotation axis of the Sun) than for a localized 3D $\varOmega$-shaped tube (see Sect. 3.1 in Fan 2008). Thus an initial field strength of $\gtrsim 1.8 \times 10^5 {\mathrm {\ G}}$ is needed for an axisymmetric toroidal ring to rise nearly radially (Jouve and Brun 2007). The simulations of Jouve and Brun (2007) also recovered the previous results from Cartesian simulations that if the flux tube is not twisted, it splits into two counter rotating vortices before reaching the top of the envelope.

Fournier et al. (2017) presented highly-resolved 3D compressible MHD simulations of the buoyant rise of non-axisymmetric magnetic flux tubes in an adiabatically stratified rotating stellar interior envelope with varying rotation rates, without the presence of convection. The simulations considered flux tubes that are sufficiently twisted (satisfying the minimum twist requirement eq. 30) to ensure a coherent rise. With the use of AMR, the simulations well resolve the rising flux tube, with the initial tube diameter near the bottom of the domain being resolved by at least 50 grid points. They found that the compressible simulations show results that are consistent with the previous thin flux tube and anelastic simulations in regard to the rising trajectories and rise times. Through parameter studies, they derived a control parameter that determines the rise time and the regime of the rise (buoyancy-dominated or rotation-dominated), in terms of the stellar rotation rate, the magnetic field strength of the flux tube, and the azimuthal wavenumber of the rise pattern.

The rise of highly twisted, kink unstable magnetic flux tubes as a possible origin of $\delta$-sunspots

As discussed in Sect. 5.2, most of the solar active regions are observed to have very small twists, with an averaged value of $\alpha \equiv \langle J_z/B_z \rangle$ (the averaged ratio of the vertical electric current over the vertical magnetic field) measured to be on the order of $0.01 \mathrm {\ Mm}^{-1}$ (e.g. Pevtsov et al. 1995, 2001). However there is a small but important subset of active regions, called the $\delta$-sunspots, which are observed to be highly twisted with $\alpha$ reaching a few times $0.1 \mathrm {\ Mm}^{-1}$ (Leka et al. 1996), and to have unusual polarity orientations that are sometimes reversed from Hale’s polarity rule (see Zirin and Tanaka 1973; Zirin 1988; Tanaka 1991). These $\delta$-sunspots are compact structures where umbrae of opposite polarity are contained within a common penumbra. They are found to be the most flare productive active regions (see Zirin 1988). Through careful analysis of the evolution of flare-active $\delta$-sunspot groups, Tanaka (1991) proposed a model of an emerging twisted flux rope with kinked or knotted geometry to explain the observed evolution of these regions.

Motivated by the observations of $\delta$-sunspots, MHD calculations of the evolution of highly twisted, kink unstable magnetic flux tubes in the solar convection zone have been carried out (Linton et al. 1996, 1998, 1999; Fan et al. 1998b, 1999). For an infinitely long twisted cylindrical flux tube with axial field $B_z (r)$, azimuthal field $B_{\theta } (r) = q\,(r)\,r B_z (r)$, and plasma pressure $p\,(r)$ in hydrostatic equilibrium where $dp/dr = -(B_{\theta }^2 / 4 \pi r) - d(B_z^2+B_{\theta }^2) / dr$, a sufficient condition for the flux tube to be kink unstable is (see Freidberg 1987)

$$\begin{aligned} \frac{r}{4} \left( \frac{q'}{q} \right) ^2 + \frac{8 \pi p'}{B_z^2} < 0 \end{aligned}$$

(32)

to be true somewhere in the flux tube. In Eq. (32) the superscript ’ denotes the derivative with respect to r. This is known as Suydam’s criterion. Note that condition (32) is sufficient but not necessary for the onset of the kink instability and hence there can be cases which are kink unstable but do not satisfy condition (32). One such example are the force-free twisted flux tubes which are shown to be always kink unstable without line-tying (i.e., infinitely long) (Anzer 1968), but for which $p' = 0$. Force-free fields are the preferred state for coronal magnetic fields under low plasma-$\beta$ conditions and are not a likely state for magnetic fields in the high-$\beta$ plasma of the solar interior. Linton et al. (1996) considered the linear kink instability of uniformly twisted cylindrical flux tubes with $q = B_{\theta } / r B_z$ being constant, confined in a high $\beta$ plasma. They found that the equilibrium is kink unstable if q exceeds a critical value $q_\mathrm {cr} = a^{-1}$, where $a^{-2}$ is the coefficient for the $r^2$ term in the Taylor series expansion of the equilibrium axial magnetic field $B_z$ about the tube axis: $B_z(r) = B_0 (1 - a^{-2} r^2 + \cdots )$. This result is consistent with Suydam’s criterion. They further argued that an emerging, twisted magnetic flux loop will tend to have a nearly uniform q along its length since the rise speed through most of the solar convection zone is sub-Alfvénic and torsional forces propagating at the Alfvén speed will equilibrate quasi-statically. Meanwhile expansion of the tube radius at the apex as it rises will result in a decrease in the critical twist $q_\mathrm {cr} = a^{-1}$ necessary for the instability. This implies that as a twisted flux tube rises through the solar interior, a tube that is initially stable to kinking may become unstable as it rises, and that the apex of the flux loop will become kink unstable first because of the expanded tube cross-section there (Parker 1979; Linton et al. 1996).

The non-linear evolution of the kink instability of twisted magnetic flux tubes in a high-$\beta$ plasma has been investigated by 3D compressible MHD simulations (Linton et al. 1998, 1999) and 3D anelastic MHD simulations (Fan et al. 1998b, 1999). Fan et al. (1998b, 1999) modeled the rise of a kink unstable flux tube through an adiabatically stratified model solar convection zone.

Fig. 26

The rise of a kink unstable magnetic flux tube through an adiabatically stratified model solar convection zone (result from a simulation in Fan et al. (1999) with an initial right-handed twist that is 4 times the critical level for the onset of the kink instability). In this case, the initial twist of the tube is significantly supercritical so that the e-folding growth time of the most unstable kink mode is smaller than the rise time scale. The flux tube is perturbed with multiple unstable modes. The flux tube becomes kinked and arches upward at the center where the kink concentrates, with a rotation of the tube orientation at the apex that exceeds $90^{\circ }$

Fig. 27

A horizontal cross-section near the top of the upward arching kinked loop shown in the last panel of Fig. 26. The contours denote the vertical magnetic field $B_z$ with solid (dotted) contours representing positive (negative) $B_z$. The arrows show the horizontal magnetic field. One finds a compact bipolar region with sheared transverse field at the polarity inversion line. The apparent polarity orientation (i.e., the direction of the line drawn from the peak of the positive pole to the peak of the negative pole) is rotated clockwise by about $145^{\circ }$ from the $+x$ direction (the east-west direction) of the initial horizontal flux tube

In the case where the initial twist of the tube is significantly supercritical such that the e-folding growth time of the most unstable kink mode is smaller than the rise time scale, Fan et al. (1999) found sharp bending of the flux tube as a result of the non-linear evolution of the kink instability. During the onset of the kink instability, the magnetic energy decreases while the magnetic helicity is approximately conserved. The writhing of the flux tube also significantly increases the axial field strength and hence enhances the buoyancy of the flux tube. The flux tube rises and arches upward at the portion where the kink concentrates, with a rotation of the tube orientation at the apex that exceeds $90^{\circ }$ (see Fig. 26). Based on the orientation of the magnetic bipoles seen in a horizontal cross-section (Fig. 27) taken near the top of the kinked loop approaching the top boundary, it is conjectured that the emergence of this kinked flux tube may give rise to a compact magnetic bipole with polarity order inverted from the Hale polarity rule (Fig. 27) as often seen in $\delta$-sunspots.

However the aforementioned simulations (Linton et al. 1998, 1999; Fan et al. 1998b, 1999) are limited to modeling the rise of the kink unstable flux tubes within an adiabatically stratified model convection zone, and thus it is not shown whether the emergence of the kinked tubes from the convection zone into the solar atmosphere can produce the observed characteristics of the $\delta$-sunspots on the photosphere. To address this question, Takasao et al. (2015)(see also review by Toriumi and Wang (2019)) carried out a 3D compressible MHD simulation of a buoyant, kink-unstable flux tube that becomes kinked in the top layer of an adiabatically stratified model convection zone and subsequently emerges into the solar atmosphere. It is found that due to the development of the kink instability before the emergence, the magnetic twist at the apex of the kinked tube is greatly reduced as a result of conversion of twist into writhe, although the two legs of the kinked tube are still strongly twisted. Instead of forming a bipolar structure, the emergence of the subsurface kinked flux tube produces at the photosphere a complex quadrupole structure (see e.g. Fig. 35 and associated movie in Toriumi and Wang 2019), containing a narrow elongated bipolar pair sandwiched between a pair of coherent twisted bipolar spots. The central narrow bipolar channel is formed due to the submergence of U-shaped loops that develop at the apex of the kinked tube.

The conservation of magnetic helicity requires that the writhing of the tube due to the kink instability is of the same sense as the twist of the field lines. Hence for a kinked emerging tube, the rotation or tilt of the emerging magnetic bipole from the east-west polarity orientation defined by the Hale’s polarity rule should be related to the twist of the tube. The rotation or tilt should be clockwise (counterclockwise) for right-hand-twisted (left-hand-twisted) flux tubes. This tilt–twist relation can be used as a means to test the model of kinked flux tubes as the origin of $\delta$-sunspots (Tanaka 1991; Leka et al. 1994, 1996; López Fuentes et al. 2003). Observations have found with both consistent and opposing cases (Leka et al. 1996; López Fuentes et al. 2003). A study (Tian et al. 2005) which includes a large sample (104) of complex $\delta$-configuration active regions shows that 65–67% of these $\delta$-regions have the same sign of twist and writhe, supporting the model of kinked flux tubes.

Another scenario that explains the origin of the compact $\delta$-sunspot configuration is the “multi-buoyant segment model” (see review by Toriumi and Wang 2019) first simulated by Toriumi et al. (2014) to explain the quadrupolar flux emergence pattern of active region (AR) NOAA 11158. In this scenario, two adjacent buoyant segments of a single subsurface twisted flux tube rise as an M-shaped loop towards the surface to form two bipolar emerging regions. The adjacent inner polarities with opposite signs of the two emerging bipolar regions collide to form a compact $\delta$-sunspot with highly sheared and compressed polarity inversion line (PIL), reminiscent of the flux emergence pattern observed in AR 11158. The inner polarities collide to form the compact $\delta$-sunspot because they are connected beneath the surface by downward moving U-shaped fields. In a recent realistic radiation MHD simulation of active region formation in a deep convecting domain that encompasses both the bulk of the convection zone and the near surface layer, Toriumi and Hotta (2019) successfully simulated the spontaneous formation of $\delta$-sunspots through a multi-buoyant segment scenario that naturally develops due to the interaction between the emerging magnetic flux and turbulent convection (see Sect. 9.1).

3D MHD simulations of buoyant flux tubes in a stratified convective velocity field

General considerations

To understand how active region flux tubes emerge through the solar convection zone, it is certainly important to understand how 3D convective flows in the solar convection zone affect the rise and the cohesion of the buoyant flux tubes. 3D MHD simulations in the presence of stratified convective flows are needed to fully address the above question. The thin flux tube model (e.g., Weber et al. 2011) suggests that in order for convection not to significantly affect the buoyant rise of the flux tube, the magnetic buoyancy of the flux tube should dominate the downward hydrodynamic force from the convective downflows:

$$\begin{aligned} \frac{B^2}{8 \pi H_p }> C_{\mathrm {D}}\frac{\rho v_{\mathrm {c}}^2}{\pi a} \,\,\Rightarrow \,\, B > \left( \frac{2 C_{\mathrm {D}}}{\pi } \right) \left( \frac{H_p}{a}\right) ^{1/2} B_{\mathrm {eq,downflow}}, \end{aligned}$$

(33)

where $B_{\mathrm {eq,downflow}}\equiv (4 \pi \rho )^{1/2} v_{\mathrm {c}}$ is the field strength at which the magnetic energy density is in equipartition with the kinetic energy density of the convective downdrafts, $v_{\mathrm {c}}$ is the flow speed of the downdrafts, $H_p$ is the local pressure scale height, a is the tube radius, and $C_{\mathrm {D}}$ is the aerodynamic drag coefficient which is of order unity. In Eq. (33) we have used the aerodynamic drag force as an estimate for the magnitude of the hydrodynamic forces. The estimate (33) leads to the condition that the field strength of the flux tube needs to be significantly higher than the equipartition field strength by a factor of $\sqrt{H_p / a}$. For flux tubes responsible for active region formation, $\sqrt{H_p / a} > 3$ near the bottom of the solar convection zone. Thus we call $B \gtrsim 3 B_{\mathrm {eq,downflow}}$ the “magnetic buoyancy dominated regime”, and expect $B < 3 B_{\mathrm {eq,downflow}}$ to be the regime where convective downflows become dominant.

Simulations in a local Cartesian geometry without rotation

Fan et al. (2003) carried out direct 3D anelastic MHD simulations of the evolution of a buoyant magnetic flux tube in a stratified convective velocity field in a Cartesian box that spans 3 density scale heights. The density contrast between the bottom and top of the domain is approximately equal to that between the bottom of the solar convection zone and about 37 Mm depth the photosphere. The basic result of the simulations is illustrated in Fig. 28.

Fig. 28

The evolution of a uniformly buoyant magnetic flux tube in a stratified convective velocity field from the simulations of Fan et al. (2003). Top-left image: A snapshot of the vertical velocity of the 3D convective velocity field in a superadiabatically stratified fluid. The density ratio between the bottom and the top of the domain is 20. Top-right image: The velocity field (arrows) and the tube axial field strength (color image) in the vertical plane that contains the axis of the uniformly buoyant horizontal flux tube inserted into the convecting box. Lower panel: The evolution of the buoyant flux tube with $B = B_{\mathrm {eq,downflow}}$ (left column) and with $B = 10 B_{\mathrm {eq,downflow}}$ (right column). The color indicates the absolute field strength of the flux tube scaled to the initial tube field strength at the axis. A movie corresponding to the lower panel, showing the evolution for the two cases with $B = B_{\mathrm {eq,downflow}}$ and $B = 10 B_{\mathrm {eq,downflow}}$ is available as a supplement

They first computed a 3D convective velocity field in a superadiabatically stratified fluid, until the convection reaches a statistical steady state. The resulting velocity field (see top-left image in Fig. 28) shows the typical features of overturning convection in a stratified fluid as found in many previous investigations. In the bulk of the convecting domain, the downflows are concentrated into narrow filamentary plumes, some of which extend all the way across the domain, while the upflows are significantly broader and are of smaller velocity amplitude in comparison to the downdrafts. A uniformly buoyant, twisted horizontal magnetic flux tube having an entropy that is equal to the entropy at the base of the domain is inserted into the convecting box (see top-right image in Fig. 28).

In the case where the field strength of the tube is in equipartition to the kinetic energy density of the strongest downdraft (left column in the bottom panel of Fig. 28), i.e. $B=B_{\mathrm {eq,downflow}}$, the evolution of the tube depends sensitively on the local condition of the convective flows. Despite being buoyant, the portions of the tube in the paths of downdrafts are pushed downward and pinned down to the bottom, while the rise speed of sections within upflow regions is significantly boosted. $\varOmega$-shaped emerging tubes can form between downdrafts. It is found that the three-dimensional evolution and the cohesion of the flux tubes with $B = B_{\mathrm {eq,downflow}}$ no longer depend sensitively on the initial twist of the tube, in contrast to the results obtained in the absence of convection. In the case of convection-dominated evolution, the flux tube is being bent by the flow in an incoherent manner along the tube. The flux tube is no longer able to develop vortex tubes coherent along the tube axis, which is the main reason for the flux tube to break up and cease to rise in the absence of convection. Despite being severely distorted, the $\varOmega$-tube that emerge between downdrafts can not be ruled out as a possible source of solar active regions, given the fact that the observed emerging magnetic regions often show complex morphologies.

On the other hand in the case where the tube field strength is 10 times the equipartition value (right column in the bottom panel of Fig. 28), the horizontal flux tube rises under its uniform buoyancy, nearly unaffected by the convection. In this magnetic buoyancy dominated regime, a sufficient initial twist is needed to prevent the tube from breaking up into two vortex tubes and rise coherently, similar to the result shown in the previous simulations of rising flux tubes in the absence of convection (Sect. 5.3).

In the anelastic simulations of Fan et al. (2003) discussed above, the physical values of the downflow speed and $B_{\mathrm {eq,downflow}}$ are all scaled to the value of the superadiabaticity $\delta _r$ at the base of the domain used for the reference state. If we assume a value of $2 \times 10^{-8}$ for the superadiabaticity near the base of the solar convection zone for $\delta _r$, the $B_{\mathrm {eq,downflow}}$ described in the above result would correspond to about 10 kG.

The 3D simulations of Fan et al. (2003) have very limited spatial resolution with the initial radius of the tube being resolved by about 6 grid points and the simulations also incorporate explicit viscosity and magnetic diffusion. As has been shown in Martínez-Sykora et al. (2015), who have carried out 3D MHD simulations of buoyant flux tubes in the absence of convection achieving a much higher spatial resolution (and hence significantly lower diffusions) through the use of AMR, the results change significantly when the low-diffusion regime is reached compared to the high-diffusion regime. Therefore the results such as those discussed above in Fan et al. (2003) of buoyant flux tubes in convection need to be further examined with higher resolution simulations. However it is difficult to achieve the low-diffusion regime using AMR in the case where convection is present and small scale features develop everywhere.

Global rotating convective spherical-shell simulations

Jouve and Brun (2009) have carried out the first set of global anelastic MHD simulations of the buoyant rise of an initially toroidal flux ring in a rotating, fully convective spherical shell, possessing self-consistently generated mean flows such as meridional circulations and differential rotation, representative of the conditions of the solar convective envelope (see, e.g., review by Miesch 2005). They inserted into the fully developed convecting envelope a buoyant toroidal flux ring with different initial field strengths, twist rates, and initial latitudes, to study how the flux tube rises in the presence of convection and the associated mean flows, and how the dynamic evolution depends on the above initial parameters.

It is found that the magnetic field strength corresponding to the value that is in equipartition with the kinetic energy of the strongest downflows is rather high, $B_{\mathrm {eq,downflow}}\approx 6.1 \times 10^4 {\mathrm {\ G}}$. The initial field strength B of the toroidal flux rings considered in the simulations are all significantly greater than $B_{\mathrm {eq,downflow}}$, being $2.5 B_{\mathrm {eq,downflow}}$, $5 B_{\mathrm {eq,downflow}}$, and $10 B_{\mathrm {eq,downflow}}$. Thus, except for the case with $B= 2.5 B_{\mathrm {eq,downflow}}$, all of the other cases simulated are in the magnetic buoyancy dominated regime (with $B > 3 B_{\mathrm {eq,downflow}}$ as discussed in Sect. 5.6.1). As a result, the simulations recovered many of the findings obtained from previous simulations in the absence of convective flows. These include the dependence of the poleward deflection of the tube on the initial tube field strength (e.g., Choudhuri and Gilman 1987; Fan 2008), the critical dependence on the initial twist for the cohesion of the buoyantly rising flux tube (e.g., Emonet and Moreno-Insertis 1998; Abbett et al. 2000), and the dependence of the tilt angle of the emerging tube on the initial twist (Sect. 5.4 and Fan 2008). Due to the relatively high magnetic diffusivity in the code, flux tubes with a very large initial field strength (ranging from $1.5 \times 10^5 {\mathrm {\ G}}$ to $6 \times 10^5 {\mathrm {\ G}}$) and a large radius, corresponding to a total flux on the order of a few times $10^{23} {\mathrm {\ Mx}}$, significantly greater than the typical active region fluxes, are considered, such that the rise times of the flux tubes are $\lesssim$ the diffusive time scale of about 14.5 days. Because most of the cases considered are essentially in the magnetic buoyancy dominated regime, the rising toroidal flux tube only develops rather moderate undulations by the influence of the convective flows (see Fig. 29), and $\varOmega$ tubes with undulations extending the depth of the convection zone are not found.

Fig. 29

Image reproduced with permission from Jouve and Brun (2009), copyright by AAS

Cut at the latitude of $30^{\circ }$ of the radial velocity (color) and of the magnetic energy (line contours) for three different simulations of the rise of a buoyant toroidal flux ring with different initial field strengths: $2.5 B_{\mathrm {eq,downflow}}$ (top panel), $5 B_{\mathrm {eq,downflow}}$ (middle panel), and $10 B_{\mathrm {eq,downflow}}$ (bottom panel).

It is also found that flux tubes introduced at lower latitudes (e.g., at $15^{\circ }$) have difficulty reaching the top of the domain (even with a strong initial field strength of $5 B_{\mathrm {eq,downflow}}\approx 3 \times 10^5 {\mathrm {\ G}}$), and the authors attributed the cause of this to the differential rotation. For the weakest field strength case (with $B = 2.5 B_{\mathrm {eq,downflow}}= 1.5 \times 10^5 {\mathrm {\ G}}$), it is found that portions of the toroidal ring are pinned down by the convective downdrafts, and eventually the tube loses its buoyancy due to magnetic diffusion and is unable to rise to the top (see top panel of Fig. 29).

Jouve et al. (2013) have extended the above work to consider initial toroidal flux rings at the base of the convection zone with a longitudinally localized buoyancy distribution to simulate the buoyant rise of a single $\varOmega$-shaped loop of flux in the rotating, convective spherical shell with self-consistently generated mean flows (i.e. the differential rotation and meridional circulation). It is found that the rise and the characteristics of the emerging regions are strongly affected by the convective motions when loops with initial field strengths $\le 10^5$ G are considered, however emerging regions with the correct tilt and a dominant leading polarity are still found in these simulations. However most of these simulations have used initial toroidal flux tubes with a right-handed initial twist in the northern hemisphere, which is opposite to the observed preferred sign of twist (left-handed) for active regions in the northern hemisphere (e.g., Pevtsov et al. 2001). It has been shown in the simulations in the absence of convection (e.g. Fan 2008) that with a magnitude of the twist that reaches the critical twist needed for the buoyant flux tube to rise cohesively, the orientation of the tilt angle of the final emerging region is strongly influenced by the sign of the twist of the rising $\varOmega$ loops, where a left-handed twist tends to produce a tilt that is opposite to the observed tilt of solar active regions in the northern hemisphere. It is still not clear whether, in the presence of the rotating convection, the buoyant rise of an $\varOmega$-shaped tube with a left-handed twist in the northern hemisphere (consistent with the observed hemisphere preference of the sign of active region twist) can produce an emerging region with the correct tilt and a dominant leading polarity, as were found for the right-hand twisted cases in Jouve et al. (2013).

It should be emphasized that so far, all 3D simulations of isolated rising flux tubes in a global rotating spherical convective envelope have to use initial toroidal flux tubes with a large radius, and hence a large total flux (a few times $10^{23}$ Mx), about an order of magnitude greater than the flux of typical large solar active regions of $10^{22}$ Mx, due to the large numerical diffusion (that erodes the magnetic buoyancy) resulting from the limited numerical resolution. Clearly significantly higher resolution simulations with a reduced magnetic diffusion are necessary to model the evolution of rising flux tubes from the bottom of the solar convection zone in more realistic parameter regimes. Specifically, it is important to model cases with a weaker initial field strength ($10^4 {\mathrm {\ G}} \lesssim B \lesssim 10^5 {\mathrm {\ G}}$) under the significant influence of the rotating solar convection, as well as the influence of the turbulent magnetic field of the convective dynamo (e.g., Pinto and Brun 2013), to study whether $\varOmega$-shaped emerging flux bundles with properties consistent with solar active regions can develop.

Turbulent pumping of a magnetic field in the solar convection zone

As discussed in Sect. 5.6, for buoyant flux tubes with significantly super-equipartition field strength $B \gtrsim (H_p / a)^{1/2} B_{\mathrm {eq,downflow}}$, where $B_{\mathrm {eq,downflow}}$ is in equipartition with the kinetic energy density of the convective downflows, the magnetic buoyancy of the tubes dominates the hydrodynamic force from the convective downflows and the flux tubes can rise unaffected by convection. On the other hand if the field strength of the flux tubes is comparable to or smaller than the equipartition value $B_{\mathrm {eq,downflow}}$, the magnetic buoyancy is weaker than the hydrodynamic force from the convective downflows and the evolution of the tubes becomes largely controlled by the convective flows. In this regime of convection dominated evolution, due to the strong asymmetry between up- and downflows characteristic of stratified convection, it is found that magnetic flux is preferentially transported downward against its magnetic buoyancy out of the turbulent convection zone into the stably stratified overshoot region below. This process of “turbulent pumping” of a magnetic field has been demonstrated by several high resolution 3D compressible MHD simulations (see Tobias et al. 1998, 2001; Dorch and Nordlund 2001).

Tobias et al. (2001) carried out a series of 3D MHD simulations to investigate the turbulent pumping of a magnetic field by stratified convection penetrating into a stably stratified layer. A thin slab of a unidirectional horizontal magnetic field is introduced into the middle of an unstably stratified convecting layer, which has a stable overshoot layer attached below. It is found that the fast, isolated downflow plumes efficiently pump flux from the convecting layer into the stable layer on a convective time scale. Tobias et al. (2001) quantify this flux transport by tracking the amount of flux in the unstable layer and that in the stable layer, normalized by the total flux. Within a convective turnover time, the flux in the stable layer is found to increase from the initial value of 0 to a steady value that is greater than 50% of the total flux (reaching 80% in many cases), i.e., more than half of the total flux is settled into the stable overshoot region in the final steady state. Moreover the stable overshoot layer is shown to be an effective site for the storage of a toroidal magnetic field. If the initial horizontal magnetic slab is put in the stable overshoot layer, the penetrative convection is found to be effective in pinning down the majority of the flux against its magnetic buoyancy, preventing it from escaping into the convecting layer. It should be noted however that the fully compressible simulations by Tobias et al. (2001) assumed a polytropic index of $m=1$ for the unstable layer which corresponds to a value for the non-dimensional superadiabaticity $\delta$ of 0.1. Thus the convective flow speed $v_{\mathrm {c}}$ for the strong downdrafts is on the order of $\sqrt{\delta } \sim 0.3$ times the sound speed, i.e., not very subsonic. On the other hand, the range of initial magnetic field strength considered in the simulations corresponds to a plasma $\beta$ ranging from $2 \times 10^3$ to $2 \times 10^7$. Thus comparing to the kinetic energy density of the convective downflows, the strongest initial field considered is of the order $0.1 B_{\mathrm {eq,downflow}}$, i.e., below equipartition, although a field with strength up to $B_{\mathrm {eq,downflow}}$ may be generated as a result of amplification by the strong downflows during the evolution. Therefore the above results obtained with regard to the efficient turbulent pumping of a magnetic field out of the convection zone into the stable overshoot region against its magnetic buoyancy apply only to fields weaker than or at most comparable to $B_{\mathrm {eq,downflow}}$.

Abbett et al. (2004) found that turbulent pumping is very weak and ineffective in an MHD convection model without a stable overshoot layer at the bottom. Considering both the results of Tobias et al. (2001) and Abbett et al. (2004) it appears that the presence of the stable overshoot layer below the convection zone is an essential ingredient for effective turbulent pumping.

The turbulent pumping of magnetic flux with field strength $B \lesssim B_{\mathrm {eq,downflow}}$ out of the convection zone into the stable overshoot region demonstrated by the high resolution 3D MHD simulations has profound implications for the working of the interface mean field dynamo models (Parker 1993; Charbonneau and MacGregor 1997) as discussed by Tobias et al. (2001). The interface dynamo models require efficient transport of the large scale poloidal field generated by the $\alpha$-effect of the cyclonic convection out of the convection zone into the stably stratified tachocline region where strong rotational shear generates and amplifies the large scale toroidal magnetic field. Turbulent pumping is shown to enhance both the transport of magnetic flux into the stable shear layer and the storage of the toroidal magnetic field there. It further implies that the transport of magnetic flux by turbulent pumping should not be simply treated as an enhanced isotropic turbulent diffusivity in the convection zone as is typically assumed in the mean field dynamo models. Tobias et al. (2001) noted that a better treatment would be to add an extra advective term to the mean field equation characterizing the effect of turbulent pumping, which would correspond to including the antisymmetric part of the $\alpha$-tensor known as the $\gamma$-effect (see Moffatt 1978).

Amplification of a toroidal magnetic field by conversion of potential energy

Thin flux tube models of emerging flux loops through the solar convective envelope (Sect. 5.1) have inferred a strong super-equipartition field strength of order $10^5 {\mathrm {\ G}}$ for the toroidal magnetic field at the base of the solar convection zone. Generation of such a strong field is dynamically difficult since the magnetic energy density of a $10^5 {\mathrm {\ G}}$ field is about 10–100 times the kinetic energy density of the differential rotation (Parker 1994; Rempel and Schüssler 2001). An alternative mechanism for amplifying the toroidal magnetic field has been proposed which converts the potential energy associated with the stratification of the convection zone into magnetic energy. It is shown that upflow of high entropy plasma towards the inflated and “exploding” top of a rising $\varOmega$-loop developed from an initial toroidal field of equipartition field strength ($\sim 10^4 {\mathrm {\ G}}$) can significantly intensify the submerged part of the field by extracting plasma out of it (Parker 1994; Moreno-Insertis et al. 1995; Rempel and Schüssler 2001). This process is a barometric effect and is caused by the entropy gradient in the solar convection zone maintained by the energy transport.

In the thin flux tube simulations of rising $\varOmega$-loops in the solar convection zone, it is found that flux loops with a low initial field strength of $\sim 10^4 {\mathrm {\ G}}$ do not reach the upper half of the solar convection zone before the apexes of the loops loose pressure confinement and effectively “explode” (Moreno-Insertis et al. 1995). This loss of pressure confinement at the top of the emerging loop occurs as plasma inside the tube establishes hydrostatic equilibrium along the tube which happens if the emerging loop rises sufficiently slowly (Moreno-Insertis et al. 1995). The loop rises adiabatically carrying the high entropy plasma from the base of the solar convection zone while the entropy outside the flux tube decreases with height in the superadiabatically stratified convection zone. Hydrostatic equilibrium therefore dictates that the plasma pressure inside the flux tube decreases with height slower than the outside and becomes equal to the external pressure at a certain height where the magnetic field can no longer be confined. This “explosion” height for the emerging loop is found to be a function of the initial tube field strength at the base of the solar convection zone (see Fig. 30).

Fig. 30

Image reproduced with permission from Christensen-Dalsgaard et al. 1993, copyright by AAS

Depth from the surface where the apex of an emerging flux loop with varying initial field strength rising from the bottom of the convection zone looses pressure confinement or “explodes” as a result of tube plasma establishing hydrostatic equilibrium along the tube. The explosion height is computed by considering an isentropic thin flux loop with hydrostatic equilibrium along the field lines (see Moreno-Insertis et al. 1995) in a model solar convection zone of Christensen-Dalsgaard.

For loops with an initial field strength $\sim 10^4 {\mathrm {\ G}}$, the explosion height is at about the middle of the solar convection zone. When the loop apex approaches the explosion height, it expands drastically and the buoyancy of the high entropy material in the tube is expected to drive an outflow which extracts plasma out of the lower part of the flux tube at the base of the solar convection zone. This process has been demonstrated by Rempel and Schüssler (2001), who performed MHD simulations of exploding magnetic flux sheets in two-dimensional Cartesian geometry.

The simulations of Rempel and Schüssler (2001) start with a magnetic sheet with a higher value of entropy placed at the bottom of an adiabatically stratified layer (constant entropy layer). This setup avoids the complication of involving convective flows in the simulations while keeping the essential effect of the entropy decrease in the solar convection zone by assuming a constant entropy difference between the flux sheet and the isentropic layer. The central portion of the flux sheet is perturbed upward which subsequently forms a rising loop as a result of its magnetic buoyancy (see Fig. 31).

Fig. 31

Image reproduced with permission from Rempel and Schüssler (2001), copyright by AAS

Evolution of magnetic field strength (gray scale: darker gray denotes stronger field) and velocity field (arrows) during the flux loop explosion. The horizontal part of the field is amplified by a factor of 3.

The apex of the rising loop explodes into a cloud of weak magnetic field as it crosses the predicted explosion height (middle panel) and high entropy plasma, driven by buoyancy, continues to flow out of the “stumps”, draining mass from the lower horizontal part of the flux sheet (bottom panel). The field strength of the horizontal part of the flux sheet is visibly intensified. It is found that the final field strength the horizontal part of the field can reach is roughly the value for which the explosion height is close to the top of the stratification. For the solar convection zone, this value corresponds to $\sim 10^5 {\mathrm {\ G}}$ (see Fig. 30). This implies that the large field strength of order $10^5 {\mathrm {\ G}}$ may be achieved by the process of flux “explosion”, which draws energy from the potential energy associated with the stratification of the solar convection zone. A coherent picture maybe as follows. Differential rotation in the tachocline shear layer generates and amplifies the toroidal magnetic field to an equipartition value of about $10^4 {\mathrm {\ G}}$, at which point magnetic buoyancy becomes important dynamically, and magnetic buoyancy instability, radiative heating or other convective perturbations drive the formation of buoyant flux loops rising into the solar convection zone. These rising loops explode in the middle of the convection zone and fail to rise all the way to the surface. These “failed” eruptions “pump” out the plasma from the toroidal field at the base of the solar convection zone (Parker 1994) and amplify the toroidal field until it reaches the strongly super-equipartition field strength of order $10^5 {\mathrm {\ G}}$, whose eruptions then lead to the emergence of solar active regions at the surface.

The simulations by Rempel and Schüssler (2001) are 2D, with invariance in the horizontal direction perpendicular to the magnetic field across the flux sheet. Hotta et al. (2012a) extend the simulation to the more realistic 3D case where a finite horizontal extent (in the direction perpendicular to the magnetic field) of the flux sheet at the base of the convection zone is perturbed and emerges. It is found that a similarly strong intensification of the magnetic field at the base of the convection zone as that found in the 2D simulations of Rempel and Schüssler (2001) can be achieved if the spatial scale of the flux sheet in the direction perpendicular to the magnetic field that participates in the flux emergence is sufficiently large. However, if this spatial scale is small, the foot points of the emerging flux are not as strongly anchored and rise up, resulting in a significant decrease of the magnetic field amplification.

Formation of active region emerging flux from convective dynamos in the bulk of the solar convection zone: Towards a new paradigm of active region flux generation and emergence

Significant progress has been made in the past decade by global 3D MHD convective dynamo simulations in producing a large-scale magnetic field that shows some aspects of the solar-like cyclic behavior (see review by Charbonneau (2020). Several simulations have shown the self-consistent formation of buoyant emerging loops with super-equipartition field strengths from the dynamo generated fields in the bulk of the convection zone, with characteristics suitable as the progenitors of solar active regions (e.g., Nelson et al. 2011, 2013, 2014; Fan and Fang 2014).

Using the anelastic spherical harmonic (ASH) code, Nelson et al. (2011, 2013, 2014) have carried out global 3D MHD simulations of convection and dynamo action in a spherical convective envelope of a Sun-like star that rotates at three times the solar rate ($3 \, \varOmega _{\odot }$). The simulations use a spherical shell domain that corresponds to the bulk of the solar convection zone, extending from $0.72 R_{\odot }$ to $0.97 R_{\odot }$ ($R_{\odot }$ is the solar radius), with a density contrast of about 25. With the use of the dynamic Smagorinsky model for the subgrid-scale turbulent diffusion, the high resolution simulations of Nelson et al. (2013) are able to reach a significantly lower viscosity and magnetic diffusion than what had been achieved previously with the ASH simulations. The simulations obtained a solar-like differential rotation with faster rotation at the equator than the poles, and a complex multi-cell meridional flow pattern. The simulations demonstrate that convective dynamos can maintain large-scale toroidal magnetic structures, or magnetic wreaths, that undergo cyclic reversals in the bulk of the turbulent convective envelope without a stably stratified overshoot region or a tachocline at the base. With decreasing magnetic diffusion and viscosity in the simulation, it is found that enhanced turbulent intermittency can further amplify the shear-generated magnetic structures to produce localized, coherent fibril magnetic fields (wreath cores) with super-equipartition field strengths (reaching peak field strengths of 45 kG) relative to the maximum kinetic energy density of convection at mid-convection zone. These fibril magnetic fields become buoyant loops that rise to the near-surface layer through combined actions of magnetic buoyancy and advection by giant-cell convection. Examples of such buoyant loops from the magnetic wreaths are shown in Fig. 32.

Fig. 32

Image reproduced with permission from Nelson et al. (2013), copyright by AAS

Magnetic wreaths and buoyant magnetic loops evolving from small-scale wreath sections amplified by turbulent intermittency, in the convective dynamo simulation (case S3) of Nelson et al. (2013). a Field line rendering of magnetic wreaths at low latitudes. Field lines are colored by $B_{\phi }$ (netative in blue, positive in red) to highlight the two wreaths present. b Zoom-in on region indicated in a showing field line tracings of the core of the buoyant magnetic loops at the same instant colored by magnitude of B (weak fields in purple, intense fields in green). Volume rendering shows $B_{\phi }$ using the same color scheme as in (a). c The same region 4 days later, showing the continued rise of the loops through the stratified domain and their expansion.

By identifying a sample of 158 such buoyant loops in the course of the convective dynamo simulation, Nelson et al. (2014) analyzed the statistical trends in the properties of the buoyant loops. The buoyant loops clearly show a hemisphere polarity orientation preference in accordance with Hale’s polarity law for solar active regions, although showing a slightly higher rate of violations. The buoyant emerging loops are measured to have a mean latitudinal tilt of $7.3^{\circ }$, with the leading side (in the direction of rotation) closer to the equator than the following side, consistent with the sense and the magnitude of the observed mean tilt of solar active regions. The measured tilt angles show a wide range of scatter similar to the observed active region tilts. The buoyant loops also show a distribution of twist that is peaked at a value that is consistent with the observed hemisphere preferred sign and magnitude of the mean twist of solar active regions. Whether the loops rise to the top of the domain does not seem to depend on the twist values. The results from the lowest diffusivity convective dynamo simulation described in Nelson et al. (2011, 2013, 2014) clearly indicate the key roles turbulent convection plays in both the generation and the transport of super-equipartition buoyant flux ropes in the bulk of the solar convection zone, unlike much of the previous studies of buoyant magnetic flux, which generally considered convection as a purely disruptive process.

In another study, Fan and Fang (2014) have carried out a 3D anelastic MHD simulation of a convective dynamo in a model solar convective envelope extending from $0.72 R_{\odot }$ at the base of the convection zone to $0.97 R_{\odot }$, rotating at the solar rotation rate $\varOmega _{\odot }$, and without a stably stratified overshoot region at the base. In this simulation, the convection is driven by the heating due to the divergence of the solar radiative diffusive heat flux in the solar convection zone. The resulting convective dynamo is found to maintain a large-scale mean magnetic field that undergoes irregular polarity reversals. The mean axisymmetric toroidal magnetic field is of opposite signs in the two hemispheres, and is more concentrated towards the bottom of the convection zone compared to the magnetic wreaths in the convective dynamos of Nelson et al. (2013). It is found in this convective dynamo simulation at the solar rotation rate $\varOmega _{\odot }$, that the presence of the magnetic fields plays a critical role in the self-consistent maintenance of a solar-like differential rotation, without which the convective flows drive a differential rotation with a faster rotating polar region. The magnetic fields have an effective role of an enhanced viscosity, which suppresses the amplitude of the large-scale convective motions such that they become more rotationally constrained (lower Rossby number) to produce the necessary angular momentum transport to drive a solar-like differential rotation.

It is also found that in the midst of the turbulent fields, there are relatively coherent bundles of buoyant loops with strong super-equipartition toroidal field strengths relative to the mean kinetic energy of convection at that depth (Fig. 33e, f), which rise to the top of the domain and produce active region like flux emergence events. An example of such an emerging flux region is shown in Fig. 33, marked by an arrow. The emerging region is characterized by a diverging bipolar pattern in the radial field $B_r$ (panel (a)), with the leading polarity tilted towards the equator, and the emergence of a strong super-equipartition longitudinal field patch reaching a peak field strength of 9800 G (panel (b)). It corresponds to an up flow region in $v_r$ (panel (c)), but the upward velocity ($\sim 50$ m/s) is not significantly different from that of the other up flow convective cells. The zonal velocity $v_{\phi }$ of the emerging region shows a diverging pattern, and when averaged over the emerging region, is $\sim 100$ m/s faster than the mean zonal velocity of that latitude.

Fig. 33

Image reproduced with permission from Fan and Fang (2014), copyright by AAS

Panels a–d show respectively snapshots of $B_r$, $B_{\phi }$, $v_r$, and $v_{\phi }$ at a shell slice at the depth of 30 Mm below the photosphere, displayed on the full sphere in Mollweide projection. Panels e and f show respectively 3D views of the magnetic field lines and the equipartition field iso-surfaces of $v_a / v_{\mathrm{rms}} = 1$ with $v_a$ being the Alfvén speed and $v_{\mathrm{rms}}$ being the r.m.s. convective velocity for the corresponding depth.

Fan and Fang (2014) has done a statistical study of the tilt angles of the horizontal fields in the super-equipartition emerging field areas at $r = 0.957 R_{\odot }$ near the top, for a period of about 1 year centered at a cycle maximum phase. It is found that there is a preference for the longitudinal field in the strong emerging field regions to conform to Hale’s polarity rule by a ratio of 2.4 to 1 in area, and a statistical significant mean tilt angle of $7.5^\circ \pm 1.6^\circ$ from the east-west direction for the emerging horizontal fields, consistent with the sense and magnitude of the active region mean tilt. However, the violation from Hale’s rule is far greater than that observed for solar active regions Stenflo and Kosovichev (e.g., 2012).

Fan and Fang (2014) showed that the coherent emerging flux bundles of super-equipartion field strengths (see e.g. Fig. 33e) are not isolated flux tubes rising from the bottom of the CZ. They are the product of continued shear amplification by the giant-cell convection. The fact that the emerging flux has a prograde zonal speed relative to the mean zonal speed of the local latitude indicates that it is not a toroidal flux tube rising in isolation from the bottom of the CZ. Because if it were it would have a retrograde flow due to angular momentum conservation as is found in many previous studies of isolated rising flux tubes in the rotating solar CZ (e.g., Caligari et al. 1995; Weber et al. 2013; Fan 2008). It has been pointed out that the retrograde motion of the tube plasma with respect to the local rotation rate is in direct contradiction to the observation that sunspots rotate faster than the local plasma, and is one of the main difficulties associated with explaining active region and sunspot fields as buoyantly rising flux tubes from the bottom of the solar convection zone. Here the coherent emerging flux bundles generated by the convective dynamo in the bulk of the convective envelope are continually amplified by the differential rotation and the local shear by the giant cell convection against resistive dissipation, and are well coupled to the local giant-cell convective flows. Because of the positive correlation of the radial and longitudinal velocities for the giant-cell convection in the low latitude region of the convective envelope, the magnetic loops have the tendency to develop a forward leaning shape towards the direction of rotation, as shown in the r-$\phi$ slices in Fig. 34. It can be seen in the top panel (a) that the emerging flux bundle approaching the top boundary at about 200 deg longitude (corresponding to emerging flux region indicated with the arrow in Fig. 33), is sheared by the local prograde-moving giant-cell flow into a “hairpin” shape with the leading end of the emerging flux bundle pushed against the down flow lane of the giant cell. A similar “hairpin” shaped emerging flux bundle (with the opposite longitudinal field at the top) whose leading end is pushed against a strong downflow lane can also be seen at about the same longitude location in the southern hemisphere slice in panel (b). Such an arrangement of the emerging flux in relation to the giant-cell flow pattern is found to cause the earlier formation of the stronger and more coherent leading sunspots of an active region as shown in the near-surface layer 3D MHD simulations of flux emergence by Chen et al. (2017) (see Sect. 9).

Fig. 34

r-$\phi$ slices of the longitudinal magnetic field $B_{\phi }$ and the $(v'_r, v'_{\phi })$ velocity vectors, where $v'_r$ and $v'_{\phi }$ are the fluctuating parts (with the longitudinal averages subtracted) of the radial and the longitudinal velocities. a is the r-$\phi$ slice through the center of the strong emerging flux bundle indicated with arrow in Fig. 33e, at about $11^{\circ }$ latitude. b is the r-$\phi$ slice at about $-5^{\circ }$ latitude in the southern hemisphere. These slices are made from the same convective dynamo simulation of Fan and Fang (2014) at the same time instant as that shown in Fig. 33

However it should be cautioned that there are major unresolved issues with the current 3D global-scale simulations of the solar convection zone, such as those discussed above. One such issue is the so called “convective conundrum” (see review in O’Mara et al. 2016). Observational estimate based on time-distance helioseismology (Hanasoge et al. 2012, 2016) has suggested an upper bound for the velocity amplitude for the large-scale convection (with $l < 60$, where l is the spherical harmonic degree) that is more than an order of magnitude smaller than the giant-cell convection velocities typically obtained from modern high-resolution global solar convection simulations (e.g. Miesch et al. 2008), which are similar to what are obtained in the above solar convective dynamo simulation (Fan and Fang 2014). It appears that the convective velocities required to transport the solar luminosity in global models of solar convection are systematically larger than those required to maintain the solar differential rotation and those inferred from solar observations (O’Mara et al. 2016), although the most recent unprecidentedly high-resolution simulations of the global solar convection zone is showing promising results that may resolve this difficulty (Hotta and Kusano 2021). Furthermore, the ab initio global convective dynamo simulations are still far from being able to produce a large-scale mean field that reproduces the basic solar cycle behavior, and the result continues to show significant changes when the numerical resolution and the Reynolds numbers are increased (e.g. Hotta et al. 2016).

Implications of near-surface-layer simulations of active region formation and helioseismic investigations of emerging flux

Evolution in the top layer of the solar convection zone and the photosphere

The domains of global-scale 3D MHD simulations of rising flux tubes or convective dynamo in the solar convective envelope have so far been extending from the bottom of the convection zone to about 30 to 20 Mm depth below the photosphere (e.g., Fan 2008; Jouve et al. 2013; Nelson et al. 2013; Fan and Fang 2014; Hotta et al. 2016). Because of the rapid decrease of the various scale heights in the top layer of the solar convection zone which demands increasing numerical resolution, global-scale 3D MHD simulations that encompass the entire convection zone all the way to the photosphere have not been achieved, although promising efforts toward that are underway (e.g., Hotta and Iijima 2020). Furthermore, there is an increased complexity in the physics of the top layer of the solar convection zone. The thermodynamics of the plasma is complicated by ionization effects and the radiative exchange is expected to play an important role in the heat transport (see review by Nordlund et al. 2009). The anelastic approximation breaks down because the plasma flow speed is no longer slow compared to the sound speed. Therefore it is not straightforward to connect the properties of the emerging flux from the global convection zone simulations, whose upper boundaries are at about 20 Mm below the photosphere, to the observed properties of solar active regions and sunspots. The emergence of magnetic flux through the uppermost layer of the convection zone and further into the stably stratified solar atmosphere needs to be investigated by fully compressible MHD simulations, taking into account the complex physics in the near-surface convective and atmosphere layers (see review by Cheung and Isobe 2014).

Significant progress has been made in recent years in realistic 3D radiation MHD simulations of magneto-convection and emerging magnetic flux through the topmost 30 Mm of the solar convection zone and the overlying photospheric layer to model active region and sunspot formation, incorporating the physics of partial ionization and radiative transfer (see, e.g., Cheung et al. 2010; Stein and Nordlund 2012; Rempel and Cheung 2014; Chen et al. 2017). These simulations have produced results that can be directly compared with photospheric observations of the solar active region formation and evolution. Also note that most of these near-surface-layer simulations (except Stein and Nordlund 2012) have ignored the rotational terms in the equations because of the relative short time scales of the processes studied compared to the solar rotation period.

Cheung et al. (2010) carried out the first 3D radiation MHD simulation of the formation of a solar active region at the solar surface using the MURaM MHD code in a simulation domain that spans $92\,\mathrm{Mm} \times 49\,\mathrm{Mm}$ in the horizontal directions and 8.2 Mm in the vertical direction with the lower boundary located at 7.5 Mm below the photosphere. The emerging flux is provided by imposing at the lower boundary the kinematic advection of the top half of a twisted magnetic torus of $7 \times 10^{21}$ Mx into the domain with a vertical rise speed of 1 km/s. Due to the strong stratification of the top layer of the convection zone, the rise of the magnetic flux is accompanied by a strong lateral expansion, which leads to a scaling relation between the plasma density and the magnetic field strength of $B \propto {\rho }^{1/2}$. Due to the fragmentation of the rising magnetic torus and the undulation of the field lines by the convective flows, the emergence of magnetic flux at the photosphere first appears as an extended area of a mixed polarity pattern with small-scale bipoles that emerge with a systematic orientation. It is shown that granular convection plays an important role in causing the reconnection of the submerged U-loops of the serpentine field lines to remove heavy plasma and allow the emergence of the flux into the atmosphere (see e.g. Fig. 37 in Cheung and Isobe 2014). With time, due to the magnetic tension from the subsurface roots of the emerging flux, the opposite polarity magnetic elements at the surface counterstream and coalesce to their corresponding polarity concentrations, leading to the formation of coherent pores and sunspots with kilo-Gauss field strengths. Such flux emergence pattern and evolution are consistent with photospheric observation of emerging active regions.

Rempel and Cheung (2014) extended the simulation of Cheung et al. (2010) by using a larger ($147\,\mathrm{Mm} \times 74\,\mathrm{Mm}$ in horizontal dimensions) and deeper (reaching a depth of 15.5 Mm below the photosphere) domain and an untwisted emerging magnetic torus with a larger total flux of $1.7 \times 10^{22}$ Mx. Furthermore, they included a field-aligned flow of 500 m/s in the emerging magnetic torus (in addition to its upward advection speed of 500 m/s at the lower boundary), to investigate the effect of the retrograde flows along the apex of the emerging loops predicted by previous simulations of rising flux tubes from the bottom of the convection zone due to the conservation of angular momentum (Caligari et al. 1995; Weber et al. 2011; Fan 2008). It is found that even in the absence of twist, the magnetic flux is able to rise through the 15.5 Mm of the convection zone and emerge into the photosphere to form sunspots. The presence of the field-aligned retrograde flow in the emerging magnetic torus leads to an asymmetric formation of the sunspot pair, with the leading spot being more axisymmetric and coherent (consistent with observations), but also forming later compared to the following spot, which is opposite to the observed behavior of the majority of active regions. The presence of sustained outflows from the center where the leading spot is to develop, driven by the stronger inflow of mass through the leading foot point of the emerging torus at the lower boundary (due to the presence of the torus-aligned retrograde flow) delays the formation of the leading spot.

Chen et al. (2017) have further extended upon the works of Cheung et al. (2010) and Rempel and Cheung (2014) to simulate the sunspot and active region formation resulting from the emergence of the coherent buoyant flux bundles generated in a global-scale convective dynamo simulation (Fan and Fang 2014). Instead of advecting an idealized magnetic torus, they have used the magnetic and velocity fields extracted from a horizontal slice (at 30 Mm depth) near the top boundary of the solar convective dynamo simulation, centered on the emerging region indicated in Fig. 33, to drive the emerging flux at the lower boundary of the realistic radiation MHD simulations of the top layers of the convection zone with the MURaM code. The simulations show that the emerging flux bundles rise with the mean speed of convective upflows and fragment into small-scale magnetic elements that further rise to the photosphere, where bipolar sunspot groups are formed through the coalescence of the small-scale magnetic elements. The formation of the sunspot groups reproduces the morphological asymmetries of the observed solar active regions, where the leading polarity sunspots form earlier and are more coherent, less fragmented compared to the following polarity spots. It is found that sunspots tend to form above the downflow lanes of the giant-cell convection imposed at the lower boundary, and a well-formed sunspot is mostly a monolithic magnetic structure that is anchored in a persistent deep-seated downflow lane. As shown in the evolution in the subsurface vertical slice through the developing bipolar sunspot pair in Fig. 35, the prograde flow which pushes the leading end of the emerging flux bundle closer to the downflow lane seen in the convective dynamo (Fig. 34) is carried into the near-surface layer domain, similarly causing the apex and the leading side of the emerging loops to be closer to the strong downdraft. This results in a greater amplification of the vertical magnetic field in the leading side of the emerging loops and hence the earlier formation of the leading polarity sunspot (see panels (b)–(d)).

Fig. 35

Image reproduced with permission from Chen et al. (2017), copyright by AAS

Magnetic field strength $|\mathbf{B}|$ in a vertical slice through the emerging flux bundle. Arrows show the direction of the velocity vectors in the x-z slice. Note that the length of the arrows does not correspond to the speed of the flow.

Chen et al. (2017) have carried out the simulations using different domain sizes with the horizontal width varying from 98 Mm to 196 Mm and the depth varying from 8 Mm to 32 Mm. It is found that the asymmetric formation of the sunspot groups is a robust result with the asymmetry being more pronounced in the simulation with the largest and deepest domain.

Stein et al. (2011) and Stein and Nordlund (2012) have also carried out realistic radiation MHD simulations of active region formation in the top layer of the convection zone (using a domain of 48 Mm wide by 20 Mm depth), where a minimally structured, uniform, untwisted, horizontal magnetic field is advected into the domain by inflows at the lower boundary. The influence of solar rotation on the convective motions is included via f-plane rotation at a latitude of $30^{\circ }$ north. The simulation of Stein and Nordlund (2012) is a particularly interesting case, where the uniform, untwisted, horizontal magnetic field advected into the domain at the bottom boundary at 20 Mm depth is of a relatively weak field strength of only 1   kG, and thus the emerging magnetic flux rises to the surface with speed not significantly different from the convective upflows. It is found that the emerging flux is undulated by the up and down flows of convection to produce a hierarchy of magnetic loops with a wide range of scales, with smaller loops riding “piggy-back” on larger ones. Eventually a large loop approaches the surface and produces an active region with a compact leading spot and more diffuse following spots. The orientation of the active region is approximately aligned with the orientation of the uniform magnetic field at the bottom. As pointed out by Rempel and Cheung (2014), although their simulation did not impose the emergence of a discrete magnetic flux tube at the lower boundary, their imposing a uniform horizontal field (with constant strength and orientation over the course of two days) in the inflows at the lower boundary implicitly assumes the existence of a large-scale, coherent magnetic structure at depths below 20 Mm. The results of the “gentle” flux emergence presented here, where the emerging flux rises with a speed not significantly different from the convective upflows and where the convective downflow lanes of the largest convective cells strongly influence the location for sunspot formation, are consistent with the results by Chen et al. (2017) of active region formation resulting from the emergence of coherent flux bundles generated by the convective dynamo. These results are also supported by the constraints put forth by the helioseismic investigations of the properties of the subsurface active region emerging flux (Sect. 9.2).

Helioseismic constraints of the subsurface emerging flux

Local helioseismology (see review by Gizon and Birch 2005), which uses acoustic wave propagation to probe the solar interior, is a tool that can be applied to potentially measure and detect the dynamic signatures associated with the subsurface active region emerging flux before it appears at the surface. However, because of the high plasma $\beta$ and the extremely subsonic motions expected of the rising flux tubes in most of the solar convection zone (except when they reach the very top layer where sunspots form), detecting their pre-emergence signatures through wave travel-time perturbations at a deep depth of $\sim 30$ Mm is estimated to be extremely difficult (e.g., Birch et al. 2010).

Several local helioseismic studies of emerging active regions have reported isolated events where pre-emergence seismic signatures were detected, however so far the results have not been definitive (see an overview of these in Birch et al. 2013). To reduce the uncertainties, Birch et al. (2013) have taken a statistical approach and applied helioseismic holography to a large number (over 100) samples of two types of regions, pre-emergence and without emergence as control, to determine the statistically significant average signatures of the pre-emergence regions compared to the control population. The measured results place strong constraints on models of active region emergence. They rule out the presence of any significant large-scale retrograde flow exceeding 15 m/s at 20 Mm depth for the emerging flux, expected by the simulations of a magnetic buoyancy dominated flux tube rising from the bottom of the convection zone (e.g., Caligari et al. 1995; Weber et al. 2011; Fan 2008). They also indicate that the rapid emergence process simulated by Cheung et al. (2010), which predicts horizontal diverging flows of order km/s extending over tens of Mm in the top layer of the convection zone, is not typical for the observed emerging active regions. The model that is most compatible with the observation is the “gentle” convection determined active region formation described in the simulation of Stein and Nordlund (2012).

Birch et al. (2016) have carried out a further study where they combine the measurements of surface horizontal flows using both helioseismology and local correlation tracking of granulations, together with realistic simulations of near-surface layer active region formation to constrain the physical conditions of the subsurface rising magnetic flux concentrations that give rise to active regions. Using observations from the Helioseismic and Magnetic Imager (HMI) on the Solar Dynamic Observatory (SDO), they measured the surface horizontal flows associated with 70 selected emerging active regions, paired with 70 corresponding regions with no flux emergence as control to determine the flow signatures due to flux emergence. It is found that at 3 hours before the surface emergence, the helioseismically inferred near-surface flows are dominated by the supergranular-scale convective flows. On average, there is not a statistical significant radial outflow from the emergence site detected associated with the magnetic flux emergence. For comparison, near-surface layer simulations of active region formation were carried out that used a set up similar to that of Rempel and Cheung (2014) but with a varying imposed rise speed for the emerging magnetic torus at the lower boundary, ranging from 70 to 500 m/s. The simulations show that the pre-emergence radial out flow at the surface depends on the rise speed of the emerging flux imposed at the lower boundary. In order for the pre-emergence radial out flow at the surface to be compatible with the observed result of no detectable significant outflow at 3 hours before the surface emergence time, the rise speed for the emerging flux at the lower boundary depth of about 20 Mm needs to be below the maximum speed for the convective upflow, about 140 m/s. This observational constraint is compatible with the model of active region formation resulting from the emergence of the convective dynamo generated emerging flux bundles described in Chen et al. (2017) and the “gentle” convection determined active region formation scenario described in Stein and Nordlund (2012). In both of these models, convection strongly influence the locations of sunspot formation.

Through a similar statistical observational study, Birch et al. (2019) extended the work of Birch et al. (2016) and measured the spatial variation and temporal evolution of the average near-surface flows before and during the emergence of the active regions. They found that in the day before emergence, active region emergence is preceded by an east-west elongated converging flow of an amplitude of about 40 m/s that is located to the east (the retrograde direction) from the emergence location. They suggest that this result may be explained if the emergence locations are related to the supergranulation-scale converging flow regions. The nature of such a pre-emergence flow pattern needs to be investigated in future near-surface-layer flux emergence simulations.

Simulations that encompass the deep convection zone and the near-surface layer

Hotta and Iijima (2020) have carried out the first radiation MHD simulations of a rising magnetic flux tube and the resulting active region formation in a deep domain that encompasses the entire depth of the convection zone, extending from the base of the convection zone at 200 Mm depth to the photosphere, including the realistic physics of ionization effects, radiative energy transport, and compressible convection of the near-surface layer. Such a whole-convection-zone simulation is achieved by using the RSST numerical approach (Sect. 2.3). It avoids the artificial effects of an imposed lower boundary condition in the previous near-surface layer simulations of active region formation and enables the natural two-way coupling between the deep convection zone and the near surface layer. The simulation domain has horizontal widths of 98 Mm and extends vertically from the bottom of the convection zone to 700 km above the photosphere. A horizontal force-free twisted flux tube with an axial field strength of 10 kG and a flux of $10^{22}$ Mx is inserted into the evolved convection at the depth of 35 Mm in the domain. It is found that the flux tube is undulated into an $\varOmega$-shaped structure by two strong anchoring downflows and a broad upflow in the central region. The central portion of the $\varOmega$-shaped flux bundle rises buoyantly to the photosphere and the emerged flux elements are then coalesced to form two coherent sunspots whose concentrated fluxes are rooted in the two deep downflows with the deeper root reaching 80 Mm depth. The morphology of the formed sunspot is found to follow the morphology of the downflow lane in which the sunspot flux is rooted. This property is also found in the simulation of sunspot formation driven at the lower boundary with the emergence of the convective dynamo generated flux bundles and the associated giant-cell convective flows Chen et al. (2017).

The simulation by Hotta and Iijima (2020) found that the rise speed of the apex of the $\varOmega$-shaped flux tube tends to be larger than the typical upward convection velocity because of the growth of the buoyancy in the flux tube caused by the suppression of mixing by the magnetic field with the surrounding super-adiabatically stratified convecting fluid. Differing from the constrain obtained from the study of Birch et al. (2016), the simulation shows that the rising speed of the flux tube exceeds 250 m/s at a depth of 18 Mm, without incurring an observable divergent flow at the surface 3 hours before the onset of flux emergence, whereas Birch et al. (2016) put an upper limit of 150 m/s for the rise speed of the flux tube at the depth of 18 Mm in order to satisfy the observation of no observable significant divergent flow at 3 hours before active region flux emergence. Hotta and Iijima (2020) suggested that the discrepancy is caused by the imposed lower boundary condition of the near-surface layer simulations in Birch et al. (2016) where a uniformly upward rise speed is prescribed for the entire magnetic torus, which might have a stronger impact at the surface compared to the $\varOmega$-shaped tube in the deep domain simulation for which the flow structure contains both upflows and downflows naturally developed under the influence of the convection.

In a similar realistic radiation MHD simulation of active region formation in a deep convecting domain (98 Mm horizontal widths and vertically extending from a depth of 140 Mm below the photosphere to 700 km above), Toriumi and Hotta (2019) successfully modeled the spontaneous formation of $\delta$-sunspot active regions. Similar to Hotta and Iijima (2020), a force-free left-hand-twisted flux tube is inserted into the evolved (hydrodynamic) convection at a depth of 16.7 Mm. As illustrated in Fig. 36, because of the pattern of convection at the location of the flux tube, two $\varOmega$-shaped rising segments develop and rise to the photosphere to form two bipolar emerging regions with flux concentrations P1 and N1, and P2 and N2. Since the legs of the two adjacent $\varOmega$-loops are connected below the surface as U-loops which are pushed downward by the convective downflows, the legs approach each other, causing the collision of the opposite polarity spots N1 with P2, and N2 with P1. This results in the formation of two compact $\delta$-sunspots N1-P2 and N2-P1, each containing opposite polarity umbrae with a shared penumbra (see the two bottom left panels for $t=42.3$ hr in Fig. 36). The $\delta$-sunspots formed in the simulation reproduce several key observed features of the observed flare-productive $\delta$-sunspots. The colliding opposite polarity umbrae of the $\delta$-spot show coherent rotational motions as a result of unwinding of the subsurface twisted flux tubes, causing strong velocity shear and producing strong sheared horizontal magnetic field reaching 4 KG at the polarity inversion line (PIL) of the $\delta$-spot. A magnetic channel with a pattern of alternating elongated positive and negative polarities also develops at the PIL.

Fig. 36

Image reproduced with permission from Toriumi and Hotta (2019), copyright by AAS

Time sequence snapshots of (column 1) the emergent intensity normalized by the quite-Sun value ($I/I_0$), (column 2) the vertical magnetic field $B_z$ sampled at $\tau = 1$, (column 3) the vertical velocity ($V_z$) at the initial depth of the inserted flux tube, and (column 4) the absolute field strength averaged over a range in the y-direction and normalized by the local background density. Turquoise contours in column 1 indicate where the smoothed intensity is less than $I/I_0 = 0.45$ (umbra) and 0.9 (penumbra). Black contours in column 3 show where $|B| = 5$ and 10 kG. The two emerging bipoles P1-N1 and P2-N2 collide to form the two $\delta$-spots N1-P2 and N2-P1.

The results of Hotta and Iijima (2020) and Toriumi and Hotta (2019) further stress the importance of the interaction between the emerging magnetic flux and turbulent convection in determining the locations of sunspot formation and the properties of the active region that forms. The multi-buoyant segment scenario modeled by Toriumi and Hotta (2019) suggests that the formation of flare and eruptive active regions may be a stochastically determined process.

Summary and discussion

For some time, a prevailing picture has been that solar active region magnetic flux originates from a strong toroidal magnetic field stored in the overshoot region at the base of the convection zone, generated by a deep seated solar dynamo process. Consequently, a large body of theoretical, numerical and observational studies has been devoted to addressing the processes of how the toroidal flux is destabilized and rise through the convection zone to the photosphere to form the observed solar active regions. These studies have provided insights into the origin of several observed properties of solar active regions, such as the various asymmetries between the leading and the following polarities of an active region (Sects. 5.1, 9.1) and the active region magnetic twist (Sects. 5.2). However they have also raised new questions and difficulties with the picture of active regions as magnetic buoyancy dominated rising flux tubes originating from the bottom of the solar convection zone.

If the solar cycle dynamo generates toroidal magnetic field at the base of the convection zone, the strength B of this field remains uncertain. Whether B is significantly greater than or comparable to $B_{\mathrm {eq}}\sim 10^4 {\mathrm {\ G}}$, which is the field strength in equipartition with the kinetic energy density of the convective motions, will critically affect the formation, dynamic evolution, and properties of the emerging active region flux tubes. As was described in Sect. 5.6, for a buoyant flux tube with $B \gtrsim (H_p / a)^{1/2} B_{\mathrm {eq,downflow}}\sim 3 B_{\mathrm {eq,downflow}}$, the magnetic buoyancy force of the flux tube dominates the hydrodynamic force of the strongest downdrafts, and the flux tube can rise not significantly affected by convection. On the other hand, for $B_{\mathrm {eq,downflow}}\lesssim B \lesssim 3 \times B_{\mathrm {eq,downflow}}$ the strong convective downdrafts can overcome the magnetic buoyancy and hence plays a significant role in affecting the dynamics and structure of the emerging $\varOmega$-shaped tubes. Thin flux tube simulations of emerging flux loops in the solar convective envelope (Sect. 5.1) suggest that the toroidal magnetic fields at the base of the solar convection zone is in the range of about $4 \times 10^4$ to $10^5 {\mathrm {\ G}}$, significantly higher than the equipartition field strength, in order for the emerging loops to satisfy the Joy’s Law trend for the active region mean tilt angles as well as the observed amount of scatter of the tilt angles about the mean Joy’s Law behavior. However, there are major difficulties associated with explaining active regions as rising flux tubes in such magnetic buoyancy dominated regime (with $B \sim 10^5$ G at the base of the convection zone) as listed in the following:

• (1) The retrograde flow of $\sim 100$ m/s for the tube plasma at the apex of the emerging loop found in both the thin flux tube simulations (Sect. 5.1.4) and 3D MHD simulations (Sect. 5.4), due to the conservation of angular momentum of the rising flux tubes from the bottom of the convection zone, is not detected by helioseismic investigations of subsurface emerging active regions (Sect. 9.2).

• (2) The minimum magnetic twist rate required to counteract the vorticity generation by the magnetic buoyancy, which tends to break up the buoyant flux tube and suppress its rise, is too high compared to the observed mean twist of the majority of solar active regions (Sect. 5.3), and furthermore drives a tilt opposite to the observed active region mean tilt if the twist sign follows the observed hermisphere preference (Sects. 5.4, 5.6.3).

• (3) The mean-field flux-transport dynamo models which take into account the dynamic effects of the Lorentz force from the large-scale mean fields have shown that the toroidal magnetic field generated at the base of the solar convection zone is $\sim 1.5 \times 10^4$ G (Rempel 2006), significantly below the field strengths suggested by the thin flux tube simulations for active region progenitor flux tubes. Nevertheless, the amplification of a toroidal magnetic field by conversion of potential energy associated with the superadiabatic stratification of the convection zone may be a means to reach field strength that is significantly above the equipartition value (Sect. 7).

The need to put the site for the generation and storage of the strong toroidal magnetic field, responsible for the formation of solar active regions, to the overshoot layer at the bottom of the solar convection zone has been put in question (Sect. 8, see also Brandenburg 2005; Charbonneau 2020). Recent global 3D MHD convective dynamo simulations have shown that a large-scale mean magnetic field that shows some aspects of the solar-like cyclic behavior can be generated entirely within the convective envelope without an overshoot layer (see review by Charbonneau 2020). Some of these simulations with sufficiently low magnetic diffusivity have shown the self-consistent formation of buoyant emerging flux bundles with super-equipartition field strengths in the bulk of the convection zone, with characteristics suitable as the progenitors of solar active regions (Sect. 8). It is found that these coherent super-equipartion-strength flux bundles are the result of continued amplification by turbulent intermittency or giant-cell convection shear. They rise at a speed not significantly different from the typical convective upflow speed and move prograde with the local giant-cell convective flows, and hence avoiding the difficulty (1) above. The emerging flux bundles tend to develop a forward leaning shape towards the direction of rotation with their leading ends pushed closer to the down flow lane of the giant-cell. Such an arrangement of the emerging flux bundle in relation to the giant-cell flow pattern is found to cause the earlier formation of the more coherent leading sunspot of an active region as shown in a near-surface layer 3D radiation MHD simulation of active region formation (Chen et al. 2017, Sect. 9). It also appears that such convection generated emerging flux bundles do not show a magnetic twist that is too high compared to the observed mean magnetic twist of solar active regions (Nelson et al. 2014, Sect. 8) and therefore avoids the difficulty (2) above. However it should be emphasized that the global convective dynamo simulations are still far from being able to produce a large-scale mean field that reproduces the basic solar cycle behavior, and that the result continues to show significant changes when the numerical resolution and the Reynolds numbers are increased (e.g. Hotta et al. 2016). Thus the question with regard to where the active region flux is generated remains uncertain.

Significant advances in realistic radiation MHD simulations of active region formation, and helioseismic investigations of emerging active regions have provided new insights into the properties of the subsurface emerging flux (Sect. 9). These studies suggest the “gentle” flux emergence picture, where the emerging flux rises with a speed not significantly different from the convective upflows and where the convective downflow lanes of the largest convective cells strongly influence the location for sunspot formation. The most recent radiation MHD simulations of active region formation that encompass the bulk of the convection zone and the near surface layer further stress the important role the interaction between the emerging magnetic flux and turbulent convection plays in determining the locations of sunspot formation and the development of flare productive $\delta$-sunspot active regions (Sect. 10).

The question of whether, or to what extent, a strong toroidal magnetic field stored in the overshoot region at the base of the convection zone, generated by a deep seated solar dynamo process, is responsible for the formation of solar active regions remains to be more rigorously investigated. Simulations of the dynamic rise of buoyantly unstable, active region scale flux tubes in the global solar convective envelope, with the influence of solar rotation, have mainly resorted to the thin flux tube model (Sect. 5.1), due to the insufficient numerical resolution to resolve such active region scale flux tubes at the base of the solar convection zone by the global 3D MHD models, which have so far only considered initial toroidal flux tubes with fluxes much larger than those of typical active regions (Sects. 5.4, 5.6.3). Global-scale 3D MHD simulations of the solar convective envelope with the presence of both the turbulent magnetic fields and convection (e.g., those in Sect. 8), and with an adequate resolution to resolve active region scale flux tubes at the bottom of the solar convection zone, are needed to investigate whether a buoyantly unstable toroidal magnetic field at the bottom of the convection zone can rise to the surface as emerging flux consistent with the properties of solar active regions. Such investigations are becoming feasible with the recent advances in the 3D computational MHD models of the solar convection zone (e.g., Hotta et al. 2016; Hotta and Iijima 2020).

On a connected subject, the modeling of rising flux tubes in stellar outer convection zones have been carried out to understand the properties of starspots and stellar dynamos. For a review on this area of research, the readers are referred to the Living Review in Solar Physics article by Berdyugina (2005).