Abstract
The quiet Sun is the region of the solar surface outside of sunspots, pores, and plages. In continuum intensity it appears dominated by granular convection. However, in polarized light the quiet Sun exhibits impressive magnetic activity on a broad range of scales, from the 30,000 km of supergranular cells down to the smallest magnetic features of about 100 km resolvable with current instruments. Quiet Sun fields are observed to evolve in a coherent way, interacting with each other as they are advected by the horizontal photospheric flows. They appear and disappear over surprisingly short time scales, bringing large amounts of magnetic flux to the solar surface. For this reason they may be important contributors to the heating of the chromosphere. Peering into such fields is difficult because of the weak signals they produce, which are easily affected, and even completely hidden, by photon noise. Thus, their evolution and nature remain largely unknown. In recent years the situation has improved thanks to the advent of high-resolution, high-sensitivity spectropolarimetric measurements and the application of state-of-the-art Zeeman and Hanle effect diagnostics. Here we review this important aspect of solar magnetism, paying special attention to the techniques used to observe and characterize the fields, their evolution on the solar surface, and their physical properties as revealed by the most recent analyses. We identify the main open questions that need to be addressed in the future and offer some ideas on how to solve them.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The quiet Sun is the area of the solar surface devoid of sunspots and active regions. For a long time it was thought to be nonmagnetic, since only the photospheric granulation could be seen in continuum images (Fig. 1, top panel). However, this idea proved wrong: in polarized light, the quiet Sun shows a reticular pattern of intense kilogauss fields called the magnetic network and a myriad of weaker, small-scale flux concentrations in the regions in between them—the solar internetwork (Fig. 1, middle panel).
Quiet Sun fields are intimately connected to supergranulation, the largest convective pattern on the solar surface. Supergranular cells have characteristic diameters of 30,000 km and lifetimes of 1–2 days. They harbor vertical upflows of 30 ms\(^{-1}\) and horizontal flows of 300 ms\(^{-1}\). These properties have been reviewed by Rieutord and Rincon (2010).
The network (Sheeley 1967) outlines the boundaries of supergranular cells, precisely where the horizontal flows turn into downdrafts. Network magnetic fields are organized in discrete, kG flux tubes whose walls expand with height until they merge with adjacent tubes in the chromosphere (Pneuman et al. 1986; Solanki 1993). This forms large flux concentrations, with sizes that often exceed 1\(^{\prime \prime }\). Network patches are persistent and can be followed for hours and even days. During their evolution, they undergo frequent shape changes and interactions with other flux elements and granular flows (Requerey et al. 2015, 2017), which makes the network a highly dynamic region.
The internetwork (IN) closely corresponds to the interior of supergranular cells. IN magnetic fields appear as individual flux concentrations and immediately start to move toward the network, following more or less radial trajectories that are perturbed by the local granulation pattern. These elements have weaker fields, smaller sizes, and shorter lifetimes than network flux concentrations, but they are even more dynamic.
Quiet Sun at disk center as observed by the Hinode spectropolarimeter on 10 March 2007 between 11:37 and 14:37 UT. The top panel shows a continuum intensity map at 630 nm. The other panels display the corresponding maps of longitudinal magnetic flux density (middle) and transverse flux density (bottom). They were derived from the circular and linear polarization signals observed in the Fe i 630 nm line pair. The gray scales saturate at \(\pm 50\) Mx cm\(^{-2}\) and 200 Mx cm\(^{-2}\), respectively. Images reproduced with permission from Lites et al. (2008), copyright by AAS
A significant fraction of the photospheric magnetic flux resides in the quiet Sun. The network contains \((6.8 \pm 1.2) \times 10^{23}\) Mx over the entire solar surface, while the IN harbors \((1.1 \pm 0.2) \times 10^{23}\) Mx (Gošić 2015). This is comparable to the total flux carried by active regions during the maximum of the solar cycle (e.g., \(6 \times 10^{23}\) Mx in cycle 23 according to Jin et al. 2011). Quiet Sun fields are important also for the dynamics and energetics of the solar atmosphere: through processes of emergence and cancellation, they couple the different atmospheric layers and may contribute effectively to the heating of the chromosphere and the corona. These are just some of the reasons why their characterization has been pursued vigorously for almost five decades now.
Quiet Sun fields are difficult to observe because they are organized on small spatial scales, evolve rapidly, produce very weak signals, and their detection requires polarimetric measurements. Thus, progress in this research area has generally been brought about by advances in polarimetric sensitivity and spatial resolution. At the same time, developments in theory and numerical models have helped interpret the observations. The realism of current numerical simulations is now sufficient to allow direct comparisons with observations, a strategy that holds great promise to further our understanding of quiet Sun magnetism. Despite all the tools at our disposal, however, the inherent difficulty of observing the magnetic structures of the quiet Sun has inevitably led to dissenting views and controversies on fundamental aspects, such as the strength and inclination of IN fields. Some of the controversies have already been solved, but others are still a matter of discussion.
This article presents a global description of quiet Sun magnetic fields, their properties, their nature, and the processes whereby they appear and disappear on the solar surface. Since the IN is at the forefront of solar physics research today, we focus on this fascinating but largely unknown component of the quiet Sun, leaving the network for a future update. Our goal is to review the current understanding of IN magnetic fields and the aspects which are still under debate. The capabilities and limitations of the observations and methods used to investigate the quiet Sun are often at the origin of the discrepancies, so we start the presentation with a thorough description of them (Sect. 2). Next, we describe the dynamics and evolution of IN fields (Sect. 3) and their magnetic properties (Sect. 4). In Sect. 5 we offer a unifying picture which could explain the available Zeeman and Hanle observations of the quiet Sun. Finally, we discuss a number of open issues in Sect. 6. Our approach is observational for the most part, as numerical simulations are already covered in detail elsewhere (Stein 2012).
Reviews on the magnetism of the quiet Sun have been presented by, among others, Solanki (1993), de Wijn et al. (2009), Sánchez Almeida and Martínez González (2011), Guglielmino (2012), Martínez Pillet (2013), and Borrero et al. (2017). The reader is referred to these for further information on aspects not dealt with here, such as network fields and flux-tube physics, magnetic fields in the polar regions, and small-scale dynamo action.
2 Characterization of quiet Sun magnetic fields
Solar magnetic fields are best seen in polarized light. The stronger fields generate polarization in spectral lines through the Zeeman effect, while the weaker ones modify the polarization produced by scattering processes via the Hanle effect. By interpreting these signals it is possible to determine the field properties. Indeed, much of our present knowledge about quiet Sun magnetism is based on polarimetric observations of the solar surface. The observations can include the four Stokes parameters (I, Q, U, and V) or only a combination thereof, in one or more spectral lines, and in one or more wavelengths.Footnote 1 For an introduction to solar polarimetry and the Stokes formalism, see Rees (1987), Landi Degl’Innocenti (1992), or del Toro Iniesta (2003).
In this section we summarize the methods used to study quiet Sun magnetic fields via intensity-based magnetic proxies and the Zeeman and Hanle effects, highlighting their strengths and limitations. We also show examples of the type of observations that can be made with current instruments and how they are interpreted. Finally, we discuss the importance of high spatial resolution and the effects of noise in the characterization of vector magnetic fields from weak signals.
2.1 Magnetic proxies
It has long been known that strong magnetic fields in the quiet Sun can be detected as bright structures in intensity measurements taken through selected UV filters (e.g., Chapman 1970). With typical widths of 1 nm, such filters cover spectral regions dominated by temperature-sensitive molecular bands, atomic lines, or both.
Sheeley (1969) used the CN band head at 388.3 nm to investigate the evolution of the photospheric network. At much higher spatial resolution, Muller and Roudier (1984) first observed network elements as tiny bright points in Fraunhofer’s G band, a spectral region around 430.5 nm dominated by absorption lines of the CH molecule. G-band bright points are sub-arcsec (\(\sim \)0\(.{2}^{\prime \prime }\)) structures located in intergranular lanes that have characteristic peak intensities of 1.4 times the quiet Sun intensity (Zakharov et al. 2005). Their mean lifetime is about 10 min, with some elements lasting up to 70 min (Berger et al. 1998b). They turn out to be cospatial with magnetic flux concentrations (Berger and Title 2001). Filtergrams in or near the CN band head also show magnetic elements as bright points (Zakharov et al. 2005; Uitenbroek and Tritschler 2006, 2007; Riethmüller et al. 2010).
The high contrast of magnetic elements in the G band is due to their lower density compared with the external medium, which reduces the abundance of CH molecules and thus the opacity of the gas. Through the more transparent flux concentrations one can see deeper layers (when observing at disk center) or the walls of the granules behind them (when observing near the limb). Both are hotter than the surroundings, producing bright structures (Spruit 1976, 1977). The effect has been confirmed by Schüssler et al. (2003), Carlsson et al. (2004) and Uitenbroek and Tritschler (2006), among others.
For such a process to work the magnetic element must be partially evacuated. This requires a sufficiently strong magnetic field, so the weakest flux concentrations are unlikely to be observed as bright points in molecular bands. However, not all bright points have kG fields. In fact, Sánchez Almeida et al. (2004) detected large amounts of G-band bright points in a quiet IN region, where strong elements should be scarce. Also in the IN, Requerey et al. (2017) observed CN bright points with longitudinal fields significantly weaker than 1 kG. From a simultaneous inversion of seven spectral lines in the visible and near infrared using a free magnetic filling factor, Beck et al. (2007) found that G-band bright points in the granulation area surrounding sunspots show a flat distribution of field strengths spanning the range 500–1500 G. They also found a tendency for the contrast of the bright points to be larger for more vertical fields and ascribed this pattern to the deeper layers reachable within the magnetic element when the line of sight is aligned with its axis. Thus, weak features may be as prominent in the G band as kG features if they show a better alignment with the observer. This can be expected to occur frequently because magnetic elements experience deviations from the vertical due to buffeting by the surrounding granulation (Steiner et al. 1998).
Not only molecular bands, but also photospheric and chromospheric atomic lines including H\(\alpha \) (Dunn and Zirker 1973) and Ca ii K (Mehltretter 1974), as well as selected spectral regions in the UV down to 214 nm (Riethmüller et al. 2010), show intense flux concentrations as bright points. A comparison of some of these diagnostics has been given by Leenaarts et al. (2006), who concluded that the blue wing of H\(\alpha \) is the best option for proxy magnetometry of the quiet Sun. Magnetic elements appear bright in both photospheric and chromospheric layers as demonstrated by, e.g., filtergrams spanning the extended wings of the Ca ii K and H lines. This offers an opportunity to investigate their evolution throughout the atmosphere. Interestingly, imaging observations of magnetic elements at different heights can be used to estimate the magnetic field inclination by comparing their spatial position in at least two layers, as recently done by Jafarzadeh et al. (2014b) using SUNRISE data. This geometrical approach nicely complements more direct inversion techniques, which have difficulties in retrieving the inclination of nearly vertical fields in the presence of noise. However, one must keep in mind that the position of maximum brightness in continuum images does not always coincide with the center of the magnetic structure, since conspicuous intensity enhancements often occur at the periphery of the flux patches. Those brightenings are associated with upflows that develop within the magnetic elements as they interact with the adjacent granular flows (Requerey et al. 2014).
Finally, magnetic elements also appear bright in continuum radiation (Dunn and Zirker 1973). A prominent example recorded by the Hinode spectropolarimeter is shown in the inset of Fig. 6. However, due to the lower contrasts compared with molecular bands and atomic lines, very high spatial resolution and stable image quality are required to use the continuum as a proxy of magnetic elements. For many years, the superb conditions at the Observatoire du Pic du Midi allowed network magnetic elements to be studied using white-light filtergrams (Muller 1983; Muller and Keil 1983). Higher spatial resolution observations are now possible both from the ground (e.g., the Dunn Solar Telescope, the Swedish 1-m Solar Telescope, or the 1.6-m Goode Solar Telescope) and from space (e.g., the Hinode satellite).
In summary, bright points provide a convenient means to identify and follow the evolution of quiet Sun magnetic elements using relatively simple imaging observations. However, it is important to realize that there is no perfect one-to-one correspondence between magnetic fields and brightness: only a fraction of the elements produce bright points and, when they do, the brightness enhancement may disappear well before the flux concentration. This shows that the visibility of bright points depends not only on the properties of the magnetic elements themselves, but also on how those properties change with time (Berger and Title 2001; de Wijn et al. 2008; Requerey et al. 2017).
2.2 The Zeeman effect
2.2.1 Principle
The Zeeman effect is the splitting of spectral lines into several components under the action of a magnetic field (Zeeman 1897a, b). Soon after its discovery in the laboratory, Hale (1908) reported the first observations of split lines (hence of magnetic fields) in sunspots. A historical overview of these two milestones can be found in del Toro Iniesta (1996). The Zeeman effect has since provided us with an invaluable tool for the characterization of solar magnetic fields.
In the presence of an external magnetic field, an atomic level of angular momentum J splits into \(2J+1\) Zeeman sublevels with magnetic quantum numbers \(M= -J, \dots , +J\). Let J and \(J'\) be the lower and upper levels of an absorption spectral line. Transitions between the different magnetic sublevels (with quantum numbers M and \(M'\)) give rise to different Zeeman components. For electric dipole transitions, the appropriate selection rules are \(\varDelta M \equiv M' - M = 0\) and \(\varDelta M = \pm 1\). Transitions with \(\varDelta M =0\) generate the so-called \(\pi \) components, while \(\varDelta M = -1\) and \(\varDelta M = +1\) produce \(\sigma _r\) and \(\sigma _b\) components, respectively. The wavelength shifts of these components are
where e and \(m_{\mathrm{e}}\) represent the charge and mass of the electron, \(\lambda _0\) is the wavelength of the unperturbed line, c the speed of light, B the magnetic field strength, and g and \(g'\) the Landé factors of the atomic levels. In LS coupling,
L and S are the orbital and spin angular momentum quantum numbers, respectively. The \(\sigma _b\) components appear blueward of the unperturbed line, the \(\sigma _r\) components redward of it, and the \(\pi \) components in between the \(\sigma \) components.
In general, the various Zeeman components are elliptically polarized. For a description, see Fig. 3.1 of Landi Degl’Innocenti and Landolfi (2004) and note that it refers to the case of a spectral line in emission. When the magnetic field points to the observer, the \(\sigma _b\) and \(\sigma _r\) components show circular polarization in the clockwise and counterclockwise directions, respectively, i.e., they generate positive and negative Stokes V signals. The \(\pi \) components show no circular polarization. If the field points away from the observer, the circular polarizations of the \(\sigma \) components change sign. This is the so-called longitudinal Zeeman effect.
When the magnetic field is perpendicular to the observer, the \(\sigma \) components display linear polarization parallel to the magnetic field, giving rise to Stokes Q and U, but no Stokes V. The \(\pi \) components are also linearly polarized perpendicular to the magnetic field. This is the so-called transverse Zeeman effect.
The simplest Zeeman pattern, a normal triplet, occurs when either \(J=0\), \(J'=0\), or both Landé factors are equal, in which case there are only one unshifted \(\pi \) component and two \(\sigma \) components displaced from the line center by
Here, g is the Landé factor of the level with non-zero angular momentum, or the common Landé factor of the two levels. The wavelength shift can be rewritten as
with \(\varDelta \lambda _{\mathrm{B}}\) in mÅ, \(\lambda _0\) in Å, and B in G. Since the fine structure of the Zeeman components is usually not resolved, more complicated patterns can effectively be treated as an equivalent Zeeman triplet by substituting the various \(\sigma _r\), \(\sigma _b\) and \(\pi \) components by a single component located at the corresponding center of gravity. For symmetry reasons, the equivalent \(\pi \) component is unshifted with respect to the unperturbed line, and the two equivalent \(\sigma \) components are displaced by
where the effective Landé factor of the transition is defined as
This expression is independent of the coupling scheme (e.g., Landi Degl’Innocenti 1982).
The polarization of the different Zeeman components can be used to determine the orientation of the vector magnetic field relative to the observer, whereas their wavelength separation informs about the field strength. A Stokes V profile with a positive (negative) blue lobe indicates a magnetic field pointing to (away from) the observer. The relation between Stokes V and Stokes Q, U gives the inclination of the field with respect to the line of sight. Finally, the relation between Q and U depends on the azimuth of the vector magnetic field projected on the plane perpendicular to the line of sight. There is a 180\(^\circ \)-azimuth ambiguity, in the sense that fields with azimuths differing by \(180^\circ \) produce exactly the same Q and U signals and are thus indistinguishable.
An important parameter is the ratio between the Zeeman splitting and the Doppler width of the line, \(\varDelta \lambda _{\mathrm{B}}/\varDelta \lambda _{\mathrm{D}}\). The Doppler width can be expressed as
where T represents the temperature of the plasma, c the speed of light, k the Boltzmann constant, and m the mass of the atom, so \(\varDelta \lambda _B / \varDelta \lambda _D \propto g_{\mathrm{eff}} \lambda _0\). This ratio indicates the magnetic sensitivity of a given spectral line. When \(\varDelta \lambda _B / \varDelta \lambda _D \gg 1\), the magnetic splitting is larger than the thermal line width and the individual Zeeman components are clearly separated in the polarization profiles. When that happens, the distance between them is a good indicator of the field strength. With small ratios, the components are not sufficiently separated and their distance cannot be used to derive the field strength. The transition between the two regimes occurs at around \(\varDelta \lambda _B / \varDelta \lambda _D = 1.5\) (Stenflo et al. 1987).
2.2.2 Zeeman measurements
In this section we briefly describe the various types of Zeeman measurements that can be used to investigate the magnetism of the solar photosphere. We will follow a systematic approach from simpler to more complex observations.
2.2.3 Stokes I measurements
Most spectral lines do not show complete Zeeman splitting in the quiet Sun. The \(\sigma \) components are often mixed with the \(\pi \) components in the intensity spectrum, making it difficult to determine the magnetic field strength from their wavelength separation. The only exception is the emission line of Mg i at 12.32 \(\upmu \)m (Brault and Noyes 1983; Bruls and Solanki 1995). This line is formed in the upper photosphere (\(\log \tau _{\mathrm{500}} \sim -2.7\)) and has a modest Landé factor of \(g_{\mathrm{eff}} =1\), but its extremely long wavelength means that the Zeeman components are completely split for fields as weak as a few hundred G. Brault and Noyes (1983) and Zirin and Popp (1989) presented Mg i 12.32 \(\upmu \)m observations of plages taken at the MacMath–Pierce telescope on Kitt Peak. Unfortunately, measurements in the thermal infrared are very challenging and Mg i 12.32 \(\upmu \)m remains a difficult target. Another disadvantage is the low spatial resolution that can be achieved: at 12 \(\upmu \)m, the diffraction limit of a 1.5 m telescope is only 2\(^{\prime \prime }\).
For the other lines, the Zeeman splitting still produces some effects that can be measured. One is the broadening of the intensity profile, which depends on the Landé factor of the transition. The line broadening has been used to set upper limits on the strength of the magnetic field in the very quiet solar photosphere by comparing lines with different magnetic sensitivity. The first attempts by Unno (1959) resulted in a maximum strength of 300 G. Later, Stenflo and Lindegren (1977) analyzed 402 unblended Fe i lines of the solar spectrum and found a dependence of the line width on the Landé factor. Such a relation allowed them to set an upper limit of about 90 G for the ’turbulent’ field of the quiet Sun. Also from magnetic broadening arguments, Solanki and Stenflo (1984) came to the conclusion that plage and network flux tubes have approximately the same field strength in the kG range. The method was abandoned as new, more sensitive techniques became available (e.g., full Stokes polarimetry or the Hanle effect discussed in Sect. 2.5).
Another effect induced by the presence of magnetic fields is line weakening. Absorption lines, especially those of neutral atoms, weaken at the position of small-scale magnetic elements, giving rise to conspicuous line “gaps” or discontinuities in spectrograms (Sheeley 1967; Kneer and von Uexkuell 1991). This is partly due to the Zeeman splitting, which desaturates the line, but also to the different thermal structure of the flux concentrations relative to the surroundings (Chapman and Sheeley 1968). Strong magnetic elements show higher temperatures at the same optical depth and, as a result, the ionization is enhanced, the number of absorbers decreases, and the line weakens. Sometimes the line even disappears from the spectrum, leading to a significant increase in the central intensity (e.g., Lagg et al. 2010). Because of this temperature dependence, it is difficult to determine the properties of the field from measurements of the line weakening. However, the effect has an interesting application: maps of the solar surface taken in the core of neutral atom lines show brightenings at the position of magnetic elements, which makes it possible to identify them without the help of polarization measurements (see examples in Chapman and Sheeley 1968).
Nowadays it is not common to use Stokes I to diagnose quiet Sun magnetic fields. The reason is that the full power of the intensity spectrum can be exploited only in combination with the other three Stokes parameters. In addition, until very recently the intensity profiles observed in the quiet Sun had little asymmetries or other spectral signatures that could be interpreted in terms of magnetic fields. The situation has now changed with the advent of very high spatial resolution data. In any case, Stokes I remains a useful proxy of magnetic fields through the line weakening and enhanced line core intensities mentioned above.
2.2.4 Magnetograph observations
In the early 1950s, Babcock invented the photoelectric magnetograph to measure the circular polarization in the wings of Zeeman-sensitive lines (Babcock 1953). The amplitude of the Stokes V signal can, in principle, be translated into a longitudinal field strength or, more precisely, into a longitudinal magnetic flux if the field is not resolved and occupies only a fraction f of the resolution element (see Sect. 2.2.3 below). The measurements can be taken in one wing only, but it is preferable to observe two or more wavelength positions, symmetrically distributed around the line center, to eliminate the influence of Doppler shifts (at least to first order). The same principle is used by vector magnetographs, the only difference being that they measure the four Stokes parameters to obtain also the transverse component of the field.
One of the most successful magnetographs ever built is the Michelson Doppler Imager (MDI; Scherrer et al. 1995) on board the Solar Heliospheric Observatory (SOHO). This instrument provided seeing-free observations of the solar surface for years, leading to important discoveries despite its relatively modest spatial resolution of 1\(.{25}^{\prime \prime }\). In 2011, MDI was superseded by the Helioseismic Magnetic Imager (HMI; Scherrer et al. 2012) on the Solar Dynamics Observatory (SDO). With a resolution of 1\(^{\prime \prime }\), HMI performs continuous full Stokes observations of the entire solar disk at a cadence of 10 min. Another very successful magnetograph is the Narrowband Filter Imager (NFI; Ichimoto et al. 2008) on board Hinode (Kosugi et al. 2007; Tsuneta et al. 2008). It is capable of measuring the four Stokes parameters in a number of spectral lines at a resolution of about 0\(.{3}^{\prime \prime }\). The seeing-free observations provided by the Hinode NFI make it possible to follow the evolution of the small-scale magnetic elements of network and IN regions with unprecedented accuracy and sensitivity (an example is given in Fig. 11). On the ground, several magnetographs have been or are being operated at the Big Bear Solar Observatory, including a videomagnetograph that was used to investigate the quiet Sun IN thoroughly (e.g., Varsik 1995), a full digital magnetograph (Wang et al. 1998), and the Infrared Imaging Magnetograph (IRIM; Cao et al. 2006). For many years, the highest resolution magnetograms were obtained with the Solar Optical Universal Polarimeter (SOUP; Title and Rosenberg 1981) at the Swedish 1-m Solar Telescope on La Palma (e.g., Berger et al. 2004).
Magnetographs allow a good characterization of the temporal evolution of the magnetic field over large areas. However, they are of limited use for accurate determinations of the magnetic flux because complicated geometries can change the signal in unpredictable ways and the few observables they provide do not allow us to know when that happens. For example, the presence of opposite polarities in the resolution element may reduce the signal, which would lead to a severe underestimation of the flux density without a hint that cancellation is taking place. When complex geometries or large flows occur (as frequently observed at high spatial resolution), full line profiles are to be preferred. Until recently, the only way to obtain such observations was to use grating spectrographs, but in the last few years imaging spectropolarimeters have been developed to bridge the gap between classical magnetographs and spectrographs. Like magnetographs, imaging spectropolarimeters are based on tunable filters, but they can perform line scans with much higher spectral resolution. These instruments provide 2D spectropolarimetric observations suitable for image restoration. Examples of such devices include the Interferometric Bidimensional Spectrometer (IBIS; Cavallini 2006), the Göttingen Fabry–Pérot Interferometer (GFPI; Bendlin et al. 1992, Bello González and Kneer 2008), the CRisp Imaging Spectro-Polarimeter (CRISP; Scharmer 2006), the Visible Imaging Polarimeter working with the Triple Etalon Solar Spectrometer (VIP+TESOS; Beck et al. 2010), and the GREGOR Fabry-Pérot Interferometer (Puschmann et al. 2012). All of them use short exposures to minimize seeing fluctuations. This leads to modest polarimetric sensitivities which are sufficient to study the photospheric network but not the IN. The first imaging spectropolarimeter providing sufficient sensitivity to detect the weak fields of the internetwork was the Imaging Magnetograph eXperiment (IMaX; Martínez Pillet et al. 2011) of the SUNRISE balloon-borne observatory (Barthol et al. 2011). On two occasions, IMaX flew at an altitude of 40 km to avoid the distortions caused by the Earth’s atmosphere, which made it possible to increase the integration time up to 6 s per wavelength point and reach a noise level of \(10^{-3} \, I_{\mathrm{QS}}\) (with \(I_{\mathrm{QS}}\) the quiet-Sun continuum intensity) at a resolution of 0\(.{15}^{\prime \prime }\) (Solanki et al. 2010). The data acquired by IMaX show the evolution and dynamics of internetwork fields with unprecedented detail (e.g., Solanki et al. 2010; Danilovic et al. 2010a; Borrero et al. 2010, and the movie of Fig. 12).
2.2.5 Full Stokes spectropolarimetry
For quantitative inferences of solar magnetic fields and their variation with height one needs measurements of the four Stokes parameters in as many lines as possible, with high signal-to-noise ratios, and high spectral and spatial resolution. This requires the use of grating spectrographs, whose main disadvantage is that the spectrograph slit has to be stepped across the solar surface to create 2D maps. Thus they offer modest cadences when observing large fields of view. However, the disadvantages are more than compensated by the fact that the full line profiles are recorded at once, which leads to excellent spectral integrity. Grating spectropolarimeters allow for simultaneous observations of many spectral lines—often spanning widely separated wavelength ranges—and very long exposure times. The latter do not necessarily mean poor spatial resolution, thanks to the use of adaptive optics systems (on the ground) or the absence of seeing fluctuations (in space).
Historically, the Stokes I and V spectra acquired with the Fourier Transform Spectrometer at the McMath–Pierce telescope on Kitt Peak played a very important role in our understanding of small-scale magnetic elements in the quiet Sun, owing to their extraordinary spectral resolution and low noise (e.g., Stenflo et al. 1984; Solanki and Stenflo 1984). The FTS spectra were obtained through a 10\(^{\prime \prime }\)-circular aperture with integration times of more than 20 min, so they lack spatial and temporal resolution. The Advanced Stokes Polarimeter (ASP; Elmore et al. 1992) at the Dunn Solar Telescope was the first instrument that provided spatially resolved spectropolarimetric observations of the solar surface. Under good seeing conditions, it was able to measure the Fe i 630 nm lines at a resolution of 1\(^{\prime \prime }\). The ASP served as a model for more sophisticated spectropolarimeters, including the Tenerife Infrared Polarimeter (TIP; Martínez Pillet et al. 1999), the Diffraction-Limited Spectro-Polarimeter (DLSP; Sankarasubramanian et al. 2004), the POlarimetric Littrow Spectrograph (POLIS; Beck et al. 2005), the Spectro-Polarimeter for INfrared and Optical Regions (SPINOR; Socas-Navarro et al. 2006), and the GREGOR Infrared Spectrograph (GRIS; Collados et al. 2012).
Most of these instruments focus on polarimetric sensitivity and spatial resolution, rather than multi-line capabilities. Thus, the first simultaneous observations of visible and near-IR lines with TIP and POLIS at the German Vacuum Tower Telescope (VTT) on Tenerife represented a major breakthrough (Khomenko et al. 2005a; Bellot Rubio and Beck 2005; Beck et al. 2007). Spectral lines in the visible and near infrared have different magnetic sensitivities, so it is useful to observe them simultaneously to better constrain the properties of the field (e.g., Cabrera Solana et al. 2005; Martínez González et al. 2008). SPINOR extends the capabilities of TIP and POLIS by allowing the observation of up to 5 spectral lines. A still better wavelength coverage can be obtained with the spectrograph of the THEMIS telescope, which was designed to observe as many as 10 different spectral regions (see López Ariste et al. 2000 and references therein).
Another breakthrough was achieved in 2006 when the spectropolarimeter (SP; Lites et al. 2001, 2013) on board the Japanese Hinode satellite started operations. The Hinode SP performs seeing-free observations of the full Stokes profiles of the Fe i line pair at 630 nm, with a spatial sampling of 0\(.{16}^{\prime \prime }\) and a sensitivity of \(10^{-3} \, I_{\mathrm{QS}}\). As we shall see later, this instrument has greatly advanced our understanding of quiet Sun magnetism.
In the near future, integral field units will revolutionize solar spectropolarimetry. These devices make it possible to observe two-dimensional fields of view with standard grating spectrographs, bringing all their benefits at much faster cadence and the possibility of applying restoration techniques to the acquired images. Two integral field spectropolarimeters are now under construction: the DL-NIRSP (see Tritschler et al. 2016) for the Daniel K. Inouye Solar Telescope and MuSICa (Calcines et al. 2013) for the European Solar Telescope. The first is based on optical fibers, while the second uses an image slicer.
2.2.6 Interpretation
The polarization of Zeeman-sensitive spectral lines depends nonlinearly on the physical properties of the atmosphere in which the lines are formed. Recovering this information from the observed Stokes profiles is not easy. In principle, the complete line transfer problem has to be solved, i.e., the radiative transfer equation must be integrated in a given model atmosphere with appropriate values of the absorption matrix and the source function vector to compute the Stokes spectra that would emerge at the surface (Landi Degl’Innocenti 1992). If the synthetic profiles do not coincide with the observed ones, the model atmosphere has to be changed to improve the fit. This can be done manually or automatically, leading to the concept of Stokes inversions.
Under certain idealized conditions, however, much simpler solutions of the radiative transfer equation exist (Landi Degl’Innocenti and Landolfi 2004). They are commonly used to infer the magnetic field strength from the observations. In what follows, some of them will be discussed because of their historical significance, but also because they illustrate important properties of the Stokes profiles. These approximate solutions have largely been superseded by more sophisticated inversion methods, which we will also consider in detail below. Finally, we will describe methods to separate the magnetic field strength from the filling factor using lines with hyperfine structure.
2.2.7 Strong field regime
When the magnetic splitting is much larger than the line width, i.e., when \(\varDelta \lambda _B / \varDelta \lambda _D \gg 1\), the wavelength separation between the \(\sigma \) components is directly measurable in the circular polarization profiles and can be used to determine the field strength through Eq. (5).
Since \(\varDelta \lambda _B / \varDelta \lambda _D \propto g_{\mathrm{eff}} \lambda _0\), this method is very useful in the infrared, where many spectral lines are almost completely split with relatively modest field strengths. In the case of the \(g_{\mathrm{eff}}= 3\) Fe i line at 1564.9 nm, for example, the strong field regime can be considered to be a good approximation for Stokes V when the field strength exceeds about 500 G (Solanki et al. 1992). Analyses based on the Zeeman splitting of Fe i 1564.9 nm and the nearby Fe i line at 1565.2 nm (\(g_{\mathrm{eff}}=1.53\)) have been presented by, among others, Rabin (1992), Lin (1995), and Khomenko et al. (2003). In all these cases, simple Gaussian fits were performed to determine the field strength from the Stokes V peak separation of the Fe i 1564.9 nm line.
In the strong field regime, the separation between the \(\sigma \) components increases linearly with B, but the amplitudes of the Stokes profiles do not change.
2.2.8 Weak field regime
When the Zeeman splitting is negligible compared with the line width (\(\varDelta \lambda _{\mathrm{B}}/\varDelta \lambda _{\mathrm{D}} \ll 1\)), a series expansion of the absorption matrix, assuming a height-independent field, leads to the following expression for Stokes V (e.g., Jefferies et al. 1989; Landi Degl’Innocenti and Landolfi 2004):
Here, \(\gamma \) is the inclination of the vector magnetic field to the line of sight, \(I_0\) the intensity that would emerge from the same atmosphere with zero magnetic field, and \(\varDelta \lambda _{\mathrm{B}} = 4.6686 \times 10^{-10} \lambda _0^2 \, g_{\mathrm{eff}} B\). The filling factor f accounts for the possibility that the field occupies only a fraction f of the surface area covered by the pixel.
In the weak field regime described by Eq. (8), the shape of the Stokes V profile is given by the derivative of the intensity profile and does not change with the field strength. In contrast, the amplitude of Stokes V is proportional to the longitudinal field (\(B_\parallel = B \cos \gamma \)) and to the magnetic filling factor f. Since the profile shape remains constant, it is in principle not possible to separate \(B_\parallel \) from f, and only their product can be determined. This is precisely the longitudinal magnetic flux density, defined as
with A the area of integration perpendicular to the line of sight. If the magnetic field is homogeneous and occupies a fraction f of the integration domain, then \(\varphi = f B \cos \gamma \) and \(V \propto \varphi \). Although B and \(\varphi \) have the same units, it is customary to distinguish between intrinsic fields and flux densities by using G and Mx cm\(^{-2}\), respectively (see Keller et al. 1994). Note that longitudinal fields and longitudinal flux densities coincide when the field is resolved (\(f=1\)).
Equation (8) is often used to convert magnetograph measurements into longitudinal flux densities through a standard calibration that is explained in detail by Landi Degl’Innocenti (1992). However, one must be careful with its range of applicability, as it is valid only when the field is weak and constant with height. In the quiet Sun network, where fields of up to 2 kG can be found, its use would be questionable.Footnote 2 Even if the magnetic field is weak, we still have a calibration problem because \(I_0\) cannot be observed directly and must be estimated. Normally, one uses the quiet Sun intensity profile in the hope that it will give a good approximation to \(I_0\), but this is not always the case, according to the results of numerical simulations. A discussion of some of the limitations of Eq. (8) for the interpretation of magnetograph measurements can be found in Beckers (1971).
Equation (8) is applicable not only to magnetograph measurements, but also to full Stokes I and V spectra. When more than one wavelength sample is available, a least-squares fit of the observations to Eq. (8) increases the precision of the calculations by reducing the dependence on noise. The fit is analytical and the longitudinal flux density can be obtained as
where index i runs through the different wavelength points (Domínguez Cerdeña et al. 2006; Martínez González and Bellot Rubio 2009). Another advantage of having full Stokes I and V spectra is that the derivative of the intensity profile can be computed for each pixel individually, without having to rely on a generic calibration based on the average quiet Sun profile.
In the weak field approximation, Stokes Q and U are zero to first order in \(\varDelta \lambda _{\mathrm{B}}\). To second order,
where \(\gamma \) and \(\chi \) are the inclination and azimuth of the magnetic field, H(a, v) the Voigt function, a the damping parameter, \(v = \varDelta \lambda /\varDelta \lambda _{\mathrm{D}}\) the specific wavelength, and primes represent derivatives with respect to v (see Jefferies et al. 1989 for details). In the limit of weak lines, the intensity profile has the same form as the line absorption coefficient, so \((H''/H') (\mathrm{d} I_0 /\mathrm{d} \lambda ) \approx \mathrm{d}^2 I_0/\mathrm{d} \lambda ^2 \) and Eqs. (11) and (12) can be rewritten in terms of the second derivative of the intensity profile.
From these expressions we see that Q and U depend quadratically on the transverse component of the magnetic field (\(B_\perp = B \sin \gamma \)) but linearly on the magnetic filling factor. While Stokes V admits a straightforward interpretation in terms of a longitudinal flux density, Stokes Q and U cannot be transformed directly into a transverse flux density. First of all, the very definition of transverse flux is problematic, because it requires a surface whose normal is perpendicular to the line of sight, hence it is not accessible to the observations. Secondly, the magnetic filling factor in that surface may be significantly different from the f corresponding to the horizontal plane. Thirdly, taking the 4th root of \(Q^2 + U^2\) results in \(B_\perp \) being multiplied by \(f^{1/2}\), not by f. Therefore, one needs to obtain f by other means to be able to compute a “transverse” flux density as \(f B_\perp \) (by pure analogy with the longitudinal flux density). Because of these problems, the transverse flux densities reported by Lites et al. (2008) were defined as the strength of the resolved (\(f=1\)) field that would explain the observed amplitudes of Q and U, i.e., they represent a convenient means of quantifying the abundance of linear signals.
According to the weak field approximation, it is not possible to determine the three components of the vector magnetic field and the filling factor from measurements of Q, U, and V alone, since there are four unknowns (f, B, \(\gamma \), and \(\chi \)) and only three observables. However, adding Stokes I solves the problem: at very high spatial resolution, the intensity profile appears to contain sufficient information to determine f uniquely on a pixel-by-pixel basis (Orozco Suárez et al. 2007c). This is because the magnetic atmosphere and the nonmagnetic surroundings contribute different signals to Stokes I, owing to their different temperatures and flow fields. The two contributions are weighted by the filling factor, which allows f to be derived. Once f is known, the strength and orientation of the field can be obtained from Q, U, and V by combining Eqs. (8), (11), and (12).
For many years, the weak field approximation has been used to interpret ground-based observations of the quiet Sun that did not show linear polarization signals. However, with Hinode we have found an unexpected amount of linear signals associated with weak fields (e.g., Fig. 2). Large Stokes Q and U amplitudes are also observed in the Fe i line at 1564.9 nm (Collados 2001). These measurements offer us the possibility of abandoning the weak field approximation in favor of exact radiative transfer calculations: with the four Stokes parameters well above the noise level, not only longitudinal flux densities but also the full vector magnetic field and the magnetic filling factor can be obtained more accurately through Stokes inversions (Orozco Suárez et al. 2007c).
Example of Stokes profiles observed with the Hinode spectropolarimeter in a quiet Sun IN region. Note the prominent Stokes Q and U signals exhibited by the Fe i 630.25 nm line. The dashed lines represent the best-fit profiles using a simple Milne–Eddington model atmosphere with a homogeneous magnetic field. The observations are well reproduced by a field of 177 G which is inclined 107\(^\circ \) to the local vertical and occupies 42% of the pixel. Image reproduced with permission from Orozco Suárez et al. (2007b), copyright by AAS
2.2.9 Line ratio technique
When the Zeeman splitting is large, the magnetic field strength and the filling factor can be separated thanks to their different effects on the shapes of the Stokes profiles. In general, however, the splitting is not complete and small changes in the separation of the \(\sigma \) components can be masked very efficiently by the noise. Therefore, with simple methods it is often not possible to say whether a small Stokes V signal is due to a strong field with small filling factor, or to a weak field with a large filling factor.
To distinguish between these cases, Stenflo (1973) invented the magnetic line ratio technique. The method is based on the use of two lines (1 and 2) with identical thermodynamic behavior but different magnetic sensitivities. To ensure the same thermal response, the lines must have very similar wavelengths, excitation potentials, and oscillator strengths. In this way, both will show the same intensity profile \(I_0\) and the same derivative \(\mathrm{d}I_0/\mathrm{d}\lambda \) at all heights in the atmosphere. The only difference between them should be their different Landé factors \(g_1\) and \(g_2\).
If the field is weak, the ratio of the Stokes V amplitudes of the two lines \(V_1/V_2\) is equal to \(g_1/g_2\), independently of the magnetic filling factor (Eq. 8). This result holds even when the field is not constant with height, because the two lines have exactly the same shape in all layers of the atmosphere. With stronger fields, the weak field regime breaks down earlier for the line having the larger Landé factor. Owing to Zeeman saturation, the Stokes V signal of that line is no longer proportional to B and \(V_1/V_2 \not = g_1/g_2\). This behavior can be used to distinguish between intrinsically weak and strong fields, regardless of the magnetic filling factor. The ratio \(V_1/V_2\) can be calibrated as a function of B, but not very precisely because the relation between the two quantities depends on the details of line formation and the magnetic structure assumed in the resolution element.
The best magnetic line ratio pair is Fe i 525.021 and 524.705 nm. These lines belong to multiplet 1 of neutral iron and are sufficiently close in the spectrum as to be observable simultaneously. Their \(\log gf\) values, where g is the multiplicity of the lower level and f the oscillator strength, are very similar and therefore the two lines show nearly the same strength. However, they have different Landé factors of 3 and 2, respectively. Thus, in the presence of weak fields their Stokes V amplitude ratio should be 3 / 2. A smaller ratio was observed in network and facular regions, which led to the conclusion that the fields are intrinsically strong there (Stenflo 1989; Solanki 1993).
Another useful line pair is the Fe i doublet at 630.25 and 630.15 nm. In this case, however, the two lines have different atomic parameters and are formed at slightly different heights. With Landé factors of 2.5 and 1.67, respectively, their Stokes V amplitude ratio should vary from about 1.5 for weak fields to about 1 for strong fields. However, high resolution observations show many instances where Fe i 630.15 nm has stronger Stokes V signals than Fe i 630.25 nm, which in principle is not possible. This unexpected behavior reflects the different formation heights of the two lines: if the magnetic field increases with height, then the Fe i 630.15 nm line will show larger V signals than Fe i 630.25 nm because it is formed higher in the atmosphere. Such gradients of the field can be produced by, e.g., the canopies of magnetic flux tubes.
The diagnostic capabilities of these line pairs and that formed by the Fe i 1564.9 and 1565.2 nm lines have been investigated by Khomenko and Collados (2007) using magnetoconvection simulations with flux levels appropriate for the IN. They concluded that the 525.021/524.705 and 1564.9/1565.2 line ratios show good correspondence with the field strength. However, they found a bad performance of the 630.25/630.15 ratio which was ascribed to the large difference in formation heights. Steiner and Rezaei (2012) also investigated the behavior of the 630.25/630.15 line ratio with the help of numerical simulations. They showed that it can lead to the wrong conclusion that hG fields have kG strengths in the presence of magnetic canopies (or, for that matter, in the presence of strong vertical gradients of the field). This result may explain why some analyses using the 630.25/630.15 line ratio show a preponderance of kG fields in the IN (Stenflo 2010a).
Smitha and Solanki (2017) have recently proposed two new ratios based on the Fe i 1553.4/1554.3 nm and 682.0/684.2 nm lines. The near-IR transitions produce larger Stokes V signals than Fe i 1564.8 and 1565.2 nm, so they appear to be well suited to studying quiet Sun magnetic fields. For the moment, however, no observations of those lines are available in the literature.
The line ratio technique is very useful to distinguish between strong and weak fields independently of the filling factor, but the exact field strength cannot be derived without a more sophisticated analysis. In particular, we should warn that using scatter plots of the Stokes V amplitudes of a line pair to draw general conclusions as to whether the fields are strong or weak is dangerous, since the slope of the data point cloud gives only a single value which does not need to apply to every individual pixel. In fact, the scatter seen in those plots is often large, making it possible for many pixels to harbor weak fields even if the statistical result indicates strong fields, and vice versa.
2.2.10 Stokes inversions
The shapes of the observed polarization profiles are determined by the thermal, magnetic, and dynamic conditions of the solar atmosphere. To extract this information as accurately as possible, inversion methods based on analytical or numerical solutions of the radiative transfer equation have been developed over the years. Reviews on inversions techniques can be found in del Toro Iniesta and Ruiz Cobo (1996, 2016), Socas-Navarro (2001), Bellot Rubio (2006), and Ruiz Cobo (2007).
The basic idea behind inversions is to compute synthetic Stokes profiles from a guess model atmosphere and fit them to the observations by means of a nonlinear, least-squares algorithm. In this process, the parameters of the model are modified iteratively until the best fit is reached. The main advantages of inversion techniques are: (a) the complete line transfer problem is solved, so there is no need for simplifying assumptions or uncertain calibrations; (b) the four Stokes parameters are used simultaneously to better constrain the atmosphere; and (c) complex scenarios, such as magnetic flux tubes or two-component model atmospheres, can be implemented in order to interpret the observations more realistically.
Auer et al. (1977) developed the first inversion technique using the Unno–Rachkovsky solution of the radiative transfer equation (Unno 1956). This solution yields analytical Stokes profiles under the assumptions that the atmospheric parameters are constant with height and that the source function changes linearly with optical depth—the so-called Milne–Eddington (ME) approximation. Skumanich and Lites (1987) extended the method of Auer et al. (1977) in various ways and developed a new ME inversion code to interpret the observations of the ASP. This code was used to investigate the properties of virtually all the magnetic structures present in the solar surface, from sunspots to IN magnetic fields (e.g., Lites et al. 1996). Currently operational ME codes include MELANIE (Socas-Navarro 2001), HELIXFootnote 3 (Lagg et al. 2004), MILOSFootnote 4 (Orozco Suárez and del Toro Iniesta 2007), MERLINFootnote 5 (Lites et al. 2007a), and VFISVFootnote 6 (Borrero et al. 2011).
With only nine free parameters, the ME approximation provides a simple but accurate description of the formation of spectral lines in the presence of magnetic fields. This explains its popularity. Strictly speaking, the ME model is applicable to only one spectral line because the so-called thermodynamical parameters of the model represent the properties of both the atmosphere and the chosen line. In practice, however, many ME codes invert the pair of Fe i lines at 630.15 and 630.25 nm simultaneously. They are formed in slightly different layers and may sense different atmospheric conditions, but this appears not to be critical for ME inversions. As shown by Orozco Suárez et al. (2010b), it is indeed possible to analyze them simultaneously using the same thermodynamic parameters and a constant opacity ratio. Rather than being a source of error, the use of the two lines improves the determination of the ME parameters because the influence of noise is reduced.
ME inversions cannot explain asymmetric or anomalous Stokes profiles (e.g., three-lobed Stokes V spectra). These profiles arise from complex magnetic and dynamic geometries, with vertical gradients of the atmospheric parameters. To treat those cases, which are rather common in the quiet Sun, more general inversion techniques were developed in the 1990s. The first one was SIRFootnote 7 (Stokes Inversion on Response functions; Ruiz Cobo and del Toro Iniesta 1992). SIR is a general purpose code capable of dealing with arbitrary stratifications of the atmospheric parameters. It is computationally expensive because the radiative transfer equation has to be solved numerically, but there exists a parallel version based on MPI that offers the possibility of inverting large data sets with much better samplings of the parameter space than were affordable before (Thonhofer et al. 2015). To improve the determination of the physical properties of the atmosphere, the code can fit several lines simultaneously, taking into account all four Stokes parameters or any combination thereof. Other codes that work with gradients of the atmospheric parameters include SPINOR (Frutiger and Solanki 1998) and NICOLEFootnote 8 (Socas-Navarro et al. 2015). The former can handle atomic and molecular lines in LTE, while the latter was designed to invert atomic lines under non-LTE conditions.
To investigate the properties of unresolved magnetic fields beyond the line ratio technique, specific inversion codes implementing the thin flux tube approximation were developed by different groups. Keller et al. (1990) pioneered this kind of analyses. By fitting the continuum intensity and a number of observables extracted from Stokes V, they derived the temperature stratification and the field strength of magnetic elements in facular and network regions. The flux tube inversion code of Bellot Rubio et al. (2000a) was designed to obtain the thermal, dynamic, and magnetic properties of unresolved magnetic elements by fitting the shapes of the Stokes I and V spectra of an arbitrary number of lines observed at disk center. For the first time, this code made it possible to determine the parameters of quiet Sun magnetic elements and their immediate surroundings (Bellot Rubio et al. 2000b). SPINOR can also invert the Stokes profiles of an arbitrary number of lines in terms of thin flux tubes and is not restricted to observations at disk center (Frutiger et al. 2003). These codes were applied to ground-based observations of facular and network regions taken without adaptive optics systems. Such observations did not resolve the magnetic elements and therefore had to be interpreted in terms of models that implement the full structure of a flux tube in the pixel, including its central core and the magnetic canopy. Modern instruments, however, allow one to see individual features and study their different parts independently. For this reason, column-by-column inversions with general-purpose codes like SIR, SPINOR or NICOLE have become the preferred way to analyze high-resolution measurements such as those provided by Hinode, IMaX and CRISP.
At very high spatial resolution one can expect to find vertical discontinuities of the atmospheric parameters almost everywhere. They occur when the line of sight pierces the interface between different magnetic regions, like for example the canopy of a resolved flux tube. To analyze the asymmetric Stokes profiles resulting from such discontinuous atmospheres one can use the SIRJUMP code, which implements a discontinuity at a given optical depth and makes it possible to retrieve the position and amplitude of the jump for the various atmospheric parameters (Bellot Rubio et al., in preparation). Figure 3 shows an application of this code to single-lobed Stokes V profiles observed in the quiet Sun (Sainz Dalda et al. 2012). SIRJUMP has also been applied to IMaX data to determine the height structure of a resolved network patch where the canopy is clearly seen (Martínez González et al. 2012a).
The method of choice when the line of sight traverses two magnetic interfaces is SIRGAUSSFootnote 9 (Bellot Rubio 2003). This code can be used to model localized perturbations of one or more atmospheric parameters at a given height as Gaussian functions. Ishikawa et al. (2010) recently inferred the properties of small-scale magnetic loops in the solar IN through an application of SIRGAUSS to Hinode/SP data.
Examples of single-lobed Stokes V profiles observed by Hinode in the quiet Sun at disk center. Blue-only profiles are shown on the left and red-only profiles on the right. Top: Stokes I and V profiles of the Fe i line pair at 630 nm (solid lines) and best-fit profiles computed with SIRJUMP (dots). Middle and bottom: Atmospheric stratifications resulting from a SIRJUMP inversion of the observed profiles (temperature, LOS velocity, magnetic field strength, and field inclination). Note the discontinuities around \(\log \, \tau _{500} = -0.9\), well within the line formation region (indicated with vertical dashed lines). Images reproduced with permission from Sainz Dalda et al. (2012), copyright by AAS
MIcro-Structured Magnetic Atmospheres (MISMAs) represent an alternative view of the solar atmosphere (Sánchez Almeida et al. 1996). The MISMA hypothesis assumes that the magnetic field is organized on scales much smaller than the photon mean free path, producing optically thin fluctuations of the physical parameters along the line of sight. Each resolution element would therefore contain a collection of magnetic fibrils with different strengths, inclinations, azimuths, and possibly also velocities and temperatures. To model this situation, Sánchez Almeida (1997) developed an inversion code based on MISMAs.
The MISMA scenario has demonstrated a remarkable ability to reproduce the Stokes V profile shapes and asymmetries observed in the network and IN (Sánchez Almeida and Lites 2000; Viticchié et al. 2011). This success is partly due to the complexity of the model and the way it is implemented in practice: by using two, or even three, magnetic atmospheres in the resolution element it is possible to have opposite polarities coexisting next to each other. This provides a great deal of flexibility to fit all kinds of Stokes V asymmetries and anomalous shapes. The price to be paid is a larger number of free parameters, typically twice as many as those of ME models.
MISMAs represent a limiting case of the meso-structured atmospheres considered by Carroll and Kopf (2007). These authors derived a stochastic radiative transfer equation for arbitrary fluctuating magnetic fields using a statistical description based on probability densities and spatial correlations. The correlation length is the key parameter allowing the macro- and micro-structured scenarios to be treated within the same formalism. An inversion code for meso-structured atmospheres exists (Carroll 2007), but it has not been applied systematically to high spatial resolution observations of the solar surface.
Another approach to investigating the magnetism of the quiet Sun is the tomographic inversion based on artificial neural networks developed by Carroll and Kopf (2008). Neural networks have long been used in solar physics (Socas-Navarro 2001), but this is the first time they are trained with 3D models from magnetoconvection simulations. The inversion thus retrieves the atmospheric stratifications of the model that best fits the observed profiles. The validity of the approach clearly depends on the realism of the simulation and on the way the synthetic profiles are degraded to mimic instrumental effects.
2.2.11 Lines with hyperfine structure
In some atoms, the interaction between the nuclear angular momentum and the orbital angular momentum gives rise to hyperfine structure effects. López Ariste et al. (2002) proposed to use them to study the magnetism of the quiet Sun, pointing to two lines of particular interest: Mn i 553.77 and 874.09 nm. Both exhibit reversals in the core of the circular polarization profile, as well as multiple peaks in Stokes Q and U, but only for weak fields. These “anomalies” depend on the magnetic field strength, rather than on the magnetic flux, which makes it possible to derive the former directly from the shape of the observed profiles. Since the polarization amplitudes are not used, the field strength can be recovered without an explicit knowledge of the magnetic filling factor. The diagnostic, however, is not completely free from uncertainties when the atmosphere is unresolved (Sánchez Almeida et al. 2008).
Mn i 1526.27 nm is another interesting line identified by Asensio Ramos et al. (2007). Both its intensity and polarization profiles are sensitive to the presence of hyperfine structure. In particular, the shape of the intensity profile varies with the magnetic field strength. By using a line ratio technique, Asensio Ramos et al. (2007) were able to determine the average strength of quiet Sun magnetic fields and the horizontal scale on which they are organized.
To fully exploit the diagnostic potential of these lines, however, it is necessary to implement the appropriate Zeeman patterns in existing inversion codes and to lower the noise level of current observations, which is barely sufficient to detect the subtle signatures induced by hyperfine structure (e.g., López Ariste et al. 2006).
2.3 The importance of spatial resolution
All measurements of the light coming from the solar surface are degraded to a larger or smaller extent by telescope diffraction and, in the case of ground-based observations, atmospheric turbulence. Moreover, the signal is sampled on a CCD camera with a given pixel size. These effects set the spatial resolution of the observations and limit our ability to diagnose quiet Sun magnetic fields, so it is important to understand them.
There are two main consequences of telescope diffraction and atmospheric seeing: a general reduction of the polarization signal and a modification of the shape of the polarization profiles. Both are caused by the spatial mixing of signals dictated by the telescope and the seeing point spread functions (PSFs). The CCD pixel size, on the other hand, may limit the spatial resolution if it does not critically sample the telescope PSF according to the Shannon theorem.
In what follows we examine these effects and their implications. We will start with a simple description of the problem, ending up with a full simulation of the effects of telescope diffraction and CCD pixelation on Hinode SP data. This will help us understand the importance of spatial resolution and the methods used to take account of diffraction in the analysis of space-borne measurements.
2.3.1 Unresolved magnetic fields and Zeeman cancellation
When individual magnetic features are not resolved by the instrument, the light we record in each pixel comes from the magnetized areas in the pixel and their non-magnetic surroundings. In that case, the emergent Stokes vector \(\mathbf {S}\) can be expressed asFootnote 10
where the subscripts M and NM label the magnetic and non-magnetic atmospheres, respectively, \(A_{\mathrm{M}}\) and \(A_{\mathrm{NM}}\) are the surface areas they occupy, and the magnetic filling factor \(f= A_{\mathrm{M}}/(A_{\mathrm{M}}+A_{\mathrm{NM}}) < 1\) represents the fraction of the pixel covered by magnetic fields. Since the non-magnetic atmosphere does not produce polarization, Eq. (13) simplifies to
This two-component model implicitly assumes that the magnetic field in the pixel is homogeneous and can be described using just one magnetic atmosphere. The expressions above reflect an important property of the Stokes parameters: the circular and linear polarization signals come only from the magnetic features present on the solar surface, independently of their size. Thus, the mere detection of polarization in Zeeman-sensitive lines implies the existence of magnetic fields. By contrast, the intensity spectrum is less useful to diagnose magnetic fields because it also gets contributions from the non-magnetic areas.
Equation (13) shows that the observed polarization signals are proportional to the magnetic filling factor f, so they weaken as the spatial resolution worsens because f decreases. Photon noise then becomes more important, distorting the measurements and hiding the weakest signals.
The situation is more complex when fields of different strengths and orientations coexist in the resolution element. If the fields are of opposite polarity, their Stokes V signals may cancel out. This problem is particularly relevant for small-scale magnetic fields such as those found in the quiet Sun. The amount of cancellation depends on the number of canceling features and the similarity of the signals they produce. In general, the larger the resolution element or the smaller the magnetic structures, the stronger the cancellation that can be expected to occur. However, complete cancellation is highly unlikely, as it requires that for each element of positive polarity there is another of negative polarity having the same magnetic properties, thermal stratification, and flow field.
The linear polarization profiles are insensitive to the polarity of the fields and therefore do not cancel out in the same way as Stokes V. Complete cancellation of Stokes Q and U is possible, but only if the pixel contains fields spanning the full range of azimuths or the azimuths differ by exactly 90 degrees, together with matching field strengths, field inclinations, flows, and thermal properties. For this reason, even if strong cancellation happens in Stokes V, the presence of magnetic fields would still be detectable through the observation of Stokes Q and U.
In summary, cancellation of opposite-polarity fields is expected to produce weaker Stokes V signals but relatively unchanged Stokes Q and U amplitudes. The resulting magnetic field inclinations would be too large compared with the real ones, because of the larger linear to circular polarization ratio (see Eqs. 8, 11 and 12). This bias makes it difficult, if not impossible, to derive accurate field inclinations in the presence of strong Zeeman cancellation.
2.3.2 Effects of diffraction at high spatial resolution
Here, we analyze in a more quantitative way the effects of telescope diffraction on spectropolarimetric measurements. We will focus on observations by the Hinode SP, since the absence of atmospheric seeing makes it easier to reach the diffraction limit as compared with ground-based measurements. This is because the PSF induced by seeing is much wider than the instrumental PSF accounting for diffraction (essentially an Airy function defined by the telescope aperture). However, we should not forget that diffraction is present also in ground-based observations.
The best way to understand how the telescope influences space-based measurements is to simulate the measurement process itself. One can use 3D numerical models of the solar surface, compute the emergent Stokes profiles through radiative transfer calculations, degrade them according to the instrumental PSF and CCD pixelation in order to produce synthetic observables, and make comparisons with the original spectra. This has been done by Orozco Suárez et al. (2007c) and van Noort (2012) for the case of the Hinode SP and by Orozco Suárez et al. (2010a) for SUNRISE/IMaX, using MHD simulations of the quiet Sun by Vögler et al. (2005).
Example of the effects of telescope diffraction on the asymmetries of the Stokes profiles emerging from an MHD model with mean field strength of 10 G. The selected pixel is located in an intergranular lane. The degradation corresponds to the Hinode PSF. Black and red are used to show the original and degraded profiles, respectively. From Orozco Suárez (2008)
Maps of total circular polarization in Fe i 630.25 nm from a MHD model with mean field strength of 10 G before and after degradation by the Hinode PSF (left and middle panels). The panel on the right shows an histogram of the circular polarization ratio for pixels having degraded Stokes Q, U or V amplitudes larger than 4.5 times the noise level of \(10^{-3} \, I_{\mathrm{QS}}\). The rest of pixels cannot be inverted because their signals are too small. Image reproduced with permission from Orozco Suárez et al. (2007c), copyright by ASJ
Diffraction mixes the light from nearby pixels and modifies the shapes of the Stokes profiles quite significantly (Fig. 4). In general, the blurring caused by the telescope PSF reduces the complexity of the profiles, i.e., the spectra look smoother and more symmetric as a result of the spatial mixing. However, there is also a general reduction of the polarization signal, since the light emitted by individual features gets spread over a larger area. This can be observed in Fig. 5 for the case of the Hinode SP. Shown are maps of the total circular polarization of Fe i 630.25 nm before (left) and after (middle) spatial degradation of the synthetic profiles with the Hinode PSF. Both maps are rebinned to the Hinode/SP pixel size. Clearly, most of the signals weaken, although some pixels located next to strong features get larger signals. The histogram on the right quantifies the amount of signal reduction: up to 80% of the pixels show smaller polarization after degradation by the instrumental PSF. The linear polarization behaves in a similar way.
This signal reduction has important consequences for the interpretation of the data. Quiet Sun magnetic fields are weak and most of the time measurable only through Stokes V. In the weak field regime, the Stokes V amplitudes depend linearly on the field strength. Thus, to first order, the smaller circular polarization signal caused by diffraction is equivalent to a weaker field strength. Without allowance for diffraction effects, one would systematically obtain fields that are too weak. A simple way to avoid the problem is to model the signal reduction as
where \(\alpha _{\mathrm{d}}\) is a dilution factor intended to decrease the polarization generated by the magnetic atmosphere. The role of \(\alpha _{\mathrm{d}}\) is similar to that of the stray-light factor introduced by Lites and Skumanich (1990) to account for the effects of scattered light and atmospheric seeing in ground-based observations.Footnote 11
To retrieve the actual field strengths one can invert the data with a single magnetic atmosphere and a free dilution factor, as pointed out by Orozco Suárez et al. (2007c). Since diffraction mixes information from nearby pixels, the intensity profile \(I_{\mathrm{d}}\) needed to determine the dilution factor must be computed locally. For Hinode/SP observations, Orozco Suárez et al. (2007c) proposed to calculate \(I_{\mathrm{d}}\) as the average of the intensity profiles observed in a 1\(^{\prime \prime }\)-wide box containing the pixel under analysis.
Figure 5 shows that, in the case of the Hinode SP, most of the polarization signals are reduced to about 45% of their original value. Very roughly, this is equivalent to \(\alpha _{\mathrm{d}} = 0.55\). However, leaving \(\alpha _{\mathrm{d}}\) as a free parameter results in a range of values, some of which are substantially larger than the most probable dilution factor of 0.55. To understand why, it is important to realize that the model used to describe the effects of diffraction is formally identical to the two-component model of Eqs. (14)–(17), meaning that \((1-\alpha _{\mathrm{d}})\) also carries information on the magnetic filling factor. Indeed, \(\alpha _{\mathrm{d}} \gg 0.55\) would indicate that the magnetic field does not occupy the whole resolution element, but only a fraction of it. In that case, the filling factor would approximately be given by \(f=(1-\alpha _{\mathrm{d}})/0.45\), which already takes into account the 55% average signal reduction caused by diffraction. Pixels that get larger signals cannot be treated properly with this approach. They represent 20% of the total number of pixels with signals above 4.5 times the noise level. In those pixels, fields stronger than the real ones can be expected from the inversion.
The method described above has been successfully applied to Hinode/SP observations (Orozco Suárez et al. 2007b; Orozco Suárez and Bellot Rubio 2012), but is very crude. In particular, it does not account for the shape variations of the Stokes profiles induced by diffraction. A more realistic approach is to deconvolve the observations using the known telescope PSF, which leads to significant improvements when diffraction is the main cause of spatial smearing. Deconvolving ground-based data with the telescope PSF also enhances the image quality, but does not remove the main source of blurring and signal mixing (atmospheric turbulence). Unfortunately, the seeing-induced PSF changes continuously both in time and in space, so it is difficult to correct. Despite the lack of a proper treatment, a number of ground-based data have been deconvolved using empirical seeing functions. Their parameters were estimated by comparing a small set of observables with MHD simulations and therefore are not particularly well constrained (e.g., Scharmer et al. 2011).
Correction of Hinode/SP data using the telescope PSF has been carried out in two different ways. The first one, proposed by van Noort (2012), is actually a convolution rather than a deconvolution. He developed a spatially coupled inversion scheme where many adjacent pixels are inverted simultaneously and their synthetic profiles convolved with the telescope PSF before being compared with the observed ones. This method holds great promise because it provides a strictly correct treatment of telescope diffraction. The advantage of convolution over deconvolution is that the noise does not increase in the process. The second approach, proposed by Ruiz Cobo and Asensio Ramos (2013), performs a direct deconvolution of the telescope PSF. To avoid artifacts due to the noise, the method uses a regularization based on a principal component decomposition of the observed Stokes profiles. The regularization reduces the noise of the profiles by expressing each of them as a truncated linear combination of the principal components derived from the full data set. Only the maps with the coefficients of the expansion are deconvolved. The first application of this technique to Hinode/SP observations of the quiet Sun has been presented by Quintero Noda et al. (2015). The method works well in practice and allows the deconvolved Stokes profiles to be inverted using existing codes. From a mathematical point of view, it is equally correct and has the advantage of being much less demanding in terms of computational resources.
2.3.3 Benefits of high spatial resolution
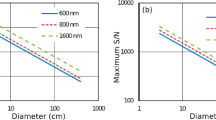
The spatial resolution of quiet Sun observations has increased over the years thanks to advances in instrumentation—particularly image stabilization devices, from the typical 1\(^{\prime \prime }\) of ground-based spectropolarimeters using correlation trackers, to the 0\(.{5}^{\prime \prime }\) made possible by adaptive optic systems and the 0\(.{3}^{\prime \prime }\) allowed by the Hinode SP, which performs seeing-free observations from space. This evolution is illustrated in Fig. 6.
The main advantage of space-borne instruments is that they reach the diffraction limit of the telescope more easily, avoiding the blurring caused by the Earth’s atmosphere and improving the spatial resolution of the observations. Better spatial resolution means that the filling factor of magnetic structures is larger, leading to increased polarization signals (Eq. 13). An example is given in Fig. 7, where the profiles of an isolated flux concentration observed by Hinode at original and degraded resolutions are compared. As expected, the former show much larger amplitudes. These signals are less affected by photon noise and permit a better determination of the properties of quiet Sun magnetic fields.
Evolution of the spatial resolution of spectropolarimetric measurements. From left to right we show continuum intensity maps of the quiet solar surface near the disk center observed with TIP at 1565 nm, the DLSP at 630 nm, and the Hinode SP at 630 nm. The TIP and DLSP observations were made from the ground and reach resolutions of 1\(^{\prime \prime }\) and 0\(.{6}^{\prime \prime }\), respectively (Martínez González et al. 2007; Lites and Socas-Navarro 2004). The Hinode SP performs observations at 0\(.{32}^{\prime \prime }\). Images reproduced with permission, copyright by ESO (left) and AAS (middle)
Hinode/SP observations showing that higher spatial resolution often leads to stronger polarization signals. The Stokes V profile from the central pixel of a quiet Sun magnetic patch at original resolution (0\(.{16}^{\prime \prime }\) per pixel, white curve) is about 5 times larger than that observed at degraded resolution (0\(.{96}^{\prime \prime }\) per pixel, red curve)
In addition, the reduced mixing occurring at high spatial resolution minimizes the possibility of Zeeman cancellation of opposite-polarity Stokes V profiles. This, again, leads to larger circular polarization signals. By means of a controlled experiment using Hinode/SP and SUNRISE/IMaX data, we will show in Sect. 4.3 that the amplitudes of the observed Stokes V profiles (or, alternatively, the longitudinal magnetic flux densities derived from them) do indeed increase with spatial resolution, but only below about 1\(^{\prime \prime }\), which is the threshold at which the observations seem to start resolving the magnetic structures that make up the quiet Sun.
The larger magnetic filling factors and the smaller degree of Zeeman cancellation associated with high spatial resolution bring the following benefits:
Mixing of different magnetic components in the pixel is reduced.
Individual magnetic features can be identified more clearly.
Physical processes occurring on small spatial scales are better resolved.
Since the need to consider different magnetic fields in the resolution element is less pressing, analyses can use simple one-component models with a dilution factor or two-component models consisting of a magnetized atmosphere and a field-free medium. The filling factor can also be expected to approach unity when the spatial resolution is comparable to the typical size of the magnetic features, so the contribution of the non-magnetic atmosphere decreases. All these improvements facilitate the inference of physical parameters from the observations.
The fact that the spectra are not smeared out by the mixing of disparate signals from different structures means there is a much richer variety of Stokes profile shapes at high spatial resolution, reflecting the specific conditions of the individual features (e.g., Viticchié and Sánchez Almeida 2011; Viticchié et al. 2012; Sainz Dalda et al. 2012). The observed profiles show spectral signatures that are not visible at lower resolution, providing a wealth of new information on vertical gradients of the atmospheric parameters. The intensity profile represents a good example of the improvements brought about by spatial resolution. At low resolution, especially from the ground, the observed Stokes I profiles are mostly symmetric and cannot be used to determine gradients of velocity or other atmospheric parameters.Footnote 12 The situation is completely different from space, where high resolution can be achieved without adaptive optics or post-facto restoration techniques. The spectral signatures and asymmetries of high-resolution intensity profiles are extremely rich (e.g. Bellot Rubio 2009; Quintero Noda et al. 2014) and make it possible to determine parameters that are otherwise difficult to obtain, including the magnetic filling factor and the field strength in the weak field regime.Footnote 13 While Stokes I provides the best example, in general all the four Stokes parameters show clear spectral signatures and/or enhanced asymmetries at high resolution, which helps infer the physical properties of the solar atmosphere more accurately.
2.4 Reliability of inversions at high spatial resolution
In the previous section we described a simple inversion strategy to account for the effects of telescope diffraction on Hinode/SP observations using a one-component model with a free dilution factor. Here we test how well the method works in practice. The effects of noise are also examined, since this is perhaps the main factor limiting our ability to diagnose quiet Sun fields.
Photon noise changes the shapes of the Stokes profiles and hides the weakest signals, notably Stokes Q and U. Without clear linear polarization—the typical situation in network and IN regions—, the inference of the magnetic field inclination is difficult. Inversion codes may even interpret pure noise in Stokes Q or U as real signals. Since the fields are weak, the generation of Q or U amplitudes at the level of the noise requires strong transverse fields (Eqs. 11–12), which can induce a bias toward too large field inclinations (e.g., Khomenko et al. 2003). Borrero and Kobel (2011) confirmed the problem simulating Stokes profiles from purely vertical fields and adding noise to them. They showed that ME inversions of the synthetic data always result in inclined fields unless the noise is lowered to very small levels. Also from ME inversions, Asensio Ramos (2009) demonstrated that the information content of Hinode/SP spectra without clear linear polarization signals is not sufficient to set strong constraints on the field inclination, although the field strength can be well determined only from Stokes I and V.
Inversion of synthetic Stokes profiles from a magnetoconvection simulation representing quiet IN conditions. Maps of field strength, inclination, and azimuth are shown from top to bottom. The left column displays the original MHD model at \(\log \tau _{500} = -2\). The other columns give the maps inferred from a one-component ME inversion of the synthetic profiles degraded spatially and spectrally without noise (second column), with noise of \(10^{-3} \, I_{\mathrm{QS}}\) and \(\alpha _{\mathrm{d}}=0\) (third column), and with noise of \(10^{-3} \, I_{\mathrm{QS}}\) leaving the dilution factor as a free parameter (fourth column). Image reproduced with permission from Orozco Suárez et al. (2007a), copyright by AAS
To quantify the typical errors of the magnetic parameters inferred from the inversion of noisy quiet Sun data, Orozco Suárez et al. (2007a) simulated Hinode/SP observations with the help of MHD models. They computed the Stokes spectra emerging from the models and degraded them with the appropriate spatial and spectral PSFs. The data were then rebinned to the SP pixel size and noise was added at the level of \(10^{-3} \, I_{\mathrm{QS}}\). Finally, the synthetic profiles were inverted and the results compared with the original MHD models. Such a comparison allowed the errors and uncertainties of the recovered parameters to be determined with high accuracy in realistic atmospheres, limited only by the approximations of the model.
Figure 8 shows the results of that experiment. With an average field strength of 10 G, the MHD model used by Orozco Suárez et al. (2007a) is representative of quiet Sun IN conditions (Vögler et al. 2005). As with most of the Hinode/SP observations analyzed so far, the simulated data were inverted in terms of a one-component ME atmosphere and a dilution factor, following the strategy proposed by Orozco Suárez et al. (2007c). Two inversions were carried out: one assuming that there is no reduction of the polarization signals (\(\alpha _{\mathrm{d}}=0\)), and another leaving \(\alpha _{\mathrm{d}}\) as a free parameter, to account for telescope diffraction effects.
The first column in Fig. 8 shows the magnetic parameters of the MHD model at \(\log \tau _{500} = -2\), a typical height sampled by the Fe i 630.2 nm lines. Note that the simulation domain contains very weak fields, often below 10 G. The second column displays the results of the inversion of the Stokes profiles emerging from the model after having been degraded spatially and spectrally. For that inversion a zero dilution factor was used, resulting in too weak field strengths, as explained in Sect. 2.3.2. So far the spectra do not contain any noise. In the third and fourth columns we show the magnetic parameters resulting from the inversion of the degraded profiles with noise of \(10^{-3} \, I_{\mathrm{QS}}\) using \(\alpha _{\mathrm{d}}=0\) and \(\alpha _{\mathrm{d}} \not = 0\), respectively. White pixels represent locations where Stokes Q, U, and V are clearly below the noise level, which makes the inversion unfeasible.
We can now compare the inversions of the noisy profiles with the MHD simulations. In Fig. 9 we plot the mean field strength and field inclination errors along with their standard deviations. The errors are defined as the difference between the retrieved parameters and the original MHD model at \(\log \tau _{500} = -2\). Forcing the dilution factor to zero leads to a strong underestimation of the field strength as a consequence of the signal reduction induced by diffraction (upper left panel, solid line). The field inclination is well recovered on average, with errors of less than 5 degrees in the whole range of field strengths (bottom left panel, solid line). However, individual pixels may show very large errors (especially for the weaker fields), as revealed by the dashed line in the same panel.
Errors and uncertainties in the field strengths (top) and field inclinations (bottom) inferred from one-component ME inversions of simulated Hinode/SP observations. The error (solid lines) represents the difference between the inferred parameters and the MHD model at \(\log \tau _{500} = -2\). We show mean errors averaged over all the pixels with sufficient polarization signal (Stokes Q, U, or V amplitudes larger than 4.5 times the noise level of \(10^{-3} \, I_{\mathrm{QS}}\)). The uncertainties (dashed lines) are the standard deviation of the individual errors. Both errors and uncertainties are plotted as a function of field strength. The panels on the left correspond to inversions assuming \(\alpha _{\mathrm{d}}=0\), while those on the right correspond to inversions in which the dilution factor is left as a free parameter, in order to account for the effects of telescope diffraction. Reproduced with permission from Orozco Suárez et al. (2007a) and Orozco Suárez and Bellot Rubio (2012), copyright by AAS
The inversion where the dilution factor is allowed to vary does a very good job in retrieving the field strength, although the inferred values are slightly overestimated (by some 80 G on average) owing to the noise and the limitations of the approach. The field inclination shows slightly larger average errors, probably as a consequence of the increased number of free parameters, but they never exceed 10 degrees. All in all, these results indicate that one-component ME inversions using a dilution factor provide reasonable estimates of both field strengths and field inclinations when at least one of the Stokes profiles is clearly above the noise level, i.e., when the observations carry some magnetic information. Individual pixels may show large errors in field strength and particularly field inclination, but the overall distributions seem to be relatively well determined.
The only effective way to avoid the systematic errors and uncertainties induced by noise is to lower the noise itself. This requires collecting more photons during the same exposure time, which calls for larger telescope apertures than are currently available. The next generation of solar telescopes will therefore be extremely helpful for quiet Sun studies. Particularly promising are the 4-m Daniel K. Inouye Solar Telescope under construction on Maui, the 4-m European Solar Telescope now in its design phase, and the 1.5-m SUVIT telescope planned for SOLAR-C, but also the 1.6-m Goode Solar Telescope at Big Bear Observatory and the 1.5-m GREGOR telescope at Teide Observatory, both of which are already operational.
In the meantime, the following strategies can be used to lower the impact of noise on the determination of quiet Sun magnetic fields:
Denoise the observations using Principal Component Analysis techniques, at the cost of modifying the original signals (as done by, e.g., Martínez González et al. 2008, 2010b).
Invert only Stokes I and V when the linear polarization signals do not stand out clearly above the noise level, assuming that the field is vertical (e.g., Viticchié et al. 2011).
Restrict the inversion to pixels with clear linear polarization signals, even if they represent only a fraction of the total quiet Sun area and their analysis introduces a bias toward the more inclined fields (e.g., Orozco Suárez and Bellot Rubio 2012).
Reduce the noise by using longer effective exposure times, at the cost of lower spatial resolution and increased temporal mixing of the signals (Bellot Rubio and Orozco Suárez 2012).
Use additional diagnostics to constrain the field inclination whenever possible, such as multi-layer intensity measurements of magnetic bright points (Jafarzadeh et al. 2014b, see Sect. 2.1).
2.5 The Hanle effect
2.5.1 Principle
Besides the Zeeman effect, another physical mechanism that can be used to study the weak fields of the quiet Sun is the Hanle effect (Stenflo 1982). It consists in the modification of the scattering polarization of spectral lines due to the presence of a magnetic field. The field alters the coherences (phase relations) between the different magnetic sublevels involved in the transition, which usually leads to a reduction of the polarization signal and a rotation of the plane of polarization. For an intuitive explanation of this process based on the oscillatory model of the electron, the reader is referred to Trujillo Bueno (2001). The full theory of the Hanle effect can be found in, e.g., Landi Degl’Innocenti and Landolfi (2004).
The coherent scattering of anisotropic radiation by atoms produces linear polarization. In the solar atmosphere, the anisotropy is caused by the predominantly vertical radiation field and also by local inhomogeneities (the granulation). It increases with height above the surface as the incident illumination becomes more and more unidirectional. If no magnetic fields are present, the polarization of the scattered radiation is perpendicular to the scattering plane. Thus, for a 90\(^\circ \) scattering angle, i.e., for observations at the limb, the light is linearly polarized parallel to the limb. This is usually chosen to be the positive Stokes Q direction, so U is zero.
Consider now a limb observation of a weak magnetic field pointing to the observer. That is, the field is horizontal (parallel to the solar surface). In this case, the Hanle effect produces depolarization, and the amplitude of Stokes Q decreases. Also, the polarization plane is rotated in the counterclockwise direction. This leads to \(U > 0\). If the field is horizontal and points away from the observer, a similar depolarization occurs but the polarization plane rotates clockwise, generating \(U < 0\). Thus, if the two fields coexist in the resolution element, cancellation of U will happen but we will still see depolarization in Stokes Q. Note that the Hanle effect does not work for fields that are perpendicular to the line of sight or aligned with the symmetry axis of the radiation field (e.g., Stenflo 1982). The latter means that vertical fields at the limb cannot change the scattering polarization of spectral lines.
The Hanle effect also operates in forward scattering (zero scattering angle). At disk center, the polarization due to scattering is zero for symmetry reasons, but the Hanle effect creates linear polarization in the presence of weak inclined fields (Trujillo Bueno et al. 2002).
The Hanle effect is sensitive to fields from about \(0.1 B_{\mathrm{H}}\) to \(10 B_{\mathrm{H}}\), where \(B_{\mathrm{H}}\) is the critical field for which the Zeeman splitting and the natural width of the level are the same (see Trujillo Bueno 2001). The critical Hanle field depends on the transition, but it typically ranges from a few G to tens of G. Stronger fields lead to Hanle saturation. In that regime, the amount of depolarization is maximum and no longer changes with the field strength, but Stokes Q and U still inform about the azimuth and inclination of the field.
2.5.2 Hanle measurements in the photosphere
There are few photospheric lines suitable for the analysis of quiet Sun magnetic fields via the Hanle effect. One of the reasons is that the collisional rates in the photosphere are very high, which quickly destroys the coherences between the Zeeman sublevels and leads to unpolarized scattering. The vast majority of Hanle measurements in the photosphere have been performed in the resonance line of Sr i at 460.7 nm. The left column of Fig. 33 shows an example of Sr i 460.7 nm observations. This line has a large polarizability factorFootnote 14 and is relatively immune to depolarizing collisions because of its large radiative de-excitation rate (Faurobert et al. 2001). It forms 200–300 km above \(\tau _{500} = 1\) (e.g., Bommier et al. 2005) and has \(B_{\mathrm{H}} \sim 20\) G (Faurobert-Scholl 1996; Trujillo Bueno et al. 2006). The Sr i 460.7 nm line shows one of the strongest scattering polarizations of the second solar spectrum, with maximum Q / I signals of the order of 1.5% at \(\upmu =0.1\) (\(\upmu \) represents the cosine of the heliocentric angle) and some 0.1% at \(\upmu = 0.8\) (Stenflo et al. 1997). The rapid decrease of the polarization toward the disk center is partly due to the changing scattering geometry (which modulates the Q / I amplitude as \(1-\upmu ^2\)) and partly to the progressively deeper line formation height, which increases the depolarizing collision rates.
Magnetic fields weaker than the Hanle saturation limit reduce the amplitude of the scattering polarization signal. As can be seen in Fig. 34, the changes in Q / I are typically smaller than a few 0.1%. Thus, detecting the Hanle signatures requires a polarimetric sensitivity of the order of \(10^{-4} \, I_{\mathrm{QS}}\). The usual way to achieve such low noise levels is to keep the spectrograph slit parallel to the limb and integrate for long periods of time. It is also common to average the spectra along the slit. For this reason, most of the Sr i 460.7 nm measurements presented to date lack spatial and temporal resolution. The observations of Stenflo et al. (1980), for example, have typical integration times of 10 min, which are longer than the mean granular lifetime. The ZIMPOL measurements carried out by Stenflo et al. (1997) had shorter integration times, but the data were averaged along the 49 arcsec slit to improve the signal-to-noise ratio. Bommier et al. (2005) made Sr i observations with THEMIS and also averaged the profiles along their \(0.5^{\prime \prime }\times 60^{\prime \prime }\) slit. Similar strategies were followed by Malherbe et al. (2007) at Pic du Midi: they integrated the spectra recorded during 1 h of observations or summed the signals over the \(0.6^{\prime \prime }\times 140^{\prime \prime }\) slit, depending on whether the slit was perpendicular or parallel to the limb, respectively.
Judging from the above mentioned papers, the effective spatial resolution of most of the available Sr i measurements is not better than, say, 10\(^{\prime \prime }\)–50\(^{\prime \prime }\), with integration times that often exceed several minutes. The highest resolution to date seems to have been provided by THEMIS. According to López Ariste et al. (2007b), their measurements reach 1\(^{\prime \prime }\), although they do not specify the effective integration time of the spectra.
Molecules can also be used to study the magnetism of the quiet Sun via the Hanle effect. One of the unexpected properties of the second solar spectrum is that molecules often produce large scattering polarization signals (Stenflo and Keller 1997). Some of them, such as C\(_2\), MgH, and CN, are formed in the photosphere. The scattering polarization of molecular lines shows little spatial and temporal variation (Fig. 33, right panels). This led Berdyugina et al. (2002) to conclude that they are relatively immune to the Hanle effect because of their small Landé factors. An alternative explanation is that molecular lines form above the hot granular cells, where only a small fraction of the fields are sufficiently strong to produce significant Hanle depolarization (Trujillo Bueno 2003).
A great advantage of molecular lines for Hanle studies is that they allow the application of differential analyses based on line ratios (Stenflo et al. 1998; Berdyugina and Fluri 2004; Trujillo Bueno et al. 2006). The idea is to compare the polarization signals in selected lines of the same molecule in order to determine the strength of the underlying field without complex radiative transfer calculations of the scattering polarization. This is possible if the lines have different Landé factors (hence different Hanle sensitivities) but otherwise similar parameters such as lower level populations, radiative rates, and collisional rates. The molecular line-ratio technique provides a relatively model-independent diagnostic of the magnetic field responsible for the observed Hanle depolarization (Faurobert and Arnaud 2003; Berdyugina and Fluri 2004; Bommier et al. 2006; Asensio Ramos and Trujillo Bueno 2007). One variant of the method, suggested by Trujillo Bueno (2003) for the C\(_2\) lines of the Swan system, involves selecting a line with a very large critical Hanle field. Such lines do not undergo Hanle depolarization and can effectively be used as a non-magnetic reference (Trujillo Bueno et al. 2006). The differential Hanle effect can also be applied to atomic lines. A particularly useful combination is the \(a^5F\)–\(y^5F^o\) multiplet of Ti i (Manso Sainz et al. 2004).
2.5.3 Interpretation
To extract information on the underlying magnetic field via the Hanle effect it is necessary to compare the observed linear polarization with that expected in the absence of magnetic fields. This involves three steps: (1) calculation of the zero-field reference case; (2) determination of the Hanle depolarization using the observations and the reference; and (3) derivation of the magnetic field that produces the observed depolarization.
Computing the amount of polarization in the absence of magnetic fields requires a good knowledge of how the scattering polarization is generated. Such an understanding is not always available. Indeed, when the first systematic surveys of the second solar spectrum were made, the theory of scattering polarization could not explain many of the observed signals, which led to the conclusion that it was full of ’enigmas’. Some of these enigmas are now resolved, but others await explanation.
Several methods have been developed to compute the zero-field reference case. For Sr i 460.7 nm one can use the last scattering approximation and assume that the emergent polarization is due only to the last scatterer, which sees a particular anisotropic illumination and a given magnetic field (Stenflo 1982, 2001). This approximation, valid when there is no lower-level atomic polarization, avoids the need to solve the radiative transfer problem with multiple scattering. The next step in complexity is to integrate the radiative transfer equation using a source function with scattering terms, as done by Faurobert-Scholl (1993), Faurobert-Scholl et al. (1995), and Faurobert et al. (2001). In general, however, one has to solve the coupled equations of radiative transfer and statistical equilibrium for the elements of the atomic density matrix. The steps have been summarized by Trujillo Bueno (2001, 2009). This is the approach followed by Bommier et al. (2005) to interpret their Sr i 460.7 nm observations. Independently of the method, the calculations are complicated by the fact that one often does not know with precision the degree of anisotropy of the radiation field (for example, local inhomogeneities due to the granulation are usually neglected) or the depolarizing collision rates, to name a few. The latter are particularly important, because they change in an efficient way the linear polarization to be expected in the absence of fields. The 3D multilevel radiative transfer code developed by Štěpán and Trujillo Bueno (2013) solves some of these problems. It is currently the most sophisticated tool for the calculation of scattering polarization and the Hanle effect in MHD models of the solar atmosphere.
The second step consists in determining the exact amount of depolarization through a comparison of the observed and the zero-field polarization. This requires precise Stokes Q amplitudes and therefore correction of instrumental effects such as fringes and \(I \rightarrow Q\) crosstalk. Unfortunately, the corrections are difficult to perform because the continuum is intrinsically polarized and cannot be used to estimate the magnitude of the effectsFootnote 15. To circumvent these problems, the Stokes Q continuum is usually placed at the level indicated by theoretical calculations, the most sophisticated of which rely on 3D hydrodynamical models (e.g., Trujillo Bueno and Shchukina 2009).
Finally, it is necessary to calculate the amount of Hanle depolarization induced by a given magnetic field. Since the introduction of the method by Stenflo (1982), the usual choice has been to assume a distribution of weak, turbulent magnetic fields in every resolution element. The fields are taken to be horizontal with a random distribution of azimuths or to have an isotropic distribution of orientations (in inclination and azimuth). Both arrangements produce very similar depolarizations (Stenflo 1982). For simplicity, a single-valued field strength is often assumed. However, a distribution of field strengths is more realistic and can be modeled by means of statistical probability density functions (PDFs). It is important to realize that the assumption of turbulent fields is equivalent to assuming that each spatio-temporal resolution element of the observations contains the full distribution of fields.
With only one observable per resolution element (the Hanle depolarization in the core of a spectral line) the actual distribution of field strengths cannot be constrained unambiguously. The magnetic field PDF is usually described in terms of a single parameter and then fitted to the observations. As shown by Frisch et al. (2009), a given Hanle depolarization value can often be explained by rather different PDFs. Thus, the resulting field strengths are uncertain. The same happens with the field inclination, which is not well constrained by the observations.
One way to improve the precision of Hanle diagnostics is to combine lines with different Hanle sensitivities spanning a large range of field strengths. Another way is to use the differential Hanle effect with pairs of molecular or atomic lines, a procedure that should make the analysis rather model-independent. Finally, it is clear that higher spatial resolution could help narrow the range of field strengths and inclinations present in the resolution element.
3 The quiet Sun internetwork: dynamics and evolution
The terms intranetwork (Martin 1984) or internetwork (Lites et al. 1993) refer to the areas of the solar surface that appear devoid of magnetic activity in full-disk longitudinal magnetograms, i.e., quiet Sun regions outside of sunspots, pores, plages, and the network. The lack of magnetic activity is only apparent, as high-sensitivity Zeeman measurements reveal that these regions are permeated by ubiquitous polarization signals. Using short exposures, most of the signals observed in longitudinal magnetograms correspond to the strong flux concentrations of the network and ephemeral regions.Footnote 16 However, when deep integrations are carried out, IN regions show a wealth of circular polarization signals. An example from the Hinode SP is displayed in the left panel of Fig. 10.
Longitudinal (left) and transverse (right) magnetogram signals in a 40\(^{\prime \prime }\) \(\times \)40\(^{\prime \prime }\) IN area observed by the Hinode SP at a resolution of 0\(.{3}^{\prime \prime }\). The full maps are shown in Fig. 1. White and black in the longitudinal flux density map represent positive and negative polarity fields, respectively. Black in the transverse magnetogram indicate large linear polarization signals. The left panel saturates at ± 50 \(\hbox {Mx cm}^{-2}\), the right panel at 200 \(\hbox {Mx cm}^{-2}\). Image reproduced with permission from Lites et al. (2008), copyright by AAS
The existence of magnetic fields in the IN was discovered by Livingston and Harvey (1971, 1975) and Smithson (1975). Using low resolution longitudinal magnetograms, they observed discrete magnetic features of mixed polarities within the limits of the photospheric network. Those features were small in size and had typical fluxes of \(10^{16}\) – \(10^{17}\) Mx. They seemed to appear in the interior of supergranular cells, moving radially away toward the network during their lifetimes. Under good seeing conditions, individual IN elements could sometimes be traced for hours. These early observational findings describe pretty well the quiet Sun IN fields as seen in longitudinal magnetograms, although their intrinsic magnetic properties were not known at the time (Livingston and Harvey 1975; Martin 1984, 1988; Livi et al. 1985; Zirin 1985, 1987).
The IN is also pervaded by linear polarization signals (Fig. 10, right panel). This aspect of the quiet Sun magnetism was hidden to longitudinal magnetographs and required full vector spectropolarimetry to be unveiled. Linear polarization signals were known to exist in the quiet Sun since the work of Lites et al. (1996), but their spatial distribution could not be investigated in detail until Hinode came into operation. At the sensitivity of current instruments those signals are detected as roundish patches scattered over the solar surface, both in visible and in near-IR lines (e.g., Lites et al. 2008; Beck and Rezaei 2009). According to Lites et al. (2008), the linear polarization tends to appear at the edges of granules while the circular polarization patches are stronger in intergranular lanes. Thus, they are not completely cospatial on small scales. On larger scales, both linear signals (Lites et al. 2008; Ishikawa and Tsuneta 2010; Danilovic et al. 2010a; Ishikawa and Tsuneta 2011) and circular signals (Domínguez Cerdeña 2003; Yelles Chaouche et al. 2011) seem to trace the boundaries of mesogranules.Footnote 17 Clearly, mesogranulation is important for the organization of IN magnetic fields, but its origin is still a matter of debate.
Modern observations from space show the dynamics and evolution of IN flux concentrations with unprecedented detail, owing to their high spatial resolution and sensitivity. For example, longitudinal magnetograms by the Hinode NFI made it possible to observe the evolution of IN elements and their interactions for periods of more than 20 h (Fig. 11). Likewise, the IMaX instrument aboard SUNRISE has provided an accurate view of the evolution of linear polarization patches in the IN (Fig. 12). The movies from both instruments show that IN flux elements appear and disappear continuously.
In this section we describe the properties of IN magnetic fields as observed in longitudinal and vector magnetograms, paying special attention to their fluxes, dynamics, lifetimes, emergence rates, and modes of appearance and disappearance.
Still from a movie showing the evolution of a quiet Sun region at the disk center, as observed by the Hinode NFI within the framework of the Hinode Operation Plan 151 (Flux replacement in the solar network and internetwork) on 20–21 January 2010. The measurements consists of longitudinal magnetograms obtained in the two wings of Na i 589.6 nm at \(\pm 16\) pm from line center. The total exposure time per magnetogram was 6.4 s, resulting in a sensitivity of 6 G. The sequence lasts 20 h and has a cadence of 1 min. There is a gap of about 29 min in the middle. The dimensions of the field of view are \(93^{\prime \prime }\times 123^{\prime \prime }\), with a pixel size of 0\(.{16}^{\prime \prime }\). (For movie see Electronic Supplementary Material.)
Still from a movie showing the linear polarization signals observed by SUNRISE/IMaX in the IN on 9 June 2009. The sequence has a total duration of 32 min and a cadence of 30 s. The FOV measures \(40^{\prime \prime }\times 40^{\prime \prime }\) with a pixel size of 0\(.{055}^{\prime \prime }\). More details can be found in Solanki et al. (2010). Courtesy V. Martínez Pillet and the SUNRISE team. (For movie see Electronic Supplementary Material.)
3.1 Magnetic flux distribution and flux budget
IN elements appear on the solar surface with a variety of fluxes. It is important to determine this distribution as accurately as possible to estimate the total flux they contribute to the quiet Sun and the corresponding flux emergence rates. The shape of the flux distribution may also shed light on the origin and nature of IN fields.
Using a feature identification algorithm, Parnell et al. (2009) studied the distribution of fluxes in longitudinal magnetograms taken by Hinode/NFI and SOHO/MDI (see Fig. 13). Individual IN patches were found to have fluxes from about \(10^{16}\) to some \(10^{18}\) Mx (blue line). The weakest elements are the most abundant. The stronger ones contain fluxes comparable to small network patches, but they are very rare. Indeed, the flux distribution of IN features turns out to be well represented by a power law of index \(-1.85\). Parnell et al. (2009) demonstrated that the same law is valid also for ephemeral regions, network elements, and sunspots (green and red curves), covering more than 5 decades in flux. They interpreted this result as an indication that all the magnetic features are produced by the same physical mechanism or, alternatively, that they have different origins, but that surface processes shape their flux contents and ultimately the observed flux distribution.
Distribution of longitudinal magnetic fluxes observed in Hinode/NFI magnetograms of the quiet Sun (blue curve) and SOHO/MDI high resolution and full disk magnetograms (green and red lines, respectively). Image reproduced with permission from Parnell et al. (2009), copyright by AAS
To distinguish between the two possibilities, Thornton and Parnell (2011) focused on newly emerged features observed with the Hinode NFI. They found that all magnetic elements appearing on the solar surface, from the weakest IN flux patches to the largest sunspots, follow a single power law with slope \(-2.69\), spanning a flux range of nearly 7 orders of magnitude between \(10^{16}\) and \(10^{23}\) Mx. This led them to conclude that all the features are created by the same (dynamo) mechanism.
The IN is a fundamental ingredient of the quiet Sun. Using deep Big Bear magnetograms, Wang et al. (1995) estimated that up to 20% of the total quiet Sun flux is in the form of IN elements at any time. Such a result was confirmed by Gošić et al. (2014) through the analysis of long-duration magnetogram sequences acquired by the Hinode NFI. These authors determined the flux content of NE and IN regions over the entire solar surface to be about \(6.8 \times 10^{23}\) and \(1.1 \times 10^{23}\) Mx, respectively. Thus, the IN accounts for 15% of the quiet Sun flux, with very little temporal fluctuations (see chapter 4 of Gošić 2015 for details). The flux content of the quiet Sun, in turn, is slightly larger than the total flux of active regions at solar maximum (\(6 \times 10^{23}\) Mx in cycle 23, according to Jin et al. 2011).
3.2 Flux appearance and disappearance rates
Another important parameter is the flux appearance rate in the IN. Already from the early observations it was obvious that IN elements bring a substantial amount of magnetic flux to the surface. Zirin (1987), for example, estimated the typical rate of IN dipole formation to be 5 events per hour in a single network cell, resulting in \(10^{24}\) Mx per day over the entire solar surface. This is twice as large as the \(5 \times 10^{23}\) Mx day\(^{-1}\) carried by ephemeral regions and 3 times larger than the \(\sim 3 \times 10^{23}\) Mx contained in the entire network (as determined by Hagenaar 2001 from SOHO/MDI observations), highlighting the importance of IN fields for the global magnetism of the Sun.
More recently, Thornton and Parnell (2011) estimated a total flux emergence rate of \(2.7 \times 10^{25}\) Mx day\(^{-1}\) considering all the magnetic features that appear on the solar surface (IN elements, ephemeral regions, active regions). Since the index of the power law describing their flux distribution is smaller than \(-2\), most of the flux turns out to be carried by the weak IN elements.Footnote 18 Such an emergence rate is enormous compared with the \(\sim 6 \times 10^{21}\) Mx day\(^{-1}\) brought to the surface by active regions at solar maximum (Schrijver and Harvey 1994). Zhou et al. (2013) reported an even larger value of \(3.8 \times 10^{26}\) Mx day\(^{-1}\), combining the total IN flux observed in Hinode/NFI magnetograms with the mean lifetime of IN features given by Zhou et al. (2010). This estimate, however, may be affected by the extremely short lifetimes used in the calculations.
Sources and sinks of IN magnetic flux in the interior of a supergranular cell near the disk center, as observed by the Hinode NFI on 2–3 November 2010. The top panel shows the instantaneous flux appearance rates considering the total flux carried by the detected IN features (solid line) and only their initial flux (dashed line). The middle panel displays the rates at which magnetic flux is removed from the cell by transfer to the network (purple), in situ fading (orange) and cancellation (green). The bottom panel compares the total flux appearance and disappearance rates, computed by adding the three processes mentioned above. Image reproduced with permission from Gošić et al. (2016), copyright by AAS
From an analysis of very deep Hinode/NFI magnetograms spanning almost 38 h of continuous measurements, Gošić et al. (2016) determined the instantaneous flux appearance rates in two individual supergranular cells located near the disk center (see Fig. 14, upper panel). Instead of fitting the observed flux distribution, they tracked every single IN feature from birth to death and added their fluxes as a function of time. This led to an average flux appearance rate of \(120 \pm 3\) Mx cm\(^{-2}\) day\(^{-1}\), or \((3.7 \pm 0.4) \times 10^{24}\) Mx day\(^{-1}\) over the entire solar IN, which is a factor of 3 smaller than the value given by Thornton and Parnell (2011) but still enormous.
The extremely large appearance rates reported in the literature pose several problems. First, the emerged flux cannot stay on the solar surface for long, otherwise the total flux would increase without limit, which is obviously not observed. This means that the flux removal rate has to be very high too. Gošić et al. (2016) estimated \(125 \pm 6\) Mx cm\(^{-2}\) day\(^{-1}\) or \((3.9 \pm 0.5) \times 10^{24}\) Mx day\(^{-1}\) over the whole IN, confirming suspicions that flux removal is as important a process as flux emergence in explaining the flux balance of the quiet Sun (Schrijver et al. 1997; Lamb et al. 2013). However, we still do not understand the mechanism(s) through which magnetic flux disappears from the surface. Secondly, some authors have suggested that the observed emergence rates are not real (e.g., Lamb et al. 2008, 2010). This would be the case if part of the IN elements become visible as a result of the coalescence of already existing flux which is too dispersed to be detectable. Coalescence would make the flux show up, but would not inject new flux into the surface. The actual emergence rate would therefore be smaller than the observed one. This scenario is finding growing support in the community, as we will see in Sect. 3.5.2.
3.3 Dynamics of internetwork fields
Space-based observations such as those of Fig. 11 illustrate in a dramatic way the dynamics of IN fields. IN patches appear in the interior of supergranular cells and then move toward the network. During their migration they often interact with other IN elements, merging with like-polarity features or canceling with opposite-polarity patches. Fragmentation is also common. Some elements disappear in situ, fading below the detection limit. Others reach the cell boundaries, where they merge or cancel with network flux concentrations. The complex dynamics of IN fields was first described by Martin (1984) and Livi et al. (1985). In the early literature, IN elements were reported to appear near the center of supergranules (Martin 1990), but Zhang et al. (1998b) demonstrated that in reality they emerge everywhere within the cell interiors.
Trajectories of 375 IN magnetic patches within a supergranular cell. The observations were taken by the Hinode NFI in the framework of HOP 151. Different magnetic elements are shown with different colors. The border of the supergranular cell is marked with red and yellow corks as derived through local correlation tracking of continuum intensity and LOS velocity structures, respectively. Image reproduced with permission from Gošić (2012)
The way IN elements move after they appear on the solar surface provides clues on their nature and origin. Two different horizontal velocity patterns have been identified: a random walk on small scales and a more systematic, radial motion toward the network on large scales. The former is believed to result from the continual buffeting by granular convection (e.g., Manso Sainz et al. 2011), although interactions between IN element can also produce random velocities (Martin 1984). The latter is due to mesogranular and supergranular flows (e.g., Orozco Suárez et al. 2012). The observation that IN patches are influenced by granular motions suggests that they are intrinsically weak, with strengths below the equipartition value of \(\sim 500\) G at which the magnetic energy density equals the kinetic energy density of the gas in the photosphere. Moreover, since they seem to be passively advected by supergranular flows, they cannot be rooted very deeply in subphotospheric layers, otherwise they would withstand the drag exerted by the external flow field.
The migration of IN patches to the network is shown in Fig. 15. As can be seen, the trajectories followed by individual elements are not straight because of their random velocity component. The most recent determination of the proper motion of IN elements has been carried out by de Wijn et al. (2008), who quoted an rms velocity of \(1.57 \pm 0.08\) km s\(^{-1}\). The instantaneous velocities can be large. The footpoints of newly emerged loops, for example, show a ballistic velocity of 3 km s\(^{-1}\) during the emergence phase, until they reach the adjacent intergranular lanes (Martínez González and Bellot Rubio 2009; Manso Sainz et al. 2011). The net velocity (net displacement divided by elapsed time) is much smaller than the instantaneous velocity, of order 0.35 km s\(^{-1}\) (Zirin 1987), although it changes with distance from the center of the supergranular cell (Orozco Suárez et al. 2012). The estimates of the mean radial component of the net velocity range from 0.15 km s\(^{-1}\) (Orozco Suárez et al. 2012) to 0.2 km s\(^{-1}\) (de Wijn et al. 2008) and 0.4 km s\(^{-1}\) (Zhang et al. 1998c). Interestingly, de Wijn et al. (2008) reported systematic differences between the radial velocities of positive and negative IN elements, but this behavior needs to be confirmed using more observations.
The motion of IN elements on the solar surface can be described as a diffusion process characterized by a diffusion coefficient \(K(\tau ) \propto \tau ^{\gamma -1}\) that depends on the temporal scale \(\tau \) and the diffusion index \(\gamma \) (e.g., Berger et al. 1998a; Cadavid et al. 1999; Hagenaar et al. 1999; Abramenko et al. 2011; Giannattasio et al. 2013). The mean squared displacement of the moving elements after a time \(\tau \) is \(\langle (\varDelta l)^2 \rangle \sim \tau ^{\gamma }\). The case \(\gamma =1\) represents a random walk (normal diffusion). When the transport of flux occurs faster, \(\gamma > 1\) and the diffusion coefficient increases with both the temporal and spatial scales. This is called superdiffusion. The latest results point to a superdiffusive regime in the IN, with \(\gamma = 1.44 \pm 0.08\) (Giannattasio et al. 2014) and even \(\gamma = 1.69 \pm 0.08\) (Jafarzadeh et al. 2014a). Giannattasio et al. (2013) found a double regime in the quiet Sun, without distinguishing between network and IN elements. In a subsequent paper, they demonstrated that it is actually the network features that show two different behaviors: superdiffusion on short temporal scales (\(\le \) 600 s) and normal diffusion on longer scales (Giannattasio et al. 2014). The latter reflects the reduced transport rates occurring at the supergranular cell boundaries, which act as stagnation points where magnetic features get trapped efficiently.
Yang et al. (2015) studied the dispersal of magnetic elements in the network and active region plage as a function of their field strengths and also found superdiffusive regimes. However, the diffusion indices were observed to decrease with increasing field strength, from \(\gamma \sim 1.6\) at 100 G to \(\gamma \sim 1\) above 900 G. Thus, the stronger features diffuse more slowly, which suggests that they are more capable of withstanding the perturbations induced by granular and supergranular flows.
3.4 Lifetimes
Using Hinode/NFI observations, the lifetimes of IN elements have been found to range from 1 to 20 min, with a mean value of 2.9 min (Zhou et al. 2010). Based on similar Hinode/NFI magnetograms and a careful analysis of the interactions between elements, Gošić (2015) estimated a longer mean lifetime of \(\sim 9\) min, with individual features lasting from 2 min (a limit set by the cadence of the observations) to 200 min. de Wijn et al. (2008) also reported an average lifetime of about 10 min from another Hinode/NFI data set.
These results are not always comparable because of the different definitions and criteria used by different authors (see discussion in DeForest et al. 2007). Zhou et al. (2010), for example, considered the life of fragmenting patches to be terminated when they split, with the fragments being regarded as new elements. Likewise, two merging elements would be pronounced dead during the merger, which would in turn generate a new feature. By contrast, Gošić (2015) attempted to follow individual elements for as long as possible. Thus, the strongest fragment of a splitting feature would not be taken as a newly born element but as the evolution of the parent. In a similar way, the patch resulting from a merger would be identified as the evolution of the strongest contributor. Not surprisingly, Gošić (2015) reported longer lifetimes than Zhou et al. (2010).
Most authors agree that the lifetime distribution of IN features can be described as an exponential, at least up to some duration (Gošić 2012; Giannattasio et al. 2013). Gošić (2015) reports that an exponential law with a decay time of \(230 \pm 10\) s fits the observed distributions well up to 20 min, although a power law provides a better fit in the whole range from 2 to 40 min.
There is also agreement that the longer-lived elements are the stronger ones, pointing to a positive correlation between lifetime and flux. In general, however, IN elements are short-lived features and most of them survive for less than the typical granulation time scales. This conclusion greatly differs from earlier ground-based results quoting lifetimes of hours. The difference is probably due to the improved resolution attained from space, which allows a better separation of IN elements.
3.5 Sources of internetwork fields
In Sect. 3.2 we discussed the flux appearance rates observed in the quiet Sun. Here we describe the various mechanisms through which the field actually appears on the solar surface. A good understanding of these processes is needed to constrain the origin of the fields.
The modes of appearance of IN magnetic elements have been investigated by, among others, Zhang et al. (1998a) using Big Bear magnetograms, Lamb et al. (2008) using SOHO/MDI observations, and Zhou et al. (2010), Lamb et al. (2010), Wang et al. (2012), and Gošić et al. (2016) using Hinode/NFI data. In general, the results vary significantly with the spatial resolution and sensitivity of the measurements. Since both are essential to identifying individual elements and tracing their evolution, the more recent analyses are to be preferred.
The observations reveal that magnetic flux is brought to the solar IN by bipolar and unipolar elements. The latter are far more common than the former, but are also less well understood. We will describe their main properties in the following sections.
Emergence of a small-scale magnetic loop as observed by the Hinode SP at a resolution of 0\(.{32}^{\prime \prime }\). From top to bottom: continuum intensity, total linear polarization, and total circular polarization. The cadence of the observations is 30 s. Contours mark the position of the circular (black and white) and linear (red) polarization patches. Distances are given in arcsec. Image reproduced with permission from Martínez González and Bellot Rubio (2009), copyright by AAS
3.5.1 Bipolar features
Part of the IN magnetic flux emerges on the solar surface in the form of bipolar features. These are observed as two elements of opposite polarity that separate from each other with time, or as clusters of mixed polarities appearing in small areas. The opposite-polarity features are called small-scale magnetic loops and sometimes IN ephemeral regions. Clusters of mixed polarities are probably formed by individual loops that emerge together. Therefore, they essentially represent the same phenomenon.
Figure 16 shows the photospheric signatures of a prototypical IN magnetic loop. Initially, a small patch of linear polarization emerges in a granular cell and grows in size over time (top and middle panels). At some point, two circular polarization patches of opposite polarity appear at the ends of the linear patch and begin to move apart (bottom panels). The linear polarization patch represents the loop top with horizontal fields and the circular patches the more vertical loop footpoints. Soon thereafter, the linear signal vanishes and the circular signals reach the adjacent intergranular lanes, where they follow the plasma motion. The emergence process lasts 3–5 min.
Observations have shown that these loops can get to the low chromosphere (Martínez González and Bellot Rubio 2009; Gömöry et al. 2013). The movie presented in Fig. 17 illustrates the evolution of a magnetic loop in four different atmospheric layers. The loop is first detected in the photosphere and 5 min later in the temperature minimum region (sampled by Mg i 517.3 nm magnetograms). Eight minutes after the start of the event, chromospheric Ca ii H brightenings are observed at the position of the loop footpoints.
Still from a movie showing the ascent of a small magnetic loop through the solar atmosphere. The observations were acquired with all three instruments of the Hinode Solar Optical Telescope (the SP, the NFI, and the BFI). From left to right: CN intensity filtergrams, longitudinal flux density in the photosphere calculated from Fe i 630.1 and 630.2 nm, longitudinal flux density in the temperature minimum region computed from Mg i b 517.3 nm measurements, and Ca ii H 396.85 nm intensity filtergrams. The contours mark circular (black, white) and linear (red) polarization patches. Image reproduced with permission from Martínez González and Bellot Rubio (2009), copyright by AAS. (For movie see Electronic Supplementary Material.)
The first observations of isolated, small-scale magnetic loops in the IN were reported by Lites et al. (1996) using the ASP. These structures (or Horizontal Internetwork Fields—HIFs—as they were called) harbor weak fields (< 600 G) and show blueshifts, suggesting that they emerge from subsurface layers in the form of \(\varOmega \)-loops, carried by granular upflows or magnetic buoyancy (Zwaan 1987). Low-lying loops were also detected in near-IR spectropolarimetric observations by Martínez González et al. (2007). These authors found horizontal magnetic fields in between the two opposite-polarity footpoints, where the field was clearly vertical, although they could not distinguish between U-loops and \(\varOmega \)-loops. Martínez González et al. (2007) estimated that at least 10%–20% of the photospheric IN flux is connected by low-lying loops.
High-resolution observations of emerging loops have been taken with the Hinode SP (Centeno et al. 2007; Ishikawa and Tsuneta 2009; Martínez González and Bellot Rubio 2009; Jin et al. 2009). The SP measurements allowed the Doppler velocity of the linear polarization patches to be determined. Using this information, it is easy to decide whether the observed events correspond to U-shaped or \(\varOmega \)-shaped loops. For instance, Centeno et al. (2007) analyzed an event in which the apex of the tube was clearly blueshifted, indicating the emergence of an \(\varOmega \)-loop. The linear polarization signals characterizing these events disappear at some point because the loop top reaches high atmospheric layers, outside of the formation region of the observed spectral lines. The three-dimensional structure of the loops has been reconstructed by Martínez González et al. (2010a) and Ishikawa et al. (2010). Figure 18 shows the results of Martínez González et al. (2010a). As can be seen, the loop is rather flat in the photosphere and much more elongated higher up. Gömöry et al. (2010) developed a geometrical model of rising magnetic loops using near-IR observations taken with TIP at the German VTT on Tenerife. They also detected blueshifts in the linear polarization patch. Their model confirms the basic picture described above.
Three-dimensional reconstruction of a small-scale \(\varOmega \)-loop observed with the Hinode SP, as derived from a potential field extrapolation. The loop encompasses the photosphere and low chromosphere. Different colors represent different field lines. The image on the horizontal plane shows the continuum intensity and the projection of several field lines. The short dashes indicate the inclination of the vector magnetic field at the loop footpoints, with blue and red marking positive and negative polarities. Image reproduced with permission from Martínez González et al. (2010a), copyright by AAS
A statistical analysis of the emergence of small-scale magnetic loops was carried out by Martínez González and Bellot Rubio (2009) based on 69 events observed with the Hinode SP. They determined the typical lifetimes, sizes, vertical velocities, and magnetic fluxes of these structures and came to the conclusion that about 23% of the loops make it to the chromosphere. It is still unknown whether the loops continue their rise to the corona, although Martínez González et al. (2010a) have shown, using potential field extrapolations, that the apex of the loops can be located as high as 2–3 Mm above the continuum forming layer (Fig. 18). The ascent of granular-sized magnetic bubbles up to the transition region has actually been observed in active regions (Ortiz et al. 2014; de la Cruz Rodríguez et al. 2015; Ortiz et al. 2016), but not in the quiet Sun. To investigate this problem, combined observations of the Interface Region Imaging Spectrograph (IRIS; De Pontieu et al. 2014) and other space assets are highly desirable.
A number of authors have concentrated on the analysis of so-called Transient Horizontal Magnetic Fields (THMFs; Ishikawa and Tsuneta 2009). THMFs represent the linear polarization patches that are seen to emerge in high spatial and temporal resolution spectropolarimetric observations of the quiet Sun. THMFs and HIFs are probably the same features. They have been associated with emerging loops but could also represent submerging loops or canceling fields. Jin et al. (2009) analyzed 446 such events and found a correlation between their lifetimes and magnetic flux densities, but only when the linear signals are accompanied by circular polarization signals of opposite polarity. Isolated THMFs with no circular signals have weaker fluxes and shorter lifetimes. The most complete statistical analysis of these features has been performed using SUNRISE/IMaX data. Danilovic et al. (2010a) analyzed 4536 events at high temporal (\(\sim 30\) s) and spatial (0\(.{15}^{\prime \prime }\)) resolution with a noise level of \(10^{-3} \, I_{\mathrm{QS}}\). They reported an emergence rate of \(7\times 10^{-4}\) arcsec\(^{-2}\) s\(^{-1}\), one or two orders of magnitude larger than previous estimates, thanks to the high sensitivity of the instrument. They also found a correlation of the lifetimes and sizes with the mean linear polarization signals. The features observed by SUNRISE/IMaX show both upflows and downflows, although the upflows are more common. About 8% are fully embedded in downflowing plasmas and have different properties. They could be associated with the submergence of U-shaped field lines, but their origin is still unknown.
The main properties of small-scale IN magnetic loops can be summarized as follows:Footnote 19
They tend to appear at the edges of granules and show no preferred orientation (Centeno et al. 2007; Ishikawa et al. 2008; Ishikawa and Tsuneta 2009; Martínez González and Bellot Rubio 2009).
The mean size of the linear polarization patch representing the horizontal fields of the loop top is 1\(^{\prime \prime }\)–2\(^{\prime \prime }\) in Hinode/SP observations. At higher spatial resolution, about 97% of the linear polarization patches show sizes smaller than 1\(^{\prime \prime }\) (Danilovic et al. 2010a). The loop cross section is elongated, with a vertical extent of 100–200 km and a horizontal extent of \(\sim 400\) km (Ishikawa et al. 2010; Martínez González et al. 2010a).
The loop tops and loop footpoints show blueshifts in the photosphere, indicating upward motions. The average ascent speed is of order 1 km s\(^{-1}\). In the low chromosphere, the footpoints harbor downflows of \(\sim 0.6\) km s\(^{-1}\), perhaps as a consequence of the drainage of plasma along the legs of the magnetic flux tube. Gömöry et al. (2010) also detected redshifts of 2 km s\(^{-1}\) in the footpoints of a loop at photospheric levels.
The loop footpoints separate steadily at a mean speed of \(\sim 2\) km s\(^{-1}\) during the initial stages of the emergence. They slow down when the loop top reaches the chromosphere. The mean maximum distance between the footpoints is 1200 km. In some cases, separations of up to 4000 km are observed, with the footpoints straddling a few granules. Thus, the loops remain coherent structures despite the photospheric convective flows.
The average loop lifetime is 12 min, with individual values ranging from 2 to 40 min. Jin et al. (2009) found a mean lifetime of 5.6 min. Danilovic et al. (2010a) derived an exponential distribution of lifetimes, from 0.5 to 10.5 min. Thus, the loops evolve on typical granulation time scales (Title et al. 1989; Hirzberger et al. 1999). Again, we stress that the meaning of lifetime varies between papers: while Martínez González and Bellot Rubio (2009) defined it as the total duration of the event, from the appearance of linear polarization to the disappearance of the footpoints, Jin et al. (2009) and Danilovic et al. (2010a) considered only the interval during which linear signals are observed. For this reason, the lifetimes given by Martínez González and Bellot Rubio (2009) are usually longer.
The loops are weak field structures, with strengths below the equipartition value (Lites et al. 1996; Martínez González and Bellot Rubio 2009; Ishikawa and Tsuneta 2009). Field strengths of \(\sim 200\) G (Martínez González et al. 2010a) and \(\sim 400\) G (Gömöry et al. 2010; Ishikawa et al. 2010) have been inferred for single events. There are no direct measurements of the field strength in the chromosphere, but using flux conservation arguments Martínez González et al. (2010a) estimated 50 G at a height of 500 km. At the resolution of the Hinode SP, the loops fill 30% of the pixel (Martínez González et al. 2010a).
The loop emergence rate has been reported to be \(5.5 \times 10^{-6}\) arcsec\(^{-2}\) s\(^{-1}\) (Martínez González and Bellot Rubio 2009), \(2.8 \times 10^{-5}\) arcsec\(^{-2}\) s\(^{-1}\) (Lites et al. 1996), \(4.5 \times 10^{-5}\) arcsec\(^{-2}\) s\(^{-1}\) (Jin et al. 2009), and \(5.7 \times 10^{-5}\) arcsec\(^{-2}\) s\(^{-1}\) (Ishikawa and Tsuneta 2009). At higher spatial and temporal resolution the emergence rate increases up to \(\sim 7\times 10^{-4}\) arcsec\(^{-2}\) s\(^{-1}\) (Danilovic et al. 2010a). It is very similar in quiet Sun and plage regions (Ishikawa and Tsuneta 2009).
The loop footpoints have a mean longitudinal flux of \(9\times 10^{16}\) Mx at photospheric levels. The longitudinal flux density is 26 \(\hbox {Mx cm}^{-2}\) in the photosphere and some 13 \(\hbox {Mx cm}^{-2}\) in the chromosphere.
Small-scale loops bring an enormous amount of flux to the surface, with values over the entire Sun ranging from \(1.1 \times 10^{24}\) Mx day\(^{-1}\) (Martínez González and Bellot Rubio 2009) to \(9.8 \times 10^{24}\) Mx day\(^{-1}\) (Jin et al. 2009). The most recent estimate based on Hinode/NFI magnetograms is \(4.1 \times 10^{24}\) Mx day\(^{-1}\) (Gošić 2015). This includes loops and clusters of mixed-polarity elements.
The loops inject \(\sim 2 \times 10^6\) erg cm\(^{-2}\) s\(^{-1}\) of magnetic energy into the solar atmosphere (Ishikawa and Tsuneta 2009; Martínez González et al. 2010a). For comparison, the radiative losses of the quiet Sun chromosphere are in the range \(4 \times 10^6\) erg cm\(^{-2}\) s\(^{-1}\) (Withbroe and Noyes 1977) to \(10^7\) erg cm\(^{-2}\) s\(^{-1}\) (Anderson and Athay 1989). Thus, small-scale loops could supply anything from 20% to 50% of the energy needed to balance the chromospheric losses, provided of course they reach such heights.
3.5.2 Unipolar magnetic flux
Magnetic flux also appears on the solar surface in the form of unipolar patches which are not clearly related to any other magnetic element of opposite polarity in the surroundings. Figure 19 shows an example recorded by the Hinode NFI. This is the most common mode of flux appearance in the solar IN, according to longitudinal magnetograms such as those used to construct the movie of Fig. 11. In a 24-h sequence of SOHO/MDI magnetograms with a resolution of 1\(.{2}^{\prime \prime }\), Lamb et al. (2008) observed a factor of 10 more flux appearing in the form of unipolar patches than emerging as bipolar features.
The mechanism that drives the appearance of unipolar flux in the solar photosphere is not known. Clearly, the patches must be connected with flux of opposite polarity, but the absence of obvious candidates near the emergence site is a mystery. Lamb et al. (2008) suggested two possible explanations: either the emergence is bipolar (i.e., in the form of small-scale magnetic loops) but the opposite-polarity footpoint escapes detection because it is more dispersed and does not stand above the noise level, or the unipolar patches do not represent newly emerged flux but already existing flux which coalesces and becomes strong enough to be detectable (see their Fig. 4). Using a model of asymmetric bipolar emergence, they concluded that the first scenario cannot be responsible for more than a small fraction of the unipolar flux, which led them to favor the coalescence mechanism. The idea that the appearance of unipolar flux is due to concentration of previously undetected flux was confirmed by Lamb et al. (2010) from simultaneous SOHO/MDI and Hinode/NFI measurements. Also the larger flux appearance rates observed toward the boundaries of supergranular cells by, e.g., Wang (1988), Stangalini (2014) and Gošić (2015) are compatible with this mechanism: close to the network one can expect a larger amount of recycled flux and, therefore, more vigorous coalescence leading to increased flux appearance rates.
The example of Fig. 19 illustrates what seems to be a coalescence process in the solar IN. No negative-polarity patches exist near the positive-polarity element that emerges at the center of the field of view. One frame before the appearance, however, there are hints of dispersed, very weak positive flux at the position of the feature. This flux is not easily detectable because the signal remains close to the noise level, but it is likely the precursor of the unipolar patch that will appear in the following frame. During the first minutes of its life, the patch contracts and gets stronger, as expected from a coalescence process.
Appearance of unipolar flux concentrations in the solar IN. This event was observed with the Hinode NFI at a cadence of 1.5 min. The data belongs to the Hinode Operation Plan 151 (Flux replacement in the solar network and internetwork). The contours outline an isolated magnetic patch with no obvious opposite-polarity patches nearby. It probably appears as a consequence of the coalescence of unresolved magnetic flux. There are hints of very weak positive polarity flux at the position of the feature one frame before the element is detected. Note also the contraction of the patch during the first frames. Image reproduced with permission from Gošić (2012)
As pointed out in Sect. 3.1, coalescence may solve the problem posed by the enormous flux appearance rates observed in the solar IN. However, the actual amount of unipolar flux still needs to be determined at the resolution of Hinode. This is not an easy task owing to the large number of features present in the magnetograms. Without additional information other than their temporal evolution, it is often difficult to distinguish genuine unipolar patches from the footpoints of magnetic loops or clusters of bipolar features. The use of complementary tools, such as magnetic field extrapolations (e.g., Wiegelmann and Sakurai 2012) and magnetofrictional simulations (e.g., Cheung and DeRosa 2012), may be of help in identifying the poles of magnetic loops when they are far apart or when the loops appear in crowded regions. In those cases, feature tracking algorithms may fail to detect the opposite polarity patch associated with a newly observed loop footpoint, which would be interpreted as the appearance of unipolar flux. This strategy holds great promise for a better interpretation of the observations.
The first data-driven magnetofrictional simulation of the quiet Sun was performed by Gošić (2015) using Hinode/NFI magnetogram sequences. The resulting magnetic field lines helped determine the connectivity of IN magnetic patches with a view to separating bipolar features from unipolar flux concentrations. According to this analysis, 75% of the features that show up in the interior of supergranular cells are unipolar. Together, they account for \(1.8 \times 10^{24}\) Mx day\(^{-1}\), or 45% of the total flux appearance rate in the IN (Gošić 2015). This would not be fresh flux but coalesced flux that was already present in the photosphere. The remaining 55% correspond to bipolar features—the only entities deemed capable of bringing new flux to the surface.
Emergence of unipolar magnetic fields in granular convection. This event was observed with the Hinode SP at a cadence of 2 min on 10 March 2007. From top to bottom, we show the normalized continuum intensity, the integrated (unsigned) circular polarization signal, the total linear polarization signal, Ca ii H intensity filtergrams, and line-of-sight velocity maps calculated from the Stokes V zero-crossing point (blue means upward). The red contours enclose pixels with circular polarization signals well above the noise level. Image reproduced with permission from Orozco Suárez et al. (2008), copyright by ESO
The appearance of unipolar flux can also be due to the mechanism proposed by Pietarila et al. (2011). They suggested that the localized descent of chromospheric magnetic fields by downward convective plumes may explain the sudden appearance of unipolar patches in the photosphere. The mechanism has received some support from MHD simulations, but it should be investigated further. A definite confirmation will require simultaneous observations in chromospheric and photospheric lines to follow the evolution of the field and demonstrate its downward motion.
Alternatively, changes in the inclination of already existing horizontal magnetic fields may explain the appearance of unipolar flux. Through interactions with granular flows, the fields may become more vertical during part of their lifetimes, showing up up as new features in longitudinal magnetograms. This mechanism requires vector magnetograms to be confirmed or refuted.
The scenarios described above can be expected to work mainly in intergranular lanes. However, the appearance of unipolar flux within granules is well documented, which points to the existence of additional mechanisms. De Pontieu (2002) reported the first examples using high-resolution magnetograms taken at the Swedish Vacuum Solar Telescope on La Palma, although they were interpreted as HIFs observed at large viewing angles. Bello González et al. (2008) detected them also near the disk center. Those events are better seen in Hinode data. Figure 20 shows an example from Orozco Suárez et al. (2008). A unipolar circular polarization patch (red contours) appears above a granular convective cell. It grows in size until it reaches a stable configuration and then disappears in situ after 14 min, undisturbed by other magnetic elements. No linear polarization or circular polarization of opposite polarity is observed near the structure at any time, which makes this process conceptually different from the emergence of magnetic loops. We know that the unipolar patch is emerging on the solar surface because it exhibits strong blueshifts. The Stokes V profiles associated with these features show extreme asymmetries and sometimes only one lobe, pointing to the existence of sharp discontinuities of the vector magnetic field and velocity along the line of sight (for a discussion of the mechanisms generating single-lobed profiles see Sect. 4.2).
The emerged flux seems to be confined to the photosphere because no response is detected in chromospheric Ca ii H filtergrams or Mg i b\(_2\) 517.3 nm magnetograms sampling the temperature minimum region. These unipolar patches have a mean lifetime of 13 min and a mean size of 4 arcsec\(^2\), with flux densities of about 30 \(\hbox {Mx cm}^{-2}\) and total fluxes of \(\sim 5.5\times 10^{17}\) Mx. Their average upward velocity is 2–3 km s\(^{-1}\). Interestingly, they do not seem to be perturbed by convective flows. The magnetic patch of Fig. 20, for example, is never advected or shredded by the horizontal motions of the hosting granule. Actually, it lives longer than the granule itself. Both the occurrence rate of these features, only 6 events in 10 h of observations, and their location away from intergranular lanes suggest that coalescence is not the main driver behind them.
3.6 Sinks of internetwork fields
Magnetic flux is observed to disappear from the solar IN through cancellation and in situ fading of magnetic elements, possibly after fragmentation. Figure 21 displays examples of these processes as seen in high-resolution longitudinal magnetograms taken by the Hinode NFI. The IN also loses flux when IN magnetic features interact with network patches and merge or cancel with them. The rates of these flux removal mechanisms are shown in the middle panel of Fig. 14 as determined by Gošić et al. (2016) from long-duration Hinode/NFI magnetogram sequences.
Examples of cancellation, in-situ disappearance, and fragmentation of flux features observed in Hinode/NFI magnetograms. White represents positive polarity. The magnetograms are saturated to ± 30\(\hbox {Mx cm}^{-2}\) to better follow the evolution of the flux. The measurements were taken in the framework of Hinode Operation Plan 151. Tickmarks are separated by 1\(^{\prime \prime }\)
3.6.1 Flux cancellation
At any time, the IN is pervaded by magnetic elements of both polarities. Their continuous motions give rise to encounters between features of opposite polarity, resulting in a mutual loss of magnetic flux. This process, known as flux cancellation (Livi et al. 1985; Martin 1988), is the only mechanism that can truly remove flux from the solar surface. The cancellation can be total or partial, depending on whether the features disappear completely or not.
Zwaan (1987) proposed two physical models to explain the cancellation of flux in the solar photosphere, namely, the retraction of \(\varOmega \)-shaped field lines (Fig. 22a) and magnetic reconnection of opposite-polarity fields (Fig. 22b, c). In the first case, the two canceling features belong to the same magnetic system. In the second, they belong to different systems. If reconnection occurs below the photosphere, the reconfiguration of the field lines causes the emergence of a U-loop, driven by both magnetic tension and buoyancy forces (Fig. 22b). If reconnection takes place above the photosphere, an \(\varOmega \)-loop is generated and pushed downward as the magnetic tension force overcomes magnetic buoyancy (Fig. 22c). Reconnection can also happen within the same flux system, generating O-loops (Kubo et al. 2010). This occurs when the footpoints of an \(\varOmega \)-loop are pushed together into close contact and reconnect in the photosphere while the loop top is still in the chromosphere. All the processes described above remove magnetic flux from the solar surface, decreasing its total flux content.
The submergence of \(\varOmega \)-loops (Fig. 22c) is the most likely mechanism of flux cancellation because reconnection processes are more efficient near the temperature minimum region (Litvinenko 1999). Hence, flux cancellation events are expected to show photospheric redshifts and horizontal fields at the neutral line separating the two magnetic polarities, as the loop top crosses the photosphere and dips into subsurface layers. However, low-altitude reconnection is also possible. In MHD simulations, it has been observed to occur where horizontal fields are pulled down by the flows of a new intergranular lane developing over a decaying granule. This forms a U-shaped loop whose opposite-polarity legs are forced into close contact until they eventually reconnect below the surface (Tortosa-Andreu and Moreno-Insertis 2009)
Cancellation scenarios proposed by Zwaan (1987). Case (a) represents the retraction of existing field lines forming an \(\varOmega \)-loop. Cases (b) and (c) imply prior reconnection of unrelated field lines below (b) or above (c) the photosphere. After reconnection takes place, the flux is removed by the emergence of a U-loop or the submergence of an \(\varOmega \)-loop. Image reproduced with permission, copyright by Annual Reviews
Cancellation processes have been observed in active regions and the quiet Sun by many authors, including Martin et al. (1985), Livi et al. (1985), Zhang et al. (2001), Yurchyshyn and Wang (2001), Goodman (2001), Chae et al. (2002, 2004, 2010), Bellot Rubio and Beck (2005), Kubo and Shimizu (2007), Cheung et al. (2008), Park et al. (2009), Yang et al. (2009), Zhang and Jin (2009), and Kubo et al. (2010). For a review, see Chae (2012). However, the question of whether they are due to the submergence of \(\varOmega \)-loops or the emergence of U-loops is not yet settled from an observational point of view. With a focus on network regions, Wang and Zhang (1999) analyzed the time delay between cancellation events observed in the chromosphere and the photosphere, concluding that the cancellation is produced by reconnection above the photosphere and thus involves the retraction of \(\varOmega \)-loops. Iida et al. (2010) investigated a single cancellation event in a quiet Sun region using Hinode/SP data and detected both inclined fields and redshifts at the cancellation site. This also points to the submergence of an \(\varOmega \)-loop as the cause of the cancellation. However, Zhang et al. (2009) analyzed the relation of small cancellation events with the granular flow and found strong blueshifts at the cancellation site, which led them to favor the rise of U-loops generated by magnetic reconnection below the photosphere. They also suggested that cancellation processes can modify the granular evolution and even suppress convection.
What is now established is that the footpoints of small-scale IN loops (Sect. 3.5.1) often interact and cancel with preexisting magnetic patches of opposite polarity (Gömöry et al. 2010). Indeed, the emergence of magnetic loops and their subsequent cancellation with ambient fields is the likely cause of the supersonic magnetic upflows discovered by Borrero et al. (2010) in the IN. According to Quintero Noda et al. (2013), these flows tend to occur near the polarity inversion lines created by one of the loop footpoints and a preexisting opposite-polarity patch, which suggests a reconnection-driven event.
Litvinenko (1999) and Ryutova et al. (2003) studied the cancellation of small magnetic features from a theoretical point of view. These and other efforts have recently been summarized by Ryutova (2015). Cancellation processes often involve complex dynamics and more than just two opposite polarity fields. To grasp the full complexity of the problem one can perform MHD simulations. They show that magnetic flux is removed from the solar surface as opposite polarity fields advected by granular motions come into contact and reconnect above the photosphere (Cameron et al. 2011). The resulting U-loop quickly rises to higher layers, whereas the associated \(\varOmega \)-loop retracts much more slowly. Simulations have also been used to find the observational signatures of the cancellation of ambient and emerging fields, with a view to understanding the nature of supersonic magnetic flows in the IN (Danilovic et al. 2015).
Cancellation is an efficient way of removing flux from the quiet Sun. Using Big Bear observations, Livi et al. (1985) determined an average flux cancellation rate of \(\sim 1.7 \times 10^{23}\) Mx day\(^{-1}\) in enhanced network regions and their associated IN areas. The value of \(4.2 \times 10^{23}\) Mx day\(^{-1}\) reported by Lamb et al. (2013) is only slightly larger, despite the improved angular resolution of the Hinode/NFI. These rates refer to the quiet Sun as a whole because none of the authors separated the network from the IN. In the IN, Gošić et al. (2016) estimated a cancellation rate of \((7 \pm 1) \times 10^{23}\) Mx day\(^{-1}\), with little temporal and spatial variations. This represents 18% of the total IN flux observed to disappear in their Hinode/NFI magnetogram sequences. However, it is important to realize that the actual cancellation rates must be larger, for two reasons. First, partial cancellations where the intervening features do not disappear completely are very hard to detect and are therefore usually ignored in the calculations. The work of Gošić et al. (2016) is no exception. The second reason is that cancellations of IN magnetic elements with network patches were counted as instances of flux transfer to the network, not as cancellations occurring within supergranular cells. The rates at which IN flux is transferred to the network will be discussed in Sect. 3.6.3.
3.6.2 In situ disappearance
High-resolution magnetogram movies (Fig. 11) demonstrate that small magnetic flux elements can disappear without interacting with other features. They are just observed to fade in situ. This is the dominant mode of flux disappearance in the solar IN (e.g., Zhou et al. 2010; Lamb et al. 2013). Fading proceeds at a rate of \((1.6 \pm 0.3) \times 10^{24}\) Mx day\(^{-1}\), which accounts for 42% of the total flux loss in the IN (Gošić et al. 2016). The central panels of Fig. 21 show an example where a single polarity magnetic element fades away leaving no trace of its flux.
In situ disappearance implies that the signal decreases below the noise level and becomes undetectable. This can be caused by, e.g., a rapid dissipation of the magnetic field, a gradual dispersal of the flux, or an increase in the field inclination. All these mechanisms would reduce the magnetogram signal. The third process is often not considered, but it may play an important role given the complex dynamics of the solar IN. Unfortunately, it is difficult to assess its contribution without vector magnetograms. The fading of magnetic patches could also be due to undetected cancellations occurring at subresolution scales. However, Lamb et al. (2013) have shown that this is very unlikely because no weak opposite-polarity flux can be detected in ensemble averages of such events. Thus, contrary to flux cancellation, in situ disappearance does not remove magnetic energy from the solar surface, it only reorganizes the field.
The dispersal of magnetic flux can be thought of as the process opposite to flux coalescence. It requires advection of flux by horizontal flows. One way of dispersing magnetic flux is to first split it into smaller pieces. Fragmentation of magnetic patches is observed to occur frequently at the resolution of Hinode and may proceed also at smaller scales. Figure 21c shows an example of an element splitting into three fragments (clearly visible at 11m 50s). The central fragment vanishes while the others separate with time. The fragmentation of flux tubes can be triggered by the surrounding granulation, which deforms their boundaries. The so-called interchange instability may then set in and eventually break the tubes (Parker 1975; Steiner 2007). Flux tubes of less than \(10^{19}\) Mx are liable to the interchange instability (Meyer et al. 1977), implying that most of the patches observed in the solar IN could undergo this process. However, the instability does not develop if the field is twisted or the tube is surrounded by whirl flows (Schüssler 1984). Another mechanism for destabilizing and disintegrating a magnetic flux tube is the Kelvin–Helmholtz instability due to shear between the flows inside and outside the tube. All these processes disperse the magnetic structures and would be observed as in situ disappearances.
3.6.3 Transfer of internetwork flux to the network
Early observations already showed that many IN features survive long enough to reach the supergranular cell borders, where they merge with network patches of the same polarity or cancel with patches of opposite polarity (Livi et al. 1985; Martin 1988, 1990). In both cases, the IN loses flux. This complex process has been characterized by Gošić et al. (2014, 2016).
The central panel of Fig. 14 shows the rates of flux transfer from the IN to the network in a supergranular cell observed with the Hinode/NFI (Gošić et al. 2016). The instantaneous rates exhibit strong fluctuations, caused by large IN features that appear in bipolar clusters or small IN ephemeral regions and end up interacting with network patches. The mean flux transfer rate turns out to be \((1.53 \pm 0.02) \times 10^{24}\) Mx day\(^{-1}\), i.e., about 40% of the total flux lost by the IN (Gošić et al. 2014, 2016).
Thus, the IN provides the network with an enormous amount of flux. Approximately half of it is positive and half is negative, so the net contribution is almost zero (Gošić 2015). However, in absolute value the IN is capable of supplying as much flux as the network contains in only about 10 h. The subsequent evolution of that flux is not known, but there must be efficient ways to remove it from the surface, otherwise the network flux would grow indefinitely.
3.7 Flux balance in the internetwork
Table 1 summarizes the mean flux appearance and disappearance rates observed in two different supergranular cells near the disk center, as reported by Gošić et al. (2016) from the analysis of long-duration Hinode/NFI magnetogram sequences.Footnote 20 Although these rates have previously been determined by other authors, none of the works published in the literature offers the consistency of the analysis by Gošić et al. (2016), who used the same magnetic feature tracking algorithm and the same methods on the same data sets to derive all the rates at once, thus providing a complete overview of the flux budget of individual supergranular cells.
As can be seen in the table, the flux appearance rates are nearly identical in the two cases. Also the disappearance rates are very similar. This is a remarkable result, given the different properties of the two supergranular cells: one of them (data set 2) was highly unipolar, while the other showed no polarity imbalance.
Table 1 demonstrates that the flux appearance and disappearance rates agree to within 5%, i.e., flux appears in the supergranules at the same rate as it disappears, keeping the flux content unchanged. This almost perfect balance is maintained also instantaneously, as can be seen in the lower panel of Fig. 14. The curves showing the appearance and disappearance rates are very similar, and where they differ the reason is the temporal delay between the appearance and disappearance of strong IN features within the cells, which is non negligible in most cases.
The rates given in Table 1 should be considered as lower limits, as higher sensitivity measurements are likely to increase them. Analysis of SUNRISE/IMaX data by Smitha et al. (2017), for example, suggests a total flux appearance rate of 1100 Mx cm\(^{-2}\) day\(^{-1}\), nearly one order of magnitude larger than indicated by the Hinode/NFI magnetograms of Gošić et al. (2016). The IMaX data have both higher sensitivity and higher spatial resolution, but shorter duration. The spectral line is also different, Fe i 525.02 nm instead of Na i 589.6 nm. This means IMaX was able to observe weaker flux concentrations in deeper layers of the photosphere where the fields are stronger. The two effects can be expected to produce increased flux rates.
4 The quiet Sun internetwork: magnetic properties
The quest for characterizing the properties of quiet Sun IN fields has been pursued for more than 30 years and represents a beautiful example of the scientific method, with discoveries, pitfalls, independent verification of results, dissenting views, controversies, and many heated debates that spurred new ideas, and that are finally appearing to converge toward a relatively simple picture of quiet Sun magnetism. Although much progress has been made in the intervening years, some aspects are still open to discussion and further scrutiny.
Here we take a close look at the Zeeman polarization signals observed in the IN and the information they give us on the properties of the fields. We examine how the longitudinal magnetic flux density changes with spatial resolution in the IN. This allows us to draw conclusions as to whether the fields are resolved or not. We also review the field strength and field inclination estimates reported by different authors and the controversies they have fueled. The Hanle view of the solar IN will be presented in Sect. 4.6.
4.1 Zeeman polarization signals
The magnetogram movies of Figs. 11 and 12 show a wealth of magnetic features in the solar IN. However, these are only the strongest signals and many areas look empty. Such regions also contain magnetic fields, but their signals are very weak. To detect them one needs the higher sensitivity provided by grating spectropolarimeters. Figure 23 shows Hinode/SP observations carried out in the so-called deep mode with an integration time of 9.6 s. The slit was kept fixed at a disk center position and repeated measurements were taken there. The first four panels of the figure display the Stokes I, Q, U, and V spectra recorded in one of the 9.6 s integrations. They show circular polarization nearly everywhere along the slit, but few patches of linear polarization.
To increase the signal-to-noise ratio of the measurements, Lites et al. (2008) averaged seven consecutive slits, resulting in an effective integration time of 67.2 s and a noise level of \(3\times 10^{-4} \, I_{\mathrm{QS}}\) (middle panels of Fig. 23). At this point, 100% of the pixels exhibit measurable Stokes V signals and some start to show clear linear polarization signals. However, the noise is still high. The integration can be pushed even further to reveal the weakest signals (Bellot Rubio and Orozco Suárez 2012). With integrations of 9.8 min (rightmost panels in Fig. 23), the noise is reduced down to \(10^{-4} \, I_{\mathrm{QS}}\) and more than 60% of the pixels show Stokes Q or U amplitudes larger than 4.5 times the noise level. Many other pixels exhibit recognizable linear signals, albeit with smaller amplitudes. Interestingly, the two lines recorded by Hinode have the same characteristic shapes in Stokes Q (and in Stokes U). One may also notice that the Stokes Q and U profiles detected so clearly in the longer integrations were also present in the other datasets, but buried in the noise. This gives confidence that they are genuine signals. The price to pay for reaching such sensitivities is a degraded spatial resolution and the possibility of signal mixing due to the long integrations. For example, if the lifetime of the magnetic structures is shorter than the integration time, the fields contributing to a given pixel may disappear and be replaced by different ones during the measurement process, intermingling the signals. Still, the rms contrast of the granulation after 10 min of integration is 5.6%, much larger than the typical contrasts of equivalent ground-based measurements.
Stokes I, Q, U, and V slit images of the quiet Sun at disk center taken with the Hinode SP. The first four panels corresponds to an integration of 9.6 s. The middle panels have an effective integration time of 67.2 s and the right ones 9.8 min. The horizontal axis represents wavelength and the vertical axis is spatial distance along the slit, which was oriented in the N-S direction. The Stokes Q, U, and V panels are saturated at \(\pm 10^{-3}\, I_{\mathrm{QS}}\). Image reproduced with permission from Bellot Rubio and Orozco Suárez (2012), copyright by AAS
The deep mode observations of Hinode show an important aspect of the IN magnetism that is worth highlighting here: the circular and linear polarization signals do not change in a random manner along the slit. Rather, they vary smoothly with spatial position. In linear polarization one can observe patches with sizes ranging from 0\(.{5}^{\prime \prime }\) to 2\(^{\prime \prime }\)–3\(^{\prime \prime }\). This suggests that the measured signals are not created by disorganized fields within the resolution element, but by well defined, discrete structures. Some of them are the ones observed in magnetogram movies with relatively long lifetimes of 2–15 min (Sect. 3). Also, the high abundance of linear signals along the slit already suggests that IN fields are highly inclined to the vertical.
4.2 Stokes V profile shapes
The IN exhibits a large diversity of Stokes V profile shapes, reflecting the richness of physical conditions and processes that take place there.
In static plane–parallel atmospheres, Stokes V is antisymmetric, with a well defined zero-crossing point and two lobes of opposite sign and equal amplitudes (e.g., Landi Degl’Innocenti and Landolfi 1983). However, the observed IN profiles often show area and amplitude asymmetries.Footnote 21 The existence of gradients of velocity with height is a necessary and sufficient condition for generating non-zero area asymmetry (Auer and Heasley 1978; Landolfi and Landi Degl’Innocenti 1996). The area asymmetry is further enhanced by gradients of field strength, field inclination, or field azimuth (e.g., Illing et al. 1975; Sanchez Almeida and Lites 1992; Makita 1986). Its sign depends on the sign of the gradients themselves (Solanki and Pahlke 1988; Solanki and Montavon 1993), which gives some information on how the atmospheric parameters vary with height. Vertical gradients also produce amplitude asymmetries, but other mechanisms do so too. For example, the coexistence of several magnetic components with different velocities in the resolution element is a very efficient means of generating Stokes V amplitude imbalances. Distinguishing between the different possibilities is not easy, which explains the limited diagnostic potential of the amplitude asymmetry compared to the area asymmetry.
Various classifications of quiet-Sun Stokes V profile shapes at spatial resolutions on the order of 1\(^{\prime \prime }\) exist in the literature for visible and near-IR spectral lines (e.g., Sigwarth et al. 1999; Sigwarth 2001; Khomenko et al. 2003; Domínguez Cerdeña et al. 2003b). In Fig. 24 we present a compilation of IN Stokes V profiles recorded by Hinode at 0\(.{3}^{\prime \prime }\). The classification has been done manually, using as fewer classes as possible to illustrate the broad range of variation of the spectra. Other classifications of Hinode profiles have been presented elsewhere (e.g., Viticchié and Sánchez Almeida 2011).
Classification of Fe i 630.15 and 630.25 nm Stokes V profiles observed by Hinode in a quiet Sun IN region at disk center with a resolution of 0\(.{3}^{\prime \prime }\). The dotted lines indicate the central wavelengths of the two lines. The profiles exhibit distinct spectral signatures. Panel a displays a prototypical regular profile with two lobes of opposite sign. The other panels show profiles with increasingly larger asymmetries (b), only one lobe (c and d), three lobes (e), bumps in the one of the lobes (f and g), and even four lobes (h). The cause of these spectral features can be traced back to the physical processes at work on the solar surface. The numbers shown in each panel give the fraction of IN profiles belonging to the different classes, considering only those pixels with signals above 6 times the noise level
In the following, the different classes will be described using the terminology introduced by Sigwarth (2001). When the asymmetries are small and two antisymmetric lobes can be recognized we have normal profiles (Fig. 24, panel [a]). Profiles with strong area asymmetries indicate the existence of vertical gradients (panel [b]). In extreme cases, one of the lobes is completely suppressed (panels [c] and [d]). The origin of these single-lobed profiles has been investigated using different magnetic configurations (e.g., Grossmann-Doerth et al. 2000; Steiner 2000, 2001; Ploner et al. 2001; Sainz Dalda et al. 2012). In general, they require sharp discontinuities of the atmospheric parameters along the line of sight, such as those occurring in magnetic canopies—the interface between a magnetized and a field-free region. An example is given in Fig. 3. Multiple polarity reversals along the atmosphere (Ploner et al. 2001) and even smooth stratifications (Viticchié 2012; Borrero et al. 2013) can also generate one-lobed profiles.
Circular polarization profiles with three lobes, similar to Stokes Q or U, can be found as well (Fig. 24, panel e). Sometimes the central lobe is strongly suppressed. These mixed-polarity profiles can be produced, for instance, by the superposition of two Stokes V signals of opposite polarity and different Doppler shifts. They suggest the presence of distinct magnetic field structures within the resolution element (Rüedi et al. 1992; Sánchez Almeida et al. 1996; Sánchez Almeida and Lites 2000). However, such profiles are also generated by sharp vertical gradients of field inclination and velocity (e.g., Ploner et al. 2001). This means that the opposite polarities do not need to coexist side by side, as they can also occur along the line of sight.
Dynamic profiles are those that exhibit a blue (or red) lobe with two humps, indicating the presence of an additional V signal with the same polarity but larger Doppler shifts (panels [f] and [g]). This class is similar to the mixed-polarity one since it requires distinct magnetic structures within the same resolution element or along the line of sight. The only difference would be the polarity of the two components, which in this case is the same. An example of dynamic profiles with very large Doppler shifts producing four lobes is shown in panel [h].
The classification presented in Fig. 24 is almost identical to that of Sigwarth (2001), with the exception of the profiles with many lobes and erratic shapes he found (classes IIIa, IIIb, and IIIc in his Fig. 4). We have not seen such profiles in Hinode/SP data, possibly because of the better spatial resolution and absence of atmospheric seeing. However, we cannot rule out the existence of IN profiles with even more complicated shapes or extreme asymmetries at higher spatial resolution and sensitivity. Magnetoconvection simulations seem to generate a very broad range of Stokes V profile shapes (Ploner et al. 2001; Steiner 2001; Sánchez Almeida et al. 2003b; Khomenko et al. 2005b; Bello González et al. 2009), so it is likely that future observations will reveal more complex Stokes V spectra.
To categorize the IN Stokes V profiles observed by Hinode into the eight families shown in Fig. 24 we used the Euclidean distance as the metric of choice and considered only pixels with circular signals above 6 times the noise level. The fraction of profiles belonging to each class is indicated in the corresponding panel. These values should be considered as approximate, given the limitations of current classification methods. The Euclidean distance is a popular metric, but it fails to capture the subtleties of the profiles and may lead to errors. For example, dynamic profiles can be classified as profiles with strong area and/or amplitude asymmetries, because the dip between the two humps in the red or blue lobe produces a very small change in the metric. Therefore, it is sometimes impossible to distinguish between a highly asymmetric profile and one with two visible components in the red or blue lobe. To avoid this problem, other parameters need to be considered together with the Euclidean distance, e.g., the amplitude and area asymmetries or the profile width, in order to improve the reliability of the classification. Another difficulty is that the profile shape changes with the strength of the signal. For example, one- and three-lobed profiles are often weak and therefore noiser and more difficult to classify.
Keeping in mind these caveats, the populations given in Fig. 24 show that two-lobed asymmetric profiles are the most abundant in the IN (38%), followed by one-lobed profiles (24%), dynamic profiles (22%), regular anti-symmetric profiles (16%), and mixed-polarity profiles (1%). The distribution varies significantly when weaker signals are included in the analysis.
4.3 How is the magnetic field organized in the internetwork?
To estimate the magnetic energy stored in the solar atmosphere it is necessary to have a good knowledge of how quiet Sun magnetic fields are structured. This is because the inference of the field strength—the basic quantity determining the magnetic energy—depends critically on a precise understanding of the field organization, with different models producing different results, as we shall see later. Of utmost importance is whether or not the fields are spatially resolved in current observations.
Unresolved fields are expected to produce cancellation of opposite-polarity Stokes V signals, as described in Sect. 2.3.1. We still do not know if this problem affects our measurements, but several indirect arguments suggest that some degree of Zeeman cancellation might be present in the observations. For example, the existence of mixed-polarity profiles (Sect. 4.2) already demonstrates that some pixels contain fields of opposite polarity (although in this case they are well recognizable in the Stokes V profiles and do not produce complete Zeeman cancellation). Also, the magnetic energy of IN fields inferred through Hanle diagnostics appears to be larger than that calculated from Zeeman measurements (e.g., Trujillo Bueno et al. 2004). This led to the concept of very small-scale, turbulent fields which would permeate the whole solar surface and would be invisible to Zeeman-sensitive lines because of complete cancellation of the correspondig Stokes V signals. Another argument is based on the abundance of asymmetric Stokes V profiles. Sánchez Almeida et al. (1996) argued that the existence of mixed-polarity magnetic fibrils with sizes of a few tens of km within the resolution element would be able to explain the large fraction of asymmetric profiles. Also possible is the operation of a local dynamo on the solar surface (Vögler and Schüssler 2007). In that case, the observed magnetic structures would be the result of the stretching of field lines by turbulent plasma motions, which would create a pattern of highly mixed-polarity fields prone to Zeeman cancellation.
Interestingly, the longitudinal magnetic flux density defined by Eq. (9) is a good indicator of the amount of Zeeman cancellation that may affect the observations. Depending on how the magnetic field is organized, the observed longitudinal flux density will behave differently as the spatial resolution improves. There are three possibilities:
- (i)
The magnetic structures have extremely small characteristic sizes. As a consequence, each pixel is filled with a homogeneous distribution of fields with random orientations. In this case, the longitudinal flux density does not change with spatial resolution because the fields are too small to be resolved and the amount of Zeeman cancellation they produce is always the same.
- (ii)
The magnetic structures are large and spatially resolved. Therefore, there is no Zeeman cancellation and the longitudinal flux density remains constant with spatial resolution.
- (iii)
The structures have intermediate sizes. The IN is unevenly permeated by magnetic fields of both polarities which are not yet fully resolved. Improvements in the spatial resolution will make it possible to separate some of them, decreasing the amount of Zeeman cancellation and therefore increasing the longitudinal flux density in the pixel.
Effects of spatial degradation on magnetograms generated from SUNRISE/IMaX V5-6 data using the weak field approximation. The top left panel is the longitudinal flux density map at the original resolution of IMaX. The other panels show the maps corresponding to different resolutions. The gray scale is the same in all panels. Note that the spatial degradation is applied to the observed Stokes profiles and not to the magnetograms themselves
To decide which of these situations better represents reality, we perform here a controlled experiment using data from SUNRISE/IMaX. This instrument has delivered the highest resolution observations of the quiet Sun available to date. We first spatially degrade the monochromatic Stokes I and V images with a Gaussian PSF whose FWHM is set to the desired resolution and compute the longitudinal flux density for each pixel using the weak field approximation (Eq. 8). Then we study how much of the original longitudinal flux density gets canceled as the resolution worsens.
Figure 25 shows the resulting flux density maps for the data at highest resolution (top left panel) and degraded resolutions (from left to right, and from top to bottom). The original phase-diversity reconstructed data show magnetic features of both polarities in close proximity. These elements have a broad distribution of spatial sizes and fluxes. As the observations are artificially degraded, the number of features that remain visible decreases. At 0\(.{88}^{\prime \prime }\), magnetic elements about 1\(^{\prime \prime }\) in diameter are still clearly distinguishable, but at 3\(^{\prime \prime }\) most of the features have canceled and the magnetogram looks rather diffuse.
Variation of the longitudinal magnetic flux density with spatial resolution calculated using SUNRISE/IMaX data (solid and dotted) and Hinode/SP observations (dashed). The longitudinal flux density values were computed taking into account all the pixels within the field of view except for the dotted line, in which only pixels with circular polarization signals exceeding twice the noise level of the data at original resolution have been included
To quantify the degree of cancellation, in Fig. 26 we present the variation with spatial resolution of the unsigned longitudinal flux density averaged over the field of view (i.e., the mean value of \(| \varphi |\), considering all pixels). The black curve shows that the longitudinal flux changes little from 3\(.{5}^{\prime \prime }\) to about 1\(^{\prime \prime }\). Below 1\(^{\prime \prime }\), however, the flux quickly increases. This simple exercise strongly suggests that the magnetic structures of the solar IN start to be resolved by the observations at \(\sim 1\) \(^{\prime \prime }\). As a consequence of the reduced Zeeman cancellation, higher fluxes are detected. The variation of the longitudinal flux density with resolution r is well described by an exponential of the form \(\overline{|\varphi |} \propto \exp {(-1.1r)}\).
The flux increase observed below 1\(^{\prime \prime }\) could be due to the noise of the magnetograms, which is larger at high resolution. To rule out this possibility, the dotted curve in Fig. 26 shows the mean unsigned longitudinal flux density calculated taking into account only those pixels whose circular polarization amplitudes are at least twice the noise level of the data with the best resolution. In this way we use the same noise threshold to analyze all the maps. Now the longitudinal flux density increase is steeper at better resolutions because the averages no longer include the weakest signals in the FOV, but the general trend remains the same. The similarity between the solid and the dotted curves demonstrates that the increase of the flux below 1\(^{\prime \prime }\) is due to the smaller degree of Zeeman cancellation (we are resolving the magnetic structures) and not to the noise. Very remarkably, the same functional dependence is obtained from Hinode/SP normal-map observations (red dashed line in Fig. 26). As in the IMaX case, the variation of the longitudinal flux density with spatial resolution has been calculated using the weak field approximation and all pixels within the FOV. The only difference between the IMaX and Hinode curves is a small offset of 1–2 G, which possibly reflects the different sensitivities of the Fe i 525.02 nm and Fe i 630 nm lines, given that the same diagnostic was applied and neither of the two datasets is affected by seeing fluctuations.
We can compare the results of our experiment with magnetoconvection simulations, which have also been employed to determine the dependence of the longitudinal flux density on spatial resolution (e.g., Sánchez Almeida et al. 2003b; Abbett 2007). In the MHD models, the flux decreases because of the cancellation of opposite polarities on small spatial scales. However, the rate at which this happens differs between simulations. For instance, in the convective dynamo simulations of Abbett (2007) the longitudinal flux density decreases as \(\exp {(-1.0r)}\), similarly to the \(\exp {(-1.1r)}\) drop deduced from the SUNRISE/IMaX and Hinode/SP measurements (Fig. 26). The Boussinesq dynamo simulations of Sánchez Almeida et al. (2003b) show a rather different functional dependence, with the flux decreasing drastically as soon as the resolution deteriorates. The flux cancellation is less pronounced in mixed-polarity simulations compared to dynamo simulations (e.g., Khomenko et al. 2005b). In the former, fields of opposite polarity are inserted into the computational domain in an ad-hoc manner, since no dynamo action occurs, while in the latter the fields are the result of amplification by turbulent convective motions. The different magnetic topology generated by the two setups is responsible for the different degree of Zeeman cancellation.
In summary, the analysis presented here suggests that we are starting to resolve the magnetic structures of the solar IN, at least the largest ones. Actually, this is not a surprising result, given the myriad of coherent IN features that are detected by high-sensitivity instruments. Those magnetic features have a range of lifetimes and evolve smoothly, interacting with the granulation and with other IN magnetic elements. The fact that (part of) the IN fields are being resolved in current observations substantiates the use of simple models to derive their properties, e.g., one-component model atmospheres. The sharp increase of the flux below 1\(^{\prime \prime }\) observed in our controlled experiment using SUNRISE/IMaX and Hinode/SP data is very similar to that indicated by the dynamo simulations of Abbett (2007), but differ from others, pointing to fundamental differences in the structuring and organization of the magnetic field between simulations.
4.4 Magnetic flux in the solar internetwork
The mean longitudinal magnetic flux of the solar IN is an important quantity for direct comparisons with numerical simulations and therefore it has been measured by many authors over the years. Here we discuss the available estimates, including the ones derived from seeing-free SUNRISE/IMaX and Hinode/SP observations, and assess their reliability.
Figure 27 shows the results of a survey of the mean unsigned longitudinal magnetic flux densities reported in the literature as a function of spatial resolution. We have imposed strict selection criteria considering only publications that (i) explicitly provide the unsigned longitudinal flux density averaged over the field of view and (ii) clearly indicate the effective spatial resolution of the observations (frequently limited by seeing in the case of ground-based measurements). Publications providing enough information to calculate the flux in the full field of view have been included too. In total, 31 estimates met these criteria. For the most part they refer to the quiet Sun as a whole, since no separation between IN and network regions is usually made. The plot shows a large scatter that gets worse at higher resolutions. However, there is a trend of longitudinal flux densities increasing as the resolution improves, from the 3\(^{\prime \prime }\) of the early studies to the 0\(.{15}^{\prime \prime }\) achieved by SUNRISE/IMaX. This is consistent with the results of the experiment carried out in Sect. 4.3.
Compilation of quiet Sun longitudinal flux densities reported in the literature against spatial resolution of the observations. Each of the symbols represents a measurement, as indicated on the right. Blue colors mark flux values derived from simultaneous observations in visible and near-IR lines. Red stands for near-IR lines alone. Error bars are present when the authors provide them or when different values for the flux and the spatial resolution are reported in the publication
The often contradictory values reported by different authors at similar resolutions reflect the many uncertainties of flux density measurements. The estimates are affected by atmospheric seeing that blurs and distorts the images and can alter the flux very efficiently (Lee et al. 1997), by the noise of the observations (Lites et al. 2008), by the different sensitivities of the spectral lines, by the specifics of the diagnostic techniques (Beck and Rezaei 2009), and by systematic instrumental errors (zero-point calibration, stray-light contamination, etc.). The scatter observed in Fig. 27 is the result of the combination of these problems. Another source of scatter is the intrinsic differences between different regions of the solar surface. As shown by Table 1 in Viticchié et al. (2011), the flux densities in the IN, the network, and the entire quiet Sun, including all the pixels or only the analyzed ones, may differ by up to 60 G even when the same observations and analysis technique are used.
With the large scatter of Fig. 27, the extrapolation of the data points toward infinite spatial resolution is questionable. Note that representing the data on a logarithmic scale may give the wrong impression that the scatter is small. For example, Figure 3 of Sánchez Almeida and Martínez González (2011) is similar to ours but uses a logarithmic scale. A fit to the data suggested that the flux varies with spatial resolution as \(\phi (r) \propto r^{-1}\). However, the fluxes obtained from the best quality measurements deviate from the fit by up to a factor of 3. Extrapolations are not warranted in this case, as they may produce even larger errors. Another problem with extrapolations is that there is no guarantee that the flux density will keep the same behavior on scales not yet resolved by the observations.
For these reasons, plots like the one shown in Fig. 27 should not be used to draw conclusions about the organization of the field on still unresolved scales. They are useful, though, to estimate the longitudinal magnetic flux in the solar IN at the resolution of 0\(.{15}^{\prime \prime }\)–0\(.{5}^{\prime \prime }\) achievable nowadays, which seems to be between 10 and 20 Mx cm\(^{-1}\).
4.5 Magnetic field strength and inclination distribution in the IN
4.5.1 Early determinations
The first attempts to determine the field strength of IN features were made by Keller et al. (1994). They used the Zürich Imaging Polarimeter (ZIMPOL; Povel 1995) attached to the German VTT on Tenerife to record the circular polarization profiles of the visible Fe i 524.7 and 525.02 nm lines. At the attained spatial resolution (probably \(\sim 5\) \(^{\prime \prime }\)), the observations yielded an upper 1\(\sigma \)-limit of 500 G on the strength of IN fields via the line-ratio technique (Sect. 2.2.3).
Soon thereafter, Lin (1995) reported the first spectrograph measurements of circularly polarized light in the IN using the near-IR Fe i 1564.8 and 1565.2 nm lines (see also Rüedi et al. 1992). From the observed Zeeman splittings he obtained weak IN fields, with a mean strength of 500 G, consistent with the results of Keller et al. (1994). Lin (1995) suggested that IN fields might be in the form of small flux tubes with an average size of \(\sim 75\) km, implying small filling factors. Given the relatively long exposure time (90 s) and large slit width (1\(^{\prime \prime }\)) of the observations, the spatial resolution was not very different from that achieved in the visible. The same data were later analyzed by Solanki et al. (1996), who obtained an average field strength of about 280 G and further suggested that IN features are flux tubes that either are in equipartition with convection or have undergone weak convective collapse. At the time, no linear polarization signals were detected in visible or near-IR lines.
Using the ASP, Lites et al. (1996) performed observations of the four Stokes profiles of the Fe i lines at 630.15 and 630.25 nm in the quiet Sun. These observations represented a breakthrough since for the first time they showed linear polarization signals in the IN, leading to the discovery of Horizontal Internetwork Fields (HIFs) at 1\(^{\prime \prime }\) resolution. A two-component Milne–Eddington inversion (Sect. 2.2.3) of the data suggested weak field strengths and large inclinations. The HIFs were considered to be an additional ingredient of the global IN magnetism. Lites (2002) analyzed the same data and identified two magnetic components in IN regions: spatially concentrated fields that are observed mainly in intergranular lanes and large-scale, diffuse fields above granules. He estimated a longitudinal flux density of 9.2 \(\hbox {Mx cm}^{-2}\) in the IN, using all pixels with flux densities of less than 40 \(\hbox {Mx cm}^{-2}\). Furthermore, he argued that the weak IN flux detected in these ASP observations must be close to being spatially resolved (within a factor of 2–3).
In the same year, Grossmann-Doerth et al. (1996) observed the Fe i 524.71 and 525.02 nm lines with ZIMPOL at the 1.5-m McMath–Pierce telescope and, for the first time, reported field strengths in the kG range. This result was obtained through the application of a modified line-ratio technique (Sánchez Almeida et al. 1988). The spatial resolution was about 2\(.{3}^{\prime \prime }\). Unfortunately it is not clear whether the inferred field strengths correspond to the IN proper or most probably to network patches, given the fact that only 15% of the FOV was subjected to analysis.
Contradicting the results of Grossmann-Doerth et al. (1996), further observations of the Fe i 1565 nm lines at a resolution of 2\(.{5}^{\prime \prime }\) by Meunier et al. (1998) yielded weak fields. Lin and Rimmele (1999) found field strengths in the range from 200 to 1000 G and small filling factors (\(<1\%\)) using the same lines. They noted that IN fields evolve in close association with the solar granulation and suggested that such “granular” fields might be an additional weak field component of the IN.
Sigwarth et al. (1999) also analyzed observations of the Fe i 630 nm lines taken with the ASP. The spatial resolution was claimed to be 0\(.{8}^{\prime \prime }\) and the noise about \(10^{-4}\) in units of the continuum intensity. These authors calculated the distribution of field strengths using the ASP ME inversion code with a single magnetic component and a nonmagnetic atmosphere. They found clear indications that IN fields are weak, in contrast to the network which showed kG fields.
The work of Sigwarth et al. (1999) revealed for the first time the existence of a large variety of Stokes V profile shapes in the IN, from regular antisymmetric profiles to very asymmetric single-lobed profiles, caused by complex magnetic topologies and dynamics (Sect. 4.2). Several configurations have been proposed to explain the observed shapes, including magnetic canopies in flux tubes, small-scale magnetic loops, and MISMAs.
4.5.2 Visible vs near-infrared lines: controversy and suggested solutions
The MISMA hypothesis (Sánchez Almeida et al. 1996) was applied to Fe i 630 nm observations of the IN by Sánchez Almeida and Lites (2000), Sánchez Almeida (2001), and Socas-Navarro and Sánchez Almeida (2002). A model consisting of two magnetic components and one non-magnetic component, plus stray-light contamination, was shown to be able to reproduce the asymmetric Stokes V profiles observed by the ASP. The main conclusions of these analyses were: (i) a large proportion of IN fields are in the kG regime, although weak fields also exist; (ii) the filling factors are small, of order 1%; (iii) a sizable fraction of the observed Stokes V profiles require two magnetic components with opposite polarities; and (iv) an unknown amount of the flux remains undetected. The IN flux density obtained from the MISMA inversion was 10 \(\hbox {Mx cm}^{-2}\).
Sánchez Almeida and Lites (2000) argued that their strong fields were compatible with the fields derived from the Fe i lines at 1565 nm, because in a model MISMA the visible lines trace the kG fields while the near-IR lines are more sensitive to the weaker fields present in the atmosphere (for example, due to vertical field gradients). However, this explanation does not account for the hG fields inferred from the Fe i 630 nm lines by other authors.
Left: Distribution of field strengths calculated from the Zeeman splitting of the Fe i lines at 1564.8 and 1565.2 nm. The solid, dashed, and dotted lines represent all pixels in the FOV, only granules, and only intergranular lanes, respectively. Right: Histogram of the field inclinations derived by comparing the Stokes Q and U amplitudes with the Stokes V amplitudes. The solid line represents all pixels. The dashed (dotted) line stands for the pixels with Stokes V (Stokes Q or U) signals above the noise level. The right part of the field strength distribution corresponding to all pixels is well represented by an exponential of the form \(A \exp {(-B/B_0)}\), with \(B_0=200\) G and A a normalization constant. Image reproduced with permission from Khomenko et al. (2003), copyright by ESO
The controversy about the strength of IN fields continued with Khomenko et al. (2003) finding hG fields from near-IR measurements (see also Collados 2001) and Domínguez Cerdeña et al. (2003a, b) favoring kG fields from observations of the 630 nm lines. The former authors measured the Fe i 1565 nm lines with TIP at the VTT. Their maps show 50% (20%) of pixels with circular (linear) polarization signals above \(10^{-3} \, I_{\mathrm{QS}}\) (3 times the noise level), with most of the features located in intergranular lanes. Figure 28 depicts the field strength and field inclination distributions they obtained using the Zeeman splitting of the Stokes profiles with well-defined shapes (about 70% of the selected pixels). According to their results, the fields are weak with a distribution that peaks at 350 G. The mean inclination is \(\sim \)20\(^\circ \), but the distribution is broad with only 5% of the pixels having inclinations larger than 70\(^\circ \). The other 30% of the profiles showed three lobes, suggesting mixed polarities within the pixel. Khomenko et al. (2003) estimated a longitudinal flux density of 8 \(\hbox {Mx cm}^{-2}\) and filling factors of order 2%.
Domínguez Cerdeña et al. (2003a, b), on the other hand, employed observations taken with the GFPI at the German VTT. They recorded the Stokes I and V profiles of the 630 nm lines at 28 wavelength positions and reconstructed the data to reach a spatial resolution of 0\(.{5}^{\prime \prime }\). Using the weak field approximation, they found longitudinal flux densities of 17–21 \(\hbox {Mx cm}^{-2}\), twice as large as any other observation thus far. The line ratio technique yielded field strengths between 900 and 1600 G and filling factors around 2%. Most of the magnetic signals were located in intergranular lanes, although some patches could be observed in granules.
These results appeared to be confirmed when Lites and Socas-Navarro (2004) analyzed high resolution (\(\sim \)0\(.{6}^{\prime \prime }\)) observations of the Fe i 630 nm lines by the DLSP and found intrinsic field strengths in the kG range and small filling factors (< 1%) using the line ratio technique.
Theoretical arguments were then proposed to elucidate the origin of the discrepancy between visible and near-IR measurements. A solution can be found if one assumes that there is a continuous distribution of fields in the pixel, with the hG fields occupying a larger fractional area than the kG fields (Socas-Navarro and Sánchez Almeida 2003). Analyzed in terms of a single magnetic component, the near-IR lines would be more sensitive to the weak fields and the visible lines to the strong fields. The reason is the quadratic dependence of the Zeeman splitting on wavelength, which makes the polarization signals generated by the field spread over a longer wavelength interval in the near-IR. When the pixel contains a mixture of weak and strong fields, the polarization of near-IR lines will come mainly from the former because they buid up a larger signal than the strong fields which are further away. For visible lines, the signals produced by the weak and the strong fields overlap in wavelength, but the latter are dominant due to their larger amplitudes. As a consequence, the near-IR lines would pick out the weaker fields while the visible lines would trace the stronger fields, unless multi-component models are used to interpret the observations.
The possibility of having a subpixel distribution of fields with both hG and kG strengths was examined by Socas-Navarro and Lites (2004) using data from the DLSP and the ASP (see also Socas-Navarro 2004a, b). They considered a model with one field-free component and two magnetic atmospheres whose strengths were fixed at 300 G and 1700 G. Many of the observed profiles could be reproduced by changing the relative occupation factor of the two magnetic components. In those cases, the analysis yielded 300 G fields in 70–90% of the magnetized area within the pixel and 1700 G in the remainder 10–30%. Surprisingly, also the network elements were found to harbor a similar mixture of weak and strong fields on subresolution scales.
Yet another possibility was suggested by Bellot Rubio and Collados (2003). They simulated Stokes V profiles assuming an exponential distribution of field strengths, and interpreted them in terms of a single magnetic component in the pixel. Their results showed that photon noise changes the amplitudes of the Fe i 630 nm lines efficiently, which for small signals is prone to result in kG strengths even when the fields are weak. The Fe i 1565 nm lines are less affected because of their larger Zeeman splitting. To minimize the bias of the visible lines, Bellot Rubio and Collados (2003) recommended to use Stokes V measurements with signal-to-noise ratios of at least 10–15.
Finally, Martínez González et al. (2006) showed that the Fe i 630 nm lines can be affected by crosstalk between the magnetic and thermodynamic parameters of the atmosphere, which decreases the reliability of the field strengths inferred from Stokes inversions. The reason, again, is their small Zeeman splitting. The Fe i 524.7 and 525.0 nm lines also suffer from this drawback (Martínez González 2007).
At that point it was natural to try to observe the same IN region in visible and near-IR lines simultaneously. Sánchez Almeida et al. (2003a) made the first attempts. Two data sets were taken 1 min apart with TIP at the German VTT and the Multi-Raie (MTR) mode at THEMIS, but the achieved spatial resolutions were different (1\(^{\prime \prime }\) vs 1\(.{7}^{\prime \prime }\)). Using ME inversions, Sánchez Almeida et al. (2003a) found a preponderance of kG fields from the Fe i 630 nm lines while the Fe i 1565 nm lines yielded fields of about 300 G. This was taken as a proof that the visible and near-IR lines trace different fields in the resolution element. Further support for the coexistence of mixed field strengths was claimed on the ground that 25% of the analyzed pixels showed Stokes V profiles with opposite polarities in the two spectral regions.
Circular polarization maps of a quiet Sun area taken simultaneously in the Fe i 1564.8 nm line (left panel, TIP) and in the Fe i 630.25 nm line (right panel, POLIS). The red and blue contours outline positive and negative polarities, respectively. The scale is the same in both maps. Image reproduced with permission from Khomenko et al. (2005a), copyright by ESO
Khomenko et al. (2005a) were the first to observe the Fe i 630 and 1565 nm lines simultaneously at the same telescope, thus under the same seeing conditions. This was achieved using TIP and POLIS at the German VTT. The Stokes V maps resulting from the visible and near-IR observations turned out to be rather similar (see Fig. 29), with only 5% of the pixels showing opposite polarities. Also, the simultaneous observations of Martínez González et al. (2008) at the VTT showed very few pixels with one polarity in Fe i 630 nm and the opposite in Fe i 1565 nm. This suggests that the opposite polarities observed by Sánchez Almeida et al. (2003a) in the two spectral lines were probably caused by the different seeing conditions prevailing at the telescopes.
Simulations have also been used to understand how the limitations of the analysis techniques may generate discrepancies between visible and near-IR observations. Khomenko and Collados (2007) examined the line ratio method, coming to the conclusion that the Fe i lines at 630 nm do not provide a good diagnostics of the field strength because of their different formation heights and the existence of strong vertical gradients in the atmosphere. The Fe i 525.0/524.7 and Fe i 1564.8/1565.2 line ratios allow much better inferences to be made. This suggests that the IN field strengths derived from 630.25/630.15 line ratios may be compromised, including those of Socas-Navarro and Sánchez Almeida (2003), Domínguez Cerdeña et al. (2003a, b), Socas-Navarro et al. (2004), and Lites and Socas-Navarro (2004). The field strength determinations by Keller et al. (1994) and Grossmann-Doerth et al. (1996) would also be affected because the Fe i 525.0/524.7 line ratio carries information from high photospheric layers, where the field is already below 1 kG even in the network.
4.5.3 The Hinode era
The unprecedented stability and spatial resolution provided by the Hinode SP opened up new avenues to explore the magnetism of the quiet Sun, particularly the weakest IN signals. The SP measures the full Stokes vector of the Fe i 630 nm lines with a resolution of 0\(.{32}^{\prime \prime }\), close to the diffraction limit of the telescope. Such an enormous leap in spatial resolution helped settle the controversy between visible and near-IR lines. Here we review this result and others from ground-based facilities that appeared almost simultaneously.
Soon after the Hinode launch, Lites et al. (2007b, 2008) discovered ubiquitous linear polarization signals in the IN from an analysis of SP observations taken at different noise levels (see Figs. 10 and 23). The “apparent” longitudinal and transverse magnetic flux densities of the IN were determined assuming spatially resolved signals. The calculations yielded a longitudinal flux density of 11 \(\hbox {Mx cm}^{-2}\) and a transverse flux density of 55 \(\hbox {Mx cm}^{-2}\). This result came as a surprise because nobody had predicted such a large abundance of transverse fields. Although noise and other systematic effects could have affected the estimates, Schüssler and Vögler (2008) and Steiner et al. (2008) later reported ratios of horizontal to vertical field components of 4–6 in the mid-photospheric layers of their MHD simulations, confirming the value of 5 derived from the Hinode/SP data. Lites et al. (2008) argued that the mean IN field strength has to be at least 55 G to explain the apparent transverse flux densities indicated by the observations. They also showed that the circular polarization patches tend to be located in dark intergranular lanes, whereas the linear patches are mostly associated with intermediate intensities, i.e., they occur at the edges of granular cells (see their Figs. 8 and 9). This spatial separation suggests that the linear signals are not produced by the buffeting of flux tubes anchored in the intergranular lanes. However, Ishikawa and Tsuneta (2011) found that 53% of the linear patches occur in between circular signals of opposite polarity, so there is a relation between them. They proposed that both structures trace different parts of small-scale magnetic loops emerging in the solar surface, of the type observed by Centeno et al. (2007) and Martínez González and Bellot Rubio (2009). Lites et al. (2008) and Ishikawa and Tsuneta (2011) also found the IN polarization signals to be structured on mesogranular scales, as had been suggested by Domínguez Cerdeña (2003).
Some of the IN measurements taken by the Hinode SP were inverted in terms of ME atmospheres (e.g., Orozco Suárez et al. 2007b, c; Lites et al. 2008; Asensio Ramos 2009; Ishikawa et al. 2008; Ishikawa and Tsuneta 2009; Borrero and Kobel 2011; Jin et al. 2012; Orozco Suárez and Bellot Rubio 2012). ME models cannot reproduce asymmetric profiles such as those observed in the IN. However, as pointed out in Sect. 2.4, they do a very good job in retrieving the average properties of the atmosphere (Fig. 9). A similar conclusion was reached by Westendorp Plaza et al. (1998), Orozco Suárez et al. (2010a), and Borrero et al. (2014), who used asymmetric profiles generated from prescribed atmospheres and MHD simulations, respectively, and inverted them in terms of ME models. The reason why ME atmospheres have been employed to analyze Hinode/SP observations of the IN is the weakness of the signals, which makes the application of more sophisticated atmospheres challenging. ME inversions do not provide information about gradients of atmospheric parameters with height. However, they are robust and the averages along the line of sight obtained from them were deemed sufficient for a first exploratory investigation of the IN magnetism at very high resolution. According to Borrero et al. (2014), the parameters returned by ME inversions describe the properties of a corrugated surface whose height can be calculated pixel by pixel using generalized response functions. They can also be ascribed to a fixed optical depth, albeit with larger errors.
The main results of ME analyses are summarized in Fig. 30. It shows the magnetic field strength and field inclination probability density functions (PDFs) calculated by Orozco Suárez and Bellot Rubio (2012). They were obtained assuming that the resolution element contains a homogeneous magnetic atmosphere, in line with the arguments put forward in Sect. 4.3. Orozco Suárez and Bellot Rubio (2012) included a “local” non-magnetic component in the inversion to account for the effects of the instrumental PSF (see Sect. 2.3.2).
Magnetic field strength (left) and inclination (right) probability density functions for IN regions resulting from a ME inversion of Hinode/SP data with a noise level of \(3 \times 10^{-4} \, I_{\mathrm{QS}}\). Only pixels whose Stokes profile amplitudes exceed a polarization threshold of 4.5 times the noise level were included in the analysis. Inclinations are measured from the local vertical. Image reproduced with permission from Orozco Suárez and Bellot Rubio (2012), copyright by AAS
The PDFs shown in Fig. 30 correspond to a deep integration data set with a noise level of \(3 \times 10^{-4} \, I_{\mathrm{QS}}\) and represent 72.7% of the analyzed IN area. The field strength distribution peaks at \(\sim 100\) G and then decreases rapidly toward stronger fields. This indicates that the IN consists of hG flux concentrations for the most part. There is no hump at kG values because network pixels were excluded from the PDF. The average field strength is 170 G and the FWHM of the distribution 190 G. The field inclination PDF shows a large abundance of highly inclined fields, with a maximum at 90\(^\circ \) (horizontal fields). Near 0\(^\circ \) and 180\(^\circ \) the distribution increases again, reflecting the existence of vertical fields in intergranular lanes.
The weak nature of IN fields was confirmed by Beck and Rezaei (2009) using Fe i 1565 nm measurements taken with TIP under very good seeing conditions (\(\sim 0\) \(.{7}^{\prime \prime }\)). The observations achieved a noise level of \(2\times 10^{-4} \, I_{\mathrm{QS}}\), thanks to relatively long exposures of 30 s. The data were inverted with SIR using a two-component model atmosphere (one magnetic and another field free) plus stray-light contamination. The distribution of field strengths showed a clear preponderance of weak fields and a peak around 250 G. A nearly flat distribution of field inclinations between 45\(^\circ \) and 90\(^\circ \) was inferred for fields weaker than 500 G (see their Fig. 8). Beck and Rezaei (2009) suggested that the smaller fraction of inclined fields resulting from the TIP observations as compared to the Hinode/SP measurements may be related to the deeper formation height of the Fe i 1565 nm lines.
The strictly simultaneous and co-spatial quiet Sun observations made by Martínez González et al. (2008) at the German VTT using TIP and POLIS shed additional light on the contradictory results obtained from visible and near-IR lines. The spatial resolution of the data was 1\(.{2}^{\prime \prime }\) and the noise level \(2\times 10^{-4} \, I_{\mathrm{QS}}\) after PCA filtering. The four Stokes profiles of the visible and near-IR lines were first inverted separately and then simultaneously with the SIR code. A two-component model consisting of one magnetic and one field-free atmosphere was assumed. The inversion of the visible lines delivered kG fields, while that of the near-IR lines and the simultaneous inversion of the two spectral ranges resulted in weak fields, despite the fact that the magnetic fluxes derived from the visible and near-IR lines were completely consistent. This confirmed the limitations of the visible lines for retrieving the field strength from weak IN signals when the thermodynamics is not constrained independently. The analysis also clearly showed that all the Stokes profiles observed at 1\(^{\prime \prime }\) resolution are compatible with weak IN fields.
Viticchié et al. (2011) inferred a strong decrease of the field with height from MISMA inversions of Hinode/SP normal map measurements. They used two magnetic components in each pixel to fit the asymmetrical shapes and irregularities of the observed Stokes V profiles. Such a model returned mixed polarities in 25% of the analyzed pixels. The inversions showed strong kG fields near the continuum forming layer and a predominance of hG fields in the mid photosphere, at the height of formation of the 630 nm lines. Once again, a MISMA interpretation of the data indicated a large abundance of kG fields in the solar IN, which is at odds with most of the ME analyses of Hinode/SP data published so far. However, the fraction of hG fields derived from the analysis was much larger than that reported by Sánchez Almeida and Lites (2000). Also, the fact that hG fields were detected in the mid photosphere partly reconciles the MISMA results with those from ME inversions.
Hinode/SP observations of a 7.4\(^{\prime \prime }\) \(\times \)7.4\(^{\prime \prime }\) area of the solar IN. From left to right and top to bottom: normalized continuum intensity, total (circular plus linear) polarization signal, field strength, and field inclination. The field strength and inclination have been inferred from an ME inversion of the observed Stokes vector. Contours outline the photospheric granulation (\(\mathrm{I_c}/ I_{\mathrm{QS}} > 1.05\)). Masked areas are black and correspond to pixels with polarization signals below 4.5 times the noise level. Image reproduced with permission from Orozco Suárez et al. (2007b), copyright by AAS
The spatial resolutions reachable nowadays allow granules and intergranular lanes to be studied separately. Both types of structures show clear polarization signals (Orozco Suárez et al. 2007b). The spatial distribution of field strengths and inclinations is displayed in Fig. 31. As can be seen, the fields in granular cells tend to be dispersed, weaker, and more inclined than those located in intergranular lanes. The fields observed in intergranular lanes are less inclined and seem to carry most of the magnetic flux (Beck and Rezaei 2009).
4.5.4 Latest results
Danilovic et al. (2016) recently achieved a major milestone in the analysis of Hinode/SP measurements. Using the code by van Noort (2012), these authors performed a spatially coupled inversion of a quiet Sun region near the disk center. A model featuring vertical gradients of the parameters was employed, with three nodes at log \(\tau _{500} = 0, -8\), and \(-2.0\). This type of inversion goes beyond the limits of ME atmospheres and is therefore well suited to determining the height variation of the vector magnetic field. In addition, it accounts for the effects of the telescope PSF without requiring a local stray light profile. After a meticulous test of the code on MHD simulations, the authors concluded that spatially coupled inversions are less prone to errors due to photon noise, because they use the information contained in the observations more efficiently. As a result, the magnetic field maps look less noisy and show finer small-scale details.
Danilovic et al. (2016) found magnetic fields decreasing with height in most of the observed area. Their field strength distributions are dominated by weak fields like those in Orozco Suárez et al. (2007b). However, they increase monotonically toward the weakest fields rather than showing a peak around 100 G. The average field is 130 G at optical depth unity. The field inclination also changes with height, becoming more horizontal in the upper layers. At \(\log \tau _{500} = -0.8\), the inclination distribution shows the usual peak near 90\(^\circ \), but it is less pronounced than indicated by ME inversions. At \(\log \tau _{500} = -2.0\), the amplitude of the peak is larger and the distribution comes closer to previous results. In the future, it would be desirable to apply the same code to deep-mode Hinode/SP observations, as they have significantly better signal-to-noise ratios.
Some of these results have been verified independently by Lites et al. (2017). To avoid the problems associated with the different sensitivities of circular and linear polarization to photon noise, they followed the approach of Stenflo (2013) and studied only the linear polarizations signals recorded by the Hinode SP in the IN. A total of 153 deep-mode maps taken at different positions on the solar disk were considered. Their results strictly refer to the weakest signals and show that most of IN fields have a preferred horizontal orientation, with the strongest ones being more vertical. This is in line with the conclusions of Stenflo (2013). Interestingly, Lites et al. (2017) applied the same technique to a set of MHD models by Rempel (2014), simulating instrumental effects and observing conditions. A comparison with the observations led them to suggest that the most intense and vertical fields are related to the presence of magnetic loops along the line of sight, in combination with large oblique viewing angles. From a physical point of view, such fields would correspond to the magnetic flux that is expelled from the photosphere upward in the form of small-scale loops.
4.5.5 Results from lines with hyperfine structure
The analysis of spectral lines with hyperfine structure (HFS) provided independent constraints on the distribution of magnetic fields in the quiet Sun. The first attempts to use HFS effects to determine the average intrinsic field strengths were carried out by López Ariste et al. (2006). They observed the Mn i 553.7 nm line with the ASP and estimated the field strength in different magnetic structures. The network yielded fields in the kG range, as expected, although hG fields were also detected. After averaging the profiles over a wide area to reduce the effects of noise (hence degrading the spatial resolution), they found that the IN is dominated by weak fields below 600 G. Strong fields (above kG) are also present in the IN, but filling a surface area about 10 times smaller.
Soon thereafter, López Ariste et al. (2007a) performed simultaneous observations of the solar IN in the Mn i 553.7 nm and Fe i 630 nm lines, using the MTR mode of THEMIS. They analyzed the 630 nm data by means of line ratios and SIR inversions, and compared the results with those from the Mn i 553.7 nm line. The 630 nm lines delivered kG fields with both methods, while the Mn i line gave field strengths below 600 G. These results confirmed the drawbacks of the 630 nm line pair identified by Martínez González et al. (2006) and Khomenko and Collados (2007). The distribution of field strengths in the solar IN was later derived from THEMIS observations of the Mn i 553.7 nm line by Ramírez Vélez et al. (2008). Their results showed a quiet Sun IN dominated by weak fields.
Sánchez Almeida et al. (2008) warned that the detection of the Mn i 553.7 nm HFS feature indicating hG fields does not preclude the existence of kG fields. They showed examples where the HFS hump can be seen when both hG and kG fields coexist in the pixel. Thus, the presence of strong fields cannot be ruled out using simple analyses. To exploit the diagnostic potential of this line, inversion schemes capable of dealing with vertical gradients and unresolved structure in the pixel are necessary.
In the near-IR, the Mn i 1526.27 nm line is sensitive to HFS effects not only in Stokes V but also in Stokes I, which allows the average strength and organization of the field to be determined (Asensio Ramos et al. 2007). The analysis of Mn i 1526.27 nm observations gathered at the German VTT with a spatial resolution of 1\(.{4}^{\prime \prime }\) revealed the presence of weak (\(<700\) G) fields with a mean strength of about 200 G and filling factors of \(\sim 10\)%. From a comparison of the total and net flux densities inferred from the Stokes I and V signals observed in each pixel, Asensio Ramos et al. (2007) concluded that more than 90% of the total IN flux cancels out at a resolution of 1\(.{4}^{\prime \prime }\) and is therefore not detectable through Stokes V.
4.5.6 Agreed facts
Based on the results presented so far, we summarize here the consensus that appears to be emerging on the physical properties of quiet Sun IN fields. Our list of “agreed facts” heavily relies on the conclusions drawn from full spectropolarimetric data taken at very high spatial resolution and/or different spectral regions assuming that only one magnetic field exists in the pixel. Alternative views will be discussed in the next section.
4.5.7 Internetwork fields are weak for the most part
The analysis of space-borne Fe i 630 nm observations shows a clear tendency for weak fields, in agreement with the results derived from ground-based measurements of the Fe i 1565 nm lines and the Mn i 553.7 and 1526.27 nm lines. Combined inversions of visible and near-IR data taken simultaneously at the same telescope also indicate weak fields. This agreement appears to bring to an end the debate about the distribution of field strengths in the IN. Hinode has been instrumental in resolving the controversy between visible and near-IR lines thanks to its unprecedented angular resolution and sensitivity, which allows unbiased interpretations of the weak Fe i 630 nm polarization signals to be made.
Still, a number of authors concluded that IN fields are strong (above 1 kG) or found a combination of weak and strong fields in the pixel. Some of them applied the line ratio technique to Fe i 630.15 and 630.25 nm (Grossmann-Doerth et al. 1996; Socas-Navarro and Sánchez Almeida 2003; Domínguez Cerdeña et al. 2003a, b; Socas-Navarro et al. 2004; Lites and Socas-Navarro 2004; Stenflo 2010a) but doubts about the robustness of the 630.15/630.25 line ratio exist (Khomenko and Collados 2007). Other authors used forward modeling or inversions of the radiative transfer equation (Solanki et al. 1996; Socas-Navarro and Lites 2004). However, these techniques do not seem to return correct field strengths from the 630 nm lines when the fields are very weak and the spatial resolution is low (Martínez González et al. 2006).
The ME inversions of the Fe i 630 nm lines carried out by Sigwarth et al. (1999) and Sánchez Almeida et al. (2003a) also delivered kG fields. This remains an unsolved problem, but we note that it is possible that they were biased by the modest angular resolution of the observations, since ME inversions seem to be adequate to analyze high resolution data (Orozco Suárez et al. 2007a). In fact, Fe i 630 nm observations gathered by the POLIS instrument at the German VTT under excellent seeing conditions and with the help of adaptive optics indicated weak fields in the solar IN (see appendix from Rezaei et al. 2007). Earlier ME inversions of the visible lines gave weak fields too (Lites et al. 1996; Lites 2002).
4.5.8 Internetwork magnetic fields are highly inclined
Prior to Hinode, the inclination of IN fields was poorly known. Only Lites et al. (1996), Collados (2001), and Khomenko et al. (2003) had presented results based on Fe i 630 and 1565 nm measurements. Orozco Suárez et al. (2007b) carried out the first inversion of Hinode/SP data and found large inclination angles. This is in general agreement with the estimates of Lites et al. (1996), Beck and Rezaei (2009), Danilovic et al. (2016), and others. Actually, except for Khomenko et al. (2003), there is now a consensus that IN fields are highly inclined—some authors find a most probable inclination of 90\(^\circ \) and others favor smaller inclinations, but all report fields that are far from being purely vertical.
However, concerns have been raised about the large abundance of near horizontal fields indicated by high-resolution observations. This specific result could be an artifact of the noise (de Wijn et al. 2009; Asensio Ramos 2009; Borrero and Kobel 2011) or could reflect the failure of ME inversions to separate the magnetic field parameters from the filling factor (e.g., Bommier et al. 2009).
Investigating the accuracy of the field inclinations derived from ME analyses of Hinode/SP data has been arduous. Both theoretical and pragmatic arguments were used to support the view that ME inversions of full spectropolarimetric measurements can disentangle the field strength, inclination, and filling factor properly (Orozco Suárez and del Toro Iniesta 2007; del Toro Iniesta et al. 2010). First of all, the combined analysis of the four Stokes profiles increases the sensitivity to the vector magnetic field and the filling factor. Indeed, when the field is weak, Stokes I turns out to show greater sensitivity to the inclination than other Stokes parameters (del Toro Iniesta et al. 2010). Moreover, the response of Stokes I to changes in field strength and filling factor are very different. Hence, Stokes I was identified as an essential ingredient for disentangling these two parameters (Orozco Suárez et al. 2007c), which in turn leads to more accurate inclination values.
Statistical analyses have been employed to elucidate whether or not the distribution of inclinations is affected by the noise of the measurements. For instance, Orozco Suárez et al. (2007c) applied ME inversions to a set of Stokes profiles from different initial models to analyze the effects of noise. Their tests showed that ME inversions are capable of distinguishing between field strength, inclination, and filling factor. Also the analysis of Orozco Suárez et al. (2007a), in which Stokes profiles were synthesized from magnetoconvection simulations and then analyzed as real observations, indicated that ME inversions return field strengths and inclinations with small errors even at the noise level of Hinode/SP normal map measurements (cf. Sect. 2.4).
A comprehensive study of the effects of noise on ME inferences was carried out by Asensio Ramos (2009) using a Bayesian approach. He analyzed a Hinode/SP data set from a small quiet Sun region with a noise level of \(10^{-3} \, I_{\mathrm{QS}}\). His results show that it is possible to disentangle the field strength from the filling factor. However, the information contained in the observations is not sufficient to constrain the inclination of the field when Stokes Q and U are buried in the noise. As a consequence, the inclination distribution may show an overabundance of fields with large inclinations. Also, he pointed out that the inclination distribution derived from the Hinode/SP data is compatible with a quasi-isotropic distribution of magnetic fields.
Borrero and Kobel (2011) further analyzed the problem of noise. They performed an experiment in which a distribution of purely vertical fields was used to simulate the Stokes profiles of the Fe i line at 632.05 nm. The synthetic profiles were contaminated with noise and inverted using the VFISV code. Very surprisingly, the resulting field inclination distributions showed a large fraction of nearly horizontal fields. The reason argued by the authors confirms the suspicion of Khomenko et al. (2003), namely that the inversion code fits the noise in Q and U as real signals, which leads to large transverse fields because of the small sensitivity of Stokes Q and U to weak fields. This experiment does not represent the actual conditions of the solar atmosphere because only zero Stokes Q and U signals were considered, but it illustrates in a dramatic way the risks associated with the analysis of noisy polarization profiles, especially when only one line is considered.
To minimize these problems, most authors set stringent criteria to invert real observations. For example, Orozco Suárez et al. (2007a) restricted their analysis to pixels with Stokes Q, U, or V amplitudes larger than 4.5 times the noise level. However, even that criterion is probably insufficient—one needs to include more information to be able to retrieve the field inclination with confidence. As suggested by Asensio Ramos (2009) and Borrero and Kobel (2011), the use of measurable Stokes Q and U signals in the inversion increases the reliability of the results. This was demonstrated by Borrero and Kobel (2012) for the case of a uniform distribution of vector magnetic fields. Indeed, limiting the analysis to pixels that show Stokes Q or U signals above 4.5 times the noise level ensures that the inferred field strength and inclination distributions are correct, although the method induces a bias because it selects the more inclined fields within the sample.
With that in mind, Orozco Suárez and Bellot Rubio (2012) carried out an ME analysis of high-sensitivity Hinode/SP observations. The data had a noise level of \(3 \times 10^{-4} \, I_{\mathrm{QS}}\), four times smaller than standard normal map measurements. Only pixels showing linear polarization amplitudes larger than 4.5 times the noise level were inverted, accounting for 27.4% of the surface area covered by the IN. The distributions of field strength and field inclination resulting from the inversions are displayed in Fig. 32. The PDF depicted on the right confirms the large abundance of inclined fields in the IN at disk center, with most of them being horizontal. The inferred inclinations are very reliable, thanks to the low noise of the observations and the fact that all four Stokes parameters contributed information to retrieve the vector magnetic field. The inversions of data with even lower noise presented by Bellot Rubio and Orozco Suárez (2012) confirm the results shown in Fig. 32. Interestingly, the inclination PDF indicates the existence of more vertical fields toward 0\(^\circ \) and 180\(^\circ \). These fields could be associated with the footpoints of small-scale magnetic loops, with vertical structures in intergranular lanes, or with magnetic bright points (Sánchez Almeida et al. 2010; Bonet et al. 2012). The latter may be connected with the small fraction of kG fields detected in the IN (shallow hump at \(\sim 1.4\) kG in the field strength distribution of Fig. 32).
Distribution of magnetic field strengths and inclinations derived from an ME inversion of Hinode/SP data with noise at the level of \(3 \times 10^{-4} I_{\mathrm{QS}}\), including only pixels with clear linear polarization signals (Stokes Q or U amplitudes exceeding 4.5 times the noise level). About 90% of those pixels show also Stokes V amplitudes above the same threshold. The distributions represent 27.4% of the field of view. Image reproduced with permission from Orozco Suárez and Bellot Rubio (2012), copyright by AAS
Actually, there is growing evidence that the inclination of IN fields depends on the field strength (e.g., Beck and Rezaei 2009; Martínez González et al. 2016). The stronger fields are found in intergranular lanes and are also the more vertical. The weak fields tend to be more horizontal. This behavior may partly explain some discrepant results presented in the literature. If no distinction between strong and weak fields is made, or if network fields are not excluded from the analysis, then the shape of the inclination distribution will vary depending on the exact mixture of field strengths in the observed region. Thus, both predominantly horizontal and predominantly vertical fields may be obtained in the same IN area as a result of subtle choices like noise treatment, removal of network patches, etc.
4.5.9 Larger average filling factors are obtained at higher spatial resolution
ME analyses of Hinode/SP data show broad distributions of filling factors in the IN, with a peak at 25%–30% and extended tails toward larger values (e.g., Borrero and Kobel 2011; Orozco Suárez and Bellot Rubio 2012). Ground-based Fe i 1565 nm measurements taken with adaptive optics delivered distributions peaking at 5%–10% at a resolution of 0\(.{8}^{\prime \prime }\) (Beck and Rezaei 2009). From an analysis of visible and near-IR observations, Martínez González et al. (2008) found the maximum to be at 2%. This demonstrates that the filling factors have increased by at least one order of magnitude from the 0.5–2% derived at \(\sim 1\) \(^{\prime \prime }\) up to the 25% observed at 0\(.{32}^{\prime \prime }\). The actual filling factors deduced from Hinode/SP observations may even be larger—by a factor of 2—if the degradation induced by telescope diffraction is considered (Sect. 2.3.2).
Thus, in regions where there is sufficient polarization signal, Hinode infers the existence of magnetic fields occupying more than 25% of the pixel area. This suggests we are nearly resolving the magnetic structures that make up the IN, lending support to case (iii) discussed in Sect. 4.3. Lites (2002) reached a similar conclusion by combining the apparent longitudinal fluxes observed by the ASP with the range of fields allowed by Hanle depolarization measurements.
However, recent Fe i 1565 nm measurements with GRIS at the 1.5 m GREGOR telescope have resulted in filling factors typically below 20%, with a maximum around 1% (Martínez González et al. 2016). These values are smaller than those derived by Beck and Rezaei (2009) despite their superior resolution (0\(.{4}^{\prime \prime }\)), but they refer to a small fraction of the observed FOV, only the 12% of the area where the vector magnetic field could be determined reliably. More studies using new GRIS data are needed to shed light on this discrepancy.
4.5.10 Alternative views
4.5.11 Micro-structured model atmospheres
MISMA inversions have consistently returned a mixture of strong and weak fields in the resolution element, often with opposite polarities (e.g., Sánchez Almeida and Lites 2000; Socas-Navarro and Sánchez Almeida 2002; Domínguez Cerdeña et al. 2006; Viticchié et al. 2011). The mixture is dominated by kG fields. These results follow from an interpretation of the asymmetries and irregularities of the observed Stokes profiles in terms of unresolved structure in the pixel and are independent of the spectral line used. Therefore, it seems likely that the preponderance of kG strengths indicated by MISMA inversions is a consequence of the underlying hypothesis, viz., the existence of optically thin structures at subresolution scales. While there are theoretical arguments supporting such an organization of the magnetic field in the solar atmosphere, no direct proofs of it exist. Model MISMAs are complicated structures requiring several magnetic components and a fairly large number of free parameters, which make them prone to noise-induced errors. Under these conditions, and in the absence of direct proofs of the MISMA hypothesis, most authors prefer to follow Occam’s Razor and choose simpler scenarios to interpret the observations. Models featuring vertical gradients of the parameters seem to be able to reproduce the observed asymmetries without requiring the presence of kG fields everywhere (e.g., Fig. 3), but have not been explored systematically as of yet. Only when such an analysis is carried out will we be able to assess the need for unresolved structure in the pixel and perhaps also understand why MISMA inversions tend to favor kG fields.
4.5.12 Collapsed and uncollapsed fields
Stenflo (2010a) challenged the consensus reached by the community with an analysis of the Hinode/SP observations of Lites et al. (2008). Using the line ratio technique, he found the quiet Sun to consist of two different flux populations that show up prominently in scatter plots of the Stokes V amplitudes of the Fe i 630 nm lines. Stenflo (2010a) argued that these populations correspond to collapsed and uncollapsed magnetic fields. The former would be associated with kG flux-tube like structures, while the latter would represent weak fields. Both populations are predominantly vertical. The collapsed fields have a preference for the intergranular lanes and the uncollapsed ones for the granular cells (Stenflo 2011). According to his analysis, most of the observed flux is carried by fields in the kG range, i.e., by the collapsed population. This interpretation of the Hinode/SP data is clearly at odds with previous analyses, which delivered weak and highly inclined IN fields under the assumption of nearly resolved structures.
The discrepancy can be solved if the kG structures found by Stenflo (2010a) represent strong network fields. This remains an open possibility because network and IN signals were not separated. A more important drawback of the analysis is the application of the line ratio technique to Fe i 630.15 and 630.25 nm. Stenflo (2010a) estimated the field strength from these lines despite the problems associated with their different formation height (Khomenko and Collados 2007). To minimize the errors, he introduced an offset to the line ratio, calculated using the same data. However, a constant offset is of little use because the conditions of the atmosphere—in particular the vertical gradient of magnetic field—change from pixel to pixel. Figure 2 of Khomenko and Collados (2007) illustrates this situation: the field strength distribution obtained from the 630.15/630.25 line ratio is completely different from the original one and cannot be recovered applying a single offset. Since the inferred field strengths were used to determine the corresponding inclinations, the latter may not be valid either.
On the other hand, Steiner and Rezaei (2012) have demonstrated using MHD simulations that the 630.15/630.25 line ratio may return strong kG fields in the presence of canopy-like structures, even when all the fields are weak. Again, this behavior is due to the different formation heights of the two lines. Fe i 630.25 nm samples slightly deeper photospheric layers and may result in too small Stokes V amplitudes when the magnetized region is located higher up, leading to an apparent saturation of the line ratio which is interpreted as evidence of strong fields. Thus, Steiner and Rezaei (2012) suggested that the collapsed kG population of Stenflo (2010a) represents nothing but weak canopy fields.
The existence of canopy fields appears to be supported by the analysis of Stenflo (2013), who finds a transition from preferentially vertical fields deep in the atmosphere to more horizontal fields above, based on the symmetry properties of Stokes Q and U. This suggests that there must be non-zero vertical gradients of the field inclination in the solar IN. The detection of such gradients would lend credence to the magnetic canopy scenario and therefore remains an important target for future investigations. As pointed out before, the first inversion of Hinode/SP data implementing gradients of the atmospheric parameters along the line of sight suggests that IN fields become more horizontal with height (Danilovic et al. 2016). It would be of great interest to know whether this result applies to individual structures as well or is valid only in a statistical sense.
4.5.13 A hierarchy of fields
At the resolution of current telescopes, the solar IN exhibits a broad range of scales, field strengths, and field inclinations (see Figs. 10, 11 and 32). We observe a hierarchy of structures with sizes from the roughly 1500 km of the largest IN magnetic elements down to the \(\sim 110\) km limit achieved by SUNRISE/IMaX. Some of the structures are resolved, such as the footpoints and apexes of small-scale emerging magnetic loops, while others are nearly resolved, as indicated by the large filling factors obtained from the inversion of full spectropolarimetric measurements. The question naturally arises as to whether this hierarchy extends beyond the resolution limit presently attainable and, if so, at which scale it stops.
Some authors have claimed a high degree of self-similarity in magnetograms taken at different spatial resolutions, concluding that the quiet Sun must consist of randomly oriented magnetic fields with sizes as small as 10 m (Stenflo and Holzreuter 2003). Self-similarity is a typical property of fractals. The fractal dimension of solar magnetic structures determined by Janßen et al. (2003) from 0\(.{5}^{\prime \prime }\) resolution magnetograms is \(D=1.2\), which also points to a self-similar organization of the field over a large range of scales. The extrapolation of this behavior to subresolution scales implies that every pixel contains the full distribution of magnetic fields. By further assuming that these fields have mixed polarities one arrives at the concept of turbulent fields invisible to the Zeeman effect (but detectable through the Hanle effect). However, it is not clear to what degree magnetoconvection should produce a perfect balance of mixed polarities on all spatial scales. This question must be addressed with future numerical simulations at much lower magnetic Prandtl numbers than are affordable nowadays (see discussion in Martínez Pillet 2013). The MISMA hypothesis also postulates the existence of optically thin magnetic irregularities with opposite polarities filling the resolution element, in agreement with a fractal structuring of the field.
This hierarchical view of quiet Sun magnetism has received support from analyses of how the polarization amplitudes observed by the Hinode SP and other ground-based instruments change with spatial resolution. The lack of significant variations reported by Martínez González et al. (2010b) was interpreted as evidence that most of the fields are still unresolved. However, their results are incompatible with the experiment presented in Sect. 4.3. We believe this is due to the way the data were degraded to the stated resolutions. Martínez González et al. (2010b) further suggested that, despite the hierarchical organization of the field in the quiet Sun, some of the magnetic structures in the extended tail of the distribution are starting to be resolved by Hinode at 0\(.{32}^{\prime \prime }\). A similar conclusion was reached by López Ariste and Sainz Dalda (2012) from an analysis of the Stokes V asymmetries observed by the Hinode SP at different heliocentric angles. These authors also estimated the correlation lengths of the field, finding a broad range of scales from hundreds of km down to 10 km, as expected from a turbulent cascade.
The existence of structures with different sizes and magnetic properties in the solar IN is clear from both observations and theoretical arguments. However, there is a big difference in the way competing scenarios assume them to be distributed spatially. While ME inversions explain the Hinode/SP measurements with a single magnetic component in each resolution element, Hanle depolarization analyses, MISMA models, and fractal-like scenarios make the assumption that the full range of field strengths and inclinations is present in every resolution element. Further improvements in angular resolution are needed to provide additional constraints on the actual organization of the magnetic fields in the solar IN.
4.6 The Hanle view of the solar internetwork
For a long time, the Hanle effect was believed to be the only means of investigating the photospheric volume not covered by strong network fields (e.g., Stenflo 1989, 2008, 2010b). Hanle and Zeeman measurements were considered complementary, with both diagnostics sampling different tails of the IN magnetic field distribution. In particular, the Hanle effect was charged with the task of revealing the “hidden” magnetism of the quiet Sun, i.e., the turbulent, volume-filling, weak fields with mixed polarities that would be tangled at subresolution scales, producing nearly perfect Stokes V cancellation and hence escaping detection by longitudinal Zeeman measurements.
ZIMPOL observations of scattering polarization in photospheric lines. Left: Sr i 460.7 nm measurements taken at THEMIS on 7 August 2007. The spectrograph slit scanned a quiet region near the W limb (\(\upmu = 0.08\)). The Sr i line exhibits a prominent Q signal. Except for a clear patch at \(y\sim 25^{\prime \prime }\), Stokes U is zero. The atomic line to the right shows very weak Stokes V signals all along the slit. Image courtesy J.O. Stenflo. Right: Molecular CN lines around 377.3 nm. The measurements were taken at the McMath–Pierce Telescope on 28 March 2005 with the slit parallel to the limb (\(\upmu =0.1\)). The CN lines are unconspicuous in Stokes I, but produce clear Q signals (the white vertical bands). Image reproduced with permission from Stenflo (2007), copyright by SAIt
This research field has been very active, from both an observational and a theoretical point of view, leading to significant advances in our knowledge of quiet Sun magnetic fields. Here we show examples of Hanle observations and summarize some of the main results derived from them.
4.6.1 Observations and interpretation
The left panels of Fig. 33 display ZIMPOL observations of the photospheric Sr i 460.7 nm line taken at THEMIS. The slit was oriented parallel to the limb and the spectra were integrated for 35 min. This example illustrates the following properties of the Hanle effect in quiet regions of the solar photosphere: (a) Stokes U is essentially zero, i.e., there is no significant rotation of the plane of polarizationFootnote 22; (b) Stokes Q shows Hanle depolarization, with no strong spatial variation of the signal along the slit; and (c) circular polarization signals may or may not be present, but when observed they show spatial fluctuations on rather large scales (5\(^{\prime \prime }\)–10\(^{\prime \prime }\) or more). At the resolution of most Hanle measurements, these properties seem to be quite robust (e.g., Fig. 1 in Bommier et al. 2005).
The classical interpretation of the observations is the following. (a) There is no Hanle rotation (Stokes U is zero) because every resolution element contains an isotropic distribution of field orientations. An isotropic distribution of field azimuths would suffice, but isotropy of the field inclination is often presumed too. (b) The Hanle depolarization does not vary spatially because each pixel contains the full distribution of field strengths. Alternatively, all the pixels are permeated by the same single-valued isotropic field. (c) Stokes V is the signature of the longitudinal Zeeman effect. The large scale of variation of Stokes V shows that the measurements are unresolved. In fact, the Stokes V fluctuations seen in Hanle measurements are clearly different from those detected at very high spatial resolution using the Zeeman effect (compare Fig. 33 with Fig. 23 from Hinode/SP observations, and note the different spatial scales).
The strength of the photospheric fields determined from these kinds of observations ranges from 10 G to some 100 G. The first estimates of Stenflo (1982) were based on the last scattering approximation and showed that the Hanle depolarization of the Sr i 460.7 nm line could be explained by an isotropic distribution of fields with a mean strength of 50–100 G. Such fields were compatible with the upper limit of 90 G that Stenflo and Lindegren (1977) had estimated earlier from the magnetic broadening of Stokes I (Sect. 2.2.2). The more detailed radiative transfer calculations of Faurobert-Scholl (1993), including multiple scattering, depolarizing elastic collisions, and partial frequency redistribution, were applied to center-to-limb observations of Sr i 460.7 nm. The results indicated the presence of a turbulent field with strengths in the range 30 to 60 G at a height of 150 km above \(\tau _{500} = 1\), and some 10–30 G at 250 km. Slightly lower values of 20 and 10 G were derived by Faurobert-Scholl et al. (1995) in a refined analysis, this time including more accurate collisional cross-sections. Bommier et al. (2005) assumed a unimodal distribution of isotropic fields, finding a strength of 54 G at a height of 220 km and a gradient of \(-0.12\) G/km. Their calculations were based on the atomic density matrix formalism in a plane-parallel atmosphere with macro- and micro-turbulent velocities. Surprisingly, Derouich et al. (2006) came to the opposite conclusion following the same approach: the field strength first increases with height up to 300 km and then drops. Trujillo Bueno et al. (2006) criticized the use of macro- and micro-turbulence because these parameters can introduce errors in the depolarization rates. Instead, they proposed to perform radiative transfer calculations with model atmospheres from 3D hydrodynamical simulations.
Molecular lines appear to indicate weaker fields than atomic lines. The study of Faurobert and Arnaud (2003), based on the center-to-limb variation of C\(_2\) lines, suggested the presence of a turbulent field of about 15 G in the upper photospheric layers. This value was confirmed by Berdyugina and Fluri (2004) using a different set of C\(_2\) lines. Trujillo Bueno et al. (2006) pointed out that the absence of \(\varLambda \) doubling in the C\(_2\) molecule implies even weaker fields, of only 7 G. Asensio Ramos and Trujillo Bueno (2007) detected a height variation of the field from about 4 G to 2 G very near the limb, using the C\(_2\) lines proposed by Berdyugina and Fluri (2004). These values agree well with the horizontal fields of 2 G inferred by Lites et al. (2010) from an analysis of the scattering polarization of the atomic Fe i lines at 630 nm, seen in emission for the first time with Hinode. The Fe i 630 nm signals were detected 0\(.{3}^{\prime \prime }\) above the limb, or 550 km above the \(\tau =1\) level, already at the base of the chromosphere. The weaker fields indicated by the C\(_2\) lines (as compared with the Sr i line) may be a consequence of the C\(_2\) molecule being present almost exclusively in granules, where the fields are intrinsically weaker (see Sect. 4.6.2).
To determine the height variation of the magnetic field strength, Milić and Faurobert (2012) inverted the linear polarization in six C\(_2\) triplets and one MgH line observed at nine positions on the solar disk. These lines have different Hanle sensitivities and are formed at different heights in the atmosphere, spanning the range from \(z =200\) to 400 km. Their inversion method is based on 2-level atom radiative transfer calculations in a standard 1D model atmosphere and takes into account elastic depolarizing collisions. The magnetic field is assumed to be horizontal with an isotropic distribution of azimuths and a strength varying with height (as described by three parameters). Their results indicate a rapid height variation of the field strength, from 95 G at 200 km to 5 G at 400 km. Such a stratification provides a reasonable fit to all the data points, and may explain why different lines (formed at different heights) yielded different field strengths in previous analyses. Milić and Faurobert (2012) further argued that the existence of such a strong vertical gradient is incompatible with the assumption of isotropic fields.
Using surface dynamo simulations by Vögler and Schüssler (2007), Shchukina and Trujillo Bueno (2011) came to the conclusion that the average magnetic field in the simulation needs to be multiplied by a factor of 12 at all heights to explain the Hanle measurements of the Sr i 460.7 nm line near the solar limb. However, this enhancement of the magnetic field would lead to too strong fields deep in the photosphere where the Fe i 630 nm lines are formed, producing unrealistically large Zeeman signals. Thus, since the Sr i 460.7 nm line is formed in the upper photosphere, they proposed a modified magnetic field stratification with an average strength of 160 G at \(z = 60\) km and 130 G at \(z = 300\) km to explain the Hanle and Zeeman signals at the same time. The fields deduced by Shchukina and Trujillo Bueno (2011) are much stronger than those by Milić and Faurobert (2012), reflecting differences in observables, atmospheric models, and treatments of the radiative transfer problem. Despite this discrepancy, both investigations agree on the existence of a magnetic field weakening with height.
The “turbulent” fields deduced from existing Hanle measurements are volume-filling and would produce little (if any) fluctuations of the signal from one resolution element to the next. Also the MISMA fields conjectured by Sánchez Almeida et al. (1996) are tangled on very small scales and have mixed polarities, so in principle they could represent the same structures. Despite these similarities, there is a serious contradiction between the results of Hanle and MISMA analyses, as the former indicate very weak fields and the latter favor kG strengths (Sect. 4.5.2).
4.6.2 Spatial variations of the Hanle signals
While most measurements of scattering polarization in photospheric lines do not show large spatial variations, some observations and theoretical calculations suggest that significant fluctuations will be detected at high angular resolution (better than 1\(^{\prime \prime }\)).
Spatial variations of the Hanle effect were first observed by Stenflo et al. (1998), mostly in chromospheric lines. According to the authors, “they shatter the view that the turbulent magnetic field that fills the space (99% of the photospheric volume) between the kG flux tubes has unique and invariant properties”. Spatial fluctuations of the Hanle depolarization were also seen by Stenflo et al. (2002) in Stokes vector images acquired through a narrow-band filter in the Na i D\(_1\) and D\(_2\) lines, also mapping the chromosphere. The Hanle depolarization was found to be intermittent, with a pattern associated with the supergranular network and facular regions.
The first indications of spatially varying Hanle signals in the photosphere were gathered by Malherbe et al. (2007). Even with integrations of several minutes, these authors were able to detect a change in the scattering polarization of the Sr i 460.7 nm line as a function of continuum intensity. The observed signals were larger above granules as compared with intergranular lanes. This difference could reflect differences in line formation conditions (e.g., anisotropic illumination) and/or different magnetic fields. The existence of spatial fluctuations on granular scales has been confirmed by Snik et al. (2010), who used the Broadband Filter Imager on Hinode to observe the scattering polarization of the CN band head at 388 nm. Their seeing-free measurements have an unprecedented spatial resolution of 0\(.{2}^{\prime \prime }\) and demonstrate that granules show significantly larger fractional polarization than intergranular lanes. Unfortunately, Stokes U was assumed to be zero everywhere, so it is not possible to assess whether there is Hanle rotation of the polarization plane and, if so, whether it also undergoes spatial fluctuations.
Recently, Bianda et al. (2018) used ZIMPOL and the 1.5m GREGOR telescope to perform full Stokes measurements of the Sr i 460.7 nm line at \(\upmu =0.3\). Integrating for 2 min, they recorded clear spatial variations of the Stokes Q signal along the slit, together with prominent signals in Stokes U and V. The effective resolution of the measurements is about 1\(^{\prime \prime }\), judging from the intensity and circular polarization spectra presented in the paper. This is sufficient to separate granules and intergranular lanes. Actually, Bianda et al. (2018) found the spatial scale of the fluctuations to be comparable to that of granulation, with granules generally showing larger Stokes Q signals. This confirms the results of Malherbe et al. (2007).
Sr i 460.7 nm linear polarization measurements at different heliocentric angles \(\theta \) (symbols) and theoretical modeling (curves). The fractional polarizations that would be produced by isotropic turbulent fields of different strengths are indicated by the green curves, as resulting from NLTE radiative transfer calculations in realistic 3D hydrodynamical models of the solar photosphere (from top to bottom: 0, 5, 10, 15, 20, 30, 40, 50, 60 80, 100, 150, 200, 250, and 300 G). The orange curve corresponds to the best-fitting field strength of 60 G. The black curve shows the variation of the linear polarization assuming an exponential distribution of fields with average strength of 130 G. Image reproduced with permission from Trujillo Bueno et al. (2004), copyright by Macmillan
On the theoretical side, a breakthrough occurred when Trujillo Bueno et al. (2004) predicted strong spatial fluctuations of the Hanle depolarization on small scales, due to the very different strengths of granular and intergranular fields. Using detailed radiative transfer calculations in 3D hydrodynamical simulations, Trujillo Bueno et al. (2004) first showed that the observed center-to-limb variation of the linear polarization of Sr i 460.7 nm is consistent with an isotropic turbulent field of \(\sim 60\) G, or with an exponential distribution having \(\langle B \rangle \sim 130\) G (see Fig. 34). Then they argued that the Hanle depolarization measured in C\(_2\) lines is consistent only with an exponential distribution of turbulent fields having \(\langle B \rangle \sim 15\) G, since stronger fields would produce too large depolarizations.
The paradox was solved by noting that the scattering polarization of the C\(_2\) lines is influenced only by the conditions of the granular upflows, where the abundance of the molecule is significantly different from zero and where the largest anisotropic illumination occurs. Thus, Trujillo Bueno et al. (2004) proposed that the turbulent fields have a strength of 15 G in the granules. To explain the observed Sr i data, which get contributions from both granules and intergranular lanes, the latter must harbor stronger fields than the 60–130 G deduced from the spatially unresolved measurements. Indeed, most of the fields in intergranular lanes must reach the Hanle saturation limit to produce the maximum depolarization possible. This limit is attained at about 200 G, although fields of 150 G already yield similar depolarizations.
The work of Trujillo Bueno et al. (2004) demonstrated for the first time that strongly different fields must exist in granules and intergranular lanes. As noted by Sánchez Almeida (2005), it is not possible to know the strength of the intergranular fields because they are above the Hanle saturation limit, but this difficulty does not invalidate the main result, namely that the magnetic field varies on granular scales. Further support for the existence of Hanle fluctuations on small spatial scales has been presented by Trujillo Bueno and Shchukina (2007).
We still do not know whether the observed spatial fluctuations of the scattering polarization of Sr i 460.7 nm are due to different illumination anisotropies or to different magnetic fields in granules and intergranular lanes. The second possibility would be consistent with Trujillo Bueno et al. (2004). However, we want to stress that the existence of different fields in granular and intergranular regions would speak against the concept of a volume-filling, microturbulent field in every resolution element, as has been assumed in most Hanle studies. In fact, the observed Hanle depolarizations may not be incompatible with a more deterministic field varying on scales nearly resolved by current instrumentation. Even if those fields produce some degree of cancellation in Stokes V, they could still be detectable through Stokes Q and U and hence be accessible to Zeeman measurements. This possibility is examined in the next section.
5 An unifying view of the quiet Sun internetwork
In this section we elaborate on the idea that both Zeeman and Hanle measurements actually trace the same magnetic fields, thus merging the seemingly different views of the solar IN provided by both diagnostics. We also briefly discuss a scenario to explain the observed distributions of IN vector fields taking into account the surface processes in which they participate.
5.1 The Zeeman and Hanle effects trace the same IN magnetic fields
Zeeman and Hanle measurements have often been thought to provide complementary views of quiet Sun magnetism. This idea is reinforced by the fact that the highly structured fields revealed by the former on scales of 0\(.{2}^{\prime \prime }\)–0\(.{3}^{\prime \prime }\) seem to be essentially different from the homogeneous, unstructured, isotropic field that would cover the whole solar surface according to the latter.
The main argument for the existence of turbulent fields is the lack of spatial variations of the Hanle depolarization in photospheric lines. However, this may simply be a result of the poor resolution attained by most Hanle measurements, insufficient to distinguish the individual elements seen in Figs. 10 and 11. Actually, we believe that the IN fields detected by the Hinode SP and SUNRISE/IMaX are the fields traced by the Hanle effect, and, therefore, that they can explain the Hanle observations discussed in Sect. 4.6. The differences between the conclusions drawn from Hanle and Zeeman measurements of the photosphere would not be real but an artifact of their vastly different angular resolutions.
To support this idea we have used the high sensitivity Hinode/SP measurements of Lites et al. (2008) to determine the distribution of fields that would be seen in the typical spatio-temporal resolution element of Hanle observations. Its size is taken to be \(0.{5}^{\prime \prime } \times 5^{\prime \prime }\) (slit width \(\times \) resolution along the slit) and we assume integrations of 5 min. This is indeed a very conservative estimate because most Hanle measurements represent spatial averages over the full slit length. The surface area covered by such a resolution element at \(\upmu = 0.1\) is equivalent to \(5^{\prime \prime }\times 5^{\prime \prime }\) at disk center, due to projection effects. This area of 25 arcsec\(^2\) is almost exactly the same as the 26.2 arcsec\(^2\) sampled by one Hinode/SP slit with 1024 pixels of 0\(.{16}^{\prime \prime }\)\( \times 0.{16}^{\prime \prime }\). Therefore, a single slit measurement of 67 s in Lites et al. (2008) would account for the area of the typical Hanle resolution element at \(\upmu =0.1\). To account for the 5 min integration time, we just consider five consecutive slit measurements. In the end, a \(0.{5}^{\prime \prime } \times 5^{\prime \prime }\) Hanle measurement at \(\upmu =0.1\) is simulated using \(5 \times 1024\) pixels of \(0.{16}^{\prime \prime } \times 0.{16}^{\prime \prime }\) taken at disk center.
We have computed the field strength, inclination, and azimuth in each of the \(5 \times 1024\) pixels from a Milne–Eddington inversion based on a single magnetic component in the pixel. It is worth recalling here that the Hinode observations used for this experiment have a noise level of \(3 \times 10^{-4} \, I_{\mathrm{QS}}\). We only considered the magnetic field parameters coming from pixels with polarization signals larger than 4.5 times the noise level. In this way we use the most reliable inversion results. The Zeeman observations performed by the Hinode SP are very sensitive and show Stokes Q or U signals larger than this threshold in 30% of the field of view. The percentage of pixels with sufficiently large Stokes V amplitudes is 70%. The observations thus provide a rather complete coverage of the solar surface, with outstanding sensitivity and spatial resolution.
The distributions of field strength, inclination, and azimuth in the simulated Hanle resolution element are presented in Fig. 35. The field strength PDF is dominated by weak fields in the range 0–200 G. Stronger fields of up to 1.5 kG do exist, but they are not common (the observations correspond to a very quiet IN region with just one network patch). The inclination distribution shows a predominance of horizontal fields, with the same amount of positive and negative polarities (\(\gamma < 90^\circ \) and \(\gamma > 90^\circ \), respectively). Finally, the azimuth PDF is nearly flat, indicating a random distribution of orientations in the horizontal plane.
Distribution of field strengths, field inclinations, field azimuths and, filling factor in a typical Hanle resolution element of size \(0.{5}^{\prime \prime } \times 5^{\prime \prime }\) after integrating for 5 min. The distributions have been derived from real Hinode/SP observations with a pixel size of \(0.{16}^{\prime \prime } \times 0.{16}^{\prime \prime }\) and a noise level of \(3 \times 10^{-4} \, I_{\mathrm{QS}}\)
These distributions are compatible with the photospheric Hanle measurements discussed in Sect. 4.6, for the following reasons:
- 1.
The magnetic fields present in the Hanle resolution element do not change much from one element to the next. This explains the small spatial variations of Q / I along the slit found in the observations.
- 2.
The fields are mostly horizontal, as required to produce Hanle depolarization. The PDF suggests that the field inclination is not isotropic.
- 3.
The azimuth is randomly distributed, i.e., the resolution element contains horizontal fields with all orientations, leading to cancellation of Stokes U. Thus, the plane of linear polarization is not rotated (at the resolution of Hanle measurements).
- 4.
The average field strength is \(\langle B \rangle = 135\) G, i.e., significantly larger than the values resulting from some Hanle measurements such as those by Kleint et al. (2010) and others described in Sect. 4.6.1. However, it is surprisingly similar to that inferred by Trujillo Bueno et al. (2004). Although the agreement is probably coincidental, we note that \(\sim 20\%\) of the fields are stronger than the Hanle saturation limit of about 200 G for Sr i 460.7 nm. The percentage of fields stronger than 150 G is \(\sim 40\)%. This means that a significant fraction of the fields produce the maximum depolarization possible, as required to explain the C\(_2\) and Sr i observations considered by Trujillo Bueno et al. (2004).
- 5.
When the field distribution is split according to granules and intergranular lanes, the average field strengths are 105 and 150 G, respectively. The fields are weaker in the granules, consistent with the results of Trujillo Bueno et al. (2004). The granular fields in our simulated Hanle resolution element are still stronger than those of Trujillo Bueno et al. (2004), but the amount of weak fields below 30 G is relatively large. Interestingly, 22% of the intergranular area is covered by fields stronger than 200 G and 51% by fields stronger than 150 G. Thus, a substantial fraction of the intergranular lanes would produce the maximum possible saturation in Sr i 460.7 nm.
These considerations support the idea that the IN fields detected with Hinode via the Zeeman effect contribute significantly to the Hanle signals observed in photospheric lines. The fields are organized on very small scales, but they cannot be considered turbulent at a resolution of 0\(.{32}^{\prime \prime }\). In particular, the existence of opposite polarities within the same pixel does not seem to be warranted: the polarization patches detected by Hinode in the IN are larger than the resolution limit and have well defined signs that do not change randomly from one pixel to the next. This result also holds true at the resolution of 0\(.{15}^{\prime \prime }\) provided by the vector magnetograph observations of SUNRISE/IMaX. For this reason, the Zeeman polarization maps of the IN obtained by high-resolution instruments do not show a typical noise-like, salt-and-pepper appearance. The key ingredient that has enabled the Zeeman detection of these weak fields is high spatial resolution. The polarization signals recorded by Hinode in its \(0.{16}^{\prime \prime } \times 0.{16}^{\prime \prime }\) pixels can be explained reasonably well with a single magnetic field of given inclination and azimuth within the pixel, perhaps varying with height (cf. Danilovic et al. 2016). If the resolution is degraded to several arcsec, those fields would certainly look isotropic and turbulent, as inferred from Hanle observations.
The Hinode measurements cannot not rule out the existence of another population of weak fields contributing to the Hanle signals. However, those fields would necessarily have very small strengths, a few G or tens of G at most, in order not to produce clear Zeeman signals. Such fields might be detectable in the future as higher angular resolution and sensitivity become available.
In the meantime, it seems important to back up this idea by performing detailed radiative transfer calculations of the Sr i 460.7 nm and C\(_2\) lines with the field distributions shown in Fig. 35 (or, better, with full model atmospheres determined from inversions of Hinode/SP data with gradients of the atmospheric parameters) to see if they can reproduce the existing depolarization measurements.
5.2 Origin of the internetwork magnetic field distributions
There is growing consensus that the quiet Sun IN is pervaded by magnetic fields which are weak and highly inclined for the most part. The key question now is to identify the mechanism(s) producing the observed PDFs. This mechanism is probably related to the way the field is generated and/or the way it emerges on the solar surface.
In the quiet Sun IN, observations show the continuous appearance of magnetic structures exhibiting large linear polarization signals. These magnetic events have been identified as “horizontal” IN fields (Lites et al. 1996; Jin et al. 2009), emerging small-scale magnetic loops (Martínez González et al. 2007; Centeno et al. 2007; Martínez González and Bellot Rubio 2009; Gömöry et al. 2010; Guglielmino et al. 2012; Martínez González et al. 2012b), and transient “horizontal” magnetic fields (Ishikawa et al. 2008, 2010; Ishikawa and Tsuneta 2011). In all cases one witnesses the transient appearance of a linear polarization patch, followed by two circular polarization patches (of opposite polarity) that separate from each other with time. The frequency of these events has been found to increase with the sensitivity and spatial resolution of the observations, from single cases (Lites et al. 1996; Martínez González et al. 2007) to hundreds of them (Danilovic et al. 2010a; Martínez González et al. 2012b). The magnetic field extrapolations of SUNRISE/IMaX data presented by Wiegelmann et al. (2010) also show small-scale loops all over the IN. Half of them (51%) close within the photosphere, while the others reach chromospheric and even coronal heights.
Thus, it is possible that the observed distributions of magnetic field strength and inclination are a result of the presence of many of these structures, with different sizes and lifetimes, in the quiet Sun. This idea is supported by the fact that the PDFs of the vector magnetic field in the solar IN and in loop structures have similar shapes. An example is given in Fig. 36, where we display the parameters resulting from a ME inversion of a small-scale loop observed by the Hinode SP in slit-and-stare mode. The combination of the distributions of many such loops would be able to explain the PDFs inferred in the IN, including the isotropic distribution of azimuths (due to the random orientation of the loop axes).
This scenario is gaining momentum within the solar community (Bommier 2011; Ishikawa and Tsuneta 2011; Orozco Suárez and Katsukawa 2012). In combination with our claim that the Hanle measurements trace the very same IN fields detected by Hinode and SUNRISE, it implies that the presence of small-scale magnetic loops all over the solar surface may ultimately be the reason of the Hanle depolarization observed in photospheric lines. The existence of a hierarchy of coherent loops appearing and disappearing continuously would also explain the detection of Zeeman signals in 100% of the solar surface when sufficiently long integrations are used (Fig. 23).
Small-scale magnetic loop recorded in sit-and-stare deep-mode Hinode/SP observations of the quiet Sun at disk center. Left: Maps of the total circular and linear polarization (top and bottom panels, respectively). Time goes from left to right and spatial position along the slit from bottom to top. The signatures of the loop emerging in the solar photosphere are clearly seen: a conspicuous linear polarization patch flanked by two circular polarization patches of opposite polarity. The linear polarization signal is thought to represent the nearly horizontal loop top and the circular signal the more vertical loop footpoints. Right: Magnetic field PDFs for the structure displayed on the left panels, as derived from a ME inversion of the data. Clockwise from upper left: field strength, field inclination, magnetic filling factor, and field azimuth. Inclinations and azimuths are given in the line-of-sight reference frame. The PDFs have shapes similar to those deduced for the solar IN (Fig. 30), except for the azimuth distribution which reflects the orientation of the vector magnetic field in the loop. Image reproduced with permission from Orozco Suárez and Katsukawa (2012), copyright by AAS
6 Open questions
Thanks to the progress made in recent years we now have a relatively accurate view of the properties of IN magnetic fields. As this initial characterization period comes to an end, we face the need to study the IN all over the solar disk, to investigate how the vector magnetic field varies with height in the atmosphere, to improve the spatial resolution of Hanle measurements, and to determine the origin of the fields. Below we describe these aspects in some detail and summarize the main results obtained so far.
6.1 Center-limb variation of internetwork polarization signals
The properties of IN magnetic fields away from disk center are poorly known. If the IN is pervaded by coherent magnetic structures, then their properties should change when observed at different viewing angles. If the fields are isotropic (randomly oriented), the distribution of magnetic parameters will be the same independently of the position on the disk. Thus, the center-to-limb variation of the polarization signals may help determine the topology of the field.
The first analyses of the IN at different heliocentric angles were based on full disk longitudinal magnetograms and found a small decrease of the polarization amplitudes toward the limb (Zwaan 1987; Martin 1988). The spectropolarimetric measurements of Meunier et al. (1998) pointed in the same direction. This behavior suggests that the IN consists of weak fields with mixed polarities. Such fields would be isotropically oriented, unlike the vertical magnetic flux tubes of the network. Indeed, using 1\(^{\prime \prime }\)-resolution observations, Lites (2002) found that strong network elements outside of the disk center show an inclination to the line of sight which is consistent with vertical flux tubes. However, the weaker fields surrounding the network elements have a distribution of inclinations skewed away from the local vertical. Lites (2002) argued that this shift could signal the presence of unresolved, mixed polarities. Observations in the near-IR Fe i 1565 nm lines at 0\(.{7}^{\prime \prime }\)–1\(^{\prime \prime }\) showed no variations of the circular and linear polarization amplitudes and area asymmetries with heliocentric angle, which also suggests an isotropic distribution of fields.
In contrast, Harvey et al. (2007) used 3\(^{\prime \prime }\)-resolution longitudinal photospheric magnetograms from SOLIS and GONG to discover a background of dynamic, patchy structures whose visibility increases toward the solar limb. These structures were associated with seething horizontal fields in the quiet Sun, possibly driven by convective processes and field reconfigurations.
Lites et al. (2008) also provided new but yet unexplained insights on the variation of the IN polarization signals with the heliocentric angle. Using Hinode/SP data, they showed that both the apparent longitudinal and transverse magnetic flux densities decrease toward the limb. Since there are about five times more transverse flux than longitudinal flux at disk center, one would expect the longitudinal flux to increase toward the limb as the inclined fields become more and more aligned with the line of sight. However, this naive expectation was not confirmed by the observations. A magnetic field decreasing with height could explain (part of) the flux reduction toward the limb.
Magnetic field strength, inclination, azimuth, and filling factor distributions in the IN as calculated from ME inversions of high signal-to-noise ratio Hinode/SP measurements at different heliocentric angles. The inset in the field strength panel shows the weak-field end of the distribution in linear scale. Inclinations are measured with respect to the line of sight. Image reproduced with permission from Orozco Suárez and Katsukawa (2012), copyright by AAS
Similar Hinode/SP measurements were analyzed by Orozco Suárez and Katsukawa (2012). Figure 37 shows the distributions of field strengths, inclinations, azimuths, and filling factors they obtained from an ME inversion of four data sets at different heliocentric angles. Here, the inclination is measured with respect to the line of sight. As can be seen, IN fields are weak at all disk positions and the distributions show small variations when going from disk center to the limb. The shape of the inclination distribution is slightly squeezed for large viewing angles, suggesting a larger abundance of inclined fields near the limb, in agreement with the results of Lites et al. (2008). The small variations of the inclination PDF found by Orozco Suárez and Katsukawa (2012) would be compatible with an isotropic distribution of fields within the FOV. However, a detailed analysis revealed that for fields stronger than 200 G there exist indeed variations of the inclination distributions with viewing angle, associated with network fields (vertical and intermediate orientations at the disk center, horizontal orientations near the limb). Moreover, the distribution of fields weaker than 200 G could be associated, for 30% of the analyzed pixels, with loop-like structures in the field of view, which are still clearly visible at large heliocentric angles. This partly rules out the idea of an IN locally made of isotropic fields suggested by Martínez González et al. (2010b), as small-scale magnetic loops are coherent structures with fields having a well-defined orientation.
Also from Hinode/SP data, Borrero and Kobel (2013) argued that the observed center-to-limb variation of the circular and linear polarization amplitudes cannot be explained by either an isotropic distribution of IN fields or line-of-sight effects. On the contrary, it requires the field distribution to be intrinsically different depending on the solar latitude. The reason could be the different formation height of the spectral lines as the heliocentric angle changes or an influence of the solar dynamo. The study of the solar cycle dependence of the weak IN flux using high resolution measurements of the quiet Sun (including the poles) can thus provide additional information about the nature and distribution of IN fields.
In summary, while the field inclination distributions derived from Hinode/SP measurements may resemble that of isotropic fields, the latest results suggest that the field is actually not isotropic. It could even show spatial and temporal variations. This highlights the need for more observations and synoptic programs to understand how the polarization signals change both with the heliocentric angle and with the solar cycle.
6.2 Height variation of the vector magnetic field in the IN
As discussed in Sect. 4.6.1, most Hanle analyses agree that IN fields weaken with height in the atmosphere, although no consensus has been reached on the exact range of variation.
The only analyses of Hinode/SP data that have considered vertical variations of the atmospheric parameters are the tomographic inversions of Carroll and Kopf (2008), the MISMA inversions of Viticchié et al. (2011), and the spatially coupled inversions of Danilovic et al. (2016). Carroll and Kopf (2008) found weak fields, with an unsigned averaged flux that goes from \(\sim 16\) \(\hbox {Mx cm}^{-2}\) at the bottom of the photosphere to about 4 \(\hbox {Mx cm}^{-2}\) at 500 km. Thus, a strong decrease of the longitudinal field with height is indicated. The reliability of this analysis rests on that of the MHD models used to train the neural network (see Sect. 2.2.3). The MISMA inversions of Viticchié et al. (2011) also inferred a rapid vertical decrease of the field, with kG values near the base of the photosphere and sub-kG strengths at \(z = 150\) km, where the Fe i 630 nm lines are formed.
MISMA inversions have gone one step further than other analyses by successfully reproducing the observed asymmetries, hence determining the stratification of the atmospheric parameters much more precisely than had been possible before. However, other (simpler) scenarios are known to be able to reproduce strongly asymmetric profiles too (e.g., Fig. 3). Therefore, there is an urgent need to analyze the Hinode/SP data in terms of models featuring vertical gradients of the parameters with codes such as SIR, NICOLE, or SPINOR. This will help verify the outcome of the MISMA inversions and shed new light on the magnetism of the quiet Sun. A first analysis has been performed by Danilovic et al. (2016). Their inversions assume a single magnetic component filling the whole pixel and show magnetic fields decreasing with height. Further examination of the results of these inversions is highly desirable, in particular to assess the ability of the model to reproduce the shapes and asymmetries of the observed profiles.
Using ZIMPOL observations of the Fe i 524.7 and 525.0 nm lines taken at THEMIS, Stenflo (2013) came to the conclusion that the weak IN fields become preferentially horizontal beyond \(\upmu =0.2\), whereas they are mostly vertical until that point. Since observations toward the solar limb sample progressively higher layers of the photosphere, this appears to indicate a height variation of the magnetic field inclination. IN fields would be more vertical in the deep and mid photosphere, transitioning to horizontal in the upper photosphere. Therefore this analysis, independent of model assumptions but based on low resolution observations, also suggests that vertical gradients may be important to understand IN fields.
6.3 Hanle measurements at high spatial resolution
Without resolved observations, the Hanle effect cannot be used to determine the spatial organization of IN fields or the actual distribution of field strengths and inclinations over the solar surface. The lack of spatial resolution is without doubt the major limitation of current Hanle studies of the quiet Sun. This situation must be improved to make further progress.
The aim should be to obtain high resolution observations of the solar photosphere in Sr i 460.7 nm and selected molecular lines. Granules and intergranular lanes have to be clearly separated to test (and possibly refine) the predictions of large spatial variations made by Trujillo Bueno et al. (2004). High-resolution Sr i 470.6 nm observations will also make it possible to perform comparisons with Zeeman-based observations and confirm or refute the scenario proposed in Sect. 5.
These measurements, however, represent a challenge. The signals are very weak and require long integrations to be detected. Moreover, the need to distinguish granules and intergranular lanes calls for observations close to disk center, where scattering polarization signals are even weaker or just absent. Fortunately, the Sr i line should show measurable effects there. Using 3D hydrodynamical models of the photosphere, Trujillo Bueno and Shchukina (2007) calculated the scattering polarization of Sr i 460.7 nm at disk center and found polarization amplitudes from \(10^{-4}\) to a few times \(10^{-3} \, I_{\mathrm{QS}}\) at the diffraction limit of a 1 m telescope. These signals appear because of symmetry breaking effects: the granulation produces horizontal illumination inhomogeneities, leading to sizable scattering polarization variations on granular scales. Such signals will be modified in different ways by tangled fields on still unresolved scales and by coherent magnetic structures such as those inferred from Zeeman measurements. Thus, observing the Sr i line at high spatial resolution is of considerable interest to distinguish between scenarios. The latest investigations are based on small-scale dynamo simulations and confirm that the scattering polarization of the Sr i 460.7 nm line is very sensitive to the model magnetic field, showing spatial variations that should be detectable with the next generation of solar telescopes (del Pino Alemán et al. 2018). Interestingly, the scattering polarization signals resulting from the simulations are anticorrelated with the continuum intensity everywhere on the disk.
The challenge is then to perform spectropolarimetric measurements at a resolution of 0\(.{1}^{\prime \prime }\) and a noise level of \(10^{-4} \, I_{\mathrm{QS}}\). This is hard to achieve with filter instruments. Even with 1-m telescopes under the best seeing conditions, the throughput is not sufficient to reach such polarimetric sensitivities. One could use slit spectrographs to scan the solar surface, but this would mix the information on the anisotropy of the local radiation field. The only solution left is integral field spectropolarimetry based on, e.g., image slicers, or new instrumental concepts specifically tailored to the observation of the Sr i line. Hopefully, the sensitivity requirement will soon be met with large aperture telescopes such as the 1.5-m GREGOR and particularly the 4-m Daniel K. Inouye Solar Telescope.
6.4 Origin of internetwork fields
Much of our current knowledge of the origin of IN fields comes from numerical MHD simulations of the solar atmosphere. We have seen in the previous sections that small-scale loops emerge continually in the solar surface, and that they may explain both the observed distribution of IN fields and the Hanle depolarization of photospheric lines. According to the simulations, magnetic loops appear to be a natural consequence of the interaction of convective flows with the magnetic field. Stein and Nordlund (2006) were the first to identify rising loops in MHD simulations of the quiet Sun (see Fig. 38). Small-scale loops can also be identified in simulations by Abbett (2007), Isobe et al. (2008), and Stein et al. (2011). The latter show a hierarchy of loop-like structures of smaller and smaller sizes as the horizontal field approaches the solar photosphere. This gives rise to a magnetic topology at the surface similar to the one represented in Fig. 39, with loops straddling one or more granules.
An example of magnetic loops emerging in the solar atmosphere as observed in 3D magnetoconvection simulations. The panels on the left show renderings of the magnetic field strength and those on the right display sample field lines. The temporal cadence of the snapshots is 1 min. Image reproduced with permission from Stein and Nordlund (2006), copyright by AAS
Magnetic field lines overlying a map of the vertical velocity in the solar photosphere. The image shows the common occurrence of low-lying loop-like structures straddling one or more granules. Image reproduced with permission from Abbett (2007), copyright by AAS
The simulations demonstrate that low-lying magnetic loops are a natural configuration for the magnetic field in the solar photosphere. However, they do not say much about the origin of the field itself. In fact, most simulations proceed by injecting horizontal fields at the lower boundary of the computational box and letting them evolve. Such fields may represent, for example, recycled flux from decaying active regions or flux generated by the solar dynamo that emerges from deep in the convection zone. Despite these limitations, the simulations offer insight into crucial aspects of quiet Sun magnetism, such as the preponderance of horizontal fields over vertical fields. Steiner et al. (2008) found that the emerging magnetic flux is transported by overshooting convection to the mid and upper photosphere, where it accumulates in a layer of mainly horizontal fields near the temperature minimum region (\(\sim 500\) km). The ratio of horizontal to vertical field components was found to depend on the initial conditions and other details of the simulations, but it always shows a strong variation with height.
Ultimately, IN fields have to be produced by the global solar dynamo or by a local surface dynamo, as these are the only sources of magnetic energy in the Sun. The simulations described above, which could well represent the global dynamo scenario, produce a hierarchy of loop-like structures all over the solar surface. But also sophisticated simulations of surface dynamo action, attaining large magnetic Reynolds numbers, appear to explain the organization of the field observed by Hinode at 0\(.{32}^{\prime \prime }\). Using simulations by Vögler and Schüssler (2007), Danilovic et al. (2010a) computed synthetic Stokes profiles for the Fe i lines at 630 nm and degraded them to mimic Hinode/SP measurements. The resulting maps of longitudinal and transverse flux densities look similar to those recorded by the Hinode SP (Fig. 40). To produce a good match to the observed flux values, however, the magnetic field in the simulation had to be multiplied by a factor of 2–3. Shchukina and Trujillo Bueno (2011) also found it necessary to increase the field by a factor of 12 in the upper layers of the simulated photosphere, in order to explain the Hanle depolarization of the Sr i line. The excessive weakness of the fields may not be a serious limitation, though, as the field strength is expected to scale with the magnetic Reynolds number of the simulation. Indeed, stronger saturation fields have been obtained by Rempel (2014) using a combination of high grid resolution, low numerical diffusivities, and different bottom boundary conditions. The simulations of Rempel (2014) set an upper limit of 85 G for the average vertical magnetic field at optical depth unity. The dynamo model that best fits the Hinode/SP data analyzed by Danilovic et al. (2010a) has a mean vertical field strength of 60 G at the same depth.
The operation of a small-scale dynamo on the solar surface, however, remains an open question. It has been observed in MHD simulations, but it may be quenched at low magnetic Prandtl numbers \(P_{\mathrm{m}}\). In the solar photosphere, \(P_{\mathrm{m}} = \nu /\eta \sim 10^{-5}\), with \(\nu \) the viscosity and \(\eta \) the magnetic diffusivity. The magnetic Prandtl number cannot be computed easily in existing simulations, but it is of the order of unity and therefore much larger than that of the real Sun. Exploratory calculations by Thaler and Spruit (2015) show that no dynamo action occurs below a critical \(P_{\mathrm{m}} \approx 1\). This implies that simulations at lower magnetic Prandtl numbers may not produce small-scale dynamos (cf. Martínez Pillet 2013).
Comparison of the vertical and transverse field components generated by a surface dynamo simulation (left) with Hinode/SP observations (right), after calculation of synthetic Fe i 630 nm Stokes profiles and suitable degradation to match the specifications of the Hinode SP (middle). Image reproduced with permission from Danilovic et al. (2010b), copyright by ESO
Actually, Katsukawa and Orozco Suárez (2012) did not find indications of local dynamo action in their analysis. These authors calculated velocity and magnetic power spectra from Hinode/SP observations and compared them with the simulations of Vögler and Schüssler (2007) and Pietarila Graham et al. (2009, 2010). They found the slope of the magnetic power spectrum to be close to \(-1\) on subgranular scales, suggesting that the magnetic energy comes mainly from granular-sized structures or from a mixture of granular- and small-scale fields, not from small-scale fields only as it would be the case if a local dynamo is at work on the solar surface. This illustrates the controversies regarding the origin of IN fields.
Even if the magnetic topology of the quiet Sun IN can be explained by current simulations, it is important to go beyond morphological comparisons and study also the temporal evolution of the field in the simulations. Especially in the case of surface dynamos, it is not clear whether the small-scale structuring of the field may survive for as long as is required to explain the lifetimes of IN magnetic features. Also, it is necessary to verify that the evolution of loop-like structures in surface dynamo simulations resembles that observed in the real Sun.
Observationally, there are different ways to distinguish between global and local dynamos. One is to look for net imbalances of magnetic flux of opposite polarities in IN regions or changes in the net unsigned flux. Another is to study possible latitudinal and/or solar-cycle related variations of the magnetic field. No flux imbalances or cycle dependence would favor local dynamo action as the origin of the fields.
Lites (2011) used a large number of Hinode/SP maps to perform the first analysis. He did not find obvious polarity imbalances or changes of the unsigned flux in the weakest flux regions. On the contrary, the regions with larger fields (corresponding to the network) showed a marked polarity imbalance. This led him to suggest that IN fields may be generated by a local dynamo.
So far, no conclusive evidence for variations of IN fields with latitude or with the solar cycle exists, except perhaps near the poles. Two complementary approaches have been followed. On the one hand, Kleint et al. (2010) used the differential Hanle effect in two C\(_2\) triplets around 514.1 nm to monitor the IN at different disk positions. They found no variations of the IN fields—assumed to be turbulent—in two years around the solar minimum between cycles 23 and 24. However, complementing their observations with earlier measurements, they reported a possible small variation of the turbulent field strength with the solar cycle. This detection is only marginal and needs to be confirmed with additional observations, ideally from a homogeneous dataset. The linear polarization signals of Sr i 460.7 nm do not seem to be modulated by the solar cycle either (Trujillo Bueno et al. 2004). On the other hand, Buehler et al. (2013) analyzed the long-term evolution of the weak IN signals observed with Hinode at disk center. No variations of the polarization signals or magnetic flux could be detected, leading them to conclude that IN fields are not driven by the global dynamo but rather by a local dynamo, probably acting on small (granular) scales. Their results were later confirmed by Faurobert and Ricort (2015) comparing Hinode/SP maps from the maximum and miminum of the solar cycle and by Jin and Wang (2015a, b) using more than 1000 Hinode maps taken in the period 2007–2014.
The properties and evolution of magnetic fields in the poles have been studied by several authors. According to Ito et al. (2010), the weak fields of polar and equatorial regions have the same magnetic properties. This suggest a common origin. Shiota et al. (2012) found a clear variation of the stronger polar fields with the solar cycle, which is related to the global polarity reversal. By contrast, the weaker fields do not seem to vary significantly. Lites et al. (2014) studied the full range of latitudes using synoptic maps taken by Hinode during the period 2008–2013. They found no variations at mid latitudes for the weakest flux, so local dynamo action remains a plausible physical scenario for the generation and maintenance of IN fields there. At higher latitudes, and especially near the poles, they detected clear changes in the magnetic flux associated with the solar cycle and the polarity reversal. Those variations can also be seen in the weak polar flux, albeit with much lower amplitudes.
In summary, more observational and theoretical work is required to fully understand the origin of IN fields in the quiet Sun. While observations show a slight preference for local dynamo action, a definite conclusion on this topic will have to await confirmation that simulations at very low magnetic Prandtl numbers and high magnetic Reynolds numbers can explain the observed evolution of the field on the solar surface, including their modes of appearance and disappearance.
Notes
Stokes I represents the intensity, Q and U the linear polarization, and V the circular polarization. In practice, I is measured as the sum of the intensities transmitted through linear polarizers oriented at \(0^\circ \) and \(90^\circ \), Q as the difference of the intensities transmitted through linear polarizers at \(0^\circ \) and \(90^\circ \), and U as the difference of the intensities transmitted through linear polarizers at \(45^\circ \) and \(135^\circ \). V is measured as the difference of the intensities transmitted through a quarter wave plate followed by linear polarizers at \(45^\circ \) and \(135^\circ \). In this way, V represents the difference between right (clockwise) and left (counterclockwise) circularly polarized light.
Recall that the Stokes parameters are defined per unit area.
Actually, \(\alpha _{\mathrm{d}}\) was called stray-light factor in Orozco Suárez et al. (2007c). Here, we prefer to use the term dilution factor to avoid misinterpretations.
The C-shaped bisector of the mean quiet Sun profile is not produced by a real variation of the velocity with height in the solar atmosphere, but by the mixing of granular and intergranular profiles according to the areas they occupy.
At high spatial resolution, the mismatch between the observed intensity profile and the non-magnetic intensity profile is used to estimate the magnetic filling factor. Once this parameter is known, the amplitudes of Stokes Q, U and V give the field strength. See Orozco Suárez et al. (2007c) for details.
The polarizability factor \(W_2\) represents the fraction of scattering processes that occur as classical dipole scattering. It depends on the angular momentum J of the upper and lower transition levels (Stenflo 1994). The source function for Stokes Q is proportional to \(W_2\), so this factor measures the intrinsic scattering polarization of the line. For Sr i 460.7 nm, \(W_2\) reaches the maximum value of 1.
The polarization of the Sun’s continuum spectrum is mainly due to Rayleigh scattering by hydrogen and Thomson scattering by free electrons (e.g., Stenflo 2005). It is larger at shorter wavelengths and increases toward the limb. The continuum around Sr i 460.7 nm is polarized by \(Q/I \sim 0.1\%\) at \(\upmu =0.1\) (Stenflo 2005; Trujillo Bueno and Shchukina 2009).
Ephemeral regions are bipolar magnetic features that appear on the solar surface and remain visible for a few hours before merging or canceling with other flux concentrations (Harvey and Martin 1973). They have typical fluxes in the range \(3\times 10^{18}\) – \(1\times 10^{20}\) Mx and sizes of 30 Mm.
Mesogranular cells have characteristic sizes of 3–12 Mm and lifetimes of up to 6 h. They were discovered by November et al. (1981).
This can be seen by integrating the flux distribution between given limits. The emergence rate of features with fluxes between \(10^{16}\) and \(10^{20}\) Mx is 450 Mx cm\(^{-2}\) day\(^{-1}\), while that of features with fluxes above \(10^{20}\) Mx is only 1 Mx cm\(^{-2}\) day\(^{-1}\), according to Eq. (3) in Thornton and Parnell (2011).
Taken from Martínez González and Bellot Rubio (2009), unless otherwise stated.
The area asymmetry is the difference between the areas of the Stokes V blue and red lobes, normalized to their sum. The amplitude asymmetry is the difference between the amplitudes of the blue and red lobes, also normalized to their sum.
A very weak patch of negative Stokes U signal can be seen around \(y \sim 25^{\prime \prime }\). Such features are not common. Indeed, this is the first time that Hanle rotation is detected in Sr i measurements.
References
Abbett WP (2007) The magnetic connection between the convection zone and corona in the quiet Sun. Astrophys J 665:1469–1488. https://doi.org/10.1086/519788
Abramenko VI, Carbone V, Yurchyshyn V, Goode PR, Stein RF, Lepreti F, Capparelli V, Vecchio A (2011) Turbulent diffusion in the photosphere as derived from photospheric bright point motion. Astrophys J 743:133. https://doi.org/10.1088/0004-637X/743/2/133. arXiv:1111.4456
Anderson LS, Athay RG (1989) Model solar chromosphere with prescribed heating. Astrophys J 346:1010–1018. https://doi.org/10.1086/168083
Asensio Ramos A (2009) Evidence for quasi-isotropic magnetic fields from Hinode quiet-Sun observations. Astrophys J 701:1032–1043. https://doi.org/10.1088/0004-637X/701/2/1032. arXiv:0906.4230
Asensio Ramos A, Trujillo Bueno J (2007) THEMIS observations of the Hanle effect in C\(_2\) lines. Mem Soc Astron Ital 78:42–47
Asensio Ramos A, Martínez González MJ, López Ariste A, Trujillo Bueno J, Collados M (2007) A near-infrared line of Mn i as a diagnostic tool of the average magnetic energy in the solar photosphere. Astrophys J 659:829–847. https://doi.org/10.1086/511951. arXiv:astro-ph/0612389
Auer LH, Heasley JN (1978) The origin of broad-band circular polarization in sunspots. Astron Astrophys 64:67–71
Auer LH, House LL, Heasley JN (1977) The determination of vector magnetic fields from Stokes profiles. Solar Phys 55:47–61. https://doi.org/10.1007/BF00150873
Babcock HW (1953) The solar magnetograph. Astrophys J 118:387–396. https://doi.org/10.1086/145767
Barthol P, Gandorfer A, Solanki SK et al (2011) The Sunrise mission. Solar Phys 268:1–34. https://doi.org/10.1007/s11207-010-9662-9. arXiv:1009.2689
Beck C, Rezaei R (2009) The magnetic flux of the quiet Sun internetwork as observed with the tenerife infrared polarimeter. Astron Astrophys 502:969–979. https://doi.org/10.1051/0004-6361/200911727. arXiv:0903.3158
Beck C, Schmidt W, Kentischer T, Elmore D (2005) Polarimetric Littrow Spectrograph—instrument calibration and first measurements. Astron Astrophys 437:1159–1167. https://doi.org/10.1051/0004-6361:20052662
Beck C, Bellot Rubio LR, Schlichenmaier R, Sütterlin P (2007) Magnetic properties of G-band bright points in a sunspot moat. Astron Astrophys 472:607–622. https://doi.org/10.1051/0004-6361:20065620. arXiv:0707.1232
Beck C, Bellot Rubio LR, Kentischer TJ, Tritschler A, del Toro Iniesta JC (2010) Two-dimensional solar spectropolarimetry with the KIS/IAA visible imaging polarimeter. Astron Astrophys 520:A115. https://doi.org/10.1051/0004-6361/200913441. arXiv:1007.1153
Beckers JM (1971) The measurement of solar magnetic fields. In: Howard R (ed) Solar magnetic fields. IAU symposium, vol 43. Reidel, Dordretch, pp 3–23
Bello González N, Kneer F (2008) Narrow-band full Stokes polarimetry of small structures on the Sun with speckle methods. Astron Astrophys 480:265–275. https://doi.org/10.1051/0004-6361:20078567
Bello González N, Okunev O, Kneer F (2008) Small-scale magnetic field dynamics on the Sun at high spatial and temporal resolution. Astron Astrophys 490:L23–L26. https://doi.org/10.1051/0004-6361:200810464
Bello González N, Yelles Chaouche L, Okunev O, Kneer F (2009) Dynamics of small-scale magnetic fields on the Sun: observations and numerical simulations. Astron Astrophys 494:1091–1106. https://doi.org/10.1051/0004-6361:200810448
Bellot Rubio LR (2003) The fine structure of the penumbra: from observations to realistic physical models. In: Trujillo-Bueno J, Sánchez Almeida J (eds) Solar polarization 3. ASP conference series, vol 307. Astronomical Society of the Pacific, San Francisco, pp 301–323
Bellot Rubio LR (2006) Stokes inversion techniques: recent advances and new challenges. In: Casini R, Lites BW (eds) Solar polarization 4. ASP conference series, vol 358. Astronomical Society of the Pacific, San Francisco, pp 107–118 arXiv:astro-ph/0601483
Bellot Rubio LR (2009) Detection of supersonic horizontal flows in the solar granulation. Astrophys J 700:284–291. https://doi.org/10.1088/0004-637X/700/1/284. arXiv:0905.3719
Bellot Rubio LR, Beck C (2005) Magnetic flux cancellation in the moat of sunspots: results from simultaneous vector spectropolarimetry in the visible and the infrared. Astrophys J Lett 626:L125–L128. https://doi.org/10.1086/431648
Bellot Rubio LR, Collados M (2003) Understanding internetwork magnetic fields as determined from visible and infrared spectral lines. Astron Astrophys 406:357–362. https://doi.org/10.1051/0004-6361:20030704
Bellot Rubio LR, Orozco Suárez D (2012) Pervasive linear polarization signals in the quiet Sun. Astrophys J 757:19. https://doi.org/10.1088/0004-637X/757/1/19. arXiv:1207.0692
Bellot Rubio LR, Ruiz Cobo B, Collados M (2000a) Inversion of Stokes profiles from solar magnetic elements. Astrophys J 535:475–488. https://doi.org/10.1086/308806
Bellot Rubio LR, Ruiz Cobo B, Collados M (2000b) Structure of plage flux tubes from the inversion of Stokes spectra. I. Spatially averaged Stokes I and V profiles. Astrophys J 535:489–500. https://doi.org/10.1086/308807
Bendlin C, Volkmer R, Kneer F (1992) A new instrument for high resolution, two-dimensional solar spectroscopy. Astron Astrophys 257:817–823
Berdyugina SV, Fluri DM (2004) Evidence for the Hanle effect in molecular lines. Astron Astrophys 417:775–784. https://doi.org/10.1051/0004-6361:20034452
Berdyugina SV, Stenflo JO, Gandorfer A (2002) Molecular line scattering and magnetic field effects: resolution of an enigma. Astron Astrophys 388:1062–1078. https://doi.org/10.1051/0004-6361:20020587
Berger TE, Title AM (2001) On the relation of G-band bright points to the photospheric magnetic field. Astrophys J 553:449–469. https://doi.org/10.1086/320663
Berger TE, Löfdahl MG, Shine RA, Title AM (1998a) Measurements of solar magnetic element dispersal. Astrophys J 506:439–449. https://doi.org/10.1086/306228
Berger TE, Löfdahl MG, Shine RS, Title AM (1998b) Measurements of solar magnetic element motion from high-resolution filtergrams. Astrophys J 495:973–983. https://doi.org/10.1086/305309
Berger TE, Rouppe van der Voort LHM, Löfdahl MG, Carlsson M, Fossum A, Hansteen VH, Marthinussen E, Title A, Scharmer G (2004) Solar magnetic elements at 0.1 arcsec resolution. General appearance and magnetic structure. Astron Astrophys 428:613–628. https://doi.org/10.1051/0004-6361:20040436
Bianda M, Berdyugina S, Gisler D, Ramelli R, Belluzzi L, Carlin ES, Stenflo JO, Berkefeld T (2018) Spatial variations of the Sr i 4607 Å scattering polarization peak. Astron Astrophys 614:A89. https://doi.org/10.1051/0004-6361/201731887. arXiv:1803.03531
Bommier V (2011) The quiet Sun magnetic field: statistical description from THEMIS observations. Astron Astrophys 530:A51. https://doi.org/10.1051/0004-6361/201015761
Bommier V, Derouich M, Landi Degl’Innocenti E, Molodij G, Sahal-Bréchot S (2005) Interpretation of second solar spectrum observations of the Sr i 4607 Å line in a quiet region: turbulent magnetic field strength determination. Astron Astrophys 432:295–305. https://doi.org/10.1051/0004-6361:20035773
Bommier V, Landi Degl’Innocenti E, Feautrier N, Molodij G (2006) Collisional influence on the differential Hanle effect method applied to the second solar spectrum of the \(A^{2}{\varPi }-X^{2}{\varSigma }^{+}\) (0, 0) band of MgH. Astron Astrophys 458:625–633. https://doi.org/10.1051/0004-6361:20054591
Bommier V, Martínez González M, Bianda M, Frisch H, Asensio Ramos A, Gelly B, Landi Degl’Innocenti E (2009) The quiet Sun magnetic field observed with ZIMPOL on THEMIS. I. The probability density function. Astron Astrophys 506:1415–1428. https://doi.org/10.1051/0004-6361/200811373
Bonet JA, Cabello I, Sánchez Almeida J (2012) Center-to-limb variation of the area covered by magnetic bright points in the quiet Sun. Astron Astrophys 539:A6. https://doi.org/10.1051/0004-6361/201118215. arXiv:1112.2513
Borrero JM, Kobel P (2011) Inferring the magnetic field vector in the quiet Sun. I. Photon noise and selection criteria. Astron Astrophys 527:A29. https://doi.org/10.1051/0004-6361/201015634. arXiv:1011.4380
Borrero JM, Kobel P (2012) Inferring the magnetic field vector in the quiet Sun. II. Interpreting results from the inversion of Stokes profiles. Astron Astrophys 547:A89. https://doi.org/10.1051/0004-6361/201118238. arXiv:1209.4830
Borrero JM, Kobel P (2013) Inferring the magnetic field vector in the quiet Sun. III. Disk variation of the Stokes profiles and isotropism of the magnetic field. Astron Astrophys 550:A98. https://doi.org/10.1051/0004-6361/201118239. arXiv:1212.0788
Borrero JM, Martínez-Pillet V, Schlichenmaier R, Solanki SK, Bonet JA, del Toro Iniesta JC, Schmidt W, Barthol P, Gandorfer A, Domingo V, Knölker M (2010) Supersonic magnetic upflows in granular cells observed with SUNRISE/IMaX. Astrophys J Lett 723:L144–L148. https://doi.org/10.1088/2041-8205/723/2/L144. arXiv:1009.1227
Borrero JM, Tomczyk S, Kubo M, Socas-Navarro H, Schou J, Couvidat S, Bogart R (2011) VFISV: very fast inversion of the Stokes vector for the helioseismic and magnetic imager. Solar Phys 273:267–293. https://doi.org/10.1007/s11207-010-9515-6. arXiv:0901.2702
Borrero JM, Martínez Pillet V, Schmidt W, Quintero Noda C, Bonet JA, del Toro Iniesta JC, Bellot Rubio LR (2013) Is magnetic reconnection the cause of supersonic upflows in granular cells? Astrophys J 768:69. https://doi.org/10.1088/0004-637X/768/1/69. arXiv:1303.2557
Borrero JM, Lites BW, Lagg A, Rezaei R, Rempel M (2014) Comparison of inversion codes for polarized line formation in MHD simulations. I. Milne-Eddington codes. Astron Astrophys 572:A54. https://doi.org/10.1051/0004-6361/201424584. arXiv:1409.3376
Borrero JM, Jafarzadeh S, Schüssler M, Solanki SK (2017) Solar magnetoconvection and small-scale dynamo. Recent developments in observation and simulation. Space Sci Rev 210:275–316. https://doi.org/10.1007/s11214-015-0204-5. arXiv:1511.04214
Brault J, Noyes R (1983) Solar emission lines near 12 microns. Astrophys J Lett 269:L61–L66. https://doi.org/10.1086/184056
Bruls JHMJ, Solanki SK (1995) Infrared lines as probes of solar magnetic features. IX. Mg i 12 \(\mu \)m diagnostics of solar plage. Astron Astrophys 293:240–251
Buehler D, Lagg A, Solanki SK (2013) Quiet Sun magnetic fields observed by Hinode: support for a local dynamo. Astron Astrophys 555:A33. https://doi.org/10.1051/0004-6361/201321152. arXiv:1307.0789
Cabrera Solana D, Bellot Rubio LR, del Toro Iniesta JC (2005) Sensitivity of spectral lines to temperature, velocity, and magnetic field. Astron Astrophys 439:687–699. https://doi.org/10.1051/0004-6361:20052720
Cadavid AC, Lawrence JK, Ruzmaikin AA (1999) Anomalous diffusion of solar magnetic elements. Astrophys J 521:844–850. https://doi.org/10.1086/307573
Calcines A, López RL, Collados M (2013) MuSICa: the multi-slit image slicer for the EST spectrograph. J Astron Instrum 2:1350009. https://doi.org/10.1142/S2251171713500098
Cameron R, Vögler A, Schüssler M (2011) Decay of a simulated mixed-polarity magnetic field in the solar surface layers. Astron Astrophys 533:A86. https://doi.org/10.1051/0004-6361/201116974. arXiv:1108.1155
Cao W, Jing J, Ma J, Xu Y, Wang H, Goode PR (2006) Diffraction-limited polarimetry from the infrared imaging magnetograph at Big Bear Solar Observatory. Publ Astron Soc Pac 118:838–844. https://doi.org/10.1086/505408
Carlsson M, Stein RF, Nordlund Å, Scharmer GB (2004) Observational manifestations of solar magnetoconvection: center-to-limb variation. Astrophys J Lett 610:L137–L140. https://doi.org/10.1086/423305. arXiv:astro-ph/0406160
Carroll TA (2007) Stokes profile inversion in meso-structured magnetic atmospheres. In: Kneer F, Puschmann KG, Wittmann AD (eds) Modern solar facilities—advanced solar science, p 297 arXiv:astro-ph/0703315
Carroll TA, Kopf M (2007) The meso-structured magnetic atmosphere. A stochastic polarized radiative transfer approach. Astron Astrophys 468:323–339. https://doi.org/10.1051/0004-6361:20066975. arXiv:astro-ph/0703329
Carroll TA, Kopf M (2008) Zeeman-tomography of the solar photosphere. Three-dimensional surface structures retrieved from Hinode observations. Astron Astrophys 481:L37–L40. https://doi.org/10.1051/0004-6361:20079197. arXiv:0803.1048
Cauzzi G, Smaldone LA, Balasubramaniam KS, Keil SL (1993) On the calibration of line-of-sight magnetograms. Solar Phys 146:207–227. https://doi.org/10.1007/BF00662010
Cavallini F (2006) IBIS: a new post-focus instrument for solar imaging spectroscopy. Solar Phys 236:415–439. https://doi.org/10.1007/s11207-006-0103-8
Centeno R, Socas-Navarro H, Lites BW, Kubo M, Frank Z, Shine R, Tarbell T, Title A, Ichimoto K, Tsuneta S, Katsukawa Y, Suematsu Y, Shimizu T, Nagata S (2007) Emergence of small-scale magnetic loops in the quiet-Sun internetwork. Astrophys J Lett 666:L137–L140. https://doi.org/10.1086/521726. arXiv:0708.0844
Chae J (2012) Magnetic reconnection in the photosphere and chromosphere. In: Bellot Rubio L, Reale F, Carlsson M (eds) 4th Hinode science meeting: unsolved problems and recent insights. ASP conference series, vol 455, p 187
Chae J, Moon YJ, Wang H, Yun HS (2002) Flux cancellation rates and converging speeds of canceling magnetic features. Solar Phys 207:73–85
Chae J, Moon YJ, Pevtsov AA (2004) Observational evidence of magnetic flux submergence in flux cancellation sites. Astrophys J Lett 602:L65–L68. https://doi.org/10.1086/382222
Chae J, Goode PR, Ahn K, Yurchysyn V, Abramenko V, Andic A, Cao W, Park YD (2010) New solar telescope observations of magnetic reconnection occurring in the chromosphere of the quiet Sun. Astrophys J Lett 713:L6–L10. https://doi.org/10.1088/2041-8205/713/1/L6
Chapman GA (1970) An interference filter for observing the photospheric network. Solar Phys 13:78–84. https://doi.org/10.1007/BF00963943
Chapman GA, Sheeley JNR (1968) The photospheric network. Solar Phys 5:442–461. https://doi.org/10.1007/BF00147012
Cheung MCM, DeRosa ML (2012) A method for data-driven simulations of evolving solar active regions. Astrophys J 757:147. https://doi.org/10.1088/0004-637X/757/2/147. arXiv:1208.2954
Cheung MCM, Schüssler M, Tarbell TD, Title AM (2008) Solar surface emerging flux regions: a comparative study of radiative MHD modeling and Hinode SOT observations. Astrophys J 687:1373–1387. https://doi.org/10.1086/591245. arXiv:0810.5723
Collados M (2001) Infrared polarimetry. In: Sigwarth M (ed) Advanced solar polarimetry—theory, observation, and instrumentation. ASP conference series, vol 236. Astronomical Society of the Pacific, San Francisco, pp 255–271
Collados M, López R, Páez E, Hernández E, Reyes M, Calcines A, Ballesteros E, Díaz JJ, Denker C, Lagg A, Schlichenmaier R, Schmidt W, Solanki SK, Strassmeier KG, von der Lühe O, Volkmer R (2012) GRIS: the GREGOR infrared spectrograph. Astron Nachr 333:872. https://doi.org/10.1002/asna.201211738
Danilovic S, Beeck B, Pietarila A, Schüssler M, Solanki SK, Martínez Pillet V, Bonet JA, del Toro Iniesta JC, Domingo V, Barthol P, Berkefeld T, Gandorfer A, Knölker M, Schmidt W, Title AM (2010a) Transverse component of the magnetic field in the solar photosphere observed by SUNRISE. Astrophys J Lett 723:L149–L153. https://doi.org/10.1088/2041-8205/723/2/L149. arXiv:1008.1535
Danilovic S, Schüssler M, Solanki SK (2010b) Probing quiet Sun magnetism using MURaM simulations and Hinode/SP results: support for a local dynamo. Astron. Astrophys 513:A1. https://doi.org/10.1051/0004-6361/200913379. arXiv:1001.2183
Danilovic S, Cameron RH, Solanki SK (2015) Simulated magnetic flows in the solar photosphere. Astron Astrophys 574:A28. https://doi.org/10.1051/0004-6361/201423779. arXiv:1408.6159
Danilovic S, van Noort M, Rempel M (2016) Internetwork magnetic field as revealed by two-dimensional inversions. Astron Astrophys 593:A93. https://doi.org/10.1051/0004-6361/201527842. arXiv:1607.00772
DeForest CE, Hagenaar HJ, Lamb DA, Parnell CE, Welsch BT (2007) Solar magnetic tracking. I. Software comparison and recommended practices. Astrophys J 666:576–587. https://doi.org/10.1086/518994. arXiv:0704.2921
de la Cruz Rodríguez J, Hansteen V, Bellot-Rubio L, Ortiz A (2015) Emergence of granular-sized magnetic bubbles through the solar atmosphere. II. Non-LTE chromospheric diagnostics and inversions. Astrophys J 810:145. https://doi.org/10.1088/0004-637X/810/2/145. arXiv:1503.03846
De Pontieu B (2002) High-resolution observations of small-scale emerging flux in the photosphere. Astrophys J 569:474–486. https://doi.org/10.1086/339231
De Pontieu B, Title AM, Lemen JR et al (2014) The Interface Region Imaging Spectrograph (IRIS). Solar Phys 289:2733–2779. https://doi.org/10.1007/s11207-014-0485-y. arXiv:1401.2491
de Wijn AG, Lites BW, Berger TE, Frank ZA, Tarbell TD, Ishikawa R (2008) Hinode observations of magnetic elements in internetwork areas. Astrophys J 684:1469–1476. https://doi.org/10.1086/590237. arXiv:0806.0345
de Wijn AG, Stenflo JO, Solanki SK, Tsuneta S (2009) Small-scale solar magnetic fields. Space Sci Rev 144:275–315. https://doi.org/10.1007/s11214-008-9473-6. arXiv:0812.4465
del Pino Alemán T, Trujillo Bueno J, Štěpán J, Shchukina N (2018) A novel investigation of the small-scale magnetic activity of the quiet Sun via the Hanle effect in the Sr i 4607 Å line. Astrophys J 863:164. https://doi.org/10.3847/1538-4357/aaceab. arXiv:1806.07293
del Toro Iniesta JC (1996) On the discovery of the Zeeman effect on the sun and in the laboratory. Vistasn Astron 40:241–256. https://doi.org/10.1016/0083-6656(96)00005-0
del Toro Iniesta JC (2003) Introduction to spectropolarimetry. Cambridge University Press, Cambrigde. https://doi.org/10.1017/CBO9780511536250
del Toro Iniesta JC, Ruiz Cobo B (1996) Stokes profiles inversion techniques. Solar Phys 164:169–182. https://doi.org/10.1007/BF00146631
del Toro Iniesta JC, Ruiz Cobo B (2016) Inversion of the radiative transfer equation for polarized light. Living Rev Sol Phys 13:4. https://doi.org/10.1007/s41116-016-0005-2. arXiv:1610.10039
del Toro Iniesta JC, Orozco Suárez D, Bellot Rubio LR (2010) On spectropolarimetric measurements with visible lines. Astrophys J 711:312–321. https://doi.org/10.1088/0004-637X/711/1/312. arXiv:1001.3022
Derouich M, Bommier V, Malherbe JM, Landi Degl’Innocenti E (2006) Second solar spectrum of the Sr i 4607 Å line: depth probing of the turbulent magnetic field strength in a quiet region. Astron Astrophys 457:1047–1052. https://doi.org/10.1051/0004-6361:20065782
Domínguez Cerdeña I (2003) Evidence of mesogranulation from magnetograms of the Sun. Astron Astrophys 412:L65–L68. https://doi.org/10.1051/0004-6361:20034617
Domínguez Cerdeña I, Kneer F, Sánchez Almeida J (2003a) Quiet-Sun magnetic fields at high spatial resolution. Astrophys J Lett 582:L55–L58. https://doi.org/10.1086/346199. arXiv:astro-ph/0211454
Domínguez Cerdeña I, Sánchez Almeida J, Kneer F (2003b) Inter-network magnetic fields observed with sub-arcsec resolution. Astron Astrophys 407:741–757. https://doi.org/10.1051/0004-6361:20030892. arXiv:astro-ph/0306329
Domínguez Cerdeña I, Sánchez Almeida J, Kneer F (2006) Quiet Sun magnetic fields from simultaneous inversions of visible and infrared spectropolarimetric observations. Astrophys J 646:1421–1435. https://doi.org/10.1086/505129. arXiv:astro-ph/0604381
Dunn RB, Zirker JB (1973) The solar filigree. Solar Phys 33:281–304. https://doi.org/10.1007/BF00152419
Elmore DF, Lites BW, Tomczyk S, Skumanich AP, Dunn RB, Schuenke JA, Streander KV, Leach TW, Chambellan CW, Hull HK (1992) The advanced Stokes polarimeter: a new instrument for solar magnetic field research. In: Goldstein DH, Chipman RA (eds) Polarization analysis and measurement. Proceedings of SPIE, vol 1746. SPIE, Bellingham, WA, pp 22–33. https://doi.org/10.1117/12.138795
Faurobert M, Arnaud J (2003) Center-to-limb variation of scattering polarization in molecular solar lines: observations and modeling. Astron Astrophys 412:555–565. https://doi.org/10.1051/0004-6361:20031468
Faurobert M, Ricort G (2015) Solar-cycle variations of the internetwork magnetic field. Astron Astrophys 582:A95. https://doi.org/10.1051/0004-6361/201526298
Faurobert M, Arnaud J, Vigneau J, Frisch H (2001) Investigation of weak solar magnetic fields. New observational results for the Sr i 460.7 nm linear polarization and radiative transfer modeling. Astron Astrophys 378:627–634. https://doi.org/10.1051/0004-6361:20011263
Faurobert-Scholl M (1993) Investigation of microturbulent magnetic fields in the solar photosphere by their Hanle effect in the Sr i 4607 Å line. Astron Astrophys 268:765–774
Faurobert-Scholl M (1996) Diagnostics with the Hanle effect. Solar Phys 164:79–90. https://doi.org/10.1007/BF00146624
Faurobert-Scholl M, Feautrier N, Machefert F, Petrovay K, Spielfiedel A (1995) Turbulent magnetic fields in the solar photosphere: diagnostics and interpretation. Astron Astrophys 298:289
Frisch H, Anusha LS, Sampoorna M, Nagendra KN (2009) The Hanle effect in a random magnetic field. Dependence of the polarization on statistical properties of the magnetic field. Astron Astrophys 501:335–348. https://doi.org/10.1051/0004-6361/200911696
Frutiger C, Solanki SK (1998) Do solar magnetic elements harbor downflows? Astron Astrophys 336:L65–L68
Frutiger C, Solanki SK, Gandorfer A (2003) Magnetic elements near the solar limb: inversions based on a flux-tube model. In: Trujillo-Bueno J, Sánchez Almeida J (eds) Solar polarization 3. ASP conference series, vol 307. Astronomical Society of the Pacific, San Francisco, pp 344–351
Giannattasio F, Del Moro D, Berrilli F, Bellot Rubio L, Gošić M, Orozco Suárez D (2013) Diffusion of solar magnetic elements up to supergranular spatial and temporal scales. Astrophys J Lett 770:L36. https://doi.org/10.1088/2041-8205/770/2/L36. arXiv:1305.4006
Giannattasio F, Stangalini M, Berrilli F, Del Moro D, Bellot Rubio L (2014) Diffusion of magnetic elements in a supergranular cell. Astrophys J 788:137. https://doi.org/10.1088/0004-637X/788/2/137. arXiv:1405.0677
Gömöry P, Beck C, Balthasar H, Rybák J, Kučera A, Koza J, Wöhl H (2010) Magnetic loop emergence within a granule. Astron Astrophys 511:A14. https://doi.org/10.1051/0004-6361/200912807. arXiv:0910.4449
Gömöry P, Balthasar H, Puschmann KG (2013) Evidence of quiet-Sun chromospheric activity related to an emerging small-scale magnetic loop. Astron Astrophys 556:A7. https://doi.org/10.1051/0004-6361/201321410. arXiv:1306.3393
Goodman ML (2001) The necessity of using realistic descriptions of transport processes in modeling the solar atmosphere, and the importance of understanding chromospheric heating. Space Sci Rev 95:79–93
Gošić M (2012) Properties and evolution of magnetic elements in the solar internetwork. Master’s thesis, Universidad de Granada, Spain
Gošić M (2015) The solar internetwork. PhD thesis, Universidad de Granada, Spain
Gošić M, Bellot Rubio LR, Orozco Suárez D, Katsukawa Y, del Toro Iniesta JC (2014) The solar internetwork. I. Contribution to the network magnetic flux. Astrophys J 797:49. https://doi.org/10.1088/0004-637X/797/1/49. arXiv:1408.2369
Gošić M, Bellot Rubio LR, del Toro Iniesta JC, Orozco Suárez D, Katsukawa Y (2016) The solar internetwork. II. Flux appearance and disappearance rates. Astrophys J 820:35. https://doi.org/10.3847/0004-637X/820/1/35. arXiv:1602.05892
Grossmann-Doerth U, Keller CU, Schüssler M (1996) Observations of the quiet Sun’s magnetic field. Astron Astrophys 315:610–617
Grossmann-Doerth U, Schüssler M, Sigwarth M, Steiner O (2000) Strong Stokes V asymmetries of photospheric spectral lines: what can they tell us about the magnetic field structure? Astron Astrophys 357:351–358
Guglielmino SL (2012) Observational consequences of flux emergence from the photosphere to the corona: the role of interactions. In: Bellot Rubio L, Reale F, Carlsson M (eds) 4th Hinode science meeting: unsolved problems and recent insights. ASP conference series, vol 455, p 109
Guglielmino SL, Martínez Pillet V, Bonet JA, del Toro Iniesta JC, Bellot Rubio LR, Solanki SK, Schmidt W, Gandorfer A, Barthol P, Knölker M (2012) The frontier between small-scale bipoles and ephemeral regions in the solar photosphere: emergence and decay of an intermediate-scale bipole observed with SUNRISE/IMaX. Astrophys J 745:160. https://doi.org/10.1088/0004-637X/745/2/160. arXiv:1110.1405
Hagenaar HJ (2001) Ephemeral regions on a sequence of full-disk Michelson Doppler Imager magnetograms. Astrophys J 555:448–461. https://doi.org/10.1086/321448
Hagenaar HJ, Schrijver CJ, Title AM, Shine RA (1999) Dispersal of magnetic flux in the quiet solar photosphere. Astrophys J 511:932–944. https://doi.org/10.1086/306691
Hale GE (1908) On the probable existence of a magnetic field in Sun-spots. Astrophys J 28:315. https://doi.org/10.1086/141602
Harvey KL, Martin SF (1973) Ephemeral active regions. Solar Phys 32:389–402. https://doi.org/10.1007/BF00154951
Harvey JW, Branston D, Henney CJ, Keller CU (2007) Seething horizontal magnetic fields in the quiet solar photosphere. Astrophys J Lett 659:L177–L180. https://doi.org/10.1086/518036. arXiv:astro-ph/0702415
Hirzberger J, Bonet JA, Vázquez M, Hanslmeier A (1999) Time series of solar granulation images. II. Evolution of individual granules. Astrophys J 515:441–454. https://doi.org/10.1086/307018
Ichimoto K, Lites B, Elmore D, Suematsu Y, Tsuneta S, Katsukawa Y, Shimizu T, Shine R, Tarbell T, Title A, Kiyohara J, Shinoda K, Card G, Lecinski A, Streander K, Nakagiri M, Miyashita M, Noguchi M, Hoffmann C, Cruz T (2008) Polarization calibration of the solar optical telescope onboard Hinode. Solar Phys 249:233–261. https://doi.org/10.1007/s11207-008-9169-9
Iida Y, Yokoyama T, Ichimoto K (2010) Vector magnetic fields and doppler velocity structures around a cancellation site in the quiet Sun. Astrophys J 713:325–329. https://doi.org/10.1088/0004-637X/713/1/325
Illing RME, Landman DA, Mickey DL (1975) Broad-band circular polarization of sunspots: spectral dependence and theory. Astron Astrophys 41:183–185
Ishikawa R, Tsuneta S (2009) Comparison of transient horizontal magnetic fields in a plage region and in the quiet Sun. Astron Astrophys 495:607–612. https://doi.org/10.1051/0004-6361:200810636. arXiv:0812.1631
Ishikawa R, Tsuneta S (2010) Spatial and temporal distributions of transient horizontal magnetic fields with deep exposure. Astrophys J Lett 718:L171–L175. https://doi.org/10.1088/2041-8205/718/2/L171
Ishikawa R, Tsuneta S (2011) The relationship between vertical and horizontal magnetic fields in the quiet Sun. Astrophys J 735:74. https://doi.org/10.1088/0004-637X/735/2/74. arXiv:1103.5556
Ishikawa R, Tsuneta S, Ichimoto K, Isobe H, Katsukawa Y, Lites BW, Nagata S, Shimizu T, Shine RA, Suematsu Y, Tarbell TD, Title AM (2008) Transient horizontal magnetic fields in solar plage regions. Astron Astrophys 481:L25–L28. https://doi.org/10.1051/0004-6361:20079022. arXiv:0802.1769
Ishikawa R, Tsuneta S, Jurčák J (2010) Three-dimensional view of transient horizontal magnetic fields in the photosphere. Astrophys J 713:1310–1321. https://doi.org/10.1088/0004-637X/713/2/1310. arXiv:1003.1376
Isobe H, Proctor MRE, Weiss NO (2008) Convection-driven emergence of small-scale magnetic fields and their role in coronal heating and solar wind acceleration. Astrophys J Lett 679:L57–L60. https://doi.org/10.1086/589150
Ito H, Tsuneta S, Shiota D, Tokumaru M, Fujiki K (2010) Is the polar region different from the quiet region of the Sun? Astrophys J 719:131–142. https://doi.org/10.1088/0004-637X/719/1/131. arXiv:1005.3667
Jafarzadeh S, Cameron RH, Solanki SK, Pietarila A, Feller A, Lagg A, Gandorfer A (2014a) Migration of Ca ii H bright points in the internetwork. Astron Astrophys 563:A101. https://doi.org/10.1051/0004-6361/201323011. arXiv:1401.7522
Jafarzadeh S, Solanki SK, Lagg A, Bellot Rubio LR, van Noort M, Feller A, Danilovic S (2014b) Inclinations of small quiet-Sun magnetic features based on a new geometric approach. Astron Astrophys 569:A105. https://doi.org/10.1051/0004-6361/201423414. arXiv:1408.2443
Janßen K, Vögler A, Kneer F (2003) On the fractal dimension of small-scale magnetic structures in the Sun. Astron Astrophys 409:1127–1134. https://doi.org/10.1051/0004-6361:20031168
Jefferies J, Lites BW, Skumanich A (1989) Transfer of line radiation in a magnetic field. Astrophys J 343:920–935. https://doi.org/10.1086/167762
Jin C, Wang J (2015a) Solar cycle variation of the inter-network magnetic field. Astrophys J 806:174. https://doi.org/10.1088/0004-637X/806/2/174
Jin CL, Wang JX (2015b) Does the variation of solar intra-network horizontal field follow Sunspot cycle? Astrophys J 807:70. https://doi.org/10.1088/0004-637X/807/1/70
Jin C, Wang J, Zhou G (2009) The properties of horizontal magnetic elements in quiet solar intranetwork. Astrophys J 697:693–700. https://doi.org/10.1088/0004-637X/697/1/693. arXiv:0904.1010
Jin CL, Wang JX, Song Q, Zhao H (2011) The Sun’s small-scale magnetic elements in Solar Cycle 23. Astrophys J 731:37. https://doi.org/10.1088/0004-637X/731/1/37. arXiv:1102.3728
Jin CL, Wang JX, Xie ZX (2012) Solar intranetwork magnetic elements: intrinsically weak or strong? Solar Phys 280:51–67. https://doi.org/10.1007/s11207-012-0050-5
Katsukawa Y, Orozco Suárez D (2012) Power spectra of velocities and magnetic fields on the solar surface and their dependence on the unsigned magnetic flux density. Astrophys J 758:139. https://doi.org/10.1088/0004-637X/758/2/139. arXiv:1209.0548
Keller CU, Steiner O, Stenflo JO, Solanki SK (1990) Structure of solar magnetic fluxtubes from the inversion of Stokes spectra at disk center. Astron Astrophys 233:583–597
Keller CU, Deubner FL, Egger U, Fleck B, Povel HP (1994) On the strength of solar intra-network fields. Astron Astrophys 286:626–634
Khomenko E, Collados M (2007) On the Stokes V amplitude ratio as an indicator of the field strength in the solar internetwork. Astrophys J 659:1726–1735. https://doi.org/10.1086/512098
Khomenko EV, Collados M, Solanki SK, Lagg A, Trujillo Bueno J (2003) Quiet-Sun inter-network magnetic fields observed in the infrared. Astron Astrophys 408:1115–1135. https://doi.org/10.1051/0004-6361:20030604
Khomenko EV, Martínez González MJ, Collados M, Vögler A, Solanki SK, Ruiz Cobo B, Beck C (2005a) Magnetic flux in the internetwork quiet Sun. Astron Astrophys 436:L27–L30. https://doi.org/10.1051/0004-6361:200500114
Khomenko EV, Shelyag S, Solanki SK, Vögler A (2005b) Stokes diagnostics of simulations of magnetoconvection of mixed-polarity quiet-Sun regions. Astron Astrophys 442:1059–1078. https://doi.org/10.1051/0004-6361:20052958
Kleint L, Berdyugina SV, Shapiro AI, Bianda M (2010) Solar turbulent magnetic fields: surprisingly homogeneous distribution during the solar minimum. Astron Astrophys 524:A37. https://doi.org/10.1051/0004-6361/201015285
Kneer F, von Uexkuell M (1991) On the structure of spectral line gap regions. Astron Astrophys 247:556–564
Kosugi T, Matsuzaki K, Sakao T, Shimizu T, Sone Y, Tachikawa S, Hashimoto T, Minesugi K, Ohnishi A, Yamada T, Tsuneta S, Hara H, Ichimoto K, Suematsu Y, Shimojo M, Watanabe T, Shimada S, Davis JM, Hill LD, Owens JK, Title AM, Culhane JL, Harra LK, Doschek GA, Golub L (2007) The Hinode (Solar-B) mission: an overview. Solar Phys 243:3–17. https://doi.org/10.1007/s11207-007-9014-6
Kubo M, Shimizu T (2007) Magnetic field properties of flux cancellation sites. Astrophys J 671:990–1004. https://doi.org/10.1086/523080
Kubo M, Low BC, Lites BW (2010) Granular-scale magnetic flux cancellations in the photosphere. Astrophys J 712:1321–1330. https://doi.org/10.1088/0004-637X/712/2/1321. arXiv:1003.2863
Lagg A, Woch J, Krupp N, Solanki SK (2004) Retrieval of the full magnetic vector with the He i multiplet at 1083 nm. Maps of an emerging flux region. Astron Astrophys 414:1109–1120. https://doi.org/10.1051/0004-6361:20031643
Lagg A, Solanki SK, Riethmüller TL, Martínez Pillet V, Schüssler M, Hirzberger J, Feller A, Borrero JM, Schmidt W, del Toro Iniesta JC, Bonet JA, Barthol P, Berkefeld T, Domingo V, Gandorfer A, Knölker M, Title AM (2010) Fully resolved quiet-Sun magnetic flux tube observed with the SUNRISE/IMaX instrument. Astrophys J Lett 723:L164–L168. https://doi.org/10.1088/2041-8205/723/2/L164. arXiv:1009.0996
Lamb DA, DeForest CE, Hagenaar HJ, Parnell CE, Welsch BT (2008) Solar magnetic tracking. II. The apparent unipolar origin of quiet-Sun flux. Astrophys J 674:520–529. https://doi.org/10.1086/524372
Lamb DA, DeForest CE, Hagenaar HJ, Parnell CE, Welsch BT (2010) Solar magnetic tracking. III. Apparent unipolar flux emergence in high-resolution observations. Astrophys J 720:1405–1416. https://doi.org/10.1088/0004-637X/720/2/1405
Lamb DA, Howard TA, DeForest CE, Parnell CE, Welsch BT (2013) Solar magnetic tracking. IV. The death of magnetic features. Astrophys J 774:127. https://doi.org/10.1088/0004-637X/774/2/127. arXiv:1307.4019
Landi Degl’Innocenti E (1982) On the effective Landé factor of magnetic lines. Solar Phys 77:285–289. https://doi.org/10.1007/BF00156111
Landi Degl’Innocenti E (1992) Magnetic field measurements. In: Sáanchez F, Collados M, Vázquez M (eds) Solar observations: techniques and interpretation. Cambridge University Press, Cambridge, pp 71–72
Landi Degl’Innocenti E, Landolfi M (1983) Asymmetries in Stokes profiles of magnetic lines: a linear analysis in terms of velocity gradients. Solar Phys 87:221–231. https://doi.org/10.1007/BF00224835
Landi Degl’Innocenti E, Landolfi M (2004) Polarization in spectral lines. Astrophysics and space science library, vol 307. Kluwer Academic, Dordrecht. https://doi.org/10.1007/1-4020-2415-0
Landolfi M, Landi Degl’Innocenti E (1996) Net circular polarization in magnetic spectral lines produced by velocity gradients: some analytical results. Solar Phys 164:191–202. https://doi.org/10.1007/BF00146633
Lee J, Chae JC, Yun HS, Zirin H (1997) The effect of seeing on solar magnetic flux measurements. Solar Phys 171:35–48. https://doi.org/10.1023/A:1004962105138
Leenaarts J, Rutten RJ, Carlsson M, Uitenbroek H (2006) A comparison of solar proxy-magnetometry diagnostics. Astron Astrophys 452:L15–L18. https://doi.org/10.1051/0004-6361:20065182
Lin H (1995) On the distribution of the solar magnetic fields. Astrophys J 446:421. https://doi.org/10.1086/175800
Lin H, Rimmele T (1999) The granular magnetic fields of the quiet Sun. Astrophys J 514:448–455. https://doi.org/10.1086/306925
Lites BW (2002) Characterization of magnetic flux in the quiet Sun. Astrophys J 573:431–444. https://doi.org/10.1086/340120
Lites BW (2011) Hinode observations suggesting the presence of a local small-scale turbulent dynamo. Astrophys J 737:52. https://doi.org/10.1088/0004-637X/737/2/52
Lites BW, Skumanich A (1990) Stokes profile analysis and vector magnetic fields. V. The magnetic field structure of large sunspots observed with Stokes II. Astrophys J 348:747–760. https://doi.org/10.1086/168284
Lites BW, Socas-Navarro H (2004) Characterization of magnetic flux in the quiet Sun. II. The internetwork fields at high angular resolution. Astrophys J 613:600–609. https://doi.org/10.1086/422836
Lites BW, Rutten RJ, Kalkofen W (1993) Dynamics of the solar chromosphere. I. Long-period network oscillations. Astrophys J 414:345–356. https://doi.org/10.1086/173081
Lites BW, Leka KD, Skumanich A, Martínez Pillet V, Shimizu T (1996) Small-scale horizontal magnetic fields in the solar photosphere. Astrophys J 460:1019. https://doi.org/10.1086/177028
Lites BW, Elmore DF, Streander KV (2001) The Solar-B spectro-polarimeter. In: Sigwarth M (ed) Advanced solar polarimetry—theory, observation, and instrumentation. ASP conference series, vol 236. Astronomical Society of the Pacific, San Francisco, p 33
Lites BW, Casini R, Garcia J, Socas-Navarro H (2007a) A suite of community tools for spectro-polarimetric analysis. Mem Soc Astron Ital 78:148
Lites BW, Socas-Navarro H, Kubo M, Berger T, Frank Z, Shine RA, Tarbell TD, Title AM, Ichimoto K, Katsukawa Y, Tsuneta S, Suematsu Y, Shimizu T (2007b) Hinode observations of horizontal quiet Sun magnetic flux and the ‘hidden turbulent magnetic flux’. Publ Astron Soc Japan 59:571
Lites BW, Kubo M, Socas-Navarro H, Berger T, Frank Z, Shine R, Tarbell T, Title A, Ichimoto K, Katsukawa Y, Tsuneta S, Suematsu Y, Shimizu T, Nagata S (2008) The horizontal magnetic flux of the quiet-Sun internetwork as observed with the Hinode spectro-polarimeter. Astrophys J 672:1237–1253. https://doi.org/10.1086/522922
Lites BW, Casini R, Manso Sainz R, Jurčák J, Ichimoto K, Ishikawa R, Okamoto TJ, Tsuneta S, Bellot Rubio L (2010) Scattering polarization in the Fe i 630 nm emission lines at the extreme limb of the Sun. Astrophys J 713:450–457. https://doi.org/10.1088/0004-637X/713/1/450
Lites BW, Akin DL, Card G, Cruz T, Duncan DW, Edwards CG, Elmore DF, Hoffmann C, Katsukawa Y, Katz N, Kubo M, Ichimoto K, Shimizu T, Shine RA, Streander KV, Suematsu A, Tarbell TD, Title AM, Tsuneta S (2013) The Hinode spectro-polarimeter. Solar Phys 283:579–599. https://doi.org/10.1007/s11207-012-0206-3
Lites BW, Centeno R, McIntosh SW (2014) The solar cycle dependence of the weak internetwork flux. Publ Astron Soc Japan 66:S4. https://doi.org/10.1093/pasj/psu082
Lites BW, Rempel M, Borrero JM, Danilovic S (2017) Are internetwork magnetic fields in the solar photosphere horizontal or vertical? Astrophys J 835:14. https://doi.org/10.3847/1538-4357/835/1/14
Litvinenko YE (1999) Photospheric magnetic reconnection and canceling magnetic features on the Sun. Astrophys J 515:435–440. https://doi.org/10.1086/307001
Livi SHB, Wang J, Martin SF (1985) The cancellation of magnetic flux. I. On the quiet sun. Aust J Phys 38:855–873
Livingston W, Harvey J (1971) The kitt peak magnetograph. IV: 40-channel probe and the detection of weak photospheric fields. In: Howard R (ed) Solar magnetic fields. IAU symposium, vol 43, p 51
Livingston WC, Harvey J (1975) A new component of solar magnetism—the inner network fields. Bull Am Astron Soc 7:346
López Ariste A, Sainz Dalda A (2012) Scales of the magnetic fields in the quiet Sun. Astron Astrophys 540:A66. https://doi.org/10.1051/0004-6361/201118191. arXiv:1202.5436
López Ariste A, Rayrole J, Semel M (2000) First results from THEMIS spectropolarimetric mode. Astron Astrophys Suppl Ser 142:137–148. https://doi.org/10.1051/aas:2000144
López Ariste A, Tomczyk S, Casini R (2002) Hyperfine structure as a diagnostic of solar magnetic fields. Astrophys J 580:519–527. https://doi.org/10.1086/343111
López Ariste A, Tomczyk S, Casini R (2006) Quiet sun magnetic field diagnostics with a Mn line. Astron Astrophys 454:663–668. https://doi.org/10.1051/0004-6361:20054657
López Ariste A, Martínez González MJ, Ramírez Vélez JC (2007a) Determination of field strengths in the quiet Sun. Astron Astrophys 464:351–356. https://doi.org/10.1051/0004-6361:20065593
López Ariste A, Malherbe JM, Manso Sainz R, Asensio Ramos A, Ramírez Vélez JC, Martínez González M (2007b) Turbulent fields in the quiet sun from Hanle and Zeeman effects with THEMIS. In: Bouvier J, Chalabaev A, Charbonnel C (eds) SF2A-2007. Société Francaise d’Astronomie et d’Astrophysique, France, p 592
Makita M (1986) An interpretation of the broad-band circular polarization of sunspots. Solar Phys 106:269–286. https://doi.org/10.1007/BF00158497
Malherbe JM, Moity J, Arnaud J, Roudier T (2007) First observations of the second solar spectrum with spatial resolution at the Lunette Jean Rösch. Astron Astrophys 462:753–762. https://doi.org/10.1051/0004-6361:20065910
Manso Sainz R, Landi Degl’Innocenti E, Trujillo Bueno J (2004) Concerning the existence of a ‘turbulent’ magnetic field in the quiet Sun. Astrophys J Lett 614:L89–L91. https://doi.org/10.1086/425176. arXiv:astro-ph/0408360
Manso Sainz R, Martínez González MJ, Asensio Ramos A (2011) Advection and dispersal of small magnetic elements in the very quiet Sun. Astron Astrophys 531:L9. https://doi.org/10.1051/0004-6361/201117042
Martin SF (1984) Dynamic signatures of quiet Sun magnetic fields. In: Keil SL (ed) Small-scale dynamical processes in quiet stellar atmospheres, p 30
Martin SF (1988) The identification and interaction of network, intranetwork, and ephemeral-region magnetic fields. Solar Phys 117:243–259. https://doi.org/10.1007/BF00147246
Martin SF (1990) Small-scale magnetic features observed in the photosphere. In: Stenflo JO (ed) Solar photosphere: structure, convection, and magnetic fields. IAU symposium, vol 138, p 129
Martin SF, Livi SHB, Wang J (1985) The cancellation of magnetic flux. II. In a decaying active region. Aust J Phys 38:929–959
Martínez González MJ (2007) Internetwork magnetic fields observed in the visible. Mem Soc Astron Ital 78:59
Martínez González MJ, Bellot Rubio LR (2009) Emergence of small-scale magnetic loops through the quiet solar atmosphere. Astrophys J 700:1391–1403. https://doi.org/10.1088/0004-637X/700/2/1391. arXiv:0905.2691
Martínez González MJ, Collados M, Ruiz Cobo B (2006) On the validity of the 630 nm Fe i lines for magnetometry of the internetwork quiet Sun. Astron Astrophys 456:1159–1164. https://doi.org/10.1051/0004-6361:20065008. arXiv:astro-ph/0605446
Martínez González MJ, Collados M, Ruiz Cobo B, Solanki SK (2007) Low-lying magnetic loops in the solar internetwork. Astron Astrophys 469:L39–L42. https://doi.org/10.1051/0004-6361:20077505. arXiv:0705.1319
Martínez González MJ, Collados M, Ruiz Cobo B, Beck C (2008) Internetwork magnetic field distribution from simultaneous 1.56 \(\mu \)m and 630 nm observations. Astron Astrophys 477:953–965. https://doi.org/10.1051/0004-6361:20078506. arXiv:0711.0267
Martínez González MJ, Manso Sainz R, Asensio Ramos A, Bellot Rubio LR (2010a) Small magnetic loops connecting the quiet surface and the hot outer atmosphere of the Sun. Astrophys J Lett 714:L94–L97. https://doi.org/10.1088/2041-8205/714/1/L94. arXiv:1003.1255
Martínez González MJ, Manso Sainz R, Asensio Ramos A, López Ariste A, Bianda M (2010b) Statistical analysis of the very quiet Sun magnetism. Astrophys J Lett 711:L57–L60. https://doi.org/10.1088/2041-8205/711/2/L57. arXiv:1001.4551
Martínez González MJ, Bellot Rubio LR, Solanki SK, Martínez Pillet V, del Toro Iniesta JC, Barthol P, Schmidt W (2012a) Resolving the internal magnetic structure of the solar network. Astrophys J Lett 758:L40. https://doi.org/10.1088/2041-8205/758/2/L40. arXiv:1209.2584
Martínez González MJ, Manso Sainz R, Asensio Ramos A, Hijano E (2012b) Dead calm areas in the very quiet Sun. Astrophys J 755:175. https://doi.org/10.1088/0004-637X/755/2/175. arXiv:1206.4545
Martínez González MJ, Pastor Yabar A, Lagg A, Asensio Ramos A, Collados M, Solanki SK, Balthasar H, Berkefeld T, Denker C, Doerr HP, Feller A, Franz M, González Manrique SJ, Hofmann A, Kneer F, Kuckein C, Louis R, von der Lühe O, Nicklas H, Orozco D, Rezaei R, Schlichenmaier R, Schmidt D, Schmidt W, Sigwarth M, Sobotka M, Soltau D, Staude J, Strassmeier KG, Verma M, Waldman T, Volkmer R (2016) Inference of magnetic fields in the very quiet Sun. Astron Astrophys 596:A5. https://doi.org/10.1051/0004-6361/201628449. arXiv:1804.10089
Martínez Pillet V (2013) Solar surface and atmospheric dynamics. The photosphere. Space Sci Rev 178:141–162. https://doi.org/10.1007/s11214-013-9967-8. arXiv:1301.6933
Martínez Pillet V, Collados M, Sánchez Almeida J, González V, Cruz-Lopez A, Manescau A, Joven E, Paez E, Diaz J, Feeney O, Sánchez V, Scharmer G, Soltau D (1999) LPSP & TIP: full Stokes polarimeters for the Canary Islands observatories. In: Rimmele TR, Balasubramaniam KS, Radick RR (eds) High resolution solar physics: theory, observations, and techniques. ASP conference series, vol 183. Astronomical Society of the Pacific, San Francisco, p 264
Martínez Pillet V, del Toro Iniesta JC, Álvarez-Herrero A et al (2011) The Imaging Magnetograph eXperiment (IMaX) for the Sunrise balloon-borne solar observatory. Solar Phys 268:57–102. https://doi.org/10.1007/s11207-010-9644-y. arXiv:1009.1095
Mehltretter JP (1974) Observations of photospheric faculae at the center of the solar disk. Solar Phys 38:43–57. https://doi.org/10.1007/BF00161822
Meunier N, Solanki SK, Livingston WC (1998) Infrared lines as probes of solar magnetic features. XIII. The relative flux in weak and strong quiet-Sun magnetic fields. Astron Astrophys 331:771–781
Meyer F, Schmidt HU, Weiss NO (1977) The stability of sunspots. Mon Not R Astron Soc 179:741–761
Milić I, Faurobert M (2012) Hanle diagnostics of weak solar magnetic fields: inversion of scattering polarization in c\(_{2}\) and mgh molecular lines. Astron Astrophys 547:A38. https://doi.org/10.1051/0004-6361/201219737
Muller R (1983) The dynamical behavior of facular points in the quiet photosphere. Solar Phys 85:113–121. https://doi.org/10.1007/BF00148262
Muller R, Keil SL (1983) The characteristic size and brightness of facular points in the quiet photosphere. Solar Phys 87:243–250. https://doi.org/10.1007/BF00224837
Muller R, Roudier T (1984) Variability of the quiet photospheric network. Solar Phys 94:33–47. https://doi.org/10.1007/BF00154805
November LJ, Toomre J, Gebbie KB, Simon GW (1981) The detection of mesogranulation on the Sun. Astrophys J 245:L123–L126. https://doi.org/10.1086/183539
Orozco Suárez D (2008) Diffraction-limited spectropolarimetry of quiet Sun magnetic fields. PhD thesis, Universidad de Granada, Spain
Orozco Suárez D, Bellot Rubio LR (2012) Analysis of quiet-Sun internetwork magnetic fields based on linear polarization signals. Astrophys J 751:2. https://doi.org/10.1088/0004-637X/751/1/2. arXiv:1203.1440
Orozco Suárez D, del Toro Iniesta JC (2007) The usefulness of analytic response functions. Astron Astrophys 462:1137–1145. https://doi.org/10.1051/0004-6361:20066201
Orozco Suárez D, Katsukawa Y (2012) On the distribution of quiet-Sun magnetic fields at different heliocentric angles. Astrophys J 746:182. https://doi.org/10.1088/0004-637X/746/2/182
Orozco Suárez D, Bellot Rubio LR, del Toro Iniesta JC (2007a) Quiet-Sun magnetic fields from space-borne observations: simulating Hinode’s case. Astrophys J Lett 662:L31–L34. https://doi.org/10.1086/519279. arXiv:0705.0096
Orozco Suárez D, Bellot Rubio LR, del Toro Iniesta JC, Tsuneta S, Lites BW, Ichimoto K, Katsukawa Y, Nagata S, Shimizu T, Shine RA, Suematsu Y, Tarbell TD, Title AM (2007b) Quiet-Sun internetwork magnetic fields from the inversion of Hinode measurements. Astrophys J Lett 670:L61–L64. https://doi.org/10.1086/524139. arXiv:0710.1405
Orozco Suárez D, Bellot Rubio LR, del Toro Iniesta JC, Tsuneta S, Lites BW, Ichimoto K, Katsukawa Y, Nagata S, Shimizu T, Shine RA, Suematsu Y, Tarbell TD, Title AM (2007c) Strategy for the inversion of Hinode spectropolarimetric measurements in the quiet Sun. Publ Astron Soc Japan 59:837 arXiv:0709.2033
Orozco Suárez D, Bellot Rubio LR, del Toro Iniesta JC, Tsuneta S (2008) Magnetic field emergence in quiet Sun granules. Astron Astrophys 481:L33–L36. https://doi.org/10.1051/0004-6361:20079032. arXiv:0712.2663
Orozco Suárez D, Bellot Rubio LR, Martínez Pillet V, Bonet JA, Vargas Domínguez S, del Toro Iniesta JC (2010) Retrieval of solar magnetic fields from high-spatial resolution filtergraph data: the Imaging Magnetograph eXperiment (IMaX). Astron Astrophys 522:A101. https://doi.org/10.1051/0004-6361/201014217. arXiv:1006.5510
Orozco Suárez D, Bellot Rubio LR, del Toro Iniesta JC (2010) Milne-eddington inversion of the Fe i line pair at 630 nm. Astron Astrophys 518:A3. https://doi.org/10.1051/0004-6361/201014374. arXiv:1005.5013
Orozco Suárez D, Katsukawa Y, Bellot Rubio LR (2012) The connection between internetwork magnetic elements and supergranular flows. Astrophys J Lett 758:L38. https://doi.org/10.1088/2041-8205/758/2/L38
Ortiz A, Bellot Rubio LR, Hansteen VH, de la Cruz Rodríguez J, Rouppe van der Voort L (2014) Emergence of granular-sized magnetic bubbles through the solar atmosphere. I. Spectropolarimetric observations and simulations. Astrophys J 781:126. https://doi.org/10.1088/0004-637X/781/2/126. arXiv:1312.5735
Ortiz A, Hansteen VH, Bellot Rubio LR, de la Cruz Rodríguez J, de Pontieu B, Carlsson M, Rouppe van der Voort L (2016) Emergence of granular-sized magnetic bubbles through the solar atmosphere. III. The path to the transition region. Astrophys J 825:93. https://doi.org/10.3847/0004-637X/825/2/93
Park S, Chae J, Litvinenko YE (2009) Rates of photospheric magnetic flux cancellation measured with Hinode. Astrophys J Lett 704:L71–L74. https://doi.org/10.1088/0004-637X/704/1/L71
Parker EN (1975) The nature of the sunspot phenomenon. IV: The intrinsic instability of the magnetic configuration. Solar Phys 40:291–301. https://doi.org/10.1007/BF00162376
Parnell CE, DeForest CE, Hagenaar HJ, Johnston BA, Lamb DA, Welsch BT (2009) A power-law distribution of solar magnetic fields over more than five decades in flux. Astrophys J 698:75–82. https://doi.org/10.1088/0004-637X/698/1/75
Pietarila A, Cameron RH, Danilovic S, Solanki SK (2011) Transport of magnetic flux from the canopy to the internetwork. Astrophys J 729:136. https://doi.org/10.1088/0004-637X/729/2/136. arXiv:1102.1397
Pietarila Graham J, Danilovic S, Schüssler M (2009) Turbulent magnetic fields in the quiet Sun: implications of Hinode observations and small-scale dynamo simulations. Astrophys J 693:1728–1735. https://doi.org/10.1088/0004-637X/693/2/1728. arXiv:0812.2125
Pietarila Graham J, Cameron R, Schüssler M (2010) Turbulent small-scale dynamo action in solar surface simulations. Astrophys J 714:1606–1616. https://doi.org/10.1088/0004-637X/714/2/1606. arXiv:1002.2750
Ploner SRO, Schussler M, Solanki SK, Sheminova VA, Gadun AS, Frutiger C (2001) The formation of one-lobed Stokes V profiles in an inhomogeneous atmosphere. In: Sigwarth M (ed) Advanced solar polarimetry—theory, observation, and instrumentation. ASP conference series, vol 236, pp 371–378
Pneuman GW, Solanki SK, Stenflo JO (1986) Structure and merging of solar magnetic fluxtubes. Astron Astrophys 154:231–242
Povel HP (1995) Imaging Stokes polarimetry with piezoelastic modulators and charge-coupled-device image sensors. Opt Eng 34:1870–1878. https://doi.org/10.1117/12.200596
Puschmann KG, Denker C, Kneer F, Al Erdogan N, Balthasar H, Bauer SM, Beck C, Bello González N, Collados M, Hahn T, Hirzberger J, Hofmann A, Louis RE, Nicklas H, Okunev O, Martínez Pillet V, Popow E, Seelemann T, Volkmer R, Wittmann AD, Woche M (2012) The GREGOR Fabry–Pérot interferometer. Astron Nachr 333:880. https://doi.org/10.1002/asna.201211734. arXiv:1210.2921
Quintero Noda C, Martínez Pillet V, Borrero JM, Solanki SK (2013) Temporal relation between quiet-Sun transverse fields and the strong flows detected by IMaX/SUNRISE. Astron Astrophys 558:A30. https://doi.org/10.1051/0004-6361/201321719. arXiv:1309.0627
Quintero Noda C, Ruiz Cobo B, Orozco Suárez D (2014) Photospheric downward plasma motions in the quiet Sun. Astron Astrophys 566:A139. https://doi.org/10.1051/0004-6361/201423461. arXiv:1405.1561
Quintero Noda C, Asensio Ramos A, Orozco Suárez D, Ruiz Cobo B (2015) Spatial deconvolution of spectropolarimetric data: an application to quiet Sun magnetic elements. Astron Astrophys 579:A3. https://doi.org/10.1051/0004-6361/201425414. arXiv:1505.03219
Rabin D (1992) Spatially extended measurements of magnetic field strength in solar plages. Astrophys J 391:832–844. https://doi.org/10.1086/171392
Ramírez Vélez JC, López Ariste A, Semel M (2008) Strength distribution of solar magnetic fields in photospheric quiet Sun regions. Astron Astrophys 487:731–740. https://doi.org/10.1051/0004-6361:20078654. arXiv:0806.1326
Rees DE (1987) A gentle introduction to polarized radiative transfer. In: Kalkofen W (ed) Numerical radiative transfer. Cambridge University Press, Cambridge, p 213
Rees DE, Semel MD (1979) Line formation in an unresolved magnetic element—a test of the centre of gravity method. Astron Astrophys 74:1–5
Rempel M (2014) Numerical simulations of quiet Sun magnetism: on the contribution from a small-scale dynamo. Astrophys J 789:132. https://doi.org/10.1088/0004-637X/789/2/132. arXiv:1405.6814
Requerey IS, del Toro Iniesta JC, Bellot Rubio LR, Bonet JA, Martínez Pillet V, Solanki SK, Schmidt W (2014) The history of a quiet-Sun magnetic element revealed by IMaX/SUNRISE. Astrophys J 789:6. https://doi.org/10.1088/0004-637X/789/1/6. arXiv:1405.2837
Requerey IS, del Toro Iniesta JC, Bellot Rubio LR, Martínez Pillet V, Solanki SK, Schmidt W (2015) Dynamics of multi-cored magnetic structures in the quiet Sun. Astrophys J 810:79. https://doi.org/10.1088/0004-637X/810/1/79. arXiv:1508.06998
Requerey IS, del Toro Iniesta JC, Bellot Rubio LR, Martínez Pillet V, Solanki SK, Schmidt W (2017) Convectively driven sinks and magnetic fields in the quiet-Sun. Astrophys J Suppl Ser 229:14. https://doi.org/10.3847/1538-4365/229/1/14. arXiv:1610.07622
Rezaei R, Schlichenmaier R, Beck CAR, Bruls JHMJ, Schmidt W (2007) Relation between photospheric magnetic field and chromospheric emission. Astron Astrophys 466:1131–1144. https://doi.org/10.1051/0004-6361:20067017. arXiv:astro-ph/0701896
Riethmüller TL, Solanki SK, Martínez Pillet V, Hirzberger J, Feller A, Bonet JA, Bello González N, Franz M, Schüssler M, Barthol P, Berkefeld T, del Toro Iniesta JC, Domingo V, Gandorfer A, Knölker M, Schmidt W (2010) Bright points in the quiet Sun as observed in the visible and near-UV by the balloon-borne observatory SUNRISE. Astrophys J Lett 723:L169–L174. https://doi.org/10.1088/2041-8205/723/2/L169. arXiv:1009.1693
Rieutord M, Rincon F (2010) The Sun’s supergranulation. Living Rev Solar Phys 7:lrsp-2010-2. https://doi.org/10.12942/lrsp-2010-2. arXiv:1005.5376
Rüedi I, Solanki SK, Livingston W, Stenflo JO (1992) Infrared lines as probes of solar magnetic features. III. Strong and weak magnetic fields in plages. Astron Astrophys 263:323–338
Ruiz Cobo B (2007) Inversion techniques: from observations to atmospheres. In: Kneer F, Puschmann KG, Wittmann AD (eds) Modern solar facilities—advanced solar science. Universitätsverlag Göttingen, Göttingen, p 287
Ruiz Cobo B, Asensio Ramos A (2013) Returning magnetic flux in sunspot penumbrae. Astron Astrophys 549:L4. https://doi.org/10.1051/0004-6361/201220373. arXiv:1211.6335
Ruiz Cobo B, del Toro Iniesta JC (1992) Inversion of Stokes profiles. Astrophys J 398:375–385. https://doi.org/10.1086/171862
Ryutova M (2015) Physics of magnetic flux tubes. Astrophysics and space science library, vol 417. Springer, Berlin. https://doi.org/10.1007/978-3-662-45243-1
Ryutova M, Tarbell TD, Shine R (2003) Interaction and dynamics of the photospheric network magnetic elements. Solar Phys 213:231–256
Sainz Dalda A, Martínez-Sykora J, Bellot Rubio L, Title A (2012) Study of single-lobed circular polarization profiles in the quiet Sun. Astrophys J 748:38. https://doi.org/10.1088/0004-637X/748/1/38. arXiv:1202.0593
Sánchez Almeida J (1997) Physical properties of the solar magnetic photosphere under the MISMA hypothesis. I. Description of the inversion procedure. Astrophys J 491:993. https://doi.org/10.1086/304999
Sánchez Almeida J (2001) Thermal relaxation of very small solar magnetic structures in intergranules: a process that produces kilogauss magnetic field strengths. Astrophys J 556:928–936. https://doi.org/10.1086/321532. arXiv:astro-ph/0103415
Sánchez Almeida J (2005) On the Sr i \(\lambda \)4607 Å Hanle depolarization signals in the quiet Sun. Astron Astrophys 438:727–732. https://doi.org/10.1051/0004-6361:20042394. arXiv:astro-ph/0504339
Sanchez Almeida J, Lites BW (1992) Observation and interpretation of the asymmetric Stokes Q, U, and V line profiles in sunspots. Astrophys J 398:359–374. https://doi.org/10.1086/171861
Sánchez Almeida J, Lites BW (2000) Physical properties of the solar magnetic photosphere under the MISMA hypothesis. II. Network and internetwork fields at the disk center. Astrophys J 532:1215–1229. https://doi.org/10.1086/308603
Sánchez Almeida J, Martínez González M (2011) The magnetic fields of the quiet Sun. In: Kuhn JR, Harrington DM, Lin H, Berdyugina SV, Trujillo-Bueno J, Keil SL, Rimmele T (eds) Solar polarization 6. ASP conference series, vol 437, p 451 arXiv:1105.0387
Sánchez Almeida J, Collados M, del Toro Iniesta JC, Solanki SK (1988) Magnetic field strength in solar flux tubes: a model atmosphere independent determination. Astron Astrophys 196:266–268
Sánchez Almeida J, Landi Degl’Innocenti E, Martínez Pillet V, Lites BW (1996) Line asymmetries and the microstructure of photospheric magnetic fields. Astrophys J 466:537. https://doi.org/10.1086/177530
Sánchez Almeida J, Domínguez Cerdeña I, Kneer F (2003a) Simultaneous visible and infrared spectropolarimetry of a solar internetwork region. Astrophys J Lett 597:L177–L180. https://doi.org/10.1086/379969. arXiv:astro-ph/0309727
Sánchez Almeida J, Emonet T, Cattaneo F (2003b) Polarization of photospheric lines from turbulent dynamo simulations. Astrophys J 585:536–552. https://doi.org/10.1086/346077. arXiv:astro-ph/0211175
Sánchez Almeida J, Márquez I, Bonet JA, Domínguez Cerdeña I, Muller R (2004) Bright points in the internetwork quiet Sun. Astrophys J Lett 609:L91–L94. https://doi.org/10.1086/422752. arXiv:astro-ph/0405515
Sánchez Almeida J, Viticchié B, Landi Degl’Innocenti E, Berrilli F (2008) Quiet-Sun magnetic field measurements based on lines with hyperfine structure. Astrophys J 675:906–919. https://doi.org/10.1086/524928. arXiv:0710.5393
Sánchez Almeida J, Bonet JA, Viticchié B, Del Moro D (2010) Magnetic bright points in the quiet Sun. Astrophys J Lett 715:L26–L29. https://doi.org/10.1088/2041-8205/715/1/L26. arXiv:1004.1885
Sankarasubramanian K, Gullixson C, Hegwer S, Rimmele TR, Gregory S, Spence T, Fletcher S, Richards K, Rousset E, Lites BW, Elmore D, Streander K, Sigwarth M (2004) The diffraction limited spectro-polarimeter: a new instrument for high-resolution solar polarimetry. In: Fineschi S, Gummin MA (eds) Telescopes and instrumentation for solar astrophysics. Proceedings of SPIE, vol 5171. SPIE, Bellingham, WA, pp 207–218. https://doi.org/10.1117/12.508790
Scharmer GB (2006) Comments on the optimization of high resolution Fabry–Pérot filtergraphs. Astron Astrophys 447:1111–1120. https://doi.org/10.1051/0004-6361:20052981
Scharmer GB, Henriques VMJ, Kiselman D, de la Cruz Rodríguez J (2011) Detection of convective downflows in a sunspot penumbra. Science 333:316. https://doi.org/10.1126/science.1206429
Scherrer PH, Bogart RS, Bush RI, Hoeksema JT, Kosovichev AG, Schou J, Rosenberg W, Springer L, Tarbell TD, Title A, Wolfson CJ, Zayer I (1995) The solar oscillations investigation: Michelson Doppler Imager. Solar Phys 162:129–188. https://doi.org/10.1007/BF00733429
Scherrer PH, Schou J, Bush RI, Kosovichev AG, Bogart RS, Hoeksema JT, Liu Y, Duvall TL, Zhao J, Title AM, Schrijver CJ, Tarbell TD, Tomczyk S (2012) The helioseismic and magnetic imager (HMI) investigation for the solar dynamics observatory (SDO). Solar Phys 275:207–227. https://doi.org/10.1007/s11207-011-9834-2
Schrijver CJ, Harvey KL (1994) The photospheric magnetic flux budget. Sol Phys 150:1–18. https://doi.org/10.1007/BF00712873
Schrijver CJ, Title AM, van Ballegooijen AA, Hagenaar HJ, Shine RA (1997) Sustaining the quiet photospheric network: the balance of flux emergence, fragmentation, merging, and cancellation. Astrophys J 487:424. https://doi.org/10.1086/304581
Schüssler M (1984) The interchange instability of small flux tubes. Astron Astrophys 140:453–458
Schüssler M, Vögler A (2008) Strong horizontal photospheric magnetic field in a surface dynamo simulation. Astron Astrophys 481:L5–L8. https://doi.org/10.1051/0004-6361:20078998. arXiv:0801.1250
Schüssler M, Shelyag S, Berdyugina S, Vögler A, Solanki SK (2003) Why solar magnetic flux concentrations are bright in molecular bands. Astrophys J Lett 597:L173–L176. https://doi.org/10.1086/379869
Shchukina N, Trujillo Bueno J (2011) Determining the magnetization of the quiet Sun photosphere from the Hanle effect and surface dynamo simulations. Astrophys J Lett 731:L21. https://doi.org/10.1088/2041-8205/731/1/L21. arXiv:1103.5652
Sheeley JNR (1967) Observations of small-scale solar magnetic fields. Solar Phys 1:171–179. https://doi.org/10.1007/BF00150852
Sheeley JNR (1969) The evolution of the photospheric network. Solar Phys 9:347–357. https://doi.org/10.1007/BF02391657
Shiota D, Tsuneta S, Shimojo M, Sako N, Orozco Suárez D, Ishikawa R (2012) Polar field reversal observations with Hinode. Astrophys J 753:157. https://doi.org/10.1088/0004-637X/753/2/157. arXiv:1205.2154
Sigwarth M (2001) Properties and origin of asymmetric and unusual Stokes V profiles observed in solar magnetic fields. Astrophys J 563:1031–1044. https://doi.org/10.1086/323963
Sigwarth M, Balasubramaniam KS, Knölker M, Schmidt W (1999) Dynamics of solar magnetic elements. Astron Astrophys 349:941–955
Skumanich A, Lites BW (1987) Stokes profile analysis and vector magnetic fields. I. Inversion of photospheric lines. Astrophys J 322:473–482. https://doi.org/10.1086/165743
Smitha HN, Solanki SK (2017) Probing photospheric magnetic fields with new spectral line pairs. Astron Astrophys 608:A111. https://doi.org/10.1051/0004-6361/201731261. arXiv:1709.08926
Smitha HN, Anusha LS, Solanki SK, Riethmüller TL (2017) Estimation of the magnetic flux emergence rate in the quiet Sun from Sunrise data. Astrophys J Suppl Ser 229:17. https://doi.org/10.3847/1538-4365/229/1/17. arXiv:1611.06432
Smithson RC (1975) Observations of weak solar magnetic fields with the Lockheed diode array magnetograph. Bull Am Astron Soc 7:346
Snik F, de Wijn AG, Ichimoto K, Fischer CE, Keller CU, Lites BW (2010) Observations of solar scattering polarization at high spatial resolution. Astron Astrophys 519:A18. https://doi.org/10.1051/0004-6361/201014500. arXiv:1005.5042
Socas-Navarro H (2001) Stokes inversion techniques: recent achievements and future horizons. In: Sigwarth M (ed) Advanced solar polarimetry—theory, observation, and instrumentation. ASP conference series, vol 236. Astronomical Society of the Pacific, San Francisco, pp 487–501
Socas-Navarro H (2004a) Multiline Stokes analysis for the study of small-scale solar magnetic fields. Astrophys J 613:610–614. https://doi.org/10.1086/422837
Socas-Navarro H (2004b) A simple procedure for optimizing the height resolution in spectral line inversions. Astrophys J 614:457–463. https://doi.org/10.1086/423662
Socas-Navarro H, Lites BW (2004) Observational evidence for small-scale mixture of weak and strong fields in the quiet Sun. Astrophys J 616:587–593. https://doi.org/10.1086/424796. arXiv:astro-ph/0410562
Socas-Navarro H, Sánchez Almeida J (2002) Magnetic properties of photospheric regions with very low magnetic flux. Astrophys J 565:1323–1334. https://doi.org/10.1086/324688. arXiv:astro-ph/0110025
Socas-Navarro H, Sánchez Almeida J (2003) Magnetic fields in the quiet Sun: observational discrepancies and unresolved structure. Astrophys J 593:581–586. https://doi.org/10.1086/376504
Socas-Navarro H, Martínez Pillet V, Lites BW (2004) Magnetic properties of the solar internetwork. Astrophys J 611:1139–1148. https://doi.org/10.1086/422379
Socas-Navarro H, Elmore D, Pietarila A, Darnell A, Lites BW, Tomczyk S, Hegwer S (2006) Spinor: visible and infrared spectro-polarimetry at the National Solar Observatory. Solar Phys 235:55–73. https://doi.org/10.1007/s11207-006-0020-x. arXiv:astro-ph/0508685
Socas-Navarro H, de la Cruz Rodríguez J, Asensio Ramos A, Trujillo Bueno J, Ruiz Cobo B (2015) An open-source, massively parallel code for non-LTE synthesis and inversion of spectral lines and Zeeman-induced Stokes profiles. Astron Astrophys 577:A7. https://doi.org/10.1051/0004-6361/201424860. arXiv:1408.6101
Solanki SK (1993) Smallscale solar magnetic fields: an overview. Space Sci Rev 63:1–188. https://doi.org/10.1007/BF00749277
Solanki SK, Montavon CAP (1993) Uncombed fields as the source of the broad-band circular polarization of sunspots. Astron Astrophys 275:283
Solanki SK, Pahlke KD (1988) Can stationary velocity fields explain the Stokes V asymmetry observed in solar magnetic elements? Astron Astrophys 201:143–152
Solanki SK, Stenflo JO (1984) Properties of solar magnetic fluxtubes as revealed by Fe i lines. Astron Astrophys 140:185–198
Solanki SK, Rüedi IK, Livingston W (1992) Infrared lines as probes of solar magnetic features. II. Diagnostic capabilities of Fe i 15648.5 Å and 15652.9 Å. Astron Astrophys 263:312–322
Solanki SK, Zufferey D, Lin H, Rüedi I, Kuhn JR (1996) Infrared lines as probes of solar magnetic features. XII. Magnetic flux tubes: evidence of convective collapse? Astron Astrophys 310:L33–L36
Solanki SK, Barthol P, Danilovic S, Feller A, Gandorfer A, Hirzberger J, Riethmüller TL, Schüssler M, Bonet JA, Martínez Pillet V, del Toro Iniesta JC, Domingo V, Palacios J, Knölker M, Bello González N, Berkefeld T, Franz M, Schmidt W, Title AM (2010) SUNRISE: instrument, mission, data, and first results. Astrophys J Lett 723:L127–L133. https://doi.org/10.1088/2041-8205/723/2/L127. arXiv:1008.3460
Spruit HC (1976) Pressure equilibrium and energy balance of small photospheric fluxtubes. Solar Phys 50:269–295. https://doi.org/10.1007/BF00155292
Spruit HC (1977) Heat flow near obstacles in the solar convection zone. Solar Phys 55:3–34. https://doi.org/10.1007/BF00150871
Stangalini M (2014) Photospheric supergranular flows and magnetic flux emergence. Astron Astrophys 561:L6. https://doi.org/10.1051/0004-6361/201322831. arXiv:1312.2477
Stein RF (2012) Solar surface magneto-convection. Living Rev Solar Phys 9:lrsp-2012-4. https://doi.org/10.12942/lrsp-2012-4
Stein RF, Nordlund Å (2006) Solar small-scale magnetoconvection. Astrophys J 642:1246–1255. https://doi.org/10.1086/501445
Stein RF, Lagerfjärd A, Nordlund Å, Georgobiani D (2011) Solar flux emergence simulations. Solar Phys 268:271–282. https://doi.org/10.1007/s11207-010-9510-y. arXiv:0912.4938
Steiner O (2000) The formation of asymmetric Stokes V profiles in the presence of a magnetopause. Solar Phys 196:245–268
Steiner O (2001) The formation of asymmetric Stokes V profiles in the presence of a magnetopause. In: Sigwarth M (ed) Advanced solar polarimetry—theory, observation, and instrumentation. ASP conference series, vol 236, p 587
Steiner O (2007) Photospheric processes and magnetic flux tubes. In: Hasan SS, Banerjee D (eds) Kodai school on solar physics. American Institute of Physics conference series, vol 919, pp 74–121. https://doi.org/10.1063/1.2756784. arXiv:0709.0081
Steiner O, Rezaei R (2012) Recent advances in the exploration of the small-scale structure of the quiet solar atmosphere: vortex flows, the horizontal magnetic field, and the Stokes-\(V\) line-ratio method. In: Golub L, De Moortel I, Shimizu T (eds) Fifth Hinode science meeting. ASP conference series, vol 456, p 3 arXiv:1202.4040
Steiner O, Grossmann-Doerth U, Knoelker M, Schüssler M (1998) Dynamical interaction of solar magnetic elements and granular convection: results of a numerical simulation. Astrophys J 495:468. https://doi.org/10.1086/305255
Steiner O, Rezaei R, Schaffenberger W, Wedemeyer-Böhm S (2008) The horizontal internetwork magnetic field: numerical simulations in comparison to observations with Hinode. Astrophys J Lett 680:L85–L88. https://doi.org/10.1086/589740. arXiv:0801.4915
Stenflo JO (1973) Magnetic-field structure of the photospheric network. Solar Phys 32:41–63. https://doi.org/10.1007/BF00152728
Stenflo JO (1982) The Hanle effect and the diagnostics of turbulent magnetic fields in the solar atmosphere. Solar Phys 80:209–226. https://doi.org/10.1007/BF00147969
Stenflo JO (1989) Small-scale magnetic structures on the sun. Astron Astrophys Rev 1:3–48. https://doi.org/10.1007/BF00872483
Stenflo J (ed) (1994) Solar magnetic fields: polarized radiation diagnostics. Astrophysics and space science library, vol 189. Springer, Dordrecht. https://doi.org/10.1007/978-94-015-8246-9
Stenflo JO (2001) Observation of scattering polarization and the diagnostics of solar magnetic fields. In: Sigwarth M (ed) Advanced solar polarimetry—theory, observation, and instrumentation. ASP conference series, vol 236. Astronomical Society of the Pacific, San Francisco, pp 97–108
Stenflo JO (2005) Polarization of the Sun’s continuous spectrum. Astron Astrophys 429:713–730. https://doi.org/10.1051/0004-6361:20041667
Stenflo JO (2007) Solar polarimetry with ZIMPOL. Plans for the future. Mem Soc Astron Ital 78:181
Stenflo JO (2008) Solar magnetic fields. J Astrophys Astron 29:19–28. https://doi.org/10.1007/s12036-008-0003-4
Stenflo JO (2010a) Distribution functions for magnetic fields on the quiet Sun. Astron Astrophys 517:A37. https://doi.org/10.1051/0004-6361/200913972
Stenflo JO (2010b) Measuring the hidden aspects of solar magnetism. In: Hasan SS, Rutten RJ (eds) Magnetic coupling between the interior and atmosphere of the Sun, pp 101–117. https://doi.org/10.1007/978-3-642-02859-5_8. arXiv:0903.4935
Stenflo JO (2011) Collapsed, uncollapsed, and hidden magnetic flux on the quiet Sun. Astron Astrophys 529:A42. https://doi.org/10.1051/0004-6361/201016275
Stenflo JO (2013) Horizontal or vertical magnetic fields on the quiet Sun. Angular distributions and their height variations. Astron Astrophys 555:A132. https://doi.org/10.1051/0004-6361/201321608. arXiv:1306.3581
Stenflo JO, Holzreuter R (2003) Distribution of magnetic fields at scales beyond the spatial resolution limit. In: Pevtsov AA, Uitenbroek H (eds) Current theoretical models and future high resolution solar observations: preparing for ATST. ASP conference series, vol 286, p 169
Stenflo JO, Keller CU (1997) The second solar spectrum. A new window for diagnostics of the Sun. Astron Astrophys 321:927–934
Stenflo JO, Lindegren L (1977) Statistical analysis of solar Fe i lines: magnetic line broadening. Astron Astrophys 59:367–378
Stenflo JO, Baur TG, Elmore DF (1980) Resonance-line polarization. IV. Observations of non-magnetic line polarization and its center-to-limb variations. Astron Astrophys 84:60–67
Stenflo JO, Solanki S, Harvey JW, Brault JW (1984) Diagnostics of solar magnetic fluxtubes using a Fourier transform spectrometer. Astron Astrophys 131:333–346
Stenflo JO, Solanki SK, Harvey JW (1987) Diagnostics of solar magnetic fluxtubes with the infrared line Fe i \(\lambda \) 15648.54 Å. Astron Astrophys 173:167–179
Stenflo JO, Bianda M, Keller CU, Solanki SK (1997) Center-to-limb variation of the second solar spectrum. Astron Astrophys 322:985–994
Stenflo JO, Keller CU, Gandorfer A (1998) Differential Hanle effect and the spatial variation of turbulent magnetic fields on the Sun. Astron Astrophys 329:319–328
Stenflo JO, Gandorfer A, Holzreuter R, Gisler D, Keller CU, Bianda M (2002) Spatial mapping of the Hanle and Zeeman effects on the Sun. Astron Astrophys 389:314–324. https://doi.org/10.1051/0004-6361:20020580
Štěpán J, Trujillo Bueno J (2013) PORTA: a three-dimensional multilevel radiative transfer code for modeling the intensity and polarization of spectral lines with massively parallel computers. Astron Astrophys 557:A143. https://doi.org/10.1051/0004-6361/201321742. arXiv:1307.4217
Thaler I, Spruit HC (2015) Small-scale dynamos on the solar surface: dependence on magnetic Prandtl number. Astron Astrophys 578:A54. https://doi.org/10.1051/0004-6361/201423738. arXiv:1305.04575
Thonhofer S, Bellot Rubio LR, Utz D, Hanslmeier A, Jurçák J (2015) Parallelization of the SIR code for the investigation of small-scale features in the solar photosphere. In: Nagendra KN, Bagnulo S, Centeno R, Martínez González MJ (eds) Polarimetry. IAU symposium, vol 305, pp 251–256. https://doi.org/10.1017/S1743921315004858. arXiv:1503.03710
Thornton LM, Parnell CE (2011) Small-scale flux emergence observed using Hinode/SOT. Solar Phys 269:13–40. https://doi.org/10.1007/s11207-010-9656-7
Title AM, Rosenberg WJ (1981) Tunable birefringent filters. Opt Eng 20:815–823. https://doi.org/10.1117/12.7972820
Title AM, Tarbell TD, Topka KP, Ferguson SH, Shine RA (1989) Statistical properties of solar granulation derived from the SOUP instrument on Spacelab 2. Astrophys J 336:475–494. https://doi.org/10.1086/167026
Tortosa-Andreu A, Moreno-Insertis F (2009) Magnetic flux emergence into the solar photosphere and chromosphere. Astron Astrophys 507:949–967. https://doi.org/10.1051/0004-6361/200912394
Tritschler A, Rimmele TR, Berukoff S, Casini R, Kuhn JR, Lin H, Rast MP, McMullin JP, Schmidt W, Wöger F, DKIST Team (2016) Daniel K. Inouye solar telescope: high-resolution observing of the dynamic Sun. Astron Nachr 337:1064. https://doi.org/10.1002/asna.201612434
Trujillo Bueno J (2001) Atomic polarization and the Hanle effect. In: Sigwarth M (ed) Advanced solar polarimetry—theory, observation, and instrumentation. ASP conference series, vol 236. Astronomical Society of the Pacific, San Francisco, p 161
Trujillo Bueno J (2003) New diagnostic windows on the weak magnetism of the solar atmosphere. In: Trujillo Bueno J, Sánchez Almeida J (eds) Solar polarization 3. ASP conference series. Astronomical Society of the Pacific, San Francisco, vol 307, pp 407–424
Trujillo Bueno J (2009) The second stellar spectrum and the non-LTE problem of the 2nd kind. In: Hubeny I, Stone JM, MacGregor K, Werner K (eds) Recent directions in astrophysical quantitative spectroscopy and aradiation hydrodynamics. AIP conference proceedings, vol 1171. AIP, Boulder, pp 27–42. https://doi.org/10.1063/1.3250067
Trujillo Bueno J, Shchukina N (2007) The scattering polarization of the Sr i \(\lambda \)4607 line at the diffraction limit resolution of a 1 m telescope. Astrophys J Lett 664:L135–L138. https://doi.org/10.1086/520838. arXiv:0706.2386
Trujillo Bueno J, Shchukina N (2009) Three-dimensional radiative transfer modeling of the polarization of the Sun’s continuous spectrum. Astrophys J 694:1364–1378. https://doi.org/10.1088/0004-637X/694/2/1364. arXiv:0812.3494
Trujillo Bueno J, Landi Degl’Innocenti E, Collados M, Merenda L, Manso Sainz R (2002) Selective absorption processes as the origin of puzzling spectral line polarization from the Sun. Nature 415:403–406 arXiv:astro-ph/0201409
Trujillo Bueno J, Shchukina N, Asensio Ramos A (2004) A substantial amount of hidden magnetic energy in the quiet Sun. Nature 430:326–329. https://doi.org/10.1038/nature02669. arXiv:astro-ph/0409004
Trujillo Bueno J, Asensio Ramos A, Shchukina N (2006) The Hanle effect in atomic and molecular lines: a new look at the Sun’s hidden magnetism. In: Casini R, Lites BW (eds) Solar polarization 4. ASP conference series, vol 358. Astronomical Society of the Pacific, San Francisco, p 269
Tsuneta S, Ichimoto K, Katsukawa Y, Nagata S, Otsubo M, Shimizu T, Suematsu Y, Nakagiri M, Noguchi M, Tarbell T, Title A, Shine R, Rosenberg W, Hoffmann C, Jurcevich B, Kushner G, Levay M, Lites BW, Elmore D, Matsushita T, Kawaguchi N, Saito H, Mikami I, Hill LD, Owens JK (2008) The solar optical telescope for the Hinode mission: an overview. Solar Phys 249:167–196. https://doi.org/10.1007/s11207-008-9174-z. arXiv:0711.1715
Uitenbroek H (2003) The accuracy of the center-of-gravity method for measuring velocity and magnetic field strength in the solar photosphere. Astrophys J 592:1225–1233. https://doi.org/10.1086/375736
Uitenbroek H, Tritschler A (2006) The contrast of magnetic elements in synthetic CH- and CN-band images of solar magnetoconvection. Astrophys J 639:525–533. https://doi.org/10.1086/499331. arXiv:astro-ph/0510333
Uitenbroek H, Tritschler A (2007) Narrow-band imaging in the CN band at 388.33 nm. Astron Astrophys 462:1157–1163. https://doi.org/10.1051/0004-6361:20066286. arXiv:astro-ph/0611407
Unno W (1956) Line formation of a normal Zeeman triplet. Publ Astron Soc Japan 8:108–125
Unno W (1959) Turbulent motion in the solar atmosphere. I. Doppler widths of photospheric lines. Astrophys J 129:375–400. https://doi.org/10.1086/146630
van Noort M (2012) Spatially coupled inversion of spectro-polarimetric image data. I. Method and first results. Astron Astrophys 548:A5. https://doi.org/10.1051/0004-6361/201220220. arXiv:1210.4636
Varsik JR (1995) Calibration of the Big Bear videomagnetograph. Solar Phys 161:207–228. https://doi.org/10.1007/BF00732067
Viticchié B (2012) On the polarimetric signature of emerging magnetic loops in the quiet Sun. Astrophys J Lett 747:L36. https://doi.org/10.1088/2041-8205/747/2/L36. arXiv:1201.6501
Viticchié B, Sánchez Almeida J (2011) Asymmetries of the Stokes V profiles observed by HINODE SOT/SP in the quiet Sun. Astron Astrophys 530:A14. https://doi.org/10.1051/0004-6361/201016096. arXiv:1103.1987
Viticchié B, Sánchez Almeida J, Del Moro D, Berrilli F (2011) Interpretation of HINODE SOT/SP asymmetric Stokes profiles observed in the quiet Sun network and internetwork. Astron Astrophys 526:A60. https://doi.org/10.1051/0004-6361/201015391. arXiv:1009.6065
Viticchié B, Sánchez Almeida J, del Moro D, Berrilli F (2012) Stokes V asymmetries in the quiet Sun. In: Bellot Rubio L, Reale F, Carlsson M (eds) 4th Hinode science meeting: unsolved problems and recent insights. ASP conference series, vol 455, p 271
Vögler A, Schüssler M (2007) A solar surface dynamo. Astron Astrophys 465:L43–L46. https://doi.org/10.1051/0004-6361:20077253. arXiv:astro-ph/0702681
Vögler A, Shelyag S, Schüssler M, Cattaneo F, Emonet T, Linde T (2005) Simulations of magneto-convection in the solar photosphere. Equations, methods, and results of the MURaM code. Astron Astrophys 429:335–351. https://doi.org/10.1051/0004-6361:20041507
Wang H (1988) On the relationship between magnetic fields and supergranule velocity fields. Solar Phys 117:343–358. https://doi.org/10.1007/BF00147252
Wang J, Zhang J (1999) Flux, evolution and velocity pattern of solar intranetwork magnetic fields. In: Schmieder B, Hofmann A, Staude J (eds) Third advances in solar physics Euroconference: magnetic fields and oscillations. ASP conference series, vol 184. Astronomical Society of the Pacific, San Francisco, pp 222–226
Wang J, Wang H, Tang F, Lee JW, Zirin H (1995) Flux distribution of solar intranetwork magnetic fields. Solar Phys 160:277–288. https://doi.org/10.1007/BF00732808
Wang H, Denker C, Spirock T, Goode PR, Yang S, Marquette W, Varsik J, Fear RJ, Nenow J, Dingley DD (1998) New digital magnetograph at Big Bear solar observatory. Solar Phys 183:1–13
Wang J, Zhou G, Jin C, Li H (2012) Solar intranetwork magnetic elements: bipolar flux appearance. Solar Phys 278:299–322. https://doi.org/10.1007/s11207-012-0128-0. arXiv:1203.0807
Westendorp Plaza C, del Toro Iniesta JC, Ruiz Cobo B, Martínez Pillet V, Lites BW, Skumanich A (1998) Optical tomography of a Sunspot. I. Comparison between two inversion techniques. Astrophys J 494:453–471. https://doi.org/10.1086/305192
Wiegelmann T, Sakurai T (2012) Solar force-free magnetic fields. Living Rev Solar Phys 9:lrsp-2012-5. https://doi.org/10.12942/lrsp-2012-5. arXiv:1208.4693
Wiegelmann T, Solanki SK, Borrero JM, Martínez Pillet V, del Toro Iniesta JC, Domingo V, Bonet JA, Barthol P, Gandorfer A, Knölker M, Schmidt W, Title AM (2010) Magnetic loops in the quiet Sun. Astrophys J Lett 723:L185–L189. https://doi.org/10.1088/2041-8205/723/2/L185. arXiv:1009.4715
Withbroe GL, Noyes RW (1977) Mass and energy flow in the solar chromosphere and corona. Annu Rev Astron Astrophys 15:363–387. https://doi.org/10.1146/annurev.aa.15.090177.002051
Yang S, Zhang J, Borrero JM (2009) Dipolar evolution in a coronal hole region. Astrophys J 703:1012–1020. https://doi.org/10.1088/0004-637X/703/1/1012. arXiv:0908.0578
Yang Y, Ji K, Feng S, Deng H, Wang F, Lin J (2015) Dispersal of G-band bright points at different longitudinal magnetic field strengths. Astrophys J 810:88. https://doi.org/10.1088/0004-637X/810/2/88
Yelles Chaouche L, Moreno-Insertis F, Martínez Pillet V, Wiegelmann T, Bonet JA, Knölker M, Bellot Rubio LR, del Toro Iniesta JC, Barthol P, Gandorfer A, Schmidt W, Solanki SK (2011) Mesogranulation and the solar surface magnetic field distribution. Astrophys J Lett 727:L30. https://doi.org/10.1088/2041-8205/727/2/L30. arXiv:1012.4481
Yurchyshyn VB, Wang H (2001) Magnetic flux cancellation observed in the Sunspot moat. Solar Phys 202:309–318
Zakharov V, Gandorfer A, Solanki SK, Löfdahl M (2005) A comparative study of the contrast of solar magnetic elements in CN and CH. Astron Astrophys 437:L43–L46. https://doi.org/10.1051/0004-6361:200500135
Zeeman P (1897a) On the influence of magnetism on the nature of the light emitted by a substance. Astrophys J 5:332. https://doi.org/10.1086/140355
Zeeman P (1897b) On the influence of magnetism on the nature of the light emitted by a substance. Philos Mag 43:226
Zhang J, Jin C (2009) Emergence and cancellation of small-scale magnetic flux in a quiet region. Science in China G. Phys Astron 52:1691–1695. https://doi.org/10.1007/s11433-009-0253-4
Zhang J, Lin G, Wang J, Wang H, Zirin H (1998a) The evolution of intranetwork magnetic elements. Astron Astrophys 338:322–328
Zhang J, Lin G, Wang J, Wang H, Zirin H (1998b) Lifetime of intranetwork magnetic elements. Solar Phys 178:245–250
Zhang J, Wang J, Wang H, Zirin H (1998c) The motion patterns of intranetwork magnetic elements. Astron Astrophys 335:341–350
Zhang J, Wang J, Deng Y, Wu D (2001) Magnetic flux cancellation associated with the major solar event on 2000 July 14. Astrophys J Lett 548:L99–L102. https://doi.org/10.1086/318934
Zhang J, Yang S, Jin C (2009) Interaction between granulation and small-scale magnetic flux observed by Hinode. Res Astron Astrophys 9:921–932. https://doi.org/10.1088/1674-4527/9/8/008. arXiv:0905.1553
Zhou GP, Wang JX, Jin CL (2010) Solar intranetwork magnetic elements: evolution and lifetime. Solar Phys 267:63–73. https://doi.org/10.1007/s11207-010-9641-1
Zhou G, Wang J, Jin C (2013) Solar intranetwork magnetic elements: flux distributions. Solar Phys 283:273–282. https://doi.org/10.1007/s11207-013-0229-4
Zirin H (1985) Evolution of weak solar magnetic fields. Aust J Phys 38:961–969
Zirin H (1987) Weak solar fields and their connection to the solar cycle. Solar Phys 110:101–107. https://doi.org/10.1007/BF00148205
Zirin H, Popp B (1989) Observations of the 12 micron Mg i lines in various solar features. Astrophys J 340:571–578. https://doi.org/10.1086/167418
Zwaan C (1987) Elements and patterns in the solar magnetic field. Annu Rev Astron Astrophys 25:83–111. https://doi.org/10.1146/annurev.aa.25.090187.000503
Acknowledgements
It is a pleasure to thank our collaborators at the Instituto de Astrofísica de Andalucía, the Instituto de Astrofísica de Canarias, the Kiepenheuer Institut für Sonnenphysik, and the National Astronomical Observatory of Japan for helping us study the quiet Sun over the years. In particular, we want to thank Jose Carlos del Toro Iniesta for many fruitful discussions, his revision of this article, and his continued support, and Juan Manuel Borrero for endless discussions on solar spectropolarimetry. Terry Mahoney carried out a thorough and professional English correction of the manuscript, which is gratefully acknowledged. Many of the results presented here are based on the analysis of Hinode and SUNRISE data. We have been fortunate enough to be closely related to both missions. The generous dedication and deep knowledge of Hinode’s Chief Observers is greatly appreciated, as is Hinode’s open data policy, which has permitted significant advances in our understanding of the quiet Sun. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC (UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organized at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway). The German contribution to SUNRISE is funded by the Bundesministerium für Wirtschaft und Technologie through Deutsches Zentrum für Luft- und Raumfahrt e.V. (DLR), grant number 50 OU 0401, and by the Innovationsfond of the President of the Max Planck Society (MPG). The Spanish contribution has been funded by the Spanish MICINN under projects ESP2006-13030-C06 and AYA2009-14105-C06 (including European FEDER funds). The HAO contribution was partly funded through NASA grant number NNX08AH38G. This work has been supported by the Spanish Ministerio de Economía y Competitividad through projects ESP2014-56169-C6-1-R and ESP2016-77548-C5-1-R, including European FEDER funds. Use of NASA’s Astrophysics Data System, in this and all our papers, is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
41116_2018_17_MOESM1_ESM.mov
Movie of Fig. 11 showing the evolution of a quiet Sun region at the disk center, as observed by the Hinode NFI within the framework of the Hinode Operation Plan 151 (Flux replacement in the solar network and internetwork) on 20–21 January 2010. The measurements consists of longitudinal magnetograms obtained in the two wings of Na i 589.6 nm at ± 16 pm from line center. The total exposure time per magnetogram was 6.4 s, resulting in a sensitivity of 6 G. The sequence lasts 20 h and has a cadence of 1 min. There is a gap of about 29 min in the middle. The dimensions of the field of view are 93ʺ × 123ʺ, with a pixel size of 0.16ʺ. (mp4 31,531KB)
41116_2018_17_MOESM2_ESM.wmv
Movie of Fig. 12 showing the linear polarization signals observed by SUNRISE/IMaX in the IN on 9 June 2009. The sequence has a total duration of 32 min and a cadence of 30 s. The FOV measures 40ʺ× 40ʺ with a pixel size of 0.055ʺ. Courtesy V. Martínez Pillet and the SUNRISE team. (mp4 4,175KB)
41116_2018_17_MOESM3_ESM.mov
Movie of Fig. 17 showing the ascent of a small magnetic loop through the solar atmosphere. The observations were acquired with all three instruments of the Hinode Solar Optical Telescope (the SP, the NFI, and the BFI). From left to right: CN intensity filtergrams, longitudinal flux density in the photosphere calculated from Fe i 630.1 and 630.2 nm, longitudinal flux density in the temperature minimum region computed from Mg i b 517.3 nm measurements, and Ca ii H 396.85 nm intensity filtergrams. The contours mark circular (black, white) and linear (red) polarization patches. (mp4 3,992KB)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bellot Rubio, L., Orozco Suárez, D. Quiet Sun magnetic fields: an observational view. Living Rev Sol Phys 16, 1 (2019). https://doi.org/10.1007/s41116-018-0017-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41116-018-0017-1