Abstract
Due to the increasingly complex and interconnected nature of global supply chain networks (SCNs), a recent strand of research has applied network science methods to model SCN growth and subsequently analyse various topological features, such as robustness. This paper provides: (1) a comprehensive review of the methodologies adopted in literature for modelling the topology and robustness of SCNs; (2) a summary of topological features of the real world SCNs, as reported in various data driven studies; and (3) a discussion on the limitations of existing network growth models to realistically represent the observed topological characteristics of SCNs. Finally, a novel perspective is proposed to mimic the SCN topologies reported in empirical studies, through fitness based generative network models.
Similar content being viewed by others
Introduction
Global supply chain networks (SCNs) play a vital role in fuelling international trade, freight transport by all modes, and economic growth. Due to the interconnectedness of global businesses, which are no longer isolated by industry or geography, disruptions to infrastructure networks caused by natural disasters, acts of war and terrorism, and even labour disputes are becoming increasingly complex in nature and global in consequences (Manuj and Mentzer, 2008). Disruptions ripple through global SCNs, potentially magnifying the original damage. Even relatively minor disturbances, such as labour disputes, ground traffic congestion or air traffic delays can result in severe disruptions to local and international trade. Therefore, this ‘fragility of interdependence’ creates new risks to global and local economies (Vespignani, 2010).
At the local level, disturbances to SCNs can have major social and economic ramifications. For instance, during the 2011 Queensland floods in Australia, the key transportation routes were shut down, preventing supermarkets from restocking and leading to critical food shortages (Bartos, 2012). However, at the global level, these consequences can be magnified, resulting in more significant and longer lasting damage. A recent example of such a global SCN disruption is the 2011 Tohoku earthquake and ensuing tsunami in the northeast coast of Japan. Alongside the appalling humanitarian impact, this tsunami caused destruction of critical infrastructure in Japan, resulting in a domino effect, which propagated through global SCNs, with significant global economic consequences. It is reported that for several weeks following the disaster, Toyota in North America experienced shortages of over 150 parts, leading to curtailed operations at only 30% of capacity (Canis, 2011). Similar impacts were observed following the September 11th terrorist attacks on the United States in 2001, where movement of electronic and automotive parts were disrupted due to the shutdown of air and truck transportation networks (Sheffi, 2001). These high impact low probability disruptions have affected a large number of economic variables such as industrial production, international trade and logistics operations, thus revealing vulnerabilities in the global SCNs, which are traditionally left unaddressed (Tett, 2011). Therefore, the design of supply chains that can maintain their function in the face of perturbations, both expected and unexpected, is a key goal of contemporary supply chain management (Lee, 2004).
Until recently, the primary focus of supply chain management was on increasing efficiency and reliability by means of globalization, specialization and lean supply chain procedures. Although, these practices enable cost savings in daily operations, they have also made the SCNs more vulnerable to disruptions (World Economic Forum, 2013). Under a low probability high impact disruption, lean supply chains would shut down in a matter of hours, with global implications. Supply concentration and IT reliance make the supply chains vulnerable to targeted attacks. This is particularly evident in the SCNs with low levels of ‘buffer’ inventory (Jüttner et al., 2003).
A recent strand of publications, by both academic and industry communities, has revealed the importance of understanding and quantifying robustness in global SCNs. Increasing focus has been given to modelling SCNs as complex adaptive systems, in recent years, using network science methods to examine the robustness of various network topologies (Choi et al., 2001; Surana et al., 2005; Brintrup et al., 2016).
The aim of this paper is to present a critical assessment of the research published, mainly in the last decade, in the field of modelling the topology and robustness of SCNs using network science concepts. A novel perspective is then presented in relation to the way forward. The subsequent sections of this paper are structured as follows; From complex systems theory to network science section discusses the complex system nature of modern SCNs and introduces key network science concepts in the context of SCNs; Network science approach to modelling the topology and robustness of SCNs section presents the network science approach to modelling the topology and robustness of SCNs; Discussion of literature – Limitations and improved methodological directions section presents a discussion, including comparisons, critiques and potential methodological improvements, of the research reviewed, and Conclusions and future directions section provides conclusions and outlines possible directions for future research.
From complex systems theory to network science
Complex systems theory
Complex systems theory is a field of science that is used to investigate how the individual components and their relationships give rise to the collective behaviour of a given system (Ladyman et al., 2013). In essence, complex systems possess collective properties that cannot easily be derived from their individual constituents. For example, social systems which comprise relationships between individuals, the nervous system which functions through individual neurones and connections, and life on Earth itself, can all be regarded as complex systems (Kasthurirathna, 2015).
Although complex systems do not have a formal definition, the following three key features broadly characterise such systems (Bar-Yam, 2002);
-
1.
Emergence: Macro level properties, which dynamically originate from the activities and behaviours of the individual agents of the system, cannot be easily explained at the agent level alone (Kaisler and Madey, 2009). Therefore, emergence is governed by micro level interactions that are ‘bottom-up’ rather than ‘top-down’ rules.
-
2.
Interdependence: Individual components depend on each other to varying degrees (Buckley, 2008).
-
3.
Self-organisation: This is the attribute that is most commonly shared by all complex systems, where large scale organisation manifests itself spontaneously without any central control, based on local feedback mechanisms that either amplify or dampen disturbances (Mina et al., 2006).
Complex system characteristics of modern supply chain networks
Traditionally, a focal firm is assumed to be responsible for shaping the structure of a given SCN by selecting different suppliers for various purposes, such as reduced cost, increased flexibility/redundancy, and so on. However, the ability of a single firm to shape its supply chain seems to significantly diminish as SCNs become more global and complex in nature. Therefore, the topological structure of a SCN can increasingly be considered as emergent. As such, in a global and a complex business landscape, an individual firm may benefit more from positioning itself within the SCN rather than attempting to shape the SCN’s overall topology (Xuan et al., 2011).
Choi et al. (2001) note the complex adaptive system nature of large scale SCNs, where an interconnected network of multiple entities exhibit adaptiveness in response to changes in both the environment and the system itself. System behaviour emerges as a result of the large number of activities made in parallel by interacting entities (Pathak et al., 2007). Therefore, from the point of view of a single firm, the overall SCN is a self-organising system, which consists of various entities engaging in localised decision-making. Given this distributed nature of decision making, the configuration of the final SCN is beyond the realm of control of one organisation. Indeed, individual firms may pursue their own goals with the SCN emerging over time (Choi and Hartley, 1996; Choi et al., 2001).
Network modelling of supply chains
Traditionally, supply chains have been modelled as multi agent (or agent based) systems, in order to represent explicit communications between the various entities involved (Gjerdrum et al., 2001; Julka et al., 2002; Nair and Vidal, 2011). The earliest example of such a model is Forrester’s supply chain model (Forrester, 1961; Forrester, 1973), which comprised four types of agents, representing various organisations involved in a supply chain (namely; retailers, wholesalers, distributors and manufacturers), interacting with each other. Such agent-based models (ABMs) provide autonomy to each entity involved and define behaviours in terms of observables accessible to each agent and its goals, norms and decision rules (Parunak et al., 1998; Rahmandad and Sterman, 2008). ABMs are a form of logical deduction, since, given a set of basic rules and initial conditions, the emergent outcomes are embedded in the rules, however surprising they may be (Epstein and Axtell, 1996; Berryman and Angus, 2010).
ABMs are considered to be micro-models, since they facilitate system level inference from explicitly programmed, micro-level rules in simulated agent populations over time and space in a given environment. While such a bottom-up approach maybe suitable for relatively small systems, the exponential increase in the number of connected entities that comprise modern global SCNs favour a top-down approach to system modelling (Pruteanu, 2013).
In this regard, the macro perspective offered by network models are particularly valuable. A recent surge in interest in the area of networks has paved the way for what is now known as ‘network science’. Starting from the mathematical field of graph theory (Bondy and Murty, 1976; West, 2001), network science has now matured into a separate field, borrowing concepts from other domains such as statistical mechanics (Albert and Barabasi, 2002; Newman et al., 2011).
Network models focus on how topological properties affect various system properties. Such models typically do not have an environment or coevolution of the environment with the system. Rather, they consist of an ensemble of nodes that behave coherently. This top-down approach considers the network as a single entity and in some models, the individual nodes may exchange information and update the state of the system based on global specifications, which makes the system less prone to unpredictable emergent behaviour (Pruteanu, 2013).
Basic network models
The series of papers published by Erdȍs and Rényi on random graphs, between 1950 and 1960, sparked initial interest in network science. However, since the introduction of small-world networks by Watts and Strogatz in 1998, interest in the field of network science has surged, as evident in literature.
The following networks are now widely regarded as benchmarks;
-
1)
Erdȍs-Rényi (ER) Random graphs:
-
Nodes are randomly connected to each other.
-
Modelled using the Erdös-Rényi model (Erdȍs and Rényi, 1959).
-
-
2)
Small-world networks:
-
Most nodes are not neighbours of one another, but can be reached from every other node by a small number of steps.
-
Modelled using the Watts–Strogatz model (Watts and Strogatz, 1998).
-
3)
Scale-free networks:
-
The degree distribution follows power-law, at least asymptotically.
-
Modelled using the Barabasi-Albert (BA) model (Barabási and Albert, 1999).
The key characteristics of the above mentioned network topologies are presented in Fig. 1.
Comparison of random, small-world and scale free networks. Topological structure of benchmark network models. Random and Small-world network topologies do not include hub nodes. In contrast, scale-free topologies are characterised by the presence of small number of highly connected hub nodes and a high number of feebly connected nodes. Presence of distinct hubs in scale-free networks make them more vulnerable to targeted attacks, compared to random and small-world networks
Modelling network topology
A wide range of network models are available in network science literature. They can be broadly categorised into two distinct classes as follows;
-
1.
Generative models – the aim of these models is to generate a snapshot of a topology. Among generative models, some are static (time independent topologies) while some use growth (and other mechanisms). Furthermore, some generative models include predefined global properties (such as degree distribution, hierarchy and modularity) while others predefine a local property (such as the attachment probability).
-
2.
Evolving models – the aim of these models is to capture the microscopic mechanisms underlying the temporal evolution of a network topology. These models include growth and in some instances may include node deletion and link rewiring. For a comprehensive summary of mechanisms underlying various evolving network models, readers are referred to Albert and Barabasi (2002).
Figure 2 outlines the different perspectives offered by generative and evolving network models.
Based on the above classification, both ER random and small-world network models are static generative models as they imply a fixed number of nodes where links are placed between nodes using some random algorithm. These models are therefore less widely used to model dynamical open systems, such as SCNs. However, the ER random model is generally used by researchers as a null model to test whether a real network property is statistically significant or simply attributable to random connectivity (Kito et al., 2014).
It is noted that the result of any static generative model can also be obtained by an evolving model (for example, an ER random network can be conveniently generated using an evolving model with a specified growth process). In fact, any evolving model can be used for generative purposes. In this regard, the BA model, which is generally considered as an evolving network model, can also be used for generative purposes, depending on the study requirement.
An evolving network growth model governs the time evolution of networks by specifying the way in which the new nodes connect with the existing nodes in the network (Zhao et al., 2011a). This process is referred to as ‘attachment’ and various network growth models comprise various ‘attachment rules’, which subsequently generate networks with distinct topologies as they evolve. For example, the mechanism underlying generation of scale free networks has been successfully captured by the growth (in terms of nodes) and preferential attachment mechanism presented in the BA model (Barabási and Albert, 1999). Under preferential attachment, the probability p i that a new node makes a connection to an existing node i with degree k i is given by:
where N is the set of nodes to which the new node could connect.
The BA model represents a ‘rich get richer’ process and the resulting scale-free network topology can be used to model many real world networks, such as the World Wide Web, power grids, metabolic networks and social networks (Surana et al., 2005). This concept explains the existence of ‘hubs’ (a few nodes with a large number of connections), which is a defining feature of scale-free networks.
The degree distribution P k of a scale free network is approximated with power-law as follows;
where k is the degree of the node and γ is the power-law exponent.
Many network properties depend on the value of the power-law exponent, γ (Barabasi, 2014). Therefore, it is important to accurately estimate the power-law exponent of the degree distribution of a given network topology, as this enables us to compare network topologies on a continuous spectrum. Newman (2005) presents a reliable methodology accurately estimating the power-law exponent of a given degree distribution, which involves plotting the complementary cumulative distribution function. This method does not require data binning and as a result eliminates the plateau observed in linear binning approach for high degree regime by extending the scaling region. Interested readers are referred to Clauset et al. (2009), for a comprehensive review of power-law distributions in empirical data.
Fitness based network models
In the BA model, it is assumed that a node’s growth rate (in terms of new link acquisition) is determined solely by its degree. Accordingly, it predicts that the oldest node always has the most links – this concept is often referred to as the first mover advantage in the economics literature. However, this approach does not take into consideration the intrinsic characteristics of the nodes which may influence the rate at which they acquire new links. For instance, in many real world networks such as Hollywood actor networks and global business networks, some nodes despite being latecomers, acquire links within a short timeframe whereas others are present within the network from early on but fail to acquire high numbers of links (Barabasi, 2014). As such, modelling SCN growth based on a growth model which views new link acquisitions from a purely topological perspective may not be suitable.
Therefore, rather than relying entirely on the node degree, the attachment probability and subsequent network growth should rely on a more basic factor, referred to as node ‘fitness’ (Caldarelli et al., 2002; Ghadge et al., 2010; Smolyarenko, 2014). The concept of ‘fitness’ can be thought of as the amalgamation of all the attributes of a given node that contribute to its propensity to attract links, which could also include the node degree.
In order to overcome the limitations mentioned above, a model was proposed by Bianconi and Barabasi (2001). This model is referred to as the Bianconi-Barabasi Model (hereinafter referred to as the BB model) and has the following characteristics;
-
Growth – At each time step, a new node j with m links and fitness ϕ j is added to the network. In generating an ensemble of networks, ϕ j is sampled from a fitness distribution. Once assigned, the fitness of a node remains constant.
-
Preferential Attachment – the probability of a new node connecting to node i is proportional to the product of node i’s degree k i and its fitness ϕ i ;
As can be seen from the above formulation, between two nodes i and j with the same fitness (ϕ i = ϕ j ), the one with the higher degree will have the higher probability of selection. Conversely, between two nodes i and j with the same degree (k i =k j ) the node with the higher fitness will be selected with a higher probability, thus indicating that even a relatively new node, with only a few links, can acquire more new links rapidly, if it has a higher level of fitness. As such, consideration is given to both fitness and the degree of the nodes in the above growth model.
More recently, Ghadge et al. (2010) proposed a purely fitness based network growth model, which accounts for the various factors that contribute to the likelihood of a new node being attracted to an existing node within a network. Such fitness based attachment models can indeed be categorised as generative models. This type of models offers greater flexibility owing to their ability to reproduce network topologies with fixed global properties.
In the model proposed by Ghadge et al. (2010), the fitness ϕ i , which represents the propensity of node i to attract links, is formed from the product of relevant attributes {φ i1, …, φ iL };
Where each attribute, φi is represented as a real non-negative value. Subsequently, it is assumed that the number of attributes affecting a node’s attractiveness is sufficiently large and are statistically independent. Therefore, by a version of the Central Limit Theorem, the overall fitness ϕ i will tend to be lognormally distributed, regardless of the type of distribution of the individual factors (Nguyen and Tran, 2012). In a SCN context, the attributes, which contribute to fitness, could include cost, service or product quality, reliability, and so on. Finally, the probability of connecting a new node j to an existing node i is taken to be proportional to its fitness ϕ i , as follows;
The above attachment rule, named the ‘Lognormal Fitness Attachment’ (LNFA), differs from the BA model in that node fitness replaces node degree (Nguyen and Tran, 2012). Therefore, in LNFA, a new node which has a large fitness, despite being in the network for a short period of time, can make itself a preferential choice for new nodes entering the network.
Recent work by Bell et al. (2017) have investigated the evolutionary mechanisms that would give rise to a fitness-based attachment process. In particular, it is proven by analytical and numerical methods that in homogeneous networks, the minimisation of maximum exposure to unfitness by each node, leads to attachment probabilities that are proportional to fitness. This result is then extended to heterogeneous networks, with strictly tiered SCNs being used as examples.
Generating null models using configuration model
Similar to the LNFA model, the configuration model belongs to the wider class of network generative models. A generative model allows us to choose parameters and draw a single instance of a network. Since a single generative model can generate many instances of networks, the model itself corresponds to an ensemble of networks.
The configuration model is commonly used to generate networks with pre-defined degree sequences. It is particularly useful for generation of null models for the purposes of hypothesis testing. Comparison of properties of an empirical network with the properties of an ensemble of networks generated by the configuration model allows one to identify if the properties observed in the empirical network are unique and meaningful or whether they are common to all networks with that degree sequence (Fosdick et al., 2016). When data is available for an empirical network, a technique termed degree preserving randomisation (DPR) is often used in literature to generate random networks which correspond to the configuration model. DPR involves rewiring the original network, to generate an ensemble of null models, while preserving the degree vector (Maslov and Sneppen, 2002). At each time step, the DRP process randomly picks two connected node pairs and switch their link targets. This switching is repeatedly applied to the entire network until each link is rewired at least once. The resulting network represents a null model where each node still has the same degree, yet the paths through the network have been randomised.
For example, Becker et al. (2014) have constructed a manufacturing system network model from real world data (where nodes represent separate work stations and links represent material flows between work stations). By applying the DPR process to generate an ensemble of networks with the same degree distribution, the authors observe that nodes (work stations) with a particularly high betweenness centrality are over-represented in the manufacturing system studied. They concludes that the manufacturing system topology is therefore non-random and favours the existence of a few highly connected work stations.
Network science approach to modelling the topology and robustness of SCNs
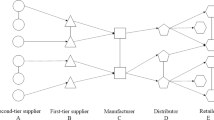
So far, the published research in the area of modelling SCNs as complex networks have demonstrated that a network perspective can indeed be used to successfully represent a supply chain as nodes and links (Thadakamalla et al., 2004; Xuan et al., 2011; Zhao et al., 2011a; Zhao et al., 2011b; Wen and Guo, 2012; Li et al., 2013; Li, 2014; Mari et al., 2015 and Kim et al., 2015). A typical SCN model consists of nodes, which represent individual firms (such as suppliers, manufacturers, distributers and retailers), and links, which represent interactions between nodes (such as exchange of information, transportation of material, and financial transactions). Such abstractions can be beneficial in identifying the properties of various types of SCN, as representing too many details could be detrimental to identifying the network properties (Shen et al., 2006). On the other hand, important node or link information could be lost. The level of detail to be represented by a given complex network model is an important decision to be made by the network scientist (Kasthurirathna, 2015).
Given the ultimate goal of obtaining generalizable results for real world SCNs, the theoretical research in this area should be well informed by empirical studies. In particular, empirical studies should be used to establish the key characteristics that need to be represented in the network topologies being generated by a given growth mechanism. Figure 3 illustrates the general methodological framework of research on topological modelling and robustness analysis of SCNs.
Modelling SCN topologies through growth models
In order to characterise the dynamical processes on complex SCNs, the first step is to construct realistic network growth models. Such models can be used to generate an ensemble of networks with the required topological properties, from which insights can be gained into the relationship between the topology and the dynamics of complex networks (Bianconi, 2016).
In the context of supply chains, the concept of growth describes how newcomer firms join existing firms in a SCN. As new entrants join the SCN, trading partners are assigned from within the network. In the above regard, the BA model, despite its simplicity and elegance, includes a number of known limitations, as listed in Table 1 against their respective implications for SCNs.
Indeed, firm partner selection is, in reality, a multi-objective problem and involves numerous factors, such as price, performance, quality, goodwill, transport cost (Jain et al., 2009; Li et al., 2013). However, it is not practical to consider all these factors, so researchers have adopted simple yet intuitive approaches which extend the basic BA model concept. These include specifying selection (attachment) rules based on basic topological properties, such as the node degree (i.e. the connectedness of a given firm), in conjunction with other parameters (such as the number of links entering the system with each type of new node, the rewiring probability, and the topological distance between source and target nodes). Examples of such customised attachment rules are summarised in Table 2.
Each of the aforementioned attachment rules, over time, generate networks with distinct topologies. It is evident, that when constructing network topologies representative of SCNs, the attachment preference is generally governed by three factors;
-
1)
The type of node entering the system (which determines the number of links that enter the system with addition of new nodes and to which existing nodes these links will be connected).
-
2)
Type and degree of existing nodes (preference is given to existing high degree nodes over the low degree nodes, representing the market power and visibility of highly connected firms).
-
3)
Type and topological or geographical distance of existing nodes (preference is given to closer nodes than farther away ones, in terms of either the topological or the geographical distance, representing the ‘relationship distance’ or the cost of goods movement, respectively).
Concept of SCN robustness
From the contemporary literature in the area of modelling SCN robustness, it is evident that the terms resilience and robustness have been used interchangeably by researchers. However, in the field of network science, the terms resilience and robustness have distinct meanings. For example, a system is called robust, if it can maintain its basic functions in the presence of internal and external perturbations. Hence, a robust SCN would include redundant or parallel components, which if needed can be relied upon to maintain the overall functionality.
In contrast, resilience is defined as the capability of a system to adapt to internal or external perturbations by changing mode of operation, without losing its ability to function (Barabasi, 2014). Therefore, a resilient supply chain should respond quickly and effectively to a given perturbation, such as a change in supply or demand, or to the failure of a component (such as a firm or a material transport route) within the system. The response mechanism of a resilient SCN is attributable to its flexibility to rewire the lost connections away from disrupted nodes (Sheffi and Rice, 2005). As opposed to resilience, the robustness of a SCN does not relate to response mechanisms – it merely reflects the extent to which a given SCN can withstand loss of its components, without losing its basic functions. It is worth noting that most studies have focussed mainly on the topological robustness of SCNs, rather than their resilience.
Analytical measurements of SCN topological robustness
Network science offers a rich set of tools for topological robustness analysis. Refer to Costa et al. (2007) and Rubinov and Sporns (2010) for a comprehensive range of measures used for the characterization of complex networks. Some key metrics used in network science, and their corresponding SCN implications at node and network level are presented in Appendix 1 and 2, respectively.
As can be seen from the metrics presented in Appendix 1 and 2, the analytical measures in network science can be used to gain important insights on network structure and robustness quickly and with low computational difficulty. However, the key limitation of using analytical measures is that they are unable to account for the heterogeneity of nodes, in terms of their functionality within a given SCN, since the metrics consider all nodes to be homogeneous in function. In order to overcome the above limitation, researchers have relied on simulations to analyse the topological robustness of SCNs. Furthermore, simulations allow flexibility in analysis through customised robustness metrics (see section below).
Using simulations to determine the topological robustness of SCNs
Node failures in networks can be categorised either as ‘random failures’ or ‘targeted attacks’. Random failures entail the same probability of failure across each node within a given network. In contrast, a ‘targeted attack’ refers to when an attacker selectively compromises the nodes with probabilities proportional to their degrees, where highly connected nodes are compromised with higher probability (Ruj and Pal, 2014).
In the network science literature, random failures and targeted attacks in networks are typically simulated as follows;
-
1)
Random failure: Each robustness metric established for the network is recorded at each time step by randomly removing the nodes from the network.
-
2)
Targeted attacks: Each robustness metric established for the network is recorded at each time step by sequentially removing the nodes, based on their degree, removing higher degree nodes first, from the network.
The robustness values recorded for each metric, for each network considered, are then compared. It has, so far, been established that the random networks respond similarly to both random failures and targeted attacks. In comparison, the scale-free networks are robust against random failures but are highly sensitive to targeted attacks (Albert et al., 2000). This is due to the presence of hubs (highly connected nodes) in scale-free networks, which are the nodes targeted by an attacker.
A number of researchers have modelled various SCN topologies under both random failures and targeted attacks, and attempted to establish an optimal topology which can withstand each type of failure without compromising the overall network functionality (Thadakamalla et al., 2004; Zhao et al., 2011a, Li and Du, 2016). Each study has established a set of robustness metrics, in order to assess and compare the robustness of each network topology simulated under random failures and targeted attacks. These robustness metrics are variations of the existing standard topological metrics from network science. The most commonly used network topology metrics in supply network research are;
-
1.
Size of the largest connected component (LCC) of a network - As nodes are sequentially removed, the graph disintegrates into sub-graphs. The number of nodes in the LCC (or the largest sub-graph) of a fragmented network therefore provides insights into its overall connectivity.
-
2.
Average or maximum path length in the LCC - The average or maximum shortest path length between any two nodes in the largest connected component of a network. This provides insights into the overall accessibility of the network.
The above metrics consider the roles of entities (nodes and links) within a distribution network to be homogeneous. Such an assumption is far from reality, since the entities within a real-world supply network play different roles with different characteristics – for example, the distance between two supply nodes or two demand nodes are not as important as that between a supply and a demand node (Zhao et al., 2011b).
Therefore, various researchers (such as Thadakamalla et al., 2004; Zhao et al., 2011a and Zhao et al., 2011b, Xu et al., 2014) have developed new metrics, which realistically represent the heterogeneous roles of nodes within the network. For example, Zhao et al. (2011a) have developed the following customised robustness metrics for distribution networks;
-
Supply availability rate is represented as the percentage of demand nodes that have access to supplies from at least one supply node.
-
The network connectivity is determined through the size of the largest functional sub-network (LFSN), namely the number of nodes in the LFSN in which there is a path between any pair of nodes and there exists at least one supply node.
-
Accessibility is determined by;
-
○ Average supply path lengths in the LFSN, i.e. the average shortest supply path length between all pairs of supply and demand nodes in the LFSN.
-
○ Maximum supply path lengths in the LFSN, i.e. the maximum shortest path length between any pair of supply and demand nodes in the LFSN.
Empirical studies on SCN topologies
A review of contemporary literature on SCN topologies reveals that only a limited number of data driven studies are available in this domain. This is mainly due to difficulty in obtaining specific information about supplier/customer relationships, which is often proprietary and confidential. Table 3 presents a summary of a number of empirical studies available to date. It is noted that these studies generally focus on overall topological character of SCNs rather than robustness.
Discussion of literature – Limitations and improved methodological directions
This section will critically discuss the existing methodologies in contemporary literature, on modelling SCN topologies and robustness.
Modelling SCN topologies
Insights revealed by empirical studies
While SCNs in real world may not evolve through a single mechanism, it is possible to infer general growth and design principles from the global properties of existing SCNs. In this regard, empirical studies play a major role in pointing the theoretical research work on modelling SCN topologies in a meaningful direction.
A number of past theoretical studies have relied upon the BA model for SCN growth and/or benchmarking purposes (Thadakamalla et al., 2004; Xuan et al., 2011; Zhao et al., 2011a). However, based on the results of empirical studies summarised in this paper, it is understood that the BA model (due to its minimal nature) cannot sufficiently represent the growth mechanism underlying SCNs, due to the following:
-
1)
The BA model generates networks with a constant power-law exponent, γ = 3, as shown by both analytical and simulation methods in Barabasi (2014). The SCNs reported in empirical studies indicate topologies with γ ≈ 2 (it is noted that γ = 2 is the boundary between hub and spoke (γ < 2) and scale-free (γ > 2) network topologies).
-
2)
The BA model cannot generate networks with pronounced community structure, which has been observed in real SCNs, since all nodes in the network belong to a single weakly connected component (Newman, 2003).
-
3)
Assortative (or disassortative) mixing as observed in real SCNs, is not a feature of networks generated by the BA model - as shown analytically (in the limit of large network size) by Newman (2002).
As can be seen above, although some real world networks have been convincingly modelled by the preferential attachment mechanism presented in the BA model (Barabasi et al., 1999, Albert et al., 1999), this is not so for SCNs. Therefore, a convincing network growth mechanism for SCNs is yet to be formulated.
Suitability of network models in literature for SCN modelling purposes
Considering the limitations of the BA model in representing the topologies of real SCNs (as discussed in the previous section), the generative models which predefine a global property (such as the degree distribution, hierarchy, modularity, etc.) are a good starting point for the researchers in the SCN domain, especially when the interest of research is directed towards understanding the role of network topology on its robustness. In particular, the SCNs in the real world may have evolved based on various non generalizable principles. Therefore, when aiming to study and understand the topological character of SCNs, researchers will benefit more from simply mimicking the observed topologies, than trying to understand the underlying growth mechanism – which may indeed be complex and non-generalizable, beyond the realm of a single mathematical algorithm.
Generative models allow the researchers to recreate a network topology, as observed at a single cross section in time, and undertake further investigations on various phenomena, such as topological efficiency, robustness etc. When information on the adjacency matrix is available for real-world networks, one can simply use the DPR to generate an ensemble of random networks (which correspond to the configuration model) to establish whether the degree distribution on its own is sufficient to describe the property observed in the network at hand. It is worth noting that in tiered SCNs, the DPR process should be restricted to each tier, in order to ensure that links are not swapped between non-compatible tiers.
In many cases, adjacency matrix information for real networks are not readily available. Such situations require the researcher to recreate the degree distribution of the SCN, using only the basic network metrics (such as the power-law exponent) or simply through qualitative descriptions. In this regard, fitness based generative models have recently gained prominence in theoretical research (Caldarelli et al., 2002; Bedogne et al., 2006; Smolyarenko, 2014; Perera et al., 2016a). In fitness based models, the fitness distribution and the connection rules are given by a priori arbitrary functions, which enables considerable amount of tuning (Smolyarenko, 2014). Indeed, this tunability makes such models a useful and practical modelling tool.
For example, the LNFA includes a tunable parameter σ (the shape parameter of the lognormal distribution), which can be manipulated to generate a large spectrum of networks. At one extreme, when σ is zero, all nodes have the same fitness and therefore at the time a new node joins the network, it chooses any existing node as a neighbour with equal probability, thus replicating the random graph model. On the other hand, when σ is increased beyond a certain threshold, very few nodes will have very large levels of fitness while the overwhelming majority of nodes have extremely low levels of fitness. As a result, the majority of new connections will be made to a few nodes which have high levels of fitness. The resulting network therefore resembles a monopolistic/“winner-take-all” scenario, which can sometimes be observed in the real world (however, in some instances, it may be necessary to place a restriction on the highest degree achievable by a single node, in order to represent the ‘contractual capacity’ of firms). Between the above two extremes (random and monopolistic) lies a spectrum of power law networks which can closely represent many real networks (Ghadge et al., 2010). Figure 4 illustrates the spectrum of network topologies generated by the LNFA model.
Nguyen and Tran (2012) have illustrated that the LNFA model can indeed generate network topologies with γ ≈ 2, which represents many observed SCN topologies in empirical research work (Büttner et al., 2013; Orenstein, 2016). However, the ability of LNFA to generate modular and disassortative networks, as observed in SCNs, remains an open research question.
Directionality of links
The inter-firm relationships in SCNs are generally modelled using undirected links. However, the links between nodes in a SCN can include a direction, depending on the specific type of relationship being modelled. The inter-firm relationships in a SCN can be broadly categorised into three classes, namely; (1) material flows, (2) financial flows, and (3) information exchanges. Material flows are usually unidirectional from suppliers to retailers, while financial flows are unidirectional in the opposite direction. Both material and financial flows mostly occur vertically, across the functional tiers of a SCN (however, in some cases, two firms within the same tier, such as two suppliers, could also exchange material and finances) (Lazzarini et al., 2001). In contrast, information exchanges are bidirectional (i.e. undirected) and includes both vertical and horizontal connections (i.e. between firms across tiers and between firms within the same tier). Therefore, the same SCN can include different topologies based on the specific type of relationship denoted by the links in the model. For instance, unlike material and financial flows, SCN topology for information exchanges can exhibit shorter path lengths and high clustering due to relatively larger number of horizontal connections (Hearnshaw and Wilson, 2013).
Compared to undirected network representation, in directed networks, the adjacency matrix is no longer symmetric. As a result, the degree of a node in a directed network is characterised by both in-degree and out-degree. On this basis, the degree distribution of directed networks is analysed separately for in and out degrees. Also, unlike undirected networks, in directed networks the distance between node i and node j is not necessarily the same as the distance between node j and node i. In fact, in directed networks, the presence of a path from node i to node j does not necessarily imply the presence of a path from node j to node i (Barabasi, 2014). This has implications on node centrality metrics, such as closeness and betweenness. In addition, it is noted that many dynamics, such as synchronizability and percolation, are different in directed networks compared to undirected networks (Schwartz et al., 2002; Park and Kim, 2006). Therefore, when modelling SCNs, it is important to first identify the specific type of relationship denoted by the links, so that network can be correctly represented as undirected or directed.
Additional considerations for robustness testing
From a SCN point of view, the position of an individual firm with respect to the others can influence both its strategy and behaviour (Borgatti and Li, 2009). Accordingly, analysis of each firm’s role and importance based on its position in the SCN can reveal important properties, such as its structural robustness. In this regard, future studies could simulate targeted attacks based on node centrality measures, such as betweenness and closeness centrality, rather than node degree. Such considerations will capture the critical nodes in various perspectives. Also, as Piraveenan et al. (2012) notes, when simulating targeted attacks on empirical networks, one could also rank nodes on the basis of non-topological attributes (such as firm size, output, and geographic location).
Depending on the structure of the overall SCN, disruptions can be experienced in various forms, such as; supply disruptions, logistics disruptions, coordination disruptions and demand disruptions (Yi et al., 2013). These various disruptions can be attributed to either nodes or links or both, for modelling purposes. So far, the focus of modelling has been on unweighted links in SCNs, which essentially indicate that all relationships are considered to be homogeneous in terms of their relative importance. However, real SCNs exhibit large levels of heterogeneity in the capacity and intensity of the connections (links) between the nodes. Rui and Ban (2012) state that empirical observations have shown the existence of nontrivial correlations and associations between link weights and topological quantities in complex networks. In the context of SCNs, the connections, be they physical flows or relationships between organisations, are heterogeneous in terms of the strength and importance. Therefore, the SCN can be better reflected and understood in terms of weighted networks, where weights reflect volume, frequency or the criticality of flows (Hearnshaw and Wilson, 2013). If such information is available, targeted attacks could also be simulated by link removal on the basis of link weights.
Conclusions and future directions
This paper has presented a comprehensive and critical review of the research undertaken on the use of network science techniques to model the topology and robustness of SCNs. The key challenge in this research is the tailoring of network science principles to SCNs, by identifying the fundamental SCN features. Although network science offers a rich conceptual representation of SCNs, a number of potential improvements to the existing modelling approach have been identified and are proposed for future research.
From the literature reviewed, it is evident that most of the previous research undertaken in the field of modelling SCNs as complex networks have given primary consideration to network topology. Based on the empirical studies, it is evident that most real world SCNs tend to have power-law exponents which fluctuate around 2. It is noted that γ = 2 is the boundary between hub and spoke (γ < 2) and scale-free (γ > 2) network topologies. Also, most SCN topologies indicate disassortative mixing and modularity (the presence of communities). The well-known BA model is not able to generate network topologies with the above mentioned features. Therefore, researchers are advised to focus on generative models to mimic the SCN topologies observed in empirical studies. This approach is deemed more effective and reliable than the existing methodology of investigating the mechanisms underlying SCN evolution, particularly since the overarching goal of research in this area is to understand the role of network topology on properties such as robustness. It is emphasised that future theoretical work on development of SCN growth models should ideally aim to reflect the above outlined topological features in the network topologies obtained from generative models. A natural extension of this work would be to investigate the ability of fitness based growth models, coupled with node and link heterogeneity, to mimic the topological features, such as modularity and disassortativity, of real world SCNs.
So far, empirical studies have investigated a cross sectional view of real SCNs at a given point in time. However, databases such as Bloomberg offer rich data sets to investigate the evolution of SCNs across time. Therefore, researchers could investigate the evolution of SCNs, using temporal data. Such empirical tests can validate the theoretical network growth models developed so far in the literature.
References
Albert R, Barabási AL (2002) Statistical mechanics of complex networks. Rev Mod Phys 74(1):47
Albert R, Jeong H, Barabási AL (1999) Internet: diameter of the world-wide web. Nature 401(6749):130–131
Albert R, Jeong H, Barabási AL (2000) Error and attack tolerance of complex networks. Nature 406:378–382
Barabási, A. L. (2014). Network science book. Boston: Center for Complex Network, Northeastern University. Available online at: http://barabasi.com/networksciencebook
Barabási A-L, Albert R (1999) Emergence of scaling in random networks. Science 286(5439):509–512
Bartos S (2012) Resilience in the Australian food supply chain. Department of agriculture Australian government, fisheries and forestry, Commonwealth of Australia, Canberra Retrieved from http://www.tisn.gov.au/Documents/Resilience%20in%20the%20Australian%20food%20supply%20chain%20-%20PDF%20copy%20for%20web.PDF
Bar-Yam Y (2002) General features of complex systems. Encyclopedia of Life Support Systems (EOLSS), UNESCO, EOLSS Publishers, Oxford
Becker T, Meyer M, Windt K (2014) A manufacturing systems network model for the evaluation of complex manufacturing systems. Int J Product Perform Manag 63(3):324–340
Bedogne C, Rodgers GJ (2006) Complex growing networks with intrinsic vertex fitness. Phys Rev E 74(4):046115
Bell M, Perera S, Piraveenan M, Bliemer M, Latty T, Reid C (2017) Network growth models: a behavioural basis for attachment proportional to fitness. Sci Rep 2017:7
Berryman MJ, Angus SD (2010) Tutorials on agent-based modelling with NetLogo and network analysis with Pajek, Complex physical, biophysical and Econophysical systems, pp 351–375
Bianconi G, Barabási AL (2001) Competition and multiscaling in evolving networks. EPL (Europhysics Letters) 54(4):436
Bianconi, Ginestra. "Processes on networks". 2016. Lecture
Bondy JA, Murty USR (1976) Graph theory with applications, vol 290. Macmillan, London
Borgatti SP, Li X (2009) On social network analysis in a supply chain context*. J Supply Chain Manag 45(2):5–22
Brintrup, A., Wang, Y., & Tiwari, A. (2015). Supply networks as complex systems: a network-science-based characterization
Brintrup A, Ledwoch A, Barros J (2016) Topological robustness of the global automotive industry. Logist Res 9(1):1–17
Buckley W (2008) Society as a complex adaptive system. Emergence: Complexity and Organization 10(3):8
Büttner K, Krieter J, Traulsen A, Traulsen I (2013) Static network analysis of a pork supply chain in northern Germany—characterisation of the potential spread of infectious diseases via animal movements. Preventive veterinary medicine 110(3):418–428
Caldarelli G, Capocci A, De Los Rios P, Munoz MA (2002) Scale-free networks from varying vertex intrinsic fitness. Phys Rev Lett 89(25):258702
Canis, Bill. (2011). Motor vehicle supply chain: effects of the Japanese earthquake and tsunami: DIANE publishing
Choi TY, Hartley JL (1996) An exploration of supplier selection practices across the supply chain. J Oper Manag 14(4):333–343
Choi TY, Hong Y (2002) Unveiling the structure of supply networks: case studies in Honda, Acura, and DaimlerChrysler. J Oper Manag 20(5):469–493
Choi TY, Dooley KJ, Rungtusanatham M (2001) Supply networks and complex adaptive systems: control versus emergence. J Oper Manag 19(3):351–366
Clauset A, Shalizi CR, Newman ME (2009) Power-law distributions in empirical data. SIAM Rev 51(4):661–703
Cohen R, Erez K, Ben-Avraham D, Havlin S (2000) Resilience of the internet to random breakdowns. Phys Rev Lett 85(21):4626
Costa LDF, Rodrigues FA, Travieso G, Villas Boas PR (2007) Characterization of complex networks: a survey of measurements. Adv Phys 56(1):167–242
Epstein JM, Axtell R (1996) Growing artificial societies: social science from the bottom up. Brookings Institution Press, Massachusetts
Erdős P, Rényi A (1959) On random graphs. I. Publ Math 6:290–297
Forrester JW (1961) Industrial dynamics. MIT Press, Cambridge
Forrester JW (1973) World dynamics. MIT Press, Cambridge
Fosdick, B. K., Larremore, D. B., Nishimura, J., & Ugander, J. (2016). Configuring random graph models with fixed degree sequences. arXiv preprint arXiv:1608.00607
Freeman LC (1977) A set of measures of centrality based on betweenness. Sociometry 1:35–41
Gang Z, Ying-Bao Y, Xu B, Qi-Yuan P (2015) On the topological properties of urban complex supply chain network of agricultural products in mainland China. Transportation Letters 7(4):188–195
Ghadge S, Killingback T, Sundaram B, Tran DA (2010) A statistical construction of power-law networks. International Journal of Parallel, Emergent and Distributed Systems 25(3):223–235
Gjerdrum J, Shah N, Papageorgiou LG (2001) A combined optimization and agent-based approach to supply chain modelling and performance assessment. Prod Plan Control 12(1):81–88
Hearnshaw EJ, Wilson MM (2013) A complex network approach to supply chain network theory. Int J Oper Prod Manag 33(4):442–469
Jain V, Wadhwa S, Deshmukh SG (2009) Select supplier-related issues in modelling a dynamic supply chain: potential, challenges and direction for future research. Int J Prod Res 47(11):3013–3039
Julka N, Srinivasan R, Karimi I (2002) Agent-based supply chain management—1: framework. Comput Chem Eng 26(12):1755–1769
Jüttner U, Peck H, Christopher M (2003) Supply chain risk management: outlining an agenda for future research. Int J Log Res Appl 6(4):197–210
Kaisler S, Madey G (2009) Complex adaptive systems: emergence and self-organization. Presentation, University of Notre Dame, Notre Dame
Kasthurirathna D (2015) The influence of topology and information diffusion on networked game dynamics (ph.D). University of Sydney, Sydney
Keqiang W, Zhaofeng Z, Dongchuan S (2008) Structure analysis of supply chain networks based on complex network theory, In Semantics, Knowledge and Grid, 2008. SKG'08. Fourth International Conference on. IEEE, USA, pp 493–494
Kim Y, Choi TY, Yan T, Dooley K (2011) Structural investigation of supply networks: a social network analysis approach. J Oper Manag 29(3):194–211
Kim Y, Chen YS, Linderman K (2015) Supply network disruption and resilience: a network structural perspective. J Oper Manag 33:43–59
Kito T, Brintrup A, New S, Reed-Tsochas F (2014) The structure of the Toyota supply network: an empirical analysis. Saïd Business School WP 2014:3
Ladyman J, Lambert J, Wiesner K (2013) What is a complex system?.European. Journal for Philosophy of Science 3(1):33–67
Lazzarini S, Chaddad F, Cook M (2001) Integrating supply chain and network analyses: the study of netchains. Journal on chain and network science 1(1):7–22
Lee HL (2004) The triple-a supply chain. Harv Bus Rev 82(10):102–113
Li Y (2014) Networked analysis approach of supply chain network. Journal of Networks 9(3):777–784
Li Y, Du ZP (2016) Agri-food supply chain network robustness research based on complex network, In proceedings of the 6th international Asia conference on industrial engineering and management innovation. Atlantis Press, Paris, pp 929–938
Li G, Gu YG, Song ZH (2013) Evolution of cooperation on heterogeneous supply networks. Int J Prod Res 51(13):3894–3902
Manuj I, Mentzer JT (2008) Global supply chain risk management strategies. Int J Phys Distrib Logist Manag 38(3):192–223
Mari SI, Lee YH, Memon MS, Park YS, Kim M (2015) Adaptivity of complex network topologies for designing resilient supply chain networks. International Journal of Industrial Engineering 22(1):102–116
Maslov S, Sneppen K (2002) Specificity and stability in topology of protein networks. Science 296(5569):910–913
Mina AA, Braha D, Bar-Yam Y (2006) Complex engineered systems: a new paradigm, In complex engineered systems. Springer, Heidelberg, pp 1–21
Nair A, Vidal JM (2011) Supply network topology and robustness against disruptions–an investigation using multi-agent model. Int J Prod Res 49(5):1391–1404
Newman ME (2002) Assortative mixing in networks. Phys Rev Lett 89(20):208701
Newman ME (2003) The structure and function of complex networks. SIAM Rev 45(2):167–256
Newman ME (2005) Power laws, Pareto distributions and Zipf's law. Contemp Phys 46(5):323–351
Newman ME, Girvan M (2004) Finding and evaluating community structure in networks. Phys Rev E 69(2):026113
Newman M, Barabasi AL, Watts DJ (2011) The structure and dynamics of networks. Princeton University Press, Princeton
Nguyen K, Tran DA (2012) Fitness-based generative models for power-law networks, In handbook of optimization in complex networks. Springer US, New Mexico, pp 39–53
Noldus R, Van Mieghem P (2015) Assortativity in complex networks.Journal of. Complex Networks 3(4):507–542
Orenstein P (2016) How does supply network evolution and its topological structure impact supply chain performance? In 2016 Second International Symposium on Stochastic Models in Reliability Engineering, Life Science and Operations Management (SMRLO). IEEE, USA, pp 562–569
Parhi M (2008) Impact of the changing facets of inter-firm interactions on manufacturing excellence: a social network perspective of the Indian automotive industry. Asian Journal of Technology Innovation 16(1):117–141
Park SM, Kim BJ (2006) Dynamic behaviors in directed networks. Phys Rev E 74(2):026114
Parunak HVD, Savit R, Riolo RL (1998) Agent-based modeling vs. equation-based modeling: a case study and users’ guide, In Multi-agent systems and agent-based simulation. Springer, Heidelberg, pp 10–25
Pathak SD, Day JM, Nair A, Sawaya WJ, Kristal MM (2007) Complexity and adaptivity in supply networks: building supply network theory using a complex adaptive systems perspective*. Decis Sci 38(4):547–580
Perera S, Bell MGH, Bliemer MCJ (2016a) Resilience characteristics of supply network topologies generated by fitness based growth models. 95th Annual Meeting of the Transportation Research Board TRB, Washington, D.C. United States, 14th January 2016
Perera S, Bell M, Piraveenan M, Bliemer M (2016b) Empirical investigation of supply chain structures using network theory. 6th International Conference on Logistics and Maritime Systems, Sydney Retrieved from http://logms2016.org/authors-information/
Piraveenan M, Uddin S, Chung KSK (2012, August) Measuring topological robustness of networks under sustained targeted attacks, In Advances in Social Networks Analysis and Mining (ASONAM), 2012 IEEE/ACM International Conference on. IEEE, USA, pp 38–45
Pruteanu, A. (2013). Mastering emergent behavior in large-scale networks
Rahmandad H, Sterman J (2008) Heterogeneity and network structure in the dynamics of diffusion: comparing agent-based and differential equation models. Manag Sci 54(5):998–1014
Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabási AL (2002) Hierarchical organization of modularity in metabolic networks. Science 297(5586):1551–1555
Rubinov M, Sporns O (2010) Complex network measures of brain connectivity: uses and interpretations. NeuroImage 52(3):1059–1069
Ruhnau B (2000) Eigenvector-centrality—a node-centrality? Soc Networks 22(4):357–365
Rui Y, Ban Y (2012) Nonlinear growth in weighted networks with neighborhood preferential attachment. Physica A: Statistical Mechanics and its Applications 391(20):4790–4797
Ruj S, Pal A (2014, May) Analyzing cascading failures in smart grids under random and targeted attacks, In Advanced Information Networking and Applications (AINA), 2014 IEEE 28th International Conference on. IEEE, USA, pp 226–233
Sabidussi G (1966) The centrality index of a graph. Psychometrika 31(4):581–603
Schwartz N, Cohen R, Ben-Avraham D, Barabási AL, Havlin S (2002) Percolation in directed scale-free networks. Phys Rev E 66(1):015104
Sheffi Y (2001) Supply chain management under the threat of international terrorism. The International Journal of logistics management 12(2):1–11
Sheffi Y, Rice JB Jr (2005) A supply chain view of the resilient enterprise. MIT Sloan Manag Rev 47(1):41
Shen Z, Ma KL, Eliassi-Rad T (2006) Visual analysis of large heterogeneous social networks by semantic and structural abstraction.Visualization and. Computer Graphics, IEEE Transactions on 12(6):1427–1439
Smolyarenko IE (2014) Fitness-based network growth with dynamic feedback. Phys Rev E 89(4):042814
Song C, Havlin S, Makse HA (2006) Origins of fractality in the growth of complex networks. Nat Phys 2(4):275–281
Sun JY, Tang JM, Fu WP, Wu BY (2017) Hybrid modeling and empirical analysis of automobile supply chain network. Physica A: Statistical Mechanics and its Applications 473:377–389
Surana A, Kumara S, Greaves M, Raghavan UN (2005) Supply-chain networks: a complex adaptive systems perspective. Int J Prod Res 43(20):4235–4265
Tett G. (2011). Japan supply chain risk reverberates globally - financial Times.Com. Retrieved from https://www.ft.com/content/fc3936a6-4f2f-11e0-9038-00144feab49a
Thadakamalla HP, Raghavan UN, Kumara S, Albert R (2004) Survivability of multiagent-based supply networks: a topological perspective. Intelligent Systems, IEEE 19(5):24–31
Vázquez A (2003) Growing network with local rules: preferential attachment, clustering hierarchy, and degree correlations. Phys Rev E 67(5):056104
Vespignani A (2010) Complex networks: the fragility of interdependency. Nature 464(7291):984–985
Watts DJ, Strogatz SH (1998) Collective dynamics of ‘small-world’ networks. Nature 393(6684):440–442
Wen L, Guo M (2012) Statistic characteristics analysis of directed supply chain complex network. International Journal of Advancements in Computing Technology 4(21)
West DB (2001) Introduction to graph theory, vol 2. Prentice hall, Upper Saddle River
Willems, SP (2008) Data set—Real-world multiechelon supply chains used for inventory optimization. Manufacturing & Service Operations Management 10(1):19–23.
World Economic Forum. (2013). Building resilience in supply chains. Retrieved from http://www3.weforum.org/docs/WEF_RRN_MO_BuildingResilienceSupplyChains_Report_2013.pdf
Xu M, Wang X, Zhao L (2014) Predicted supply chain resilience based on structural evolution against random supply disruptions. International Journal of Systems Science: Operations & Logistics 1(2):105–117
Xu NR, Liu JB, Li DX, Wang J (2016) Research on evolutionary mechanism of agile supply chain network via complex network theory. Math Probl Eng 2016:9
Xuan Q, Du F, Li Y, Wu TJ (2011) A framework to model the topological structure of supply networks. Automation Science and Engineering, IEEE Transactions on 8(2):442–446
Yi CQ, Meng SD, Zhang DM, Li JD (2013) Managing disruption risks in supply chain based on complex networks. Journal of Convergence Information Technology 8(5):175–184
Zhang Y, Xiong J, Feng C (2012) Robustness analysis of supply chain network based on complex networks. Computer Simulation 11:087
Zhao K, Kumar A, Yen J (2011a) Achieving high robustness in supply distribution networks by rewiring. Engineering Management, IEEE Transactions 58(2):347–362
Zhao K, Kumar A, Harrison TP, Yen J (2011b) Analyzing the resilience of complex supply network topologies against random and targeted disruptions. Systems Journal, IEEE 5(1):28–39
Funding
The authors would like to acknowledge the Australian Research Council (ARC) for funding this work under grant DP140103643.
Availability of data and materials
Not applicable.
Author information
Authors and Affiliations
Contributions
SP carried out the initial review of literature and prepared the draft manuscript. M.G.H. Bell and M.C.J. Bliemer participated in discussions where limitations in existing research methods were identified and improvements proposed. SP and M.G.H. Bell prepared the final manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
LIST OF NETWORK LEVEL METRICS AND THEIR SCN IMPLICATIONS.
Appendix 2
LIST OF NODE LEVEL METRICS AND THEIR SCN IMPLICATIONS.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Perera, S., Bell, M.G. & Bliemer, M.C. Network science approach to modelling the topology and robustness of supply chain networks: a review and perspective. Appl Netw Sci 2, 33 (2017). https://doi.org/10.1007/s41109-017-0053-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41109-017-0053-0