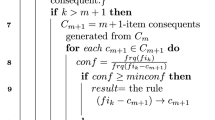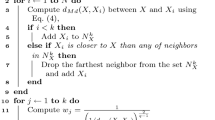Local means-based fuzzy k-nearest neighbor classifier with Minkowski distance and relevance-complementarity feature weighting

Abstract

This paper introduces an enhanced fuzzy k-nearest neighbor (FKNN) approach called the feature-weighted Minkowski distance and local means-based fuzzy k-nearest neighbor (FWM-LMFKNN). This method improves classification accuracy by incorporating feature weights, Minkowski distance, and class representative local mean vectors. The feature weighting process is developed based on feature relevance and complementarity. We improve the distance calculations between instances by utilizing feature information-based weighting and Minkowski distance, resulting in a more precise set of nearest neighbors. Furthermore, the FWM-LMFKNN classifier considers the local structure of class subsets by using local mean vectors instead of individual neighbors, which improves its classification performance. Empirical results using twenty different real-world data sets demonstrate that the proposed method achieves statistically significantly higher classification performance than traditional KNN, FKNN, and six other related state-of-the-art methods.

1 Introduction

Fuzzy k-nearest neighbor (FKNN) (Keller et al. 1985), a variation of the traditional k-nearest neighbor (KNN) (Cover and Hart 1967) classifier, is considered a more robust classifier than the traditional KNN (Derrac et al. 2015). In the traditional KNN classifier, each instance in the data set is assigned a single class label based on the majority class of its k nearest neighbors. By contrast, the FKNN classifier assigns a degree of membership to each instance in a specific class in the data set based the distances of its k nearest neighbors (Keller et al. 1985). These membership degrees are used as weights in the classification process, which makes the FKNN more robust to noise at the class boundaries (Keller et al. 1985; Maillo et al. 2020). The FKNN classification is an active topic of recent research and is being used in various applications (for examples, see González et al. 2021; Kumar and Thakur 2021; Maillo et al. 2020). However, the classical FKNN method has several limitations, such as sensitivity to the choice of the membership function (Derrac et al. 2016), number of nearest neighbors (k) (Derrac et al. 2015), and difficulty in handling high-dimensional data (Maillo et al. 2020). To address these limitations, researchers, such as Kassani et al. (2017) and Biswas et al. (2018), have proposed several enhancements. Recently, Zeraatkar and Afsari (2021) introduced two novel extensions of the FKNN classifier by incorporating the concepts of interval-valued fuzzy (IVF) sets, intuitionistic fuzzy (IF) sets, and the resampling method known as SMOTE, with a focus on addressing class imbalance classification problems. The primary purpose of these new FKNN variants, SMOTE-IVF and SMOTE-IVIF, was to enhance the classification performance of instances in the minority class. Moreover, González et al. (2021) proposed a novel fuzzy KNN method, called MonFKNN, based on monotonic constraints to enhance classification performance by addressing the issue of class noise. Based on the concept of multiple pseudo-metrics of fuzzy parameterized fuzzy soft matrices (fpfs-matrices), Memis et al. (2022) introduced the fuzzy parameterized fuzzy soft KNN (FPFS-kNN) classifier. This classifier takes into account the impact of model parameters on classification. A distinctive feature of this method is its use of five distance measures within the fpfs-matrices to generate multiple k nearest neighbors. Additionally, Bian et al. (2022) proposed a new FKNN approach, the fuzzy KNN method with adaptive nearest neighbors (A-FKNN), which focuses on determining a fixed k value for each test data instance. The core idea of A-FKNN is to find the optimal k value for each training instance during the training phase and to build a decision tree, called the A-FKNN tree. During the testing phase, A-FKNN identifies the optimal k for each testing instance by searching through the A-FKNN tree and then runs FKNN with the optimal k for each testing instance. Regarding specific application context, several enhancements for the FKNN algorithm have also been proposed, for example, a boosted particle swarm optimization with FKNN (bSRWPSO-FKNN) classifier for predicting atopic dermatitis disease (Li et al. 2023) and a Harris Hawks optimization and Sobol sequence and stochastic fractal search based FKNN (SSFSHHO-FKNN) model for diagnosis of Alzheimer’s disease (Zhang et al. 2023).

Furthermore, Kumbure et al. (2019) particularly focused on FKNN to address class imbalance problems. They proposed a new variant of FKNN that employs class-representative local means, which are locally representative of their respective classes, to enhance classification accuracy. This method was further improved in Kumbure et al. (2020) by introducing a Bonferroni mean-based local mean computation process that outperforms traditional FKNN and other competitive classifiers. In the present study, we focus on further improving the performance of the local means-based FKNN method.

Our research aims to design and develop a local means-based FKNN classifier that effectively addresses the noise and uncertainty in the data, thereby yielding improved performance. To achieve this goal, we employ a feature weighting process based on fuzzy entropy (De Luca and Termini 1971), similarity measures (Luukka 2011), and feature selection concepts, such as relevance and complementarity (Ma and Ju 2022; Vergara and Estevez 2014; Yu and Liu 2004), to assess feature importance. We also used Minkowski distance to calculate distance between instances and employed class representative local mean vectors from class subsets instead of individual nearest neighbors to find class memberships.

In the context of feature selection, the theoretical concepts of relevance and complementarity have been widely employed as effective methods to identify optimal feature subsets (Ma and Ju 2022). Feature relevance recognizes the features that carry out valuable information regarding the target variable (Vergara and Estevez 2014). By contrast, feature complementarity highlights that combining two or more features, even those that may be individually insufficient, can collectively provide meaningful information about the class variable (Ma and Ju 2022; Vergara and Estevez 2014). Thus, we focus on these theoretic feature selection measures to generate weights for features across the importance of each feature by estimating relevance and complementarity information. This enables us to obtain better weights for features, which can then be utilized, in conjunction with distance calculation to identify more suitable nearest neighbors for the new instance. Furthermore, entropy is used to measure the level of uncertainty in the values of a feature (Luukka 2011; Vergara and Estevez 2014). This can be useful in cases where the data are uncertain or noisy, as it can help identify features that are more informative or relevant for classification. Therefore, we specifically focus on fuzzy entropy and similarity-based relevance and complementarity weighting methods to improve the accuracy of the proposed classifier.

The Minkowski distance, a generalized distance measure, is characterized by a specific parameter (called order parameter), making it more flexible and adaptable to various types of data distributions and feature spaces. Therefore, by using the Minkowski distance with an appropriate order parameter, can achieve better performance for nearest neighbor search in such data sets, as it can handle different types of data distributions more effectively. Accordingly, the Minkowski distance is employed in combination with fuzzy entropy and class prototypes to develop and propose the feature-weighted Minkowski distance-based local mean fuzzy k-nearest neighbor (FWM-LMFKNN) method.

The flowchart in Fig. 1 outlines the steps of the proposed FWM-LMFKNN method. The process consists of two main phases. The first phase generates feature weights by combining the effects of feature relevance and complementarity. The second phase performs the classification, which includes the following steps: calculating the Minkowski distance between training instances ($X_i$) and the query sample (y), finding the k nearest neighbors for each class (j), calculating the class representative local mean ($V_j$), determining the distance between local means and the query sample, computing class memberships, and finally classifying the query sample.

Fig. 1

Flowchart of the proposed method

The main contributions of this paper can be summarized as follows:

• Feature weights that are generated using a combined effect of feature relevance and complementarity are used to weight the distances between testing and training instances in the learning process of the FKNN algorithm.

• Minkowski distance is adopted for distance calculation to identify the most reasonable nearest neighbors, thereby achieving better class representative local mean vectors (i.e., class prototypes).

• The decision rule on classification is made by considering the membership values, which are calculated using weighted Minkowski distances between the new instance and class representative local mean vectors.

The effectiveness of the proposed FWM-LMFKNN classifier is examined using various real-life data sets in both low- and high-dimensional spaces, covering binary- and multi-class problems. In the empirical analysis, the proposed method is compared with classical KNN (Cover and Hart 1967) and FKNN (Keller et al. 1985) methods and six more competitive methods, including LM-FKNN (Kumbure et al. 2019), LM-PNN (Gou et al. 2014), MLM-KHNN (Pan et al. 2017), FPFS-kNN (Memis et al. 2022), generalized mean distance-based KNN (GMD-KNN) (Gou et al. 2019), and interval-valued k-nearest neighbor (IV-KNN) (Derrac et al. 2015).

2 Preliminaries

This section briefly discusses the related KNN methods, fuzzy entropy, similarity measure, (relevance- and complementarity-based) feature weighting strategy, and the Minkowski distance.

2.1 Related KNN methods

The KNN algorithm (Cover and Hart 1967) is simple and effective, and it is based on the idea that an unseen data instance can be classified by looking at its closest “neighbors" from the training data set. It starts by calculating the distance between the unknown instance and all the instances in the training set. The distance can be computed using various distance metrics, but the Euclidean distance is the most commonly used (Derrac et al. 2015). Once the distances are calculated, the k nearest neighbors are selected based on their nearness to the unknown data instance. Then, the class labels of the k nearest neighbors are counted, and the class with the majority number of votes is assigned to the unknown instance.

By contrast, the FKNN method (Keller et al. 1985) uses fuzzy set theory (Zadeh 1965) to assign class membership degrees to each data instance instead of crisp labels. The basic idea of the FKNN is to assign a membership degree to the unknown instance in each class based on the degree of similarity to its k nearest neighbors and their memberships to each class. The membership degree of the unknown instance (y) in each class (j) represented by its k nearest neighbors is calculated as follows:

$$\begin{aligned} u_j(y)=\frac{\sum _{i=1}^k u_{ij}(1/\left\| y-x_i\right\| ^{2/(m-1)})}{\sum _{i=1}^{k}(1/\left\| y-x_i\right\| ^{2/(m-1)})} \end{aligned}$$

(1)

where $x_i$ is the ith neighboring instance in the training set, and $u_{ij}$ is the membership degree of ith neighboring instance in the jth class. $m>1$ is the fuzzy strength parameter. There are two approaches to calculating $u_{ij}$: the crisp membership method and fuzzy membership method—detailed information about these methods can be found in Keller et al. (1985).

As previously noted, the KNN and FKNN methods are both affected by the value of parameter k (Yang and Sinaga 2021), and are particularly susceptible to the effects of outliers. To deal with these issues, particularly to the KNN classifier, the idea of class representative local mean (LM) vectors was first introduced by Mitania and Hamamotob (2006). The resulting LM-KNN classifier (Mitania and Hamamotob 2006) computes a local mean vector of nearest neighbors from each class. The unknown instance is then assigned to the class represented by the local mean vector that is closest to it. The effectiveness of this method has led to the development of several variants that aim to improve performance by addressing not only the impact of outliers but also the sensitivity to the neighborhood size k. The local mean-based pseudo k-nearest neighbor (LM-PNN) (Gou et al. 2014) and multi-local means-based k-harmonic nearest neighbor (MLM-KHNN) (Pan et al. 2017) classifiers are examples of variants that have demonstrated improved classification performance. Based on the concept of class prototypes, recent enhancements to the classical FKNN method have been proposed, such as the multi-local power means fuzzy k-nearest neighbor (MLPM-FKNN) (Kumbure et al. 2019) and Bonferroni mean-based fuzzy k-nearest neighbor (BM-FKNN) (Kumbure et al. 2020) methods. These methods have been successful in achieving appropriate local class prototypes by incorporating various mean operators, such as generalized and Bonferroni means.

In this paper, our objective is to enhance the performance of the local means-based FKNN method by incorporating the Minkowski distance measure, class prototypes, and a feature weighting scheme.

2.2 Minkowski distance

Minkowski distance is a generalization of the Euclidean distance and Manhattan distance. It is a measure of the distance between two points in a metric space, which is defined by a norm. The Minkowski distance between two instances $x_i$ and $x_r$ in d-feature space is defined as:

$$\begin{aligned} d_{mink\_dis}(x_i, x_r) = \left( \sum _{l=1}^{d}\vert x_i^l- x_{r}^l\vert ^p\right) ^{1/p} \text { for}\, p\ge 1 \end{aligned}$$

(2)

where the parameter p is called the order of the Minkowski distance. By using different values for p, we can define several different distances; for example, when $p = 2$, the Minkowski distance is equivalent to the Euclidean distance, which is the most commonly used distance measure for continuous features. Further, we can obtain the Manhattan distance by setting $p = 1$ and harmonic distance with $p = -1$ as examples. Due to this special property of Minkowski distance, it has been used in many applications, such as Bergamasco and Nunes (2019) and Gueorguieva et al. (2017). Additionally, the weighted Minkowski distances can be defined with feature weights $w^{l}$ for $l=1,\dots ,d$ according to:

$$\begin{aligned} d^w_{mink\_dis}(x_i, x_r) = \left( \sum _{l=1}^{d}w^{l}\vert x_i^l- x_{r}^l\vert ^p\right) ^{1/p} \text { for}\, p\ge 1 \end{aligned}$$

(3)

2.3 Fuzzy entropy

Entropy (H) is a concept used in information theory to measure the uncertainty or randomness of a system or feature (Vergara and Estevez 2014). Entropy, usually discussed in a probability space (De Luca and Termini 1971), measures the amount of information required to describe the outcome of a random feature. The higher the entropy, the more uncertain or unpredictable the feature is. Fuzzy entropy, first defined by De Luca and Termini (1971), is an expanded version of classical entropy in the fuzzy sets theory. It is a measure that quantifies the degree of fuzziness of a fuzzy set (Al-sharhan et al. 2001). It is defined based on the concept of Shannon entropy (Shannon 1948), which is a measure of randomness in a probability distribution. However, fuzzy entropy differs from Shannon entropy, as it deals with vagueness and ambiguity uncertainties rather than probabilistic concepts (Al-sharhan et al. 2001). According to De Luca and Termini (1971) and Luukka (2011), the fuzzy entropy (h) can be defined for a given fuzzy set A defined over a universe U as:

$$\begin{aligned} h(A) = -\sum _{i=1}^{n} (\mu _A(x_i) log \, \mu _A + (1-\mu _A(x_i))log(1-\mu _A(x_i))) \end{aligned}$$

(4)

where, $\mu _A(x_i)$ represents the membership degree of an element $x_i$ in the set A. The fuzzy entropy has been used to find feature importance concerning the target variable in the feature selection process (Luukka 2011; Lohrmann et al. 2018). It has also been applied for classification problems, especially to improve the KNN performance; for example, see Morente-Molinera et al. (2017).

2.4 Similarity measure

In feature selection, a similarity measure quantifies the degree of closeness or correlation between two features. It helps assess how similar or related two features are to each other. Łukasiewicz similarity (Łukasiewics 1970) is a specific similarity measure based on the Łukasiewicz t-norm, which is a triangular norm used in fuzzy set theory (Zadeh 1965). For our study, the Łukasiewicz similarity is utilized together with fuzzy entropy to find feature relevance, and it can defined according to Luukka et al. (2001) as follows:

$$\begin{aligned} S \langle x, y\rangle =({1-|x^p-y^p|})^{1/p} \end{aligned}$$

(5)

where $x, y \in [0,1]$¹ and $x, y \in {\mathbb {R}}^d$. This is chosen because it satisfies monotonicity, symmetricity, and transitivity properties (Luukka et al. 2001).

2.5 Mutual information

Mutual information is a well-known method for measuring the amount of information one random feature provides compared to another feature (Vergara and Estevez 2014). This notion has been dominant and valuable in the context of feature selection, where mutual information is measured for each feature concerning the target variable. Features with higher mutual information are considered more relevant, as they contribute more information to predicting or classifying the target variable. In Meyer et al. (2008) and Vergara and Estevez (2014), for given X and Y two random features, mutual information (I) is defined as follows:

$$\begin{aligned} I(X;Y) = {\left\{ \begin{array}{ll} H(X) - H(X \backslash Y) \\ H(Y) - H(Y \backslash X) \\ H(X) + H(Y) - H(X,Y) \end{array}\right. } \end{aligned}$$

(6)

where H(X) and H(Y) represent the entropy of features X and Y, respectively. H(X, Y) denotes the joint entropy of X and Y, while $H(X \backslash Y)$ indicates the conditional entropy of X given Y. $H(Y \backslash X)$ is the conditional entropy of Y given X. I(X; Y) measures the degree of correlation between features X and Y or the amount of information X covers about Y.

2.6 Feature relevance and complementarity

This subsection briefly discusses the concepts of relevance and complementarity in the context of feature selection. Before briefly describing these concepts, we first introduce some basic notations and terminologies in Table 1.

Table 1 Basic notations and their meaning

The sets mentioned in Table 1 are related as follows: $X=f_i \cup A \cup \lnot \{f_i,A\}$, $\emptyset =f_i \cap A \cap \lnot \{f_i,A\}$.

2.6.1 Relevance

A feature is considered relevant if individually or together with other features it provides information about class variable C. There are many definitions of “relevance” in the literature, but roughly, they can be divided into probabilistic framework (Kohavi and John 1997) and mutual information framework (Meyer et al. 2008). The probabilistic framework defines three levels of relevance: strongly relevant, weakly relevant, and irrelevant features. Strongly relevant features give unique information about C and cannot be replaced by other features. Weakly relevant features also provide information about C, but other features can replace them without losing information about C. Irrelevant features do not give information on C, and they can be removed without losing any vital information. Similarly, a mutual information framework is defined into these three categories as given in Eq. (6).

2.6.2 Complementarity

The notion of complementarity (also called information synergy) signifies that the working of two features together could carry more information than the sum of their individual values to the target variable (Singha and Shenoy 2018). It is used to measure the degree of interaction between an individual feature $f_i$ and feature subset A given C (Vergara and Estevez 2014). This can be again measured, for example, by using mutual information [$I(f_i;A|C)$]. One way to understand the complementarity effect is the following: when information that A has about C is greater when it interacts with feature $f_i$ compared to when it does not interact, then complementarity information is present.

Feature selection is a critical step in preparing data for machine learning models. Most feature selection approaches are usually based on notions of relevance, redundancy, and complementarity (Sun et al. 2017; Singha and Shenoy 2018). Redundancy occurs when multiple features provide the same or similar information about the class variable (Singha and Shenoy 2018). Redundant features are often highly correlated with each other and do not offer new or additional information to the model. Therefore, in a typical feature selection task. redundant features are identified and removed. However, to create the feature weighting criterion in the proposed method, we focus solely on relevance and complementarity concepts and do not consider the redundancy measure. This is because this approach avoids the calculation of pairwise correlations and interdependencies between features, reducing computational time. Especially in cases where the number of features is very large, redundancy checks can be more computationally expensive. Moreover, in some sense, complementarity is closely related to redundancy (Sun et al. 2017), and it is also known that complementarity approach is efficient that redundancy approach (Singha and Shenoy 2018). For these reasons, relevance and complementarity are considered in our study to have an efficient and effective feature weighting strategy. In general, relevant and complementary features maximize the mutual information with the class variable, ensuring that the feature informativeness is observed reasonably well (Singha and Shenoy 2018).

3 The proposed FWM-LMFKNN classifier

This section introduces the feature-weighted Minkowski distance-based local mean fuzzy k-nearest neighbor (FWM-LMFKNN) method, which is based on the concepts of feature weighting, Minkowski distance, and class representative local mean vectors. The feature weighting employs fuzzy entropy and similarity measures, incorporating relevance and complementarity notions. We begin by defining the calculation of feature relevance and complementarity and, subsequently, the weighting strategy for the new classifier.

3.1 Feature weighting based on relevance and complementarity

The calculation of relevance is based on fuzzy entropy and similarity measures. Suppose a training data set $\{X_i \in {\mathbb {R}}^d, \omega _i\}_{i=1}^n$ consisting n number of instances in d-dimensional feature space [i.e., $X_i = (x_i^1, x_i^2,\ldots , x_i^d)$] and t different classes [i.e., $\omega \in (C= (c_1, c_2, \ldots , c_t)$)]. Given these, relevance of features to class variable is calculated using the following steps:

• (1) Normalize feature data into unit interval, that is, $X_i \rightarrow [0,1]^d$

• (2) Obtain ideal vectors²$v_j \in {\mathbb {R}}^d$ for each class j from the training set data using arithmetic mean.

  $$\begin{aligned} v_{j} = \left( \frac{1}{n_j} \sum _{i=1}^{n_j} X_{i}\right) , \quad j=1,\ldots ,t \end{aligned}$$

  (7)

  where $n_j$ denotes the number of instances belonging to class j, that is, the mean calculation is restricted to only those samples that belong to class j. $X_i$ is an instance belonging to jth class.

• (3) Compute similarity measure S from each training instance $X_i = (x_i^1, x_i^2,\ldots , x_i^d)$ to corresponding ideal vector $v_j = (v_j^1, v_j^2,\ldots , v_j^d)$ as follows:

  $$\begin{aligned} S \langle x_i, v_j\rangle = \frac{1}{d} \sum _{l=1}^{d}(1-\vert (x_i^l)^p - (v_j^l)^p\vert \big )^{1/p} \end{aligned}$$

  (8)

  for $x_i, v_j \in [0, 1]^d$. For the sake of simplicity, we use $p=1$ in the proposed method. Notice that the matrix $[S]_{n \times d \times t}$ needs to be reshaped by reducing the dimensions as $n \times t$ and d.

• (4) Compute relevance (denoted by $f^{REL}$) by measuring fuzzy entropy (h) for each feature $l \in [1, d]$ using the similarity values ($S \langle x_i, v_j\rangle$) from the previous step and Eq. (4) as:

  $$\begin{aligned} f^{REL} = h(l) = -\sum _{i=1}^{n} (S^l log \, S^l + (1-S^l)log(1-S^l)) \end{aligned}$$

  (9)

  where $S^l$ is the similarity for feature l of a sample $X_i$ with ideal vector $v_j$ of class j is summed over all samples ($i=1, \ldots ,n$) and classes ($j=1,\ldots ,t$).

The calculation of complementarity ($f^{COMP}$) is performed for $l=1,\dots ,d$ using following steps:

• (1) Compute intersection between lth feature and all the other features by using algebraic product, that is,

  $$\begin{aligned} x^{l}_{i} \cap x^{l^{'}}_{i}=x^{l}_{i} x^{l^{'}}_{i} \end{aligned}$$

  (10)

  where $l^{'}=1,\dots ,d$ and this way, the intersection matrix $T_1$ is formed.

• (2) Add class variable C to the intersection matrix as $T_2=\{T_1,C\}$.

• (3) Compute correlation³ between features, $Corr(T_2)$.

• (4) Subtract identity matrix I from the correlation matrix and take absolute values from it, that is, $T_3=|Corr(T_2)-I|$.

• (5) Find the maximum correlation, $H_c=\max (T_3)$

• (6) Compute complementarity value ($f^{COMP}$) using the negation of correlation, such as $f^{COMP}=1-H_{c}$, and collect the complementarity information in the matrix.

In the proposed method, we generate feature weights focusing on an aggregate effect of relevance and complementarity in the learning process. Both relevance and complementarity have positive influence on feature weights, in fact, their combined effect could offer a best trade-off considering model’s performance and flexibility with small data sets (Singha and Shenoy 2018). Moreover, combining relevance with complementarity may identify individually relevant features to the class variable and provide unique information when considered simultaneously. This strategy can weigh features by considering different characteristics of the class distribution and features. This ensures the identification of more suitable nearest neighbors to the query instance based on distance, ultimately enhancing the classification performance of the method.

3.2 The FWM-LMFKNN algorithm

Based on the fundamental concepts of the previously discussed classifiers, the feature weighting strategy, Minkowski distance, and local means, we propose an extension of the FKNN method: the FWM-LMFKNN classifier.

The proposed classification method utilizes a two-phase approach: it calculates weights for each feature, and then it employs nearest neighbor classification to an unknown instance. In the first phase, a strategy incorporating the concepts based on relevance and complementarity is utilized to calculate the feature weights. The second phase involves finding sets of k nearest neighbors for an unknown instance (y) from each class based on the feature-weighted Minkowski distances between y and each training instance, followed by calculating local mean vectors for each set of k nearest neighbors. Next, the Minkowski distance between y and each local mean vector is calculated (feature weights are also applied), and fuzzy memberships for each class concerning y are computed. Finally, y is classified into the class with the highest membership degree. A formal definition of the proposed FWM-LMFKNN algorithm can be defined as follows. Suppose that we have a training data set $\{x_i, \omega _i\}_{i=1}^n$ that is composed of n number of instances in d-dimensional feature space [i.e., $x_i = (x_i^1, x_i^2,\ldots , x_i^d)$] and t different classes [i.e., $\omega \in (c = (c_1, c_2,\ldots , c_t)$)]. In the FWM-LMFKNN method, the class label $\omega ^*$ for a given unknown instance [$y = (y^1, y^2,\ldots , y^d)$] is achieved as described below.

Phase 1:

Calculate of relevance and complementarity measures using the notions presented in Sect. 3.1 and consider a combined effect of those measures by summing them (i.e., $f^{REL}+f^{COMP}$). It is well-known that higher entropy values correspond to lower similarity and increased uncertainty in the corresponding feature, while lower entropy values indicate greater similarity and increased importance. This is reflected in the relevance value, which is based on fuzzy entropy and similarity. Therefore, the complementary values of relevance are employed as feature weights (w). This principle holds for complementarity as well. Accordingly, for a given feature l, the weight ($w^{l}$) can be defined as:

$$\begin{aligned} w^{l} = 1- \frac{(f^{REL}+f^{COMP})}{\sum _{l=1}^{d}(f^{REL}+f^{COMP})} \end{aligned}$$

(11)

Phase 2:

• (1) Compute the Minkowski distance, $d_{mink\_dis}(y, x_j)$ between y and each training instance $x_i$ according to:

  $$\begin{aligned} d_{mink\_dis}(y, x_i) = \left( \sum _{l=1}^{d} w^{l} \vert y^{l}- x^{l}_i\vert ^p\right) ^{1/p}. \end{aligned}$$

  (12)

  As shown in this computation, a feature weight $w^{l}$, which is computed in the previous phase, is allocated to distance, which allows instances that are closer to y to be given a higher weight (lower distance), while instances that are farther away are given a lower weight (higher distance). This can help to mitigate the effects of noise and outliers in the training data.

• (2) Find the set of k nearest neighbors, $\{x^{nn}_{ij}\}_{i=1}^k$ of y from each class j based on the ordered distances computed in the previous step. Here, nn stands for “nearest neighbor.”

• (3) Compute a local mean vector (z) using the set of k nearest neighbors in each class j according to:

  $$\begin{aligned} z_{j}= \frac{1}{k}\sum _{i=1}^{k}x^{nn}_{ij} \end{aligned}$$

  (13)

• (4) Compute the Minkowski distances between y and each local mean vector as:

  $$\begin{aligned} d_{mink\_dis}(y, z_{j}) = \left( \sum _{l=1}^{d} w^{l} \vert y^{l}- z^{l}_j\vert ^p\right) ^{1/p} \end{aligned}$$

  (14)

• (5) Compute fuzzy membership ($u_j$) to class j concerning y using the distances $d_{mink\_dis}(y, z_{j})$ for $j=1,2,\ldots ,t$ according to:

  $$\begin{aligned} u_j(y)=\frac{\sum _{j=1}^t u_{jj}(1/d_{mink\_dis}(y, z_{j})^{2/(\gamma -1)})}{\sum _{j=1}^{t}(1/d_{mink\_dis}(y, z_{j}))^{2/(\gamma -1)})} \end{aligned}$$

  (15)

  where $u_{jj}$ is 1 for the known class and 0 is for the other classes. Notice that here $u_{jj}$ has twice j, and it is because number of classes and the number of local mean vectors are the same.

• (6) Return the class $\omega ^*$ of y, which has the highest membership degree [i.e., $\omega ^* = \text {arg}\,\max _{\omega _i}\, u_i(y)$].

By incorporating a combination of relevance and complementarity into the feature weighting process, the FWM-LMFKNN method can effectively handle uncertainty and vagueness in the data, leading to more reasonable decision boundaries. Using the Minkowski distance metric also allows for more flexible and powerful distance computations, further improving the classifier’s performance. The steps of the proposed method discussed under Phase 1 and Phase 2 are summarized as Algorithm 1 and Algorithm 2.

Algorithm 1

FWM-LMFKNN (Phase 1:Feature weights generation)

Algorithm 2

FWM-LMFKNN (Phase 2: Classification)

To demonstrate the impact of using Minkowski distance in the proposed method, a simple experiment was conducted, as indicated by Karimi and Torabi (2022), by selecting the Vehicle data set from UCI repository (Dheeru and Taniskidou 2017). Three data instances, labeled $x_1, x_2$, and $x_3$, were selected from the data set. The Minkowski distances between $x_1$ and $x_2$ and between $x_2$ and $x_3$ were then calculated for varying values of p, as depicted in Fig. 2. The results, as shown in the figure, indicate that when p is less than 4, $x_3$ is closer to $x_2$ than $x_1$. Conversely, when p is greater than 4, $x_1$ is closer to $x_2$ than $x_3$. Accordingly, when $x_2$ is used as a test instance with $x_1$ and $x_3$ serving as training instances, the performance of FWM-LMFKNN classifier can be highly dependent on the value of the parameter p. This clearly indicates that using the Minkowski distance rather than the Euclidean distance in the proposed method allows it to find nearest neighbors in a more flexible way.

Fig. 2

Minkowski distance between $x_1$ and $x_2$, and $x_2$ and $x_3$ with respect to different values of p

Furthermore, incorporating class representative local mean vectors in the FWM-LMFKNN enhances the classifier’s robustness and effectively addresses challenges arising from data distribution, including class imbalance, feature noise, and the impact of outliers. Previous studies in Kumbure et al. (2019, 2020) have comprehensively examined and demonstrated the significance of utilizing class prototypes in the FKNN classifier. This strategy contributes to the classifier’s ability to handle complex data sets, providing a more reliable and accurate classification results.

3.3 Computational complexity analysis

In this subsection, we briefly discuss the computational complexities of the proposed FWM-LMFKNN method. Let us consider n, which indicates the number of training instances characterized by c classes in d-dimensional feature space, and query sample y (the sample to be classified). The KNN (Cover and Hart 1967) classifier consists of a calculation of the distances from y to all training instances to find k nearest neighbors and then observes the majority class among them. Therefore, according to Guo et al. (2014, 2019), the computational complexity of the KNN method is $O(nd+nk+k)$. The FKNN (Keller et al. 1985) algorithm extends the KNN method by adding an additional step for computing the membership of y considering each class based on the distances between y and k nearest neighbors. Therefore, its computational complexity is $O(nd+nk+ck+c)$. Compared to the FKNN, the LM-FKNN consists of an additional step of the local mean computation using the set of k nearest neighbors from each class, thus it requires the computation of $O(nd+nk+cdk+cd+c)$. According to Duarte et al. (2019), the computational complexity of the Minkowski distance between two points of dimension d is O(d). But when we have n data instances, it requires O(nd). Then the computational complexity of the LM-FKNN method combined with the Minkowski distance is $O(2nd+nk+cdk+cd+c)$. The computation of feature relevance includes the calculation of ideal vectors from each class, the similarity measure, and fuzzy entropy. Therefore, it requires a computational complexity of O(3ncd). The calculation of the feature complementarity contains the steps of forming an intersection matrix, computation of the correlation, and complementarity values. Therefore, its computational complexity is $O(nd^2+n+n) \approx O(nd^2)$. The proposed FWM-LMFKNN combined those steps; therefore, its computational complexity is $O(2nd+nk+cdk+cd+c+3ncd+ nd^2)$, and when the constant terms are ignored and $n>>k, c, d$, it is $\approx O(nd+ncd+nk+ nd^2)$.

Based on the above analysis, it is evident that the FWM-LMFKNN method requires more computation time, particularly compared to the classical KNN, FKNN, and LM-FKNN methods. The primary reason for this is the additional computation involved in generating feature weights using relevance and complementarity, as well as the use of the Minkowski distance measure.

4 Experiment

To evaluate the performance of the proposed classifier, a series of experiments were conducted using real-world data sets and comparing the results to well-established baseline models. The following sub-sections describe the data sets used, the models compared, the evaluation metrics, and the experimental procedure.

4.1 Data sets

We used 20 real-world data sets to evaluate the performance of the proposed approach. These data sets are freely available at the UCI (Dheeru and Taniskidou 2017) and KEEL (Alcala-Fdez et al. 2011) machine learning repositories. Table 2 provides a summary of the main characteristics of the data sets, including the number of instances, features, classes, and corresponding data repository. The data sets ranged in size from 106 to 5500 instances and encompass binary and multi-class problems.

Table 2 The used data sets from UCI and KEEL repositories

4.2 Testing methodology

This study employed a thirty-fold holdout validation procedure across all experiments with the data. In each run, utilizing the stratified random sampling technique, the data set was randomly divided into training and testing sets, while $30\%$ of instances were allocated to the test set. The average classification accuracies with a $95\%$ level of confidence of 30 splits of each data set were reported as the final results. This experimental setup was adopted based on the indications by Gou et al. (2014, 2019) and Pan et al. (2017). As classification accuracy alone may not be sufficient in evaluating the performance of a classifier, additional measures such as sensitivity and specificity are often necessary to provide a more comprehensive evaluation (Kumbure et al. 2019, 2020). For this reason, in addition to the accuracy, we calculated sensitivity and specificity values in our analysis, as they are commonly used measures in this context.

To provide a comprehensive comparison, several well-established models were chosen as baselines for the proposed classifier. The models included classical KNN (Cover and Hart 1967), FKNN (Keller et al. 1985), and six other competitive classifiers: MLM-KHNN (Pan et al. 2017), LM-PNN (Gou et al. 2014), LM-FKNN (Kumbure et al. 2019), FPFS-kNN (Memis et al. 2022), GMD-KNN (Gou et al. 2019) and IV-KNN (Derrac et al. 2015). The number of nearest neighbors (k) and the Minkowski distance parameter (p) were systematically varied during the validation process to optimize the performance of the proposed method and baseline models (i.e., grid search was performed). Specifically, the range of k was set from 1 to 20, and the set of p values considered were $\{1,1.5,\ldots ,4\}$ for all the data sets. In fuzzy KNN-based methods, the fuzzy strength parameter (m) was fixed at a value of 2 for all FKNN classifiers throughout the experiments, as suggested by Derrac et al. (2015). Lastly, statistical tests, including Friedman and Bonferrni-Dunn tests, were applied to evaluate the statistical significance of the performance improvement of the proposed method compared to benchmark methods.

5 Results

This section presents the experimental results of the proposed method’s performance against selected real-world data sets compared to the related baseline models. Optimal parameter values are also presented and discussed. Finally, a statistical analysis demonstrates that the proposed method achieved statistically significantly higher performance than the benchmark methods.

5.1 Evaluation of the proposed method

Table 3 presents a comprehensive comparison of the classification accuracy results and corresponding standard deviations of the proposed FWM-LMFKNN classifier and seven other baseline models, across 20 data sets. Note that the highest classification performance among the competing methods is highlighted in bold for each data set.

Table 3 The accuracy (%) results of each classifier, along with the corresponding standard deviations (in brackets), in all tested data sets

The table results show that the proposed FWM-LMFKNN method outperformed all other classifiers in terms of accuracy in 15 data sets (achieving the highest average accuracy of $82.50\%$). The table also shows the second-best performance in four data sets (Balance and Texture). Additionally, the proposed method had the lowest average standard deviation (of $2.57\%$) among all the classifiers, indicating that its performance was more consistent across the different data sets. This suggests that the proposed method was not only more accurate but also more robust than the other classifiers evaluated. In addition, corresponding sensitivity and specificity values (see Table 4 and Table 5) were reasonable and supported indications given by accuracy results. Besides, the performance of the LM-FKNN classifier appeared to be the second best (gaining average accuracy of $81.24\%$), indicating the effectiveness of using class representative local means in the FKNN classifier, as indicated by related classifiers presented by Kumbure et al. (2019, 2020).

Considering the optimal parameter values (see Table 4), the proposed method achieved the highest performance with a 1–3.5 range for the Minkowski distance parameter across all data sets. Among them, the Manhattan distance ($p=1$) appeared to have worked reasonably well in most cases, which is in line with the previous study by Kumbure and Luukka (2022). Regarding the parameter k, classification performance significantly improved with higher k values in the proposed method as well as the local means-based KNN methods. This finding aligns with previous research (Gou et al. 2014; Pan et al. 2017), demonstrating that multi-local mean vectors with nearest neighbors represented each class more accurately. This outcome is expected, as more data instances make local mean vectors more representative.

Table 4 The sensitivity (%) results of each classifier with optimal k and p values in all tested data sets

Table 5 The specificity (%) results of each classifier in all tested data sets

To further illustrate the performance of the proposed method in comparison to the baseline models, the accuracy results of all classifiers with varying values of parameter k on four selected cases, Appendicitis, Bupa, Cleveland, and Retinopathy data sets are presented in Fig. 3. As clearly shown in these sample cases, the proposed method generally outperformed the benchmark methods across a range of k values, particularly at high values of k.

Fig. 3

The accuracy of each method with respect to parameter k in the Appendicitis (a), Bupa (b), Cleveland (c), and Retinopathy (d)) data sets

Furthermore, the classification performances of each method are depicted in box plots in Fig. 4, where each box represents the distribution of accuracy values over 30 runs during the validation on the Cleveland, Ionosphere, Spambase, and Vehicle data sets. A box plot analysis was conducted for the selected cases to understand the variability of each method’s performance across the cross-validation. As shown in the box plots, the proposed FWM-LMFKNN method had the highest median accuracy among all the classifiers, with a minimal interquartile range (IQR) across all cases considered, indicating that the accuracy values are relatively consistent across all runs.

Fig. 4

Box-plot distributions of accuracy by each classifier in the Cleveland (a), Ionosphere (b), Spambase (c), and Vehicle (d) data sets

5.2 Statistical analysis for benchmark comparison

To evaluate the significance of this improvement, we performed the Friedman test (Friedman 1937) and subsequently conducted the Bonferroni-Dunn test (Dunn 1961), following the methodology presented by Demšar (2006). In the Friedman test, classifiers were ranked individually for each data set—the top-performing classifier received a rank of 1, followed by the second-best with a rank of 2, and so forth, as detailed in Table 6. Subsequently, we calculated the Friedman statistic using the following formula:

$$\begin{aligned} \chi ^2 = \frac{12N}{c_n(c_n+1)}\left[ \sum _{j=1} R_j^2 - \frac{c_n(c_n+1)^2}{4}\right] \end{aligned}$$

(16)

In the formula, $R_j=\frac{1}{n}\sum _{i=1}r_i^j$, where $r_i^j$ represents the rank of the jth classifier on the ith data set, and there are $c_n$ classifiers and N data sets. In line with this, we computed $\chi ^2=42.9$ based on the averaged ranks presented in Table 6 (here, $c_n=9$ and $N=20$), resulting in a corresponding p-value of $9.17 \times 10^{-7}$. This result offers sufficient evidence to reject the null hypothesis that all classifiers perform equally. In other words, this result supports the conclusion that the chosen classifiers exhibited statistically significant differences in mean accuracies at a significance level of 0.05. Since the null hypothesis was rejected, a post-hoc test can be applied now.

Table 6 Ranking of each classifier according to its performance on each data set for the Friedman test

Accordingly, we conducted the Bonferroni-Dunn test to compare the performance of the proposed FWM-MLFKNN classifier with each other method, as indicated by Demšar (2006). In this test, the performances of two classifiers are considered significantly different if the corresponding average rank difference is greater than or equal to the critical difference (CD), which is defined as:

$$\begin{aligned} CD = q_\alpha \sqrt{\frac{c_n(c_n+1)}{6N}} \end{aligned}$$

(17)

where $q_\alpha$ represents the critical value from the two-tailed Bonferroni-Dunn test. After we applied the test to our analysis, we observed $CD=2.401$ ($q_{0.05}=2.72$, $c_n=9$, and $N=20$). By comparing this statistic with the difference in average rank between the FWM-LMFKNN method and each baseline method, we found that the proposed method demonstrated statistically significantly higher performance in terms of mean accuracy compared to all other methods. Table 7 presents the test results, where “Yes" denotes a significant difference between the mean accuracy of the proposed FWM-LMFKNN method and each benchmark classifier.

Table 7 The results of the Bonferroni-Dunn test on the mean accuracy of the FWM-LMFKNN classifier against six baseline models

5.3 Ablation studies

In machine learning research, an ablation study is used to determine the significance of various components or aspects of a model and to evaluate their impact on overall performance (Meyes et al. 2019; Kwon and Lee 2024). Accordingly, we conducted ablation studies on the main components of our proposed method—namely feature weights (based on relevance and complementarity) and Minkowski distance—to demonstrate their effectiveness on classification performance. For the ablation studies, the performance of the original method, ML-FKNN (Kumbure et al. 2019), was compared with its variants: one using feature weights based on the feature relevance and complementarity and another utilizing a Minkowski distance metric-based similarity calculation. These methods were also compared with the proposed method (FWM-LMFKNN), which combines both feature weighting and the Minkowski distance. Models’ performances were compared using the experimental setup described in Sect. 4. The best average accuracy values (along with their standard deviations) across all data sets are presented in Table 8.

Table 8 The accuracy (%) results of each case with corresponding standard deviations (in brackets) in all tested data sets in the ablation study

The results in Table 8 indicate that LM-FKNN with feature weights slightly improved performance compared to the original method, with an increase in average accuracy from 81.54 to 81.69%. By contrast, LM-FKNN with Minkowski distance considerably improved performance, with an increase from 81.54 to 82.45%. This improvement may be due to the parameterized Minkowski distance allowing the classifier to adopt the most suitable distance metric for the data, thus achieving a more accurate set of nearest neighbors. However, the proposed FWM-LMFKNN method, which combines both feature weighting and the Minkowski distance measure, achieved the best overall results, with the highest average accuracy of 82.52%. Although the overall performance difference between the proposed method and LM-FKNN with Minkowski distance was not large, FWM-LMFKNN performed the best on many data sets, highlighting the positive impact of feature weighting. The standard deviation results of the proposed method were also low and reasonable, further supporting its robustness.

6 Conclusion

In this paper, we proposed a new fuzzy k-nearest neighbor method called FWM-LMFKNN based on feature weighting, Minkowski distance, and class representative local mean vectors. To determine the optimal feature weights in the proposed approach, we explicitly developed a feature weighting scheme considering a combined effect of relevance and complementarity. The proposed method was evaluated using a variety of real-world data sets, and the results show that it outperformed the baseline models in terms of used evaluation metrics. The use of feature weights and Minkowski distance allows for a more accurate calculation of the distances between new instance and training instances based on their nearness, which improves the accuracy of the proposed FWM-LMFKNN method. The ablation study conducted demonstrated the effectiveness of these aspects of the FMW-LMFKNN. Additionally, the proposed method takes into account the local structure of class subsets by using local mean vectors, further improving the performance of the classification. The results of this study demonstrate that the proposed method is a powerful tool for classification tasks and can be applied to a wide range of data sets.

Future work includes further testing of various data sets, evaluating the reliability of the proposed method, and investigating the possibility of incorporating other mean operators, such as generalized mean, in the local mean and ideal vector computation.