Introduction

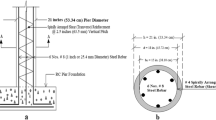
Damaged or under-strength concrete bridge repair and strengthening is an important issue, especially with the current poor state of the bridge infrastructure [4]. The deficiency could be due to fire, poor design or construction, time-dependent deterioration, corrosion or impact of vehicles. One of the most common problems is the impact caused by over-height vehicles that exceed the posted clearance for a bridge. The Lyndon B. Johnson (LBJ) Express construction project in the greater Dallas, Texas, area experienced such a vehicle impact event. The LBJ Freeway is a 59.5 km loop traversing from I-20 in the south of the city to SH 121 to the north. In 2011, a remodeling of 21 km length of the LBJ Freeway between I-35 and US-75 was initiated with a large number of bridges and overpasses. One of the most important factors in the tight project schedule was traffic control. Keeping the traffic flowing to a maximum level caused the coexistence of new traffic routes with old or temporary routes. Bridge 54 on Preston Road was impact damaged during one of these overlapping phases. The overpass had been completed, while the old route was open below, causing a temporary vertical lower clearance than the final design leading to the impact and damage. The bridge has three spans in the north–south direction with different number of girders. The damaged girder was situated on the western edge on the middle span in the southbound direction, as shown in Fig. 1. The southbound structure included 23 standard Tx46 prestressed I-girders [28] in the north span, nine Tx46 girders in the middle span and 11 Tx28 girders in the south span. The middle span had a total width of 29.11 m, with a precast composite deck of 203 mm thickness. The spacing between the girders was 3.5 m, with two overhangs having widths of 1.07 and 0.69 m. Table 1 shows some pertinent properties of the Tx46 girder.

Fig. 1
figure 1

Location of damaged girder on the middle southbound span of bridge 54

Full size image
Table 1 Tx46 girder section properties
Full size table

The damaged girder had 42 low-lax prestressing strands (with 12.7 mm diameter each and 1861 MPa ultimate strength) placed according to the patterns shown in Fig. 2, with no debonding and four harped strands. The corresponding eccentricities were 396 mm at mid-span and 309 mm at the end. The girder concrete compressive strength in service was 58.6 MPa. The non-prestressed mild steel had a yield strength of 414 MPa.

Fig. 2
figure 2

Prestresing strand patterns. a Mid-span, b end

Full size image

The vehicle impact resulted in severe damage on the girder (Fig. 3), causing a 4.3 m long damage along the bottom flange with spalled concrete and three rows of exposed but undamaged strands (total of nine strands exposed). The center of the damaged area was at 6.7 m from the left support. A sketch of the damaged section is presented in Fig. 4.

Fig. 3
figure 3

Damaged girder photograph

Full size image
Fig. 4
figure 4

Schematic of damaged section

Full size image

The study described herein theoretically modeled the full-scale damaged girder before and after repair to analyze its structural behavior through comparison with actual load testing information. The objectives of this study were to provide a better understanding of the structural behavior and propose adequate modeling techniques of beams repaired with GFRP rebars. The proposed techniques will help to establish adequate repair procedures and to anticipate the structural behavior of damaged girders prior to the repair process.

Most prior investigations on bridge strengthening involved only the Carbon Fiber Reinforced Polymer (CFRP) systems. However, investigation on the use of GFRP systems has increased in recent years, mainly on the use of GFRP rebars for bridge decks and the durability aspects. Most of the past studies involved scale models in laboratories.

Nanni et al. [21] mentioned that carbon fibers have three times higher strength than glass fibers and are ten times more expensive. Glass fibers, however, have good thermal and electrical insulation properties. Hutchinson [13] found that externally bonded CFRP sheets were effective in improving the shear strength of prestressed concrete I-girders. Recommendations and guidance for using CFRP sheets were included. Pantelides et al. [23] provided guidelines for repair of bridge girders using FRP wrapping. The girders considered were reinforced or prestressed with shear and flexural deficiencies from end cracking or vehicular collision. Hasenkamp et al. [11] established criteria for repair materials and methods for prestressed concrete girders with end zone cracking caused by prestress release. Rosenboom and Rizkalla [26] published a shear design model for a section repaired with CFRP. Cha [8] demonstrated how the use of carbon fiber composites strengthened prestressed concrete beams up to 86 % for high-strength concrete and 58 % for normal strength concrete. Klaiber et al. [16] inferred, based on laboratory investigation, that CFRP repair for prestressed concrete girders is feasible when about 15 % of the strands are severed. Green and Boyd [10] showed that external CFRP systems can restore up to 90 % of the moment capacity loss after a vehicle impact of girders. Brinkman [6] studied three different types of CFRP repair systems: near surface mounted, externally bonded and bonded post-tensioned. The last system was the most effective in restoring the lost girder capacity.

Rosenboom [25] tested 30 full-scale prestressed concrete bridge girders retrofitted with FRP materials. The FRP repair and the bond behavior were studied from an engineering point of view. Kasan [15] investigated 22 prototype prestressed concrete bridge girders, including spread boxes, AASHTO type I girders and adjacent boxes, with varying degrees of damage and CFRP repair techniques. It was concluded that when 25 % or more of the strands no longer contributed to the capacity, the best option is to replace the affected girder. Other researchers [7] undertook field investigations, analyzing the effectiveness of FRP repair system on I-565 bridges in Huntsville, Alabama.

Two advantages of GFRP are corrosion resistance and durability. Abushagur [3] found that the GFRP wrapping not only creates a corrosion protective layer for steel structures, but also improves the flexural capacity of steel sections. Ragaby [24] investigated the use of GFRP bars as deck reinforcement. They were found to work well for bridge decks with corrosion problems. Bridge decks reinforced with GFRP rebars had superior fatigue performance. Huang [12] investigated durability behavior and degradation mechanism of GFRP rebars in concrete. He developed more accurate environmental reduction factors that those given by the design codes. Yan [31] investigated the durability of GFRP as bridge deck reinforcement subject to weathering conditions. Laosiriphong [18] found that the use of GFRP wraps increased the durability of railroad crossties and enhanced the flexural rigidity by 44 % and the shear modulus by 18 %. Memon and Sheikh [20] investigated the use of GFRP sheets to repair square columns under simulated earthquake loads. The sheets significantly enhanced ductility, energy dissipation ability, and moment capacity of deficient columns. Smith [27] investigated the rehabilitation of timber railroad bridges using GFRP wraps. All specimens showed 55–60 % recovery of initial strengths with GFRP retrofit. Mahmood [19] compared the cracking of concrete members reinforced with GFRP and steel rebars. No difference between the crack width with either systems was found. Johnson [14] conducted an experimental program with 24 large scale beams with different types of GFRP rebars. The study concluded that the bent GFRP rebar stirrups exhibited acceptable thermal and mechanical properties.

It is apparent that significant prior work has been undertaken with external CFRP wrapping for concrete bridge strengthening. Several studies have looked at GFRP rebar application in bridge decks and girders. However, no prior study has investigated the use of GFRP rebars in the repair and strengthening of full-scale impact damaged concrete bridge girders, the theoretical modeling aspects of this application and validation with in situ load testing.

Repair procedure

Repair of a damaged bridge girder has to satisfy three important criteria of safety, minimum repair time and economy. Among other steps satisfying these factors, an important and novel approach herein was the use of transverse and longitudinal fiberglass rebars to increase the girder capacity and durability.

NCHRP 20-07/task 307 report is a widely accepted source for classifying girder damage and associated repair needed [22]. Based on the NCHRP damage classification, because the exposed strands on the damaged girder were not severed, the damage was categorized as “moderate”. Although there was no structural damage, an adequate repair was required to prevent further deterioration and the corrosion of the strands. The repair process used three different materials: an adequate bonding agent, embedded GFRP rebars and a one component shrinkage-compensated micro concrete mortar (designed for large volume repair). The use of GFRP rebars was motivated by its high resistance to corrosion and to reduce the aesthetic impact that could be caused by an external FRP wrapping on a new bridge. The pertinent properties of the rebars and mortar are presented in Tables 2 and 3, respectively.

Table 2 Fiber glass rebar properties
Full size table
Table 3 Repair mortar properties
Full size table

The repair procedure consisted of the following steps: (1) remove all loose concrete; (2) chip existing concrete to provide a rough surface; (3) drill holes for GFRP rebar placement; (4) place GFRP rebar after cleaning all surfaces; (5) apply bonding agent; (6) install formwork; (7) fill with repair mortar; and (8) remove formwork after 12 h of curing. Chipped concrete had a minimum depth of 38 mm. The GFRP rebar placement scheme is shown in Fig. 5. The rebars were arranged both longitudinally and transversally. The length of the transverse rebars was 203 mm, embedded 101 mm inside the girder section, and spaced at 152 mm along the damage and located at 216 mm from the bottom. The longitudinal rebars were placed along the damage above and below the transverse rebars with a length of 4.3 m. These rebars enhanced the flexural capacity of the repaired section and supplemented the mortar strength that was lower than the girder concrete strength.

Fig. 5
figure 5

Repair scheme

Full size image

Load testing

The load testing consisted of placing a loaded truck on the damaged span before and after the repair and monitoring the corresponding strains. The test protocol followed the AASHTO guidelines [2]. The test truck weighed 400 kN over six axles, as compared to the AASHTO HL-93 truck weight of 320 kN (Fig. 6). The truck length and width were 12.8 and 2.4 m, respectively. It was placed at two different positions on the span. Phases 1 and 2 corresponded to load testing on the damaged and the repaired bridge, respectively. For Phase 1, as shown in Fig. 7, in truck position 1, the truck was centered on the damage (1.1 m from the barrier) for 650 s. Thereafter, in position 2, the truck was moved to the adjacent undamaged girder for 200 s, 3.34 m from the barrier (Fig. 8). The same truck locations were used in Phase 2, creating truck positions 3 and 4 for the repaired girder. Six strain gages were utilized in Phase 1, while a seventh gage was added at the bottom of the repaired girder for Phase 2 (Figs. 9, 10). Strain data were automatically acquired through a strain box and data acquisition system.

Fig. 6
figure 6

Test truck characteristics

Full size image
Fig. 7
figure 7

Truck position 1, phase 1

Full size image
Fig. 8
figure 8

Truck position 2, phase 1

Full size image
Fig. 9
figure 9

Strain gage locations, phase 1 damaged girder

Full size image
Fig. 10
figure 10

Strain gage locations, phase 2 repaired girder

Full size image

Finite element modeling (FEM)

The software used herein was ABAQUS [9] to model the behavior of the girder under review, both in the damaged and repaired stages. The software is highly sophisticated and allows the modelling of structural behavior under external loads. ABAQUS has an extensive library of materials, including elastic and elastic–plastic solids, and elements such as beams or plates.

The concrete girder, as well as the deck and haunch sections, was defined with a 3D deformable extrusion solid from ABAQUS. The effective girder flange width was calculated as 2.8 m, based on AASHTO LRFD provisions [1]. The transformed width is not necessary, because ABAQUS allows the use of sections with different materials properties.

The Concrete Damaged Plasticity (CDP) model is the most realistic in ABAQUS and was used herein, considering the inelastic behavior of concrete in both compression and tension. For the elastic behavior, the modulus of elasticity of the girder concrete was computed as 38.5 GPa, based on AASHTO LRFD [1] for a concrete compressive strength of 58.6 MPa. For the slab and haunch concrete, the compressive strength and elastic moduli were 27 MPa and 26.4 GPa, respectively. For concrete, AASHTO provides a Poisson’s Ratio of 0.2. The CDP default parameters were based on published values in the literature [17]. In the absence of experimental data, the approach suggested by Wight and MacGregor [30] for the concrete compressive behavior was used, valid for concrete strengths from 13.8 to 124 MPa. The needed damage parameters were adopted from Birtel and Mark [5]. A maximum stress and the corresponding strain must be defined as a limit for total compression crushing failure of the concrete, and were taken as 0.5 and 0.3 times the concrete compressive strength [29]. The resulting concrete compressive stress–strain curve is shown in Fig. 11. The tensile behavior of concrete was represented with a model proposed by Wahalathantri et al. [29]. Applying the modified tension stiffening model for ABAQUS, the tensile behavior of the concrete girder is shown in Fig. 12.

Fig. 11
figure 11

Concrete compressive stress–strain diagram

Full size image
Fig. 12
figure 12

Concrete tension stress–strain diagram

Full size image

The steel and GFRP rebars were represented with 3D deformable wires with a truss section. Elastic–plastic stress–strain behavior was assumed for the regular steel rebars. For the steel elastic behavior, an elastic modulus of 200 GPa and a Poisson’s Ratio of 0.3 were assumed. The ABAQUS assembly module was used to embed the rebars into the concrete girder. The union between the girder and the slab/haunch was performed via interaction ties. These two interactions constrain the nodal degrees of freedom in contact, and guarantee the compatibility of deformation and adequate stress transmission. The elastic stress–strain diagram for the GFRP rebars is shown in Fig. 13. The modulus of elasticity and Poisson’s ratio were 53.6 GPa and 0.26, respectively.

Fig. 13
figure 13

GFRP rebar stress–strain diagram

Full size image

The effective prestress was obtained using AASHTO LRFD procedure [1]. The total loss of prestress was determined as the sum of the short-term losses (elastic shortening) of 98.2 MPa and long-term losses (shrinkage/creep, steel relaxation) of 154 MPa, resulting in a total loss of 252 MPa. The approximate method given by AASHTO LRFD, article 5.9.5.3, was used herein to find the long-term losses, with an assumed relative humidity of 70 %. A relaxation loss of 16.5 MPa for low-lax strands was used. The resulting effective prestress was 1144 MPa. To reduce the computational time and because the contribution of prestressing steel to the girder stiffness was negligible, the prestressing strands were not directly modeled in the FEM. Instead, equivalent forces were applied using the load-balancing method. The prestress force was equivalent to a combination of a compressive axial force equal to the effective prestress in each strand (113 kN) and a vertical force component applied at the draping points of 9.1 kN.

The girder was considered as simply supported on elastomeric bearing pads. To compare the FEM results and the load test data, the input loads were not factored. The load case modeled was dead load plus prestress force plus live load for various truck positions. The dead loads came from the barrier, slab, haunch and girder. A C221 type barrier was used on the bridge with a weight of 7.34 kN/m. The slab tributary area and the haunch were assumed to have a concrete weight of 23.8 kN/m3. The live load transmitted by each truck axle was found by the lever rule. To introduce the live loads into ABAQUS, they were applied on a surface equivalent to the tire contact area over the deck, assumed as 232,257 mm2.

The computation was performed first using 381 mm mesh size and then gradually reduced to 76 mm. Mesh sizes smaller than 76 mm resulted in very long computational times. Therefore, a 76 mm mesh size was used herein (Fig. 14).

Fig. 14
figure 14

Damaged girder FEM with 76 mm mesh size

Full size image

Results and discussion

To compare the FEM strains to the average strains measured from load testing, the FEM strains from the closest nodes to each strain gage were used herein. Figure 15 presents the FEM strains for Phase 1 loading and truck position 1. The deformed shape of the girder and the stress concentration around the damaged area are evident. The time variation of the measured strains for Phase 1 truck position 1 is shown in Fig. 16. The strains for each gage remained about constant with time with minor fluctuations. This trend was demonstrated in results from other gages and truck positions.

Fig. 15
figure 15

FEM model strains, phase 1, truck position 1

Full size image
Fig. 16
figure 16

Truck position 1 strain measurements

Full size image

The strains from the model and the load testing are presented in Fig. 17. Most of the FEM strains were slightly higher than those from the load testing for truck position 1. For position 2, the live loads applied on the girder were lower than those from position 1, resulting in decreased strains (Fig. 17b). The model prediction was more accurate for truck position 2 than position 1. The difference between the strains from the model and the testing is small; the greatest difference was about 6.3 μm. This validates the Phase 1 FEM model. In Phase 2 repaired girder, truck position 3, the strains (Fig. 17c) decreased from those for truck position 1 by about 50 %. The greatest difference between the FEM and actual strains was for gage number 4. Gages 3 and 4 were located at the same height in the girder cross section and separated 0.61 m longitudinally. Therefore, the measured strains in the gages should have been similar. The FEM strains for these two gages were close. It may be inferred that gage 4 was not placed appropriately or did not work properly during load testing.

Fig. 17
figure 17

Theoretical and measured strains. a Truck position 1, b truck position 2, c truck position 3, d truck position 4

Full size image

Because the loads applied to the girder for truck position 4 were lower than those for position 3, the strains values were relatively lower as well, with a maximum strain of about 17 micron. Figure 17d shows that the differences between the theoretical and actual strains were small.

In general, for a prestressed girder, the bottom fiber stress can be obtained as the summation of the compressive stress caused by the prestress force and the tensile stress due to the gravity loads, as shown in Eq. 1:

$$\sigma = \frac{M \times y}{I} - \frac{P}{A}$$
(1)

where σ is the net stress, P is the prestress force, A is the cross-sectional area, M is the bending moment from gravity loads, y is the distance from the neutral axis to the bottom fiber, and I is the moment of inertia.

The repair procedure was expected to recover the damaged section capacity by primarily increasing its moment of inertia, through which the gravity tensile stresses would be reduced. This should result in increased compressive stresses at the bottom fiber of the repaired girder. To demonstrate this, FEM stresses at the girder bottom fiber at the center of the damage (located at 6.7 m from the left support) were reviewed herein. For Phase 1, stresses from FEM nodes closest to points 1, 2 and 3, shown in Fig. 18a, were considered. For Phase 2, in addition to the three points, two additional points 4 and 5 were considered (Fig. 18b). The corresponding FEM stresses are presented in Table 4. For the damaged girder, the maximum compression occurred at point 3 for both truck positions, while the minimum compression occurred at point 1 which was closest to the damage. As expected, for the repaired girder, the compressive stress values are quite a bit greater than those obtained for the damaged girder. At point 1, the compressive stress after repair is nearly three times that from before repair. At point 2, the increase is almost 50 %. The increase in the moment of inertia for the repaired girder and corresponding decrease in the tensile stresses from gravity loads are evident. For both phases, the stress values obtained indicated that the girder was under elastic behavior. The maximum compressive stress for the repaired girder concrete was 8.93 MPa, well below the assumed concrete compressive elastic limit of 29.3 MPa.

Fig. 18
figure 18

Analyzed stress points. a Phase 1, b phase 2

Full size image
Table 4 FEM stresses at girder bottom
Full size table

The maximum stresses developed in the longitudinal GFRP rebars in the repaired girder are given in Table 5. It can be observed that the rebar compressive stresses decreased slightly from truck position 3–4. This is expected, because for these truck positions the loads applied on the girder were greater than those applied for the other two positions. The stresses in the GFRP rebars were under the elastic limit.

Table 5 Maximum stresses in GFRP rebars
Full size table

Conclusions

The following conclusions can be drawn based on the results from this study:

  1. 1.

    GFRP rebars, together with an appropriate bonding agent and repair mortar, can be effectively used to repair and strengthen prestressed concrete bridge girders damaged due to impact from an over-height vehicle. These rebars enhance the flexural capacity of the repaired section and supplement the repair mortar strength if it is lower than the girder concrete strength.

  2. 2.

    GFRP rebars can impart durability to the repaired section due to its high resistance to corrosion. The rebars can help in reducing the aesthetic impact that could be caused by an external FRP wrapping on a new bridge.

  3. 3.

    The damaged and the repaired girders on the LBJ Express Project were effectively modeled with a finite element software with appropriate model parameters for concrete, steel and GFRP rebars.

  4. 4.

    In situ full-scale load testing with various loaded truck positions on the composite bridge showed good comparison with the FEM results. Strain values from the theoretical modeling were slightly larger than those from actual strain gage readings, meaning that the modeled bridge was slightly less stiff than the actual bridge. The theoretical model and load testing accurately predicted the reduction of strain in the girder when the truck position moved away from on top of the girder.

  5. 5.

    The repair scheme drastically increased the stiffness of the damaged girder, resulting in about 50 % reduction in the bottom strains, as evidenced in the theoretical and actual values.

  6. 6.

    The beneficial effect of the repair resulted in large increases in the net compressive stresses (by about 200–300 %) at the girder bottom through the increase of the section stiffness and reduction of the gravity load stresses. Stresses remained well below the elastic range for concrete.

  7. 7.

    The stresses in the GFRP rebars after repair also remained well below the elastic limit.