Introduction

The pile foundations are adopted to transfer the load from the structure to soil when the structure is embedded in a weak soil stratum. In an axially loaded pile, the load is transferred to the soil through the side friction at the soil–pile interface and base resistance offered by the soil bed. Pile foundations are subjected to significant amount of lateral forces in addition to the vertical forces. The lateral forces are due to the wind, wave, earthquake, dredging, and impact loads [20, 35, 60, 63, 66]. When the pile is subjected to lateral loads, the load carrying mechanism changes. The lateral load is resisted by the soil–pile interaction effect [87], which in turn depends on pile material, pile diameter, soil properties, and bed slope of ground. Studies showed that the influence of vertical load on the lateral response is not so significant when the vertical load is applied simultaneously with the lateral load [53]. The current design practices consider the influence of these two loadings independently and hence pile designs are carried out separately for vertical and lateral loads. The effects of vertical loads on the piles are well established through these years, whereas studies on vertical piles under lateral loads are limited and are continuing to establish a well-defined method of analysis considering the effect of all the influencing parameters [27]. The present study focuses on the significant factors affecting the soil–structure interaction of laterally loaded pile foundation (LLP). For better understanding, the literatures have been grouped into different categories based on: type of investigations, characteristics of soil, characteristics of pile, and type of loading.

Types of investigations

Reviewing the available literature it was observed that the studies on LLP are generally carried out by conducting the theoretical, numerical, and experimental investigation of soil–pile system. For better understanding of the literature, they are grouped based on the type of investigation carried out to study the behavior of LLPs.

Theoretical investigation

Theoretical investigations are the basis of numerical formulations. The theoretical formulations are to be studied for the advanced modifications in the numerical formulations. Earlier developments in the theoretical formulations are also discussed here. Lateral loads on piles cause deflection and rotation of pile caps. To calculate the pile cap deflection and rotation the pile has been idealized as a beamas shown in Fig. 1 [18, 20]. LLP analysis had been conducted by considering a cantilever action with tip load. Further the soil–structure interaction can be incorporated by considering the effect of soil parameters. Such an attempt was done by Mazurenko et al. to analyze the behavior of a LLP [57].

Fig. 1
figure 1

General beam column element [18, 20]

Full size image

In a LLP the point of zero deflection or the point of maximum bending moment is considered to be the point at which failure of the soil–pile system occurs. An analytical method to calculate the point of zero deflection and the point of maximum bending moment was suggested by Mironov [58]. To develop this general method the factors considered are, flexural rigidity of the pile, nature of variation of stiffness of soil mass with depth and the ratio between the deflections and soil reactions. Better understanding on the behavior of LLPs can be obtained from the soil reaction–pile deflection (p–y) curves of the soil. Reese et al. [81] have developed non-dimensional curves from the numerical solution of the differential equation describing the pile behavior as shown in Fig. 2 and it can be used to estimate the p–y curves. He had further suggested p–y method of analysis for LLPs by taking into account, the nonlinear and inelastic characteristics of soil [82].

Fig. 2
figure 2

Behavior of laterally loaded pile [81]

Full size image

Later, p–y analysis method was modified by Duncan et al. and is referred as the characteristic load method [25]. It is simpler than p–y analyses initially developed by Reese et al. The method used dimensional analysis to characterize the nonlinear behavior of LLPs and drilled shafts by means of relationships among dimensionless variables. The characteristic load method has been found to be in good agreement with values measured in field load test also. More advancement in this was suggested by Brown et al. and his analytical method proves a rigorous and reliable method of interpreting lateral load tests on piles or drilled shafts using inclinometer data [15]. The method utilizes a least square regression technique that will converge to a solution for analytical p–y curves which produce minimum error between the predicted and measured deflection versus depth profile over a range of loading.

Fig. 3
figure 3

Basic strain wedge model [45]

Full size image

Further, the strain wedge (SW) model as shown in Fig. 3 was suggested and was found to have advantages over p–y curve method [3, 45]. SW model analysis predicts the response of LLPs and had shown very good agreement with actual field tests in sand, clay and layered soils. The advantage of the SW model is that it is capable of taking into account the effect of changes in soil and pile properties on the resulting p–y curves.

The studies on laterally loaded single pile were extended to pile groups also. Reese et al. who have already developed p–y method for laterally loaded single pile have presented the analysis of a cluster of piles [83]. The importance of various parameters involved in the solution is studied using different analytical approaches. A modification of this has been suggested by Poulos–Focht–Koch in which the pile group has been considered as a large diameter pile. Later, Chore et al. have extended the work of Reese and derived finite element formulation for the nonlinear analysis of pile groups subjected to lateral loads using p–y curves [20, 21, 91]. In the study, pile was idealized as one-dimensional beam element, pile cap as two-dimensional plate element and soil as nonlinear elastic springs using modified p–y curves [31]. It was observed in the study that the nonlinearity of the soil is found to increase the top displacement of the pile group and decrease the fixed moments and positive moments. Kim et al. have conducted studies on pile–soil system subjected to lateral loads in clay soil by improved wedge failure model and hyperbolic p–y criteria [45]. The proposed p–y curves with an improved wedge model are more appropriate and realistic for representing a pile–soil interaction for LLP in clay than the existing p–y method.

The behavior of soil becomes complex when the change in its property along the vertical profile is considered. In a simplified analysis the vertical soil profile was considered uniform, suggested by Reissner as shown in Fig. 4. It was modified by Horwath [37] with additional case of Young’s modulus varying with depth for layer of finite thickness.

Fig. 4
figure 4

Reissner type simplified elastic continuum applied to laterally loaded pile [37]

Full size image

The response of single pile subjected to lateral load in layered soil was further studied by Rongqing et al. and developed an analytical method which uses fundamental basis of structural mechanics to obtain the governing equation of the soil–pile system [54]. Both free head and fixed head methods are considered here. The pile deflection, bending moment and soil reaction can be calculated using this method.

The modulus of soil resistance was further modified as an exponential function with depth and derived a new γ parameter to predict the pile response [43]. The direct shear test was used to determine modulus of soil resistance and ultimate soil resistance. The existing methods were later modified considering the nonlinear elastic properties and modulus degradation characteristics of soil [106]. The stress strain behavior of most geo-materials is highly nonlinear at all phases of loading and s-shaped degradation curve as shown in Fig. 5 is commonly found. Furthermore, certain studies suggest two-dimensional mapped infinite elements and nonlinear stress–strain behavior of the soil using hyperbolic fit [34].

Fig. 5
figure 5

Degradation curve of shear modulus of soil [32]

Full size image

Later, a detailed investigation by Banerjee et al. incorporated layering effect of soil in finite element method (FEM) and boundary element method (BEM). Studies present inelastic pile–soil–structure interaction under static loading with piles modeled using linear beam column finite elements and soil was modeled using nonlinear springs [10]. Researchers have developed finite element formulations and its MATLAB coding by considering modulus of subgrade reaction approach to analyze fixed head and free head single piles in cohesionless soil [62, 73, 74, 91, 102]. Solutions are obtained for pile response with various cohesionless soils taking into account the short pile and long pile behavior.

Through these years, theoretical investigations have developed solutions for LLPs and pile groups embedded in homogeneous as well as layered soil. Even though the incorporation of soil layering in the theoretical formulation of LLP makes the solution more complicated, adopting finite element analysis techniques as well as computational power of latest computers can produce accurate results.

Numerical investigation

A set of numerical formulations for advanced analysis of soil–structure interaction is developed by many researchers [46, 47, 50, 99, 100]. A new frequency domain method for evaluating the earthquake input energy to a structure–pile system or a superstructure alone subjected to horizontal ground motion was developed by Takewaki et al. [100].

The soil–pile–structure system is idealized as shown in Fig. 6 and derived the energy transfer function, which plays a key role in the input energy calculation. Input energy was expressed in time domain as,

$$E_{I}^{A} = \mathop \int \limits_{ - \infty }^{\infty } F_{A} (\omega )|A(\omega )|^{2} {\text{d}}\omega \quad {\text{and}}\quad E_{I}^{S} = \mathop \int \limits_{ - \infty }^{\infty } F_{S} (\omega )|A(\omega )|^{2} {\text{d}}\omega ,$$
(1)

where \(F_{A} \left( \omega \right)\,\;and \;F_{S} \left( \omega \right)\) are called the energy transfer function for the soil–pile system and the energy transfer function for the structure, respectively. The method was developed in frequency domain approach and hence has the advantage of being able to include directly the frequency dependent characteristics such as stiffness and damping of the soil considered. Takewaki et al. [99] have also incorporated the effect of pile group on the seismic stiffness and strength design of buildings. Pile group effect is taken into account through the influence coefficients among piles, which are defined for inter-story drifts and pile head bending moments. It has been shown that pile group effect reduces the inter-story drift of buildings and increases the bending moment of pile at the top.

Fig. 6
figure 6

Free-body diagram showing the forces in a soil–pile–structure system [100]

Full size image

Takewaki et al. [46] have further extended the method to analyze the earthquake energy input in soil–pile structure system with uncertain soil parameters. Taking the advantage of frequency domain approach the earthquake input energy to the structure can be obtained in a compact form. The method was further modified as a unified response spectrum method incorporating the kinematic and inertial effects as shown in Fig. 7 [47, 50]. The equilibrium equation is derived for the structure–pile–soil system and is represented in Eq. 2

Fig. 7
figure 7

Simple structure–pile–soil system connected to free-field ground [50]

Full size image
$$\mathop \sum \limits_{i = 0}^{1} m_{i} \left( {\"u_{G} + \"u_{i} } \right) + k_{i} (u_{0}^{\left( I \right)} + u_{0}^{\left( k \right)} - u_{G} ) + k_{p} (u_{0}^{\left( I \right)} + u_{0}^{\left( k \right)} ) = 0.$$
(2)

To verify the numerical model with winkler type soil model, Takewaki et al. have considered an onsite building pile system in Yokohama, Japan. The building consists of 12 storied steel frame structure supported by 20 cast in situ concrete piles of 35 m long and 1.7 m in diameter. The numerical model adopted for the analysis is as shown in Fig. 8. The bending strains at the top of the pile were compared and it was found that the strain values obtained using continuum model with winkler type soil element was in good agreement with the measured values of stains.

Fig. 8
figure 8

Building pile system supported by the free-field ground through winkler type soil model [50]

Full size image

A newly developed updated reference point (URP) method was used by Okada et al. [69], to study the seismic pile response of a structure–pile–soil system with uncertain soil and concrete properties. A ten storied building was modeled and the pile head bending moments were compared in URP and NURP methods. It was confirmed in the studies that the NURP method can be applied to the seismic pile response in terms of the structure–pile–soil system with an acceptable accuracy and the worst variation for weak soil parameter are to be clarified. It was also found that the variability of equivalent shear wave velocities of soil, even at a deep underground influences the bending moment at the pile head.

Seismic soil–structure interaction of a pile group was studied using equivalent pier method (EPM) by Badry et al. [9]. The study was conducted on an axisymmetric multistoried building and the peak response of the building under fixed base condition and flexible base condition were studied. It was observed that the response of flexible base structure was more, about 15–20 % compared to fixed base structures. Also it was concluded that EPM approach reduces the analysis time by 68 %, since in this method, equivalent piers give rise to larger elements during meshing, which facilitates to take larger time steps and hence less duration of analysis.

Increased computational power of computers has made the numerical investigations the most cost-effective and accurate method of investigation. Most of the numerical investigations reported include the analysis based on the finite element method using software, such as ABAQUS [22], ANSYS [96], FLAC [56], FLIPER [105], GROUP [88], LPILE [59], PLAXIS Foundation 1.1 [8, 19, 65, 102], PLAXIS 3D [94] etc.

Studies on the coupled bridge foundation-superstructure finite element was conducted by Zhang et al. [105] using the finite element code FLPIER to predict the lateral response of the single piles and pile groups (3 × 3–3 × 7 pile groups) founded in both loose and medium dense sands. FLIPER incorporates Reese et al.’s p–y curves, Brown et al.’s p-multiplier approach and Mc Way et al.’s p-multiplier factor for large pile groups. The studies involved the predictions of lateral load versus lateral deflection of the group, the shears and bending moments developed in the individual piles, and the distributions of the lateral loads in each pile row, which were all in good agreement with the measured results. The suggested variation of bending moment in a fixed head pile group is shown in Fig. 9.

Fig. 9
figure 9

Sketch of bending moment distribution in fixed head pile group [105]

Full size image

The effect of pile–soil interaction was effectively represented using CONTACT 49 element (5 node, 3 DOF) element in ANSYS in a set of analyses conducted by Soltani et al. [96] and the results were compared with linear method of Hetenyi, nonlinear method of Matlock and finite element program of Bowles. The 3D pile–soil interaction effect was incorporated in ANSYS model and it leads to the difference in maximum bending moment and pile top deflection in comparison to the other’s methods. Many researchers have performed the finite element analysis using the software PLAXIS 3D Foundation using embedded pile element and the analysis results are in good agreement with the pile load test conducted by various researchers.

Piles in cohesive soil were analyzed by a series of numerical analyses conducted by Moayed et al. [59] using the LPILE software. Broms (1964) proposed graphs to obtain ultimate lateral bearing capacity of such piles. Broms solution does not consider the effect of vertical loading on lateral bearing capacity of piles. This study incorporates the effect of vertical load also in predicting the lateral capacity of pile. Avaei et al. [5] have investigated the effects of different parameters, such as pile properties, soil– stress–strain behavior, pile–soil interaction, etc., on the behavior of pile subjected to lateral load. A comparison has been made between the results derived from finite difference and equivalent spring methods. Finite difference program has been developed in Turbo Pascal and the equivalent spring method is solved using SAP 2000 package. The results obtained using both the methods are found to be in good agreement. Parametric study on a LLP with the length of 15 m and diameter of 1 m subjected to a lateral load of 300 kN showed that the properties of soil near the pile head greatly influence the pile head displacement. It was also noticed that the pile end displacement was influenced by the pile length and after a particular length (9 m in this case) the influence of pile length decreases and this length is called the depth of fixity.

The lateral behavior of single pile in cohesionless soil subjected to both vertical and horizontal loads was studied by Chik et al. [103] by conducting numerical analysis using the software PLAXIS 3D Foundation 1.1. The verification of the model is done by comparing the results with the field pile load test results. Babaei [8] performed numerical investigation on axial bearing capacity of piles embedded in sloping sandy ground, using PLAXIS 3D Foundation. The results have shown that the pile axial capacity increases with increase in upward slope and decreases with increase in downward slope. Nonlinear finite element modeling using PLAXIS 3D Foundation was done by Kim et al. (2011) to investigate numerically the pile deflection, bending moment and p–y curves along the length of the pile. Based on the findings of this study, it was found that pile elastic modulus (E p ), interface property (R inter), and pile toe condition exert no significant influence on the p–y characteristics.

Conte et al. [20] have used the finite element code ABAQUS to predict the response of reinforced concrete pile to horizontal loading. Finite element codes are supplied with several constitutive models. However, the choice of a constitutive model is generally influenced by the material parameters that are available for the case study. Sophisticated soil models could not be justified if all the material properties related to the model are not available. Hence, the present study uses a linear elastic perfect plastic soil model with Mohr–Coulomb failure criteria which uses five soil parameters, such as shear modulus (G), Poisson’s ratio (ν′), shearing resistance angle (φ′), effective cohesion (c′), and angle of dilatancy (ψ).

Numerical example in PLAXIS-3D

Pile load test on laterally loaded pile

A pile load test conducted by Ismael et al. has been modeled and studied. The pile was 0.3 m in diameter and had a length of 5 m situated in Kuwait. The surface soil was found to a depth of 3.5 m and was characterized as having both component of shear strength, c and φ. The soil profile consisted of a medium dense cemented silty sand layer to a depth 3 m. This was underlain by medium dense to very dense silty sand with cemented lumps to the bottom of the borehole. All properties of soil are listed in Table 1. Ground water was not encountered within the depth of the borehole. In conclusion, the comparison between the PLAXIS 3D simulation and the reported lateral data is shown in Figs. 10, 11 and 12 [39]. The piles were deflecting not in the same magnitude at the field test due to the variability of soil properties. Also, the numerical simulation is reasonably accurate for the problem of LLPs and piles oil interaction over a wide range of deformation for 5-m piles.

Table 1 Geotechnical properties of the soil layers and the pile
Full size table
Fig. 10
figure 10

PLAXIS 3D output

Full size image
Fig. 11
figure 11

Comparison of PLAXIS 3D with field test

Full size image
Fig. 12
figure 12

Shadow stress zone and gap formation in LLP group [86]

Full size image

PLAXIS 3D curve manager is used to plot the load deflection curve of the present analysis and is shown in Fig. 10. The load deflection curve available from the literature [39] and the curve obtained from the present study are plotted together using plot digitizer as shown in Fig. 11. It was observed that both the experimental and numerical results are comparable. Hence it can be concluded that the software is capable of incorporating the nonlinear soil–structure interaction effect.

Experimental investigation

Experimental investigations were conducted either on full-scale field piles or on model piles. Though the full-scale test results are considered to be more reliable, the costs of full-scale tests being very high, properly engineered model tests were usually adopted for the studies. Even though the experimental investigations are costly and difficult, the most commonly adopted numerical investigation results are validated with properly conducted experimental results. Some of the widely used experimental results are also discussed here. Rollins et al. [84–87] and Gandhi et al. [29] have conducted a number of full-scale tests on LLP and the same has been adopted for many researchers for the verification of other studies. Experimental model tests are also conducted to study the behavior of LLPs by researchers like Gandhi, Mostafa, Rao, Cox, etc. [23, 27, 28, 72, 79, 89, 93, 95].

Full-scale field tests conducted by a number of researchers had studied the behavior of group piles in comparison to single pile with the intension of predicting the group effect from the behavior of a single pile. The pile group deflection and the maximum bending moment under the same average load per pile are reported to be almost twice as that of a single pile. Similar investigations were conducted using model piles also by applying laws of similitude, and experiments were carried out similar to that of field tests. Laws of similitude are adopted to model the piles from the available field piles. Field piles are generally concrete or steel. A suitable material capable of predicting the deflection and bending moment is adopted for a model pile. Model piles can be made using aluminum [27, 61, 95], mild steel [23, 79, 93] or PVC [49].

It was observed from the studies that for a particular load, aluminum pipe piles showed more deformation at the top of the pile and strains along the length of the pile, compared to steel pipe piles [89]. Considering the above fact, aluminum pipes piles are more suited for model studies since it can give strain readings even for a small variation of load. Model tests were conducted to plot the load deflection curve as well as the bending moment variation along the depth of pile. Based on the studies it was observed that individual pile efficiency can be increased by increasing the spacing between the piles. Researchers have suggested that at a spacing of eight to nine times the pile diameter the individual piles attain 100 % efficiency [23]. A similar study revealed that the optimum spacing between piles for maximum resistance to be about two times relative stiffness factor T [27]

$$T = \left( {\frac{\text{EI}}{{n_{h} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 5}}\right.\kern-0pt} \!\lower0.7ex\hbox{$5$}}}} ,$$
(3)

where EI is the flexural rigidity of the pile material and n h is the coefficient of modulus variation (possible range values of n h from 2.5 to 20 MN/m3) [11, 24]. Studies have also inferred that the pile group efficiency decreases with increase in the number of piles in the group even for same spacing between the piles. Piles embedded in slopes showed a decreased load carrying capacity in comparison to piles in level ground. Model studies on sloping ground have found that the effect of slope on the strength reduction of the pile soil system could be neglected for piles located beyond five pile diameters from the crest of the slope [95].

The pile cap imparts fixity to the pile head. Experiments show that fixed head pile exhibits 40 % reduction in pile head deflection in comparison to free head pile [29]. The influence of pile cap on the lateral load carrying capacity of piles was also studied by Nath et al. [68] and it was found that an increase in embedment depth of pile cap increases the lateral resistance offered by the pile cap to the pile group.

Factors influencing SSI analysis of laterally loaded pile

From the detailed review of the different investigation methods, it was understood that, proper assessment of the characteristics of soil and pile, loading details, etc., are essential in the accurate modeling of the soil–pile system. Hence, a brief review on the characteristics of soil, characteristics of pile and type of loading are also incorporated in the present study.

Characteristics of soil

In soil–structure interaction analysis the distribution of load from the structure to the soil is investigated. In this load transfer mechanism, the characteristics of soil has very important role. The behavior of soil is predicted based on the engineering properties of soil, vertical soil profile and the alignment of ground surface.

Soil properties

The behavior of soil is anisotropic, nonlinear, and time dependent [32]. However, the soil parameters such as unit weight (γ), shear modulus (E s ), Poisson’s ratio (ν), shearing resistance angle (φ), effective cohesion (c), and angle of dilatancy (ψ) play a very important role in representing the soil behavior. Soil properties vary from very soft to very stiff consistency, based on which there will be changes in the soil–structure interaction. Most of the studies on LLP are conducted with pile-embedded sandy soil [3, 24, 27, 28, 77]. Only a very few studies are available for LLP embedded in clay [78, 95, 99].

The engineering properties of soil could be found out using the standard test methods like ASTM and BIS [95]. Proper assessment of the properties of the soil is required for the prediction of the behavior of the structure under external loading. It is also required for the accurate modeling of soil during numerical analysis. It was observed in certain studies that reduction in soil moisture content causes an increase in the lateral soil resistance [51]. In clayey soil, studies revealed that drying the soil sample affects the index properties, the compressibility and the shear strength behavior especially for clays in which Kaolinite is the major constituent [71, 80].

The improvement of lateral capacity of pile can be achieved by compaction of surrounding soil and thereby reducing the number of piles and hence saving the cost [24, 73, 74]. This is true only up to a certain depth, and it was found that when the thickness of densified soil increases beyond a certain height there is not much increase in lateral load.

Vertical soil profile

In the actual ground surface, the vertical soil profile is always layered and the properties vary from layer to layer though it is considered to remain constant for a particular layer for the purpose of analysis [7]. For example in the Winkler approach which considers the soil as a layered system to study the lateral resistance of piles, the soil pressure p is related to lateral deflection y through the modulus of subgrade reaction k h of the particular layer,

$$p = k_{h} y .$$
(4)

Various geotechnical engineers such as Terzaghi, Broms, Poulos, Matlock, and Reese have suggested an equation for subgrade reaction in terms of E s , the soil modulus and D, the diameter of the pile [76]

$$k_{h} = (0.48 \;{\text{to}} \;1.8){\raise0.7ex\hbox{${E_{s} }$} \!\mathord{\left/ {\vphantom {{E_{s} } D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}.$$
(5)

Alignment of ground surface

Generally a level ground surface is assumed in a soil–structure system. But when the ground surface is sloping or when the slope of the ground is varying with time, it is found that the surface profile of the ground affects the structural behavior of the pile. Hence, a sloping ground surface should be taken into consideration while analyzing a soil–pile system.

Prediction of the behavior of a LLP could be obtained from the theoretical solution derived based on the force-equilibrium model of rigid piers embedded in cohesionless and c–φ soil profiles in sloping ground surfaces [26]. A parametric study indicated that the amount of reduction in load carrying capacity due to the slope is dependent on the value of the surface slope angle θ and soil strength properties. Later, operating charts were developed using finite element method for estimating behavior of the slopes under different submergence conditions, under complex geometries and properties of slope stability problems [52]. The charts developed using finite element method are claimed to be superior to the traditional charts of Morgernstern, used for the same purpose.

The load-carrying capacity of a LLP decreases as the bed slope increases [95]. The decrease in the load-carrying capacity is due to the decrease in the resistance offered by soil at the top portion of the soil mass, as there is a reduction in soil mass due to the formation of sloping bed. It was found that as the slope increases, there is an increase in the magnitude of maximum bending moment [11]. The increase in relative density is found to be significant for piles embedded in sloping ground [40]. The relative stiffness between the pile and soil has an important role in determining the failure mode of the pile [56]. It was also found that in a pile group, with the increase in the pile spacing, the critical slip surface becomes deeper [103]. Scour can also cause reduction in lateral load-carrying capacity [48, 49].

Researchers have developed relationships to predict the pile top displacement and the maximum bending moment of a LLP in sloping ground based on the corresponding values for the piles embedded in horizontal ground [92]. Based on the experimental results it was concluded that slope reinforcement significantly increases the lateral capacity of pile groups. Geo-grid layer provided with sufficient length and breadth beyond the potential failure surface could improve the slope stability [93].

Sleeving can also be provided to minimize the transfer of lateral loads from the buildings to shallow depths of slopes [18]. The load transfer mechanism from the laterally loaded sleeved pile to sloping ground is through a shear load transfer mechanism in the vertical plane. Under large lateral loads, the influence of the sleeving on pile performance appears to diminish because of the wide spread plastic zone developed around the pile.

Characteristics of pile

The characteristics of pile also play a very important role in determining the behavior of pile under external loading. The characteristics of pile include the length of pile, stiffness of pile, and the arrangement of pile.

Flexibility of pile

Based on the flexibility condition, piles can be categorized into short and long piles. The influence of pile length in the variation of bending moment was studied and it was concluded that short piles behave linearly and long piles behave nonlinearly [6]. Unlike long piles, in short piles maximum bending moment is affected by the length of the pile. It is also observed that in the displacement plots, the pile length could have a substantial influence on the maximum displacement at the pile end. However, this influence decreases from a particular length. Beyond that length, the pile is considered to be a long pile. Thus, for a long pile the changes in the length of the pile will not considerably affect the displacement as well as bending moment.

Stiffness of pile

Stiffness properties of a pile depend on the Young’s modulus of the material of the pile and the cross-sectional area or moment of inertia of the pile. The generally adopted material properties for pile foundations are concrete, steel, and timber [77]. Depending upon the availability, cost, and the strength requirements, a suitable material will be selected. In India, concrete piles are widely used as onsite piles. Young’s modulus of concrete is E c  = 500 (fck)1/2.

Circular and square are the generally adopted cross-sectional shapes of pile. Square shape is adopted for precast piles. Most of the cast in situ piles are circular in shape. Certain researchers have made a serendipitous finding that there is a significant shape factor affecting the ability of pile to mobilize soil resistance to lateral loads [33]. Under a given lateral load applied to free head piles having approximately equal moment of inertia, those having circular cross sections were more resistant to lateral movements than square or H-beam cross section. Investigations were also done to study the effect of pile shape for both circular and square cross section on pile response. In a particular study, the 1.2-m circular piles (MI = 0.03 m4) and 1.2-m sided square piles (MI = 0.05 m4) were considered and it was concluded that square pile is more resistant to lateral load than a circular pile due to high contact surface area between the pile and the surrounding soil, and due to high bending resistance [40].

Arrangement of pile

Single pile arrangement or group pile arrangement can be adopted to transfer the structural load to the ground depending on the load to be transferred and the type of soil. Researches show that the average pile group response was softer than the single pile response. However, the single pile test can be a good indicator of the pile group behavior. It was also found that the p-multipliers work well to account for the group effect [87, 88].

Studies have already established the influence of pile group rigidity of LLP in marine clay. The group efficiency under lateral loading is estimated from the ultimate lateral capacity of the pile group, Q g and ultimate lateral capacity of single pile, Q s for a group of ‘n’ number of piles using the formula,

$${\text{Lateral group efficiency}\,=\,}{\raise0.7ex\hbox{${Q_{g} }$} \!\mathord{\left/ {\vphantom {{Q_{g} } {nQ_{s} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${nQ_{s} }$}}.$$
(6)

It was also concluded that short and rigid piles are more resistant to lateral loads when they are arranged in a parallel configuration than in a series, whereas the reverse is true in cases of long and flexible piles [66].

Researchers have developed p-multiplier concept which provides a reasonable means of accounting for the reduction in capacity produced by group effects and the resulting lateral group effect by considering the shadow stress zone and soil gapping as shown in Fig. 1 [38, 86, 87]. The studies show that p-multiplier is unity for pile spacing greater than 5D–6D spacing.

Certain studies show that the ultimate lateral capacity of pile group depends on the length to diameter ratio of pile, pile friction angle, pile group geometry, spacing of piles in a group and the sand placement density [68, 77]. The pile group deflection and the maximum bending moment under the same average load per pile were investigated to be twice as that of a single pile [86]. Experiments showed that in a pile group, trailing rows of piles carried less loads in comparison to leading rows of piles [1, 2]. Back calculated p-multipliers were 0.8 for front rows and 0.4 for trailing rows [85]. It is interesting to note that group interaction effects vanish after liquefaction [40]. Pile groups with pile cap showed more lateral resistance in comparison to free head piles and it was observed that pile cap contributed 40 % of the total resistance [29, 87].

Type of loading

The structure is designed to resist the external loads acting on it. The structure may be subjected to static or dynamic loading. The behavior of the structure will be different under different loading conditions.

Static loading

The magnitude and direction of the static loading on the structure are given the prime consideration while designing the pile foundations and the structure as a whole. Even though the pile material is considered to be linearly elastic, the nonlinear behavior of soil is to be incorporated in the load-deflection analysis of piles.

The governing equation to represent pile under lateral static loading incorporating the bending stiffness of the pile (EI), subgrade modulus of soil (k) and deflection of the pile element considered (y) is expressed as [5, 15, 90]:

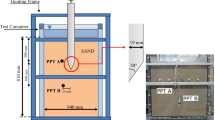
$${\text{EI}}\frac{{\partial^{4} y}}{{\partial x^{4} }} - ky = 0 .$$
(7)

Researchers have conducted full scale and model tests on LLPs subjected to static loading. The basic arrangement of a LLP and soil resistance is shown in Fig. 13. Load will be applied at the pile top at regular intervals of time and the pile top deflections were noted [94, 95]. Corresponding to each load, the dial gauge reading at the top of the pile and the strain gauge readings along the length of the pile were studied. The bending moment (M) is proportional to strain gauge reading (ɛ) and hence the constant of proportionality ‘C’ is obtained from simple bending test. The relation thus obtained can be expressed as [11]:

$$M = C \times \varepsilon .$$
(8)
Fig. 13
figure 13

Lateral load and components of resistance offered by soil–pile system [87]

Full size image

The influence of axial loads on the lateral response of piles was studied and it was found that the lateral deflection and the bending moment of the pile increased with the increase in axial load [53]. The influence of combined loading on lateral capacity decreases as the L/D ratio of the pile increases. The study was extended in layered soil and the variation of displacement along the depth of pile is studied. It was found that when a sand layer is present within a clay deposit, there is reduction in displacement and when a clay layer is present within a sand deposit there is increase in displacement [104].

Dynamic loading

Dynamic loadings are time dependent in nature. The behavior of structure under dynamic loading depends on the natural frequency of the structure. Hence, the possible changes in the natural frequency of the structure with the changes in the soil and the structure are to be studied. The dynamic flexural differential equation of the pile under free vibration condition can be written as [30]:

$$m_{p} \frac{{\partial^{2} y}}{{\partial t^{2} }} + C_{p} \frac{\partial y}{\partial t} + K_{ds} Dy + E_{p} J_{p} \frac{{\partial^{4} y}}{{\partial x^{4} }} + N_{p} \frac{{\partial^{2} y}}{{\partial x^{2} }} = 0 ,$$
(9)

where m p is the mass of the pile per unit length, C p structural damping coefficient of the pile, K ds dynamic stiffness of the soil, E p young’s modulus of pile, J p polar moment of inertia of the pile, N p axial load on pile, and y is the lateral deflection of the pile.

The fundamental natural frequency of the pile for the first mode is:

$$f_{1} = \frac{{ak_{1}^{2} }}{2\pi } ,$$
(10)

where \(a = \frac{{E_{p} J_{p} }}{{m_{p} }}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} ,\,\,k_{1} = \frac{1.875}{{l_{e} }}\), l e is the effective length of pile.

Fig. 14
figure 14

Schematic diagram of dynamic p–y analysis model [14]

Full size image

Dynamic p–y analysis was suggested for analyzing seismic soil–pile–structure interaction represented as in Fig.14 [14]. A simplified analytical model for the lateral harmonic response of single pile and pile group in layered soil was developed by Mylonakis et al. [67]. The predictions of the model are in agreement with the earlier results, while its simplicity offers a versatile alternative to rigorous solutions. The governing equation for the vertical elastic pile embedded in winkler medium is:

$$\frac{{{\text{d}}^{4} y}}{{{\text{d}}x^{4} }} + 4\lambda^{4} y = \frac{q}{\text{EI}} ,$$
(11)

where EI is the flexural rigidity of the pile, q the distributed force along the pile, and λ is the complex wave number associated with the propagation of flexural waves along the pile.

The soil–pile system behaves predominantly in a nonlinear fashion close to the resonance region under dynamic loads [6, 7, 13]. The maximum dynamic BM is magnified by about 1.5 times the maximum static BM for model piles in clay. The maximum dynamic BM occurs at a depth of about 1.5 times the depth of maximum static BM for model piles, which indicates an increase of active length under dynamic load [13, 17].

A new approach to model the material nonlinearity of soil media for the dynamic analysis of pile foundations is proposed by Maheshwari et al. [55]. They incorporated the effects of material nonlinearity of soil on the free-field response which depend very much on the frequency of excitation [98]. Due to the material nonlinearity of the soil, at low frequencies (as compared to the natural frequency of the soil–pile system) the seismic response increases as much as 30 % and at higher frequencies the reverse is true.

Conclusion

A detailed literature review on the soil–structure interaction analysis of LLPs is presented in this paper. Properties of soil and pile, type of loading, analysis methods, etc., play important roles in predicting the behavior of a soil–structure system.

  • The five significant soil parameters are identified such as, unit weight (γ), shear modulus (E s ), Poisson’s ratio (ν), shearing resistance angle (φ), effective cohesion (c), and angle of dilatancy (ψ) which can contribute to soil behavior in a soil–structure system. Standard methods such as ASTM, BIS, etc., should be adopted to quantify the above properties for the accurate analysis of the soil behavior.

  • The vertical profile of soil is also very important in predicting the soil–pile behavior. However, for simplicity in conducting various studies, soil profile may be considered to be either homogeneous or layered.

  • The gradient of the ground surface is also significant in predicting the soil–pile behavior under lateral load.

  • Pile stiffness contributes toward the lateral load carrying capacity of pile. Stiffness of pile is mainly governed by the material property (E) and the moment of inertia (I) of the pile. Hence, pile characteristics such as cross sectional shape, cross sectional area, and material properties are also significant in the structural behavior of LLPs.

  • Seismic loads are considered to be the most complex dynamic loading condition. It could be studied in a simplified manner using sinusoidal loading condition. During the dynamic analysis of soil–pile system, the variations in the natural frequency of the system with the variation in soil properties are to be studied and accounted.

  • A softer soil consistency causes an increase in the depth of fixity of the pile which in turn decreases the natural frequency of the soil–pile system.

  • The method of analysis to study LLP can be analytical, experimental or numerical investigation of soil–pile system. Each of the methods has its own advantages and disadvantages. Analytical solutions are much developed now-a-days but are found to be lengthy and complicated. Developing computer programs of the formulation can solve the difficulty to a large extentd.

  • Experimental investigations on field pile are found to be superior to all the other analysis methods. But it is found to be costly and time consuming. Experimental investigations using model test set up is a good alternative to study the present problem, if all the parameters involved in the study could be modeled using the laws of similitude.

  • Numerical simulation and analysis of the problem solved using finite element or finite difference methods are becoming popular with the increasing computational power of computers and the availability of reliable software particularly designed by considering the influence of soil–structure interaction. Proper validation of model created in the numerical software could ensure better results.