1 Introduction

1.1 Topological data analysis

Data analytical techniques are being far outstripped by the exponential growth and availability of raw data in the modern era. Consequently, efforts made to discover answers are primarily reliant on modern technology, with computational techniques such as machine learning (ML) and deep learning (DL) being prevalent analytical methods. In mathematics, the study of shape presents itself in the form of topology, to understand and describe three-dimensional shapes and deformations [1]. With advances in the field, low-dimensional topological features can represent complex and high-dimensional datasets through topological data analysis (TDA) [2]. Notably, correlation measures can serve as valuable input data for TDA, extending the analytical toolkit to capture complex and nonlinear relationships in high-dimensional datasets and providing a more comprehensive understanding of the underlying structures and patterns [2].

1.2 Point sets in topological spaces

Pairwise correlation measures, such as Pearson’s correlation coefficient denoted by ’r,’ are fundamental tools in statistical analysis, quantifying the statistical relationship between pairs of variables in a dataset and providing insights into the degree and direction of their linear association [3]. It is essential to recognise that Pearson’s correlation assumes linearity and may not capture nonlinear associations [4]. In cases involving nonlinearity, alternative measures like Spearman rank correlation or Kendall tau rank correlation, assessing monotonic relationships, can be employed [5]. In contrast, in TDA, the representation of data hinges on modelling proximity relationships using distance measures, often the Euclidean metric, though alternative metrics can be task-specific [6]. These alternative metrics may account for non-Euclidean aspects, such as temporal dynamics or intrinsic geometries, emphasising the intricacies and application-dependent nature of choosing an appropriate distance metric to optimally represent the underlying geometric and topological features in TDA [7]. To address these challenges, distance correlation measures, also known as dissimilarity correlation measures, emerge as non-Euclidean-based metrics. They quantify the relationship between variables by considering the pairwise distances between data points rather than their actual values. These measures assess the similarity or dissimilarity of variables while providing insights into nonlinear associations and dependencies in the data [8]. Distance correlation has proven to be a useful for TDA, offering a more versatile approach compared to traditional correlation measures [7, 9, 10].

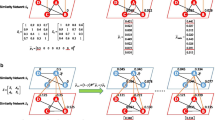
In the context of tasks based on gene expression data, topological overlap measures (TOMs) emerge as highly useful non-Euclidean-based metrics, specifically designed to mitigate the sensitivity of networks to connections formed due to random noise [11]. Similarly, to address challenges associated with noise in network connections, TOM provides an effective tool for uncovering meaningful relationships in co-expression networks, prominently used by weighted gene co-expression analysis (WGCNA) [12]. The core idea of TOM is a cumulative measure of direct and shared connections (i.e. mediated by neighbours) [13]. TOM takes into account two important features including connection strengths and the correlation direction (i.e. sign). Vertices exhibiting negative correlations are not connected, and as the correlation decreases, their connection strength approaches zero. Conversely, for vertices with positive correlations, as the correlation strengthens, so does their connection strength. This phenomenon is discussed in detail by Zhang et al. [14]. TOM removes antireinforcing connections while preserving both direct and reinforcing (shared neighbour) connections, with careful considerations to mitigate arbitrary factors during the transformation of correlation strengths, as discussed by Yip et al. [15]. For TDA, careful deliberation is necessary to select the most suitable representation of the data. Consequently, this study aims to improve phenotype prediction by taking into consideration the distance measures between point sets prior to TDA computation. The objective is to assess whether these measures can more effectively capture more definitive topological signatures from the data.

2 Background theory

The concepts of TDA are explained including the construction of the simplicial complex, persistence homology (PH), and vector-based transformation of the PH.

2.1 Persistent homology

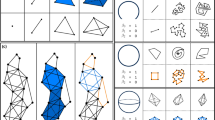
The basis of TDA relies on the identification of homology groups in a simplicial complex. Simplices on their own are mathematical objects consisting of a collection of vertices, edges, triangles, tetrahedra, octahedra, and other polyhedra. A simplicial complex can be defined as the collection of simplices by the intersection of simplex faces [16].

Fig. 1
figure 1

Construction of simplex units

Full size image
Fig. 2
figure 2

Filtration process resulting in the construction of the simplicial complex. Followed by summarising the topological signature across multiple dimensional spaces

Full size image

The \({ k}\)-dimensional simplex unit is built by \({ k}\) + 1 vertices. Such that, for each dimensional space, exists every face of a \({ k}\)-dimensional simplex. For example, a zero simplex is a single vertex, a one simplex is a connected edge with two vertices, a two simplex is a triangle with three vertices, and so on (see Fig. 1). A high-dimensional simplicial complex contains numerous \({ k}\)-dimensional simplices and is termed the Vietoris–Rips simplicial complex (VR Complex) [6]. The VR complex VR(X, r) associated with a metric space (X, d) is constructed by considering all possible simplices formed by subsets of points in X with pairwise distances less than or equal to a chosen radius parameter r. Each simplex in the complex represents a geometric configuration of points, and the complex captures the topological features of the underlying space in various dimensions [17]. The high dimensionality of the simplicial complex arises from the consideration of simplices of different orders. Specifically, a k-dimensional simplex corresponds to a set of (k+1) vertices within the given distance threshold. The VR complex provides a combinatorial representation of the topological structure of the metric space, enabling the study of its shape and connectivity [18].

The central idea of TDA is PH, and it is determined by a process known as filtration. This process involves the connection of data points over a changing distance parameter, termed the filtration value. As the filtration value increases, so does the overlap between point connections giving rise to \({ k}\)-dimensional simplices subsequently constructing the simplicial complex (see Fig. 2).

During filtration, various topological features emerge through a sequence of filtration steps (termed ’birth’), and as the filtration value increases, some topological features disappear (termed ’death’), within the context of the growing simplicial complex. Topological features are classified into different homology groups termed Betti numbers. The \(k^{th}\) Betti number represents the rank of the connectivity of vertices within the simplicial complex of the \(k^{th}\)-dimensional cycle or ’hole,’ forming a part of the simplicial complex (see Fig. 3). Notably, it is important to acknowledge the combinatorial complexity associated with computing high-order Betti numbers, like Betti-2, Betti-3, Betti-4, and so forth [19, 20].

Fig. 3
figure 3

The first three Betti numbers shown by possible shapes found in a simplicial complex. A Betti-0 topological feature shown as a vertex (can also be illustrated by two connected vertices), a Betti-1 topological feature shown as a circle and a Betti-2 topological feature shown as a sphere

Full size image

The first three Betti numbers include:

  • Betti-0: Number of connected data points

  • Betti-1: Number of one-dimensional cycles/circles

  • Betti-2: Number of two-dimensional holes/cavities

During filtration, the timeline of the formation of sequences of topological features is recorded, giving information about the birth and death of each topological feature [21]. As such, a topological feature is defined by the value of the filtration value where each feature arises (i.e. birth coordinate) and disappears (i.e. death coordinate). Topological features that persist for prolonged filtration iterations (i.e. also termed persistent Betti numbers) are deemed to be more informative compared to those that occur for short filtration iterations (which are likely to represent noise) [22,23,24,25]. The Betti numbers condense the actual data and reduce them to a purely topological representation valuable for understanding the underlying structure of the data. The Betti numbers are typically collated to a persistence diagram (PD) and is a useful representation that encode the PH by collating Betti numbers [26]. Every point on a PD can be represented by equation 1.

$$\begin{aligned} { D} = {b_{{ i}}, b_{{ j}}} | b{_{{ i}} < d{_{{ i}}}} \end{aligned}$$
(1)

where \(b_{{ i}}\) denotes the birth (the independent variable) and \(d_{{ i}}\) the death coordinate (the dependent variable) of the \(k^{th}\)-Betti topological feature. PDs embed useful information for all topological features detected during filtration. However, the output is a multiset which cannot be directly implemented in ML and DL machinery. As such, vector transformation of the PD’s multiset is required, where multiple techniques exist.

The simplest forms of vector-transformation techniques that exist include total persistence and persistence entropy. However, these representations oversimplify PD’s and poorly characterise data for ML and DL prediction tasks [27]. More stable and comprehensive vector representations, including persistent landscape (PL) and persistence image (PI), have been used to improve prediction [24, 28]. We exclude PLs as it is beyond the scope of this study. PIs are determined by applying a Gaussian kernel to each topological point in the persistence diagram (PD), transforming them into a collection of pixels on a standardised rectangular grid. The Gaussian kernel serves to weight the contributions of individual points, emphasising their significance based on proximity and intensity [29]. This gridded representation forms a structured array of values, encoding persistent topological information with spatial coherence. The choice of the Gaussian kernel enables a smooth and continuous transformation of topological features, allowing for nuanced extraction of Betti numbers that robustly characterise the underlying geometric and topological properties of the data [30]. Consequently, the intensity of each pixel represents the weighting function applied to each feature. More persisting topological features (i.e. long lifespan) are deemed more significant than less persisting topological features (i.e. short lifespan). The weight is defined as the absolute value of equation 2 proven by [24]:

$$\begin{aligned} \mathrm{Topological\;feature} = | b_{{ i}} - d_{{ j}} | \end{aligned}$$
(2)

The topological features for each point, denoted as (\({b, d}\)), provide a description of persistence intervals. Pixels on the PI are then converted into numerical values organised in a fixed-dimensional vector. These PIs serve as fixed-dimensional vectors encapsulating essential topological information, characterising gene expression data for each patient. This representation demonstrates promising utility in downstream classification tasks, where the distinctive features captured by PIs contribute to the effectiveness of the classification models [24, 30].

2.2 TDA for biological research

In the realm of biological sciences, TDA has proven to be a versatile tool, contributing to various applications ranging from classifying phenotypes based on imaging data [31] to characterising proteins at a topological level [32]. In genomics, TDA has continued to emerge as a breakthrough technique for extracting information from sequence data and has been applied to topics such as evolution and complex diseases, as detailed by [33]. In Parkinson’s disease research, gene expression has been combined with TDA to classify and predict phenotype [10]. In this study, we propose and evaluate a novel method that replaces distance correlation with TOM to construct a set of data points from gene expression data. Preliminary results indicate that this workflow enhances the VR complex, subsequently revealing numerous persistent topological features. Importantly, robust topological signatures representing the data were obtained in the current study, leading to an improvement in the prediction accuracy of the DL model.

3 Methods

3.1 Experimental workflow

Fig. 4
figure 4

A simple workflow detailing the methods followed in order to evaluate the DNN model performance based on learning from topological features obtained from PH computation generated from distance correlation measures and TOM. DGE Differential gene expression, DCM distance correlation measures, TOM topological overlap measures, PH persistent homology, DNN deep neural network

Full size image

3.2 Datasets

Patient transcriptomic data generated from RNA Sequencing (RNA-Seq) were obtained from The Cancer Genome Atlas (TCGA) data portal (https://portal.gdc.cancer.gov/). Four different cancer types including Breast Adenocarcinoma (BRCA), Lung Adenocarcinoma (LUAD), Colonic Adenocarcinoma, Rectal Adenocarcinoma (COAD/READ) and Prostate Adenocarcinoma (PRAD) cancers were focused on to evaluate the framework for various types of disease. The details of the datasets are summarised in Table 1.

Table 1 Cancer datasets obtained from TCGA
Full size table

To mitigate the computational cost for PH computation, two parameters, namely the size (n) and dimensionality of the VR complex (k), were considered. Our approach achieved this by selecting biologically relevant genes to reduce the dimensionality, aiming to address the expected combinatorial complexity associated with computing up to Betti-2 for each patient.

3.3 Gene filtering

3.3.1 Differential gene expression

The selection of biologically relevant genes was conducted through Differential Gene Expression (DGE) analysis, serving as the initial step to identify genes significantly up- and downregulated between cancer-afflicted and healthy cancer samples, thereby distinguishing the two sample groups. Before initiating the DGE analysis, we conducted a principal component analysis (PCA) to visually assess the separation between cancer-afflicted and healthy patient groups based on the gene expression profiles. PCA begins by calculating the covariance matrix of the standardised data. The covariance matrix describes the relationships between all pairs of variables, indicating the degree to which they vary together [45]. As such, PCA provides a comprehensive overview of the overall variance in the dataset and enables the observation of any distinct clustering patterns.

After obtaining raw counts for each gene, these counts were subjected to size factor normalisation to account for variations in library size across patient samples. Size factors were estimated individually for each sample, effectively scaling the counts based on library size differences [46]. Subsequently, normalised quotient counts were derived from the raw gene count values and the mean count value per gene across all patient samples, with the exclusion of gene count values below ten following the approach implemented by [47]. To facilitate a more robust analysis and visualisation, variance stabilising transformation (VST) was applied to the normalised counts before fitting the negative binomial model to identify DGE’s and for PCA.

For the DGE analysis, a negative binomial linear model was individually fitted for each gene. Subsequently, a Wald test was employed for significance testing to evaluate the differences between the actual and predicted estimates, as defined by a weighted distance [48]. The significance of the results was determined using the Benjamin–Hochberg-adjusted probability value (BH-adjusted p-value), with significance declared at p-values less than 5%. The BH-adjusted p-value was used as a false discovery rate (FDR), a correction method applied to p-values to account for the multiple comparisons problem. It helps control the proportion of false positives among significant findings [49]. Genes with a fold change (FC) greater than one were selected to represent up-regulation, while values less than one indicated down-regulation. Furthermore, log2FC were used instead of raw FC values, to linearise the FC values, making them more interpretable (i.e. a log2FC of one indicated a two-fold change) [50]. The R programming package DESeq2 [51] played a central role in the entire differential gene expression (DGE) analysis process, encompassing normalisation, transformation, identification of differentially expressed genes (DEGs), and principal component analysis (PCA).

Additionally, to elucidate the underlying genetic regulation of DEGs, we performed functional enrichment analysis using the R programming package clusterProfiler [52]. Our focus was specifically on Reactome, a well-established knowledgebase, to discern significantly enriched pathways associated with the observed gene expression changes [53]. To minimise the false FDR, we applied a stringent threshold of a BH-adjusted p-value of 5% or less. This approach enabled us to gain valuable insights into the molecular mechanisms and pathways implicated in neoplasm regulation relative to healthy or normal function. Overall, this analysis provides a robust foundation for the subsequent interpretation of biological significance in the obtained results. These comprehensive analyses collectively contribute to a deeper understanding of the molecular distinctions between cancer-afflicted and healthy patient samples. Gene expression matrices were then subsetted by preselecting significantly up- and down-regulated genes. The modified gene expression matrices were optimally split into train (\(X_{\textrm{train}}\)) (70%) and test (\(X_{\textrm{test}}\)) (30%) data [54, 55]. \(X_{\textrm{train}}\) was used to compute the distance correlation and TOM.

3.4 Distance correlation approaches

Measurement of the dependence between variables is the central way of projecting data into a topological space. In particular, the strength of the dependency (i.e. the correlation coefficient) with the Pearson correlation coefficient is the most used to evaluate linear relationships and is defined by equation 3 and proved by [56].

$$\begin{aligned} cor(X,Y) = \frac{cov(X,Y)}{\sqrt{Var(X)Var(Y)}} \end{aligned}$$
(3)

The Pearson correlation coefficient is defined by the quotient of the pairwise covariance and the variance of variable X and Y. The cor(X, Y) is a measure of \(\epsilon [-1,1]\). A \(|cor(X,Y)| = 1\) shows dependence and \(cor(X,Y) = 0\) shows independence between variable X and Y. However, variable X and Y can be non-independent whilst the \(cor(X,Y) = 0\), highlighting the importance of considering nonlinear relationships as shown in Fig. 5.

Fig. 5
figure 5

The correlation of data points between two random variables shown by the blue points. Positive correlations are shown to have positive gradients and negative correlations with negative gradients. Whilst non-independent correlations may have a Pearson correlation coefficient of zero, they appear to have nonlinear relationships depicted by the shape of the data points

Full size image

Distance correlations are unique in that they are more sensitive to detecting nonlinear relationships. Let two random variables be X and Y with finite second moments. The distance covariance can be defined by the following function. Let (X, Y), \((X',Y')\) and \((X'',Y'')\) be the independent and identically distributed duplicates. The distance covariance can therefore be defined by equation 4 and proved by [57].

$$\begin{aligned} dCor^{2}(X,Y):= & {} E(|X - X'||Y - Y'|)\nonumber \\{} & {} + E(|X-X'|)E(|Y-Y'|)\nonumber \\{} & {} - 2E(|X-X'||Y-Y''|) \end{aligned}$$
(4)

The distance correlation coefficient can be determined by equation 5.

$$\begin{aligned} dCor(X,Y):= \frac{dCov(X,y)}{\sqrt{dCov(X,Y)dCov(Y,Y)}} \end{aligned}$$
(5)

Distance correlation (dCor(X, Y)) is a nonnegative measure defined by dCor(X, Y) \(\epsilon [0, 1]\). The difference is that the distance correlation coefficient (that is, \(dCor(X,Y) = 0\)) is invariant with respect to linear transformations. Calculating the covariance between two variables determines the correlation. As such, covariance tending to zero indicates independence between variables and vice versa. The Python package dcor was used to calculate the covariance between pair of genes [58].

3.5 Topological overlapping measures

TOMs are an extension of the Pearson correlation coefficient; however, this measure considers neighbour-mediated strengths to recalculate correlation measures. Standard TOM measures (i.e. unsigned) consider that all neighbour-mediated strengths reinforce direct connections. However, this may not always be the case, and signed-TOM attempts to account for these considerations. In a signed-TOM network negative correlations are considered unconnected with their connection strength tending to zero, whereas unsigned-TOM considers negative correlations to have high connection strengths [14]. As such, unsigned-TOM take the absolute values of correlations failing to distinguish between positive and negative correlations. Signed-TOM corrects the direct connection strength by removing anti-reinforcing mediated connections. The input of signed-TOM requires the negative/positive sign of the correlation measure. This can be achieved by first defining the weighted network adjacency measures \({\hat{a}}_{i,j}\) as per equation 6 and shown by [59].

$$\begin{aligned} {\hat{a}}_{i,j} = \textrm{sign}(\textrm{cor}(x_{i},x_{j}))^\beta \end{aligned}$$
(6)

The \(x_{i}\) and \(x_{j}\) represent the \(i^{th}\) and \(j^{th}\) pair of vertices (i.e. pair of genes in a gene expression matrix). And the \(cor(x_{i},x_{j})\) of the similarity measures the pairwise similarity of genes using the Pearson correlation coefficient metric. The weighted adjacency measures are calculated by transforming the similarity measure by raising to the power value \(\beta \ge 1\). The adjacency encodes the network connection strength between a gene pair (\(x_{i}\) and \(x_{j}\)). The \(\beta \) value is determined by applying the scale-free topology criterion that implies that the degree distribution of the adjacency network must follow a power law. Following the computation of the adjacency network, the signed-TOM was determined as per equation 7 and proved by [14]:

$$\begin{aligned} \textrm{TOM}_{i,j} = \frac{|a_{i,j} + \sum _{u\ne i,j} {\hat{a}}_{i,u} {\hat{a}}_{u,j}|}{\min (k_{i},k_{j}) + 1 - |a_{aj}|} \end{aligned}$$
(7)

where \(k_{i}\) and \(k_{j}\) represent the connectivity of the \(i^{th}\) and \(j^{th}\) vertex. Signed-TOM preserves the sign of the relationship between vertices with respect to connections by shared neighbours. Both distance correlation measures and signed-TOM were used to form the VR complex for PH computation.

3.6 TDA implementation

Using the Python package Gudhi (https://gudhi.inria.fr), data were projected into a topological space from distance correlations and signed-TOM into VR complexes. A collection of topological features were collated by a weighted filtration approach during PH computation. Topological birth and death coordinates for the zero, first and second Betti numbers were determined for BRCA, LUAD, COAD/READ and PRAD datasets. To determine the weighted filtration rate for each patient’s VR complex, the Gudhi implementation shown in equation 8 was performed [60].

$$\begin{aligned} \textrm{filtration} = \max (2 \times F_{i}, 2 \times F_{j}, \textrm{dist}_{i, j} + F_{i} + F_{j}) \end{aligned}$$
(8)

Equation 8 determines the filtration rate based on the expression value of each gene pair. Such that, the largest value of the mathematical expression becomes the filtration rate for a specific gene pair. \(F_{i}\) describes the \(i^{th}\) gene, and \(F_{j}\) describes the \(j^{th}\) gene. The weighted filtration rates were based on the distance correlations and signed-TOM (i.e. \(\textrm{dist}_{i, j}\)) constructed from \(X_{\textrm{train}}\) for both \(X_{\textrm{train}}\) and \(X_{\textrm{test}}\) datasets. Consequently, \(X_{\textrm{test}}\) was omitted from the distance correlation/signed-TOM computation to prevent data leakage during model training and testing.

Patient-level topological signatures were represented as PDs (shown in Fig. 10a–h). PDs play a key role in TDA, by collating all the identified topological features (grouped by Betti numbers). The topological signatures in the form of PD multisets were vector-transformed into PIs for model prediction.

Fig. 6
figure 6

The developed TDA framework for the prediction of phenotype from gene expression data following DGE analysis. Distance correlations and signed-TOM are compared to assess the most appropriate representation of pairwise gene measures to infer topology

Full size image

3.7 Phenotype prediction

A deep neural network (DNN) was fitted on each patient’s PI to classify their phenotype. Following hyper-parameter tuning, the DNN model architecture included ten layers, a Rectified Linear Unit (ReLU) activation function with a regularisation step added to the loss function. Forward and back-propagation to adjust neural weights was performed with 2000 epochs to learn from topological signatures. The TDA framework was repeated five times using a reshuffled \(X_{\textrm{train}}\) and \(X_{\textrm{test}}\), and the mean and standard deviation were reported on \(X_{\textrm{test}}\) data (the mentioned process also known as the Monte Carlo cross-validation) [61]. Model training and testing were performed using the Python package scikit-learn ( https://scikit-learn.org/stable/). The entirety of the framework can be summarised by Fig. 6.

4 Results and discussion

4.1 Genetic filtering process

PCA was conducted on the RNA-Seq count matrices for each cancer dataset to evaluate the association between cancer-afflicted and healthy patient groups. The objective of this analysis in the context of gene expression was to visualise and explore the variation in expression patterns among the two groups. This facilitated the identification of sample clusters with similar expression profiles, the detection of outliers, and to highlight the most significant sources of variability in the data. This preliminary exploration was performed before engaging in the subsequent analysis for DGE.

Fig. 7
figure 7

PCA plots for cancer gene expression datasets, each point represents a patient sample, with its position determined alongside the Principal Components 1 (PC1) and 2 (PC2). The colour scheme distinguishes between cancer-afflicted patients (depicted in orange) and healthy patients (depicted in blue). The spread of points along the PC axes reflects the variance within the dataset; a broader distribution indicates higher variance. This visualisation highlights the differences in gene expression patterns between cancer-afflicted and healthy patients

Full size image

The PCA plots provide insights into the complexity of the phenotype classification task at hand, aiming to stratify cancer-afflicted and healthy patient groups. This complexity is particularly evident in the TCGA-BRCA, PRAD, and LUAD datasets. Within these datasets, the two phenotypes display a 10% variance across the PC1 axis. However, there is no clear clarification of sample disparities. When there is substantial overlap between classes or no clear separation in the reduced-dimensional space, it suggests that the task may be more challenging, and models might encounter difficulties in achieving high accuracy without overfitting. This observation emphasises the importance of conducting a DGE analysis to identify specific genetic factors contributing to the observed variations and challenges in phenotype classification. When there is substantial overlap between classes or no clear separation in the reduced-dimensional space, as indicated by PCA, it suggests that the task may be more challenging, and models might encounter difficulties in achieving high accuracy without overfitting [62]. Following the performance of the DGE analysis, the number of DEGs identified is summarised in Table 2. This information serves as a crucial foundation for further exploration and interpretation of the genetic changes associated with the phenotype differences observed in the PCA analysis.

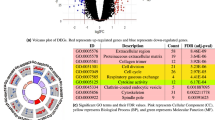
The PCA plots reveal less variance in the PRAD datasets, indicating a comparatively more homogenous gene expression pattern among samples within this dataset. In contrast, the COAD/READ datasets exhibit the most pronounced stratification, suggesting a higher degree of heterogeneity in gene expression profiles. This observation is consistent with the magnitude of the changes in gene expression reported earlier, reinforcing the notion that the extent of genetic alterations may contribute to the observed variance in the PCA plots. The magnitude of these changes provides insights into the genetic alterations associated with each cancer type, aiding further investigations into the potential biological mechanisms and pathways involved in cancer development. Functional enrichment was carried out to link the identified DEGs to interpret the level of genetic regulation, and the enriched Reactome pathways for both up-regulated and down-regulated genes are reported.

Table 2 Number of significant DEGs identified for each cancer gene expression dataset
Full size table
Fig. 8
figure 8

Dot plot illustrating enriched biological pathways in up- and down-regulated genes in cancer gene expression datasets. Each dot represents a specific pathway, with its position along the x-axis indicating the gene ratio (proportion of genes in the pathway among all analysed genes). The colour of each dot represents the significance of enrichment, with warmer colours indicating lower BH-adjusted p-values. Pathways associated with up-regulated genes are positioned on the right, while those associated with down-regulated genes are on the left

Full size image

The enriched biological pathways identified in this study offer a comprehensive view of the functional consequences of gene regulation. Up-regulated genes demonstrated heightened activity in several crucial pathways. G Protein-coupled receptor (GPCR) ligand binding suggested increased sensitivity to extracellular signals, potentially influencing cell signalling and communication [63]. Ion channel transport enrichment pointed to an enhancement in cellular responsiveness, emphasising the significance of ion flux in cellular homeostasis and communication [64]. The involvement of Class A/1 (Rhodopsin-like receptors) indicated specific regulation of receptors associated with sensory perception and cellular signalling [65]. Enrichment in potassium channels highlighted a potential impact on cellular excitability and signalling [66]. Furthermore, protein ligand binding enrichment underscored the importance of protein–protein interactions in mediating cellular processes [67].

Moving beyond pathway analysis, ligand–receptor binding is a fundamental process in cell signalling, orchestrating the transmission of information between cells [68]. Ligands, whether autocrine, paracrine, or endocrine, interact with specific receptors, categorised as cell surface or intracellular, initiating a sequence of events leading to cellular responses. Molecular recognition and binding between ligands and receptors trigger conformational changes, activating receptors [69]. Subsequently, signal transduction pathways are activated, involving various intracellular molecules, second messengers, and protein kinases. This intricate signalling cascade culminates in a cellular response, influencing processes such as gene expression, cell growth, and differentiation [70]. Understanding ligand–receptor interactions is crucial for unravelling the complexities of cell signalling and holds significance in drug development for targeting specific pathways in the treatment of diseases, including cancer and neurological disorders [71].

Conversely, down-regulated genes revealed distinctive sets of pathways associated with regulatory processes and cell cycle control. Moreover, the enrichment in cell cycle checkpoints implies the potential suppression of cell cycle progression, suggesting a regulatory mechanism to control cell division [72]. Mitotic spindle checkpoint enrichment suggests a potential disruption in the fidelity of chromosome segregation during cell division. All three observations are indicative of potential mechanisms to reduce cell growth and proliferation [73]. In addition, the presence of the keratinisation pathway, related to the formation of protective layers in epithelial tissues, may indicate alterations in tissue development or differentiation that could contribute to limiting cell growth [74]. Moreover, the enrichment in the condensation of phosphate chromosome pathway suggests potential modifications in chromatin structure and organisation, which could further influence the regulation of gene expression and cellular processes related to cell proliferation [75].

In summary, the identified enriched biological pathways provide detailed insights into the functional consequences of gene regulation in the studied dataset, covering a wide range of cellular processes, including signal transduction, ion transport, cell cycle regulation, and tissue development. Understanding these pathways is crucial for unravelling the molecular mechanisms underlying the observed gene expression patterns and their potential implications in cellular functions and diseases. Constructing topological features based on this level of genetic regulation in the analysed cancer datasets can provide further insights into the network properties and interactions shaping the observed gene expression patterns.

4.2 Discovering genetic interactions

The construction of the distance correlation and signed-TOM was used to form the VR complex. The distance correlation measures remains a popular correlation metric since it considers both linear and nonlinear association between two random variables. However, signed-TOM has been successful in computing weighted co-expression networks. Shown below is the distance correlation measure and signed-TOM from pre-selected cancer datasets.

Fig. 9
figure 9

Distance correlation and signed-TOM for each cancer dataset. The correlation coefficient measure is shown by the colour bar, the measurement of dependence (or strong connection strength for signed-TOM) is shown by yellow and independence (or weak connection strength for signed-TOM) is shown by blue colour (colour figure online)

Full size image

It is evident from figure 9 that a more complex mixture of dependence and independence (i.e. \(dCor(X,Y) \rightarrow 1\) and \(dCor(X,Y) \rightarrow 0\), respectively) exists between gene pairs for a VR complex constructed from a distance correlation measures. Signed-TOM depicts larger patterns of regions indicating strong and weak connection strengths between gene pairs, whereas distance correlation measures shows more complex interactions between gene pairs. This highlights the application of signed-TOM to identify coordinated gene clusters for the co-expression analysis highlighted by numerous published work [76,77,78,79].

The utility of distance correlation measures in bioinformatics research is recently emerging. Studies have highlighted that distance correlation better depicts the complexity of the coordination of gene expression levels than Pearson correlation measures which are the building blocks of signed-TOM [57, 80,81,82]. Research outputs following the implementation of distance correlation to co-expression analysis reveal that complex biological associations are identified compared to other correlation metrics including Pearson correlation coefficients [57]. This is the same observation seen in Fig. 9, whereby more definitive differences are observed between smaller groups of genes when constructed from distance correlation measures, whereas signed-TOM reveals the overall topology of the gene expression network (depicted by larger regions of gene groups of both strong and weak connection strengths) rather than the individual magnitudes of the relationship each gene pair. Furthermore, signed-TOM builds a more organised and structured VR complex by clustering larger groups of strongly connected and weakly connected genes.

Although signed-TOM may be limited to identifying linear dependence measures in the constructing the VR complex, nonlinear associations may be still embedded in the form of topology of the gene expression network. As such, the identification of complex topological features may be better suited from a simpler representation that highlights the topology of the dataset. We argue that the TDA implementation augments the identification of independent measures, oblivious to the signed-TOM, and the distance correlation measures may be directly obtained. Importantly, the structured nature of the VR complex may justify why during PH computation more topological features are identified and more informative (or higher dimensional) topological features are embedded. This combats limitations associated with the more disordered distance correlation measure that focuses on obtaining the individual distance magnitude between gene pairs, which reduces the potential to capture the overall topology of the gene expression network.

A depiction of this is illustrated in Fig. 10 where PDs for randomly selected cancer-afflicted patients from each cancer dataset were constructed from distance correlation and signed-TOM. The PDs summarise the topological signature for each patient by collating the birth and death coordinates for the \(k^{th}\)-Betti numbers.

Fig. 10
figure 10

A comparison between the topological signatures generated using distance correlation and signed-TOM are shown for randomly selected cancer patients in each TCGA cohort. The data points are coloured by the \(k^th\)-Betti number. Red points (Betti-0), blue points (Betti-1) and green points (Betti-2) are topological features identified during PH computation. The grey areas represent regions that do not contain topological features to satisfy \(b_{i} < d_{j}\)

Full size image

From the topological signatures summarised in the PDs (shown in Fig. 10) larger numbers of identified topological features are evident, in particular elevated volume of higher-dimensional topological features in the homology groups, Betti-1 and more specifically Betti-2 when using signed-TOM. The computation of higher-dimensional Betti numbers (greater than Betti-2) has seen sparked interest in the field of quantum computing, highlighting their potential importance to improve data representation [83]. Classical computers are prohibitively expensive for high-dimensional Betti number computation, compared to quantum algorithms that can approximate them in polynomial time [84]. As such, there is limited evidence to suggest that high-dimensional Betti numbers are more informative signals to understand the data. Regardless of the lack of supporting literature, we claim that the signed-TOM representation embeds far more high-dimensional topological features for the capacity of classical computer algorithms (i.e. up until Betti-2 topological features) compared to distance correlation measures. We also claim that Betti numbers greater than Betti-1 reveal more intricate and high resolution signals embedded in the VR complex. One study that supports these claims by Shi et al., showed that high-ordered topological features (computed up to Betti-3) played an important role in better explaining the complexity of brain function [85].

We hypothesise that higher-dimensional topological features in the VR complex constructed from the signed-TOM may reveal more information with regard to the complexity of gene expression data. To validate this hypothesis, vector transformation of the PDs was performed to form PI’s prior to phenotype prediction. Shown below are PI’s (randomly selected cancer-afflicted patients) showing a matrix of pixels generated by imposing a weight function to the points in the PD (i.e. identified topological features) to define the probability distribution for the points. From these distributions, a surface is constructed over the diagram to form the fixed-dimensional feature vector.

Fig. 11
figure 11

PI from an individual cancer-afflicted patient generated from distance correlation measures and signed-TOM summarising the vector-based transformed PD into a pixelised topological signature shown in the yellow regions. The intensity of the yellow spot is proportional to the density of the most appropriate persistent topological features

Full size image

4.3 Phenotype classification

The topological signature generated from signed-TOM not only indicates an increase in higher-dimensional Betti numbers (i.e. Betti-2) but also an increase in persistent topological features. This is depicted by the bright yellow pixels observed in higher frequencies in cancer patients with topological signatures built from signed-TOM (Fig. 11). As stated previously, low-persistence Betti numbers are more likely to be topological noise, while those with a high persistence values tend to correspond to meaningful information [86, 87]. To validate whether topological signatures embedded with more persisting topological features better represent a dataset, phenotype prediction using a DNN was performed. This was achieved using topological features in the form of PIs generated from signed-TOM on the selected cancer datasets as outlined in table 1.

Table 3 Topological data analysis built with distance correlations measures
Full size table
Table 4 Topological data analysis built with topological overlapping measures
Full size table

To evaluate the overall model performance, the Monte Carlo cross-validation method was employed (table 3 and 4). True-positive rate (TPR), also known as recall, represents how accurate the model was in predicting the phenotype correctly by measuring true positives (TP) divided by the sum of TP and false negatives (FN). Precision measures the number of TP over the sum of TP and false positives (FP). F1 scores are the mean of precision and accuracy. F1 (Macro) is computed using the arithmetic mean of all the F1 scores in each class, whereas F1 (Micro) computes a global average F1 score. The use of multiple metrics obtains a finer-grained idea of the performance of the classification model. In particular, by taking into account class imbalances observed for the selected cancer datasets in table 1.

Clear observations of improved phenotype prediction on topological signatures constructed from signed-TOM are shown in Table 4, with F1 scores moving from 60 s and 70 s to the high 80 s and 90 s. Furthermore, Table 4 highlights that in a sample size of approximately 60–70 unlabelled patients, the TDA framework constructed from signed-TOM correctly classifies the phenotype up to 90% of the time. From up-stream results, more high-dimensional and persistent topological features are identified from the VR complex constructed from signed-TOM. This is a remarkable observation since distance correlation measures have become the gold standard in measuring dependence and independence between two random variables. This may be attributed to signed-TOM taking into account gene neighbourhoods to determine the connection strength. This approach is observed to better defined gene groups, highlighted by its success in weighted gene co-expression analysis [88,89,90].

4.4 Further investigations

To further improve the constructed TDA framework, the incorporation of biological explainability should be investigated. Recall that Betti numbers are formed by vertices (or genes) and are identified using concepts of topology perspective. Therefore, gene sets representing Betti numbers can be related to biological function by performing functional enrichment analysis. Many of the ML/DL models are black boxes that do not explain their predictions in a way that humans can understand. The lack of transparency of predictive models can have consequences caused by bias. Incorporating biological annotation to the identified topological features will provide explainability to black-box ML/DL models but can uncover the underlying biological mechanisms that are used to classify a patient’s phenotype.

The field of biology stands to gain substantial advantages through the integration of TDA, particularly in the domains of phenotype prediction and biomarker discovery. The application of TDA within the biological context benefits from the insights provided by domain experts. In the realm of phenotype prediction, experts in biology can guide the selection of pertinent features (i.e. as performed by DGE analysis in this work), facilitate the integration of multi-omics data, and optimise algorithm parameters. TDA, in turn, captures the nuanced relationships among these features, unveiling intricate patterns resulting in the enhancement of prediction tasks. For biomarker discovery, TDA has the potential to become crucial as it aids in the identification of potential biomarkers, interpretation of topological networks, and integration of diverse data types. Furthermore, the integration of contextual knowledge is paramount for effective pathway analysis, validation, and interactive exploration of TDA results, ensuring their alignment with known biological mechanisms. The collaborative synergy between data scientists and experts in biology holds the key to unlocking the full potential of TDA, providing valuable insights into the complexities of biological datasets, such as cancer gene expression data.

This study emphasises the importance of marrying the implementations of domain knowledge to further improve computational methods. Our findings leads us to recommend the use of signed-TOM for the encoding RNA-Seq generated gene expression data into topological signatures using TDA. The results show that signed-TOM enhances the construction of the VR complex. Furthermore, the results show that the simplicial complex is enhanced due to the larger numbers of topological features (particularly higher-dimensional features—highlighted in the PDs) and more persistent topological features (highlighted in PIs), which are embedded in the VR complex. These findings are validated using a DNN to learn from the topological signatures constructed from distance correlations and signed-TOM and observe an increase in phenotype prediction performance using signed-TOM. Further work aims to apply this framework to datasets constructed from a variety of gene profiling platforms to eliminate the possibility of technical interference of the construction of the correlation measures. Furthermore, expanding the phenotype prediction using other diseases to validate our framework will also be pursued.

5 Conclusions

The concepts of topology are introduced as an ideal representation of nonlinear relationships in data as the overall structure is maintained despite homeomorphisms that shrink and stretch data [91]. We illustrate that TDA is also able to retain significant features through Betti numbers of the data despite excess noise through variability. Lastly, TDA computed with signed-TOM outperformed the popularly used distance correlations measures to create more informative PDs with more measurable features in various datasets. We make four observations to validate the enhancement of the VR complex. The first, we show the signed-TOM outputs large organised groups of genes, showing clear patterns of strong and weak connections of genes. The second observation is that the VR complex constructed from signed-TOM shows more data spread in a topological space and embeds numerous topological features of high dimensions. From this observation, we speculate that high-dimensional topological features can be seen as a measure of resolution. The third observation shows signed-TOM forms more persistent topological features during PH computation. Lastly, we show that the topological signature generated from signed-TOM with all the above stated attributes, improves cancer phenotype prediction accuracy scores by almost 20% compared to the popular distance correlation metric. As such, we recommend the use of signed-TOM for TDA encoding and the subsequent use for phenotype prediction on gene expression data generated from RNA-Seq.