Tracking Time Evolving Data Streams for Short-Term Traffic Forecasting

Abstract

Data streams have arisen as a relevant topic during the last few years as an efficient method for extracting knowledge from big data. In the robust layered ensemble model (RLEM) proposed in this paper for short-term traffic flow forecasting, incoming traffic flow data of all connected road links are organized in chunks corresponding to an optimal time lag. The RLEM model is composed of two layers. In the first layer, we cluster the chunks by using the Graded Possibilistic c-Means method. The second layer is made up by an ensemble of forecasters, each of them trained for short-term traffic flow forecasting on the chunks belonging to a specific cluster. In the operational phase, as a new chunk of traffic flow data presented as input to the RLEM, its memberships to all clusters are evaluated, and if it is not recognized as an outlier, the outputs of all forecasters are combined in an ensemble, obtaining in this a way a forecasting of traffic flow for a short-term time horizon. The proposed RLEM model is evaluated on a synthetic data set, on a traffic flow data simulator and on two real-world traffic flow data sets. The model gives an accurate forecasting of the traffic flow rates with outlier detection and shows a good adaptation to non-stationary traffic regimes. Given its characteristics of outlier detection, accuracy, and robustness, RLEM can be fruitfully integrated in traffic flow management systems.

1 Introduction

Data streams are ordered, potentially unbounded sequences of observations (data elements) made available over time [24, 43, 57, 58]. Data stream mining, the process of extracting knowledge from them, has arisen as a relevant topic in the machine learning field during the past decade [3].

In many data stream mining applications where data exhibit a time series nature, the goal is to predict information about future instances in the data stream given some knowledge about previous ones. This can be approached either by modelling of the dynamics of the system, or by autoregressive models. Within the field of road traffic analysis and forecasting, the latter approach has rapidly become widespread in recent years [48] due to the increase in both availability of sensed data and processing power to deal with them.

A common requirement in the task of mining data streams is the ability to distinguish the useful information from the useless ones. This may be required for limiting the usage of resources, for instance transmission bandwidth or storage memory; for summarization purposes; or even for relieving the user from information overload. As an example of this latter case, a sensor network may provide just the information that requires attention by the human supervisor, rather than transmitting all records. This task goes by the name of anomaly or outlier detection [7, 11].

One common approach to anomaly detection makes use of unsupervised learning: we learn a baseline model of the phenomenon of interest, and then measure the discrepancy of subsequent data from the baseline. An anomalous observation is the one that is not well explained by the model.

When operating within non-stationary environments for an extended time, the source of the stream may change over time. We distinguish between two types of change: for evolutionary, smooth changes, we use the term concept drift, while a radical, sudden change is labelled concept shift.

In this paper, we approach the problem of short-term traffic forecasting by employing the autoregressive approach, more suitable than a model-based one in the short-term because it can exploit the local time information, contained in recent observations and is computationally less demanding.

To tackle the issues of anomalies and non-stationarity, we employ an extension of the possibilistic clustering approach [34, 35] named Graded Possibilistic c-Means [15, 38] as a means to perform clustering of the non-stationary streaming data and employ the knowledge accumulated into the clusters to build a robust, accurate short-term traffic forecaster. Our proposed method has the ability to prevent outliers in the data stream from having a strong effect on the forecasting accuracy and is capable of both learning the data stream and analysing its evolution for the purpose of tracking it. To this end, an index to measure data stream change is proposed, based solely on the memberships to clusters, and not on additional measures.

We focus on the online approach to track and adapt to concept drift and shift and on using this knowledge to improve the ensemble forecasting model that was proposed in [1] by making the model able to not only detect outliers, but also track the changes in data streams.

An incremental retraining strategy is adopted, where the amount of retraining, and therefore the required computational effort, is modulated by the proposed measure of model change.

This paper is organized as follows. The next section summarizes the state of the art in streaming data clustering and traffic modelling, motivating the specific design choices of our proposal. Section 3 describes the proposed methodology. Section 4.1 presents the experimental validation and the discussion of results. Conclusions are given in Sect. 5.

2 Previous Work in the Fields of Data Stream Mining and Short-Term Traffic Forecasting

The subject of this work is traffic forecasting. This is one of the most relevant problems related to data stream mining. It can be cast either in the long term, where forecasts are used to configure and validate road management plans, or in the short term, for real-time decision-making. Short-term forecasting is the subject of this work.

Forecasting can be done with a system identification approach, often with macroscopic models [22]. Although it gives the most reliable results in the long-term forecasting problem, this approach is often not feasible for short-term forecasting, due to the inherent complexity of an accurate, first-principles model. The computation time required is often not compatible with the response time required.

The usual practice in this case is to use methods that forecast based on observations. This approach has developed out of the growing availability of data and, in parallel, of methods from data science, machine learning and computational intelligence [48].

Methods presented in the recent literature can be categorized into parametric models [16, 21, 46] and nonparametric or hybrid models [44, 47, 56].

Many traffic forecasting approaches focus on the problem of freeway/motorway traffic forecasting in which the state of the road traffic is quite stable. In contrast, traffic forecasting in urban and network-scale areas is more complex because of the rapid change of traffic behaviour and of the limited availability of sensors that can cover the whole network.

Many approaches based on nonparametric models to tackle this problem have been proposed, such as multilayer perceptron with a learning rule based on a Kalman filter [49], wavelet-based neural network [18], fuzzy-neural model [52], ARIMA models [23], graphical-lasso neural network [20], multi-task neural network [19], multi-task ensemble neural network [45], k-nearest neighbour nonparametric regression [53].

Most of these approaches are not meant to track changes in traffic behaviour [48]. This is the main motivation for our proposal, which is described in the next section.

Since our method is centred around data stream clustering, we also survey some related work on this topic. Most algorithms in this area [2, 4, 5, 26] focus on two aspects: detecting outliers without taking concept drift tracking into consideration and clustering irregularly distributed data, which is a challenging direction of research in the field.

Data stream clustering methods can be of the batch type, collecting a number of instances and then performing clustering on these accumulated data [31, 40]. Other methods are single-pass, storing summaries of past data as they are scanned [25]. The strategies of these algorithms can be incremental [9] or divide-and-conquer [4]. Yet other algorithms alter the structure of the data themselves so that they can be more effectively accessed [55].

Some popular stream clustering methods are density-based: they aim to find clusters of arbitrary shape by modelling them as dense regions separated by sparse regions [6, 13].

While this class of algorithms is popular and effective, they all produce only crisp partitions with no direct way to evaluate the outlierness of incoming data. An alternative strategy is to use fuzzy modelling for clustering.

Several incremental fuzzy clustering algorithms based on fuzzy c-means (FCM) [8] to track non-stationarity in data streams have been developed. Under the fuzzy modelling paradigm, each data point belongs to a cluster to a degree specified by a membership value. In general, as no membership is exactly null, a data point belongs to all clusters with different degrees.

Popular incremental fuzzy clustering algorithms for data streams include single-pass FCM [27] and online FCM (OFCM) [28]. Both process data chunk by chunk (by-pattern) and estimate centroids for entire data set by extracting summary information from each chunk, but the ways they handle chunks are different.

In [36], two algorithms based on fuzzy c-medoids (FCMD) [33], called online fuzzy c-medoids (OFCM) and history-based online fuzzy c-medoids (HOFCMD), are developed for clustering large relational data sets. In [39], it is shown that one medoid may not be sufficient to capture the underlying structure of a cluster. As a solution, in [50] an incremental fuzzy clustering approach called incremental multiple medoids-based fuzzy clustering (IMMFC) was proposed, which is based on the idea of OFCM and HOFCMD and includes a mechanism to select multiple medoids instead of a single one to represent each of the clusters in each chunk.

3 Methodology

Our choice has fallen on an autoregressive approach which forecasts one step in future after observing a suitable interval of past observations.

3.1 Data Pre-processing

The observed data are samples of traffic flow on a road network. At any given time, each arc of the network graph contains a given number of vehicles. Flow is defined as the number of vehicles per unit time. An arc is characterized by a maximum number of vehicles, its capacity. When flow approaches this value, the traffic slows down and enters a stop-and-go regime. Once the capacity is reached, traffic is entirely congested. We will be mainly concerned with relative flow, the ratio of flow to the arc capacity. Flow is sampled at discrete time intervals of the order of some minutes.

As already mentioned, data are organized in chunks of observations corresponding to a time lag vector. To forecast $f^a_t$, the traffic flow on arc a at time t, a vector of length T (the lag period) is used to represent a given chunk:

$$\begin{aligned} {\mathbf {x}}= \left[ f^a_{t-T}, f^a_{t-T+1},\ldots , f^a_{t-1}\right] . \end{aligned}$$

(1)

The vector ${\mathbf {x}}$ thus obtained describes the pattern of traffic flow variation over one past time interval of duration T in a neighbourhood of size n of arc a. In the rest of this paper, ${\mathbf {x}}$ will be the input to the method that is being described.

3.2 Forecasting Model Issues

The design of autoregressive methods requires solving the following issues.

Lag Period Proper selection of the lag period T, the size of the chunks, is crucial because it affects the correct representation of the data stream source. If the lag period is chosen too small, then we will not be able to distinguish between the time lag vectors in the vector space [10]; hence, the prediction process will be practically impossible because data do not carry enough valuable information. If the lag period is chosen too large, measurement will refer to times which are too far to have a significant correlation with the present, and therefore they will be irrelevant and act as noise [30].

In this paper, we adopt the minimum of the time-delayed mutual information as an estimation of the time lag [17]:

$$\begin{aligned} S(\tau )= - \sum \limits _{ij} p_{ij}(\tau ) \ln \frac{p_{ij}(\tau )}{p_{i}p_{j}} \end{aligned}$$

(2)

where for some partition of the real line into intervals:

• $p_{i}$ is the probability to find a time series value in the ith interval,

• $p_{ij}(\tau )$ is the joint probability that an observation at any time t falls into the ith interval and the observation at time $t+\tau$ falls into the jth one.

Unlike the autocorrelation function, the mutual information takes into account also nonlinear correlations. If the time-delayed mutual information exhibits a marked minimum, then $T=\arg \min _\tau S(\tau )$ is a good candidate for a suitable time delay. The obtained values are then confirmed by checking them against domain knowledge.

Note that if the minimum is not sufficiently prominent, then another method should be used. In the case of road traffic, the “memory” of the system is limited and this problem did not occur in our experiments.

Training Set Size This refers to the number of observation patterns that will be used to train the forecasters. This is usually not under the control of the designer, but in the problem at hand the availability of data has been found to be sufficient.

Outliers Handling Learning patterns with a different behaviour using the same model tends to reduce the model's performance. This can occur for both diversity in the operating conditions, in the presence of a stationary source, and changes in the underlying source itself (concept drift and shift), in the non-stationary case.

Accordingly, the proposed model focuses on two strategies: learning an ensemble of locally specialized models and explicitly measuring outlierness.

3.3 Robust Layered Ensemble Model

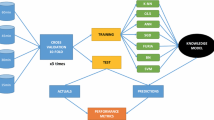
The proposed robust layered ensemble model (RLEM) for short-term traffic forecasting consists of two layers as shown in Fig. 1 and is able to track the changes in data streams, such as traffic flows, and to use this information to improve the forecasting accuracy.

Fig. 1

Diagram of the training stage in the RLEM. See text for details on the quantities and on the operational blocks mentioned in the diagram

The first layer of RLEM consists in a fuzzy clustering process having as its goals to cluster traffic flow chunks into c fuzzy clusters, where chunks with high membership to the same cluster represent similar temporal patterns, and at the same time to measure the outlierness degree of each chunk and consequently to measure the density of outliers.

To this aim, we employ an incremental clustering process based on the Graded Possibilistic c-Means (GPCM) [38] that is able to adapt to the changes in the traffic flow, by implementing a continuous learning that exploits the input chunks as they arrive. Intrinsic to this clustering method is a measure of outlierness that provides information about the goodness of fit of each input chunk to the clustering model.

In the second layer, an ensemble of a number of base learners acting as forecasters equal to the number c of clusters is used, each of them specialized on a homogeneous region of the data space. This approach follows the mixture of local experts model proposed in [29].

To obtain the c homogeneous regions of the data space needed for base learner training, we defuzzify the fuzzy segmentation performed by the first layer by assigning each chunk to the cluster where it has the highest membership (nearest neighbour criterion). To implement the base forecasters, we employ time-delayed neural networks (TDNN) [14] trained with the error back-propagation algorithm. Other choices may be implemented as well. The TDNN model is simply a multilayer perceptron neural network whose input is a time lag vector. In this work, one-hidden-layer networks are used for this purpose. We will indicate the network topology by specifying just the number of input, hidden and output units as a triplet, ni-nh-no, with the understanding that each layer is fully connected to the following and that hidden units are sigmoidal while output units are linear.

The measure of outlierness evaluated by the first layer is used in the second layer to assess and improve the forecasting accuracy.

In the following, we describe the specific clustering technique used.

3.4 The Graded Possibilistic c-Means

In central clustering, we have a training set of n instances (random vectors) and c clusters represented by means of their central points or centroids ${\mathbf {y}}_j$. Many central clustering methods perform the minimization of a objective function [8], that usually is the expectation of the distortion:

$$\begin{aligned} D&=\frac{1}{n}\sum _{l=1}^n\sum _{j=1}^c {u_{lj}}\,{d_{lj}}, \end{aligned}$$

(3)

$$\begin{aligned} l&=1, \ldots , n,\nonumber \\ j&=1, \ldots , c,\nonumber \\ {d_{lj}}&=\Vert {\mathbf {x}}_l-{\mathbf {y}}_j\Vert ^2 \end{aligned}$$

(4)

optimized with respect to centroids ${\mathbf {y}}_j$ and memberships ${u_{lj}}$, with some constraints placed on the total mass of membership to clusters

$$\begin{aligned} \zeta _l \equiv \sum ^{c}_{j=1} {u_{lj}}. \end{aligned}$$

(5)

In Eqs. 3 and 5, n is the cardinality of the data set, c is the number of clusters, while $\zeta _l$ can be interpreted as the total membership mass of observation ${\mathbf {x}}_l$. In the following of this subsection, we outline some relevant fuzzy central cluster models.

The first model we present is the maximum entropy (ME) or deterministic annealing approach [42] that imposes $\zeta _l=1$. In this case, we are in the probabilistic case, where memberships are formally equivalent to probabilities.

In addition to the expectation of the distortion (Eq. 3), the objective function $J_{\text {ME}}$ of ME includes the probabilistic constraint. The necessary conditions for the minimum of $J_{\text {ME}}$ are $\nabla J_{\mathrm {ME}} = 0$ that yields:

$$\begin{aligned} {u_{lj}}= \frac{e^{-{d_{lj}}/\beta }}{\zeta _l} \end{aligned}$$

(6)

and

$$\begin{aligned} {\mathbf {y}}_j = \frac{\sum _{l=1}^n {u_{lj}}{\mathbf {x}}_l}{\sum _{l=1}^n {u_{lj}}}\;. \end{aligned}$$

(7)

Equations 6 and 7 can be interpreted as the basis of a Picard iteration that leads to the minimum of a free energy at different levels of temperature (or fuzziness) that is regulated by the value of $\beta$ (deterministic annealing procedure). When $\beta$ is large, the free energy is equivalent to the unconstrained optimization of the expectation of the distortion (Eq. 3).

The objective function of ME is formally equivalent to the one of fuzzy c-means [8], and both of them show the problem of low outlier rejection: The memberships of outliers can be very large, not different from those of inliers.

In contrast to ME, the possibilistic c-means (PCM) [35] does not impose any constraint on $\zeta _l$, so memberships are not formally equivalent to probabilities but represent degrees of typicality to clusters.

The objective of PCM, $J_{\mathrm {PCM}}$ includes an individual parameter $\beta _j$ for each cluster, and $\nabla J_{\mathrm {PCM}} = 0$ yields

$$\begin{aligned} {u_{lj}}= e^{-{d_{lj}}/\beta _j} \end{aligned}$$

(8)

for membership of instances to clusters and Eq. 7 for cluster centres. Again, Eqs. 7 and 8 can be interpreted as the basis of a Picard iteration for the minimization of $J_{\mathrm {PCM}}$.

As discussed in [35], while the PCM produces membership functions that can be interpreted as measures of typicality of instances to clusters and shows a strong outlier rejection, the Picard iterations may fail to converge due to the lack of competitive terms in Eq. 8.

The graded possibilistic c-means (GPCM) clustering model proposed by our group [38] exploits the similarities of Eqs. 6 and 8 to obtain both the nice properties of memberships with the meaning of typicality and strong outlier rejection of the PCM and the convergence ability of the ME.

In this paper, we present a new simpler version of the GPCM. To this aim, we propose the following formula that unifies the Eqs. 6 and 8:

$$\begin{aligned} {u_{lj}}= \frac{v_{lj}}{Z_l}, \end{aligned}$$

(9)

where

$$\begin{aligned} v_{lj} \equiv e^{- {d_{lj}}/\beta _j} \end{aligned}$$

(10)

is called the free membership and $Z_l$ is the generalized partition function that is a function of the membership mass $\zeta _l$.

This allows us to add a continuum of other, intermediate cases to the two limit case models just described, respectively, characterized by $Z_l = \zeta _j$ (probabilistic) and $Z_l = 1$ (possibilistic). Here, we use the following formulation:

$$\begin{aligned} Z_l \equiv \zeta _l^\alpha = \left( \sum _{j=1}^c v_{lj}\right) ^\alpha , \quad \alpha \in [0, 1], \end{aligned}$$

(11)

where the parameter $\alpha$ controls the possibility level, from a totally probabilistic ($\alpha =1$) to a totally possibilistic ($\alpha =0$) model, with all intermediate cases for $0<\alpha <1$. The Picard iteration implementing the GPCM iterates the membership evaluation (Eq. 9), and the cluster centres evaluation (Eq. 7) until convergence.

In the GPCM model at each iteration of the Picard procedure, $\beta _j$ is updated [35] according to:

$$\begin{aligned} \beta _j = \frac{\sum ^{N}_{i=1} u_{ij} \, d_{ij}}{k \,\sum ^{N}_{i=1} u_{ij}}, \quad j= 1, \ldots , c \end{aligned}$$

(12)

Note that in the GPCM after training $\zeta _l \in (0, c)$ depends on the value of $\alpha$. More specifically:

• values $\zeta _l \approx 1$ are typical of regions well covered by centroids;

• but $\zeta _l\gg 1$ is very unlikely for good clustering solutions, since it implies many overlapping clusters;

• finally, $\zeta _l \ll 1$ characterizes regions not covered by centroids, and any observation occurring there is an outlier.

In order to reject outliers, let us define the degree of outlierness index $\varOmega$, corresponding to the concept of being an outlier, as follows:

$$\begin{aligned} \varOmega ({\mathbf {x}}_l) = \max \left\{ 1-\zeta _l, 0\right\} . \end{aligned}$$

(13)

For each threshold on $\varOmega$ we set, we obtain a region of inlier in the data space and we define as outliers the data outside this region.

Differently from other approaches based on analysing instance-centroid distances [54], the GPCM provides a direct measure of outlierness that is not referred to local density or to individual clusters, but is defined with respect to a whole clustering model.

Outlierness can be modulated by an appropriate choice of $\alpha$. Low values correspond to sharper outlier rejection, while higher values imply wider cluster regions and therefore lower rejection. For $\alpha =1$, the GPCM becomes probabilistic and loses its ability to identify or reject outliers.

We can define the initial outlier density $\rho _0\in [0, 1)$ as the average degree of outlierness:

$$\begin{aligned} \rho _0 = \frac{1}{|W_0|}\sum _{l\in W_0} \varOmega ({\mathbf {x}}_l), \end{aligned}$$

(14)

where $W_0$ is an initial window of data to “bootstrap” GPCM and provides an initial clustering.

The average density $\rho _0$ accounts for both frequency and intensity, or degree of anomaly, of outliers. This is a mean, so quantity and intensity can compensate each other, so that the effect of few strong outliers is the same as that of many moderate outliers.

During execution, outlier intensity at step $l>|W_0|$ is computed as follows:

$$\begin{aligned} \rho _{l} = 0.01 \, \varOmega ({\mathbf {x}}_{l-1}) \, + 0.99 \, \rho _{l-1}, \end{aligned}$$

(15)

where $\varOmega _l$ is the measure of outlierness at step l. Note that the density is a function of the past values, being a convex combination of current outlierness and past density (exponentially weighted moving average). The exponential time constant is $-\ln 100\approx 4.6$, similar to the typical lag periods T used in this study.

The updating formula can also be rewritten as

$$\begin{aligned} \rho _{l} = \rho _{l-1} \, +\,0.01\,\left( \;\varOmega ({\mathbf {x}}_{l-1}) - \rho _{l-1}\;\right) \end{aligned}$$

(16)

to make it evident that it is a Robbins–Monro-type [41] formula for approximating $\varOmega$, with step size of 0.01 kept fixed to enable continuous tracking, and with $\varOmega ({\mathbf {x}}_{l-1}) - \rho _{l-1}$ acting as the stochastic gradient estimate at step $t-1$.

The GPCM parameters are updated during the execution as follows. To avoid premature convergence, the possibility degree $\alpha$ is made dependent on $\rho$, so as to increase centroid coverage when outliers are detected:

$$\begin{aligned} \alpha _l = \alpha _0 + \rho _l (1-\alpha _0) \end{aligned}$$

(17)

Note that $\alpha _l$ is a function of the current density and of $\alpha _0$, its baseline value, so this formula is not a moving average.

The spread parameter for each centroid, $\beta _{j}$, is similarly updated during the execution as follows:

$$\begin{aligned} \beta _{j,l+1} = \beta _{j,l} + \rho _l \, (\beta _{j,0}-\beta _{j,l}), \end{aligned}$$

(18)

which provides the ability to roll back closer to the initial values of $\beta$ when the model is not adequate any more, as indicated by the value of $\rho$.

3.5 Ensemble Forecast Model

As shown in Fig. 1, for each cluster, a forecaster with architecture shown in Table 1 is trained and $\zeta _l$ is obtained, which is quantity computed for each chunk in the training data set.

Table 1 RLEM model parameters used for the short-term traffic forecasting for the three data sets

After the training stage, we start the forecasting stage as shown in Fig. 2 where chunks come as a stream. For each upcoming input chunk i, $\zeta _i$ is computed and compared to a threshold. In the proposed model, the threshold is selected as the minimum of $\zeta _l$ observed on the training set:

$$\begin{aligned} \varTheta \equiv \min \limits _l \; \; \zeta _l. \end{aligned}$$

(19)

Fig. 2

Diagram of the forecasting stage in the RLEM. See text for details on the quantities and on the operational blocks mentioned in the diagram

However, other choices, more or less restrictive, are possible based on the quantity and reliability of the training data.

After the training stage, we start the online forecasting stage. When a new chunk is presented to RLEM, if $\zeta <\varTheta$ it is considered an extreme outlier and will be dropped.

Technically, this is implemented as follows. We compute the binarized membership mass of the input chunk, defined as:

$$\begin{aligned} \zeta ^B= \left\{ \begin{array}{ll} {\displaystyle 0 } &{} {\text{ for }}\,\zeta <\varTheta \\ {\displaystyle 1 } &{} {\text{ otherwise }} \\ \end{array} \right. . \end{aligned}$$

(20)

The upcoming chunk is considered as an extreme outlier and is dropped (rejected) if $\zeta _i^B=0$.

The drop rate of the input chunks depends on the value of $\alpha$ which controls the sensitivity of the model to outliers. A high value of $\alpha$-means less sensitivity to outliers and a lower drop rate.

For detecting concept shift in traffic flows, we use average density $\rho$ as an indicator of the reliability of the forecasting model.

The final output of the RLEM is computed as a weighted sum of the individual base learner forecasts [29], as follows:

$$\begin{aligned} f= \sum ^{c}_{j=1} f_ju_j/\zeta \end{aligned}$$

(21)

In Eq. (21), we see that the output $f_j$ of each forecaster is weighted by $u_j$, which is the membership degree of each chunk to each cluster, so that $u_j$ will have a high value for the most suitable forecaster(s) and low to the others.

Note that, despite the possibilistic nature of the GPCM method, this weighting is convex ($\sum _j u_j/\zeta = 1$) because of the use of $\zeta$ as a partition function, since outliers and concept drift/shift have been taken into account in the previous layer.

3.6 Retraining

During operation, the system collects a sliding window of a fixed number of past observations from the input stream. When the outlier density $\rho$ is over a certain threshold $\rho _t$, the model is considered inadequate and a retraining step is triggered.

In the retraining step, the centroids and forecasters are trained on the current data window, so as to make them up to date.

4 Experiments and Results

The experimental validation of proposed robust layered ensemble model included the test of the clustering procedure based on the Graded Possibilistic c-Means on an artificial data set with built-in concept drift and shift. Then, we applied RLEM to the short-term forecasting of three traffic flow data sets.

4.1 Data Sets

The data sets employed in our experimental analysis are:

• Gaussian data set that is a synthetic data set with four evolving two-dimensional Gaussian distributions [12]. Along time, one new data point is added and one removed randomly so that the total number stays constant. However, the underlying data source (centroid positions) is slowly changed, leading to concept drift. Concept shift is obtained by removing a whole segment of the sequence at time 4000 where the stream changes abruptly. The data set was generated using the Matlab program ConceptDriftData.m available at https://github.com/gditzler/ConceptDriftData.

• PeMS that is a data set by the Caltrans Performance Measurement System (PeMS) available at http://pems.dot.ca.gov. The traffic flow data are collected every 30 s from over 15,000 detectors deployed across California. The collected data are aggregated in 5-min periods. In [37], a deep learning model was developed using these data.

• UK road network that contains multiple data sets obtained from different road links in the United Kingdom (UK) available at http://www.highways.gov.uk. This data series provides traffic flow information for 15-min periods since 2009 on most of road links in UK. The data set obtained from the loop sensor id AL2989A (TMU Site 30012533) containing traffic flow between 2009 and 2013 was used in [51] for the validation of traffic forecasting approach.

• Genoa Data set containing traffic data of a town obtained via simulation as follows as a part of our contribution to the PLUG-IN project.¹ An urban area of the city of Genoa, a town in the north-west of Italy, was mapped with the aid of Open Street Map data available at https://www.openstreetmap.org. Traffic parameters were obtained from actual observations and several days of traffic were simulated by using the SUMO open source traffic simulator [32]. Figure 5 shows the area of interest and the graph used to model it which consists of 27 nodes, 74 links, 7 external points and 19 connections. The simulation yielded observations at time intervals of 5 min obtained from a specific link and from a fixed number of adjacent links to forecast the traffic to a short-term timescale.

4.2 Implemented Models

The learning task associated with the Gaussian data set is non-stationary data streaming tracking and outlier detecting. We approach this problem using the GPCM clustering model.

Table 1 shows the values of parameters of the RLEM implementations for the short-term traffic forecasting for PeMS, UK and Genoa data sets. Each data corresponds to the average traffic flow measured in the observation period.

The size of the data chunk is the time lag estimated as the minimum of the time-delayed mutual information, as noted in Sect. 3.2. The estimated time lags for PeMS, UK and Genoa data sets correspond, respectively, to 35 min, one day and 20 min.

For the first stage of RLEM that implements a GPCM model for chunk clustering, we set five clusters for all data sets.

The base learners of the second layer of the RLEM are time-delayed neural networks (TDNN) using multilayer perceptrons with three layers. The dimension of the input layer of multilayer perceptrons is identical to the size of the chunk and the hidden layers are set to 10 units for the three cases, while the output is unidimensional and corresponds to estimation of the traffic flow.

4.3 Choice of Parameters

As most adaptive methods, the RLEM model includes three types of parameters: Model parameters, optimization parameters, and evaluation parameters.

Model parameters directly influence the operation of the system in the inference (forecasting) phase. Although the model just described includes several parameters, the only actual, user-selected model parameters are the number of forecasters c and the topology of the individual forecasters. When the number of forecasters is increased, it has been observed that the performance of the system increases accordingly, although not proportionally. Additional model parameters influencing the trade-off between stability and reactivity of the system are the adaptation gain for the moving-average update of $\rho$ and the lag period T. For both the user can choose an arbitrary value, but reasonable, objective selection criteria have been previously discussed [Eqs. (16), (2)]. The membership threshold $\varTheta$ should operate on extreme observations. Even if criteria other than Eq. (19) are employed to set its value, it should not impact normal operation.

Most parameters described are optimization parameters. These have an indirect influence on the system’s behaviour, being related to the evolution of the system in time. These include initial values for $\alpha$ and $\beta$, the size of the initial window $W_0$, and the optimization parameters for the individual forecasters which depend on the training strategy adopted (in this study, we used the error back-propagation algorithm) but do not have a strong influence on the result due to the use of an ensemble. As for the actual numerical values of these parameters, $\alpha$ has an absolute interpretation and values in [0.85, 1) can be used. However, $\beta$ strongly depends on the magnitude, distribution and dimensionality of the data and on the location of clusters, so a general indication cannot be given, although empirical methods like analysing the histogram of pairwise distances between samples can be attempted.

Finally, evaluation parameters include the metrics employed to measure performance and the relative size of training set and test set. These do not have a strong influence on the results provided that the metrics are reasonably related to actual performance on the field, that they are used consistently in comparisons and that the absolute size of training and test set are sufficient. Repeated experiments have shown that this latter point was not an issue with the data sets used in this study.

4.4 Experimental Results and Discussion

4.4.1 Gaussian Data Set

Figure 4 shows the outlierness index $\rho$ (Eq. 14) during the tracking of the Gaussian data set. Five snapshots, taken at different times, are shown in Fig. 3 and labelled with numbers corresponding to those in Fig. 4. Dots represent the 100 most recent data points of the evolving data set. Stars are the current centroids.

Fig. 3

The five snapshots taken during the clustering process of the Gaussian data set (see Fig. 4). In each snapshot, red stars are centroids. Dots are the 100 previous data points, with the 30 most recent in darker colour

Fig. 4

Degree of outlierness during the tracking of the Gaussian data set. The numbers under the curve correspond to the five snapshots in Fig. 3

The outlierness index is high when the clustering model does not fit well the data, indicating an inadequacy situation. Observing the snapshots in Fig. 3 and referring to the outlierness indicator in Fig. 4 show that the model can quickly adapt to the novelty:

• 1. After recovering from a moderate drift with respect to initial configuration.

• 2. After some outliers have appeared (note the fast recovery of the outlierness indicator in Fig. 4).

• 3. Clusters are changing their relative position but the data support stays approximately the same. Outlierness slightly increased.

• 4. Concept shift. The data support changes abruptly from the south-west to the north-east part of the graph. Outlierness peaks.

• 5. Recovery from concept shift. Incoming data points are no longer considered as outliers (Fig. 5).

Fig. 5

The road network for the short-term traffic forecasting study and the corresponding graph

4.4.2 PeMS

In Fig. 6, a forecasting experiment on the traffic flow data that were used in [37] for comparing the forecasting capabilities of the stacked autoencoder (SAE), the back-propagation neural network (BP-NN) and the radial basis function neural network (RBF-NN) using three days data for training and the upcoming seven days data for testing. The figure shows the forecasting results obtained by the RLEM using the same training and test sets.

Fig. 6

PeMS data set: forecasting results of RLEM (measured values are in blue; forecasted values are in red)

In Table 2, we compare forecasting performances of the models studied in [37] with the RLEM. The performance indexes used in the table are:

• The mean squared error (MSE) measuring the average error of the forecasting results:

  $$\begin{aligned} {\mathrm{RMSE}}= \sqrt{\frac{1}{N}\sum ^{N}_{i=1}(t_i - \hat{t}_i)^2}, \; \; i=1, \ldots , N, \end{aligned}$$

  (22)

  where $t_i$ is the observed traffic value, $\hat{t}_i$ is its forecasted value and N is the size of the test set.

• The drop rate (DR) is defined as follows:

  $$\begin{aligned} \mathrm{DR} = 1 - \frac{\sum ^{i=N}_{i=1} \zeta ^B_i}{N} \end{aligned}$$

  (23)

Table 2 Performance comparison on PeMS data set

With a drop of 9 outliers corresponding to a DR $=$ .0044, the RLEM shows the best root mean squared error.

4.4.3 UK and Genoa Data Sets

Figure 7 shows the effect of $\alpha$ on the accuracy (mean square error) of the RLEM model for the UK road network data set. The selected range of $\alpha$ values are $.93\le \alpha \le 1$. An appropriate value of $\alpha$ allows us to control the degree of outlierness, drop unwanted outliers and improve the accuracy rate. The values of the RMS are very small, but this magnitude depends on the range of the data. What carries useful information is actually the change in these values, i.e. the relative differences between values.

Fig. 7

RLEM model accuracy w.r.t $\alpha$ in UK for 3 months

Figure 8 shows the scatter plots of the traffic flow forecasting using the UK road network data set (a), and the one for Genoa data set (b), both with zero drop rate. The correlation coefficients are, respectively, .98 and .99. Figure 9 shows data from the UK data set as a continuous line, with forecast output superimposed as round dots, with a similar representation as in Fig. 6.

Fig. 8

Results of the two forecasting problems. a Scatter plot between the target and the output (UK data set), b forecast output and the target (Genoa data set). The regression curves are in blue

Fig. 9

Forecasted output and the target on the UK data set with 0 drop rate

Figure 10 shows the binarized mass of membership $\zeta ^B_i$ for the chunks of the test set. Where the value of $\zeta ^B_i$ drops the forecasting performance decreases, because the data are not well explained by the model. This makes $\zeta ^B_i$ a good indicator of model reliability and forecasting performance even during the inference phase, i.e. when targets are not available.

Fig. 10

Binarized sum of membership of each chunk to all clusters during a run on the UK data set

5 Conclusions

In this paper, we have proposed the RLEM model for short-term traffic flow forecasting. The model combines the graded possibilistic c-means clustering and ensembles of time-delayed neural networks and uses an outlierness density index to measure the reliability of the forecaster model.

We evaluated the performance of clustering model on synthetic data set, for which the ground truth is available, and then we evaluated the performance of RLEM model on three data sets. For the PeMS data set, we compared our results with SAE, BP NN and RBF NN models, and the results show that the proposed method gives an accurate forecasting of the traffic flow rates with outlier detection and shows a good adaptation to non-stationary traffic regimes. For the UK data sets, we show that the proper selection of $\alpha$ improves the forecasting accuracy.

Given its characteristics of outlier detection, accuracy and robustness, RLEM can be fruitfully integrated into real-time traffic flow management systems.