Abstract
The increasing size of RDF data requires efficient systems to store and query them. There have been efforts to map RDF data to a relational representation, and a number of systems exist that follow this approach. We have been investigating an alternative approach of maintaining the native graph model to represent RDF data, and utilizing graph database techniques (such as a structure-aware index and a graph matching algorithm) to address RDF data management. Since 2009, we have been developing a set of graph-based RDF data management systems that follow this approach: gStore, gStore-D and gAnswer. The first two are designed to support efficient SPARQL query evaluation in a centralized and distributed/parallel environments, respectively, while the last one aims to provide an easy-to-use interface (natural language question/answering) for users to access a RDF repository. In this paper, we give an overview of these systems and also discuss our design philosophy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Resource Description Framework (RDF) data model was originally proposed by W3C for modeling WebObjects as part of developing the semantic web. However, its use is now wider than the semantic web. For example, Yago and DBpedia extract facts from Wikipedia automatically and store them in RDF format to support structural queries over Wikipedia [5, 26]; biologists encode their experiments and results using RDF to communicate among themselves leading to RDF data collections, such as Bio2RDF (bio2rdf.org) and Uniprot RDF (http://www.uniprot.org/format/uniprot_rdf). Related to semantic web, Linking Open Data (LOD) project builds an RDF data cloud by linking more than 3000 datasets. The use of RDF has further gained popularity due to the launching of “knowledge graph” by Google in 2012.
An RDF dataset is a collection of triples of the form \(\langle\)subject, property, object\(\rangle\). A triple can be naturally seen as a pair of entities connected by a named relationship or an entity associated with a named attribute value. In contrast to relational databases, an RDF dataset is self-describing and does not need to have a schema (although one can be defined using RDFS). The simplicity of this representation makes it easy-to-use RDF for modeling various types of data and favors data integration.
There exist many large-scale RDF datasets, e.g., FreebaseFootnote 1 has 2.5 billion triples [6] and DBpeidaFootnote 2 has more than 170 million triples [17]. LOD now connects more than 3000 datasets and currently has more than 84 billion triples,Footnote 3 with the number of data sources doubling within three years (2011–2014). The growth of RDF dataset sizes and the expansion of their use, coupled by the definition of a declarative query language (SPARQL) by W3C, have made RDF data management an active area of research and development, and a number of RDF data management systems have been developed.
As with any database management system (DBMS), an RDF data management system has to address the challenges of efficiency, scalability and usability. However, these exhibit themselves in somewhat different ways, as we describe below:
-
1.
Efficiency Flexible pattern-matching capabilities of SPARQL language and the large volume of RDF repositories entail efficiency challenges for complex queries. Furthermore, SPARQL queries tend to involve more join steps compared to relational queries. Thus, an RDF system requires specific query optimization techniques to improve its efficiency.
-
2.
Scalability The computational and storage requirements coupled with rapidly growing RDF datasets have stressed the limits of single machine processing. For further scalability, a distributed/parallel RDF system is likely required.
-
3.
Usability Although SPARQL is a standard language to access a RDF dataset, it remains tedious and difficult for end users, because of the complexity of the SPARQL syntax and the RDF schema. Thus, providing end users an easy-to-use interface is of crucial importance in many knowledge graph applications.
-
4.
Ability to deal with change Many of the early work assume that RDF datasets are stationary. However, a number of more recent applications deal with dynamic, and streaming RDF datasets from RDF-encoded social networks.Footnote 4 Interest has now shifted to managing and querying dynamic and streaming RDF datasets [36].
There are two typical approaches to designing RDF data management systems: relational approaches and graph-based approaches [22]. The relational approaches map RDF data to a tabular representation in a number of ways and then execute SPARQL queries on them—sometimes mapping SPARQL queries to SQL. These can further be grouped into four categories:
-
Direct relational mappings This approach (e.g., Sesame [8] and Oracle [9]) exploits the fact that RDF triples have a natural tabular structure and directly maps RDF triples to a single table with three columns (subject, property, object).Footnote 5 The SPARQL query can then be translated into SQL and executed on this table. The advantage is that the mature relational query processing and optimization techniques can be utilized. However, many queries involve a large number of self-joins that are difficult to optimize.
-
Single table exhaustive indexing These systems (e.g., Hexastore [30] and RDF-3X [20, 21]) incorporate a native storage system that allows extensive indexing of the triple table, for example one index for each possible permutation of the subject, property and object attributes. Each of these indexes is sorted lexicographically by the first column, followed by the second column, followed by the third column. These are then stored in the leaf pages of a clustered B\(^{+}\)-tree. Consequently, SPARQL queries can be efficiently processed regardless of where the variables occur (subject, property, object) since one of the indexes will be applicable. The downside is the space overhead as well as the computational overhead of maintaining these indexes for dynamic datasets.
-
Property tables This approach exploits the regularity exhibited in RDF datasets where there are repeated occurrences of patterns of statements. Consequently, it stores “related” properties in the same table. Example systems include Jena [31] and IBM’s DB2RDF [7].
-
Binary tables This approach [1, 2] follows column-oriented database schema organization and defines a two-column table for each property containing the subject and object, resulting in a set of tables each of which are ordered by the subject. This is a typical column-oriented database organization and benefits from the usual advantages of such systems such as reduced I/O due to reading only the needed properties and reduced tuple length, compression due to redundancy in the column values, etc.
The second major category of systems is graph-based, which model both RDF data and the SPARQL query as a graph and evaluate the query by subgraph matching using homomorphism, e.g., [3, 34, 38, 39]. The advantage of this approach is that it maintains the original representation of the RDF data and enforce the intended semantics of SPARQL. Also, some graph database techniques, such as the structure-aware indices [38, 39] and graph-based query algorithms [34], are more suitable for RDF data. The challenge is to perform subgraph matching efficiently—this is a well-known computationally expensive problem. We have been developing a graph-based RDF data management system, called gStore, since 2009.Footnote 6 In this paper, we review our research results and provide an overview of our graph-based data management techniques.
There are three pieces of gStore that warrant description. The first is a centralized graph-based RDF triple store that stores a RDF graph using adjacency lists [38, 39]. Two key techniques incorporated in gStore are (a) a neighborhood structure-aware index that encodes the neighborhood structure of vertices in data graphs into “signatures” and builds a tree-structured index over them, and (b) employing graph homomorphism-based subgraph match algorithm to find answers to SPARQL queries instead of relational join processing. Furthermore, gStore can also handle the dynamic updates to the RDF data efficiently. This is described in Sect. 3.
The second piece is a distributed version of gStore, called gStore-D [23] that addresses scale-out issues. The novel aspect of gStore-D is the adoption of “partial evaluation and assembly” framework. A large graph is divided into several fragments, each of which is resident at one site (we do not consider replication at this point). The key issue then becomes how to find the subgraph matches (of SPARQL query Q) that cross multiple fragments—these are called crossing matches. We address this using the partial evaluation approach where a SPARQL query is executed over each fragment of RDF graph to find local partial matches that are then assembled to compute the crossing matches. This is described in Sect. 4.
The third piece addresses usability. Although SPARQL is the standard query language for RDF, it is not an easy language to learn and use, especially for casual users. Therefore, we also design a RDF question/answering system, called gAnswer [37], to answer users’ natural language questions over RDF repositories. The core idea is to translate a natural language question to a semantic query graph and employ subgraph pattern-matching technique to figure out the answers. This is described in Sect. 5.
2 Preliminaries
In this section, we provide an overview of RDF and SPARQL. Readers can refer to W3C documents (such as RDF primerFootnote 7 and SPARQL 1.1 RecommendationFootnote 8) for more details.
RDF represents data as a collection of triples of the form \(\langle\)subject, property, object\(\rangle\), where subject is an entity, class or blank node, a property is one attribute associated with one entity and object is an entity, a class, a blank node or a literal value. In RDF, entities, classes and properties are denoted by URIs (Uniform Resource Identifier) that refers to named resources. Blank nodes refer to anonymous resources that do not have a name.
Definition 1
(RDF dataset) Let pairwise disjoint infinite sets I, B and L denote URI, blank nodes and literals, respectively. An RDF dataset is a collection of triples, each of which is denoted as \(t(\mathrm{subject},\mathrm{property},\mathrm{object}) \in (I \cup B) \times I \times (I\cup B \cup L)\).
A triple can be naturally seen as a pair of nodes connected by a named relationship. Hence, an RDF dataset can be represented as a graph where subjects and objects are vertices, and triples are edges with property names as edge labels. Note that there may exist more than one property between a subject and an object, that is, multiple-edges may exist between two vertices in an RDF graph.
Definition 2
(RDF graph) An RDF graph is a four-tuple \(G=\langle V,L_\mathrm{V}, E,L_\mathrm{E} \rangle\), where
-
1.
\(V=V_\mathrm{c}\cup V_\mathrm{e} \cup V_\mathrm{b} \cup V_\mathrm{l}\) is a collection of vertices that correspond to all subjects and objects in RDF data, where \(V_\mathrm{c}\), \(V_\mathrm{e}\), \(V_\mathrm{b}\) and \(V_\mathrm{l}\) are collections of class vertices, entity vertices, blank vertices and literal vertices, respectively.
-
2.
\(L_\mathrm{V}\) is a collection of vertex labels. Given a vertex \(u \in V_\mathrm{l}\), its vertex label is its literal value. Given a vertex \(u \in V_\mathrm{c} \cup V_\mathrm{e}\), its vertex label is its corresponding URI. The vertex label of a vertex in \(V_\mathrm{b}\) (blank node) is NULL.
-
3.
E is a collection of directed edges \(\{\overrightarrow{u_i,u_j}\}\) that connect the corresponding subjects (\(u_i\)) and objects (\(u_j\)).
-
4.
\(L_\mathrm{E}\) is a collection of edge labels. Given an edge \(e \in E\), its edge label is its corresponding property.
An edge \(\overrightarrow{u_iu_j}\) is an attribute property edge if \(u_j \in V_\mathrm{l}\); otherwise, it is a link edge. \(\square\)
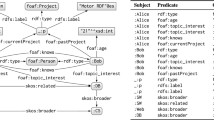
A sample of RDF dataset is given in Table 1, whose corresponding RDF graph is given in Fig. 1a.Footnote 9
SPARQL is the query language for RDF. The fundamental building block of SPARQL is the basic graph pattern (BGP), which is a collection of triples.
Definition 3
(Basic Graph Pattern) A basic graph pattern is a connected graph, denoted as \(Q=\{V(Q),\) \(E(Q)\}\), such that (1) \(V(Q) \subseteq (I \cup L \cup V_\mathrm{Var})\) is a set of vertices, where I denotes URI, L denotes literals, and \(V_\mathrm{Var}\) is a set of variables; (2) \(E(Q) \subseteq V(Q) \times V(Q)\) is a set of edges in Q; and (3) each edge e in E(Q) either has an edge label in I (i.e., property) or the edge label is a variable.
A match of BGP over RDF graph is defined as a partial function \(\mu\) from \(V_\mathrm{Var}\) to the vertices in the RDF graph. Formally, we define the match as follows:
Definition 4
(BGP Match) Consider an RDF graph G and a connected query graph Q that has n vertices \(\{v_1,\ldots ,v_n\}\). A subgraph M with m vertices \(\{u_1,\ldots ,u_m\}\) (in G) is said to be a match of Q if and only if there exists a function \(\mu\) from \(\{v_1,\ldots ,v_n\}\) to \(\{u_1,\ldots ,u_m\}\) (\(n \ge m\)), where the following conditions hold:
-
1.
if \(v_i\) is not a variable, \(\mu (v_i)\) and \(v_i\) have the same URI or literal value (\(1\le i \le n\));
-
2.
if \(v_i\) is a variable, there is no constraint over \(\mu (v_i)\) except that \(\mu (v_i)\in \{u_1,\ldots ,u_m\}\);
-
3.
if there exists an edge \(\overrightarrow{v_iv_j}\) in Q, there also exists an edge \(\overrightarrow{\mu {(v_i)}\mu {(v_j)}}\) in G; furthermore, \(\overrightarrow{\mu {(v_i)}\mu {(v_j)}}\) has the same property as \(\overrightarrow{v_iv_j}\) unless that the label of \(\overrightarrow{v_iv_j}\) is a variable.
The set of matches for Q over RDF graph G is denoted as \(\llbracket Q \rrbracket _G\), based on which, we return variable bindings that are defined in the SELECT clause.
Example 1
“Find all movies directed by Stanley Kubrick and report their movie names.” The SPARQL query is given as follows.

Note that this is a BGP query, since it contains a set of triples without UNION, OPTIONAL and FILTER clauses. The variables are prefixed by “?” and each triple ends with a period (.).
The graph representation of this query is given in Fig. 1b. The answers to the query are bindings to variable ?moviename as shown bellow.

A general SPARQL query may contain FILTER, UNION, OPTIONAL clauses. Note that these are optional according to SPARQL syntax. Formally, a general graph pattern in SPARQL is defined as follows:
Definition 5
Graph Pattern A graph pattern in SPARQL is defined as follows:
-
1.
if P is a BGP, P is a graph pattern;
-
2.
if \(P_1\) and \(P_2\) are both graph patterns, \(P_1\) AND \(P_2\), \(P_1\) UNION \(P_2\), \(P_1\) OPTIONAL \(P_2\) are all graph patterns;
-
3.
If P is a graph pattern and R is a SPARQL built-in condition, then the expression (P FILTER R) is a graph pattern.
A SPARQL built-in condition is constructed using the variables in SPARQL, constraints, logical connectives (\(\lnot\), \(\wedge\), \(\vee\)), inequality symbols (\(\le\), \(\ge\), <, >), the equality symbol (\(=\)), unary predicates like bound, isBlank and isIRI, plus other features [24, 29]. We formally define the answers of SPARQL based on BGP matches.
Definition 6
(Compatibility) Given two BGP queries \(Q_1\) and \(Q_2\) over RDF graph G, \(\mu _1\) and \(\mu _2\) define two matching functions from vertices in \(Q_1\) (denoted as \(V(Q_1)\)) and \(Q_2\) (denoted as \(V(Q_2)\)) to the vertices in RDF graph G, respectively. \(\mu _1\) and \(\mu _2\) are compatible when for all \(x \in V(Q_1 ) \cap V(Q_2 )\), \(\mu _1(x)=\mu _2(x)\), denoted as \(\mu _1 \sim \mu _2\); otherwise, they are not compatible, denoted as \(\mu _1 \not \sim \mu _2\).
Definition 7
(SPARQL Matches) Given a SPARQL query with graph pattern Q over a RDF graph G, a set of matches of Q over G, denoted as \(\llbracket Q \rrbracket _{G}\), is defined recursively as follows:
-
1.
If Q is a BGP, \(\llbracket Q \rrbracket _G\) is defined in Definition 4.
-
2.
If \(Q=Q_1 \; \mathrm{AND} \; Q_2\), then \(\llbracket Q \rrbracket _G = \llbracket Q_{1} \rrbracket _G \bowtie \llbracket Q_{2} \rrbracket _G= \{ \mu _1 \cup \mu _2 \, {\big |} \, \mu _1 \in \llbracket Q_{1} \rrbracket _G \wedge \mu _2 \in \llbracket Q_{2} \rrbracket _G \wedge (\mu _1 \sim \mu _2 ) \}\)
-
3.
If \(Q=Q_1 \; \mathrm{UNION} \; Q_2\), then \(\llbracket Q \rrbracket _G = \llbracket Q_{1} \rrbracket _G \cup \llbracket Q_{2} \rrbracket _G = \{ \mu \, {\big |} \, \mu \in \llbracket Q_{1} \rrbracket _G \vee \mu \in \llbracket Q_{2} \rrbracket _G \}\)
-
4.
If \(Q=Q_1 \; \mathrm{OPT} \; Q_2\), then \(\llbracket Q \rrbracket _G = (\llbracket Q_{1} \rrbracket _G \bowtie \llbracket Q_{2} \rrbracket _G \cup (\llbracket Q_{1} \rrbracket _G \backslash \llbracket Q_{2} \rrbracket _G = \{ \mu _1 \cup \mu _2 \, {\big |} \, \mu _1 \in \llbracket Q_{1} \rrbracket _G \wedge \mu _2 \in \llbracket Q_{2} \rrbracket _G \wedge (\mu _1 \not \sim \mu _2) \}\)
-
5.
If \(Q=Q_1 \; \mathrm{Filter} \; F\), then \(\llbracket Q \rrbracket _G = \Theta _F (\llbracket Q_{1} \rrbracket _G = \{ \mu _1 {\big |} \mu _1 \in \llbracket Q_{1} \rrbracket _G \; \mathrm{and} \; \mu _1 \; \mathrm{satisfies} \; F\}\)
The following example illustrates SPARQLs with “OPTIONAL”.
Example 2
“Report all movie names directed by Stanley Kubrick and their related book names if any.”

whose results are:

Note that most existing work focus on BGP query processing and optimization, which is also the focus of this paper, although gStore can support full graph pattern queries as defined in Definition 7.
3 gStore: A Graph-Based Triple Store
gStore [38, 39] is a graph-based RDF data management system (or what is commonly called a “triple store”) that maintains the graph structure of the original RDF data. Its data model is a labeled, directed multiedge graph (called RDF graph—see Fig. 1a), where each vertex corresponds to a subject or an object. We also represent a given SPARQL query by a query graph Q (Fig. 1b). Query processing involves finding subgraph matches of Q over the RDF graph G. gStore incorporates an index over the RDF graph (called VS*-tree) to speedup query processing. VS*-tree is a height-balanced tree with a number of associated pruning techniques to speedup subgraph matching.
3.1 Techniques
In this subsection, we briefly review the main techniques employed in gStore. As mentioned earlier, we process SPARQL queries by subgraph matching, which is computationally expensive. To reduce the search space and improve query performance, there are two key techniques in gStore: vertex encoding and indexing/querying techniques.
Encoding Techniques
Answering SPARQL queries is equivalent to finding subgraph matches of query graph Q over RDF graph G. If vertex v (in query Q) can match vertex u (in RDF graph G), each neighbor vertex and each adjacent edge of v should match to some neighbor vertex and some adjacent edge of u. In other words, the neighbor structure of query vertex v should be preserved around vertex u in RDF graph. We call this as the neighbor-structure preservation principle. Accordingly, for each vertex u, we encode each of its adjacent edge labels and the corresponding neighbor vertex labels into bitstrings, denoted as vSig(u), which we call a signature. We also encode query Q using the same encoding method. Consequently, the match between Q and G can be verified by simply checking the match between corresponding signatures. This is helpful because matching fixed-length bitstrings is much easier than matching variable length strings.
Given a vertex u, we encode each of its adjacent edges e(eLabel, nLabel) into a bitstring, where eLabel is the edge label and nLabel is the vertex label. This bitstring is called edge signature (i.e., eSig(e)). It has two parts: eSig(e).e, eSig(e).n. The first part (M bits) denotes the edge label (i.e., eLabel), and the second part (N bits) denotes the neighbor vertex label (i.e., nLabel). eSig(e).e and eSig(e).n are computed as follows:
\({{Computing }eSig(e).e}\) Given an RDF repository, let |P| denote the number of different properties. If |P| is small, we set \(|eSig(e).e|=|P|\), where |eSig(e).e| denotes the length of the bitstring and build a 1-to-1 mapping between the property and the bit position. If |P| is large, we resort to the hashing technique. Let \(|eSig(e).e | = M\). Using an appropriate hash function, we set m out of M bits in eSig(e).e to be "1". Specifically, we employ m different string hash functions \(H_i\) (\(i=1,\ldots ,m\)), such as BKDR and AP hash functions [12]. For each hash function \(H_i\), we set the (\(H_i(eLabel)\) mod M)-th bit in eSig(e).e to be "1", where \(H_i(eLabel)\) denotes the hash function value. The parameter setting problem is discussed in detail in our research paper [39].
\({{Computing } eSig(e).n}\) We first represent nLabel by a set of q-grams [14], where an q-gram is a subsequence of q characters from a given string. For example, “The\(\_\)Shining\(\_\)(film)” is represented by a set of 3-grams: \(\{\)(The),(he\(\_\)),(e\(\_\)S),...,\(\}\). Then, we use a string hash function H for each q-gram g to obtain H(g). We set the (H(g) mod N)-th bit in eSig(e).n to be '1". We also use n different hash functions for each q-gram. Finally, the string’s hash code is formed by performing bitwise OR over all q-gram’s hash codes. Figure 2 demonstrates the whole process.
\({{Computing } vSig(u)}\) Assume that u has n adjacent edges \(e_i\), \(i=1,\ldots ,n\). We first compute \(eSig(e_i)\) according to the above methods. Then, \(vSig(u)=eSig(e_1)\vee eSig(e_2) \vee \ldots \vee eSig(e_n)\), \(\vee\) is a bitwise OR operator.
For a query vertex v in SPARQL query Q, we have the analog encoding technique to compute vSig(v) (Fig. 3).
Theorem 1
Consider a query vertex v (in SPARQL query Q ) and a data vertex u (in RDF graph G ), if vSig(v) & \(vSig(u) \ne vSig(v)\), where “&” represents the bitwise ADD operation, vertex u cannot match v; otherwise, u is a candidate to match v.
Proof
If vSig(v) & \(vSig(u) \ne vSig(v)\), it means that there exists at least one edge e(eLable, nLabel) adjacent to v that does not match any edge adjacent to u. This contradicts the neighbor-structure preservation principle. Thus, u cannot match v. \(\square\)
Index Structure and Query Evaluation
According to the encoding technique, each node in both the query graph and the RDF graph is encoded into bitstrings. Theorem 1 tells us the basic pruning principle. In order to speedup filtering, we design an index, called VS\(^*\)-tree, which is a height-balanced tree [38], where each node is a bitstring that corresponds to each vertex’s code. It is a multi-level summary tree where the leaves contain the vertices in the original encoded RDF graph, and higher levels summarize the structure of the level below it. An example of VS\(^*\)-tree is given in Fig. 4. In the filtering process, we visit VS\(^*\)-tree from the root and judge whether the visited nodes are candidates. We prove that if a node at one level does not meet the condition, none of its children can match that condition. Thus, the subtree rooted at that node is pruned safely from VS\(^*\)-tree. Then, each vertex in query graph has a candidate list of nodes in the data graph. Finally, applying a depth-first search strategy, we perform a multi-way join over these candidate lists to find subgraph matches.
3.2 System Architecture
In this section, we present the system architecture, as illustrated in Fig. 5. The whole system consists of an offline part and an online part.
The offline process stores the RDF dataset and builds the VS\(^*\)-tree index. RDF Parser accepts a number of popular RDF file formats, such as N3, Turtle. The parsing result is a collection of RDF triples. We build an RDF graph using adjacency list representation for these triples, where each entity is a vertex (represented by its URI) and each triple corresponds to an edge connecting two corresponding vertices. We use a key-value store to index the adjacency lists, where URIs are keys. In the Encoding Module, we encode the RDF graph G into a signature graph \(G^*\) using the encoding technique discussed earlier. Finally, VS\(^*\)-tree builder constructs a VS\(^*\)-tree over \(G^*\). The signature graph \(G^*\) and the VS\(^*\)-tree are stored in key-value store and VS\(^*\)-tree store, respectively.
The online system consists of four modules. A SPARQL statement is the input to the SPARQL Parser, which is generated by a parser generator library called ANTLR3.Footnote 10 The SPARQL query is parsed into a syntax tree, based on which, we build a query graph Q and encode it into a query signature graph \(Q^*\) as discussed earlier.
The online query evaluation process consists of two steps: filtering and joining. First, we generate the candidates for each query node using VS\(^*\)-tree (Filter Module). Then, applying a depth-first search strategy, we perform the multi-way join (Join Module) over these candidate lists to find the subgraph matches of SPARQL query Q over RDF graph G.
gStore’s code is publicly released on Github,Footnote 11 including source codes, documents and benchmark test report. It currently has more than 140,000 lines of C++ code, not including generated SPARQL parser code. It provides both the console and the API interfaces (including C++, Java, Python, PHP). A client/server development is also supported.
4 gStore-D: A Distributed Graph Triple Store
The increasing size of RDF data requires a solution with good scale-out characteristics. Furthermore, the increasing amount of RDF data published on the Web requires distributed computing capability. We address this issue by developing a distributed version of gStore that we call gStore-D [23].
Given a RDF graph G, we adopt a vertex-disjoint graph partitioning algorithm (such as METIS [16]) to divide G into several fragments, such as Fig. 6. In the vertex-disjoint graph partitioning, any vertex u is only resident at one fragment and we also say that vertex u is an inner vertex of the fragment. If a vertex u is linked to another vertex in the other fragment, u is called a boundary vertex. In our method, we allow some replica of the boundary vertices between different fragments. In Fig. 6, vertex 008 (in fragment \(F_2\)) is a boundary vertex, since it is linked to vertex 003 in fragment \(F_1\). Thus, we allow the replica of 008 in fragment \(F_1\). The replica is called an extended vertex in \(F_1\). We note that gStore-D does not require a specific graph partitioning strategy, although different partitioning strategies may lead to different performance. For now, we consider each fragment being placed at one site. The main challenge in gStore-D is that evaluating a query may involve accessing multiple fragments. Some partition of the query may be answered within a fragment (i.e., subgraph matches are evaluated locally) that we call local partial matches (defined in Definition 8). Others, however, may require determining matches across fragments that we call crossing matches. Local partial matches can be handled using the technique of the previous section, but evaluating crossing matches requires a new approach. For this, we adopt a “partial evaluation and assembly” strategy. We send the SPARQL query Q to each fragment \(F_i\) and find local partial matches of query Q over fragment \(F_i\). If a local partial match is a complete match of Q, it is called an “inner match” in fragment \(F_i\). The main issue of answering SPARQL queries over the distributed RDF graph is finding crossing matches efficiently. We illustrate the main idea of gStore-D using the following example.
Example 3
Assume that an RDF graph G is partitioned into two fragments as shown in Fig. 6. Considering the following SPARQL query, its query graph is given in Fig. 7. The subgraph induced by vertices 003,006, 007,008, 012, 013 and 014 (shown in the shaded vertices and the red edges in Fig. 6) is a crossing match of Q.

As noted above, the key issue in the distributed environment is how to find crossing matches; this requires subgraph matching across fragments. For query Q in Fig. 7, the subgraph induced by vertices 003,006, 007,008, 012, 013 and 014 is a crossing match between fragments \(F_1\) and \(F_2\) in Fig. 6 (shown in the shaded vertices and red edges).
As mentioned earlier, we adopt the partial evaluation and assembly [15] strategy in our distributed RDF system design. Each site \(S_i\) treats fragment \(F_i\) as the known input s and other fragments as yet unavailable input \({\overline{G}}\). Each site \(S_i\) finds all local partial matches of query Q within fragment \(F_i\). We prove that an overlapping part between any crossing match and fragment \(F_i\) must be a local partial match in \(F_i\). Then, these local partial matches are assembled into the complete matches of SPARQL query Q.
Figure 8 demonstrates how to assemble local partial matches. For example, the subgraph induced by vertices 003, 006, 008 and 012 is an overlapping part between M and \(F_1\). Similarly, we can also find the overlapping part between M and \(F_2\). We assemble them based on the common edge \(\overrightarrow{008,003}\) to form a crossing match.
To summarize, there are three major steps in our method.
-
Step 1 (Initialization) A SPARQL query Q is input and sent to all sites.
-
Step 2 (Partial Evaluation) Each site finds local partial matches of Q over fragment \(F_i\). This step is executed in parallel at each site.
Recall that each site \(S_i\) receives the full query graph Q (i.e., there is no query decomposition). In order to answer query Q, each site \(S_i\) computes the partial answers (called local partial matches) based on the known input \(F_i\). Intuitively, a local partial match \(\mathrm{PM}_i\) is an overlapping part between a crossing match M and fragment \(F_i\) at the partial evaluation stage. Moreover, M may or may not exist depending on the yet unavailable input \({\overline{G}}\) . Based only on the known input \(F_i\), we cannot judge whether or not M exists. For example, the subgraph induced by vertices 003, 006, 008 and 012 (shown in shaded vertices and red edges) in Fig. 6 is a local partial match between M and \(F_1\).
Definition 8
(Local Partial Match) Given a SPARQL query graph Q with n vertices \(\{v_1,\ldots ,v_n\}\) and a connected subgraph PM with m vertices \(\{u_1,\ldots ,u_m\}\) (\(m \le n\)) in a fragment \(F_k\), PM is a local partial match in fragment \(F_k\) if and only if there exists a function \(f:\{v_1,\ldots ,v_n\}\rightarrow \{u_1,\ldots ,u_m\} \cup \{\mathrm{NULL}\}\), where the following conditions hold:
-
1.
If \(v_i\) is not a variable, \(f(v_i)\) and \(v_i\) have the same URI or literal or \(f(v_i)=\mathrm{NULL}\).
-
2.
If \(v_i\) is a variable, \(f(v_i) \in \{u_1,\ldots ,u_m\}\) or \(f(v_i)=\mathrm{NULL}\).
-
3.
If there exists an edge \(\overrightarrow{v_iv_j}\) in Q (\(1 \le i\ne j \le n\)), then PM should meet one of the following five conditions: (1) there also exists an edge \(\overrightarrow{f{(v_i)}f{(v_j)}}\) in PM with property p, and p is the same to the property of \(\overrightarrow{v_iv_j}\); (2) there also exists an edge \(\overrightarrow{f{(v_i)}f{(v_j)}}\) in PM with property p, and the property of \(\overrightarrow{v_iv_j}\) is a variable; (3) there does not exist an edge \(\overrightarrow{f{(v_i)}f{(v_j)}}\), but \(f{(v_i)}\) and \(f{(v_j)}\) are both in \(V_k^e\); (4) \(f{(v_i)}=\mathrm{NULL}\); (5) \(f{(v_j)}=\mathrm{NULL}\).
-
4.
PM contains at least one crossing edge, which guarantees that an empty match does not qualify.
-
5.
If \(f(v_i) \in V_k\) (i.e., \(f(v_i)\) is an internal vertex in \(F_k\)) and \(\exists \overrightarrow{v_i v_j} \in Q\) (or \(\overrightarrow{v_j v_i} \in Q\)), there must exist \(f(v_j) \ne \mathrm{NULL}\) and \(\exists \overrightarrow{f(v_i)f(v_j)} \in \mathrm{PM}\) (or \(\exists \overrightarrow{f(v_j)f(v_i)} \in \mathrm{PM}\)). Furthermore, if \(\overrightarrow{v_i v_j}\) (or \(\overrightarrow{v_j v_i})\) has a property p, \(\overrightarrow{f(v_i)f(v_j)}\) (or \(\overrightarrow{f(v_j)f(v_i)}\)) has the same property p.
-
6.
Any two vertices \(v_i\) and \(v_j\) (in query Q), where \(f(v_i)\) and \(f(v_j)\) are both internal vertices in PM, are weakly connected in Q. We say that two vertices are weakly connected if there exists a connected path between two vertices when all directed edges are replaced with undirected edges.
Vector \([ f{(v_1)},\ldots , f{(v_n)}]\) is a serialization of a local partial match.
Step 3 (Assembly) Each site finds all local partial matches in the corresponding fragment. The next step is to assemble partial matches to compute crossing matches and compute the final results. We propose two assembly strategies: centralized and distributed (or parallel). In centralized, all local partial matches are sent to a single site for assembly. For example, in a client/server system, all local partial matches may be sent to the server. In distributed/parallel, local partial matches are combined at a number of sites in parallel.
We first define the conditions under which two partial matches are joinable. Obviously, crossing matches can only be formed by assembling partial matches from different fragments.
Definition 9
(Joinable) Given a query graph Q and two fragments \(F_i\) and \(F_j\) (\(i \ne j\)), let \(\mathrm{PM}_i\) and \(\mathrm{PM}_j\) be the corresponding local partial matches over fragments \(F_i\) and \(F_j\) under functions \(f_i\) and \(f_j\). \(\mathrm{PM}_i\) and \(\mathrm{PM}_j\) are joinable if and only if the following conditions hold:
-
1.
There exist no vertices u and \(u^\prime\) in \(\mathrm{PM}_i\) and \(\mathrm{PM}_j\), respectively, such that \(f^{-1}_i(u)=f^{-1}_j(u^\prime )\).
-
2.
There exists at least one crossing edge \(\overrightarrow{uu^\prime }\) such that u is an internal vertex and \(u^\prime\) is an extended vertex in \(F_i\), while u is an extended vertex and \(u^\prime\) is an internal vertex in \(F_j\). Furthermore, \(f^{-1}_i{(u)}=f^{-1}_j{(u)}\) and \(f^{-1}_i{(u^\prime )}=f^{-1}_j{(u^\prime )}\).
The first condition says that the same query vertex cannot be matched by different internal vertices in joinable partial matches. The second condition says that two local partial matches share at least one common crossing edge that corresponds to the same query edge.
The join result of two joinable local partial matches is defined as follows.
Definition 10
(Join Result) Given a query graph Q and two fragments \(F_i\) and \(F_j\), \(i\ne j\), let \(\mathrm{PM}_i\) and \(\mathrm{PM}_j\) be two joinable local partial matches of Q over fragments \(F_i\) and \(F_j\) under functions \(f_i\) and \(f_j\), respectively. The join of \(\mathrm{PM}_i\) and \(\mathrm{PM}_j\) is defined under a new function f (denoted as \(\mathrm{PM}=\mathrm{PM}_i \bowtie _{f} \mathrm{PM}_j\)), which is defined as follows for any vertex v in Q:
-
1.
if \(f_i(v) \ne \mathrm{NULL} \wedge f_j(v)=\mathrm{NULL}\) Footnote 12, f(v) \(\leftarrow\) \(f_i(v)\) Footnote 13;
-
2.
if \(f_i(v) = \mathrm{NULL} \wedge f_j(v)\ne \mathrm{NULL}\), f(v) \(\leftarrow\) \(f_j(v)\);
-
3.
if \(f_i(v) \ne \mathrm{NULL} \wedge f_j(v) \ne \mathrm{NULL}\), f(v) \(\leftarrow\) \(f_i(v)\) (In this case, \(f_i(v)=f_j(v)\))
-
4.
if \(f_i(v) = \mathrm{NULL} \wedge f_j(v) = \mathrm{NULL}\), f(v) \(\leftarrow\) NULL
Example 4
Let us recall query Q in Fig. 7. Figure 8 shows two different local partial matches \(\mathrm{PM}_1^2\) and \(\mathrm{PM}_2^2\). We also show the functions in Fig. 8. There do not exist two different vertices in the two local partial matches that match the same query vertex. Furthermore, they share a common crossing edge \(\overrightarrow{008,003}\), where 008 and 003 match query vertices \(v_3\) and \(v_5\) in the two local partial matches, respectively. Hence, they are joinable. Figure 8 also shows the join result of \(\mathrm{PM}_1^2 \bowtie _{f} \mathrm{PM}_2^2\).
In the centralized assembly, all local partial matches are sent to a final assembly site. We propose an iterative join algorithm to find all crossing matches. In each iteration, a pair of local partial matches is joined. When the join is complete (i.e., a match has been found), the result is returned; otherwise, it is joined with other local partial matches in the next iteration. In order to reduce the join space of the iterative join algorithm, we divide all local partial matches into multiple partitions such that two local partial matches in the same set cannot be joinable; we only consider joining local partial matches from different partitions. In the distributed assembly, we adopt Bulk Synchronous Parallel (BSP) model [28] to design a synchronous algorithm for distributed assembly. A BSP computation proceeds in a series of global supersteps, each of which consists of three components: local computation, communication and barrier synchronization. In the local computation step, each site adopts the iterative join algorithm to assemble local partial matches within the site. If a join result is a complete match of query graph Q, it will be returned directly; otherwise, these join results (i.e., the intermediate results) will be sent to the other sites in the communication step. The details about the communication and system termination condition are discussed in [23].
5 gAnswer: Answering Natural Language Questions Using Subgraph Matching
As mentioned earlier, gStore and gStore-D aim to answer users’ structural languages (SPARQL) efficiently. As noted earlier, the complexity of the SPARQL syntax and the lack of a schema make it hard for end users to use SPARQL. Providing end users an easy-to-use interface to access RDF datasets in an effective way has been recognized as an important concern. This has lead to research for RDF question/answering (Q/A) systems [4, 32, 33, 37]. We have designed gAnswer [37] to address the problem from the perspective of a graph database.
Usually, there are two stages in RDF Q/A systems: question understanding and query evaluation. Existing systems in the first stage translate a natural language question N into SPARQL queries [11, 18, 32], which are evaluated in the second stage. The focus of the existing solutions is on query understanding.
The inherent hardness in RDF Q/A is the ambiguity of natural language. In order to translate N into SPARQL queries, each phrase in N should map to a semantic item (i.e., an entity or a class or a predicate) in RDF graph G. However, some phrases have ambiguities. For example, phrase “Philadelphia” may refer to entity \(\langle\)Philadelphia(film)\(\rangle\) or \(\langle\)Philadelphia(city)\(\rangle\). Similarly, phrase “play in” also maps to predicates \(\langle\)starring\(\rangle\) or \(\langle\)director\(\rangle\). Although it is easy for humans to know that the mapping from phrase “Philadelphia” (in question N) to \(\langle\)Philadelphia(city)\(\rangle\) is wrong, this is not easy for machines. Disambiguating one phrase in N can influence the mapping of other phrases. The most common technique is joint disambiguation [32]. Existing disambiguation methods only consider the semantics of a question sentence N. They have high cost in the query understanding stage; thus, it is most likely to result in slow response time in online RDF Q/A processing.
gAnswer [37] deals with the disambiguation in RDF Q/A from a different perspective. We do not resolve the disambiguation problem in the question understanding stage, i.e., the first stage. We take a lazy approach and push down the disambiguation to the query evaluation stage. The main advantage of our method is it can avoid the expensive disambiguation process in the question understanding stage and speedup the entire process. We illustrate the intuition of our method by an example as follows:
Example 5
Given a RDF graph in Fig. 1a, assume that a user asks “Who was married to an actor that plays in Philadelphia?”
Consider a subgraph of graph G in Fig. 1a (the subgraph induced by vertices 001, 011, 002 and 009). Edge \(\overrightarrow{001,011}\) says that “Antonio Banderas is an actor”. Edge \(\overrightarrow{009,001}\) says that “Melanie Griffith is married to Antonio Banderas”. Edge \(\overrightarrow{001,002}\) says that “Antonio Banderas starred in a film \(\langle\)Philadelphia(film)\(\rangle\)”. The natural language question N is “Who was married to an actor that plays in Philadelphia”. Obviously, the subgraph formed by edges \(\overrightarrow{001,011}\), \(\overrightarrow{009,001}\) and \(\overrightarrow{001,002}\) is a match of N. “Melanie Griffith” is a correct answer. On the other hand, we cannot find a match (of N) containing \(\langle\)Philadelphia(city)\(\rangle\) in RDF graph G. Therefore, the phrase “Philadelphia” (in N) cannot map to \(\langle\)Philadelphia(city)\(\rangle\). This is the basic idea of our graph data-driven approach. Different from traditional approaches, we resolve the ambiguity problem in the query evaluation stage.
A challenge of our method is how to define a “match” between a subgraph of G and a natural language question N. Because N is unstructured data and G is graph structure data, we should fill the gap between two kinds of data. Therefore, we propose a semantic query graph \(Q^\mathrm{S}\) to represent the question semantics of N. We formally define \(Q^\mathrm{S}\) in Definition 12. An example of \(Q^\mathrm{S}\) is given in Fig. 9, which represents the semantic of the question N. Each edge in \(Q^\mathrm{S}\) denotes a semantic relation. For example, edge \(\overline{v_1v_2}\) denotes that “who was married to an actor.” Intuitively, a match of question N over RDF graph G is a subgraph match of \(Q^\mathrm{S}\) over G (formally defined in Definition 13).
Definition 11
(Semantic Relation) A semantic relation is a three-tuple \(\langle rel, arg1,arg2 \rangle\), where rel is a relation phrase in the paraphrase dictionary D, arg1 and arg2 are the two argument phrases.
In the running example of Fig. 9, \(\langle\)“be married to,” “who,” “actor”\(\rangle\) is a semantic relation, in which “be married to” is a relation phrase, “who” and “actor” are its associated arguments. We can also find another semantic relation \(\langle\)“play in,” “that,” “Philadelphia”\(\rangle\) in N. The two semantic relations are joined to form a semantic query graph, which is defined as follows.
Definition 12
(Semantic Query Graph) A semantic query graph, denoted as \(Q^\mathrm{S}\), is a graph in which each vertex \(v_i\) is associated with an argument and each edge \(\overline{v_iv_j}\) is associated with a relation phrase, \(1\le i,j \le |V(Q^\mathrm{S})|\).
There are offline and online phases in our solution. In the offline phase, we build a paraphrase dictionary D, which records the semantic equivalence between relation phrases and predicates. In the online phase, given a natural language question N, we interpret N as a semantic query graph \(Q^\mathrm{S}\) and find answers to N by matching \(Q^\mathrm{S}\) over RDF graph G.
5.1 Offline
To enable the semantic relation extraction from N, we build a paraphrase dictionary D to match relation phrases with predicates. For example, in the running example, natural language phrases “be married to” and “play in” have semantics similar to predicates \(\langle\)spouse\(\rangle\) and \(\langle\)starring\(\rangle\), respectively. There are some relation phrase datasets, such as Patty [19] and ReVerb [13] that can be used for this purpose. We propose a graph mining algorithm to align these relation phrases with the corresponding predicates. For example, “be married to” is matched with predicate \(\langle\)spouse\(\rangle\), as shown in Table 2.
5.2 Online
Although there are still two stages “question understanding” and “query evaluation” in our method, we do not adopt the existing framework, i.e., SPARQL query generation-and-evaluation. We propose a graph-driven solution to answer a natural language question N. The coarse-grained framework is given in Fig. 9.
-
(1) \({Question\, Understanding}\) As mentioned earlier, we use a semantic query graph to understand users’ query intension. Specifically, we interpret a natural language question N as a semantic query graph \(Q^\mathrm{S}\). Given a natural language question N, we use Stanford parser to obtain the dependency tree Footnote 14 Y of N. Based on the dependency tree, we first extract all semantic relations in N, each of which corresponds to an edge in \(Q^\mathrm{S}\). Figure 10 demonstrates an example of semantic relation extraction. If the two semantic relations have one common argument, they share one endpoint in \(Q^\mathrm{S}\). In the running example, there are two semantic relations, i.e., \(\langle\)“be married to,” “who,” “actor”\(\rangle\) and \(\langle\)“play in,” “that,” “Philadelphia”\(\rangle\), as shown in Fig. 10. Although they do not share any argument, arguments “actor” and “that” refer to the same thing because of “coreference resolution” [25].
-
(2) \({Query\, Evaluation}\) As a structural representation of users’ natural language question N, we need to find a subgraph (in RDF graph G) that matches the semantic query graph \(Q^\mathrm{S}\). The match is defined according to the subgraph isomorphism (formally defined in Definition 13).
First, each argument in vertex \(v_i\) of \(Q^\mathrm{S}\) is mapped to some entities or classes in the RDF graph, which is exactly the entity linking problem [35]. In Fig. 9b, argument “Philadelphia” is mapped to three two entities \(\langle\)Philadelphia(city)\(\rangle\) and \(\langle\)Philadelphia(film)\(\rangle\), while argument “actor” is mapped to a class \(\langle\)Actor\(\rangle\). We can distinguish a class vertex and an entity vertex according to RDF’s syntax. If a vertex has an incoming adjacent edge with predicate \(\langle\)rdf:type\(\rangle\) or \(\langle\)rdf:subclass\(\rangle\), it is a class vertex; otherwise, it is an entity vertex. Furthermore, if arg is a wh-word, we assume that it can match all entities and classes in G. Therefore, for each vertex \(v_i\) in \(Q^\mathrm{S}\), it also has a ranked list \(C_{v_i}\) containing candidate entities or classes. Note that each linked item is associated with a confidence probability.
Each relation phrase \(rel_{\overline{v_iv_j}}\) (in edge \(\overline{v_iv_j}\) of \(Q^\mathrm{S}\)) is also mapped to a list of candidate predicates and predicate paths. This list is denoted as \(C_{\overline{v_iv_j}}\). The candidates in the list are also ranked by the confidence probabilities. We resolve this by building a paraphrase dictionary, like Table 2. In the running example, “Philadelphia” maps to two possible entities, \(\langle\)Philadelphia(city)\(\rangle\) and \(\langle\)Philadelphia(film)\(\rangle\). Although the former matching is wrong for “Philadelphia” in the running example (in Fig. 9), gAnswer does not resolve the ambiguity issue in this step. We allow all possible matches and push down the disambiguation to the query evaluation step.
Second, a subgraph in RDF graph can match \(Q^\mathrm{S}\) if and only if the structure (of the subgraph) is isomorphic to \(Q^\mathrm{S}\). We have the following match definition.
Definition 13
(Match) Given a semantic query graph \(Q^\mathrm{S}\) with n vertices \(\{v_1\),...,\(v_n\}\), each vertex \(v_i\) has a candidate list \(C_{v_i}\), \(i=1,\ldots ,n\). Each edge \(\overline{v_iv_j}\) also has a candidate list of \(C_{\overline{v_iv_j}}\), where \(1\le i \ne j \le n\). A subgraph M containing n vertices \(\{u_1\),...,\(u_n\}\) in RDF graph G is a match of \(Q^\mathrm{S}\) if and only if the following conditions hold:
-
1.
If \(v_i\) maps to an entity \(u_i\), \(i=1,\ldots ,n\), \(u_i\) must be in list \(C_{v_i}\); and
-
2.
If \(v_i\) maps to a class \(c_i\) , \(i=1,\ldots ,n\), \(u_i\) is an entity whose type is \(c_i\) (i.e., there is a triple \({\langle }u_i\) rdf:type \(c_i{\rangle }\) in RDF graph) and \(c_i\) must be in \(C_{v_i}\); and
-
3.
\(\forall \overline{v_i v_j } \in Q^\mathrm{S} ; \overrightarrow{u_i u_j } \in G\) \(\vee\) \(\overrightarrow{u_j u_i} \in G\). Furthermore, the predicate \(P_{ij}\) associated with \(\overrightarrow{u_i u_j}\) (or \(\overrightarrow{u_j u_i}\)) is in \(C_{\overline{v_iv_j}}\), \(1\le i,j \le n\).
Let us recall the running example in Fig. 9b. Although “Philadelphia” can map two different entities, in the query evaluation stage, we can only find a subgraph (included by vertices 001, 002, 009 and 011 in G in Fig. 1a) containing \(\langle\)Philadelphia\(\_\)film\(\rangle\) that matches the semantic query graph \(Q^\mathrm{S}\). According to the subgraph graph, we know that the result is “Melanie\(\_\)Griffith”; meanwhile, the ambiguity is resolved. Mapping phrases “Philadelphia” to \(\langle\)Philadelphia(city)\(\rangle\) of \(Q^\mathrm{S}\) is false positive for the question N, since there are no data to support that.
6 Conclusion
In this paper, we review our recent work on graph-based RDF data management. Specifically, we give an overview of the systems developed in our project: gStore, gStore-D and gAnswer. The design philosophy behind our systems is to employ graph database techniques for RDF data management. As a native implementation, graph-based approaches maintain the original representation of the RDF data and enforces the intended semantics of RDF and SPARQL. The practice of our projects proved the effectiveness and efficiency of graph-based RDF data management techniques.
We note that gStore is not the only graph-based solution for RDF data management. To the best of our knowledge, GRIN [27] is the first work that considers a graph-structural index. It uses a distance-based height-balanced tree to index the RDF graphs. Specifically, each leaf node contains a set of vertices in RDF graph. The set of leaf nodes in the tree forms a partition of all vertices in RDF graph. Interior nodes are constructed by finding a “central” vertex, denoted c, and a radius value, denoted r. All vertices within the distance r from the center c are included in the interior vertex. Note that if interior node x is a child of y in GRIN tree, all vertices included in x are a subset of that included in y. During query evaluation, GRIN derives a set of inequality constraints based on the query graph structure. For example, if the distance between two query vertices \(v_1\) and \(v_2\) (in Q) is l, the distance between their matching vertices (in RDF graph G) is no longer than l. Based on these inequality constraints, some nodes of the index can be safely pruned to reduce the search space. The intuition of GRIN is similar to M-tree [10] that is designed to support similarity search in metric spaces.
Another system that we would like to mention is Trinity. RDF [34], a distributed, memory-based graph engine for web-scale RDF data. Due to the poor locality of graph operations, it is argued that maintaining the whole RDF graph in a memory cloud is feasible. Instead of join processing, graph exploration is used to boost the system’s performance. The exploration-based approach uses the binding information of the explored subgraphs to prune candidate matches in a greedy manner [34].
Notes
Recently, W3C has set up a community interested in addressing problems of high velocity streaming RDF data (www.w3.org/community/rsp/).
There usually are additional auxiliary tables, but they are not essential to this discussion.
RDF primer.
Note that in Fig. 1 we do not put rectangles around vertices that represent literals.
\(f_j(v)=\mathrm{NULL}\) means that vertex v in query Q is not matched in local partial match \(\mathrm{PM}_j\). It is formally defined in Definition 8 condition (2).
In this paper, we use “\(\leftarrow\)” to denote the assignment operator.
The dependencies are grammatical relations between a governor (also known as a regent or a head) and a dependent. Usually, we can map straightforwardly these dependencies into a tree, called dependency tree.
References
Abadi DJ, Marcus A, Madden S, Hollenbach K (2009) SW-Store: a vertically partitioned DBMS for semantic web data management. VLDB J 18(2):385–406
Abadi DJ, Marcus AS, Madden R, Hollenbach K (2007) Scalable semantic web data management using vertical partitioning. In: Proceedings of the 33rd international conference on very large data bases, pp 411–422
Aluç G (2015) Workload matters: a robust approach to physical RDF database design. PhD thesis, University of Waterloo
Androutsopoulos I, Malakasiotis P (2010) A survey of paraphrasing and textual entailment methods. J Artif Intell Res 38:135–187
Bizer C, Lehmann J, Kobilarov G, Auer S, Becker C, Cyganiak R, Hellmann S (2009) Dbpedia—a crystallization point for the web of data. J Web Semant 7(3):154–165
Bollacker KD, Evans C, Paritosh P, Sturge T, Taylor J (2008) Freebase: a collaboratively created graph database for structuring human knowledge. In: Proceedings of the ACM SIGMOD international conference on management of data, pp 1247–1250
Bornea MA, Dolby J, Kementsietsidis A, Srinivas K, Dantressangle P, Udrea O, Bhattacharjee B (2013) Building an efficient RDF store over a relational database. In: Proceedings of the ACM SIGMOD international conference on management of data, pp 121–132
Broekstra J, Kampman A, van Harmelen F (2002) Sesame: a generic architecture for storing and querying RDF and RDF schema. In: Proceedings of the 1st international semantic web conference, pp 54–68
Chong E, Das S, Eadon G, Srinivasan J (2005) An efficient SQL-based RDF querying scheme. In: Proceedings of the 31st international conference on very large data bases, pp 1216–1227
Ciaccia P, Patella M, Zezula P (1997) M-tree: an efficient access method for similarity search in metric spaces. In: Proceedings of the 23rd international conference on very large data bases, pp 426–435
Cimiano P, Lopez V, Unger C, Cabrio E, Ngomo A-CN, Walter S (2013) Multilingual question answering over linked data (QALD-3): lab overview. In: Proceedings of the CLEF 2013 conference on information access evaluation, pp 321–332
Cormen TH, Leiserson CE, Rivest RL, Stein C (2001) Introduction to algorithms. The MIT Press, Cambridge
Fader A, Soderland S, Etzioni O (2011) Identifying relations for open information extraction. In: Proceedings of the conference on empirical methods in natural language processing, pp 1535–1545
Gravano L, Ipeirotis PG, Jagadish HV, Koudas N, Muthukrishnan S, Pietarinen L, Srivastava D (2001) Using q-grams in a DBMS for approximate string processing. IEEE Data Eng Bull 24(4):28–34
Jones ND (1996) An introduction to partial evaluation. ACM Comput Surv 28(3):480–503
Karypis G, Kumar V (1995) Analysis of multilevel graph partitioning. In Proceedings of the IEEE/ACM Supercomputing95 conference, p 29
Lehmann J, Isele R, Jakob M, Jentzsch A, Kontokostas D, Mendes PN, Hellmann S, Morsey M, van Kleef P, Auer S, Bizer C (2015) DBpedia—a large-scale, multilingual knowledge base extracted from wikipedia. Semant Web 6(2):167–195
Lopez V, Unger C, Cimiano P, Motta E (2013) Evaluating question answering over linked data. J Web Semant 21:3–13
Nakashole N, Weikum G, Suchanek FM (2012) Patty: a taxonomy of relational patterns with semantic types. In: Proceedings of the conference on empirical methods in natural language processing and computational natural language learning, pp 1135–1145
Neumann T, Weikum G (2008) RDF-3X: a RISC-style engine for RDF. Proc VLDB Endow 1(1):647–659
Neumann T, Weikum G (2009) The RDF-3X engine for scalable management of RDF data. VLDB J 19(1):91–113
Özsu MT (2016) A survey of RDF data management systems. Front Comput Sci 10(3):418–432
Peng P, Zou L, Özsu MT, Chen L, Zhao D (2016) Processing SPARQL queries over distributed RDF graphs. VLDB J 25(2):243–268
Pérez J, Arenas M, Gutierrez C (2006) Semantics and complexity of SPARQL. CoRR, arXiv:cs/0605124
Soon WM, Ng HT, Lim DCY (2001) A machine learning approach to coreference resolution of noun phrases. Comput Linguist 27(4):521–544
Suchanek FM, Kasneci G, Weikum G (2007) Yago: a core of semantic knowledge. In: Proceedings of the 16th international world wide web conference, pp 697–706
Udrea O, Pugliese A, Subrahmanian VS (2007) GRIN: a graph based RDF index. In: Proceedings of the 22nd national conference on artificial intelligence, pp 1465–1470
Valiant LG (1990) A bridging model for parallel computation. Commun ACM 33(8):103–111
W3C. W3C: SPARQL 1.1 overview. https://www.w3.org/tr/rdf-sparql-query/. 21 March (2013)
Weiss C, Karras P, Bernstein A (2008) Hexastore: sextuple indexing for semantic web data management. Proc VLDB Endow 1(1):1008–1019
Wilkinson K (2006) Jena property table implementation. Technical Report HPL-2006-140, HP Laboratories Palo Alto, October 2006
Yahya M, Berberich K, Elbassuoni S, Ramanath M, Tresp V, Weikum G (2012) Natural language questions for the web of data. In: Proceedings of the conference on empirical methods in natural language processing and computational natural language learning, pp 379–390
Yahya M, Berberich K, Elbassuoni S, Weikum G (2013) Robust question answering over the web of linked data. In: Proceedings of the 22nd ACM international conference on information and knowledge management, pp 1107–1116
Zeng K, Yang J, Wang H, Shao B, Wang Z (2013) A distributed graph engine for web scale RDF data. Proc VLDB Endow 6(4):265–276
Zhang W, Su J, Tan CL, Wang W (2010) Entity linking leveraging automatically generated annotation. In: Proceedings of the 23rd international conference on computational linguistics, pp 1290–1298
Zhang Y, Pham M, Corcho Ó, Calbimonte J (2012) Srbench: a streaming RDF/SPARQL benchmark. In: The Semantic Web—ISWC 2012—11th international semantic web conference, Boston, MA, USA, November 11–15, 2012, Proceedings, Part I, pp 641–657
Zou L, Huang R, Wang H, Yu JX, He W, Zhao D (2014) Natural language question answering over RDF: a graph data driven approach. In: Proceedings of the ACM SIGMOD international conference on management of data, pp 313–324
Zou L, Mo J, Chen L, Özsu MT, Zhao D (2011) gStore: answering SPARQL queries via subgraph matching. Proc VLDB Endow 4(8):482–493
Zou L, Özsu MT, Chen L, Shen X, Huang R, Zhao D (2014) gStore: a graph-based SPARQL query engine. VLDB J 23(4):565–590
Acknowledgements
Lei Zou was funded by National Key Research and Development Program of China under grant 2016YFB1000603 and NSFC under grant No. 61622201. M. Tamer Özsu’s research was funded by a grant from Natural Sciences and Engineering Research Council (NSERC) of Canada.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zou, L., Özsu, M.T. Graph-Based RDF Data Management. Data Sci. Eng. 2, 56–70 (2017). https://doi.org/10.1007/s41019-016-0029-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41019-016-0029-6