1 Introduction

Steel plate shear wall (SPSW) systems have suitable performance in experimental and numerical studies. This system has enjoyed high stiffness and strength and considerable energy absorption. In the SPSW system, the infill plate plays an important role as a ductile lateral force-resisting system [1,2,3]. Buckling and dynamics are pressing problems in many engineering applications, e.g., thin-frame, column-like, thin-wall, and aerospace/automotive structures. These types of structures are often susceptible to instability, failure due to buckling, and dynamics issues [4, 5]. In steel shear walls, due to the low buckling capacity of the infill plate, buckling appears under the service load, which is a problem mainly under wind loads. To overcome this problem, some ideas have been presented, such as: utilizing stiffener, covering infill plates with concrete [6] or Fiber Reinforced Polymer (FRP) [7], utilizing semi-supported SPSW [8], and utilizing corrugated infill plates [9]. Among the proposed methods, utilizing corrugated infill plates is the most practical and easier to build than other ones.

The steel plate shear wall utilizing corrugated plates (C-SPSW) has shown acceptable seismic behavior. The C-SPSW enjoys larger out-of- and in-plane stiffness and lateral resistance than the conventional steel plate shear walls (SPSWs) under lateral loading [10]. The shape of corrugated infill plates was sinusoidal [11], rectangular [12], or trapezoidal corrugations [13]. The trapezoidal corrugated form was most commonly utilized in practice [14].

The use of corrugated plates as shear-resistant members was first developed in the late 1930s by Bergman and Reissner [15]. After the finding of Bergman, the shear buckling of the corrugated plates was widely studied [16,17,18,19,20,21].

The behavior of the C-SPSW was investigated comprehensively [22, 23] and research was focused on predicting the load–displacement curve of the system under monotonic loading.

Several researchers [24,25,26,27,28,29,30,31] studied the hysteretic behavior of the C-SPSW experimentally and numerically, and they confirmed the capability of the C-SPSW as a successful system under lateral loading.

Although the C-SPSW system has significant advantages but corrugated plates are produced from flat steel plates using cold rolling machines, so their thickness must be limited. The maximum thickness of corrugated plates used in practice is 8 mm. If high ultimate strength is required in the design, a thick corrugated plate should be used. To overcome the problem, Tong et al. [32] proposed utilizing double corrugated plates in the C-SPSW system. He investigated the behavior of the double corrugated plates in C-SPSW numerically and parametrically [33, 34].

The present study intends to provide an investigation into the behavior of double corrugated steel plate shear walls (DC-SPSWs). Although double corrugated plate has high elastic stiffness and strength, it suffered from low ductility due to the bucking of the infill plate. This dilemma was confirmed by Tong et al. [33]. To overcome the problem, an infill plate made of low-yield-point (LYP) steel was proposed. Since LYP steel possesses lower strength than A36, it is expected to have higher ductility. Herein, the finite element method is used to simulate the double corrugated steel plate shear wall (DC-SPSW). The effects of the corrugated angle (θ), the ratio of length (L) to height (H), and the steel type (A36 and LYP) of the infill plate on the behavior of the DC-SPSW are investigated.

2 Method of Study

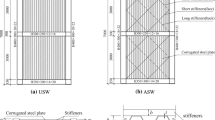
In this study, the behavior of SPSW, composed of double corrugated plates for infill plate (DC-SPSW) made of low-yield-point steel (LYP) or ordinary steel (ASTM A36), is investigated numerically and parametrically. To do this, first, a wall with L = H = 3000 mm and A36 steel is designed based on Ref. [32]. The designed boundary frame is shown in Fig. 1. In this model, the thickness of the double infill plate was measured as 2 × 2 mm. The boundary frame was designed according to the stress transferred from the infill plate. To do so, it was designed based on the AISC-guide 20 [35]. the wall was determined with a corrugated angle θ of 30 degrees, and the corrugations were considered horizontal. To investigate the effect of the LYP steel on the behavior of the wall system, by keeping the strength of the plate, its thickness was increased by \(\frac{{Fy_{A36} }}{{Fy_{LYP} }}\), where the \(Fy_{A36}\) and \(Fy_{LYP}\) are the yielding stress of infill wall with A36 steel and LYP steel, respectively [36]. Since the ratio is \(\frac{{Fy_{A36} }}{{Fy_{LYP} }} = 2.5\), for models with LYP steel, double corrugated plates with a thickness of 2 × 5 mm were used. For both walls with different yielding stress, the lateral strength of the infill plate is the same.

Fig. 1
figure 1

Schematic view of DC-SPSW

Full size image

To investigate the effect of the L/H ratio with a fixed height of 3000 mm, the walls with L/H = 1, 1.5, and 2 were analyzed for both LYP steel and A36 steel. Also, models with θ equal to 30, 45, 60, and 90 (degrees) were investigated.

3 Numerical Study

3.1 Numerical Models

The introduced 24 numerical models are listed in Table 1, where for each numerical model, a name has been designed. The first letters of the name stand for the Double Corrugated (DC) SPSW. The second and third letter represents the L/H ratio and θ, respectively. Finally, the last letter, A and L, shows the material of the infill plates that are A36 and LYP, respectively.

Table 1 Numerical model properties
Full size table

The finite element (FE) method and the ABAQUS software [37] were used to simulate the DC-SPSW through a set of one-story, one-bay frame models. Beams, columns, and corrugated infill panels were modeled with the four-node shell element (S4R). This element is a doubly curved thin or thick shell, with reduced integration, hourglass control, and finite membrane strain. Each element node has six degrees of freedom [38, 39]. The finite element models were loaded under horizontal load. Geometric nonlinearities were applied in the analysis of the finite element models under monotonic loading. The stress–strain curve of the material was modeled with a bilinear representation. Therefore, the material nonlinearities were applied in all the finite element analyses.

3.2 Verification of Results

In this study, the experimental investigation carried out by Hosseinzadeh et al. [9] was used for the verification of the finite element (FE) model, as shown in Fig. 2. The specimens of C-SPSW with one-story and single-bay in half-scale were tested. The load–displacement curves and the model's overall behavior were compared with those of the experimental studies. The results, as depicted in Fig. 3, show a very good comparison between the experimental results and the FE results.

Fig. 2
figure 2

a Experimental model; b FE model

Full size image
Fig. 3
figure 3

Comparison of the load–displacement curves between the experimental [9] and the FE results

Full size image

3.3 Loading Regime and Boundary Conditions

Lateral loads are applied to the beam-column connections and are gradually increased from zero to a magnitude beyond the system’s capacity. The ultimate displacement limit is considered to occur at a drift ratio of 2.5% per ASCE/SEI 7–22 [40]. To simulate the fixed condition of the column-to-base plate connections, the bottom nodes of both columns’ flanges and webs are restrained from displacement and rotation in all directions. To simulate the constraints imposed by slabs of the story floors, the out-of-plane displacements of beam webs were restrained from translation in the global z-direction. The connections of the two corrugated plates are completely interlocked, and the screw connections are omitted to simplify the calculations.

3.4 Materials Properties

The ASTM A36 and LYP steels were selected for numerical models. The boundary frame was made of ASTM A36 steel, and the wall plate was made of ASTM A36 and LYP steel. The material stress–strain behavior curves [35] are shown in Fig. 4, where Young’s modulus is 200 GPa, and Poison’s ratio is 0.3.

Fig. 4
figure 4

The stress–strain behavior curves of the material

Full size image

3.5 Defining the Seismic Behavior Parameters

To estimate the seismic parameters, the actual load–displacement response curves are usually idealized, as illustrated in Fig. 5. This idealization is based on the following assumptions and definitions:

  • The maximum displacement of the structure, \({\Delta }_{\mathrm{max}}\), will be considered based on the requirements of the local regulations.

  • The ductility factor is \(\upmu ={\Delta }_{\mathrm{max}} / {\Delta }_{\mathrm{y}}\).

  • The elastic stiffness is equal to the initial slope of the load-deformation curve and is \(\mathrm{K}={\mathrm{V}}_{\mathrm{y}} /{ \Delta }_{\mathrm{y}}\).

  • The over-strength factor, Ω, is defined as the ratio of yield resistance, Vy, to the lateral force corresponding to the first yield of structure, Vs.

  • The energy absorbed by the system, E, is equal to the closed area under the load–displacement curve.

  • The response modification factor is \({\mathrm{R}}_{u}={\mathrm{V}}_{\mathrm{e}} / {\mathrm{V}}_{\mathrm{s}}\)

Fig. 5
figure 5

Actual and idealized response curves of a common structure

Full size image

4 Discussions and Results

4.1 General Finding

Load versus displacement and also stiffness versus displacement plots, which are drawn in Fig. 6, reveal some valuable information conserving the behavior of structures. In addition, the structural parameters are listed in Table 2. According to Fig. 6 and Table 2, both the corrugated angle and infill materials affect the behavior of walls. An overall view reveals that the larger ultimate strength, energy dissipating capacity, and elastic stiffness are obtained by the corrugated plate with an angle of 30°. Moreover, the LYP steel has a better performance than the A36 steel walls. In doing so, the exact influence of the parameters on the behavior of the models is investigated in the next sections.

Fig. 6
figure 6

Comparing the pushover curve of the FE models

Full size image
Table 2 Structural parameters of numerical models with L/H = 1
Full size table

To have a fair comparison, the load has been normalized with (t.Fy). As shown in Fig. 7, the LYP walls showed a better performance in the case of ultimate strength and dissipating energy. Also, for both walls with A36 and LYP steels, the walls with a corrugated angle of 30° possess greater performance. The lowest curve is obtained by corrugated walls with an angle of 90°.

Fig. 7
figure 7

Comparing the normalized response curves

Full size image

4.2 Effect of the Corrugated Angle θ on the Behavior of Walls

Figure 8 illustrates the share of the infill plate considering the corrugated angle, θ, in resisting lateral loading. As shown in Fig. 8, the corrugated angle affects the behavior of walls with A36 and LYP steels. The comparison results driven by the pushover curves of FE results, and Table 2, are listed in Table 3. The results indicate that by increasing the angle θ, the seismic performance of the wall decreases. The effect of θ on the structural parameters of walls with LYP steel is more than on walls with A36 steel. For both walls, by the θ = 90°, the stiffnesses of the walls are significantly reduced. The elastic stiffness of the walls is reduced by 24% for A36-wall by changing the θ from 30° to θ = 60°, whereas it is reduced by 36% for LYP walls. Also, it has a similar effect on the Ru and Ω. The Ru for A-36 walls is reduced by 24% by changing the θ = 30° to θ = 60°, whereas it is reduced by 56% for LYP walls. This decrease is considerable. The θ has a lower effect on the ultimate strength, Vu, and energy absorption, E, in comparison with other structural parameters. Increasing the θ reduces 2 to 9% of the Vu and E.

Fig. 8
figure 8

The effect of angle θ on the infill plate behavior

Full size image
Table 3 Comparing the results of walls to investigate the effect of angle θ on the wall’s behavior
Full size table

In addition to the θ, the L/H ratio also affects the share of the infill plate (which will be examined in the next section) in lateral loading. For all L/H ratios, by increasing the θ, the share of the infill plate in lateral load-bearing is reduced. For L/H = 1 with A36 materials, during drift equals 0.23 to 0.27, the θ does not affect the share of infill plate in load-bearing that is drift = 0.1 to 0.255 for wall with LYP steels. As the L/H ratio increases, the interval between the effect of angle on the shear share of the infill plate increases; of course, LYP-steel sheets are less affected.

4.3 Effect of Infill Plate’s Materials Properties

In Fig. 9, the comparison of the wall to investigate the effect of the infill plate’s materials properties on the behavior of walls is plotted. As shown in Fig. 9, the LYP materials improve the behavior of walls.

Fig. 9
figure 9

Comparing the pushover curve of the FE models considering the LYP effect

Full size image

According to the structural parameters listed in Table 4, using the LYP steel instead of A36, the ultimate strength is increased by around 31%. But, the Δs and Vs are reduced by 55 to 62% and 27 to 17%, respectively. Reducing the parameters leads the structures to yield to reach better performance. Therefore, the μ, Ω, and Ru are improved by around 50, 54 to 75%, and 1.84 to 2.14 times, respectively. This comparison confirms the ability of the LYP to improve the behavior of the wall.

Table 4 Comparing the results of walls to investigate the effect of LYP steel on the wall’s behavior
Full size table

Figure 10 reveals that by changing the materials from A36 to LYP, the share of the infill plate in load-bearing is considerably amplified. As the share of the infill plate in load-bearing is raised, the susceptibility of hinge formation in columns is reduced. Therefore, it is expected that by using LYP steel for the infill plate, the safety of the structure is enhanced.

Fig. 10
figure 10

Comparing the effect of materials in the share of infill plate in load-bearing

Full size image

4.4 Investigating the L/H Ratio on the Behavior of the Wall

In Fig. 11, the response of walls has been compared to investigate the L/H aspect ratio. As the L/H ratio increases, the pushover diagram moves upwards, which increases the seismic parameters. Therefore, by increasing the L/H ratio with a constant thickness, which leads to an increase in the slender ratio of the infill plate, not only does it not reduce seismic performance, but it also improves the seismic performance of the wall. In DC-2-30-A and DC-1.5-30-A models, compared to the DC-1-30-A model, the resistance has increased by about 33% and 13%, respectively; also, for all models by doubling the dimensional ratio (L/H), we have seen an increase in resistance of about 25% to 35%. According to Fig. 11, with increasing the aspect ratio, we see an increase in sheet stiffness, which was 66% and 33% in DC-2–30-A and DC1.5–30-A models compared to DC-1-30-A, respectively. As shown in Fig. 12, the stiffness of the LYP steel models (with double and a half thickness) is about twice that of the A36 steel models. According to the results, it can be explained that increasing the length of the filler plate, in any case, is more important than increasing the thickness. However, increasing the thickness of the sheet has a greater effect on the stiffness of the samples. It is suggested to use of wall with a L/H ratio greater than 1 for both A36 and LYP steel walls.

Fig. 11
figure 11

Comparing the pushover curve of the FE models considering the L/H ratio

Full size image
Fig. 12
figure 12

Stiffness diagram of models with a wave angle of 30 degrees

Full size image

5 Proposed Relation to Predicting the Ultimate Strength

Figure 13 shows the load vs. drift diagram for all models. According to Fig. 13, the frame behaves almost the same for all dimensional ratios (L/H). However, with the increase of the dimensional ratio (L/H) for all models, we see an increase in the contribution of the filler plate to the frame, which is more in LYP steel.

Fig. 13
figure 13

Interaction of wall-frame

Full size image

Therefore, according to Refs. [41, 42], the ultimate strength of the boundary frame is measured as Eq. (1) and (2). The shear force of the frame after the formation of the plastic joint in the columns, \({F}_{f}\), was introduced as the shear capacity or ultimate shear force of the frame. The displacement \({\Delta }_{f}\) was corresponded to the displacement of the elastic limit (beginning of the plastic displacement) of the frame and considered:

$${\Delta }_{f}=\frac{{M}_{fp}{ H}^{2}}{6{E}_{c} {I}_{c}}$$
(1)
$${F}_{f}=\frac{4{M}_{fp}}{H}$$
(2)

where \({E}_{c}\) is the modulus of elasticity of columns, \({I}_{c}\) is the moment of inertia of the column, and \({M}_{fp}\) is the lowest plastic moment capacity.

Based on the fitting of the results, the following relation is proposed for predicting the ultimate strength of the infill plate

$${F}_{w}=L.{t}_{p}{F}_{y,walll}\left(0.01+\frac{L}{H\mathrm{sin}\theta }\frac{{F}_{y,col}}{{F}_{y,walll}}\right)$$
(3)

where \({F}_{y,col}\) and \({F}_{y,walll}\) are the yielding stress of columns and infill wall, respectively, and \({t}_{p}\) is the total thickness of the double corrugated infill plate.

Therefore, the ultimate strength of the double corrugated SPSW is proposed as follows:

$${F}_{u}={F}_{f}+{F}_{w}$$
(4)

As shown in Fig. 14, the simple proposed relation (4) predicts the ultimate strength of the double corrugated SPSW with good accuracy. Since the proposed relation predicts the ultimate strength lower than FE modeling, it would be conservative in the design of the system.

Fig. 14
figure 14

Comparing the FE results with the proposed relation

Full size image

6 Conclusions

To increase the buckling resistance of the infill steel plate, its thickness can be increased, but with the increase in thickness, the amount of stress transferred to the boundary frame increases. For this reason, made the assumption of equal capacity where increased thickness and decreased yield stress. In this paper, the effects of the steel type (A36 and LYP) of the infill plate on the behavior of the double corrugated steel plate shear walls were investigated. The results are summarized as follows:

  • The results showed that LYP steel improves the seismic behavior of corrugated double walls.

  • In walls with both materials (A36 and LYP), by increasing the θ, the seismic performance of the wall is reduced. But The effect of θ on the structural parameters of walls with LYP steel is more than that of walls with A36 steel.

  • For a wall with both materials (A36 and LYP), by θ = 90 o, the strength and stiffness of the wall are significantly reduced.

  • The elastic stiffness of walls is reduced by 24% for A36-walls by changing the θ from 30° to θ = 60 o, whereas it is reduced by 36% for LYP walls. Also, it has a similar effect on Ru and Ω. The Ru for A36 walls is reduced by 24% by changing the θ = 30° to θ = 60 o, whereas it is reduced by 56% for LYP walls.

  • The θ has a lower effect on the ultimate strength, Vu, and energy absorption, E, in comparison with other structural parameters. Increasing the θ reduces 2% to 9% of the Vu and E.

  • For L/H = 1 with A36 materials, during drift equals 0.23 to 0.27, the θ does not affect the share of infill plate in load-bearing that is drift = 0.1 to 0.255 for wall with LYP steel.

  • As the L/H ratio increases, the seismic parameters improve.

  • Increasing the L/H ratio, which leads to an increase in the slender ratio of the infill plate, not only does not reduce seismic performance, but also improves the seismic performance of the wall. It is suggested to use of wall with a L/H ratio greater than 1 for both the A36 wall and the LYP wall.

  • A practical relation was proposed for predicting the ultimate strength of the double corrugated SPSW with good accuracy.