Novel Observer-Based Input-Constrained Control of Nonlinear Second-Order Systems with Stability Analysis: Experiment on Lever Arm

Abstract

In this survey, the stability of input-constrained control for a widely used class of second-order systems is investigated. A continuous prediction-based approach is utilized to calculate the limited current control input by minimizing the next tracking error of nonlinear second-order system. The Karush–Kuhn–Tucker theorem is used to analytically solve the resulting constrained optimization problem. The constrained stability is analyzed by equating the constrained solution with the solution obtained from an optimal controller with time-varying weight on the control input. The proposed constrained controller adapts itself to real conditions by using information about the perturbations obtained from an extended state observer (ESO). Simulation studies for a lever arm indicates that the constrained controller presented in the closed form is much faster than the common nonlinear model predictive control method which requires an online dynamic optimization at each sampling time. Accordingly, experimental implementation of the proposed controller is conducted on a fabricated platform consisting of a lever arm. The results show that the proposed constrained controller can successfully track different time-varying positions for the arm by admissible torques generated by a DC motor. The comparative results with an adaptive backstepping controller indicate higher performance for the proposed ESO-based controller in compensating for the perturbations and external disturbance.

Appendices

Appendix 1: Nonlinear Model Predictive Control Algorithm

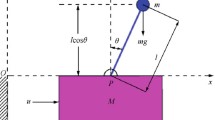
The nonlinear model predictive control (NMPC) is an conventional effective method to constrained control of nonlinear systems. In order to show the performance of the proposed constrained controller for the lever arm, the results are compared with a constrained NMPC. The overall structure of constrained NMPC algorithm is shown in Fig. 14. According to Fig. 14, the NMPC algorithm includes, prediction block predicts the future states, cost function block, and minimization block that minimize the cost function in the presence of state constraints. The discrete model of lever arm is used in this algorithm. According to Fig. 15, the control and predictive horizon of the NMPC algorithm is chosen 5 and 10 steps, respectively. Consequently, when $k = 0$, the control horizon will be from $k = 0$ to $k = 4$ and the predictive horizon will be from $k = 1$ to $k = 10$.

Fig. 14

The overall structure of NMPC algorithm for a lever arm

Fig. 15

A discrete NMPC approach

Appendix 2: Adaptive Back-stepping with Tuning Function for Strict Feedback System

An adaptive controller is formulated by combining a parameter estimator, which furnishes estimations of unknown parameters, with a control law.

$$\begin{aligned} \left\{ \begin{array}{lc} \dot{x}_{1}=x_{2} + \phi ^T_{1}(x_1)\theta + \psi _1 (x_1), \\ \dot{x}_{2}=au+\phi ^T_{2}(x)\theta + \psi _2 (x), \end{array}\right. \end{aligned}$$

(52)

where $\theta$ is unknown constant, $\phi _i$ and $\psi _i$, $i = 1, 2$ are known functions, sign(a) is known but a is an unknown function.

Step 1 defining the change of coordinates as

$$\begin{aligned} z_1&= x_1 - x_r , \end{aligned}$$

(53)

$$\begin{aligned} z_2&= x_2 - \alpha _1 - \dot{x}_r, \end{aligned}$$

(54)

which $\alpha _1$ is virtual control. Derivative of the tracking error $z_1$ is calculated as

$$\begin{aligned} \begin{aligned} \dot{z}_1&= \dot{x}_1-\dot{x}_r = x_2+\phi ^T_1\theta +\psi _1-\dot{x}_r \\&= z_2+\alpha _1+\phi ^T_1\theta +\psi _1. \end{aligned} \end{aligned}$$

(55)

First Lyapunov function is defined as

$$\begin{aligned} V_1 = \frac{1}{2}z^2_1 + \frac{1}{2}{\tilde{\theta }}^T \Gamma ^{-1}{\tilde{\theta }}, \end{aligned}$$

(56)

where ${\tilde{\theta }}=\theta -{\hat{\theta }}$ and $\Gamma$ is an arbitrary positive definite matrix.

$$\begin{aligned} \dot{V}_1 = z_1 \dot{z}_1- {\tilde{\theta }}^T \Gamma ^{-1}\dot{{\hat{\theta }}}. \end{aligned}$$

(57)

Substituting (55) in (57)

$$\begin{aligned} \dot{V}_1 = z_1\left( z_2+\alpha _1+\phi ^T_1 {\hat{\theta }}+\psi _1\right) -{\tilde{\theta }}^T \Gamma ^{-1}\dot{{\hat{\theta }}}. \end{aligned}$$

(58)

Choosing $\dot{{\hat{\theta }}}=\Gamma \phi _1 z_1$ and $\alpha _1 = -c_1 z_1-\phi ^T_1 {\hat{\theta }}-\psi _1$ leads to $\dot{V}_1\le 0$, where $c_1$ and ${\hat{\theta }}$ are a positive constant and an estimate of $\theta$, respectively.

Considering $\tau _1=\Gamma \phi _1 z_1$ as first tuning function, first derivative of Lyapunov function is rewritten as

$$\begin{aligned} \dot{V}_1 = z_1 z_2-c_1z^2_1-{\tilde{\theta }}^T \Gamma ^{-1}\left( \dot{{\hat{\theta }}}-\tau _1\right) . \end{aligned}$$

(59)

Step 2 Derivative of the second tracking error $z_2$ is calculated as

$$\begin{aligned} \begin{aligned} \dot{z}_2 &=\dot{x}_2-{\dot{\alpha }}_1-\ddot{x}_r \\&=au+\phi ^T_2\theta +\psi _2-\frac{\partial \alpha _1}{\partial x_1}(x_2+\psi _1)-\frac{\partial \alpha _1}{\partial x_1}\phi ^T_1 \theta - \frac{\partial \alpha _1}{\partial {\hat{\theta }}}\dot{{\hat{\theta }}}-\ddot{x}_r. \end{aligned} \end{aligned}$$

(60)

Second lyapunov function is proposed as

$$\begin{aligned} V_2 = V_1+\frac{1}{2}z^2_2+\frac{|a|}{\gamma }{\tilde{p}}^2 \end{aligned}$$

(61)

where ${\tilde{p}}=p-{\hat{p}}$ and $p=\frac{1}{a}$ and $\gamma$ is a constant value. First derivative of this Lyapunov function is written as

$$\begin{aligned} \begin{aligned} \dot{V}_2&= \dot{V}_1 +z_2\dot{z}_2-\frac{|a|}{\gamma }{\tilde{p}}\dot{{\hat{p}}} \\&=z_1 z_2-c_1z^2_1-{\tilde{\theta }}^T \Gamma ^{-1}\left( \dot{{\hat{\theta }}}-\tau _1\right) \\&\quad +z_2\left( au+\phi ^T_2\theta +\psi _2-\frac{\partial \alpha _1}{\partial x_1}(x_2+\psi _1)-\frac{\partial \alpha _1}{\partial x_1}\phi ^T_1 \theta - \frac{\partial \alpha _1}{\partial {\hat{\theta }}}\dot{{\hat{\theta }}}-\ddot{x}_r\right) \\&\quad +{\tilde{\theta }}^T\Gamma ^{-1}(\tau _1-\dot{{\hat{\theta }}}). \end{aligned} \end{aligned}$$

(62)

The aim is to make $\dot{V}_2\le 0$. The stabilizing function $\alpha _2$ is selected as

$$\begin{aligned} \begin{aligned} \alpha _2&= -c_2z_2-z_1-\psi _2+\frac{\partial \alpha _1}{\partial x_1}(x_2+\psi _1)-\left( \phi _2-\frac{\partial \alpha _1}{\partial x_1}\phi _1\right) {\hat{\theta }}\\&\quad +\frac{\partial \alpha _1}{\partial {\hat{\theta }}}\tau _2, \end{aligned} \end{aligned}$$

(63)

where $\tau _2$ is second tuning function. It is determined as below

$$\begin{aligned} \tau _2 = \tau _1+\Gamma \left( \phi _2-\frac{\partial \alpha _1}{\partial x_1}\phi _1\right) z_2. \end{aligned}$$

(64)

First derivative of error variable can be rewritten as

$$\begin{aligned} \dot{z}_2 = -c_2 z_2 -z_1+\left( \phi _2-\frac{\partial \alpha _1}{\partial x_1} \phi _1\right) ^T{\tilde{\theta }}+\frac{\partial \alpha _1}{\partial {\hat{\theta }}}\left( \tau _2-\dot{{\hat{\theta }}}\right) -a{\tilde{p}}{\bar{u}}. \end{aligned}$$

(65)

Substituting (65) in (62) is resulted in

$$\begin{aligned} \dot{V}_2 = -c_1 z^2_1-c_2z^2_2+{\tilde{\theta }}^T \Gamma ^{-1}\left( \tau _2-\dot{{\hat{\theta }}}\right) -\frac{|a|}{\gamma }\left( \gamma sign(a) {\bar{u}}z_2+\dot{{\hat{p}}}\right) \end{aligned}$$

(66)

Considering

$$\begin{aligned} u&={\hat{p}}{\bar{u}}, \ \ \ {\bar{u}}=\alpha _2+\ddot{x}_r \end{aligned}$$

(67)

$$\begin{aligned} \dot{{\hat{\theta }}}&=\tau _2 \end{aligned}$$

(68)

$$\begin{aligned} \dot{{\hat{p}}}&=-\gamma sign{(a)}{\bar{u}}z_2, \end{aligned}$$

(69)

lead to $\dot{V}_2\le 0.$