3D Numerical Cross-Section Analysis of a Tapered Beam Slice

Abstract

Cross-section analysis is an important tool used to recover stresses and strains in a structure at specific cross-sections of arbitrary geometries, without the need for a full 3D model. This is particularly essential for large-scale structures such as aircrafts, wind turbine blades, etc. where making a full model can be computationally very expensive or impractical. The majority of currently available cross-section analysis frameworks are based on stepwise prismatic assumptions, which are hardly suited for the analysis of tapered beams. In fact, high-fidelity stress analysis obtained from analytical and full 3D models shows that predictions of stepwise prismatic approximations can significantly deviate from the correct solution of tapered beams. In this work, a prismatic 3D cross-section analysis method is extended to analyze a symmetrically tapered finite cross-section slice. In this study, the cross-section slice is discretized with 8-node and 20-node solid elements. The boundary conditions are applied as six constraint equations via the Lagrange multiplier method. The external nodal forces acting on the cross-section faces are obtained from the equivalent tractions induced by the cross-section forces. The developed numerical model is validated against the exact analytical solutions of a wedge as well as commercial finite element (FE) software COMSOL and it is shown that the numerically predicted displacement and stress fields agree well with those provided by the wedge’s analytical solution and the FE COMSOL results. This work contributes to the advancement of high-fidelity numerical tapered cross-section analysis methods with an application for many engineering structures.

1 Introduction

Non-prismatic beams find a wide field of application in engineering such as e.g. aircrafts, vessels, bridges, wide span space structures and wind turbine blades to name a few. Especially wind turbine rotor blades are strictly non-prismatic as they exhibit Longitudinal Geometric Variations (LGVs) in the form of taper, twist and pre-curvature. The taper defined in this work refers to a continuous variation of the cross-section dimensions along the beam axis. Particularly sectors working with large-scale structures, such as the wind industry, are currently facing great difficulties in accurately predicting cross-section responses of tapered structures such as wind turbine rotor blades. It should be noted that full 3D models of such large structures are impractical for high fidelity time-domain fluid–structure interaction analyses. For instance, aeroelastic analysis of wind turbine blades involves several thousand time steps in each load case. Therefore, in general aeroelastic simulations are performed on beam element level for the entire wind turbine interacting with the surrounding fluid and provide the cross-section force history in the beam element nodes. For this purpose, cross-section analysis is essential to provide the beam cross-section stiffnesses—arising from complex geometries and anisotropic material properties—as input to the aeroelastic model. Moreover, the output of such aeroelastic simulations is the internal cross-sectional force history, which can hardly be used for accurate stress–strain recovery from a classic 3D finite element (FE) model. That is because the application of the six internal cross-section forces as external forces to 3D models locally disturbs the response due to improper force application conditions, eventually restraining or disturbing cross sectional warping displacements at the load application points. In order to avoid inaccurate cross-section warping displacement and stress/strain results, cross-section analysis tools are essential to accurately recover stresses and strains at specific cross-sections from internal cross-section forces without the need for a full 3D model, which can be impractical for large-scale structures.

Giavotto et al. (1983) were among the first to formulate a general cross-section analysis framework for arbitrary cross-section geometries and anisotropic material behaviour. The theory of Giavotto et al. has been implemented in the commercially available software packages Blasques (2012). Another commercially available cross-section analysis tool—Cesnik (1997)—draws from Hodges’ theory (Hodges 2006)that was further extended by Yu et al. (2012).

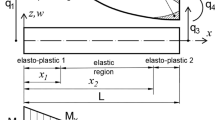
Although the available cross-section analysis tools are based on different formulations, they predominantly share one common assumption—the stepwise prismatic approximation. Figure 1a depicts the stepwise prismatic approach for cross section analysis of tapered beams.

Fig. 1

Generic beam length with a continuous non-constant taper with a stepwise prismatic cross-section approximation with a differential slice thickness $dz$ and b piecewise linearly tapered cross-section approximation with a finite slice thickness $\Delta z$ and c detail of the piecewise linear approximation of the continuous taper by the local tangent

Literature provides an abundance of theoretical work dedicated to tapered beams among which the pioneering works of Carothers (1914), Bleich (1932) and Boley (1963) show that prismatic formulations do not hold in case of tapered beams. More recently, the analytical solutions of Bennati et al. (2016), and Bertolini et al. (2019a, b, 2020) showed that the stress fields in tapered beams can be strongly at variance with prismatic beams. A numerical study on tapered beams (Bertolini et al. 2019a, b) comparing the predictions of BECAS with that of an equivalent 3D finite element shell model shows that even perceivably small taper gradients induce shear-extension and shear-bending coupling effects that cannot be predicted by prismatic beam theories. Moreover, the study (Bertolini et al. 2019a, b) showed that the magnitude of the deviation of stepwise prismatic approaches is a strong function of the taper angle. Bertolini et al. (2020) investigated a finite element method to analyze a tapered cross-section slice. Despite its success, the presented method was not able to provide a consistent prediction accuracy for all cross-section stress components. Moreover, the results exhibited a pronounced thickness dependency. It is worth mentioning two different studies on tapered beams by Hodges et al. (2008a, b) based on the variational asymptotic method—the underlying theory of VABS. The importance of a taper-correction factor for stress recovery and cross-section stiffness prediction is emphasized in (Ho et al. 2010). Later, a full theory for cross-section analysis of tapered beams was presented by Rajagopal (2014) but according to the best knowledge of the authors, a validation against analytical or numerical models is currently not available.

Migliaccio (2023) derived closed form solutions for the shear flow in tapered beams with rectangular and circular cross-sections. Balduzzi et al. (2017) compared the most common stress-recovery procedures with proposed new non-prismatic planar beam model by example of an I-cantilever beam. Mercuri et al. (2020) derived an analytical model for a non-uniformly tapered 2D planar cantilever beam. Vilar et al. (2021) and Ojo and Weaver (2021) proposed a method for the stress analysis of non-prismatic beams. They formulated a strong anisoparametric unified formulation (SUF) by combining a beam element with solid elements. The method was successfully applied to cantilever beams with various forms of taper.

Later Vilar et al. (2022) developed an analytical method to recover stresses in cantilever beams with lengthwise variation subject to cross section forces and distributed surface loads. Their method was able to predict the transverse stresses more accurately than state-of-the-art models. Chockalingam (2020) derived an analytical expression for the shear stress in doubly tapered bi-symmetric I-beams with excellent accuracy. Chockalingam (2021) derived an analytical Timoshenko beam formulation providing the finite element stiffness matrix of an I-beam with constant taper. Murakami et al. (1996) and Karttunen et al. (2016) developed analytical solutions for anisotropic beams.

Carrera (2011) has developed a unified formulation—CUF—based on the Taylor expansion of generic function describing the beam displacement field. The method employs higher order terms to describe nonlinear in and out-of-plane cross-section warping. The method is based on a prismatic cross-section formulation assuming that the cross-section surface geometry is not a function of the beam axis coordinate. This makes the application of the CUF to tapered beams challenging as the limits of the integral of the strain energy density are a function of the beam axis. Balduzzi et al. (2016) and Auricchio et al. (2015) solved the 2D tapered cantilever beam problem by applying discrete boundary conditions. In (Auricchio et al. 2015) Timoshenko kinematics are used to obtain the stress distributions in the beam. Good agreement was obtained for the axial and transverse stress components, but deviations of the shear stress distribution became apparent when they compared the predicted shear stress with 2D finite element analysis. The reason for the deviation was independently investigated and discussed by Taglialegne (2018). Assuming Timoshenko kinematics prevents the accurate prediction of the non-linear warping displacements which were obtained by the exact analytical solution of Taglialegne (2018). The method is not lending itself to cross-section analysis since the imposition of discrete boundary conditions at the cross-section faces would prevent the cross-section from warping.

Building on the valuable findings and insights provided by the literature, this work attempts a feasibility study of an extension of the numerical stepwise prismatic approach toward a stepwise tapered cross-section slice approximation (c.f. Fig. 1). The study is based on a symmetrically tapered beam. Figure 1b depicts the principle of the proposed approach in which a beam with non-constant taper is approximated with a series of finite cross-section slices exhibiting a piecewise constant taper. The work builds on two existing approaches: Ghiringhelli and Montegazza (1994) derived a method along the lines of (Giavotto et al. 1983) to predict the cross-section stiffness matrix of a prismatic untwisted beam using a finite cross-section slice discretized with 3D solid elements with one element layer in the slice thickness direction. In their formulation, a constant interpolation was assumed in the slice thickness direction. More recently, Couturier and Krenk (2016) suggested a similar method but using solid elements with Hermitian type shape functions. They obtain the prismatic cross-section stiffness matrix by imposing the six 3D deformation modes that correspond to extension, bending, shear and torsion.

To the best knowledge of the authors, no such method is currently available in the open literature and currently, no commercial cross-section analysis tool can make such predictions. Our method is a 3D model with no plane stress assumption (3D elements are used) and is indeed applicable to general cross-sections beyond the availability of analytical solutions. A plane stress wedge example whose analytical solution was available in the literature was used solely for the purpose of validating the proposed numerical 3D model. For the torsion load case and composite tapered slices under axial and bending load cases, the predicted stress components were validated against their correspondings predicted by commercial FE software COMSOL.

This work demonstrates that stepwise prismatic 3D cross-section analysis approaches can indeed be extended into piecewise tapered formulations. The proposed approach provides accurate predictions of the stress field in a 3D tapered cross-section, which currently available stepwise prismatic approaches fail to provide. The predictive accuracy of such a formulation is validated against closed form analytical solutions and the effect of cross-section slice thickness and taper angle on the field variables is investigated. Cross-section analysis of tapered beams is a highly active research area in the analysis of large-scale structures—predominantly for dynamic time domain analysis. The findings presented serve the need of many different industry sectors dealing with tapered structures such as wind, aeronautic, space and marine.

The remainder of this article is structured in the following fashion: Sect. 2.1 provides the theoretical framework of the proposed approach and contrasts its differences with the classic cross-section analysis approach. Section 2.2 presents the implementation of the approach into a 3D Finite Element framework. Section 3 compares the numerically predicted field variables with a wedge example whose analytical solution was available in the literature as well as COMSOL FE results. The implications of the results are discussed in Sect. 4 and the major findings are compiled in Sect. 5.

2 Methodology

2.1 Theoretical Background

It is well-known that in stepwise prismatic formulations, neither the material properties nor the geometry vary along the differential cross section element ${\text{d}}z$. In cross-section analysis, this allows the internal work to be calculated as the area integral of the strain energy density (Giavotto et al. 1983; Blasques 2012) according to Eq. (1).

$${\partial W}_{{\text{int}}}/\partial z={\int }_{A}{\varepsilon }_{ij}{ \sigma }_{ij}\mathrm{ d}A$$

(1)

In stepwise prismatic formulations with a differential slice thickness, the internal energy is therefore, defined in energy per unit length. However, in tapered slices the cross-section dimensions are a function of the beam axis direction, which compels the integration of the strain energy density over the cross-section volume according to Eq. (2).

$${W}_{{\text{int}}}={\int }_{V}{\varepsilon }_{ij}{ \sigma }_{ij}\mathrm{ d}V$$

(2)

This detail has in fact considerable implications since a tapered cross section analysis can no longer be treated as a quasi-planar 2D problem but needs to be formulated as a 3D problem. In its weak formulation, this means that the cross-section can no-longer be discretized with plane strain elements but needs to be discretized with solid elements (see Sect. 2.2). On the other hand, for the purpose of cross-section analysis it is desired to make the 3D formulation adhere to the particular or central solution of the governing second order ODE as originally defined by Giavotto et al. (1983) in a sense that (i) it provides the 6 × 6 cross-section stiffness matrix and (ii) it recovers stress and strain fields from internal cross section forces. The remainder of this section is concerned with providing a framework that makes tapered 3D cross sectional analysis compliant with the classic beam theory.

This can be done by accepting the transition from a differential slice formulation to a finite slice thickness formulation $dz\to \Delta z$. Figure 1a shows that the cross-section will be treated as tapered cross-section slice with a finite thickness $\Delta z$ possessing two initially parallel cross section planes that are perpendicular to the beam axis. The cross-section plane in the negative and positive z-direction are denoted with the subscript $-$ and $+$ respectively. The slice thickness is assumed small relative to the characteristic in-plane cross section dimensions i.e. $\Delta z\ll h$ where $h$ could be the cross-section height.

Figure 2a and b show the kinematics of a tapered finite cross-section slice when undergoing an arbitrary deformation. Figure 2b shows that the total cross section plane deformation comprises of two parts namely a rigid body motion (RBM) and the warping deformation as coined by Giavotto et al. (1983). The RBM itself consists of three rigid body translations $\chi$ and three rigid body rotations $\varphi$, where the dashed polygon in Fig. 2b represents the deformation of the slice associated with the RBM of the two cross section planes. The dashed polygon would represent the deformation resulting from the assumption that cross-sectional planes remain plane. The warping deformation is consequently defined as the portion that distorts the cross section in the out-of-plane and in-plane directions.

Fig. 2

a Linearly tapered beam with a finite beam slice $\Delta z$ in the undeformed state with a cross-section fibre (red line) and b the beam slice in an arbitrarily deformed configuration with total displacement and rigid body translation vector $\chi$ and rigid body rotation $\varphi$ and c cross-section deformation of the beam slice without the rigid body motions representing the result of the cross-sectional analysis method

In cross section analysis only the cross section deformation or the relative displacements are meaningful which is exemplified by the red cross section fibre depicted in Fig. 2a and b. The change in length of the cross sectional fibre due to deformation is given by the difference of the position vectors in the initial configuration and the primed configuration: $\overrightarrow {{A_{ + } \grave{A}_{ + } }} - \overrightarrow {{A_{ - } \grave{A}_{ - } }}$. Figure 2c shows that the RBM is hence redundant when determining this change in fibre length, which is only a function of the relative displacement. Figure 2c depicts the so called central solution representing a cross-section slice located in the far field of a beam undisturbed by boundary effects. In other words, the RBMs depend on the beam boundary conditions that must remain unknown in cross-section analysis. Hence, in order to remove the RBM we demand that the weighted integral of the translations and rotations of all material points pertaining to the cross section slice are null. Defining the cross-section displacement vector as ${\varvec{u}}={\left(\begin{array}{ccc}{u}_{x}& {u}_{y}& {u}_{z}\end{array}\right)}^{T}$, the three translation and three rotation restraint equations can be written in continuous form as follows:

$$\int {\left[{\varvec{I}}\boldsymbol{ }{{\varvec{n}}}^{T}\right]}^{T}{\varvec{u}}\boldsymbol{ }{\text{d}}V=0$$

(3)

$${\varvec{n}}=\left[\begin{array}{ccc}0& -z& y\\ z& 0& -x\\ -y& x& 0\end{array}\right]$$

(4)

Equation 3 can be seen as a set of non-discrete boundary conditions enforcing that the average translations and rotations of all material points are cancelling one another. Referring to Fig. 2c this means that both the net translation with respect to the y-axis and that the net rotation with respect to the x-axis of the two cross-section planes are zero. Figure 3a, b shows the six cross section forces and the associated generalised cross-section strains and curvatures as stipulated in this work.

Fig. 3

Beam coordinate system on positive cross-section surface with a cross-section forces $T$ and moments $M$ and b the associated generalized cross-section strains ${\varepsilon }_{0}$ and $\kappa$

The generalized beam cross-section strains and curvatures (Bathe 1982; Blasques 2012) are in the case of a tapered finite cross-section slice the finite differences of the rigid body translations and rotations given by Eq. (5), which concludes the kinematics of the tapered cross-section slice.

$$\begin{array}{ccc}{\varepsilon }_{0x}=\frac{{\chi }_{+x}-{\chi }_{-x}}{\Delta z}-\left(\frac{{\varphi }_{+y}+{\varphi }_{-y}}{2}\right)& {\varepsilon }_{0y}=\frac{{\chi }_{+y}-{\chi }_{-y}}{\Delta z}+\left(\frac{{\varphi }_{+x}+{\varphi }_{-x}}{2}\right)& {\varepsilon }_{0z}=\frac{{\chi }_{+z}-{\chi }_{-z}}{\Delta z}\\ {\kappa }_{x}=\frac{{\Delta \varphi }_{x}}{\Delta z}& {\kappa }_{y}=\frac{\Delta {\varphi }_{y}}{\Delta z}& {\kappa }_{z}=\frac{{\Delta \varphi }_{z}}{\Delta z}\end{array}$$

(5)

The coupling of the cross section force vector ${\left[\begin{array}{cc}{\varvec{T}}& {\varvec{M}}\end{array}\right]}^{T}={\left[\begin{array}{cccccc}{T}_{x}& {T}_{y}& {T}_{z}& {M}_{x}& {M}_{y}& {M}_{z}\end{array}\right]}^{T}$ with the cross-section slice is established via the tractions ${\varvec{p}}={\left[\begin{array}{ccc}{\sigma }_{zz}& {\sigma }_{yz}& {\sigma }_{xz}\end{array}\right]}^{T} \overrightarrow{{\varvec{e}}}$ using the beam equilibrium conditions that can be written for the finite cross-section slice as follows:

$$\left[\begin{array}{c}{{\varvec{T}}}_{-}\\ {{\varvec{M}}}_{-}\end{array}\right]=\underset{{A}_{-}}{\overset{}{\int }}{\left[{\varvec{I}}\boldsymbol{ }{{\varvec{n}}}_{-}^{T}\right]}^{T} {{\varvec{p}}}_{-} {\text{d}}A$$

(6)

$$\left[\begin{array}{c}{{\varvec{T}}}_{+}\\ {{\varvec{M}}}_{+}\end{array}\right]=\underset{{A}_{+}}{\overset{}{\int }}{\left[{\varvec{I}}\boldsymbol{ }{{\varvec{n}}}_{+}^{T}\right]}^{T} {{\varvec{p}}}_{+} {\text{d}}A$$

(7)

The issue with Eqs. (6) and (7) is that the tractions on the two cross-section planes for a tapered slice with arbitrary geometry and anisotropic material behaviour are unknown beforehand, which prevents the calculation of the external work done by the cross-section forces. Giavotto et al. (1983) have resolved this problem by separating the total cross-section deformation into a so-called rigid body displacement and a warping displacement. By coupling the cross-section forces with the rigid body displacements, it is possible to formulate the work equations in such a way that the tractions do not appear explicitly, which resolves the problem. In the current formulation presented in this work the total cross-section deformations cannot be separated into a rigid body and a warping displacement. For this reason, in the present study the tractions acting on the two cross section planes need to be assumed to be known.

It has been demonstrated by Bertolini et al. (2019a, b, 2020) and Taglialegne (2018) through comparison with 3D finite element models, that accurate approximate predictions of the stresses in homogeneous isotropic linearly tapered beams are possible with the assumptions that Navier’s equation holds, under the proviso that the taper angle is small. That is to say, it has been shown that the axial stress distributions in moderately tapered beams can be well approximated by the prismatic solution, where the remaining stress components can accurately be obtained from the axial stress distribution using the Cauchy equilibrium conditions. In this work, the same approach is utilised inasmuch the nodal forces acting on the cross-section slice planes are obtained with the prismatic formulations as will be explicated in detail in Sect. 2.2.

The numerical predictions obtained by the proposed method are validated against the exact analytical solution of a symmetrical 2D wedge depicted in Fig. 4. The geometrical parameters $L=H/\mathit{tan}\alpha$ and ${H}_{0}=2H$ defining the wedge are chosen in such a way, that the cross-section slice geometry located at mid-span corresponds to the finite element model in order to allow direct comparison.

Fig. 4

a Geometry and coordinate system of the symmetric plane stress wedge with constant taper angle $\alpha$ showing the cross-section slice with the dashed control section at mid-span and external uniaxial tip load triple ${\overline{F} }_{x}, {\overline{F} }_{y}, {\overline{M} }_{x}$ defined in force per unit width and b rectangular cross-section at mid-span of width $B$ used to validate the proposed numerical method

Taglialegne (2018) derived the three Cauchy stress components for the plane stress wedge using Carothers equilibrium conditions and proper transformation from Cartesian to polar coordinate system (CSYS)which are reproduced by Eq. (8) through (10) as a function of the three external wedge tip loads (c.f. Fig. 4).

$${\sigma }_{zz}=\frac{1}{{\left({y}^{2}+{\left(L-z\right)}^{2}\right)}^{2}}\left(\frac{{\overline{F} }_{z}{\left(L-z\right)}^{3}}{\alpha +{\text{sin}}\alpha {\text{cos}}\alpha }-\frac{{\overline{F} }_{y}y{\left(L-z\right)}^{2}}{\alpha -{\text{sin}}\alpha {\text{cos}}\alpha }+\frac{{4\overline{M} }_{x}y\left(L-z\right)\left({y}^{2}-{\left(L-z\right)}^{2}-\left({y}^{2}+{\left(L-z\right)}^{2}\right){\left({\text{sin}}\alpha \right)}^{2}\right)}{\left(2\alpha {\text{cos}}2\alpha -{\text{sin}}2\alpha \right)\left({y}^{2}+{\left({L}_{0}-z\right)}^{2}\right)}\right)$$

(8)

$${\sigma }_{yy}=\frac{1}{{\left({y}^{2}+{\left(L-z\right)}^{2}\right)}^{2}}\left(\frac{{\overline{F} }_{z}{y}^{2}\left(L-z\right)}{\alpha +{\text{sin}}\alpha {\text{cos}}\alpha }-\frac{{\overline{F} }_{y}{y}^{3}}{\alpha -{\text{sin}}\alpha {\text{cos}}\alpha }+\frac{{4\overline{M} }_{x}y\left(L-z\right)\left({y}^{2}-{\left(L-z\right)}^{2}+\left({y}^{2}+{\left(L-z\right)}^{2}\right){\left({\text{cos}}\alpha \right)}^{2}\right)}{\left(2\alpha {\text{cos}}2\alpha -{\text{sin}}2\alpha \right)\left({y}^{2}+{\left({L}_{0}-z\right)}^{2}\right)}\right)$$

(9)

$${\sigma }_{yz}=\frac{1}{{\left({y}^{2}+{\left(L-z\right)}^{2}\right)}^{2}}\left(\frac{-{\overline{F} }_{z}y{\left(L-z\right)}^{2}}{\alpha +{\text{sin}}\alpha {\text{cos}}\alpha }+\frac{{\overline{F} }_{y}{y}^{2}\left(L-z\right)}{\alpha -{\text{sin}}\alpha {\text{cos}}\alpha }+\frac{{2\overline{M} }_{x}\left(\left({\left({L}_{0}-z\right)}^{4}-{y}^{4}\right){{\text{cos}}\alpha }^{2}-{\left({L}_{0}-z\right)}^{2}\left({\left({L}_{0}-z\right)}^{2}-3{y}^{2}\right)\right)}{\left(2\alpha {\text{cos}}2\alpha -{\text{sin}}2\alpha \right)\left({y}^{2}+{\left({L}_{0}-z\right)}^{2}\right)}\right)$$

(10)

The total deformations of the wedge were obtained from the Cauchy stress components using constitutive relations and subsequent integration of the strain components (Taglialegne 2018). In order to shed light on the range of validity for a taper angle small enough to comply with the Navier traction assumption, it is useful to inspect the non-dimensionalisation of the solution for ${\sigma }_{zz}$ (Eq. 8). Using the natural coordinates $-1\le \eta \le 1$ (corresponding to the y-direction) and $0\le \zeta \le 1$ (corresponding to the z-direction), Taglialegne (2018) derived the following non-dimensionalised expression for pure axial loading:

$${\sigma }_{zz}=\frac{2{\text{tan}}\alpha }{\left(\alpha +{\text{sin}}\alpha {\text{cos}}\alpha \right)\left(1-\zeta \right){\left(1+{\eta }^{2}{\left({\text{tan}}\alpha \right)}^{2}\right)}^{2}}\frac{{\overline{F} }_{z}}{2{H}_{0}B}$$

(11)

Linearisation of Eq. (11) with ${\text{sin}}\alpha \cong {\text{tan}}\alpha \cong \alpha$ and ${\text{cos}}\alpha \cong 1$ the following expression is obtained:

$${\sigma }_{zz}\approx \frac{1}{\left(1-\zeta \right){\left(1+{\eta }^{2}{\alpha }^{2}\right)}^{2}}\frac{{\overline{F} }_{z}}{2{H}_{0}B}$$

(12)

Equation 12 shows that the constant stress distribution (i.e. no variation along $\eta$) is obtained for taper angles approaching zero such that $\underset{\alpha \to 0}{{\text{lim}}}{\sigma }_{zz}={\overline{F} }_{z}/\left(1-\zeta \right)2{H}_{0}B$. It is now possible to define a small taper angle to satisfy the condition ${\alpha }^{2}\ll \alpha \Rightarrow \alpha \ll 1$.

2.2 Numerical Implementation

In this section, the numerical implementation of the proposed method is presented and explicated in detail. The following underlying assumptions have been made for the implementation of the method:

• Isotropic homogeneous linear elastic material

• Small strain theory (linearized Green–Lagrange strain tensor)

• The taper angle is small i.e. $\alpha \ll 1$

Figure 5 shows the geometry of the tapered wedge slice with a symmetric constant taper of slope $k={\text{tan}}\alpha$ defined at the outer boundary. The slice is discretized with 8-noded and 20-noded isoparametric solid elements. Since the analytical solution is based on a plane stress wedge, the geometry was discretized with one element through the thickness. The cross-section forces were applied through their equivalent nodal forces using the integration of their tractions as schematically depicted in Fig. 6. The numerical procedure was implemented in the Matlab programming language (MATLAB 2020).

Fig. 5

a 3D cross section slice of a symmetrically tapered planar wedge with global CSYS, main dimensions $B,H,\Delta z$ and taper angle $\alpha$ discretized with $n$ elements along the y-direction and with one element along the z-direction and b orientation of the 20-noded isoparametric solid element with natural CSYS aligned with the global CSYS. The same orientation of the CSYS is considered for the 8-node element

Fig. 6

Beam CSYS, uniaxial cross-section forces and the associated tractions following prismatic beam theory applied to both planes of the symmetrically tapered finite cross-section slice for a axial force ${T}_{z}$ and b shear force ${T}_{y}$ and c bending moment ${M}_{x}$

The cross-section slice was discretized with both 8-noded and 20-noded isoparametric solid elements where the shape functions of the latter are provided in Appendix A. With the strain–displacement matrix ${\varvec{B}}=\left[{{\varvec{B}}}_{1} {{\varvec{B}}}_{2} {{\varvec{B}}}_{3} \cdots {{\varvec{B}}}_{i}\right]$ assembled using Eq. (13) and the linear elastic isotropic constitutive stiffness tensor ${\varvec{Q}}={{\varvec{S}}}^{-1}$ was used with the compliance tensor provided below:

$$S=\left[\begin{array}{cccccc}\frac{1}{E}& -\frac{\nu }{E}& -\frac{\nu }{E}& 0& 0& 0\\ -\frac{\nu }{E}& \frac{1}{E}& -\frac{\nu }{E}& 0& 0& 0\\ -\frac{\nu }{E}& -\frac{\nu }{E}& \frac{1}{E}& 0& 0& 0\\ 0& 0& 0& \frac{1}{G}& 0& 0\\ 0& 0& 0& 0& \frac{1}{G}& 0\\ 0& 0& 0& 0& 0& \frac{1}{G}\end{array}\right]$$

(13)

The elemental stiffness matrix is given by Eq. (15) using the standard Finite Element formulation (Bathe 1982).

$${{\varvec{B}}}_{{\varvec{i}}}={\left[\begin{array}{cccccc}\frac{\partial {N}_{i}}{\partial x}& 0& 0& \frac{\partial {N}_{i}}{\partial y}& 0& \frac{\partial {N}_{i}}{\partial z}\\ 0& \frac{\partial {N}_{i}}{\partial y}& 0& \frac{\partial {N}_{i}}{\partial x}& \frac{\partial {N}_{i}}{\partial z}& 0\\ 0& 0& \frac{\partial {N}_{i}}{\partial z}& 0& \frac{\partial {N}_{i}}{\partial y}& \frac{\partial {N}_{i}}{\partial x}\end{array}\right]}^{T}$$

(14)

$${{\varvec{K}}}_{e}={\int }_{{V}^{e}}{{\varvec{B}}}^{T}{\varvec{Q}}\boldsymbol{ }{\varvec{B}} {\text{d}}V$$

(15)

Integration of Eq. (15) was done with a Gaussian quadrature using a full integration scheme (Dhondt 2004). The global stiffness matrix is eventually obtained by exploiting the standard assembly procedure according to ${\varvec{K}}={\sum }_{e}{{\varvec{K}}}_{e}$. Consequently, the weak form of the cross-section equilibrium conditions is given as ${\varvec{K}}\boldsymbol{ }{\varvec{u}}={\varvec{f}}$. In order to make ${\varvec{K}}$ positive definite, requires the removal of the six redundant equations represented by the RBMs. In order to avoid restraining the cross-section warping displacements by assigning discrete essential boundary conditions, a set of six homogeneous constraint equations is used. Equations 16 represent the discrete formulation of Eq. (3) where the first and second rows of Eqs. (16) pertains to the rigid body translations and rigid body rotations, respectively.

$$\begin{array}{ccc}{\sum }_{i=1}^{{n}_{n}}{u}_{x}^{\left(i\right)}=0& {\sum }_{i=1}^{{n}_{n}}{u}_{y}^{\left(i\right)}=0& {\sum }_{i=1}^{{n}_{n}}{u}_{z}^{\left(i\right)}=0\\ {\sum }_{i=1}^{{n}_{n}}-{z}_{i}{ u}_{y}^{\left(i\right)}+{y}_{i}{ u}_{z}^{\left(i\right)}=0& {\sum }_{i=1}^{{n}_{n}}{z}_{i}{ u}_{x}^{\left(i\right)}-{x}_{i}{ u}_{z}^{\left(i\right)}=0& {\sum }_{i=1}^{{n}_{n}}{-y}_{i}{ u}_{x}^{\left(i\right)}+{x}_{i}{ u}_{y}^{\left(i\right)}=0\end{array}$$

(16)

where ${n}_{n}$ represents the number of nodes in both the front and back surfaces of the tapered cross-section slice. The constraints (Eqs. 16) can be applied in the virtual work principle through the Lagrange multiplier method. In matrix form, Eq. (16) can be written as ${\varvec{C}}\boldsymbol{ }{\varvec{u}}=0$ where ${\varvec{C}}=\left[{\left[{\varvec{I}}\boldsymbol{ }{{\varvec{n}}}_{1}^{T}\right]}^{T} {\left[{\varvec{I}}\boldsymbol{ }{{\varvec{n}}}_{2}^{T}\right]}^{T} {\cdots \left[{\varvec{I}}\boldsymbol{ }{{\varvec{n}}}_{i}^{T}\right]}^{T}{\cdots \left[{\varvec{I}}\boldsymbol{ }{{\varvec{n}}}_{{n}_{n}}^{T}\right]}^{T}\right]$. The total potential can now be formulated with the $6\times 1$ Lagrange multiplier vector ${\varvec{\lambda}}$ as follows:

$$\Pi =\frac{1}{2}\left({{\varvec{u}}}^{T} {\varvec{K}} {\varvec{u}}-{{\varvec{u}}}^{T} {\varvec{f}}\right)+{\varvec{\lambda}}\left({\varvec{C}} {\varvec{u}}\right)=0$$

(17)

The solution of Eq. (17) is obtained by minimizing the potential energy $\Pi$ according to:

$${\nabla }_{u,\lambda }=\frac{\partial\Pi }{\partial u}\delta {\varvec{u}}+\frac{\partial\Pi }{\partial \lambda }\delta{\varvec{\lambda}}=0$$

(18)

Equation 18 must hold for any arbitrary $\delta {\varvec{u}}$ and $\delta{\varvec{\lambda}}$ which means that $\partial\Pi /\partial u=0$ and $\partial\Pi /\partial \lambda =0$ which renders the following constrained system of equilibrium equations:

$$\left[\begin{array}{cc}{\varvec{K}}& {{\varvec{C}}}^{T}\\ {\varvec{C}}& 0\end{array}\right] \left[\begin{array}{c}{\varvec{u}}\\{\varvec{\lambda}}\end{array}\right]=\left[\begin{array}{c}{\varvec{f}}\\ 0\end{array}\right]$$

(19)

The solution of Eq. (19) provides the nodal displacement vector corresponding to the relative cross-section slice deformation depicted in Fig. 2c in bold lines. The LHS diagonal of Eq. (19) contains zero entries rendering the matrix positive semi-definite that prevents direct solution methods such as e.g. the Cholesky factorisation method. A lower–upper (LU) factorization method is used to solve the system of Eqs. 19.

The element nodal force vector of Eq. (19) is obtained from the following equation:

$${\varvec{f}}=\int {{\varvec{N}}}^{T}\left(\xi ,\eta ,\zeta \right){\varvec{p}}\left(x,y,z\right) {\text{d}}A$$

(20)

where ${\varvec{N}}$ is evaluated at the back and front surfaces of the cross section ($\zeta =\pm 1$). For a slice with rectangular cross section of height ${H}^{-}$ and ${H}^{+}$ and width ${B}^{-}$ and ${B}^{+}$ at the back and front side respectively, the corresponding element nodal force components at the back and front sides resulted from axial force ${T}_{z}$, bending moment ${M}_{x}$ and shear force ${T}_{y}$ are given as follows:

$${f}_{i}^{\pm }={T}_{z}{\int }_{-1}^{1}{\int }_{-1}^{1}\frac{{N}_{i}^{\pm }}{{A}^{\pm }}\left|{{\varvec{J}}}_{{A}^{\pm }}\right|{\text{d}}\xi {\text{d}}\eta$$

(21)

$${f}_{i}^{\pm }={M}_{x}{\int }_{-1}^{1}{\int }_{-1}^{1}\frac{{N}_{i}^{\pm }}{{I}_{x}^{\pm }}\left(J\left(\mathrm{2,2}\right)\eta +{y}_{c}\right)\left|{{\varvec{J}}}_{{A}^{\pm }}\right|{\text{d}}\xi {\text{d}}\eta$$

(22)

$${f}_{i}^{\pm }=\frac{{T}_{y}}{B}{\int }_{-1}^{1}{\int }_{-1}^{1}\frac{{N}_{i}^{\pm }}{{I}_{x}^{\pm }}\left(\frac{{{H}^{\pm }}^{2}}{8}-\frac{{\left(J\left(\mathrm{2,2}\right)\eta +{y}_{c}\right)}^{2}}{2}\right)\left|{{\varvec{J}}}_{{A}^{\pm }}\right|{\text{d}}\xi {\text{d}}\eta$$

(23)

The secondary field variables in terms of Cauchy stress and linearized Green strain are obtained following standard finite element procedure. The secondary variables are computed by averaging over all elemental Gauss points and reporting the value in the element center.

A flowchart illustrating the major steps of the solution process is shown in Fig. 7.

Fig. 7

Major steps of the solution process

3 Results

3.1 Isotropic Material

In this section, the results obtained from the numerical implementation of the method in Matlab are presented. Linear elastic isotropic mechanical properties of the material used for validating the model are as follows. $\nu =0.25$ and $E=1\times {10}^{5} {\text{MPa}}$.

Table 1 denotes the relative error percentage between the numerical and analytical solutions for the normal stress ${\sigma }_{zz}$ and shear stress ${\sigma }_{yz}$ in a prismatic slice. As expressed in Table 1, the error for the axial load case is numerically zero for both 8-noded and 20-noded elements whereas in the case of bending moment load, the error for the 8-noded element is higher than the 20-noded element. This difference is due to shear locking that occurs in linear elements (e.g. 8-noded element) with full integration under bending, while the shear locking problem is eliminated when using quadratic elements (e.g. 20-noded element). In the torsion load case, the error is negligible for 8-noded and 20-noded elements. Both, the 8-noded and 20-noded elements were implemented in the Matlab code. However, the discretization with the 20-noded element did not significantly improve the numerical results in the present cases, therefore, the results of the 8-noded element are presented for the taper slice modeling. It should be noted that the 8-noded element discretization is the preferred choice—if possible—in order to reduce- the computational time of the cross-section analysis.

Table 1 Deviation percentage between numerical and analytical stresses in a prismatic slice for axial, bending and torsion load cases as well as different element types

Figure 8 shows a good agreement between the analytical solution (blue) and the numerical solution (dash-dot) for the cross-section displacements under pure bending. The former was obtained by removing the RBMs from the total displacements using the method presented in Appendix B. Figure 8 shows that shear bending induced S-shaped warping displacements are present in addition to the shortening (top) and elongation (bottom) of the slice. Consequently, the S-shaped warping displacement vanishes in a prismatic slice. Comparison of the analytical solution with the numerical prediction in Fig. 8 shows that the latter is more compliant.

Fig. 8

Grey, black dash-dot and blue are the initial configurations, the numerical solution and the analytical solution, respectively for the cross-section displacements of a tapered cross-section slice for pure bending with a taper angle of 5° and a scale factor of 50. The non-linear and unsymmetrical cross-section warping under pure bending is different to the response of a prismatic cross-section which is accurately predicted

Figure 9 compares the numerical and analytical solutions for shear and normal stress components of a 5° tapered cross-section slice under axial loading. All stresses are evaluated at the mid-plane of the cross-section slice at z = 0. As seen in Fig. 9, the numerical results agree well with the analytical solution for all the three stress components ${\sigma }_{yy}$, ${\sigma }_{yz}$ and ${\sigma }_{zz}$.

Fig. 9

Marker points and continuous lines represent the numerical and analytical solutions, respectively for stress components of a cross-section slice of 5° taper angle under the axial loading case T_z. It is noteworthy to mention that both components ${\sigma }_{yy}$ and ${\sigma }_{yz}$ would be zero and ${\sigma }_{zz}$ would be incorrectly predicted as a constant value in stepwise prismatic cross-section analysis predictions

Figure 10 shows the numerical and analytical solutions of the shear and normal stress components for a 5° tapered cross-section slice under pure bending. A very good agreement is observed for the shear ${\sigma }_{yz}$ and normal ${\sigma }_{zz}$ stress components. A small variance between the analytical and the numerical solutions for the normal stress ${\sigma }_{yy}$ becomes apparent (see Fig. 10a). It was found that the deviation error can be reduced by using a 20-noded element discretization.

Fig. 10

Marker points and continuous lines represent the numerical and analytical solutions, respectively for stress components of a cross-section slice of 5° taper angle under the pure bending moment load case M_x. It is noteworthy to mention that both components ${\sigma }_{yy}$ and ${\sigma }_{yz}$ would be zero in stepwise prismatic cross-section analysis predictions. The assumed linearly distributed tractions are a good approximation of the axial stress distribution ${\sigma }_{zz}$

Figure 11 demonstrates the shear stresses predicted by the proposed numerical method and the finite element (FE) software COMSOL Multiphysics (COMSOL Multiphysics® v. 5.6). In order to make a true comparison of the stress results predicted by COMSOL software and the proposed method, the geometrical parameters of the tapered beam are chosen so that the cross-section slice at the midspan of the COMSOL model corresponds to the cross-section geometry modeled in the proposed method. Figure 11a and b depict the mesh geometry and COMSOL contour plot of shear stresses at the midspan cross-section slice of the clamped tapered beam under torsion, respectively. The predicted shear stresses by the proposed numerical method agree well with the COMSOL results (c.f. Fig. 11c).

Fig. 11

Shear stresses predicted by the proposed numerical method and commercial FE software COMSOL for a cross-section slice of 5° taper angle under a torsion load M_z a Finite element mesh in COMSOL software b COMSOL contour plot of the shear stresses at the midspan cross-section slice of the tapered beam clamped at one end and under torsion at the other end c Comparison between the shear stresses predicted by the proposed numerical method and COMSOL software

Figure 12 shows the effect of the tapered slice thickness on the accuracy of the numerical solutions. As seen in Fig. 12, there is no significant dependency between the accuracy of the numerical results and the slice thickness. The maximum and minimum deviation errors are around 3.5% and 0.5% for slice thicknesses of 1 m and 3 m, respectively. It is worth noting that the deviation error decreases slightly when the thickness to width aspect ratio approaches one. It is important to discretize the model in such a way that high-quality elements are obtained to achieve the highest accuracy.

Fig. 12

Deviation percentage between the numerical stress components at the slice mid-plane and the corresponding analytical solutions versus the taper slice thickness for an axial load case

Figure 13 shows the deviation error between the numerical and the analytical solutions of a tapered slice under axial and bending moment loading for different taper angles. The results show a good agreement between the numerical and analytical results for 3°, 4°and 5° taper angles, especially in the case of axial loading. The maximum error is around 5% for normal stress ${\sigma }_{yy}$ in the case of bending and a taper angle of 5° c.f. Fig. 13b. The deviation error increases slightly with taper angle as seen in Fig. 13b.

Fig. 13

Deviation percentage between the maximum values of numerical stress components and the corresponding analytical ones versus the slice taper angle for both a axial load case and b bending load cases

3.2 Composite Material (Transversely Isotropic)

Mechanical material properties of the composite (i.e. transversely isotropic) tapered beam used for the validation of the proposed numerical method against commercial FE software COMSOl are as follows.

$${E}_{z}=1e5 {\text{MPa}}, {E}_{x}={E}_{y}=1e4 {\text{MPa}}, {\nu }_{xz}={\nu }_{yz}=0.3, { \nu }_{xy}=0.25, {G}_{xz}={G}_{yz}=8000 {\text{MPa}}$$

The tapered beam’s length along the Z direction in the COMSOL model is considered long enough (L = 100 m) to avoid the effect of boundary condition and loads on the stress results at the midspan cross-section.

Figure 14 depicts the shear and normal stresses predicted by the proposed numerical method and the FE software COMSOL for a 3° tapered cross-section slice under axial loading. Similar to the torsion case (c.f. Fig. 11a), to make a true comparison, the geometry of the cross-section slice at the midspan of the tapered beam modeled by COMSOL FE corresponds to the slice geometry modeled by the proposed method. The predicted shear and normal stress components agree relatively well with their corresponding COMSOl results (c.f. Fig. 14). The composite tapered slice exhibits slightly higher deviation errors than the isotropic tapered slice for normal stress components ${\sigma }_{yy}$ and ${\sigma }_{zz}$ (c.f. Fig. 14 and Fig. 9).

Fig. 14

Normal and shear stress components predicted by the proposed numerical method (marker points) and commercial FE software COMSOL (continuous lines) for a 3° tapered cross-section slice under axial loading

Figure 15 demonstrates normal and shear stress components for a 3° tapered cross-section slice under pure bending. The predicted shear ${\sigma }_{yz}$ and normal ${\sigma }_{zz}$ stress components match very well with their correspondings predicted by FE software COMSOL, however there is a slight deviation error in ${\sigma }_{yy}$ stress component. It is noteworthy that the normal stress component ${\sigma }_{zz}$ does not change linearly with the slice’s height (i.e. Y axis) for the composite tapered slice, and it deviates from linearity at the top and bottom of the slice (c.f. Fig. 15c).

Fig. 15

Normal and shear stress components predicted by the proposed numerical method (marker points) and commercial FE software COMSOL (continuous lines) for a 3° tapered cross-section slice under pure bending moment

4 Discussion

The Lagrange multiplier method used for applying the boundary conditions provides the capability to accurately predict the warping deformation in tapered cross-sections without restraining the response. In the FE formulation, the nodal forces were calculated assuming prismatic assumptions for the tractions, however, the numerically predicted results agreed well with the FE results predicted by COMSOL software and analytical solutions for the displacement and stress components. Applying approximate prismatic tractions enables coupling of the cross-section forces to the nodal forces without compromising the accuracy of the predicted displacement and stress. The applicability of the approximate prismatic assumption has been confirmed in other research works (Taglialegne 2018; Bertolini et al. 2019a, b). The numerical prediction of the slice displacement was slightly more compliant compared to the analytical solution, which is likely caused by neglecting the shear tractions when calculating the nodal forces.

The effect of the slice thickness on the accuracy of the numerical results was found to be insignificant. As only one element was used to discretize the slice through the thickness, the slight change in the numerical prediction error (i.e. approx. 1%) with slice thickness can be attributed to a change in the element aspect ratio and accordingly the element quality. In order to eliminate the numerical error due to element quality, the slice thickness and the model discretization should be chosen such that elements with aspect ratios much larger or smaller than one are avoided.

The numerical model predicted the stress components well with high accuracy for slices with small taper angles between 3° and 5° which is the case for the majority of beam-type structures in engineering applications (e.g. wind turbine blades). With increasing slice taper angle, the error caused by the prismatic traction formulation increases which reduces the accuracy of the numerical model. This deviation however, is not a shortcoming of the method per se but rather a limitation of the currently adopted prismatic coupling between the cross-section force and the nodal forces. Future research will focus on coupling the cross-section forces to the cross-section slice faces in such a way that the nodal forces do not explicitly appear in the formulation. It is expected that the method will also provide accurate predictions for large taper angles.

5 Conclusions

In this work, a numerical framework was developed for analyzing tapered cross-sections. The method was implemented using Matlab programming and the numerical results were validated against closed-form analytical solutions and COMSOL FE results. The following conclusions can be drawn from this work:

• i. It was demonstrated that the proposed method can provide accurate predictions of warping deformation and stress/strain fields of tapered 3D cross sections, which is not possible with stepwise prismatic formulations.

• ii. The feasibility of tapered 3D cross-section analysis was demonstrated and validated.

• iii. The Lagrange multiplier method was applied successfully to the cross-section analysis of tapered finite cross-section slices, allowing for warping displacement to be modelled.

• iv. The numerically predicted stress and strains at the slice mid-plane are largely independent of the slice thickness.

• v. The numerically predicted cross-section displacements and stresses agree well with the analytical solution for small taper angles which are the case for many engineering structures such as wind turbine blades.

Appendices

Appendix 1

The shape functions for 20-noded isoparametric solid element used in the numerical approach proposed in this work:

$${N}_{i}=\frac{1}{8}\left(1+\xi {\xi }_{i}\right)\left(1+\eta {\eta }_{i}\right)\left(1+\zeta {\zeta }_{i}\right)\left(\xi {\xi }_{i}+\eta {\eta }_{i}+\zeta {\zeta }_{i}-2\right) {\text{for}} i=1, 3, 5, 7, 13, 15, 17, 19$$

(A1)

$${N}_{i}=\frac{1}{4}\left(1-{\xi }^{2}\right)\left(1+\eta {\eta }_{i}\right)\left(1+\zeta {\zeta }_{i}\right) {\text{for}} i=2, 6, 14, 18$$

(A2)

$${N}_{i}=\frac{1}{4}\left(1-{\eta }^{2}\right)\left(1+\xi {\xi }_{i}\right)\left(1+\zeta {\zeta }_{i}\right) {\text{for}} i=4, 8, 16, 20$$

(A3)

$${N}_{i}=\frac{1}{4}\left(1-{\zeta }^{2}\right)\left(1+\xi {\xi }_{i}\right)\left(1+\eta {\eta }_{i}\right) {\text{for}} i=9, 10, 11, 12$$

(A4)

Appendix 2

For direct comparison of the cross-section displacements obtained from the numerical method, it was necessary to remove the RBMs from the total displacements $\widetilde{{\varvec{u}}}$ provided by the analytical 2D wedge solution. Using the constraints in Eq. (16) it is possible to define the following identity for the two rigid body translations ${\overline{{\varvec{u}}} }_{T}$:

$${\sum }_{i=1}^{{n}_{n}}{\widetilde{u}}_{y}^{\left(i\right)}={\overline{u} }_{Ty} {n}_{n}$$

(B1)

$${\sum }_{i=1}^{{n}_{n}}{\widetilde{u}}_{z}^{\left(i\right)}={\overline{u} }_{Tz} {n}_{n}$$

(B2)

The displacement vector components due to rigid body rotation ${\varphi }_{x}$ of the cross-section slice are given by ${\overline{{\varvec{u}}} }_{R}={{\varvec{n}}}^{T}\boldsymbol{ }{\left[\begin{array}{ccc}{\varphi }_{x}& 0& 0\end{array}\right]}^{T}={\varphi }_{x} {\left[\begin{array}{cc}-z& y\end{array}\right]}^{T}$. In a similar fashion, the following identity can be established by substituting the displacement components due to rigid body rotation into Eq. (21):

$${\sum }_{i=1}^{{n}_{n}}-{z}_{i}{ \widetilde{u}}_{y}^{\left(i\right)}+{y}_{i}{ \widetilde{u}}_{z}^{\left(i\right)}={\varphi }_{x}{\sum }_{i=1}^{{n}_{n}}{z}_{i}^{2}+{y}_{i}^{2}$$

(B3)

The rigid body rotation can be obtained from Eq. x and the components of the cross-section deformation without RBMs are ${\varvec{u}}=\widetilde{{\varvec{u}}}-{\overline{{\varvec{u}}} }_{T}-{\overline{{\varvec{u}}} }_{R}$ which in expanded form is notably:

$$\left(\begin{array}{c}{u}_{y}^{(i)}\\ {u}_{z}^{(i)}\end{array}\right)=\left(\begin{array}{c}{\widetilde{u}}_{y}^{(i)}\\ {\widetilde{u}}_{z}^{(i)}\end{array}\right)-\frac{1}{{n}_{n}}\left(\begin{array}{c}{\sum }_{i=1}^{{n}_{n}}{\widetilde{u}}_{y}^{\left(i\right)}\\ {\sum }_{i=1}^{{n}_{n}}{\widetilde{u}}_{z}^{\left(i\right)}\end{array}\right)-\frac{{\sum }_{i=1}^{{n}_{n}}-{z}_{i}{ \widetilde{u}}_{y}^{\left(i\right)}+{y}_{i}{ \widetilde{u}}_{z}^{\left(i\right)}}{{\sum }_{i=1}^{{n}_{n}}{z}_{i}^{2}+{y}_{i}^{2}}\left(\begin{array}{c}-{z}_{i}\\ {y}_{i}\end{array}\right)$$

(B4)