1 Introduction

The piezometric instrument is generally installed in dams to measure the hydraulic pressure to examine dam seepage. The distribution of the pore pressure due to the gravity seepage is determined using the flow grid method, although the finite element method used in this field. Clough et al. were the first researchers who utilized finite element method in predicting the behavior of an earth dam in 1967. In their study, Clough et al. used the linear elastic model to analyze stresses and deformations in the dam. However, with the development of powerful computers, more complex models are developed to represent the stress-strain behavior of materials and used in the finite element analysis such as the non-linear hyperbolic model developed by Duncan and Chang, in (1970) and application of this procedure to simulate wetting effects described by Nobari and Duncan (1972). Dams built on alluvial deposits or permeable bedrock have been subjected to fatal seepage (Fu and Jin 2009). Therefore, foundation treatment cut-off systems, such as a clay core or concrete cutoff wall, are often utilized (Wieland 2016; Uromeihy and Barzegari 2007; Zhong et al. 2011). Concrete cutoff walls can be deformed by unevenly distributed pressures, which form cracks that can lead to seepage of the dam. Pueyo Anchuela et al. (2018) investigated the crack distribution in a dam using ground penetration radar. The integrity of the cutoff wall system and the influence on dam seepage were then analyzed. Geotechnical problems, which earth dams could experience during their operational stages, are mainly related to slope instability and internal erosion phenomena (Jannati et al. 2010). Updating dam safety and efficiency concerning such concerns are becoming a crucial matter, especially for those structures that have been in operation for several decades. To accomplish this task, dam loading history should be preventively known; also, monitored physical quantities and results from periodical inspections should be suitably collected and interpreted during the different stages of the dam's life (Nayebzadeh et al. 2000). The pore water pressure created in the core of earth dams is very important in terms of soil mechanics, and its increase can endanger the stability of the dam. Increasing pore water pressure may reduce effective stress, thus reduce the shear strength of core materials, and ultimately create cracks or ruptures in the dam body. Reducing the pore water pressure in the dam body during the construction and operation of the dam is a very important issue (Johansson et al. 1997). According to the ICOLD (International Commission on Large Dams), the majority of failed dams either did not have any monitoring system or had a system that was out of order. This finding, therefore, demonstrates the importance of inspection and an appropriate monitoring system for regular observation of dam performance. The objective of dam monitoring, which plays a significant role in dam safety, is to provide data to evaluate dam performances throughout its whole life cycle. In the analysis of the earth's dam in the conditions where the reservoir is full and permanent seepage is established, a conventional and simple method of using effective stress is based on the pore pressure caused by gravity seepage from the dam. Usually, the pore pressure distribution is caused by gravity seepage from within the dam (Rahimi 2011). The distribution of the pore pressure due to the gravity seepage is determined using the flow grid method, although the finite element method used in this field. The finite element method for solving geotechnical problems was first proposed by Clough and Woodward in 1967. Also, Clough and Zienkiewicz in 1967 provided general reports for the static analysis of earth dams, but the use of finite element methods for the analysis of large soil structures, such as dams, was popularized by Duncan and Chang (1970). Also, Abhilasha and Balan (2014) compared to the existing and common earth dam seepage modeling software. The results of analysis and comparison of different software showed that modeling with Seep/w software has acceptable and high accuracy and can be efficient and economical for complex problems. Rashedi et al. (2017) assessed the pore water pressure and settlement of the Gavshan earth dam and the comparison of instrumentation data, numerical modeling using FLAC (2D) software concluded that dam performance in terms of pore water pressure, and finally stability of the dam is positive. Haghighi et al. (2012) studied the seepage of earth dam's foundation with blanket and cut-off wall. He provides a simple equation for calculating the seepage from earth dams based on the blanket composition and the cut-off wall. In another study, (Moradi et al. 2017), studied the pore water pressure in the body of the earth dams in the construction stages. By modeling the Damghan earth dam with Plaxis software and layer-to-layer analysis of dam construction steps and using the Mohr–Coulomb behavioral model, they achieved positive results regarding the software's ability to simulate pore pressure stress. Also, Mousavi Khansari et al. (2009) studied and evaluated the pore pressure at the core of the Karkheh Dam during construction and impounding simultaneously using the instrumentation results. Luo et al. (2018) studied the behavioral variation of the Chengbihe reservoir dam in 18 years. Using the results of the piezometric pressure and instrumentation settlement concluded that the maximum settlement of the dam in the central part is 178 mm, which is gradually from the center to the wings reduced. The maximum settlement at the wings was 65.8. Also, most settlements are observed at the upstream of the seals, which can be due to changes in water level and reservoir pressure. Javanmard et al. (2019) in an article on the pore water pressure of the Taham Dam used the results of instrumentation and Plaxis software. Khassaf and Madhloom (2017) studied the effect of permeability and core thickness on the determination of hydraulic gradient, output gradient, saturation, and total pressure using numerical methods. Also, Lee et al. (2018), Al-Janabi et al. (2020), Aboelela (2016), Venkatesh and Karumanch (2016), Jiang and He (2018), Qiu et al. (2016) and Kheiri et al. (2020) in separate studies examined the seepage of earth dams. In this study, the results of the pore water pressure and seepage discharge of the Eyvashan earth dam were compared with the results of the numerical analysis by Geostudio software. Also, the function of the cut-off wall will be checked. By comparing the observational results and numerical analysis while verifying the geo-studio software, the proper sealing function of the dam is confirmed using the cut-off wall method.

2 Materials and Methods

2.1 Specification of the Eyvashan Dam

Eyvashan Reservoir Dam has located 1.5 km from the upstream of the village of Eyvashan and about 57 km from Khorramabad in the coordinates of 48° 49′ 2″ and 33° 28′ 31″, located on the Horod River. The area of the Horod river drainage basin up to the axis of the dam of Eyvashan is 120 km2. The dam is a rock fill-earth dam type with a vertical clay of core that has a height of 64 m, a crest height of 68 m (1868 masl), and a normal elevation of 64 m (1864 masl). The volume of the reservoir in the normal value of the dam is 52 million m3 and the area of the lake at a normal level is 2.3 km2. Figure 1 presents the Eyvashan earth dam.

Fig. 1
figure 1

Eyvashan earth dam

Full size image

The construction site of the Eyvashan earth dam from the geological point of view of the rock bed consists of conglomerate rocks that have outcrops in the boundaries of these rocks but deposited on the conglomerate rock in the bottom of the valley of alluvial sedimentary deposits. In terms of lithology, the conglomerate of the axis and lake is composed of limestone, sandstone, slate, metamorphic rocks and igneous rocky parts with a silty-sandy and sometimes silt–clay matrix. In terms of lithology, the conglomerate of the axis and lake is composed of radiolarite parts, sandstone, slate, metamorphic rocks and igneous rocks with a silty-sandy and sometimes-silty clay matrix. In the study of the site of the Eyvashan dam axis, the first rock mass rating system (RMR), first presented by Bieniawski, has been used as the most comprehensive geomechanical classification system for rock masses to classify rock mass (Table 1).

Table 1 Geomechanical classification of rock mass of Eyvashan dam based on RMR system
Full size table

According to the results, the rock mass class of the Eyvashan dam (very good) is very suitable for soil excavation.

2.2 Governing Equation for Seepage Analysis

The long-term study state and the transient analysis of the seepage are conducted by using numerical models. SEEP/W, a numerical model, is used in which an instrument is using the finite element method to simulate the water flowing through porous media (SEEP/W, 2012). SEEP/W is used to simulate the groundwater movement in both the steady or transient states. The program is formulated based on the flow of water through both saturated and unsaturated soils following Darcy’s Law, which may be expressed as:

$$q = k \cdot i.$$
(1)

With q being the specific discharge, k being the hydraulic conductivity, and i being the gradient of the total hydraulic head. The hydraulic conductivity in Eq. (1) is maintained as a constant value for the full saturated soil, while it is modeled as various values for the unsaturated soil changing with the water content of the soil. The general governing differential equation for two-dimensional seepage can be expressed mathematically as (SEEP/W, 2012):

$$\frac{\partial }{\partial x}\left( {k_{x} \frac{\partial H}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {k_{y} \frac{\partial H}{{\partial y}}} \right) + Q = \frac{\partial \theta }{{\partial t}}.$$
(2)

With H the total head, kx the hydraulic conductivity in the x-direction, ky the hydraulic conductivity in the y-direction, Q the applied boundary flux, Θ the volumetric water content, and t time. Mainly, this equation equates the water flux flowing through a two-dimensional elemental volume in x- and y-directions plus the applied boundary flux to the volumetric water content with consideration to the time (SEEP/W, 2012). The change in the volumetric water content is related to the changes in the stress state variables: (σ − ua) and (ua − uw), where σ is the total stress, ua is the pore-air pressure, and uw is the pore water pressure. SEEP/W (2012) considers the total stress in the soil is constant, which means there is no change in the variable of (σ − ua). Also, the program assumes no change in the pore air pressure (ua). Therefore, the change in the volumetric water content of soil depends only on the change in the pore water pressure (uw). The volumetric water content is calculated by using the following equation:

$$\partial \theta = m_{{\text{w}}} \gamma_{{\text{w}}} \partial \left( {H - y} \right).$$
(3)

With mw the storage curve slope, γw the unite weight of water, H the total hydraulic head, and y the elevation. By substituting Eq. (3) into Eq. (2), the general governing differential equation may be stated as (SEEP/W, 2012):

$$\frac{\partial }{\partial x}\left( {k_{x} \frac{\partial H}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {k_{y} \frac{\partial H}{{\partial y}}} \right) + Q = m_{{\text{w}}} \gamma_{{\text{w}}} \partial \left( {H - y} \right).$$
(4)

2.3 Instrumentation Installed in Eyvashan Earth Dam

Installed instruments in the Eyvashan earth dam include Casagrande standpipe piezometers for measuring pore water pressure, observation wells for determining groundwater level and settlement meters to measure the body's settlement and v-notch seepage to measure the discharge of water seepage from the dam body used, which is a mechanical device and is one of the simplest types of instruments installed in this dam. Electrical instruments have higher accuracy, and the reading of them is possible by the reader's devices and the possibility of remote reading. Electric piezometers for measuring pore water pressure, pressure gauge cells for measuring total stress, Inclinometer for measurement of change shapes, Extensometers for measuring elongation, Jointmeters for Openings in rocky and earthy masses, Crack meters to measure crack widths, earth dam accelerometers for measuring and recording the motion of the vibration of the earth, and dozens of other instruments are the most commonly used electrical instruments in the earth and concrete dams, tunnels, caverns, railways and bridges used. The general status of the installed instrument of the Eyvashan Dam is presented in Table 2. Also, in the numerical analysis, the behavioral model of Mohr–Coulomb has been used, which is shown in Table 3.

Table 2 General condition of the equipment installed in the Eyvashan earth dam (Abdan Faraz Consulting Engineers Co)
Full size table
Table 3 Parameters of materials used in numerical analysis
Full size table

The instrumentation of the Eyvashan dam considered in four sections of 228–228, 229–229, 230–230 and 231–231, in the 0 + 249, 0 + 356, 0 + 477 and 0 + 546 km, respectively. In the present study, the characterization of the instrument installed in the section of 229 Eyvashan Reservoir Dam was investigated. The maximum level of instrumentation is related to the 229–229 cross section with seven levels and the minimum number of instrumentation levels related to the 231–231 section with five levels (Fig. 2).

Fig. 2
figure 2

Position of the instrument on the plan and section of the Eyvashan earth dam

Full size image

2.4 Monitoring of Electrical Piezometer Foundations (EPF)

In the level of 1778 masl, two piezometers mounted upstream, downstream, and equidistant from the axis. The trend of piezometric pressure variations on this level is such that during rising landings, it shows a rising trend and shows a slight decrease in the grazing course at the time of embankment stall. This process has become an incremental process during impounding. In the upstream watershed, after the start of impounding and at the last reading, the piezometric pressure is about 692 kPa and downstream 581 kPa, and the pressure difference is lower than the low 111 kPa. The piezometric alignment in this upstream and downstream level is 1849 and 1837 m, respectively (Abdan Faraz Consulting Engineers) (Fig. 3).

Fig. 3
figure 3

Pore water pressure changes in foundation piezometers, level 1778 masl

Full size image

At 1788 masl, two piezometers in the upstream and downstream of the axis and two electric piezometers adjacent to the Casagrande piezometers in the downstream axis (Fig. 4). The piezometric alignment in upstream and downstream at the last readings is 1855 and 1819 masl, respectively. Also, the pressure upstream is about 351 kPa above the lower pressure. Also, this difference accompanied by an increase in the level of the lake, which could be somewhat indicative of the proper functioning of the cut-off wall. The downstream piezometers also show a nearly identical trend with their near-described piezometers, and the piezometric balance calculated in this instrument (EPF-229-5, 6) reaches 1802 and 1803 masl, respectively. Also, it shows a roughly identical trend at the downstream (Fig. 4).

Fig. 4
figure 4

Pore water pressure changes in foundation piezometers, level 1788 masl

Full size image

With rising reservoir water levels up to 1862 masl, upstream piezometers are affected by piezometric changes in their surroundings, which is followed by a decrease in the piezometric balance at the same time.

2.5 Monitoring of Electrical Piezometer Embankment (EPE)

At 1799 masl, two piezoelectric dams were installed at the top and bottom of the clay core. The variation in the pore pressure created in the clay core was due to the increase in the embankment and late 2013, with increasing reservoir water level; the pore volume increased ascending, at the last readings provided in the upstream 649 kPa and downstream 298 kPa (Fig. 5).

Fig. 5
figure 5

Pore water pressure changes in embankment piezometers, level 1799 masl

Full size image

At an altitude of 1812 masl, two piezometers of electricity in the clay core and 1809 masl, three electrical piezometers in the bottom shell installed. Piezometers that have been installed inside the clay core have experienced a uniformity since the installation so far after the completion of the embankment operation and the beginning of the impounding period, the pore pressure created is depleted, and in both the piezometers upstream and downstream of this pressure are negligible (Fig. 6).

Fig. 6
figure 6

Pore water pressure changes in embankment piezometers, level 1809 masl

Full size image

In the downstream shell, the amount of pore pressure generated is uniform and constant, and the pore pressure created is negligible (Fig. 7).

Fig. 7
figure 7

Pore water pressure changes in embankment piezometers, level 1812 masl

Full size image

At an altitude of 1825 masl, two piezometers are located on the upstream and downstream of the clay core and two piezometers in the bottom crest, the piezometer mounted above the hand after the start of intake and at the last reading, the pressure of 276 kPa. Also, the piezometer mounted at the bottom of the last revision shows a pore pressure near 138 kPa, but a piezometer mounted in the bottom-down filter since the beginning of the year 2011, with the start of a gentle ascension garlic embankment And at the last reading it shows a pressure of about 31 kPa. The piezometer fitted in the bottom shell at the last reading recorded a piezometric pressure of 75 kPa (Fig. 8).

Fig. 8
figure 8

Pore water pressure changes in embankment piezometers, level 1825 masl

Full size image

At an altitude of 1838 masl, there are three piezometers of electricity in the clay core and a lane filter. The upper piezometer of the cluster of the jet pressure is 276 kPa, and the lower piezometer of the pressure limit is 268 kPa. The piezometer inside the filter material shows a very small pore pressure, which appears to be natural due to the surrounding environment. The electrical piezometer installed at the level 1851 masl has shown that the pore pressure is negligible at zero, which can be due to a dry area around the instrument (Fig. 9).

Fig. 9
figure 9

Pore water pressure changes in embankment piezometers, level 1838 masl

Full size image

3 Results and Discussion

3.1 Numerical Analysis of Seepage of Eyvashan Dam

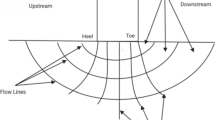
In this research, the Geostudio software suite was used to determine the seepage rate of the Eyvashan Dam using the results of instrument reading and comparing it with the results of the numerical analysis. The capabilities of this program include plotting the flow of water through the soil and velocity vectors, plotting flow lines and potential lines, and calculating the flow rate for a specific section of the soil or, in other words, the section of a dam. In the finite element method, the body and the dam with the small elements are element sized and after the application of boundary conditions, according to different levels of water, the amount of seepage flow is calculated. Quad and triangle elements were used to mesh the dam and other parts in the FEM models. The number of elements and nods used in the Eyvashan model is 2315 and 2992, respectively. The boundary conditions for the seepage analysis and the finite element mesh are presented in Fig. 10. For analysis of the seepage from the body and foundation of the Eyvashan earth dam and to achieve acceptable results and comparing better seepage, six different levels of water were used for analysis by software and in steady state, and the results obtained after the impact of the lake width (dam length) compared with actual data.The results of the seepage analysis are shown in Fig. 11 in 1812, 1820, 1830, 1840, 1850, and 1861.20 levels.

Fig. 10
figure 10

Boundary conditions for the seepage analysis and the finite element mesh (Eyvashan earth dam)

Full size image
Fig. 11
figure 11

Numerical analysis of Eyvashan seepage at different water levels a 1812, b 1820, c 1830, d 1840, e 1850, f 1861.40

Full size image

As shown in Table 4, the seepage rate is calculated per unit and is calculated by the impact length of the dam, which is 600 m. The numerical analysis (Table 4) illustrates the actual seepage flow rates and seepage analysis results.

Table 4 Actual seepage rate (instrument) and numerical analyses (Geostudio software)
Full size table

According to the results of numerical and numerical analysis, the maximum seepage rate in the full reservoir conditions is equal to 831,604,320 l/year. Also, according to Fig. 12, the seepage discharge values obtained from the numerical analysis are approximately the same with the actual results and do not differ significantly. Part of this difference in values can be due to differences in the specific gravity of materials in the design and reality. To evaluate and compare the statistical accuracy of the results of the observational and simulated data, the ratio of normalized mean error (NRMSE) (5) and relative error (RSE) (6) and mean absolute error percentage (MAPE) (7), as well as the mean absolute magnitude error (MAE) of relation (8), is used in calculating the relative error (RE) of relation (9).

$${\text{NRMSE}} = \frac{{\sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {P_{i} - O_{i} } \right)^{2} }}{n}} }}{{O_{{{\text{max}}}} - O_{{{\text{min}}}} }},$$
(5)
$${\text{RSE}} = \frac{{\sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {P_{i} - O_{i} } \right)^{2} }}{n}} }}{{O_{{{\text{ave}}}} }},$$
(6)
$${\text{MAE}} = \mathop \sum \limits_{i = 1}^{n} \frac{{\left| {P_{i} - O_{i} } \right|}}{n},$$
(7)
$${\text{MAPE}} = \mathop \sum \limits_{i = 1}^{n} \left| {\frac{{\left( {P_{i} - O_{i} } \right)}}{{O_{i} }}} \right|{ } \times \frac{100}{n},$$
(8)
$${\text{RE}} = \frac{{{\text{MAE}}}}{{O_{{{\text{ave}}}} }} \times 100.$$
(9)
Fig. 12
figure 12

Comparison of instrument seepage results and numerical analysis

Full size image

In the above relations, Pi is simulated (software), Oi is the observational value (instrumentation), Oave, average observation values, Omax, maximum observation values, Omin, minimum observation values, and n number of data. After applying the relationships on observational and simulated data, the results of the average normalized error, relative standard error, mean absolute magnitude error and the mean absolute magnitude of the relative error for the results of seepage discharge were 95.57, 92.20, 91.63 and 91.12, which indicates the model's performance and the conformance of the measured values with the software. Also, to evaluate and compare the exact performance of the instrumentation and the Geostudio model, a multi-variable regression is used from the criterion of the coefficient of determination (Eq. 10).

$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {P_{i} - O_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {P_{i} - O_{{{\text{ave}}}} } \right)^{2} }}.$$
(10)

In (10) n is the number of samples, O, and P are, respectively, the observed values and the predicted values, and Oave is the mean of observational values. The coefficient of determination indicates that the regression line between the predicted and measured values is close to that of the regression line with a slope of one. In calculations, the closer R2 to the number one, the more efficient the model is. Indeed, if the value of R2 is equivalent to one, it shows a perfect fit, indicating a complete fit between the observational and predicted data. By applying (10) on observed and predicted data, the value of the coefficient of determination was 0.9892, which indicates the correspondence of the results of the seepage for the actual instrument values and the values of the software Geostudio (Fig. 13).

Fig. 13
figure 13

Comparison of instrument (observed values) and finite element methods (predicted values) for estimating seepage

Full size image

3.2 Investigation of the Results of the Water Pressure of the Dam of Eyvashan

Increasing the pore pressure of the water leads to failure in the excavation. Among the destructive effects of increasing pore pressure, we can mention the following:

  1. A.

    The most common effect of increasing the pore pressure on earth dams is the unsteadiness of the gravel slope.

  2. B.

    Increasing the pressure of the pore water leads to an increase in compressive forces upstream of the hydraulic structures and instability of the structures.

  3. C.

    The pressure of the pore water may result in the upward force rising in the soil of the enclosed soil located downstream of the dam. The destruction begins when the force reaches upward from the force due to the weight of the layer destroying a scouring or flood phenomenon. The confidence level used for upward forces is the expression it is from the ratio of overhead forces to the upward force of water, which is expressed as 11.

    $${\text{Sf}} = \frac{{{\text{Gs}} \times t}}{{\left( {1 + e} \right) \times h}}.$$
    (11)

In relation (11), Gs is the relative density of solids, t is thickness, e is the porosity of the enclosing soil layer, h is the piezometric height in the substrate, and the minimum confidence coefficient 2 is required. To check the pore pressure of the block in the dam of Eyvashan, the instruments installed in section 229 selected. Section 229 is a cross-section with the maximum height of the dam of Eyvashan. The results include readings made on June 21, 2016, at the level of the reservoir equal to 1861.20 m. In this research, for verifying the data obtained from instrumentation readings, the pore water pressure of the Eyvashan earth dam using Geostudio software presented in two-dimensional and under the conditions of the flattened geometric model, which simplifies the calculations. Then, the results of a numerical analysis are compared with the results of the observation. Table 5 presents the permeability of the materials used in the leak analysis. The displacement of the body piezometric and the pore, the pore pressure contours, and the total head contours in the Geostudio model are shown in section 229 of the Eyvashan earth dam (Figs. 14, 15). The pore water pressure at the reserve floor level is 53.5 m, which is equivalent to the reservoir water level (1861.20 m). The phreatic line does not show a drop in the upper shell due to the high permeability of the upstream crust, and a significant hydraulic gradient is observed in the core, which is evidence of the proper functioning of the core, that is, counteracting the permeability of the flow of water. As can be seen, the equilibrium of the pressure lines in the earth's dam is indicative of the continuity of the permafrost in the body of the earth dam.

Table 5 Permeability of various materials of Eyvashan Dam
Full size table
Fig. 14
figure 14

Pore water pressure contours (kPa) of the Eyvashan earth Dam

Full size image
Fig. 15
figure 15

Total head contours (m) of the Eyvashan earth dam

Full size image

In Table 6, the values of the water pressure of the pore water pressure read by the piezometers and the results of computer modeling presented as a pressure height. Generally, phreatic line in the dam is the boundary between the positive and negative pore pressures as the points below the free surface flow line have positive pore water pressure values and the points located above this line have negative water pressure values due to the occurrence of the suction phenomenon in the upper regions. In this research, zero indicates negative values of pore water pressure.

Table 6 Measured and predicted values of pore pressure of core and foundation Eyvashan earth dam for the instruments installed in the section of 229
Full size table

Figure 16 compares readings from instrumentation and numerical modeling results for foundation and embankment piezometers.

Fig. 16
figure 16

Comparison of the observed and predicted values of the pore water head of section 229, a Electric Piezometers Embankment, b Electric Piezometers Foundation

Full size image

These values relate to the pore water pressure of the body and foundation of the Eyvashan earth dam. In this study, the pore water pressure at zero above the free flow level is considered. In general, the values obtained from instrumental readings and numerical analysis are in good agreement with each other. As you can see, the results of reading the electric piezometers in the clay core at the 1806 and 1825 m level indicate lowering the pressure from the upstream–downstream of the core, which indicates the correct functioning of these piezometers (Fig. 17).

Fig. 17
figure 17

Pressure drop from upstream and downstream of the core at two different levels (observational and numerical analysis), a 1806 masl, b 1825 masl

Full size image

As shown in Fig. 18, the values obtained from numerical analysis, both quantitatively and formally, are very consistent with the results of instrumentation readings. EPF-1 and EPF-3 piezoelectric devices are located on the upstream side of the cut-off wall and the EPF-2 and EPF-4 piezometer are on the lower side and close to it. Also, the amount of pressure on the downstream side of the cut-off wall in both the numerical and observational modeling results has dropped sharply, indicating the correct operation of the injection cut-off wall.

Fig. 18
figure 18

Pressure drop from upstream and downstream of the cut-off wall at different levels, a 1778 masl, b 1888 masl

Full size image

To evaluate and compare the performance of the instrumentation and the Geostudio model, multivariate regression was used from the criterion of the coefficient of explanation (Eq. 10). By applying Eq. (10) on observed and predicted data, the coefficient of explanation for Geostudio software was 0.9834, which showed the correspondence of the results of pore water pressure for values Instrumentation and predicted values (Fig. 19).

Fig. 19
figure 19

Distribution pore water pressure for observed (instrument) and predicted values (Geostudio software)

Full size image

4 Conclusions

The values obtained from the numerical analysis are very consistent with the results of accurate instrument readings. Also, the free surface line of the flow (phreatic line) obtained from numerical modeling in the dam body is quantitatively and qualitatively very similar to the actual free surface line of the extracted stream from the installed piezometers. In fact, the performance of the core in dealing with the amount of dam seepage is in good agreement with the initial design conditions and indicates the stable behavior of the dam in terms of permeability. Installed piezometers upstream of the core shows a higher pressure than the downstream, due to the high saturation state of the phreatic line. According to the results of numerical and numerical analysis, the maximum seepage rate in the full reservoir conditions is equal to 831,604,320 l/year. The slight changes in the phreatic line seen in the numerical model with respect to the actual flow conditions of the object and the dam may be due to the use of materials with different mechanical parameters in the operation. Therefore, the material of the actual materials used in the body of the Eyvashan dam and parameters such as the design may differ from the design values. In addition, the numerical analysis of the two-dimensional seepage was performed while the actual current in the earthen dams was somewhat three-dimensional, so this difference in the phreatic line is justifiable. The amount of pressure on the downstream side of the cut-off wall in both the numerical and observational modeling results has dropped sharply, indicating the correct operation of the injection cut-off wall.