1 Introduction

In 1950, Szász operators (Szász (1950)) are defined by

$$\begin{aligned} P_m(h;u)=\sum _{i=0}^{\infty }h\left( \frac{i}{m}\right) p_{m,i}(u), \end{aligned}$$
(1.1)

where \(u\in [0,\infty ),m=1,2,...,\)

$$\begin{aligned} p_{m,i}(u)=e^{-mu}\frac{(mu)^i}{i!}. \end{aligned}$$
(1.2)

The classical Sz\(\acute{a}\)sz–Mirakjan operators are linear positive operators and approximate the continuous functions over the positive semi-axis. Several mathematicians have constructed various generalizations of Sz\(\acute{a}\)sz–Mirakjan operators given by (1.1), e.g., Agrawal et al. 2014; Alotaibi 2022, 2023, ; Wafi and Rao 2018; Raiz et al. 2022, 2023; Acu and Rasa 2020; Mursaleen and Nasiruzzaman 2017; Aslan 2022; Aslan and Mursaleen 2022; Aslan 2022; Aslan and Mursaleen 2022; Rao et al. 2021; Ayman-Mursaleen 2017, 2022; Mishra et al. 2023; Mohiuddine et al. 2017; Nasiruzzaman et al. 2021, 2023; Ayman-Mursaleen and Serra-Capizzano 2022; Al-Abied et al. 2021 and Kajla et al. 2021, etc. We also refer to reader for a deep historical background (Mohiuddine 2020; Mohiuddine et al. 2022; Yadav et al. 2023; Mohiuddine et al. 2023; Nasiruzzaman et al. 2023; Mohiuddine et al. 2021; Mohiuddine and Özger 2020; Özger et al. 2022; Ansari et al. 2022; Cheng and Mohiuddine 2023).

Motivated with the above development, we define Szász–Durrmeyer type operators \(S^{\nu }_{m}:L _{B}[0,\infty ) \rightarrow \mathbb {R},\) with generalized beta function as \((L _{B}[0,\infty )\) denotes the space of bounded and Lebesgue measurable functions:

$$\begin{aligned} S^{\nu }_{m}(h;u)=\sum _{i=0}^{\infty }p_{m,i}(u)C^{\nu }_{m,i}(t)h(t), \end{aligned}$$
(1.3)

where \(C_{m, i}^{\nu }(t)=\int _{0}^{1} D_{m, i}^{\nu }(t)dt\) and \(D_{m, i}^{\nu }(t)\) is given by the formula

$$\begin{aligned} D_{m, i}^{\nu }(t)=\frac{t^{i \nu -1}(1-t)^{(m-i) \nu -1}}{B(i \nu ,(m-i) \nu )}. \end{aligned}$$

Now, we calculate some estimates for operators defined in equation (1.3).

Let \(e_{k}(t)=t^k\), \(k=0,1,2,3,4\). Then, in the following Lemmas, we give the some moments and estimate for the operators given by (1.3).

2 Basic Estimates

Lemma 2.1

For the operators \(S^{\nu }_{m}(.;.)\) given by (1.3), the following identities are obtained:

$$\begin{aligned} S^{\nu }_{m}(1;u)&= 1,\\ S^{\nu }_{m}(t;u)&= u,\\ S^{\nu }_{m}(t^2;u)&= \left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{\nu +1}{m\nu +1}\right) u,\\ S^{\nu }_{m}(t^3;u)&= \left( \frac{m^2\nu ^2}{m^2\nu ^2+3m\nu +2}\right) u^3\\ &\quad+ \left( \frac{3m\nu (\nu +1)}{m^2\nu ^2+3m\nu +2}\right) u^2\\ &\quad+ \left( \frac{\nu ^2+3\nu +2}{m^2\nu ^2+3m\nu +2}\right) u,\\ S^{\nu }_{m}(t^4;u)&= \left( \frac{m^3\nu ^3}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) u^4\\&\quad+ \left( \frac{6m^2\nu ^2(\nu +1)}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) u^3\\&\quad+ \left( \frac{7m\nu ^3+18m\nu ^2+11m\nu }{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) u^2\\&\quad+ \left( \frac{\nu ^3+6\nu ^2+11\nu +6}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) u, \end{aligned}$$

Proof

If \(k=0\), then

$$\begin{aligned} (i) \quad S^{\nu }_{m}(1;u)= & {} \sum _{i=0}^{\infty }p_{m,i}(u)\int _{0}^{1} D_{m, i}^{\nu }(t) dt\\= & {} \sum _{i=0}^{\infty }\frac{p_{m,i}(u)}{B(i\nu ,(m-i)\nu )}\times B(i\nu ,(m-i)\nu )\\= & {} \sum _{i=0}^{\infty }p_{m,i}(u)\\= & {} 1. \end{aligned}$$

If \(k=1\), then

$$\begin{aligned} (ii)\quad S^{\nu }_{m}(t;u)= & {} \sum _{i=0}^{\infty }\frac{p_{m,i}(u)}{B(i\nu ,(m-i)\nu )}\int _{0}^{1} t^{i\nu }(1-t)^{(m-i)\nu -1}dt\\= & {} \sum _{i=0}^{\infty }\frac{p_{m,i}(u)}{B(i\nu ,(m-i)\nu )}\times B\left( i\nu +1,(m-i)\nu \right) \\= & {} \sum _{i=0}^{\infty }\left( \frac{i}{m}\right) p_{m,i}(u)\\= & {} u. \end{aligned}$$

If \(k=2\), then

$$\begin{aligned} (iii)\quad S^{\nu }_{m}(t^2;u) &= \sum _{i=0}^{\infty }\frac{p_{m,i}(u)}{B(i\nu ,(m-i)\nu )}\int _{0}^{1} t^{i\nu +1}(1-t)^{(m-i)\nu -1}dt\\ & = \sum _{i=0}^{\infty }\frac{p_{m,i}(u)}{B(i\nu ,(m-i)\nu )}\times B\left( i\nu +2,(m-i)\nu \right) \\ &= \left( \frac{m\nu }{m\nu +1}\right) \sum _{i=0}^{\infty }\left( \frac{i^2}{m^2}\right) p_{m,i}(u)\\ & \quad+ \left( \frac{1}{m\nu +1}\right) \sum _{i=0}^{\infty }\left( \frac{i}{m}\right) p_{m,i}(u)\\ & = \left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{m\nu }{\nu +1}\right) u. \end{aligned}$$

If \(k=3\), then

$$\begin{aligned} (iv)\quad S^{\nu }_{m}(t^3;u) &= \sum _{i=0}^{\infty }\frac{p_{m,i}(u)}{B(i\nu ,(m-i)\nu )}\int _{0}^{1} t^{i\nu +2}(1-t)^{(m-i)\nu -1}dt\\ &= \sum _{i=0}^{\infty }\frac{p_{m,i}(u)}{B(i\nu ,(m-i)\nu )}\times B\left( i\nu +3,(m-i)\nu \right) \\ &= \left( \frac{m^2\nu ^2}{m^2\nu ^2+3m\nu +2}\right) \sum _{i=0}^{\infty }\left( \frac{i^3}{m^3}\right) p_{m,i}(u)\\ &\quad+ \left( \frac{3m\nu }{m^2\nu ^2}{m^2\nu ^2+3m\nu +2}\right) \sum _{i=0}^{\infty }\left( \frac{i^2}{m^2}\right) p_{m,i}(u)\\ &\quad + \left( \frac{2}{m^2\nu ^2}{m^2\nu ^2+3m\nu +2}\right) \sum _{i=0}^{\infty }\left( \frac{i}{m}\right) p_{m,i}(u)\\ & = \left( \frac{m^2\nu ^2}{m^2\nu ^2+3m\nu +2}\right) u^3+\left( \frac{3m^2\nu ^2+3m^2\nu ^2}{m(m^2\nu ^2+3m\nu +2)}\right) u^2\\ &\quad + \left( \frac{3m^2\nu ^2+3m^2\nu ^2}{m^2(m^2\nu ^2+3m\nu +2)}\right) u. \end{aligned}$$

If \(k=4\), then

$$\begin{aligned} (v)\quad S^{\nu }_{m}(t^4;u) & = \sum _{i=0}^{\infty }\frac{p_{m,i}(u)}{B(i\nu ,(m-i)\nu )}\\{} & {} \int _{0}^{1} t^{i\nu +3}(1-t)^{(m-i)\nu -1}dt\\ & = \sum _{i=0}^{\infty }\frac{p_{m,i}(u)}{B(i\nu ,(m-i)\nu )}\times B\left( i\nu +4,(m-i)\nu \right) \\ & = \left( \frac{m^3\nu ^3}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) \\{} & {} \sum _{i=0}^{\infty }\left( \frac{i^4}{m^4}\right) p_{m,i}(u)\\ &\quad+ \left( \frac{6m^2\nu ^2}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) \\{} & {} \sum _{i=0}^{\infty }\left( \frac{i^3}{m^3}\right) p_{m,i}(u) \\ &\quad + \left( \frac{11m\nu }{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) \\{} & {} \sum _{i=0}^{\infty }\left( \frac{i^2}{m^2}\right) p_{m,i}(u)\\ &\quad + \left( \frac{6}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) \\{} & {} \sum _{i=0}^{\infty }\left( \frac{i}{m}\right) p_{m,i}(u)\\ & = \left( \frac{m^3\nu ^3}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) u^4\\ &\quad + \left( \frac{6m^2\nu ^3+6m^2\nu ^2}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) u^3\\ &\quad + \left( \frac{7m\nu ^3+18m\nu ^2+11m\nu }{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) u^2\\ &\quad + \left( \frac{\nu ^3+6\nu ^2+11\nu +6}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) u. \end{aligned}$$

\(\square\)

Lemma 2.2

The central moments of beta Szász–Mirakjan operators using Lemma 2.1 are easily calculated as follows:

$$\begin{aligned} S^{\nu }_{m}((t-u)^2;u) & = \left( \frac{m\nu }{m\nu +1}-1\right) u^2+\left( \frac{\nu +1}{m\nu +1}\right) u=A_{m}^{\nu },\nonumber \\ S^{\nu }_{m}((t-u)^4;u) & = \bigg (\frac{m^3\nu ^3}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\nonumber \\ & \quad - \, \frac{4m^2\nu ^2}{m^2\nu ^2+3m\nu +2}\nonumber \\ & \quad +\, \frac{6m\nu }{m\nu +1}-3\bigg )u^4\nonumber \\ & \quad +\, \bigg (\frac{6m^2\nu ^3(\nu +1)}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\nonumber \\ & \quad -\, \frac{12m\nu (\nu +1)}{m^2\nu ^2+3m\nu +2}\nonumber \\ & \quad +\, \frac{6(\nu +1)}{m\nu +1}\bigg )u^3\nonumber \\ & \quad +\, \left( \frac{7m\nu ^3+18m\nu ^2+11m\nu }{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right. \nonumber \\ & \quad -\, \left. \frac{4\nu ^2+12\nu +8}{m^2\nu ^2+3m\nu +2}\right) u^2\nonumber \\ & \quad +\, \left( \frac{\nu ^3+6\nu ^2+11\nu +6}{m^3\nu ^3+6m^2\nu ^2+11m\nu +6}\right) \nonumber \\ & = B_m^{\nu }. \end{aligned}$$
(2.1)

3 Rate of Convergence

Definition 3.1

The modulus smoothness for a uniformly continuous function \(\tau\) is presented as follows:

$$\begin{aligned} \omega (\tau ;\eta ) = \sup _{|t-u|\le \eta }\{|\tau (t)-\tau (u)|, t, u\in [0,\infty )\}, \end{aligned}$$

for \(\tau \in C[0, \infty ).\)

For a uniformly continuous function \(\tau\) in \(C[0,\infty )\) and \(\eta >0\), one has

$$\begin{aligned} |\tau (t)-\tau (u)|\le \left( 1+\dfrac{(1-t)^{2}}{\eta ^{2}}\right) \omega (\tau ;\eta ). \end{aligned}$$
(3.1)

Theorem 3.1

For \(S^{\nu }_{m}(.;.)\), the operators introduced by (1.3) and for each \(\tau \in C[0,\infty )\cap E\), \(S^{\nu }_{m}(\tau ;u)\longrightarrow \tau (u)\) on each compact subset of \([0,\infty )\), where \(E= \big \{\tau :u\ge 0,\dfrac{\tau (u)}{1+u^{2}}\)is convergent as \(u\longrightarrow \infty \big \}.\)

Proof

In view of Korovkin-type property (iv) of Theorem 4.1.4 in Altomare and Campiti (1994), it is sufficient to show that \(S^{\nu }_{m}(e_k;u)\longrightarrow e_k,\) for \(k=0,1,2\). Using Lemma 2.1, it is obvious \(S^{\nu }_{m}(e_{0};u)\longrightarrow e_{0}(u)\) as \(n\longrightarrow \infty\) and for \(k=1\)

$$\begin{aligned} \lim _{m}S^{\nu }_{m}(e_{1};u)=\, & {} lim_{m\longrightarrow \infty }\left( \left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{\nu +1}{m\nu +1}\right) u\right) \\= \,& {} e_{1}(u). \end{aligned}$$

Similarly, we can prove for \(k=2,\) \(S^{\nu }_{m}(e_{2};u)\longrightarrow e_{2}(u)\), which completes the proof of Theorem 3.1. \(\square\)

Theorem 3.2

(See Shisha and Bond (1968)) Let \(L:C[c,d] \longrightarrow B[c,d]\) be the positive linear operator and let \(\gamma _{u}\) be the function defined by

$$\begin{aligned} \beta _{u}(y)= |y-u|, (u,y)\in [c,d]\times [c,d]. \end{aligned}$$

If \(\tau \in C_{B} ([c,d]),\) for any \(u\in [c,d]\) and \(\delta >0\), the operator L verifies:

$$\begin{aligned}{} & {} |(L\tau )(u)-\tau (u)|\le |\tau (u)||(L e_{0})(u)-L|(Le_{0})(u)\\{} & {} \quad +\lambda ^{-1}\sqrt{(Le_{0})(u)(L\gamma ^{2}_{u}(u))}\omega _{\tau }(\lambda ). \end{aligned}$$

Theorem 3.3

Let \(\tau \in C_{B}[0,\infty )\). Then, for the operator \(S^{\nu }_{m}(.;.)\) presented by (1.3), one has

$$\begin{aligned} |S^{\nu }_{m}(\tau ;u)-\tau (u)|\le 2\omega (\tau ;\lambda ), \text { where } \lambda =\sqrt{S^{\nu }_{m}(A_{m}^{\nu };u)}. \end{aligned}$$

Proof

In terms of Lemma 2.1, 2.2 and Theorem 3.1, one has

$$\begin{aligned} \left| S^{\nu }_{m}(\tau ;u)-\tau (u)\right| \le \bigg \{1+\lambda ^{-1}\sqrt{S^{\nu }_{m}(A_{m}^{\nu };u)}\bigg \} \omega (h;\lambda ), \end{aligned}$$

which prove the Theorem 3.3 choosing \(\lambda =\sqrt{S^{\nu }_{m}(A_{m}^{\nu };u)}.\) \(\square\)

4 Numerical and Graphical Analysis

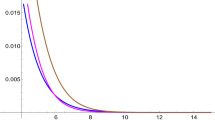
In this section, we depict the convergence behaviour of the operators given by (1.3) for the function \(f(u)=\dfrac{u}{2}e^{-18u}.\) In table 1, we discuss numerical behaviour for different values of \(m= 10, 15, 25\) for the operators (1.3), with \(\nu =0\) in terms of error formula \(E^{\nu }_{m}(h; u)=|S^{\nu }_{m}(f; u)-f(u)|.\) Furthermore, graphical representation of the convergence and error of the operator (1.3) are given in Figs. 1 and 2, respectively, using \(f(u)= \dfrac{u}{2}e^{-18u}\) and \(m=10, 15, 25.\)

Here, the error approximation table 1 is given, which supports our analytical and numerical results.

Table 1 Error Approximation Table
Full size table
Fig. 1
figure 1

Convergence of operator \(S^{\nu }_{m}(.;.)\) for \(m=10,15,25\)

Full size image
Fig. 2
figure 2

Error approximation \(E^{\nu }_{m}(h; u)=|S^{\nu }_{m}(f; u)-f(u)|.\)

Full size image

5 Local Approximations

The local approximation results in \(C_{B}[0,\infty )\), which is the space of real-valued continuous and bounded functions equipped with norm, \(||h||= sup_{0\le u<\infty }|h(u)|\). For any \(h\in C_{B}[0,\infty )\) and \(\delta >0,\), Peetre K-functional is defined as follows:

$$\begin{aligned} K_{2}(h;\delta )= inf\bigg \{||h-f||+\delta ||f^{''}||: f\in C^{2}_{B}[0,\infty )\bigg \}, \end{aligned}$$

where \(C^{2}_{B}[0,\infty )=\bigg \{f\in C_{B}[0;\infty ):f^{'}, f^{''}\in C_{B}[0,\infty )\bigg \}\).

By DeVore and Lorentz (1993p.177, Theorem 2.4), there is fixed real constant \(C>0.\) As a result, it exists

$$\begin{aligned} K_{2}g(h,f)\le C_{B}(h,\sqrt{\delta }). \end{aligned}$$
(5.1)

The modulus of smoothness of second order is denoted by \(\omega _{2}(.;.)\) and is defined as follows:

$$\begin{aligned} \omega _{2}(h;\sqrt{\delta }) & = sup_{0<h\le \sqrt{\delta }}sup_{u\in [0,\infty )}|h(u+2h) \\ & -2h(u+h)+h(u)|. \end{aligned}$$

Now, for \(h\in C_{B}[0,\infty ), u\ge 0\), the auxiliary operator is taken into consideration \(\widehat{S}^{\nu }_{m}(.;.)\) as follows:

$$\begin{aligned} \widehat{S}_{m}^{\nu }(h;u)= {S}_{m}^{\nu }(h;u)+h(u)-h\left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{\nu +1}{m\nu +1}\right) u. \end{aligned}$$
(5.2)

Lemma 5.1

Let \(f\in C^{2}_{B}[0,\infty )\). Then, for all \(u\ge 0\), one has

$$\begin{aligned} |\widehat{S}_{m}^{\nu }(h;u)-h(u)|\le \xi _{m}(u)||f^{''}||, \end{aligned}$$

where

$$\begin{aligned} \xi _{m} (u) = & \left( {\frac{{m^{2} \nu ^{2} }}{{m^{2} \nu ^{2} + 3m\nu + 2}}} \right)u^{3} \\ & \quad + \left( {\frac{{3m\nu (\nu + 1)}}{{m^{2} \nu ^{2} + 3m\nu + 2}}} \right)u^{2} \\ & \quad + \left( {\frac{{\nu ^{2} + 3\nu + 2}}{{m^{2} \nu ^{2} + 3m\nu + 2}}} \right)u. \\ \end{aligned}$$

Proof

For the auxiliary operators are defined in the Definition (5.2), we have

$$\begin{aligned} \widehat{S}_{m}^{\nu }(1;u)=1, \text { } \widehat{S}^{\nu }_{m}(\eta _{u};u)=0 \text { and } |\widehat{S}^{\nu }_{m}(h;u)|\le 3||h||. \end{aligned}$$
(5.3)

By Taylor’s expansion and \(h\in C^{2}_{B}[0,\infty ),\), we have

$$\begin{aligned} f(t)= f(v)+(t-v)f^{'}(v)+\int ^{t}_{v}(t-w)g^{''}(w)dw. \end{aligned}$$
(5.4)

Operating (5.2) both the sides in above equation, we have

$$\begin{aligned}{} & {} \widehat{S}_{m}^{\nu }(h;u)-h(u)=f^{'}(u)\widehat{S}_{m}^{\nu }(t-u;u)\\{} & {} \quad +\widehat{S}_{m}^{\nu }\left( \int ^{1}_{u}(t-v)g^{''}(v)dv\right) . \end{aligned}$$

From (5.2) and (5.3), we have

$$\begin{aligned} \widehat{S}_{m}^{\nu }(h;u)-h(u) & = \widehat{S}_{m}^{\nu }\left( \int ^{1}_{u}(t-v)(g)^{''}(v)dv;u\right) \nonumber \\ &= S_{m}^{\nu }\left( \int ^{1}_{u}(t-u)g^{''}(v)dv;u\right) \nonumber \\ &\quad - \int ^{\left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{\nu +1}{m\nu +1}\right) u}_{u}\nonumber \\{} & {} \left( \left( \frac{m\nu }{m\nu +1}\right) u^2 +\left( \frac{\nu +1}{m\nu +1}\right) u-v\right) \nonumber \\{} & {} g^{''}(v)dv. \end{aligned}$$
(5.5)

Since,

$$\begin{aligned} \left| \int ^{1}_{u}(t-v)g^{''}(v)dv\right| \le (t-u)^{2}||g^{''}||. \end{aligned}$$
(5.6)

Then, we get

$$\begin{aligned}{} & {} \left| \int ^{\left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{\nu +1}{m\nu +1}\right) u}_{u}\left( \left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{\nu +1}{m\nu +1}\right) u-v\right) g^{''}(v)dv\right| \nonumber \\{} & {} \quad \le \left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{\nu +1}{m\nu +1}-u\right) ^{2}||g^{''}||. \end{aligned}$$
(5.7)

Applying (5.6) and (5.7) in (5.5), we obtain

$$\begin{aligned}{} & {} \left| S^{\nu }_{m}(h; u)-h(u)\right| \\{} & {} \quad \le \left\{ S^{\nu }_{m}((t-u)^{2};u)+\left( \frac{m\nu }{m\nu +1}\right) u^2 +\left( \frac{\nu +1}{m\nu +1}\right) u \right\} ||h^{''}||\\{} & {} \quad =\xi _{m}(u)||h^{''}||, \end{aligned}$$

which completes the proof of Lemma 5.1. \(\square\)

Theorem 5.2

Let \(h\in C^{2}_{B}[0,\infty ).\) Then, there exists a constant \(C>0\) such that

$$\begin{aligned} |S^{\nu }_{m}(h; u)-h(u)|\le C\omega _{2}(h;\sqrt{\xi _{m}})+\omega (h;S^{\nu }_{m}(\xi _{m};u)), \end{aligned}$$

where \(\xi _{m}(u)\) is defined by the Lemma 5.1.

Proof

For \(g\in C^{2}_{B}[0,\infty )\), \(h\in C_{B}[0,\infty )\) and in view of the definition of \(\widehat{S}^{\nu }_{m}(.;.)\), one has

$$\begin{aligned}{} & {} |S^{\nu }_{m}(h; u)-h(u)|\le |{\widehat{S}^{\nu }_{m}}(h-g;u)| +|(h-g)(u)|+|\widehat{S}_{m}^{\nu }(g;u)-g(u)|\\{} & {} \quad +\left| h\left( \left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{\nu +1}{m\nu +1}\right) \right) -h(u)\right| . \end{aligned}$$

With the aid of Lemma 5.1 and relation in (5.3), we get

$$\begin{aligned} \left| S^{\nu }_{m}(h; u)-h(u)\right|\le & {} 4||h-g||+|S^{\nu }_{m}(h; u)-h(u)|\\+ & {} \left| h\left( \left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{\nu +1}{m\nu +1}\right) \right) -h(u)\right| \\\le & {} 4||h-g||+\xi _{m}(u)||g^{''}||+\omega (h;S^{\nu }_{m}(\xi _{u};u)). \end{aligned}$$

From definition of Peetre’s K-functional

$$\begin{aligned} \left| S^{\nu }_{m}(h;u)-h(u)\right| \le C \omega _{2}\left( h;\sqrt{\xi _{m}(u)}\right) +\omega (h;S^{\nu }_{m}(\xi _{u};u)), \end{aligned}$$

which completes the proof of Theorem 5.2.

Let \(\rho _{1}>0\) and \(\rho _{2}>0\) are two fixed real values. Then, we recall Lipschitz-type space here Özarslan and Aktŭglu (2013) as follows:

\(Lip^{\rho _{1}\rho _{2}}_{M}(\gamma ):= \bigg \{h\in C_{B}[0,\infty ):|h(t)-h(u)| \le M\dfrac{|t-u|^{\gamma }}{(t+\rho _{1}u+\rho _{2}u^{2})^{\gamma /2}}:u,t\in (0,\infty )\bigg \},\) \(M>0\) is a constant and \(0<\gamma \le 1\). \(\square\)

Theorem 5.3

Let \(h\in Lip^{\rho _{1},\rho _{2}}_{M}(\gamma )\) and \(u\in (0,\infty ).\) Then, for the operators defined by (1.3), one has

$$\begin{aligned} \left| S^{\nu }_{m}(h;u)-h(u)\right| \le M \left( \dfrac{\eta _{m}(u)}{\rho _{1}u+\rho _{2}u^{2}}\right) ^{\dfrac{\gamma }{2}}, \end{aligned}$$
(5.8)

where \(\gamma \in (0,1)\) and \(\eta _{m}(u)= S^{\nu }_{m}(\xi ^{2}_{u};u).\)

Proof

For \(\gamma =1\) and \(u\in [0,\infty ),\), one has

$$\begin{aligned} \left| S^{\nu }_{m}(h;u)-h(u)\right|\le & {} S^{\nu }_{m}(|h(t)-h(u);u)\\\le & {} M S^{\nu }_{m}\left( \dfrac{|t-u|}{(t+\rho _{1}u+\rho _{2}u^{2})^{1/2}};u\right) . \end{aligned}$$

It is obvious that

$$\begin{aligned} \dfrac{1}{t+\rho _{1}u+\rho _{2}u^{2}}<\dfrac{1}{(\rho _{1}u+\rho _{2}u^{2})},\\ \end{aligned}$$

for all \(u\in [0;\infty ),\), we have

$$\begin{aligned} \left| S^{\nu }_{m}(h;u)-h(u)\right|\le & {} \dfrac{M}{(\rho _{1}u+\rho _{2}u^{2})^{1/2}}\left( S^{*}_{m}(t-u)^{2};u\right) ^{1/2}\\\le & {} M\left( \dfrac{\eta _{(m)}(u)}{\rho _{1}u+\rho _{2}u^{2}}\right) ^{1/2}. \end{aligned}$$

Using H\(\ddot{o}\)lder’s inequality, the Theorem 5.3 now holds for \(\gamma =1\) and \(\gamma \in (0,\infty )\). with \(q_{1}=2/\gamma\) and \(q_{2}=2/2-\gamma\), we have

$$\begin{aligned} \left| S^{\nu }_{m}(h;u)-h(u)\right| \le \left( S^{\nu }_{m}(|h(t)-h(u)|^{\gamma /2};u)\right) ^{\gamma /2}\\ \le M S^{\nu }_{m}\left( \dfrac{|t-u|^{2}}{t+\rho _{1}u+\rho _{2}u^{2}};u\right) ^{\gamma /2}. \end{aligned}$$

Since \(\dfrac{1}{t+\rho _{1}u+\rho _{2}u^{2}}<\dfrac{1}{\rho _{1}u+\rho _{2}u^{2}}\) for all \(u\in (0,\infty )\), we have

$$\begin{aligned} |S^{\nu }_{m}(h;u)-h(u)|\le & {} M\left( \dfrac{S^{\nu }_{m}(|t-u|^{2};u)}{\rho _{1}u+\rho _{2}u^{2}}\right) ^{\gamma /2}\\\le & {} M\left( \dfrac{\eta _{m}(u)}{\rho _{1}u+\rho _{2}u^{2}}\right) ^{2}. \end{aligned}$$

This completes the proof of Theorem 5.3.

Now, we recall \(r^{th}\) term order Lipschitz-type maximal function suggested by Lenze (1988) as follows:

$$\begin{aligned} \widetilde{\omega }(h;u)=\sup _{t\ne u},_{t\in (0,\infty )} \dfrac{|h(v)-f(u)|}{|v-u|^{r}}, u\in [0;\infty ), \end{aligned}$$
(5.9)

and \(r\in (0,1]\). \(\square\)

Theorem 5.4

Let \(h\in C_{B}[0,\infty )\) and \(r\in (0,1]\). Then, for all \(u\in [0,\infty )\), one has

$$\begin{aligned} \left| S^{\nu }_{m}(h;u)-h(u)\right| \le \widetilde{\omega }_{r}(h;u)(\eta _{m}\left( u)\right) ^{\gamma /2}. \end{aligned}$$

Proof

We know that

$$\begin{aligned} \left| S^{\nu }_{m}(h;u)-h(u)\right| \le S^{\nu }_{m}\left( |h(v)-h(u)|;u\right) . \end{aligned}$$

From equation (5.9), one has

$$\begin{aligned} \left| S^{\nu }_{m}(h;u)-h(u)\right| \le \widetilde{\omega _{r}}\left( (h;u)(S^{\nu }_{m}|v-u|^{r};u)\right) . \end{aligned}$$

By H\(\ddot{o}\)lder’s inequality with \(q_{1}=2/r\) and \(q_{2}=2/2-r\), we have

$$\begin{aligned} \left| S^{\nu }_{m}(h;u)-h(u)\right| \le \widetilde{\omega _{r}}(h;u)\left( S^{\nu }_{m}|v-u|^{2};u\right) ^{r/2}, \end{aligned}$$

we arrive at our the desired result. \(\square\)

6 Weighted Approximation

To establish the next result, we recall some notation from Gadziev (1976). Assume that \(B_{1+u^{2}}[0,\infty )= \left\{ h(u):|h(u)|\le M_{h}(1+u^{2})\right\}\), is weighted functional space, \(M_{h}\) is a constant that is determined by h and in \(B_{1+u^{2}}[0,\infty )\), \(u\in\) \([0,\infty ), C_{1+u^{2}}[0,\infty )\) is the space continuous functions with the norm

$$\begin{aligned} ||h(u)||_{1+u^{2}} = \sup _{u\in [0,\infty )}\dfrac{|h(u)|}{1+u^{2}}, \end{aligned}$$

and

$$\begin{aligned} C^{k}_{1+u^{2}}[0,\infty )=\left\{ h\in C_{1+u^{2}}[0,\infty ):\lim _{|u|\longrightarrow \infty }\dfrac{h(u)}{1+u^{2}}=K\right\} , \end{aligned}$$

K is a constant that depends on h.

The modulus of continuity for the function h with \(a>0\) and a closed interval [0, a] is as follows:

$$\begin{aligned} \omega _{a}(h;\delta )= \sup _{|v-u|\le \delta }\sup _{u,v\in [0,a]}\left| h(v)-h(u)\right| . \end{aligned}$$
(6.1)

Here, we observe that for \(h\in C_{1+u^{2}}[0,\infty )\), the modulus of continuity tends to zero.

Theorem 6.1

For \(h\in C_{1+u^{2}}[0,\infty )\) and its modulus of continuity \(\omega _{b+1}(h;\delta )\) defined on \([0,b+1]\in [0,\infty )\), we have

$$\begin{aligned} ||S^{\nu }_{m}(h;u)-h(u)||_{C[0,b]}\le 6 M_{h}(1+b)\delta _{(m)}(b)+2\omega _{b+1}\left( h;\sqrt{\delta _{(m)}(b)}\right) , \end{aligned}$$

where

$$\begin{aligned} \delta _{m}(b)=S^{\nu }_{m}(\phi ^{2}_{b};b). \end{aligned}$$

Proof

From (Ibikli and Gadjieva (1995) p. 378) for \(u\in [a,b]\) and \(v\in [0,\infty )\), we have

\(|h(v)-h(u)|\le 6M_{h}(1+b^{2})(v-u)^{2}+\left( 1+\dfrac{|v-u|}{\delta }\right) \omega _{b+1}(h;\delta ).\)

Applying both sides \(S^{\nu }_{m}(.;.),\), one has

$$\begin{aligned} |S^{\nu }_{m}h(v)-h(u)|\le 6M_{h}(1+b^{2})|S^{\nu }_{m}(v-u)^{2}\\ +\left( 1+\dfrac{|S^{\nu }_{m}(1+\sqrt{|v-u|})}{\delta }\right) \omega _{b+1}(h;\delta ). \end{aligned}$$

In view of Lemma (2.2) and \(u\in [a,b]\), we get

$$\begin{aligned} |S^{\nu }_{m}(h;u)-h(u)|\le 6M_{h}(1+b)\delta _{(m)}(b)+\left( 1+\dfrac{\sqrt{\delta _{(m)}(b)}}{\delta }\right) \omega _{b+1}(h;\delta ). \end{aligned}$$

Choosing \(\delta =\delta _{m}(b)\), we arrive at our desired result \(\square\)

Theorem 6.2

If the operators \(S^{\nu }_{m}(.;.)\) given by (1.3) from \(C^{k}_{1+u^{2}}[0;\infty )\) to \(B_{1+u^{2}}[0;\infty )\) satisfying the conditions

$$\begin{aligned} \lim _{m\longrightarrow \infty }||S^{\nu }_{m}(e_{j};.)-e_j||_{1+u^{2}}=0, \end{aligned}$$

for \(j=0, 1, 2\) Then, for each \(h\in C^{k}_{1+u^{2}}[0,\infty )\), one has

$$\begin{aligned} \lim _{m\longrightarrow \infty }||S^{\nu }_{m}(h;.)-h||_{1+u^{2}}=0. \end{aligned}$$

Proof

To prove this Theorem, it is enough to show that

$$\begin{aligned} \lim _{m\longrightarrow \infty }||S^{\nu }_{m}(e_{j};.)-e_{j}||_{1+u^{2}}=0, j=0,1,2. \end{aligned}$$

From Lemma 2.2, we have for \(j=0\)

$$\begin{aligned} ||S^{\nu }_{m}(e_{0};.)-e_{0}||_{1+u^{2}}=\sup _{u\in [0,\infty )}\dfrac{|S^{\nu }_{m}(e_{0};.)-1|}{1+u^{2}}=0. \end{aligned}$$

For \(j=1\), it is obvious.

For \(j=2\)

$$\begin{aligned} ||S^{\nu }_{m}(e_{2};.)-e_{2}||_{1+u^{2}}=\sup _{u\in [0;\infty )}\dfrac{\left| \left( \frac{m\nu }{m\nu +1}\right) u^2+\left( \frac{\nu +1}{m\nu +1}\right) u-u^2\right| }{1+u^{2}},\\ =\sup _{u\in [0,\infty )}\dfrac{u^2}{1+u^{2}}\left( \frac{m\nu }{m\nu +1}\right) + \left( \frac{\nu +1}{m\nu +1}\right) sup_{u\in [0,\infty )}\dfrac{u}{1+u^{2}}. \end{aligned}$$

This implies that \(||S^{\nu }_{m}(e_{2};.)-e_2||_{1+u^{2}}\longrightarrow 0\) as \(m\longrightarrow \infty\). Hence, we complete the proof of Theorem 6.2. \(\square\)

Theorem 6.3

Let \(h\in C^{k}_{1+u^{2}}[0,\infty )\) and \(\gamma >0\) Then, we have

$$\begin{aligned} \lim _{m\longrightarrow \infty } sup_{u\in [0,\infty )} \dfrac{|S^{\nu }_{m}(h;u)-h(u)|}{(1+u^{2})^{1+\gamma }}=0. \end{aligned}$$

Proof

For fixed number \(u_{0}>0\), one possesses

$$\begin{aligned} sup_{u\in (0,\infty )}\dfrac{|S^{\nu }_{m}(h;u)-h(u)|}{(1+u^{2})^{1+\gamma }}\le & {} sup_{u\le u_{0}}\dfrac{|S^{\nu }_{m}(f;u)-f(u)|}{(1+u^{2})^{1+\gamma }}\\+ & {} sup_{u\ge u_{0}}\dfrac{|S^{\nu }_{m}(h;u)-h(u)|}{(1+u^{2})^{1+\gamma }}\\\le & {} ||S^{\nu }_{m}(h.;.)|-h||_{C[0,u_{0}]}\\+ & {} ||h||_{1+u^{2}}sup_{u\ge u_{0}}\dfrac{|S^{\nu }_{m}(1+v^{2};u)|}{(1+u^{2})^{1+\gamma }}\\+ & {} sup_{u\ge u_{0}}\dfrac{|h(u)|}{(1+u)^{1+u}} \end{aligned}$$
$$\begin{aligned} = T_{1}+T_{2}+T_{3}. \end{aligned}$$
(6.2)

Since

\(|h(a)|\le ||h||_{1+u^{2}}(1+u^{2})\), we have

$$\begin{aligned} T_{3}=sup_{u\ge u_{0}}\dfrac{|h(u)|}{(1+u^{2})^{1+\gamma }}\le sup_{u\ge u_{0}}\dfrac{||h||_{1+u^{2}}}{(1+u^{2})^{1+\gamma }}\le \dfrac{||h||_{1+u^{2}}}{(1+u^{2})^{\gamma }}. \end{aligned}$$

Let \(\epsilon >0\) be random real number. Then, from (3.1), there exists \(m_{1}\in \mathbb {N},\) such that

$$\begin{aligned} T_{2}>\dfrac{1}{(1+u^{2})^{\gamma }}||h||_{1+u^{2}}\left( 1+u^{2}+\dfrac{\epsilon }{3||h||_{1+u^{2}}}\right) , \end{aligned}$$

for all

$$\begin{aligned} m_{1}\ge m\le \dfrac{||h||_{1+u^{2}}}{(1+u^{2})^{\gamma }}+\dfrac{\epsilon }{3}, \end{aligned}$$

for all \(m_{1}\ge m\). This implies that \(T_{2}+T_{3}<2\dfrac{||h||_{1+u^{2}}}{1+u^{2}}+\dfrac{\epsilon }{3}\).

For a large enough value of \(u_{0}\), we get \(\dfrac{||h||_{1+u^{2}}}{1+u^{2}}+\dfrac{\epsilon }{6}\),

$$\begin{aligned} T_{2}+T_{3}<\dfrac{2\epsilon }{3} \text { for all } m_{1}\ge m. \end{aligned}$$
(6.3)

By Theorem 6.2, there exists \(m_{2}> m\) such that

$$\begin{aligned} T_{1}=||S^{\nu }_{m}(h)-h||_{C[0,u_{0}]}<\dfrac{\epsilon }{3} \text { for all } \text { } m_{2}\ge m. \end{aligned}$$
(6.4)

Let \(m_{3}= max\{m_{1}, m_{2}\}\). Then, joining (6.2), (6.3) and (6.4), we get

$$\begin{aligned} sup_{u\in [0,\infty )}\dfrac{|S^{\nu }_{m}(h;u)-h(u)|}{(1+u^{2})^{\gamma }}<\epsilon . \end{aligned}$$

The proof of the above theorem (6.2) is complete. \(\square\)

7 Bivariate Case of Extended Beta-Type Sz\(\acute{a}\)sz–Mikjan Operator \(S^{\nu }_{m}(h;u)\)

Take \(T^2=\{(u_1, u_2):0\le u_1\le 1, 0\le u_2 \le 1\}\) and \(C(T^2)\) is the class of all continuous function on \(T^2\) equipped with norm \(||f||_{C(T^2)}=\sup _{(u_1, u_2)\in T^2}|f(u_1, u_2)|.\) Then, for all \(g\in C(T^2)\) and \(m_1, m_2\in \mathbb {N},\), we introduce a bivariate sequence as follows:

$$\begin{aligned}{} & {} S_{m_1, m_2}^{\nu }(h; u_1, u_2)\nonumber \\{} & {} \quad = \sum _{j=0}^{\infty }\sum _{k=0}^{\infty }C_{m_{1}, m_{2},j,k}^{\nu }(t_{1}, t_{2})p_{m_{1}, m_{2},j,k}(u_1, u_2)h(t_{1}, t_{2}) \end{aligned}$$
(7.1)

where

$$\begin{aligned} C_{m_{1}, m_{2},j,k}^{\nu }(t_{1}, t_{2})= & {} C_{m_{1},j}^{\nu }(t_{1})C_{m_{2},k}^{\nu }(t_{2}),\\ with~ C_{m_{i},j}^{\nu }(t_{i})= & {} \int _{0}^{1}D_{m_i, j}^{\nu }(t_i)dt_i,~for~i=1, 2 \\ \end{aligned}$$

and

$$\begin{aligned} p_{m_{1}, m_{2},j,k}(u_1, u_2)= & {} p_{m_{1}, j}(u_1)p_{m_{2}, k}(u_2),\\ with~ p_{m_{i}, j}(u_i)= & {} e^{-m_{i}u_i}\dfrac{(m_{i}u_{i})^j}{j!}, ~for~ i=1, 2.\\ \end{aligned}$$

Lemma 7.1

Let \(e_{j, k}= u_{1}^{j}u_{2}^{k}.\) Then, for the operator (7.1), we get

$$\begin{aligned} {S}^{\nu }_{m_1, m_2}(e_{0, 0}; u_{1}, u_{2}) & = 1,\\ {S}^{\nu }_{m_1, m_2}(e_{1, 0}; u_{1}, u_2) &= u_{1},\\ {S}^{\nu }_{m_1, m_2}(e_{0, 1}; u_{1}, u_2) &= u_{2},\\ {S}^{\nu }_{m_1, m_2}(e_{2, 0}; u_1, u_2) &= \left( \frac{m_1\nu }{m_1\nu +1}\right) u^{2}_{1}+\left( \frac{\nu +1}{m_1\nu +1}\right) u_{1},\\ {S}^{\nu }_{m_1, m_2}(e_{0, 2}; u_1, u_2) &= \left( \frac{m_2\nu }{m_2\nu +1}\right) u^{2}_{2}+\left( \frac{\nu +1}{m_2\nu +1}\right) u_{2},\\ {S}^{\nu }_{m_1, m_2}(e_{3, 0}; u_{1}, u_{2}) & = \left( \frac{m^{2}_1\nu ^2}{m^{2}_1\nu ^2+3m_1\nu +2}\right) u^{3}_1\\ &\quad + \left( \frac{3m_1\nu (\nu +1)}{m^{2}_1\nu ^2+3m_1\nu +2}\right) u^{2}_1\\ & \quad + \left( \frac{\nu ^2+3\nu +2}{m^{2}_1\nu ^2+3m_1\nu +2}\right) u_1, \\ {S}^{\nu }_{m_1, m_2}(e_{0, 3}; u_{1}, u_{2}) & = \left( \frac{m^{2}_2\nu ^2}{m^{2}_2\nu ^2+3m_2\nu +2}\right) u^{3}_2\\ &\quad + \left( \frac{3m_2\nu (\nu +1)}{m^{2}_2\nu ^2+3m_2\nu +2}\right) u^{2}_2\\ & \quad + \left( \frac{\nu ^2+3\nu +2}{m^{2}_2\nu ^2+3m_2\nu +2}\right) u_2. \end{aligned}$$

Proof

From (2.1) and linearity, property we get

$$\begin{aligned} S^{\nu }_{m_1, m_2}(e_{0, 0}; u_{1}, u_{2})= & {} S^{\nu }_{m_1, m_2}(e_{0}; u_{1}, u_{2})S^{\nu }_{m_1, m_2}(e_{0}; u_{1}, u_{2}),\\ S^{\nu }_{m_1, m_2}(e_{1, 0}; u_{1}, u_{2})= & {} S^{\nu }_{m_1, m_2}(e_{1}; u_{1}, u_{2})S^{\nu }_{m_1, m_2}(e_{0}; u_{1}, u_{2}),\\ S^{\nu }_{m_1, m_2}(e_{0, 1}; u_{1}, u_{2})= & {} S^{\nu }_{m_1, m_2}(e_{0}; u_{1}, u_{2})S^{\nu }_{m_1, m_2}(e_{1}; u_{1}, u_{2}),\\ S^{\nu }_{m_1, m_2}(e_{2, 0}; u_{1}, u_{2})= & {} S^{\nu }_{m_1, m_2}(e_{2}; u_{1}, u_{2})S^{\nu }_{m_1, m_2}(e_{0}; u_{1}, u_{2}),\\ S^{\nu }_{m_1, m_2}(e_{0, 2}; u_{1}, u_{2})= & {} S^{\nu }_{m_1, m_2}(e_{0}; u_{1}, u_{2})S^{\nu }_{m_1, m_2}(e_{2}; u_{1}, u_{2}),\\ S^{\nu }_{m_1, m_2}(e_{3, 0}; u_{1}, u_{2})= & {} S^{\nu }_{m_1, m_2}(e_{3}; u_{1}, u_{2})S^{\nu }_{m_1, m_2}(e_{0}; u_{1}, u_{2}),\\ S^{\nu }_{m_1, m_2}(e_{0, 3}; u_{1}, u_{2})= & {} S^{\nu }_{m_1, m_2}(e_{0}; u_{1}, u_{2})S^{\nu }_{m_1, m_2}(e_{3}; u_{1}, u_{2}). \end{aligned}$$

\(\square\)

8 Degree of Convergence

For any \(g\in C(\mathcal {T}^2)\) and \(\eta >0,\), the modulus of continuity of the second order is given by

$$\begin{aligned} \omega \left( g;\delta _{n_1},\eta _{n_2}\right) = \sup _{(u_1, u_2)\in T^2}\{\mid g(t,s)-g(u_{1},u_{2})\mid : (t,s),(u_{1},u_{2})\in \mathcal {T}^2\}, \end{aligned}$$

with \(\mid t-u_{1}\mid \le \eta _{n_1},\; \mid s-u_{2}\mid \le \eta _{n_2}\) defined by the partial modulus of continuity as follows:

$$\begin{aligned} \omega _1\left( g;\eta \right) = \sup _{0 \le u_{2}\le \infty }\sup _{\mid x_1-x_2 \mid \le \eta } \{\mid g(x_1,u_{2})-g(x_2,u_{2})\mid \}, \\ \omega _2\left( g;\eta \right) = \sup _{0 \le u_{1}\le \infty }\sup _{\mid u_{1}-u_{2} \mid \le \eta } \{\mid g(u_{1},u_{1})-g(u_{1},u_{2})\mid \}. \end{aligned}$$

Theorem 8.1

For any \(g \in C(\mathcal {T}^2),\), we have

$$\begin{aligned} \mid S_{m_1, m_2}^{\nu } (g;u_{1},u_{2})-g(u_{1},u_{2})\mid \le 2\bigg (\omega _1(g;\delta _{u_{1},n_1})+\omega _2(g;\delta _{n_2,u_{2}})\bigg ). \end{aligned}$$

Proof

In order to give the proof of Theorem 8.1, generally, we use the well-known Cauchy–Schwarz inequality. Thus, we see that

$$\begin{aligned}{} & {} \mid S_{m_1, m_2}^{\nu }(h; u_{1}, u_{2})-g(u_{1},u_{2})\mid \\{} & {} \quad \le S_{m_1, m_2}^{\nu }\left( \mid g(t,s) -g(u_{1},u_{2})\mid ;u_{1},u_{2} \right) \\{} & {} \quad \le S_{m_1, m_2}^{\nu }\left( \mid g(t,s)-g(u_{1},s)\mid ;u_{1},u_{2} \right) \\{} & {} \qquad + S_{m_1, m_2}^{\nu }\left( \mid g(u_{1},s)-g(u_{1},u_{2})\mid ;u_{1},u_{2} \right) \\{} & {} \quad \le S_{m_1, m_2}^{\nu }\left( \omega _1(g;\mid t-u_{1}\mid );u_{1},u_{2} \right) \\{} & {} \qquad + S_{m_1, m_2}^{\nu }\left( \omega _2(g;\mid s-u_{2}\mid );u_{1},u_{2} \right) \\{} & {} \quad \le \omega _1(g;\delta _{n_1})\\{} & {} \qquad \left( 1+\delta _{n_1}^{-1} S_{m_1, m_2}^{\nu }(\mid t-u_{1}\mid ;u_{1},u_{2}) \right) \\{} & {} \qquad +\omega _2(g;\delta _{n_2})\\{} & {} \quad \left( 1+\delta _{n_2}^{-1} S_{m_1, m_2}^{\nu }(\mid s-u_{2}\mid ;u_{1},u_{2}) \right) \\{} & {} \quad \le \omega _1(g;\delta _{n_1})\\{} & {} \quad \left( 1+\frac{1}{\delta _{n_1}} \sqrt{ S_{m_1, m_2}^{\nu } ((t-u_{1})^2;u_{1},u_{2})}\right) \\{} & {} \qquad +\omega _2(g;\delta _{n_2})\\{} & {} \quad \left( 1+\frac{1}{\delta _{n_2}} \sqrt{ S_{m_1, m_2}^{\nu } ((s-u_{2})^2;u_{1},u_{2})}\right) . \end{aligned}$$

If we choose \(\delta _{n_1}^2=\delta _{n_1,u_{1}}^2= S_{m_1, m_2}^{\nu } ((t-u_{1})^2;u_{1},u_{2})\) and \(\delta _{n_2}^2=\delta _{n_2,u_{2}}^2= S_{m_1, m_2}^{\nu } ((s-u_{2})^2;u_{1},u_{2}),\), then we can simply achieve our objectives. \(\square\)

Here, we analyse convergence in terms of the Lipschitz class for bivariate functions. For \(M>0\) and \(\tau ,\tau \in [0,1],\), maximal Lipschitz function space on \(E \times E \subset \mathcal {T}^2\) given by

$$\begin{aligned} \mathcal {L}_{\tau ,\tau }(E\times E)= & {} \bigg \{g: \sup (1+t)^{\tau }(1+s)^{\tau }\\{} & {} \left( g_{\tau ,\tau }(t,s)- g_{\tau ,\tau }(u_{1},u_{2}) \right) \\\le & {} M \frac{1}{(1+u_{1})^{\tau }}\frac{1}{(1+u_{2})^{\tau }} \bigg \}, \end{aligned}$$

where g is continuous and bounded on \(\mathcal {T}^2\), and

$$\begin{aligned}{} & {} g_{\tau ,\tau }(t,s)-g_{\tau ,\tau }(u_{1},u_{2})= \frac{\mid g(t,s)-g(u_{1},u_{2})\mid }{\mid t-u_{1} \mid ^{\tau }\mid s-u_{2} \mid ^{\tau } }; \nonumber \\{} & {} \quad (t,s),(u_{1},u_{2})\in \mathcal {T}^2. \end{aligned}$$
(8.1)

Theorem 8.2

Let \(g\in \mathcal {L}_{\tau ,\tau }(E\times E).\) Then, for any \(\tau ,\tau \in [0,1],\), there exists \(M>0\) such that

$$\begin{aligned} \mid S_{m_1, m_2}^{\nu }(h; u_{1}, u_{2})-g(u_{1},u_{2})\mid\le & {} M \bigg \{\bigg (\left( d(u_{1},E)\right) ^{\tau }+\left( \delta _{n_1,u_{1}}^2\right) ^{\frac{\tau }{2}} \bigg )\\\times & {} \bigg (\left( d(u_{2},E)\right) ^{\tau }+\left( \delta _{n_2,u_{2}}^2\right) ^{\frac{\tau }{2}} \bigg )\\+ & {} \left( d((u_{1},E))^{\tau } \left( d(u_{2},E)\right) ^{\tau }\right) \bigg \}, \end{aligned}$$

where \(\delta _{n_1,u_{1}}\) and \(\delta _{n_2,u_{2}}\) defined by Theorem 8.1.

Proof

Consider \(\mid u_{1}-x_0 \mid =d(u_{1}, E)\) and \(\mid u_{2}-y_0 \mid =d(u_{2}, E)\), for any \((u_{1},u_{2})\in \mathcal {T}^2\), and \((x_0,y_0)\in E\times E.\)

Let \(d(u_{1}, E)=\inf \{ \mid u_{1}-u_{2} \mid : u_{2} \in E \}\). Then, we write here

$$\begin{aligned}{} & {} \mid g(t,s)-g(u_{1},u_{2})\mid \le M \mid g(t,s)-g(x_0,y_0)\mid \nonumber \\{} & {} \quad + \mid g(x_0,y_0)-g(u_{1},u_{2})\mid . \end{aligned}$$
(8.2)

Apply \(S_{m_1, m_2}^{\nu }(.;.,.)\), we obtain

$$\begin{aligned}{} & {} \mid S_{m_1, m_2}^{\nu }(h; u_{1}, u_{2})-g(u_{1},u_{2})\mid \\{} & {} \quad \le S_{m_1, m_2}^{\nu }\left( \mid g(u_{1},u_{2})-g(x_0,y_0)\mid + \mid g(x_0,y_0)-g(u_{1},u_{2})\mid \right) \\{} & {} \quad \le M S_{m_1, m_2}^{\nu }\left( \mid t-x_0\mid ^{\tau }\mid s-y_0\mid ^{\tau };u_{1},u_{2} \right) \\{} & {} \quad +M\mid u_{1}-x_0\mid ^{\tau }\mid u_{2}-y_0\mid ^{\tau }. \end{aligned}$$

For all \(A,B \ge 0\) and \(\tau \in [0,1],\), the inequality \((A+B)^{\tau }\le A^{\tau }+B^{\tau },\) thus

$$\begin{aligned} \mid t-x_0\mid ^{\tau } \le \mid t-u_{1}\mid ^{\tau } +\mid u_{1}-x_0\mid ^{\tau }, \\ \mid s-y_0\mid ^{\tau } \le \mid s-u_{2}\mid ^{\tau } +\mid u_{2}-y_0\mid ^{\tau }. \end{aligned}$$

Therefore,

$$\begin{aligned}{} & {} \mid S_{m_1, m_2}^{\nu }(h; u_{1}, u_{2})-g(u_{1},u_{2})\mid \\{} & {} \quad \le M S_{m_1, m_2}^{\nu }\left( \mid t-u_{1}\mid ^{\tau }\mid s-u_{2}\mid ^{\tau };u_{1},u_{2} \right) \\{} & {} \quad +M\mid u_{1}-x_0\mid ^{\tau } S_{m_1, m_2}^{\nu }\left( \mid s-u_{2}\mid ^{\tau };u_{1},u_{2} \right) \\{} & {} \quad +M\mid u_{2}-y_0\mid ^{\tau } S_{m_1, m_2}^{\nu }\left( \mid t-u_{1}\mid ^{\tau };u_{1},u_{2} \right) \\{} & {} \quad + 2 M\mid u_{1}-x_0\mid ^{\tau } \mid u_{2}-y_0\mid ^{\tau } S_{m_1, m_2}^{\nu }\left( \mu _{0,0};u_{1},u_{2} \right) . \end{aligned}$$

Apply Hölders inequality on \(S_{m_1, m_2}^{\nu }(.;.,.)\), we get

$$\begin{aligned}{} & {} S_{m_1, m_2}^{\nu }\left( \mid t-u_{1}\mid ^{\tau }\mid s-u_{2}\mid ^{\tau };u_{1},u_{2} \right) = \mathcal {U}_{n_1,k}^{\lambda _1}\left( \mid t-u_{1}\mid ^{\tau };u_{1},u_{2} \right) \\{} & {} \quad \times \mathcal {V}_{n_2,l}^{\lambda _2}\left( \mid s-u_{2}\mid ^{\tau };u_{1},u_{2} \right) \\{} & {} \quad \le \left( S_{m_1, m_2}^{\nu } (\mid t-u_{1}\mid ^{2};u_{1},u_{2})\right) ^{\frac{\tau }{2}}\\{} & {} \quad \times \left( S_{m_1, m_2}^{\nu }(\mu _{0,0};u_{1},u_{2} ) \right) ^{\frac{2-\tau }{2}}\\{} & {} \quad \times \left( S_{m_1, m_2}^{\nu } (\mid s-u_{2}\mid ^{2};u_{1},u_{2})\right) ^{\frac{\tau }{2}}\\{} & {} \quad \times \left( S_{m_1, m_2}^{\nu }(\mu _{0,0};u_{1},u_{2} ) \right) ^{\frac{2-\tau }{2}}. \end{aligned}$$

Thus, we can obtain

$$\begin{aligned} \mid S_{m_1, m_2}^{\nu }(h; u_{1}, u_{2})-g(u_{1},u_{2})\mid\le & {} M\left( \delta _{n_1,u_{1}}^2\right) ^{\frac{\tau }{2}} \left( \delta _{n_2,u_{2}}^2\right) ^{\frac{\tau }{2}} \\+ & {} 2M \left( d(u_{1},E)\right) ^{\tau }\left( d(u_{2},E)\right) ^{\tau }\\+ & {} M \left( d(u_{1},E)\right) ^{\tau } \left( \delta _{n_2,u_{2}}^2\right) ^{\frac{\tau }{2}}\\+ & {} L \left( d(u_{2},E)\right) ^{\tau }\left( \delta _{n_1,u_{1}}^2\right) ^{\frac{\tau }{2}} \end{aligned}$$

which completes the proof. \(\square\)

9 Numerical and Graphical Analysis

It is observed by given below example, table and figure for the different set of parameters \(\nu =0.3\), the operator \(S_{m_1, m_2}^\nu (.;.,.)\) converges uniformly to the function \(f(u_{1}, u_{2})=\dfrac{u_1u_2}{2}e^{-16(u_{1}u_{2})}\) (Yellow), and using error formula \(E_{m_1, m_2}^{\nu }(f; u_1, u_2)=|S_{m_1, m_2}^{\nu }(h; u_{1}, u_{2})-f(u_{1}, u_{2})|\), the error of the operator (7.1) is given in Fig. 4. Further, as \(m_{1}=m_{2}=10\) (Blue), \(m_{1}=m_{2}=15\) (Green) and \(m_{1}=m_{2}=25\) (Red).

Table 2 Error Approximation Table
Full size table
Fig. 3
figure 3

\(S_{m_1, m_2}^{\nu }(.;.,.)\) converges to \(f(u_{1}, u_{2})=\dfrac{u_1u_2}{2}e^{-16(u_{1}u_{2})}\)

Full size image
Fig. 4
figure 4

\(E_{m_1, m_2}^{\nu }(.;.,.)\) converges to \(f(u_{1}, u_{2})=\dfrac{u_1u_2}{2}e^{-16(u_{1}u_{2})}.\)

Full size image

10 Conclusion

In this study, we introduce generalized beta Sz\(\acute{a}\)sz–Mirakjan operators and study their approximation properties. Further, we prove a Korovkin-type convergence theorem, the order of convergence concerning the usual modulus of continuity as well as Peetre’s K-functional and Lipschitz-type class of functions. Moreover, we introduced global approximation results and A-Statistical approximation properties of the constructed operators. We provided several graphical representations as convergence and error of approximation in terms of the values of some selected parameters in order to make our article comprehensible and to demonstrate the accuracy and efficacy of the proposed operators.