Approximation by bivariate Chlodowsky type Szász–Durrmeyer operators and associated GBS operators on weighted spaces

Abstract

In this article, we consider a bivariate Chlodowsky type Szász–Durrmeyer operators on weighted spaces. We obtain the rate of approximation in connection with the partial and complete modulus of continuity and also for the elements of the Lipschitz type class. Moreover, we examine the degree of convergence with regard to the weighted modulus of continuity and Peetre’s K-functional. Further, we construct the associated GBS type of these operators and estimate the degree of approximation using the mixed modulus of continuity and a class of the Lipschitz of Bögel type continuous functions. Finally, with the help of Maple software, we present the comparisons of the convergence of the bivariate Chlodowsky type Szász–Durrmeyer operators and associated GBS type operators to certain functions with some graphs and error estimation tables.

1 Introduction

The approximation of the continuous functions via the sequences of linear positive operators, which have many applications in disciplines such as engineering and physics, besides mathematics, has been an important research topic since the last century. In [1], Bernstein proposed one of the elegant proof of the Weierstrass approximation theorem. A generalization of Bernstein operators on an unbounded set was introduced by Chlodowsky [2]. In 1930, an integral modification of the classical Bernstein operators was presented by Kantorovich [3]. In [4, 5], Szász–Mirakjan considered the linear positive operators on $[0,\infty )$, which are related to the Poisson distribution. In 1957, Baskakov [6] studied a sequence of positive linear operators for the convenient functions defined on the interval $[0,\infty )$. To approximate the Lebesgue integrable functions, Durrmeyer [7] introduced and studied the integral modification of the Bernstein operators. In recent years, a lot of generalizations and modifications of above-mentioned operators over finite or infinite intervals have been studied by several authors. One of the prominent components of approximation theory, the Korovkin type theorems, on weighted spaces was introduced by Gadzhiev [8, 9]. Ispir [10] presented a modification of the Baskakov operators for the interval $[0,b_{m}]$ and derived some approximation results in terms of the Korovkin theorems. In [11], Ditzian studied a necessary and adequate condition on the degree of convergence of Szász–Mirakjan and Baskakov operators on weighted spaces. In 2005, Ibikli and Karsli [12] proposed the Bernstein–Chlodowsky operators in terms of Durrmeyer type operators and reached some approximation results of these operators. Mazhar and Totik [13] considered a modification of the integral type of the Szász–Mirakjan operators and proved direct estimates and saturation results of these operators. In [14], Mursaleen and Ansari defined the Chlodowsky version of the Szász operators by the Brenke type polynomials and established degree of convergence with a classical method, Peetre’s K-functional and second-order modulus of continuity. Dogru [15] investigated some properties of the continuous functions on $[0,\infty )$ by the modified positive linear operators. In 2013, Izgi [16] introduced and studied the following composition of the Chlodowsky and Százs–Durrmeyer operators on weighted spaces

$$ Z_{m}(\mu ;x)=\frac{m}{b_{m}}\sum_{k=0}^{m}p_{m,k} \biggl( \frac{x}{b_{m}}\biggr) \int _{0}^{\infty }s_{m,k}\biggl( \frac{t}{b_{m}}\biggr)\mu (t)\,dt,\quad (0\leq x\leq b_{m}), $$

(1.1)

where $p_{m,k}(q)=\binom{m}{k}q^{k}(1-q)^{m-k}$, ($0\leq k\leq m$), $q\in {}[ 0,1]$, $s_{m,k}(w)=e^{-mw}\frac{(mw)^{j}}{j!}$, $w\in {}[ 0,\infty )$, and $(b_{m})$ is a positive and increasing sequence with the following assumption:

$$ \lim_{m\rightarrow \infty }b_{m}=\infty , \qquad \lim_{m \rightarrow \infty } \frac{b_{m}^{2}}{m}=0. $$

He investigated the uniform convergence, rate of approximation on weighted spaces, and proved a Voronovskaya type asymptotic formula for the operators (1.1). Recently, the univariate or bivariate cases of several well-known linear positive operators have been studied in many papers [17–24].

The structure of this research is organized as follows: In Sect. 2, we propose the bivariate extension of operators (1.1). We introduce the uniform convergence of these operators and estimate the order of approximation in terms of the partial and complete modulus of continuity for the elements of the Lipschitz type class, weighted modulus of continuity, and Peetre’s K-functional, respectively. In Sect. 3, we discuss the associated GBS type of these operators and investigate the order of convergence by the mixed modulus of smoothness and the Lipschitz class of the Bögel continuous functions. In the final section, we present some graphs and error estimation tables to compare the convergence of bivariate and associated GBS type operators to certain functions.

2 Construction of the operators

Let $I_{\alpha _{n}\beta _{m}}:=[0,\alpha _{n}]\times {}[ 0,\beta _{m}]$ and the space $C(I_{\alpha _{n}\beta _{m}})$ be the set of all real-valued functions of bivariate continuous on $I_{\alpha _{n}\beta _{m}}$. The weighted function is given by

$$ \rho (z,y)=1+z^{2}+y^{2}, \quad (z,y)\in I_{\alpha _{n} \beta _{m}}.$$

It is endowed with the norm $\Vert \mu \Vert _{\rho }= \sup_{(z,y)\in I_{\alpha _{n}\beta _{m}}} \frac{\mu (z,y)}{\rho (z,y)}$. Moreover, by $B_{\rho }(I_{\alpha _{n}\beta _{m}})$, we denote the real-valued continuous functions on $I_{\alpha _{n}\beta _{m}}$ and verify $\vert \mu (z,y) \vert \leq C_{\mu }\rho (z,y)$; here $C_{\mu }$ is fixed and depends just on μ. We also denote by $C_{\rho }(I_{\alpha _{n}\beta _{m}})$ the subspace of every continuous function depending on $B_{\rho }(I_{\alpha _{n}\beta _{m}})$, and by $C_{\rho }^{a}$ the subspace of every functions $\mu \in C_{\rho }(I_{\alpha _{n}\beta _{m}})$, satisfying $\lim_{(z,y)\rightarrow \infty } \frac{\mu (z,y)}{\rho (z,y)}=a$, where a is a constant depending on μ. In what follows, let $e_{u,v}(z,y)=z^{u}y^{v}$, $(z,y)\in I_{\alpha _{n}\beta _{m}}$, $( u,v ) \in \mathbb{N} _{0}\times \mathbb{N} _{0}$ with $0\leq u,v\leq 4$ be the bivariate test functions.

Now, based on the method of parametric extensions (see: [25, 26]), we define two-dimensional Chlodowsky–Szász–Durrmeyer operators as follows:

$$\begin{aligned} R_{n,m}(\mu ;z,y)={}&\frac{n}{\alpha _{n}}\frac{m}{\beta _{m}} \sum_{k=0}^{n}\sum _{j=0}^{m}P_{n,m,k,j}\biggl(\frac{z}{\alpha _{n}}, \frac{y}{\beta _{m}}\biggr) \\ &{}\times \int _{0}^{\infty } \int _{0}^{\infty }S_{n,m,k,j}\biggl( \frac{t}{\alpha _{n}},\frac{s}{\beta _{m}}\biggr)\mu (t,s)\,dt\,ds, \end{aligned}$$

(2.1)

where $P_{n,m,k,j}(u_{1},v_{1})=\binom{n}{k}\binom{m}{j}u_{1}^{k}v_{1}^{j}(1-u_{1})^{n-k}(1-v_{1})^{m-j}$, ($0\leq k\leq n$, $0\leq j\leq m$), $(u_{1},v_{1})\in [ 0,1]\times [0,1]$, and $S_{n,m,k,j}(u_{2},v_{2})=e^{-nu_{2}}e^{-mv_{2}}\frac{(nu_{2})^{k}}{k!} \frac{(mv_{2})^{j}}{j!}$, $(u_{2},v_{2})\in {}[ 0,\infty )\times[0,\infty )$; $(z,y) \in I_{\alpha _{n}\beta _{m}}$ and the sequences $(\alpha _{n})$, $(\beta _{m})$ are increasing of positive numbers, satisfying:

$$ \lim_{n\rightarrow \infty }\alpha _{n}=\infty ,\qquad \lim_{m\rightarrow \infty }\beta _{m}=\infty \quad \text{and}\quad \lim_{n\rightarrow \infty } \frac{\alpha _{n}^{2}}{n}=0,\qquad \lim_{m\rightarrow \infty }\frac{\beta _{m}^{2}}{m}=0. $$

(2.2)

Lemma 2.1

([16])

For the test functions $e_{p}(t)=t^{p}$, $p=0,1,2,3,4$, the following identities hold:

$$\begin{aligned} &Z_{m}(e_{0};y) =1,\qquad Z_{m}(e_{1};y)=y+ \frac{b_{m}}{m}, \\ &Z_{m}(e_{2};y) =y^{2}+\frac{(4b_{m}-y)y}{m}+ \frac{2b_{m}^{2}}{m^{2}}, \\ &Z_{m}(e_{3};y) =y^{3}+ \frac{(18b_{m}^{2}+9(m-1)b_{m}y-(3m-2)y^{2})y}{m^{2}}+ \frac{6b_{m}^{3}}{m^{3}}, \\ &Z_{m}(e_{4};y) =y^{4}+ \bigl\{ 96b_{m}^{3}+72(m-1)b_{m}^{2}y+16(m-1) (m-2)b_{m}y^{2} \\ & \hphantom{Z_{m}(e_{4};y) =}{} -\bigl(6m^{2}-11m+6\bigr)y^{3} \bigr\} \frac{y}{m^{3}}+ \frac{24b_{m}^{4}}{m^{4}}. \end{aligned}$$

Lemma 2.2

Let the operators $R_{n,m}(\mu ;z,y)$ be given by (2.1). Then the following identities hold true:

$$\begin{aligned}& \textup{(i)}\quad R_{n,m}(e_{0,0};z,y) =1, \\& \textup{(ii)} \quad R_{n,m}(e_{1,0};z,y) =z+\frac{\alpha _{n}}{n}, \\& \textup{(iii)} \quad R_{n,m}(e_{0,1};z,y) =y+\frac{\beta _{m}}{m}, \\& \textup{(iv)}\quad R_{n,m}(e_{2,0};z,y) =z^{2}+ \frac{ \{ 4\alpha _{n}-z \} z}{n}+ \frac{2\alpha _{n}^{2}}{n^{2}}, \\& \textup{(v)}\quad R_{n,m}(e_{0,2};z,y) =y^{2}+ \frac{ \{ 4\beta _{m}-y \} y}{m}+\frac{2\beta _{m}^{2}}{m^{2}}, \\& \textup{(vi)}\quad R_{n,m}(e_{3,0};z,y) =z^{3}+ \frac{ \{ 18\alpha _{n}^{2}+9(n-1)\alpha _{n}z-(3n-2)z^{2} \} z}{n^{2}}+ \frac{6\alpha _{n}^{3}}{n^{3}}, \\& \textup{(vii)}\quad R_{n,m}(e_{0,3};z,y) =y^{3}+ \frac{ \{ 18\beta _{m}^{2}+9(m-1)\beta _{m}y-(3m-2)y^{2} \} y}{m^{2}}+ \frac{6\beta _{m}^{3}}{m^{3}}, \\& \textup{(viii)} \quad R_{n,m}(e_{4,0};z,y) =z^{4}+ \bigl\{ 96 \alpha _{n}^{3}+72(n-1)\alpha _{n}^{2}z+16(n-1) (n-2)\alpha _{n}z^{2} \\& \hphantom{\textit{(viii)} \quad R_{n,m}(e_{4,0};z,y) =}{} -\bigl(6n^{2}-11n+6\bigr)z^{3} \bigr\} \frac{z}{n^{3}}+ \frac{24\alpha _{n}^{4}}{n^{4}}, \\& \textup{(ix)}\quad R_{n,m}(e_{0,4};z,y) =y^{4}+ \bigl\{ 96\beta _{m}^{3}+72(m-1)\beta _{m}^{2}y+16(m-1) (m-2)\beta _{m}y^{2} \\& \hphantom{\textup{(ix)}\quad R_{n,m}(e_{0,4};z,y) =}{} -\bigl(6m^{2}-11m+6\bigr)y^{3} \bigr\} \frac{y}{m^{3}}+ \frac{24\beta _{m}^{4}}{m^{4}}. \end{aligned}$$

Proof

The desired result can be obtained easily from Lemma 2.1 and (2.1). □

Lemma 2.3

Let the operators $R_{n,m}(\mu ;z,y)$ be given by (2.1). Then in view of Lemma 2.2, we have

$$\begin{aligned}& \textup{(i)}\quad R_{n,m}(e_{1,0}-z;z,y) =\frac{\alpha _{n}}{n}, \\& \textup{(ii)}\quad R_{n,m}(e_{0,1}-y;z,y) =\frac{\beta _{m}}{m}, \\& \textup{(iii)}\quad R_{n,m}\bigl((e_{1,0}-z)^{2};z,y\bigr) = \frac{ ( 2\alpha _{n}-z ) z}{n}+ \frac{2\alpha _{n}^{2}}{n^{2}}, \\& \textup{(iv)}\quad R_{n,m}\bigl((e_{0,1}-y)^{2};z,y\bigr) = \frac{ ( 2\beta _{m}-y ) y}{m}+ \frac{2\beta _{m}^{2}}{m^{2}}, \\& \textup{(v)}\quad R_{n,m}\bigl((e_{1,0}-z)^{4};z,y\bigr) = \frac{z}{n^{3}} \bigl( 72 \alpha _{n}^{3}-12(6n-1)\alpha _{n}^{2}z-4(n-8)\alpha _{n}z^{2} \\& \hphantom{\textup{(v)}\quad R_{n,m}\bigl((e_{1,0}-z)^{4};z,y\bigr) =}{} +3(n-2)z^{3} \bigr) +\frac{24\alpha _{n}^{4}}{n^{4}}, \\& \textup{(vi)}\quad R_{n,m}\bigl((e_{0,1}-y)^{4};z,y\bigr) = \frac{y}{m^{3}} \bigl( 72 \beta _{m}^{3}-12(6m-1)\beta _{m}^{2}y-4(m-8)\beta _{m}y^{2} \\& \hphantom{\textup{(vi)}\quad R_{n,m}\bigl((e_{0,1}-y)^{4};z,y\bigr) =}{} +3(m-2)y^{3} \bigr) +\frac{24\beta _{m}^{4}}{m^{4}}. \end{aligned}$$

Proof

Since the proofs of (ii), (iv), and (vi) can be obtained with similar calculations, we will only prove (i), (iii), and (v).

Using the properties of linearity of operators (2.1) and Lemma 2.1, one has

$$\begin{aligned}& \textup{(i)}\quad R_{n,m}(e_{1,0}-z;z,y) =R_{n,m}(e_{1,0};z,y)-zR_{n,m}(e_{0,0};z,y) \\& \hphantom{\textup{(i)}\quad R_{n,m}(e_{1,0}-z;z,y)} =\frac{\alpha _{n}}{n}, \\& \textup{(iii)}\quad R_{n,m}\bigl((e_{1,0}-z)^{2};z,y\bigr) =R_{n,m}(e_{2,0};z,y)-2zR_{n,m}(e_{1,0};z,y)+z^{2}R_{n,m}(e_{0,0};z,y) \\& \hphantom{\textup{(iii)}\quad R_{n,m}\bigl((e_{1,0}-z)^{2};z,y\bigr)} =z^{2}+\frac{ \{ 4\alpha _{n}-z \} z}{n}+ \frac{2\alpha _{n}^{2}}{n^{2}}-2z \biggl( z+ \frac{\alpha _{n}}{n} \biggr) +z^{2} \\& \hphantom{\textup{(iii)}\quad R_{n,m}\bigl((e_{1,0}-z)^{2};z,y\bigr)} =\frac{ ( 2\alpha _{n}-z ) z}{n}+ \frac{2\alpha _{n}^{2}}{n^{2}}, \\& \textup{(v)}\quad R_{n,m}\bigl((e_{1,0}-z)^{4};z,y\bigr) \\& \hphantom{\textup{(v)}\qquad}{}=R_{n,m}(e_{4,0};z,y)-4zR_{n,m}(e_{3,0};z,y)+6z^{2}R_{n,m}(e_{2,0};z,y) \\& \hphantom{\textup{(v)} \qquad=}{}{} -4z^{3}R_{n,m}(e_{1,0};z,y)+z^{4}R_{n,m}(e_{0,0};z,y) \\& \hphantom{\textup{(v)}\qquad} =z^{4}+ \bigl\{ 96\alpha _{n}^{3}+72(n-1) \alpha _{n}^{2}z+16(n-1) (n-2) \alpha _{n}z^{2} - \bigl(6n^{2}-11n+6\bigr)z^{3} \bigr\} \frac{z}{n^{3}} \\& \hphantom{\textup{(v)}\qquad=}{} +\frac{24\alpha _{n}^{4}}{n^{4}}-4z \biggl( z^{3}+ \frac{ \{ 18\alpha _{n}^{2}+9(n-1)\alpha _{n}z-(3n-2)z^{2} \} z}{n^{2}}+ \frac{6\alpha _{n}^{3}}{n^{3}} \biggr) \\& \hphantom{\textup{(v)}\qquad=}{} +6z^{2} \biggl( z^{2}+\frac{ \{ 4\alpha _{n}-z \} z}{n}+ \frac{2\alpha _{n}^{2}}{n^{2}} \biggr) -4z^{3} \biggl( z+ \frac{\alpha _{n}}{n} \biggr) +z^{4} \\& \hphantom{\textup{(v)}\qquad}{} =\frac{z}{n^{3}} \bigl\{ 72\alpha _{n}^{3}-12(6n-1) \alpha _{n}^{2}z-4(n-8)\alpha _{n}z^{2}+3(n-2)z^{3} \bigr\} + \frac{24\alpha _{n}^{4}}{n^{4}}. \end{aligned}$$

 □

Lemma 2.4

As a consequence of Lemma 2.3, we have

$$\begin{aligned}& \textup{(i)} \quad \sup_{0\leq z\leq \alpha _{n}}R_{n,m} \bigl((e_{1,0}-z)^{2};z,y\bigr) \leq \frac{3\alpha _{n}^{2}}{n}, \\& \textup{(ii)}\quad \sup_{0\leq y\leq \beta _{m}}R_{n,m} \bigl((e_{0,1}-y)^{2};z,y\bigr) \leq \frac{3\beta _{m}^{2}}{m}, \\& \textup{(iii)}\quad \sup_{0\leq z\leq \alpha _{n}}R_{n,m} \bigl((e_{1,0}-z)^{4};z,y\bigr) \leq \biggl( 12 \frac{\alpha _{n}^{2}}{n} \biggr) ^{2}, \\& \textup{(vi)}\quad \sup_{0\leq y\leq \beta _{m}}R_{n,m} \bigl((e_{0,1}-y)^{4};z,y\bigr) \leq \biggl( 12 \frac{\beta _{m}^{2}}{m} \biggr) ^{2}. \end{aligned}$$

Proof

In view of Lemma 2.3, one can obtain

$$ \mathrm{(i)}\quad \sup_{0\leq z\leq \alpha _{n}}R_{n,m} \bigl((e_{1,0} -z)^{2};z,y\bigr) \leq \frac{2(n+1)\alpha _{n}^{2}}{n^{2}}\leq \frac{3\alpha _{n}^{2} }{n} $$

and

$$ \mathrm{(iii)}\quad \sup_{0\leq z\leq \alpha _{n}}R_{n,m} \bigl((e_{1,0} -z)^{4};z,y\bigr) \leq \frac{3(n+47)\alpha _{n}^{4}}{n^{3}}\leq \biggl( 12 \frac{\alpha _{n}^{2}}{n} \biggr) ^{2}. $$

Analogously, the proof of the inequalities (ii) and (iv) can be obtained by the same methods; thus we get the desired result. □

In the next theorem, with the help of theorems related to the weighted approximation of functions of several variables proved by Gadzhiev et al. [27], we show the uniform convergence of the operators given by (2.1) on $I_{\alpha _{n}\beta _{m}}$.

Theorem 2.5

Let the linear positive operators $R_{n,m}:C_{\rho }(I_{\alpha _{n}\beta _{m}})\rightarrow B_{\rho }(I_{\alpha _{n}\beta _{m}})$ verify the following conditions:

$$\begin{aligned}& \lim_{n,m\rightarrow \infty } \bigl\Vert R_{n,m}(e_{0,0})-1 \bigr\Vert _{\rho } =0, \\& \lim_{n,m\rightarrow \infty } \bigl\Vert R_{n,m}(e_{1,0})-z \bigr\Vert _{\rho } =0, \\& \lim_{n,m\rightarrow \infty } \bigl\Vert R_{n,m}(e_{0,1})-y \bigr\Vert _{\rho } =0, \\& \lim_{n,m\rightarrow \infty } \bigl\Vert R_{n,m} \bigl(e_{1,0}^{2}+e_{0,1}^{2}\bigr)- \bigl(z^{2}+y^{2}\bigr) \bigr\Vert _{\rho } =0. \end{aligned}$$

Hence,

$$ \lim_{n,m\rightarrow \infty } \bigl\Vert R_{n,m}( \mu )-\mu \bigr\Vert _{\rho }=0 $$

for all $\mu \in C_{\rho }^{a}(I_{\alpha _{n}\beta _{m}})$.

Proof

Taking into account the following relations from Lemma 2.2:

$$\begin{aligned}& \textup{(i)} \quad R_{n,m}(e_{0,0};z,y) =1, \qquad \textup{(ii)}\quad R_{n,m}(e_{1,0};z,y)=z+ \frac{\alpha _{n}}{n}, \\& \textup{(iii)}\quad R_{n,m}(e_{0,1};z,y) =y+\frac{\beta _{m}}{m}, \qquad \textup{(iv)}\quad R_{n,m}(e_{2,0};z,y)=z^{2}+ \frac{ \{ 4\alpha _{n}-z \} z}{n}+ \frac{2\alpha _{n}^{2}}{n^{2}}, \\& \textup{(v)}\quad R_{n,m}(e_{0,2};z,y) =y^{2}+ \frac{ \{ 4\beta _{m}-y \} y}{m}+\frac{2\beta _{m}^{2}}{m^{2}}. \end{aligned}$$

Thus, it clear that $\Vert R_{n,m}(e_{0,0})-1 \Vert _{\rho }\rightarrow 0$ as $n,m\rightarrow \infty$ on $I_{\alpha _{n}\beta _{m}}$.

$$ \bigl\Vert R_{n,m}(e_{1,0})-z \bigr\Vert _{\rho }= \sup_{(z,y)\in I_{\alpha _{n}\beta _{m}}} \frac{ \vert R_{n,m}(e_{1,0})-z \vert }{1+z^{2}+y^{2}}= \frac{\alpha _{n}}{n} \sup_{(z,y)\in I_{\alpha _{n}\beta _{m}}} \frac{1}{1+z^{2}+y^{2}}. $$

Hence, we get

$$ \lim_{n,m\rightarrow \infty } \bigl\Vert R_{n,m}(e_{1,0})-z \bigr\Vert _{\rho }=0. $$

Similarly, one can obtain

$$ \lim_{n,m\rightarrow \infty } \bigl\Vert R_{n,m}(e_{0,1})-y \bigr\Vert _{\rho }=0. $$

Also,

$$\begin{aligned} & \bigl\Vert R_{n,m}\bigl(e_{1,0}^{2}+e_{0,1}^{2} \bigr)-\bigl(z^{2}+y^{2}\bigr) \bigr\Vert _{\rho } \\ &\quad =\sup_{(z,y)\in I_{\alpha _{n}\beta _{m}}} \frac{ \vert R_{n,m}(e_{2,0};z,y)+R_{n,m}(e_{0,2};z,y)-(z^{2}+y^{2}) \vert }{1+z^{2}+y^{2}} \\ &\quad \leq 2 \biggl( \frac{\alpha _{n}^{2}}{n^{2}}+ \frac{\beta _{m}^{2}}{m^{2}} \biggr) \sup_{(z,y) \in I_{\alpha _{n}\beta _{m}}} \frac{1}{1+z^{2}+y^{2}}+4 \biggl( \frac{\alpha _{n}}{n}+ \frac{\beta _{m}}{m} \biggr) \sup_{(z,y)\in I_{\alpha _{n}\beta _{m}}} \frac{z+y}{1+z^{2}+y^{2}}. \end{aligned}$$

Thus, we have

$$ \lim_{n,m\rightarrow \infty } \bigl\Vert R_{n,m} \bigl(e_{1,0}^{2}+e_{0,1}^{2} \bigr)-\bigl(z^{2}+y^{2}\bigr) \bigr\Vert _{\rho }=0. $$

Since all conditions of the bivariate Korovkin type theorem are satisfied, we arrive

$$ \lim_{n,m\rightarrow \infty } \bigl\Vert R_{n,m}(\mu )- \mu \bigr\Vert _{\rho }=0, $$

for all $\mu \in C_{\rho }^{a}(I_{\alpha _{n}\beta _{m}})$. Consequently, the proof is complete. □

Let $I_{cd}:=[0,c]\times {}[ 0,d]\subset I_{\alpha _{n}\beta _{m}}$. For $\mu (z,y)\in C(I_{cd})$, we give the complete modulus of continuity as follows:

$$\begin{aligned} \varpi (\mu ,\gamma _{n,}\gamma _{m}) ={}&\sup \bigl\{ \bigl\vert \mu (u,v)-\mu (z,y) \bigr\vert :(u,v),(z,y)\in I_{cd}, \\ & {} \vert u-z \vert \leq \gamma _{n}, \vert v-y \vert \leq \gamma _{m} \bigr\} \end{aligned}$$

where $\varpi (\mu ,\gamma _{n,}\gamma _{m})$ verify the subsequent properties:

$$\begin{aligned}& (1)\quad \varpi (\mu ,\gamma _{n,}\gamma _{m}) \rightarrow 0,\quad \gamma _{n}\rightarrow 0, \gamma _{m}\rightarrow 0 \\& (2)\quad \bigl\vert \mu (u,v)-\mu (z,y) \bigr\vert \leq \varpi (\mu , \gamma _{n,}\gamma _{m}) \biggl( 1+ \frac{ \vert u-z \vert }{\gamma _{n} } \biggr) \biggl( 1+ \frac{ \vert v-y \vert }{\gamma _{m}} \biggr). \end{aligned}$$

For the integers z and y, the partial modulus of continuity is given by

$$\begin{aligned}& \omega _{1}(\mu ,\gamma ) =\sup \bigl\{ \bigl\vert \mu (u_{1},y)- \mu (u_{2},y) \bigr\vert :y\in {}[ 0,d], \vert u_{1}-u_{2} \vert \leq \gamma ,\gamma >0 \bigr\} , \\& \omega _{2}(\mu ,\gamma ) =\sup \bigl\{ \bigl\vert \mu (z,v_{1})- \mu (z,v_{2}) \bigr\vert :z\in {}[ 0,c], \vert v_{1}-v_{2} \vert \leq \gamma ,\gamma >0 \bigr\} . \end{aligned}$$

Let the space $C^{2}(I_{cd})$ denote the functions of μ such that $\frac{\partial _{j}\mu }{\partial z_{j}}$, $\frac{\partial _{j}\mu }{\partial y_{j}}$ ($j=1,2$) belongs to $C(I_{cd})$. For $\mu \in C(I_{cd})$, the norm on $C^{2}(I_{cd})$ and Peetre’s K-functional are defined as follows:

$$ \Vert \mu \Vert _{C^{2}(I_{cd})}= \Vert \mu \Vert _{C(I_{cd})}+ \sum ^{2} _{j=1} \biggl( \biggl\Vert \frac{\partial _{j}\mu }{\partial z_{j}} \biggr\Vert _{C(I_{cd})}+ \biggl\Vert \frac{\partial _{j}\mu }{\partial y_{j}} \biggr\Vert _{C(I_{cd})} \biggr) $$

and

$$ K_{2}(\mu ,\zeta )=\inf \bigl\{ \Vert \mu -h \Vert _{C(I_{cd})}+\zeta \Vert h \Vert _{C^{2}(I_{cd})}:h\in C^{2}(I_{cd}) \bigr\} , $$

respectively, where $\zeta >0$. Also, the following inequality:

$$ K_{2}(\mu ,\zeta )\leq D\overset{\ast }{\omega _{2}}(\mu ,\sqrt{\zeta }) $$

(2.3)

holds, where $\overset{\ast }{\omega _{2}}(\mu ,\sqrt{\zeta })$ denotes the second order of the modulus of continuity, and $D>0$ is an absolute constant independent of μ, ζ and $\overset{\ast }{\omega _{2}}$.

Theorem 2.6

For any $(z,y)\in I_{cd}$ and all $\mu \in C(I_{cd})$, we arrive

$$ \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \leq 2\varpi \bigl( \mu ,\gamma _{n,m}(z,y)\bigr), $$

where $\gamma _{n}=\gamma _{n}(z)=\sqrt{R_{n,m}((e_{1,0}-z)^{2};z,y)}$, $\gamma _{m}=\gamma _{m}(y)=\sqrt{R_{n,m}((e_{0,1}-y)^{2};z,y)}$ and $\gamma _{n,m}=\gamma _{n,m}(z,y)=\sqrt{\gamma _{n}^{2}(z)+\gamma _{m}^{2}(y)}$.

Proof

Taking into account the properties of $\varpi (\mu ,\gamma _{n,m})$ and utilizing the linearity of the operators (2.1) yield

$$\begin{aligned} \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert & = \bigl\vert R_{n,m}\bigl(\mu (t,s);z,y\bigr)-R_{n,m}\bigl(\mu (z,y);z,y\bigr) \bigr\vert \\ & \leq R_{n,m}\bigl( \bigl\vert \mu (t,s)-\mu (z,y) \bigr\vert ;z,y \bigr) \\ & \leq R_{n,m}(\varpi \bigl(\sqrt{(e_{1,0}-z)^{2}+(e_{0,1}-y)^{2}};z,y \bigr) \\ & \leq \varpi (\mu ,\gamma _{n,m}) \biggl[ 1+\frac{1}{\gamma _{n,m}}R_{n,m}\bigl(\sqrt{(e_{1,0}-z)^{2}+(e_{0,1}-y)^{2}};z,y \bigr) \biggr] . \end{aligned}$$

Next, using the Cauchy–Schwarz inequality and Lemma 2.2, one can obtain

$$\begin{aligned} & \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \\ &\quad \leq \varpi (\mu ,\gamma _{n,m}) \biggl[ 1+\frac{1}{\gamma _{n,m}} \bigl( R_{n,m}\bigl((e_{1,0}-z)^{2}+(e_{0,1}-y)^{2};z,y \bigr) \bigr) ^{ \frac{1}{2}} \biggr] \\ &\quad =\varpi (\mu ,\gamma _{n,m}) \biggl[ 1+\frac{1}{\gamma _{n,m}} \bigl( \gamma _{n}^{2}(z)+\gamma _{m}^{2}(y) \bigr) ^{\frac{1}{2}} \biggr] \\ &\quad =2\varpi \bigl(\mu ,\gamma _{n,m}(z,y)\bigr), \end{aligned}$$

which gives the proof. □

Theorem 2.7

Suppose that the operators $R_{n,m}(\mu ;z,y)$ are given by (2.1), and $\mu \in C(I_{cd})$. Then the following relation verifies

$$ \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \leq 2 \bigl( \omega _{1}(\mu ,\gamma _{n})+\omega _{2}(\mu ,\gamma _{m}) \bigr), $$

where $\gamma _{n}=\gamma _{n}(z)$ and $\gamma _{m}=\gamma _{m}(y)$ are given as in Theorem 2.6.

Proof

Using the linearity of operators (2.1) and Lemma 2.2, we arrive

$$\begin{aligned} & \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \\ &\quad = \bigl\vert R_{n,m}\bigl(\mu (t,s);z,y\bigr)-R_{n,m} \bigl(\mu (z,y);z,y\bigr) \bigr\vert \\ &\quad \leq R_{n,m}\bigl( \bigl\vert \mu (t,s)-\mu (z,y) \bigr\vert ;z,y \bigr) \\ &\quad \leq R_{n,m}\bigl( \bigl\vert \mu (t,s)-\mu (z,s) \bigr\vert ;z,y \bigr)+R_{n,m}\bigl( \bigl\vert \mu (z,s)-\mu (z,y) \bigr\vert ;z,y \bigr) \\ &\quad \leq \omega _{1}(\mu ,\gamma _{n}) \biggl[ 1+ \frac{1}{\gamma _{n}}R_{n,m}\bigl( \vert t-z \vert ;z,y\bigr) \biggr] \\ &\qquad {} +\omega _{2}(\mu ,\gamma _{m}) \biggl[ 1+ \frac{1}{\gamma _{m}}R_{n,m}\bigl( \vert s-y \vert ;z,y\bigr) \biggr]. \end{aligned}$$

Utilizing the Cauchy–Schwarz inequality,

$$\begin{aligned} \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \leq{} &\omega _{1}( \mu ,\gamma _{n}) \biggl[ 1+\frac{1}{\gamma _{n}} \bigl\{ R_{n,m}\bigl((e_{1,0}-z)^{2};z,y\bigr) \bigr\} ^{\frac{1}{2}} \biggr] \\ & {}+\omega _{2}(\mu ,\gamma _{m}) \biggl[ 1+ \frac{1}{\gamma _{m}} \bigl\{ R_{n,m}\bigl((e_{0,1}-y)^{2};z,y \bigr) \bigr\} ^{\frac{1}{2}} \biggr]. \end{aligned}$$

Hence, for all $(z,y)\in I_{cd}$, taking $\gamma _{n}=\gamma _{n}(z)$ and $\gamma _{m}=\gamma _{m}(y)$ as in Theorem 2.6, we have the proof of this theorem. □

With the help of the Lipschitz class, we will also estimate the order of approximation of operators (2.1). Let $\mu \in C(I_{cd})$, $(z,y),(t,s)\in I_{cd}$ and $\varphi _{1},\varphi _{2}\in ( 0,1 ]$ the class of Lipschitz for the bivariate case is given by

$$ \operatorname{Lip}_{L}(\mu ;\varphi _{1}, \varphi _{2})= \bigl\{ \mu \in C(I_{cd}): \bigl\vert \mu (t,s)-\mu (z,y) \bigr\vert \leq L \vert t-z \vert ^{\varphi _{1}} \vert s-y \vert ^{\varphi _{2}} \bigr\} . $$

(2.4)

Theorem 2.8

Suppose that $\mu \in \operatorname{Lip}_{L}(\mu ;\varphi _{1},\varphi _{2})$. Then for all $(z,y)\in I_{cd}$, we obtain

$$ \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \leq L \bigl( \delta _{n}(z) \bigr) ^{\frac{\varphi _{1}}{2}} \bigl( \delta _{m}(y) \bigr) ^{\frac{\varphi _{2}}{2}}, $$

where $\delta _{n}(z)$ and $\delta _{m}(y)$ are given as in Theorem 2.6.

Proof

Using the linearity and monotonicity properties of operators (2.1), in view of Lemma 2.2, it becomes

$$\begin{aligned} \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert & \leq R_{n,m} \bigl( \bigl\vert \mu (t,s)-\mu (z,y) \bigr\vert ;z,y \bigr) \\ & \leq L R_{n,m} \bigl( \vert t-z \vert ^{\varphi _{1}} \vert s-y \vert ^{\varphi _{2}};z,y \bigr) \\ & =L R_{n,m} \bigl( \vert t-z \vert ^{\varphi _{1}};z,y \bigr) R_{n,m} \bigl( \vert s-y \vert ^{\varphi _{2}};z,y \bigr). \end{aligned}$$

Utilizing the Hölder’s inequality for $( p_{1},q_{1} ) = ( \frac{2}{\varphi _{1}}, \frac{2}{2-\varphi _{1}} )$, $( p_{2},q_{2} ) = ( \frac{2}{\varphi _{2}}, \frac{2}{2-\varphi _{2}} )$, one has

$$\begin{aligned} \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \leq{}& L \bigl( R_{n,m} \bigl( (e_{1,0}-z)^{2};z,y \bigr) ^{\frac{\varphi _{1}}{2}}R_{n,m} ( e_{0,0};z,y ) ^{\frac{2-\varphi _{1}}{2}} \\ &{} \times R_{n,m} \bigl( (e_{0,1}-y)^{2};z,y \bigr) ^{ \frac{\varphi _{2}}{2}}R_{n,m} ( e_{0,0};z,y ) ^{\frac{2-\varphi _{2}}{2}} \bigr) \\ \leq{}& L \bigl( \delta _{n}(z) \bigr) ^{ \frac{\varphi _{1}}{2}} \bigl( \delta _{m}(y) \bigr) ^{ \frac{\varphi _{2}}{2}}. \end{aligned}$$

Hence, the proof is completed. □

Next, we will examine the degree of approximation of functions $\mu \in C_{\rho }^{a}$ on $I_{\alpha _{n}\beta _{m}}$. Analogously as in [18], for each $\mu \in C_{\rho }^{a}$, we consider the weighted modulus of continuity as below:

$$ \Delta _{n,m}(\mu ;\gamma _{1},\gamma _{2})= \underset{\underset{(z,y)\in I_{\alpha _{n}\beta _{m}}}{ \vert r \vert \leq \gamma _{1,} \vert s \vert \leq \gamma _{2}}}{\sup } \frac{ \vert \mu (z+r,y+s)-\mu (z,y) \vert }{\rho (r,s)\rho (z,y)}.$$

Additionally, $\Delta _{n,m}(\mu ;\gamma _{1},\gamma _{2})\rightarrow 0$ for $\gamma _{1}\rightarrow 0$, $\gamma _{2}\rightarrow 0$. Also, for $\mu _{1}>0$, $\mu _{2}>0$, the following relation satisfies

$$ \Delta _{n,m}(\mu ;\mu _{1}\gamma _{1},\mu _{2}\gamma _{2})\leq 4(1+ \mu _{1}) (1+\mu _{2})\Delta _{n,m}(\mu ;\gamma _{1},\gamma _{2}). $$

Theorem 2.9

Let $R_{n,m}(\mu ;z,y)$ operators be given by (2.1). For all $\mu \in C_{\rho }^{a}$ and n, m the following inequality

$$ \sup_{(z,y)\in I_{\alpha _{n}\beta _{m}}} \frac{ \vert R_{n,m}(\mu ;z,y)-\mu (z,y) \vert }{1+z^{2}+y^{2}} \leq K\Delta _{n,m}\biggl(\mu ;\sqrt{\frac{\alpha _{n}^{2}}{n}}, \sqrt {\frac{\beta _{m}^{2}}{m}}\biggr) $$

holds and is sufficiently large, where $K>0$ is a constant.

Proof

For all $(z,y)\in I_{\alpha _{n}\beta _{m}}$, $(t,s)\in {}[ 0,\infty )\times {}[ 0,\infty )$, using the definition of operators (2.1), we get

$$\begin{aligned} & \bigl\vert R_{n,m}\bigl(\mu (t,s);z,y\bigr)-\mu (z,y) \bigr\vert \\ &\quad \leq R_{n,m} \bigl( \bigl\vert \mu (t,s)-\mu (z,y) \bigr\vert ;z,y \bigr) \\ & \quad \leq 8\bigl(1+z^{2}+y^{2}\bigr)\Delta _{n,m}(\mu ;\gamma _{n},\gamma _{m})R_{n,m} \bigl( B_{1}(z)B_{2}(y);z,y \bigr), \end{aligned}$$

(2.5)

where

$$ B_{1}(z)=\biggl(1+\frac{ \vert t-z \vert }{\gamma _{n}}\biggr) \bigl(1+(t-z)^{2} \bigr), $$

and

$$ B_{2}(y)=\biggl(1+\frac{ \vert s-y \vert }{\gamma _{m}}\biggr) \bigl(1+(s-y)^{2} \bigr). $$

It is clear that since

$$ B_{1}(z)\leq \textstyle\begin{cases} 2(1+\gamma _{n}^{2}), &\vert t-z \vert \leq \gamma _{n}, \\ 2(1+\gamma _{n}^{2}), & \vert t-z \vert \geq \gamma _{n},\end{cases} $$

then for each $z,t\in {}[ 0,\infty )$, we derive

$$ B_{1}(z)\leq \biggl\{ 1+\frac{(e_{1,0}-z)^{4}}{\gamma _{n}^{4}} \biggr\} . $$

(2.6)

Analogously, we get

$$ B_{2}(y)\leq \biggl\{ 1+\frac{(e_{0,1}-y)^{4}}{\gamma _{m}^{4}} \biggr\} . $$

(2.7)

Using (2.6) and (2.7) in (2.5) yields

$$\begin{aligned} & \bigl\vert R_{n,m}\bigl(\mu (t,s);z,y\bigr)-\mu (z,y) \bigr\vert \\ & \quad \leq 4\bigl(1+z^{2}+y^{2}\bigr)\Delta _{n,m}(\mu ;\gamma _{n},\gamma _{m}) \\ &\qquad {} \times \biggl[ 1+ \frac{R_{n,m}((e_{1,0}-z)^{4};z,y)}{\gamma _{n}^{4}} \biggr] \biggl[ 1+ \frac{R_{n,m}((e_{0,1}-y)^{4};z,y)}{\gamma _{m}^{4}} \biggr] \\ &\quad \leq 4\bigl(1+z^{2}+y^{2}\bigr)\Delta _{n,m}(\mu ;\gamma _{n},\gamma _{m}) \\ &\qquad {} \times \biggl[ 1+\frac{144}{\gamma _{n}^{4}} \biggl( \frac{\alpha _{n}^{2}}{n} \biggr) ^{2} \biggr] \biggl[ 1+\frac{144}{\gamma _{m}^{4}} \biggl( \frac{\beta _{m}^{2}}{m} \biggr) ^{2} \biggr] . \end{aligned}$$

Choosing $\gamma _{n}=\sqrt{\frac{\alpha _{n}^{2}}{n}}$, $\gamma _{m}=\sqrt{\frac{\beta _{m}^{2}}{m}}$ and taking the assumptions for the sequences $(\alpha _{n})$, $(\beta _{m})$ in (2.2), we get the proof of this theorem. □

Theorem 2.10

Suppose that $\mu \in C(I_{cd})$. Then the following inequality satisfies

$$\begin{aligned}& \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \\& \quad \leq N \{ \overset{\ast }{\omega _{2}}\bigl(\mu ;\sqrt{A_{n,m}(z,y)} \bigr)+\min \bigl\{ 1,A_{n,m}(z,y) \Vert \mu \Vert _{C^{2}(I_{cd})} \bigr\} +\varpi \bigl(\mu ; \xi _{n,m}(z,y)\bigr) \end{aligned}$$

where a constant $N>0$ independent of μ and $A_{n,m}(z,y)$. $\xi _{n,m}= \sqrt{ ( \frac{\alpha _{n}}{n} ) ^{2}+ ( \frac{\beta _{m}}{m} ) ^{2}}$, $A_{n,m}(z,y)=\gamma _{n}^{2}(z)+\gamma _{m}^{2}(y)+\xi _{n,m}^{2}$ and $\gamma _{n}(z)$, $\gamma _{m}(y)$ are given by Theorem 2.6.

Proof

Firstly, we consider the following auxiliary operators:

$$ \overline{R_{n,m}}(\mu ;z,y)=R_{n,m}(\mu ;z,y)-\mu \biggl(z+ \frac{\alpha _{n}}{n},y+\frac{\beta _{m}}{m}\biggr)+\mu ( z,y ). $$

(2.8)

It follows by Lemma 2.2 that

$$ \overline{R_{n,m}}(t-z;z,y)=0\quad \text{and}\quad \overline{R_{n,m}}(s-y;z,y)=0. $$

For $\mu \in C^{2}(I_{cd})$, $(s,t)\in I_{cd}$, using the Taylor expansion formula, we get

$$\begin{aligned} \mu (s,t)-\mu (z,y) ={}&\mu (s,y)-\mu (z,y)+\mu (s,t)-\mu (s,y) \\ ={}&\frac{\partial \mu (z,y)}{\partial z}(s-z)+ \int_{z}^{s}(s-u)\frac{\partial ^{2}\mu (u,y)}{\partial ^{2}u}\,du \\ & {}+\frac{\partial \mu (z,y)}{\partial y}(t-y)+\int _{y}^{t}(t-v)\frac{\partial ^{2}\mu (z,v)}{\partial ^{2}v}\,dv. \end{aligned}$$

(2.9)

Operating $\overline{R_{n,m}}$ on (2.9), it becomes

$$\begin{aligned} & \overline{R_{n,m}}(\mu ;z,y)-\mu (z,y) \\ &\quad =\overline{R_{n,m}} \biggl(\int _{z}^{s}(s-u)\frac{\partial ^{2}\mu (u,y)}{\partial ^{2}u}\,du;z,y \biggr) + \overline{R_{n,m}} \biggl( \int_{y}^{t}(t-v)\frac{\partial ^{2}\mu (z,v)}{\partial ^{2}v}\,dv;z,y \biggr) \\ &\quad =R_{n,m} \biggl(\int _{z}^{s}(s-u)\frac{\partial ^{2}\mu (u,y)}{\partial ^{2}u}\,du;z,y \biggr) - \int _{z} ^{z+\frac{\alpha _{n}}{n}} \biggl( z+\frac{\alpha _{n}}{n}-u \biggr) \frac{\partial ^{2}\mu (u,y)}{\partial ^{2}u}\,du \\ &\qquad {} +R_{n,m} \biggl( \int _{y}^{t}(t-v)\frac{\partial ^{2}\mu (z,v)}{\partial ^{2}v}\,dv;z,y \biggr) - \int_{y}^{y+\frac{\beta _{m}}{m}}\biggl( y+\frac{\beta _{m}}{m}-v \biggr) \frac{\partial ^{2}\mu (z,v)}{\partial ^{2}v}\,dv. \end{aligned}$$

Hence,

$$\begin{aligned} & \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \\ &\quad \leq R_{n,m} \biggl( \biggl\vert \int _{z}^{s} \vert s-u \vert \biggr\vert \frac{\partial ^{2}\mu (u,y)}{\partial ^{2}u}\biggr\vert \,du \biggr\vert ;z,y \biggr) + \biggl\vert \int_{z}^{z+\frac{\alpha _{n}}{n}} \bigg\vert z+\frac{\alpha _{n}}{n}-u \bigg\vert \biggr\vert \frac{\partial ^{2}\mu (u,y)}{\partial ^{2}u} \biggr\vert \,du \biggr\vert \\ &\qquad {} +R_{n,m} \biggl( \biggl\vert \int _{y}^{t} \vert t-v \vert \bigg\vert \frac{\partial ^{2}\mu (z,v)}{\partial ^{2}v} \bigg\vert \,dv \bigg\vert ;z,y \biggr) + \biggl\vert \int_{y}^{y+\frac{\beta _{m}}{m}} \bigg\vert y+\frac{\beta _{m}}{m}-v \bigg\vert \bigg\vert \frac{\partial ^{2}\mu (z,v)}{\partial ^{2}v} \bigg\vert \,dv \bigg\vert \\ &\quad \leq \biggl\{ R_{n,m}\bigl((s-z)^{2};z,y\bigr)+\biggl(z+ \frac{\alpha _{n}}{n}-z\biggr)^{2}\\ &\qquad {}+R_{n,m} \bigl((t-y)^{2};z,y\bigr)+\biggl(y+\frac{\beta _{m}}{m}-y \biggr)^{2} \biggr\} \Vert \mu \Vert _{C^{2}(I_{cd})}. \end{aligned}$$

Choosing $\xi _{n,m}= \sqrt{ ( \frac{\alpha _{n}}{n} ) ^{2}+ ( \frac{\beta _{m}}{m} ) ^{2}}$, $A_{n,m}(z,y)=\gamma _{n}^{2}(z)+\gamma _{m}^{2}(y)+\xi _{n,m}^{2}$, we obtain

$$ \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \leq A_{n,m}(z,y) \Vert \mu \Vert _{C^{2}(I_{cd})}. $$

(2.10)

Additionally, using Lemma 2.2 and (2.1), (2.10), we derive

$$ \bigl\vert \overline{R_{n,m}}(\mu ;z,y) \bigr\vert \leq \bigl\vert R_{n,m}(\mu ;z,y) \bigr\vert + \biggl\vert \mu \biggl(\frac{\alpha _{n}}{n}, \frac{\beta _{m}}{m}\biggr) \biggr\vert + \bigl\vert \mu (z,y) \bigr\vert \leq 3 \Vert \mu \Vert _{C(I_{cd})}. $$

(2.11)

Next, (2.1) and (2.11) yield

$$\begin{aligned} & \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \\ &\quad \leq \bigl\vert \overline{R_{n,m}}(\mu -h;z,y) \bigr\vert + \bigl\vert \overline{R_{n,m}}(h;z,y)-h(z,y) \bigr\vert \\ &\qquad {} +\big\vert h(z,y)-\mu (z,y) \big\vert + \biggl\vert \mu \biggl( \frac{\alpha _{n}}{n}, \frac{\beta _{m}}{m}\biggr)-\mu (z,y) \biggr\vert \\ &\quad \leq 4 \Vert \mu -h \Vert _{C(I_{cd})}+ \bigl\vert R_{n}(\mu ;z,y)-\mu (z,y) \bigr\vert + \biggl\vert \mu \biggl( \frac{\alpha _{n}}{n},\frac{\beta _{m}}{m}\biggr)-\mu (z,y) \biggr\vert \\ & \quad \leq \bigl( 4 \Vert \mu -h \Vert _{C(I_{cd})}+A_{n,m}(z,y) \Vert h \Vert _{C^{2}(I_{cd})} \bigr) +\varpi \bigl(\mu ;\xi _{n,m}(z,y)\bigr). \end{aligned}$$

(2.12)

Consequently, in (2.12), utilizing the infimum on the right-hand side over all $\mu \in C^{2}(I_{cd})$ and taking (2.3), we attain

$$\begin{aligned}& \bigl\vert R_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \\& \quad \leq N \{ \overset{\ast }{\omega _{2}}\bigl(\mu ;\sqrt{A_{n,m}(z,y)} \bigr)+\min \bigl\{ 1,A_{n,m}(z,y) \Vert \mu \Vert _{C^{2}(I_{cd})} \bigr\} +\varpi \bigl(\mu ; \xi _{n,m}(z,y)\bigr). \end{aligned}$$

Hence, the required result is obtained. □

3 The GBS type of $R_{n,m}(\mu ;z,y)$

The notion of the B-continuous and B-differentiable functions were firstly used by Bögel [28, 29]. Dobrescu and Matei [30] proposed the Generalized Boolean Sum (GBS) type of Bernstein operators. Next, Badea [31, 32] presented the B-continuous functions with the GBS type operators. We refer readers to interesting research in this direction [33–38].

Let us now give some definitions that we will use in this section.

A function $\mu :U\times V\rightarrow \mathbb{R}$, where U, V are compact intervals of $\mathbb{R}$. For any $(z,y),(t_{0},s_{0})\in U\times V$, the mixed difference of μ is given as

$$ \phi _{(t_{0},s_{0})}\mu (z,y)=\mu (z,y)-\mu (z,s_{0})- \mu (t_{0},y)+ \mu (t_{0},s_{0}).$$

(3.1)

If a real-valued function μ satisfies the following relation, it is called a Bögel-continuous (B-continuous) at $(t_{0},s_{0})\in U\times V$.

$$ \lim_{(t_{0},s_{0})\rightarrow (z,y)}\phi _{(t_{0},s_{0})} \mu (z,y)=0. $$

If the following limit denoted by $D_{B}\mu (z,y)$ exists and is finite, then a function μ is called a Bögel-differentiable (B-differentiable) at $(t_{0},s_{0})\in U\times V$.

$$ \lim_{(t_{0},s_{0})\rightarrow (z,y)} \frac{\phi _{(t_{0},s_{0})}\mu (z,y)}{(t_{0}-z)(s_{0}-y)}=D_{B}\mu (z,y). $$

(3.2)

Note that by $C_{b}(U\times V)$ and $D_{b}(U\times V)$, we denote the sets of each B-continuous and B-differentiable functions on $U\times V$, respectively. Considering the definition of B-continuous, one gets $C(U\times V)\subset C_{b}(U\times V)$, see [39] for details.

A function $\mu :U\times V\rightarrow \mathbb{R}$ is called a Bögel-bounded (B-bounded) on $U\times V$ if there exists $W>0$ such that $\vert \phi _{(t_{0},s_{0})}\mu (z,y) \vert \leq W$ for all $(t_{0},s_{0}),(z,y)\in U\times V$.

Also, if $U\times V$ is a compact subset of $\mathbb{R} ^{2}$, hence all Bögel-continuous functions are Bögel-bounded on $U\times V\rightarrow \mathbb{R}$.

Further, by $B_{b}(U\times V)$, we denote the space of all B-bounded functions on $U\times V$, and it is endowed with the norm $\Vert \mu \Vert _{B}= \sup_{(z,y),(t_{0},s_{0})\in U\times V} \vert \phi _{(t_{0},s_{0})} \mu (z,y) \vert$.

For $\mu \in B_{b}(I_{\alpha _{n}\beta _{m}})$, the mixed modulus of smoothness is defined as:

$$ \omega _{\mathrm{mixed}} ( \mu ;\delta _{1},\delta _{2} ) := \sup \bigl\{ \bigl\vert \phi _{(t_{0},s_{0})}\mu (z,y) \bigr\vert : \vert t_{0}-z \vert < \delta _{1}, \vert s_{0}-y \vert < \delta _{2} \bigr\} , $$

where $(z,y),(t_{0},s_{0})\in U\times V$ and $\delta _{1},\delta _{2}\in \mathbb{R} ^{+}$. Also, for all $\lambda _{1},\lambda _{2}\geq 0$, the following inequality holds

$$ \omega _{\mathrm{mixed}} ( \mu ;\lambda _{1}\delta _{1},\lambda _{2} \delta _{2} ) \leq ( 1+\lambda _{1} ) ( 1+ \lambda _{2} ) \omega _{\mathrm{mixed}} ( \mu ; \delta _{1},\delta _{2} ), $$

(3.3)

for more details, see [31, 32].

Let $C_{b}(I_{cd})$ denote the set of all Bögel-continuous functions on $I_{cd}$. For $\mu \in C_{b}(I_{cd})$, the Lipschitz class $\operatorname{Lip}_{L}(\varphi _{1},\varphi _{2})$ by $L>0$, $(z,y),(t_{0},s_{0})\in I_{cd}$ and $\varphi _{1},\varphi _{2}\in ( 0,1 ]$ is given by

$$ \operatorname{Lip}_{L}(\varphi _{1},\varphi _{2})= \bigl\{ \mu \in C_{b}(I_{cd}): \bigl\vert \phi _{(t_{0},s_{0})}\mu (z,y) \bigr\vert \leq L \vert t_{0}-z \vert ^{\varphi _{1}} \vert s_{0}-y \vert ^{ \varphi _{2}} \bigr\} . $$

Now, we construct the associated GBS type of operators (2.1). For $n,m\in \mathbb{N}$, for each $(z,y)\in U\times V$ and any $\mu \in C_{b}(I_{cd})$, we derive

$$ G_{n,m}(\mu ;z,y)=R_{n,m}\bigl(\mu (z,s_{0})+\mu (t_{0},y)-\mu (t_{0},s_{0});z,y\bigr). $$

Exactly, for any $(z,y)\in I_{cd}$ and $\mu \in C_{b}(I_{cd})$, the GBS type operators related to the $R_{n,m}$ operators are defined as:

$$\begin{aligned} & G_{n,m}(\mu ;z,y) \\ &\quad =\frac{n}{\alpha _{n}} \frac{m}{\beta _{m}}\sum_{k=0}^{n}\sum _{j=0}^{m}P_{n,m,k,j}\biggl( \frac{z}{\alpha _{n}}, \frac{y}{\beta _{m}}\biggr) \\ &\qquad {} \times \int _{0}^{\infty } \int _{0}^{\infty }S_{n,m,k,j}\biggl( \frac{t}{\alpha _{n}},\frac{s}{\beta _{m}}\biggr) \bigl[ \mu (z,s_{0})+ \mu (t_{0},y)-\mu (t_{0},s_{0}) \bigr]\,dt_{0}\,ds_{0}. \end{aligned}$$

(3.4)

It is clear that the operators given by (3.4) are positive and linear.

Now, with the help of the mixed modulus of continuity, we will estimate the degree of approximation of operators (3.4).

Theorem 3.1

Let $\mu \in C_{b}(I_{cd})$. Then for each $(z,y)\in I_{cd}$ and $n,m\in \mathbb{N}$, we arrive

$$ \bigl\vert G_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \leq 8 \omega _{\mathrm{mixed}} \Bigl( \mu ;\sqrt{\alpha _{n}^{2}/n}, \sqrt{\beta _{m}^{2}/m} \Bigr) . $$

Proof

In view of (3.3), we get

$$\begin{aligned} \bigl\vert \phi _{(t_{0},s_{0})}\mu (z,y) \bigr\vert & \leq \omega _{\mathrm{mixed}} \bigl( \mu ; \vert t_{0}-z \vert , \vert s_{0}-y \vert \bigr) \\ & \leq \biggl( 1+\frac{ \vert t_{0}-z \vert }{\delta _{1}} \biggr) \biggl( 1+ \frac{ \vert s_{0}-y \vert }{\delta _{2}} \biggr) \omega _{\mathrm{mixed}} ( \mu ;\delta _{1},\delta _{2} ), \end{aligned}$$

(3.5)

where $(z,y),(t_{0},s_{0})\in I_{cd}$, and $\delta _{1},\delta _{2}\in \mathbb{R} ^{+}$.

From (3.1), it is clear that

$$ G_{n,m}(\mu ;z,y)-\mu (z,y)=-R_{n,m}\bigl(\phi _{(t_{0},s_{0})}\mu (z,y);z,y\bigr). $$

(3.6)

Utilizing the Cauchy–Schwarz inequality to (3.6) and using (3.5) and Lemma 2.2 yield

$$\begin{aligned} & \bigl\vert G_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \\ &\quad \leq R_{n,m}\bigl( \bigl\vert \phi _{(t_{0},s_{0})}\mu (z,y) \bigr\vert ;z,y\bigr) \\ & \quad \leq \biggl( R_{n,m}(e_{0,0};z,y)+\delta _{1}^{-1} \sqrt{R_{n,m} \bigl( (t_{0}-z)^{2};z,y \bigr) }+\delta _{2}^{-1} \sqrt{R_{n,m} \bigl( (s_{0}-y)^{2};z,y \bigr) } \\ &\qquad {} + \frac{1}{\delta _{1}\delta _{2}} \sqrt{R_{n,m} \bigl( (t_{0}-z)^{2};z,y \bigr) R_{n,m} \bigl( (s_{0}-y)^{2};z,y \bigr) } \biggr) \omega _{\mathrm{mixed}} ( \mu ;\delta _{1},\delta _{2} ) . \end{aligned}$$

Using Lemma 2.4 and choosing $\delta _{1}=\sqrt{\alpha _{n}^{2}/n}$ and $\delta _{2}=\sqrt{\beta _{m}^{2}/m}$, we obtain the proof. □

The next result gives the order of convergence of operators (3.4) in connection with the Lipschitz type class.

Theorem 3.2

Let $\mu \in \operatorname{Lip}_{L}(\varphi _{1},\varphi _{2})$. For any $(z,y)\in I_{cd}$, $L>0$ and $\varphi _{1},\varphi _{2}\in ( 0,1 ]$, we derive

$$ \bigl\vert G_{n,m}(\mu ;z,y)-\mu (x,y) \bigr\vert \leq L \bigl( \delta _{n}(z) \bigr) ^{\frac{\varphi _{1}}{2}} \bigl( \delta _{m}(y) \bigr) ^{\frac{\varphi _{2}}{2}},$$

where $\delta _{n}(z)$ and $\delta _{m}(y)$ are given as in Theorem 2.6.

Proof

From (3.6), we get

$$\begin{aligned} \bigl\vert G_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert & \leq R_{n,m} \bigl( \bigl\vert \phi _{(t_{0},s_{0})}\mu (z,y) \bigr\vert ;z,y \bigr) \\ & \leq LR_{n,m} \bigl( \vert t_{0}-z \vert ^{\varphi _{1}} \vert s_{0}-y \vert ^{\varphi _{2}};z,y \bigr) \\ & =LR_{n,m} \bigl( \vert t_{0}-z \vert ^{\varphi _{1}};z,y \bigr) R_{n,m} \bigl( \vert s_{0}-y \vert ^{\varphi _{2}};z,y \bigr) . \end{aligned}$$

Utilizing the Hölder’s inequality with $( p_{1},q_{1} ) = ( \frac{2}{\varphi _{1}}, \frac{2}{2-\varphi _{1}} )$, $( p_{2},q_{2} ) = ( \frac{2}{\varphi _{2}}, \frac{2}{2-\varphi _{2}} )$ and Lemma 2.2, we derive

$$\begin{aligned} \bigl\vert G_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \leq {}&L \bigl( R_{n,m} \bigl( (t_{0}-z)^{2};z,y \bigr) ^{\frac{\varphi _{1}}{2}}R_{n,m} ( e_{0,0};z,y ) ^{\frac{2-\varphi _{1}}{2}} \\ & {}\times R_{n,m} \bigl( (s_{0}-y)^{2};z,y \bigr) ^{ \frac{\varphi _{2}}{2}}R_{n,m} ( e_{0,0};z,y ) ^{ \frac{2-\varphi _{2}}{2}} \bigr) \\ \leq{}& L \bigl( \delta _{n}(z) \bigr) ^{ \frac{\varphi _{1}}{2}} \bigl( \delta _{m}(y) \bigr) ^{ \frac{\varphi _{2}}{2}}. \end{aligned}$$

Hence, the proof is complete. □

Theorem 3.3

Let $\mu \in D_{b}(I_{cd})$ with $D_{B}\mu \in B(I_{cd})$ (the set of every bounded function on $I_{cd}$). There exists a constant $C>0$ such that for all $(z,y)\in I_{cd}$, one has

$$ \bigl\vert G_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \leq C \sqrt {\frac{\alpha _{n}^{2}}{n}\frac{\beta _{m}^{2}}{m}} \biggl( \Vert D_{B} \mu \Vert _{\infty }+\omega _{\mathrm{mixed}}\biggl(D_{B}\mu ; \sqrt{\frac{\alpha _{n}^{2}}{n}},\sqrt{\frac{\beta _{m}^{2}}{m}}\biggr) \biggr). $$

Proof

For $\mu \in D_{b}(I_{cd})$, we get

$$ \phi _{(t_{0},s_{0})}\mu (z,y)=(z-t_{0}) (y-s_{0})D_{B} \mu (u,v),\quad (t_{0}< u< z \text{ and }s_{0}< v< y), $$

see details in [39]. Therefore,

$$ D_{B}\mu (u,v)=\phi _{(t_{0},s_{0})}D_{B}\mu (u,v)+D_{B}\mu (u,y)+D_{B} \mu (z,v)-D_{B}\mu (z,y). $$

(3.7)

Since $D_{B}\mu \in B(I_{cd})$, then using (3.7), we may write

$$\begin{aligned} & \bigl\vert R_{n,m} \bigl( \phi _{(t_{0},s_{0})}\mu (z,y);z,y \bigr) \bigr\vert \\ &\quad = \bigl\vert R_{n,m}\bigl((z-t_{0}) (y-s_{0})D_{B} \mu (u,v);z,y\bigr) \bigr\vert \\ &\quad \leq R_{n,m}\bigl( \vert z-t_{0} \vert \vert y-s_{0} \vert \bigl\vert D_{B}\mu (u,v) \bigr\vert ;z,y\bigr) \\ &\qquad {} +R_{n,m}( \vert z-t_{0} \vert \vert y-s_{0} \vert \bigl( \bigl\vert D_{B}\mu (u,y) \bigr\vert + \bigl\vert D_{B}\mu (z,v) \bigr\vert + \bigl\vert D_{B}\mu (z,y) \bigr\vert ;z,y\bigr) \\ &\quad \leq R_{n,m}\bigl( \vert z-t_{0} \vert \vert y-s_{0} \vert \omega _{\mathrm{mixed}} \bigl( D_{B}\mu ; \vert u-z \vert , \vert v-y \vert \bigr) ;z,y\bigr) \\ & \qquad {}+3 \Vert D_{B}\mu \Vert _{\infty }R_{n,m}\bigl( \vert z-t_{0} \vert \vert y-s_{0} \vert ;z,y\bigr). \end{aligned}$$

(3.8)

From (3.3), we get

$$\begin{aligned} & \omega _{\mathrm{mixed}} \bigl( D_{B}\mu ; \vert u-z \vert , \vert v-y \vert \bigr) \\ &\quad =\omega _{\mathrm{mixed}} \bigl( D_{B} \mu ; \vert t_{0}-z \vert , \vert s_{0}-y \vert \bigr) \\ &\quad \leq \biggl( 1+\frac{1}{\gamma _{n}} \vert t_{0}-z \vert \biggr) \biggl( 1+\frac{1}{\gamma _{m}} \vert s_{0}-y \vert \biggr) \omega _{\mathrm{mixed}} ( D_{B}\mu ;\gamma _{n}, \gamma _{m} ). \end{aligned}$$

(3.9)

Taking into account (3.8) and (3.9) and utilizing the Cauchy–Schwarz inequality, we get

$$\begin{aligned} & \bigl\vert G_{n,m}(\mu ;z,y)-\mu (z,y) \bigr\vert \\ &\quad = \bigl\vert R_{n,m} \bigl( \phi _{(t_{0},s_{0})}\mu (z,y);z,y \bigr) \bigr\vert \\ &\quad \leq 3 \Vert D_{B}\mu \Vert _{\infty } \sqrt{R_{n,m}\bigl((z-t_{0})^{2}(y-s_{0})^{2};z,y \bigr)} \\ &\qquad {} + \biggl[ R_{n,m}\bigl( \vert z-t_{0} \vert \vert y-s_{0} \vert ;z,y\bigr)+\frac{1}{\gamma _{n}}R_{n,m} \bigl((z-t_{0})^{2} \vert y-s_{0} \vert ;z,y \bigr) \\ &\qquad {} + \frac{1}{\gamma _{m}}R_{n,m}\bigl( \vert z-t_{0} \vert (y-s_{0})^{2};z,y\bigr) \\ &\qquad {} +\frac{1}{\gamma _{n}\gamma _{m}}R_{n,m}\bigl((z-t_{0})^{2}(y-s_{0})^{2};z,y \bigr) \biggr] \omega _{\mathrm{mixed}} ( D_{B}\mu ;\gamma _{n}, \gamma _{m} ) \\ &\quad \leq 3 \Vert D_{B}\mu \Vert _{\infty } \sqrt{R_{n,m}\bigl((z-t_{0})^{2}(y-s_{0})^{2};z,y \bigr)} \\ &\qquad {} + \biggl[ \sqrt{R_{n,m}\bigl((z-t_{0})^{2}(y-s_{0})^{2};z,y \bigr)}+ \frac{1}{\gamma _{n}}\sqrt{R_{n,m}\bigl((z-t_{0})^{4}(y-s_{0})^{2};z,y \bigr)} \\ & \qquad {} +\frac{1}{\gamma _{m}} \sqrt{R_{n,m}\bigl((z-t_{0})^{2}(y-s_{0})^{4};z,y \bigr)} \\ & \qquad {} +\frac{1}{\gamma _{n}\gamma _{m}}R_{n,m}\bigl((z-t_{0})^{2}(y-s_{0})^{2};z,y \bigr) \biggr] \omega _{\mathrm{mixed}} ( D_{B}\mu ;\gamma _{n}, \gamma _{m} ) . \end{aligned}$$

Moreover, for $(t_{0},s_{0}),(z,y)\in I_{cd}$ and $\alpha ,\beta \in \{ 1,2 \}$, we have

$$ R_{n,m}\bigl((z-t_{0})^{2\alpha }(y-s_{0})^{2\beta };z,y \bigr)=R_{n,m}\bigl((z-t_{0})^{2 \alpha };z,y\bigr)\times R_{n,m}\bigl((y-s_{0})^{2\beta };z,y\bigr). $$

From Lemma 2.4, choosing $\gamma _{n}=\sqrt{\frac{\alpha _{n}^{2}}{n}}$, $\gamma _{m}=\sqrt{\frac{\beta _{m}^{2}}{m}}$ and taking the assumptions for the sequences $(\alpha _{n})$, $(\beta _{m})$ in (2.2), we have the desired result. □

4 Graphics and error estimation tables

In this section, with the help of Maple software, we compare the convergence of operators (2.1) and (3.4) to the certain functions $\mu (z,y)$.

Example 4.1

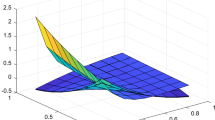
Let $\mu (z,y)=y^{2}e^{-\frac{z}{3}}$ (yellow). In Fig. 1, we illustrate the convergence of operators (2.1) to $\mu (z,y)=y^{2}e^{-\frac{z}{3}}$ for ${n,m}=5$ (red), ${n,m}=10$ (blue), ${n,m}=30$ (green), $\alpha _{n}=\ln (n+1)$ and $\beta _{m}=\ln (m+1)$. In Table 1, we also estimate the error estimation of operators (2.1) to $\mu (z,y)$ for $n,m=20,50,150$, respectively.

Figure 1

The convergence of operators $R_{n,m}$ to $\mu (z,y)=y^{2}e^{-\frac{z}{3}}$ (yellow) for ${n=m}=5$ (red), ${n=m}=10$ (blue), ${n=m}=30$ (green)

Table 1 Error of approximation of the operators $R_{n,m}$ to $\mu (z,y)=y^{2}e^{-\frac{z}{3}}$ for $n=m=20,50,150$

Figure 1 clearly shows that since the values of n, m increase, the order of convergence of operators (2.1) to $\mu (z,y)$ becomes better. Further, from Table 1, it is obvious that as the values of n, m are increasing, the absolute difference between operators (2.1) and $\mu (z,y)=y^{2}e^{-\frac{z}{3}}$ is decreasing.

Example 4.2

Let $\mu (z,y)=\frac{3}{2}-zye^{-\frac{y}{2}}$ (yellow). In Fig. 2, we compare the convergence of operators (2.1) (green) and (3.4) (purple) to the function $\mu (z,y)=\frac{3}{2}-zye^{-\frac{y}{2}}$ with ${n,m}=10$ and $\alpha _{n}=\sqrt[3]{n}$, $\beta _{m}=\sqrt[3]{m}$. Also, in Table 2, we compute the error estimation of operators (2.1) and (3.4) to $\mu (z,y)$ for $n=m=35$ and certain values of $0\leq z,y\leq 2$.

Figure 2

The convergence of operators $R_{n,m}$ (green) and $G_{n,m}$ (purple) to $\mu (z,y)=\frac{3}{2}-zye^{-\frac{y}{2}}$ (yellow) for ${n=m}=10$

Table 2 Error of approximation of the operators $R_{n,m}$ and $G_{n,m}$ to $\mu (z,y)=\frac{3}{2}-zye^{-\frac{y}{2}}$ for ${n=m}=35$

If Fig. 2 and Table 2 are analyzed in detail, it becomes obvious that the GBS type operators (3.4) are approximated much better than operators (2.1).