Abstract
In this paper we investigate an interesting subclass \(\mathcal {BS}(\alpha )\) (\(0\le \alpha <1\)) of starlike functions in the unit disc \(\Delta\). The class \(\mathcal {BS}(\alpha )\) was introduced by Kargar et al. (Anal Math Phys, 2017. https://doi.org/10.1007/s13324-017-0187-3) which is strongly related to the Booth lemniscate. Some geometric properties of this class of analytic functions, including radius of starlikeness of order \(\gamma\) (\(0\le \gamma <1\)), the image of \(f(\{z:|z|<r\})\) when \(f\in \mathcal {BS}(\alpha )\), an special example and estimate of bounds for \(\mathrm{Re}\{f(z)/z\}\), are studied.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \({\mathcal {H}}\) denote the class of analytic functions in the open unit disc \(\Delta = \{z\in {\mathbb {C}} : |z| < 1\}\) on the complex plane \({\mathbb {C}}\). Also let \({\mathcal {A}}\) denote the subclass of \({\mathcal {H}}\) including of functions normalized by \(f(0)=f'(0)-1=0\). The subclass of \({\mathcal {A}}\) that consists of all univalent functions f(z) in \(\Delta\) is denoted by \({\mathcal {S}}\). We denote by \({\mathfrak {B}}\) the class of functions w(z) analytic in \(\Delta\) with \(w(0) = 0\) and \(|w(z)| < 1\), \((z \in \Delta )\). For two analytic and normalized functions f and g, we say that f is subordinate to g, written \(f \prec g\) in \(\Delta\), if there exists a function \(w\in {\mathfrak {B}}\) such that \(f (z) = g(w(z))\) for all \(z\in \Delta\). In special case, if the function g is univalent in \(\Delta\), then
It is easy to see that for any complex numbers \(\lambda \ne 0\) and \(\mu\), we have:
The set of all functions \(f\in {\mathcal {A}}\) that are starlike univalent in \(\Delta\) will be denoted by \({\mathcal {S}}^*\) and the set of all functions \(f\in {\mathcal {A}}\) that are convex univalent in \(\Delta\) will be denoted by \({\mathcal {K}}\). Robertson (see Robertson 1985) introduced and studied the class \({\mathcal {S}}^*(\gamma )\) of starlike functions of order \(\gamma \le 1\) as follows
We note that if \(\gamma \in [0,1)\), then a function in \({\mathcal {S}}^*(\gamma )\) is univalent. Also we say that \(f\in {\mathcal {K}}(\gamma )\) (the class of convex functions of order \(\gamma\)) if and only if \(zf'(z)\in {\mathcal {S}}^*(\gamma )\). In particular we put \({\mathcal {S}}^*(0)\equiv {\mathcal {S}}^*\) and \({\mathcal {K}}(0)\equiv {\mathcal {K}}\).
Recently, Kargar et al. (2017) introduced and studied a class functions related to the Booth lemniscate as follows.
Definition 1.1
(see Kargar et al. 2017) The function \(f\in {\mathcal {A}}\) belongs to the class \(\mathcal {BS}(\alpha )\), \(0\le \alpha <1\), if it satisfies the condition
Recall that (Piejko and Sokół 2013), a one-parameter family of functions given by
are starlike univalent when \(0\le \alpha \le 1\) and are convex for \(0 \le \alpha \le 3-2\sqrt{2}\approx 0.1715\). We have also \(F_{\alpha }(\Delta )=D(\alpha )\), where
and
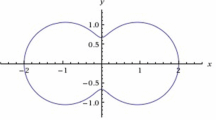
It is clear that the curve
is the Booth lemniscate of elliptic type (see Fig. 1, for \(\alpha =1/3\)). For more details, see Kargar et al. (2017).
Lemma 1.1
(see Kargar et al. 2017) Let\(F_{\alpha }(z)\)be given by (1.3). Then for\(0\le \alpha <1\), we have
Therefore by definition of subordination and by Lemma 1.1, \(f\in {\mathcal {A}}\) belongs to the class \(\mathcal {BS}(\alpha )\), if it satisfies the condition
The following lemma will be useful.
Lemma 1.2
(see Ruscheweyh and Stankiewicz 1985) Let\(F,G\in {\mathcal {H}}\)be any convex univalent functions in\(\Delta\). If\(f\prec F\)and\(g\prec G\), then
In this work, some geometric properties of the class \(\mathcal {BS}(\alpha )\) are investigated.
2 Main Results
We start with the following lemma that gives the structural formula for the function of the considered class.
Lemma 2.1
The function\(f\in {\mathcal {A}}\)belongs to the class\(\mathcal {BS}(\alpha )\), \(0\le \alpha <1\), if and only if there exists an analytic functionq, \(q(0)=0\)and\(q\prec {F_{\alpha }}\)such that
The proof is easy. Putting \(q={F_{\alpha }}\) in Lemma 2.1 we obtain the function
which is extremal function for several problems in the class \(\mathcal {BS}(\alpha )\). Moreover, we consider
From (1.7) we conclude that \(f \in \mathcal {BS}(\alpha )\) is starlike of order \(\frac{\alpha }{\alpha -1} < 0,\) hence f may not be univalent in \(\Delta\). It may therefore be interesting to consider a problem to find the radius of starlikeness of order \(\gamma\), \(\gamma \in [0,1)\) (hence univalence) of the class \(\mathcal {BS}(\alpha )\), i.e. the largest radius \(r_s(\alpha ,\gamma )\) such that each function \(f \in \mathcal {BS}(\alpha )\) is starlike of order \(\gamma\) in the disc \(|z|< r_s(\alpha ,\gamma )\). For this purpose we recall the following property of the class \({\mathfrak {B}}.\)
Lemma 2.2
(Schwarz lemma) (see Duren 1983) Letwbe analytic in the unit disc\(\Delta\), with\(w(0)=0\)and\(|w(z)|<1\)in\(\Delta .\)Then\(|w'(0)|\le 1\)and\(|w(z)|\le |z|\)in\(\Delta .\)Strict inequality holds in both estimates unlesswis a rotation of the disc:\(w(z)=e^{i\theta }z.\)
Theorem 2.1
Let\(\alpha \in (0,1)\)and\(\gamma \in [0,1)\)be given numbers. If\(f\in \mathcal {BS}(\alpha )\), thenfis starlike of order\(\gamma\)in the disc\(|z|< r_s(\alpha ,\gamma )=\frac{\sqrt{1+4\alpha (1-\gamma )}-1}{2\alpha (1-\gamma )}.\)The result is sharp.
Proof
Let \(f\in \mathcal {BS}(\alpha ),\)\(\alpha \in (0,1).\) Then through (1.2) we have \(\left( \frac{zf'(z)}{f(z)}-1\right) \prec \frac{z}{1-\alpha z^2}\) so there exists \(w\in {\mathfrak {B}}\) such that
for all \(z\in \Delta\). Applying the Schwarz lemma we obtain
where \(r=|z|<1\). Let us consider a function \(h(r)=1-\frac{r}{1-\alpha r^2},\)\(r \in (0,1).\) Note that \(h'(r)=-\frac{1+\alpha r^2}{(1-\alpha r^2)^2}<0\) for all \(r \in [0,1)\) hence h is a strictly decreasing function and it decreases from 1 to \(\frac{\alpha }{\alpha -1}<0.\) Therefore the equation \(h(r)=\gamma\) has for given \(\alpha\) and \(\gamma\) the smallest positive root \(r_s(\alpha ,\gamma )\) in (0, 1). Therefore f is starlike of order \(\gamma\) in \(|z|<r\le r_s(\alpha ,\gamma )\). Note that for the function \({\tilde{f}}\) given in (2.2) we obtain
and \(A(-r_s(\alpha ,\gamma ))=\gamma\). \(\square\)
Putting \(\gamma =0\) in Theorem 2.1, we obtain.
Corollary 2.1
Let\(\alpha \in (0,1)\). If\(f\in \mathcal {BS}(\alpha )\)thenfis starlike univalent in the disc\(|z|< r_s(\alpha )=\frac{\sqrt{1+4\alpha }-1}{2\alpha }\). The result is sharp.
Remark 2.1
Note that \(\lim _{\alpha \longrightarrow 0^+} r_s(\alpha )= \lim _{\alpha \longrightarrow 0^+} \frac{2}{\sqrt{1+4\alpha }+1}=1.\) Moreover, it is worth mentioning that \(\lim _{\alpha \longrightarrow 1^-} r_s(\alpha )=\frac{\sqrt{5}-1}{2}= 0,618\dots\), i.e. this limit is a reciprocal of the golden ratio \(\frac{\sqrt{5}+1}{2}.\)
Now we consider the following question:
For a given number \(r \in (0,1]\) find \(\alpha (r)\) such that for each function \(f\in \mathcal {BS}(\alpha (r))\) the image \(f(\{z:|z|<r\})\) is a starlike domain.
Theorem 2.2
Let\(r \in (0,1]\)be the given number. If \(0\le \alpha < \frac{1-r}{r^2}\), then each function\(f\in \mathcal {BS}(\alpha )\)maps a disc\(|z|<r\)onto a starlike domain.
Proof
After using the same argument as in the proof of Theorem 2.1 we conclude that \(f \in \mathcal {BS}(\alpha )\) satisfies the equality
for all \(z \in \Delta\) with some \(w\in {\mathfrak {B}}\). Then we have by Schwarz’s lemma that
Consequently, for \(|z|<r\), we obtain \(\mathrm{Re} \left\{ \frac{zf'(z)}{f(z)}\right\} >1-\frac{r}{1-\alpha r^2}.\) Let us note that a function \(g(\alpha )=1-\frac{r}{1-\alpha r^2},\)\(\alpha \in [0,1),\) has positive values for \(0\le \alpha < \frac{1-r}{r^2}\). Therefore the image of the disc \(|z|<r\) is a starlike domain. \(\square\)
Theorem 2.3
Let\(n\ge 2\)be integer. If one of the following conditions holds
- (i):
-
\(\frac{1}{\alpha +n(1-\alpha )}< |c|<1,\)
- (ii):
-
\(n > \frac{3-\alpha }{1-\alpha }\) and \(\frac{1}{\alpha -2+n(1-\alpha )}< |c|<1,\)
- (iii):
-
\(n\ge \frac{2-\alpha }{1-\alpha }\) and \(|c|>1,\)
- (iv):
-
\(n<\frac{2-\alpha }{1-\alpha }\) and \(1<|c|<\frac{1}{2-\alpha +n(\alpha -1)},\)
then the function\(g_n(z)=z+cz^n\)does not belong to the class\(\mathcal {BS}(\alpha )\).
Proof
Let us put \(G(z)=\frac{zg'_n(z)}{g_n(z)}-1=\frac{1+cnz^{n-1}}{1+cz^{n-1}}-1.\) To prove our assertion it suffices to show that the function G is not subordinate to \(F_{\alpha }\) or equivalently, because of the univalence of the dominant function \(F_{\alpha }\), that the set \(G(\Delta )\) is not included in \(F_{\alpha }(\Delta )=D(\alpha ).\) Upon performing simple calculation we find that the set \(G(\Delta )\) is the disc with the diameter from the point \(x_1=\frac{|c|(n-1)}{|c|-1}\) to the point \(x_2=\frac{|c|(n-1)}{|c|+1}.\) The set \(D(\alpha )\) is bounded by the curve
We have \(\min _{|z|=1}\mathrm{Re}\{F_{\alpha }(z)\}=F_{\alpha }(-1)=\frac{1}{\alpha -1}\) and \(\max _{|z|=1}\mathrm{Re}\{F_{\alpha }(z)\}=F_{\alpha }(1)=\frac{1}{1-\alpha }.\) If one of the conditions \((i)-(iv)\) is satisfied then \(\min \{x_1,x_2\}<\frac{1}{\alpha -1}\) or \(\max \{x_1,x_2\}>\frac{1}{1-\alpha },\) and then \(G(\Delta )\) is not included in \(D(\alpha ).\) The proof of theorem is completed. \(\square\)
Recently, one of the interesting problems for mathematician is to find bounds for \(\mathrm{Re}\{f(z)/z\}\) (see Kargar et al. 2016; Sim and Kwon 2013). In the sequel, we obtain lower and upper bounds for \(\mathrm{Re}\{f(z)/z\}\). We first get the following result for the function F(z) given by (2.3).
Theorem 2.4
The functionF(z) of the form (2.3) is convex univalent in\(\Delta\).
Proof
A simple calculation gives us
It is sufficient to show that (2.4) has positive real part in the unit disc. From Lemma 1.1 we obtain
It is easily seen that \(K'(\alpha )=\frac{1}{(\alpha -1)^2}>0\). Thus \(K(\alpha )\ge K(0)=0\), and hence F(z) is convex univalent function. \(\square\)
In the proof of the next theorem we will use the following result concerning the convexity of the boundary of \(D(\alpha )\).
Lemma 2.3
(see Piejko and Sokół 2013) Suppose that\(F_\alpha\)is given by (1.3). If \(0 \le \alpha \le 3-2\sqrt{2}\approx 0.1715\), then the curve\(F_\alpha (e^{i\varphi })\), \(\varphi \in [0,2\pi )\), is convex. If \(\alpha \in (3-2\sqrt{2},1)\), then the curve\(F_\alpha (e^{i\varphi })\), \(\varphi \in [0,2\pi )\), is concave.Moreover, in both cases this curve is symmetric with respect to both axes.
Theorem 2.5
If a functionfbelongs to the class\(\mathcal {BS}(\alpha )\), \(0 \le \alpha \le 3-2\sqrt{2}\), then
whereF(z) is given by (2.3).
Proof
Let \(0 \le \alpha \le 3-2\sqrt{2}\) and let f be in the class \(\mathcal {BS}(\alpha )\). Then we have
where \(F_\alpha\) is given by (1.3). It is well known that the normalized function
belongs to the class \({\mathcal {K}}\) and for \(f\in {\mathcal {A}}\) we get
By Lemma 2.3 we deduce that the function \(F_\alpha\) is convex. Thus applying Lemma 1.2 in (2.6) we obtain
Now from (2.7) and (2.8), we can obtain
Thus
This completes the proof of theorem. \(\square\)
Here by combining Theorem 2.4, Theorem 2.5 and (1.1), we get:
Theorem 2.6
Let \(f\in \mathcal {BS}(\alpha )\), \(0 \le \alpha \le 3-2\sqrt{2}\)and\(|z|=r<1\). Then
The result is sharp.
Proof
By the subordination principle, we have:
From Theorem 2.4, since F(z) is convex univalent in \(\Delta\), and it is real for real z, thus it maps the disc \(|z|=r<1\) onto a convex set symmetric which respect to the real axis laying between \(F(-r)-1\) and \(F(r)-1\). Now the assertion is obtained from Theorem 2.5. \(\square\)
References
Duren PL (1983) Univalent functions. Springer, Berlin
Kargar R, Ebadian A, Sokół J (2016) On subordination of some analytic functions. Sib Math J 57:599–604
Kargar R, Ebadian A, Sokół J (2017) On Booth lemniscate and starlike functions. Anal Math Phys. https://doi.org/10.1007/s13324-017-0187-3
Piejko K, Sokół J (2013) Hadamard product of analytic functions and some special regions and curves. J Inequal Appl 2013:420
Robertson MS (1985) Certain classes of starlike functions. Mich Math J 32:135–140
Ruscheweyh St, Stankiewicz J (1985) Subordination under convex univalent function. Bull Pol Acad Sci Math 33:499–502
Sim YJ, Kwon OS (2013) Notes on analytic functions with a bounded positive real part. J Inequal Appl 2013:370. https://doi.org/10.1186/1029-242X-2013-370
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kargar, R., Ebadian, A. & Trojnar-Spelina, L. Further Results for Starlike Functions Related with Booth Lemniscate. Iran J Sci Technol Trans Sci 43, 1235–1238 (2019). https://doi.org/10.1007/s40995-018-0588-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40995-018-0588-7