1 Introduction

Bulk metallic glasses (BMGs) combine high strength and hardness with an elastic limit of up to 2% [1]. These properties make them attractive for highly stressed applications. To obtain a glassy metal and prevent the formation of a crystalline structure the liquid phase must be cooled rapidly. In casting, the lowest cooling rate at which crystallization does not occur is called the critical cooling rate (CCR) [2]. It is roughly in a range between 1 and 100 K/s for Zr-based BMGs [3]. The CCR inherently limits the size of components manufactured through casting. These limitations can be overcome with additive manufacturing (AM) techniques such as laser powder bed fusion of metals (PBF-LB/M) [4, 5]. The layer-by-layer approach, along with localized laser-energy input, creates very small melt pools, ensuring large cooling rates of up to 106 K/s [6, 7]. The freedom of design enables the production of large and complex geometries, such as lattice structures [8, 9], topologically optimized structures [4], or compliant mechanisms [10], which is an innovation for BMGs. However, the quality of additively manufactured BMGs is still challenged by factors such as porosity, (nano-) crystallization, and structural relaxation, which can strongly affect their mechanical performance [11,12,13,14,15]. Despite the presence of high cooling rates, there is still a possibility that partial or complete crystallization may occur due to low glass-forming ability (GFA) or unfavorable processing conditions [16,17,18]. Currently Zr-based BMGs, such as Zr59.3Cu28.8Al10.4Nb1.5 (tradename Zr01, former AMZ4) [19], are predominantly established for PBF-LB/M. Here, additively manufactured samples can achieve the yield strength of high-purity cast material [12, 20, 21]. However, it is important to note that Zr-based BMGs have a high oxygen affinity. Due to the unfavorable surface-to-volume ratio, higher oxygen levels within the powder feedstock compared to cast materials are inevitable [22]. Oxygen is well-known to trigger nucleation and crystallization, which drastically increases the CCR of AMZ4 from roughly 6 K/s (high purity) [23] up to 1.4 × 104 K/s [24]. This eventually deteriorates the process stability and part quality [12, 25]. Therefore, robust alloy compositions are desirable for a broader establishment of BMGs through AM. A promising extension of the current BMG selection for PBF-LB/M is the Cu–Ti-based alloy, Cu47Ti34Zr11Ni8 (Vit101) [26], due to its higher strength and lower material cost [27]. Although it exhibits a lower GFA in casting, its distinctive performance makes it a notable choice. Albeit, especially in view of lowered GFAs, a thorough understanding of the actual thermal cycling during PBF-LB/M is necessitated to ensure an amorphous structure of the part.

In this matter, thermal simulations of the processing of BMGs by PBF-LB/M can provide important insights into the solidification behavior, including devitrification in the heat-affected zone (HAZ). Such simulations are typically performed at different scale levels, distinguished by their geometric magnitude. The most common subdivisions are part [28], layer [29], and melt-pool [30] simulations. At the macroscopic part level, the structure of an entire geometry is modeled and examined in terms of the temperature distribution within the component [28]. Mesoscale layer models usually focus on representing the exposure of single layers or laser tracks [29]. Finally, the melt pool itself can also be simulated, which typically involves considerations of fluid dynamics [30]. The replication of the PBF-LB/M process through a numerical model requires the simplification or neglect of scale-dependent physical phenomena. Input parameters such as material properties can be subject to uncertainties, which makes calibration an important step in the development of a valid model [31]. Lindwall et al. developed numerical models, analyzing the processing of AMZ4 at different scale levels [32, 33]. In a macroscopic approach [32], the energy was simultaneously introduced onto the entire surface. The prediction of crystallization is implemented through a phase model and based on thermal history. This approach was calibrated by determining the released heat by the devitrification through differential scanning calorimetry (DSC) measurements of suction cast samples. In a mesoscopic simulation of multiple remelting of a single laser track, Lindwall et al. were able to successfully simulate crystallization within the HAZ [33]. The results were then verified using scanning electron microscope (SEM) and transmission electron microscopy (TEM) images of additively manufactured samples. Yang et al. employed an alternative method to verify the results of a mesoscopic multi-single-track remelting simulation by comparing them with a physical specimen made from AMZ4 [34]. Their analysis focused on the micromechanical characteristics of the HAZ and its adjacent regions. Utilizing nanoindentation, they successfully discerned the crystalline segment of the HAZ based on its elevated hardness and Young's modulus in comparison to the amorphous surrounding. These calibration and validation approaches focus primarily on the crystalline/amorphous ratio and the location of the devitrification based on time–temperature-transformation (TTT) diagrams, which are not yet available for Vit101. Given the CCR of BMGs, the temperature during solidification is also of particular importance and should be considered as a calibration factor. Especially in terms of process monitoring, utilizing the temperature appears to be a potent method.

A potential approach for measuring temperature in-situ at high frequencies is using high-speed pyrometry. For quality assurance purposes, pyrometers are commercially integrated coaxially into the scanning system of a PBF-LB/M machine by separating the temperature radiation to be examined from the laser beam using filter and mirror systems [35, 36]. In this way the measuring spot is coupled to the moving laser beam, so that the temperature of the melt pool can be monitored by the pyrometer. Hence, it is typically not possible to determine the cooling cycles after the laser passed. Opposed to that, a static off-axis integration allows to investigate the full thermal history of a fixed point. This makes it a feasible choice for acquiring temperature profiles to calibrate a numerical simulation.

Since the thermal history during PBF-LB/M processing remains the key aspect for predictive parameter and process development, this study focuses on a method to calibrate the thermal simulation of the PBF-LB/M process. In this matter, the thermal profiles of single laser scan tracks were measured and simulated using off-axis high-speed pyrometry as well as a thermal finite element method (FEM) model and subsequently compared with the resulting scan track morphologies.

2 Materials and methods

2.1 Experimental setup

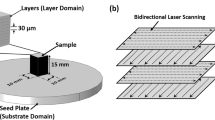
The measurements were carried out on a SLM 280HL PBF-LB/M system with a Sensortherm METIS H322 high-speed ratio pyrometer, using a spectral emissivity value of 0.59 determined by Wegner in [37]. The pyrometer has a measuring range of 673 to 1473 K and a maximum measuring frequency of 25 kHz. The pyrometer lens is mounted at an angle of 30° to the z-axis on the ceiling of the build chamber and pointed at the build platform (Fig. 1).

Fig. 1
figure 1

The build chamber of the SLM 280HL machine equipped with a pyrometer lens mounted at an angle of 30° to the ceiling. A schematic representation illustrates the test geometry, including the scan strategy and placement of the measuring spot. In addition, a microscopic image provides an approximation of the resulting measuring spot size

Full size image

The optical fiber of the pyrometer is led out of the build chamber through a sealed cable gland. This integration results in an elliptical measuring spot with a width of about 0.35–0.5 mm and an aspect ratio of 1.16, centered on the surface of the substrate plate. To prepare a base layer made of Vit101, serving as a substrate for subsequent single tracks, a cuboid with a width of 3 mm and a length of 5 mm is built using Vit101 powder. The powder was supplied by the IWT Bremen and atomized as described in [38], resulting in a particle size range of 20–63 µm. Laser exposure was conducted under an argon atmosphere with an oxygen content below 0.01% using a layer height of 0.02 mm and a preheating temperature of 423 K. Using a scanning strategy identical for each layer, parallel vectors along the y-axis without contour exposure are employed. Although 80 W and 1600 mm/s showed good process stability and a relative density above 99.9% in a previous parameter study [39], to ensure a sufficient pyrometer signal, an elevated laser power of 160 W was chosen. The single track is placed in the center of the pyrometer spot and scanned after powder application. The emitted radiation is detected on a wavelength band of 1.45–1.65 µm using the pyrometer.

2.2 Numerical model

The FEM software COMSOL Multiphysics (Version 6.1) is used for the numerical implementation of the process. The sample geometry of the tests is transferred to the program for this purpose. Since particularly high temperature gradients are to be expected in the top layers, the upper three layers are represented separately and discretized with a finer 45 µm hexahedral mesh compared to the part below (Fig. 2).

Fig. 2
figure 2

The upper three layers of the geometry are discretized with a fine 45 µm hexahedral mesh due to the expected high temperature gradients. The mesh resembling the pyrometer spot was further refined to a maximal element size of 30 µm. The path of the heat source is marked by a blue line

Full size image

Further mesh refinement is applied where the measurement spot was located during the tests to improve the comparability of the experimentally determined and simulated values without significantly extending the computing time. Previous layers are assigned the thermal properties of the solid material (Fig. 3), while the top layer initially represents the properties of powder.

Fig. 3
figure 3

Thermal material properties used in the simulation with Tx marking the crystallization temperature. For simplification, the glass transition temperature was assumed to be equal to Tx. The heat capacity was sourced from Bochtler [27, 40], the thermal conductivity of the bulk material up to Tx from Schönrath et al. [41], and the thermal conductivity of the powder was determined using the transient hot-bridge method at room temperature, and extrapolated following the methodology of Ciew et al. [42]

Full size image

The heat-capacity data were sourced from Bochtler [27], combining DSC measured values up to the glass transition temperature and a subsequential fit according to Kubaschewski et al. [43]. Thermal conductivity was taken up to the glass transition temperature from Schönrath et al. [41]. At elevated temperatures, calculations were based on Lindwall's [44] assumption that density and thermal diffusivity remain constant in the undercooled liquid region, a concept extrapolated from AMZ4 to Vit101. The thermal conductivity of the powder was obtained through the transient hot-bridge method using a Linseis THB 100 at room temperature and extrapolated for higher temperatures following the methodology outlined by Chiew et al. [42]. Due to the low thermal conductivity of the metal powder in comparison to bulk material [45], the side surfaces of the specimen geometry are simplified as thermally isolated [32]. This means that heat losses only occur on the component surface. Laser energy is introduced onto the top layer by a moving heat source. The intensity follows a Gaussian distribution with a standard deviation corresponding to the laser radius of the PBF-LB/M machine. This form of energy input leads to a locally resolved heating of the uppermost layer and, if the liquidus temperature is exceeded, to an irreversible transformation of the powder into a solid material by overwriting the material properties. To establish the comparability between the simulated temperature curves with those measured during the experiments, an approximation of the pyrometer’s measurement method was included. Since the intensity of the laser beam corresponds to a Gaussian distribution and thus the energy input is not spatially uniformly resolved, the material is also not uniformly heated. Supplemented by the non-uniform cooling of the melt pool, caused by the continuous movement of the laser and the heating of the sample, the emission of a radiation mixture of the different temperatures within the measuring spot occurs. For this reason, an average temperature within the spot is calculated. The simulation was iteratively calibrated regarding the cooling behavior, which holds particular significance for the amorphous processing of BMGs due to their CCR. This calibration utilized the pyrometer temperature data from a single track at 1600 mm/s and 160 W by adjusting the absorption coefficient, ultimately yielding a value of 0.29, which is in good agreement with the empirical data on the absorption coefficient of 0.318 determined for Vit101 by Wegner in [37].

Both the measured and simulated temperature profiles initially show a rapid increase (Fig. 4). In the measured profile, this results in a plateau of 100 µs at 1473 K due to the measurement limit of the pyrometer. The simulated profile also exhibits a plateau of approximately 100 µs at 2532 K, but with a significant decrease in the heating rate preceding it. This behavior is attributed to the presence of the heat source within the measurement spot. Following the plateaus, both profiles show an exponential temperature decrease, with the simulated temperature trends toward 423 K while the measured data reach the lower measurement limit of the pyrometer before reaching a stable temperature.

Fig. 4
figure 4

The temperature measured by pyrometry (black) and simulated (gray) plotted over time. The gray-shaded areas indicate the measurement range limits of the pyrometer. An estimated progression of the pyrometer data beyond the lower detection limit is illustrated with an exponential fit. The dashed box symbolizes the area shown enlarged in the upper right corner

Full size image

Because of the low signal intensity due to the small measurement spot, the signal is susceptible to noise, especially at low temperatures (Fig. 4). To ensure comparability of the measured with the simulated values in this temperature range, the pyrometer temperature data were fitted accordingly (dashed line in Fig. 4). The time frame between heating and cooling multiplied by the scan speed corresponds to the spot size of the pyrometer. Based on this calculation, the measuring spot’s diameter is 0.45 mm, and is therefore in agreement with the simulation and the microscopic observation of the targeting laser (Fig. 1). The deviation in the heating behavior can be attributed to the inertia of the measuring system. The instantaneous rise in temperature caused by the laser entering the measuring spot cannot be sensed accurately by the pyrometer. This is due to its response time, which defines the time it takes for 90% of the signal of a sudden increase in temperature to be present at the output, limiting the temporal accuracy of the heating cycle. This limitation is not considered in the simulation; hence the average simulated heating rate is 3.9 times higher than the measured rate. Further measurement-related deviations occur due to the detection range of the pyrometer, which lies between 673 and 1473 K. For this reason, the simulated temperatures outside this range cannot be verified. The measured and simulated cooling phases are sufficiently consistent, whereby the average cooling rate of the simulation in the pyrometer measurement spectrum is 3.33 × 105 K/s, the average measured rate is 2.01 × 105 K/s. In the range above the glass transition temperature of 674 K [27], both the minimal simulated cooling rate at 6.17 × 104 K/s and the minimal measured rate of 7.35 × 104 K/s are above the nominal CCR of < 250 K/s [26]. However, it is important to note that the real CCR of the material could be elevated due to a higher oxygen content or other impurities. Nevertheless, the significantly higher observed cooling rate indicates that the devitrification of the material is not a result of the melt cooling down too slow. Instead, other mechanisms, such as the thermal conditions in the HAZ or cyclic reheating [33, 34] are of greater importance.

To assess the simulation's capability to accurately replicate reality, a validation process was conducted following calibration. Four additional scanning speeds (800, 1200, 1600, 2000 mm/s) were simulated at a constant laser power of 80 W to investigate parameter variations adjacent to the optimal settings found at 80 W and 1600 mm/s. The resulting melt-pool widths were compared with experimentally determined values (Fig. 5).

Fig. 5
figure 5

The measured and simulated melt-pool widths at 80 W are plotted over the scanning speeds of 800, 1200, 1600 and 2000 mm/s. The simulated melt-pool widths are indicated by gray, hollow circles, while the measured ones are represented by black, filled circles. Above each data point, a microscopic image of the melt track at the corresponding scanning speed is depicted

Full size image

In the simulation, the melt-pool widths were determined by the longest distance orthogonal to the direction of motion of the heat source, where the temperature exceeded the liquidus temperature of 1168 K [27].

By doubling the laser-scanning speed from 800 to 1600 mm/s, the measured melt-pool width shrank from 177 µm to 122 µm (Table 1), representing a decrease of 31%. A similar decrease of approximately 28% can be observed in the simulated widths.

Table 1 Measured and simulated melt-pool widths at different scanning speeds and a constant laser power of 80 W
Full size table

Across the scanning speeds from 800 to 1600 mm/s, the differences between measured and simulated widths are within a range of 0.47 to 3.17%, showing a speed dependent correlation. Notably, the highest deviation was calculated at a scanning speed of 2000 mm/s, reaching 14.16%. Microscopic observations revealed that at this high speed, the formation of a consistent melt track was not possible anymore. This is likely attributed to an insufficient energy density to form a stable melt track. The high scanning speed leads to a narrow scan track, which results in a decrease in the wetting ability, and the flowing and spreading characteristics become unfavorable, eventually resulting in plateau-rayleigh instabilities, also called the balling phenomenon [46]. As these phenomena are not implemented into the numerical model, the melt-pool width is overestimated for parameters resulting in balling. However, since the simulated results aligned well with the experimentally determined melt-pool widths for laser parameters resulting in a stable melt track, it can be inferred that the presented model can adequately represent the real process.

3 Conclusion

Single track experiments and simulations were conducted using the Cu–Ti-based BMG Vit101. The simulation underwent calibration regarding the cooling behavior based on pyrometry data. A consistent agreement in the measuring spot diameter of the pyrometer between experimental observation and simulation was observed. Notably, a good match was found in the cooling behavior across the temperature range of 673–1473 K, the detection range of the pyrometer used. It should be noted that the validation of the maximum temperatures achieved was constrained by the measurement range limitations of the pyrometer. Addressing this issue is an important aspect for future work. Nonetheless, the comparison of cooling rates between experimental measurements and simulations yielded favorable results. The minimum measured and simulated cooling rates above the glass transition temperature were in the range of 104 K/s and are therefore well above the critical cooling rate of Vit101. The validation process extended to the assessment of melt-pool widths, where a comparison was made between simulated results and microscopic imagery obtained from experiments for four different scanning speeds. A high degree of agreement in widths was observed for scan speeds below 2000 mm/s, with discrepancies ranging from 0.47 to 3.17%. Nevertheless, it is crucial to highlight that, at scan speeds exceeding 2000 mm/s, fluid dynamic effects dominate, leading to melt-pool disruptions and, consequently, higher deviations occur. Overall, these findings suggest that the presented simulation model effectively captures the cooling behavior and melt-pool dimensions of the laser processing of Vit101, particularly within specified energy–density ranges, offering valuable insights for further optimization and application.

Looking forward, the ongoing refinement of the numerical model presents two critical directions for further exploration. First, there is a need to validate temperatures exceeding 1473 K, considering the limitations of the current pyrometer measurement range. Exploring other wavelengths or measuring ranges will be essential to accurately predict and understand behaviors in higher temperature regimes similar to Yang et al. [18, 47]. However, this also requires fundamental knowledge of the TTT diagram obtainable through Flash DSC. Another crucial step involves the integration of crystallization and fluid dynamic processes into the simulation. Simultaneously, expanding the scope to encompass entire layers, with a specific focus on different scan strategies, holds significant promise. These advancements aim not only to improve the accuracy of the simulation but also to unlock new possibilities for advanced applications in laser processing, especially for the material class of BMGs.