1 Introduction

Fused deposition modeling (FDM) is an additive manufacturing process where a thermoplastic filament is selectively dispensed through an extruder [1]. FDM is one of the most commonly used 3D printing technologies and has the potential to democratize manufacturing by enabling low-cost production of goods by users outside the manufacturing sector [2,3,4]. FDM 3D printing is constantly expanding into new feedstock materials, including polymer composites, and commonly recycled thermoplastics such as high-density polyethylene (HDPE) and polyethylene terephthalate (PET) [5, 6]. Unfortunately, the 3D printing process is sensitive to any change in system configuration, especially the feedstock. Calibrating a printer to a new feedstock requires a time-consuming trial-and-error process to identify optimal settings for a large number of process parameters [7]. The experience required to efficiently navigate this high-dimensional parameter space acts as a barrier to entry for non-expert users; improper settings often result in failed prints that are time consuming and wasteful and can discourage users from using 3D printers in the future [8, 9].

Autonomous experimentation (AE) systems [10] capable of iteratively planning, executing, and analyzing experiments toward human-directed research outcomes have shown great promise in accelerating optimization in complex and high-dimensional materials problems such as carbon nanotube synthesis [11], chemical reactions [12], and direct ink writing (DIW) [13, 14]. Inspired by these advances, this paper presents the first low-cost AE system for closed-loop calibration of FDM 3D printers that demonstrates optimizing process parameters for printing complex 3D models with submillimeter dimensional accuracy. The system is implemented on a low-cost FDM printer and requires only a consumer-grade camera and computer capable of running modern 3D printing software, making it easily deployable. Autonomous calibration is realized through a computer vision-based quality analysis that computes a metric between a camera image of a calibration object and its 3D model. The computer vision-based analysis is combined with the simulated annealing metaheuristic to efficiently explore candidate process parameter settings.

System performance is evaluated based on the dimensional accuracy of a popular benchmark 3D model printed using three materials: polylactic acid (PLA), PLA blended with several additives (PLA Pro), and polyvinyl butyral (PVB). Results show that the system is capable of autonomously calibrating a 3D printer to print the benchmark with an average deviation in dimensional accuracy of 0.047 mm using a calibration budget of just 30 g of filament (~ $1 USD). The time and material savings enabled by the demonstrated automation represents a significant step forward to increase the accessibility of 3D printing to non-expert users.

2 Related work

The tight link between printer configuration and part quality has motivated research into the optimization of process parameters for a variety of materials and models [15,16,17,18,19]. A common approach is to evaluate a matrix of process parameter settings determined using design of experiments (DOE) [7]. Since each experiment requires physically printing a part, calibration objects that are designed to be printed quickly while still having geometric features that are representative of more complex models are typically utilized [20,21,22]; however, these methods can still be inefficient and time consuming when the parameter space is large [7].

Metaheuristics represent a family of approximate optimization techniques able to provide sufficiently good solutions for complex and high-dimensional problems and have been shown to be effective at optimizing process parameters for 3D printing [23,24,25]. Abdollahi, et al. [24] developed an expert guided hill-climbing algorithm to optimize process parameters for 3D printing the experimental material polydimethylsiloxane (PDMS). The algorithm involved three steps; expert screening to select the parameter space, factors, and factor levels; using hill-climbing with a rubric-based evaluation method to search the expert-defined parameter space for the best set of parameter settings; and using expert knowledge to define a new parameter space if hill climbing converged to an unsatisfactory set of parameters. The algorithm was able to find a high-quality set of parameters for a set of simple calibration objects that were shown to be transferable to more complex models such as a human toe and ear.

In a similar study, Oberloier, et al. [25] used particle swarm optimization (PSO) to optimize process parameter settings for FDM 3D printing using recycled low-density polyethylene (LDPE) filament. Utilizing a fitness function based on physical measurements, PSO was able to optimize six process parameters to print three calibration objects: a line, planar surface, and cube. The parameter settings were also found to be transferable to printing other objects such as the legs for a stool.

Common to the studies above is the need for human assessment (physical measurement, subjective assessment, etc.) within the optimization loop. Computer vision techniques offer a potential low-cost solution for “closing the loop”, enabling an autonomous research loop similar to those demonstrated by AE systems on several complex and high-dimensional materials problems [10]. Existing research on computer vision-based defect monitoring includes methods that compare an ideal reference model with images of the printed part [26, 27], and machine learning methods that classify, localize, or segment printed part defects by training a model using a large dataset of defect examples [28,29,30,31].

Nuchitprasitchai, et al. [26] developed single and double camera systems capable of detecting simple failure conditions such as a clogged nozzle and incomplete printing based on deviations from the expected part geometry. In the single camera setup deviations were detected through image subtraction with a reference image depicting the ideal geometry generated from the 3D model. In the double camera setup, the two images were used to create a two-view 3D reconstruction that was compared to the 3D model in terms of height and width. Petsiuek and Pearce [27] developed a more complex single camera system able to detect additional printing errors including layer shifting and infill deviation. Pseudo top-down and side views of the part were generated by applying perspective projection to images captured from a digital camera at a fixed angle. In combination with the position of the camera and toolpath trajectories, the side view images enabled detection of deviations in the height of the part as it is being printed. Top-down images were utilized to detect deviations in the trajectory of the outer shell using multi-template matching and the iterative closest point algorithm, as well as to assess infill texture quality using texton-based texture segmentation.

The use of convolutional neural networks (CNN) for defect detection and process monitoring in 3D printing has grown in popularity in recent years [28]. This is largely due to the discovery that features generated by CNNs pretrained on very large datasets such as ImageNet can be transferred to other problem domains with only modest changes to the original network [29]. Jin, et al. [30] utilized images collected from a consumer-grade webcam mounted to the extruder of an FDM printer to train a CNN for material extrusion evaluation. Images of three classes of extrusion quality created by varying the material flow rate were collected and used to fine-tune a RestNet 50 architecture. The trained CNN was deployed in a closed-loop system and its predictions were used to correct the flow rate of the printer in real-time. Brion and Pattinson [31] extended this work with two additional process parameters, lateral speed, and Z offset, by utilizing a CNN with an attention mechanism and multiple output layers and showed that their system could be used to improve prints that would otherwise fail without intervention. Despite these promising demonstrations, CNNs require a very large number of training images and it is often difficult or impractical to collect a dataset that is representative of all operating conditions the system may encounter.

Closest to this work is the Additive Manufacturing Autonomous Research System (AM ARES) developed by Deneault, et al. [13]. AM ARES utilized computer vision in combination with Bayesian methods for closed-loop optimization of a DIW system. Whereas AM ARES demonstrated closed-loop optimization of process parameters for direct-writing single-layer 2D prints, the system presented in this paper targets the FDM process and is capable of optimizing process parameters for printing complex 3D models.

3 Methodology

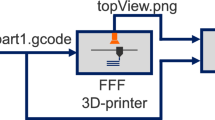
Figure 1 shows a high-level overview of the system pipeline. Since the real-world function relating the 3D printer's process parameters to the printed part quality is unknown, the 3D printing process is modeled as a black box function. The function receives a set of process parameter settings that are used to print a calibration object, and outputs a computer vision-based metric representing the quality of the settings. Unlike recent methods [30, 31], the quality analysis does not require a large dataset of images to train a computer vision model. Instead, it leverages a calibration object that prints quickly and is representative of more complex models. The evaluation method extracts local shape features from a camera image of the calibration object and a synthetic image based on the calibration object’s 3D model that is generated using computer graphics. The quality metric is computed as a minimum cost matching between the feature vectors of the two images and represents the dissimilarity between the printed object and the 3D model. Simulated annealing is used to efficiently search the parameter space for parameter settings that minimize the quality metric. The calibration process is run until a user-defined budget is expended.

Fig. 1
figure 1

High-level diagram of the closed-loop calibration system

Full size image

3.1 System configuration

Figure 2 shows the system configuration. It consists of a Creality Ender-3 FDM 3D printer and Raspberry Pi High Quality Camera controlled using a Raspberry Pi 4 Model B. The Ender-3 is configured to deposit 1.75 mm plastic filament from a nozzle with a 0.4 mm diameter at a maximum extrusion temperature of 240 °C and is capable of printing at a maximum speed of 180 mm/s with an accuracy range of 0.1–0.4 mm and a printing precision of ± 0.1 mm. The Ender-3 has a maximum print area of 220 mm × 220 mm × 250 mm that can be heated to a temperature of 100 °C. The Raspberry Pi High Quality Camera utilizes a Sony IMX477R stacked CMOS sensor. The sensor consists of a 4072 × 3040 square pixel array with a pixel size of 1.55 μm × 1.55 μm and employs an RGB pigment primary color mosaic filter. The camera is mounted on a 50-inch lightweight tripod stand and equipped with a 16 mm C-mount telephoto lens. The system is controlled by a workstation equipped with an Nvidia Quadro P5200 GPU, an Intel Xeon E-2186 M CPU, and 64 GB of RAM; however, any computer that meets the minimum requirements to run modern 3D printing software can be utilized. PrusaSlicer v2.5.0. is used to set the printer configuration and generate toolpaths.

Fig. 2
figure 2

System configuration consisting of a the Creality Ender-3, Raspberry Pi HQ Camera, and b modified Stanford bunny model used as the calibration object

Full size image

The calibration object is a modified Stanford bunny model [32] that was smoothed and resized to have dimensions 25.6 mm × 19.2 mm × 24.1 mm. The modifications enable it to print in 25 min at a speed of 20 mm/s using just 1 g of filament with a cubic infill density of 7%. The Stanford bunny model was chosen due to having several geometric structures that can pose a challenge for FDM printers. For example, the model’s ears test the printer’s ability to print structures that extend outward with no direct support, whereas the model’s spherical back tests the printer’s surface finish ability.

3.2 Calibration object evaluation using computer vision

3.2.1 Object segmentation

The first step in the computer vision evaluation pipeline is to segment the object from the background using color-based thresholding. The Red, Green, and Blue (RGB) image from the camera is converted to Hue, Saturation, and Value (HSV), which separates the color and luminance into separate channels [33]. The calibration object is separated from the background by thresholding with a hue range that corresponds to the color of the filament used to print the object.

3.2.2 Synthetic image generation

Synthetic image generation renders a synthetic image of the 3D model in the same position and orientation as the printed object, and at the same resolution as the camera image, enabling the use of pixel-based comparison methods. Approximation of the physical camera uses a calibrated camera model based on the pinhole camera model. Let the 3D model of the calibration object be represented by the graph \(G=(V,E)\) where each vertex \(v\in V\) is a homogeneous coordinate in a three-dimensional Cartesian coordinate frame and each edge \(e\in E\) maintains the adjacency of two vertices in \(V\). The mapping of each vertex \(v\in {\mathbb{R}}^{4}\) to a point \(u\in {\mathbb{R}}^{3}\) on the image plane is given by

$$u = K\left[ {R|t} \right]v$$
(1)

where the matrix \(K\in {\mathbb{R}}^{3x3}\), also known as the intrinsic parameter matrix, describes the intrinsic parameters of the camera. The intrinsic parameter matrix has the form

$$K = \left[ {\begin{array}{*{20}c} {f_{x} } & 0 & {p_{x} } \\ 0 & {f_{y} } & {p_{y} } \\ 0 & 0 & 1 \\ \end{array} } \right]$$
(2)

where \(f_{x}\) and \(f_{y}\) are the focal length of the camera along the \(x\) and \(y\) axes, and \({p}_{x}\) and \({p}_{y}\) are the coordinates of the principal point, which is the point where the image plane intersects the image’s optical axis. The matrix \([R|t]\), known as the extrinsic parameter matrix, is composed of rotation matrix \(R\in {\mathbb{R}}^{3x3}\) and translation vector \(t\in {\mathbb{R}}^{3}\) and describes the position and orientation of the camera with respect to the world coordinate frame.

Perspective projection requires estimating the physical camera’s intrinsic parameters along with models for radial and tangential distortion induced by the lens. OpenCV’s implementation of Zhang, et al.’s [34] algorithm was utilized due to its ease of implementation, accuracy, and robustness under different conditions. Zhang’s algorithm takes a set of images of a known planar pattern captured in different positions and orientations and uses the known geometry of the pattern to establish correspondences between the 2D image points and the 3D world coordinates of the pattern points. An asymmetric chessboard with 10 × 7 vertices and 11 × 8 squares was chosen as the planar pattern to detect the internal corners [35]. The chessboard was scaled to have a 90 mm width and 70 mm height and was printed on A4 cardstock. A total of 31 chessboard images were used to estimate the camera’s intrinsic parameters with a reprojection error of 0.42 pixels. The reprojection error indicates that on average, each of the projected points is displaced 0.42 pixels from their true position.

The problem of estimating the matrix \([R|t]\) is known as the pose estimation problem [36] and can be solved by minimizing the norm of the reprojection error of \(n> 3\) point correspondences between the image plane and the world frame [37]. Generating the required 2D–3D point correspondences utilizes four circular markers shown in Fig. 3a. The markers are printed onto the printer bed using a filament with a known set of process parameter settings so that the coordinates of their centers are known accurately relative to the origin of the world coordinate frame. The marker centers in the image plane are determined by first performing object segmentation on the markers using the same methods described earlier and then performing contour detection (Sect.  3.2.3). The extracted contours are then filtered using Eq. 3 so that only contours with a minimum circularity of 0.7 are retained.

Fig. 3
figure 3

a The circular markers used to establish 2D-3D correspondences, b point cloud generated using Eq. 1, and c graphics pipeline used to generate the synthetic image

Full size image
$$Circularity= \frac{4 \cdot \pi \cdot Area}{Perimete{r}^{2}}$$
(3)

Finally, the marker centers are estimated by computing the centroid of each contour. After obtaining the intrinsic matrix and the point correspondences between the image marker centers and their position in the world frame, the extrinsic parameter matrix is solved for by minimizing the norm of the reprojection error of the 2D-3D point correspondences using OpenCV’s implementation of the Levenberg–Marquardt algorithm [38].

Applying Eq. 1 to the vertex set specified by the 3D model results in the projection of the points onto the image plane shown in Fig. 3b. The projected points form an unstructured 2D point cloud that is unsuitable for computing rich shape representation since it does not contain any connectivity information between adjacent points. To better facilitate the comparison of shape features between the 3D model of the calibration object and the image of the printed part, the perspective projection of a polygon mesh representation of the 3D model is rendered using the computed camera matrices and the open-source computer graphics API OpenGL [39]. The rendering pipeline is shown in Fig. 3c. The pipeline begins with the geometric data specified by the 3D model formatted as a Wavefront .obj file. The projected position in screen space is computed for each vertex according to

$${u}_{screen}=\left[\begin{array}{cccc}2\cdot \frac{{k}_{00}}{w}& 0& \frac{w-2\cdot {k}_{02}}{w}& 0\\ 0& -2\cdot \frac{{k}_{11}}{h}& \frac{h-2\cdot {k}_{12}}{h}& 0\\ 0& 0& \frac{-f-n }{f-n}& \frac{-2\cdot f\cdot n}{f-n}\\ 0& 0& -1& 0\end{array}\right]\left[\begin{array}{cccc} & R& & t\\ 0& 0& 0& 1\end{array}\right]v$$
(4)

where \({k}_{ij}\) is the \((i,j)\) entry of the intrinsic parameter matrix, \(R\) and \(t\) are the rotation matrix and translation vector that compose the extrinsic parameter matrix, \(w\) and \(h\) are the width and height of the camera image, and \(n\) and \(f\) specify the coordinates for the near and far clipping planes that specify how much of the scene is seen by the camera in the viewport. The projected vertices are assembled into triangles and parts of the triangles that fall outside the screen are clipped and discarded. The remaining parts are tessellated into an array of pixels and the vertex colors are blended across the array. The resulting rendering is then saved in image format.

3.2.3 Contour detection

After performing object segmentation and synthetic image generation, the boundary information of the calibration object is extracted from both images using OpenCV’s implementation of the border tracing algorithm by Suzuki and Abe [40]. The output of the contour detection phase is a pair of lists of the pixel coordinates representing the contours of the calibration object in the camera and synthetic images.

3.2.4 Shape representation using shape context

For each extracted contour, the shape context [41], a boundary-based local feature that represents shape as a distribution over relative positions of the extracted contour points, is computed. A boundary-based representation was chosen as they are more sensitive to small deviations than region-based methods [42]. For example, shape context can account for minor defects in the ears of the calibration object, whereas this information is thrown away by region-based representations such as the area of the segmentation mask. Additionally, shape context’s translation invariance and partial rotation invariance make it insensitive to the reprojection error introduced in the camera calibration process. The process for computing the shape context is shown in Fig. 4. For each point \({p}_{i}\) belonging to the extracted contour, a 3D histogram \({h}_{i}\) with bins that are uniform in log-polar space is computed according to

$${h}_{i}\left(k\right)=\left|\left\{q\ne {p}_{i} :D\left(q,{p}_{i}\right)\in bi{n}_{k}\right\}\right|$$
(5)

where \(k\) is the bin number and \(D(q,{p}_{i})\) is the log of the Euclidean distance between points \(q\) and \({p}_{i}\). Each histogram uses 12 angle bins and 5 range bins for a total of 60 bins per histogram. The feature vector is taken as the set of computed histograms and forms a compact and highly discriminative representation of the printed calibration object’s shape.

Fig. 4
figure 4

Extracting the shape context feature: a the log-polar bins for an arbitrary contour point and b the corresponding histogram

Full size image

3.2.5 Print quality metric computation

Given the feature vectors \(H=\left\{{h}_{1}, {h}_{2}, \dots , {h}_{n}\right\}\) from the camera image and \(H^{\prime} = \left\{ {h_{1}^{{}} , h_{2}^{{}} , \ldots h_{{n^{\prime}}}^{{}} } \right\}\) from the synthetic image, the print quality metric is computed by solving for a minimum cost feature matching formulated as:

$$\min \sum\limits_{{(h,h^{\prime}) \in H \times H^{\prime}}} {C(h,h^{\prime}} )x(h,h^{\prime})$$
$$s.t.\,\,\,\,\,\,\,\,\,\,\,\sum\limits_{{h^{\prime} \in H^{\prime}}} x(h,h^{\prime}) = 1\,\,\,\,\,\forall h\, \in H,$$
(6)
$$\sum\limits_{h \in H} {x(h,h^{\prime}) = 1\,\,\,\,\,\forall h^{\prime}\,\, \in H^{\prime}}$$

where \(x\left( {h,h^{\prime}} \right)\) is an indicator function that takes value 1 if \(\left( {h,h^{\prime}} \right)\) is included in the matching and 0 otherwise, and \(C\left( {h,h^{\prime}} \right)\) is the distance between \(h\) and \(h^{\prime}\) given by

$$c(h,h^{\prime}) = \frac{1}{2}\sum\nolimits_{k = 1}^{k} {\frac{{\left[ {h\left( k \right) - h^{\prime}(k)} \right]^{2} }}{{h(k) + h^{\prime}(k)}}}$$
(7)

The formulation above is an instance of the weighted bipartite matching problem, which is solved using the Jonker-Volgenant algorithm [43].

3.3 Process parameter optimization using simulated annealing

Simulated annealing, a popular single-solution metaheuristic that was inspired by the annealing process in metallurgy [44], is used to find a high performing set of process parameters. The algorithm is initialized with a set of process parameter settings \(S\) and a temperature hyperparameter \(T\) that controls the exploration–exploitation trade-off. Table 1 shows the five process parameters selected for optimization, their minimum and maximum values that form the boundaries of the search space, and the standard deviation used to generate candidate solutions. All process parameters are set using PrusaSlicer v2.5.0. Extrusion temperature, bed temperature, printing speed, and fan speed were selected as they have been shown to have a significant impact on part quality [16, 45, 46]. Additionally, many manufacturers of thermoplastic filaments provide a recommended range for these parameters that can be used for system validation. Extrusion multiplier was also selected as the amount of filament extruded by the nozzle can vary depending on material type and quality [47]. At each iteration, a candidate set of process parameter settings \(S^{\prime}\) is generated by sampling from a set of Gaussian distributions centered on S. If a sample falls outside a parameter’s associated range, a new sample is drawn until it is within range.

Table 1 Process parameters optimized by simulated annealing, corresponding ranges, and standard deviation
Full size table

The candidate settings are used to print the calibration object that is evaluated using the methods described in Sect. 3.2. If the quality of the candidate settings is higher than that of the current settings, they are accepted as the current settings of the next iteration. Otherwise, they are accepted according to

$$\exp \left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (s) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (s^{\prime})}}{T}} \right) > \xi$$
(8)

where \(\hat{f}\) is the part quality estimated using the computer vision evaluation and \(\xi \sim U\left( {0,1} \right)\). Thus, for a sufficient \(T\), Eq. 8 allows the algorithm to escape from local minima. The temperature is updated according to the cooling schedule given by

$$T\left( {t + 1} \right) = T\left( t \right) - \eta T\left( t \right)$$
(9)

where t is the current iteration and \(\eta\) is the cooling rate. The starting temperature and cooling rate were determined experimentally to balance exploration and exploitation at 20 and 0.01, respectively. After each iteration, a custom toolpath script is called that utilizes the print head to remove the current calibration object from the print bed. As a criterion for terminating the algorithm, we set a budget of 30 iterations that corresponds to a consumption of approximately 30 g of filament (~ $1 USD). Although this stopping criterion does not ensure convergence, the following section shows that the best-found settings are able to transfer to printing high quality parts that are more complex than the calibration object, which is demonstrated by printing a popular benchmark 3D model with submillimeter dimensional accuracy.

4 Results and discussion

The autonomous calibration system was evaluated on three types of thermoplastic material: PLA, PLA Pro, and PVB. PLA is the most popular thermoplastic used in FDM 3D printing due to its low melting point and good layer adhesion. PLA Pro is a stronger, more durable, and more temperature-resistant form of PLA that contains additional additives that give it improved mechanical properties and thermal resistance. PVB is a more recently adopted thermoplastic that has similar mechanical and printing properties to PLA and PLA Pro but can be easily post-processed with isopropyl alcohol for better surface finishes. Table 2 shows the recommended settings range provided by the manufacturer for each material. Two experimental runs were conducted for each material. Each experimental run was initialized with an extrusion temperature of 240 °C, bed temperature of 22 °C, print speed of 100 mm/s, extrusion multiplier of 160%, and fan speed of 0%, which are outside each material’s manufacturer’s recommended range.

Table 2 Manufacturer recommended settings for the thermoplastic materials used in the experiments
Full size table

Figure 5 shows the convergence plots for the experiments and Table 3 lists the optimized process parameter settings. In each experimental run, the initial settings caused various printing defects including over-extrusion, stringing, overheating, and bed adhesion issues. These defects caused significant deviations from the expected geometry of the part, resulting in high initial dissimilarity scores. In the case of the first run using PLA Pro (Fig. 5b), the part detached from the printer bed early in the printing process, resulting in the only complete failure and thus the highest dissimilarity score across all experimental runs. Simulated annealing was highly effective in optimizing process parameter settings for each experimental run, resulting in a significant improvement in print quality over the initial settings. The optimized settings for extrusion temperature and bed temperature fell within the corresponding manufacturer’s recommended range in each run. Interestingly, the optimized print speed fell below the lower bound of the manufacturer’s recommended range in at least one run for each material. Furthermore, the optimized settings for each material varied between runs, and no two runs yielded the same set of process parameter settings. The similarity in print quality despite differences in process parameter settings between the optimized settings for each material suggests the presence of many local minima close in fitness to the global minima [23].

Fig. 5
figure 5

Convergence plots for the a PLA, b PLA Pro, and c PVB experiments

Full size image
Table 3 The best-found settings in each experiment and corresponding dissimilarity scores
Full size table

To evaluate the ability of the optimized settings to transfer to more complex objects, the optimized settings from each experimental run were used to print a 3DBenchy, a popular 3D model for benchmarking 3D printer configurations. The quality of the settings was assessed by taking 9 physical measurements of the printed benchmarks and comparing them with the expected measurements of the 3D model. Measurements were made using a Mitutoyo 500-196-30 digital caliper with a resolution of 0.01 mm. Figure 6 shows the ideal dimensions of the benchmark 3D model, box plots, and radar charts depicting the deviations in millimeters for the experiments. All sets of process parameter settings were able to print a benchmark object with an average deviation from the 3D model of 0.047 mm, which is more accurate than the Creality Ender-3’s published tolerance of 0.1–0.4 mm. All individual measurement deviations were also smaller or within the published tolerance, demonstrating that the system is capable of optimizing settings that can be used to print high quality parts that are more complex than the calibration object.

Fig. 6
figure 6

a The ideal measurements used to evaluate the dimensional accuracy of the benchmark object, b box plots, and radar plots of the deviation from the ideal measurements in millimeters for the c PLA, d PLA Pro, and e PVB experiments

Full size image

5 Conclusion and future work

This paper presents the first low-cost AE system for closed-loop calibration of FDM 3D printers that demonstrates optimizing process parameters for printing complex 3D models with submillimeter dimensional accuracy. Autonomous calibration is achieved through modeling the 3D printing process as a black box function that is evaluated using computer vision and optimized using the simulated annealing metaheuristic. Print quality is formulated as a minimum cost matching between shape context feature vectors extracted from a camera image of a calibration object and a synthetic image of the object’s 3D model generated using computer graphics. Simulated annealing is used to efficiently search the parameter space for parameter settings that minimize the computer vision evaluation. The system is evaluated on three popular thermoplastic materials and is shown to be able to find process parameter settings capable of printing high quality parts even when initialized with settings known to cause printing defects. Results show that the best-found settings are able to transfer to printing 3D models that are more complex than the calibration object as demonstrated by printing a popular benchmark with an average deviation in dimensional accuracy of 0.047 mm using a calibration budget of just 30 g of filament. The automated parameter tuning not only reduces the occurrence of defects in the 3D printing process, but also lowers the minimum user skill requirement for effective operation, reducing the barrier to entry for non-expert users.

A limitation of the system is its ability to miss geometric deviations due to occlusions as a result of using a single, fixed camera. Future work includes extending the system to incorporate images from multiple viewing angles using a 3D printable gantry similar to [48]. A set of multi-view images also enables incorporating more complex computer vision techniques such as a comparison of the 3D model with a photogrammetric 3D reconstruction of the printed object as in [49]. This could enable quantifying not only shape-based deviations, but deviations in the printed surface as well.