1 Introduction

1.1 Overview

Pressure loaded components such as heat exchangers or hydraulic valves are often enclosed volumes with channel systems. Nowadays production is characterized by common combinations of manufacturing techniques, such as rolling and welding or casting and drilling, which are highly evolved and cost-effective, but geometrically limited.

Additive manufacturing (AM) technologies enable realization of complex 3-D geometries to achieve highly functional components. Powder bed fusion of metals using a laser beam (PBF-LB/M), used for this work, is one of the dominating additive manufacturing techniques for production of fully dense metal parts reaching mechanical properties, which can fulfill common material standards [1, 2].

Besides a lot of promising opportunities (part integration, functional integration, geometric freedom, structural lightweight design, customizability and fabrication on demand), a lack of trust in quality is often present [3]. Qualification of AM components is challenging due to a high amount of quality influencing factors and the fact, that producing companies become the material manufacturers, because of fully re-melting the feedstock.

Additionally, costs per part are comparatively high, because of typical build rates below 10 cm3 per hour (mid-size single laser system) and post-processing steps like support removal and testing [4]. Business cases arise especially for complex components as costs do not directly increase with geometric complexity during manufacturing process.

The European Pressure Equipment Directive (PED) 2014/68/EU regulates the conformity assessment of pressure equipment in its markets. Resulting standards have a good comparability to the US markets standards defined by American Society of Mechanical Engineers (ASME).

EN 13445, which is one important European standard, is publicly available not yet considering AM methods [5]. Thus, AM pressure equipment must have cost-intensive single-component qualification to be realized with high expenses in testing [3, 6].

To enable series qualification procedures, German Institute for Standardisation (DIN) Standards Committee Technology of Materials (NWT) is working since 2019 on adapting DIN EN 13445. The pre-normative result of this work DIN/TS 17026 “Unfired pressure vessels—Additional requirements for pressure equipment and pressure components fabricated with additive manufacturing methods” and is textual related to prEN 13445 – Part 14 which is under developement by European Committee for Standardization (CEN) Technical Committee (TC) 54 for AM in future [7].

To support this normative efforts, the presented work investigates a predetermined point of failure by a surface notch, which is integrated by design and directly fabricated using PBF-LB/M. This enables a controlled failure position due to pressure overload. Henceforth, maintenance testing effort could be reduced using this component position for targeted testing. Validation and to help closing the gap of component and multiaxial testing in present literature, this work presents destructive burst testing of AM fabricated vessels.

1.2 Methodological approach

The authors introduce a validated novel design approach aiming to outline a guideline for the application of pre-defined point of failures on pressure vessels using a surface notch (see Fig. 1). A solution for the optimization challenge in applying a safe malfunction, which fulfills simultaneously part specific strength requirements, is presented.

Fig. 1
figure 1

Methodological approach for the integration of a predetermined failure location

Full size image

Due to the layer-wise building process, AM often leads to anisotropic material behavior and component properties (e.g. strength or surface roughness) [8]. Thus, location and orientation of functional geometric features highly affect their reliability. Following, machine capabilities at that location, especially geometric resolution, limit the design space for theoretical or experimental failure geometry analysis. The mechanism for non-experimentally found geometries can be validated experimentally, e.g. by tensile testing. Further on, validated features and functions are implemented in construction and validated by computational analysis as well as experiments (burst testing).

2 Methodology

2.1 Manufacturing and material

EOS M290 (EOS GmbH, Krailling, Germany) PBF-LB/M system was used to manufacture all specimens (Table 2). The standard parameter set “316L 040 FlexM291 1.00” was used with skywriting and vector flow optimization turned on (Table 1). Part exposure was set to “against argon flow direction” and platform preheating was set to 80 °C. Table 2 gives more details about the machine specification.

Table 1 Main Infill Process Parameters
Full size table
Table 2 Manufacturing machine specification
Full size table

Austenitic steel 1.4404 (316L) powder feedstock produced by thyssenkrupp (thyssenkrupp Materials Services GmbH, Essen, Germany) with a nominal particle size distribution of D10 = 15 µm and D90 = 45 µm was used for manufacturing. Table 3 lists the measured and normative chemical composition.

Table 3 Chemical composition of 1.4404 in wt.% (I) measured, (II) reference values according to DIN EN 10088–1
Full size table

Tensile specimens were cut by wire-cut electrical discharge machining (EDM) of the build platform. Pressure vessels were cut using a band saw. No post-process heat treatment was performed. Testing is applied without any thermal or mechanical post-processing except reaming (M6 × 1.0) for burst testing to focus investigations on as-built conditions.

2.2 Computational analysis

Abaqus software (Dassault-Systèmes SE, Vélizy-Villacaoublay, France) was used for finite element analysis. Material data measured at the exact same machine with comparable 1.4404 material feedstock and same process parameters were used as data input for simulation [9]. The numerical analysis software must use isotropic material data. Hence, inferior values are used and given by Table 4. Full integrational eight-node axisymmetric elements (CAX8) were used considering the component geometry. Element size plausibility was checked by stress difference due to halving and doubling element sizes. Nominal element size of 0.75 mm was used for the raw vessel without notch, based only on its quarter, because of its symmetry. Nominal element size of 1.1 mm was used for evaluating the vessel with predetermined breaking point as half. Element refinement to 0.1 mm was applied at the notch area. Nodal floating bearings fix the device at its connection front surface.

Table 4 Material data for finite element analysis
Full size table

2.3 Part testing

2.3.1 Tensile testing

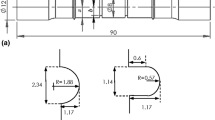
Quasi-static tensile tests were performed according to DIN EN ISO 6892–1 using tensile test device Zwick Roell Z050 (ZwickRoell GmbH & Co. KG, Ulm, Germany) with 50 kN load cell and strain gage multiXtens (ZwickRoell GmbH & Co. KG, Ulm, Germany) [10]. Testing rate was based on strain rate with 0,002 s−1. Specimen geometries were in accordance with form E from DIN 50125 and are presented in Fig. 2 [11].

Fig. 2
figure 2

Flat tensile test specimen geometry DIN 50125-E 2 × 20 x 46 with additional surface notch

Full size image

2.3.2 Burst testing

Burst testing was performed together with TÜV SÜD (TÜV SÜD Industrie Service GmbH, Filderstadt, Germany) using a 100 MPa hand pump HP32/8 (URACA GmbH & Co. KG, Bad Urach, Deutschland). The specimens were attached using a M6 screw connection with copper shim, a 70 shore acrylnitril butadien kautschuk (NBR 70) O-ring and thread sealing tape (Figs. 3, 4). Testing medium was water and accurate venting was performed before applying high pressure loads to avoid explosive volume expansion. Load increase was done by constant manual pumping until break.

Fig. 3
figure 3

Experimental setup for burst test

Full size image
Fig. 4
figure 4

Base pressure vessel burst test geometry

Full size image

2.3.3 Scanning Electron Microscopy (SEM)

Analysis of break surfaces was conducted using a Hitachi (Chiyoda, Tokyo, Japan) TM3030Plus scanning electron microscope (SEM). All images were acquired with 15 kV of accelerating voltage in scanning electron image mode using build-in automatic adjustment of contrast and brightness.

2.3.4 Metrology 3-D scanning

Metrology measurement of deviation after burst testing was done by structured light using ATOS Core 300 (Carl Zeiss GOM Metrology GmbH, Braunschweig, Germany). Specimens were prepared with optical markings and stepwise rotated and scanned. The software automatically calculates a tessellation file representing the specimen surface.

Analysis was done with GOM Inspect Software (Carl Zeiss GOM Metrology GmbH, Braunschweig, Germany). Geometric comparison is based on a three point pre-alignment followed by an automatic best-fit alignment using only surface vertices in the connection area of the pressure vessel. This strategy produces a repeatable and robust geometric alignment, because of nonexistent or marginal deformation in this component area. All results were calculated between the raw Computer-Aided Design (CAD) geometry and the 3-D measurement result.

3 Results

3.1 Location for integration

Finding an adequate location for applying the surface notch marks the starting point of the introduced method. The authors use a computational stress analysis (finite element method) to identify a part surface with homogeneous stress distribution and which is one of the weakest surface areas according to a specified failure load case (inner pressure overload). Figure 4 shows the underlying component geometry with an inner diameter Di of 40 mm and a wall thickness ea of 2 mm which is based on DIN EN 13445–3:2018–12 [5]. To reduce support structures and allow powder removal, the marked upright build direction is targeted (Fig. 4). Pel of 52.8 N/mm2 reaches the yield strength Rp0.2 at the verification point. The pressure Ppl = 57.4 N/mm2 reaches the full plastic load capacity resulting in plastic form factor Kp = 1.087 regarding FKM guideline [12]. Hence, component strength σSK is 570.1 N/mm2.

Higher loads will result in plastic deformation and component failure. Figure 5 shows the equivalent plastic strain (PEEQ) at Ppl. It comes clear, that highest mechanical stresses and plastic deformation start at the cylinder barrel right at the verification point (red color marks high stresses). This fits the expectations, due to a design regarding DIN EN 13445, which prevent areas like the bottom and those with non-constant diameters from failure. Tangent stress at the marked location is twice as big as axial stress and will cause longitudinal cracking, which is well known by “Barlow's formula”.

Fig. 5
figure 5

Equivalent plastic strain distribution using FEM

Full size image

Following “Barlow’s Formula” and Table 5, a longitudinal fracture behavior in the cylinder barrel area (verification point) is probable. Thus, the advised location of failure for a device in case of overload is its weakest (the barrel surface). The targeted surface notch should follow the expected longitudinal fracture direction. Another location or orientation would need to have less strength and would weaken the total component or waste material. Mechanical stress decreases within the vessel wall from inside to outside. Applying the surface notch at the outer hull maximizes overall strength and enables visual inspection after manufacturing.

Table 5 Calculated mechanical stress at verification point due to inner pressure of 50 N/mm2 assuming isotropic linear-elastic material behaviour
Full size table

3.2 Geometric capability

A longitudinal surface notch applied at the outer cylinder barrel is targeted (Sect. 3.1) to realize the predetermined point of failure. The component orientation for manufacturing defines the surface notch to be parallel to the build direction (Fig. 4). Figure 6 shows a test artifact to evaluate geometric accuracy for several notch and bulge radii in three manufacturing orientations.

Fig. 6
figure 6

Geometry testing artefact for surface notch in different orientations

Full size image

Notch and bulges radii were varied between R0.1 and R1.0 mm according to Renard series R5 according DIN 323–1 [13]. The measurements attest to the underlying machine parameter combination repeatability of notch radii greater R0.25 mm for upskin and vertical located notches. The authors accept a standard deviation of less than 10% for measured radii.

3.3 Notch geometry investigation

The notch geometry is investigated numerically using Abacus Isight simulation execution software (Dassault-Systèmes SE, Vélizy-Villacaoublay, France). Surface notch radii φ between R0.16 and R1 mm as well as notch depths t between 0.16 and 1 mm were varied [14]. The opening angle ω is fixed to 90° (Fig. 7).

Fig. 7
figure 7

Mesh representation and surface notch geometry

Full size image

Element size is refined to 0.1 mm in the notch area to achieve accurate results. Pressure load is set to 20 N/mm2. The analysis goal is to find the geometry causing the smallest stress concentration evaluated by the stress concentration factor ak [12]. Figure 8 shows a stronger relationship of notch depth to stress concentration compared to notch radii. Stress concentration decreases with higher radii and smaller depths. The minimum ak = 1.07 is achieved by φ = R0.75 and t = 0.219 mm leading to maximum local stress of 217.5 N/mm2. Maximum ak was 2.1 and local stress up to 746.9 N/mm2.

Fig. 8
figure 8

Simulation result: stress concentration factor ak in relation to notch depth t and radii φ at constant pressure load

Full size image

3.4 Material behavior/tensile testing

Flat tensile testing is used for evaluation of fundamental material behavior (Fig. 2). Five different specimens were evaluated in 15 measurements. Specimens c, d, and e have the defined notch geometry applied symmetrically. The notch is shifted by 5 mm with specimen d. Specimen b equals c, except its doubled notch depth (Fig. 9).

Fig. 9
figure 9

Tensile specimens after testing: (a) without, (b) 1.5 × notch depth, (c) centered, (d) shifted and (e) rotated notch

Full size image

Fracture surface passes perpendicular to tensile testing direction. Fracture position of specimens with notch shows a high focus to the notch center, except specimen e (notch rotation of 45°), which could not achieve the alignment of notch and fracture surface.

Ultimate tensile strength (UTS) related to nominal transverse section shows only small reduction for notched specimens. A significant reduction of break elongation accompanied with applied notch, except for the rotated notch of specimen e. Notch shifting by 5 mm shows no effect (compare c and d) to the strain measurement. The sharpest notch (b) results in the highest decrease of break elongation from around 32% (a) to 14% (b) (see Fig. 10).

Fig. 10
figure 10

Standard force versus elongation (tensile testing)

Full size image

Yield strengths Rp0.2 and Rp1.0 are highly relevant for construction via EN 13445. Both values show no significant change due to application of notch geometries (Fig. 11). One measurement of un-notched specimen differs to higher values, which corresponds to an incorrect positioning of the strain gage.

Fig. 11
figure 11

Measured yield strength Rp0.2 due to tensile testing

Full size image

3.5 Construction and computational validation

A longitudinal outer surface notch as predetermined point of failure is applied to the introduced vessel geometry (Fig. 4) as discussed before. The notch length follows the calculation by [15] to fit the criteria leakage before break. For longitudinal failure of tubes, a critical crack length of 10.39 mm can be calculated. Thus, the notch length is set to 10.5 mm.

Additionally to a raw and a notched vessel, a version with a bulge to limit or stop crack growth is investigated experimentally. Figure 12 shows the bulge geometry, which is constructed using the method of stress reducing triangles and length lw = φ = 0.75 mm [16].

Fig. 12
figure 12

Bulge geometry for crack growth limitation

Full size image

From 26.5 MPa of inner pressure, yield strength is exceeded locally at the notch ground. With ak and Rp0.2(min), a nominal calculation pressure of σP = 41.55 N/mm2 results for the vessel with notch and bulge. Full exceedance of yield strength within the vessels wall is reached at 50 N/mm2 of inner pressure (elastic ideal-plastic material behavior). According to FKM guideline, a static occupancy rate of 96.25% (at room temperature and for low consequence of failure) follows at [12]. Similarly, a dynamic strength verification can be calculated, which results in a dynamic occupancy rate of 92.25% for a pulsating pressure load σM = σP/2 ± σP/10 (10^5 load cycles).

3.6 Experimental validation

Pressure vessels without a notch (A, F, H, J), with notch (C, D, I, K) and with notch and bulge (B, E, G, L) were fabricated as described in Sect. 2.1 and experimentally tested (see Sect. 2.3.2). Figure 13 shows one of each tested geometry. All specimens failed between 67 and 70 N/mm2 of inner pressure and, meeting the expectations, with a longitudinal fracture and nearly 45° rotated break surface. Nominal pressure at failure is around 100 N/mm2 above calculations (Ppl), although material properties were evaluated with an identical setup (system, parameter, and material). In accordance with tensile testing, notched specimens show less plastic deformation compared to those without. While the failure location of vessels without notch seems to be random, all notched specimens failed exactly within the predetermined location.

Fig. 13
figure 13

Pressure vessel types after burst testing

Full size image

Differences in plastic deformation come clear in Fig. 14. Plastic deformation versus base CAD geometry is drawn for three representative specimens. The outer hull at the failure location of notched vessels elongates with around 6 mm half as far as the vessel without notch. On the opposite side, the difference is bit higher. The vessel without notch shows approx. 6.2 mm of deviation, with notch 2.4 mm and with notch and bulge 2.9 mm.

Fig. 14
figure 14

3-D scanned deviation color plot at deformed geometry (top) cross cut section and (below) side view

Full size image

Figure 15 shows fracture surfaces acquired using SEM. One piece was cut from the central fracture region for one vessel with (a) and without (b) predefining notch. Both specimen cuts are aligned with inside to the left in Fig. 15 (pressure loaded side). Due to constriction, specimen b (without) has less width compared to a (with notch) and its fracture surface seems to be less rough in a wider region, indicating less residual forced rupture. Both fracture surfaces show an overall comb structure at high magnification as well as small dimples pointing to trans-crystalline fracture at grain boundaries (ductile fracture) [17].

Fig. 15
figure 15

Fracture surface analysis using SEM imaging: (a) burst specimen with, (b) without notch

Full size image

4 Discussion

Location, orientation, and geometry for a fracture predetermining surface notch were successfully found. In this case, the application meets the base component’s weakest region. Location finding is based on linear elastic analysis for a well-known austenitic steel and geometry (tube-like). More complex components or missing material data would lead to challenges, especially if a geometry is highly sensitive to anisotropic material behavior or low ductility. In terms of manufacturing restrictions (overhang), a surface notch orientation parallel to the build orientation or applied to upskin surfaces is ideal. An application on downskin areas would be much more challenging due to geometric accuracy and surface roughness.

The used system and parameter set combination allows notch radii from R0.25 mm for upskin as well as vertical areas. Downskin surfaces with 45° degree were investigated too, but a robust measurement failed due to high roughness.

A linear elastic simulation study-based one finite element method found the correlation between notch radii, depth, and local stress concentration as well as a possible optimum solution successfully (Fig. 8).

Comparing the found optimum with a less good-rated geometry (increased depth) by tensile testing corresponds to this result. Further tensile testing showed only small decreases in ultimate tensile strength which can be interpreted as notch hardening. Simultaneously, hardening due to geometry is based on stress elevation and reduces ductility in accordance to reduced break elongation. Moving the fracture location by a moved notch position was successful, but is limited to the measurement length of a tensile test specimen. Fracture rotation by 45° was not successful. One explanation is the high constriction due to the materials ductility. Stress increase due to plastic deformation and surface notch meets at the exact specimen center, which leads to a centered fracture location. On top of that, ductility is the dominating influence factor to stress increase in this case. On that basis, tensile test specimen (e) intends that, elongation at break does not decrease if the predetermination fails (Fig. 9).

Construction was done based on the previous steps and in accordance to EN 13445–3. An additional geometry for stopping crack growth aiming on leakage before break is introduced. To do so, the surface notch length follows a calculation for critical crack length and leakage area [15]. Those are designed for a dynamic failure initiation and are not appropriate for static overload. Computational strength verification in accordance to FKM guideline successfully rated the chosen geometry to be sufficient with occupancy rates of 96.25 and 92.25% (see 3.5).

Experimental validation is successfully achieved. All notched specimens followed the predetermined fracture location, while non-notched specimens fail at random locations around the diameter. Besides, this is good news for the manufacturing process as neither gas flow nor re-coating direction shows influence to the fracture location. SEM imaging shows in accordance to simulation results less roughness at the inner specimen side, which can be explained by more plasticization as result of higher local stresses (Fig. 15). This supports a notch application outside the vessel for higher component strength. As it was discussed before, additional bulges do not limit fracture length significantly, which can be explained by the dynamic calculation base for critical crack length and leakage area. Despite this, bulges show a positive effect to break elongation due to additional material. Maximal load capacity during testing exceeds calculated full plastic load capacity for all test vessels, which can be explained with conservative approximations by FKM guideline regarding its aim for a safe design instead of exact failure load forecast.

3-D scanning showed significantly reduction in ultimate elongation for specimens with surface notches (Fig. 14). This means in effect, that vessels without notch suffer higher loads (same pressure, but increased volume). Nevertheless, the authors opine that extreme plastic elongations shown are not accepted in industrial applications and would be stopped earlier (e.g. by gage strain measurement or visual inspection). Thus, predetermining the exact failure location could be a valid functional integration by design.

In future, dynamic investigation of crack growth stop mechanisms should be done using e.g. cyclic compact tension tests. Furthermore, anisotropy behavior of additive manufactured materials could be based on multiaxial testing combined with strain and elongation measurements, as it is presented in this work.

5 Conclusion

A general method for the application of a predetermined failure location using a surface notch is described and successfully validated using a simple pressure loaded vessel. Tensile testing is performed to evaluate overall material behavior due to the applied safety function in an early design state. Computational analysis and formula-based design rules from literature enable a short development time for the component geometry. Burst tests were performed and evaluated using SEM imaging and 3-D scanning. The manufactured components made from austenitic steel 316L using PBF-LB/M fulfill the expectations. Implementation of directly manufactured predetermined failure locations work especially well.