1 Introduction

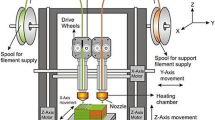
Additive manufacturing (AM) of metal components is increasingly gaining traction in the fabrication of prototypes, tools, and end-use products. Most frequently applied AM metal processes are represented by selective laser melting (SLM), electron beam melting (EBM), metal-based binder jetting (BJ), and indirect AM processes such as investment- and sand casting. Furthermore, a potentially cost-effective alternative for small-scale components can be found in the metal-fused filament fabrication (FFF) process, since even desktop FFF printers could be used for this filament-based part fabrication approach. To prepare such metal–polymer composite filaments, metal powder is mixed with a polymeric binder system to enable filament fabrication. After the “green” parts are fabricated, a debinding process step to remove the polymer and a sintering step to fuse the metal particles together (“brown” part) need to be conducted. Thus, this sintering process results in shrinkage of the components, which is dependent on several key aspects such as design, material, and print parameter settings, leading to challenges in its accurate process control.

Interestingly, studies investigating the metal FFF process are dating back to the year 1996 or even earlier [1]. In this study, metal–polymer composite filaments are produced with a 50–65 vol% of metal particle loading, allowing it to fabricate parts out of, e.g., stainless steel, WC–Co, and SiO2. New materials for metal FFF were developed, as demonstrated by [2] as an example for rapid tooling applications using iron–nylon composite or by [3] using Sn-Bi alloys.

Recently, new commercially available filaments (“Ultrafuse 316LX”) for metal FFF with high metal filler ratios of 80 vol% were introduced [4], allowing it to reduce the volumetric shrinkage and to integrate AM machines into existing metal injection molding process chains using the same catalytic debinding parameters and comparable sintering temperature profiles. This material has been tested and compared to SLM by [5], showing successful 3D prints with x/y-shrinkages of 13–18% and z-shrinkages of 15–23%, reaching yield strength of 167 MPa and an ultimate tensile strength of 465 MPa (as expected, both tensile strength indicators below SLM).

However, to expand on the mentioned study and to analyze the mechanical and shrinkage performance of metal FFF parts using the Ultrafuse 316LX material more deeply, this study investigates the effect of the print orientation on tensile testing results, different theoretical infill levels (infill percentages based on print parameters in the slicing software, not consistent with the actual material infill) on compression testing results, and the possibility to produce more complex-shaped industrial components for digital spare part production scenarios [6].

2 Materials and methods

The manufacturing process chain of metal FFF using plastic–metal composite filaments consists of 3D printing, debinding/sintering, and post-processing to fabricate functional metal components. The 3D printing system used in this study was a “Funmat HT” (Intamsys, China). The applied material was an “Ultrafuse 316LX” (BASF, Germany) plastic–metal composite filament, containing 80-vol% austenitic stainless steel 316L. As shown in Table 1, all specimens were fabricated with the listed print settings using “Cura 2.7.0” (Ultimaker, Netherlands) for print preparations. The theoretical infill level percentage was kept constant at 100% for all tensile testing samples and the 3D-printed wood tool. In contrast, the infill level percentages were varied from 25 to 125% for the compression testing pins to investigate its influence on the relative part density, mechanical performance, and shrinkage behavior. The selected infill pattern is described by lines with repetitive orientations in every second layer.

Table 1 Print parameters
Full size table

Fabricated samples were debinded and sintered externally (Plastoco oy, Finland) with process parameters confidential to the company. However, process parameters match or are similar to the recommended “Catamold 316 LG” metal injection molding standard, which consists of debinding at 110 °C using HNO3, sintering under argon atmosphere with a ramp rate of 5 K/min from room temperature to 600 °C (hold of 1 h), and temperature increase from 600 to 1380 °C with the same ramp rate and a hold of 3 h. Finally, the furnace is cooled down [7]. The orientation of the components during the debinding and sintering stage is as-printed, except for the tensile testing bars, which are orientated flat onto the platform. Mechanical testing (tensile and compression testing) was conducted using a “MTS Insight 30-kN” tensile testing equipment (Material Testing Systems, USA) and a “MTS 810 100-kN” compression testing equipment (Material Testing Systems, USA) in accordance with ASTM E8 M-04 and ASTM D695-15, respectively. To estimate the relative part density, an “Upyc 1200e” (Quantachrome Instruments, USA) pycnometer was used applying helium gas with a target pressure of 131 kPa. Each sample was measured five times and results were averaged. Consequently, the relative part density values were obtained by comparing the measured volume from the pycnomoter with the outer volume of the cylindrical samples measured with a caliber (repetitive three-point analysis of the diameter). 3D-scanning was performed with an “Atos core 3D scanner” (GOM, Germany) and the underlying inspection software “GOM Inspect 2018” (GOM, Germany) is used to estimate the dimensional shrinkage percentages of an industrial wood tool acting as a spare part. Shrinkage percentages of the analyzed tensile and compression testing specimens were measured using a caliber due to their simple geometries as compared to the wood tool. Consequently, the shrinkage behavior is analyzed using linear regression models for potential shrinkage-influencing factors.

3 Results and discussions

In Fig. 1, fabricated tensile testing designs, an industrial wood tool, and a lattice structure representing “green” parts are shown. Except for the lattice design, all samples successfully passed the sintering step. The lattice design collapsed due to its delicate shape, not being able to hold its mass, representing one major design-dependent limitation of the metal FFF process.

Fig. 1
figure 1

Fabricated tensile testing specimens (flat, flipped, vertical), a lattice structure, and an industrial wood tool (before sintering)

Full size image

As shown in Fig. 2, sintered parts are presented. In this case, cylindrical pins for compression testing contain different theoretical infill levels. Visually, differences between the samples cannot be observed.

Fig. 2
figure 2

Sintered compression testing pins with varying theoretical infill levels ranging from 25 to 125%

Full size image

The established design of experiments comprises varying theoretical infill levels and varying print orientations for fabricated compression- and tensile testing samples, respectively. Thus, the number of experiments is kept at a minimum as compared to one-factor-at-a-time experimental setups while guaranteeing the transferability of results and maximizing the number of analyzed factors. In this regard, it can be assumed that varying theoretical infill levels do not affect the shrinkage behavior of tensile testing specimens in a different manner when being compared to the compression testing specimens, and that the compressive strength of the compression testing samples is affected comparably by its print orientation.

3.1 Tensile testing

In a first analysis step, the tensile testing samples printed in different orientations (vertical, flipped, flat) were mechanically tested, their stress–strain relations are presented in Fig. 3, and their key performance indicators are presented in Table 2.

Fig. 3
figure 3

Tensile properties of vertically, flipped, and flat tensile testing specimens (three samples each)

Full size image
Table 2 Tensile properties of tensile testing bars with varying print orientations (i.e., vertical, flipped, and flat)
Full size table

On average, the highest yield strength and ultimate tensile strength are reached when printing the samples flat onto the platform, followed by flipped and vertically fabricated specimens. Similarly, the elongation at break shows higher values in accordance with increased tensile stress levels.

Elasticity is fulfilled up to a strength of 104.77 ± 6.97 MPa, from which a plastic deformation zone to a maximum level of 311.81 ± 6.97 MPa is present.

The reason behind the inferior results of vertically and flipped tensile testing bars is most likely linked to weak layer adhesion. Since the number of layers is at a maximum if parts are printed vertically (layers perpendicular to tensile testing direction), strength is at its lowest level. Similar results for print orientation-dependent polymer-based FFF tensile testing can be found in literature [8]. Deviations in particular for the “flipped” orientation are based on defects resulting from necessary support structures under the horizontal middle section of the tensile testing samples.

The number of tensile testing samples for each orientation should be increased to five or more samples, each to provide an enhanced statistical validation of results. Since observed differences of the stress–strain behavior of the tensile testing specimens were not expected to occur at this level when designing the experiments, the initial number of samples was set to three samples per orientation to lower the cost for printing and sintering. Further tensile tests are planned to validate results on the print orientation-specific tensile testing behavior.

3.2 Compression testing

In Fig. 4, the stress–strain graphs of the compression testing pins containing varying infill levels are shown.

Fig. 4
figure 4

Compression properties for three samples of each infill level

Full size image

As expected, compressive stress levels increase with higher theoretical infill levels; from 53.23 ± 1.51 to 167.38 ± 2.51 MPa for yield strengths and 152.32 ± 3.73 to 667.62 ± 15.03 MPa for stresses at 20% strain when comparing 25–125% theoretical infill levels. The observation of increased mechanical strength by applying higher infill levels is backed up by polymer-based FFF testing in literature, demonstrating the positive effect of higher infill levels on mechanical strength [9]. Furthermore, yield strength is not increasing linearly with the theoretical infill percentages, whereas this is the case when measuring stresses at 20% compressive strain.

This observation could show that lower levels of theoretical infills (i.e., 25%, 50%) prevent higher stress levels, because their internal structures crack more rapidly when tested for compression. However, these results assist in targeting a certain compressive performance when aiming at material savings using specific infill levels (Table 3).

Table 3 Compression properties of compression testing cylinders with varying theoretical infill levels (i.e., 25%, 50%, 75%, 100%, and 125%)
Full size table

3.3 Relative part density

Since the relative part density of fabricated (post-sintered) compression testing parts has a significant effect on the mechanical performance, the relation between the theoretical infill and relative part density is investigated further. As presented in Fig. 5, a linear dependency between those two parameters is verified, resulting in relative part density levels of 40.99–95.4%.

Fig. 5
figure 5

Resulting relative part density for varying theoretical infill levels

Full size image

Higher relative part density levels appear possible when comparing these results to [5], in which a level of 98.5% is presented. Lower tensile testing results, e.g., 104.77 ± 6.97 MPa as compared to 167 MPa for yield strengths and 311.81 ± 6.97 MPa versus 465 MPa can be explained by lower relative part density levels used in this study (theoretical infill level of 100% for tensile testing with a relative part density of approx. 82.20%).

3.4 Shrinkage behavior

Finally, the shrinkage behavior applying the metal FFF process is investigated in detail. The shrinkage analysis process is presented in Fig. 6. Starting with a digital model of an industrial wood tool, the component is manufactured, debinded and sintered, and ultimately compared by taking the manufactured and sintered stages as the basis using 3D scanning techniques.

Fig. 6
figure 6

Process for shrinkage analysis for a wood tool acting as a demonstrator. From top: digital model, 3D-printed component, debinded and sintered component (post-processed front), comparison of 3D-printed and sintered stage using 3D scanning techniques

Full size image

In Fig. 7, the detailed dimensional comparison for the top, the side, and the frontal view of the wood tool is shown. Several measuring points are defined and shrinkage results are averaged.

Fig. 7
figure 7

Three-directional shrinkage analysis in GOM Inspect

Full size image

To analyze the dimensional shrinkage using linear regression models, data of fabricated samples are averaged for each 3D-printed geometry, compared to the nominal 3D model data, and analyzed based on three potential influencing factors (i.e., volume, height, and surface area). Resulting values are shown in Table 4; the linear fitting is presented in Fig. 8.

Table 4 Averaged shrinkage results based on nominal volume (vol), nominal height (z), and nominal surface area (A)
Full size table
Fig. 8
figure 8

Dimensional z- and x–y regression model fitting for the nominal volume (vol), nominal height (z), and nominal surface area (A)

Full size image

Linear regression with moderate confidence levels is exclusively observed for the nominal part height (z); unlike nominal part volume (vol) and nominal surface area (A). Therefore, two shrinkage predictability functions ((1) and (2)) for part dimensions are established:

$$ z\left( \% \right)\; = \; - \;0.0 4 8 7*z\; + \; 2 3. 3 5 8 { }\,\,\left( {R^{ 2} = \, 0. 6 3 7} \right) $$
(1)
$$ x - y\;\left( \% \right)\; = \;0.0 2 2 6*z\; + \; 1 6. 2 8 6 { }\,\,\left( {R^{ 2} \; = \;0. 7 5 3} \right) $$
(2)

Currently, the shrinkage predictability analysis is based on 27 samples, and more data are required to improve the model. Furthermore, a larger variety of part geometries including special design features such as overhangs, holes, and engraved details should be investigated further to account for a holistic analysis; in addition, the part orientation during the sintering stage may have an influence on the shrinkage behavior.

Furthermore, a potential influencing factor on dimensional shrinkage is represented by the theoretical infill level when analyzing the compression testing pins. However, as demonstrated in Fig. 9, the shrinkage percentages remain constant over varying theoretical infill percentages, and thus for varying density levels (as demonstrated in Fig. 5).

Fig. 9
figure 9

Shrinkage behavior for varying theoretical infill levels

Full size image

4 Conclusions

Print orientation has a crucial effect on resulting tensile testing performance for metal FFF. Furthermore, specific mechanical performances can be targeted by varying infill levels (no effect on shrinkage), making it possible to save manufacturing time and material. Finally, it could be demonstrated that this process is applicable for small-scale spare part production incorporating mentioned limitations and challenges. In this context, part height-dependent shrinkage predictability is assisted by established functions for a range of part geometries.