1 Introduction

Crack tip opening displacement (CTOD) is the displacement at the original crack tip or the 90° intercept (Rice 1964; Anderson 2017), and is also defined as the separation between the two surfaces of a physical crack tip (Nunes and Reis 2012). The double clip gauge technique was developed to directly measure CTOD (Willoughby and Garwood 1981). Hereby, the extrapolation of two clip gauge measurements at different heights above or at the crack mouth allows to directly measure the position of the plastic hinge. International Standard for Submarine pipeline systems accepted the double clip gauge technique to measure CTOD for specimens (DNV OS F101 2012), and recently British Standards Institution adopted the double clip gauge method to measure the plastic contribution of CTOD (BSI 2018). In elastic–plastic fracture mechanics, CTOD is generated from the elastic and plastic deformation of the specimen. However, in rocks, minor component of CTOD is due to elastic–plastic deformation. Microcracks and microdamage within FPZ should be the main contributors to CTOD (Dugdale 1960; Barenblatt 1962; Yang and Cox 2005; Dong et al. 2019). SEM analysis reveals an increase in microcrack density in FPZ with increased loading of the specimen (Hoagland et al. 1973; Brooks et al. 2013). Therefore, CTOD should be calculated considering FPZ effect in rock.

The measurement of CTOD is a vital and fundamental task for studying the fracture of solid materials. In the previous work (Tagawa et al. 2014), the actual CTOD was experimentally measured by using two different methods, one being observation of the sectioned crack tip after unloading and the other, replication of the loaded crack tip by silicone rubber casting. Therefore, CTOD is commonly measured using single or double clip gauge techniques and applying a plastic hinge model. However, clip gauge CTOD calculations merely provide information related to the center of the notch. For the case of a finite-length surface breaking notch, where CTOD is variable along the notch front, exact knowledge of CTOD over the entire front is not possible by the clip gauge measurement techniques (Kawabata et al. 2016). Thus, Samadian et al. (2019) proposed a novel technique based on full field three-dimensional profile measurement of the notched surface utilizing stereoscopic Digital Image Correlation (3D-DIC) to measure CTOD over the entire crack front. The proposed method was verified by the measurement of silicone replicas cast inside the notch in addition to a supporting FEM investigation. Lin et al. (2013, 2014) used DIC techniques to compute CTOD and FPZ length in sandstone under a three-point bending test. At the onset of unstable propagation (peak load), CTOD was 45 μm under mixed mode loading and 30 μm under mode I, and FPZ length was 10–12 mm for the mixed mode and 5–7 mm for mode I. Wu et al. (2020) proposed a new digital image correlation-based method to calculate and measure the FPZ length and crack opening displacement of heat-treated granite specimens, and found that CTOD increases parabolically as a function of the heat treatment temperature. At the temperature of 20 °C, the average CTOD is 9.86 μm. At 900 °C, the average CTOD is 90.20 μm. In summary, it is known that CTOD measurement values vary greatly in different methods, rocks and even temperatures. However, theoretical studies on CTOD can explain these variations.

After proposed CTOD, Wells (1963) conducted an approximate analysis that related the CTOD to the stress intensity factor in the limit of small-scale yielding. Considering a crack with a small plastic zone, Irwin (1968) postulated that crack-tip plasticity makes the crack behave as if it were slightly longer. Thus, the CTOD was estimated by determining the displacement at the physical crack tip (Anderson 2017). The strip-yield model provided an alternative means for analyzing CTOD (Burdekin and Stone 1966). The plastic zone was modeled by yield magnitude closure stresses. The size of the strip-yield zone was defined by the requirement of finite stresses at the crack tip. CTOD can be defined as the crack-opening displacement at the end of the strip-yield zone. According to this definition, CTOD in a through crack can be computed (Burdekin and Stone 1966). The British Standard Institution (BSI) standardized a CTOD estimation method based on a plastic hinge model from crack mouth opening displacement (BS5762:1979), however, American Society for Testing and Materials (ASTM) revised the estimation method based CTOD calculation (ASTM 2003). Following the revision mentioned above, the definition of CTOD was discussed (Wolfenden et al. 1992; Tagawa et al. 2010), and based on numerous CTOD test results, it was suggested that CTODASTM gives a smaller value than CTODBSI, Thus, a new CTOD calculation method was investigated by Kawabata et al. (2016), considering the variation of crack tip blunting due to strain hardening. A new factor f was introduced to correct the plastic term. In this factor, the blunted crack tip shape depends on the strain hardening exponent, and f is given as a function of the yield-to-tensile ratio of the material and the specimen thickness. These theories for calculating CTOD are based on a small range yield assumption and are still from elastic–plastic fracture mechanics. However, the FPZ size around crack tip is of the same order of magnitude as the specimen size at the peak load, making the small range yield assumption invalid (Planas and Elices 1991; Dutler et al. 2018). Moreover, CTOD is depend on cohesion (or closure stresses) in FPZ and there is a direct correlation between the magnitude of cohesion and the degree of damage in FPZ (Yang et al. 2019, 2021). Therefore, CTOD caused by elastic–plastic deformation is relatively small, CTOD generated by micro-damage in the FPZ is dominant.

The above reveals the need to consider FPZ in CTOD calculation. Therefore, this paper modifies the strip-yield model and plastic zone model for calculating CTOD by taking into the FPZ and the effective Young’s modulus, and verifies the revised theoretical models through three-point beam experiments.

2 Fracture experiment

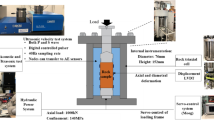
A sandstone in a quarry of Sichuan, China was selected to manufacture three-point bending beams, considering that sandstone is a common rock in coal mines and other fields related to natural resources such as the petroleum industry. The uniaxial compressive strength of the sandstone was 52.4 MPa. The minimum and maximum grain sizes of the sandstone were 0.11 mm and 0.54 mm, respectively, and the proportion of grain sizes between 0.15 and 0.3 mm was about 74%. The specimens had a central crack and a rectangular cross-section, and the pre-cracks were cut by a diamond wire with a diameter of 0.2 mm. The International Society of Rock Mechanics requires that the pre-crack width should be less than 1.5 mm ± 0.2 mm. The pre-crack widths in the tests ranged from 0.3 to 0.4 mm. The sizes of the specimens followed the suggested method by the International Society for Rock Mechanics (ISRM) and shown in Table 1 and Fig. 1.

Table 1 Dimensions of specimens
Full size table
Fig. 1
figure 1

Loading system and specimen

Full size image

The images with 2048 × 2048 pixels were acquired by Zeiss high-speed camera with a 100 mm fixed-focus lens. When the center deflection of the specimen changed each 0.001 mm, a photo was taken. The LED light sources were placed close to the camera. To control the loading process of the mechanical testing machine, the intermediate beam displacement was used as a servo feedback signal, and the loading rate was 0.0002 mm/s. The specimen loading system is shown in Fig. 1.

3 Results and analysis

3.1 Horizontal displacement distribution

The images collected from the experiments were processed by software (VIC-2D) to obtain horizontal displacements in each specimen. The software automatically established coordinates for the observation area. When the software processed the speckle photos, the subset and the step were set after carefully considering the photo quality and the data precision. The size of the subset was closely related to the accuracy of the data. When calculating the pixel displacement as a data point, the software matched the unloaded subset with the subset after loading to obtain the relevant point. The more relevant the points are, the better the matching and displacement accuracy. Therefore, the size of the subset was set as large as possible so that more relevant points could be matched to improve the calculation accuracy. In our case, the subset was set to 27 pixels. The size of the step was closely related to the data density. The step was the number of pixels between two data points. In this study, the step was 4 pixels, and the average accuracy allowed was set to 0.05 pixels.

Figure 2 shows the results of the horizontal displacements of specimens at the peak load. A contour line represents the same horizontal displacement level, and the difference between two adjacent contour lines is equal. Therefore, the density of the contours reflects the variation gradient of the horizontal displacements. The horizontal displacement contours are dense and diverge around the crack tip.

Fig. 2
figure 2

Horizontal displacement measured by DIC

Full size image

3.2 Crack tip opening displacement (CTOD) at peak load

According to CTOD definition, the CTOD is equal to the difference between the displacement values on both sides of the crack tip, and the displacement is obtained by the crack tip displacement field from the DIC. Vertical reference lines are placed at 2 mm on both sides of the crack of each size specimen, as shown in Fig. 3. Take the difference in displacement on reference lines between the two sides of the crack tip at the peak load as the CTOD. All experimental CTOD are shown in Fig. 4.

Fig. 3
figure 3

Vertical reference lines

Full size image
Fig. 4
figure 4

Crack tip opening displacement (CTOD) at peak load

Full size image

3.3 FPZ length at peak load

Using DIC technology, the displacements in the fracture ligaments of rock specimens were measured at peak load. By analyzing the displacement distribution of fracture ligament, the fluctuation coefficient of displacement was calculated to determine the FPZ length. The fluctuation coefficient is defined as a function of the horizontal displacement of five adjacent data points, as shown in Eq. 1.

$$\lambda_{i} = \sqrt {\mathop \sum \limits_{n = i - 2}^{i + 2} \left( {u_{n} - u} \right)^{2} }$$
(1)

where λi is the fluctuation coefficient of the data point i, un is the horizontal displacement value of the n-th data point, u is the average of five consecutive horizontal displacement values, and n is the horizontal displacement sequence number of the data point.

The fluctuation coefficient and FPZ are presented in Fig. 5. The FPZ length of all specimens are in Table 2.

Fig. 5
figure 5

Fluctuation coefficient distribution along fracture ligament at peak load

Full size image
Table 2 FPZ length at peak loading
Full size table

4 Theoretical analysis of CTOD

In this section, the theoretical CTOD is compared with the measured CTOD, and their difference is analyzed. The FPZ and the effective Young’s modulus are introduced to modify plastic zone model and strip-yield model for calculating CTOD.

4.1 Plastic zone model and strip-yield model

Considering a crack with a small plastic zone, Irwin (1968) postulated that crack-tip plasticity makes the crack behave as if it were slightly longer. Thus, we can estimate the CTOD by solving the displacement at the physical crack tip, assuming an effective crack length of \({a}_{0}\) + \({r}_{y}\). The displacement at the effective crack tip is given by (2)

$$u_{y} = \frac{{4K_{I} }}{E}\sqrt {\frac{{r_{y} }}{2\pi }}$$
(2)

where E is the Young’s modulus. The Irwin plastic zone length (\({r}_{y}\)) is:

$$r_{y} = \frac{1}{2\pi }\left( {\frac{{K_{I} }}{{\sigma_{t} }}} \right)^{2}$$
(3)

Substituting Eq. 3 into Eq. 2 gives

$$CTOD_{PZM} = 2u_{y} = \frac{4}{\pi }\frac{{K_{I}^{2} }}{{\sigma_{t} E}}$$
(4)

The strip-yield model provides an alternate means for analyzing CTOD (Burdekin and Stone 1966). The size of the strip-yield zone was defined by the requirement of finite stresses at the crack tip. The CTOD can be defined as the crack-opening displacement at the end of the strip-yield zone. According to this definition, CTOD in a through crack can be computed by Eq. 5 (Burdekin and Stone 1966).

$$CTOD_{SYM} = \frac{{8\sigma_{t} a_{0} }}{\pi E}ln\, sec\frac{\pi \sigma }{{2\sigma_{t} }} = \frac{{K_{I}^{2} }}{{E\sigma_{t} }}$$
(5)

As described above, fracture toughness and tensile strength are also required to calculate CTOD. Tensile strength and fracture toughness can be computed by Eqs. 6 and 7 (Tada et al. 2010; Wang and Hu 2017). Substituting both parameters and Young’s modulus (E = 12.35 GPa) into Eqs. 4 and 5, respectively, the CTOD can be determined. The result is shown in Fig. 6.

$$\sigma_{t} = \frac{{3P_{max} S}}{{2B\left( {H - a_{0} } \right)^{2} }}$$
(6)
$$K_{Ic} = \frac{{3SP_{max} }}{{2BH^{2} }}\sqrt {a_{0} } f\left( {\frac{{a_{0} }}{H}} \right)$$
(7)

\(f\left( {\frac{{a_{0} }}{H}} \right) = \frac{{1.99 - \frac{{a_{0} }}{H}\left( {1 - \frac{{a_{0} }}{H}} \right)\left[ {2.15 - 3.93\frac{{a_{0} }}{H} + 2.7\left( {\frac{{a_{0} }}{H}} \right)^{2} } \right]}}{{\left( {1 + 2\frac{{a_{0} }}{H}} \right)\left( {1 - \frac{{a_{0} }}{H}} \right)^{1.5} }}\)

Fig. 6
figure 6

CTOD comparison between two unmodified theoretical models and experiment

Full size image

where \({P}_{max}\) is the peak load to the specimen, S is the distance between the two supports below the three-point bending beam, B is the thickness of the specimen, H is the height of the specimen, and \({a}_{0}\) is the pre-crack length.

Figure 6 (Blue and yellow line) shows that the theoretical CTOD values were much smaller than the experimental values, i.e., they were only 8–19% of the experimental values. This is because the two models are derived from elastic–plastic fracture mechanics. However, the FPZ size is of the same order of magnitude as the specimen size at the peak load, making the small plastic zone assumption invalid. Thus, the theoretical formulation needs to be revised. The experimentally-measured CTOD consists of: (1) the displacement generated by the elastic–plastic deformation in the crack tip, and (2) the displacement generated by micro-damage in the FPZ. Based on the experimental data, it can be seen (Fig. 6) that the CTOD caused by elastic–plastic deformation is relatively small, accounting for about 8–19% of the overall CTOD. However, the CTOD generated by micro-damage in the FPZ is 81–92%.

4.2 Modified plastic zone model and strip-yield model

The modified models are based on the correction to tensile strength, fracture toughness and Young’s modulus. As mentioned above, the source of the CTOD at the peak load is not only the elastic–plastic deformation of the crack tip, but also micro-scale damage such as microcracking. These damages are from the FPZ, so the influence of the FPZ on the above three parameters needs to be considered.

The fracture process of rock under Three-pointed bend loading condition can be divided into four phases (Hashida and Takahashi 1993): (1) pre-existing microcracks before loading; (2) a few tensile micro-cracks initiate on the weakest plane near the notch tip and beginning of detectable non-linearity of load–displacement record; (3) growth and linkage of microcracks and increasing non-linear deformation; (4) large scale linkage of micro-cracks and fracture of the remaining strongest bonding occur and onset of macroscopic crack extension. The corresponding load–displacement curve is shown in Fig. 7.

Fig. 7
figure 7

The load- displacement curve of the micro-fracture process (Hashida and Takahashi 1993)

Full size image

The partially developed FPZ is formed at the peak load and fully developed FPZ is formed after the peak load and their corresponding locations on the load–displacement curve are marked in Fig. 7. Because of microcrack, frictional sliding and pull-out of grains, the stress corresponding the partially developed FPZ is almost equal to the tensile strength around the crack tip. While stress corresponding a fully developed FPZ varies from zero to the direct tensile strength (Wittmann and Hu 1991). The shapes of the load–displacement curves (Fig. 8) in this study are similar to the load–displacement curve in Fig. 7.

Fig. 8
figure 8

The load- displacement curve

Full size image

For simplicity, a constant stress within the partially developed FPZ, akin to those in the literature (Chamberlain and Boswell 1983; Guinea et al. 2000), is assumed. This is acceptable if the length of FPZ does not exceed one-tenth of the height or width of the specimen. Then, tensile strength was corrected by applying the FPZ length from experiment, and we need to consider the stress condition along the FPZ and two equilibrium conditions for bending stress and bending moment to establish four equations. Assume that the stress in the FPZ is equal to the tensile strength and is uniformly distributed. Using the stress distribution along the crack plane in Fig. 9, we have:

$$y = \frac{{\sigma_{c} }}{{\sigma_{t}^{*} }}x$$
(8)

where \(x\) is the distance from the FPZ tip to the neutral axis and y is the distance from the point of Pmax to the neutral axis, as shown in Fig. 9. It can be written that:

$$x + y = H - a_{0} - l_{p}$$
(9)
Fig. 9
figure 9

Specimen parameters

Full size image

The force equilibrium condition along the crack plane in Fig. 6 is:

$$0.5 \times \sigma_{c} \times y = 0.5 \times \sigma_{t}^{*} \times x + l_{p} \times \sigma_{t}^{*}$$
(10)

The moment equilibrium condition gives:

$$\frac{1}{4} \times \frac{{SP_{max} }}{B} = \frac{1}{3}\sigma_{c} y^{2} + \frac{1}{3}\sigma_{t}^{*} x^{2} + \sigma_{t}^{*} l_{p} \left( {\frac{1}{2}l_{p} + x} \right)$$
(11)

There are four unknown parameters, \(\sigma_{t}^{*}\), \(\sigma_{c}\), \(x {\text{and}} y\), in the above four equations, Eqs. (8–11). Eliminating \(\sigma_{c}\), \(x\;{\text{and}}\;y\) from the above relations, it can be obtained that:

$$\sigma_{t}^{*} = \frac{{\frac{S}{B} \times P_{max} }}{{\frac{{\left( {H - a_{0} - l_{p} } \right)\left( {H - a_{0} + l_{p} } \right)^{3} + \left( {H - a_{0} - l_{p} } \right)^{4} + 6l_{p} \left( {H - a_{0} - l_{p} } \right)^{2} \left( {H - a_{0} } \right)}}{{3\left( {H - a_{0} } \right)^{2} }} + 2l_{p}^{2} }}$$
(12)

where \({P}_{max}\) is the peak load to the specimen, S is the distance between the two supports below the three-point bending beam, B is the thickness of the specimen, H is the height of the specimen, and \({a}_{0}\) is the pre-crack length. \({\sigma }_{c}\) is the compressive stress, and \({l}_{p}\) is the FPZ length obtained experimentally. These parameters are also shown in Fig. 9.

The FPZ makes rock fracture behavior no longer strictly conform to LEFM (Friedman et al. 1972; Hoagland et al. 1973). The FPZ can be regarded as a damaged but uncracked area (Labuz et al. 1987). Many modified models are based on the concept of effective crack length to consider the effect of FPZ on material fracture behavior (Labuz et al. 1985, 1987; Kramarov et al. 2020), and Labuz et al. (1985, 1987) experimentally concluded that the effective crack length in rock fracture tests should include the FPZ length. Therefore, the modified fracture toughness takes the FPZ length as part of the crack length.

$$a_{eff}^{*} = a_{0} + l_{p}$$
(13)
$$K_{Ic}^{*} = \frac{{3SP_{max} }}{{2BH^{2} }}\sqrt {a_{eff}^{*} } f\left( {\frac{{a_{eff}^{*} }}{H}} \right)$$
(14)

Micro-damage caused by stress perturbations and locally high stresses can reduce the elastic modulus of rock (Heap and Faulkner 2008; Heap et al. 2009). Experimental data are added to support this conclusion. The average strain value in the sampling line was first obtained using DIC, and the sampling line was 1 mm from and perpendicular to the crack tip. This average value was taken as the strain value around the crack tip. Two loading moments, pre-peak 40% and peak load, were selected. According to Eqs. (6) and (12), the crack tip stress is approximately proportional to the loading force. According to 1D Hooke's law. we calculate the tensile Young's modulus ratio between at pre-peak 40% and peak load, \({E}_{eff}^{*}/{E}_{t}\), as shown in the Table 3. The tensile Young's modulus at the peak moment is taken as the corrected effective Young's modulus (\({E}_{eff}^{*}\)), and the tensile Young's modulus at pre-peak 40% is the normal tensile Young's modulus (\({E}_{t}\)).

Table 3 Tensile Young's modulus ratio
Full size table

Rocks show different Young’s modulus in compression and tension (Fairhurst 1961). The limited data in the literature including both compressive and tensile elastic modulus indicates that the compressive modulus is always larger than the tensile modulus of rock (Jianhong et al. 2009; Fuenkajorn and Klanphumeesri 2011; Ye et al. 2012). For instance, the tensile modulus was found to be 65.4% \({(E}_{t}/E)\) of the compressive modulus (Patel and Martin 2018). Integrating the stress state and degree of damage at the crack tip, the average value of \({E}_{eff}^{*}/{E}_{t}\) is 0.501784, and \({E}_{t}/E\) is 65.4%. Therefore, the effective Young's modulus is 1/3 of the Young's modulus in compression.

$$E_{eff}^{*} = \frac{1}{3}E$$
(15)

The modified tensile strength, fracture toughness and effective Young's modulus were taken into Eqs. 4 and 5 to obtain Eqs. 16 and 17. The CTOD values from modified models and experiments are shown in Fig. 10.

$$CTOD_{PZM}^{*} = \frac{4}{\pi }\frac{{\left( {K_{Ic}^{*} } \right)^{2} }}{{\sigma_{t}^{*} E_{eff}^{*} }}$$
(16)
$$CTOD_{SYM}^{*} = \frac{{\left( {K_{Ic}^{*} } \right)^{2} }}{{\sigma_{t}^{*} E_{eff}^{*} }}$$
(17)
Fig. 10
figure 10

CTOD values from two modified models and experiment

Full size image

Figure 11 shows that the errors between the experimental CTOD and theoretical CTOD from strip-yield mode (SYM) and plastic zone model (PZM) are 85–92% and 81–90%, respectively. However, the errors between the experimental CTOD and theoretical CTOD from the modified SYM and modified PZM are 50–15% and 4–34%, respectively. The modified plastic zone model (PZM) matches well the experimental results, and nearly half of the specimens have an error less than 10%. These data prove that the modified plastic zone model is a good predictor of experimental results.

Fig. 11
figure 11

Errors between calculated CTOD values from fours models (two modified models and two unmodified models) and measured CTOD values from experiment

Full size image

5 Discussion

In this study, the CTOD generation is clarified as the elastic–plastic deformation and the micro-damage, both of which contribute 8–19% and 81–92% to CTOD respectively. The plastic zone model for calculating CTOD are also modified to reduce the error between them and the experimental values to 4–34%.

In this study, the measured CTOD values at the peak load are 0.018–0.028 mm, which are close to the CTOD of 0.030 mm obtained by Lin et al (2014). However, the measured CTOD values in this study are significantly different from the measured CTOD values by Chen et al. (2023) (6.67–6.97 um), Dong et al. (2019) (4.34 um) and Pan et al. (2021) (3.09 um). This because rock type, specimen configuration and specimen size all affect the measured CTOD values. In addition, the testing standards in the forementioned studies are not uniform. In this and Lin et al.’s study, a CTOD value was obtained by subtracting the displacement values on both sides of the crack tip, but in Chen et al.’ study the virtual extensometer functions from the DIC corresponding software was used, and in Dong et al.’s study microscale observations and solution analytical fitting were used. Note that the first CTOD test standard was published in Great Britain in 1979. Several years later, ASTM published E 1290, an American version of the CTOD standard. ASTM E 1290 has been revised several times, and the most recent version was published in 2008. With the widespread use of DIC in rock testing, the measured CTOD standards applicable to DIC test should be established.

CTOD as a parameter for determining material fracture behavior has an advantage since it is an intuitive parameter that requires no further calculations comparing to fracture toughness (\({K}_{Ic}\)) and energy release rate (G). Only when the CTOD reaches this critical value does the crack extend unstably. In addition, a CTOD value may be independent on rock specimen size, according to the CTOD values in Fig. 4. For instance, the sizes of TPB1-3 and TPB4-6 are different in Table 1, but these two specimens do not show much different CTOD values (Fig. 4). However, this needs more experiments to further confirm.

To make the CTOD more obtainable, according to the rigid hinge model (Anderson 2017), the crack opening displacement at a certain place can be converted to the crack tip opening displacement. The opening displacement \(\delta\) at any point of crack can be measured, and the CTOD can be inferred by geometric relationship with \(\delta\), as illustrated in Fig. 12. Referring to this figure, we can estimate CTOD from a similar triangle’s construction:

$$\frac{CTOD}{{\left( {H - L} \right)r}} = \frac{\delta }{{L + \left( {H - L} \right)r}}$$
(18)
Fig. 12
figure 12

The geometric model for estimating CTOD from three-point bend specimens

Full size image

Therefore

$$CTOD = \frac{{\delta \left( {H - L} \right)r}}{{L + \left( {H - L} \right)r}}$$
(19)

where \(r\) is the rotational factor, a dimensionless constant between 0 and 1. The CTOD can be obtained easily by the methods above.

6 Conclusions

The measured CTOD consists of two parts: (1) the displacement generated by elastic–plastic deformation in the crack tip region, and (2) the displacement generated by micro-damage in the FPZ. Based on the experimental data and theoretical analysis from strip-yield mode (SYM) and plastic zone model (PZM), the CTOD value caused by elastic–plastic deformation and micro-damage in the FPZ accounts for about 8–19% and 81–92% of the overall CTOD.

The modified plastic zone model is better than the strip-yield mode, the plastic zone model and the modified strip-yield mode in calculating the CTOD of the rock specimens. The CTOD error is reduced from 81 to 90% between the plastic zone model and the experiment to 4–34% between the modified plastic zone model and the experiment, with nearly half of the specimens having an error of less than 10%.