Evaluation of Tensile Young’s Modulus and Poisson’s Ratio of a Bi-modular Rock from the Displacement Measurements in a Brazilian Test

Abstract

Unlike metals, rocks show bi-modularity (different Young’s moduli and Poisson’s ratios in compression and tension). Displacements monitored during the Brazilian test are used in this study to obtain the Young’s modulus and Poisson’s ratio in tension. New equations for the displacements in a Brazilian test are derived considering the bi-modularity in the stress–strain relations. The digital image correlation technique was used to monitor the displacements of the Brazilian disk flat surface. To validate the Young’s modulus and Poisson’s ratio obtained from the Brazilian test, the results were compared with the values from the direct tension tests. The results obtained from the Brazilian test were repetitive and within 3.5% of the value obtained from the direct tension test for the rock tested.

Appendix

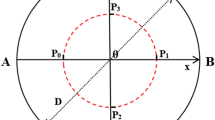
1.1 Displacement Along Horizontal and Vertical Line in a Brazilian Test

Figure 8 shows the Brazilian disk loaded along its vertical diameter EF. For a particular value of load (P), the horizontal displacement (u(x)) along the horizontal diameter (AB) and the vertical displacement (v(y)) along the vertical diameter (EF) are functions of x, y, E _c, E _t, ν _c and ν _t (due to symmetry, the vertical displacement along AB and the horizontal displacement along EF are zero). The derivations for u(x) and v(y) here follow the methodology that is adopted by Ye et al. (2012). However, the bi-modularity relation between the elastic constants as given by Ambartsumyan (1969) and Sundaram and Corrales (1980) is considered in the Brazilian stress–strain equations.

Fig. 8

Brazilian sample loaded along the diameter

The horizontal and vertical stress along the horizontal diameter AB are:

$$\sigma_{xx} = \frac{2P}{\pi Dt}\left[ {1 - \frac{{16D^{2} x^{2} }}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}} \right]$$

(6)

$$\sigma_{yy} = \frac{2P}{\pi Dt}\left[ {1 - \frac{{4D^{4} }}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}} \right]$$

(7)

and the horizontal and vertical stress along the vertical diameter EF are:

$$\sigma_{xx} = \frac{2P}{\pi Dt}$$

(8)

$$\sigma_{yy} = \frac{2P}{\pi Dt}\left[ {1 - \frac{{4D^{2} }}{{\left( {D^{2} - 4y^{2} } \right)^{2} }}} \right]$$

(9)

(Hondros 1959; Ye et al. 2012).

According to Ambartsumyan (1969) and the model adopted by Sundaram and Corrales (1980), the strain–stress relationships for a plane stress condition (σ _zz  = 0) with bi-modularity can be written as:

$$\varepsilon_{xx} = \frac{{\sigma_{xx} }}{{E_{\text{t}} }} - C_{0} \sigma_{yy}$$

(10)

and

$$\varepsilon_{yy} = \frac{{\sigma_{yy} }}{{E_{\text{c}} }} - C_{0} \sigma_{xx}$$

(11)

where

$$C_{0} = \frac{{\nu_{\rm t} }}{{E_{\rm t} }} = \frac{{\nu_{\rm c} }}{{E_{\rm c} }}$$

(12)

Considering a small segment dx at a distance x from the center of the disk along the horizontal diameter AB (Fig. 8), the small displacement of this segment is:

$$\begin{aligned} {\text{d}}u & = \varepsilon_{xx} {\text{d}}x \\ {\text{d}}u & = \left[ {\frac{{\sigma_{xx} }}{{E_{\text{t}} }} - \frac{{\nu_{\rm c} \sigma_{yy} }}{{E_{\text{c}} }}} \right]{\text{d}}x \\ \end{aligned}$$

and the total horizontal displacement of the point at distance x is:

$$u\left( x \right) = \mathop \int \nolimits_{0}^{x} \left[ {\frac{{\sigma_{xx} }}{{E_{\text{t}} }} - \frac{{\nu_{\text{c}} \sigma_{yy} }}{{E_{\text{c}} }}} \right]{\text{d}}x$$

Substituting the value of σ _xx and σ _yy from Eqs. (6) and (7), u(x) can be written as:

$$\begin{aligned} u\left( x \right) = & \frac{2P}{{\pi DtE_{\text{t}} }}\mathop \int \nolimits_{0}^{x} {\text{d}}x - \frac{2PD}{{\pi tE_{\text{t}} }}\mathop \int \nolimits_{0}^{x} \frac{{16x^{2} }}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}{\text{d}}x - \frac{{2\nu_{\text{c}} P}}{{\pi DtE_{\text{c}} }}\mathop \int \nolimits_{0}^{x} {\text{d}}x + \frac{{2\nu_{\text{c}} PD^{4} }}{{\pi DtE_{\text{c}} }}\mathop \int \nolimits_{0}^{x} \frac{4}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}{\text{d}}x \\ & \Rightarrow u\left( x \right) = \frac{2Px}{{\pi DtE_{\text{t}} }} - \frac{2PD}{{\pi tE_{\text{t}} }}\mathop \int \nolimits_{0}^{x} \frac{{16x^{2} }}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}{\text{d}}x - \frac{{2\nu_{\text{c}} Px}}{{\pi DtE_{\text{c}} }} + \frac{{2\nu_{\text{c}} PD^{4} }}{{\pi DtE_{\text{c}} }}\mathop \int \nolimits_{0}^{x} \frac{4}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}{\text{d}}x \\ & \Rightarrow u\left( x \right) = \frac{2Px}{{\pi DtE_{\text{t}} }} - \frac{2PD}{{\pi tE_{\text{t}} }}\left. {I_{1} } \right]_{0}^{x} - \frac{{2\nu_{\text{c}} Px}}{{\pi DtE_{\text{c}} }} + \frac{{2\nu_{\text{c}} PD^{4} }}{{\pi DtE_{\text{c}} }}\left. {I_{2} } \right]_{0}^{x} \\ \end{aligned}$$

where

$$I_{1} = \mathop \int \nolimits \frac{{16x^{2} }}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}{\text{d}}x$$

and

$$\begin{aligned} I_{2} & = \mathop \int \nolimits \frac{4}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}{\text{d}}x \\ I_{1} & = \mathop \int \nolimits \frac{{16x^{2} }}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}{\text{d}}x = 4\mathop \int \nolimits \frac{{4x^{2} }}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}{\text{d}}x \\ & \Rightarrow I_{1} = 4\mathop \int \nolimits \frac{{D^{2} + 4x^{2} - D^{2} }}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}{\text{d}}x \\ & \Rightarrow I_{1} = 4\mathop \int \nolimits \frac{{{\text{d}}x}}{{\left( {D^{2} + 4x^{2} } \right)}} - 4D^{2} \mathop \int \nolimits \frac{{{\text{d}}x}}{{\left( {D^{2} + 4x^{2} } \right)^{2} }} \\ & \Rightarrow I_{1} = \frac{4}{{D^{2} }}\mathop \int \nolimits \frac{{{\text{d}}x}}{{\left( {1 + \frac{{4x^{2} }}{{D^{2} }}} \right)}} - 4D^{2} \mathop \int \nolimits \frac{{{\text{d}}x}}{{\left( {D^{2} + 4x^{2} } \right)^{2} }} \\ \end{aligned}$$

Let’s assume w $= 2x/D$ for the first part and $x = \frac{D}{2} \tan z$ for the second part.

$$\begin{aligned} {\text{i}} . {\text{e}} .\,{\text{d}}w &= \frac{2}{D}{\text{d}}x;\,\left( {D^{2} + 4x^{2} } \right)^{2} = D^{4} \sec^{2} z\,{\text{and}}\,{\text{d}}x = \frac{1}{2}D \sec^{2} z\,{\text{d}}z \hfill \\ &\Rightarrow I_{1} = \frac{2}{D}\mathop \int \nolimits \frac{{{\text{d}}w}}{{\left( {1 + w^{2} } \right)}} - \frac{2}{D}\mathop \int \nolimits \cos^{2} z {\text{d}}z \hfill \\ &\Rightarrow I_{1} = \frac{2}{D}\tan^{ - 1} w - \frac{\sin 2z}{2D} - \frac{z}{D} \hfill \\ \end{aligned}$$

substituting the values of w and z

$$\begin{aligned} & \Rightarrow I_{1} = \frac{2}{D}\tan^{ - 1} \frac{2x}{D} - \frac{1}{D}\frac{{\left( {{\raise0.7ex\hbox{${2x}$} \!\mathord{\left/ {\vphantom {{2x} D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}} \right)}}{{\left( {{\raise0.7ex\hbox{${2x}$} \!\mathord{\left/ {\vphantom {{2x} D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}} \right)^{2} + 1}} - \frac{1}{D}\tan^{ - 1} \frac{2x}{D} \\ & \Rightarrow I_{1} = \frac{1}{D}\tan^{ - 1} \frac{2x}{D} - \frac{2x}{{4x^{2} + D^{2} }} \\ & I_{2} = \mathop \int \nolimits \frac{4}{{\left( {D^{2} + 4x^{2} } \right)^{2} }}{\text{d}}x \\ \end{aligned}$$

Assuming $x = \frac{D}{2} {\text{tan }}w$

$$\begin{aligned} & {\text{i}} . {\text{e}} .\,\left( {D^{2} + 4x^{2} } \right)^{2} = D^{4} \sec^{2} w\,{\text{and}}\,{\text{d}}x = \frac{1}{2}D \sec^{2} w\,{\text{d}}w \\ & \Rightarrow I_{2} = \frac{2}{{D^{3} }}\mathop \int \nolimits \cos^{2} w{\text{d}}w \\ & \Rightarrow I_{2} = \frac{1}{{D^{3} }}\mathop \int \nolimits \left( {\cos 2w + 1} \right){\text{d}}w \\ & I_{2} = \frac{1}{{D^{3} }}\left( {\frac{\sin 2w}{2} + w} \right) \\ \end{aligned}$$

Substituting the value of w,

$$I_{2} = \frac{1}{{D^{2} }}\tan^{ - 1} \frac{2x}{D} + \frac{2x}{{D^{2} \left( {4x^{2} + D^{2} } \right)}}$$

Hence,

$$u\left( x \right) = \frac{2Px}{\pi Dt}\left( {\frac{1}{{E_{\rm t} }} - \frac{{\nu_{\rm c} }}{{E_{\rm c} }}} \right) - \frac{2PD}{{\pi tE_{\rm t} }}\left. {I_{1} } \right]_{0}^{x} + \frac{{2\nu_{\rm c} PD^{4} }}{{\pi DtE_{\rm c} }}\left. {I_{2} } \right]_{0}^{x}$$

Substituting the vales for I ₁ and I ₂ and rearranging u(x) can be written as:

$$u\left( x \right) = \frac{2P}{\pi t}\left[ {\left( {\frac{x}{D} - \tan^{ - 1} \frac{2x}{D}} \right)\left( {\frac{1}{{E_{\rm t} }} - \frac{{\nu_{\rm c} }}{{E_{\rm c} }}} \right) + \frac{2Dx}{{4x^{2} + D^{2} }} \left( {\frac{1}{{E_{\rm t} }} + \frac{{\nu_{\rm c} }}{{E_{\rm c} }}} \right)} \right]$$

(13)

or in terms of du/dP

$${\text{d}}u/{\text{d}}P = \frac{1}{{m_{x} }} = \frac{2}{\pi t}\left[ {\left( {\frac{x}{D} - \tan^{ - 1} \frac{2x}{D}} \right)\left( {\frac{1}{{E_{\rm t} }} - \frac{{\nu_{\rm c} }}{{E_{\rm c} }}} \right) + \frac{2Dx}{{4x^{2} + D^{2} }} \left( {\frac{1}{{E_{\rm t} }} + \frac{{\nu_{\rm c} }}{{E_{\rm c} }}} \right)} \right]$$

(14)

where $m_{x} = {\text{d}}P/{\text{d}}u$ (slope of u-P plot, Fig. 7).

Similarly, considering a small segment dy at a distance y from the center of the disk along the vertical diameter EF (Fig. 8), the small displacement of this segment is:

$${\text{d}}v = \left[ {\frac{{\sigma_{yy} }}{{E_{\rm c} }} - \frac{{\nu_{\rm t} \sigma_{xx} }}{{E_{\rm t} }}} \right]{\text{d}}y = \left[ {\frac{{\sigma_{yy} }}{{E_{\rm c} }} - \frac{{\nu_{\rm c} \sigma_{xx} }}{{E_{\rm c} }}} \right]{\text{d}}y$$

and the total vertical displacement of the point at distance y is:

$$\begin{aligned} v\left( y \right) & = \mathop \int \nolimits_{0}^{y} \left[ {\frac{{\sigma_{yy} }}{{E_{\rm c} }} - \frac{{\nu_{\rm c} \sigma_{xx} }}{{E_{\rm c} }}} \right]{\text{d}}y \\ & \Rightarrow v\left( y \right) = \frac{1}{{E_{\rm c} }}\mathop \int \nolimits_{0}^{y} \sigma_{yy} {\text{d}}y - \frac{{\nu_{\rm c} }}{{E_{\rm c} }}\mathop \int \nolimits_{0}^{y} \sigma_{xx} {\text{d}}y \\ \end{aligned}$$

substituting the value of σ _xx and σ _yy from Eqs. (8) and (9), $v\left( y \right)$ can be written as:

$$\begin{aligned} v\left( y \right) & = \frac{1}{{E_{\rm c} }}\mathop \int \nolimits_{0}^{y} \frac{2P}{\pi Dt}\left( {1 - \frac{{4D^{2} }}{{D^{2} - 4y^{2} }}} \right){\text{d}}y - \frac{{\nu_{\rm c} }}{{E_{\rm c} }}\mathop \int \nolimits_{0}^{y} \frac{2P}{\pi Dt}{\text{d}}y \\ & \Rightarrow v\left( y \right) = \frac{2P}{{\pi DtE_{\rm c} }}\mathop \int \nolimits_{0}^{y} {\text{d}}y - \frac{8DP}{{\pi tE_{\rm c} }}\mathop \int \nolimits_{0}^{y} \left( {\frac{1}{{D^{2} - 4y^{2} }}} \right){\text{d}}y - \frac{{2P\nu_{\rm c} }}{{\pi DtE_{\rm c} }}\mathop \int \nolimits_{0}^{y} {\text{d}}y \\ & \Rightarrow v\left( y \right) = \frac{2Py}{{\pi DtE_{\rm c} }}\left( {1 - \nu_{\rm c} } \right) - \frac{8DP}{{\pi tE_{\rm c} }}\left. {I_{3} } \right]_{0}^{y} \\ \end{aligned}$$

where,

$$I_{3} = \mathop \int \nolimits \frac{{{\text{d}}y}}{{\left( {D^{2} - 4y^{2} } \right)}}$$

Assuming 2y = t, i.e., 2dy = dt

$$\begin{aligned} I_{3} & = \frac{1}{2}\mathop \int \nolimits \frac{{{\text{d}}t}}{{\left( {D^{2} - t^{2} } \right)}} \\ & \Rightarrow I_{3} = \frac{1}{2} \left( {\frac{1}{2D}\ln \left[ {\frac{D + t}{D - t}} \right]} \right) \\ & \Rightarrow I_{3} = \frac{1}{4D}\ln \left[ {\frac{D + 2y}{D - 2y}} \right] \\ \end{aligned}$$

substituting the value of I ₃

$$\begin{aligned} & \Rightarrow v\left( y \right) = \frac{2Py}{{\pi DtE_{\rm c} }}\left( {1 - \nu_{\rm c} } \right) - \frac{8DP}{{\pi tE_{\rm c} }}\left( {\frac{1}{4D}\ln \left[ {\frac{D + 2y}{D - 2y}} \right]} \right) \\ & \Rightarrow v\left( y \right) = \frac{2Py}{{\pi DtE_{\rm c} }}\left( {1 - \nu_{\rm c} } \right) - \frac{2P}{{\pi tE_{\rm c} }}\ln \left[ {\frac{D + 2y}{D - 2y}} \right] \\ & v\left( y \right) = - \frac{2P}{{\pi tE_{\rm c} }}\left[ {\ln \frac{D + 2y}{D - 2y} - \frac{y}{D}\left( {1 - \nu_{\rm c} } \right)} \right] \\ \end{aligned}$$

(15)

or in terms of dv/dP

$$\frac{{{\text{d}}v}}{{{\text{d}}P}} = \frac{1}{{m_{y} }} = - \frac{2}{{\pi tE_{\rm c} }}\left[ {\ln \frac{D + 2y}{D - 2y} - \frac{y}{D}\left( {1 - \nu_{\rm c} } \right)} \right]$$

(16)

where $m_{y} = {\text{d}}P/{\text{d}}v$ (slope of v-P plot, Fig. 7).

1.2 Calculation of Tensile Modulus from the Displacement Measurements

The horizontal displacement equation

$$u\left( x \right) = \frac{2P}{\pi t}\left[ {\left( {\frac{x}{D} - \tan^{ - 1} \frac{2x}{D}} \right)\left( {\frac{1}{{E_{\rm t} }} - \frac{\nu }{{E_{\rm c} }}} \right) + \frac{2Dx}{{4x^{2} + D^{2} }} \left( {\frac{1}{{E_{\rm t} }} + \frac{{\nu_{\rm c} }}{{E_{\rm c} }}} \right)} \right]$$

can be written as:

$$C = A\left( {\frac{1}{{E_{\rm t} }} - \frac{{\nu_{\rm c} }}{{E_{\rm c} }}} \right) + B\left( {\frac{1}{{E_{\rm t} }} + \frac{{\nu_{\rm c} }}{{E_{\rm c} }}} \right)$$

(17)

where,

$$A = \left( {\frac{x}{D} - \tan^{ - 1} \frac{2x}{D}} \right); B = \frac{2Dx}{{4x^{2} + D^{2} }} \,{\text{and}}\,C = \frac{\pi ut}{2P} = \frac{\pi t}{{2m_{x} }}$$

(18)

The vertical displacement equation

$$v\left( y \right) = - \frac{2P}{{\pi tE_{\rm c} }}\left[ {\ln \frac{D + 2y}{D - 2y} - \frac{y}{D}\left( {1 - \nu_{\rm c} } \right)} \right]$$

can be written as:

$$F = \frac{1}{{E_{\rm c} }}\left[ {G - H\left( {1 - \nu_{\rm c} } \right)} \right]$$

where,

$$F = - \frac{\pi vt}{2P} = - \frac{\pi t}{{2m_{y} }};\quad G = \ln \frac{D + 2y}{D - 2y} \,{\text{and}}\,H = \frac{y}{D}$$

(19)

$$\frac{1}{{E_{\rm c} }} = \frac{F}{{\left[ {G - H\left( {1 - \nu_{\rm c} } \right)} \right]}}.$$

(20)

substituting the value of $\frac{1}{{E_{\rm c} }}$ in Eq. (17) and rearranging, E_t can be expressed as:

$$E_{\rm t} = \frac{A + B}{{C + \frac{{\left( {A - B} \right)F\nu_{\rm c} }}{{F + G\left( {\nu_{\rm c} - 1} \right)}}}}$$

(21)

The elastic constants are related by the equation (Ambartsumyan 1969):

$$\frac{{\nu_{\rm t} }}{{E_{\rm t} }} = \frac{{\nu_{\rm c} }}{{E_{\rm c} }}$$

Substituting the value of 1/E _c and E _t, ν _t can be written as:

$$\nu_{\rm t} = \frac{{\left( {A + B} \right)F\nu_{\rm c} }}{{\left[ {G - H\left( {1 - \nu_{\rm c} } \right)} \right]\left[ {C + \frac{{\left( {A - B} \right)F\nu_{\rm c} }}{{G + H\left( {\nu_{\rm c} - 1} \right)}}} \right]}}$$

(22)

1.3 Sample Calculation for Young’s Modulus and Poisson’s Ratio in Tension form the Displacement Measurements

The typical value obtained for a sample and the parameters A, B, C, F, G, H, E _c, E _t and ν _t as per the (18), (19), (20), (21) and (22) are shown in Table 5. The coefficient of variation for the tensile Young’s modulus and Poisson’s ratio are 6.0 and 3.7%, respectively. These variations within the sample are acceptable considering the different kinds of mineral grains present in the sample as discussed in Sect. 3 and because some plastic strain may have developed in the sample even at 50% of the peak load.

Table 5 Typical values measured and the tensile modulus and Poisson’s ratio obtained for a sample