Combined effect mechanism of linear loading and disturbance with different amplitudes on sandstone

Abstract

To comprehend the stress state and response characteristics of materials under complex conditions, researchers have decomposed stress states into fundamental paths and investigated diverse path combinations. To ensure comparability, four identical samples were carefully selected from a pool of 100 samples using ultrasonic tests based on the wave speed and waveform characteristics. These samples underwent specially designed stress paths to analyze the combined effects of linear loading and perturbation. Our result analysis centred on the perturbation amplitude and stress levels during composite action, revealing intricate relationships between the stress levels, strain, and nonlinear/linear energy evolution under complex stress paths. Simultaneously, 3D surface fractures were precisely reconstructed using the YOLOv5 and FAST feature point detection algorithms, elucidating the evolving patterns of the fractures. As a result of our study, the rotation trend of the main fracture was validated by integrating mechanics and P-wave reflection rules. Notably, our experimental results closely aligned with the theoretical predictions, showing the reliability of our study. These findings can significantly contribute to guiding safety protocols in the field of underground engineering.

Article highlights

• The combined effects of the stress paths under linear loading and perturbation conditions were investigated via a comprehensive analysis of the experimental results integrating mechanical theory and prior research findings.

• The YOLOV5 and FAST feature point detection algorithms were used for three-dimensional crack reconstruction, providing insights into the fracture morphology of the experimental specimens and showing the crack propagation patterns on the specimen surfaces.

• The energy evolution trend was explored, revealing a notable linear trend in the cumulative values. The stiffness evolution trend under compound paths was examined, elucidating the change mechanism through integration with established laws.

1 Introduction

The omnipresent dynamic stresses resulting from human activities pose a continuous challenge, and rocks emerge as pivotal players in transmitting this dynamic stress (Zhou et al. 2024; Zou et al. 2023a). Rocks not only serve as conduits for various ground disturbances from source points to buildings or structures but also act as carriers of disasters. Numerous studies, including those by Ding (2010), Gu et al. (2012), and Li et al. (2015), highlight the critical impact of the dynamic stress paths on the catastrophic behaviour of rocks under stress waves. Given the significant role rocks play in the transmission and response to dynamic stresses, the changes in their physical and mechanical properties need to be studied. This is particularly crucial in environments where the static forces and dynamic stresses overlap, creating complex stress conditions (Shu et al. 2023; Zou et al. 2023b). Understanding how rocks respond to these combined stress environments is essential not only for mitigating potential disasters but also for optimizing the design and safety of structures.

Environmental and anthropogenic loads impose cyclic stress actions on man-made engineering structures (Ran et al. 2023a, b), as highlighted by Cerfontaine and Collin (2018). Engineered structures undergo repetitive, time-dependent loads arising from various sources, including wind, traffic, and stress wave propagation caused by earthquakes, among others. Examples of scenarios where structures are exposed to such cyclic stress include the following: (1) utilizing abandoned coal mines for pumped hydro storage: Steffen (2012) and Pujades et al. (2016) discussed the conversion of abandoned coal mines into reservoirs for pumped hydro storage. This process involved cyclic stress actions due to the dynamic nature of water movement. (2) Storage of oil and gas in salt mines: Voznesenskii et al. (2017) explored the storage of oil and gas in salt mines, introducing cyclic stress factors associated with the extraction and storage processes. (3) Oil and shale gas production: Gong and Zhao (2007) and Altindag (2010) contributed to the understanding of cyclic stresses in the context of oil and shale gas production, where extraction processes subjected structures to repetitive loading conditions. (4) Tunnel boring machines (TBM) Tunnelling: tunnelling with TBM introduces cyclic stress actions, as studied by Hajiabdolmajid and Kaiser (2003). The mechanical interactions during tunnelling exposed the structures to repeated dynamic loads.

The intricate process of rock deformation and damage evolution is intricately linked to energy transformation and is often guided by various energy evolution activities. This comprehensive process involves the generation and recovery of deformation, as well as the accumulation, dissipation, and release of energy, as highlighted by studies such as Chen et al. (2017, 2018), and Xie et al. (2005). The fracturing process in rock fundamentally involves energy transfer and exchange, making energy-related properties crucial for describing the mechanical characteristics of the rock materials, as emphasized by research from Wang et al. (2018) and Gong et al. (2018). Existing research in the realm of energy-related studies has focused predominantly on the relationship between the elastic energy (or dissipated energy) and the stress or strain of rock specimens during loading. However, there has been a notable gap in the literature emphasizing the relationship between input energy density (IED), elastic energy density (EED), and dissipated energy density (DED), as highlighted by Li et al. (2020a, b). To address this gap, in our study, an in-depth study specifically on the changes in several energy densities is conducted, with the aim of contributing to a more holistic understanding of the energy dynamics involved in the deformation and damage evolution of rocks.

The conventional stress‒strain response has long served as a prevalent method for characterizing the mechanical properties of rock materials and has been a primary tool for assessing the failure of rock engineering structures over many decades, as noted by Meng et al. (2016) and Ning et al. (2022). However, due to its inherent limitations, this traditional method does not fully describe or elucidate the destruction behaviour of rocks. The scarcity of rock materials and the complexity of failure mechanisms, as highlighted by Xie et al. (2009), Luo and Gong (2020), and Dang and Konietzky (2022), highlight the need for additional research techniques to supplement traditional rock mechanics studies and address practical challenges. Recognizing this urgency, the integration of data science and intelligent algorithms has emerged as a transformative approach in various fields. In this study, a pioneering approach is used by tentatively applying advanced techniques, specifically the YOLOv5 and FAST feature point detection algorithms, to explore the surface cracks in rock specimens. Thus, the objective of this study is to establish new concepts into traditional rock mechanics, demonstrating the potential of combining established methods with cutting-edge technologies for a more comprehensive understanding of rock behaviour and failure mechanisms.

Most current rock fatigue studies concentrate on the isolated parameters such as uniaxial compressive strength (UCS) degradation under cyclic loading (Erarslan and Williams 2012; Gong et al. 2019), maximum stress (Bagde and Petros 2005a; b; Eremin 2020), stress amplitude (Roberts et al. 2015; Thongprapha et al. 2020), dynamic frequency (Cerfontaine and Collin 2018), loading waveform (Singh. 1998a, b), and strain rate (Li et al. 2020a, b; Singh 1998a, b). However, these studies often neglect the combined effect of cyclic action and other path forces.

Our research uses a novel approach by focusing on the design of a slope path to investigate the combined impact of a linear loading path and a cyclic loading and unloading path. Simultaneously, in this study, the influences of amplitudes in this process on the energy evolution characteristics, strain evolution characteristics, and surface crack evolution characteristics are examined. By delving into these combined effects, we aim to deepen our understanding of the damage and fracture behaviour of materials under complex loads. The outcomes of this study are anticipated to contribute significantly to the field, providing valuable insights that can guide the development of underground engineering fissures. By considering the holistic impact of combined loading scenarios, we seek to enhance our ability to predict, manage, and design structures in complex geological environments, ultimately advancing the field of rock mechanics.

2 Rock sample preparation and experimental procedures

2.1 Sample preparation

The test rock samples were sourced from an active mining site in Hunan, China, and were specifically drilled from identical geological strata. To ensure the integrity of the experimental outcomes and mitigate the impact of sample heterogeneity, all specimens were meticulously extracted from a single rock block while maintaining a consistent coring orientation. Upon retrieval, the surface of the samples exhibited distinctive grey‒white colouration, indicative of a well-defined block-like structure. Given the susceptibility of the rock samples to swelling and disintegration upon contact with water, a waterless grinding approach was employed during the sample production phase. In accordance with the standards set by the International Society for Rock Mechanics (ISRM), the samples were subjected to precision machining to form standardized cylinders with a diameter of 50 mm and a height of 100 mm. Stringent quality control measures were implemented, ensuring a length deviation of less than 2 mm for all samples. The uniformity of both ends post-grinding was maintained within ± 0.05 mm, with the end face perpendicular to the axis and a maximum deviation not exceeding 0.25°.

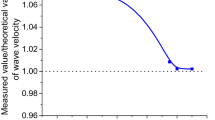
The wave velocity of a batch of 100 rock samples collected from a specific location was measured using a wave velocity measuring device (Fig. 1). Subsequently, samples with wave speeds falling within the range v ∈ (2.8–2.9 km/s) were selected for further analysis. From this preselected group, 8 samples were selected for detailed wave velocity testing using the measuring device. The purpose of this focused testing on a subset of samples was to gather more specific and in-depth information on their wave characteristics, contributing to a more comprehensive understanding of the rock properties in this particular location.

Fig. 1

Wave velocity measuring device

The wave details were thoroughly analysed using MATLAB through the following steps:

• 1. Time difference measurement: The temporal differences between the waves were measured, and an alignment process was applied to synchronize them.

• 2. Inverse Fast Fourier Transformation (IFFT): The inverse fast Fourier transform was employed to transform the signals back to the time domain, providing a detailed representation of the wave characteristics.

• 3. Spectral coherence calculation: The spectral coherence between the signals was calculated using the Mscohere function. This step involved assessing the degree of consistency or correlation between the wave signals and was based on the acoustic test results and the spectral coherence analysis.

• 4. Sample Selection: Four similar samples were selected based on the coherence estimate. The coherence estimate rate was crucial in identifying samples with consistent and significant wave characteristics.

• 5. Coherence in the major frequency area: Fig. 2 reveals that during the major frequency area with frequencies ∈ (20–50 Hz), Test1, Test3, Test4, and Test5 exhibited the highest coherence estimate rates.

Fig. 2

Wave speed measurement results

Consequently, these four samples were selected as the final experimental samples because they demonstrated the most robust and coherent wave characteristics within the specified frequency range. This rigorous analysis and selection process contributes to the precision and reliability of the experimental data.

2.2 Experimental system

This study employed a 60-ton electrohydraulic servo test machine for conducting the experiments. The test machine featured a maximum output pressure of 600 kN, with a loading range spanning from 50 to 10 kN/s. The force value resolution was finely tuned to 1/800,000, and the specific loading rate applied was set at 400 N/s. The relative error of the displacement value in the machine test was carefully controlled within ± 0.5%, ensuring precision and accuracy in the measurements.

The measurement system was a dynamic strain test system consisting of sensors and signal processors. The sensors used are specialized dynamic strain gauges designed to measure strain; strain is the deformation or elongation of a material, particularly under dynamic or rapidly changing conditions. Unlike traditional strain gauges that are suitable for static measurements, dynamic strain gauges are optimized for applications involving varying or cyclic loads, such as those encountered in dynamic testing and vibration analysis. This setup was designed to capture and process dynamic strain data, providing critical information for the analysis of the mechanical properties of the materials under varying conditions. The integration of advanced testing equipment and a reliable measurement system ensured the quality and reliability of our experimental results (Fig. 3).

Fig. 3

Experimental system diagram

2.3 Problem introduction and experimental design

2.3.1 Changes in the stress rate and mean stress level

The value and the rate of the stress change are kept constant. However, different stress paths may occur with different amplitudes of the disturbance. As shown in Fig. 4, when the disturbance amplitudes are 1A, 2A, and 3A, the stress changes are the same, but the stress paths are very different. Therefore, to characterize the difference in this process, the following three parameters are introduced to quantify the path: stress level s, disturbance amplitude A, and disturbance frequency f.

Fig. 4

Influence of the disturbance amplitude and frequency on the overall stress level

The following relationships exist between the magnitude, frequency, and total stress change value of the stress path:

$$Y = 4A \cdot {\text{f}}$$

(1)

where Y is the total amount of stress change in the stress path, A is the path disturbance fluctuation amplitude, and f is the number of disturbances completed by the path per unit time.

The influence of several variables on the physical and mechanical properties of materials needs to be determined experimentally. In the following formula, the default path overall stress level is the mean value of the stress path:

$$s_{1} = A{\text{ + s}}_{0}$$

(2)

The determination of the overall stress level may not be solely governed by the above formula. Hence, we posit the existence of an adjustment factor, denoted as ‘k,’ which potentially influences the stress values in reflecting the comprehensive stress level:

$$s_{2} = {\text{k}}A{\text{ + s}}_{0}$$

(3)

where S₀ is the stress level of the disturbance path, and its specific form is shown in the following figure.

One of the forms on the left shows that the overall level of stress increases with time, as shown in Fig. 5. To represent the change in the overall level of stress, the slope angle is used to characterize the rate of change. Characterization method: The median points of each disturbance peak in the disturbance signal are connected to form a slope of the overall stress level change. In this process, the following formula is satisfied:

$${\overline{\text{v}}} = \frac{{\Delta {\text{s}}}}{{\Delta {\text{t}}}}$$

(4)

$$\theta = {\text{arctan}}\left( {\frac{{{\overline{\text{v}}}}}{{{\text{v}}_{{{\text{ucs}}}} }}} \right)$$

(5)

where ${\overline{\text{v}}}$ is the rate of change in the stage stress, ${\text{v}}_{{{\text{ucs}}}}$ is the rate of change in the strength test, $\Delta {\text{s}}$ is the change in the stress path change slope in a certain section (in MPa), and $\Delta {\text{t}}$ is the elapsed time in the process (in units of s).

Fig. 5

Two ways to affect the stress level during stress wave action

To calculate the value according to the actual stress path, the following formula can be used:

$${\overline{\text{v}}} = \frac{{\left( {s_{1} - s_{0} } \right)}}{{\left( {Y/{\text{v}}} \right)}}$$

(6)

where s₀ is the initial stress, s₁ is the stress at the end of the overall change in the path, Y is the numerical value of the stress change during the process, and v is the stress change rate of the testing machine during this process.

The relationship between the stress change rate of the test machine and the stage average stress change rate in the setting is as follows:

$${\overline{\text{v}}} = \frac{A}{{\left( {Y/{\text{v}}} \right)}}$$

(7)

Combined with the stress path disturbance effect and the overall stress level, an experimental scheme is designed to explore the influence of the amplitude change on the rock physical and mechanical properties under the same slope angle.

2.3.2 Experimental program

In the experiment, to ensure the same slope angle for different amplitudes, the force change rate of the servo needed to be changed. The loading rate for strength testing in the experiment was v = 20 N/s, as indicated by the red arrow in Fig. 6. The other three sets of test paths were the superposition of the linear loading paths and disturbance paths. The amplitudes of the disturbance paths are A, 2A, and 3A. The stress level at any time is a function of the position of the linear path.

Fig. 6

Experimental stress path diagram

To ensure that the comprehensive stress level under the slope stress path is consistent with the strength test path of linear loading, the value of $\overline{{\text{v}}}$ needs to be the same, and the following formula is satisfied:

$${\overline{\text{v}}} = {\overline{\text{v}}}_{1} = \frac{{\left( {s_{M} - s_{0} } \right)}}{{{\text{v}}_{1} }} = \frac{{\left( {s_{M} - s_{0} } \right)}}{{\left( {Y_{OA} + Y_{AM} } \right)/{\text{v}}_{2} }}{ = }\frac{{\left( {s_{M} - s_{0} } \right)}}{{\left( {Y_{OB} + Y_{BM} } \right)/{\text{v}}_{3} }}{ = }\frac{{\left( {s_{M} - s_{0} } \right)}}{{\left( {Y_{OC} + Y_{CM} } \right)/{\text{v}}_{4} }}$$

(8)

where YOA, YAM, YOB, YBM, YOC, and YCM are the absolute values of the ordinate value change between the two points in the figure and SO and SM are the ordinate values corresponding to the O point and the M point, respectively. v₁ is the change speed of the servo machine force in the linear loading path, v₂ is the loading speed of the servo machine under the condition of 0.1UCS amplitude, v₃ is 0.2UCS, and v₄ is 0.3UCS.

According to the condition and amplitude relationship shown in Eq. (8), the following can be defined:

$$A_{2} = A = 0.1UCS,\quad A_{3} = 2A = 0.2UCS ,\quad A_{4} = 3A = 0.3UCS$$

(9)

Then, the servo load change rate can be obtained as follows:

$$\left\{ \begin{gathered} V_{2} = \frac{{Y_{2} }}{{\text{t}}}{ = }\frac{{4A_{2} - \left( {s_{M} - s_{0} } \right)}}{{\left( {s_{M} - s_{0} } \right)/{\text{v}}_{1} }} \hfill \\ V_{3} = \frac{{Y_{3} }}{{\text{t}}}{ = }\frac{{4A_{3} - \left( {s_{M} - s_{0} } \right)}}{{\left( {s_{M} - s_{0} } \right)/{\text{v}}_{1} }} \hfill \\ V_{4} { = }\frac{{Y_{4} }}{{\text{t}}}{ = }\frac{{4A_{4} - \left( {s_{M} - s_{0} } \right)}}{{\left( {s_{M} - s_{0} } \right)/{\text{v}}_{1} }} \hfill \\ \end{gathered} \right.$$

(10)

The final experimental design parameters are shown in Table 1 and include the number of experimental groups, the loading rate of the testing machine, the growth rate of the comprehensive stress level, and the disturbance amplitude.

Table 1 Experimental parameter design

2.4 3D reconstruction algorithm for the crack detection based on YOLOv5 and FAST feature point algorithms

In this section, we propose a fully intelligent algorithm for rock fracture detection and 3D reconstruction. Based on YOLOv5 target detection and the FAST feature point detection algorithms, our algorithm uses the concept of "pretraining and fine-tuning" in the field of deep learning to construct a model for rock crack detection and 3D reconstruction on the existing open-source pretrained YOLOv5 model.

The algorithm implementation is divided into three modules: (1) a YOLOv5 detection module with enhanced pretraining; (2) a FAST feature point detection module; and (3) a crack 3D reconstruction module. The data acquisition part (0) is also included to obtain the surface crack information of the sample through the camera. A schematic diagram is shown in Fig. 7.

Fig. 7

YOLOv5 and FAST feature point detection algorithm flowchart

2.4.1 Pretrained YOLOv5

(1) YOLOv5 model pretraining and fine-tuning

The YOLO objective algorithm was first proposed in 2016 (Redmon et al. 2016). The image information in this algorithm can be predicted by only one forward propagation. The main principle is to flatten the fully connected layer of the convolutional network to achieve detection of the area frame. In the following years, Redmon improved upon the algorithm and proposed YOLOv2 and YOLOv3, which achieved improved performance. In 2020, researchers proposed YOLOv4 (Bochoknovskiy et al. 2020), followed by the better-performing YOLOv5 algorithm in 2021 (Jocher et al. 2021). At present, the YOLOv5 algorithm has good target recognition performance in the field of deep learning, and the algorithm has a large number of open-source pretraining models. Users can fine-tune their own models on the existing large-scale image pretraining models. This saves time and effort.

In this study, we introduce a pretrained YOLOv5 model and fine-tune it on the resulting rock fracture image data.

To generate a trainable dataset, we initiated the process by subjecting the raw rock fracture image data to image augmentation. This involved employing various techniques to enrich the dataset, including the following steps:

• (1) Sampling: The rock fracture images are captured from diverse angles.

• (2) Rotation: Rotations are applied to the original rock fracture image to produce similar images.

• (3) Cropping: Different yet similar fracture images are extracted through cropping.

Subsequently, we curated a dataset comprising 200 labelled rock fracture images using Labelme. To enhance the informational content of these images, we fine-tuned the fusion of the 200 rock fracture images with a pretrained YOLOv5 model, aiming to capture the intricate characteristics of rock fractures.

In the final stage, the image needing crack position information extraction was input into the YOLOv5 network. The detection accuracy was gauged by an AUC threshold of ≥ 0.8, determining the extraction frame, which served as our conclusive result.

(2) Image cutting and binarization

Following the YOLO detection frame results, the next step involves cutting the image to focus on the specific rock fracture area of interest. This process is crucial for isolating the relevant information for further analysis. The images obtained are then subjected to binarization, a technique that converts the images into binary form. Binarization simplifies the image, representing it in terms of black and white pixels, and prepares it for the subsequent processing steps.

In Fig. 8, an example of the final detection result is shown, revealing a total of nine crack detection frames. These frames pinpoint areas of interest within the rock fracture images. To enhance the detection of feature points within the cracks, it is essential to cut and binarize the rock crack map. This additional step optimizes the identification of the critical feature points, setting the stage for subsequent analysis and characterization of the rock fractures.

Fig. 8

YOLO detection cuts the image

2.4.2 FAST feature point detection algorithm

The FAST feature point detection algorithm efficiently determines feature point locations by detecting local pixel grayscale changes (Rosten and Drummond 2005). In the context of the rock fracture analysis, where binary images of the fractures have been obtained, the algorithm is applied to identify feature points along the edges of the cracks.

The process involves the following steps: (1) Noise removal: Prior to feature point detection, salt and pepper noise present in the binary image is removed. This step is crucial because non-rock fracture areas may introduce unwanted noise, and eliminating unwanted noise ensures accurate detection of the relevant features in the rock fractures; (2) Feature Point Detection (Contour Detection): The algorithm then performs feature point detection, which is essentially contour detection in the context of the rock fractures. The grayscale information change at the edges of the binary image is leveraged to obtain discrete crack point information. This step helps identify key points along the cracks, providing valuable data for the further analysis and characterization. The FAST algorithm coupled with contour detection on binary images enhances the identification of the feature points along the rock fractures, contributing to a comprehensive understanding of the fracture characteristics (Fig. 9).

Fig. 9

Binarization, noise reduction and point extraction

2.4.3 3D reconstruction of fissures

Using the YOLOv5 and FAST feature point detection algorithms, we obtained discrete crack coordinate information (x, y) from the two-dimensional images, and we aimed to reconstruct the coordinates via projection. Specifically, (1) the Y axis of the fracture in the 2D image is projected as the Z axis in 3D, and (2) the parametric equation is constructed using the rock radius, height and length. Based on this parametric equation, the x-coordinate in the image is spatially nonlinearly projected. The fracture coordinate point (X, Y) in three-dimensional space is obtained, and the transformation equation is as follows:

$$\left\{ \begin{gathered} {\text{x}} = \frac{D}{2}\cos \left( {\frac{{360x_{{\bullet}} }}{\pi D}} \right) \hfill \\ {\text{y}} = \frac{D}{2}sin\left( {\frac{{360x_{{\bullet}} }}{\pi D}} \right) \hfill \\ z = y_{{\bullet}} \hfill \\ \end{gathered} \right.$$

(11)

where D is the diameter of the bottom surface of the cylindrical specimen; x· and y· are the coordinates of the lateral expansion plane of the specimen; and x, y, and z are the spatial coordinates of the reconstructed crack. The specific form is shown in Fig. 10.

Fig. 10

Coordinate transformation

3 Results

The experimental results, as shown in Fig. 11, align with the outlined experimental design. Notably, under identical slope angles, various sample groups experienced an equivalent number of stress disturbances within the same time frame, leading to a consistent increase in comprehensive stress levels across all experiments. Interestingly, the strength of the sandstone samples exhibits a decreasing trend as the specimens are disturbed, with a simultaneous increase in stress levels.

Fig. 11

Actual diagram of the experimental stress path

Furthermore, a clear correlation emerges, indicating that larger disturbance amplitudes result in more pronounced reductions in strength. Notably, these reductions, while notable, remain within a range of 10% of the uniaxial compressive strength (UCS). The intricacies of the strength reduction phenomena warrant further exploration and will be addressed in the subsequent discussion section.

During the experiment, we employed a set of samples exhibiting consistent acoustic test results. By analysing the stress‒strain curves, the curves of the samples clearly exhibit a remarkable degree of coincidence, with the hysteresis loop curves in each cycle displaying a parallel nature. These congruent results indicate that the mechanical properties of the samples are similar, highlighting the efficacy of the acoustic selection method. Notably, the force required for the specimen to induce an equivalent amount of deformation under the applied load remains consistent.

According to the data shown in Fig. 12, the strains at the final failure of the samples converge at approximately 0.01. Notably, when subjected to combined linear loading and perturbation, the strain at specimen failure is lower than that in the case of linear loading alone. As the amplitude of the perturbation increases, the strain at failure decreases. This trend is attributed to the consistent integrated stress level throughout the experiment and the relatively uniform strain rate. Larger amplitudes lead to a shorter time for sample failure, resulting in insufficient development of the deformation.

Fig. 12

Stress‒strain curves

Examining the temporal evolution of strain in Fig. 13, the rate of change in strain with time remains essentially constant. This uniformity is explained by the consistent integrated stress level along the stress path (with a constant slope angle in the loading path). Based on these findings, during the sample deformation process, the stress level emerges as the primary controlling factor, while the influence of the perturbation on the strain evolution during the deformation development is minimal.

Fig. 13

Strain‒time curve

The fracture images of the experimental samples were analysed using the YOLOv5 and the FAST feature point detection algorithms, as illustrated in Fig. 14. Based on the examination of the spatial distribution of surface cracks, under linear loading alone, only a minimal number of lateral cracks are observed. However, a significant increase in the number of cracks oriented in the lateral direction is observed when the linear loading action is combined with perturbation. Notably, in this study, the fractures are limited by the method; thus, we predominantly discuss the main cracks in the sample, and some horizontal microfractures are not fully identified.

Fig. 14

3D reconstructed image of the fissure

Furthermore, an assessment of the main fracture angle indicates a deflection under the influence of combined stress conditions. The specific pattern of change in the fracture surface angle is further explored in the subsequent discussion, elucidating the complex dynamics of fracture behaviour under these complex loading conditions.

4 Discussion

4.1 Strain evolution under different amplitudes

Normally, elastic deformation recovers after the external load is removed, but rock material belongs to plastically deformable material, there will have some irreversible plastic deformation at the same time. Moreover, in the initial stage of loading, irreversible deformation may change the initial properties of the rock. Chen et al. (2020) found that the irreversible deformation increases sharply in the first cycle and then increases steadily with increase of cycle times. Zhang et al. (2021) found that irreversible deformation is the reason for fatigue failure, and fatigue damage is directly affected by the level of irreversible deformation, and the increase of irreversible deformation can reflect fatigue damage under cyclic loading. In order to understand how the irreversible deformation develops, the irreversible strain of the specimen was investigated to explore the relationship between the cyclic load and irreversible strain, and the influence of slope-shaped stress path.

By related scholars Gatelier (2002), Jia et al. (2018), Peng et al. (2019), the calculation method of irreversible strain adopted in this paper is as follows:

$$\left\{ \begin{gathered} \varepsilon_{{\text{i}}}^{{\text{i}}} = \varepsilon_{{1{\text{i}}}} - \varepsilon_{{1({\text{i}} - 1)}} \hfill \\ \varepsilon_{{\text{i}}}^{{\text{e}}} = \varepsilon_{{1{\text{i}}}} - \varepsilon_{{2{\text{i}}}} \hfill \\ \end{gathered} \right.$$

(12)

where $\varepsilon_{{\text{i}}}^{{\text{i}}}$ is irreversible strain of i cycles, $\varepsilon_{{\text{i}}}^{{\text{e}}}$ is elastic strain of i cycles, $\varepsilon_{{{\text{1i}}}}$ is elastic strain of i cycles, $\varepsilon_{{{\text{1i}}}}$ is initial strain of i cycles, $\varepsilon_{{{\text{2i}}}}$ is final strain of i cycles, $\varepsilon_{{{\text{1(i}} - {1)}}}$ is initial strain of i − 1 cycles, these parameters are described in Fig. 15.

Fig. 15

Irreversible strain calculation method

From Fig. 16, the stain change rule of the sample under the slope force path is explore. The specimens have largest irreversible strain generated by first cycle load, which is much larger than the subsequent irreversible strain. After that, the irreversible strain accumulation of specimens remain stable. By comparison, the irreversible strain does not change much with the amplitude, and irreversible strain curves are basically overlapped. But the total irreversible strain decreases with the increase of the amplitude at the period of specimen failure. Additional changes have occurred inside the sample during the disturbance part in stress path acting. The superposition of the cyclic disturbance path makes the sample have lower breaking threshold because disturbance wave reflect to influent horizontal direction part of rock sample.

Fig. 16

Single cycle irreversible strain and irreversible strain

From Fig. 17, the elastic deformation inside the sample is quite different from the irreversible strain which conforms to the general elastic stress–strain relationship. In the case of larger amplitude, larger elastic deformation occurs. Under the three amplitude conditions, the elastic deformation of the sample conforms to the proportional relationship of the amplitude value. For the total amount of elastic deformation, the total strain is larger under the higher amplitude disturbance before the failure of the sample, and it follow a linear rule.

Fig. 17

Single cycle elastic deformation and cumulative value

Mathematically fit the irreversible strain, elastic strain and elastic strain in a single cycle in the above figure, with the number of cycles N as the independent variable. Because the time of each single cycle in the experiment is the same, the formula obtained by fitting can be converted with time, and the conversion relationship is as follows:

$$T = \sum {T_{{\text{i}}} } { = }N \cdot T_{{\text{i}}}$$

(13)

This formula can be used to predicate the time-dependent change of the deformation inside the sample under the condition of slope loading (Table 2).

Table 2 Strain data fitting results

Combined with the above data, the development trend of irreversible strain level with the total deformation of the specimen is finally obtained from Fig. 18. It is clear the irreversible strain presents a good linear characteristic with the increase of the total strain value.

$$\left\{ \begin{gathered} (\varepsilon^{i} /\varepsilon^{0} ) = 0.9935(\varepsilon^{{}} /\varepsilon^{0} ) + 0.2683\quad \, (R^{2} = 0.99) \hfill \\ (\varepsilon^{i} /\varepsilon^{0} ) = 0.9941(\varepsilon^{{}} /\varepsilon^{0} ) + 0.3169\quad \, (R^{2} = 0.99) \hfill \\ (\varepsilon^{i} /\varepsilon^{0} ) = 0.9949(\varepsilon^{{}} /\varepsilon^{0} ) + 0.0398\quad \, (R^{2} = 0.99) \hfill \\ \end{gathered} \right.$$

(14)

Fig. 18

Linear relationship between irreversible reaction and strain value

4.2 Energy evolution of sandstone

Essentially, the progressive process of rock material failure from initial deformation to final failure is driven by the coupled effects of input energy, dissipated energy, and elastic energy. The study of these three energies has been widely used to analyze the stability of rock engineering, and some scholars have also used them to describe rock damage or failure behavior and established relevant failure criteria (Li et al. 2017).

According to the evolution of energy rule, many scholars have also applied relevant energy criteria to guide engineering. For example, Zhang et al. (2021) based on the analysis of the external input energy of the fracture zone, plastic zone and elastic stress increase zone of the lateral coal seam staggered roadway to derive the corresponding energy dissipation formula. Then, the damage variable of the surrounding rock was determined using the ratio of the internal dissipated energy to the external input energy. So they found that the support pressure produces compressive and plastic deformations in the rock mass, when loose gangue is above the roadway, dissipating more energy and making the roadway easier to maintain.

In the process of studying the energy evolution, three energy parameters (external input energy, internal elastic energy and internal dissipated energy) are usually used to describe the energy changes during the pre-peak failure process of rocks. The external input energy (energy generated by the load of testing machine) acts on the sample and is absorbed by the rock sample. Part of the absorbed energy is stored and accumulated in the interior due to elastic deformation of specimen. The other part is dissipated by the compaction, initiation and propagation of cracks in the specimen or dissipated in other forms of energy. For example, the thermal energy generated by the compression process due to the reduction in volume. The three energies are calculated as follows:

$$\left\{ \begin{gathered} {\text{u}}_{i}^{o} = \int_{{\varepsilon_{o} }}^{{\varepsilon_{2} }} {\sigma {\text{d}}\varepsilon } \hfill \\ {\text{u}}_{i}^{e} = \int_{{\varepsilon_{1} }}^{{\varepsilon_{2} }} {\sigma {\text{d}}\varepsilon } \hfill \\ {\text{u}}_{i}^{d} = \int_{{\varepsilon_{o} }}^{{\varepsilon_{2} }} {\sigma {\text{d}}\varepsilon } - \int_{{\varepsilon_{1} }}^{{\varepsilon_{2} }} {\sigma {\text{d}}\varepsilon } \hfill \\ \end{gathered} \right.$$

(15)

where ${\text{u}}_{i}^{o}$, ${\text{u}}_{i}^{e}$ and ${\text{u}}_{i}^{d}$ are the external input energy, internal elastic energy and internal dissipated energy calculated according to the stress–strain relationship under the cyclic loading and unloading experimental conditions, respectively; $\varepsilon_{1} { = }\varepsilon_{1}^{{\text{i}}}$ is the residual deformation, and $\varepsilon_{2}$ represents the total axial deformation. (Park et al. 2014; Wasantha et al. 2014a, b) In Fig. 19, ${\text{u}}_{i}^{o}$ represents the area of OAC, ${\text{u}}_{i}^{e}$ represents the area of ABC and ${\text{u}}_{i}^{d}$ represents the area of AOB.

Fig. 19

Energy calculation method

Elastic energy density (EED) plays an important role in the study of rock mechanical properties, and has a wide range of applications in many rock mechanics problems. Wang and Part (2001) used elastic energy to study the occurrence of shock and rockburst. Xie et al. (2009) gave the expression of elastic energy under uniaxial test, which was used to establish the overall failure criterion of rock. Later Tarasov and Randolph (2011), Tarasov and Potvin (2013) discussed the ultrabrittleness of rocks and a general criterion for elastic properties considering rock brittleness.

However, in actual engineering practice, rock usually subjected to the superposition forces due to the complexity of the stress from multiple force sources. Therefore, it is necessary to explore the change of elastic energy of the sample under complex path. Figure 20 shows the relationship between the EED and IED of the specimen under the slope loading path. From Fig. 20, there is a strong linear correlation between input energy density and elastic energy density. When the amplitudes are 0.1 UCS, 0.2 UCS, and 0.3 UCS, the slopes of the fitting curves of the three are basically same. The results reveal that after the superposition of disturbance and static load, the overall level of stress has dominated influence on the elastic energy of the sample, and the change of the amplitude does not change the proportion of elastic energy in the process of cyclic loading and unloading.

Fig. 20

Linear relationship between total input energy and elastic energy

Figure 21 shows the variation of dissipated energy under different loading cycles. Results show that under the action of the slope path, the dissipated energy is very large at the beginning of loading, then decreases sharply, and then fluctuates within a range. The larger the amplitude of slope loading, the lower the proportion of dissipated energy in the total input energy. Under 0.1UCS amplitude, the percentage of dissipated energy is mainly concentrated and below 10%, the 0.2UCS amplitude fluctuates within 10–15%, and 0.3UCS amplitude, the proportion of dissipated energy of the sample is mainly concentrated in 15–20%. It is clear that the proportion of dissipated energy will increase before the failure of the sample.

Fig. 21

Relationship between dissipated energy and number of cycles

Compare it with previous study, the dissipative energy is different from the research results of Gong et al. (2019) caused by different experimental paths. When the rock material is subjected to complex stress condition, the energy dissipation rule is different, and the relationship between the dissipated energy and the total input energy shows a nonlinear relationship. In order to explore the energy dissipation characteristics of the sample under complex stress conditions, the rule between the accumulated dissipated energy and the accumulated input energy was investigated in this experiment.

$$\left\{ \begin{gathered} {\text{u}}_{i}^{{{\text{t}}o}} { = }\sum\limits_{1}^{i} {{\text{u}}_{i}^{o} } \hfill \\ {\text{u}}_{i}^{te} { = }\sum\limits_{1}^{i} {{\text{u}}_{i}^{e} } \hfill \\ {\text{u}}_{i}^{td} { = }\sum\limits_{1}^{i} {{\text{u}}_{i}^{d} } \hfill \\ \end{gathered} \right.$$

(16)

From Fig. 22, the ratio of the total amount of dissipated energy to the total amount of elastic energy exhibits a linear correlation. Due to the linear correlation between the total amounts, under the complex path, compared with the simple strength test experiment, the energy change of the sample has different phenomena. The result is related to the dissipative energy statistics including the energy that is too late to be released in the disturbance process.

Fig. 22

Linear relationship between total dissipated energy and total elastic energy

As shown in Fig. 23, there is a linear correlation between the accumulated dissipated energy and the total input energy, and the curve represents the dynamic ratio between TDED and TIED at any time. Based on the total input energy at any time, the total dissipated energy value under this condition can be estimated. This has a certain guiding role for energy monitoring of complex construction spot.

Fig. 23

Linear relationship between total input energy and total dissipated energy

Table 3 shows the fitting relationship between the elastic energy, dissipated energy and input total energy of rock under the slope shape signal. From the fitting equation, the slopes in the fitting equation decrease with the increase of the disturbance amplitude. Based on the fitting formula, the relationship between several energies can be deduced as follows:

$$\left\{ \begin{gathered} {\text{u}}_{i}^{{\text{e}}} {\text{ = Au}}_{i}^{{\text{o}}} + B \hfill \\ \sum\limits_{1}^{i} {{\text{u}}_{i}^{d} } {\text{ = C}}\sum\limits_{1}^{i} {{\text{u}}_{i}^{o} - D} \hfill \\ \end{gathered} \right.$$

(17)

where A, B, C, D are the constants related to the path received in the complex disturbance process, and the values can be obtained by testing the corresponding rock mass.

Table 3 Energy evolution fitting relationship

After obtaining the values, the ratio between the dissipated energy and the elastic energy at the process can be calculated in the corresponding scenario:

$$\left\{ \begin{gathered} {\text{u}}_{i}^{{\text{d}}} { = }\sum\limits_{1}^{i} {{\text{u}}_{i}^{d} } - \sum\limits_{1}^{i - 1} {{\text{u}}_{i}^{d} } \hfill \\ M_{e}^{d} = \frac{{{\text{Au}}_{i}^{{\text{o}}} + B}}{{\sum\limits_{1}^{i} {{\text{u}}_{i}^{d} } - \sum\limits_{1}^{i - 1} {{\text{u}}_{i}^{d} } }} = \frac{{{\text{Au}}_{i}^{{\text{o}}} + B}}{{{\text{C}}\left( {\sum\limits_{1}^{i} {{\text{u}}_{i}^{o} } - \sum\limits_{1}^{i} {{\text{u}}_{{i{ - }1}}^{o} } } \right)}} \hfill \\ \end{gathered} \right.$$

(18)

If it is deduced from the free energy of the sample system (Madkour 2021), following the same

$$W = W\left( {\sigma ,\alpha ,\beta } \right)$$

(19)

The expanded formula includes elastic deformation due to stress, which is reversible during loading and unloading. The second part is the energy consumed by the deformation caused by the internal shaping development of the sample, and the third part is the energy contained in the internal reversible variables:

$$\delta W = \left( {\varepsilon - \frac{\partial W}{{\partial \varepsilon }}} \right){\text{d}}\sigma - \frac{\partial W}{{\partial \alpha }}{\text{d}}\alpha - \frac{\partial W}{{\partial \beta }}d\beta$$

(20)

Among them, the first term $\left( {\varepsilon - \frac{\partial W}{{\partial \varepsilon }}} \right){\text{d}}\sigma$ is zero because the difference between the storage and release of elastic energy in the cyclic process is:

$$\left( {\varepsilon - \frac{\partial W}{{\partial \varepsilon }}} \right){\text{d}}\sigma = 0$$

(21)

Because the two parameters $\alpha$ and $\beta$ are independent of each other, because during the cyclic disturbance process $\delta W \ge 0$, the internal energy change of the sample is shown in the following formula:

$$- \frac{\partial W}{{\partial \alpha }}{\text{d}}\alpha \ge 0_{{}} ,\quad - \frac{\partial W}{{\partial \beta }}d\beta \ge 0$$

(22)

Here: $W^{\alpha }$ is the deformation dissipation energy generated by the internal plastic development of the sample, and the energy contained in the internal reversible variable of $W^{\beta }$, as shown in the following formula

$$- \frac{\partial W}{{\partial \alpha }}{\text{d}}\alpha { = }W^{\alpha } ,\quad - \frac{\partial W}{{\partial \beta }}d\beta { = }W^{\beta }$$

(23)

Since it is assumed in the experiment that $\varepsilon_{{{\text{ij}}}}^{{^{\beta } }}$ cannot be recovered due to continuous loading then:

$$\vartriangle \varepsilon = \varepsilon_{{{\text{ij}}}}^{\beta } = \Delta \varepsilon_{{{\text{ij}}}}^{{}} - \varepsilon_{{{\text{ij}}}}^{{\text{r}}}$$

(24)

Combining the above formula, the following formula can be obtained:

$$\varepsilon_{{{\text{ij}}}}^{{\text{r}}} = \varepsilon_{{{\text{ij}}}}^{\alpha } - \varepsilon_{{{\text{ij}}}}^{{^{\beta } }} = - \frac{{\partial W^{\alpha } }}{{\partial \sigma_{{{\text{ij}}}} }}{ + }\frac{{\partial W^{\beta } }}{{\partial \sigma_{{{\text{ij}}}} }}$$

(25)

By combining the above formula with the existing elastic–plastic evolution equation, it can be deduced that the energy that cannot be released in time inside the sample is caused by the strain in the sample that cannot be recovered in time. However, due to the lack of monitoring of strains that are too late to recover, there is no way to verify the total amount of energy. Is the total amount of energy that cannot be recovered during this process equal to the energy of the strain that the specimen has no time to recover? Or are there other energy changes included in the energy that cannot be recovered in time? The next step for verification requires further application of more complete monitoring methods. In general, this section obtains the variation of dissipative energy and elastic energy at any time during the slope deformation process.

4.3 Unloading stiffness and secant modulus evolution

The “elastic modulus method” in damage theory is a method to define or measure damage by the change of material elastic modulus before and after damage based on the strain equivalence hypothesis (Xie et al. 2005). Subsequent scholars have improved this method and obtained a description of elastic modulus damage that is more consistent with elastic–plastic materials (Li et al 2020a, b). They introduced unloading stiffness to characterize the hypothetical “damaged material elastic modulus” to distinguish it from unloading stiffness.

Before researches mainly aimed at the quasi-static process, when the deformation is completely recovered after unloading. However, under the condition of continuous loading and unloading, the unloading deformation cannot be completely recovered, which poses a great challenge to the solution of unloading stiffness. To explore the damage effect under continuous disturbance, an attempt was made to solve the “unloading stiffness”.

Taking point A in Fig. 24 as an example, the plastic damage and elastic–plastic damage of point A are explored. The elastic modulus at this time is as follows:

$${\text{E}} = \mathop {{\text{lim}}}\limits_{{\varepsilon \to \varepsilon_{O} }} \frac{{{\text{d}}\sigma }}{{{\text{d}}\varepsilon }}$$

(26)

Fig. 24

Secant modulus calculation method

The secant modulus of the OA segment can be expressed as:

$${\text{E}}_{{\text{i}}} { = }\frac{{\sigma_{{{\text{i + }}1}} - \sigma_{{\text{i}}} }}{{\varepsilon_{{{\text{i + }}1}} - \varepsilon_{{\text{i}}} }}$$

(27)

According to the elastic modulus and the tangent modulus of the OA segment, the unloading stiffness satisfies the following formula:

$${\text{E}}_{{\text{i}}}^{s} = \frac{{{\text{E}}_{{\text{i}}} { + }E}}{k(\sigma ,\alpha ,\beta )}$$

(28)

Among them, the function k is the relationship equation between unloading stiffness and secant modulus and unloading stiffness. $\alpha$ is caused by plastic deformation and internal irreversible damage, $\beta$ is caused by deformation, but the recovery of deformation takes time, and the two are independent parameters that do not affect each other. The formula is as follows:

$${\text{E}}_{i}^{s} = \frac{{\sigma_{A} }}{{\varepsilon_{i}^{e} + \Delta \varepsilon }} = \frac{{\sigma_{A} }}{{\varepsilon_{A} - \varepsilon_{i}^{{\text{r}}} }}$$

(29)

The damage deformation of the sample is:

$$D{ = }1{ - }\frac{{\varepsilon_{A} - \varepsilon_{{\text{i}}}^{{\text{r}}} }}{{\varepsilon_{A} }}\left( {\frac{{{\text{E}}_{i}^{s} }}{E}} \right)$$

(30)

It can be obtained that the deformation of the specimen cannot be recovered due to continuous loading and unloading:

$$\Delta \varepsilon = \frac{{\sigma_{A} }}{{{\text{E}}_{i}^{s} }} - \varepsilon_{i}^{e}$$

(31)

By exploring the deformations that cannot be quickly recovered during the loading and unloading process. The irreversible strain accumulated inside the specimen during this process can be further explored, as well as the energy stored before the deformation can be recovered. This is consistent with the results described in Sect. 4.2. Combining the two parts can explore the change of specimen stiffness during loading and unloading.

From Fig. 25, it's evident that the cyclic loading and unloading experiments on concrete materials, as discussed by Xie et al. (2005) and other scholars, reveal consistent patterns in the changes of loading modulus, unloading modulus, and unloading stiffness of the samples after loading and unloading disturbances. During the loading and unloading cycles, stiffness initially increases and then decreases with the rising strain. Notably, the unloaded stiffness slightly surpasses the unloaded modulus, which, in turn, is slightly greater than the elastic modulus of the loaded section.

Fig. 25

Elastic modulus change of concrete under cyclic action (Xie et al. 2005)

Turning to Fig. 26, it is observed that the loaded and unloaded modulus of sandstone specimens in cyclic loading and unloading experiments generally exhibit a monotonically increasing trend, with the unloaded modulus surpassing the loaded modulus. Interestingly, under equivalent stress levels, the amplitude of disturbance has minimal impact on the elastic modulus, maintaining the material properties quite consistently.

Fig. 26

Evolution law of secant modulus for loading and unloading

Comparing these findings with previous results and those presented in this paper, when sandstone material undergoes loading and unloading along a slope path, the sample typically doesn't reach the stiffness decay stage before failure. Instead, it often remains in the stiffness increase stage. Formula 27, derived in this study, indicates that the rise in loaded elastic modulus, unloaded elastic modulus, and sample stiffness is primarily attributed to recoverable deformation within the sample. This deformative recovery takes some time after exposure to external forces. However, due to continuous loading, the sample's deformation can't fully recover, leading to an increase in the elastic modulus of the unloading section, surpassing that of the loading section, and subsequently influencing the subsequent loading phases.

From Figs. 27, 28 and 29, the fitting relationship of the secant modulus of the sample with the deformation is obtained based on the change of the loading and unloading modulus of the sample with the development of deformation. The relationship between the loading and unloading modulus of the sample under the three amplitude conditions follows the same formula:

$${\text{(E}}_{{\text{i}}}^{{}} /{\text{E)}} = {\text{a(}}\varepsilon_{{\text{i}}}^{{}} /\varepsilon_{0} {)}^{2} + {\text{b(}}\varepsilon /\varepsilon_{0} {)} + {\text{c}}$$

(32)

$$\left\{ \begin{gathered} {\text{(E}}_{{}}^{ + } /{\text{E)}} = {0}{\text{.428(}}\varepsilon /\varepsilon_{0} {)}^{2} - {0}{\text{.0516(}}\varepsilon /\varepsilon_{0} {)} + {0}{\text{.627}}\quad ({\text{R}}^{2} = {0}{\text{.949)}} \hfill \\ {\text{(E}}_{{}}^{ - } /{\text{E)}} = {0}{\text{.475(}}\varepsilon /\varepsilon_{0} {)}^{2} - {0}{\text{.0635(}}\varepsilon /\varepsilon_{0} {)} + {0}{\text{.592}}\quad ({\text{R}}^{2} = {0}{\text{.966)}} \hfill \\ \end{gathered} \right.$$

(33)

$$\left\{ \begin{gathered} {\text{(E}}_{{}}^{ + } /{\text{E)}} = {0}{\text{.589(}}\varepsilon /\varepsilon_{0} {)}^{2} - {0}{\text{.063(}}\varepsilon /\varepsilon_{0} {)} + {0}{\text{.444}}\quad ({\text{R}}^{2} = {0}{\text{.993)}} \hfill \\ {\text{(E}}_{{}}^{ - } /{\text{E)}} = {0}{\text{.616(}}\varepsilon /\varepsilon_{0} {)}^{2} - {0}{\text{.069(}}\varepsilon /\varepsilon_{0} {)} + {0}{\text{.411}}\quad ({\text{R}}^{2} = {0}{\text{.974)}} \hfill \\ \end{gathered} \right.$$

(34)

$$\left\{ \begin{gathered} {\text{(E}}_{{}}^{ + } /{\text{E)}} = {0}{\text{.707(}}\varepsilon /\varepsilon_{0} {)}^{2} - {0}{\text{.075(}}\varepsilon /\varepsilon_{0} {)} + {0}{\text{.411}}\quad ({\text{R}}^{2} = {0}{\text{.914)}} \hfill \\ {\text{(E}}_{{}}^{ - } /{\text{E)}} = {0}{\text{.785(}}\varepsilon /\varepsilon_{0} {)}^{2} - {0}{\text{.084(}}\varepsilon /\varepsilon_{0} {)} + {0}{\text{.385}}\quad ({\text{R}}^{2} = {0}{\text{.922)}} \hfill \\ \end{gathered} \right.$$

(35)

Fig. 27

Nonlinear relationship between secant modulus and strain under 0.1UCS

Fig. 28

Nonlinear relationship between secant modulus and strain under 0.2UCS

Fig. 29

Nonlinear relationship between secant modulus and strain under 0.3UCS

Examining the figure above alongside the corresponding fitting equation reveals that the quadratic coefficient in the fitting relation for both loading and unloading modulus increases with the amplitude. Notably, the quadratic coefficients for the unloading modulus equations consistently surpass those of the loading modulus. This suggests that, under identical stress levels, variations in amplitude lead to changes in the physical and mechanical properties of the sandstone material, causing alterations in the material's elastic variables.

In contrast to findings from prior studies, the loading and unloading process for general materials appears to be a dynamic sequence involving both increasing and decaying stiffness. This phenomenon aligns with existing theories that describe the material's behavior as a balance between strengthening and damage effects throughout the loading and unloading cycles. These insights contribute to a more comprehensive understanding of the intricate interplay between stress, amplitude, and the mechanical response of sandstone materials.

4.4 Comprehensive analysis of influence on rock material stability under slope loading

4.4.1 Overall stress level and force change rate in slope loading

When considering the information presented in Sects. 3 and 4.1 in conjunction, it becomes evident that, under the slope stress path, the primary factor influencing the overall deformation rate of the specimen is the stress level. Surprisingly, the disturbance parameters seem to exert minimal influence on the strain rate of the specimen. Across the four experimental sample groups, the strain rates exhibit a remarkable consistency.

As the experiments approach final failure, an interesting observation emerges: the maximum strain reached by each specimen is essentially uniform. This suggests a robustness in the response of the specimens, indicating that, regardless of the specific disturbance parameters, the ultimate failure point remains consistent across the different experimental conditions. These findings underscore the dominance of stress levels in determining deformation rates and provide valuable insights into the material's behavior under the slope stress path (Fig. 30).

Fig. 30

Stress level determines strain rate

During the experiment, the force change rates of the experimental servos were very different at 375 N/s, 775 N/s, and 1175 N/s, respectively. But the difference in loading rate did not cause a huge change in the strength of the specimen. According to expert (Wasantha et al. 2014a, b; Zhang et al. 2021, Xie et al 2022), under a simple linear loading path, the peak strength of sandstone increases with a nonlinear gradient with the increase of strain rate. Therefore, in order to judge the stability of the sample due to the complex stress state, it is necessary to judge the final stress level of the rock material according to the interaction of various forces.

4.4.2 Recoverable strain in slope loading

For the change of secant modulus discussed in Sect. 4.3, the secant modulus first increases and then decreases during the disturbance process of cyclic loading and unloading. In this process, the deformation of the specimen that is too late to recover plays an important role in the early stage of loading. Although the sandstone material used in this experiment only showed a rise in the secant modulus at this stage, it did not begin to show a decrease. In the process of continuous loading and unloading, the cause of the phenomenon may be that the strain that is too late to recover accumulates a large amount of energy, which leads to the direct destruction of the sample. The sample did not enter the self-propelled damage inside the late sample, and then the failure occurred (Fig. 31).

Fig. 31

Recoverable strain induces secant modulus change

As shown in Fig. 32, the rock material's composition is depicted, showcasing a diverse array of minerals that collectively form the rock's main structure. Delving deeper into the phenomenon of increasing and decreasing secant modulus, as explored by Li et al. (2017), reveals a crucial aspect related to the initial loading stage. At this point, the sample harbors numerous pores. As the loading cycles progress, these pores gradually contract under increasing stress and exhibit a recovery trend during stress reduction. However, when stress is released, the recovery of the shrunken pores takes time.

Fig. 32

Mechanism analysis of secant modulus change

Despite this recovery process, the constant disturbance to the pores causes them to develop directly into through fractures. This leads to experimental results that deviate from conventional expectations. Only when the sample's pores are essentially closed does the development of cracks initiate again. Remarkably, throughout this process, the loading and unloading stiffness, as well as the secant modulus of the samples, show a consistent trend of continuous increase.

This nuanced understanding of the interplay between pore dynamics, stress, and fractures sheds light on the complex behavior of the rock material, highlighting the non-trivial factors contributing to the observed trends in the experimental results.

In general tests, after the pores are closed during the loading and unloading process of the sample, the initiation, development and penetration of cracks occur inside the sample, and may also be accompanied by slippage between mineral crystals. Compare such a process with those formulas in Sect. 4.3. When the secant modulus decreases, the recoverable deformation inside the sample begins to self-drive. The energy of the internal crack initiation comes from the compression deformation energy between some crystals accumulated in the early stage and part of the energy input by the machine at this time.

4.4.3 Energy evolution in slope loading

Showing in Fig. 33, the evolution of energy in the sample presents an irregular state of change as the number of cycles increases. Despite this irregularity, there is a discernible overall trend in the energy variation, albeit with fluctuations around the theoretical change trend. This fluctuation is reminiscent of the relationship between true values and measured values in the measurement process, as highlighted by Faranda and Vaienti (2014).

Fig. 33

Fluctuation problem in energy evolution

To address the nonlinearity observed in energy changes during loading and unloading, this study employs an approach of accumulating energy. By examining the total energy and exploring its evolution, a remarkable linear regularity emerges. This elimination of nonlinear results through the accumulation of energy provides a meaningful insight into the law governing energy evolution.

Understanding the linear regularity in the total energy evolution is particularly significant, offering valuable contributions to the exploration of energy dynamics within the context of the study. It underscores the importance of considering cumulative energy changes to unveil a clearer and more regular pattern in the complex energy evolution process.

When comparing these results to those presented in Sect. 4.2, a compelling linear relationship emerges when using accumulated energy to explore specimen force under complex loading conditions. This simplification of the prediction formula for the energy evolution process, in contrast to many nonlinear studies, carries substantial value for engineering applications. The streamlined approach provides a clearer understanding of energy dynamics.

4.5 P-wave reflection caused by disturbance and specimen failure mode

Based on the results of Sect. 3, the failure modes of the samples were investigated. The effects of linear loading and perturbation on materials under complex stress conditions were superimposed, to explore the combined effect on the state of the specimen. Figure 34 shows a schematic diagram of the force transmission and displacement changes of the mineral crystal unit inside the sample under complex stress conditions. During this process, the up and down vibration of the particles after the disturbance of the mineral crystal unit can be seen. The force is transmitted by the particles moving up and down. This process enables the propagation of stress waves.

Fig. 34

Transmission of stress waves inside matter

Figure 35 shows the stress of the specimen under uniaxial action and complex stress conditions. Under linear loading conditions, the fracture of the specimen is shear fracture. We take stress elements along the fracture surface for force analysis.

Fig. 35

Force analysis under the superposition of two forces

Taking a mechanical unit in the sample as the research object, the fracture angle of the sample is explored. As shown in Fig. 35, the normal stress and shear stress of the fracture surface of the sample can be expressed as:

$$\left\{ \begin{gathered} \sigma_{{{\text{xy}}}} { = }\frac{{\sigma_{{\text{x}}} { + }\sigma_{{\text{y}}} }}{2}{ + }\frac{{\sigma_{{\text{x}}} - \sigma_{{\text{y}}} }}{2}\cos \left( {2\theta } \right) \hfill \\ \tau_{{{\text{xy}}}} { = }\frac{{\sigma_{{\text{x}}} - \sigma_{{\text{y}}} }}{2}\sin \left( {2\theta } \right) \hfill \\ \end{gathered} \right.$$

(36)

where $\sigma_{{\text{x}}}$ and $\sigma_{{\text{y}}}$ are the plane force of the sample under this stress condition, and $\theta$ is the rupture angle of the sample under this condition.

According to the Mohr–Coulomb criterion (Jaeger 1979), It can be obtained that the relationship when the sample breaks at this time is as follows:

$$\frac{{\sigma_{{\text{x}}} - \sigma_{{\text{y}}} }}{2}\sin \left( {2\theta } \right) = {\text{tan}}\varphi \cdot \sigma_{{{\text{xy}}}} + c$$

(37)

where $\varphi$ is the angle of internal friction and $c$ is the cohesion.

Based on the elastic wave theory (Wei 2022), a longitudinal wave with an incident angle of θ propagates in the elastic half-space, and the P wave and the SV wave are reflected on the theoretical fracture surface. Assuming no energy loss during propagation, the potential function of the incident longitudinal wave in the two-dimensional Cartesian coordinate system can be derived as follows:

$$\left. {\left\{ \begin{gathered} {\text{u}}_{x}^{{}} \hfill \\ u_{y}^{{}} \hfill \\ \end{gathered} \right.} \right\}\left. { = \left\{ \begin{gathered} \frac{\partial }{{\partial \sigma_{x}^{{}} }} \hfill \\ \frac{\partial }{{\partial \sigma_{y}^{{}} }} \hfill \\ \end{gathered} \right.} \right\}A\exp \left[ {ik_{1}^{{}} \left( {x\sin \beta + y\cos \beta - v_{p} t} \right)} \right] + \left. {\left\{ \begin{gathered} - \frac{\partial }{{\partial \sigma_{y}^{{}} }} \hfill \\ \frac{\partial }{{\partial \sigma_{x}^{{}} }} \hfill \\ \end{gathered} \right.} \right\}A\exp \left[ {ik_{1}^{{}} \left( {x\sin \gamma + y\cos \gamma - v_{s} t} \right)} \right]$$

(38)

According to the conditions of this paper, the expression of stress can be obtained as follows:

$$\left\{ \begin{gathered} \sigma_{x}^{{}} = \lambda \left( {\frac{{\partial u_{{\text{x}}} }}{{\partial {\text{x}}}} + \frac{{\partial u_{y} }}{\partial y}} \right) + 2G\frac{{\partial u_{{\text{x}}} }}{{\partial {\text{x}}}} \hfill \\ \sigma_{{\text{y}}}^{{}} = \lambda \left( {\frac{{\partial u_{{\text{x}}} }}{{\partial {\text{x}}}} + \frac{{\partial u_{y} }}{\partial y}} \right) + 2G\frac{{\partial u_{y} }}{\partial y} \hfill \\ \tau_{{}}^{T} = G\left( {\frac{{\partial u_{{\text{x}}} }}{\partial y} + \frac{{\partial u_{y} }}{\partial x}} \right) \hfill \\ \end{gathered} \right.$$

(39)

In the above formula: the expression of each parameter is very complex, and it needs to be deduced in combination with formula (9) and formula (A12)– (A14) in (Huang et al 2017). Finally, the resulting spatial stress distribution changes are shown in Fig. 36c.

Fig. 36

a Force analysis under disturbance, b stress wave model with oblique incidence, c periodic variation of stress caused by disturbance

The superimposed stress path of linear loading and perturbation can cause three phenomena as shown in Fig. 37.

Fig. 37

Directional deflection of maximum shear stress caused by linear loading and disturbance

Such modifications can be verified by the results showed in Fig. 38. As the amplitude of perturbation increases, the angle of the fracture surface also increases. Additionally, compared to the linear loading condition, the failure form of the specimen becomes more complex. Since the stress changes with time during the disturbance process, the failure often presents in the form of multiple fracture surfaces, making the failure form more complicated than that of the linear loading.

Fig. 38

Experimentally obtained fracture surface changes

4.6 Engineering significance

Fault rockburst refers to the violent energy release phenomenon at the coal mine scale caused by sudden fault slip caused by coal mining activities (Cai et al 2021). This sudden fault slip, also known as fault reactivation, is a key factor in the occurrence of fault-induced rock bursts. The critical condition for the activation of the interrupted layer in this process is as follows:

$$\tau_{{{\text{xy}}}}^{{}} \le \left[ \tau \right]$$

(40)

Combined with the results obtained above, as shown in Fig. 39, it can be seen that the stress wave disturbance will induce fractures around the fault to expand around the fault. Crack propagation reduces the critical shear strength for fault activation.

$$\left[ {\tau_{{}}^{ - } } \right] = {\text{k}}_{1} \left[ \tau \right]$$

(41)

where $\left[ {\tau_{{}}^{ - } } \right]$ is the weakened fault activation strength, k is the fault activation parameter, and $\left[ \tau \right]$ is the fault activation strength before undisturbed.

Fig. 39

Disturbance-induced fissure development around faults

At the same time, the disturbance will promote the change of the direction of the maximum shear stress. It can be seen from Fig. 40 that if the direction of the maximum shear stress coincides with the direction of the fault, the risk of fault activation will be greatly increased, as shown in the following formula:

$$\tau_{{{\text{xy}}}}^{ + } = {\text{k}}_{{2}} \tau_{{{\text{xy}}}}^{{}}$$

(42)

where $\tau_{{{\text{xy}}}}^{ + }$ is the shear stress value after the shear stress has changed, ${\text{k}}_{{2}}$ is a parameter related to the disturbance stress, and $\tau_{{{\text{xy}}}}^{{}}$ is the shear stress value before the undisturbed fault activity.

Fig. 40

Disturbance-induced maximum shear stress direction deflection induced fault activation

This outcome offers a potential explanation for the occurrence of fissures in the walls of underground parking structures. The practical aspects of underground engineering involve in-situ stress induced by the overlying rock and adjacent buildings, as illustrated in Fig. 41. Concurrently, the movements associated with transportation and construction projects generate stress waves. The underground walls and roof of the space experience distinct force influences, amalgamating into a complex set of stress conditions. This insight proves valuable in comprehending issues like wall leakage in underground garages or the formation of fissures in various underground engineering projects.

Fig. 41

Development of underground wall fissures caused by ground disturbance

5 Conclusions

In this study, we used a combination of innovative methodologies, including a novel slope loading path design, acoustic identification for sample selection through waveform analysis, and a 3D reconstruction algorithm for crack detection utilizing the YOLOv5 and the FAST feature point detection algorithms. Our focus was on understanding the behaviour of sandstone samples under a combined loading path, with particular emphasis on stress‒strain evolution, energy dynamics, secant modulus changes, and crack development.

The key conclusions drawn from our comprehensive investigation are as follows:

• 1. Deformation Rate Determination: The deformation rate of a sample under complex stress is intricately linked to the cumulative stress level resulting from the superposition of various stresses. The stress level of the superposition result determines the deformation rate of the sample.

• 2. Energy Evolution Trend: In the context of complex stress, the internal energy evolution exhibits nonlinear changes. However, a more robust linear trend is observed from the statistical analysis of the accumulated energy.

• 3. Perturbation Effect on the Fracture Development: Under identical stress levels, the perturbation effects play a crucial role in promoting more comprehensive development of the internal fracture system. This induces fractures perpendicular to the perturbation direction within the sample.

• 4. Crack Detection and Three-Dimensional Reconstruction: By leveraging YOLOv5 and FAST feature points for crack detection, we successfully achieved three-dimensional reconstruction, providing valuable insights into surface crack morphology and the fracture mode of the sample.

• 5. Disturbance Stress Wave Influence: Disturbance stress waves cause periodic deflection of the maximum shear stress surface inside the sample, leading to the induction of more fracture surfaces and altering the angle of the fracture surface.

In summary, our findings contribute to a deeper understanding of the intricate interactions within sandstone samples under complex loading conditions. Moreover, the integration of advanced methodologies facilitates practical applications in engineering. Through theoretical analysis, we elucidated the underlying reasons for the observed phenomena, emphasizing the potential value of our research in the field.