1 Introduction

The study of the strength behaviors of rock materials under three-dimensional (3D) stress conditions is always a difficult and challenging field. To determine the failure strength of intact rocks and rock masses, numerous strength criteria have been developed (Hoek et al. 1992; Li et al. 2022; Wu et al. 2017; Zhu and Shao 2020). The Hoek–Brown (HB) strength criterion based on the statistical analysis of polyaxial test data is widely used in geotechnical engineering and has been gradually developed to create a relatively complete system (Chen et al. 2021; Gao et al. 2019; Hoek and Brown 1980; Li et al. 2021). The required empirical parameters are related to uniaxial strength behaviors, mineral compositions and structural characteristics of rocks (Hoek et al. 1992). Because this strength criterion can describe the inherent nonlinear failure of rock materials, it is useful in related engineering applications (Merifield et al. 2006; Yang et al. 2018). However, the factor of intermediate principal stress σ2 is not reflected in the original HB criterion, and many studies (Gong et al. 2019; Zhang et al. 2019, 2022) have illustrated the influence of σ2 on rock failure. Mogi (1971) conducted high triaxial compression tests on Mizuho trachyte and Dunhan dolomite and revealed the critical effect of σ2 on rock strength. Takahashi and Koide (1989), Ma and Haimson (2016), Gao et al. (2018), Du et al. (2020) and other scholars reached similar conclusions by performing true triaxial tests on different types of rock.

Thus, developing a 3D version of the HB criterion that reflects the role of σ2 is vital to understand the strength characteristics of rock materials under 3D stress conditions. Pan and Hudson (1988) elevated the original two-dimensional (2D) HB strength criterion to a 3D version with a circular envelope in the π-plane. Singh et al. (1998) replaced the minimum principal stress σ3 in the power-law term with (σ2 + σ3)/2 to realize the three-dimensionalization of the generalized HB (GHB) criterion. Priest (2005) established a new 3D version by combining the Drucker–Prager (DP) criterion (Drucker and Prager 1952) and the GHB strength criterion (Hoek et al. 1992) and reduced it to a simplified version with higher prediction accuracy. Jiang and Zhao (2015) summarized the relationships between the stress invariants of multiple 3D HB criteria and proposed a unified expression and a modified 3D HB criterion. However, the existing 3D HB strength criteria cannot directly or clearly describe the influence of σ2 and σ3 on the failure strength of rock materials, and their complex expressions are inconvenient for engineering applications. Therefore, it is crucial to establish a 3D HB strength criterion that is simple in expression and can quantitatively describe the effects of σ2 and σ3.

The existing 3D and original 2D HB criteria are primarily used to characterize the failure of intact rocks. Directly using them to explore the failure and strength properties of the jointed rock mass will produce significant errors and cannot reflect the strong joint orientation dependence (Zhang 2008). Many studies (Colak and Unlu 2004; Nasseri et al. 2003; Wen et al. 2021) have demonstrated the differences in the empirical parameter mb in the HB criterion corresponding to different inclination angles, and a marginal deviation in mb will lead to large predicted errors. Accurate determination of mb at different dip angles is a crucial factor in solving the strength parameters of jointed rock mass. Hoek et al. (1992), Tien and Kuo (2001), Lee and Pietruszczak (2008) and other scholars (Ismael and Konietzky 2019; Saroglou and Tsiambaos 2008) successively proposed the relationships mb(β) between the empirical parameter mb and inclination angle β, and then developed the HB criterion to grasp the strength characteristics of the jointed rock mass under conventional triaxial stress states. Existing empirical equations describe the simple monotonic or quadratic function relationship between mb and β, and are not suitable for all types of jointed rock masses. Therefore, seeking a universal variation law and establishing an accurate empirical relation mb(β) is critical. It is also necessary to combine this empirical relationship with a reliable 3D HB strength criterion to effectively determine the true triaxial failure strength properties of a jointed rock mass.

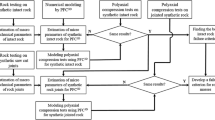
In this study, a new 3D expression of HB criterion was first established for intact rocks. To reflect the effects of σ2 and σ3 on the rock strength, a weighting factor n was introduced into the 3D criterion, and σ3 in the power-law term was replaced by (nσ2 + σ3)/(n + 1). The proposed 3D version was verified using true triaxial test results, and the prediction accuracy was compared with that of five other 3D HB criteria. Results show the least deviation between the predicted strengths of the proposed criterion and the test values, and the overall prediction effect is superior to the other five. Then, a new empirical relation mb(β) was established to apply the proposed 3D HB criterion to jointed rock masses. The proposed empirical relation mb(β) can describe the monotonic or quadratic function relationship between the parameter mb and the dip angle β, and also achieves good fitting on the similar periodic variation of mb. Thus, the proposed 3D HB criterion has good prediction accuracy for the polyaxial strength values of jointed rock masses. The modified 3D HB criterion in this study achieves good predictions and exhibits potential in related engineering applications.

2 Failure criteria for intact rocks

2.1 Existing 3D HB strength criteria

To describe the nonlinearity between the maximum principal stress σ1 and the minimum principal stress σ3 of intact rocks, Hoek and Brown (1980) presented the well-known HB strength criterion:

$$\sigma_{1} = \sigma_{3} + \sigma_{ci} \left( {m_{i} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + 1} \right)^{0.5}$$
(1)

where σci is the failure strength under uniaxial stress, and mi is the material parameter.

The HB criterion has since been continuously improved while being widely used. Hoek et al. (1992) developed the GHB criterion that can be applied to rock masses with poor quality:

$$\sigma_{1} = \sigma_{3} + \sigma_{ci} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{a}$$
(2)

where mb, s, and a are the empirical parameters of rock mass. For intact rock, s and a are set equal to 1 and 0.5, respectively.

Because both the original and generalized HB criteria overlook the role of σ2, the true 3D strength behavior cannot be clearly described. Pan and Hudson (1988) first established a novel 3D criterion, which expresses the relation between the first stress invariant I1 and second deviatoric stress invariant J2:

$$\frac{3}{{\sigma_{ci} }}J_{2} + \frac{\sqrt 3 }{2}m_{i} \sqrt {J_{2} } - m_{i} \frac{{I_{1} }}{3} = s\sigma_{ci}$$
(3)

where the specific expressions of I1 and J2 are

$$I_{1} = \sigma_{1} + \sigma_{2} + \sigma_{3}$$
(4)
$$J_{2} = \frac{{\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{3} - \sigma_{1} } \right)^{2} }}{6}$$
(5)

Singh et al. (1998) replaced σ3 in the power-law term with (σ2 + σ3)/2 to realize the three-dimensionalization of the GHB criterion:

$$\sigma_{1} = \sigma_{3} + \sigma_{ci} \left( {m_{b} \frac{{\sigma_{2} + \sigma_{3} }}{{2\sigma_{ci} }} + s} \right)^{a}$$
(6)

By combining the GHB and the DP criteria, Priest (2005) established a comprehensive 3D version and developed a simplified expression that performs better than the comprehensive version. The specific expression of the simplified Priest criterion is

$$\sigma_{1} =\, 3\left[ {\mu \sigma_{2} + \left( {1 - \mu } \right)\sigma_{3} } \right] + \sigma_{ci} \left[ {m_{b} \frac{{\mu \sigma_{2} + \left( {1 - \mu } \right)\sigma_{3} }}{{\sigma_{ci} }} + s} \right]^{a} - \left( {\sigma_{2} + \sigma_{3} } \right)$$
(7)

where μ is an empirical parameter reflecting the influence of σ2, and its value ranges between 0 and 1.

Jiang and Zhao (2015) summarized a unified relationship between I1 and J2 by analyzing the GHB, Singh, Pan–Hudson, Priest and other strength criteria and proposed a relatively simple version:

$$\frac{1}{{m_{b} \sigma_{{_{ci} }}^{1/a - 1} }}\left( {\sqrt {3J_{2} } } \right)^{1/a} + \frac{{2\cos \left( {\pi /3 - \theta_{L} } \right)}}{\sqrt 3 }\sqrt {J_{2} } - \frac{{I_{1} }}{3} = \frac{{s\sigma_{ci} }}{{m_{b} }}$$
(8)

where θL is the Lode angle.

2.2 Proposed 3D HB strength criterion

Neglecting the role of σ2 is a deficiency of the GHB criterion. Both the σ2 and σ3 affect the rock failure strength characteristics, but in different proportions. Mogi (1967) also pointed out that the enhancement of the failure strength is affected by σ2 to a certain extent and developed an empirical function between (σ1-σ3)/2 and (σ1 + ησ2 + σ3)/2. η is an effect weighting factor for σ2. Based on this, we initially considered adopting the ησ2 + σ3 to replace the σ3 in the power-law term of GHB criterion, thereby establishing a new 3D version. However, when σ2 = σ3, η must be equal to 0 if the 3D version is to be reduced to the 2D HB criterion. Therefore, a modified 3D HB criterion was developed to describe the effects of σ2 and σ3 on rock mass strength:

$$\sigma_{1} = \sigma_{3} + \sigma_{ci} \left[ {m_{b} \frac{{n\sigma_{2} + \sigma_{3} }}{{\left( {n + 1} \right)\sigma_{ci} }} + s} \right]^{a}$$
(9)

where n is the stress weighting factor, ranging from 0 to 1. In this criterion, (nσ2 + σ3)/(n + 1) is used to replace σ3 in the power-law term. The weighting factor n before σ2 and the coefficient 1 before σ3 are interchangeable, and the effects of σ2 and σ3 reflected by the proposed criterion are relative. When σ2 = σ3, the proposed 3D version is automatically converted to the GHB criterion. Equation (9) can be rewritten as follows:

$$\sigma_{1} = \sigma_{3} + \sigma_{ci} \left[ {m_{b} \frac{{p\sigma_{2} + q\sigma_{3} }}{{\sigma_{ci} }} + s} \right]^{a}$$
(10)

where p and q are the empirical parameters for evaluating the influence of σ2 and σ3, respectively. p equals n/(n + 1) and varies from 0 and 0.5, and q equals 1/(n + 1) and varies from 0.5 and 1. Compared with the simple Priest criterion (Eq. (7)), Eq. (10) is a more simplified form, and the ranges of the empirical parameters μ and p are different. Mogi (1967) noted that the influence of σ2 on the failure strength is smaller than that of σ3; thus, the range of the empirical parameter p set in this study is more reasonable. For intact rocks, Eq. (9) is rewritten as

$$\sigma_{1} = \sigma_{3} + \sigma_{ci} \left[ {m_{i} ^{\prime}\frac{{n\sigma_{2} + \sigma_{3} }}{{\left( {n + 1} \right)\sigma_{ci} }} + 1} \right]^{0.5}$$
(11)

where mi' is the empirical coefficient in the proposed criterion.

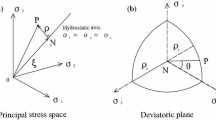
In the principal stress space, Eq. (9) is expressed by the stress invariants and the Lode angle as

$$F\left( {I_{1} ,J_{2} ,\theta_{L} } \right) = \sigma_{ci} \left[ {\frac{{m_{b} I_{1} }}{{3\sigma_{ci} }} + 2m_{b} \sqrt {J_{2} } \frac{{n\cos \left( {\theta_{L} - \frac{2\pi }{3}} \right) + \cos \left( {\theta_{L} + \frac{2\pi }{3}} \right)}}{{\sqrt 3 \left( {n + 1} \right)\sigma_{ci} }} + s} \right]^{a} - 2\sqrt {\sigma_{ci} } \cos \left( {\theta_{L} - \frac{\pi }{6}} \right)$$
(12)

To demonstrate the failure envelopes in the π-plane for different weighting factors n, Eq. (12) was applied to sandstone (Du et al. 2020) at I1 = 100 Mpa. From the expressions of the proposed and other existing 3D versions, it can be seen that Eq. (9) becomes Eq. (2) (2D HB criterion) and Eq. (9) (Singh criterion) at n = 0 and 1, respectively. Then, both the HB criterion and the Singh criterion were applied to sandstone. As shown in Fig. 1, the cross-sectional shape of Eq. (12) in the π-plane is an irregular hexagon. For different n, the failure strength values are the same at σ2 = σ3. As n increases from 0 to 1, the envelope gradually expands outward, and the strength at σ1 = σ2 increases. When n is taken to the minimum value of 0, the role of σ2 is neglected, and the envelope of the proposed strength criterion is identical to the HB criterion. When n is equal to the maximum value 1, the effects of σ2 and σ3 are considered the same, and the envelope of the proposed strength criterion coincides with that of the Singh criterion. Therefore, the Singh and the GHB criteria can be regarded as the upper and lower bounds of the proposed criterion, respectively.

Fig. 1
figure 1

Failure envelopes in the π-plane of the proposed 3D criterion at I1 = 100 MPa for sandstone with σci = 32 MPa, mi = 26, s = 1, and a = 0.5

Full size image

2.3 Validation of the proposed 3D HB criterion

Six test datasets (Table 1 or Online Resource 1) were adopted to prove the accuracy of the proposed criterion in predicting the failure strength of intact rocks. The selected test data covers uniaxial compression (σ2 = σ3 = 0), biaxial compression (σ1 > σ2 > σ3 = 0), conventional triaxial compression (σ1 > σ2 = σ3), true triaxial compression (σ1 > σ2 > σ3 ≠ 0), and triaxial tension (σ1 = σ2 > σ3) test results.

Table 1 Summary of triaxial test datasets for jointed rock masses
Full size table

Nonlinear regression fitting was performed using the curve fitting tool in the MATLAB software. After selecting the data set, the fitting function was set according to requirements in the custom equations window. The values of parameters in the expression were obtained by the nonlinear least square method. s and a equal 1 and 0.5, respectively, and σci represents the uniaxial compression strengths of the six rocks. The calibration parameters mi', n, p and q for these six intact rocks are listed in Table 2. The relative error percentage (AAREP) and the root mean squared logarithmic error (RMSLE) were employed to evaluate the accuracy of predictions. The specific expressions are

$${\text{AAREP}} = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left| {\frac{{\sigma_{{1,{\text{pred}}}} - \sigma_{{1,{\text{test}}}} }}{{\sigma_{{1,{\text{pred}}}} }}} \right|} \times 100\%$$
(13)
$${\text{RMLSE}} = \sqrt {\frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left[ {\log \left( {\sigma_{{1,{\text{test}}}} + 1} \right) - \log \left( {\sigma_{{1,{\text{pred}}}} + 1} \right)} \right]^{2} } }$$
(14)

where σ1,test is the test value of σ1; σ1,pred is the predicted value of σ1; N is the data number. The value of AAREP or RMLSE close to 0 demonstrates a better prediction. Table 2 also shows the calculated error measures for the six rocks. Figure 2 shows the best fits of the proposed 3D criterion to the test results.

Fig. 2
figure 2

Best fitting of the proposed criterion to the polyaxial test data

Full size image
Table 2 Calibration results of the proposed 3D HB criterion for six intact rocks
Full size table

Table 2 and Fig. 2 show that the proposed criterion can accurately estimate the failure strengths of six intact rocks under different stress states. The weighting factors n of the six rocks are all small. The Dunhan dolomite has the largest n, indicating that the σ2 dependence of Dunhan dolomite is higher than that of other rocks. The calculated empirical parameter p is approximately 3.26 to 21.22 times q, indicating that the influence of σ3 is greater than that of σ3.

To demonstrate the superiority and accuracy of the proposed criterion, the HB, Pan–Hudson, Singh, Priest, and Jiang–Zhao criteria were also adopted to evaluate the failure strength of these six rocks. s, a, and σci are the inherent parameters and experimental results of intact rocks, and they are the same as those used in the proposed criterion. The mi' values in Table 2 are only used in the proposed strength criterion. The mi values in other existing strength criteria are the respective fitting results with the experimental data. The error measure AAREP and RMLSE values for the six strength criteria are summarized in Fig. 3, and these criteria are ranked according to their prediction accuracy.

Fig. 3
figure 3

Error measures of the six criteria for six intact rock types

Full size image

For the Mizuho trachyte, the simple Priest criterion performs best, with AAREP and RMLSE of 3.080% and 1.781 × 10–2, respectively. AAREP and RMLSE of the proposed criterion are 3.291% and 1.814 × 10–2, respectively, indicating a prediction that is not significantly different to the Priest criterion. For the other five rocks, the proposed criterion works better than the other five strength criteria. This is because the stress weighting factor n in the proposed criterion can be adjusted according to the impacts of σ2 and σ3, thus improving its predictive ability. The Priest strength criterion also has an empirical parameter μ that describes the role of σ2. However, the adjustable range of μ is not as accurate as the range of the stress weighting factor n in the proposed criterion, and cannot reflect the fact that the influence capacity of σ3 is greater than that of σ2. For the total data of these six rocks, the proposed strength criterion performs best, followed by the simple Priest criterion, Jiang–Zhao, HB, Pan–Hudson, and Singh criteria. The prediction produced by the Singh criterion is worse than the HB criterion because the weighting factor n in the Singh criterion equals 1, overestimating the effect of σ2. The HB criterion ignores the σ2 and sets n to 0, which is closer to the calibration results of n in Table 2. The Pan–Hudson criterion achieves poor prediction accuracies and cannot be simplified to the original HB criterion in three-dimensional tension (σ1 = σ2) and compression states (σ2 = σ3). Overall, the proposed 3D version can describe the failure strength behavior well by adjusting the stress weighting factor n and quantitatively evaluate the impacts of σ2 and σ3 on the rock failure.

3 Failure criteria for jointed rock masses

3.1 Existing empirical relations for parameter m b

In some studies (Ma et al. 2020; Zhang 2008), the 3D strength criteria for intact rocks were used to estimate the failure strength parameters of jointed rock masses, but this cannot describe the high joint directional dependence of the strength behaviors, and the resulting predictions are poor. When establishing the 3D criterion for jointed rock masses, the joint orientation is an important consideration (Singh et al. 2018), including the dip direction α and dip angle β (Fig. 4).

Fig. 4
figure 4

Relationship between the joint plane and the three principal stress directions

Full size image

The dip angle β is the primary consideration in the previous true triaxial test study of jointed rock masses (Feng et al. 2019; Zhang et al. 2012; Zhao et al. 2021), and there is a lack of test data considering the comprehensive effect of α and β. Therefore, the existing modified HB criteria (Hoek et al. 1992; Lee and Pietruszczak 2008; Ismael and Konietzky 2019) for jointed rock masses only considers the single factor of β, and the effect of σ2 is neglected. The empirical parameter mb of the jointed rock mass is related to the dip angle of the joint plane (Colak and Unlu 2004), thus the original 2D HB criterion is rewritten as

$$\sigma_{1} = \sigma_{3} + \sigma_{cj} \left[ {m_{b} \left( \beta \right)\frac{{\sigma_{3} }}{{\sigma_{cj} }} + 1} \right]^{0.5}$$
(15)

where mb(β) is the empirical parameter mb at a certain angle of β, and σcj is the uniaxial compression strength at a certain angle of β. By combining the HB strength criterion expression of Eq. (15), some scholars established the empirical relations mb(β) to predict the strength parameters of anisotropic rock masses. Hoek et al. (1992) first derived an empirical relationship between mb and β:

$$\frac{{m_{b} \left( \beta \right)}}{{m_{b} \left( {0^\circ } \right)}} = 1 - k_{1} \exp \left[ { - \left( {\frac{{\beta - k_{2} }}{{k_{3} + \beta k_{4} }}} \right)^{4} } \right]$$
(16)

where mb(0°) is mb when the dip angle is 0°, and k1, k2, k3, and k4 are constant terms.

From Jaeger's strength criterion (Jaeger 1960), Tien and Kuo (2001) developed another empirical relation:

$$\frac{{m_{b} \left( \beta \right)}}{{m_{b} \left( {0^\circ } \right)}} = \frac{1}{{1 + l\sin^{2} \beta \cdot \cos^{2} \beta }}$$
(17)

where l is a constant term.

Also, Lee and Pietruszczak (2008) established a 3D HB criterion to analyze the rock strength anisotropy, and the relationship between mb and β is

$$m_{b} \left( \beta \right) = t_{1} - t_{2} \exp \left[ {t_{3} \left( {1 - 3\cos^{2} \beta } \right)} \right]$$
(18)

where t1, t2, and t3 are constant terms.

3.2 Proposed empirical relation for parameter m b

To seek the relationship between the empirical parameter mb and the dip angle β, six triaxial test datasets (Table 3 or Online Resource 2) of jointed rock masses were adopted. Combining Eq. (15), the variations in the mb value with dip angle β are plotted in Fig. 5.

Table 3 Summary of triaxial test datasets for jointed rock masses
Full size table
Fig. 5
figure 5

Variation in the mb value with dip angle β

Full size image

Figure 5 indicates that the variations in Isfahan schist, dry phyllite, and layered rock show marked quadratic function relationships, and the mb of carbonaceous phyllite, chlorite schist, and dry orthoquartzite exhibit similar periodic function relationships with dip angle β. The mb values corresponding to different β were calculated using the existing empirical relations (Eqs. (16)–(18)). Results show that Eqs. (16) and (18) exhibit a monotonic function in the range of β = 0°–90°, while Eq. (17) is a quadratic function symmetric about β = 45°. Therefore, none of these three empirical relations accurately describe the variation of mb with the dip angle, particularly for the similar periodic variation curves shown in Fig. 5.

According to the variations in the parameter mb with the dip angle β shown in Fig. 5, the following empirical function was established:

$$m_{b} \left( \beta \right) = A + B\cos \left( {w \cdot \beta } \right) + C\sin \left( {w \cdot \beta } \right)$$
(19)

where A, B, C, and w are constant terms.

Combining Eqs. (11) and (19), the proposed 3D HB criterion is rewritten as the following expression so that it can be applied to the jointed rock masses:

$$\sigma_{1} = \sigma_{3} + \sigma_{cj} \left[ {m_{b} \left( \beta \right)\frac{{n\sigma_{2} + \sigma_{3} }}{{\left( {n + 1} \right)\sigma_{cj} }} + 1} \right]^{0.5}$$
(20)

In the established 3D criterion Eq. (20) for jointed rock masses, the impacts of σ2 and joint orientation can be considered concurrently. Because the true triaxial datasets of jointed rock masses considering both α and β are lacking, the proposed strength criterion assumes that the α is fixed and only the β is considered.

3.3 Validation of the proposed empirical relation m b(β) and 3D HB criterion

First, the proposed empirical relation mb(β) and the 3D HB criterion were verified using the six conventional triaxial test datasets listed in Table 3. At this time, σ2 = σ3 and Eq. (20) becomes Eq. (15). mb in Fig. 5 are fitted with Eq. (19), and the calculated values of each constant term are shown in Table 4. The prediction effects of the proposed empirical relationship are evaluated by AAREP and RMLSE. From Table 4, the established empirical relation mb(β) achieves good prediction accuracies for the empirical parameters mb of six jointed rock masses, and the maximum AAREP and RMLSE are 3.014% and 1.367 × 10–2, respectively. To demonstrate the advantages of the proposed empirical relation, the AAREP and RMLSE of the three existing empirical functions introduced above and the proposed empirical relation are summarized in Fig. 6, and these relations are ranked according to their prediction accuracy.

Table 4 Calibration results of the proposed empirical relation mb(β) for six jointed rock masses
Full size table
Fig. 6
figure 6

Error measures of the four empirical relations for mb values of six jointed rock masses

Full size image

Because the mb of carbonaceous phyllite changes slightly with dip angle, these four empirical relations all show good prediction effects, and the proposed empirical relation performs the best. For chlorite schist and dry orthoquartzite, whose mb variations are similar to the periodic function, the predictions of the proposed empirical relation are markedly better than those of the other three relations. The mb variation of Isfahan schist is a quadratic function curve symmetrical about β = 45°; thus, the empirical relationship proposed by Tiankuo performs well, and the empirical relationship established in this paper also achieves good predictions. It can be seen that the proposed empirical relation can accurately predict the periodic and quadratic function curves presented in Fig. 5. For the mb of all six jointed rock masses, the proposed empirical relation performs markedly better than the existing three empirical relations, and the total AAREP and RMLSE of the established relationship are 2.066% and 1.060 × 10–2, respectively. The prediction qualities of the other three empirical relations are poor, and the empirical relation established by Hoek and Brown performs the worst.

Based on the constant terms in Table 4, the calculated mb values of the six jointed rock masses at different β are obtained. By combining Eq. (15), the failure strengths under different pressures σ3 are estimated. The predicted strength values and test results of each rock type are presented in Fig. 7, and the points closer to the contour line represent a better prediction effect. The predicted values of the six rock types in Fig. 7 are all within the upper/lower limit of 85%, indicating that the predicted results agree well with the test results. Table 4 shows that the proposed empirical relation mb(β) achieves the worst prediction for dry phyllite; thus, the data points in Fig. 7b are scattered, and the predictive ability is reduced. Overall, the proposed 3D HB criterion for jointed rock masses can effectively estimate the σ1 values of six jointed rock masses with different β when σ2 = σ3.

Fig. 7
figure 7

Comparison between σ1 values predicted via the proposed 3D HB criterion for jointed rock masses and experimental results

Full size image

Then, three true triaxial datasets (Online Resource 3) were used to demonstrate the effectiveness of the proposed empirical relation mb(β) and the 3D HB criterion in evaluating the strength behaviors of jointed rock masses when σ2 ≠ σ3. The three rock types include the sand-lime block (Tiwari and Rao 2007), jointed marble (Gao et al. 2020), and columnar jointed rock mass (Lu 2021). The data number for sand-lime block, jointed marble and columnar jointed rock mass is 44, 35, and 32, respectively. By fitting Eq. (20) with the test data, the variations in the mb value with the dip angle of the three rock types are shown in Fig. 8.

Fig. 8
figure 8

Variation in the mb value with dip angle β

Full size image

As shown in Fig. 8, the mb of the sand-lime block and jointed marble exhibit a quadratic function with β, and the variation curve of the columnar jointed rock is 'W-shaped'. The mb of the three jointed rock masses are fitted with Eq. (19), and the calculated constant term values and error measures AAREP and RMLSE are listed in Table 5. Overall, the proposed empirical relation mb(β) achieves good predictions of the mb for the three rock types. The AAREP and RMLSE of the sand-lime block are 12.856% and 6.246 × 10–2, respectively, indicating relatively poor prediction performance.

Table 5 Calibration results of the proposed empirical relation mb(β) for three jointed rock masses
Full size table

The constant term values in Table 5 and Eq. (19) are used to calculate the empirical parameter mb at different dip angles of the three jointed rock masses, and the calculated values are listed in Table 6. The true triaxial test values are fitted with Eq. (20), and the calculated values of weighting factor n and two error measures are also listed in Table 6. In addition, both the σ1,test and σ1,pred values are plotted in Fig. 9.

Table 6 Calibration results of the proposed 3D HB criterion for three jointed rock masses
Full size table
Fig. 9
figure 9

Comparison between σ1 values predicted via the proposed 3D HB criterion for jointed rock masses and experimental results

Full size image

According to the error measures shown in Table 6, the proposed criterion achieves the worst predictions of the failure strength of the sand-lime block due to the relatively poor prediction performance of the established mb(β) for mb. As shown in Fig. 9a, 90.909% of the points are within the error limit, and four points beyond this range correspond to dip angles of 30° and 50°. The sensitivity of the sand-lime blocks at different β to changes in the stress environment varies considerably. In particular, the variation of σ1 value with confining pressure for blocks with dip angles of 30° and 50° is different from that for blocks with other dip angles. When σ2 = σ3 = 0.31 MPa and 0.78 MPa, the failure strengths of 30° and 50° are significantly lower than those of other dip angles. The ratios between the maximum and minimum failure strengths under different confining pressures corresponding to 0°, 70° and 90° are in the range of 1.8–2.5. When β = 30° and 50°, the data are scattered, and the corresponding ratios are 4.2 and 4.1, respectively. Therefore, the predictions for the strength values of 30° and 50° are worse than those of other dip angles. For jointed marble and columnar jointed rock mass, all σ1,pred values are within the error limit, indicating that the predicted results are consistent with the test values. Overall, the proposed 3D HB strength criterion for jointed rock masses can effectively predict the strength values for different β when σ2 ≠ σ3.

4 Discussion

4.1 Physical meaning of weighting factor n

To assess the association between two variables v1 and v2, the correlation factor r is typically applied (Freund et al. 2010). The specific expression is

$$r\left[ {v_{{1}} {, }v_{{2}} } \right] = \frac{{Cov\left[ {v_{{1}} {, }v_{{2}} } \right]}}{{\sqrt {Var\left[ {v_{{1}} } \right] \cdot Var\left[ {v_{{2}} } \right]} }}$$
(21)

where Cov[v1, v2] represents the covariance between v1 and v2; Var[v1] represents the deviation of v1; and Var[v2] represents the deviation of v2. To quantitatively describe the roles of σ2 and σ3, the partial correlation factors r2 and r3 were introduced (Ma et al. 2020):

$$r_{2} = r\left[ {\sigma_{1} {, }\sigma_{2} {:}\sigma_{3} } \right] = \frac{{r\left[ {\sigma_{1} {, }\sigma_{2} } \right] - r\left[ {\sigma_{1} {, }\sigma_{3} } \right] \cdot r\left[ {\sigma_{2} {, }\sigma_{3} } \right]}}{{\sqrt {\left( {1 - r^{2} \left[ {\sigma_{1} {, }\sigma_{3} } \right]} \right) \cdot \left( {1 - r^{2} \left[ {\sigma_{2} {, }\sigma_{3} } \right]} \right)} }}$$
(22)
$$r_{3} = r\left[ {\sigma_{1} {, }\sigma_{3} {:}\sigma_{2} } \right] = \frac{{r\left[ {\sigma_{1} {, }\sigma_{3} } \right] - r\left[ {\sigma_{1} {, }\sigma_{2} } \right] \cdot r\left[ {\sigma_{2} {, }\sigma_{3} } \right]}}{{\sqrt {\left( {1 - r^{2} \left[ {\sigma_{1} {, }\sigma_{2} } \right]} \right) \cdot \left( {1 - r^{2} \left[ {\sigma_{2} {, }\sigma_{3} } \right]} \right)} }}$$
(23)

where the factors r2 and r3 are used to assess the influence of σ2 and σ3, respectively. The minimum and maximum absolute values of r2 and r3 are 0 and 1, respectively. An absolute value of r2 or r3 close to 1 means that the σ2 or σ3 has a significant effect on the failure strength.

The partial correlation factors r2 and r3 of the six intact rocks in Sect. 2.3 were calculated and compared with the weighting factor n in Table 2. Figure 10 shows the relationships between the weighting factor n in the proposed 3D criterion and the two partial correlation factors. Based on r, the plane is divided into three parts, representing different degrees of stress dependence (Ma et al. 2020).

Fig. 10
figure 10

Relationship between influence coefficient n and partial correlation factor r

Full size image

As shown in Fig. 10, most intact rocks (Mizuho trachyte, westerly granite, KTB amphibolites, Coconino sandstone, and sandstone) exhibit low and intermediate σ2 dependencies. The partial correlation factor r2 of the Dunhan dolomite is 0.802, indicating a high σ2 dependence. The relation between n and r2 exhibits a clear exponential function, and the partial correlation factor r2 increases with the weighting factor n. The partial correlation factor r3 of all intact rocks is greater than 0.8, indicating a high σ3 dependence. There is a linear relationship between n and r3, and the partial correlation factor r3 decreases with the weighting factor n. The weighting factor n in the proposed criterion is closely correlated to the partial correlation factors r2 and r3, which means that n can effectively evaluate the roles of σ2 and σ3. Meanwhile, it is worth trying to use the calculated partial correlation factors r2 and r3 to obtain the weighting factor n.

4.2 Consideration of dip direction α

The establishment of a true triaxial criterion for jointed rock masses also requires the consideration of joint dip direction α. However, because of the shortage of true triaxial datasets considering both α and β (Feng et al. 2019; Zhang et al. 2012; Zhao et al. 2021), only the inclination angle β is considered in Sect. 2.2. In this section, the dip direction α is considered separately, and the validity of establishing the relationship between mb and α in the same function form as mb(β) (Eq. (19)) is verified. To discuss the effect of α, the true triaxial dataset of gneiss performed by Liu et al. (2020) were used (Online Resource 4). The number of test data is 16. In this true triaxial compression test, the dip angle β is fixed at 30°, and the dip directions α are 0°, 30°, 60°, and 90°. The true triaxial test results are fitted with Eq. (20), and the calculated mb at different dip directions are summarized in Fig. 11. The mb corresponding to different dip directions is predicted by a function expression of Eq. (19), and the fitting curve is also plotted in Fig. 11.

Fig. 11
figure 11

Variation in the mb value with dip direction α

Full size image

As shown in Fig. 11, mb first drops and then rises with α. The fitting curve agrees well with the data points, and the AAREP and RMLSE are 7.441% and 4.295 × 10–2, respectively. Table 7 lists the mb values for different dip directions α calculated from the obtained relation mb(α). The σ1 values of gneiss at different dip directions are predicted using the proposed 3D criterion, and the calculated weighting factor n and two error measures are also shown in Table 6. The σcj values are the uniaxial compression strengths. In addition, the σ1,test and σ1,pred values of gneiss are plotted in Fig. 12.

Table 7 Calibration results of the proposed 3D HB criterion for gneiss with different dip directions α
Full size table
Fig. 12
figure 12

Comparison between σ1 values predicted via the proposed 3D HB criterion for gneiss and experimental results

Full size image

Table 7 and Fig. 12 demonstrate that the proposed criterion works well in predicting the failure strengths of gneiss at different dip directions, and the AAREP and RMLSE are 4.901% and 3.190 × 10–2, respectively. All points are within the error limit, indicating that the predicted values agree with the test results; this result demonstrates that the empirical relation mb(α) in the same form as Eq. (19) can effectively determine the mb value for different α so that the proposed 3D strength criterion shows good prediction performance.

Strengthening the true triaxial test study of jointed rock masses considering both α and β can effectively improve the 3D strength criterion for jointed rock masses. With sufficient test data, the 3D criterion established in this paper will be promoted. If possible, the following empirical relationship mb(α, β) can provide a reference for studying the effects of α and β simultaneously:

$$m_{b} \left( {\alpha ,\beta } \right) = m_{b} \left( \alpha \right) \cdot m_{b} \left( \beta \right)$$
(24)

5 Conclusions

To describe the roles of σ2 and σ3 on the strength behaviors of intact rocks, a novel 3D version of the HB criterion was developed. Subsequently, an empirical function mb(β) was established to apply the proposed 3D HB criterion to jointed rock masses. The main conclusions are summarized as follows:

  1. 1.

    The failure envelope of the proposed strength criterion in the π-plane is an irregular hexagon and gradually expands outward as n increases from 0 to 1. When n = 0, the expression of the proposed version reduces to the original HB criterion, and their envelopes are overlapping. When n = 1, the expression of the proposed criterion becomes the Singh criterion, and the two envelopes are the same.

  2. 2.

    The proposed criterion and five other existing 3D criteria for intact rocks are validated using six sets of polyaxial test data. Overall, the proposed criterion performs the best, followed by the Priest, Jiang–Zhao, HB, Pan–Hudson, and Singh strength criteria. This is because the proposed criterion can adjust the stress weighting factor n according to the impacts of σ2 and σ3 on the rock failure.

  3. 3.

    The mb of six jointed rock masses at different dip angles β were predicted using the established relationship and three other existing empirical expressions, and the prediction qualities were compared. The proposed empirical relation mb(β) performed markedly better than the other relations; thus, the proposed 3D HB criterion can effectively determine the strength values of these six rock types when σ2 = σ3.

  4. 4.

    The applicabilities of the proposed empirical relation mb(β) and the modified 3D HB criterion under unequal confining pressures were verified using three true triaxial datasets. Results showed that the established empirical relationship achieves good predictions of the mb of three jointed rock masses, and the predicted strengths at different dip angles were consistent with the test results.

  5. 5.

    The weighting factor n is closely correlated to the partial correlation factors r2 and r3 of principal stress σ2 and σ3. The expression of the established relation mb(β) can also be used to accurately describe the variation in mb with the dip direction α, providing space to develop a better 3D strength criterion for jointed rock masses.