Spontaneous cracking of thermally toughened safety glass. Part one: Properties of nickel sulphide inclusions

Abstract

Spontaneous breakage of glass in facades is under control today, due to application of a very effective prevention method, namely the Heat Soak Test (HST) following EN 14179-1 (2006/2016). Nevertheless, details of the latter are still subject to discussion, mainly due to the fact that some years ago, it was discovered in an R&D project that it’s holding temperature is too high, and it was reduced to $260 \pm 10\,^\circ \hbox {C}$ at the recent review. In the present paper we investigate the properties of nickel sulphide inclusions in order to show that there’s a huge difference in their comportment, and therewith their “criticality”, in the HST or on the façade. Namely, not only the expansivity difference between nickel sulphide and the glass plays a role. Nickel sulphide inclusions show a spectrum of possible compositions, and we approach this fact systematically, showing how the breakage probability under both conditions changes depending on the detailed composition of the inclusions. The result of this comparison is that, out of all nickel sulphide inclusions leading to breakage in HST, only 40% also lead to breakage at ambient. Another aspect is the time-to-breakage curve in the HST. By the example of a dataset where nearly only SiO$_2$ stones cause breakages therein, we show that not only the $\upalpha$ to $\upbeta$ transformation of NiSx causes these breakages. Also the HST process itself, through the fact that it’s impossible to heat up the glass panes therein in an absolutely homogeneous way, adds significant thermo-mechanic forces leading to boosting the breakages more than possible on façades. Besides this, also the potential impact of sub-critical crack growth at HST temperature is discussed. We conclude that the actual estimation of the residual breakage probability of Heat-Soak Tested Thermally Toughened Glass (according to EN 14179-1) is much too high, needs major revision, and until then, can only be looked at to be a lower limit with high safety margin of the real safety of this product. The present paper will be completed by at least two additional papers dealing with the detection of nickel sulphide inclusions in annealed glass and, on the other hand, a new way to evaluate statistically the data from nickel sulphide inclusion caused breakages.

1 Introduction

Spontaneous breakage of thermally toughened safety glass has been an issue for more than 50 years. The Heat Soak Test (HST) was invented in about 1960 to make the glass safe against this defect. Since that time, significant research has been done on the subject, summarized in a previous review article by Karlsson (2017). The article itself reveals some apparent gaps that still exist in our understanding of the spontaneous breakage phenomenon. More recent analysis presented here sheds doubt on some of the statements and conclusions in that summary. The present series of three papers will present new facts, new insights, and relevant new findings on spontaneous breakage of thermally toughened safety glass.

This paper is presented due to resurgent interest in the subject. In the 1990’s and the beginning of the 2000’s the “old HST” (e.g. according to German DIN 18516) seemed to be insufficient because numerous spontaneous breakages had been recorded on buildings in Europe. The use of toughened glass in facades came more and more in vogue, so that not only the bare number of such sheets, but also the obvious lack in heat-soaking capacity demanded the amendment of the standard. After R&D efforts that includes the collection of 1462 times-to-breakage in refined HST ovens (Kasper and Bordeaux 2000; Kasper 2000) and their statistical evaluation as its basis, a new product had been defined in EN 14179-1:2006 named “Heat Soak Tested Thermally Toughened Safety Glass”. This product is said to be safe because the heat-soaking procedure is meticulously prescribed in the standard Fraud or accidental malpractice seem to be excluded, and the product is expected to be as safe as possible in all actual conscience.

To assure the validity of the standard, a research project was coordinated by the author (Kasper) at the Grenoble University in France (SIMaP institute, Science et Ingénierie des Matériaux et Procédés). This research project served as the PhD study of O. YOUSFI. He revealed that the HST might not be as safe as presumed. YOUSFI found that above a certain compositional limit ($\hbox {x} > 1.012$ in $\hbox {NiS}_{\mathrm{x}})$, the $\upalpha$ to $\upbeta$ transformation of nickel sulphide cannot be completed if the temperature exceeds a certain limit (Yousfi et al. 2010b). This temperature limit is $280\, ^{\circ }\hbox {C}$, which is the lower temperature during the holding time in HST defined in EN 14179-1(2006). His results were published, extensively discussed, and in 2016 (in the frame of a general revision) they were integrated into said standard. The temperature level during holding time will now be $(260 \pm 10)\, ^{\circ }\hbox {C}$, an average of $30 ^{\circ }$ lower than before, putting the holding temperature safely below the limit identified by YOUSFI.

The lower holding temperature should make the HST safer; however, some experts have suggested the holding time needs to be extended due to the lower holding temperature, following ARRHENIUS’ law that requires time prolongation on temperature decrease. In Germany, where the Bauregelliste¹ requires doubling of the holding time in comparison with EN 14179-1(2006), ostensibly to reach a certain safety level corresponding to a component failure probability of less than $10^{-6}$ per year, 4 h of holding time are assertively defended.

The focus of the present publication is therefore to discuss the need for extended holding time under the light of established and new R&D results. In the present Part One of the paper the knowledge and experience on the nature of nickel sulphide inclusions are reviewed. Previously unpublished facts and findings are presented and combined with established ones, which show the relevance of some earlier findings was either misinterpreted or simply not understood at the time of gathering them. This new analysis reveals that even after more than 50 years of study of spontaneous breakage of toughened glass, all aspects of this very complicated phenomenon are still not fully understood. The present triple paper engages to make a significant step forward in this field. Its starting point is to highlight the relevant properties of the different nickel sulphide species $(\hbox {NiS}_{\mathrm{x}})$, i.e. the minerals usually found in many of the departure points of spontaneous breakages, and to work out how this variety of minerals influences the breakage probability. In another section, the breakage in HST caused by a different kind of inclusions, namely refractory stones, is discussed. These verifiably also cause breakages, and surprisingly their breakage behavior in HST is undistinguishable from that of the nickel sulphide inclusions. This fact leads to some revolutionary conclusions concerning the HST.

Part two (Kasper et al., forthcoming) will interpret the data from a series of inclusions identified in annealed glass. In part three (Kasper, forthcoming) a dataset previously published in Kasper and Bordeaux (2000) and Kasper (2000) is combined with new data collected in the past 15 years. It is split into two datasets “Breakages on Buildings” and “Breakages in HST”. This allows analysis of the significant differences in breakage probability, showing that the HST is much safer than required.

Short glossary:

±:

Standard deviation.

$\upalpha$-, $\upbeta$-NiS:

High and low temperature phase of nickel sulphide, respectively

EDX:

Energy-dispersive X-ray fluorescence, method for quantifying composition of small particles

EN:

European Standard

HST::

Heat Soak Test, if not otherwise mentioned carried out according to EN 14179-1:2006.

MPa:

Mega-Pascal (pressure)

NiS:

Nickel sulphide, atomic composition 1:1

NiSx:

Nickel sulphide with non-stoichiometric composition, or multitude of differently composed nickel sulphides

SEM:

Scanning electron microscope

SG:

Saint-Gobain (company producing, among others, flat glass)

x:

Molar or atomic fraction (e.g. in NiSx)

2 The difference between spontaneous glass breakages on buildings and in HST: criticality of the inclusions

Observed breakages in HST are more frequent than those on buildings, but up to now these differences have never been quantified. Long-term data shows that an orientating number for the breakage rate in a typical HST is between 0.5% and 1% of the panes.² Comparing this number with the breakage numbers observed in practice on un-soaked toughened glass (e.g. on full glass doors, shower cabins, buildings in countries where a HST is not mandatory or on car glazing), the glass industry would face a significant problem with un-soaked toughened glass if one out of one or two hundred such panes were to break. This is especially true for toughened car glazing. Even though the single panes are smaller and thinner, and estimated nickel sulphide inclusions would only cause the spontaneous breakage of one pane in 400 cars over their lifetime of c. 10 years, all car glass producers would face a serious problem and undoubtedly many complaints. Applying this breakage rate to the number of cars in use in Germany, namely c. 61,000,000 (c. 5% of them are replaced yearly) (Kraftfahrtbundesamt 2016), c. 7500 spontaneous breakages per year would have to be observed, even disregarding trucks, busses and other utility vehicles with normally much bigger glass panes (and, therewith, proportionally higher breakage risk). If this breakage rate were to occur, the high number of breakages could not remain unremarked.

There is no doubt that average (float) glass quality is constant if small glass lots from “pollution crisis” are disregarded. Consequently, there should not be a principal difference between glass in a façade and glass in a glass door, a shower cabin or a car body. The different thicknesses may play a certain role; this will further be discussed in Kasper et al. (forthcoming).

The root cause of this difference in spontaneous breakage numbers is the “criticality” of the inclusions. An inclusion is called “critical” if it leads to glass breakage and “uncritical” if it does not. This “black-and-white” definition, applied on every single inclusion, is not absolute. An inclusion that is normally “uncritical” can turn into being critical if external conditions change; the reverse is also true.

Fig. 1

a Print of nickel sulphide inclusion into glass (hollow calotte); b Nickel sulphide inclusion with intact surface. Photographs both taken on breakage mirror after spontaneous breakage. Notched surface structure from crystallization of NiSx of c. $\pm \, (1 {\ldots }10)\, \upmu \hbox {m}$ is clearly visible. No trace of adhering NiSx is visible or detectable by e.g. EDX in the hollow calotte. Big defects in (a) (in arrow’s direction) are maybe artifacts generated by the breakage forces, but some deeper wrinkles are visible on the untouched rest of the surface. Dotted arrow in (b): reunification step of the primary crack (explication see text). Photographs: SG (2003/2004)

For fixed external conditions, the criticality of a nickel sulphide inclusion is mostly defined by the following parameters; however, they are individual for every inclusion, and this list is not complete. Section 2.3 points out another factor to be added, namely the impact of the HST process itself.

• The position of a nickel sulphide inclusion within the glass section.

  A very important factor for criticality is the stress surrounding the inclusion within the glass, because the stress does not only depend on the distance to the next surface, but also on the toughening degree (measurable, e.g., by the glass surface compression) and on the stress distribution over the whole pane’s surface that is never homogeneous. This can easily be seen by looking at the stress distribution pattern on a toughened car lite, using polarizing (sun-) glasses.

• The size of the inclusion. Fracture mechanics of glass reveal that with increasing inclusion diameter, the criticality also increases.

  Model calculations, e.g. in Bordeaux and Kasper (1997), Swain (1980, 1981) reveal that inclusions smaller than c. $50\, \upmu \hbox {m}$ are unable to cause glass breakage. Even if a primary crack was present, it could not “grow” enough (thereby causing the breakage of the entire pane) because respective forces are too small.

• Its detailed chemical composition.

  Concerning this factor of influence, for said modeling only the physical properties of pure NiS(1:1) have so far been accounted for. The impact of varying composition has, to the author’s knowledge, never been considered in a respective model. Even in the most recent review article (Karlsson 2017) only “the NiS” with its solely relevant $\upalpha$ and $\upbeta$ phases is mentioned as a cause of spontaneous breakage. Section 2.2 shows that this is an inadmissible simplification.

• To the author’s knowledge, the effects of the notched surface structure of inclusions (see Fig. 1 below, and later in this section) have never been taken into account in such a model.

Spontaneous breakage of thermally toughened glass basically occurs in three steps as described below. However, note that this is not only true for nickel sulphide inclusions; also with other kinds of inclusions (stones, bubbles) proven to lead to spontaneous cracking, breakage follows the same pattern.

1st step: Crack initiation

Crack initiation demands local exceeding of the glass strength. It takes place in one (“the weakest”) point, normally on a surface.

Glass strength

On its outer surface, corrosion and many small scratches limit the glass strength, whereas around an inclusion the glass has never been subject to external environment; therefore, it can be much stronger; in the case of a smooth bubble, strength could be close to theoretical strength. The latter is calculated from glass composition (window glass) and atomic forces to be c. 7000 MPa (Schaeffer 2013). Typically, the highest strength of glass measured on native and undamaged glass samples is only approximately 1/10 of this value. According to Hillig (1962) and based on more modern glass theories (see e.g. Greaves 1985; Poggemann et al. 2003) this is due to atomic fluctuations in the glass structure causing clustering during cooling, so that the glass structure is not really homogeneous; this leads to structurally caused notches in the glass surface and limits its maximum strength to a value that is significantly lower than the strength calculated from atomic distances only. Its most probable real range is therefore $(800\,\pm 200)\, \hbox {MPa}$.

Toughening

Another influencing factor is the general stress situation around the inclusion: Compressive stress locally strengthens the glass, whereas tensile stress weakens. This circumstance is a key to crack initiation and propagation. It is well known that in toughened glass the stress distribution is described in good approximation by a parabola. The minimum surface compressive stress for toughened glass is, per normative definition, − 80 MPa (Mognato et al. 2011), but for product conformity reasons this value is intentionally elevated in production, so that the surface compression is supposed to be $(-100\, \pm \, 20)\, \hbox {MPa}$; this also includes the inevitable heterogeneity of the surface stress within every glass pane. Consequently, the tensile stress at the glass’ midline $[(+50 \pm 10)\, \hbox {MPa}]$ is half of the surface value. Note that this stress is not nearly high enough to initiate spontaneous breakage of faultless glass.

Fig. 2

Circular crack around (and notched surface of) nickel sulphide inclusions, a, b Observed in annealed glass by light microscope: relation (crack length)/(inclusion radius) in both c. 1.4. c Observed in thermally toughened glass in the compressive zone, without HST: relation (crack length)/(inclusion radius) c. 0.95, in both cases the crack is orientated parallel to the surface. d Observed in thermally toughened glass in the compressive zone, after HST: size $270/370\, \upmu \hbox {m}$ // crack length (dotted arrow) $450\, \upmu \hbox {m}$, relation (crack length)/(inclusion radius) c. 2.8, crack height close to inclusion estimated from Newtonian rings’ number c. $1.8\, \upmu \hbox {m}$. Photographs: SG (1968/2004/2017) [a–c: Size/magnification not reported]

Cohesion between inclusion and glass

Figure 1a shows that there’s no cohesion between glass and nickel sulphide inclusions. When the inclusion falls off or sticks in the other half of the breakage center, no significant pieces of NiS remain on the surface of such an empty calotte although nickel sulphide inclusions often show very weak inner adhesion and easily disintegrate into their inner single crystals. The lack of cohesion between glass and NiS is related to the non-wettability of and insolubility of nickel sulphide in the glass (melt) already described by Heinrichs and Becker (1928). This fact is important for the modeling of breakage mechanics because if there’s no cohesion, the stress situation around the (untransformed) inclusion resembles to that of a (notched) bubble but not to that of a “normal” (silicate, silicon, other interlocked) inclusion. It is also important for the following considerations because an (untransformed) nickel sulphide inclusion that is smaller than its surrounding bubble does not exert force onto the glass.

Size (diameter) impact

The inclusion’s size and the surrounding stress field play the deciding roles for crack initiation.

In Fig. 2, examples of initial cracks generated by nickel sulphide inclusions are shown. The crack size is in the range of the radius of the inclusion, except for the situation after HST where it is significantly more extended. The photographs in Fig. 2a, b have been taken on annealed glass, those in Fig. 2c, d in the compressive zone of toughened glass. Respective photographs from the tensile zone of toughened glass cannot be taken because the inclusions cause glass breakage; at the reverse they are then found on the surface of the “butterfly” after breakage.

Note that in Fig. 2a, b the crack is not equatorial and not orientated into a definite direction with reference to the glass surface. There is no clearly orientated stress field so that in this case, the inclusion’s properties solely decide on these parameters. In contrast, in Fig. 2c, d, the crack orientation parallel to the glass surface is forced by the stress field; consequently, microscopic stress measurement and crack observation are not the same if toughened or annealed glass is examined. The primary crack propagates perpendicularly to the glass surface under tensile stress (as is further discussed below), but parallel under compressive stress as shown above, including a transition zone around the neutral stress zone where the propagation direction is less defined.

The Newtonian rings in Fig. 2d allow to estimate the height of the crack close to the inclusion. Using the basic equation from white light interferometry, $\hbox {n}\,*\,\uplambda = 2\,*\,\hbox {d}$, and considering that three red rings $(\uplambda \approx 600\, \hbox {nm})$ are visible, the third among them in striking distance to the inclusion, the crack height at that place is estimated to be $1.8\, \upmu \hbox {m}$ or 0.5% of the inclusion’s diameter. Note that this is the value of the diameter difference calculated for a real nickel sulphide inclusion of composition NiS(1:1) at ambient temperature in Fig. 8.

Figure 3a shows an example of a small inclusion where a primary crack is not generated although weak stress around the inclusion is visible after thermal transformation. In contrast, Fig. 3b shows an example of an inclusion that is not much bigger than in Fig. 3a, but primary cracks are clearly visible after some holding time at elevated temperature. This point will be the subject of further discussion based on new findings to be published in Kasper et al. (forthcoming).

Another, and perhaps more critical point to consider is that under compressive stress initial crack formation can be suppressed. This is important also because some nickel sulphide inclusions contain a neutral matter $(\hbox {Ni}_{9}\hbox {S}_{8})$ that limits the maximum growth of the individual inclusion (on buildings only as will be shown below) to a value far below the crystallographic value for pure NiS (1:1), see Sect. 2.2.2.

Impact of the surface structure

In the case of nickel sulphide inclusions, the strength of its surrounding glass surface is affected by the notched nature of the surface of these inclusions. The physical reason thereof is the crystallization of NiS species at c. $1000\, ^{\circ }\hbox {C}$, when the glass is still smooth and perfectly molds the changing surface texture. Figure 1 shows a SEM micrograph and a light microscope photograph where the typical corrugation of such inclusions is visible. Although exact measurements are still missing,³ Fig. 1 allows an estimate of the depth of the notches to be in the range of [$1\, \upmu \hbox {m} \dots 10\, \upmu \hbox {m}$⁴]; the aspect visible in the micrographs is quite typical for nickel sulphide inclusions. The same notched structure is visible on every nickel sulphide inclusion’s surface, already under the light microscope, see Fig. 1b and findings in Kasper et al. (forthcoming), and this is a characterizing property for this kind of inclusion. Comparison of Fig. 1a, b shows that the surface structure is not exactly identical: surface structure is in detail individual for every single nickel sulphide inclusion.

These superficial wrinkles are not in-line with GRIFFITH’s assumptions on the weakening of the glass strength due to surface cracks. But, even if the “tip” of the “crack” is rounded, the stress concentration due to such a structure is not negligible. The following argument is based on Liu et al. (2015) and intents mainly to analyze the situation in the tensile zone of toughened glass.

Nomenclature:

$\hbox {K}_{\mathrm{t}}$::

stress concentration factor;

w::

finite plate dimension;

$\upsigma ^{\mathrm{max}}$::

maximum stress at tip;

$\upsigma _{\infty }$::

shear stress applied;

a::

crack length;

$\uprho$::

(tip or hole) radius

LIU mentions that around a circular hole in a glass plate of finite dimension (this can e.g. be the section of a glass plate) the stress concentration is calculated according to

$$\begin{aligned} K_{{ t}}=2\left( 1-\frac{2\rho }{w}\right) ^{-1}+\left( 1-\frac{2\rho }{w}\right) ^{2}. \end{aligned}$$

(2a)

Equation (2a) allows to estimate that, e.g., for a glass plate of 5 mm thickness and a small smooth bubble of $220\,\upmu \hbox {m}$ diameter (i.e. c. 4% of the glass thickness), $\hbox {K}_{\mathrm{t}}$ is 3.01, i.e. the impact of $[2\,*\,\uprho /\hbox {w}]$ is becoming negligible for smaller bubbles in the example. Even for a big bubble (in relation to nickel sulphide inclusions found in glass) of $500\, \upmu \hbox {m}$ diameter, for the same glass thickness, $\hbox {K}_{\mathrm{t}}$ is still 3.03. The global conclusion of this is that around a nickel sulphide inclusion, the basic stress concentration factor shows a value of three.

For the three-dimensional case of thermally toughened glass the conditions are more complicated. If there is no stress, then there is nothing to concentrate, and this is essentially the case perpendicular to the glass surface. The “toughening” stress vectors are orientated parallel to the surface; their absolute value (“length”) and sign depend on the position in the glass section, with their maximum in the middle. Regarding opening Mode I, the highest stress is induced in the points of the bubble situated closest to the glass surfaces (i.e. in both zeniths of the bubble); in the ideal case of a perfectly smooth bubble situated in the tensile zone of a perfectly toughened and homogeneous glass, an eventual spontaneous breakage would always start from the particular zenith situated closer to the glass midline because there the tensile stress is the higher. In any case, such a void is a weak point in the glass. Instead of 50 MPa, the tensile stress at the zenith of the smooth bubble increases to 150 MPa, but, in comparison with 800 MPa of basic glass strength estimated above, this is still not nearly high enough to initiate spontaneous breakage.

Based on Eq. (2a), LIU develops a model that allows calculation of the stress concentration at the tip of a notched V-crack. He shows by finite element modelling that, to a certain extent, this estimation does not depend on the opening angle of the V-crack, as long as it is not too flat. His formula, valid for a semi-infinite plate,

$$\begin{aligned} {\sigma }_{yy}^{\mathrm{max}}=3.36\sigma _{\infty }\cdot \frac{(a+\rho )}{\sqrt{\rho ^{2}+2a\rho }} \end{aligned}$$

(2b)

allows to estimate, as an example derived from the observations in Fig. 1, $\upsigma ^{\mathrm{max}}/\upsigma _{\infty } = \hbox {K}_{\mathrm{t}} = 4.8$ for a V-crack of total depth $(\hbox {a}+\uprho =) 7\, \upmu \hbox {m}$ including a calotte-form tip of $(2\,*\,\uprho =) 4\, \upmu \hbox {m}$ diameter.

This estimation should also be approximately valid if the V-crack is situated on the surface of a much bigger bubble of, e.g., $200\,\upmu \hbox {m}$ diameter. The consequence of this would be that the local stress increases even more than due to the presence of a smooth bubble alone. Again, due to the dissymmetry of the stress field in toughened glass, it does matter where the V-crack is situated. On the inclusion’s equator (where opening Mode I does not play a role and the stress concentration is minimum anyway) its impact is undoubtedly small because the V-crack is directed parallel to the stress field. In contrast, if it is situated in the zenith, perpendicular to the stress field, its impact is maximum. Continuing the example above, the maximum induced stress increases from 150 MPa to more than 700 MPa. The example illustrates how it is possible that, in contrast to a smooth bubble, an un-transformed nickel sulphide inclusion of sufficient size positioned in the middle of the glass can lead to glass failure if a comparatively small additional force interferes, such as by inhomogeneous heating, cases of which have been observed in practice.⁵

Hypothetically, if the V-crack migrates from the zenith towards the equator of the bubble, the local stress at its tip decreases due to (a) the decrease of $\hbox {K}_{\mathrm{t}}$ [ref. Eq. (2a); note that its value is not zero even at equator position] and (b) the decrease of the angle between the stress vector and the V-crack direction. Such a V-crack, therefore, would still have a significant weakening influence if it is situated near the zenith.

In the case of a nickel sulphide inclusion, the whole surface is notched. In any case, the starting point of the initial crack is defined by the weakest point on its surface. Regarding the stress concentration in toughened glass, this point must be situated near one of the zeniths of the inclusion, at a place where one groove causes the maximum impact.

Fig. 3

(No) crack formation around two nickel sulphide inclusions, observed in annealed glass by polarized light microscopy after heat treatment at constant temperature. Diameters: Sample a: $40\, \upmu \hbox {m}$; Sample b: $75\, \upmu \hbox {m}$. a1, b1 Initial state after annealing on float glass line. a2, b2 After heat treatment 24 h/$140\,^{\circ }\hbox {C}$. a3, b3 After heat treatment 44 h/$140\,^{\circ }\hbox {C}$. $40\, \upmu \hbox {m}$ inclusion causes only little stress (by color change), no cracks. $75\, \upmu \hbox {m}$ inclusion causes stress and several cracks up to c. $20\, \upmu \hbox {m}$. Photographs: SG (1968), also Ortmanns (1970)

The combination of its distance to the zenith and its effective depth also decides on the amount of additional stress needed to be induced by the transforming inclusion to initiate spontaneous failure.

2nd step: Crack propagation

After initiation at one (“the weakest”) point, the primary crack does not only propagate into the glass, but it also surrounds the inclusion and reunites on the opposite side. This is seldom symmetrical so that at the reunification line a wave or a dagger-form step is often observed (see Fig. 1).

Once a crack is initiated, it grows until at its tip, stress falls below critical stress defined by the glass’ material property $\hbox {K}_{\mathrm{Ic}}$. Because (in annealed glass) this phenomenon is subject to simple lever rule, the effect is directly related to the inclusion’s diameter. A small inclusion will generate a short crack, whereas (under, apart from diameter, identical conditions) a big inclusion will generate a proportionally longer crack. Observation in annealed glass shows that in the case of nickel sulphide inclusions, the crack length can nearly reach the diameter of the inclusion (see Fig. 2a–c).

Laboratory trials using annealed glass samples in the 1960 ’s demonstrated this relationship between the diameter of the inclusion and crack length (see Fig. 3), but also showed that around small inclusions no visible crack is initiated even after long-time heating and supposedly complete $\upalpha$ to $\upbeta$ transformation. There is some uncertainty around the second observation because the exact composition of the inclusion remained unknown, but nevertheless this is important because it shows that around small nickel sulphide inclusions (the limit seems to be about $50\, \upmu \hbox {m}$, in correlation with criticality calculations by finite element models and observations on HST breakages), cracks do not only stop, but they are not even visibly initiated.

The dependence of crack growth on the transformation degree of the inclusion is observable under laboratory conditions (heat treatment is then stopped after a certain time and continued after observation) as shown by the examples in Fig. 3.

Conversely, the conditions for crack initiation in thermally toughened glass are different from those in annealed glass because of the stress surrounding the nickel sulphide inclusions. Compression suppresses extension forces during crack initiation because on the surface of the inclusion the sum of the respective forces (environmental stress + stress induced by inclusion) determine if a crack is initiated or not. It can be observed that the direction of the primary circular crack surrounding the nickel sulphide inclusion depends on the surrounding stress field. Under compression, it is directed towards the glass surface, whereas under extension it is parallel to the glass surface.

Sub-critical crack growth also probably plays a certain role in crack initiation. Based on thermodynamics, the assumption that the NiS cavity would be dry like an artificial vacuum is likely wrong. During melting, flat glass equilibrates with the melting furnace’ atmosphere. Under gas-air flames with a moisture content of c. 20%, c. 350 ppm water are absorbed into the structure of soda-lime glass (Geotti-Bianchini et al. 1999). Because this is an equilibrium reaction, under dry conditions, water can be released by diffusion from the glass matrix. This diffusion process would proceed more rapidly at higher temperatures. At the limit (i.e. after sufficient time under given conditions) in the very small free volume surrounding a nickel sulphide inclusion, or in a primary crack caused by the same, the water vapor content can increase again. At ambient temperature this process is very slow and eventually not relevant. In contrast, even at $300\, ^{\circ }\hbox {C}$ a weak structure relaxation (“de-tempering”) is observed in toughened glass by Schneider et al. (2017). Although the effect is only in the low percent range at HST conditions, it seems to be significant. Conversely, a simple geometric calculation reveals that around a $250\, \upmu \hbox {m}$ nickel sulphide inclusion [simplifying with composition NiS(1:1)], a gap of c. $0.25\, \upmu \hbox {m}$ forms at HST temperature (at ambient temperature, it is c. $0.42\, \upmu \hbox {m}$). To fill this vacuum with e.g. 10% water vapor, a glass layer of 26 nm thickness must be completely depleted, i.e. c. only 100 atomic layers; it is even less than this for the very narrow primary cracks induced into the glass by $\upalpha$ to $\upbeta$ transformation of nickel sulphide inclusions. Unfortunately, for $\hbox {T} < \hbox {T}_{\mathrm{g,}}$ the diffusion coefficient of water in the glass matrix is unavailable and nearly impossible to estimate (Behrens 2006), so for the time being, precise calculation seems to be unfeasible. Nonetheless, the very low depletion depth, in combination with a seemingly proven structure relaxation, shows that this might be an important effect in the HST.

Another argument for this is the finding of Barry and Ford (2001). He detected a layer of NaOH on the surface of some freshly dissected nickel sulphide inclusions covering c. 50% of their surface. His interpretation is that (dry) $\hbox {Na}_{2}\hbox {O}$ would be present on the inclusions’ surface, and by quick reaction with water vapor from the atmosphere, NaOH would form; however, thermodynamic calculation reveals that in or on glass, isolated $\hbox {Na}_{2}\hbox {O}$ is extremely unstable. A much more probable thermodynamic interpretation of his finding is that both water vapor and sodium are mobile and diffuse from the glass matrix into the gap as described above. NaOH can dissolve significant amounts of water from further diffusion, and although the water is partly bounded, this “solution” causes a certain water vapor pressure that influences the crack growth.

According to Wiederhorn (1967) sub-critical crack growth depends exponentially on the water content of the surrounding atmosphere; therefore, water diffusion at HST temperature can have an impact on the time-to-breakage, not only caused by nickel sulphide inclusions, but by any inclusion causing cracks in the glass. The process of combined water diffusion and crack growth leads to delayed breakage of inclusions causing a primary crack, but not being immediately critical. More research is needed to clarify this process.

3rd Step: Sudden failure of the entire toughened glass pane

Sudden failure of entire toughened glass panes occurs due to the energy stored in the glass on toughening. This is the reason why nickel sulphide inclusions do not harm annealed glass panes: for self-destruction, enough energy is only stored in toughened, or possibly heat-strengthened glass panes.

Self-destruction (“spontaneous breakage”) takes place if the crack growth does not stop. This depends on the stress situation around the inclusion.

• In the case of high compressive stress, the glass is stronger so that eventually even no primary crack generates (see remarks above), at least if the inclusions are not too large. Even if a primary crack forms, crack growth can be stopped at a certain small distance. Additionally, under compressive stress the primary crack is always directed parallel to the glass surface (see Fig. 2b, c), so that it cannot initiate the failure of the whole pane.

  The result is, the situation stabilizes and the glass pane does not break.

Changing conditions such as wind loading or temperature changes can later make uncritical stress situations critical over time. This will be discussed later, after the general description here.

• In the case of high tensile stress, even a small primary crack extends “to infinite” so that the glass pane shatters.

  Under this condition the primary crack always points into the “right” direction, namely approximately perpendicular to the glass surface, due to the crack initiation mechanism discussed above.

These two extreme cases are obviously clear, but also this is not “black-and-white”. In between is a “gray zone” where “hazard” decides if the pane in question shatters or not, or maybe not immediately but with some delay.

Hazard, in this context, means primarily uncontrollable, but possibly statistically describable

• (a) circumstances the pane is subject to,

• (b) properties of the nickel sulphide inclusions, and

• (c) the exact direction of the primary crack, i.e. the position of the weakest point in its notched surface.

A probabilistic approach must be applied to macroscopically (statistically) describe the breakages, e.g. using probability curves. This will mainly be the theme of the continuation of the present paper in Kasper (forthcoming) and Kasper et al. (forthcoming).

2.1 Temperature influence

Under the circumstances of “Building” and “HST”, the temperature of the glass panes is quite different $(25\,^{\circ }\hbox {C}$ to $100\,^{\circ }\hbox {C}/250\,^{\circ }\hbox {C}$ to $300\,^{\circ }\hbox {C}$). This difference should have a remarkable influence on breakage occurrence. Three main reasons are responsible.

2.1.1 Nickel sulphide and glass have different coefficients of thermal expansion.

The expansivity of glass $(9\,*\,10^{-6}\, \hbox {K}^{-1})$ is significantly lower than that of pure NiS, whereas the coefficients of both the $\upalpha$ and $\upbeta$ phase of NiS only show a small difference $[16.5\,*\,10^{-6}\, \hbox {K}^{-1 }(\upalpha \hbox { phase}) / 14.5\,*\,10^{-6}\, \hbox {K}^{-1 }(\upbeta$ phase)] (Fleet 1988); see also Sect. 2.2.2.

The direct and intuitive consequence of these differences is that in the HST more glass panes break than ever would break in facades if the glass would be used un-soaked.

A hypothetical situation is presented next to better understand this.

A glass lot comprising a high number of panes (e.g. 10,000 tons), contaminated with a considerable number of nickel sulphide inclusions (referring to a HST breakage rate of one in six tons of glass or, in other words, a heat-soak loss of 1%; this would be the “normal” number), shall be toughened and installed in facades without making the HST. After perhaps 50 years, some number of panes will perhaps shatter spontaneously, caused by some nickel sulphide inclusions becoming critical at ambient temperature.⁶ Then, perhaps 20 years after the last spontaneous breakages have occurred, all remaining panes are subject to a HST.

Although the critical panes are already self-eliminated (or there has been no breakage at all), some additional breakages will be observed during the HST. In the HST, the difference in thermal expansivity (and other influencing factors, see Sect. 2.3) causes enough stress to make some become critical a posteriori, these break, and in sum, c. one breakage in six tons will be observed, just as a consequence of the actual glass quality. The relation between both breakage rates is, however, unknown at this point. Approaches to this open question are the main theme of the present small series of papers.

In a HST of the identical, but freshly toughened glass, both processes occur in parallel. Besides thermal expansion (and other HST effects), also the $\upalpha$ to $\upbeta$ transformation is forced in time-lapse, so that the result of this HST would be the same as the sum of breakages in time and in HST of the aged glass imagined above.

2.1.2 Inhomogeneous heating-up

The glass panes, standing in the HST oven on a stillage in a pile, are heated up and cooled down relatively fast (e.g. $2^{\circ }\, \hbox {K/min}$); cooling is normally slower to prevent thermal breakages. Note that the HST process uses hot or cool gas (mostly air), respectively, for temperature change.

Temperature change steps cannot be made in a totally homogeneous way. The glass rims orientated towards the air stream will lead the actual temperature change. The temperature change then propagates over the glass surface until it reaches the opposite rim. If the air flow is not symmetric or not the same at every place within the slots in the pile (e.g. because of the stillage bars, or just because it is not homogeneous), temperature differences within the surfaces (membrane stress) and between both surfaces of the same pane are induced. It has been observed (Grindatto 2017) that even glass of e.g. eight millimeters thickness can bow by several centimeters under this thermal load, thus forming a flat bowl. Bowing the glass means shifting the maximum of the stress parabola from its position on the glass midline towards one of the surfaces.

This additional mechanical load is a good explanation for the facts that: (a) annealed glass normally does not survive a HST; (b) not only glasses containing nickel sulphide inclusions break in HST, but also refractory or silicon inclusions cause failure (Jeschko 1999). In comparison with ambient conditions and in absolute contrast to nickel sulphide inclusions, in these cases stress from a phase transition can be excluded; only effects due to thermal dilatation can play a role. This topic is more extensively discussed in Sect. 2.3.

There is also another consequence of nickel sulphide inclusions. As already discussed, nickel sulphide inclusions are situated in a cavity that has a notched surface. This makes them already a weak point for glass stability, independent of their “growing potential” by $\upalpha$ to $\upbeta$ transformation. The larger the inclusion before the transformation, the worse (weaker) the glass stability at that inclusion. This is true

• (a) during the toughening process where such “over-critical” nickel sulphide inclusions practice-confirmed lead to glass breakage, and

• (b) in HST in the cases where the inclusion transforms slowly but due to said thermal load, it causes glass breakage before its transformation reaches criticality, and this is even the case if it would never reach criticality, e.g. due to its exotic composition (see examples below) or to its size.

• (c) Under normal application conditions on buildings, such a high mechanical load is difficult to imagine, or perhaps even impossible; therefore, it can be assumed that if an inclusion in un-soaked glass has not only survived the toughening process, but also the transport to the building site and the mounting into the façade, the most probable and observable cause for spontaneous breakage at ambient temperature will be $\upalpha$ to $\upbeta$ transformation of a nickel sulphide inclusion.

2.1.3 Sub-critical crack growth

Sub-critical crack growth is boosted by the presence of water vapor. As already discussed, it is possibly correlated with structure relaxation (even below $\hbox {T}_{\mathrm{g}})$, but certainly with water diffusion from the glass matrix into the vacuum around the inclusions and in the primary cracks. Because both diffusion and structural relaxation are strongly temperature-dependent, this effect is expected to be absent at ambient temperature; at HST temperature it cannot be excluded.

2.2 Influence of the composition of the Nickel sulphide inclusions

Long term study of nickel sulphide inclusions shows variability in their compositions. A number of analyses has been published [Kasper and Bordeaux 2000; Yousfi et al. 2010b, and others (review article by Karlsson 2017)], but to the author’s knowledge compositional differences of the inclusions have never really been correlated with glass breakages on buildings or in HST.

As a first step in a scientific approach, the mechanism for generation of nickel sulphide inclusions in the glass melt is summarized. This approach is the key for understanding the differences in compositions.

Fig. 4

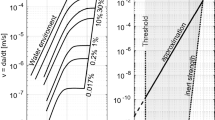
Vapor pressure of NiS$_x$ at $980\,^{\circ }\hbox {C}$. o : Sharma and Chang (1980). $\blacksquare$ : Author results from bubble sizes and x values identified in NiSx inclusions. A Linear interpolation (exponential curves). B Common best fit for both datasets, using non-exponential fit. C Transcription into linear scales. D Example calculated by $\hbox {HSC}^{\circledR }$ for $980\,^{\circ }\hbox {C}$, showing similar curve trend. a: x in $\hbox {NiS}_{\mathrm{x}} = 1.031; \hbox {P} = 5.7\, \hbox {bar}$. b: $\hbox {x} = 1.062; \hbox {P} = 7.5\, \hbox {bar}$ (LAFFITTE’s limit composition). c: $\hbox {x} = 1.12; \hbox {P} = 10.5\, \hbox {bar}$ (SHARMA’s limit composition)

Following Kasper and Stadelmann (2002), the predominating source for nickel sulphide inclusions in normal glass production is nickel-containing steel particles. Because nickel sulphide is more stable than iron sulphide, and iron oxide and sulphide are easily soluble in the glass melt,⁷ the formation of essentially iron-free nickel sulphide inclusions is generally observed, even if the steel particles only contain a low concentration of nickel. This means that a concentration of only 0.05% nickel in a sufficiently large steel particle can be enough to generate a dangerous nickel sulphide inclusion. No chemical equation is listed here because in the given context it could lead to misunderstanding rather than to clarification.

In the glass melting tank, the metal particle reacts slowly; therefore, the composition of its liquid phase develops gradually. Thermodynamic calculation and aspects of reaction kinetics reveal the composition of the liquid is $\hbox {NiS}_{\mathrm{x}}$, and “x” in this combination ranges from values of (approximately) $\approx 0.5$ (corresponding to the eutectic composition $\approx \hbox {Ni}_{2}\hbox {S}$ in equilibrium with solid nickel metal) to $\approx 1.06$ [where the sulfur vapor pressure of the liquid $\hbox {NiS}_{\mathrm{x}}$ reaches high values and the nickel sulphide inclusions are definitely no longer stable (Sharma and Chang 1980; Lin et al. 1978); Fig. 4, author calculations below]. This reaction scheme is proven by laboratory melting trials and phase identification in the inclusions generated in the respective glass melts (Kasper and Stadelmann 2002). Consequently, every nickel sulphide droplet has its individual $\hbox {x}_{\mathrm{liquid}}$ value, and the respective (statistical) distribution can be assumed to be uniform, except if the composition is in a high vapor pressure region.

2.2.1 Vapor pressure of NiSx

Sharma and Chang (1980) correlates the vapor pressure with the sulphur content in liquid $\hbox {NiS}_{\mathrm{x}}$. In his phase diagram, he draws the respective calculated isobars. Evaluating this leads to the conclusion that, at e.g. $980\,^{\circ }\hbox {C}$—this is a very low temperature for a glass melt—the vapor pressure’s logarithm depends nearly linearly on x in $\hbox {NiS}_{\mathrm{x}}$, see the red line Fig. 4A. For $\hbox {x} = 0.93$, it reaches 1 bar. For $\hbox {x} = 1$, it already reaches 10 bars, and (extrapolated) 72 bars for $\hbox {NiS}_{1.06}$. The qualitative conclusion of this is that the observed high over-pressure must lead to spontaneous thermal decomposition (“explosion”) of the liquid $\hbox {NiS}_{\mathrm{x}}$ droplet. If this threshold is stepped over, it is irreversible and the inclusion destroys itself; however, this is not a clearly fixed pressure but a range including a probabilistic fade-out of x.

According to thermodynamic calculation, the decomposition products are sulfur vapor $(\hbox {S}_{2}$ and $\hbox {S}_{3}$, see Fig. 4D) and a more stable decomposition product, e.g. fine-grained $\hbox {Ni}_{3}\hbox {S}_{2}$ powder. The latter has often been observed on the walls of the “bubbles” at respective (otherwise inconclusive) laboratory trials. The decomposition products quickly dissolve in the glass melt.

The pressure values extrapolated from SHARMA’s data are very high and would lead to the assumption that even NiS(1:1) would not be stable as an inclusion; however, these inclusions are certainly observed in the glass. Bubble nucleation, in absence of any heterogeneous nucleating matter and a perfectly smooth surface of the molten NiSx, certainly requires some bars of over-pressure, but the not as high as the extrapolated ones. This casts doubt on the validity of the simple approach of an exponential extrapolation of SHARMA’s values.

The nickel sulphide inclusions themselves present additional information. Long observed but never commented on is the fact that almost all nickel sulphide inclusions contain voids and bubbles.

Bubble and pore formation in nickel sulphide inclusions

Generally, bubbles can only generate in a liquid, and due to their surface tension, they normally show spherical shape. But in the nickel sulphide inclusions, only bubbles in strongly over-stoichiometric inclusions are approximately spherical (see examples in Figs. 13 and 14). Closer examination reveals that nearly all voids are irregularly shaped; therefore, the only reasonable explanation seems to be that they generate during crystallization. Beginning crystallization also provides nuclei for bubbles, i.e. the system crosses over from a state of latent over-pressure to a state of heterogeneous nucleation and pressure equilibration, whereas (at c. $1000\,^{\circ }\hbox {C}$) the total pressure of the inclusion is mostly kept in its original state by the surrounding viscous glass.

Consequently, as crystallization is occurring, “sweating out” of $\hbox {S}_{2}$ gas takes place (this fact follows from said thermodynamic approaches) until the diameter of the bubbles equalizes the NiSx vapor pressure. At that moment, the freezing-in temperature must be just below the melting temperature of NiS (assumed $980\,^{\circ }\hbox {C}$). With continuing crystallization, the (originally spherical) bubbles are then deformed by the growing crystals. FIB⁸ preparation of some inclusions reveals that the holes are really empty. In comparison with the heterogeneous (bi-phasic) inclusions, pores appear much more frequently in the near- and over-stoichiometric inclusions.

Sulfur vapor generation changes the stoichiometry of the inclusions. The impact of this effect is estimated by taking the maximum pore volume fraction observed in a near-stoichiometric inclusion, about 12%, and considering the over-pressure at crystallization temperature. Even for this maximum case, the bulk change of NiSx calculates to be $\Delta \hbox {x}=-0.008$. Obviously, this is almost negligible.

For the estimation of the over-pressure at the crystallization point, all examples of the present paper are used where bubbles in the nickel sulphide inclusions are observable. This is the case in Figs. 6, 9, 10, 13 and 14. All the bubble diameters are found to be between c.$2\, \upmu \hbox {m}$ and $10\, \upmu \hbox {m}$. The basic physical formula Eq. (3) allows estimates of the respective pressures.

$$\begin{aligned} \hbox {P}_{\mathrm{int}} = 2 \,*\, \upgamma /\hbox {r} + \hbox {P}_{\mathrm{envi}} \end{aligned}$$

(3)

with $\hbox {P}_{\mathrm{int}}$ Internal pressure of a bubble; $\upgamma$ Surface tension of surrounding liquid, c. 0.5 N/m for NiS; r Radius of bubble from picture; $\hbox {P}_{\mathrm{envi}}$ Environmental pressure (atmospheric + hydrostatic), 1.04 bar.

By lack of literature data, the surface tension of NiS had to be estimated (c. 0.5 N/m). This assumed value is like that of a metal (e.g.: Sn 0.56 N/m; Hg 0.48 N/m); it is chosen because the glass melt ($\upgamma = 0.35\, \hbox {N/m}$) is not wetted by NiS as well as by the metals, whereas laboratory trials (Kasper and Stadelmann 2002) revealed very clearly that the metal surface is wetted by the sulphide melt. The environmental pressure is composed of normal air pressure (1013 hPa) and the (nearly negligible) hydrostatic pressure in the glass melt in the channel of the glass melting furnace in a depth of 10 cm ($\rightarrow 25\, \hbox {hPa}$).

With these data, the internal pressure of the inclusions at their crystallization point is estimated. The pressures obtained are added into Fig. 4 (black squares). In Fig. 4A it seems as if the data would be significantly different from SHARMA’s, but trying a common fit (Fig. 4B) reveals that they can all be assembled on a common curve. The thermodynamic cause for this is the fact that NiSx is not one simple stoichiometric combination, and its vapor pressure does not come from evaporation but from its decomposition into another species and sulfur vapor. With increasing x, different nickel-sulfur species ($\hbox {Ni}_{9}\hbox {S}_{8}$, NiS, $\hbox {Ni}_{3}\hbox {S}_{4,}$ etc.) would crystallize from the melt so that the latter’s decomposition pressure does not increase exponentially like a common vapor pressure. Comparison with respective calculation by $\hbox {HSC}^{{\circledR }}$ (Fig. 4D) reveals that the curves are very similar even in linear scales where every potential deviation would be much more obvious than in the logarithmic diagrams. Consequently, both results from SHARMAS’s diagram and from the measurements on nickel sulphide inclusions closely match, the combined measurements lead to more reasonable results than simple extrapolation, and the common fit is also reasonable.

The inclusion in Fig. 13 contains parasitic elements (Se, Fe), making the calculation maybe doubtable. Nevertheless, the pressure calculated using the common fit (7.6 bar) fits very well with the measured stoichiometric composition (x $=$ 1.07), the highest x the author and his colleagues ever observed up to date in their working group. All other inclusions in question are practically pure NiSx so that the data obtained are thus valid for the diagram.

This means that the maximum possible pressure must be somewhere around 7 bars, referring to $\hbox {NiS}_{1.062}\, (\hbox {x}=1.062)$; this would then be the “stochastic” limit for the composition of nickel sulphide inclusions in glass subjected to over-pressure. Note that both over-stoichiometric inclusions shown in the present paper are untransformed, i.e. $\upalpha$ phase, because the $\upbeta$ phase does not tolerate over-stoichiometry; however, as already mentioned, Laffitte (1956) and Laffitte and Crousier (1956) fixes a maximum of $\hbox {x}= 1.060$ from X-ray micro-diffraction. Yousfi et al. (2010b) (Fig. 12) fixes a limit composition of $\hbox {x}=1.047$ for possible transformation in HST. The exact value⁹ for inclusions in glass is not known, but it seems that it does not play a significant role in view of YOUSFI’s limit. A current SG research project goal is to learn more about this.

2.2.2 Crystallization

Because their melting point is below $1000\,^{\circ }\hbox {C}$, nickel sulphide inclusions do not crystallize before they enter the float bath; glass forming therein (stretching) is the reason why they sometimes look elliptical instead of spherical. This effect is more pronounced in thin glass than in thick glass since thin glass is stretched more.

Fig. 5

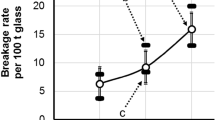
Composition range of nickel sulphide inclusions eventually leading to glass breakage. Dotted (–o–o–) curve: estimated probability of occurrence, based on LAFFITTE’s papers (limit value 1.06 for occurrence in glass), YOUSFI’s papers (limit value 1.047 for breakages), own bubble pressure calculations and x values observed in breakages

In the crystallizing inclusion, starting from given $\hbox {x}_{\mathrm{liquid}}$, crystals form according to the Ni-S phase diagram. Simplifying (because foreign elements like iron can also have a limited influence) one can distinguish two main situations, discussed below.

Wagner (1977) found, among the others, inclusions composed of $\hbox {Ni}_{3}\hbox {S}_{2}$ or $(\hbox {Ni}_{3}\hbox {S}_{2} + \hbox {Ni})$; these do not cause spontaneous fracture, in contrast to those in the composition range from “$\hbox {Ni}_{7}\hbox {S}_{6}$” (now known to be $\hbox {Ni}_{9}\hbox {S}_{8})$ to NiS. Since only nickel sulphide inclusions containing (at least partly) the 1:1-composition are of interest because this chemical compound is the only one to be subject to slow $\upalpha$ to $\upbeta$ phase transformation at ambient temperature, thereby causing spontaneous breakages. According to the Ni-S phase diagram (including the vapor pressure issue and LAFFITTE’s papers discussed above), this composition can only form if $\hbox {x}_{\mathrm{liquid}}$ is in the range $0.89< \hbox {x}_{\mathrm{liquid}} < 1.06$. Then, the solely interesting (and solely observed) phases in the crystalline high-temperature nickel sulphide inclusions are $\hbox {Ni}_{9}\hbox {S}_{8}$ (where theoretically, $\hbox {x}_{\mathrm{solid}}$ is exactly 0.888...¹⁰) and $\hbox {NiS}_{\mathrm{x}}$ where $\hbox {x}_{\mathrm{solid}}$ is in the range $1 \le \hbox {x}_{\mathrm{solid}} < 1.06$. In the transformed $\upbeta$ phase nickel sulphide inclusions, the composition $\hbox {Ni}_{3}\hbox {S}_{4}$ is occasionally observed as a subsequent product of slow diffusional transformation.

The occurrence curve (–o–o– in Fig. 5) reveals that a majority (maybe 75%) of the inclusions should be heterogeneous. This is in contradiction with some observations previously published, e.g. in Kasper et al. (2003), where only 5 out of 14 (from HST) and 2 out of 7 (from buildings) are heterogeneous, i.e. $\approx {\frac{1}{3}}$ only in every case. In Kasper et al. (2003) the data is also different in that the proportion of $\hbox {Ni}_{9}\hbox {S}_{8}$/NiS is very low in both building cases (estimated $< 10\%$) whereas in those from HST it is up to c. 50% as in Fig. 10. A reason for this could be that with increasing heterogeneity, the inclusions become more brittle and fragile. With increased brittleness of the inclusions, the mechanical polishing for sample preparation could have a significant selecting effect. The total yield of polishing is only c. 50%, meaning every second inclusion is lost during preparation. This thinking is clearly supported by Barry and Ford (2001)’s findings. Among the seven inclusions he reports this for, five (71%) are bi-phasic, and he reports $\hbox {Ni}_{9}\hbox {S}_{8}$ contents between 6% and 57%, referring to x in NiSx from 0.94 to 0.99. BARRY’s inclusions originate from spontaneous breakages and non-broken glasses on a building where the University of Queensland (Australia) had carried out successful trials to detect inclusions before breakage, so this finding supports the plot in Fig. 8.

If by chance the $\hbox {NiS}_{\mathrm{x}}$ droplet’s $\hbox {x}_{\mathrm{liquid}}$ value in glass is exactly 1, a nickel sulphide inclusion with exactly stoichiometric composition (“NiS”) will be generated. But, after the statements above, it is clear that normally this does not occur. The composition of a large majority of nickel sulphide inclusions should deviate from the 1:1 composition. Still, (approximately) this case is often found in breakages. Figure 6 shows an example identified in a glass pane after breakage.

Fig. 6

Nickel sulphide inclusion found in a toughened glass pane not broken in HST. Situated close to neutral stress zone of the glass, distance from glass midline: 28% of glass thickness (compression ends at 29%). Size $110\, \upmu \hbox {m}$; analyzed composition $\hbox {x}_{\mathrm{solid}} = 1.01 \pm 0.01$. Porosity in visible surface 11%, pore diameter $9\, \upmu \hbox {m} \rightarrow$ pressure 3.3 bar. a SEM micrograph of polished inclusion, +: 12 points analyzed by EDX for quantification. b By light microscope, before preparation for SEM. c SEM/EDX spectrum: pure $\hbox {NiS}_{\mathrm{x}}$ with Fe $< 0.2\%$. Photographs: SG (2015)

(a) $\mathbf{x}_{\mathbf{liquid}}<$ 1: Under-stoichiometric inclusions

This composition is called “under-stoichiometric” with reference to its sulphur content, in comparison with NiS(1:1). In this composition range, the crystallized nickel sulphide inclusion contains two separate phases, namely NiS and $\hbox {Ni}_{9}\hbox {S}_{8}$. Their volume proportion depends on the exact value of $\hbox {x}_{\mathrm{liquid}}$. Below $400\,^{\circ }\hbox {C}, \hbox {Ni}_{9}\hbox {S}_{8}$ is not subject to a phase transformation relevant for glass breakage;¹¹ therefore, in such a case, the volume fraction of NiS determines whether the inclusion is critical or not. If there’s not enough NiS (see Fig. 8), the $\upalpha$ to $\upbeta$ phase transformation does not make the volume of the entire inclusion grow enough to cause glass breakage at ambient temperature. In contrast to this, in HST these inclusions are all critical.

In HST, the $\upalpha$ to $\upbeta$ transformation speed of pure NiS (even up to $\hbox {x}_{\mathrm{solid}} = 1.012$) is fast (Liu et al. 2015; Yousfi et al. 2010b). It is a kind of “knock-on” transformation (resembling the martensitic transformation in steel); these inclusions must be among the very first, already causing breakages when the temperature during the heating-up phase in HST, reaches c. $150\,^{\circ }\hbox {C}$. In contrast to the over-stoichiometric inclusions (see below), this transformation is not subject to diffusion and therefore much faster.

Consequently (see also Fig. 7b):

• (a) The maximum expansion due to $\upalpha$ to $\upbeta$ transformation of a given nickel sulphide inclusion depends on its content of NiS(1:1). Maximum expansion (according to literature data measurements, c. 3.8%¹² is observed if the inclusion does not contain any $\hbox {Ni}_{9}\hbox {S}_{8}$. With decreasing $\hbox {x}_{\mathrm{liquid}}$, the proportion of $\hbox {Ni}_{9}\hbox {S}_{8}$ in the solid inclusion increases, and therefore the maximum expansion at ambient temperature decreases.

Fig. 7

Under-stoichiometric inclusions, x$_{\mathrm{liquid}}<{1}$

An additional effect is due to the very high thermal expansivity of $\hbox {Ni}_{9}\hbox {S}_{8}$; with $\Delta \hbox {V/V} = 120\,*\,10^{-6}\, \hbox {K}^{-1}$ (Stoelen et al. 1994) it is c. three times that of NiS. This causes strong relative shrinking of the $\hbox {Ni}_{9}\hbox {S}_{8}$ part on cooling, making the inclusion at ambient temperature significantly smaller than it would be if it would only be NiS. A secondary effect (and at the same time the proof for higher shrinking) is that the $\hbox {Ni}_{9}\hbox {S}_{8}$ part of such inclusions looks fissured, in contrast to the NiS part. The latter is clearly visible in Figs. 9 and 10.

• (b) The $\hbox {Ni}_{9}\hbox {S}_{8}$ content of a given inclusion is the determining factor for the crack length that can be induced into the surrounding glass. This means the $\hbox {Ni}_{9}\hbox {S}_{8}$ content also determines if the inclusion is critical or not.

• (c) Conversely, if the crystalline NiS(1:1) content of a given inclusion is above a certain limit (the limit also depends on inclusion stress environment and inclusion size), the inclusion is critical under building conditions. The respective glass pane will break after some time.

  {Example Fig. 10}

• (d) If the NiS(1:1) content is below this limit (under hypothetically identical circumstances), the inclusion is uncritical.

  {Example Fig. 9}

• (e) Subject to HST, i.e. to significant temperature increase, the inclusion can become critical, due to the high expansivity of both NiS and $\hbox {Ni}_{9}\hbox {S}_{8}$. Comprehensively, the “limit of criticality” therewith shifts to a lower NiS (1:1) content. Below, this extent will be calculated, demonstrating that every under-stoichiometric inclusion is potentially critical in the HST, but not at ambient temperature.

• (f) Transformation speed and criticality after cooling back to ambient temperature:

  Every inclusion discussed here contains the stoichiometric form of NiS(1:1) as the transformable part. It is very quickly and completely transformed in the HST; therefore, a later additional growth by $\upalpha$ to $\upbeta$ transformation (after cooling back to ambient temperature) is excluded.

  Additionally, the $\hbox {Ni}_{9}\hbox {S}_{8}$ contained in most of these inclusions helps to stabilize the inclusion after cooling to ambient temperature; due to its even higher expansion coefficient, these inclusions can never become critical ex post because the inclusion is always smaller than the surrounding bubble.

Fig. 8

Breakage triggering by different nickel sulphide inclusion species depending on x in $\hbox {NiS}_{\mathrm{x}}$. $\hbox {NiS}_{\mathrm{x}}$ can only cause a breakage if it puts pressure onto the surrounding glass, i.e. if – before or after $\upalpha$ to $\upbeta$ transformation – its diameter is bigger than that of the surrounding “bubble”. Ordinate values: $\hbox {y} = 1 - \hbox {d}_{\mathrm{Inclusion}}/\hbox {d}_{\mathrm{Bubble}}$ (d: diameters), i.e. for $\hbox {y} = 1$ the size of “bubble” and inclusion are the same. LHS/RHS [left/right hand side]

The conclusion follows that under-stoichiometric nickel sulphide inclusions cannot cause delayed breakage after HST. They have a high safety margin due to thermal re-contraction.

Quantification using literature values¹³ yields the diagram shown in Fig. 8A LHS ([Left Hand Side, i.e. only the part at left of the (1:1) vertical; RHS [Right Hand Side] will be discussed later). It includes the $\hbox {Ni}_{7}\hbox {S}_{6}$ into $\hbox {Ni}_{9}\hbox {S}_{8}$ transformation at $400\,^{\circ }\hbox {C}$, the related volume increase, and the thermal contraction of both phases. The calculation confirms the qualitative statements above. Based on the lever rule for crack length, the breakage probability increases linearly with the diameter difference if it is above a certain threshold. Applying the uniform distribution from Fig. 5 (for $\hbox {x} < 1.00$) allows the following estimation of breakage probability relation between HST and ambient temperature.

Fig. 9

Nickel sulphide inclusion (HGI930) found in a glass pane, not broken in HST: Situated in tensile stress zone of the glass, distance from glass midline: 11% of glass thickness. Size $(140 \times 190)\, \upmu \hbox {m}$. a SEM micrograph of polished inclusion, 1: NiS (1:1) (darker areas), c. 10% of area only. Rest: $\hbox {Ni}_{9}\hbox {S}_{8}$ (brighter area; more fissured). Porosity in visible surface 1%, pore diameter $8\, \upmu \hbox {m}, \rightarrow$ calculated $\hbox {S}_{2}$ pressure 3.5 bar. b By light microscope, before preparation for SEM. c SEM/EDAX spectrum: pure $\hbox {NiS}_{\mathrm{x}}$. Photographs: SG (2015)

Fig. 10

Nickel sulphide inclusion found in a glass pane (Sample A), broken on building. Size $(160 \times 180)\,\upmu \hbox {m}$, location in glass cross section not reported. SEM micrograph of polished inclusion at different magnification. 1: NiS (1:1), $\hbox {Fe} < 0.2\%$; (darker areas), c. 40% ... 50% of area. Rest: $\hbox {Ni}_{9}\hbox {S}_{8}\, \hbox {Fe} < 0.2\%$; (brighter area; more fissured). Porosity in visible surface 2.4%, pore diameter $8\, \upmu \hbox {m}, \rightarrow$ calculated $\hbox {S}_{2}$ pressure 3.5 bar. Photographs: SG (2015)

Fig. 11

Over-stoichiometric inclusions, $\mathrm{x}_{\mathrm{liquid}}>{1}$. Stability limit localized between $\hbox {x} = 1.03$ and $\hbox {x} = 1.06$. Vapor pressures calculated for $980\,^{\circ }\hbox {C}$ according to Sharma and Chang (1980) and own calculation

• At ambient temperature, without $\upalpha$ to $\upbeta$ transformation, no breakage is initiated.

  For every composition the inclusions are significantly smaller than the surrounding “bubble”, see curve (a), calculated with ambient temperature $50\,^{\circ }\hbox {C}$ continuously. Even if this temperature is unrealistically supposed to be $120\,^{\circ }\hbox {C}$, no breakages can occur.

• Heating up to HST temperature, but before $\upalpha$ to $\upbeta$ transformation, already makes inclusions within $\hbox {x} \in \{0.89,~0.96\}$ become critical [curve (b), left of big red dot in Fig. 8A LHS], due to the very high thermal expansivity of $\hbox {Ni}_{9}\hbox {S}_{8}$ (see footnote 11). At ambient temperature, $\hbox {Ni}_{9}\hbox {S}_{8}$ makes the inclusion small ($\rightarrow$ safety margin), whereas under HST conditions it helps to force breakage due to its high thermal expansion.

• After $\upalpha$ to $\upbeta$ transformation, at ambient temperature, x in $\hbox {NiS}_{\mathrm{x}}$ must be within $\hbox {x} \in \{0.93,~1\}$ for breakage [curve (c); above big blue dot in Fig. 8A LHS]. This result is supported by Barry and Ford (2001)’s findings, as discussed at the beginning of the present section.

• In contrast to this, under HST conditions, every inclusion in the LHS range can become critical [curve (d)] independently of its $\hbox {Ni}_{9}\hbox {S}_{8}$ content. This is due to the combination of the very high expansivity of $\hbox {Ni}_{9}\hbox {S}_{8}$ and the $\upalpha$ to $\upbeta$ transformation of the increasing fraction of NiS.

• Consequently, in the LHS part of the diagram, within $\hbox {x} \in \{0.89,~0.93\}, (0.04/0.11 =) 36\%$ of the total number of breakages occurring at HST temperature (within $\hbox {x} \in \{0.89,~1\}$) would never occur at ambient temperature due to lack of NiS(1:1).

• Additionally, in the range where breakages would also occur at ambient temperature due to $\upalpha$ to $\upbeta$ transformation of NiS (curve c in Fig. 8A LHS, $x\in \{0.93, 1\}$ under otherwise identical conditions (size, position, environmental stress etc.), the criticality of the inclusions at ambient temperature increases with x in $\hbox {NiS}_{\mathrm{x}}$. In the HST [curve (d)], the criticality is nearly constant and much higher. In the range $\hbox {x} \in \{0.93, 1.00\}$, only 40% of the breakages in HST are relevant for buildings.

Figuratively, this calculation estimates the relative breakage probability (see Fig. 8B) from the surfaces below curves (c) and (d) above the criticality threshold T in Fig. 8A LHS. As long as curve (c) is above T, the relative breakage probability is $< 1$. If curve (c) is below T, the breakage probability is estimated to be zero.

Additionally, the respective number from Fig. 8 RHS (below) must be considered. The estimates described here are summarized in Table 1.

Examples for under-stoichiometric inclusions

Many of the nickel sulphide inclusions are heterogeneous and show this structure. Here two examples are shown. Figure 9 represents a case where the glass pane did not break even in HST; the inclusion only contains c. 10% NiS(1:1). Remember that not only the composition of an inclusion decides on breakage triggering, but also position, size and corrugation need to have critical values. In the example of Fig. 10, the pane broke on a building; the percentage of NiS (1:1) is c. 40%,¹⁴ i.e. $\hbox {x}_{\mathrm{liquid}} \approx 0.94$.

(b)$\mathbf{x}_{\mathbf{liquid}} > \mathbf{1}$: Over-stoichiometric inclusions

In the over-stoichiometric case, the (quenched) crystallized high-temperature nickel sulphide inclusion only contains one phase, $\upalpha \hbox {-NiS}_{\mathrm{x}}$. According to the Ni-S phase diagram, $\hbox {x}_{\mathrm{solid}}$ in this combination (but only in the $\upalpha$ phase) can principally vary from 1.00 to c. 1.12 (Sharma and Chang 1980), but as pointed out above, a limit value of 1.04 to 1.06 is more realistic in the case of nickel sulphide inclusions in glass. Yousfi et al. (2011) has calculated a limit of $\hbox {x} < 1.047$ for transformation under HST conditions; therefore, x values above this value should anyway be irrelevant (Fig. 11).

The possibility for over-stoichiometry is due to the property of $\upalpha$-NiS to allow “nickel voids” within the crystal structure (but strictly no sulphur voids).¹⁵ Laffitte and Crousier (1956) and Laffitte (1956) found in his seminal work on the Ni-S phase diagram in the late 1950 ’s that the global crystal structure does not change, but the lattice is subject to systematic (anisotropic) expansion depending on stoichiometry. The exact value of $\hbox {x}_{\mathrm{solid}}$ can be measured precisely by X-ray diffraction, but the nickel sulphide inclusions in glass are generally too small for this determination method. In the inclusions, $\hbox {x}_{\mathrm{solid}}$ is only measurable using EDX, with much lower precision.

Conversely, Laffitte (1956) and Laffitte and Crousier (1956) revealed that the maximum of x is 1.060 in this over-stoichiometric compositional range, and that the $\hbox {NiS}_{\mathrm{x}}$ density in the homogeneity interval $\hbox {x} \in \{1.000 {\ldots } 1.060\}$ decreases linearly from $5.50\, \hbox {g/cm}^{3}$ to $5.36\, \hbox {g/cm}^{3}$. Simple calculation reveals that this expansion refers to an average one-dimensional elongation of $\Delta \hbox {L/L}= 0.85\%$ between the extremes of the interval. This fact is the cause for the inclination of curve (a) in Fig. 8 RHS.

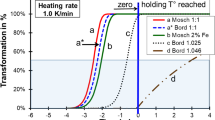
In contrast to $\upalpha \hbox {-NiS}, \upbeta \hbox {-NiS}$, the low-temperature phase, does not show this tolerance to voids. This is the reason why with increasing value of $\hbox {x}_{\mathrm{solid}}$, transformation needs more and more time because it needs more and more “diffusional purge”. As already mentioned above, phase separation into $\upbeta \hbox {-NiS}$ and $\hbox {Ni}_{3}\hbox {S}_{4}$ is necessary (at $\hbox {T} < 356\,^{\circ }\hbox {C}$), slowing down the transformation and giving it a significantly different mechanism with distinct, observable nucleation and growth (Yousfi et al. 2011; cited in Fig. 12). This kind of diffusional transformation is reversible, but as already observed by Biltz et al. (1936), the $\upbeta$ to $\upalpha$ back-transformation is relatively slow. Even at e.g. $400\,^{\circ }\hbox {C}$ it sometimes occurs over weeks. The $\upalpha$ to $\upbeta$ transformation (relevant for the success of the HST) is faster than the $\upbeta$ to $\upalpha$ back-transformation, sufficiently faster to enable phase transformation to complete in the required HST time. YOUSFI identified the following limits:

$1.000< \hbox {x} < 1.012$::

Fast $\upalpha$ to $\upbeta$ transformation without remarkable diffusion impact (martensitic-like), only slightly slower than pure NiS.

$1.012< \hbox {x} < 1.047$::

Diffusional mechanism of $\upalpha$ to $\upbeta$ transformation; range of potentially dangerous composition

$1.047 < \hbox {x}$:

Transformation speed too slow to be dangerous, no transformation in HST

YOUSFI’s most important contribution to the HST problem is the finding that at temperatures above $280\,^{\circ }\hbox {C}$, the $\upalpha$ to $\upbeta$ transformation of these slowly transforming species is principally incomplete and could cause breakages after HST due to post-transformation. For more information, please refer to his publications (Yousfi et al. 2010b, a, 2011). This finding by YOUSFI resulted in the decrease of the holding temperature range of the HST in EN 14179-1 from ($290 \pm 10)\,^{\circ }\hbox {C}$ (2002/2005) to $(260 \pm 10)\,^{\circ }\hbox {C}$ (at revision 2016) and in ISO 20675.

Fig. 12

Transformation kinetics of different nickel sulphide inclusion species. Time–Temperature-Transformation diagram cited from Yousfi et al. (2010b). Fv: transformation degree for curve calculation. Horizontal bars: New temperature limits in HST EN 14179-1:2016

The consequence of this change is that under the new conditions transformation of the slowly-transforming, over-stoichiometric inclusions can (in contrast to the HST before 2016) be completed during holding time. The “Thermally Toughened Heat Soak Tested Safety Glass” will be safer after the condition’s modification.

The facts mentioned here are quantified by detailed calculation; all known relevant facts (expansion coefficients, volume changes at phase transition, etc.) are considered therein. The result is shown in Fig. 8 RHS (“Right Hand Side”). From this, the following conclusions are drawn.

• $\upalpha$-phase [curves (a) and (b) in Fig. 8 RHS]

The density of $\upalpha \hbox {-NiS}_{\mathrm{x}}$ decreases with increasing x; according to general understanding, this means that the average bond strength decreases. The latter is (within a given system) equivalent to an increase of the thermal expansivity. By lack of measured expansivity values, these had to be estimated based on reasonable assumptions. If they were constant, curve (d) would be horizontal on RHS. According to the conclusion above, the curve must show a negative slope.

• Any over-stoichiometric $\upalpha \hbox {-NiSx}$ cooled down to ambient temperature [curve (a)] does not cause breakage.

• Due to the vapor pressure concern pointed out above, highly over-stoichiometric inclusions are rarely observed.

• If $\hbox {x} < 1.047$, the transformation speed (Yousfi et al. 2010b) is sufficient to transform the respective inclusions entirely in the revised HST (2016). This is what is assumed for the diagram: All possible compositions of $\upalpha \hbox {-NiS}_{\mathrm{x}}$ are entirely transformed.

• Simple heating-up (without $\upalpha$ to $\upbeta$ transformation) to HST temperature [curve (b)] is insufficient to cause breakage by any over-stoichiometric inclusion.

• $\upbeta$-phase [curves (c) and (d) in Fig. 8 RHS]

At both ambient and HST temperature, $\upbeta$-NiS does not allow a deviation from exact stoichiometry. This means that the sulfur excess present in the inclusions of Fig. 8 RHS leads to “sweating out” of a different phase, namely polydymite, $\hbox {Ni}_{3}\hbox {S}_{4}$, at both ambient temperature and HST temperature. Vaesite, $\hbox {NiS}_{2}$, only can play a role at temperatures above $536\,^{\circ }\hbox {C}$; i.e. it cannot be found in the inclusions even at HST temperature.

$\hbox {Ni}_{3}\hbox {S}_{4}$ has a much lower density $(4.83\, \hbox {g/cm}^{3} = -11\%)$ than $\upbeta \hbox {-NiS}\, (5.38 \hbox {g/cm}^{3})$. Consequently, similarly to the un-transformed inclusion where the density decreases as pointed out above, the density of the $\upbeta \hbox {-NiS}$ –$\hbox {Ni}_{3}\hbox {S}_{4}$ mixture decreases significantly with x due to increasing polydymite content at both ambient and HST temperature. Curves (c) and (d) in Fig. 8 RHS reveal this increase by the positive slope that is even steeper than on the LHS.¹⁶

Fig. 13

Nickel sulphide inclusion (HGI003) found in a glass pane, not broken in HST: Situated in tensile stress zone of the glass, distance from glass midline: 13% of glass thickness. Size $(95/125)\,\upmu \hbox {m}$. a SEM micrograph of polished inclusion, homogeneous, with foam-like structure. Analysis (EDX) $\hbox {NiS}_{\mathrm{x}}$ with $\hbox {x}_{\mathrm{solid}} = 1.07$. Porosity in visible surface 8%, pore size $3\, \upmu \mathrm{m} \rightarrow$ calculated $\hbox {S}_{2}$ pressure 7.4 bar. b By light microscope, before preparation for SEM; $\hbox {scale bar} = 50\, \upmu \hbox {m}$. c SEM/EDAX spectrum: $\hbox {NiS}_{\mathrm{x}}$ contaminated with Fe (0.3 at.%)/Se (1.7 at.%). Photographs: SG (2015)

• Consequently, in $\hbox {x} \in \{1.00, 1.06\}$, under otherwise identical conditions (size, position, environmental stress etc.), the criticality of the inclusions increases with x in $\hbox {NiS}_{\mathrm{x}}$, and it is by c. 23% higher in the HST in comparison with ambient temperature. Estimation is made by comparing the surfaces below curves (c) and (d) in Fig. 8, in analogy to the estimation on the under-stoichiometric (LHS) side.

• This signifies that in $\hbox {x} \in \{1.00, 1.06\}$, estimated 23% more inclusions (i.e. smaller ones etc.) become critical.

• Regarding the total range ($\hbox {x} \in \{0.89, 1.06\}$, i.e. LHS + RHS), and considering the occurrence estimation sketched in Fig. 5, this refers to 8% more critical inclusions in HST than on buildings.

This number must be added to the respective one estimated for Fig. 8 LHS (“Left Hand Side”) (above, 70%), so that the total estimation for “irrelevant breakages in HST” (with respect to the chemical composition only) is 78%, i.e. more than three quarters of the inclusions causing breakage in HST would be uncritical at ambient temperature.

Fig. 14

Nickel sulphide inclusion (412) found in a breakage center: Situated in the tensile stress zone of the glass, size $(110/120)\, \upmu \hbox {m}$; Position in glass not reported. SEM micrograph of mechanically polished inclusion, homogeneous, with foam-like structure. Multipoint analysis (EDX): $\hbox {NiS}_{\mathrm{x}}$ with $\hbox {x}_{\mathrm{solid}} = 1.035 \rightarrow$ not transformed ($\upbeta$ NiS always 1:1). Porosity in visible surface 6%, pore diameter $4\, \upmu \hbox {m}, \rightarrow$ calculated $\hbox {S}_{2}$ pressure 5.7 bar. Photographs: SG (2003)

This estimation is in good correlation with others, e.g. from the size distribution difference between ambient temperature and HST (see the findings presented in the continuation of the present paper).

Examples from practice for over-stoichiometric inclusions are seldom seen. Figure 13 shows an inclusion with high over-stoichiometry and additional contamination with some iron and selenium. Although situated in the tensile zone and of sufficient diameter, it has been unable to cause glass breakage in HST because it remained untransformed.

A similar kind of inclusion has been found in a breakage departure point from building, but with different chemical composition (Fig. 14). In that case, the metal (Ni) to sulphur ratio is about $\hbox {x}=1.035$; iron and selenium are absent. Also in this case, the visibly porous structure is due to over-stoichiometry and gas development at the time of crystallization. Among all the inclusions from breakages analyzed in the author’s laboratories, this is the only one showing this structure and apparent over-stoichiometry. The over-stoichiometry reveals that the inclusion remained, at least partly, un-transformed. As already pointed out above, $\upbeta$-NiS does not allow deviation from the 1:1-composition.

Table 1 Estimated breakage probability relation between HST and facade

2.2.3 Summary: Compositional range of NiSx

In summary, the composition of “NiS” in the nickel sulphide inclusions is normally not expected to be exactly 1:1. Unfortunately, the compositional range identifiable in breakage departure points is limited. Two limiting factors are identified, namely the content of $\hbox {Ni}_{9}\hbox {S}_{8}$ in the inclusions at the lower end of the x scale and the vapor pressure of $\hbox {NiS}_{\mathrm{x}}$ at its upper end; this latter limit is valid for both HST and building conditions because it concerns the real existence of these compositions. Due to some differences in experimental findings and theoretical calculation, it is not currently possible to exactly fix this limit. On the basis of measurements of transformation kinetics on massive samples, Yousfi et al. (2010b, 2010a, 2011) calculates a limit of x = 1.047 (rounded 1.05). Above this value in the over-stoichiometric range, inclusions cannot cause breakage even in HST because their $\upalpha$ to $\upbeta$ transformation speed is too slow; therefore, these inclusions are not relevant both in HST and on buildings.

The frequency of occurrence of under-stoichiometric inclusions in the glass (Fig. 8 LHS) does not depend on composition. Described another way, the distribution is uniform due to the continuous development of x in $\hbox {NiS}_{\mathrm{x}}$ during glass melting and no losses due to “explosion”. Figure 8 LHS reveals that every under-stoichiometric inclusion can, based on composition, cause a breakage in HST. Contrary to this, breakages on buildings seem to be almost totally excluded (even independent of size and position) for c. 25% of the inclusions, namely those in $\hbox {x} \in \{0.89 {\ldots } 0.93\}$.

But in the range where the inclusions can be critical on building, i.e. $\hbox {x} \in \{0.93 {\ldots } 1.00\}$, the diameter relation quotient is an average (Building/HST) $= 0.40$. Consequently, in this compositional range, 60% of the breakages in HST are, at the limit, not relevant for buildings.

Concerning over-stoichiometric inclusions, it has been argued above that due to the increasing self-decomposition pressure of NiSx at elevated temperatures, the occurrence of the respective inclusions fades out as depicted in Fig. 5. Figure 8 RHS reveals that the difference between HST and ambient temperature conditions depends little on composition and that the diameter relation quotient is (Building/HST) $= 0.77$. Like the previous argument above, if this relation is proportional to the breakage probability, in this composition range, 23% of the breakages in HST are, at the limit, not relevant.

Table 1 summarizes the estimated breakage probability relation between building and HST over the total physically possible compositional range $(\hbox {x} \in \{0.89 {\ldots } 1.12\})$. In the relevant range, this number is calculated to be 39% (column G); consequently, due to the NiSx composition spread, c. 61% of the breakages in HST are not relevant for buildings. If, for a worst-case estimation, in a parallel calculation the threshold T in Fig. 8A is set to zero, the relation (G) increases to 51%, i.e., c. half of the number of breakages in HST are still not relevant for buildings.

This calculation is supported by the findings shown in Fig. 2c, d although, admittedly, the number of examples is still small. In this figure the relation (crack length)/(radius of inclusion) is only 0.95 for un-soaked glass whereas for glass after HST it is 2.8, i.e. c. threefold this value. Although even this extreme difference is naturally not a proof, it points clearly into the same direction.

Because crack initiation is more probable, and the initial cracks generated in the HST are more extended (i.e. longer), the HST eliminates all inclusions that would be critical on buildings.¹⁷ Furthermore, it eliminates 1.0 to 1.5 times this number from the inclusions that would be uncritical. Note that this rating only accounts for the effects of diversification of the composition of the nickel sulphide inclusions. Other impact factors are not yet included, but they must logically lead to an even higher safety margin.

The precision of the calculated numbers should not be over-estimated because many coefficients influence the calculation, and they are not all known with high precision, e.g. the coefficients of thermal expansion of some (high and low temperature) NiSx species. Independently, size and position distribution evaluations give similar results, as revealed in Kasper (forthcoming) and Kasper et al. (forthcoming).

Besides those presented in the present paper, more examples for NiSx compositions from glass breakages can be found in Kasper et al. (2003) and Yousfi et al. (2010a).

2.3 Breakages in HST not caused by nickel sulphide inclusions

In 1994, 134 breakage centers were made available from a HST facility in Belgium. This high number of “butterflies” had been collected in the facility because at the time, the HST was generally carried out on horizontal racks where the glass panes rested on perforated steel plates so that it was easy to collect many breakage centers. At that time, twelve out of these butterflies (i.e. 9%) were identified to be refractory stones, and two were large bubbles. This is so low in relation to the nickel sulphide inclusions because the float glass quality is thoroughly checked prior to toughening (mainly online on the float line) so that stones that are large enough to cause spontaneous breakage are mostly eliminated in advance. Contrariwise, nickel sulphide inclusions were (and still are) not detectable online on a production line. This information draws attention to the fact that nickel sulphide inclusions are not the only breakage cause in HST, but at the time, its importance was not realized. However, a production incident in 1999 taught us more.

The following crisis happened nearly 20 years ago. To date, no breakage at all has been recorded on the building in question, so that it is certain that the glass production described below led to a safe product without any breakage events until now, despite significant production difficulties. This information is assured as accurate because of the very special kind of the glass produced, and because SG hosted the glass reserve in its producing factory.

In 1999, as a part of a building project in Basel (CH) (the Peter Merian House), in addition to the float glass usually used, an order was also placed for a significant quantity of toughened heat-soak tested green 8 mm and 10 mm Kathedral glass sheets. These were a patterned glass, and because the ordered number was high enough and the color specification narrow (the Kathedral’s color should not show a visible color deviation to respective green float glass used on the same facades), the decision was made to produce it by mass coloration in one of SG’s patterned glass furnaces. The production schedule was arranged to produce an excess quantity as a reserve. After production, the glass was processed, i.e. toughened and heat-soaked, in Switzerland. The issue began with the toughening when about one third of the glass broke. The remaining panes were then subject to HST where another third of the glass broke. Initially, nickel sulphide inclusions were suspected as the cause of the breakage. Breakage departure points were collected by horizontal soaking of the next best glass lot from current production; this means that the sampling was statistically random. The analytical results were very explicit: only one out of the 11 samples analyzed is a nickel sulphide inclusion. Because it was not possible to detect inclusions online in colored patterned glass at that time, the color transition in the melting furnace (correlated with a change in the temperature distribution) caused an undetected stone crisis. After the glass treatment was completed, the volume produced was insufficient for the order, and the missing glass had to be made in a second production campaign.

The 11 samples mentioned are still available; in the following the respective dataset will be called “non-nickel sulphide inclusions” although one among them is in fact a nickel sulphide inclusion. The latter remains in the evaluation as a reference. To obtain more information on the breakage mechanism, the 11 samples were recently analyzed again, using scanning electron microscopy, EDX and micro-XRD. The results are summarized in Table 2. One inclusion has the very exotic composition of cobalt sulphide. Another one composes of pure iron. The remaining eight (77%) are composed of pure $\hbox {SiO}_{2}$. XRD revealed that the mineralogical composition of these stones is combined quartz, cristobalite, tridymite and glassy $\hbox {SiO}_{2}$. According to Jebsen-Marwedel and Brückner (1980) the most probable source for this kind of stones is incomplete batch melting. Silica batch stones are almost always enrobed by a halo of $\hbox {SiO}_{2}$-rich glass, characterized by a significantly lower coefficient of thermal expansion than the normal soda-lime glass. Their occurrence can easily be explained by the processes in the melting furnace at the time. In fact, the furnace had not been tailored for (highly heat absorbing) green glass. Consequently, the average temperature in the glass melt fell, the currents (mixing vortices) were disturbed and incompletely melted batch residuals (including the iron inclusion that should normally have been digested or transformed into NiS) found their way to the furnace exit.

Table 2 Inclusions identified in Kathedral Glass, all having caused breakage in HST

Fracture-mechanic approach

Generally, $\hbox {SiO}_{2}$ stones do not have the same thermal expansion coefficient (TEC) as soda-lime silica glass; TEC can be higher (e.g. pure cristobalite) or lower (glassy $\hbox {SiO}_{2})$, and crack formation is always a local event. Whatever the details, it is obvious that in the present case the stress induced by the inclusions is sufficient to make a high number of them critical during the toughening process. It is not important if the stress induced is positive or negative. According to Varner (2001), if the difference in thermal expansion is high enough that in cases of both positive and negative stress, cracks are generated in the surrounding glass; only the direction of the primary cracks (radial/tangential) is different.

Following are some relevant remarks to the non-nickel sulphide inclusion dataset, Table 1 and Fig. 15. Full fracture-analytic discussion is beyond the scope of this document.

• With some exceptions to be discussed below, the fracture stress estimated from the radius of the breakage mirror $\hbox {s}_{\mathrm{f}}$ is that of toughened glass,¹⁸$(44 \pm 4)\, \hbox {MPa}$ in the present case.

• The stones’ distribution in the glass section is very similar to that of nickel sulphide inclusion-caused breakages [to be discussed extensively in Kasper (forthcoming) and Kasper et al. (forthcoming)], and all are situated within the tensile zone of the glass.

• Cobalt sulphide no. 7 in Table 2) is very exotic and shall not be discussed further, except that

  • The system Co–S does not show a phase transition between ambient and $422\,^{\circ }\hbox {C}$ (Friedrich 1908);

  • although the inclusion is very small, the fracture stress is in the normal range, and a circular primary crack is clearly visible like in no. 1.

• (Pure) iron has a melting point of more than $1500\,^{\circ }\hbox {C}$. Melting is essential to form a sphere as observed in no. 1 in Table 2, Fig. 15B). This proves that the inclusion had been exposed to glass melting temperature and is not, e.g., a defect coming from the refining area $(1200\,^{\circ }\hbox {C})$ or the feeder $(1100\,^{\circ }\hbox {C})$, therefore most probably being a batch relic.

  Iron has a much higher coefficient of thermal expansion than glass, and, being a metal, it is not wetted by the glass melt (i.e., there’s nearly no adhesion); therefore, at both ambient and HST temperature, the inclusion should not put pressure or tension onto the surrounding glass, and it seems improbable that the visible circular primary crack had been induced by the inclusion itself. Other forces (during toughening or HST) must have initiated it.

• Most of the inclusions $(8/11 = 72\%)$ were composed of several types of $\hbox {SiO}_{2}$. The presence of quartz and recrystallization of cristobalite/tridymite are characteristic and strong indicators that all these inclusions were batch relics (Jebsen-Marwedel and Brückner 1980).

  • Recrystallization (formation of secondary crystals during refining, shown in Fig. 15A and analyzed by XRD) is not possible without significant $\hbox {SiO}_{2}$ over-concentration (from previous dissolution) around the stones.

  • In some cases, $\hbox {s}_{\mathrm{f}}$ is significantly higher, resulting in a circular breakage mirror, significantly smaller than the “normal” case, indicating that the forces coming from the respective stones are very high, higher than the tensile stress of the glass itself.

Even without going into the fracture-analytic details this signifies clearly that the $\hbox {SiO}_{2}$ stones in question have a lower coefficient of thermal expansion than the surrounding glass; the high forces identified must have built up on cooling during glass production. In the HST, stress around the $\hbox {SiO}_{2}$ stones increases on cooling and decreases on re-heating.

Note that tensile stress from inclusions at HST holding temperature is approximately divided by two in comparison with ambient temperature stresses. Consequently, stress change due to temperature level increase in the HST cannot have been the cause for those breakages.

Fig. 15

Information on non-nickel sulphide inclusions having caused breakage in HST. A Typical SiO$_{2}$ inclusion with (a) secondary SiO$_{2}$ crystals (recrystallization). B Iron sphere. (b): The circular primary crack around the inclusion is clearly visible. C (no. 6), D (no. 3): Form of breakage mirror reveals impact of external force (bowing of pane). E (no. 8): Form and size of breakage mirror reveal extremely high force coming from inclusion (50 MPa). F Positions of non-nickel sulphide inclusions in glass cross section. Note that the dagger-form staged crack is on the opposite side of the departure point of the primary crack, see comment in Fig. 2

• In the breakage events where $\hbox {SiO}_{2}$ stones are involved, but $\hbox {s}_{\mathrm{f}}$ is not increased, the glass was assumed to have been already damaged by induction of primary cracks during the toughening process, but not strongly enough to cause a breakage immediately. This begs the question: Why does it cause breakage in HST? In these cases, sub-critical crack growth and/or external (thermo-mechanic) forces must play a major role.

• The C-form of some of the inclusion’s breakage mirrors (most pronounced examples given in Fig. 15C, D) reveals clearly the impact of additional external forces, namely bowing of the pane at the breakage point.

These finding re-enforce the preceding hypothesis, namely that in the HST thermo-mechanical forces serve to increase breakage.

Fig. 16

WEIBULL evaluation of breakages in HST not caused by nickel sulphide inclusions (A), in comparison with nickel sulphide inclusion caused breakages (B) in float glass. Total number of breakages recorded: A 319, B 1462. Thereof, during holding time: A 52 (16.3%), B 290 (19.8%). Standard deviation ± s in y direction A 6.6, B 16.2 (in numbers). Mean error $\pm \hbox {s}/\hbox {n}^{1/2}$: A 0.37, B 0.42 (in numbers). WEIBULL-parameters A$\upalpha$: 3.15 $\upbeta$: 5.19 $\Delta \hbox {x}$: $-6.5$, B$\upalpha$: 3.22 $\upbeta$: 5.15 $\Delta \hbox {x}$: $-6.0$. a: Time zero (start of holding phase). b: Temperature reaches minimum holding level $(280\,^{\circ }\hbox {C})$ everywhere. c: WEIBULL best fit curve, nearly hidden behind measuring points (green line)

Time-to-breakage curves

By chance, the processing site of the Kathedral glass panes was the same location that was, at that time, recording the time-to-breakage of breakages caused by nickel sulphide inclusions in toughened float glass. Consequently, the times to breakage were recorded for the Kathedral glass and filed separately. The author evaluated this data set of 319 observed breakages¹⁹ in the following year (Fig. 16A) but it remained unpublished until now. Some differences in comparison with nickel sulphide inclusion induced breakages in float glass (Fig. 16B) are noted below:

• 84% of the breakages occur during the heating-up phase. For nickel sulphide inclusions this number is 80%; the difference is small and probably not significant.

• Figuratively, the scattering around curve Fig. 16A seems to be higher, mainly in the low temperature range.

  Because the total number of breakages is much lower in the data set for Fig. 16A than in the float glass data set for Fig. 16B, this impression is not real. Standard deviation as well as mean error are lower for the non-nickel sulphide inclusions.

• Breakages in Fig. 16A started earlier during heating-up than in Fig. 16B.

Overall, both curves are very similar. This is also true both for their distribution over the glass section (Fig. 15C) and the estimated breakage stress $\hbox {s}_{\mathrm{r}}$ (Table 1).

Consequently,

• The conditions for glass breakage in HST are not greatly dependent on the type of inclusion causing the breakage.

• After less than 3 h holding time,²⁰ in both cases (nickel sulphide inclusions and non-nickel sulphide inclusions) no more breakages are observed.

• Other effects must over-compensate for the absence of the $\upalpha$ to $\upbeta$ transformation in the non-nickel sulphide inclusions to still cause the breakages.

These arguments are very important for understanding the entire HST process.

• One possible explanation is induction of thermal stress into the glass panes in the HST.

Reiterating the discussion in Sect. 2.1.2, it is not feasible to get completely homogenous heating of stacked large glass panes. The panes always show thermal gradients (i.e. the panes are subject to transient stress); these gradients are normally not seen so much across the pane thickness but manifest as membrane stress over their surfaces, mainly during heating-up. Also the discussion of fracture mechanics in correlation with the non-nickel sulphide inclusions identified clear indications for this effect.

• Another possible explanation is sub-critical crack growth.

A cavity in the glass (bubble, loose inclusion like a nickel sulphide inclusion) is certainly very well protected from outer atmosphere and gaseous water vapor therein, but, as discussed in Sect. 2.1.3, the glass matrix itself is not absolutely dry. According to Geotti-Bianchini et al. (1999), it contains c. 350 ppm water, mostly bonded as silanol groups (–OH) in the glass structure, and it also shows a mobility comparable to alkali ions under the form of $\hbox {H}^{+}$ detached from the silanol groups, according to Scholze (1988). Water is consequently mobile in the glass matrix and can migrate (diffuse) into gaps and cracks at elevated temperature, causing retarded sub-critical crack growth, in turn related to delayed breakages in HST.

To date the (never proven) assumption is widespread that in HST the defining step for the breakage devolution in time/time-to-breakage curve²¹ is the nickel sulphide inclusion’s transformation speed; also Karlsson (2017) mentions this in his review. This assumption is intuitive because the root cause of most of the HST breakages is doubtlessly nickel sulphide inclusions indeed; however, the conclusion thereof is illogical (“non sequitur”) that the root cause must be, at the same time, the determining process for the breakage devolution in time. The experience depicted here shows clearly that this conclusion is overhasty; the case is more complicated.

Laboratory observations using different approaches show that the nickel sulphide transformation is more rapid than what is observed in the Heat-Soak Test oven. “Normal” NiS(1:1) needs 10 min at $220\,^{\circ }\hbox {C}$ and less than 5 min at $280\,^{\circ }\hbox {C}$ for $>90\%$ transformation (see e.g. Fig. 12 from Yousfi et al. 2011). Even taking into account the slower transforming species (they contain a sulphur excess, see above), it is impossible to derive a model thereof that fits the real breakages; the relative number of slowly transforming (over-stoichiometric) nickel sulphide inclusions is not high enough (Sect. 2.2.2) and most of the inclusions are subject to fast transformation.

To explain this observation some have argued that the NiS transformation speed under pressure might be slower. This is not impossible, but is currently unproven. Approximately the first third of the $\upalpha$ to $\upbeta$ transformation in glass is taking place under pressure-free conditions because the inclusion is still smaller than the surrounding “bubble”. At least this part of the transformation will always occur with the normal speed measured e.g. by DSC, as related in Bordeaux and Kasper (1997), Yousfi et al. (2011) and other publications. It is hard to imagine that the transformation speed would slow down significantly just because the inclusion is under a pressure of some ten MPa before the glass cracks. For a solid crystalline body this pressure level is not high, and significant impacts would only be expected to result in respective pressures in the GPa range.

In 1999, Sakai and Kikuta (1999) published data revealing (in his Fig. 4) that at a heating rate of 2.86 degrees per minute, the $\upalpha$ to $\upbeta$ transformation of real inclusions is completed when reaching $180\,^{\circ }\hbox {C}$. He carried out trials with more than 20 inclusions of different composition (mentioned were $\hbox {Ni}_{7}\hbox {S}_{6}$, NiS and NiS$_{1.01})$ collected from glass production. These were heat-treated under a polarizing microscope with integrated heating stage, balancing between ambient temperature and $500\,^{\circ }\hbox {C}$. The results reveal that there is no impact of the pressurizing of the inclusions by the surrounding glass. Using the data used for the calculation of curve (a) in Fig. 17 below, but applying SAKAI’s heating rate mentioned above, the temperature calculated for 99% transformation of NiS is $179\,^{\circ }\hbox {C}$. Obviously, both results match closely under both open and glass-enclosed conditions.

Fig. 17

Comparison of transformation of NiS species with breakage occurrence in HST. HST curve from Kasper (2000) and Kasper and Bordeaux (2000); NiS transformation calculated from SG DSC results, linear heating-up from $20\,^{\circ }\hbox {C}$ with heating rate $0.83\,^{\circ }/\hbox {min}$ in every case, including the HST. a Nickel sulphide inclusion with $\hbox {x} = 1.00$. b Composition $\hbox {Ni}_{0.98}\hbox {Fe}_{0.02}\hbox {S}_{1.02}$. c WEIBULL best fit curve of the HST breakage curve (Kasper and Bordeaux 2000). d Average start of HST, ± 1.5 h depending on actual glass mass in oven. e Transformation limit where the $\hbox {NiS}_{1.00}$ inclusion exactly fills its “bubble”

This suggests there is no relevant influence of pressure on cracking. The present paper shows a better explanation. The combination of transient thermal load and (eventual) sub-critical crack growth shows good correlation with the observations from practice mentioned in Sect. 2.1 (Geotti-Bianchini et al. 1999). Additionally, (e.g. during HST oven calibration), measurements prove that within single glass panes temperature gradients are observable. In this context, Kasper (forthcoming) and Kasper et al. (forthcoming) reveals that there is an observable impact from the panes’ size.

Figure 17 quantifies the difference between the occurrence of breakages and the transformation speed of NiS.²² Under the condition of the same heating-up rate for all data, the transformation rates of two kinds of nickel sulphide (NiS(1:1); $\hbox {Ni}_{0.98}\hbox {Fe}_{0.02}\hbox {S}_{1.02})$ are compared with the breakage devolution measured in the HST in the years 1996 to 2000 (from Kasper and Bordeaux 2000; Kasper 2000). NiS(1:1) is present in the prevailing number of nickel sulphide inclusions, while the nickel sulfide-iron composition is, due to its iron content and over-stoichiometry, subject to much slower transformation. Both species’ kinetic parameters of $\upalpha$ to $\upbeta$ transformation were previously measured in the author’s laboratories using DSC. According to Fig. 5, more than 90% of the species leading to breakage in HST are contained in this compositional range, even disregarding the iron content in species Fig. 17b that is known to slow down the transformation speed even more.

As discussed above, Fig. 17curve (a) corresponds to the prevailing number of the inclusions leading to breakage in HST, referring to under-stoichiometric and near-stoichiometric NiSx liquid droplets in the glass melt. The impact of thermal expansion (mainly important for more under-stoichiometric species with $\hbox {x} \le 0.96$) is immediate and starts to play a significant role at c. $120\,^{\circ }\hbox {C}$ (derived from Fig. 8’s calculation). Fig. 17 reveals that the $\upalpha$ to $\upbeta$ transformation of both exemplary NiSx species is already completed after about 30% of the time when the breakage occurs; this means that c. 70% of the breakages take place after compete transformation. Very big inclusions or even those situated in the zone of highest tensile stress do not require 100% transformation to trigger breakage, so, these very critical inclusions are the most likely causes of the initial breakages. When these critical breakages are completed and all the NiSx is transformed, there must be another reason for the breakages to continue.

The general thinking about the processes in the HST must be reconsidered around role nickel sulphide plays in comparison to e.g. refractory stones. Generally, the time-to-breakage curves follow a probabilistic curve (applied here: WEIBULL distribution), but the detailed processes of crack initiation are clearly not the same. Based on this, the following scenario is proposed for discussion, subject to later amendments based on additional research results.

• Heating-up, low temperature, heating with reduced power for thermal glass breakage prevention:

  • Refractory stones:

    In many of these stones, cracks in glass have already been initiated during cooling at glass production or during toughening.

    The most critical refractory stones now cause breakages.

    The number of these breakages is small because the very critical ones are normally already lost during toughening; only the survivors (“the worst among the harmless”) cause some breakages during this part of the process.

  • Nickel sulphide inclusions:

    Nearly no breakages are observed because the inclusions are still untransformed. In correlation with the above observation, breakages from nickel sulphide inclusions start later in comparison with breakages from stones.

• Heating-up, temperature above c. $150\,^{\circ }\hbox {C}$, heating with full power:

  • Refractory stones:

    • Most of the stones continue to shrink in relation to glass, as discussed in this paper. Consequently, the tensile stress induced into the glass decreases.

    • Despite this, the breakage frequency first increases as the thermal gradients become stronger due to the increase of the heating power, the increase of the maximum temperature and increasing maximum possible temperature difference between hottest and coldest points in the glass surfaces.

    • With further increasing temperature, the impact of sub-critical crack growth increases, and that of thermal heterogeneity decreases.

    • Two hours before reaching holding temperature (in the example), the breakage frequency already begins to decrease significantly. This is due to the combination of temperature stabilization, the decrease in the number of still critical stones,²³ and the decreasing criticality of the remaining stones.

      This explains the acceleration at the beginning, followed by decreasing breakages later in the process.

  • Nickel sulphide inclusions:

    Inclusions transform and cause fast increasing tensile stress in the glass.

    They expand (in relation to glass) because of higher expansion coefficient, in parallel to the temperature increase.

    • Breakages start significantly when reaching c. $150\,^{\circ }\hbox {C}$.

    • 80% of the inclusions are fully transformed when the temperature (locally) reaches c. $180\,^{\circ }\hbox {C}$, at $200\,^{\circ }\hbox {C}$ this number is $>90\%$.

      Only a minority of very slowly transforming species drags behind.

    • Breakage frequency is now driven by effects like those described for the refractory stones, including increase and decrease of breakage frequency.

    • The significant difference between the two types of stones in the higher temperature region is while many of the stones shrink (in relation to the glass), the nickel sulphide inclusions expand with increasing temperature (and $\upalpha$ to $\upbeta$ transformation), and are therefore “more critical” in the HST.

• Heating-up phase macroscopically terminated, official start of holding plateau:

  • In both cases: temperature stabilizes, breakages fade out according to a statistical curve due to different effects already discussed.

    Now, at the highest temperature, sub-critical crack growth driven by water diffusion could play the major role.

• Cooling phase, survivors:

  • Refractory stones:

    Many among the eventual survivors “grow” in comparison with the glass. Higher tensile stress is induced again, and in very seldom cases breakages are observed within a few hours to a few days, while still in the factory. The additional time required for transport to the building site sorts out these “a posteriori critical” cases. Explicitly, between 2004 and 2006, every year one such a breakage was reported by our processing factories and sent to the author for analysis. In two cases, our laboratory identified the breakage cause to be a silicon sphere (elemental silicon enrobed with highly SiO2-rich glass), and in one case a large one-mm refractory inclusion. Never, neither before nor since then, a nickel sulphide inclusion was identified in a breakage center immediately after HST.

    Note that in the real case reported from the Peter-Merian-house, no breakages at all have been observed on the respective building during nearly 20 years after production.

  • Nickel sulphide inclusions:

    Survivors always shrink in relation to the glass, building up a safety margin.

    Additional analysis in Kasper et al. (forthcoming) will show that there are many survivors, in the range of 75%.

This discussion shows why a WEIBULL curve²⁴ is needed to “fit the HST” while a GAUSSIAN or the double-exponential curves describing reaction kinetics are inapplicable. Breakages are not mono-causal; multiple staged effects combine, making these less complicated mathematical descriptions obsolete.

It must be emphasized that the processes described here depend in detail on the situation in the individual HST oven types. The present section describes what is observed in a type used in 1999. That oven fulfilled the conditions of EN 14179-1, assured by tests using by multi-thermocouple temperature measurements. At that time the standard was in preparation and the measurements made in this oven type were used as the basis of the standard. More modern oven types may e.g. reach temperature stability much earlier and more evenly contributing to earlier cessation of breakages. To assure this, additional time-to-breakage measurements would have to be carried out.

3 Summary and conclusions

Observed data shows that there are always more glass breaks in HST, than on buildings. To date, only the difference in thermal expansion between glass and nickel sulphide has been assumed responsible for this effect; consequently, it has been looked at to be very small. The time-to-breakage data obtained in HST have thus been used and extrapolated to make an estimate of the residual breakage probability of Heat Soak Tested Thermally Toughened Safety Glass. The facts being presented here should help provide better estimating methods for HST toughened safety glass residual breakage probability.

In Sect. 2.2.3 the new findings and calculations of the impact of the composition of nickel sulphide inclusions onto the difference in breakage probability between HST and façades have been compiled. In short, the result of this is that the HST eliminates every inclusion that could lead to breakage on buildings and additionally more than the same number as a “safety margin”.

The Kathedral glass evaluation dataset in Sect. 2.3 reveals that heat-soak tested glass is also safe if the breakage rate during production is very high. Not only nickel sulphide inclusions, but also other stones are responsible for significant breakage in HST. The general form of the time-to-breakage curve and other findings (position in glass section, breakage stress in case of pre-damage derived from the radius of the breakage mirror) are nearly identical with those from nickel sulphide inclusions. The conclusion from this is that the nature of the inclusions causing breakage in HST is not the deciding factor for the time to breakage; the $\upalpha$ to $\upbeta$ transformation speed of the nickel sulphide inclusions is not the process determining the speed of this devolution.

This observation solves a long-existing question, namely why the time-to-breakage curve in HST cannot be explained by the measured phase transformation speed of the different relevant $\hbox {NiS}_{\mathrm{x}}$ species. Considering the occurrence frequency derived here, the latter is much faster.

This leads to the new conclusion that in HST also other impact factors than the difference in thermal expansion play an important role. Two additional influencing factors may be strong thermo-mechanical forces (temporary stress) induced into the glass during heating-up, and under-critical crack propagation driven by water diffusion at HST temperature. The first factor could be quantified by stress measurement or finite-element simulation, but the second cannot. More proofs for these hypotheses will be added in the continuation of the present paper, namely Kasper (forthcoming) and Kasper et al. (forthcoming).

Overall, the new findings are important arguments for why the existing estimations of residual breakage probability of toughened glass tested according to EN 14179-1 under-estimate actual safety. The presumption that the breakage behavior in HST and on buildings would be the same is clearly not correct. Consequently, the recommendation is to review the present safety estimation. For now, it should be considered as a minimum estimation with a big safety margin.

Additionally, the actual change of the conditions of the HST standard in 2016 will make it more reliable (and the glass safer) because the $\upalpha$ to $\upbeta$ transformation of every potentially dangerous nickel sulphide inclusion will be complete, including the seldom seen varieties with exotic over-stoichiometric composition.

New presentations and concepts in the present paper:

• Description of the impact of the surface structure of nickel sulphide inclusions on the breakage mechanics, and an explanation why even untransformed nickel sulphide inclusions can cause spontaneous breakages under certain circumstances, in contrast to smooth bubbles of the same size.

• Derivation (from NiSx phase diagram and chemical generation process) of the properties of nickel sulphide inclusions in glass in view of on their detailed composition, including the presence of $\hbox {Ni}_{9}\hbox {S}_{8}$ and $\hbox {Ni}_{3}\hbox {S}_{4}$ and elaboration of relevant compositional limits of x in $\hbox {NiSx}\, (0.89< \hbox {x} < 1.05)$. Consequences from this on the difference in both their criticality and the number of breakages on buildings and in the HST.

• Proof by example (and first publication) that not only nickel sulphide inclusions, but also refractory stones and other non-nickel sulphide inclusions lead to breakages in HST, and that the time-to-breakage curve is—except for some minor details—an S-shaped curve like for nickel sulphide inclusions with nearly identical curve expansion. The conclusion that the time to breakage in HST is not nearly as dependent on the transformation kinetics of $\hbox {NiS}_{\mathrm{x}}$ as it is on temperature level and temperature heterogeneity in the heat-soaking glass stack.

• Proof that the HST destroys much more glass than would break on buildings, derived from hard facts, i.e. publicly available physical properties of the different NiSx species involved.

  Demonstration that “criticality” of an inclusion is different under different temperature conditions.

  Derived from this, estimation that c. 60% of the breakages observed in HST are not relevant for application on building.

  Put simply, this means that the HST eliminates all inclusions that would be critical on buildings.

  Furthermore, it eliminates 1.0 to 1.5 times this number from the inclusions that would be uncritical there (see also footnote 18). This rating only accounts for the fact of diversification of the composition of the nickel sulphide inclusions. Other possible impacting factors (like mechanical stress induction) are not included, but their inclusion would logically lead to an even higher safety margin.

• Proof that the estimated residual breakage probability of “Heat-Soak Tested Thermally Toughened Safety Glass” (e.g. in Schneider et al. 2012) is much too high and far away from real safety.

An outlook on future studies will be given in the last part of the present series of publications.