Spontaneous cracking of thermally toughened safety glass Part two: Nickel sulphide inclusions identified in annealed glass

Abstract

The present paper is part two of a small series of three publications on spontaneous breakages of toughened glass. In part one, we deal with the detailed effects of the crystallographic and physical properties of the nickel sulphide species contained in those inclusions; we find that solely under this aspect, only c. 40% of the breakages in a Heat Soak Test (HST) according to, e.g., EN 14179-1:2006, would be physically able to cause a breakage in a façade. The present paper partly builds up on these findings. In the present paper, we prove experimentally that nickel sulphide inclusions are found everywhere in the raw glass section. On the other hand, their repartition is visibly influenced by gravitational settling. The resulting distribution profile is explained by a physical model. Further elaboration of this model allows to better understand the observed nickel sulphide inclusion size distribution in the raw glass. We show statistically that almost only nickel sulphide inclusions with size $>55~\upmu \hbox {m}$, situated in the middle glass portion, can lead to breakage in HST, in good correlation with data previously published. We quantify the nickel sulphide inclusions’ size impact based on the statistical evaluation of our dataset. Big nickel sulphide inclusions ($>450~\upmu \hbox {m}$) always cause very high breakage risk $> 90\%$. On the other hand, we prove experimentally that only a minority of c. 1/4 of the nickel sulphide inclusions factually existing in raw glass leads to breakages in the HST carried out in the frame of our R&D project where the glass panes were only small and thin. In the normal building glass product mix this proportion is probably higher because in the HST, the mass-related breakage rate (in numbers per ton of glass) increases with increasing glass panes’ dimensions. In Part Three we evaluate datasets from field breakages and give an overall summary of the series.

1 Introduction

The problem of nickel sulphide inclusions causing spontaneous cracking of thermally toughened glass is known since more than fifty years. Since that time, many papers have been published thereon; the state of the actual general knowledge is summarized in a well-founded review published recently by Karlsson (2017), but it cannot be ignored that some of the facts mentioned therein have to be looked at to be outdated; the present publication occupies with this, among others, in the summary. The exercise of writing a review paper shall, however, not be repeated here again and, to a certain extent, basic knowledge on the problematics of spontaneous breakage is expected from the reader.

The following is based on a recently published paper (Kasper 2018a) on the detailed effects of the crystallographic and physical properties of the nickel sulphide species contained in these inclusions in glass. The most important finding therein is that only c. 40% of the breakages in a Heat Soak Test (HST) according to, e.g., EN 14179-1:2006, are really relevant for the façade. This is mainly due to the fact that the expansion coefficients of glass and the different $\hbox {Ni}_{\mathrm{x}}\hbox {S}_{\mathrm{y}}$ species are significantly different, partly by a factor of more than ten. This literature-based calculation leads to the author’s conclusion that the HST eliminates almost all inclusions that would be critical on building. Furthermore, it eliminates 1.0 to 1.5 times this number from the inclusions that would be uncritical there. This rating solely takes into account the fact of diversification of the composition of the nickel sulphide inclusions. Other impact factors are not yet included, but they must logically lead to an even higher safety margin. A first approach to this thinking is undertaken in the present paper.

A second important result of the previous paper is that other than nickel sulphide inclusions do cause breakages in HST. Their behavior therein is a nearly perfect mimicry of that of nickel sulphide inclusions although they are not subject to the well-known and extensively discussed allotropic $\upalpha$ to $\upbeta$ phase transition. For sure, the latter is the root cause for spontaneous breakages on buildings. But the implicit and unsubstantiated, but nevertheless widespread deduction thereof that the kinetics of this transition have to define the time-to-breakage in the HST is revealed therein to be a pre-matured conclusion.

Thus, taking into account both arguments, already the previous paper should cause a paradigm shift in the safety estimation of the heat-soak tested glass. It reveals that there are significant and technologically important differences between “spontaneous breakage” on façade and in HST. It is therefore not possible to directly derive the residual breakage probability on façade from the HST’s breakage probability and time-to-breakage curve although just this is what respective estimations consist in, even including that of one of the author’s in Kasper (2000). At the time being, the result of this (simplifying) estimation, namely that for every reasonable glass pane size the yearly residual breakage probability is $<2^{*}10^{-4}$, seemed to be largely sufficient. A more detailed estimation based on the same dataset, but taking into account better fracture-mechanic calculation details, was published later (Schneider et al. 2012), leading to an estimation of even lower residual probability of breakage.

On the other hand, still not everything is clear in this theme. For example, it is known as a matter of fact that very small nickel sulphide inclusions do not cause spontaneous breakage (Swain 1981; Bordeaux et al. 1997; Schneider et al. 2012) and that the inclusions’ size is not the only criterion for this exclusion. The present paper augments this knowledge, analyzing a dataset of 140 nickel sulphide inclusions identified by automatic detection in annealed glass in SG laboratories in the Far East with the aids of statistical procedures. After identification of size and position in the glass cross section, the panes were toughened and the panes subject to a HST. Some of the remaining unbroken were characterized analytically. It is now intended to analyze more of the remaining at SG in collaboration with another institute, but this will take time and will be the subject of a later publication.

In the present introduction (Kasper 2018a) is only shortly summarized. For best understanding it is thus recommended to read this publication before plunging into the present one. Additionally, the mentioned paper contains a more detailed general introduction into the theme of spontaneous breakages that’s naturally also valid for the present one.

2 Statistical basics for dataset fitting and physical basis for nickel sulphide inclusion generation in glass melts

Some knowledge of statistical mathematics is condition to understand the following calculations and estimations. For more detailed information, it is recommended studying e.g. James et al. (2013) or another textbook on statistics.

To prevent misunderstandings, the present article does not try to model the occurrence of nickel sulphide inclusions in glass, but it evaluates the result of a detection trial in annealed glass using assorted statistical tools for their interpretation.

Two parameters were measured in this C/K-trial, namely the positions in the section of the glass and the sizes of these inclusions.

• 1. Position in the glass section.

  Purely random positioning of the inclusions would logically result in a (maybe noisy) linear position distribution over the section.

• 2. Sizes of detected nickel sulphide inclusions.

  The size spectrum is a priori unknown. Tentative fitting with different statistic distribution curves showed that the Log-Normal curve allows good fitting of the sample set that seems not to be amendable, taking into account the random noise of the results.

The second fact shall be substantiated more, namely why basically the two-parametric Log-Normal function without abscissa shift (i.e. the original function starting at $\hbox {x} = 0$), just multiplied with the total number of data in the dataset, is fitting the datasets so well. A log-normal related process output, as e.g. the datasets obtained and fitted hereunder, is principally the statistical implementation of the multiplicative product of some or many random variables. This statement is assumed to hold true without formal stochastic proof, see e.g. Redner (2002). This is, on closer examination, obvious for the nickel sulphide inclusions’ occurrence, too. These special inclusions generate from nickel containing steel particles by chemical reaction with the sulphate of the glass melt, followed by a slow oxidizing decomposition reaction with the same component (and other oxidizers like $\hbox {Fe}_{2}\hbox {O}_{3}$) of the glass and, due to the density difference of both phases, possibly subject to losses by segregation. Another significant random influence is the temperature profile, combined with the respective sojourn time, that the individual inclusion “sees” on its trajectory through the melting tank.

Nickel sulphide inclusions cannot form from the homogeneous glass melt, at least not under the common conditions of a furnace melting clear (e.g. window) glass. In a Ph.D. thesis, Shi (1993) reveals this by trials and thermodynamic calculations, and the same result is also reported in Kasper and Stadelmann (2002). Accordingly, only very exotic and, in practice, unrealistic conditions could eventually lead to this way of NiS particle formation. Additionally, however, not taken into account by Shi, but this is also an important thermodynamic effect, the formation of a separate phase needs extra energy caused by the surface energy of the (initially) very small particles. The latter is in perfect correlation with chapter 3.3.3 of the present publication, revealing that very small nickel sulphide inclusions seem to be unstable just because of their small size. The same is true for any other oxidized nickel species, e.g. from regenerator deposits transferred into the glass melt, as further explained here-below.

So, grouped and listed in chronological order as occurring in the glass melt, the most important variables of the acknowledged nickel sulphide inclusion generation process are the following.

• Nickel source

  Impact factors are size, number and nickel content of basic steel particles.

  Other nickel sources (like e.g. the nickel content of fuel oil of several ppm, or nickel-containing thin coatings on glass at recycling) can factually be excluded. Nickel sulphide inclusion formation needs definitely a particle source containing nickel metal; the alternatives listed here-above provide highly dispersed ($<1\,\upmu \hbox {m}$), oxidized NiO or $\hbox {NiSO}_{4}$ (from waste gas) or NiO (in coatings, but even if it would be the metal, the local concentration is too small). One of the authors (KASPER) carried out respective thermodynamic and mass balance calculations leading to this conclusion, published in Kasper and Stadelmann (2002) and Kasper (2000).

  However, one alternative is real, e.g. in industrial glass production, namely using a pre-mix of minor (coloring) batch components including NiO and coke at the same time. Because NiO is easily reduced in direct contact with coke, the result of this “test” is reliably (in the first step) the formation of nickel metal particles, i.e. it’s about nickel-containing particles like in the case of the steel, except that they are already pure at the beginning. On the other hand, glass coloration using (nickel metal-free) NiO in absence of a reducer, is technically possible, it does not lead to increased nickel sulphide inclusion formation and is widely applied, at least at SG. This fact disqualifies (Wagner 1977)’s assumption (still repeated in actual reviews although disproved since a long time; it is e.g. impossible with gas firing) that deposits on the fire bricks of the regenerators, containing up to 10% NiO, would cause nickel sulphide inclusions. Even if they are really peeled off by entering hot combustion air (already this presumption is doubtable because it would also lead to conspicuous, typically brownish localized glass defects), they only contain diluted NiO, but no nickel metal, and there’s no reducer in the glass to generate a sulphide thereof. Own thermodynamic calculations (Kasper 2000) and the experience that the nickel sulphide inclusion problem exists, with identical intensity, in both fuel oil and gas fired glass melting furnaces, prove that the nickel in the fuel oil has nothing to see with the nickel sulphide inclusion problem.

• Transformation of the metal into sulphide(s) (sulfidation):

  Impact factors are the chemical environment (e.g. sulphate content, oxidation state and basicity of the glass melt); the unforeseeable individual pathway of a single particle through the melting tank, i.e. residence time, temperature and (relatedly) the glass viscosity profile “seen” by the inclusion. Because the sulfur from $\hbox {SO}_{3}$ is bounded in the $\hbox {NiS}_{\mathrm{x}}$, this reaction takes place without $\hbox {SO}_{2}$ gas bubble development and, therefore, does not need to overcome the high activation energy of bubble nucleation in the viscous glass melt. More detailed descriptions of the chemical reactions involved in this sulfidation are published in Kasper (2000).

• Sulphide decomposition / digestion due to continuous oxidation by the glass melt

Both the metal particles and the nickel sulphide inclusions are thermodynamically unstable in the oxidizing soda-lime glass melt; therefore, the chemical reaction with the oxidizers (mainly $\hbox {SO}_{3}$ and $\hbox {Fe}_{2}\hbox {O}_{3}$) continues all the time until the glass solidifies, even on the surface of the solid nickel sulphide inclusions as shows, e.g. Fig. 2.

Two factors influence the decomposition speed:

• At constant reaction rate on the inclusion’s surface, the diameter diminution depends on the relation (surface [$\sim \hbox {r}^{2}$] / volume [$\sim \hbox {r}^{3}$]). Therefore, it strongly speeds up for decreasing size, namely according to a hyperbolic law.

• The reaction rate on the surface could also depend on the oxidizer’s local concentration. In order to make the decomposition reaction, the oxidizers diffuse from the glass bulk to the surface of the inclusion where they are digested. On the other hand, the reaction products diffuse away, causing a brownish halo around the inclusion, see examples below; a typical diffusion profile is measured around the inclusions Kasper and Stadelmann (2002). Logically, the oxidizer consumption rate decreases proportionally with decreasing absolute inclusion surface. Therefore, the diffusion speed of the oxidizers or of the reaction products can also influence the decomposition rate. However, if it is relevant, also this effect makes the decomposition rate speed up with decreasing size. On the other hand, in view of the obviously very long lifetime of the nickel sulphide inclusions in the glass melt, the diffusion impact most probably does not play a noticeable role.

Therefore, it is hypothesized that the hyperbolic impact predominates. This effect is certainly an important reason for observing relatively less very small inclusions in the datasets. Chapter 3.3.3.2 reveals that this hypothesis is probable.

• Position in the glass section due to gravitational settling

  Both glass and the different nickel sulphide species have significantly different densities ($2.5~\hbox {g/cm}^{3}$ and c. $5.4~\hbox {g/cm}^{3}$, respectively, at ambient temperature). The glass flow in the rear zone (“channel”) of every float or patterned glass furnace is almost free of turbulences and vortices because this would lead to optical glass defects (Jebsen-Marwedel and Brückner 1980), and the residence time of the glass in this zone of the furnace is, depending on the glass thickness and effective pull rate, in the range of several hours. Consequently, the nickel sulphide inclusions sink down due to the combination of gravitational settling and buoyancy, described by the well-known STOKES law [see below, Eq. (2)]. Qualitatively spoken, the sinking velocity depends on the density difference and, deciding, on the inclusion’s size because the glass viscosity (braking the movement) is the same for all whereas the mass (defining the gravity force) is individual.

  Consequently, if there is an observable effect, it must lead to a height-depending structure of the inclusion’s position distribution over the glass section. Gravitational settling was formerly applied in a method of indirect particle size measurement (Allen 1981); today this method is seldom used because of the invention of better, faster and more precise techniques. The background theory of this method is not directly helpful here because it does not aim to describe the position distribution development in the suspension but the weight increase on the bottom of the instrument, but it reveals that there’s a systematic and exploitable effect.

  If settling is noticeable in building glass (thickness $>4~\hbox {mm}$), one should find a higher number of inclusions in the lower zone (close to the “bath side” of the glass), eventually no inclusions in a layer (of a priori unknown thickness) close to the other (“atmosphere”) side and maybe some inclusions popping up in the bath side, but never in the atmosphere side.

The parameters listed here-above are almost deciding for size, composition and position in the cross-section of every individual nickel sulphide inclusion. But also the

• Detection method could play a role in the dataset:

  Below a certain limit defined by the detection instrument’s design, inclusions of decreasing size are detected with decreasing probability. Above the limit, the detection ability is constant and close to 100% as shown in the experimental result. In the present case, this design limit is c. $40~\upmu \hbox {m}$. According to the instrument’s performance specification based on optical calculation, the recorded image is then only $3\times 3$ pixels. All smaller “defects” detected in spite of this were therefore classified to be “irrelevant” by the instrument’s software.

  With respect to the datasets recorded and their fitting, this cut effect amplifies the size-depending decomposition effect. On the other hand, because it was known before that inclusions $<50\,\upmu \hbox {m}$ diameter cannot harm the toughened glass (this is, by the way, the reason why the design limit mentioned above is chosen $40~\upmu \hbox {m}$), this limit is low enough to record every potentially harmful inclusion.

Logically, all these influencing factors are correlated in a multiplicative way because they are consecutive steps.

As to the (non-)application of abscissa shift already mentioned above, it’s trivially logical that inclusions cannot have negative diameters; consequently, a positive shift is absolutely excluded. On the other hand, there’s no reason why some very small inclusions should not occasionally survive the glass melting process; consequently, also a negative shifting of the data does not seem adequate. Therefore, the fits based on the two-parametric LOG-NORMAL function (occasionally multiplied with an adequate constant) should (and does) match with the nickel sulphide size spectra in every case investigated in the present paper, allowing interesting conclusions and the logically well-founded quantitative comparison of different datasets.

For clearness, and although they are nearly trivial, the basic equations used in the present paper for calculating the “empirical mean standard deviation” is cited. It is a measure of the uncertainty of the approach, namely the scattering of the real data around the curve in both x and y direction, and calculates from the square root of the variance $\hbox {s}^{2}$ ($\hbox {s}=\pm \surd \hbox {s}^{2}$) according to

$$\begin{aligned} \hbox {s}^{2}{_{\mathrm{x}}}=[\Sigma (\Delta \hbox {x}^{2})] / (\hbox {N}-1);\quad \hbox {s}^{2}_{\mathrm{y}} = [\Sigma (\Delta \hbox {y}^{2})] / (\hbox {N}-1) \end{aligned}$$

(1a)

with $\Delta \hbox {x}, \Delta \hbox {y}$ : Difference between measured data point and fitted value; N : Number of $\Delta \hbox {x} / \Delta \hbox {y}$ values = number of events.

These equations are directly related to the estimation of the characteristic parameters ($\upsigma$ & $\upmu )$ of the Log-Normal curve by the least-square method. By iteration, applying the EXCEL solver, the average of both relative standard deviations [$(\hbox {s}_{\mathrm{rel.x}}+\hbox {s}_{\mathrm{rel.y}}) / 2)$] is minimized simultaneously, i.e. the mean distance between the curve and all data points in both dimensions; this is the reason why it is called below the “mean” standard deviation. At the same time, both standard deviations are obtained as estimates for the statistical quality of the curve fitting.

Another independent way to predict $\hbox {s}^{2}$ is, according to e.g. Philipp (2014), the following Eq. (1b). It allows to estimate the uncertainty of a counted result, just based on the absolute number N of events (e.g. counts; breakages) and nothing more, under the condition that $\hbox {N}>30$.¹

$$\begin{aligned} \hbox {s}_{\mathrm{rel}}{^{2}} = 1 / \hbox {N} \end{aligned}$$

(1b)

with N: number of counted events

The equation results from the theory of the one-parametric POISSON distribution; therefore, below, acronyms like “the POISSON estimation of $\pm ~\hbox {s}$” are mentioned. The equation is often used in physicochemical methods (e.g. X-ray fluorescence, EDX: number of collected counts) to estimate the analytic precision of a given measurement. In the present paper Eq. (1b) is applied to estimate the significance of some observations, differences and comparisons if they are based on counted numbers, e.g. of breakage events. However, this estimation is generally not applicable on best-fits.

For those, PEARSON’s concept of the Coefficient of Determination $\hbox {R}^{2}$ (correlation coefficient R) is applied. It is a characteristic number for the precision obtained by a best-fit, basically for linear correlations. However, like in the present paper, the latter condition is often disregarded in practice (also e.g. in spreadsheet programs like $\hbox {EXCEL}^{\circledR })$ and PEARSON’s $\hbox {R}^{2}$ is calculated in the same way for curves. In most of the cases the result is indeed significant. Therefore, and because it is easy to calculate, the utilization of $\hbox {R}^{2}$ as a quality parameter for any kind of curve fitting is widespread. If different fitting functions are applied on the same dataset, $\hbox {R}^{2}$ allows to quantify the differences between these fits, giving a useful criterion for which function fits better. This is so because the denominator in the calculation [Eq. (1c)] is then the same.

$$\begin{aligned}&\hbox {R}^{2} = 1 - (\text {explained sum of squares}) \nonumber \\&\qquad / (\text {total sum of squares}); \nonumber \\&\hbox {R}^{2}\in \{0, 1\} \end{aligned}$$

(1c)

With (explained sum of squares): $\Sigma (\hbox {y}-\hbox {Y})^{2}$ {difference between measured [y] and estimated points[Y]}; (total sum of squares): $\Sigma (\bar{\hbox {y}}-\hbox {Y})^{2}$ {[difference between average [$\bar{\hbox {y}}$] and estimated points [Y]}

$\hbox {R}^{2}=1$ signifies perfect correlation; if $\hbox {R}^{2}$ approaches zero, a correlation between the points of the data set is not notifiable (but also not forcedly disproven). – $\hbox {R}^{2}$ can be converted into t (for a STUDENT’s t-test; (Student 1908) applying the following formula.

$$\begin{aligned} \hbox {t} = \sqrt{\hbox {R}^{2}/ (1-\hbox {R}^{2}) ^{*} (\hbox {N}- 2)} \end{aligned}$$

(1d)

with N: number of data points; for null hypothesis: $\hbox {R}^{2}= 0$

However, in some cases reported below (if $\hbox {R}^{2}>0.98$; $\hbox {N}>34$), the t-test yields high numbers in every case ($\hbox {t}>40 \rightarrow$ probability $>99.9\%$ for rejection of the null hypothesis) so that in these cases, it seems to be inadequate as a discrimination criterion.

For more information on the common entities $\hbox {R}^{2}$ and t in statistics, refer e.g. to Neter et al. (2013) or nearly every other textbook on basic statistics.

3 Nickel sulphide inclusion detection in annealed glass, and trials made therewith

In 2014/2015, SG developed a non-destructive optical detection method for the identification of inclusions in (annealed) float glass in their laboratories in China and Korea (this is the trivial reason why it is given the acronym “C/K-trial”). Details of the procedure cannot be published due to the authors’ obligation to secrecy, basing on competition laws. However, it can be said that it’s about an optical method including an electronic camera system and a computer program measuring the size and the position in terms of surface coordinates and depth. Automatic image processing enables to distinguish between nickel sulphide inclusions and other glass inclusions and to differentiate from superficial contamination.

During the R&D project with acronym “C/K trial” (in contrast to the “HST-EU” [HST carried out in Europe] that’s results will be discussed in Kasper (2018b), three lots (each of several tons) of float glass potentially contaminated with nickel sulphide inclusions were examined. Besides c. 80 bubbles and refractory stones of relevant size, 140 nickel sulphide “candidates” were detected and identified by the computer program. In the frame of our R&D project, every detected inclusion was marked and cross-checked by light microscopy; in this way, the correctness of the instrument’s identification algorithms and the size measurement were proven to our satisfaction. Only one among them was identified (and later confirmed by EDX analysis) to be a partly oxidized Top Tin droplet that had cheated the instrument by imitating the characteristic NiS’ brass shine. All others were approved.

97% of the nickel sulphide inclusions (134 numbers) were detected in green (containing c. 0.6 wt% $\hbox {Fe}_{2}\hbox {O}_{3}$, 4.9 mm thick) glass originating from an identified production crisis. The other lots (common clear glass, containing c. 0.1 wt% $\hbox {Fe}_{2}\hbox {O}_{3}$) are significantly less contaminated so that only five more nickel sulphide inclusions were found in these lots. Only two inclusions were found in thicker (8 mm) glass, in all other cases the glass thickness was 4.9 mm.

Float glass is a simple soda-lime-magnesia-silicate glass of approximate composition (in wt%) 73 $\hbox {SiO}_{2}$, 13 $\hbox {Na}_{2}\hbox {O}$, 8 CaO, 4 MgO, 1 $\hbox {Al}_{2}\hbox {O}_{3}$, 0.25 $\hbox {SO}_{3}$, 0.01 to 2 $\hbox {Fe}_{2}\hbox {O}_{3}$. In the context of the present theme, among them, the sulfate content is very important because it is absolute condition for the nickel sulphide inclusion’s formation. Occasionally, other colorants than iron oxide are added. Among these, selenium is of a certain importance because if it is applied, it can accumulate in the nickel sulphide inclusions, replacing sulfur and changing the $\upalpha$ to $\upbeta$ transformation speed. An example for such an inclusion is presented in Kasper (2018a).

3.1 Parameters measured and factors influencing the measurements

The following parameters have been measured on the inclusions detected in the annealed glass.

• Position in the glass section by the detection method itself.

The automatic position measurement in the annealed glass is unfortunately not very precise because the method had not explicitly been designed to measure this parameter. Precision is c. $\pm \,0.35~\hbox {mm}$ in depth, i.e. c. $\pm \,4\%$ to $\pm \,7\%$ of the glass thickness.

Therefore, this parameter includes relatively high uncertainty. However, qualitative and semi-quantitative evaluation are possible and demonstrative.

• Size of the inclusions

Every inclusion has been sized individually by light microscopy by a laboratory operator, using an electronic size measurement program. This method is so well known and widely applied in every glass maker’s laboratory that there’s no need to describe it here. The precision of this measurement is high with c. $\pm \,~5~\upmu \hbox {m}$. The elliptic inclusion’s size is simply calculated as the average of long and short axis. Due to the observation direction (perpendicularly to the surface) and the glass production process (horizontal stretching), it can be assumed that really, these (longest / shortest) dimensions of the inclusions are observed.

• Micro-analytical composition by SEM and EDX

Some inclusions, namely those from uncolored glass that had not caused breakage, have been analyzed (up to date) in order to find out the reasons. Different SEM machines have been used in two different laboratories, but today this procedure is a well-established routine laboratory method so that there’s no need to describe it here. An early example of such analyses of nickel sulphide inclusions can be found in Barry and Ford (2001). However, technical progress has been made since that time; the method has become easier and more precise. For calibration of the EDX analysis, synthetic NiS samples of exactly known composition are used; by lack of officially available calibration standards these had been synthesized from the pure elements in the SG laboratories and cross-checked at SIMAP in Grenoble (SIMAP 2010). The synthesis method applied is the one already published in Brusetti (1980). In this way a compositional precision of $\Delta \hbox {x}<\pm 0.015$ for x in $\hbox {NiS}_{\mathrm{x}}$ is obtained and assured.

All glass samples (also those without known nickel sulphide inclusion pollution) were toughened in China in a commercial toughening furnace (Maker: LISEC) to $>80\hbox { MPa}$ compressive surface stress according to [(Glass in building 2015) EN 12150-1:2015]. The resulting compressive surface stress was measured by ellipsometry (see e.g. Fujiwara 2007) on every sample and found to be in the target range {80 MPa ... 120 MPa} in every case. Thereafter, all of the glass samples ($40 \times 50\ \hbox {cm}^{2}=0.2\hbox { m}^{2}$) were subject to a commercial HST (furnace used: TMB (Torgauer Maschinenbau) type EK 5000). The procedure applied is very close to EN 14179–1:2006, with the following key parameters.

• 3 h of heating-up ramp ($= 1.5~\hbox {K/min}$),

• 3 (instead of 2) h of holding time, but with less good temperature control ($290\pm 15)\,{^\circ }\hbox {C}$,

• 6 h of cooling ramp.

Consequently, the test conditions are even more severe than prescribed in EN 14179-1:2006, the norm applied to obtain the data of “HST-EU” to be discussed in Kasper (2018b). But the fact that 97% of the glass the nickel sulphide inclusions are detected in is only five millimeters thick, and every test pane only $0.2~\hbox {m}^{2}$ small, leads to significant differences to standard building glass as will be revealed below. In contrast to this, the green color of the glass seems not to have an impact.

3.2 Parenthesis: influence of the glass panes’ dimensions, and other factors

Before further discussing the detailed results of the C/K trial, the glass pane dimension’s impact is discussed because it seems to influence the breakage rate in HST more than presumed. Previously unpublished SG HST results (Scholze 1988) give important information. They date from the period of time when SG, in collaboration with some competitors,² started to collect data for setting up the (later so-called) EN 14179-1 and are summarized in Table 1, but they remained unpublished until now because, at the time being, their importance remained unrealized. Figure 1 shows the dependence of the measured breakage rate on glass thickness

Table 1 HST results obtained from one SG factory (1991 to 1994)

Obviously, a linear fit of the thickness dependency of the breakage rate (Fig. 1) is not reasonable because it would lead to a negative breakage rate for glass thicknesses below 4 mm. In the figure, just the connecting lines of the averages are plotted; they could eventually correspond to an exponential fit with a y-shift; due to the relatively high uncertainty of the data, the respective curve is omitted. Extrapolation is absolutely not recommended here.

Even if the HST had “only” been carried out according to DIN 18516 (the best standard available at the time being), it’s sure that in this SG factory it has been carried out with highest care and responsibility. The racks used for horizontal testing disposed of sufficiently wide space to let the hot air penetrate into every corner; 8 h of total holding time (after the reference thermocouple had reached $270\,{^\circ }\hbox {C}$) were largely long enough to guarantee more than 2 h of constant glass temperature in the respective temperature interval (by reference to the later EN 14179-1). Soaking on a rack has also the advantage that a shattering pane does not affect any other so that the number of breakages is certainly identical with the number of critical inclusions; the breakage departure points (“butterflies”) can easily be collected and inspected. In spite of these advantages, the “horizontal testing” procedure has a comparatively low productivity in comparison with modern HST ovens; this is the reason why it is no more applied today. It can be looked at to be sure that these HS-testing results are very reliable; the respective factory never faced any claims for spontaneous breakage on buildings.

A thickness dependency of the breakage rate is clearly visible in the dataset in Fig. 1. In contrast to this rather clear finding, according to Table 1, a significant impact of the glass color (colorless/iron green) is not noticeable, as well as that of the combustible used for glass melting (natural gas/fuel oil). The latter is an important observation because it reinforces the thinking explained above that fuel oil is definitely not “the” source for formation of nickel sulphide inclusions.

Fig. 1

Impact of glass thickness (and dimension) onto breakage rate in the HST according to DIN 18516. Time of data collection: 4 years (1991 to 1994). Key parameters: holding time 8 h at $(280\pm 10)\,{^\circ }\hbox {C}$ air temperature on horizontal steel racks. Total mass of glass tested 2987 tons. Total number of panes tested 120’400 thereof: green float glass 823 tons (28%). Total number of breakages recorded: 292. Average breakage rate: 1 per 10.2 tons of glass. a (circle): average breakage rate per thickness. b (block): highest/lowest recorded breakage rate per year and thickness. c (double line): error bars for $\pm 1^{*}\hbox {s}$ around (a)

The breakage rate approximately triples between 6 mm and 10 mm. Note that in practice, the average surface of the panes and their thickness increase simultaneously due to reasons of stability/statics. The breakage rates shown here are mass related, i.e. they are, under this regard, not depending on the glass pane’s dimensions due to the facts that a sufficient volume of glass was tested and that the overall breakage rate was low with only 9.97 breakages per 100 tons of glass. The glass quality (i.e. the average number of nickel sulphide inclusions) can be expected to be the same in every case because the different glass thicknesses were produced rotationally over these four years, without significant change in the furnace pull rate or the raw materials; all of the glass was produced in the same SG factory, disposing of two float lines; in one among them the melting furnace was fired with gas, in the other temporarily with fuel oil, but the raw materials used were exactly the same. Therefore, at that time, there was no good explication for the—at first sight astonishing—discovery of a significant increase with the glass thickness. But today, the findings published in Kasper (2018a) reveal how to interpret it. In thin glass with small dimensions, the nickel sulphide inclusions’ $\upalpha$ to $\upbeta$ transformation is the preponderating breakage cause, but with increasing glass thickness and size, the temporary thermo-mechanic forces increase considerably (even in horizontal heat-soaking), therewith making the breakage rate increase, too.

Another cause for the dependence of the breakage rate from glass thickness could be that the meaning of “big” nickel sulphide inclusion changes. In 5 mm glass, an inclusion’s diameter of e.g. $500~\upmu \hbox {m}$ refers to 10% of the glass thickness and even to 17% of the inner layer of the glass that is subject to tensile stress. The thicker the glass, the less critical is this direct impact of “a weak point with rough surface in the glass” [see (19) KASPER-2018 a] onto breakage prior to $\upalpha$ to $\upbeta$ transformation (i.e. breakage during toughening or shortly after, before $\upalpha$ to $\upbeta$ transformation). Therefore, some pre-matured breakages could occur before the glass reaches the HST, but in the HST, the “missing” breakages could catch up and cause higher breakage rate with increasing glass thickness. However, there’s no reason to think that this possible cause is important; seemingly causeless breakages during the toughening process are seldom in practice.

With $0.2~\hbox {m}^{2}$ and 4.9 mm thickness, the glass samples tested in the C/K trial are “small and thin” in comparison with normal building products. No breakage at all was obtained during toughening. According to what is said above and in Kasper (2018a), the mechanical impact of heat-soak testing the respective glass panes is doubtlessly much weaker than normal, according to the curve above eventually insignificant. The latter statement correlates well with the fact that refractory inclusions and bubbles, although detected, did not at all lead to breakages in the C/K trial, in contrast of the findings in a “full-size” HST, as described in Kasper (2018a).

On the other hand, this finding leads to the following interesting line of argument. It relates the argumentation of Kasper (2018a) with the findings in Fig. 1.

• (a) In “small and thin” panes, the thermo-mechanic forces in the HST play a minor role, and the nearly solely cause for breakages thereof is the $\upalpha$ to $\upbeta$ transformation of nickel sulphide inclusions. If it’s like this, the observed breakage rate of 6.2/100 t is the nickel sulphide inclusion caused baseline for breakages in HST.

  As to the C/K-Trial, the 6 mm glass panes in Fig. 1 are “small and thin” and therefore also not much subject to these thermo-mechanic forces.

  Looking at façades, Thermo-mechanic forces do not play a major role, and the nearly solely cause for this kind of spontaneous breakages is (like for thin glass in HST) the $\upalpha$ to $\upbeta$ transformation. and therefore the baseline for every glass thickness.

• (b) The breakage rate in the normal HST product mix (estimated [$9\pm 1$] mm thick) is, according to Fig. 1, c. 13/100 t. This is two times the baseline, i.e. the impact of the thermo-mechanic forces of the HST onto thicker glass leads at least to doubling of the breakage rate, compared to (1.) thin glass in HST, and (2.) every glass in façades. Reworded, the breakage frequency at the baseline is only 50% of that of the normal building product mix, and this baseline corresponds to the breakage rate on buildings.

• (c) In the paper cited above it is proven that, due to different compositions of the $\hbox {NiS}_{\mathrm{x}}$ inclusions, the temperature difference between ambient and HST more than doubles the breakage rate in the latter. Solely due to this effect, only 40% of the breakages in HST would also occur on façades.

Combining these estimates ($\hbox {P}_{\mathrm{ges}}= \hbox {P}_{1}^{*}\hbox {P}_{2}$) in order to further (not: finally) conclude on the difference between HST and Building conditions leads to the estimation that only (40% * 50% =) 20% of the HST breakages of the normal product mix would occur on façades; 80% of the breakages observed in HST would therefore be, at the limit, irrelevant for the safety of the HS-tested glass against spontaneous breakages on facades. Although this estimation is not very precise due to the considerable scattering of the breakage rates in Fig. 1, it shows how big the difference between HST and ambient conditions could be in reality.

This example-in-detail shows that the different findings published in our paper series would merit to be put into a systematic correlation in the sense of building thereof two “Bernoulli Trees” of causes, effects and correlated probabilities in order to approach a more quantitative comparison of breakage rates in both HST and on Building. However, before doing this, the facts newly presented in our papers need to be discussed officially, therewith being consolidated and, possibly and hopefully, amended and supplemented by other independent results before doing this complete approach. Also, in the sense of credibility, this approach should be made independently of the present collection of facts and partial estimations.

3.3 Result of detection trial in annealed glass (C/K trial)

Coming back to the C/K trial, in the respective ‘HST-C/K’, 35 breakages (34 in green glass, one in uncolored glass) are observed. Exclusively panes containing beforehand identified nickel sulphide inclusions broke. Explicitly, no breakages because of other reasons, i.e. from other inclusions or “causeless” ones, are observed, in full correlation of what is discussed above.

The breakage number observed refers to a breakage rate of 25% only by reference of the total number of nickel sulphide inclusions. At first sight, this seems to be low, but a coarse estimation shows that it is reasonable: Randomly, $2 x\times 21$% of the nickel sulphide inclusions are situated in the compressive zones on both sides of the glass; in the following $2 \times 12$% of the glass section, the breakage frequency is significantly reduced because the tensile stress is still comparatively low. Out of the remaining inclusions, many are too small to make the glass break. Details of this will be developed below and in Kasper (2018b). But, under the light of our results published recently in Kasper (2018a, b), referring to the different expansivity of glass and $\hbox {NiS}_{\mathrm{x}}$ species, and additionally to the high mechanical load in the HST due to thermal stress, it seems to be fully excluded that the reason for this low rate is of random-statistical nature, leading (some of) the remaining inclusions just before breakage, so that they could later break on building. The over-kill in the HST (see Kasper 2018a, b: more than a factor of two) is so enormous that this can, if at all, only be the case in seldom and exceptional cases. An approximation of the latter (c. 1 breakage in 6000 tons of glass) will be developed in Kasper (2018b).

This is important because, as already mentioned, the “normal” HST for building application is carried out with thicker glass (predominant 8 to 10 mm, total span about 6 to 15 mm) and much bigger sizes (in average c. $1.8~\hbox {m}^{2}$, partly much more) (example see chapter 2.3 here-above). This is in correlation with the finding that, except nickel sulphide inclusions, no other inclusions or big bubbles (albeit identified by the inspection method) have led to breakage in the ‘HST-C/K’, whereas in a “normal” HST this is definitely the case. The syllogism of this is that the C/K trial isolates breakages by nickel sulphide inclusions, and therefore, the breakage behavior in “a real HST of building glass” is different as will be revealed in Kasper (2018b).

Table 2 Summary of laboratory detection and tests

Table 2 summarizes the ‘HST-C/K’ results. Consequently, it seems to be “the normal case” if only ($25\pm 9$)% of the panes containing a nickel sulphide inclusion shatter in this HST, and that the majority survives. For the uncolored glass contained in the dataset, the numbers counted are too low for a simple statistical estimation, but obviously, the result at least does not contradict that of the green glass. Note well that for HST-EU conditions [in Kasper (2018b)], the conclusion is not the same; therein the breakage rate is significantly higher due to the arguments above.

Fig. 2

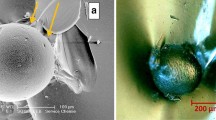
Light microscopic photographs of nickel sulphide inclusions identified by SG C/K detection method. Size = average (longest/shortest axis). Magnification the same for every picture. Arrows: decomposition halo/ream around inclusion. A–F Different sizes ($540\upmu \hbox {m}$, $290\,\upmu \hbox {m}$, $180\,\upmu \hbox {m}$, $120\,\upmu \hbox {m}$, $70\,\upmu \hbox {m}$, $35\,\upmu \hbox {m}$); among them are the very biggest and the very smallest inclusion identified. G, H Examples of inclusions found in the glass surface, all in bath side, sizes $220\,\upmu \hbox {m}$, $60\,\upmu \hbox {m}$

3.3.1 Microscopic study of the inclusions identified to be nickel sulphide inclusions

In order to understand this behavior, every inclusion identified by the laboratory identification system mentioned above was subject to manual light microscopic examination in our laboratory in China prior to thermal toughening. Figure 2 shows typical examples. Three inclusions (i.e. 2% of the total number) are detected in the bath side surface of the glass. This fact is related to gravitational settling, as forecasted in Chapter 3.3.2.2. (Position in the glass section).

Note that in every case the rough inclusion’s surface structure is clearly visible; besides the brass-like shine of the mineral³ and the exactly elliptical shape,⁴ this regular shape is an important identification criterion for the nickel sulphide inclusions, as already mentioned in Kasper (2018a) and e.g. in Karlsson (2017).

Also another observation is important: most of the inclusions show a weak brown halo that is often elongated into a brown ream (Fig. 2). This is a characteristic feature of nickel sulphide inclusions; it demonstrates that their chemical decomposition (i.e. the increase of x in $\hbox {NiS}_{\mathrm{x}}$) never stops and would lead to total digestion if the residence time in the furnace would be long enough. In other words, as already assumed earlier, nickel sulphide inclusions are, under the thermodynamic point of view, unstable in soda-lime silicate glass melts. The observation confirms what is said on nickel sulphide inclusion generation in Kasper (2018a) and other, much earlier publications of the authors’ working group, e.g. in Kasper (2000).

3.3.2 Positions of detected nickel sulphide inclusions

Due to the relatively high measurement uncertainty elucidated above, the following findings should not be overrated. Especially, extensive statistical tests are omitted; only the appearance of the curves is interpreted. Note that this whole evaluation bases on one set of data only so that over-interpretation shall be avoided. In order to prove that the observations made here are valid universally, more and independently generated datasets would be needed. However, interesting trends are observed; it would be more than interesting to consolidate these independently.

3.3.2.1 Practical findings: Positions from C/K trial

Figure 3 visualizes the measured positions of the inclusions. As already mentioned, the glass panes had been toughened and subject to the HST. Therefore, results are grouped into “All inclusions”, “Unbroken” and “Broken in ‘HST-C/K”’.

Therein, Fig. 3A shows the different data subsets figuratively as clouds of dots. In Fig. 3B, C, the cumulative curves of the positions of these three groups is shown. If “All inclusions” would be spreading uniformly over the glass section, the measured positions would be (more or less) aligned on a straight. This is obviously not the case (Fig. 3D); the difference looks absolutely systematic. Also, the difference in numbers between the upper and the lower half of the glass section is visible even in Fig. 3A. In the cumulative Fig. 3 B, C, curve (a), this generates a curvature because the concentration of the inclusions decreases continuously with the distance from the bath side.

Fig. 3

Positions of nickel sulphide inclusions detected in the glass section. a: All inclusions; b: Unbroken; c: Broken in HST-CK. Note that $\hbox {a} = \hbox {b} + \hbox {c}$. A Visualization of the positions and sizes. B Cumulative curves of positions of subsets: Curvatures in (a), “All inclusions”, due to gravitational settling ($\hbox {R}^{2} = 0.9968$); Curvatures in c, “Broken in HST”, due to higher number of breakages in center of glass ($\hbox {R}^{2}=0.9999$). C Best fit curves only, for clarity. D Linear best-fit (d; middle of triple line) with $\pm \,\hbox {s}$ straights (both outer lines)

So, this dataset is best-fitted using a 2nd degree polynomial; in view of the relatively high scattering this seems to be the best possible approach without over-fitting. A discontinuity or systematic difference or deflection from this continuous fitting curve is not visible, just a kind of voids that can be explained by random scattering (see below).

Under the statistical aspect, the linear best-fit (in Fig. 3D) yields $\hbox {s}= \pm ~5.3$ ($\hbox {R}^{2}=0.9800$), whereas the 2nd degree polynomial yields $\hbox {s}=\pm ~2.1$ ($\hbox {R}^{2}= 0.9969$). This is a significant difference, more than the double in s and remarkably better in $\hbox {R}^{2}$.⁵ Therefore, taking into account the curvature significantly amends the alignment and can doubtlessly be looked at to be reasonable, see also Fig. 3D where the linear fit including its $\pm ~\hbox {s}$ straights is figuratively compared with the real curve. Obviously, the linear fit is absolutely not satisfying.

Figure 3B, C, curve (c) shows the subset “broken in HST”. Also here, a simple 2nd degree polynomial best-fit is applied because a linear fit is not satisfying. Residual scattering estimations are $\hbox {s}=\pm ~1.00$ ($\hbox {R}^{2}=0.9998$) (linear regression); $\hbox {s}=\pm ~0.76$ ($\hbox {R}^{2}=0.9999$) (curved). Also here, the curvature is looked at to be reasonable; it’s not so much visible on $\hbox {R}^{2}$, but on s, and also obvious looking at the diagram.

Figure 3B, C, curve (b) is obtained as the difference between (a) and (c) and does therefore contain two discontinuities. Because it is derived from both other data subsets, it fits well with data subset “Unbroken”.

Close to the bath side, a void is visible in the curve; an estimated number of five inclusions seems to be missing (i.e., the ordinate intersection of the best fit curve is negative). Situated very close to the glass surface, they have most probably been lost in the float bath. As soon as they nearly reach the surface, the latter opens due to the non-wettability of NiS by the glass melt (Heinrichs et al. 1928; it’s an effect of surface energy minimization), and the inclusions are “spit out” into the tin. Nickel as well as sulfur are soluble in the liquid tin so that the inclusions are dissolved. The glass surface re-smoothens, and no visible trace is left behind if this takes place in the hot zone of the float bath. Later losses could be visible as smoothened indents, but anyway they would remain undetected because they are very small, and because this superficial defect does not fit into the detection range of the instrument developed in the SG laboratories. Even later surface opening, but with imperfect spitting, causes the appearance of those three inclusions detected sticking in the surface, see Fig. 2G, H. Obviously, they are just popping out, and in the lehr they (and the surrounding glass) are partly crushed.

This leads to the following observations and statements.

• “All inclusions”:

  Nickel sulphide inclusions are found “everywhere” in the glass. The examples in Fig. 2. show that this is also true for the lower glass surface. As expected, all superficial nickel sulphide inclusions are located in the bath side, none in the atmosphere side, and some have seemingly been lost.

  Small inclusions (c. $<140\,\upmu \hbox {m}$) are visibly more frequent than big ones.

  However, very small inclusions (c. $<50\,\upmu \hbox {m}$) are rare because of the two reasons mentioned above (limit of detection and over-proportionally fast decomposition of very small inclusions).

  Concerning the positions in the glass section, the result is surprising clear: the signature of a certain gravitational settling is visible. The cumulative curve (Fig. 3) shows a curvature, and in the lower half of the glass section (i.e. closer to the bath side of the glass), 85 inclusions (63%) are counted, whereas in the upper half it’s only 50 (37%).

  Using POISSON’s estimation for $\pm ~\hbox {s}$, the difference between these values ($=35$) is the double of the sum of both estimated standard deviations ($9+7=16$). Based on this, the difference can be looked at to be significant.

• “Broken in ‘HST-C/K”’

  Only inclusions in the center range (c. $\pm \,30\%$ from the midline of the glass) lead to breakage, as demonstrated in Fig. 3B curve b, and visible in Fig. 3A.

  Only a few bigger nickel sulphide inclusions (two among them even in the tensile zone), but many small ones survive. The latter ($<140\,\upmu \hbox {m}$) survive even in the glass center, in the highest tensile stress zone.

• “Unbroken”

  This dataset shows a ding in the middle, i.e. also this data subset shows that only inclusions in the middle zone of the toughened glass lead to breakage.

Except for the indication for gravitational settling, these findings are not really new.

But up to date, it had only been presumed that there should be more nickel sulphide inclusions in the glass than caused breakages in HST or on buildings; this had never been quantified by lack of factual observations.

3.3.2.2 A model for the explanation of the observed non-uniform position distribution

(Kasper 2018b) will point out that the localization of a nickel sulphide inclusion is not really deciding on breakage occurrence, but that the predominant factor thereon is the local tensile stress. It is therefore not always imperative to know the exact localization of the inclusions. Nevertheless, a closer look onto this phenomenon shows to be instructional, allowing interesting insight into some previously unexplained facts about nickel sulphide inclusions in glass. The same paper will also reveal that the gravitational settling observed and described in the present one is real; it is definitely also observed on datasets from Buildings and from European HST discussed there.

Although the position measurement by the C/K method is not very precise as already mentioned above, the curvature observed is explainable by a physico-mathematical model. On the other hand, this should not be overstressed; therefore, only qualitative conclusions are drawn in the following, and exact but maybe doubtable statistical analysis is omitted. The model result gives evidence for the conclusion drawn, but in order to really universalize it, the authors think that more trials and data (e.g. from different glass thicknesses) would be needed.

Settling of particles in a fluid is described by STOKES’ law; in 1851 already he derived a formula for the settling speed v of (spherical) particles under the influence of gravity and buoyancy in a viscous fluid.

$$\begin{aligned} \hbox {v} = 2^{*}(\Delta \uprho )^{*}\hbox {g}^{*} \hbox {R}^{2}/(9 ^{*} \upeta ) \end{aligned}$$

(2)

With $\Delta \uprho$: density difference; g: gravity acceleration; R: radius of particle; $\upeta$: viscosity of fluid

For details, refer to e.g. Batchelor (1967). The glass viscosity at $\hbox {T}>\hbox {T}_{\mathrm{g}}$ can well be described by the VFT (VOGEL-FULCHER-TAMMANN) equation.

$$\begin{aligned} \log (\upeta ) = \hbox {A} + \hbox {B} / (\hbox {T} - \hbox {T}_{0}) \end{aligned}$$

(3)

Therein, T is the absolute temperature; the constants $\hbox {A} = 1.86$; $\hbox {B} = 4691$; $\hbox {T}_{0}= 234$ apply for the calculation of the temperature depending viscosity [$\upeta$ in dPa*s] of a standard float glass. The constants, in turn, are calculated from the known chemical composition of the glass; for more details on viscosity calculation see e.g. Rawson (1980) or Scholze (1988).

In addition to these purely physical laws, the following frame conditions are fixed for the model.

• Temperature levels and gradients are taken from real glass production data.

• Glass: Thickness 5 mm (like in C/K-trial); production rate 500 t per day; ribbon net width 3.21 m;

  • Density $2500\hbox { kg/m}^{3}$.

  • Time dependency is calculated from these parameters.

• Nickel sulphide inclusions:

  Density $5350\hbox { kg/m}^{3}$; particles are spherical.

  As model input, uniformity in terms of size and position is postulated. No inclusions smaller than $35\,\upmu \hbox {m}$ in diameter are observed due to accelerated oxidative decomposition in the glass melt (and, eventually, the imperfection of the measuring instrumentation), see Kasper (2018a).

• No residual nickel sulphide inclusions $>630~\upmu \hbox {m}$ (value from practical observation). In fact, out of 457 nickel sulphide inclusions documented in the SG laboratories, only one is $>600~\upmu \hbox {m}$, and only three $>500~\upmu \hbox {m}$ [present paper and Kasper (2018a, b)].

• The model output, namely the cumulative curve of the positions of the inclusions over the glass section, has to fit with curve Fig. 3A.

  If this would be impossible using an adequate number of free parameters, the model would be disqualified. However, see below, fitting is reasonably possible.

• Information from glass melting furnace (exact glass flows and temperature profiles) is incomplete regarding the present model; reasonable assumptions and, naturally, some simplifications have to be made.

  In the melting zone of a glass furnace, strong mixing due to intentional induction of vortices is observed. Therefore, it is considered that the zone of the furnace responsible for the settling phenomenon is mainly the channel, i.e. the last zone of the furnace upstream the casting point into the float bath. The glass flow in this zone of the furnace is laminar and parallel-lamellar (i.e. no mixing takes place and the vertical flow velocity is zero), and the temperature therein decreases linearly from a temperature that is not exactly known (around $1200\,{^\circ }\hbox {C}$) to casting temperature of $1050\,{^\circ }\hbox {C}$. The (physically existing) vertical temperature gradient is disregarded for the model.

  In the channel, the glass “sees” the walls (i.e. the “ribbon width” is significantly smaller) and therefore, the glass thickness is much higher. These factors counteract the higher settling speed due to the higher temperature level. Additionally, the longitudinal temperature gradient (in relation to the glass thickness) is different from the one in the float bath.

  At the casting point, the thickness of the glass jumps down abruptly to glass thickness, and also the temperature makes maybe a jump down. When the glass passes under the tweel, some intentional flows (important for surface quality: they skim both surfaces) might have an impact, but most of the particles in the bulk remain more or less in their position relative to each other and to the glass section’s vertical coordinate.

  These impacts at the casting point are not calculable in detail within the present model; It is simulated in a simplified way by allowing a jump of the settling speed at the casting point (“s” in diagrams).

• Float bath temperature is going down from $1050\,{^\circ }\hbox {C}$ to $600\,{^\circ }\hbox {C}$; a linear gradient is supposed.

  Within the float bath, glass thickness is not everywhere the same. But in the places where the thickness is higher, propagation speed is lower, i.e. residence time is proportionally higher, so that the thickness effect is self-compensating.

• Conditions in the float bath are supposed to be rather exactly known (“fix parameter”), those in the channel are less known and therefore adjusted to the observations (used as “free parameter”).

• Settling does not only cause a change in the apparent position distribution, but also a loss of inclusions. The following imagination helps to understand.

  If (in a thought experiment) a number of equally-sized inclusions is aligned vertically in the glass section, and their settling is observed (but disregarding their eventual interaction), every inclusion sinks down with the same speed. When the topmost particle has settled to, e.g., 1/2 of the glass section, at the same time 1/2 of the total number of the particles has accumulated on (or broken through if there’s a possibility) the bottom surface (bath side) of the glass. In the channel, these stick to the channel floor because temperature is lower there, viscosity is very high and horizontal glass velocity very low; consequently, there is time enough for entire digestion by the glass. Concerning the loss mechanism in the float bath, see comments to Fig. 3.

  For the model discussed here, the following conclusion thereof is important. If settling calculation results in more than 100% of the glass thickness, all such inclusions (e.g. exceeding a certain size) are lost and not observable anymore in the glass. If it’s less than 100%, the respective inclusions appear in the glass (eventually only in its lower part) in a number that is proportional to the settling height.

In summary, this indicates that the nickel sulphide inclusions’ settling speed is fixed by physical parameters only (viscosity/densities/glass composition/temperature levels and gradients). The glass production process fixes the proportionality between glass thickness and residence time in the float bath. The biggest ($630\,\upmu \hbox {m}$) and smallest ($35\,\upmu \hbox {m}$) nickel sulphide inclusion ever observed are used to set the limits of sizes to be obtained in the model, whereof the small inclusions don’t really play a noticeable role.

Finally, only three free parameters are needed in the model to adjust the calculated position distribution curve to the one observed (Fig. 3A): One figure to adjust the maximum size (explicable to be relative to the residence time of the glass in the channel), another one to fix the proportion between the losses in float and channel and a third one to fit the curve maximum (situated on the bath side of the glass) with the curve observed in reality.

In a first step, the settling speed as a function of temperature is calculated; Fig. 4A shows the result for selected particle sizes of $500~\upmu \hbox {m}$ and $200~\upmu \hbox {m}$, respectively. For a given particle size, the curve form is dominated by the glass viscosity evolution. Obviously, the inclusion’s diameter has a big impact on settling velocity, too. Settling seems to be negligible at temperatures below $950\,{^\circ }\hbox {C}$.

Figure 4B shows the settling in relation to the local glass thickness for the example of a nickel sulphide inclusion of size $200~\upmu \hbox {m}$.

Under respect of the frame conditions above, two separate curves for the settling are obtained, upstream and downstream the casting point. Both curves show settling as a function of temperature under respect of the residence time in the respective region (estimated for the furnace/known for the float bath). Integration over all temperatures results in one figure for each region, namely the loss due to settling. According to the model, it’s only 1% in the float bath, but 15% in the furnace, corresponding to a total loss of 16% with reference to a (hypothetically) primarily uniform position distribution for the nickel sulphide inclusions of $200~\upmu \hbox {m}$. For other sizes, the figures are different, but the principle is the same, and there’s always much more loss in the furnace than in the float bath.

Fig. 4

Model calculation to explain the curve form of Fig. 3 a. s: Casting point (entrance of float bath). A Settling speed, calculated combining Eq. (2) with Eq. (3), for two example sizes, (a) $500\,\upmu \hbox {m}$; (b1) $200\,\upmu \hbox {m}$. B Settling distance in relation to local glass thickness (curves b1 and b2), size $200\,\upmu \hbox {m}$. Integration over temperature yields the values of the integral settling in both sectors of the diagram (see comments in text). b2: Settling within float bath; b3: Settling in furnace. C Settling as function of size (integrated over temperature in sector). fl: Settling in float bath only; co: Combined settling including float and furnace Values $>100\%$ (of the actual glass height) are losses (see text). D Simulation of occurrence curve as the integral over all sizes, relative to glass thickness. g (- - -) : Curve from Fig. 3 (a); h ($\varvec{\bigcirc }$): Circles, modelling result. k: Reference: Straight for uniform position distribution and no losses due to settling

Figure 4C shows the settling (integrated over temperature, as shown in Fig. 4B for the example of $200~\upmu \hbox {m}$) as a function of all possible inclusions’ sizes. The scale is inversed in order to draw figuratively the physical movement direction of the particles. Values (close to) zero mean that settling is not noticeable, 100% (and more) signifies that the respective inclusion is lost. According to the thinking above, the percentages in between these limits signify at the same time the settling distance of the uppermost possible particle from its starting point (the glass’ atmosphere side) and the lost particles broken through the reverse (i.e. the bath) side of the glass.

If a noticeable settling would only occur within the float chamber (curve fl), the observable size of the nickel sulphide inclusions would have to be up to $3000~\upmu \hbox {m}$; this value is obtained by extrapolation of curve “fl”. This is obviously not the reality; even inclusions bigger than $500~\upmu \hbox {m}$ are rare, see below. In order to explain the observation of maximum inclusion size of $630~\upmu \hbox {m}$, it is mandatory to hypothesize that inclusions are also lost in the melting furnace (curve co: combination of float and furnace). Only by adding up both losses, the maximum size can be fitted to real observation.

Figure 4D shows the fitting result between curve Fig. 3A and the model. Using three free parameters only, and applying the simplest hypothesis that at the beginning size and positions of the nickel sulphide inclusions are uniform, a visibly perfect congruency is obtained. Especially, the non-trivial dissymmetric curvature of the real curve is reproduced properly. The integral loss by settling below $630~\upmu \hbox {m}$ is calculated to be 37% of the original number.

The reverse conclusion of this is that settling due to gravity is the root cause for two basic properties of nickel sulphide inclusions in glass. On the one hand, the observed non-uniform position distribution of the nickel sulphide inclusions in the glass section is explained.

On the other hand, and also this had up to date been entirely unexplained, the reason for their size limitation in the glass is detected. Obviously, every “too big” inclusion runs aground, either in the furnace or in the float bath. Due to this effect, the original size distribution curve, however it would be before, is truncated in a way that only the smaller inclusions can survive, and that the relative number of survivors increases with decreasing particle size.

3.3.3 Sizes of detected nickel sulphide inclusions

The sizes of the inclusions are measured with much higher precision than the positions, as already pointed out above. Therefore, more extended statistical analysis of the findings makes sense. In order to quantify the experimental findings, two different statistical methods are applied. According to common textbooks on statistics, the simplest method is plotting histograms and comparing them. Because this does not allow quantitative evaluation and the calculation of relative breakage probabilities, the datasets are best-fitted applying or involving, as already pointed out above, the two-parametric Log-Normal distribution.

3.3.3.1 Practical findings: Sizes from C/K trial

Figure 5 shows, as an example, the histogram evaluation of the dataset “All inclusions”, using classes of $50~\upmu \hbox {m}$.

Fig. 5

Histogram of dataset “all inclusions” from C/K trial in linear (at left) and logarithmic-linear scales. Black columns: Counted numbers. Grey columns: $\pm \,\hbox {s}$ (in numbers) calculated using Eq. (1b) [POISSON]. Red line: Exponential best fit curve, excluding class $<50\,\upmu \hbox {m}$. Dotted red lines: $\pm \,\hbox {s}$ calculated from least square statistics, Eq. (1a)

With exception of the classes of the smallest ($<50\,\upmu \hbox {m}$) and maybe the biggest ($>500\,\upmu \hbox {m}$) inclusions, all counted numbers per class seem to match with a decaying exponential curve. The scattering $\pm ~\hbox {s}$ calculated using Eq. (1b) and the one calculated from the variance of the exponential best fit curve, Eq. (1a), seem to fit well (note that only the $\pm ~\hbox {s}$ level is shown in the figure). Both tolerances overlap, revealing that they are equivalent and applicable, and that the dataset is statistically consistent. The classes $>350\,\upmu \hbox {m}$ only contain a small number of members and are therefore subject to high “statistical scattering”.

However, the class of very small inclusions obviously does not match. At first sight, much more inclusions would be expected in it, e.g. (by extrapolation of the exponential best fit curve) 50 or even more. This lack is doubtlessly due to both the accelerated decomposition of very small inclusions and the detection limit of the detection method applied; these influencing factors have already been discussed above. This will further be discussed in Chapter 3.3.3.2 below.

The qualitative comparison of the histograms of the datasets “All inclusions” and “Broken in HST”, Fig. 6, reveals interesting facts.

• No breakage at all is found in the class $<50\,\upmu \hbox {m}$, as observed earlier and predicted by finite element model calculation, e.g. in Bordeaux et al. (1997), Swain (1980), and Schneider et al. (2012).

• Very low breakage rate in class ($75\pm 25$) $\upmu \hbox {m}$, only 3% (1 out of 34), however with low statistical significance (estimated $\pm 2$ numbers).

• Breakage occurrence raises to nearly 100% for big inclusions ($>450\,\upmu \hbox {m}$), but none of these seems to have been situated in the compressive stress region of the glass (see Fig. 6) Also their absolute number is small (7 in total), so that, only taking into account this counted number, statistical significance is low.

Obviously, interesting qualitative conclusions can be drawn from the histogram evaluation, and this approach is an intuitive way to make the results “comprehensive”. However, this evaluation is not really satisfying because it does not allow quantification. Therefore, on the basis of what is already said in the introducing appreciation of the Log-Normal function and on the fact that the decaying part of the data in the histogram can apparently be fitted well by an exponential function, the Log-Normal function, multiplied with the total number in the dataset, is used for the best-fit, making the evaluation continuous and avoiding subjective choice of the interval size. Figure 7 shows the result for the datasets discussed up to here⁶$^,$⁷. Fitting is done according to what was said after Eq. (1a1a).

Fig. 6

Comparison of datasets from C/K trial. A Absolute histogram (numbers). B Relative histogram (percentiles). In A and B White columns: “All inclusions”. Black columns: “Broken in HST”

Fig. 7

Log-Normal approach to datasets from C/K trial. A “All inclusions” ($\hbox {R}^{2}=0.9927$); B “Broken in ‘HST-C/K”’ ($\hbox {R}^{2}=0.9952$) ($^7$). a: Best fit curve, cumulative ($^8$), based on the Log-Normal function (see text). a1: Take-off of curve a (explication in text). b: Derivative curves (drawn in arbitrary units) belonging to a, showing figuratively the size spectrum (numbers per size). b1: Maximum of size spectrum b. Error bars $= \pm 3^{*}\hbox {s}$ (from least square fit) [a $\pm 7.5$ ($\pm 14\%$); b $\pm 3.3$ ($\pm 18\%$)]. Error bars in y direction not shown for clarity of diagram

The continuous evaluation allows the following deductions and statements.

• Applied in this way, the cumulative two-parametric Log-Normal curve ($\hbox {EXCEL}^{\circledR }$ function: LOGNORM.VERT) allows a visibly good fit for all datasets in the present paper(see also those below).

  Introduction of a third parameter (x-shift) definitively does not lead to amelioration.⁸

• According to Eq. (1a), two-dimensional least-square minimization method is used for data alignment; it leads to the estimation of the characteristic values $\upmu$ and $\upsigma$ of the individual Log-Normal curves.

• At the same time, Eq. (1a) allows deriving the mean standard deviation (i.e. the mean deviation between the dataset’s individuals and the fitting curve in both x and y direction simultaneously), and hence it is an estimation of the significance of the best-fit of the cumulative log-normal curve for the dataset.

  The respective coefficients of determination are close to the unity, $\hbox {R}^{2}>0.99$ in both cases, proving the good quality and adequateness of the fitting.

  • The related derivative curve can easily be plotted in $\hbox {EXCEL}^{{\circledR }}$, using the same best-fitted parameters. Mathematically, the maximum of this curve is normally not identical with the average, but an important (and apprehensive) characteristic of the curve form, in addition to average and median. In order to keep things easier, this maximum is just listed for comparison without mathematical interpretation. Other parameters of the derivative are not used here.

  • Both the cumulative and the derivative curves (and their characteristics in terms of $\upsigma$ and $\upmu$) are abstractions of the respective different datasets.

    Consequently, they can be used to compare the datasets, e.g. by listing their key values in a table, or making calculations and diagrams using the functions instead of the data points.

From these curves and datasets, the following key values are collected for comparison:

• (1) Number in dataset ,average and median of sizes, maximum of the derivative curve (see remarks above).

• (2) “Take-off point” of the cumulative curve.

  It is clear that, because the simple two-parametric Log-Normal function is applied to describe the datasets, all of the respective cumulative and derivative curves mathematically begin exactly at x = 0. But in their first part, the function values (y; numbers) are very close to zero; at a certain x ($\upmu \hbox {m}$) value they start to raise visibly. Figuratively spoken, this “take-off point” depends on the position of the inflection point of the curve and of its steepness. It is an important characteristic of a given dataset. In the case of, e.g., breakages in HST, it shows (with a certain uncertainty, naturally) the size limit below which the inclusions are no more dangerous. Adopting the $\pm \,3\upsigma$ criterion of the GAUSSIAN (99.7% of the members of a dataset are located within this interval 0.15% are lower, 0.15% higher), this limit (of occurrence, of breakage etc.) of 0.15% is defined arbitrarily to be the take-off point. It is calculated using the Log-normal curve from the best-fit of a given dataset, assigning a characteristic inclusion size to said function value of 0.15%.

  Naturally, it’s also possible to use the first measured point (smallest size) of a dataset to characterize the same in view of its lower limit. But this criterion is subject to much higher statistical uncertainty. The statistical relevance of a criterion derived from a whole curve, therewith taking into account all measured data, is much higher.

  According to this definition, only one out of a dataset of 667 members should (statistically) be found below the calculated 0.15%-limit. In a set of 140 or even only 35 members as in Fig. 8, the chance to find one inclusion below this limit is therefore rather low, but because it’s a statistical limit, it’s not impossible. In the concrete case of the dataset “broken in HST”, the calculated take-off point is $55~\upmu \hbox {m}$, the smallest inclusion $50\,\upmu \hbox {m}$, but both are identical within the statistical uncertainty ($\pm \,8\,\upmu \hbox {m}$) resulting from the curve fitting.

• (3) Precision of the results (scattering $\pm ~\hbox {s}$ around the best fit curve)

The precision is derived from the least-square fitting calculation between curve and respective measuring points, $\pm \,~\hbox {s}$, applying Eq. (1a) and the following description.

$\hbox {R}^{2}$ and t are then calculated using the variations obtained in this best-fit, applying Eqs. (1c) and (1d). Finally, the probability of rejection of the null hypothesis is taken from respective published spreadsheet.

Vertical error bars in the figures (length: $\pm \, 3 ^{*} \hbox {s}$) represent 99.7% of the scattering of the data around the best fit curve. Indeed, no measured point is found outside this frame, i.e. there’s no obvious systematic error. For clarity, error bars in x direction are not shown in the diagram, but listed in the following Table 3; it compares the key values of the data subsets.

Table 3 Key values of datasets from C/K trial

Fig. 8

Size spectrum, derived from position spectrum modelling in Chapter 3.3.2.2. R: Reference: Size spectrum (Fig. 7) measured and represented by Log-Normal function based curve of “All Inclusions”. a: Size spectrum, only settling by gravity [(co) in Fig. 4] accounted for. b: Multiplication of (a) with function [1–25 $\upmu \hbox {m}$ / x ; {x : size in $\upmu \hbox {m}$} ]. c: Multiplication of (b) with Logistic function [ $\hbox {k} = 0.0125$ ; $\hbox {x}0 = 140\,\upmu \hbox {m}$ ] Percent values: Relative surface between the curves

Consequently:

• The t-test reveals that all interesting key parameters of the different data subsets differ significantly. With a probability of >99.9% all values A / N and B / N (not shown in table) are different.

  • Dataset “B” (broken) is much more coarse-grained than “A” (all) and “N” (not broken).

  • This difference is significant for every parameter including the “take-off point”.

• The relation “B”/“N” is $> 2$ for all of the four relevant key values. It increases with decreasing size value, i.e. the differences are stronger for small inclusions.

This signifies that there’s a clear difference. For the first time in literature it’s proven, although it’s logical and had been presumed before, how the breakage occurrence depends on the size of the inclusions. The smaller ones are more harmless; the inclusions causing breakage are the bigger-sized. In average those causing breakage show the double diameter in comparison with the harmless ones (relation N/B). The very small (statistically, according to 3 $\upsigma$ take-off criterion, $< 55\,\upmu \hbox {m}$) do not cause breakage at all. This is in good correlation with fracture mechanical calculations and other previous experimental findings [e.g. (4) BORDEAUX–1997; (30) SWAIN-1980; see also the review paper by (13) KARLSSON-2017] postulating a respective threshold of c. $50\,\upmu \hbox {m}$.

3.3.3.2 Size spectrum derived from the model of non-uniform position distribution in the glass section

The settling model developed above (which is not a statistical model but a model based on physics) can also be used to make some predication on the size spectrum of the nickel sulphide inclusions.

The following calculations are a first trial (and as such, possibly subject to incompleteness or mistakes because no literature reference at all exists to make a comparison) to explain the size spectrum found experimentally in the C/K-Trial (and described by a function), based on natural-scientific laws of physics (STOKES, above) and chemistry (aspects of kinetics of decomposition of particles under biphasic condition).

Also, it the author’s mind, the losses described hereunder do not feedback a lot onto the position spectrum. The latter is only defined by gravitational settling. Losses due to other effects eliminate some more inclusions of any size, but independently of their position. To say it figuratively: the sinking “string” of inclusions is perforated, but the remaining members continue to sink down.

The following should be looked at to be a discussion contribution rather than absolute truth. Note well that this is the first trial into making such an evaluation: It is based on one dataset only. More datasets from other working groups are needed for cross-check. The following is therefore also meant to be an animation to carry out such trials, and it proposes a principal way how to evaluate them.

• The basis: Gravitational settling (estimated loss: 37%)

  This is curve (co) in Fig. 4. It only takes gravitational settling for the shaping of the position spectrum and the estimation of particle losses into account. But obviously, although leading to a good prediction of the inclusion’s positions, it does not lead to a correct prediction of the particle size spectrum observed.

  This curve marks the basic loss of the inclusions as a function of their size. It decreases steadily and without inflection from the very small to the biggest sizes, i.e. the very smallest should also be the most numerous survivors.

  The end of the curve on the right hand side is hypothesized to be the biggest size of a nickel sulphide inclusion ever observed to the author’s knowledge. Naturally, this assumption could be wrong; however, above, it leads to a good fitting result for the position’s spectrum observed in reality.

  The logical conclusion thereof is that, in addition to gravitational settling, also other effects must play a significant role in this curve shaping.

• The reference

  (i.e. the representation of the size spectrum by a mathematical function) is the density curve of “All Inclusions” plotted in Fig. 7A. In Fig. 8, this curve is called (R ${\bullet }~{\bullet }~{\bullet }$).

  The reason for this name change is to prevent confusion with its statistical meaning. In this chapter, it cannot be understood to be a statistical function. We use it to describe (i.e. to draw) the real measured size spectrum, whatever the functional background thereof may be. In the present case, it is (logically, see above) based on a best-fit of our dataset with the aid of the Log-Normal function, but this is not condition; the respective function could also be another one not having, coincidentally, at the same time an important meaning in statistics, it could also be e.g. a polynomial of higher order or whatever else, just fitting the dataset well.

  So, the curve obtained by additional effect’s impacts from [(co) of Fig. 4] should fit with curve (R ${\bullet }~{\bullet }~{\bullet }$) as good as possible.

• Additional effect: Faster chemical decomposition of smaller particles (estimated loss: 15%)

  It is known from the practical findings above that there’s a void in the size spectrum on the side of the small inclusions, i.e. c. $<50~\upmu \hbox {m}$, see histogram “All inclusions” in Fig. 3. The respective “take-off” criterion is $18~\upmu \hbox {m}$ (Table 3).

  As already discussed above, this truncation should follow a hyperbolic law if the lack of sensitivity of the measuring instrument does not play a role. But also if it does, as the successful result shows, the hyperbolic approach makes sense for description.

  In order to calculate the fraction of remaining inclusions after this truncation, curve (a) of Fig. 8 is simply multiplied with the function [1 – FF / x ] in order to fit the left hand side of (R ${\bullet }~{\bullet }~{\bullet }$).

  $\hbox {FF} = 25~\upmu \hbox {m}$ is the empirical fitting factor, and the variable x is the size of the inclusions in $\upmu \hbox {m}$.

  The meaning of FF is that inclusions smaller than FF are dissolved entirely (calculated sizes are negative; the stochastic fade-out of the curve is not calculable in this way); between FF and circa its double the number of residual inclusions rises steeply, then it nearly turns to constancy.

  The result of this multiplication is curve Fig. 8B.

  The estimated loss by this effect is 15% of the initial number. This signifies that this effect is rather weak in comparison with the others.

• Additional effect: Random influence (estimated loss: 35%)

  The fact that the right hand side of the diagram, curve (b) is by far not yet fitting with (R ${\bullet }~{\bullet }~{\bullet }$) indicates that there’s another impact factor that is not yet taken into account. This factor leads to a fade-out of the reference curve instead of the abrupt end predicted by the settling theory, and also, its curvature is concave instead of convex.

  This indicates that some kind of random influence, including fade-out, overlays. Whatever the cause is, it leads to the fact that relatively more big than smaller inclusions disappear, additionally to gravitational settling.

  In order to fit the curves together, multiplication of curve Fig. 8B with different (reverse) sigmoid functions was tried out. A good result was already obtained using the basic logistic curve with characteristics [$\hbox {k}=-0.0125$; $\hbox {x}_{0}=140~\upmu \hbox {m}$].⁹ Some others, as e.g. the GOMPERTZ function, revealed an even better fit, but because, at the moment, no reason can be given to apply a more complicated procedure, this simplest fit is shown here as an example in Fig. 8C, possibly to be refined by future R&D.

  The estimated loss by this effect is 35% of the initial number. This signifies that it is a strong effect.

Basically, this fitting trial does not prove that the assumptions made are correct. This would contradict the principles of logics and would also not be a proof if the fitting would be perfect. Nevertheless, in view of the simplicity of the mathematical operations applied, it is surprising good. A misfit is mainly observed at higher particle sizes. This could reveal another impact factor actually still not yet taken into account or imperfection of the dataset.

As a physical explication, this random impact factor probably bases on the following effect. The author shows in Kasper (2018a) that significant losses of nickel sulphide inclusions occur because their chemical composition shifts, with increasing sojourn time in the glass melt, towards a composition with increasing vapor pressure. Consequently, if the composition reaches a critical condition in a critical environment (the latter mainly characterized by its temperature), self-destruction (“explosion”) is the consequence. Out of the reasons discussed here-above (chapter 2), this influence is a random one, making disappear inclusions of any size. However, if a relatively high number per size of inclusions is subject to this effect (i.e. in the core area of the size spectrum), this loss appears to be stable, around 50%. If, in contrast, the absolute number per size is small (i.e. at sizes x $>400~\upmu \hbox {m}$), random becomes more important, leading to a “tailing” of the curve. Note that in the dataset discussed here, the total number of nickel sulphide inclusions $>400~\upmu \hbox {m}$ is only eight.

In summary (Table 4), the losses seem to summarize to about 85%, i.e. only c. 15% of the primary nickel sulphide inclusions survive the glass melting process. This correlates well with the author’s finding already published in 2004 (Kasper 2003) that the survival quote of artificially generated nickel sulphide inclusions in laboratory glass melts is also low, depending on the melting conditions. For example, at $1450\,{^\circ }\hbox {C}$ and 12 h of melting time or at $1550\,{^\circ }\hbox {C}$ and 2 h, the yield of nickel sulphide inclusions was 8% to 16% only.

Table 4 Losses of nickel sulphide inclusions during glass melting

In conclusion, the present physical modelling gives interesting insights in the way nickel sulphide inclusion are located and “sieved out” in the glass melting furnace and in the float bath, in a way that only a medium size arrives in the final glass whereas the smallest decompose quickly (ore remain undetected), the biggest run aground, and a non-negligible fraction decomposes spontaneously under its own vapor pressure. However, it should be noted that these hypotheses, also because they have never been published before, and because they rely on one single dataset, cannot be looked at to be proven facts. The authors would like them to be understood as a discussion contribution to be verified by future R&D.

3.3.3.3 Breakage ratio as a function of size of the nickel sulphide inclusion

Going back to the practical findings in the C/K trial, the notable observation is made that all of the seven biggest inclusions caused breakage. This leads to the assumption that for these (i.e. $>450\,\upmu \hbox {m}$, see Fig. 6) the breakage ratio approaches 100%. This assumption correlates well with the authors’ observation that big bubbles and refractory stones (mostly $>500~\upmu \hbox {m}$) also cause breakage in normal “HST-EU” (but not in the C/K trial !) as pointed out in (Kasper 2018a); this signifies that from around this size, the nature of the inclusion does not really matter anymore¹⁰; the rugged surface of the nickel sulphide inclusions [see (19), too] doubtlessly makes them more vulnerable than a smooth bubble of the same size, even before $\upalpha$ to $\upbeta$ transformation.

However, it seems to be logical that above a certain size limit correlated with the glass thickness, this breakage ratio must asymptotically reach 100%. Any inclusion with a diameter of more than 1/5 of the glass thickness is (at least partly) situated within the tensile stress zone [for memory: the compressive zone’s thickness is 21% below each surface], and the dissymmetric stress field around this kind of inclusion makes the glass very vulnerable. In the example of the present paper 1/5 of the glass thickness refers to c. 980 $\upmu \hbox {m}$, i.e. just the double of the biggest inclusion really observed here.

With this thinking, Fig. 9 is compiled, sketching the relative breakage ratio curve as a function of the nickel sulphide inclusion’s size. It’s just the division of the normalized function values [(“Broken in HST”)/(“All inclusions”)] according to the argumentation above.

Fig. 9

Breakage ratio ${B}_{{R}}$ curve as function of nickel sulphide inclusion’s size, derived from C/K trial data. a: Log-Normal curve “All inclusions”, Fig. 7, take-off at $18\,\upmu \hbox {m}$. b: Log-Normal curve “Broken in ‘HST-C/K”’, Fig. 7, take-off at $55\,\upmu \hbox {m}$. $\hbox {B}_{\mathrm{R}} = \hbox {b} / \hbox {a} =$ Relative breakage ratio in %, reaching 97% for size $550\,\upmu \hbox {m}$. Arrows indicate respective scale with the unity as the maximum in every case. Error bars $= \pm 3^{*}\hbox {s}$ (as in Fig. 7, applying error propagation law), [$\pm 3^{*}\hbox {s} =\pm 9.0\%$]

Visibly, the conditions above are fulfilled: Following a sigmoid (Log-Normal-like) function, very low breakage ratio for small inclusions (e.g., only 1% of the $50~\upmu \hbox {m}$ inclusions lead to breakage), still small below $100~\upmu \hbox {m}$ (10%), reaching 50% for $205~\upmu \hbox {m}$ and then, increasing asymptotically, showing $>90\%$ at c. $400~\upmu \hbox {m}$.

The breakage ratio curve obtained here can eventually be used in a fracture-mechanic model (maybe in the frame of a complete BERNOULLI tree model of spontaneous fracture) to estimate the breakage occurrence for a given nickel sulphide inclusion population, using the functions elaborated. But note that for this generalization the frame conditions must also be taken into account. Other influencing parameters are:

• The temperature difference between ambient (temperature depending on the place the building is situated) and HST (temperature standardized, but lower temperature applied e.g. in Japan/see ISO 20657:2017/on-line test: range 220–$300\,{^\circ }\hbox {C}$ [until 2016], now, range 220–$270\,{^\circ }\hbox {C}$);

• The inclusion’s position:

  In the present C/K dataset, the overall breakage number is not very high in the statistical sense, therefore not very precise and, strictly speaking, it is only valid for glass thickness 4.9 mm. For exact calculation, more R&D is needed to determine the factors and curves more exactly also for other glass thicknesses;

• Chemical properties:

  Besides different x in $\hbox {NiS}_{\mathrm{x}}$ (see Kasper 2018a), inclusions could contain more iron due to green glass environment (Kasper et al. 2003)); this will be specified by analyzing the remaining nickel sulphide inclusions from the unbroken panes in a future R&D project.

• The thermo-mechanic impact of the HST depends on glass thickness, pane size and position in the stack. Some information on glass thickness’ (see Fig. 1) and panes’ size influence (see Fig. 2 and its explanation) is available, but this is only one single dataset, generalization is still missing.

These unknown factors are partly hidden in the present dataset, partly they are inapplicable onto it, so that the application of this result in a complete simulation of spontaneous cracking is questionable for the case of normal (i.e. clear, thicker etc.) building glass, but it could be a first order approximation. At the reverse, to make it fully applicable, the respective influencing parameters should be better identified, differentiated and quantified by future R&D.

Figure 10 comes back to the histogram evaluation. In order to make present findings more figurative, therein, the relative breakage ratio determined by both different evaluation methods is compared.

Visibly (and logically), the scattering is much higher if the histogram’s single columns are evaluated. This is due to the small individual numbers in every class. But the key messages of both evaluating approaches are the same, as already discussed above. Consequently, both evaluations lead to the same result; no contradiction is visible.

On the other hand, this comparison shows the advantages of the complete-curve evaluation method, obviously leading to a significantly more meaningful result because the integral number of observed breakages defines residual scattering through least-square fitting.

Fig. 10

Breakage ratio ${B}_{{R}}$ from C/K trial data. Background histogram (both A and B): Inclusions identified in C/K-trial in classes of $50\,\upmu \hbox {m}$ (Fig. 6). A Relative breakage ratio (BR) estimated from breakages in individual classes of $50\,\upmu \hbox {m}$. a: BR = (number of breakages)/(total number in class) b: upper confidentially limit according to Poisson’s estimation: $\hbox {B}_{\hbox {R}}/\hbox {U} = \hbox {B}_{\hbox {R}} + \hbox {s}$. c: lower confidentially limit: $\hbox {B}_{\hbox {R}}/\hbox {L} = \hbox {B}_{\hbox {R}} -\hbox {s}$. B, curve d: Ratio estimated using Log-Normal function fitting (% scale at right) acc. to Figure 9 Error bars: $\pm \,3 ^{*} \hbox {s}$ from least square fit & error propagation ($\pm \,9\%$)

4 Summary

The present paper is part two of a small series of (previously) three publications on spontaneous breakages of toughened glass. In part one (Kasper 2018a), we deal with the detailed effects of the crystallographic and physical properties of the nickel sulphide species contained in those inclusions; we find that solely under this aspect, only c. 40% of the breakages in a Heat Soak Test (HST) according to, e.g., EN 14179-1:2006, would be physically able to cause a breakage in a façade.

The present paper partly builds up on these findings. Mainly, it describes and evaluates the findings of a nickel sulphide inclusion detection trial (“C/K-trial”) carried out at SG R&D. Before going into these details, the basics of nickel sulphide inclusion generation from nickel containing steel particles (other sources can reasonably be excluded) are mentioned in favor of general understanding of this process, but also in order to make understand why the evaluation method applied (dataset fitting with the aid of the Log-Normal function) is so successfully applied here.

The parameters measured in the C/K-trial are their size and their position in the glass section relative to the bath side of the glass. Only two of the 140 inclusions were found in thicker (8 mm) glass, in all other cases the glass thickness was 4.9 mm. After detection, every sample was subject to a HST according to EN 14179-1 leading to a total breakage rate of 25% (35 sheets) by reference to the detected nickel sulphide inclusions. Under the point of view of known facts, this is not a low number because (statistically) 42% are situated in the compressive stress zone of the toughened glass, and many among the remaining are too small to cause breakage. In order to rate this finding more correctly, the impact of the glass thickness onto the breakage rate in the common HST is revealed from older, formerly unpublished HST breakages at SG. The respective dataset bases on 3078 t of glass tested within four years, and 307 breakages recorded therein. It reveals that nor the glass color (uncolored/green) neither the kind of combustible (oil/gas) shows a significant impact onto the (mass-related, i.e. virtually thickness-independent) breakage rate, but the glass thickness does. Thicker glass breaks significantly more frequently. Reasonably assuming that the nickel sulphide inclusion’s occurrence does not depend on glass thickness, the conclusion thereof is that the HST itself acts differently onto glass of different thicknesses. This statement reinforces the findings on the thermo-mechanical impact of the HST already published recently in Kasper (2018a). On the other hand, it also makes clear that the findings in the HST-C/K within the C/K-trial cannot be directly applied onto the standard HST-EU for (systematically larger and thicker) building glass because in the HST-C/K, thermo-mechanic forces only play a minor role.

The evaluation of the C/K-trial yields the following results.

The position distribution of the inclusions in the glass section shows the signature of gravitational settling. The respective curve is approximated by a simple 2nd order polynomial. Model calculation using STOKE’s settling law and the temperature dependence of the glass viscosity (VFT equation) allows to reproduce this curve. The parameters of the model indicate that most of the significant settling takes place in the channel of the melting furnace at lamellar flow, between $1200\,{^\circ }\hbox {C}$ and the entrance of the float bath at $1050\,{^\circ }\hbox {C}$, whereas settling within the float bath is negligible. The resulting settling curve indicates that by this effect 37% of the inclusions are lost.

The size spectra of the inclusions (both “All inclusions” and subset “Broken in HST-C/K”) derived from the cumulative are again fitted well with the aid of the Log-Normal function. The comparison of these datasets reveals that coarser nickel sulphide inclusions lead more probably to breakage, and that the breakage ratio increases systematically, again following a Log-Normal function. This function could be one of the bases of future complete modelling of spontaneous breakages, e.g. building up a Bernoulli tree. On the other hand, the observed size spectrum is explained using additional physico-chemical facts, basing on the settling law already mentioned above, adding the effects of faster decomposition at smaller sizes and random self-destruction of the nickel sulphide inclusions due to shifting of their chemical composition with the sojourn time. Also these ideas could serve in future complete modeling.

5 Conclusions

In brief, the following conclusions are drawn.

The Log-Normal-function-aided fitting of datasets is in many cases applicable and useful for the generalization of nickel sulphide inclusion correlated datasets. The statistical reason for this seems to be that they are influenced by a number of consecutive (multiplicative) random factors.

Glass thickness has a non-negligible impact onto (mass-related, i.e. virtually thickness-independent) breakage occurrence in HST. As already discussed in Kasper (2018a), the assumed reason for this is the induction of non-negligible thermo-mechanic forced during heating-up of the glass stack.

Gravitational settling influences the position profile in the glass section and the size spectrum of nickel sulphide inclusions. STOKE’s settling equation alone is adequate to explain the position profile. For explanation of the size spectrum, additional hypotheses must be made.

These findings, in addition to the findings already published in Kasper (2018a), would be the basis for future complete modeling of spontaneous breakage, e.g. by aid of a Bernoulli tree. The latter, again, would be a significant basis to elaborate the real difference between breakages on buildings and in HST-EU in order to make a realistic estimation of the safety of “Heat-Soak Tested Thermally Toughened Safety Glass” (acc. EN-14179-1). Already now, the authors are, based on their findings and estimations, convinced that the latter is actually strongly under-estimated.

More facts on this technically important safety issue will be published in the subsequent publication (Kasper 2018b) of our small series.