Control of Heat Diffusion in Arc Welding Using Differential Flatness Theory and Nonlinear Kalman Filtering

Abstract

Control of the heat diffusion in the welded metal is of primary importance for successful welding of high quality (the latter being a prerequisite for efficient ship building). The paper proposes a distributed parameter systems control method that is based on differential flatness theory, aiming at solving the problem of heat distribution control in the arc-welding process. Besides it proposes a nonlinear filtering method, under the name Derivative-free nonlinear Kalman Filtering for reducing the number of real-time control measurements needed to implement the feedback control loop. The stability of the control method is confirmed analytically, while its efficiency is also evaluated through simulation experiments.

Introduction

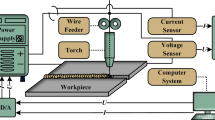
Arc welding is one of the primary tasks in ship building [1]. Automated welding in ship-building is required because of the low productivity of hand welding, which is the result of the severe environmental conditions produced in the intense heat and the fumes that are generated by the welding process. The dynamics of the welding process is given by a diffusion-type partial differential equation which describes the spatiotemporal variations of the temperature distribution in the welded workpiece (Fig. 1). The parameters (inputs) that affect this temperature distribution are the velocity of the torch and the heat input power (Fig. 2). It is important to control heat diffusion in the welding process and the associated temperature distribution in the welded material, because this finally determines the quality, strength and endurance of the weld.

According to welding theory, the temperature of the heat affected zone determines the quality of the weld [2–6]. The heat-affected zone is defined as the area round the weld bead where the temperature of the melted material varies between a lower and upper limit, where each limit is associated with transition to a different phase and structure of the material. The structure of the material that is formed after welding as well as the defects appearing in the weld depend on the temperature that is developed in the heat-affected zone and its variations during the welding process. For the monitoring of the thermal distribution in the welded workpiece several methods have been implemented, such as the use of thermocouples, infrared thermometers and infrared cameras. Efficient control of the thermal distribution during welding is still an open problem. In this manuscript a solution will be developed based on previous results on control and state estimation for distributed parameter systems with the use of differential flatness theory [7–9].

Fig. 1

Control scheme of the nonlinear heat diffusion in the welding process

Fig. 2

Control scheme of the nonlinear heat diffusion in the welding process

Methods for feedback stabilization of systems with nonlinear PDE dynamics have been a flourishing research subject in the last years [10–14]. In particular, feedback control of diffusion-type (parabolic) PDEs has been a subject of extensive research and several remarkable results have been produced [15–18]. For the control of the heat diffusion PDE, boundary and distributed control methods have been developed [19–25]. In this paper, following the procedure for numerical solution of the nonlinear PDE of heat diffusion, a set of coupled nonlinear ordinary differential equations is obtained and written in a state-space form [26, 27]. For the latter state-space description, differential flatness properties are proven. Thus, it is shown that all state variables and the control inputs of the state-space model can be written as differential functions of a vector of algebraic variables that constitute the flat output [28–32]. By applying a change of coordinates (diffeomorphism) which is based on differential flatness theory it is shown that the state-space model of the heat diffusion PDE can be written in a linear form, in which the previously noted nonlinear ordinary differential equations are now transformed into linear ones. Next, feedback control is applied to the heat diffusion PDE. For each local linear model of the aforementioned differential equations the state feedback control is selected such that asymptotic stability is assured. This can be done using for instance pole-placement methods. By computing the control input of the heat diffusion PDE, which varies both in space and time one can also compute the velocity that the welding torch should have at a specific time instant at a point of the cartesian frame, so as the temperature distribution of the workpiece to converge to the reference setpoints.

Another objective of the article is to implement state-feedback control of the nonlinear heat diffusion PDE using measurements from a small number of sensors [33, 34]. This implies that for state vector elements of the PDE’s state-space description which cannot be measured directly, state estimation with filtering methods has to be be applied. Filtering for nonlinear distributed parameter systems is again a non-trivial problem [35–38]. Both observer-based and Kalman Filter-based approaches have been proposed [39–43]. To this end, in this paper, a new nonlinear filtering method, under the name Derivative-free nonlinear Kalman Filtering, is proposed. The filter consists of the standard Kalman Filter recursion applied to the linear equivalent state-space model of the heat diffusion PDE and of an inverse transformation that enables to obtain estimates of the state variables in the initial nonlinear description [44–46].

The structure of the paper is as follows: In “Dynamic Model of the Arc Welding Process” section the dynamic model of the arc-welding process is analyzed and the associated nonlinear heat diffusion PDE is explained. In “State-Space Description of the Nonlinear Heat Diffusion Dynamics” section differential flatness properties of the welding’s heat diffusion PDE are shown and an equivalent linear state-space description is obtained. In “Solution of the Control and Estimation Problem for Nonlinear Heat Diffusion” section a feedback controller is designed for the nonlinear heat diffusion dynamics in arc welding. Moreover, a Kalman Filtering approach is introduced for implementing state feedback control using a small number of sensor measurements. In “Simulation Tests” section the efficiency of the proposed feedback control scheme for the arc-welding process is shown through simulation experiments. Finally, in “Conclusions” section concluding remarks are provided.

Fig. 3

Grid points for measuring $\phi (x,t)$

Dynamic Model of the Arc Welding Process

The reference frame of Fig. 3 is introduced and the following nonlinear heat diffusion equation is considered, describing the spatiotemporal variations of the temperature in the welded workpiece [2–4]

$$\begin{aligned} {{{{\partial }}\phi } \over {{\partial }t}}=K{{{{\partial }^2}\phi } \over {{\partial }x^2}}+f(x,t)+u(x,t) \end{aligned}$$

(1)

where K is the heat conductivity and u(x, t) is a term associated with the partial derivative of the temperature distribution with respect to the space variable x as well as with the velocity of the welding torch. This is given by

$$\begin{aligned} u(x,t)={{{\partial }\phi (x,t)} \over {{\partial }x}}v_s(t) \end{aligned}$$

(2)

with $v_s(t)$ to stand for the velocity of the torch at time instant t. Moreover, about the nonlinear term f(x, t) this is given by

$$\begin{aligned} f(x,t)=q(x)h(t) \end{aligned}$$

(3)

The term h(t) stands for the heating power provided by the torch. The term q(x) denotes the spatial distribution of the heating input and can be approximated by a Gaussian, that is [5, 6]

$$\begin{aligned} q(x)=ae^{-{{(x-x_s)}^2 \over \sigma ^2}} \end{aligned}$$

(4)

where a and $\sigma$ are constant parameters and $x_s$ is the position of the torch in the reference system used for the welding process (Fig. 1). The previous dynamic model of the welding process is the result of the energy conservation principle. In the simplest scenario of welding the following assumptions are made: (i) the thermal conductivity coefficient K remains constant throughout the process and is not affected by temperature variations of the welded material, (ii) the only heat source provided to the welded material is the one given by the torch, (iii) no heat is either produced or lost at any other part of the workpiece.

State-Space Description of the Nonlinear Heat Diffusion Dynamics

Using the approximation for the partial derivative in the partial differential equation given in Eq. (1) one has

$$\begin{aligned} {{{{\partial }^2}\phi } \over {{\partial }x^2}}{\simeq }={{\phi _{i+1}-2{\phi _i}+{\phi }_{i-1}} \over {{\Delta }x^2}} \end{aligned}$$

(5)

and considering spatial measurements of variable $\phi$ along axis x at points $x_0+i{\Delta }x, \ i=1,2,\ldots ,N$ one has

$$\begin{aligned} {{{{\partial }}\phi _i} \over {{\partial }t}}={K \over {{\Delta }x^2}}\phi _{i+1}-{{2K} \over {{\Delta }x^2}}\phi _i+{K \over {{\Delta }x}^2}\phi _{i-1}+f(\phi _i)+u(x_i,t) \end{aligned}$$

(6)

By considering the associated samples of $\phi$ given by $\phi _0, \phi _1, \ldots , \phi _N, \phi _{N+1}$ one has

$$\begin{aligned} {{{{\partial }}\phi _1} \over {{\partial }t}}= & {} {K \over {{\Delta }x}^2}\phi _{2}-{{2K} \over {{\Delta }x}^2}\phi _1+{K \over {{\Delta }x}^2}\phi _{0}+f(\phi _1)+u(x_1,t) \nonumber \\ {{{{\partial }}\phi _2} \over {{\partial }t}}= & {} {K \over {{\Delta }x}^2}\phi _{3}-{{2K} \over {{\Delta }x}^2}\phi _2+{K \over {{\Delta }x}^2}\phi _{1}+f(\phi _2)+u(x_2,t) \nonumber \\ {{{{\partial }}\phi _3} \over {{\partial }t}}= & {} {K \over {{\Delta }x}^2}\phi _{4}-{{2K} \over {{\Delta }x}^2}\phi _3+{K \over {{\Delta }x}^2}\phi _{2}+f(\phi _3)+u(x_3,t) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \cdots \nonumber \\ {{{{\partial }}\phi _{N-1}} \over {{\partial }t}}= & {} {K \over {{\Delta }x}^2}\phi _{N}-{{2K} \over {{\Delta }x}^2}\phi _{N-1}+{K \over {{\Delta }x}^2}\phi _{N-2}+f(\phi _{N-1}) \nonumber \\&+\,u(x_{N-1},t) \nonumber \\ {{{{\partial }}\phi _{N}} \over {{\partial }t}}= & {} {K \over {{\Delta }x}^2}\phi _{N+1}-{{2K} \over {{\Delta }x}^2}\phi _{N}+{K \over {{\Delta }x}^2}\phi _{N-1} \nonumber \\&+f(\phi _{N})+u(x_N,t) \end{aligned}$$

(7)

By defining the following state vector

$$\begin{aligned} x^T=\begin{pmatrix} \phi _1,\phi _2,\ldots ,\phi _N \end{pmatrix} \end{aligned}$$

(8)

one obtains the following state-space description

$$\begin{aligned} \dot{x}_1= & {} {K \over {{\Delta }x}^2}x_2-{{2K} \over {{\Delta }x}^2}{x_1}+{K \over {{\Delta }x}^2}{\phi _0}+f(x_1)+u_1 \nonumber \\ \dot{x}_2= & {} {K \over {{\Delta }x}^2}x_3-{{2K} \over {{\Delta }x}^2}{x_2}+{K \over {{\Delta }x}^2}{x_1}+f(x_2)+u_2 \nonumber \\ \dot{x}_3= & {} {K \over {{\Delta }x}^2}x_4-{{2K} \over {{\Delta }x}^2}{x_3}+{K \over {{\Delta }x}^2}{x_2}+f(x_3)+u_3 \nonumber \\&\qquad \qquad \,\,\,\qquad \qquad \cdots \nonumber \\ \dot{x}_{N-1}= & {} {K \over {{\Delta }x}^2}x_{N}-{{2K} \over {{\Delta }x}^2}{x_{N-1}}+{K \over {{\Delta }x}^2}{x_{N-2}} \nonumber \\&+f(x_{N-1})+u_{N-1} \nonumber \\ \dot{x}_{N}= & {} {K \over {{\Delta }x}^2}\phi _{N+1}-{{2K} \over {{\Delta }x}^2}{x_{N}} \nonumber \\&+{K \over {{\Delta }x}^2}{x_{N-1}}+f(x_{N})+u_N \end{aligned}$$

(9)

where $u_i, \ i=1,2.\ldots ,N$ is the control input exerted at grid point $x_0+i{\Delta }x$. Next, the following state variables are defined

$$\begin{aligned} y_{1,i}= & {} x_i \nonumber \\ y_{2,i}= & {} \dot{x}_i \end{aligned}$$

(10)

and the state-space description of the system becomes as follows

$$\begin{aligned} \dot{y}_{1,1}= & {} {K \over {{\Delta }x}^2}y_{1,2}-{{2K} \over {{\Delta }x}^2}y_{1,1}+{K \over {{\Delta }x}^2}\phi _0+f(y_{1,1})+u_1 \nonumber \\ \dot{y}_{1,2}= & {} {K \over {{\Delta }x}^2}y_{1,3}-{{2K} \over {{\Delta }x}^2}y_{1,2}+{K \over {{\Delta }x}^2}y_{1,1}+f(y_{1,2})+u_2 \nonumber \\ \dot{y}_{1,3}= & {} {K \over {{\Delta }x}^2}y_{1,4}-{{2K} \over {{\Delta }x}^2}y_{1,3}+{K \over {{\Delta }x}^2}y_{1,2}+f(y_{1,3})+u_3 \nonumber \\&\qquad \qquad \cdots \nonumber \\&\qquad \qquad \cdots \nonumber \\ \dot{y}_{1,N-1}= & {} {K \over {{\Delta }x}^2}y_{1,N}-{{2K} \over {{\Delta }x}^2}y_{1,N-1}+{K \over {{\Delta }x}^2}y_{1,N-2} \nonumber \\&+f(y_{1,N-1})+u_{N-1} \nonumber \\ \dot{y}_{1,N}= & {} {K \over {{\Delta }x}^2}\phi _{N+1}-{{2K} \over {{\Delta }x^2}}y_{1,N} +{K \over {\Delta }x^2}y_{1,N-1}+f(y_{1,N})+u_N\nonumber \\ \end{aligned}$$

(11)

The dynamical system described in Eq. (11) is a differentially flat one with flat output defined as the vector $\tilde{y}=[y_{1,1},y_{1,2},\ldots ,y_{1,N}]$. Indeed all state variables can be written as functions of the flat output and its derivatives.

Moreover, by defining the new control inputs

$$\begin{aligned} v_1= & {} {K \over {{\Delta }x^2}}\phi _0+f(y_{1,1})+u_1 \nonumber \\ v_2= & {} f(y_{1,2})+u_2 \nonumber \\ v_3= & {} f(y_{1,3})+u_3 \nonumber \\&\qquad \cdots \nonumber \\ v_{N-1}= & {} f(y_{1,N-1})+u_{N-1} \nonumber \\ v_N= & {} {K \over {{\Delta }x}^2}\phi _{N+1}+f(y_{1,N})+u_N \end{aligned}$$

(12)

the following state-space description is obtained

$$\begin{aligned} \begin{pmatrix} \dot{y}_{1,1} \\ \dot{y}_{1,2} \\ \cdots \\ \dot{y}_{1,N-1} \\ \dot{y}_{1,N} \\ \end{pmatrix}= & {} \begin{pmatrix} -{{2K} \over {{\Delta }x^2}} &{}\quad {K \over {{\Delta }x}^2} &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {K \over {{\Delta }x^2}} &{}\quad -{{2K} \over {{\Delta }x^2}} &{}\quad {K \over {{\Delta }x}^2} &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {K \over {{\Delta }x^2}} &{}\quad -{{2K} \over {{\Delta }x^2}} &{}\quad {K \over {{\Delta }x}^2} &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad {{K \over {\Delta }x^2}} &{}\quad -{{2K} \over {{\Delta }x}^2} &{}\quad {K \over {{\Delta }x}^2} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad {K \over {{\Delta }x}^2} &{}\quad -{{2K} \over {{\Delta }x}^2} \end{pmatrix}\nonumber \\&\times \begin{pmatrix} y_{1,1} \\ y_{1,2} \\ \cdots \\ y_{1,N-1} \\ y_{1,N} \\ \end{pmatrix} +\begin{pmatrix} 1 \ 0 \ 0 \ \cdots \ 0 \ 0 \\ 0 \ 1 \ 0 \ \cdots \ 0 \ 0 \\ 0 \ 0 \ 1 \ \cdots \ 0 \ 0 \\ \cdots \ \cdots \ \cdots \ \cdots \\ 0 \ 0 \ 0 \ \cdots \ 1 \ 0 \\ 0 \ 0 \ 0 \ \cdots \ 0 \ 1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ \cdots \\ v_{N-1} \\ v_N \end{pmatrix} \end{aligned}$$

(13)

Assuming that all measurements from the set of points $x_j \ j{\in }[1,2,\ldots ,m]$ are available, the associated observation (measurement) equation becomes

$$\begin{aligned} \begin{pmatrix} z_1 \\ z_2 \\ \cdots \\ z_m \end{pmatrix}= \begin{pmatrix} 1 \ 0 \ 0 \ \cdots \ 0 \ 0 \\ 0 \ 1 \ 0 \ \cdots \ 0 \ 0 \\ \cdots \ \cdots \ \cdots \ \cdots \\ 0 \ 0 \ 0 \ \cdots \ 1 \ 0 \\ 0 \ 0 \ 0 \ \cdots \ 0 \ 1 \end{pmatrix} \begin{pmatrix} y_{1,1} \\ y_{1,2} \\ y_{1,3} \\ \cdots \\ y_{1,N-1} \\ y_{1,N} \end{pmatrix} \end{aligned}$$

(14)

Thus, in matrix form one has the following state-space description of the system

$$\begin{aligned} \dot{\tilde{y}}= & {} A\tilde{y}+Bv \nonumber \\ \tilde{z}= & {} C\tilde{y} \end{aligned}$$

(15)

Moreover, denoting $a={K \over {{\Delta }x^2}}$ and $b=-{{2K} \over {{\Delta }x^2}}$, the initial description of the system given in Eq. (13) is rewritten as follows

$$\begin{aligned} \begin{pmatrix} \dot{y}_{1,1} \\ \dot{y}_{1,2} \\ \cdots \\ \dot{y}_{1,N-1} \\ \dot{y}_{1,N} \\ \end{pmatrix}= & {} \begin{pmatrix} b \ a \ 0 \ 0 \ 0 \ \cdots \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ a \ b \ a \ 0 \ 0 \ \cdots \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ a \ b \ a \ \cdots \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ \cdots \ \cdots \ \cdots \ \cdots \ \cdots \ \cdots \ \cdots \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ \cdots \ a \ b \ a \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ \cdots \ 0 \ 0 \ a \ b \end{pmatrix} \begin{pmatrix} y_{1,1} \\ y_{1,2} \\ \cdots \\ y_{1,N-1} \\ y_{1,N} \end{pmatrix} \nonumber \\&+\begin{pmatrix} 1 \ 0 \ 0 \ \cdots \ 0 \ 0 \\ 0 \ 1 \ 0 \ \cdots \ 0 \ 0 \\ 0 \ 0 \ 1 \ \cdots \ 0 \ 0 \\ \cdots \ \cdots \ \cdots \ \cdots \\ 0 \ 0 \ 0 \ \cdots \ 1 \ 0 \\ 0 \ 0 \ 0 \ \cdots \ 0 \ 1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ \cdots \\ v_{N-1} \\ v_N \end{pmatrix} \end{aligned}$$

(16)

In an outline of the above it can be noted that the PDE dynamics of the heat diffusion undergoes semi-discretization about its spatial (x-axis dimension). There are N equidistant points along the x-axis and at these points the heat diffusion dynamics is represented by a nonlinear ordinary differential equation with respect to time. Moreover, the finite differences method has been applied to compute the partial derivatives of the temperature distribution $\phi (x,t)$ with respect to the spatial variable x. After transformation of the PDE dynamics into the equivalent state-space model of Eq. (16) it can be seen that there are virtual control inputs $u_i \ i=1,2,\ldots ,N$ exerted on it. Based on the values of these control inputs and on Eq. (19) one can finally compute the speed of the torch which is the real and time varying control input exerted on the system. The outputs of the welding system’s model are specific elements of the state vector of Eq. (16). These are associated with measurements of the heat distribution (temperature) obtained at specific points of the welded element. The boundary conditions for this PDE model are $\phi (x_0,t)$ and $\phi (x_N,t)$ and these are associated with measurements about the heat distribution (temperature) obtained at the initial and final point of the x-axis dimension of the welded workpiece.

Solution of the Control and Estimation Problem for Nonlinear Heat Diffusion

Solution of the Control Problem

Using the flat outputs notation, it holds that the dynamics of the linearized equivalent model of the nonlinear heat diffusion PDE takes the form

(17)

For the dynamics given in Eq. (17), the feedback control law that assures tracking of the reference setpoint $y^d=[y_{1,1}^d,y_{1,2}^d,y_{1,3}^d,\ldots ,y_{1,N-1}^d,y_{1,N}^d]^T$ is

(18)

Next, using Eq. (18) one can compute the control action that is applied to the heat diffusion dynamics

(19)

The control input u(x, t) is a heat distribution that is generated by the moving welding torch. By knowing the spatiotemporal variations of the heat distribution u(x, t) that is provided by the torch and the associated partial derivative ${{\partial }\phi } \over {{\partial }x}$ one can also compute the speed of the torch v that is needed for making the heat distribution of the welded area reach the desirable setpoints. The proposed control scheme is depicted in Fig. 2.

For the computation of the setpoints of the speed of the welding torch one should proceed as follows: At each time instant $t_i$ and for the complete sequence of the grid points $x_1,x_2,\ldots ,x_N$ one has the set of equations:

(20)

By substituting the values of $x_j, \ j=1,2,\ldots ,x_N$ and $t_i$ in Eq. (20) the computation of $v(t_i)$, that is $v(t_i)$ can be performed in the least squares sense.

Solution of the Estimation Problem

Next, measurements are selected from a subset of points $x_j \ j{\in }[1,2,\ldots ,N]$ so as the observability of the state-space model of the welding process to be preserved (Fig. 3). For instance the associated observation (measurement) equation may take the form

$$\begin{aligned} \begin{pmatrix} z_1 \\ z_2 \\ \cdots \\ z_m \end{pmatrix}= \begin{pmatrix} 1 \ 0 \ 0 \ \cdots \ 0 \ 0 \\ 0 \ 0 \ 0 \ \cdots \ 0 \ 0 \\ \cdots \ \cdots \ \cdots \ \cdots \\ 0 \ 0 \ 0 \ \cdots \ 1 \ 0 \\ 0 \ 0 \ 0 \ \cdots \ 0 \ 0 \end{pmatrix} \begin{pmatrix} y_{1,1} \\ y_{1,2} \\ y_{1,3} \\ \cdots \\ y_{1,N-1} \\ y_{1,N} \\ \end{pmatrix} \end{aligned}$$

(21)

For the description of the system in the form of Eq. (15) one can perform estimation using the derivative-free nonlinear Kalman Filter recursion. In the filter’s algorithm, the previously defined matrices A, B and C are substituted by their discrete-time equivalents $A_{d},B_{d}$ and $C_{d}$. The discrete-time Kalman filter can be decomposed into two parts: (i) time update (prediction stage), and (ii) measurement update (correction stage).

Measurement update:

$$\begin{aligned} K(k)= & {} {P^{-}(k)}{C_d^T}[C{\cdot }P^{-}(k){C_d^T}+R]^{-1} \nonumber \\ {\hat{y}(k)}= & {} {\hat{y}^{-}(k)}+K(k)[z(k)-C_d{\hat{y}^{-}(k)}] \nonumber \\ P(k)= & {} P^{-}(k)-K(k)C_dP^{-}(k) \end{aligned}$$

(22)

Time update:

$$\begin{aligned} P^{-}(k+1)= & {} {A_d(k)}P(k)A_d^T(k)+Q(k) \nonumber \\ {\hat{y}^{-}(k+1)}= & {} A_d(k)\hat{y}(k)+B_d(k)u(k) \end{aligned}$$

(23)

Therefore, by taking measurements of $\phi (x,t)$ at time instant t at a small number of measuring points $j=1,\ldots ,n_1$ it is possible to estimate the complete state vector, i.e. to get values of $\phi$ in a mesh of points that covers efficiently the variations of $\phi (x,t)$. By processing a sequence of output measurements of the system, one can obtain estimates of the state vector $\hat{y}$. The measuring points (active sensors) can vary in time provided that the observability criterion for the state-space model of the PDE holds.

According to Eq. (22) and (23) an estimate of the system’s state vector $\hat{y}$ is obtained. Should one want to obtain an estimate of the state vector x of the initial state-space description of the nonlinear heat diffusion, he should apply the inverse differential flatness transformation connecting $x_i$’s to $y_i$’s. In the examined model of the nonlinear heat diffusion it holds that

(24)

The proposed derivative-free nonlinear Kalman Filter is of improved precision because unlike other nonlinear filtering schemes, e.g. unlike the Extended Kalman Filter it does not introduce cumulative numerical errors due to approximative linearization of the system’s dynamics. Besides it is computationally more efficient (faster) because it does not require to calculate Jacobian matrices and partial derivatives.

If state estimation-based control is applied to the state-space model of the nonlinear heat diffusion equation of the welding process, then the associated control inputs are

(25)

In complement to the modelling and control part of heat diffusion in the arc-welding model the following points are worth of further analysis:

• (i) The control problem for the welding PDE is finally formulated as a single-input one. Although, the heating power of the torch can affect the heat diffusion in the welded metal, it is finally considered that this parameter is kept constant while only the time-varying velocity of the torch stands for a control input. The term of the spatial distribution q(x) which is described in Eq. (4) depends primarily on the heating power of the torch and not on the velocity of the torch. Eq. (4) denotes that the spatial distribution of the heating input is a Gaussian centered at the present position x of the torch. If x varies in time, that is $\dot{x}{\ne }0$ then Eq. (4) still describes the spatial distribution of the heating input since parameters $\alpha$ and $\sigma$ are constants and do not depend on x.

• (ii) To implement the previously analyzed control method one can consider that the boundary conditions of the nonlinear heat diffusion PDE are known and are monitored by specific sensors. However, knowledge of boundary conditions is not necessary for the solution of the control problem for the welding process. It is not imperative to use dedicated sensors for measuring the temperature distribution at boundary points $\phi (x_0,t)$ and $\phi (x_{N+1},t)$ of the welded element. By taking measurements at specific points $\phi (x_i,t)$ of the welded element so as to assure the observability of the state-space model of the heat PDE, one can use the outcome of the Kalman Filtering procedure for estimating the temperature distribution at points which are not monitored with the use of sensors.

• (iii) Moreover, even in the case that the PDE model is not an exact one, or is characterized by missing terms or is subjected to external perturbations one can make use of robust Kalman Filtering approaches (such as the H-infinity Kalman Filter or Kalman Filter-based disturbance observers) for obtaining accurate estimates of the monitoring heat diffusion PDE.

• (iv) In the treated case study, and for purposes of computational simplicity, the heat diffusion model has been considered to be 1-dimensional. However, the evolution of the heat diffusion process make also take place in 2 or 3 dimensions. Even in the latter case one can apply the proposed PDE control and filtering method based on differential flatness theory [47]. The primary difficulty is that the order of the state space model will be elevated (doubled or tripled) and accordingly more measurement points have to be introduced.

• (v) It is possible to extend the heat-diffusion model in three dimensions, and in such a case one would come against an elevated computational burden for the control and filtering method. Instead of semi-discretization of the diffusion process at N points one would have 3N such points and the dimension of the state-space description of the system’s dynamics would be raised by a factor of 3. Up to now the problem of PDE diffusion and control with the proposed differential flatness theory approach has been treated in 1D and 2D PDE systems. Indicative multi-dimensional distributed parameter systems have been given in Ref. [48] and Ref. [49].

• (vi) It is also noteworthy that the heating power of the torch was considered to remain constant. The only varying control input was the speed of the torch. This suffices for implementing a stabilizing feedback control scheme for the heat diffusion PDE. It would be possible to apply a multi-input control scheme for the arc-welding process in which the heating power of the torch would also vary. This would not alter significantly the stages of the design of feedback controller for this process which have been explained above.

Simulation Tests

The performance of the proposed control scheme has been tested in the model of the nonlinear heat diffusion PDE that describes the arc welding process. A discretization grid of the PDE consisting of $N=50$ points, along the x axis (Fig. 1) was considered. For N grid points and M measurement sensors, process noise covariance matrix $Q{\in }R^{N{\times }N}$ is taken to be diagonal with zero elements equal to $10^{-3}$ and the measurement noise covariance matrix $R{\in }R^{M{\times }N}$ is taken to be diagonal with zero elements equal to $10^{-4}$. At each grid point the local control input $u(x_i,t)$ was exerted to the system. The state-space description of the heat-diffusion PDE comprised also a state vector of dimension $y{\in }R^{50{\times }1}$. The number of measurement points was $m{\le }N$ were m was selected such that the observability of the linearized state-space model of the PDE is preserved (actually measurements were sampled from half of the number of grid points) as shown in Fig. 3.

Fig. 4

Control of the arc welding process under moderate measurement noise a Controlled distribution $\phi (x,t)$ of the nonlinear heat diffusion PDE tracking a sinusoidal setpoint, b Control input ${{{\partial }\phi (x,t)} \over {{\partial }x}}u(t)$

Fig. 5

Control of the arc welding process (distribution $\phi (x,t)$) under moderate measurement noise a Grid points $p_1$ to $p_4$ and b Grid points $p_5$ to $p_8$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

Fig. 6

Control of the arc welding process (distribution $\phi (x,t)$) under moderate measurement noise a Grid points $p_9$ to $p_{12}$ and b Grid points $p_{13}$ to $p_{16}$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

Fig. 7

Control of the arc welding process (distribution $\phi (x,t)$) under moderate measurement noise a Grid points $p_{17}$ to $p_{20}$ and b Grid points $p_{21}$ to $p_{24}$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

Fig. 8

Control of the arc welding process (distribution $\phi (x,t)$) under moderate measurement noise a Grid points $p_{25}$ to $p_{28}$ and b Grid points $p_{29}$ to $p_{32}$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

Fig. 9

Control of the arc welding process (distribution $\phi (x,t)$) under moderate measurement noise a Grid points $p_{33}$ to $p_{36}$ and b Grid points $p_{37}$ to $p_{40}$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

The obtained results, for the case of moderate measurement noise (trace of the covariance matrix of the noise vector equal to $6.3{\times }10^{-3}$), are presented in Figs. 4, 5, 6, 7, 8, 9 and 10. The plotted variables are originally measured in SI units, however in the following diagrams their variation is presented with the use of normalized values. It can be observed that through the application of suitable control inputs the distribution function $\phi (x,t)$ can be made to track the desirable sinusoidal setpoints. Actually, the tracking of a sinusoidal reference setpoint by the distribution $\phi (x,t)$ of the nonlinear heat diffusion PDE is shown in Fig. 4a. Additionally in Fig. 4b the variations of the control input term ${{{\partial }\phi (x,t)} \over {{\partial }x}}u(t)$ are shown. Moreover, in Figs. 5, 6, 7, 8, 9 and 10 diagrams are provided about the tracking accuracy of the proposed control method at specific points of the discretization grid. It can be noticed that the state estimation-based control method resulted in fast and accurate tracking of the reference setpoints.

Fig. 10

Control of the arc welding process (distribution $\phi (x,t)$) under moderate measurement noise a Grid points $p_{41}$ to $p_{44}$ and b Grid points $p_{45}$ to $p_{48}$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

Fig. 11

Control of the arc welding process under elevated measurement noise a Controlled distribution $\phi (x,t)$ of the nonlinear heat diffusion PDE tracking a sinusoidal setpoint, b Control input ${{{\partial }\phi (x,t)} \over {{\partial }x}}u(t)$

Fig. 12

Control of the arc welding process (distribution $\phi (x,t)$) under elevated measurement noise a Grid points $p_1$ to $p_4$ and b Grid points $p_5$ to $p_8$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

Fig. 13

Control of the arc welding process (distribution $\phi (x,t)$) under elevated measurement noise a Grid points $p_9$ to $p_{12}$ and b Grid points $p_{13}$ to $p_{16}$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

Fig. 14

Control of the arc welding process (distribution $\phi (x,t)$) under elevated measurement noise a Grid points $p_{17}$ to $p_{20}$ and b Grid points $p_{21}$ to $p_{24}$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

Fig. 15

Control of the arc welding process (distribution $\phi (x,t)$) under elevated measurement noise a Grid points $p_{25}$ to $p_{28}$ and b Grid points $p_{29}$ to $p_{32}$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

Fig. 16

Control of the arc welding process (distribution $\phi (x,t)$) under elevated measurement noise a Grid points $p_{33}$ to $p_{36}$ and b Grid points $p_{37}$ to $p_{40}$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

Fig. 17

Control of the arc welding process (distribution $\phi (x,t)$) under elevated measurement noise a Grid points $p_{41}$ to $p_{44}$ and b Grid points $p_{45}$ to $p_{48}$ of the nonlinear heat diffusion PDE: tracking of the reference setpoints (red line) by the value of the distribution $\phi (x,t)$ (blue line)

The problem of robust state estimation for filtering-based control of the welding process is a significant one. Measurement data can be corrupted by noise, or there may be missing measurements or time-delays in the transmission of sensor data (for instance in visual monitoring of the welding process through distributed optical devices). Considering these cases, the simulation tests were repeated under elevated measurement noise (trace of the covariance matrix of the noise vector equal to $6.3{\times }10^{-1}$), so as to confirm the disturbance rejection capabilities and the robustness of both the filtering methods and the feedback control approach. The obtained results are depicted in Figs. 11, 12, 13, 14, 15, 16 and 17. It can be noticed, that despite functioning under measurement noise and perturbations the tracking performance of the temperature setpoints at the grid’s points remained satisfactory.

Indicative results about the variation of the root mean square error (RMSE) of the temperature setpoint tracking at grid points $i_1=10$, $i_2=25$ and $i_3=35$, under different measurement noise levels (described by the trace of the covariance matrix of the measurement noise vector $\text {trace(Cov)}_{\tilde{d}}$), are given in Table 1. It can be noticed that the filtering-based control scheme of the arc-welding process exhibited robustness to the progressively increasing intensity of disturbances.

Table 1 Tracking RMSE under disturbances

In addition to the analytical proof of the stability and convergence properties of the filtering and control methods for the heat diffusion PDE in the arc welding process the following points are outlined:

• (i) The controller is primarily designed for an infinite dimensional PDE system, which means that the number of grid points $x_1,x_2,\ldots ,x_N$ can be extended to infinity. Next, the modeling of the PDE dynamics follows the common approach for the numerical solution of PDEs, which means that the infinite number of grid points is reduced into a finite one. Consequently, instead of examining the entire x-axis about the spatial variation of the temperature distribution $\phi (x,t)$ one constrains the modeling of the PDE dynamics in a finite segment consisting of the N grid points. However, this segment can be shifted as the heat diffusion spreads in time, so as to cover subsequent areas of the x-axis. According to the above, the considered PDE model is an infinite dimensional one but its implementation on a computer requires to consider a finite approximation of it.

• (ii) The proposed Derivative-free nonlinear Kalman Filter is a nonlinear filtering method which does not suffer from the approximation errors of other nonlinear filtering methods such as the Extended Kalman Filter, while being also computationally more efficient than other nonlinear filtering methods such as Sigma Point Kalman Filters and Particle Filters [7–9]. It is known that the accuracy and stability of the Extended Kalman Filter can be set in question due to the cumulative linearization errors that characterize this method. Moreover, it is known that the Unscented Kalman Filter requires the computation of cross-covariance matrices while the Particle Filter is based on the manipulation of large sets of potential state estimates known as particles. Therefore, the latter two methods impose a significant computational burden. On the other hand, the Derivative free nonlinear Kalman Filter does not exhibit such numerical or computational weaknesses and therefore it is an estimation method of improved performance.

• (iii) Results about the numerical stability of PDEs when solved with the use of semi-discretization and the finite differences method have been given in Ref. [26]. Numerical stability methods for the discretization of PDEs have been widely studied in the relevant bibliography. By a dense sampling along both the spatial dimension x and the time dimension t of the distributed parameter system it is assured that numerical stability of the algorithm is preserved. For diffusion and wave-type PDEs it is known that the convergence condition is $2K(Dt)/Dx^2\le 1$ where Dt and Dx are the discretization steps in space and time [26].

• (iv) To confirm the observability of the state-space description of the heat diffusion PDE given in Eq. (13) and (14), the associated observability matrix has been computed and this has been found to be a full rank one. One cannot prescribe for all cases the number and position of the measurement points that assure the observability of the linearized state-space description of the PDE model. As shown in the case of the arc-welding process, the number of measurement points can be significantly reduced with respect to the number of grid points (half or less) and this is a noteworthy benefit for implementing the associated control system at minimum cost. Observability of the state-space model is also the condition for the stability of the Kalman Filter recursion. A weaker condition for the convergence of the Kalman Filter is the model’s detectability, which in turn is associated with the non-singularity of the Fisher information matrix. To provide the filtering procedure with robustness against modeling errors and external perturbations one can either apply the H-infinity Kalman Filter or can redesign the Kalman Filter as a disturbance observer [7–9, 50–52]. About testing different configurations of the measurement sensors that assure the observability of the welding model one can consider an algorithmic procedure into which the observability matrix is computed for all possible permutations of measurement sensors on the spatial grid of the PDE.

• (v) There are several approaches for improving the robustness of the proposed control and state estimation method for PDEs, with respect to modelling uncertainties and external perturbations. The controller for the individual ODEs into which the PDE model is decomposed can be made more robust by including in it H-infinity or sliding-mode terms. Another option is to use a disturbance observer in the control loop. By redesigning the Kalman Filter as a disturbances estimator it is possible to simultaneously estimate the state vector elements of the PDE’s state-space description as well as perturbation terms affecting it. By knowing such perturbation terms their annihilation becomes possible with the inclusion of an additional control term in the feedback control input. Finally, to robustify state estimation it is possible to use the H-infinity Kalman Filter in place of the typical Kalman Filter recursion [9].

Conclusions

A method for feedback control of the nonlinear heat diffusion PDE associated with the arc welding process has been provided. After showing that the PDE model of arc welding satisfies differential flatness properties it has become possible to transform it into an equivalent linear state-space form. The procedure for numerical solution of the nonlinear PDE of the heat diffusion dynamics has been followed, and a set of coupled nonlinear ordinary differential equations has been obtained. After defining state variables it has been also shown that this set of nonlinear ODEs can be finally written in a state-space form.

For the latter state-space description, differential flatness properties have been proven. Thus, it has been shown that all state variables and the control inputs of the state-space model can be written as differential functions of a vector of algebraic variables that constitute the flat output. By applying a change of coordinates (diffeomorphism) which is based on differential flatness theory it is shown that the state-space model of the heat diffusion PDE can be written in a linear matrix form, in which the previously noted nonlinear ordinary differential equations are now transformed into linear ones. For the latter description of the system the design of an asymptotically stable state feedback controller has become possible. Moreover, to implement feedback control using measurements from a small number of sensors a Kalman Filtering method has been applied. The efficiency of the proposed control and state estimation scheme has been confirmed through simulation experiments.