1 Introduction

Within lottery markets, one of the most remarkable phenomena has been the prevalence and scale of long-odds high-prize lottery products. This type of lotto game is frequently state-regulated and organized as pari-mutuel gambles where all bets of a particular type are placed together in a pool and payoffs are calculated by sharing the pool among all winning bets after deducting taxes and operational expenses. Governments worldwide have consequently authorized such lotto games based on the public’s interest in them as an alternative method for the government to raise new revenue without raising taxes. However, in recent decades, the demand for lottery seems to face a stage of maturity and in some cases even decline (Díaz & Pérez, 2021). As a response and attempt to revert this trend aiming to make playing more attractive, lottery operators across different jurisdictions started to operate multi-country lotteries, offering large prizes that would not be possible to offer operating separately. By exploiting “the peculiar scale economies of lotto” (Cook & Clotfelter, 1993) multi-country games combine the markets of the separate lottery jurisdictions which make up the new lottery marketFootnote 1.

Following the North American successful experiences of Powerball in 1992 and Mega Millions in 2002, on February 7th, 2004 the EuroMillions game was launched by a joint venture of lottery operators from France (Français des Jeux), Spain (Loterías y Apuestas del Estado), and the UK (Camelot). Later, on October 8th, 2004, Austrian, Belgian, Irish, Luxembourgish, Portuguese, and Swiss lotteries joined the EuroMillions market. On the basis of collecting funds from lottery players across all participating countries, the EuroMillions game was expected to offer jackpot prizes of sufficient size to attract and increase the number of lottery players in a given country to an unachievable level by any domestic lottery game run in that jurisdiction.

Since its introduction, the EuroMillions game, like all pari-mutuel lottery products, has been designed to distribute a proportion of the sales revenue (50%) among different prize categories. Lottery operators allocate the remaining 50% to cover their corresponding organization costs (infrastructure, salaries, advertising, etc.) and to fund good causes, such as education, sports, charities, or cultural activities. In case nobody guesses the winning combination in a particular draw, the amount of the jackpot prize rolls over to the next draw, boosting the demand for the game. A bigger jackpot may cause current players to spend more, but also it may make the game more attractive to new players who might enter the market. Following the seminal work of Forrest et al. (2002), such a positive relationship between jackpot size and lottery sales has been well documented in the literature (for some recent references, see, among others, Combs and Spry 2019; Díaz and Pérez 2021; Gabrielyan and Just 2020; Polin et al. 2021).

Notwithstanding, although the increase in the demand for EuroMillions occurs among all operators of the game, it is however quite heterogeneous across participating countries. Roger (2011) analyzed 197 draws of EuroMillions games between 2004 and 2007 and found that sales response to jackpot size sharply differs among countries with a prize elasticity of the demand ranging between 0.6 and 0.9. Accordingly, it could be possible that sales increase more in certain countries than others, increasing the sales share of high jackpot-sensitive countries and so their odds of having a national winning player as well. Therefore, high jackpot-sensitive countries could benefit from the funds that have been contributed to the prize pool by the rest of the countries throughout a particular draw cycle increasing their net payout balance. If this is the case when the jackpot is high those countries’ players would be ‘implicitly funded’ by players in other countries within the EuroMillions market.

Previous research has focused on the regressivity issue when analyzing multistate lottery games. Using data on sales from Powerball, Oster (2004) found evidence of these kind of lottery products being less regressive at higher jackpot levels. In recent papers Lee et al. (2016, 2017) also demonstrate, using data from Mega Millions, that regressivity reduces with the size of the jackpot. Finally, Comb and Spry (2019) estimate income elasticities to increase with the jackpot size in Powerball and Mega Millions games concluding these lotto games being regressive. However, as far as it is known, there is no particular contribution about implicit transfer of funds among countries (or states) within this literature.

It should be noted that participation in EuroMillions, as in any lottery market, is purely voluntary. Thus, it would be interesting to provide evidence about the current distribution of funds from prizes among countries. First, because EuroMillions consumers should be informed about how the game’s rules and design implicitly distribute the money they pay to play, a factor that may affect their purchase decision. And second, because this may provide the operator of the game an overview of the jackpot sharing, making it possible to identify the countries that receive the most (and the least), which may help in reviewing the game’s design.

All in all, this paper aims to analyze EuroMillions’ jackpot sharing among countries focusing on market share trends and on whether implicit transfer of funds among countries exist by studying the distributional consequences (across countries) of claimed jackpots. The potential regressivity character of the game is also analyzed in this paper. As far as it is known, there is no previous contribution in the literature analyzing the jackpot wins distribution among countries in multi-country (or multi-state) lotteries and its relationship with the jackpot size. Indeed, there is no study on each jurisdiction’s net payout balance and implicit funding issues from jackpot wins distribution among countries in multi-country (or multi-state) lotteries.

Why use EuroMillions data? Even though there is a lot of other lottery data about, e.g. about the UK National lottery, effects of covariates like GDP or unemployment are confounded with secular trends. The nine countries operating EuroMillions have very different and varying unemployment and socioeconomic contexts, which provides an interesting scenario to analyze how these factors affect lottery demand. Baker et al. (2016) highlighted the relevance of modelling sales at the regional level stating that it may help lottery operators by providing them guidance in understanding market trends. In addition, as lottery tickets are usually subject to tax, it is important to disentangle whether this tax increase is paid disproportionately by disadvantaged regions. Accordingly, for this study, data on the sales of EuroMillions tickets by operator for each individual drawing was collected for the period from 2004 to 2019.

2 EuroMillions: price, prizes, and changes in game design

EuroMillions drawings were held once a week, on Friday, until May 2011, when it was decided to increase the number of draws per week adding Tuesday as a draw day. The price for a single ticket differs by country depending on the local currency. As of September 2016 it is set at 2.5 euros, 2.5 GBP, or 3.50 CHF. Before this date, the price was set at 2 euros, 2 GBP, and 3 CHF, respectively. Nowadays the game is operated under a monopoly market structure in Belgium, the UK, France, Ireland, Portugal, Spain, Luxemburg, and Austria, where there is only one lottery operator allowed to sell EuroMillions lottery tickets. That was also the case of Switzerland till 2011, since then tickets are sold by two lottery operators: Swisslos and Loterie Romande - the former operates the game in the cantons of German-speaking Switzerland and Ticino, while the latter operates in the French-speaking cantons of Vaud, Friborg, Jura, Valais, Neuchâtel, and Genéve.

As previously mentioned, EuroMillions is a pari-mutuel lotto type game where prizes are based on each draw sales level and in which not claimed jackpots roll over to the next draw. The game consists in choosing five numbers from a matrix of fifty and two lucky stars (additional numbers) from a second matrix of twelve–1 chance in 140 million of winning. Table 1 details the current prize structure of the game. Top right column shows the percentage of funds that are allocated to each prize category. It should be noted that for the jackpot prize category, 50% of the prize pool is allocated for the first five draws of the cycle and it falls to 42% for the rest of the draws within a particular draws cycle. The far right column reports the average prize amount per category. The average jackpot exceeds 65 million euros, meanwhile the second and third prizes use to distribute, on average, 415,565 and 50,719 euros respectively. From these levels onwards, the amounts distributed per category are significantly reduced to 4.17 euros for the ticket holders who matched two numbers in the matrix.

It should also be noted that a minimum prize of 17 million euros is guaranteed for the first draft of each cycle (it was 15 million euros until September 2016), being a cycle the successive drafts that took place until one player guesses the winning combination, or a “SuperDraft” is carried out. In 2016, the “Big Fridays” draws were introduced offering twice a year a guaranteed minimum prize of 120 million euros.

Table 1 EuroMillions prize structure
Full size table

Just like there is a minimum prize, as for 2019 the prize structure also had a cap of 190 million euros (previously it was 185 million euros, and even before it was 180 million euros). Once the cap was reached, if there is no jackpot winner in the following draw, the corresponding amount will roll down and will be distributed among the winners of the next category.

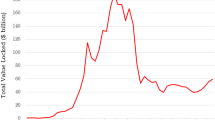
As for the jackpot size, Fig. 1 shows the EuroMillions jackpot values for the analyzed sample period, where a great volatility can be observed. From 2004 to 2019, the average jackpot was 48.7 million euros and the maximum jackpot reached was 190 million of euros (the limit set by the game rules).

Fig. 1
figure 1

EuroMillions jackpot

Full size image

3 EuroMillions’ jackpot sharing: an insight into implicit transfer of funds among countries

Who are the winners and losers from EuroMillions? If demand behaves differently across countries and so the odds of hosting a national winning player, some countries may then systematically benefit from the funds that have been contributed to the prize pool by the rest of the countries. This could lead to interesting issues about jackpot sharing in countries of different market sizes, questioning the optimality of game design and raising some concerns about implicit transfer of funds among participant countries.

This could be first addressed by studying data for EuroMillions jackpot winners’ distribution and the corresponding jackpot size claimed. Table 2 shows the amount of the jackpot prize distributed across countries within the EuroMillions market and the corresponding payout rate, the amount of euros received per euro wagered, the number of times the country won a jackpot and its proportion. In absolute terms, the UK is the jurisdiction that has received the most from the jackpot pool, followed by Spain and France, while Luxembourg and Austria are the countries that have received the least. The three countries that benefitted the most are also the ones that concentrate most of the market size (population) leading the demand for EuroMillions lottery tickets during the analyzed period. These three countries are also the countries that more times have won the jackpot. In particular, Spain has won the game 88 times, meanwhile France and United Kingdom have won the game 81 and 77 times respectively. On the other hand, Luxembourg and Ireland are also the countries that have won the least, 2 and 15 times respectively.

Notwithstanding, one would expect that countries receive their ‘fair share’ of jackpot wins given their contribution to aggregate sales, i.e., the payout rate would be similar across countries. However, it is possible that if the sensitivity of certain countries’ sales to jackpot size is particularly high, then it would be expected that their jackpot wins would be disproportionately likely to be in high payout draws (Baker et al., 2016).

Table 2 EuroMillions sales, jackpot wins’ distribution across countries and payout rate
Full size table

Such indeed has been the case. Ireland is by far the country that has the highest jackpot payout rate (0.44 euros per euro staked), even though it is located near the bottom of the sales and number of jackpots won rankings. Also, Belgium and the UK show a payout rate over the average. It seems likely therefore that the greater willingness of these countries’ players to increase their purchases when the jackpot is high will have generated relatively frequent headline-making payouts to these countries noted an ‘implicit funding’ to these countries’ players from players in other countries.

To further elaborate on this point, each country’s net payout balance is considered. The net payout balance reflects the difference between what each country receives per euro wagered, weighted for the (predicted) probability of hosting a jackpot winnerFootnote 2, and that country’s contribution to the jackpot pool, weighted for the relative size of the country with respect to the size of the market. Figure 2 shows the distribution of each country’s net payout balance for all EuroMillions draws.

Obviously, as the net payout balance variable is defined, given that in general the expected value of lotto games is negative and that outliers are excluded, it would always take negative values. The closer to zero means that the country receives as much as it contributes, the farther away, the more it contributes than it receives. Clearly, Portugal and Luxembourg seem to be the losers in the EuroMillions market (indeed, these are the two countries with the lowest jackpot elasticity), while the three countries that concentrate sales of EuroMillions lottery tickets (France, Spain, and the UK) exhibit a more balanced net payout.

Positive net payout balance values would only occur when the jackpot size is high enough to generate a positive expected value. These draws, generally considered as outliers, are displayed in Fig. 3. As already discussed in the analysis of the jackpot payout ratio, Ireland is the country with the highest net payout balance when all draws are considered including those where the size of the jackpot allows a positive expected value to be offered. Certainly, when the size of the jackpot is very high, the luck of the leprechaun seems to be with Irish players.

Fig. 2
figure 2

Net payout balance distribution by country, excluding outliers

Full size image
Fig. 3
figure 3

Net payout balance distribution by country, including outliers

Full size image

In an attempt to explain observed differences, it could be argued that as sales increase with jackpot size more in certain countries (high jackpot-sensitive countries) than in others, therefore increasing their market share, it could be expected that these countries’ chances of having a national winning player would also increase. High jackpot-sensitive countries could then benefit from the funds that have been contributed to the prize pool by the rest of the countries along a given draw cycle, increasing their net payout balance. This could raise some jackpot sharing concerns, should some countries’ demand be more sensitive to the jackpot size, and therefore these countries are more likely to win the jackpot than other countries within the EuroMillions market.

4 The market for EuroMillions and socioeconomic context

4.1 EuroMillions sales trends and market share

As mentioned, jackpot sharing and net payout balance distribution ratios could be explained by differences in EuroMillions consumption patterns. In order to analyze such correlation, data on sales for EuroMillions were collected by operator in a draw-by-draw basis from the first draw in 2004 until the one held on December 3rd, 2019, resulting in a sample of 1271 draws. Since not all the countries joined the EuroMillions market at the same time, observations for those draws when Spain, France, and the UK were the only participant countries were removed and so the first 34 draws of the game are not considered in this study.

With respect to the among-country variability of EuroMillions sales, Table 3 shows sales revenue and number of tickets sold in absolute and per capita terms (including autonomous cities) from 2004 to 2019. The overall revenue average is 7.330 million euros, with four countries (UK, France, Portugal, and Spain) having a particularly high average (well above 10 million euros). These four countries account (on average) for almost 80% of each draw sales. In terms of sales per capita Portugal is the country where the most EuroMillions tickets are sold, particularly, in this country 0.486 EuroMillions tickets are sold per inhabitant, i.e., for every two Portuguese, one EuroMillions ticket is sold. Luxembourg is the second country where EuroMillions tickets are sold the most, with 0.357 tickets per inhabitant, which means an average sales revenue of 0.748 euros per capita.

Table 3 EuroMillions sales
Full size table

Figure 4 plots each country’s sales share for each draw and jackpot level within the sample. The vertical axis measures the sales share of each country meanwhile the horizontal axis measures the jackpot (in millions of euros) reached by the game. This figure provides information about the sales share of each country and how it changes as the jackpot increases. It is evident that there are significant variations in market size among countries. For example, the UK, France, Spain, and Portugal each account for approximately 20% of the sales share, while other countries contribute less than 10%. Moreover, it can also be observed that countries such as Belgium, the United Kingdom, and Austria increase their EuroMillions sales as the jackpot size increases, while France, Portugal, and Spain significantly reduce their sales share.

The evidence from Table 3; Fig. 4 shows that sales for EuroMillions tickets have enough variability in both dimensions to allow to distinguish between temporal and geographical effects.

Fig. 4
figure 4

EuroMillions market share per country

Full size image

4.2 Socioeconomic context

It is expected that EuroMillions sales respond to changes in market socioeconomics, such as each country’s GDP (income) and the population (market size). But also, to other socioeconomic variables including the unemployment rate, the education level, and the average age by gender per country which are expected to somehow affect the demand for lottery tickets. Particularly, some previous studies found an ambiguous relationship between unemployment and lottery sales, even no correlation was found (DeBoer, 1990; Oster, 2004). Thus, some papers, including Mikesell (1994) and Scott and Garen (1994) concluded that unemployment has a positive effect on lottery tickets sales, while others, e.g. Blalock et al. (2007), found a negative relationship.

Table 4 Summary statistics on socioeconomic variables by country between 2004 and 2019
Full size table

As for the relationship between the education level (here the percentage of the population with tertiary-highest level-education) and lottery sales, a number of contributions including Clotfelter and Cook (1987 and, 1989), Kitchen and Powells (1991) and Farrell and Walker (1999) concluded that a negative correlation exists. However, in a more recent contribution, Han et al. (2016) contradict these results finding a positive relationship. Regarding age and gender, Brochado et al. (2018), using data from Portugal, concluded that elderly people tend to buy tickets of “more traditional” lotto games. Moreover, they found that lotteries, including EuroMillions, are played more by men than women, with financial reasons as the main driver of the demand.

Basic descriptive statistics of the considered socioeconomic variables are reported in Table 4. Throughout the analyzed period, economies from the countries playing EuroMillions exhibit significant heterogeneity in terms of socioeconomic factors. Income levels (measured here as quarterly GDP per capita) in Switzerland or Luxembourg are clearly above the rest of the countries, while Spain and Portugal have the lowest GDP per capita figures. In terms of population, data suggests that UK, France, and Spain would be expected to concentrate sales of EuroMillions lottery tickets as they account for 80% of the market size (almost 220 million inhabitants). Unemployment rates range between 5 and 10%, except for those countries that seem to have suffered most from the recent economic crises, such as Spain and Portugal, and, to a lesser extent, Ireland. A similar picture emerges for all countries regarding the percentage of the population with tertiary (highest level) education (with the exception of Portugal) and the age structure of the population.

5 Exploring EuroMillions market share trends

5.1 Empirical model

The available information has a panel data structure that allows observing both EuroMillions lottery tickets sales and sales market share at the country level. First, a simple model for sales, with country and draw fixed effects and socioeconomic variables as covariates is estimated. Sales of EuroMillions tickets at the country level is considered as the outcome variable and the following specification is estimated by using the within-group estimator which allows to control for the correlation of the unobserved effects at the country level and the explanatory variables:

$$ \ln Y_{{itj}} = \alpha _{i} + \gamma P_{t} + \beta X_{{ij}} + \tau T_{t} + \mu DW_{t} + \theta J_{c} + u_{{it}} $$
(1)

where Yitj is the EuroMillions sales per capita in country i in draw t of year j; αi stands for the country fixed effects; Pt is the price of a single ticket (the same in euros for all countries); Xij is a vector of the previously described covariates that could affect the outcome variable (GDP, unemployment rate, education level, and the average age by gender); Tt captures the time trend (number of draw) which allows the study to control for the effect of factors that may have simultaneously affected EuroMillions demand in all countries (this was modelled as quadratic in time); DWt is a dummy variable to indicate week-day draw; Jt is the natural logarithm of the minimum jackpot guarantee in each draw; and uit is the error term. Notice that the parameter of interest, measuring jackpot sensitivity is θ. Using a Hausman’s test we reject the null hypothesis of no correlation between the individual effects and the explanatory variables. This justifies the use of the within-group estimator.

Second, in order to estimate how EuroMillions market share varies across countries (use of ratio of sales avoids a lot of noise in the data) a fractional outcome probit model is estimated. Using quasilikehood estimators, fractional regressions model the mean of the dependent variable, each country market sales share here, conditional on the aforementioned set of covariates-including now the population-(Papke & Wooldridge, 1996, 2008):

$$ S_{{ijt}} = \phi \left( {\alpha _{i} + \gamma P_{t} + \beta X_{{ij}} + \tau T_{t} + \mu DW_{t} + \theta J_{t} } \right) $$
(2)

where now \({S}_{ijt}\) is the sales share in country i in draw t of year j.

5.2 Results

Table 5 shows the estimated coefficients for both the fixed effects model and the fractional outcome probit model. Since sales of lottery tickets depend on jackpot size but also contribute to jackpot pool-prizes are based on a percentage of sales revenue-the use of jackpot size may raise endogeneity issues. Instead, it is proposed to use the amount of the rollover (which is equal to Jt−1 when there is no jackpot winner in the immediately previous draw) or the minimum guaranteed jackpot that is offered in a given draw when there has been a winner in the immediately previous one. This provides an exogenous measure of each draw (minimum) jackpot that leads to estimated elasticities to be interpreted as lower bounds. The first column reports the estimation results of the specification in Eq. (1), where the dependent variable is the log of the EuroMillions per capita sales. Overall, the estimated lower bound of the jackpot elasticity of the demand for EuroMillions is 0.286. In order to disentangle whether some differences among countries exist, the model in Eq. (1) is re-estimated but including interaction terms between the minimum-jackpot size and a set of country dummies (Luxembourg is the reference country). Results in the second column show that Austria, Ireland and the UK are the highest jackpot-sensitive countries with an estimated lower bound of the jackpot elasticity exceeding 0.3, while Portugal exhibits the lowest one. These results are in line with those of Roger (2011), who found the demand for EuroMillions to be much less sensitive to the jackpot size in Portugal than in UK.

As for the market share model specifications, results from the fractional outcome probit model are reported in the third column. As previously discussed, although the jackpot size positively impacts the demand for EuroMillions lottery tickets in all jurisdictions, some countries experience an increase in their market share to the detriment of others, producing a significant change in the demand distribution across countries. From Table 5, it can be observed that high jackpot sensitive countries are those increasing their market share (UK, Austria, Ireland, Belgium and Switzerland), while other countries, including Portugal, France and Spain see their market share shrinking.

To check robustness of results, tests were conducted to determine whether the coefficients for the considered countries are statistically different. The p-value obtained for the coefficients corresponding to both the ticket sales and the market share model in each country are close to zero, which can be interpreted as jackpot-elasticity being significantly different across countries.

Although it is aimed to test whether the unequal jackpot distribution among countries is caused by sales patterns of lottery tickets and market share trends within the market for EuroMillions, the results of the control variables included in all model specifications in Table 5 are also commented. Since the model we are estimating corresponds to a demand equation, we included, as previously mentioned, a proxy for the income at the country level (GDP) and other socioeconomic variables (monthly unemployment rate, a proxy of the education level and the average age per gender and year), all of them having geographical and time variation. To account for time-effects, all model specifications also include categorical variables for the year, the day of the week in which every draw in the sample takes place and a quadratic time trend (draw number). The price of a single ticket is also included in all model specifications.

Table 5 Estimates of the lottery sales and market share models
Full size table

In line with previous evidence, each country’s GDP per capita positively affects both lottery sales and market share. Particularly, the results for the sales model specifications show a significant effect for the GDP per capita, with an elasticity clearly below one (i.e., EuroMillions is a normal good). In addition, the estimated income elasticities show, as in Clotfelter and Cook (1991), that sales revenue increase less than proportionately with income (GDP), which makes EuroMillions, as an implicit tax, regressive. It is worth note that estimated income elasticities for EuroMillions are lower than those estimated by Oster (2004) using data from Powerball. As for the size of the market (population), a negative effect is found for the market share specification. With regards to the age of the population, increases in males age tend to reduce per capita sales of EuroMillions sales, meanwhile, opposite results are found for females age (see Barnes et al., 2011 for a detailed discussion on the age pattern for lottery gambling).

Regarding the unemployment rate, a negative effect on lottery sales is observed. This is in line with Blalock et al. (2007), while contradict findings in Mikesell (1994) and Scott and Garen (1994). Oster (2004) also found a negative, but no significant, effect of unemployment when analyzing Powerball sales.

In contrast to Lee et al. (2016), the estimated coefficient for education level is negative in the minimum-jackpot specifications, indicating that higher level of education negatively impacts the consumption of this kind of lottery game. This may be related to the implicit bias in the complexity of calculating the winning odds linked to this type of gambles.

Overall, demand for EuroMillions is found to be sensitive to socioeconomic conditions, while other studies suggest domestic lotteries are stable.

6 Concluding remarks

Lottery operators worldwide have seen multi-country lotteries as a possible solution to the drop in sales of traditional lottery games operated in national markets. Following the success of multi-state lotteries in North America, nine European countries agreed to launch the EuroMillions game in 2004 as the first European multi-country lottery game.

Using data at a country level from the market for EuroMillions lottery tickets over a period of 1237 draws, this paper analyzed the jackpot distribution among countries reflecting that some jurisdictions tend to systematically claim higher jackpots and achieve higher payout rates. The focus was on studying whether jackpot sharing is affected by different sales patterns and market share trends in the market for EuroMillions. In particular, it is tested whether market shares respond to the jackpot size suggesting that differences in jackpot elasticity of the demand among countries, which causes, at the same time, variations in the market share and draw winning odds per country, determine distribution of the jackpot wins.

Results from a panel data regression suggest that the demand for EuroMillions lottery tickets across countries differently reacts to minimum-jackpot size. Specifically, the lower bounds of the jackpot-elasticity of EuroMillions demand varies from 0.18 (Portugal) to more than 0.3 (Ireland, UK and Austria), allowing to distinguish high jackpot-sensitive countries in the EuroMillions market. However, while jackpot size positively influences the demand for EuroMillions lottery tickets in all jurisdictions, one interesting feature in the evolution of the game has been the extent to which trends in sales market share have differed across the nine member countries. Thus, it is shown that some countries experience an increase in their market share to the detriment of others, resulting in a significant demand distribution change among countries. As a result, high jackpot-sensitive countries might also increase the odds of hosting a jackpot winner, raising some concerns about implicit transfer of funds among countries in terms of their net payout balance as a consequence of the distribution of the jackpot wins.

All this could be interpreted as the greater willingness of some country players to increase their purchases when the jackpot is high have had generated relatively frequent headline-making payouts to these countries noting an ‘implicit funding’ to these players from players in other countries.

In line with previous literature on lottery markets, evidence is also found that income positively affects EuroMillions lottery sales, but with an income elasticity clearly below one, indicating that EuroMillions could be also understood as an implicit tax, regressive.

Some policy recommendations might be derived as to creating some mechanism (e.g. by way of a compensation fund) to allocate more funds to countries with a lower payout rate, redistributing part of EuroMillions revenues between these countries that systematically received less from the jackpot pool and so exhibit a more negative net payout balance. These funds could be earmarked to good causes, such as education, sport, etc. The results might also be further explored in the context of game design and the optimality of jackpot sharing. A new game design could exploit sales market share patterns by seeking to induce a pattern of wins that would typically (in the larger countries) produce a national winner at more appropriate intervals.

Finally, as advice for stakeholders, national media coverage could give more information on the game to a much wider audience than those who seek out the official results in those countries with the lowest payouts; so, there could be a greater sales response to increases in the jackpot size. An advertising effect to boost demand may work simply by reminding the public about that buying a single ticket just might change their life.