1 Introduction

To what extent are there gender differences in altruism or prosocial behavior? The answer to this question could be important for understanding for instance gender differences on the labor market, voting, volunteer work, and charitable giving. In this paper we do a meta-analysis of gender differences in the dictator game (DG; Kahneman et al. 1986, Forsythe et al. 1994). While giving in this game is not necessarily due to altruistic concerns—for example the results of List (2007), Krupka and Weber (2013), Bardsley (2008) and Dana et al. (2006) suggest that DG giving is influenced by the strategy space, reference points and expectations of social norms—this is the most commonly studied game to understand non-strategic prosocial behavior. In the standard DG, one individual—the dictator— anonymously decides how to split a windfall endowment with another individual. In an alternative version of the DG, the dictator decides how much of the endowment to give to a charity (charity DG) (Eckel and Grossman 1996).

We include both of these standard windfall gains versions of the DG and collect raw data from 53 papers, both published work and working papers, with a total of 117 conditions and 15,016 unique individual observations. We only include experiments where monetary endowments are windfalls, the most selfish option is to give nothing, the price of giving is equal to 1, both men and women are represented, and where no reciprocity is involved.

There are several previous papers studying gender differences in DG giving (with early papers including e.g. Eckel and Grossman (1998), Bolton and Katok (1995), Andreoni and Vesterlund (2001), and with more recent reviews including e.g. Croson and Gneezy (2009) and Bertrand et al. (2010)), with individual studies typically finding that women on average give more or that there is no statistically significant gender difference. Most related to our study is the extensive meta-analysis of DG giving by Engel (2011). Engel, using reported coefficients rather than raw data, found that women on average gave 5.8 percentage points more than men.

Analyzing raw data allows us to include studies that collected gender information but either did not include gender in their analysis, or included gender but did not explicitly publish any results related to gender in the paper. Including studies where gender is not the main variable of interest could reduce publication bias; as statistically significant gender differences may be more likely to be published. Compared to Engel (2011), we have a substantially larger sample size for estimating the gender difference and we also explicitly compare DGs where the recipient is a person or a charity.

The paper is organized in the following way. Section 2 describes the inclusion criteria and data. Section 3 describes the meta-analysis methods and Sect. 4 the results. Section 5 concludes.

2 Inclusion criteria and data

2.1 Inclusion criteria

Our inclusion criteria are summarized in Table 1. We restrict our analysis to the original windfall version of the dictator game (see Forsythe et al. 1994), where the experimenter unconditionally transfers an endowment to dictators and dictators decide how much of the endowment to give to recipient players. This restriction excludes experiments where participants first earned their endowment from performing a task. We also exclude versions of the Take Game, where the dictators also have the option to take money from recipients. Both double-blind (where neither the recipient nor the experimenter can identify individual dictator decisions) and single-blind studies (where only the recipient is blind to individual dictator decisions) are included. In the initial stages of the project we had planned to only include double-blind studies, but this was revised when we realized that our sample would be too small (around 75% of our sample consists of single-blind studies). We exclude studies without a monetary endowment, but have no further restriction with respect to the size of the monetary endowment and we also allow conditions where only a randomly drawn share of participants are paid. We exclude studies where participants are matched and known to each other (for example spouses).

There is no participant age restriction, but as we require monetary incentives we exclude studies on young children. Only studies where the price of giving is equal to 1 are included (excluding studies with multipliers). We also limit the inclusion to conditions where there is no reciprocity involved, while we allow individuals to play the DG in both roles.

There is also variation between studies in the choice set of dictators. To give an example, endowments may be 4$ and dictators can give x$ to the recipient, where \(x \in \{0, 1, 2, 3, 4\}.\) We include all studies where dictators are allowed to give or keep the full endowment, making no further restriction on the choice set. Thus, in the extreme case dictators play an all or nothing game and decide whether to either give or keep the endowment, which is the case in one of our included papers (Tinghög et al. 2016). We create a variable we call Partition, to control for the choice set in an experiment, which is defined as the smallest share that can be donated. Finally, we only include studies that have data on gender and where both genders participate (excluding single-gender studies). The search for studies started on the database Econlit with a search for the keyword “Dictator game”. This gave us 513 hits and if the studies fitted our inclusion criteria we sent out an email to request the raw data from the corresponding authors. We did not systematically check for unpublished papers. In May of 2018 we also sent out a request to the experimental email group (ESA) describing our sample of included studies and our inclusion criteria, and we closed the inclusion of studies in September 2018.

Defining inclusion and exclusion criteria involves a certain degree of arbitrariness and there is a tradeoff between including studies that use as similar experimental design as possible, which allows for internal validity, and expanding the inclusion criteria to more heterogeneous designs that may increase the statistical power and the generalizability of results. We potentially lose external validity when for instance not including studies varying the price of giving and studies where the dictator earns the endowment (which excludes experiments such as the all or nothing experiment in Bekkers (2007), where the dictator earns the endowment in the experiment). However, we think the standard DG version is a reasonable starting point for analyzing gender differences in the dictator game. Generosity is unconditional, with no involvement of reciprocity, and involves no efficiency gains by changing the size of the endowment by giving and no party has done more (or less) to earn the endowment. We do include charity organizations as recipients which may increase external validity, as donating directly to anonymous individuals as in the standard DG is rare outside of the laboratory. We did not restrict our inclusion criteria to studies specifically designed to study gender differences, but included all studies meeting our inclusion criteria that had collected data on gender. It could be argued that ideally only studies designed to study gender differences should be included as they may be designed to eliminate confounding experimental designs that could influence the gender gap. However, it is not straightforward to define which studies were ex ante designed to study gender differences, and the observable “gender studies” may be published because they found gender differences and not due to their superior designs leading to publication bias. In an attempt to test if observable gender studies differ, we compare results for studies having gender in the title of the paper to the other studies in our data. An additional potential limitation of our data collection is that we did not explicitly search for discussion papers, which may induce publication bias. In Sect. 4.5 we test for publication bias using Egger’s and Begg’s tests to assess the importance of this limitation. The final sample consists of 15,016 unique observations where we also have gender data.

Table 1 Exclusion criteria used in the meta-analysis
Full size table

2.2 Data

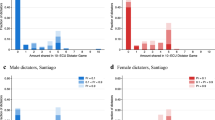
In Table 2 we present summary statistics of the included data. The full sample consists of 15,122 observations but for some observations either gender or the dictator’s decision is missing or have been incorrectly coded. Excluding those observations gives us a sample of 15,016 unique individual observations where we have both gender and the donation decision by the subject.Footnote 1 In Fig. 1 we plot the distributions of DG giving for each gender and by recipient type. As previously shown by e.g. Engel (2011), the distribution of DG giving in the standard DG is concentrated at giving nothing or half. In the charity DG a substantial fraction of subjects also give the entire endowment. When we exclude the ‘all or nothing’ study (Tinghög et al. 2016) the density on the two extreme points of the distribution decreases somewhat for the charity DG.

Fig. 1
figure 1

The full sample contains 15,016 unique individual dictator decisions. There are 11,802 observations in the standard DG and 3214 observations in the charity DG in a. Excluding the ‘all or nothing’ study in b reduces the sample size in the charity DG to 1812 observations

Full size image
Table 2 Descriptive statistics of the data included in the meta-analysis
Full size table

3 Meta-analysis methods

By collecting the individual participation data, a meta-analysis can either be done by the traditional approach of pooling effect sizes in a random effects model or with individual regression models. As Burke et al. (2017) note, these methods in general produce similar results and differences largely occur when researchers use different modelling assumptions. We begin by performing traditional random-effects meta-analysis which allows us to estimate the heterogeneity in the gender difference across the conditions included in the meta-analysis (the heterogeneity is captured by the estimate of Tau, which is the standard deviation in the true effect size across the conditions).Footnote 2 We then estimate one stage individual regression models where we also provide several robustness checks of our results. Several experiments contain multiple conditions. These conditions create a natural clustering of the individual observations in our data. In total we have 117 conditions from 53 papers, which allows us to treat each condition within an experiment as a separate cluster. We estimate a separate effect size for each condition in the random-effects model, and we cluster the standard errors on the condition level in all individual regression models.Footnote 3 Our definition of a condition follows the definition within each paper. If the same condition within an experiment is conducted in different countries (except if the study is done online (MTurk)), we define these as separate conditions to account for the country level clustering of the experiments.

We estimate Eq. (1) where \(S_{ij}\) denotes the share of the endowment donated by participant i in condition j, X is a vector of individual covariates and Z is a vector of treatment condition controls. We also replace Z with a condition fixed effect using dummy variables for each condition.Footnote 4 The gender coefficient \(\beta _1\) and the interaction between gender and charity recipient \(\beta _3\) are the coefficients of interest,

$$\begin{aligned} S_{ij} = \beta _0 + \beta _1 {\text {Female}} + \beta _2 {\text {Charity}} + \beta _3 ({\text {Female}}\star {\text {Charity}}) + \beta _4 X_{ij} + \beta _5Z_j + \epsilon _{ij}. \end{aligned}$$
(1)

4 Results

We use a significance threshold of \(p<0.005\) for “statistically significant evidence” and a threshold of \(p<0.05\) for “suggestive evidence” in our results below in line with the recent recommendation of Benjamin et al. (2018). All our tests are two-sided.

4.1 Random-effects meta-analysis

Figure 2 shows a forest plot of the estimated gender gap for each of the 117 conditions in our sample; and the random effects results are also reported in Online Appendix Table A1. We show the results both separately for the standard DG and the charity DG, and pooled for both DG versions. Women give on average 4 percentage points more than men and the gender gap is statistically significant. The average donation in our data is 32% of the endowment (see Table 2) and women on average give 13% more than men (Cohen’s \(d=0.16\))Footnote 5. The standard deviation in the true effect size–the variation between studies over and above sampling variation–is slightly higher than the average effect size at \({\hat{\tau }}\) = 4.6 percentage points. To further assess heterogeneity in the gender gap, we estimate the gender gap in the standard DG and the charity DG respectively.

In the standard DG where the recipient is another participant, women on average donate 2.3 percentage points more than men, with a standard deviation in the true effect size of \({\hat{\tau }}\) = 3.3 percentage points. In the charity DG the gender gap is larger, with women on average giving 10.9 percentage points more than men with a standard deviation in the true effect size of \({\hat{\tau }}\) = 6.4 percentage points. A meta-regression in Table A2 confirms that there is a statistically significant difference in the gender gap between the standard DG and the charity DG. The gender gaps of 2.3 percentage units in the standard DG and 10.9 percentage units in the charity DG imply that women give 9% more than men in the standard DG (Cohen’s \(d=0.10\)) and 26% more than men in the charity DG (Cohen’s \(d=0.35\)).

Excluding the ‘all or nothing’ conditions reduces the gender gap found in the overall sample from 4 to 3.1 percentage points (Cohen’s \(d=0.13\)), but it remains statistically significant with heterogeneity in the true effect size of \({\hat{\tau }}\) = 3.8 percentage points. In the charity DG the gender gap is reduced from 10.9 to 8 percentage points (Cohen’s \(d=0.27\)), with heterogeneity \({\hat{\tau }}\) = 4.7 percentage points. The smaller gender gap in the charity DG decreases the meta-regression estimate of the difference in the gender gap between the standard DG and the charity DG from 8.7 to 5.9 percentage points.

Fig. 2
figure 2figure 2

Random effects model (estimated with the Ipdmetan command in Stata). a Contains experiments with the standard DG and b contains experiments with the charity DG. The diamonds indicate the estimated effect size (and the CI) for each sub sample and the pooled (overall) effect size is at the bottom

Full size image

4.2 Individual level regression analysis

In Table 3 we report the results of the individual level regression analysis. In column 1, where we only include a binary variable for the gender of the dictator, women give on average 4.8 percentage points more than men, which is similar to the gender gap of 5.8 percentage points reported in Engel (2011). Controlling for the charity DG in column 2 gives an overall gender gap of 4 percentage points, which is identical to the gender gap found with the random-effects meta-analysis.Footnote 6 In column 3-6 we add an interaction between the female variable and the charity DG. The gender gap is statistically significantly larger in the charity DG compared to the standard DG in all four specifications, with an interaction coefficient of between 9.3 and 9.8 percentage points. Women give on average around 2 percentage points more than men in the standard DG and 11–12 percentage points more in the charity DG. These gender gaps are statistically significant for both types of DG in all the four regression models, except for the standard DG in column 3 where there is suggestive evidence of a gender difference (p = 0.0058). If we exclude the ‘all or nothing’ conditions, the results are similar (see Table 4).

Table 3 OLS results of the estimated gender gap in the DG. Standard errors clustered on the condition level in parentheses
Full size table
Table 4 OLS results of the gender difference in the DG, excluding the “all or nothing” DG study. Standard errors clustered on the condition level in parentheses
Full size table

4.2.1 Robustness checks

In a robustness test, we estimate a mixed random effects model where we allow for both the intercept and the gender gap to have random effects on the condition level.Footnote 7 These results are reported in tables A3 and A4. We find very similar results in these estimations, although the pooled gender gap of 4.6 percentage points is slightly higher. The gender gap in the standard DG is around 2 percentage points and the gender gap in the charity DG is 11 percentage points and significantly higher than in the standard DG. The gender gap is statistically significant in both the standard DG and the charity DG, both with and without the ‘all or nothing’ conditions included.

In a second robustness test, we re-estimate our results using a tobit model. The action space is limited to a donation between 0 and 1 even though some subjects may possibly prefer to take from the recipient or give more than the endowment. In the tobit model we allow censoring to occur at both 0 and 1. We report these results in tables A5 and A6, and the coefficients in these tables should be interpreted as the gender gap with respect to the latent (that in theory can take on both negative values and values above 1) dependent variable. The tobit model yields higher estimates of the gender gap, with a gender gap of 6.6 percentage points in the pooled sample. The gender gap is around 4 percentage points in the standard DG and 17 percentage points in the charity DG, and this difference is statistically significant. The gender gap is statistically significant in both the standard DG and the charity DG, both with and without the ‘all or nothing’ conditions included. As can be seen from Fig. 1, men are more likely to donate zero in both the standard DG and the charity DG and women are more likely to donate the full endowment in the charity DG. These differences at the censoring points of 0 and 1 result in a higher estimated gender gap in the tobit model when these observations are interpreted as being censored.

So far we have measured the gender gap as the difference in the share of the endowment donated. As both men and women donate more in the charity DG it is possible that the gender gap is larger in percentage points but not in terms of percentage of the average donation. We test this in an additional robustness check where we instead use the measure from Eq. (2) below, where we divide the individual share donated in the DG \((s_{ij})\) by individual i that took part in condition j by the average donation in condition j,

$$\begin{aligned} {\hat{s}}_{ij} =\frac{s_{ij}}{\overline{s_j}} . \end{aligned}$$
(2)

Multiplying this measure with 100 allows us to interpret each observation in terms of percent of the average donation within the condition that the participant took part.

Our results are confirmed by this standardization when we include all the DG studies in Table A7. Women on average give around 9% more than men in the standard DG and 25% more in the charity DG; and this difference is statistically significant. In Table A8 we carry out this analysis excluding the “all or nothing” DG study. This reduces the gender gap in the charity DG by one fifth to around 20%, and the gender gap is not statistically significantly larger in the charity DG any more (but there is suggestive evidence for a larger gender gap in the charity DG in all models). When we measure donations in relative terms the evidence of a larger gender difference in the charity DG is thus less strong, as the donations are larger on average in the charity DG compared to the standard DG.

4.3 Gender in the title of the studies

Of the 53 (117) papers (conditions) included in our study 16 (31) have gender in the title of the paper, and we test if the gender difference differs between papers with and without gender in the title.Footnote 8 If we observe such a difference we cannot tell if this is due to that studies explicitly designed to study gender differences lead to different results, or if the difference is due to that studies with gender in the title were framed as studies of gender differences and published because they found a significant gender difference. We return to the issue of publication bias in Sect. 4.5.

A meta-regression in Table A9 provides no evidence that the gender gap differs between papers with gender in the title and the other DG studies. We also estimate Eq. (1) in an OLS model in Table A10, where we include a dummy for “gender in the title”, that is interacted with the female variable to test if the gender gap is significantly larger in papers with gender in the title. The null results from the meta-regression are confirmed in the OLS model. In Table A10 we also report the estimated gender difference among the subset of papers with gender in the title (it is the sum of the gender coefficient and the interaction coefficient) and it is between 3.8 and 3.9 percentage points when we include both types of DGs, and between 2.6 and 2.9 percentage points for the standard DG and between 10 and 10.8 percentage points for the charity DG. The gender difference is statistically significant in all models except in model 3 where there is suggestive evidence.

4.4 Statistical power

In Table A11 we summarize the statistical power to detect the gender gap found in this meta-analysis. The power estimates are based on estimating the mean difference between males and females using two-sided hypothesis testing, and they are based on the average standard deviation of the standard DG papers (STD = 0.233) and the charity DG papers (STD = 0.310). We use the random effects results of a gender difference of 2.3 percentage units in the standard DG and 10.9 percentage units in the charity DG to estimate power in each DG type; but we also report power for the overall gender difference of 4 percentage units for both types of DGs. We do the power calculations for tests at the 5% level, as that is most commonly used in the literature. But we also report results for the more stringent 0.5% threshold used in this paper.

We calculate the sample size as the total number of observations in a paper, which means that we sum over all conditions within the paper. The median sample size in the standard DG papers is 130 observations, which yields a statistical power of only 9% (16%) to detect an effect size of 2.3 (4) percentage points. To reach 80% power a paper would need around 3224 (1068) observations to detect an effect size of 2.3 (4) percentage points in the standard DG. The median sample size for the charity DG papers is 192 observations, yielding 68% (14%) power to detect an effect size of 10.9 (4) percentage points. All the above estimates are based on tests at the 5% level, and using the more stringent 0.5% threshold leads to even lower power (see Table A11).

Some of the included DG studies were not designed to study gender differences, which may explain the inadequate power. However, the power for studies that have gender in the title of the paper are only slightly higher. There are 13 papers in the standard DG and three papers in the charity DG that have gender in the title of the paper. The median sample size of the 13 standard DG studies is 191, which gives 10% (22%) statistical power to detect a 2.3 (4) percentage units gender difference. The median sample size of the three charity DG studies is 216, which gives 73% (16%) statistical power to detect a 10.9 (4) percentage units gender difference.

4.5 Publication bias

Figure A1 shows funnel plots for the full sample, the standard DG sample, and the charity DG sample with the estimated effect sizes on the x-axis and the corresponding standard errors on the y-axis. An asymmetric plot could be evidence of publication bias, where only significant studies are published. The outliers at the far right in Figure A1 (a) and A1 (c) are two of the ‘all or nothing’ conditions. The funnel plots in Figure A1 do not provide any clear visual evidence of publication bias. In Figure A2 we restrict the funnel plots to papers with gender in the paper’s title. There is no clear visual evidence of any asymmetry in these plots either.Footnote 9

To statistically test if there is evidence of publication bias we have employed Egger’s and Begg’s tests of publication bias in Table A12. We find no evidence of publication bias in either the pooled sample or when looking at each dictator game separately. We furthermore carry out these tests including only papers with gender in the title, but we do not find a statistically significant publication bias in these tests either.

5 Discussion

Our results suggest that women give more than men on average in both the standard and the charity DG, but the gender gap is modest in size (4 percentage points in the pooled data and a Cohen’s d of 0.16). This is similar to the gender gap in the meta-analysis by Engel (2011). Looking at the standard DG and the charity DG separately, we find that the gender gap is 2.3 percentage points (Cohen’s \(d=0.10\)) in the former and 10.9 percentage points (Cohen’s \(d=0.35\)) in the latter (and if we exclude the “all or nothing study” this gender gap decreases to 8 percentage points; Cohen’s \(d=0.27\)). It is interesting to compare these results to the recent study by Falk et al. (2018), measuring economic preferences in a global preference survey with a sample size of about 80,000 individuals. They measured altruism by combining the answers to two survey questions. One of these was a hypothetical donation question similar to the charity DG and the other question measured the willingness to give to good causes on an 11-point scale. They found significantly higher altruism for women than for men, with an estimated gender difference of 0.10 Cohen’s d units. We find the same effect size as Falk et al. (2018) in the standard DG. For the charity DG we find a larger effect size than in Falk et al. (2018), but this effect size is also less precisely estimated in our study.Footnote 10

The estimated gender differences in our study implies that the typical DG study in the literature is underpowered to test for gender differences. Power problems have previously been reported in economics in general (Ioannidis et al. 2017) as well as for the DG (Ortmann and Zhang 2015). However, for some of the datasets included in the meta-analysis, the researchers may never have had the intention to study gender differences and may have been well powered to study their main research question. Our power results should thus mainly guide future research that aims to explore gender differences in DG giving and moving forward researchers may need substantially larger sample sizes than what has previously been the norm.

There are also several additional caveats to our conclusions. First, it is not clear whether important datasets are missing from our analysis, and whether the inclusion of these would change any of our conclusions. Publication bias may lead to inflated effect sizes in meta-analysis, which was also observed in a recent study by Kvarven et al. (2020) comparing meta-analyses to pre-registered multiple-laboratory replication projects. We tested for publication bias and found no evidence in this direction; this result, however, could be biased by the exclusion of unpublished papers from the sample. We find substantial heterogeneity in the gender gap between conditions. In our paper we explore heterogeneity with respect to if the recipient is a charity organization or another participant, but there is much more work that can be done in this regard. One should also be careful to generalize our findings to also hold in other designs such as when the price of giving varies or when the dictator earns the endowment. For example, Andreoni and Vesterlund (2001) report gender differences to be conditional on the price of giving.

Our results suggest a larger gender difference in the charity DG compared to the standard DG, although the strength of this evidence depends on if the “all or nothing” charity DG study is included or not and if the difference is measured in absolute or relative terms (as the average donations are higher in the charity DG). To draw strong conclusions about whether the gender difference is larger in the charity DG than the standard DG, it would be interesting to conduct a well-powered study to directly compare the gender difference in these two versions of the DG. A possible explanation for a larger gender difference in the charity DG could be that the charity DG is more closely related to empathy and altruism, whereas the standard DG is more related to fairness preferences (deviating from the 50/50 norm). In the standard DG it is unusual to observe donations over 50% of the endowment, whereas donating 100% of the endowment is relatively common in the charity DG. Altruism as a motivation for donations is consistent with a stronger tendency for such corner solutions of donating all or nothing. Further work is needed to better understand if the two types of DGs measure different forms of social preferences.