1 Introduction

A wealth of evidence has accumulated questioning some of the foundations of expected utility theory, and behavioral theorists have shown how these challenges can be accommodated (Wakker 2010). At the core of standard and behavioral economic modelling remains the assumption that people are endowed with well articulated and stable preferences. This fundamental assumption, however, has been challenged amongst others by Ariely et al. (2003), who have shown that preferences are initially malleable by normatively irrelevant anchors. People subsequently choose consistently with these initial preferences, and thereby end up with preferences that are characterized by what Ariely et al. (2003) call “coherent arbitrariness”. For a series of products that range from familiar (like an average bottle of wine) to unfamiliar (like listening to an unpleasant sound), they find substantial anchoring effects.

Economists often assign less weight to behavioral anomalies when they are obtained in non-repeated individual decision-making tasks. The line of reasoning is that anomalies may be eroded when people have relevant experience, for instance, as a result of trading in markets. To counter such skepticism, Ariely et al. (2003) included a treatment where subjects, after being exposed to an anchor, submitted a bid to avoid listening to an annoying sound. In the uniform-price sealed-bid auction, the three lowest bidders had to listen to the sound and each of them received a payment equal to the fourth lowest bid. Like in the individual decision-making treatment, sizable (and lasting) anchoring effects were observed in this treatment.

This paper aims to make two contributions. A first contribution is that we investigate the effects of uninformative anchoring on valuations for a familiar good in a large sample. This is important because previous papers have provided mixed evidence, from sizable anchoring effects (Ariely et al. 2003) to no anchoring effects (Fudenberg et al. 2012). Our paper stands out because of the combination of two features. First, we have a large sample of 316 subjects who are all exposed to the same anchoring protocol, while previous studies have often been based on rather small samples. Second, we use a transparently random anchor that subjects know to be uninformative because they generate it themselves with a ten-sided die.

A second contribution of our paper is that we investigate how elicited preferences are affected in a richer market setting than the one of Ariely et al. (2003), where subjects could not learn from others’ bids during the auction. We employ a standard double auction where traders are continuously updated about other traders’ bids and asks. We believe that a double auction provides a much better chance for market forces to erode initial traces of anchoring.

Our experiment consists of three phases. In the first phase, we apply a typical anchoring protocol: we ask whether subjects are willing to sell a bottle of wine for an individually drawn, random price. Then we elicit their valuation (Willingness-To-Accept) for the bottle of wine with the Becker–DeGroot–Marschak (BDM) procedure (Becker et al. 1964). In the second phase, we randomly assign subjects to either a small double auction market (n = 2) or a large double auction market (n = 8). Subjects participate in two trading periods, once as a buyer and once as a seller. In the third phase, we elicit each subject’s valuation once more.

The first phase of the experiment allows us to test whether a random anchor influences elicited valuations. We hypothesize that subjects’ valuations correlate positively with their anchors. We further conjecture that market experience will affect subjects’ elicited preferences. Subjects who are not completely sure about their preference may move into the direction of the preferences exhibited by other traders. This way, anchoring effects may diminish or even disappear. Thus, we hypothesize that the valuations elicited in the third phase will exhibit smaller (if any) anchoring effects. We also hypothesize that the large market will have a stronger effect on subjects’ preferences than the small market, and that anchoring effects are eroded more efficiently in the former.

Contrary to our first hypothesis, we observe no effect of the random anchor on subjects’ valuations. We believe our null result contributes to the literature on the robustness of anchoring effects. In Sect. 4, we position our paper in the literature and elaborate on what we can learn from our null result. There, we discuss the results of a concise meta-analysis of experimental papers that cite Ariely et al. (2003) and investigate the effects of anchoring on preferences.

We do find support for the idea that market participation affects how people value the bottle of wine. The variance in subjects’ elicited valuations after the market shrinks within trading groups. As expected, the effect of other traders’ behavior on a subject’s preference is stronger in the large market. These results underline the potential power that markets may play in eroding individual biases and noise. However, in this study, the double auction is not needed to avoid anchoring effects on valuations.

The remainder of the paper is organized as follows. Section 2 describes our experimental design and the hypotheses to be tested. Section 3 presents the results of the experiment. Section 4 provides a discussion of how our results fit in the literature.

2 Experimental design and implementation

We pre-registered our study on the American Economic Association’s registry for randomized controlled trials (Ioannidis et al. 2018).Footnote 1 The experiment was run at the CREED communication Lab of the University of Amsterdam. The communication lab has 16 soundproof, closed cubicles. The experiment was programmed in oTree (Chen et al. 2016). Subjects read the computerized instructions at their own pace (see supplementary material for instructions). No communication was allowed during the experiment. Subjects were informed that they could earn money as well as a bottle of wine. It was explained that the experiment consisted of three phases during which they would make five decisions. Subjects knew that one of those five decisions would randomly be selected for payment at the end of the experiment. In phase I, subjects made two decisions, in phase II they made two decisions and in phase III they made one decision. They only received the instructions for the next phase after a previous phase was finished.

There were two treatments which were varied between subjects. The Small market consisted of two subjects and the Large market of eight subjects. In each session, we simultaneously ran the two treatments. Subjects were randomly assigned to either one of them.

Phase I was identical for both treatments. At the start of phase I, the experimenter entered each subject’s cubicle with a ten-sided die (numbered from zero to nine). Subjects determined their own random anchor by rolling the die twice. The first outcome was the integer part and the second was the decimal part of the anchor price. For example, if a subject rolled six and four, the price was 6.4€. Hence, subjects knew that the anchor price was an uninformative draw in the range from 0€ up to 9.9€. This procedure took place in the presence of the experimenter to guarantee that the subjects entered the correct numbers.Footnote 2 We used this procedure of subjects generating the anchor themselves to make it fully transparent to our subjects that the anchor price was truly random.

The first decision of phase I was the anchoring question. The subjects were endowed with a bottle of wine, a picture of which was shown to them on their screen. Consequently, they were asked whether they were willing to sell the bottle to the experimenter for a price that corresponded to the anchor price that they had just drawn. For the second decision of phase I, each subject was asked to submit the minimum price for which they were willing to sell the same bottle of wine. This Willingness-To-Accept decision (WTA) was incentivized via the BDM procedure. The application of the BDM procedure aimed at minimizing the chance that subjects form any kind of inference from the elicitation process itself. The instructions included a description of the BDM mechanism and emphasized that it is optimal to provide the true valuation of the bottle. The explanation did not include a numerical example as we did not want any number to operate as an additional anchor. For the same reason, the upper bound of the distribution from which the BDM price was drawn was not revealed. The subjects knew that a number would be randomly drawn between 0 and two times the (unknown) price of the bottle of wine in the store. To avoid outliers, we bounded the WTA from above. Subjects were given an error message if they entered a WTA above two times the price of the wine and were asked to resubmit their decision.Footnote 3 The message did not inform them of the actual upper bound, but simply stated that their price was higher than what the experimenters believe is a reasonable price for the wine.Footnote 4

In phase II, the market treatment was implemented. In the Large market, eight subjects participated in a double auction with four buyers and four sellers. In the Small market, two subjects participated in a market with one buyer and one seller. In a typical session of 16 subjects, half were randomly assigned to the Large market (one trading group) and half to the Small market (four trading groups). The market lasted for two periods. The trading group remained the same across the two periods, but buyer and seller roles were swapped. This way all subjects were exposed to both sides of the trade before they continued to phase III.

Except for the number of traders, the market treatments were identical. Each seller was endowed with a bottle of wine and each buyer was endowed with an amount equal to the price of the bottle of wine that we paid in the store. Traders were unaware of the size of this amount. At the end of the experiment, the amount was revealed only if the market decision was chosen for payment and only to buyers.

Buyers could submit bids to buy the bottle of wine. They could increase their bid multiple times, but not decrease (or withdraw) their current highest bid. Sellers could submit asks to sell the bottle of wine. They could decrease their ask multiple times, but not increase (or withdraw) their current lowest ask. All bids and asks were automatically recorded in the Order Book, which was visible to everyone and updated in real time. A trade occurred automatically whenever any of the following two rules was satisfied. (i) When a buyer submitted a bid that was higher than or equal to the lowest ask of the sellers in the Order Book, this buyer bought from the seller with the lowest ask and the corresponding ask was the transaction price. (ii) When a seller submitted an ask that was lower than or equal to the highest bid of the buyers in the Order Book, this seller sold to the buyer with the highest bid and the corresponding bid was the transaction price. All realized trades and their corresponding prices were automatically recorded in the publicly visible Trade Book. Subjects who had already traded still saw live updated Order and Trade Books. Before the trading period opened, the subjects had to correctly answer six multiple choice questions to make sure they understood the rules of the market.

In phase III, we again elicited subjects’ WTA for the bottle of wine with the BDM mechanism. After that, subjects were asked to complete a standard demographics survey asking for their age, gender and field of study. The experiment ended at this point and the final screen shown to the subjects informed them about which of the five decisions was chosen for payment as well as their payoff. If a WTA decision was implemented, they were informed of the random BDM draw and whether this random price meant that they sold the bottle of wine or kept it.

This design allows us to test the following hypotheses. To that purpose, we use the anchors to assign subjects to a High-anchor group and a Low-anchor group on the basis of either a median split or a quartile split. We use the data of phase I to test for anchoring.

Hypothesis 1

The phase I WTA in the High-anchor group is larger than the phase I WTA in the Low-anchor group.

We use the data of phases I and III to test whether the market affects subjects’ elicited preferences and alleviates the anchoring effect.

Hypothesis 2

The difference in WTA between the High and the Low-anchor group is smaller in phase III than in phase I.

Hypothesis 3

The reduction in the difference in WTA between phase I and III is larger in the Large market treatment than the Small market treatment.

In total, 316 subjects participated in the experiment, 160 in the Large market treatment (20 trading groups) and 156 in the Small market treatment (78 trading groups). The experiment lasted approximately 75 minutes. Depending on their decisions during the experiment, subjects received on average 12.17€ including the participation fee of 8€ (excluding the bottle of wine). On top of their payment, 160 of the subjects physically received a bottle of wine. We used four different bottles of wine across sessions to avoid that prospective subjects could potentially learn the price from subjects that had participated already. Two of the bottles were priced at 6.00€ and two at 7.50€. Our subjects are on average 21 years old. Most of them \((67\%)\) are economics students, and they are evenly balanced across genders (females \(53\%\), males \(47\%\)).

3 Results

3.1 Anchoring manipulation

In this subsection, we shed light on the question whether anchoring affects subjects’ valuation of the bottle of wine. Figure 1 plots subjects’ WTA in phase I as a function of their anchor. The figure suggests that subjects’ WTA is fairly independent of their anchor.Footnote 5

Fig. 1
figure 1

Scatter plot of phase I WTA on anchor with fitted regression line

Full size image

Table 1 makes the results more precise. Hypothesis 1 states that the WTA in the group with high anchors will be larger than the WTA in the group with low anchors. First, we do a median split of our data. Contrary to the hypothesis, the WTA for the Low-anchor group does not significantly differ from the High-anchor group. The evidence is in the expected direction, but the effect size is very small and far from economically significant. The magnitudes of our anchoring effects as measured by the ratio of the valuations in the top and bottom part of the distribution varies between 1.04 (for the ratio of the quartiles) to 1.07 (for the ratio of the quintiles).Footnote 6 In comparison, for the series of products in Ariely et al. (2003) the ratio of top and bottom quintiles ranges from 2.16 to 3.03. The lack of support for an anchoring effect is further illustrated by a regression of the reported WTA on the anchor, while controlling for the price of the wine. (All regression results reported in the paper are obtained from OLS regressions.) The estimation reveals a very small and far from significant slope \((b=0.019, SE=0.061, CI=[-0.102,0.140], t=0.31, p=0.755, N=316)\).

Table 1 Mean WTA by anchor group
Full size table

The previous literature has suggested some robustness checks. For instance, Fudenberg et al. (2012) include an analysis where they test for anchoring effects after leaving out inconsistent responses. We define a response as inconsistent if the WTA is higher than the anchor price that was accepted or lower than the anchor price that was rejected. In our sample, we have 51 (16.14%) inconsistent observations from subjects resulting in a reduced sample size of 265. Using rank-sum tests, we find no anchoring effect for either median split \((\text {ratio}=1.177, z=0.239, p=0.811, N=265)\) or quartile split \((\text {ratio}=1.027, z=0.971, p=0.429, N=135)\) or quintile split \((\text {ratio}=1.022, z=0.738, p=0.460, N=105)\). A regression of valuation on anchor—again controlling for price—reveals an insignificant slope \((b=-0.015, SE=0.063, CI=[ -0.140,0.110], t=-0.24, p=0.813, N=265)\). Hence, focusing only on consistent answers does not affect our main result of no anchoring effects.

Another approach that has been used in the literature is to replace valuations above the BDM range by the maximum of the BDM range. One reason to do so is that all reports higher than the BDM range yield the same outcome. So very high reports need not reflect very high valuations, which may bias the analysis. Ariely et al. (2003) and Maniadis et al. (2014) truncate valuations in this way and find that it does not affect their results. The same approach is not directly applicable for our study as our subjects did not know the exact range of the BDM, and higher valuations than the maximum were not allowed. However, in the same spirit we can investigate whether our results are sensitive to replacing valuations above 10 by 10, the highest possible anchor. Rank-sum tests reveal no anchoring effects for either median split \((\text {ratio}=1.077, z=1.359, p=0.174, N=316)\) or quartile split \((\text {ratio}=1.081, z=1.169, p=0.242, N=163)\) or quintile split \((\text {ratio}=1.177, z=1.278, p=0.201, N=123)\). A regression of valuation on anchor and price confirms the result \((b=0.055, SE=0.051, CI=[-0.046,0.156], t=1.07, p=0.285, N=316)\). Hence, the truncation of valuations also does not qualify our null result.

As a final robustness check, we test for anchoring across demographic characteristics of our subjects (field of study and gender) as well as across different types of wine. We regress valuation on anchor, controlling for the market price of the wine and find no anchoring effect both for economic students \((b=0.049, SE=0.075, CI=[-0.099,0.198], t=0.66, p=0.511, N=211)\) as well as non-economic students \((b=-0.037, SE=0.106, CI=[-0.247,0.173], t=-0.35, p=0.735, N=105)\). We repeat the same exercise and find no anchoring effect both for male students \((b=-0.023, SE=0.089, CI=[-0.200,0.154], t=-0.26, p=0.797, N=148)\) as well as female students \((b=0.061, SE=0.085, CI=[-0.108,0.229], t=0.71, p=0.477, N=168)\). Similarly, we find no anchoring effect for any of the four types of wine we used.Footnote 7

Result 1

There is no anchoring effect in our data.

Two factors may play a role in our null-result for the effect of anchoring on valuations. The first is the familiarity of the product. Most subjects are likely to be familiar with a bottle of wine, and it may be that anchoring effects occur more easily for unfamiliar products for which people lack a clear initial preference. The other is that in our study, the anchoring procedure is transparently uninformative. In the concluding discussion, we present the results of a small meta-analysis that sheds light on these factors.

In light of Result 1, any analysis on whether market experience reduces anchoring effects is meaningless. Still, it remains interesting to investigate whether the market affects people’s preferences. Previous work showed that markets can affect people’s preferences for unfamiliar goods for which people might not have a clear initial preference to start with, such as tasting an unpleasant liquid (Tufano 2010) and lotteries (Isoni et al. 2016). It is not clear that markets can affect people’s preferences for more familiar goods like a bottle of wine. For the remainder of the analysis, we group subjects on the basis of their phase I WTA instead of their anchor and reshape the remaining two hypotheses accordingly.

3.2 Market effect on valuations

To investigate how markets affect elicited preferences, we define new groups based on the valuations. For each trading group separately, we use a median split of the phase I WTA to assign each subject to a Low- or High-WTA group.Footnote 8

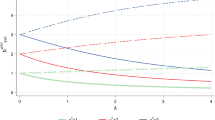
Hypothesis 2 deals with the question whether the information revealed during the market affects the valuation of subjects. Figure 2 illustrates the results. Focusing on the aggregate results of the Small and the Large markets, it is clear that subjects’ valuations move in the direction of the other WTA group.Footnote 9

Fig. 2
figure 2

Average WTA before and after the market

Full size image

To test whether the change is a statistical artifact due to regression to the mean, we compare for each subject the absolute difference between their WTA from phase I and the average WTA (from phase I) in their trading group with the same variable from phase III. The average absolute difference is 2.06€ in phase I and 1.64€ in phase III. A Wilcoxon signed-rank test reveals that traders’ WTA vary less after the market than before \((z=-5.321, p<0.001, N=316)\).

Result 2

Subjects change their WTA in the direction of the average WTA in their own trading group. WTA’s elicited in phase I vary more within their trading group than WTA’s in phase III do.

We now turn to the question whether subjects change their preferences more in the Large market than in the Small market. Figure 2 also displays the results for each market separately. In agreement with Hypothesis 3, we observe that the average decrease in WTA for the High-WTA group is larger in the Large market than in the Small market. In contrast to Hypothesis 3, subjects in the Low-WTA group increase their WTA to a somewhat larger extent in the Small market than in the Large market.

We test the differential impact of the Large market on preferences in a regression that explains the phase III WTA by the phase I WTA and observed market information, with and without interaction term for the treatment. We define observed market information as the average of the last observed actions of the other market subjects. For market subjects that traded, the last observed action is the price they agreed on. For market subjects that did not trade, it is the last bid/ask they submitted. The results in Table 2 provide supportive evidence for the idea that subjects attach more weight to their own WTA in the Small market as compared to the Large market.Footnote 10 In the first two columns, we present regressions for each market separately and in the last column, we present a regression with both markets and an interaction term.

Table 2 Effect of observed market information on WTA change by treatment
Full size table

Result 3

Subjects change their valuation more in the direction of other trading group members in the Large market than in the Small market.

4 Concluding discussion

In this paper, we find supportive evidence for the potential of markets to reduce the effects of anchoring on valuations.Footnote 11 However, in our study, the market was not needed to correct a potential individual bias due to anchoring. We find no effect of anchoring on reported valuations. This result raises doubt on the robustness of the anchoring effect on people’s preferences. Before we discuss differences between our design and other similar studies, we emphasize that our null result is not a consequence of an under-powered study. The observations of the first two sessions were used as a pilot to conduct a power analysis. We conducted a power analysis with an aim to obtain a significant result at the 5% level with 80% power in each of our market treatments separately. The power analysis resulted in an estimated sample size of 148 subjects per market treatment, so 296 subjects in total. To be on the safe side, we aimed for 320. Given that the anchoring hypothesis is based on the total sample (as no treatment has been introduced yet), we have a very high power of 99%.

The existing literature provides a mixed picture of whether anchors affect people’s valuations. Studies differ in detail in how they were run, and it is possible that anchoring effects on preferences occur in some circumstances but not in others. When trying to make sense of previous results on anchoring, a complicating factor is that many of these are based on rather small samples which makes it impossible to distinguish between true results, false positives and false negatives. However, even the large studies provide mixed results.

To make sense of previous results, we carried out a limited meta-analysis. In this analysis, we restricted our attention to the 1493 papers that cite Ariely et al. (2003). Among those, we selected the ones that reported an incentivized experiment investigating the effect of anchoring on elicited valuations. We left out results based on hypothetical payments, which includes a very large literature on the effects of anchoring on contingent valuations.Footnote 12 Table 3 lists the 19 selected studies on the anchoring of preferences, together with their main features and the reported effect. Each study result is summarized in two ways: (i) as a ratio of valuations of High- over Low-anchor group, and (ii) as Hedge’s g, defined as the difference in valuations between High- and Low-anchor group divided by the pooled standard deviation.

Table 3 Anchoring on valuation studies (ordered by publication year)
Full size table

The first feature describes the type of good for which a valuation was elicited. Familiar goods are ordinary goods that most people now and then consume, like wine, chocolate and books. Unfamiliar goods are goods for which people lack daily life experience, like consuming badly tasting liquids and listening to unpleasant sounds. People’s preferences may be more affected by anchors when they report their value for an unfamiliar product for which they do not have well-articulated preferences.

The second feature describes the extent to which the anchor may have been perceived as being informative about the price of the good. Some studies use informative anchors. One such example is provided by Jung et al. (2016), who investigate the effect of a default anchor on people’s donation in a Pay-What-You-Want pricing scheme. Naturally, a default may be perceived as a recommended donation. There are also studies that intended to provide an uninformative anchor, but which may unintentionally have been interpreted as informative by subjects. We categorize these anchors as questionable. One such approach is to let a subject’s anchor be determined by the last two digits of their social security number (SSN) (e.g., Ariely et al. 2003; Bergman et al. 2010). About one-third of the subjects of Chapman and Johnson (1999) mention that they thought that the SSN anchor was informative. Likewise, Yoon and Fong (2019) and Yoon et al. (2019) use randomly generated uninformative prices, but leave subjects in the dark about the nature of the random number. Their instructions do not exclude the possibility that the random number is somehow correlated to the true price.Footnote 13 Studies that use a randomly generated anchor, and clearly communicate the whole procedure to the subjects, are categorized as using an uninformative anchor.

The third feature in which studies differ is whether subjects’ willingness-to-accept (WTA) or willingness-to-pay (WTP) is elicited. We include this variable because initially there was some support for the idea that anchoring effects are more easily observed for WTP than for WTA (Simonson and Drolet 2004).

Before presenting the results of this concise meta-analysis, we motivate some methodological choices. First, all results need to be weighted appropriately with respect to their precision. Studies are typically weighted by the inverse of the variance of the estimated effect size. We use this approach here and weigh each study according to the variance of Hedge’s g.Footnote 14 Second, to test whether the effect size varies across different subgroups, we use the Q statistic. The Q statistic is a measure of the weighted variance of the effect sizes and is compared with the variance that would have been observed if all effect sizes where sampled from a population with the same mean.Footnote 15 Third, we use a random-effects model. Given that we are accumulating data from different studies that were carried out in different ways, we believe that the random-effects model is more appropriate than the fixed-effects model.

Figure 3 provides an overview of how these three dimensions affect the effect of anchoring on elicited valuations. We present the results in two separate forest plots, the lower one for studies that use uninformative anchors and the upper one for studies that use informative or questionable anchors. Overall, whether an anchor is uninformative or not has a strong effect on whether anchoring affects elicited valuations or not.Footnote 16 With uninformative anchors, we find a precise null-result for the effect of anchoring on elicited valuations. In contrast, with informative or questionable anchors there is a sizable and significant effect of anchoring. The difference in anchoring effects between studies with uninformative anchors and the other studies is significant \((Q=27.67, p<0.001, N=83)\).

Fig. 3
figure 3

Forest plots of results by anchor type

Full size image

Within the class of studies that use informative or questionable anchors, we find the following results of the mediating variables on the empirical relevance of anchoring: (i) anchors have a significantly stronger effect for unfamiliar goods for which people do not have a clear initial preference to start with than for familiar goods, whereas (ii) whether WTA or WTP is used to elicit subjects’ preferences does not matter; (iii) somewhat surprisingly, we find a significantly stronger effect of questionable anchors than familiar anchors, which supports the view that many of the questionable anchors were actually interpreted as informative by subjects.

Interestingly, in studies that use transparently uninformative anchors, anchoring never has an effect on elicited valuations. So far, whether a familiar or unfamiliar good is used does not matter when the anchor is clearly uninformative. Although these studies are based on relatively many data, there are only few of them, and clearly more studies in this category are welcome.

In the class of studies that use familiar goods, a final interesting comparison is between studies that use clearly uninformative anchors and those that do not. Anchoring effects on elicited valuations are only observed in the latter category, and the difference in the effect is significant \((Q=23.21, p<0.001, N=52)\). So, preferences for familiar goods can be anchored, but this requires the use of an anchor that is perceived as informative.

Overall, this meta-analysis yields the following picture: (i) if anchors are informative or perceived to be informative, then (unsurprisingly) anchoring has an effect, and mediating variables play mostly a sensible role, that is, no difference in the effect of anchoring on WTA and in the effect on WTP, while anchors have a stronger effect for valuations of unfamiliar products than familiar products; (ii) in the few studies in which anchors are uninformative, there is a quite precise null-effect, and so far none of the mediating variables plays any role.

In many cases with real-world relevance, evaluations may be made in the presence of seemingly (though not truly) informative anchors. In our view, our study sheds light on what makes anchoring of valuations actually have an impact. Originally, Tversky and Kahneman (1974) demonstrated the effect of anchors on people’s judgments with transparently uninformative numbers. On page 1128, they write “subjects were asked to estimate various quantities, stated in percentages (for example, the percentage of African countries in the United Nations). For each quantity, a number between 0 and 100 was determined by spinning a wheel of fortune in the subjects’ presence. The subjects were instructed to indicate first whether that number was higher or lower than the value of the quantity, and then to estimate the value of the quantity by moving upward or downward from the given number. Different groups were given different numbers for each quantity, and these arbitrary numbers had a marked effect on estimates.” Our study suggests that the source of the anchoring of valuations may not be that a random uninformative number is imprinted in a subject’s mind. Instead, the problem seems to be that people can be tricked into believing that an uninformative piece of information is actually a relevant piece of information. In this sense, the anchoring of valuations is more about people being too gullible when they process information. If the anchoring of preferences only reliably appears when subjects perceive the anchor as informative, then it may be less appropriate to think of the anchoring of preferences as an anchoring bias. Instead, it seems to be driven by a perception bias.