Vickrey auction vs BDM: difference in bidding behaviour and the impact of other-regarding motives

Abstract

In an experiment, we first elicit the distributional preferences of subjects and then let them bid for a lottery, either in a Becker–DeGroot–Marschak (BDM) mechanism or a Vickrey auction (VA). The standard theory predicts that altruistic subjects underbid in the VA—compared to the BDM—while spiteful subjects overbid in the VA. The data do not confirm those predictions. While we observe aggregate underbidding in the VA, the result is not driven by the choices of altruistic subjects.

1 Motivation and related literature

Deviations of bids from true valuations in second-price private-value or ‘Vickrey’ auctions (VA; Vickrey 1961) have been a recurrent theme, see Kagel et al. (1987) or Kagel and Levin (1993). The more recent literature has attributed this finding, at least partially, to spite. Andreoni et al. (2007) find that bids increase in rivals’ (known) valuations, which is consistent with the spite explanation. With unknown valuations but costly signals about the latter, Cooper and Fang (2008) also report evidence consistent with the spite hypothesis. If spite, or any form of distributional preferences, is causal for non-sincere bidding in the VA, then deviations of bids from true valuations per construction should be absent in the Becker–DeGroot–Marschak mechanism (BDM; Becker et al. 1964)—which, under the standard assumptions, is strategically equivalent to the VA. Intuitively, in the BDM, the decision is made in isolation and the outcome has only consequences for the decision maker, whereas in the VA, the outcome is also affected by the behaviour of a rivalling bidder, and by changing the own bid, a subject influences the monetary outcome for both parties involved. To test the impact of distributional preferences on bidding behaviour in the lab, we first elicit the distributional preferences of subjects and then let them bid for lottery tickets either in a BDM or in a VA. We then compare the bids across the two mechanisms. We observe underbidding in the aggregate in the VA, but the experimental data do not confirm our predictions at the individual level.

Our contribution to the existing literature is twofold. First, by keeping all details except for the treatment variation constant across treatments, our experimental design allows for a neat comparison of BDM and VA bids at the aggregate level; and second, by classifying subjects into distributional preference types and comparing their bidding behaviour across mechanisms, our design allows for a clean test of the hypotheses that distributional preferences are causal for a potential treatment difference.¹ Keeping the number of bidders constant across the two mechanisms seems indispensable, as the probability that a bidder becomes pivotal decreases in the number of rivals and because with a higher probability of pivotality, we expect bidders to perform higher cognitive effort, as their actions are more likely to influence the final monetary payoff distribution.² Keeping instructions comparable across treatments also seems important, because framing effects are known to potentially influence the behaviour in the lab (see Levin et al. 1998).

2 Experimental setup and theoretical predictions

The experiment consists of two treatments—the BDM treatment and the VA treatment—implemented in a between-subject design and paid under random lottery incentives. Each treatment consists of two parts, and subjects know that only one part is payoff-relevant:³

• 1. In part 1, we elicit the distributional preferences of subjects with the Equality Equivalence Test (EET) by Kerschbamer (2015), and then, we expose them to an incentivised survey.

• 2. In part 2, a lottery ticket (giving either $w=12$ EUR or 0 EUR with equal probabilities) is auctioned off under either the BDM or the VA. Subjects’ initial endowment in part 2 is $e=10$ EUR.⁴

EET: This procedure exposes each subject to a number (in our case 10) choices between two allocations, each specifying a payoff for the subject and a payoff for a randomly assigned anonymous second subject. In half of the choices, there is advantageous inequality (the deciding subject is ahead in monetary terms), in the other half, there is disadvantageous inequality (the deciding subject is behind in monetary terms). From the choices of the subject, x- and y-scores measuring the benevolence in the two domains of inequality are calculated. A higher x-score (y-score) means more benevolence in the domain of disadvantageous (advantageous) inequality. These scores jointly determine the distributional type of the subject.

BDM: In the BDM, each subject i is asked to submit a bid $b_i$, then a random price $p_i$ is drawn. The allocation rule is:

• (i) if $b_i>p_i$: subject i buys the lottery ticket at price $p_i$;

• (ii) if $b_i<p_i$: subject i keeps the endowment; and

• (iii) if $b_i=p_i$: either (i) or (ii) is implemented with equal probability.

VA: In the VA, subjects are randomly assigned to pairs. In each pair, the subjects—denoted i and j with $i\ne j$—are asked to submit bids $b_i$ and $b_j$. The allocation rule is:

• (i) if $b_i> b_j$: subject i buys the lottery ticket at price $b_j$, while subject j keeps the endowment;

• (ii) if $b_i< b_j$: subject j buys the lottery ticket at price $b_i$, while subject i keeps the endowment; and

• (iii) if $b_i= b_j$: either (i) or (ii) is implemented with equal probability.

Consider a subject i of distributional type $d\in \left\{ \text {self}, \text {alt}, \text {spite}\right\}$, where self stands for selfish, alt for altruistic, and spite for spiteful. Let $f_i^d\left( \cdot \right)$ be strictly increasing and normalise $f_i^d\left( 0\right) \equiv 0$. In the BDM, the unique admissible bid for subject i of type d, $b_i^d$, is implicitly defined by

$$\begin{aligned} \frac{1}{2}f_i^d\left( e+w-b_i^d\right) +\frac{1}{2}f_i^d\left( e-b_i^d\right) =f_i^d(e). \end{aligned}$$

(2.1)

Let $(x_i,x_j)$ denote the final monetary allocation and $u_i^d\left( x_i,x_j\right)$ the associated utility of subject i of distributional type d. In the VA, the utility for a selfish subject is—as in the BDM—of the form $u_i^{\text {self}}\left( x_i,x_j\right) =f^{\text {self}}_i\left( x_i\right)$. Thus, $b_i=b_i^{\text {self}}$ is a weakly dominant strategy for selfish in the VA. Sincere bidding is not necessarily a weakly dominant strategy for non-selfish subjects in the VA. An altruist i’s utility increases in the monetary payoff of j, i.e., $u_i^{\text {alt}}\left( x_i,x_j\right) =f^{\text {alt}}_i(x_i)+g^{\text {alt}}_i(x_j)$, where $g^{\text {alt}}_i(\cdot )$ is strictly increasing. Conversely, under spite, we have $u_i^{\text {spite}}\left( x_i,x_j\right) =f^{\text {spite}}_i(x_i)-g^{\text {spite}}_i(x_j)$, where $g^{\text {spite}}_i(\cdot )$ is again strictly increasing. Note that our formulation allows for a possible dependence of a subject’s risk preferences on her distributional type. That is, we explicitly allow the $f_i^d\left( \cdot \right)$ function to depend on the distributional archetype of the subject. We assume that if $x_j$ is good (bad), i.e., altruism (spite), i is more (less) risk-averse in j’s monetary gains than in her own. Empirical evidence includes, e.g., Chakravarty et al. (2011) or Mengarelli et al. (2014). In extending the distributional preferences (as defined here for certain outcomes) to a lottery framework, we follow the expected utility approach. As pointed out, among others, by Fudenberg and Levine (2012) and Saito (2013), an alternative procedure for extending distributional preferences to lotteries is to replace the certain income in the utility function with its expected value. This would allow for ex-ante fairness, while the expected utility extension does not. While the distinction between ex-ante and ex-post fairness is interesting and important, in general, it seems less relevant in our context. The reason is that our focus is on the change in the behaviour of distributional archetypes who have preferences that are monotonic in the material payoff of the other subject (i.e., selfish, altruists, and spiteful), while the ex-ante vs ex-post fairness discussion is most relevant for distributional archetypes who have preferences that are non-monotonic in the material payoff of the other subject (i.e., fairness-minded or inequality averse subjects).⁵ See Fudenberg and Levine (2012) and Saito (2013) for a discussion.

Restricting ourselves to admissible bids, we can prove (see Appendix A for details):

Proposition 1.

In the VA,

• (i) a selfish subject never has an incentive to deviate from $b_i^{\text {self}}$;

• (ii) an altruistic subject never has an incentive to overbid relative to $b_i^{\text {alt}}$ , and might have an incentive to underbid;

• (iii) a spiteful subject never has an incentive to underbid relative to $b_i^{\text {spite}}$ , and might have an incentive to overbid.

From Proposition 1 and the fact that selfish and altruistic subjects combined comprise the majority in experimental data (see Kerschbamer 2015), we derive:

Theoretical prediction 1. Comparing bids across treatments,

• (i) selfish subjects will not change their bids, while altruistic (spiteful) types will underbid (overbid) in VA relative to the BDM;

• (ii) in the aggregate, we expect underbidding in the VA relative to the BDM.

3 Results

We conducted all sessions in paper-and-pen at the University of Innsbruck in October and November 2013 and collected $n=320$ observations—146 in the BDM and 174 in the VA. We classify subjects as:

• (i) selfish, if $-0.5\le x\text { score}\le 0.5$ and $-0.5\le y\text { score}\le 0.5$;

• (ii) altruistic, if $x\text { score}\ge 0$ and $y\text { score}\ge 0$;

• (iii) spiteful, if $x\text { score}\le 0$ and $y\text { score}\le 0$.⁶

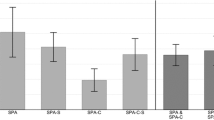
Table 1 reports the mean bid by type and treatment, and the p values for t tests comparing mean bids.⁷ Figure 1 shows the distribution of bids by type and treatment.

Fig. 1

Bids by types across treatments BDM (left) and VA (right)

Table 1 Comparison of mean bid by type and treatment (standard error in parentheses; number of observations in brackets)

We observe a difference in aggregate bidding behaviour, which is significant at the 10 % level. Given the relatively large share of altruists in the population, one might be tempted to see the predictions of Proposition 1 confirmed. However, we cannot reconcile the treatment difference measured at the aggregate level with the data at the individual level. For both selfish and spiteful types, we observe a significant (at the 10 % level) change in bids, while for altruists, there is no significant difference. This contradicts our theoretical predictions.

4 Conclusion

Our experimental design allows for a genuine comparison of BDM and VA, both at the aggregate level and at the level of the distributional type. While we observe a behavioural difference between the two mechanisms at the aggregate level, the difference cannot be explained by a purely consequentialist utility function of the form $u_i^d(x_i,x_j)=f_i^d(x_i)\pm g_i^d(x_j)$. Such functions seem to be well suited to explain behaviour in simple decision problems, such as dictator games, but less suited to explain behaviour in market environments, such as the VA.