Abstract
We classify the non-degenerate two-step nilpotent Lie algebras of dimension 8 over the field of real numbers, using known results over complex numbers. We write explicit structure constants for these real Lie algebras.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Classification lists of Lie algebras, in particular of nilpotent Lie algebras, over the field of complex numbers \({\mathbb {C}}\) and over the field of real numbers \(\mathbb {R}\), appear to be an often used tool in mathematical physics; see, for instance, [27, 28]. The problem of classification of nilpotent Lie algebras of arbitrary dimensions (even of two-step nilpotent Lie algebras of arbitrary dimension with 3-dimensional center) is wild; see [3]. However, it is possible to classify nilpotent Lie algebras in low dimensions. Up to now, nilpotent Lie algebras over some fields have been classified up to dimension 7. Lists of nilpotent Lie algebras of dimension at most 7 over different fields can be found, in particular, in [1, 16, 18, 23, 25, 30]. There is no known classification of nilpotent algebras of dimensions greater than 7, even over the field of complex numbers \({\mathbb {C}}\).
A two-step nilpotent Lie algebra over a field \(\mathbb {k}\) (synonyms: metabelian Lie algebra, nilpotent Lie algebra of class 2) is a Lie algebra L over \(\mathbb {k}\) such that
Write \(\mathfrak {z}(L)\) for the center of L:
Set \(L^{(1)}=[L,L]\). Then condition (1.1) means that \(L^{(1)}\subseteq \mathfrak {z}(L)\).
Two-step nilpotent Lie algebras form the first non-trivial subclass of nilpotent Lie algebras. A classification of two-step nilpotent Lie algebras in dimensions up to 7 was given by Gauger [15] over an algebraically closed field of characteristic different from 2, and by Stroppel [35] over an arbitrary field.
In [13], Galitski and Timashev introduced an invariant-theoretic approach to classification of two-step nilpotent Lie algebras, which allowed them to classify such Lie algebras over \({\mathbb {C}}\) up to dimension 9 (in almost all cases). They reduced the classification of two-step nilpotent Lie algebras up to dimension 9 to classification of orbits of \(\textrm{SL}\hspace{0.55542pt}(m,{\mathbb {C}})\hspace{1.111pt}{\times }\hspace{1.111pt}\textrm{SL}\hspace{0.55542pt}(n,{\mathbb {C}})\) in  for (m, n) taking values (5, 4), (6, 3), and (7, 2), and they solved the classification problems for (5, 4) and (6, 3) using the method of \(\theta \)-groups due to Vinberg [36, 37].
for (m, n) taking values (5, 4), (6, 3), and (7, 2), and they solved the classification problems for (5, 4) and (6, 3) using the method of \(\theta \)-groups due to Vinberg [36, 37].
Later, in the papers [29, 39], the two-step nilpotent Lie algebras over \({\mathbb {C}}\) of dimension 8 were classified. These results are consistent with the results of Galitski and Timashev [13]; see Sect. 3 below.
In the present paper, using the known classification of 8-dimensional non-degenerate two-step nilpotent Lie algebras over \({\mathbb {C}}\) (due to Galitski and Timashev [13], and also to Ren and Zhu [29] and to Yan and Deng [39]) we obtain a classification over \(\mathbb {R}\). See the next section for the definition of a non-degenerate two-step nilpotent Lie algebra. We start with known results over \({\mathbb {C}}\) and use Galois cohomology. We compute the Galois cohomology using the computer program [20] described in [6]. Our main results are Tables 1–3.
We performed our computations using computational algebra system GAP; see [14]. A small number of computations concerning automorphism groups of lattices were performed on Magma [10].
The plan of our paper is as follows. In Sect. 2 we reduce our classification problem to classification of orbits of the group \({\textbf {G}}(\mathbb {R})=\textrm{GL}\hspace{0.55542pt}(m,\mathbb {R})\hspace{1.111pt}{\times }\hspace{1.111pt}\textrm{GL}\hspace{0.55542pt}(n,\mathbb {R})\) in the set of non-degenerate tensors  where \({\textbf {U}}=\mathbb {R}^m\), \({\textbf {V}}=\mathbb {R}^n\) for the pair (m, n) taking values (6, 2), (5, 3), and (4, 4). In Sect. 3 we give the tables of representatives of all orbits; this is our main result.
where \({\textbf {U}}=\mathbb {R}^m\), \({\textbf {V}}=\mathbb {R}^n\) for the pair (m, n) taking values (6, 2), (5, 3), and (4, 4). In Sect. 3 we give the tables of representatives of all orbits; this is our main result.
Section 4 contains preliminaries on real algebraic groups and real Galois cohomology. In Sect. 5, for a connected reductive complex algebraic group G, we describe the action of the automorphism group \(\textrm{Aut}\hspace{0.55542pt}(G)\) on the canonical based root datum \(\textrm{BRD}\hspace{0.55542pt}(G)\). Section 6 contains preliminaries on \(\theta \)-representations. Starting Sect. 7, we compute our tables. See below the idea of the computations.
In Sect. 7, we consider a tensor \(e\in {\textbf {Y}}\) and the stabilizer \({\textbf {G}}_e\) of e in \({\textbf {G}}\). We reduce the classification of the orbits of \({\textbf {G}}(\mathbb {R})\) in \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\subset Y\) (where \(G={\textbf {G}}({\mathbb {C}})\) and \(Y={\textbf {Y}}\hspace{1.111pt}{\otimes }_\mathbb {R}\hspace{1.111pt}{\mathbb {C}})\) to computing the Galois cohomology set \(\textrm{H}^1{\textbf {G}}_e\).
In order to compute \(\textrm{H}^1{\textbf {G}}_e\), we embed \(\mathfrak {g}=\textrm{Lie}\, {\textbf {G}}\) and \({\textbf {Y}}\) into a \(\mathbb {Z}\)-graded real Lie algebra \({\hat{\mathfrak {g}}}\) such that \({\hat{\mathfrak {g}}}_0=\mathfrak {g}\) and \({\hat{\mathfrak {g}}}_1=Y\). Moreover, we embed our real tensor e into a real homogeneous \(\mathfrak {{sl}}_2\)-triple \(t=(e,h,f)\) with \(h\in {\hat{\mathfrak {g}}}_0\) and \(f\in {\hat{\mathfrak {g}}}_{-1}\). Using \({\hat{g}}\) and t, we construct a reductive \(\mathbb {R}\)-subgroup \({\textbf {P}}_t\subseteq {\textbf {G}}_e\) (not necessarily connected) such that
\(R_{\textrm{u}}\) denoting the unipotent radical. Then by Sansuc’s lemma we have
For computing \(\textrm{H}^1{\textbf {P}}_t\), we have a computer program [20], described in [6], which computes the Galois cohomology of a real algebraic group \({\textbf {H}}\), and the input for which is a real basis of the Lie algebra \(\textrm{Lie}\,{\textbf {H}}\) and a set of representatives in \(H={\textbf {H}}({\mathbb {C}})\) of the component group \(\pi _0(H)\). Thus we need \(\textrm{Lie}\,{\textbf {P}}_t\) and \(\pi _0(P_t)\). It is easy to compute \(\textrm{Lie}\,{\textbf {P}}_t\) using computer, but computing \(\pi _0(P_t)\) is tricky. We computed \(\pi _0(P_t)\) case by case via a computer-assisted calculation with participation of a human mathematician. For details see Sects. 7–11.
In Appendix A we consider an alternative approach for the case \((m,n)=(4,4)\). Namely, by duality (see Gauger [15, Section 3] or Galitski and Timashev [13, Section 1.2]) our classification problem for (4, 4) reduces to the already solved classification problems for (4, 2) and (3, 2). Our results for (4, 4) are consistent with the results of [18] for (4, 2) and (3, 2).
1.1 Notation
In this paper, by an algebraic group we mean a linear algebraic group. By letters \({\textbf {G}},{\textbf {H}},\dots \) in the boldface font we denote real algebraic groups. By the same letters, but in the usual (non-bold) font \(G,H,\dots \), we denote the corresponding complex algebraic groups \(G={\textbf {G}}\hspace{1.111pt}{\times }_\mathbb {R}\hspace{1.111pt}{\mathbb {C}}\), \(H={\textbf {H}}\hspace{1.111pt}{\times }_\mathbb {R}\hspace{1.111pt}{\mathbb {C}}\), \(\dots \) (though the standard notations are \({\textbf {G}}_{\mathbb {C}}\) and \({\textbf {H}}_{\mathbb {C}}\)) and by the corresponding small Gothic letters \(\mathfrak {g},\mathfrak {h},\dots \), we denote the Lie algebras of \(G,H,\dots \). Similarly, for real vector spaces \({\textbf {U}},{\textbf {V}}\), we write \(U= {\textbf {U}}\hspace{1.111pt}{\otimes }_\mathbb {R}\hspace{1.111pt}{\mathbb {C}}\), \(V={\textbf {V}}\hspace{1.111pt}{\otimes }_\mathbb {R}\hspace{1.111pt}{\mathbb {C}}\), \(\dots \).
For a real algebraic group \({\textbf {G}}\), we denote by \({\textbf {G}}(\mathbb {R})\) and \({\textbf {G}}({\mathbb {C}})\) the groups of the real points and the complex points of \({\textbf {G}}\), respectively; see Sect. 4 for details. By abuse of notation, we identify \(G{:=}{\textbf {G}}\hspace{1.111pt}{\times }_\mathbb {R}\hspace{1.111pt}{\mathbb {C}}\) with the group of \({\mathbb {C}}\)-points \({\textbf {G}}({\mathbb {C}})=G({\mathbb {C}})\). In particular, \(g\in G\) means \(g\in G({\mathbb {C}})\).
We gather some of our notations:
-
Z(G) denotes the center of an algebraic group G;
-
\(\textrm{Aut}\hspace{0.55542pt}(G)\) denotes the automorphism group of G;
-
\(\textrm{Inn}\hspace{0.55542pt}(G)\) denotes the group of inner automorphisms of G;
-
\(\textrm{Out}\hspace{0.55542pt}(G)=\textrm{Aut}\hspace{0.55542pt}(G)/\textrm{Inn}\hspace{0.55542pt}(G)\);
-
\(\textrm{Lie}\hspace{0.55542pt}(G)\) denotes the Lie algebra of G;
-
\(\textrm{Dyn}\hspace{0.55542pt}(G)\) denotes the Dynkin diagram of a connected reductive group G;
-
\(G^0\) denotes the identity component of an algebraic group G;
-
\(\pi _0(G)=G/G^0\) denotes the component group of G;
-
\(\textrm{H}^1{\textbf {G}}=\textrm{H}^1(\mathbb {R},{\textbf {G}})\), the first Galois cohomology of a real algebraic group \({\textbf {G}}\);
-
\(\textrm{GL}\hspace{0.55542pt}(n,{\mathbb {C}})\) denotes the complex Lie group of invertible complex \(n\hspace{1.111pt}{\times }\hspace{1.111pt}n\)-matrices, and also the complex algebraic group with this group of \({\mathbb {C}}\)-points;
-
\(\textrm{GL}\hspace{0.55542pt}(n,\mathbb {R})\) is the real Lie group of invertible real \(n\hspace{1.111pt}{\times }\hspace{1.111pt}n\)-matrices;
-
\(\textrm{GL}\hspace{0.55542pt}_{n,\mathbb {R}}\) is the connected real algebraic group with the group of real points \(\textrm{GL}\hspace{0.55542pt}(n,\mathbb {R})\).
2 First reductions
Let L be a two-step nilpotent Lie algebra over a field \(\mathbb {k}\) of characteristic different from 2. If A is a nonzero abelian Lie algebra, then the direct sum of Lie algebras \(L\hspace{1.111pt}{\oplus }\hspace{1.111pt}A\) is again a two-step nilpotent Lie algebra; we say that such a Lie algebra \(L\hspace{1.111pt}{\oplus }\hspace{1.111pt}A\) is degenerate. Clearly, in order to classify two-step nilpotent Lie algebras of dimension d over a field \(\mathbb {k}\), it suffices to classify non-degenerate two-step nilpotent Lie algebras over \(\mathbb {k}\) of dimension \(\leqslant d\).
The following lemma is almost obvious, and so we skip the proof.
Lemma 2.1
Let L be a finite-dimensional two-step nilpotent Lie algebra over a field \(\mathbb {k}\). Then L is non-degenerate if and only if \(L^{(1)}= \mathfrak {z}(L)\).
In this paper we classify non-degenerate two-step nilpotent Lie algebras of dimension 8 over \(\mathbb {R}\). Clearly, classification of degenerate two-step nilpotent Lie algebras of dimension 8 over \(\mathbb {R}\) can be reduced to classification of non-degenerate two-step nilpotent Lie algebras of smaller dimension over \(\mathbb {R}\) (which is known).
Let L be a non-degenerate two-step nilpotent Lie algebra over a field \(\mathbb {k}\) of characteristic different from 2. Set \(U=L/\mathfrak {z}(L)\) and \(V=L^{(1)}\subseteq \mathfrak {z}(L)\). The Lie bracket in L defines a skew-symmetric bilinear map
and the induced linear map

The triple \((U,V,\beta )\) is non-degenerate in the following sense: the linear map \(\beta _*\) is surjective, and for any nonzero \(u\in U\), there exists  with \(\beta (u,u')\ne 0\).
with \(\beta (u,u')\ne 0\).
Let L be a non-degenerate two-step nilpotent Lie algebra. Write \(m=\dim U\), \(n=\dim V\) where U,V are as above. Then \(m+n=\dim L\) (because L is non-degenerate). We say then that L is of signature (m, n).
A non-degenerate two-step nilpotent Lie algebra L of signature (m, n) defines a non-degenerate triple \((U,V,\beta )\) of signature (m, n) (that is, with \(\dim U=m\), \(\dim V=n\)). Conversely, a non-degenerate triple \((U,V,\beta )\) of signature (m, n) defines a non-degenerate two-step-nilpotent Lie algebra of signature (m, n) with underlying vector space
and with the Lie bracket

We see that to classify non-degenerate two-step nilpotent Lie algebras L of signature (m, n) up to an isomorphism is the same as to classify non-degenerate triples \((U,V,\beta )\) with \(\dim U=m\) and \(\dim V=n\) up to isomorphism, which in turn is equivalent to classification of the orbits of the Lie group \(\textrm{GL}\hspace{0.55542pt}(m,\mathbb {k})\hspace{1.111pt}{\times }\hspace{1.111pt}\textrm{GL}\hspace{0.55542pt}(n,\mathbb {k})\) in the set of non-degenerate skew-symmetric maps
We wish to classify non-degenerate skew-symmetric maps \(\beta \) as above over \(\mathbb {k}=\mathbb {R}\) for the signatures (m, n) with \(m+n=8\), that is,
However, if \((m,n)=(7,1)\), then \(\beta \) is a skew-symmetric bilinear form on \(\mathbb {R}^7\), but we know that there are no non-degenerate skew-symmetric bilinear forms on odd-dimensional spaces; see, for instance, Artin [2, Theorem 3.7] or Lang [22, Theorem XV.8.1]. Moreover, if \(m\leqslant 3\), then  , while \(\dim V=n\geqslant 5\), and therefore the linear map
, while \(\dim V=n\geqslant 5\), and therefore the linear map  cannot be surjective. Thus for \((m,n)=(1,7)\), (2, 6), (3, 5) there are no non-degenerate skew-symmetric bilinear maps of those signatures. It remains to classify the non-degenerate skew-symmetric maps \(\beta \) for
cannot be surjective. Thus for \((m,n)=(1,7)\), (2, 6), (3, 5) there are no non-degenerate skew-symmetric bilinear maps of those signatures. It remains to classify the non-degenerate skew-symmetric maps \(\beta \) for
3 Tables
In Tables 1, 2 and 3, we classify the orbits of the group \({\textbf {G}}(\mathbb {R})=\textrm{GL}\hspace{0.55542pt}(m,\mathbb {R})\hspace{1.111pt}{\times }\hspace{1.111pt}\textrm{GL}\hspace{0.55542pt}(n,\mathbb {R})\) acting on the set of non-degenerate skew-symmetric bilinear maps \( \mathbb {R}^m\hspace{0.55542pt}{\times }\hspace{1.111pt}\mathbb {R}^m\rightarrow \mathbb {R}^n\) for \(m+n=8\). This corresponds to the isomorphism classes of non-degenerate two-step nilpotent real Lie algebras of dimension 8.
In these tables, our real two-step nilpotent Lie algebra L is \(\mathbb {R}^8\) with the standard basis \(e_1,\dots ,e_8\). The notations like 1 and 1-bis denote two real orbits contained in the same complex orbit. The representatives \(1,2,3\dots \) in each table were taken from [13, Tables 2 and 8]. Using Galois cohomology, we determined whether there are other orbits in the same complex orbit, and if yes, we computed a representative of each real orbit. It turned out that there are at most two real orbits in each complex orbit; the other real orbit in the complex orbit containing the real orbit 1 is denoted by 1-bis.
In each row, the Lie bracket is given by the (2, 1)-tensor e given in the table, as explained in Sect. 2.
For example, in the row 3-bis in Table 2, our (2, 1)-tensor is
where we write \(e_{13{\uparrow }8}\) for the (2, 1)-tensor \((e_1^*\hspace{1.111pt}{\wedge }\hspace{1.111pt}e_3^*)\hspace{1.111pt}{\otimes }\hspace{1.111pt}e_8\). Here \(e^*_1\) and \(e^*_3\) are basis vectors of the dual space  with basis \(e_1^*,\dots ,e_5^*\), and \(e_8\) is a basis vector of the space \({\textbf {V}}=\mathbb {R}^3\) with basis \(e_6,e_7,e_8\). This tensor e of formula (3.1) defines the following Lie bracket:
with basis \(e_1^*,\dots ,e_5^*\), and \(e_8\) is a basis vector of the space \({\textbf {V}}=\mathbb {R}^3\) with basis \(e_6,e_7,e_8\). This tensor e of formula (3.1) defines the following Lie bracket:
In the columns 3–6 (\(\pi _0\), \(\mathfrak {g}_t''\), “Rep. in U”, “Rep. in V”) of each of the tables, we give certain invariants of the stabilizer \({\textbf {G}}_e\) of our tensor  in the group \({\textbf {G}}=\textrm{GL}\hspace{0.55542pt}({\textbf {U}})\hspace{1.111pt}{\times }\hspace{1.111pt}\textrm{GL}\hspace{0.55542pt}({\textbf {V}})\). We use these invariants in order to compute the Galois cohomology of \({\textbf {G}}_e\), which permits us to determine the real orbits in the complex orbit \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\).
in the group \({\textbf {G}}=\textrm{GL}\hspace{0.55542pt}({\textbf {U}})\hspace{1.111pt}{\times }\hspace{1.111pt}\textrm{GL}\hspace{0.55542pt}({\textbf {V}})\). We use these invariants in order to compute the Galois cohomology of \({\textbf {G}}_e\), which permits us to determine the real orbits in the complex orbit \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\).
We define the invariant \(\pi _0\) here: it is the component group \(\pi _0(G_e)\) of the stabilizer \(G_e\) of our tensor e. The real Lie algebra \(\mathfrak {g}_t''\) is defined in Sect. 7, and the representations in the columns “Rep. in U” and “Rep. in V” are defined in Sect. 11. We remark that the most tricky part of our calculations is the calculation of \(\pi _0(G_e)\); see Sect. 11 for an outline of the methods that we have used.
We see from the table that there are 27 isomorphism classes of non-degenerate two-step nilpotent Lie algebras of dimension 8 over \(\mathbb {R}\): seven isomorphism classes of signature (6, 2), sixteen isomorphism classes of signature (5, 3), and four isomorphism classes of signature (4, 4). Any isomorphism class over \({\mathbb {C}}\) comes from one or two isomorphism classes over \(\mathbb {R}\).
We say that a Lie algebra is indecomposable if it is not a direct sum of Lie algebras of smaller dimension. Any indecomposable two-step nilpotent Lie algebra is non-degenerate. Our tables give also a classification of non-degenerate two-step nilpotent complex Lie algebras (extracted from Galitski and Timashev [13]). We can compare our tables with results of Ren and Zhu [29] and Yan and Deng [39], who classify indecomposable two-step nilpotent complex Lie algebras of dimension 8. Using the method of characteristics (see [38, Section 4.1], [7, Section 5.4]) we can check which complex tensors (structures of two-step nilpotent Lie algebras) are equivalent. It turns out that the classifications of [29, 39] are equivalent to ours, except for that they omit the isomorphism class of Lie algebra 5 in our Table 1 and the class of Lie algebra 11 in our Table 2. This is because these two Lie algebras are decomposable:
where \(\textrm{Lie}\hspace{0.55542pt}(\hspace{1.111pt}{\cdot }\hspace{1.111pt})\) denotes the Lie algebra defined by the tensor in the parentheses. It follows that our Tables 1, 2 and 3 with these two Lie algebras removed, give a classification of indecomposable two-step nilpotent real Lie algebras.
4 Real algebraic groups and real Galois cohomology
Let \({\textbf {G}}\) be a real linear algebraic group. In the coordinate language, one may regard \({\textbf {G}}\) as a subgroup in the general linear group \(\textrm{GL}\hspace{0.55542pt}(N,{\mathbb {C}})\) (for some natural number N) defined by polynomial equations with real coefficients in the matrix entries; see Borel [4, Section 1.1]. More conceptually, one may assume that \({\textbf {G}}\) is an affine group scheme of finite type over \(\mathbb {R}\); see Milne [24, Definition 1.1]. With any of these two equivalent definitions, \({\textbf {G}}\) defines a covariant functor
from the category of commutative unital \(\mathbb {R}\)-algebras to the category of groups. We apply this functor to the \(\mathbb {R}\)-algebra \(\mathbb {R}\) and obtain a real Lie group \({\textbf {G}}(\mathbb {R})\). We apply this functor to the \(\mathbb {R}\)-algebra \({\mathbb {C}}\) and to the morphism of \(\mathbb {R}\)-algebras
and obtain a complex Lie group \({\textbf {G}}({\mathbb {C}})\) together with an anti-holomorphic involution \({\textbf {G}}({\mathbb {C}})\rightarrow {\textbf {G}}({\mathbb {C}})\), which we denote by \(\sigma _{\textbf {G}}\). The Galois group \(\Gamma \) naturally acts on \({\textbf {G}}({\mathbb {C}})\); namely, the complex conjugation \(\gamma \) acts by \(\sigma _{\textbf {G}}\). We have \({\textbf {G}}(\mathbb {R})={\textbf {G}}({\mathbb {C}})^\Gamma \) (the subgroup of fixed points).
We shall consider the linear algebraic group \(G{:=}{\textbf {G}}\hspace{1.111pt}{\times }_\mathbb {R}\hspace{1.111pt}{\mathbb {C}}\) obtained from \({\textbf {G}}\) by extension of scalars from \(\mathbb {R}\) to \({\mathbb {C}}\). Since G is an affine group scheme over \({\mathbb {C}}\), we have the ring of regular function \({\mathbb {C}}[G]=\mathbb {R}[{\textbf {G}}]\hspace{1.111pt}{\otimes }_\mathbb {R}\hspace{1.111pt}{\mathbb {C}}\). Our anti-holomorphic involution \(\sigma _{\textbf {G}}\) of \({\textbf {G}}({\mathbb {C}})\) is anti-regular in the following sense: when acting on the ring of holomorphic functions on G (by acting by \(\sigma _{\textbf {G}}^{-1}\) on the argument of a function, and by complex conjugation on the value) it preserves the subring \({\mathbb {C}}[G]\) of regular functions. An anti-regular involution of G is called also a real structure on G.
Remark 4.1
If G is a reductive algebraic group over \({\mathbb {C}}\) (not necessarily connected), then any anti-holomorphic involution of G is anti-regular. The hypothesis that G is reductive is necessary. For details and references see [9, Section 1].
A morphism of real linear algebraic groups \({\textbf {G}}\rightarrow {\textbf {G}}'\) induces a morphism of pairs  . In this way we obtain a functor \({\textbf {G}}\mapsto (G,\sigma _{\textbf {G}})\). By Galois descent this functor is an equivalence of categories; for details and references see [9, Section 1] or [6, Appendix A]. In particular, any pair \((G,\sigma )\), where G is a complex linear algebraic group and \(\sigma \) is a real structure on G, is isomorphic to a pair coming from a real linear algebraic group \({\textbf {G}}\), and any morphism of pairs
. In this way we obtain a functor \({\textbf {G}}\mapsto (G,\sigma _{\textbf {G}})\). By Galois descent this functor is an equivalence of categories; for details and references see [9, Section 1] or [6, Appendix A]. In particular, any pair \((G,\sigma )\), where G is a complex linear algebraic group and \(\sigma \) is a real structure on G, is isomorphic to a pair coming from a real linear algebraic group \({\textbf {G}}\), and any morphism of pairs  comes from a unique morphism of the corresponding real algebraic groups.
comes from a unique morphism of the corresponding real algebraic groups.
When computing the Galois cohomology \(\textrm{H}^1{\textbf {G}}\) for a real algebraic group \({\textbf {G}}\), we shall actually work with the pair \((G,\sigma )\), where G is a complex algebraic group and \(\sigma \) is a real structure on G. We shall shorten “real linear algebraic group” to “\(\mathbb {R}\)-group”.
Let \({\textbf {G}}=(G,\sigma )\) be a real algebraic group (not necessarily connected or reductive). The Galois group \(\Gamma =\{1,\gamma \}\) acts on G by
We define the first Galois cohomology set \(\textrm{H}^1(\mathbb {R},{\textbf {G}})\) by
Here \(\textrm{Z}^1{\textbf {G}}=\{z\in G\,{ |}\, g\hspace{1.111pt}{\cdot }\hspace{1.111pt}{}{^\gamma }\hspace{-1.111pt}g=1\}\) is the set of 1-cocycles, and two cocycles  are equivalent (we write \(z\sim z'\)) if \(z=g^{-1}\hspace{0.55542pt}{\cdot }\hspace{1.111pt}z'\hspace{0.55542pt}{\cdot }\hspace{1.111pt}{}{^\gamma }\hspace{-1.111pt}g\) for some \(g\in G\). We shorten \(\textrm{H}^1(\mathbb {R},{\textbf {G}})\) to \(\textrm{H}^1{\textbf {G}}\).
are equivalent (we write \(z\sim z'\)) if \(z=g^{-1}\hspace{0.55542pt}{\cdot }\hspace{1.111pt}z'\hspace{0.55542pt}{\cdot }\hspace{1.111pt}{}{^\gamma }\hspace{-1.111pt}g\) for some \(g\in G\). We shorten \(\textrm{H}^1(\mathbb {R},{\textbf {G}})\) to \(\textrm{H}^1{\textbf {G}}\).
For details see [7, Section 3.3] or [6, Section 4]. See Serre’s book [33] for the Galois cohomology \(H^1(\mathbb {k},{\textbf {G}})\) for an algebraic group \({\textbf {G}}\) over an arbitrary field \(\mathbb {k}\).
5 Action on the based root datum
Let G be a connected reductive group over an algebraically closed field \(\mathbb {k}\). Let \(T\subset G\) be a maximal torus, and let \(B\subset G\) be a Borel subgroup containing T. We consider the based root datum

Here
-
\(X=X^*(T)\) is the character group of T;
-
 is the cocharacter group of T;
is the cocharacter group of T; -
 is the root system;
is the root system; -
 is the coroot system;
is the coroot system; -
 is the system of simple roots;
is the system of simple roots; -
 is the system of simple coroots.
is the system of simple coroots.
For details see Springer [34, Sections 1 and 2].
Recall that the root system  is defined in term of the root decomposition
is defined in term of the root decomposition

where \(\mathfrak {g}_\alpha \) is the eigenspace corresponding to the root \(\alpha \). For each  we choose a nonzero element \(x_\alpha \in \mathfrak {g}_\alpha \). We write
we choose a nonzero element \(x_\alpha \in \mathfrak {g}_\alpha \). We write  and say that
and say that  is a pinning of (G, T, B).
is a pinning of (G, T, B).
We write  and consider the Cartan matrix with entries \(a_{ij}=\langle \alpha _i,\alpha _j^\vee \rangle \). Recall that the Dynkin diagram \(\textrm{Dyn}\hspace{0.55542pt}(G)\) is the graph whose set of vertices is the set of simple roots
and consider the Cartan matrix with entries \(a_{ij}=\langle \alpha _i,\alpha _j^\vee \rangle \). Recall that the Dynkin diagram \(\textrm{Dyn}\hspace{0.55542pt}(G)\) is the graph whose set of vertices is the set of simple roots  and whose set of edges is defined in the usual way using the Cartan matrix; see, for instance, [17, Section 3.1.7].
and whose set of edges is defined in the usual way using the Cartan matrix; see, for instance, [17, Section 3.1.7].
We say that  is a Borel triple in G. It is well known that if
is a Borel triple in G. It is well known that if  is another Borel triple, then there exists a unique element \(g^\mathrm{ad \,}=gZ(G)\in \textrm{Inn}\hspace{0.55542pt}(G){:=}G/Z(G)\) such that
is another Borel triple, then there exists a unique element \(g^\mathrm{ad \,}=gZ(G)\in \textrm{Inn}\hspace{0.55542pt}(G){:=}G/Z(G)\) such that  ,
,  ,
,  . This element \(g^\mathrm{ad \,}\) induces an isomorphism
. This element \(g^\mathrm{ad \,}\) induces an isomorphism  . Moreover, this induced isomorphism \(g^{\mathrm{ad \,}*}\) does not depend on the choice of the pinning
. Moreover, this induced isomorphism \(g^{\mathrm{ad \,}*}\) does not depend on the choice of the pinning  as above. Thus for given G we can canonically identify the based root data \(\textrm{BRD}\hspace{0.55542pt}(G,T,B)\) for all Borel pairs (T, B). We obtain the canonical based root datum \(\textrm{BRD}\hspace{0.55542pt}(G)\).
as above. Thus for given G we can canonically identify the based root data \(\textrm{BRD}\hspace{0.55542pt}(G,T,B)\) for all Borel pairs (T, B). We obtain the canonical based root datum \(\textrm{BRD}\hspace{0.55542pt}(G)\).
The automorphism group \(\textrm{Aut}\hspace{0.55542pt}(G)\) naturally acts on \(\textrm{BRD}\hspace{0.55542pt}(G)\), and so we obtain a canonical homomorphism
We describe \(\phi \). Choose a pinning  of (G, B, T). Write
of (G, B, T). Write
Consider the Borel triple  . Let \(a\in \textrm{Aut}\hspace{0.55542pt}(G)\). Then
. Let \(a\in \textrm{Aut}\hspace{0.55542pt}(G)\). Then  is again a Borel triple in G, and therefore there exists \(g_a\in G\) such that
is again a Borel triple in G, and therefore there exists \(g_a\in G\) such that

We see that the automorphism \(\textrm{inn}\hspace{0.55542pt}(g_a)\hspace{1.111pt}{\circ }\hspace{1.111pt}a\) of G preserves the Borel triple  and thus induces an automorphism \(\phi (a)\) of \(\textrm{BRD}\hspace{0.55542pt}(G,T,B)\). One checks that the obtained automorphism \(\phi (a)\) does not depend on the choice of
and thus induces an automorphism \(\phi (a)\) of \(\textrm{BRD}\hspace{0.55542pt}(G,T,B)\). One checks that the obtained automorphism \(\phi (a)\) does not depend on the choice of  and \(g_a\) as above. For details see [8, Section 3]. By construction, the subgroup \(\textrm{Inn}\hspace{0.55542pt}(G)\subseteq \textrm{Aut}\hspace{0.55542pt}(G)\) acts on \(\textrm{BRD}\hspace{0.55542pt}(G)\) trivially, and so we obtain an action of \(\textrm{Out}\hspace{0.55542pt}(G){:=}\textrm{Aut}\hspace{0.55542pt}(G)/\textrm{Inn}\hspace{0.55542pt}(G)\) on \(\textrm{BRD}\hspace{0.55542pt}(G)\). The action of \(\textrm{Out}\hspace{0.55542pt}(G)\) on \(\textrm{BRD}\hspace{0.55542pt}(G)\), in particular, on
and \(g_a\) as above. For details see [8, Section 3]. By construction, the subgroup \(\textrm{Inn}\hspace{0.55542pt}(G)\subseteq \textrm{Aut}\hspace{0.55542pt}(G)\) acts on \(\textrm{BRD}\hspace{0.55542pt}(G)\) trivially, and so we obtain an action of \(\textrm{Out}\hspace{0.55542pt}(G){:=}\textrm{Aut}\hspace{0.55542pt}(G)/\textrm{Inn}\hspace{0.55542pt}(G)\) on \(\textrm{BRD}\hspace{0.55542pt}(G)\). The action of \(\textrm{Out}\hspace{0.55542pt}(G)\) on \(\textrm{BRD}\hspace{0.55542pt}(G)\), in particular, on  and
and  , induces an action on \(\textrm{Dyn}\hspace{0.55542pt}(G)\).
, induces an action on \(\textrm{Dyn}\hspace{0.55542pt}(G)\).
We embed \(X^\vee \) into \(\mathfrak {t}{:=}\textrm{Lie}\, T\) as follows. Let \(\nu \in X^\vee \),  . Consider \(d\nu :\mathbb {k}\rightarrow \mathfrak {t}\) and set \(h_\nu =(d\nu )(1)\in \mathfrak {t}\).
. Consider \(d\nu :\mathbb {k}\rightarrow \mathfrak {t}\) and set \(h_\nu =(d\nu )(1)\in \mathfrak {t}\).
Consider the center Z(G), its identity component \(Z(G)^0\) (which is a torus), and the cocharacter group \(X_Z^\vee = X_*(Z(G)^0)\). We can identify

The group \(\textrm{Out}\hspace{0.55542pt}(G)\) naturally acts on the torus \(Z(G)^0\) and on its cocharacter group \(X^\vee _Z\). Moreover, it acts on the Lie algebra \(\mathfrak {z}{:=}\textrm{Lie}\, Z(G)\) and on the lattice \(\{h_\nu \in \mathfrak {z}\,{ |}\, \nu \in X_Z^\vee \}.\)
For  , we consider
, we consider  , and by abuse of notation we write \(h_\alpha \) for
, and by abuse of notation we write \(h_\alpha \) for  . The set
. The set  is a basis of the Lie algebra \(\mathfrak {t}\cap [\mathfrak {g},\mathfrak {g}]\) where \([\mathfrak {g},\mathfrak {g}]\) is the derived subalgebra of \(\mathfrak {g}\).
is a basis of the Lie algebra \(\mathfrak {t}\cap [\mathfrak {g},\mathfrak {g}]\) where \([\mathfrak {g},\mathfrak {g}]\) is the derived subalgebra of \(\mathfrak {g}\).
For each  we choose a nonzero vector \(x_\alpha \in \mathfrak {g}_\alpha \). Then we have \(\textrm{Ad }\hspace{0.55542pt}(t)\hspace{1.111pt}x_\alpha =\alpha (t)\hspace{1.111pt}{\cdot }\hspace{1.111pt}x_\alpha \) for \(t\in T\), whence
we choose a nonzero vector \(x_\alpha \in \mathfrak {g}_\alpha \). Then we have \(\textrm{Ad }\hspace{0.55542pt}(t)\hspace{1.111pt}x_\alpha =\alpha (t)\hspace{1.111pt}{\cdot }\hspace{1.111pt}x_\alpha \) for \(t\in T\), whence
because \((\alpha \hspace{1.111pt}{\circ }\hspace{1.111pt}\beta ^\vee )(t)=t^{\langle \alpha ,\beta ^\vee \rangle }\) for \(t\in {\mathbb {C}}^{\times }\).
We choose \(y_\alpha \in \mathfrak {g}_{-\alpha }\) such that \([x_\alpha , y_\alpha ]=h_\alpha \). Then \([h_\alpha ,y_\alpha ]=-2y_\alpha \). Note that the set  generates the subalgebra \([\mathfrak {g},\mathfrak {g}]\) of \(\mathfrak {g}\).
generates the subalgebra \([\mathfrak {g},\mathfrak {g}]\) of \(\mathfrak {g}\).
The set \(h_\alpha ,x_\alpha ,y_\alpha \) for  has the following properties (see [19, Section 2.9.3, formulas (2.1)]):
has the following properties (see [19, Section 2.9.3, formulas (2.1)]):

We say that \(h_\alpha ,x_\alpha ,y_\alpha \) is a canonical generating set for \([\mathfrak {g},\mathfrak {g}]\).
Now let G be a reductive group, not necessarily connected, over an algebraically closed field \(\mathbb {k}\). We consider the action of G on the Dynkin diagram \(\textrm{Dyn}\, G^0{:=}\textrm{Dyn}\, {G^{0,\mathrm{ad \,}}}\), where \({G^{0,\mathrm{ad \,}}}=(G^0)^\mathrm{ad \,}{:=}G^0/Z(G^0)\) denotes the adjoint group corresponding to the identity component \(G^0\) of the reductive group G.
As above, we choose a maximal torus \(T\subset {G^{0,\mathrm{ad \,}}}\) and a Borel subgroup \(B\subset {G^{0,\mathrm{ad \,}}}\) containing T. We consider the based root datum

For each simple root  we choose canonical generators \(x_\alpha ,y_\alpha , h_\alpha \in \textrm{Lie}\, {G^{0,\mathrm{ad \,}}}=[\mathfrak {g},\mathfrak {g}]\) as explained in Sect. 6, where \(\mathfrak {g}=\textrm{Lie}\, G\). Observe that the set
we choose canonical generators \(x_\alpha ,y_\alpha , h_\alpha \in \textrm{Lie}\, {G^{0,\mathrm{ad \,}}}=[\mathfrak {g},\mathfrak {g}]\) as explained in Sect. 6, where \(\mathfrak {g}=\textrm{Lie}\, G\). Observe that the set  generates the semisimple Lie algebra \([\mathfrak {g},\mathfrak {g}]\).
generates the semisimple Lie algebra \([\mathfrak {g},\mathfrak {g}]\).
Consider the action of G by conjugation on \(G^0\) and on \({G^{0,\mathrm{ad \,}}}\). We obtain a homomorphism
Lemma 5.1
Consider the homomorphism
and the group

Then \( \ker \phi _{\hspace{1.111pt}\textrm{Dyn}\hspace{0.55542pt}}=G^0\hspace{1.111pt}{\cdot }\hspace{1.111pt}A_1\).
Corollary 5.2
We have \(A_1\subset \ker \phi _{\hspace{1.111pt}\textrm{Dyn}\hspace{0.55542pt}}\), and the homomorphism
induced by the inclusion homomorphism \(A_1\hookrightarrow \ker \phi _{\hspace{1.111pt}\textrm{Dyn}\hspace{0.55542pt}}\) is surjective.
This corollary gives us a method to compute \(\pi _0(\ker \phi _{\hspace{1.111pt}\textrm{Dyn}\hspace{0.55542pt}})\).
Proof of Lemma 5.1
Consider the canonical homomorphism
Since the elements \(x_\alpha , y_\alpha \) generate \([\mathfrak {g},\mathfrak {g}]=\textrm{Lie}\, {G^{0,\mathrm{ad \,}}}\), we have \(A_1=\ker \psi \). On the other hand, we can factor the homomorphism \(\phi _{\hspace{1.111pt}\textrm{Dyn}\hspace{0.55542pt}}\) as follows:

It follows that \(A_1=\ker \psi \subseteq \ker \phi _{\hspace{1.111pt}\textrm{Dyn}\hspace{0.55542pt}}\). Writing  , we have that the homomorphism
, we have that the homomorphism

induces an isomorphism

see Conrad [12, Proposition 1.5.5]. It follows that \(\ker \phi _{\hspace{1.111pt}\textrm{Dyn}\hspace{0.55542pt}}\) is the preimage in G of the subgroup  . Since \({G^{0,\mathrm{ad \,}}}\) is the identity component of \(\textrm{Aut}\,{G^{0,\mathrm{ad \,}}}\), we have \(\psi (G^0)={G^{0,\mathrm{ad \,}}}\), and hence for any \(g\in \ker \phi _{\hspace{1.111pt}\textrm{Dyn}\hspace{0.55542pt}}\) there exists \(g_0\in G^0\) such that
. Since \({G^{0,\mathrm{ad \,}}}\) is the identity component of \(\textrm{Aut}\,{G^{0,\mathrm{ad \,}}}\), we have \(\psi (G^0)={G^{0,\mathrm{ad \,}}}\), and hence for any \(g\in \ker \phi _{\hspace{1.111pt}\textrm{Dyn}\hspace{0.55542pt}}\) there exists \(g_0\in G^0\) such that  , that is, \(g_0g\in \ker \psi = A_1\), as required.\(\square \)
, that is, \(g_0g\in \ker \psi = A_1\), as required.\(\square \)
6 Vinberg’s \(\theta \)-representations
Vinberg [36, 37] introduced a class of representations of algebraic groups which share many properties with the adjoint representation of a semisimple Lie algebra. This makes it possible to classify the orbits corresponding to such a representation. These representations are constructed from a \(\mathbb {Z}/m\mathbb {Z}\)-grading or a \(\mathbb {Z}\)-grading of a split semisimple Lie algebra over a field \(\mathbb {k}\). In this paper we deal exclusively with \(\mathbb {Z}\)-gradings of split semisimple real Lie algebras.
Let \(\mathfrak {g}\) be a split semisimple Lie algebra over \(\mathbb {R}\). We construct a class of \(\mathbb {Z}\)-gradings of \(\mathfrak {g}\). Fix a split Cartan subalgebra \(\mathfrak t\) of \(\mathfrak {g}\) with corresponding root system  . For
. For  , we denote the corresponding root space by \(\mathfrak {g}_\alpha \). Fix a basis of simple roots
, we denote the corresponding root space by \(\mathfrak {g}_\alpha \). Fix a basis of simple roots  of
of  . Let \((d_1,\ldots , d_\ell )\) be a sequence of non-negative integers. We define a function
. Let \((d_1,\ldots , d_\ell )\) be a sequence of non-negative integers. We define a function

We let \(\mathfrak {g}_0\) be the subspace of \(\mathfrak {g}\) spanned by \(\mathfrak t\) and all subspaces \(\mathfrak {g}_\alpha \) with \(d(\alpha )=0\). Furthermore, for \(i\in \mathbb {Z}\), \(i\ne 0\), we let \(\mathfrak {g}_i\) be the subspace of \(\mathfrak {g}\) spanned by all \(\mathfrak {g}_\alpha \) with \(d(\alpha )=i\). Then
is a \(\mathbb {Z}\)-grading of \(\mathfrak {g}\). We observe that \(\mathfrak {g}_0\) is a reductive Lie subalgebra; see [19, Theorem 8.3.1]. If

is a positive root with \(m_{i}>0\) for some i such that \(d_{i}>0\), then \(d(\alpha )\geqslant m_{i} d_{i}>0\) and hence  . It follows that the simple roots \(\alpha _i\) such that \(d_i=0\) form a basis of the root system of \(\mathfrak {g}_0\) with respect to \(\mathfrak t\).
. It follows that the simple roots \(\alpha _i\) such that \(d_i=0\) form a basis of the root system of \(\mathfrak {g}_0\) with respect to \(\mathfrak t\).
Let \({\textbf {G}}\) be the inner automorphism group of \(\mathfrak {g}\). This algebraic \(\mathbb {R}\)-group is also known as the adjoint group of \(\mathfrak {g}\), or as the identity component of the automorphism group of \(\mathfrak {g}\). For \(x\in \mathfrak {g}\) we denote its adjoint map by \(\mathrm{ad \,}x\), so \((\mathrm{ad \,}x)(y)= [x,y]\). The Lie algebra of \({\textbf {G}}\) is \(\mathrm{ad \,}\mathfrak {g}= \{ \mathrm{ad \,}x \,{|}\, x\in \mathfrak {g}\}\). Consider the Lie subalgebra \(\mathrm{ad \,}\mathfrak {g}_0 = \{ \mathrm{ad \,}x \,{|}\, x\in \mathfrak {g}_0\}\). Let \({\textbf {T}}\subset G\) be the Cartan subgroup (maximal torus) of \({\textbf {G}}\) with Lie algebra \(\mathrm{ad \,}\mathfrak t\), and let \({\textbf {G}}_0\) denote the algebraic subgroup of \({\textbf {G}}\) generated by \({\textbf {T}}\) and the elements \(\exp \hspace{0.55542pt}(\mathrm{ad \,}x)\) for \(x\in \mathfrak {g}_\alpha \) with \(d(\alpha )=0\); then \({\textbf {G}}_0\) is the connected real algebraic subgroup of \({\textbf {G}}\) whose Lie algebra is \(\mathrm{ad \,}\mathfrak {g}_0\). Since \([\mathfrak {g}_0,\mathfrak {g}_i]\subset \mathfrak {g}_i\), the action of \({\textbf {G}}_0\) on \(\mathfrak {g}_1\) leaves the subspaces \(\mathfrak {g}_i\) invariant. The representation of \({\textbf {G}}_0\) in \(\mathfrak {g}_1\) so obtained is called a \(\theta \)-representation, and \({\textbf {G}}_0\) together with its action on \(\mathfrak {g}_1\) is called a \(\theta \)-group.
For \(x\in \mathfrak {g}_1\) and \(y\in \mathfrak {g}_i\), we have \((\mathrm{ad \,}x)^k(y) \in \mathfrak {g}_{i+k}\). Since the grading is a \(\mathbb {Z}\)-grading, we have \(\mathfrak {g}_{i+k}=0\) for sufficiently big k, implying that \(\mathrm{ad \,}x\) is nilpotent. It can be shown that each real element \(x\in \mathfrak {g}_1\) lies in a real homogeneous \(\mathfrak {{sl}}_2\)-triple (h, x, y), where \(h\in \mathfrak {g}_0\) and \(y\in \mathfrak {g}_{-1}\) and
see [19, Lemma 8.3.5]. The proof of [19, Lemma 8.3.5] shows how to construct a homogeneous \(\mathfrak {{sl}}_2\)-triple (h, x, y) for a complex element x. When applied to a real element x, this method gives a real \(\mathfrak {{sl}}_2\)-triple.
Consider two elements  lying in the homogeneous \(\mathfrak {{sl}}_2\)-triples (h, x, y),
lying in the homogeneous \(\mathfrak {{sl}}_2\)-triples (h, x, y),  . Then \(x,x'\) are \(G_0\)-conjugate if and only if the two triples are \(G_0\)-conjugate if and only if \(h,h'\) are \(G_0\)-conjugate; see [19, Theorem 8.3.6]. It is possible to devise an algorithm for classifying the \(G_0\)-orbits in \(\mathfrak {g}_1\) based on this fact; see [19, Section 8.4.1]. An alternative method for this is based on Vinberg’s theory of carrier algebras; see [37]. Since a \(\theta \)-group for a \(\mathbb {Z}\)-grading or a \(\mathbb {Z}/m\mathbb {Z}\)-grading has a finite number of nilpotent orbits in \(\mathfrak {g}_{1,{\mathbb {C}}}\) (see [19, Corolary 8.3.8]), and in the case of a \(\mathbb {Z}\)-grading all \(G_0\)-orbits in \(\mathfrak {g}_1\) are nilpotent, for a \(\mathbb {Z}\)-grading there are finitely many \(G_0\)-orbits in \(\mathfrak {g}_{1,{\mathbb {C}}}\).
. Then \(x,x'\) are \(G_0\)-conjugate if and only if the two triples are \(G_0\)-conjugate if and only if \(h,h'\) are \(G_0\)-conjugate; see [19, Theorem 8.3.6]. It is possible to devise an algorithm for classifying the \(G_0\)-orbits in \(\mathfrak {g}_1\) based on this fact; see [19, Section 8.4.1]. An alternative method for this is based on Vinberg’s theory of carrier algebras; see [37]. Since a \(\theta \)-group for a \(\mathbb {Z}\)-grading or a \(\mathbb {Z}/m\mathbb {Z}\)-grading has a finite number of nilpotent orbits in \(\mathfrak {g}_{1,{\mathbb {C}}}\) (see [19, Corolary 8.3.8]), and in the case of a \(\mathbb {Z}\)-grading all \(G_0\)-orbits in \(\mathfrak {g}_1\) are nilpotent, for a \(\mathbb {Z}\)-grading there are finitely many \(G_0\)-orbits in \(\mathfrak {g}_{1,{\mathbb {C}}}\).
Now we describe the \(\mathbb {Z}\)-gradings that are relevant to this paper. They are constructed using a sequence \((d_1,\ldots ,d_\ell )\) where precisely one of the \(d_i\) is 1, and all others are 0. We give such a grading by giving the Dynkin diagram of \(\mathfrak {g}\) where the node corresponding to \(\alpha _i\) with \(d_i=1\) is colored black. We consider the following three \(\mathbb {Z}\)-gradings:

Consider such a \(\mathbb {Z}\)-grading labeled (m, n) with (m, n) taking values (4, 4), (5, 3), (6, 2). Write \({\textbf {G}}_0^{\textrm{der}}=[{\textbf {G}}_0,{\textbf {G}}_0]\), the derived subgroup of \({\textbf {G}}_0\). We see from the Dynkin diagram that the semisimple group \({\textbf {G}}_0^{\textrm{der}}\) is of type \(\textsf {A}_{m-1}\hspace{0.55542pt}{\times }\hspace{1.111pt}\textsf {A}_{n-1}\). Therefore, the universal cover \(\widetilde{\textbf {G}}_0\) of \({\textbf {G}}_0^{\textrm{der}}\) is a split simply connected semisimple group of type \(\textsf {A}_{m-1}\hspace{0.55542pt}{\times }\hspace{1.111pt}\textsf {A}_{n-1}\) and hence it is isomorphic to \(\textrm{SL}\hspace{0.55542pt}_{m,\mathbb {R}}\hspace{0.55542pt}{\times }\hspace{1.111pt}\textrm{SL}\hspace{0.55542pt}_{n,\mathbb {R}}\); we fix this isomorphism. We obtain an isogeny (surjective homomorphism with finite kernel)
Of course, to specify this isogeny we need to work with Lie algebras.
Since \({\textbf {G}}\) is of adjoint type, the set of simple roots \(\{\alpha _1,\dots ,\alpha _\ell \}\) (with \(\ell =7\)) is a basis of the character group \(\textsf {X}^*({\textbf {T}})\). Write \({\textbf {T}}_0={\textbf {T}}\cap {\textbf {G}}_0\); then the set \(\{\alpha _1,\dots ,\alpha _\ell \}\smallsetminus \{\alpha _{i_0}\}\) is a basis of \(\textsf {X}^*({\textbf {T}}_0)\), and \({\textbf {T}}={\textbf {T}}_0\hspace{1.111pt}{\times }\hspace{1.111pt}{\textbf {T}}^1\), where \({\textbf {T}}^1=Z({\textbf {G}}_0)\cong {\mathbb {G}_{\textrm{m},\mathbb {R}}}\) is a 1-dimensional split \(\mathbb {R}\)-torus with character group \(\textsf {X}^*({\textbf {T}}^1)=\mathbb {Z}\hspace{1.111pt}{\cdot }\hspace{1.111pt}\alpha _{i_0}\). Write
we obtain an isogeny \({\textbf {G}}_{m,n}\twoheadrightarrow {\textbf {G}}_0\). Since \(\mathfrak {g}_1\) is the direct sum of eigenspaces \(\mathfrak {g}_\alpha \) of \({\textbf {T}}\) in \(\mathfrak {g}\) where \(\alpha \) runs over the roots

we see that \(t\in {\textbf {T}}^1({\mathbb {C}})={\mathbb {C}}^{\times } \) acts on \(\mathfrak {g}_1\) by multiplication by t.
We compute the representation of \({\textbf {T}}_0^{\textrm{der}}\) in \(\mathfrak {g}_1\). For \(1\leqslant i \leqslant \ell =7\), let
be canonical generators of \(\mathfrak {g}\). For the root systems of types \(\textsf {D}_7\) and \(\textsf {E}_7\), this means that each \((h_i,x_i,y_i)\) is an \(\mathfrak {{sl}}_2\)-triple, that for \(i\ne j\) we have \([h_i,x_j] = -x_j\), \([h_i,y_j] =y_j\) if i, j are connected in the Dynkin diagram, otherwise \([h_i,x_j]=[h_i,y_j]=0\), and that \([x_i,y_j] =0\). Let \(i_0\) be such that \(d_{i_0}=1\). Then the elements \(h_i,x_i,y_i\) for \(i\ne i_0\) form a canonical generating set of the semisimple part \(\mathfrak {g}_0^{\textrm{der}}=[\mathfrak {g}_0,\mathfrak {g}_0]\) of \(\mathfrak {g}_0\). In the three cases above it is easy to check that \(\alpha _{i_0}\) is the unique lowest weight of \(\mathfrak {g}_1\). This means that (1) for every \(i\ne i_0\) we have that  is not a root, and (2) for every root \(\alpha \ne \alpha _{i_0}\) with \(d(\alpha )=1\), there is \(i\ne i_0\) such that \(\alpha -\alpha _i\) is a root. Here (1) is obvious, because any root must be a linear combination of simple roots with non-negative coefficients, or a linear combination of simple roots with non-positive coefficients. Assertion (2) can be checked using a list of the positive roots of the root systems of type \(\textsf {D}_7\) and \(\textsf {E}_7\), respectively. (See [36, Section 8] for a more conceptual approach.) The positive roots can be listed using a computer program like GAP; alternatively, they can be found in Bourbaki [11]. Hence
is not a root, and (2) for every root \(\alpha \ne \alpha _{i_0}\) with \(d(\alpha )=1\), there is \(i\ne i_0\) such that \(\alpha -\alpha _i\) is a root. Here (1) is obvious, because any root must be a linear combination of simple roots with non-negative coefficients, or a linear combination of simple roots with non-positive coefficients. Assertion (2) can be checked using a list of the positive roots of the root systems of type \(\textsf {D}_7\) and \(\textsf {E}_7\), respectively. (See [36, Section 8] for a more conceptual approach.) The positive roots can be listed using a computer program like GAP; alternatively, they can be found in Bourbaki [11]. Hence  is the unique (up to scalar) lowest weight vector (here “lowest weight vector" means that \([y_i,x_{i_0}]=0\) for \(i\ne i_0\)). Furthermore, \([h_i,x_{i_0}] = -x_{i_0}\) if i and \(i_0\) are connected in the Dynkin diagram, and \([h_i,x_{i_0}] = 0\) otherwise. Hence the \(\mathfrak {g}_0\)-module \(\mathfrak {g}_1\) is irreducible and we know its lowest weight \(\lambda _l\); the numerical labels \(\langle \lambda _l,\alpha _i^\vee \rangle \) are given on the Dynkin diagrams above. From this we can determine the highest weight of \(\mathfrak {g}_1\). Namely, let \(\tau \) be the only nontrivial automorphism of the Dynkin diagram \(\textsf {A}_\ell \) when \(\ell >1\), and the trivial automorphism of \(\textsf {A}_\ell \) for \(\ell =1\). Then the highest weight \(\lambda _h\) is given by \(\lambda _h=-\tau (\lambda _l)\); see [17, Section 3.2.6, Proposition 2.3 and Theorem 2.13]. We see that the numerical labels of \(\lambda _h\) are 1 at the node neighboring an extreme node of \(\textsf {A}_m\), and 1 at an extreme node of \(\textsf {A}_n\) for \(m\geqslant n\). This means that there exists an isomorphism \(\widetilde{\textbf {G}}_0\xrightarrow { \, \sim \,}\textrm{SL}\hspace{0.55542pt}_{m,\mathbb {R}}\hspace{0.55542pt}{\times }\hspace{1.111pt}\textrm{SL}\hspace{0.55542pt}_{n,\mathbb {R}}\) with \(m\geqslant n\) such that \(\mathfrak {g}_1\) is isomorphic to
is the unique (up to scalar) lowest weight vector (here “lowest weight vector" means that \([y_i,x_{i_0}]=0\) for \(i\ne i_0\)). Furthermore, \([h_i,x_{i_0}] = -x_{i_0}\) if i and \(i_0\) are connected in the Dynkin diagram, and \([h_i,x_{i_0}] = 0\) otherwise. Hence the \(\mathfrak {g}_0\)-module \(\mathfrak {g}_1\) is irreducible and we know its lowest weight \(\lambda _l\); the numerical labels \(\langle \lambda _l,\alpha _i^\vee \rangle \) are given on the Dynkin diagrams above. From this we can determine the highest weight of \(\mathfrak {g}_1\). Namely, let \(\tau \) be the only nontrivial automorphism of the Dynkin diagram \(\textsf {A}_\ell \) when \(\ell >1\), and the trivial automorphism of \(\textsf {A}_\ell \) for \(\ell =1\). Then the highest weight \(\lambda _h\) is given by \(\lambda _h=-\tau (\lambda _l)\); see [17, Section 3.2.6, Proposition 2.3 and Theorem 2.13]. We see that the numerical labels of \(\lambda _h\) are 1 at the node neighboring an extreme node of \(\textsf {A}_m\), and 1 at an extreme node of \(\textsf {A}_n\) for \(m\geqslant n\). This means that there exists an isomorphism \(\widetilde{\textbf {G}}_0\xrightarrow { \, \sim \,}\textrm{SL}\hspace{0.55542pt}_{m,\mathbb {R}}\hspace{0.55542pt}{\times }\hspace{1.111pt}\textrm{SL}\hspace{0.55542pt}_{n,\mathbb {R}}\) with \(m\geqslant n\) such that \(\mathfrak {g}_1\) is isomorphic to  as a \({\textbf {G}}_{m,n}\)-module; see [26, Table 5]. An element \((a_m,b_n,c_1)\in G_{m,n}\) acts on
as a \({\textbf {G}}_{m,n}\)-module; see [26, Table 5]. An element \((a_m,b_n,c_1)\in G_{m,n}\) acts on  as follows:
as follows:

We note that we have a canonical isomorphism  .
.
7 Using Galois cohomology
Set

with the standard action of the Galois group \(\textrm{Gal}\hspace{0.55542pt}({\mathbb {C}}/\mathbb {R})\) on Y. Write
See Notation in Introduction for the notations \(\textrm{GL}\hspace{0.55542pt}_{m,\mathbb {R}}\) and \(\textrm{GL}\hspace{0.55542pt}(m,{\mathbb {C}})\). The group \({\textbf {G}}\) acts on \({\textbf {Y}}\) in the standard way, and we have a composite homomorphism
Here the surjective homomorphism p is given by

where \(a_m\in \textrm{SL}\hspace{0.55542pt}(m,{\mathbb {C}})\), \(b_n\in \textrm{SL}\hspace{0.55542pt}(n,{\mathbb {C}})\), \(c_1\in {\mathbb {C}}^{\times } \), and we write \(c_1 b_n\) for the product of the scalar \(c_1\) and the matrix \(b_n\). Then
where \(\mu _n\) denotes the group of n-th roots of unity.
Let  , which we view as embedded into \(Y{:=}{\textbf {Y}}\hspace{1.111pt}{\otimes }_\mathbb {R}\hspace{1.111pt}{\mathbb {C}}\). As seen in Sect. 6, \(\textrm{Lie}\, G''\) is isomorphic to \({\hat{\mathfrak {g}}}_0\), the zero component of a \(\mathbb {Z}\)-graded simple complex Lie algebra \({\hat{\mathfrak {g}}}\). Moreover, Y is isomorphic as a \(G''\)-module to \({\hat{\mathfrak {g}}}_1\) (in Sect. 6 it was denoted by \(\mathfrak {g}_1\)). We use the machinery of \(\mathfrak {{sl}}_2\)-triples, as indicated in Sect. 6, to classify the \(G''\)-orbits in Y. Let \(t=(h,e,f)\) be a real homogeneous \(\mathfrak {{sl}}_2\)-triple containing e, where \(h\in {\hat{\mathfrak {g}}}_0\), \(f\in {\hat{\mathfrak {g}}}_{-1}\). We write
, which we view as embedded into \(Y{:=}{\textbf {Y}}\hspace{1.111pt}{\otimes }_\mathbb {R}\hspace{1.111pt}{\mathbb {C}}\). As seen in Sect. 6, \(\textrm{Lie}\, G''\) is isomorphic to \({\hat{\mathfrak {g}}}_0\), the zero component of a \(\mathbb {Z}\)-graded simple complex Lie algebra \({\hat{\mathfrak {g}}}\). Moreover, Y is isomorphic as a \(G''\)-module to \({\hat{\mathfrak {g}}}_1\) (in Sect. 6 it was denoted by \(\mathfrak {g}_1\)). We use the machinery of \(\mathfrak {{sl}}_2\)-triples, as indicated in Sect. 6, to classify the \(G''\)-orbits in Y. Let \(t=(h,e,f)\) be a real homogeneous \(\mathfrak {{sl}}_2\)-triple containing e, where \(h\in {\hat{\mathfrak {g}}}_0\), \(f\in {\hat{\mathfrak {g}}}_{-1}\). We write
Let \(e\in {\textbf {Y}}\). We denote by \(\mathfrak {g}_t''\) the centralizer (stabilizer) of a real \(\mathfrak {{sl}}_2\)-triple \(t=(h,e,f)\) in the real Lie algebra  . These stabilizers for the real orbits are tabulated in fourth column of each of Tables 1, 2 and 3, where by \(\mathfrak t\) we denote the Lie algebra of a one-dimensional split torus of \({\textbf {G}}\), and by \(\mathfrak u\) we denote the Lie algebra of a one-dimensional compact torus of \({\textbf {G}}\).
. These stabilizers for the real orbits are tabulated in fourth column of each of Tables 1, 2 and 3, where by \(\mathfrak t\) we denote the Lie algebra of a one-dimensional split torus of \({\textbf {G}}\), and by \(\mathfrak u\) we denote the Lie algebra of a one-dimensional compact torus of \({\textbf {G}}\).
Lemma 7.1
Assume that \(e\in {\textbf {Y}}\), and consider \({\textbf {G}}_e\), which is a real algebraic group. Then there is a canonical bijection between \(\textrm{H}^1 {\textbf {G}}_e\) and the set of real orbits (the orbits of \({\textbf {G}}(\mathbb {R})\) in \({\textbf {Y}}\)) contained in the complex orbit \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\).
Proof
By Serre [33, Section I.5.4, Proposition 36], see also [7, Proposition 3.6.5], we have a canonical bijection between \(\ker \hspace{1.111pt}[\textrm{H}^1 {\textbf {G}}_e\rightarrow \textrm{H}^1 {\textbf {G}}]\) and the set of orbits of \({\textbf {G}}(\mathbb {R})\) in \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\cap {\textbf {Y}}\). Moreover, since \({\textbf {G}}=\textrm{GL}\hspace{0.55542pt}_{m,\mathbb {R}}\hspace{1.111pt}{\times }\hspace{1.111pt}\textrm{GL}\hspace{0.55542pt}_{n,\mathbb {R}}\), we have \(\textrm{H}^1 {\textbf {G}}=1\) (see Serre [32, Section X.1, Proposition 3]), and the lemma follows.\(\square \)
We specify the map of the lemma. Recall that \(\textrm{H}^1 {\textbf {G}}_e=\textrm{Z}^1 {\textbf {G}}_e/{\sim }\) where \(\textrm{Z}^1 {\textbf {G}}_e\) is the set of 1-cocycles; see Sect. 4. Here we write \(z\sim z'\) if there exists \(g\in G_e\) such that \(z=g^{-1} z' \,{}^\gamma \hspace{-1.0pt}g\). Let \([z]\in \textrm{H}^1 {\textbf {G}}_e\) be the cohomology class represented by a cocycle z. Since \(\textrm{H}^1 {\textbf {G}}=1\), there exists \(g\in G\) such that
One can easily find such an element g using computer or by hand. We have
because \(z\in G_e\). Thus \(g\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\) is real (contained in \({\textbf {Y}}\)), and to [z] we assign the \({\textbf {G}}(\mathbb {R})\)-orbit of \(g\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\).
8 The stabilizer of e and the centralizer of \(t=(h,e,f)\)
By Lemma 7.1 we can use \(\textrm{H}^1 {\textbf {G}}_e\) in order to classify orbits of \({\textbf {G}}(\mathbb {R})\) in \({\textbf {Y}}\). Therefore, we need to compute \(\textrm{H}^1{\textbf {G}}_e\). To compute \(\textrm{H}^1 {\textbf {G}}_e\), we embed e into an \(\mathfrak {{sl}}_2\)-triple \(t=(e,h,f)\) as in Sect. 7. We compute \({\textbf {G}}''_t\) using the theory of \(\theta \)-groups. Below we describe some relations between \({\textbf {G}}''_t\) and \({\textbf {G}}_e\).
By [7, Theorem 4.3.16] we have
where \(R_{\textrm{u}}\) denotes the unipotent radical. By Sansuc’s lemma ( [31, Lemma 1.13], see also [5, Proposition 3.2] and [6, Proposition 7.1]) the inclusion \({\textbf {G}}''_t\hookrightarrow {\textbf {G}}''_e\) induces a bijection \(\textrm{H}^1 {\textbf {G}}''_t=\textrm{H}^1 {\textbf {G}}''_e\).
Lemma 8.1
For the homomorphism p of (7.1), we have \(\ker p\subseteq Z(G''_t)\) where \( Z(G''_t)\) denotes the center of \(G''_t\).
Proof
Clearly, \(\ker p\subset G''_e\). Since \(\ker p \subseteq Z(G'')\), we have \(\ker p\subseteq Z(G''_e)\). Each element \(x\in \ker p\) is semisimple, and in view of (8.1) there exists \(g\in G''_e\) such that \(gxg^{-1}\in G''_t\); see Hochschild [21, Theorem VIII.4.3]. Since \(x\in Z(G''_e)\), we see that \(x\in G''_t\) and that \(x\in Z(G''_t)\), as required.\(\square \)
Since the homomorphism p is surjective, from (8.1) we obtain that
where \(p(R_{\textrm{u}}(G''_e))\cong R_{\textrm{u}}(G''_e)\) because by Lemma 8.1 we have \(\ker p\subset G''_t\).
Now consider \(G_e\). Write
Lemma 8.2
\(G_e=D\hspace{1.111pt}{\cdot }\hspace{1.111pt}G'_e\).
Proof
Clearly \(D\subseteq G_e\) for any  , whence \(D\hspace{1.111pt}{\cdot }\hspace{1.111pt}G'_e\subseteq G_e\). Conversely, if \(g=(g_m,g_n)\in G_e\subset \textrm{GL}\hspace{0.55542pt}(m,{\mathbb {C}})\hspace{1.111pt}{\times }\hspace{1.111pt}\textrm{GL}\hspace{0.55542pt}(n,{\mathbb {C}})\), we choose \(x\in {\mathbb {C}}^{\times } \) such that \(x^m=\det \hspace{0.55542pt}(g_m)\), and we set
, whence \(D\hspace{1.111pt}{\cdot }\hspace{1.111pt}G'_e\subseteq G_e\). Conversely, if \(g=(g_m,g_n)\in G_e\subset \textrm{GL}\hspace{0.55542pt}(m,{\mathbb {C}})\hspace{1.111pt}{\times }\hspace{1.111pt}\textrm{GL}\hspace{0.55542pt}(n,{\mathbb {C}})\), we choose \(x\in {\mathbb {C}}^{\times } \) such that \(x^m=\det \hspace{0.55542pt}(g_m)\), and we set
Then \(\det \hspace{0.55542pt}(x^{-1} g_m)=1\), and therefore we have  . Since
. Since  where \(d\hspace{1.111pt}{\cdot }\hspace{1.111pt}e=e\) and \(g\hspace{1.111pt}{\cdot }\hspace{1.111pt}e=e\), we see that \(g'\hspace{1.111pt}{\cdot }\hspace{1.111pt}e = e\). Thus
where \(d\hspace{1.111pt}{\cdot }\hspace{1.111pt}e=e\) and \(g\hspace{1.111pt}{\cdot }\hspace{1.111pt}e=e\), we see that \(g'\hspace{1.111pt}{\cdot }\hspace{1.111pt}e = e\). Thus  , \(d\in D\), and \(g=d g'\), as required.\(\square \)
, \(d\in D\), and \(g=d g'\), as required.\(\square \)
We denote \({\textbf {P}}_t={\textbf {D}}\hspace{1.66656pt}{\cdot }\hspace{0.55542pt}p({\textbf {G}}''_t)\).
Corollary 8.3
\(G_e=p(R_{\textrm{u}}(G''_e))\hspace{1.111pt}{\rtimes }\hspace{1.111pt}P_t\).
Proof
We use Lemma 8.2 and formula (8.2), and obtain
as required.\(\square \)
Proposition 8.4
The inclusion \({\textbf {P}}_t\hookrightarrow {\textbf {G}}_e\) induces a bijection
Proof
Since the group \(p(R_{\textrm{u}}({\textbf {G}}''_e))\) is unipotent, by Sansuc’s lemma we have
By Corollary 8.3 we have \(\textrm{H}^1( p(R_{\textrm{u}}({\textbf {G}}''_e))\hspace{1.111pt}{\rtimes }\hspace{1.111pt}{\textbf {P}}_t)=\textrm{H}^1{\textbf {G}}_e\), as required.\(\square \)
In order to compute \(\textrm{H}^1{\textbf {P}}_t\) we need the Lie algebra of \({\textbf {P}}_t\). We have an isomorphism \(\textrm{Lie}\, G''_t\rightarrow \textrm{Lie}\hspace{0.55542pt}(G''_t/{\ker p})\) given by
Then \(\textrm{Lie}\, P_t=\textrm{Lie}\, D+\textrm{Lie}\hspace{0.55542pt}( p(G''_t)) \), where \(\textrm{Lie}\, D={\mathbb {C}}\hspace{1.111pt}{\cdot }\hspace{1.111pt}(I_m,2I_n)\). Write  ,
,  . For the differential
. For the differential  we have \(d p(a_m,b_n,c_1) = (a_m,b_n+c_1)\). Now \(\textrm{Lie}\hspace{0.55542pt}(p(G_t'')) = dp(\textrm{Lie}\hspace{0.55542pt}(G_t'')) = dp (\mathfrak {g}_t'')\), where \(\mathfrak {g}_t''\) is the centralizer of t in \(\mathfrak {g}''\). We see that it is straightforward to compute using computer the Lie subalgebra
we have \(d p(a_m,b_n,c_1) = (a_m,b_n+c_1)\). Now \(\textrm{Lie}\hspace{0.55542pt}(p(G_t'')) = dp(\textrm{Lie}\hspace{0.55542pt}(G_t'')) = dp (\mathfrak {g}_t'')\), where \(\mathfrak {g}_t''\) is the centralizer of t in \(\mathfrak {g}''\). We see that it is straightforward to compute using computer the Lie subalgebra
For classification of \({\textbf {G}}(\mathbb {R})\)-orbits in  , we need \(\textrm{H}^1 {\textbf {G}}_e\). For this end we need a real basis of \(\textrm{Lie}\, P_t\) (which is computed by our program) and the component group \(\pi _0(P_t)\).
, we need \(\textrm{H}^1 {\textbf {G}}_e\). For this end we need a real basis of \(\textrm{Lie}\, P_t\) (which is computed by our program) and the component group \(\pi _0(P_t)\).
Proposition 8.5
Consider the composite homomorphism
Then the induced homomorphism \(\varphi _*:\pi _0(G''_t)\rightarrow \pi _0(P_t)\) is surjective.
Proof
The homomorphism \(D\hspace{1.111pt}{\times }\hspace{1.111pt}G''_t\rightarrow D\hspace{1.111pt}{\cdot }\hspace{1.111pt}p(G''_t)=P_t\) is surjective. It follows that the homomorphism of the component groups
is surjective, as required.\(\square \)
We have reduced computing \(\textrm{H}^1{\textbf {G}}_e\) to computing \(\pi _0(P_t)\). Moreover, in view of Proposition 8.5, computing \(\pi _0(P_t)\) reduces to computing \(\pi _0(G''_t)\); see the end of Sect. 9 below.
9 Computing \(\textrm{H}^1{\textbf {G}}_e\)
We start with a tensor e from Tables 1, 2 and 3. These are the tensors in the rows 1–6 (but not 1-bis) in Table 1, in the rows 1–12 in Table 2, and in the rows 1–3 in Table 3. We can compute the stabilizer \(\mathfrak {g}_e=\textrm{Lie}\, G_e\) of our tensor e in the real Lie algebra \(\textrm{Lie}\, {\textbf {G}}=\mathfrak {{gl}}\hspace{0.55542pt}(m,\mathbb {R})\hspace{1.111pt}{\times }\hspace{1.111pt}\mathfrak {{gl}}\hspace{0.55542pt}(n,\mathbb {R})\). This is a linear problem, and we can easily do that using computer.
We need the Galois cohomology \(\textrm{H}^1{\textbf {G}}_e{:=}\textrm{H}^1(\mathbb {R}, {\textbf {G}}_e)\). We have a computer program [20] described in [6] for calculating the Galois cohomology \(\textrm{H}^1{\textbf {H}}\) of a real linear algebraic group \({\textbf {H}}\), not necessarily connected or reductive. We call this program “the \(\textrm{H}^1\)-program”. We assume that \({\textbf {H}}\subseteq \textrm{GL}\hspace{0.55542pt}(N,{\mathbb {C}})\) (for some natural number N) is a real algebraic subgroup (that is, defined by polynomial equations with real coefficients). The input of the \(\textrm{H}^1\)-program is the real Lie algebra \(\textrm{Lie}\, {\textbf {H}}\subset \mathfrak {{gl}}\hspace{0.55542pt}(N,\mathbb {R})\) given by a (real) linear basis, and the component group \(\pi _0(H)\) given by a set of representatives \(h_1,\dots ,h_r\in \textrm{GL}\hspace{0.55542pt}(N,{\mathbb {C}})\).
However, when working on this paper, we had only an older version of the \(\textrm{H}^1\)-program. This older \(\textrm{H}^1\)-program computes \(\textrm{H}^1{\textbf {H}}\) when \({\textbf {H}}\) is reductive (not necessarily connected). Therefore, we reduce our calculation of \(\textrm{H}^1{\textbf {G}}_e\) to the reductive case, see below.
Using computer, we embed our tensor e into a homogeneous \(\mathfrak {{sl}}_2\)-triple (h, e, f) in a \(\mathbb {Z}\)-graded Lie algebra as in Sect. 6, and we consider the reductive group \({\textbf {P}}_t={\textbf {D}}\hspace{1.66656pt}{\cdot }\hspace{0.55542pt}p({\textbf {G}}''_t)\subset {\textbf {G}}_e\), not necessarily connected; see Sect. 8. By Proposition 8.4 we have a canonical bijection \(\textrm{H}^1{\textbf {P}}_t\xrightarrow { \, \sim \,}\textrm{H}^1{\textbf {G}}_e\). It remains to compute \(\textrm{H}^1{\textbf {P}}_t\).
In order to compute \(\textrm{H}^1{\textbf {P}}_t\) using the older \(\textrm{H}^1\)-program, we need a basis of the real Lie algebra \(\textrm{Lie}\hspace{0.55542pt}({\textbf {P}}_t)\) and the component group \(\pi _0(P_t)\). Using computer, we can easily compute a basis of \(\textrm{Lie}\hspace{0.55542pt}({\textbf {P}}_t)\).
It remains to compute \(\pi _0(P_t)\). By Proposition 8.5, the homomorphism \(\pi _0(G''_t)\rightarrow \pi _0(P_t)\) is surjective. It remains to find representatives of \(\pi _0(G''_t)\) up to equivalence in \(P_t\). Here we say that \(g_1,g_2\in G''_t\) are equivalent in \(P_t\) if \(p(g_1)p(g_2)^{-1}\) is contained in the identity component \(P_t^0\) of \(P_t\).
We have a computer program checking whether an element h of a reductive algebraic group \(H\subset \textrm{GL}\hspace{0.55542pt}(N,{\mathbb {C}})\) (not necessarily connected) with Lie algebra \(\mathfrak {h}\) is contained in the identity component \(H^0\) of H. Using this program, from a set of representatives of \(\pi _0(G''_t)\) we obtain a set of representatives of \(\pi _0(P_t)\). It remains to compute \(\pi _0(G''_t)\).
10 Computing \(\pi _0(G''_t)\)
The group \(G''_t\) acts by conjugation on its identity component \({G_t^{\prime \prime \, 0}}\), whence we obtain a homomorphism
where \(\textrm{Inn}\, {G_t^{\prime \prime \, 0}}\) denotes the group of inner automorphisms of \({G_t^{\prime \prime \, 0}}\). The group of outer automorphisms \(\textrm{Out}\, {G_t^{\prime \prime \, 0}}\) naturally acts on the based root datum \(\textrm{BRD}\hspace{0.55542pt}({G_t^{\prime \prime \, 0}})\). In particular, it acts on the Dynkin diagram  and on the free abelian group \(X^\vee _Z=X_*(Z({G_t^{\prime \prime \, 0}}))\); see Sect. 5. We obtain a homomorphism
and on the free abelian group \(X^\vee _Z=X_*(Z({G_t^{\prime \prime \, 0}}))\); see Sect. 5. We obtain a homomorphism
The action of \(\pi _0(G''_t)\) on \(\textrm{Dyn}\hspace{0.55542pt}(G''_t)^0\) preserves the sets of highest weights of the representations of the derived Lie algebra \(\mathfrak {g}_t^{\prime \prime {\textrm{der}}}=[\mathfrak {g}''_t,\mathfrak {g}''_t]\) in \(U={\mathbb {C}}^m\) and in \(V={\mathbb {C}}^n\).
The group \(\textrm{Aut}\hspace{0.55542pt}(\textrm{Dyn}\, {G_t^{\prime \prime \, 0}})\) in (10.1) is finite, but \(\textrm{Aut}\hspace{0.55542pt}(X_Z^\vee )\) is infinite when\(\dim Z({G_t^{\prime \prime \, 0}})\geqslant 2\). We construct a finite subgroup of \(\textrm{Aut}\hspace{0.55542pt}(X_Z^\vee )\) containing the image of \(\pi _0(G''_t)\) in \(\textrm{Aut}\hspace{0.55542pt}(X_Z^\vee )\). Consider the symmetric bilinear form on \(\mathfrak {g}\)

where xy denotes the product of matrices. This symmetric bilinear form is G-invariant, hence \(G_t''\)-invariant. By abuse of notation, we denote again by  the restriction of the form to \(\mathfrak {z}{:=}\textrm{Lie}\, Z({G_t^{\prime \prime \, 0}})\); it is \(G_t''\)-invariant and hence \(\pi _0(G_t'')\)-invariant.
the restriction of the form to \(\mathfrak {z}{:=}\textrm{Lie}\, Z({G_t^{\prime \prime \, 0}})\); it is \(G_t''\)-invariant and hence \(\pi _0(G_t'')\)-invariant.
We observe that in all our examples, the bilinear form  on the real vector space \(\mathfrak {z}\) is positive definite. Indeed, one can see from Tables 1, 2 and 3 that the center \(\mathfrak {z}\) of the Lie algebra \(\mathfrak {g}''_t=\textrm{Lie}\, G_i''\) is split, that is, it can be diagonalized over \(\mathbb {R}\). It follows that any matrix \(x\in \mathfrak {z}\) can be diagonalized over \(\mathbb {R}\), and therefore
on the real vector space \(\mathfrak {z}\) is positive definite. Indeed, one can see from Tables 1, 2 and 3 that the center \(\mathfrak {z}\) of the Lie algebra \(\mathfrak {g}''_t=\textrm{Lie}\, G_i''\) is split, that is, it can be diagonalized over \(\mathbb {R}\). It follows that any matrix \(x\in \mathfrak {z}\) can be diagonalized over \(\mathbb {R}\), and therefore  ; moreover, if \(x\ne 0\) then
; moreover, if \(x\ne 0\) then  , as required.
, as required.
We embed \(X_Z^\vee \hookrightarrow \mathfrak {z}\): to any \(\nu \in X_Z^\vee \) we assign the element \(h_\nu =(d\nu )(1)\in \mathfrak {z}\) as in Sect. 5. We obtain a \(\pi _0(G_t'')\)-invariant positive definite bilinear form  on \(X_Z^\vee \):
on \(X_Z^\vee \):

Since  is definite, the group
is definite, the group  is finite. We can write the homomorphism (10.1) as
is finite. We can write the homomorphism (10.1) as

where both automorphism groups are finite.
11 Details of computation of Tables 1, 2 and 3
We describe the last two columns in our Tables 1, 2 and 3. We take a representative  and embed it into a homogeneous \(\mathfrak {{sl}}_2\)-triple \(t=(h,e,f)\). We consider the centralizer (stabilizer) \(\mathfrak {g}_t''\); see Sect. 7. The Lie algebra \(\mathfrak {g}_t''\) is reductive. Let \(\mathfrak {g}_t''^{\textrm{der}}=[\mathfrak {g}_t'',\mathfrak {g}_t'']\) denote its derived subalgebra. The inclusion homomorphism
and embed it into a homogeneous \(\mathfrak {{sl}}_2\)-triple \(t=(h,e,f)\). We consider the centralizer (stabilizer) \(\mathfrak {g}_t''\); see Sect. 7. The Lie algebra \(\mathfrak {g}_t''\) is reductive. Let \(\mathfrak {g}_t''^{\textrm{der}}=[\mathfrak {g}_t'',\mathfrak {g}_t'']\) denote its derived subalgebra. The inclusion homomorphism
induces complex representations of \(\mathfrak {g}_t''^{\textrm{der}}\) in U and V. We compute the highest weights of these representations and write them in the corresponding columns “Rep. in U” and “Rep. in V” of the tables.
For example, in the row 1 of Table 1, we have \(\mathfrak {g}_t''\simeq \mathfrak {{sl}}_2\hspace{0.55542pt}{\times }\hspace{1.111pt}\mathfrak {{sl}}_2\hspace{1.111pt}{\times }\hspace{1.111pt}\mathfrak {{sl}}_2\), and the representation of \(\mathfrak {g}_t''^{\textrm{der}}=\mathfrak {g}_t''\) in \(U=\mathbb {R}^6\) is the direct sum of the three 2-dimensional irreducible representations with the highest weights (1, 0, 0), (0, 1, 0), and (0, 0, 1). The representation in V is the trivial 1-dimensional irreducible representation (with highest weight (0, 0, 0)) with multiplicity 2.
Let e be one of the tensors in the rows 2, 3, 4, 5, 6 of Table 1. Looking at the last three columns of the table, we see that the Dynkin diagram \(\textrm{Dyn}\,{G_t^{\prime \prime \, 0}}\) has no non-trivial automorphisms preserving the highest weights of the representations in U and V. Thus \(\pi _0(G''_t)\), when acting on \({G_t^{\prime \prime \, 0}}\), acts trivially on \(\textrm{Dyn}\,{G_t^{\prime \prime \, 0}}\). Write r for the semisimple rank of \({G_t^{\prime \prime \, 0}}\), and let \(x_1,\dots , x_r, y_1,\dots ,y_r, h_1,\dots ,h_r\) be canonical generators of the semisimple Lie algebra \([\mathfrak {g}_t'',\mathfrak {g}_t'']\) as in Sect. 6. We add the equations
to the equations defining \(G''_t\), and compute the Gröbner basis. A calculation shows that the obtained subgroup  is contained in the diagonal maximal torus of \(G''\). This means that \(H''\) is given as the intersection of a finite number of characters of the maximal torus. This makes it possible to work with \(H''\) using the machinery of finitely-generated abelian groups. In particular we can use the Smith form of an integral matrix to find generators of \(\pi _0(H'')\). Here we do not go into the details but refer to [19, Proposition 3.9.7] and its proof. A calculation shows that the images of all these representatives are contained in the identity component \(P_t^0\) of \(P_t\). By Corollary 5.2 the image of \(\pi _0(H'')\) in \(\pi _0(P_t)\) is the whole \(\pi _0(P_t)\), and we conclude that \(\pi _0(P_t)=1\) in all these cases. A calculation (by hand or using computer) shows that \(\textrm{H}^1{\textbf {P}}_t=1\), and thus \(\textrm{H}^1{\textbf {G}}_e=1\), in all these cases. Similarly, we obtain that for the cases 8, 9, 10, 11 of Table 2 and the cases 2, 3 of Table 3 we have \(\pi _0(P_t)=1\) and \(\textrm{H}^1{\textbf {G}}_e=1\). Thus the complex orbit \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\) contains only one real orbit \({\textbf {G}}(\mathbb {R})\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\), and the corresponding complex two-step nilpotent Lie algebra has only one real form.
is contained in the diagonal maximal torus of \(G''\). This means that \(H''\) is given as the intersection of a finite number of characters of the maximal torus. This makes it possible to work with \(H''\) using the machinery of finitely-generated abelian groups. In particular we can use the Smith form of an integral matrix to find generators of \(\pi _0(H'')\). Here we do not go into the details but refer to [19, Proposition 3.9.7] and its proof. A calculation shows that the images of all these representatives are contained in the identity component \(P_t^0\) of \(P_t\). By Corollary 5.2 the image of \(\pi _0(H'')\) in \(\pi _0(P_t)\) is the whole \(\pi _0(P_t)\), and we conclude that \(\pi _0(P_t)=1\) in all these cases. A calculation (by hand or using computer) shows that \(\textrm{H}^1{\textbf {P}}_t=1\), and thus \(\textrm{H}^1{\textbf {G}}_e=1\), in all these cases. Similarly, we obtain that for the cases 8, 9, 10, 11 of Table 2 and the cases 2, 3 of Table 3 we have \(\pi _0(P_t)=1\) and \(\textrm{H}^1{\textbf {G}}_e=1\). Thus the complex orbit \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\) contains only one real orbit \({\textbf {G}}(\mathbb {R})\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\), and the corresponding complex two-step nilpotent Lie algebra has only one real form.
In the case 1 of Table 2 we have \(\pi _0(P_t)=1\), but \(\#\,\textrm{H}^1{\textbf {P}}_t=2\). Thus there are two real orbits in the complex orbit, and we computed (using computer) a representative of the second real orbit; see the row 1-bis in Table 2.
One can see that in the row 1 of Table 1, the automorphism group of the Dynkin diagram \(\textrm{Dyn}\hspace{0.55542pt}(G''_t)^0\) together with the highest weights of the representations in U and V is the symmetric group \(S_3\). A calculation shows that the homomorphisms
are isomorphisms, whence \(\pi _0(P_t)\simeq S_3\). A calculation (using the \(\textrm{H}^1\)-program or by hand) shows that \(\textrm{H}^1{\textbf {G}}_e=\textrm{H}^1 {\textbf {P}}_t\cong \textrm{H}^1(\Gamma , S_3)\) and \(\#\,\textrm{H}^1{\textbf {G}}_e=2\). Thus there are two real orbits in the complex orbit \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\); see the row 1-bis in Table 1 for a representative of the second real orbit.
Similarly, in the row 1 of Table 3, we have \(\pi _0(G_2)\cong C_2\) (a group of order 2), and
where \(c\in C_2\), \(c\ne 1\). Again we have two real orbits in the complex orbit \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\).
We consider the rows 2, 3, 4, 5, 6, 7, 11 of Table 2. We see from the table that \({G_t^{\prime \prime \, 0}}\) is a torus of dimension 2 or 3. We computed the Gröbner basis of the equations defining \(G''_t\). In the cases 4, 6, 7, 11 we obtain a subgroup contained in the diagonal maximal torus of \(G''\), and the image of this subgroup in \(P_t\) is contained in the identity component. We see that \(\pi _0(P_t)=1\), and therefore \({\textbf {P}}_t\) is a split torus. Thus \(\textrm{H}^1{\textbf {G}}_e=\textrm{H}^1{\textbf {P}}_t=1\), and the complex orbit \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\) contains only one real orbit \({\textbf {G}}(\mathbb {R})\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\).
It remains to consider the cases 2, 3, 5 of Table 2, in which \({G_t^{\prime \prime \, 0}}\) is a torus and the group \(G_t''\) is not diagonal. We provide details for the case 5; the cases 2 and 3 are similar (and easier). In the case 5 the group \({G_t^{\prime \prime \, 0}}\) is a 3-dimensional torus, and hence \(X_Z^\vee \) is a free abelian group of rank 3. We chose a basis \(e_1,e_2,e_3\) of \(X_Z^\vee \) and computed the Gram matrix  where
where  . We obtained the matrix
. We obtained the matrix

Using the function AutomorphismGroup of Magma, we computed the automorphism group  . It is a group of order 24 with generators
. It is a group of order 24 with generators

We computed the list of elements of  , and for each
, and for each  we computed the Gröbner basis for \(G_t''\) with additional equations saying that the element \(g\in G_t''\) acts on \(X_Z^\vee \) as a. For 18 elements a we got the trivial Gröbner basis \(\{1\}\), which means that the corresponding enlarged system of equations has no solutions. For the following six elements:
we computed the Gröbner basis for \(G_t''\) with additional equations saying that the element \(g\in G_t''\) acts on \(X_Z^\vee \) as a. For 18 elements a we got the trivial Gröbner basis \(\{1\}\), which means that the corresponding enlarged system of equations has no solutions. For the following six elements:

we obtained nontrivial Gröbner bases, which meant that the corresponding enlarged system did have a solution, and then it was easy to find a solution by a computer-assisted calculation. From this we obtained that \(\pi _0(G_t'')\simeq S_3\) and \(\textrm{H}^1 {\textbf {G}}_e=\textrm{H}^1{\textbf {P}}_t\simeq \textrm{H}^1(\Gamma ,S_3)\) is of cardinality 2. Similarly, we obtained that \(\pi _0(G_e)\simeq C_2\) in cases 2 and 3 of Table 2. In these two cases we also obtained that \(\#\,\textrm{H}^1{\textbf {G}}_e=2\). Thus the complex orbit \(G\hspace{1.111pt}{\cdot }\hspace{1.111pt}e\) contains exactly two real orbits, and in each case we computed a representative of the other orbit.
Data availability
All data generated or analyzed during this study are included in this published article.
References
Ancochéa-Bermúdez, J.M., Goze, M.: Classification des algèbres de Lie nilpotentes complexes de dimension \(7\). Arch. Math. (Basel) 52(2), 175–185 (1989)
Artin, E.: Geometric Algebra. Wiley Classics Library. Wiley, New York (1988)
Belitskii, G., Lipyanski, R., Sergeichuk, V.: Problems of classifying associative or Lie algebras and triples of symmetric or skew-symmetric matrices are wild. Linear Algebra Appl. 407, 249–262 (2005)
Borel, A.: Linear algebraic groups. Borel, A., Mostow, G.D. (eds.) Algebraic Groups and Discontinuous Subgroups. Proceedings of Symposia in Pure Mathematics, vol. 9, pp. 3–19. American Mathematical Society, Providence (1966)
Borovoi, M., Daw, C., Ren, J.: Conjugation of semisimple subgroups over real number fields of bounded degree. Proc. Amer. Math. Soc. 149(12), 4973–4984 (2021)
Borovoi, M., de Graaf, W.A.: Computing Galois cohomology of a real linear algebraic group (2023). arXiv:2308.04962
Borovoi, M., de Graaf, W.A., Lê, H.V.: Real graded Lie algebras, Galois cohomology and classification of trivectors in \({\mathbb{R}}^9\) (2021). arXiv:2106.00246
Borovoi, M., Kunyavskiĭ, B., Lemire, N., Reichstein, Z.: Stably Cayley groups in characteristic zero. Int. Math. Res. Not. IMRN 2014(19), 5340–5397 (2014)
Borovoi, M., Timashev, D.A.: Galois cohomology of real semisimple groups via Kac labelings. Transform. Groups 26(2), 433–477 (2021)
Bosma, W., Cannon, J., Playoust, C.: The Magma algebra system. I. The user language. J. Symbolic Comput. 24(3–4), 235–265 (1997)
Bourbaki, N.: Groupes et Algèbres de Lie. Chapitres 4–6. Éléments de Mathématique. Masson, Paris (1981)
Conrad, B.: Reductive group schemes. In: Brochard, S., Conrad, B., Oesterlé, J., Autour des Schémas en Groupes. Vol. I, pp. 93–444. Panoramas et Synthèses 42/43. Société Mathématique de France, Paris (2014)
Galitski, L.Yu., Timashev, D.A.: On classification of metabelian Lie algebras. J. Lie Theory 9(1), 125–156 (1999)
The GAP Group, GAP—Groups, Algorithms, and Programming, Version 4.12.2 (2022). https://www.gap-system.org
Gauger, M.A.: On the classification of metabelian Lie algebras. Trans. Amer. Math. Soc. 179, 293–329 (1973)
Gong, M.: Classification of Nilpotent Lie Algebras of Dimension 7 (Over Algebraically Closed Field and \(\rm R\)). Ph.D. Thesis, UWSpace (1998). http://hdl.handle.net/10012/1148
Gorbatsevich, V.V., Onishchik, A.L., Vinberg, E.B.: Lie Groups and Lie Algebras, Vol. III: Structure of Lie Groups and Lie Algebras. Encyclopaedia of Mathematical Sciences, vol. 41. Springer, Berlin (1994)
de Graaf, W.A.: Classification of 6-dimensional nilpotent Lie algebras over fields of characteristic not 2. J. Algebra 309(2), 640–653 (2007)
de Graaf, W.A.: Computation with Linear Algebraic Groups. Monographs and Research Notes in Mathematics. CRC Press, Boca Raton (2017)
de Graaf, W.A.: Computer program GalCohom (2023). https://degraaf.maths.unitn.it/galcohom.html
Hochschild, G.P.: Basic Theory of Algebraic Groups and Lie Algebras. Graduate Texts in Mathematics, vol. 75. Springer, New York (1981)
Lang, S.: Algebra. Graduate Texts in Mathematics, vol. 211, Revised 3rd edn. Springer, New York (2002)
Magnin, L.: Determination of 7-dimensional indecomposable nilpotent complex Lie algebras by adjoining a derivation to 6-dimensional Lie algebras. Algebr. Represent. Theory 13(6), 723–753 (2010)
Milne, J.S.: Algebraic Groups: The Theory of Group Schemes of Finite Type Over a Field. Cambridge Studies in Advanced Mathematics, vol. 170. Cambridge University Press, Cambridge (2017)
Morozov, V.V.: Classification of nilpotent Lie algebras of sixth order. Izv. Vyssh. Uchebn. Zaved. Matematika 4, 161–171 (1958) (in Russian)
Onishchik, A.L., Vinberg, E.B.: Lie Groups and Algebraic Groups. Springer Series in Soviet Mathematics. Springer, Berlin (1990)
Patera, J., Sharp, R.T., Winternitz, P., Zassenhaus, H.J.: Invariants of real low dimension Lie algebras. J. Math. Phys. 17(6), 986–994 (1976)
Plebański, J.F., Przanowski, M.: Generalizations of the quaternion algebra and Lie algebras. J. Math. Phys. 29(3), 529–535 (1988)
Ren, B., Zhu, L.: Classification of 2-step nilpotent Lie algebras of dimension 8 with 2-dimensional center. Comm. Algebra 39(6), 2068–2081 (2011)
Romdhani, M.: Classification of real and complex nilpotent Lie algebras of dimension 7. Linear Multilinear Algebra 24(3), 167–189 (1989)
Sansuc, J.-J.: Groupe de Brauer et arithmétique des groupes algébriques linéaires sur un corps de nombres. J. Reine Angew. Math. 327, 12–80 (1981)
Serre, J.-P.: Local Fields. Graduate Texts in Mathematics, vol. 67. Springer, New York (1979)
Serre, J.-P.: Galois Cohomology. Springer Monographs in Mathematics. Springer, Berlin (2002)
Springer, T.A.: Reductive Groups. In: Borel, A. Casselman, W. (eds.) Automorphic Forms, Representations and \(L\)-functions. Proceedings of Symposia in Pure Mathematics, vol. 33.1, pp. 3–27. American Mathematical Society, Providence (1979)
Stroppel, M.: The Klein quadric and the classification of nilpotent Lie algebras of class two. J. Lie Theory 18(2), 391–411 (2008)
Vinberg, E.B.: The Weyl group of a graded Lie algebra. Math. USSR-Izv. 10, 463–495 (1976)
Vinberg, E.B.: Classification of homogeneous nilpotent elements of a semisimple graded Lie algebra. Selecta Math. Sov. 6, 15–35 (1987)
Vinberg, E.B., Elashvili, A.G.: A classification of the trivectors of nine-dimensional space. Selecta Math. Sov. 7, 63–98 (1988)
Yan, Z., Deng, S.: The classification of two step nilpotent complex Lie algebras of dimension 8. Czechoslovak Math. J. 63 (138) (3), 847–863 (2013)
Funding
Open access funding provided by Tel Aviv University.
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Borovoi and Dina were supported by the Israel Science Foundation (Grant 1030/22).
A Appendix: Signature (4, 4): the duality approach
A Appendix: Signature (4, 4): the duality approach
We use the duality approach; see Gauger [15, Section 3] or Galitski and Timashev [13, Section 1.2]. Let U and V be finite dimensional spaces over a field \(\mathbb {k}\) of characteristic different from 2. To each surjective linear map  we assign the natural surjective linear map
we assign the natural surjective linear map

where \((\ker \beta )^\bot \) denotes the orthogonal complement (annihilator) to  in the dual space
in the dual space  to
to  . This approach reduces classification of surjective skew-symmetric bilinear maps \(\mathbb {k}^m\hspace{0.55542pt}{\times }\hspace{1.111pt}\mathbb {k}^m\rightarrow \mathbb {k}^{n_1}\) to classification of surjective skew-symmetric bilinear maps \(\mathbb {k}^m\hspace{0.55542pt}{\times }\hspace{1.111pt}\mathbb {k}^m\rightarrow \mathbb {k}^{n_2}\) where \(n_2=\left( {\begin{array}{c}m\\ 2\end{array}}\right) -n_1\). When \((m,n_1)=(4,4)\), we obtain \(n_2=\left( {\begin{array}{c}4\\ 2\end{array}}\right) -4=6-4=2\). This reduces the problem of classification of two-step nilpotent Lie algebras over \(\mathbb {k}\) of signature (4, 4) to the well-known cases of signatures (4, 2) and (3, 2) (note that the signatures (2, 2) and (1, 2) are impossible).
. This approach reduces classification of surjective skew-symmetric bilinear maps \(\mathbb {k}^m\hspace{0.55542pt}{\times }\hspace{1.111pt}\mathbb {k}^m\rightarrow \mathbb {k}^{n_1}\) to classification of surjective skew-symmetric bilinear maps \(\mathbb {k}^m\hspace{0.55542pt}{\times }\hspace{1.111pt}\mathbb {k}^m\rightarrow \mathbb {k}^{n_2}\) where \(n_2=\left( {\begin{array}{c}m\\ 2\end{array}}\right) -n_1\). When \((m,n_1)=(4,4)\), we obtain \(n_2=\left( {\begin{array}{c}4\\ 2\end{array}}\right) -4=6-4=2\). This reduces the problem of classification of two-step nilpotent Lie algebras over \(\mathbb {k}\) of signature (4, 4) to the well-known cases of signatures (4, 2) and (3, 2) (note that the signatures (2, 2) and (1, 2) are impossible).
In [18] one can find a classification of 6-dimensional nilpotent Lie algebras over a field \(\mathbb {k}\) of characteristic different from 2. This gives, in particular, a classification of surjective skew-symmetric bilinear maps
over such fields. These are representatives of the orbits with the numbering of [18, Section 4].
Here \(\beta _{6,22}(\delta )\) is equivalent to \(\beta _{6,22}(\epsilon )\) if \(\delta =\alpha ^2\epsilon \) for some \(\alpha \in \mathbb {k}^{\times } \). Thus for \(\mathbb {k}={\mathbb {C}}\) we obtain three equivalence classes with representatives
and for \(k=\mathbb {R}\) we obtain four equivalence classes with representatives
which is compatible with our Table 3.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Borovoi, M., Dina, B.A. & de Graaf, W.A. Real non-degenerate two-step nilpotent Lie algebras of dimension eight. European Journal of Mathematics 10, 16 (2024). https://doi.org/10.1007/s40879-024-00727-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40879-024-00727-3



 is the cocharacter group of T;
is the cocharacter group of T;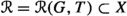 is the root system;
is the root system; is the coroot system;
is the coroot system; is the system of simple roots;
is the system of simple roots; is the system of simple coroots.
is the system of simple coroots.