Abstract
There are studied algebraic properties of quadratic Poisson brackets on non-associative non-commutative algebras, compatible with their multiplicative structure. Their relations both with derivations of symmetric tensor algebras and Yang–Baxter structures on the adjacent Lie algebras are demonstrated. Special attention is paid to quadratic Poisson brackets of Lie–Poisson type, examples of Balinsky–Novikov and Leibniz algebras are discussed. The non-associative structures of commutative algebras related with Balinsky–Novikov, Leibniz, Lie, and Zinbiel algebras are studied in detail.
Similar content being viewed by others
1 Introduction
Many integrable Hamiltonian systems, discovered during the last decades, were understood [15, 16, 24, 38] owing to the Lie-algebraic properties of their internal hidden symmetry structures. A modern Lie-algebraic approach to describing such systems in many cases allows to represent them as some specially constructed orbits of some hidden group actions on the Poisson manifolds, generated by a set of the suitably constructed Casimir invariants on the adjoint space to the corresponding symmetry Lie algebra. A first formal account of the related Hamiltonian operators and differential-algebraic structures, lying in the background of such integrable systems, was given by Gelfand and Dorfman [19, 26] and later was extended by Dubrovin and Novikov [20, 21], and also by Balinsky and Novikov [10,11,12,13]. There were also devised some new special differential-algebraic techniques [41] for studying the Lax type integrability and the structure of related Hamiltonian operators for a wide class of Riemann type hydrodynamic hierarchies. Just recently a lot of works appeared [7,8,9, 40] being devoted to the finite-dimensional representations of the Novikov algebra. Their importance for constructing integrable multi-component nonlinear Camassa–Holm type dynamical systems on functional manifolds was demonstrated by Strachan and Szablikowski in [47], where there was suggested in part the Lie-algebraic imbedding of the Novikov algebra into the general Lie–Poisson orbits scheme of classification Lax type integrable Hamiltonian systems.
In the work we succeeded in formal differential-algebraic reformulating the classical Lie algebraic scheme and developed an effective approach to classification of algebraic structures lying in the background of integrable multicomponent Hamiltonian systems. We have devised a simple Lie-algebraic algorithm, allowing to construct new algebraic structures within which the corresponding linear and quadratic Hamiltonian operators, generated by the corresponding Lie–Poisson structure on the co-adjoint orbits, exist and describe the related integrable multicomponent dynamical systems. In these cases an interesting problem of describing the Balinsky–Novikov and Leibniz type algebras, whose multiplicative structures satisfy some additional tensor r-structure type relationships naturally arises. We studied also the non-associative structures of commutative algebras related with Balinsky–Novikov, Leibniz, Lie and Zinbiel algebras, having diverse important applications both in theory of integrable dynamical systems and to modern problems of communication technology.
2 Quadratic Poisson brackets: compatibility and related algebraic structures
Let  be a finite-dimensional non-associative and non-commutative algebra of dimension \(N=\dim A\)\(\in {\mathbb {Z}}_{+}\) over an algebraically closed field \({\mathbb {K}}\). To the algebra A one can naturally relate the loop algebra \({\widetilde{A}}\) of smooth mappings
be a finite-dimensional non-associative and non-commutative algebra of dimension \(N=\dim A\)\(\in {\mathbb {Z}}_{+}\) over an algebraically closed field \({\mathbb {K}}\). To the algebra A one can naturally relate the loop algebra \({\widetilde{A}}\) of smooth mappings  and endow it with a suitably generalized natural convolution
and endow it with a suitably generalized natural convolution  on
on  , where \({\widetilde{A}}^{*}\) is the corresponding adjoint to the space \({\widetilde{A}}\).
, where \({\widetilde{A}}^{*}\) is the corresponding adjoint to the space \({\widetilde{A}}\).
First, we shall consider a general scheme of constructing non-trivial ultra-local and local [24] quadratic Poisson structures [11, 12, 14, 45] on the loop space \({\widetilde{A}}\), compatible with the internal multiplication in the algebra A. Namely, let  be a basis of the algebra A and its dual
be a basis of the algebra A and its dual  with respect to
with respect to  on
on  , that is
, that is  for all \(i,j=\overline{1,N}\), and such that for any
for all \(i,j=\overline{1,N}\), and such that for any

the quantities  for all \(s=\overline{1,N}\),
for all \(s=\overline{1,N}\),  . Denote by
. Denote by  and let
and let  be a skew-symmetric bilinear mapping. Then for linear on \({\widetilde{A}}\) functions
be a skew-symmetric bilinear mapping. Then for linear on \({\widetilde{A}}\) functions  and
and  for any \(a,b\in {\widetilde{A}}^{*}\) the expression
for any \(a,b\in {\widetilde{A}}^{*}\) the expression

defines an ultra-local quadratic skew-symmetric pre-Poisson bracket on  . Since the algebra \({\widetilde{A}}\) possesses its internal multiplicative structure “
. Since the algebra \({\widetilde{A}}\) possesses its internal multiplicative structure “ , the important problem [11, 12] arises: Under what conditions is the pre-Poisson bracket (1) Poisson and compatible with this internal structure on\({\widetilde{A}}\)? To proceed with elucidating this question, we define a co-multiplication
, the important problem [11, 12] arises: Under what conditions is the pre-Poisson bracket (1) Poisson and compatible with this internal structure on\({\widetilde{A}}\)? To proceed with elucidating this question, we define a co-multiplication  on an arbitrary element \(c\in {\widetilde{A}} ^{*}\) by means of the relationship
on an arbitrary element \(c\in {\widetilde{A}} ^{*}\) by means of the relationship

for arbitrary \(w,v\in {\widetilde{A}}\). Note that the co-multiplication  , defined this way, is a homomorphism of the tensor algebra \(\mathrm {T}^{1}({\widetilde{A}}^{*})\) into \(\mathrm {T}^{2}({\widetilde{A}}^{*})\) and the linear pre-Poisson structure
, defined this way, is a homomorphism of the tensor algebra \(\mathrm {T}^{1}({\widetilde{A}}^{*})\) into \(\mathrm {T}^{2}({\widetilde{A}}^{*})\) and the linear pre-Poisson structure  on \({\widetilde{A}}^{*}\) [see (1)] is called compatible with the multiplication “
on \({\widetilde{A}}^{*}\) [see (1)] is called compatible with the multiplication “ ” on the algebra \({\widetilde{A}}\), if the following invariance condition:
” on the algebra \({\widetilde{A}}\), if the following invariance condition:
holds for all \(a,b\in {\widetilde{A}}^{*}\) and arbitrary \(u\in {\widetilde{A}}\). Now, taking into account that multiplication in the algebra A can be represented for any \(i,j=\overline{1,N}\) by means of the relationship

where the quantities \(\sigma _{ij}^{s}\in {\mathbb {K}} \) for all i, j and \(k=\overline{1,N}\) are constants, the co-multiplication  acts on the basic functionals
acts on the basic functionals  , \(s=\overline{1,N}\), as
, \(s=\overline{1,N}\), as

Additionally, if the mapping  is given, for instance, in the simple linear form
is given, for instance, in the simple linear form

the quantities \(c_{sk}^{ij}\in {\mathbb {K}}\) are constant for all i, j and \(s,k=\overline{1,N}\) and chosen to be symmetric in their lower indices, then for the adjoint to (5) mapping  one obtains the expression
one obtains the expression

Recall that a linear mapping \(\vartheta :A\rightarrow B\) from an algebra A to the A-bimodule B is called a derivation if for any \(\lambda ,\mu \in A\) there holds the Leibniz property

The following theorem [11] gives an effective compatibility criterion for the multiplication in the algebra A.
Theorem 2.1
The pre-Poisson bracket (2) is compatible with the multiplication (3) if and only if the mapping  is a derivation of the symmetric algebra
is a derivation of the symmetric algebra  .
.
Proof
The idea of the proof consists in checking the relationships on the corresponding coefficients following both from (2) and (6) for basis elements  \(\square \)
\(\square \)
Observe now that the pre-Poisson bracket (1) can be equivalently rewritten as

giving rise, owing to the arbitrariness of elements  , to the following tensor equality:
, to the following tensor equality:

with the derivation \(\vartheta \). As was remarked in [11, 12], the following natural commutator expression:

for any  and a fixed skew-symmetric constant tensor
and a fixed skew-symmetric constant tensor  is an inner derivation of the algebra
is an inner derivation of the algebra  . Thus, one can consider a class of pre-Poisson brackets (7) in the following commutator tensor form:
. Thus, one can consider a class of pre-Poisson brackets (7) in the following commutator tensor form:

and pose a problem of finding conditions on the tensor  under which the pre-Poisson bracket (8) becomes a Poisson one.
under which the pre-Poisson bracket (8) becomes a Poisson one.
If the algebra \({\widetilde{A}}\) is non-commutative and associative, the adjacent Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\simeq {\widetilde{A}}\) makes it possible to construct the related formal Lie group  , whose tangent space at the unity can be identified with the Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\) of the right-invariant vector fields on \(G_{{\tilde{A}}}\). For a fixed element \(u\in G_{{\tilde{A}}}\) one can denote by
, whose tangent space at the unity can be identified with the Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\) of the right-invariant vector fields on \(G_{{\tilde{A}}}\). For a fixed element \(u\in G_{{\tilde{A}}}\) one can denote by  the differentials of the right and left shifts on \(G_{{\tilde{A}}}\), respectively. Let \(\rho _{u}^{*},\xi _{u}^{*}:T_{u}^{*}(G_{{\tilde{A}}})\rightarrow {\mathscr {L}}_{{\tilde{A}}}^{*}\) be dual mappings, respectively. Then the following theorem, stated in [45], holds.
the differentials of the right and left shifts on \(G_{{\tilde{A}}}\), respectively. Let \(\rho _{u}^{*},\xi _{u}^{*}:T_{u}^{*}(G_{{\tilde{A}}})\rightarrow {\mathscr {L}}_{{\tilde{A}}}^{*}\) be dual mappings, respectively. Then the following theorem, stated in [45], holds.
Theorem 2.2
The following bracket:
for any \(a,b\in T_{u}^{*}(G_{{\tilde{A}}})\) is Poisson if the homomorphism \({\mathscr {R}}:{\widetilde{A}}\rightarrow {\widetilde{A}}\), naturally related with the tensor  , is skew-symmetric and satisfies the modified Yang–Baxter relationship
, is skew-symmetric and satisfies the modified Yang–Baxter relationship
for all \(\alpha ,\beta \in {\mathscr {L}}_{{\tilde{A}}}\) subject to the Lie commutator structure in \({\mathscr {L}}_{{\tilde{A}}}\).
If to take into account that in this case there hold the expressions
for any  , where the mappings \(\Delta _{1}\) and \( \Delta _{2}\) stand for convolutions of the co-multiplication
, where the mappings \(\Delta _{1}\) and \( \Delta _{2}\) stand for convolutions of the co-multiplication  with the first and second tensor components, respectively, that is
with the first and second tensor components, respectively, that is

for any \(\alpha \in {\widetilde{A}}\), the bracket (9) will become

for any \(a,b\in T_{u}^{*}(G_{{\tilde{A}}})\), which can be easily enough computed, if to take into account the relationship (4).
The following result [14, 45] is a simple consequence of Theorem 2.2 in the case of the associative matrix algebra \({\widetilde{A}}\) and is almost classical.
Theorem 2.3
Let the algebra \({\widetilde{A}}\) be matrix associative with respect to the standard multiplication, and endowed both with the natural commutator Lie structure  and with the trace-type symmetric scalar product
and with the trace-type symmetric scalar product  . Define also for the tensor
. Define also for the tensor

the related \({\mathscr {R}}\)-homomorphism

for any \(\alpha \in {\widetilde{A}}\). Then the pre-Poisson bracket (11) is Poisson if the \({\mathscr {R}}\)-homomorphism (12) is skew-symmetric and satisfies the modified Yang–Baxter relationship (10). Moreover, the Poisson bracket (11) can be equivalently rewritten in the following simplified form:
for any  .
.
Remark 2.4
The Yang–Baxter relationship (10) is basic for finding the corresponding internal multiplication structure of the algebra \({\widetilde{A}}\), allowing the quadratic Poisson bracket (11). If, for example, to assume that the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\) allows splitting into two subalgebras,  , then the homomorphism \(\mathscr {R=P}_{+}-{\mathscr {P}}_{-}\) solves the relationship (10), where, by definition, the mappings \({\mathscr {P}}_{\pm }:{\mathscr {L}}_{{\tilde{A}} }\rightarrow {\mathscr {L}}_{{\tilde{A}}}^{\pm }\subset {\mathscr {L}}_{{\tilde{A}}}\) are the suitable projections. If to assume, that the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\) is generated by the associative multiplication “
, then the homomorphism \(\mathscr {R=P}_{+}-{\mathscr {P}}_{-}\) solves the relationship (10), where, by definition, the mappings \({\mathscr {P}}_{\pm }:{\mathscr {L}}_{{\tilde{A}} }\rightarrow {\mathscr {L}}_{{\tilde{A}}}^{\pm }\subset {\mathscr {L}}_{{\tilde{A}}}\) are the suitable projections. If to assume, that the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\) is generated by the associative multiplication “ ” of the Balinsky–Novikov loop algebra \({\widetilde{A}}\), then the related Lie structure is given by the commutator
” of the Balinsky–Novikov loop algebra \({\widetilde{A}}\), then the related Lie structure is given by the commutator

for the derivation \(D_x={d}/{dx}\) and any \(\alpha ,\beta \in {\widetilde{A}}\), giving rise to the ultra-local quadratic Poisson bracket (11). To our regret, we do not know whether the Lie structure

for any \(\alpha ,\beta \in {\widetilde{A}}\) and all  , suitably determining the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\), can be generated by some associative multiplication on the loop Balinsky–Novikov algebra, with respect to which the Lie structure (14) could entail the local quadratic Poisson bracket (11).
, suitably determining the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\), can be generated by some associative multiplication on the loop Balinsky–Novikov algebra, with respect to which the Lie structure (14) could entail the local quadratic Poisson bracket (11).
Problem 2.5
Concerning the algebraic structures discussed above the interesting problem arises: Classify associative Balinsky–Novikov loop algebras \({\widetilde{A}}\), whose adjacent Lie algebras \({\mathscr {L}}_{{\tilde{A}}}\) allow splitting into two non-trivial subalgebras subject to the Lie structure (13).
Remark 2.6
In the case of basic Leibniz loop algebra \({\widetilde{A}}\), it is well known that the usual commutator structure (13) does not generate the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\), yet the following inverse-derivative Lie structure:

suitably determined for any \(\alpha ,\beta \in {\widetilde{A}}\) and all  , already does. Yet, we do not know whether the Lie structure (15) can be generated by some associative multiplication “
, already does. Yet, we do not know whether the Lie structure (15) can be generated by some associative multiplication “ ” on the loop Leibniz algebra \({\widetilde{A}}\).
” on the loop Leibniz algebra \({\widetilde{A}}\).
3 Quadratic Poisson structures: the Lie–Poisson type generalization
Assume as above that  is a finite-dimensional algebra of the dimension \(N=\dim A\mathbb \in Z_{+}\) (in general non-associative and non-commutative) over an algebraically closed field \({\mathbb {K}}\). Based on the algebra A one can construct the related loop algebra \({\widetilde{A}}\) of smooth mappings
is a finite-dimensional algebra of the dimension \(N=\dim A\mathbb \in Z_{+}\) (in general non-associative and non-commutative) over an algebraically closed field \({\mathbb {K}}\). Based on the algebra A one can construct the related loop algebra \({\widetilde{A}}\) of smooth mappings  and endow it with the suitably generalized natural convolution
and endow it with the suitably generalized natural convolution  on
on  , where \({\widetilde{A}}^{*}\) is the corresponding adjoint space to \({\widetilde{A}}\).
, where \({\widetilde{A}}^{*}\) is the corresponding adjoint space to \({\widetilde{A}}\).
First, we will consider a general scheme of constructing non-trivial ultra-local and local Poisson structures on the adjoint space \({\widetilde{A}}^{*}\) [24] compatible with the internal multiplication in the loop algebra \({\widetilde{A}}\). Consider a basis  of the algebra A and its dual
of the algebra A and its dual  with respect to the natural convolution
with respect to the natural convolution  on
on  , that is
, that is  , \(i,j=\overline{1,N}\), and such that for any
, \(i,j=\overline{1,N}\), and such that for any

the quantities  for all \(s=\overline{1,N}\),
for all \(s=\overline{1,N}\),  . Denote by
. Denote by  and let
and let  be a skew-symmetric bilinear mapping. Then the expression
be a skew-symmetric bilinear mapping. Then the expression

defines for any \(a,b\in {\widetilde{A}}\) an ultra-local linear skew-symmetric pre-Poisson bracket on  . If the mapping
. If the mapping  is given, for instance, in the simple linear form
is given, for instance, in the simple linear form

where quantities \(c_{ij}^{s}\in {\mathbb {K}}\) are constant for all i, j and \( s=\overline{1,N}\), then for the adjoint to (17) mapping  one obtains the expression
one obtains the expression

For the pre-Poisson bracket to be a Poisson bracket on  , it should satisfy additionally the Jacobi identity. To find the corresponding additional constraints on the internal multiplication “
, it should satisfy additionally the Jacobi identity. To find the corresponding additional constraints on the internal multiplication “ ” on the algebra \({\widetilde{A}}\), define for any \( u(x)\in {\widetilde{A}}^{*}\) the skew-symmetric linear mapping
” on the algebra \({\widetilde{A}}\), define for any \( u(x)\in {\widetilde{A}}^{*}\) the skew-symmetric linear mapping

called by the Hamiltonian operator [26], via the identity

for any \(a,b\in {\widetilde{A}}\), where the mapping  is determined by the expression (18), being adjoint to it. Then it is well known [26] that the pre-Poisson bracket (16) is a Poisson one if and only if the Hamiltonian operator (19) satisfies the Schouten–Nijenhuis condition
is determined by the expression (18), being adjoint to it. Then it is well known [26] that the pre-Poisson bracket (16) is a Poisson one if and only if the Hamiltonian operator (19) satisfies the Schouten–Nijenhuis condition
for any  . Since
. Since

holds for any basis element \(e_{i}\in A\), \(i=\overline{1,N}\), the resulting pre-Poisson bracket (16) is equal to

for any \(u(x)\in {\widetilde{A}}^{*}\) and all \(a,b\in {\widetilde{A}}\). If now to define on the algebra A the natural adjacent Lie algebra structure to the algebra A

for any basis elements  , \(i,j=\overline{1,N}\), the expression (22) yields for all \(a,b\in {\widetilde{A}}\) the well-known [1, 4] classical Lie–Poisson bracket
, \(i,j=\overline{1,N}\), the expression (22) yields for all \(a,b\in {\widetilde{A}}\) the well-known [1, 4] classical Lie–Poisson bracket
Concerning the adjacent Lie algebra structure condition (23), it can be easily rewritten as the set of relationships

whose obvious solution is
for any \(i,j,s=\overline{1,N}\). As the bracket (24) is of the classical Lie–Poisson type, for the Hamiltonian operator (21) to satisfy the Schouten–Nijenhuis condition (20) it is enough to check only the weak Jacobi identity for the loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\), adjacent to the algebra \({\widetilde{A}}\) via imposing the Lie structure (23), taking into account the relationships (25). For instance, if the commutator of the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\) is given by the expression

the corresponding algebra A coincides with the well-known Balinsky–Novikov algebra, determined by means of the following relationships:
where, by definition,  for any \(a,b\in {\widetilde{A}}\). If, for instance, the commutator of the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\) is given by the expression
for any \(a,b\in {\widetilde{A}}\). If, for instance, the commutator of the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\) is given by the expression

for a suitably determined inverse-derivation mapping \(D_{x}^{-1}:{\widetilde{A}}\rightarrow {\widetilde{A}}\), the corresponding algebra A coincides with the well-known right Leibniz algebra, described by the relationships
for any \(a,b\in {\widetilde{A}}\). As a consequence of reasonings above one can formulate the following general theorem.
Theorem 3.1
The linear pre-Poisson bracket (24) on \({\widetilde{A}} ^{*}\) is Lie–Poisson on the adjoint space \({\mathscr {L}}_{{\tilde{A}}}^{*}\) if and only if the internal multiplicative structure of the algebra A is compatible with the weak Lie algebra structure on the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\).
Similarly, one can consider a simple ultra-local quadratic pre-Poisson bracket on \({\widetilde{A}}^{*}\) in the form

for any \(a,b\in {\widetilde{A}}\), where the skew-symmetric mapping  is given for any \(i,j=\overline{1,N}\) in the quadratic form
is given for any \(i,j=\overline{1,N}\) in the quadratic form

In particular, if to assume that the coefficients \(c_{ij}^{ks}=\sigma _{ij}^{k}\alpha ^{s}\) for some constant numbers \(\sigma _{ij}^{k}\) and \( \alpha ^{s}\in {\mathbb {K}}\) for all i, j and \(k,s=\overline{1,N}\), where, by definition, the multiplications

coincides with that of the algebra A, then the pre-Poissson bracket (30) yields for any \(a,b\in A\) a very compact form

generalizing the classical Lie–Poisson expression (24) and parametrically depending on the constant vector

Thus, for the pre-Lie–Poisson bracket (31) one can formulate suitable constraints on the algebraic structure of A. For instance, if the weak algebraic structure on the adjacent Lie algebra \({\mathscr {L}}_{{\tilde{A}}} \) is given, respectively, either by the Lie commutator (26) or by (28), then the corresponding multiplicative structures of the algebra A are generated, respectively, by the Balinsky–Novikov (27) and Leibniz (29) algebras relationships, augmented with the following common tensor multiplicative constraint:

which holds for any \(a\in A\) and arbitrary but fixed element \(\alpha \in A\). So, one can formulate the following theorem.
Theorem 3.2
The quadratic pre-Lie–Poisson bracket (31) on \({\widetilde{A}}^{*}\) is Poisson if and only if the internal multiplicative structure of the algebra A is compatible both with the weak Lie algebra structure on the adjacent loop Lie algebra \({\mathscr {L}}_{{\tilde{A}}}\) and with the tensor multiplicative relationships (32).
In these cases there arises an interesting problem of describing the Balinsky–Novikov and Leibniz algebras, whose multiplicative structures additionally satisfy tensor relationships (32). Such and related algebraic structure problems are planned to be studied in detail elsewhere. In the next section we proceed to study general algebraic structures related both with generalized Balinsky–Novikov and Leibniz algebras, and so-called Zinbiel algebras, having diverse important applications in communications technology.
4 Algebraic structures preliminaries
Let A be an associative commutative algebra over a field \({\mathbb {K}}\) of any finite or infinite dimension (with the addition “\(+\)” and multiplication “ ”) not necessary with identity and \(\delta \) its derivation, i.e., \(\delta :A\rightarrow A\) is a \( {\mathbb {K}}\)-linear map satisfying the Leibniz rule. Then
”) not necessary with identity and \(\delta \) its derivation, i.e., \(\delta :A\rightarrow A\) is a \( {\mathbb {K}}\)-linear map satisfying the Leibniz rule. Then

is a Balinsky–Novikov algebra (the so-called \(\delta \)-adjancent or \(\delta \)-associated Balinsky–Novikov algebra of A ) with respect to “ ” defined by the rule
” defined by the rule

(where \(\xi \) is a fixed element of A) and so

and

for all \(a,b,c\in A\). In particular,  with \(\xi =0\). Balinsky–Novikov algebras were introduced in connection with the so-called Hamiltonian operators [26] and Poisson brackets of hydrodynamic type [13]. Note here, that the term “Novikov algebra” was suggested by Osborn in [40]. Moreover,
with \(\xi =0\). Balinsky–Novikov algebras were introduced in connection with the so-called Hamiltonian operators [26] and Poisson brackets of hydrodynamic type [13]. Note here, that the term “Novikov algebra” was suggested by Osborn in [40]. Moreover,
is a Lie algebra (the so-called \(\delta \)-adjancent or \(\delta \)-associated Lie algebra of A) with respect to the Lie bracket “\([-,-]\)” defined by the rule

for any \(a,b\in A\), see [29, 30, 37, 42, p. 285] and [43, p. 245].
Let  be a (Lie, Balinsky–Novikov, Zinbiel or associative) algebra with the derivation algebra \({\mathrm{Der}}\,D\), \(\varnothing \ne \Delta \subseteq {\mathrm{Der}}\,D\) and \(\theta \in {\mathrm{Der}}\,D\). Then
be a (Lie, Balinsky–Novikov, Zinbiel or associative) algebra with the derivation algebra \({\mathrm{Der}}\,D\), \(\varnothing \ne \Delta \subseteq {\mathrm{Der}}\,D\) and \(\theta \in {\mathrm{Der}}\,D\). Then  is the annihilator of \(W\subseteq D\) and
is the annihilator of \(W\subseteq D\) and  is the center of D. If I is an ideal of D and \(\theta (I)\subseteq I\) (respectively, for any \(\theta \in \Delta \)), then we say that I is a \(\theta \)-ideal (respectively, \(\Delta \)-ideal) of D. Recall that D is called:
is the center of D. If I is an ideal of D and \(\theta (I)\subseteq I\) (respectively, for any \(\theta \in \Delta \)), then we say that I is a \(\theta \)-ideal (respectively, \(\Delta \)-ideal) of D. Recall that D is called:
\(\Delta \)-simple if
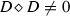 and any \( \Delta \)-ideal I of D is 0 or D,
and any \( \Delta \)-ideal I of D is 0 or D,\(\Delta \)-prime if, for any \(\Delta \)-ideals B, C of D, the condition
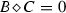 implies that \(B=0\) or \(C=0\),
implies that \(B=0\) or \(C=0\),\(\Delta \)-semiprime if, for any \(\Delta \)-ideal B of D, the condition
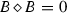 implies that \(B=0\).
implies that \(B=0\).
Every \(\Delta \)-prime algebra is \(\Delta \)-semiprime and every \(\Delta \)-simple algebra is \(\Delta \)-prime. If \(\Delta =\{ \theta \}\) and D is a \(\Delta \)-simple (respectively, \(\Delta \)-prime or \(\Delta \)-semiprime), then we say that D is \(\theta \)-simple (respectively, \(\theta \)-prime or \(\theta \)-semiprime). Moreover, if \(\Delta =\{ 0\}\), then a \(\Delta \)-simple (respectively, \(\Delta \)-prime or \(\Delta \)-semiprime) algebra is simple (respectively, prime or semiprime). Any unexplained terminology is standard as in [27, 28, 31, 34].
The purpose of this paper is also to study relationships between associative commutative algebras A, their \(\delta \)-associated Balinsky–Novikov algebras \(A^{\delta ,\xi }\) and \(\delta \)-associated Lie algebras \(A^{\delta ,L}\). Connections between properties of an associative commutative algebra A and its \(\delta \)-associated algebra \(A^{\delta ,L}\) have been investigated by Ribenboim [43], Jordan, Jordan [29, 30], and Nowicki [37]. Xu [49] found some classes of infinite-dimensional simple Balinsky–Novikov algebras of type \(A^{\delta ,\xi }\). Bai and Meng [6] proved that, if A is a finite-dimensional associative commutative algebra and \(0\ne \delta \in {\mathrm{Der}}\,A\), then \(A^{\delta ,0}\) is transitive (i.e.,  is a nilpotent right transformation operator of \(A^{\delta ,0}\) for any \(a\in A\)) and \(A^{\delta ,L}\) is a solvable Lie algebra [32]. In [48, Proposition 2.8] it is proved that the Balinsky–Novikov algebra \(A^{\delta ,\xi } \) is simple if and only if an associative commutative ring A is \(\delta \)-simple. As noted in [5], there is a conjecture: the Balinsky–Novikov algebrasNcan be realized as the algebras\(A^{\delta ,0}\), whereAis a suitable associative commutative algebras, and their (compatible) linear deformation. Recall that a binary operation
is a nilpotent right transformation operator of \(A^{\delta ,0}\) for any \(a\in A\)) and \(A^{\delta ,L}\) is a solvable Lie algebra [32]. In [48, Proposition 2.8] it is proved that the Balinsky–Novikov algebra \(A^{\delta ,\xi } \) is simple if and only if an associative commutative ring A is \(\delta \)-simple. As noted in [5], there is a conjecture: the Balinsky–Novikov algebrasNcan be realized as the algebras\(A^{\delta ,0}\), whereAis a suitable associative commutative algebras, and their (compatible) linear deformation. Recall that a binary operation  of a Balinsky–Novikov algebra
of a Balinsky–Novikov algebra  is called its linear deformation if algebras \((N,+,g_{t})\), where
is called its linear deformation if algebras \((N,+,g_{t})\), where  , are Balinsky–Novikov algebras for every t. If \(G_{1}\) is commutative, then it is called compatible.
, are Balinsky–Novikov algebras for every t. If \(G_{1}\) is commutative, then it is called compatible.
As noted in [5], a “good” structure theory for algebraic systems means an existence of a well-defined radical and the quotient by the radical is semisimple. Our result in this direction is the following.
Theorem 4.1
Let A be an associative commutative algebra with 1, \({\mathrm{char}}\,{\mathbb {K}}\ne 2\), \(0\ne \delta \in {\mathrm{Der}}\,A\) and \(\xi \in A\). Then the following conditions are equivalent:
- (i)
A is a \(\delta \)-semiprime (respectively, \(\delta \)-prime or \(\delta \)-simple) algebra,
- (ii)
\(A^{\delta ,\xi }\) is a semiprime (respectively, prime or simple) Balinsky–Novikov algebra,
- (iii)
\(A^{\delta ,L}\) is a semiprime (respectively, prime or simple) Lie algebra.
A triple  is called a Zinbiel algebra (or a dual Leibniz algebra) if
is called a Zinbiel algebra (or a dual Leibniz algebra) if
\((Z,+)\) is an abelian group,
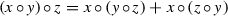 ,
, and
and 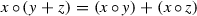
for all \(x,y,z\in Z\). As a consequence,  If
If  for all \(x,y\in Z\) (see Lemma 5.1), then
for all \(x,y\in Z\) (see Lemma 5.1), then  is an associative commutative algebra (the so-called adjacent or associated associative algebra\(Z^{A}\) of a Zinbiel algebra Z). Zinbiel algebras were introduced by Loday in [33, 34] and are very popular in the control theory (in context of “chronological” algebras, see e.g. [2, 3, 31, 44]) and in the theory of Leibniz cohomology [35]. Zinbiel rings can be defined by analogy.
is an associative commutative algebra (the so-called adjacent or associated associative algebra\(Z^{A}\) of a Zinbiel algebra Z). Zinbiel algebras were introduced by Loday in [33, 34] and are very popular in the control theory (in context of “chronological” algebras, see e.g. [2, 3, 31, 44]) and in the theory of Leibniz cohomology [35]. Zinbiel rings can be defined by analogy.
Some interesting properties of Zinbiel algebras were obtained by Dzhumadil’daev, Tulenbaev [22, 23], and Omirov [39]. In particular, Dzhumadil’daev [22] proved that any finite-dimensional Zinbiel algebra over the complex numbers field is nilpotent. We prove the next result.
Proposition 4.2
Let Z be a Zinbiel algebra over a field \({\mathbb {K}}\). If the characteristic \({\mathrm{char}}\,{{\mathbb {K}}}=p>0\) is prime, then the associated associative algebra \(Z^A\) is nil of bounded degree p.
5 An associative commutative structure of a Zinbiel algebra
Recall that a (Zinbiel or associative) algebra  is called reduced if the implication
is called reduced if the implication  is true for any \(a\in A\).
is true for any \(a\in A\).
Lemma 5.1
[18, Theorem 3.4] If  is a Zinbiel algebra, then
is a Zinbiel algebra, then  is an associative commutative algebra, where “
is an associative commutative algebra, where “ ” is defined by the rule
” is defined by the rule  for any \(a,b\in Z\).
for any \(a,b\in Z\).
An additive subgroup I of a Zinbiel ring (respectively, algebra) Z is said to be an associative ideal of Z if  . It is easy to see that I is an associative ideal of Z if and only if it is an ideal of
. It is easy to see that I is an associative ideal of Z if and only if it is an ideal of  . A Zinbiel ring Z is called 2-torsion-free if, for any \(x\in Z\), \(2x=0\) implies that \(x=0\).
. A Zinbiel ring Z is called 2-torsion-free if, for any \(x\in Z\), \(2x=0\) implies that \(x=0\).
Lemma 5.2
Let Z be a Zinbiel ring (respectively, algebra over a field \( {\mathbb {K}}\)), \(\varnothing \ne \Delta \subseteq {\mathrm{Der}}\,Z\) and \(a\in Z\). Then the following properties hold:
- (i)
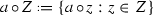 is a right ideal of Z,
is a right ideal of Z, - (ii)
if X is a non-empty subset of Z, then the right annihilator
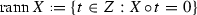 of X is an associative ideal of Z and
of X is an associative ideal of Z and 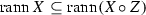 ,
, - (iii)
if I is a right \(\Delta \)-ideal of Z, then
 and
and 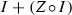 are \(\Delta \)-ideals of Z,
are \(\Delta \)-ideals of Z, - (iv)
if X is an associative \(\Delta \)-ideal of Z, then the left annihilator
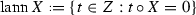 is a right \(\Delta \)-ideal of Z,
is a right \(\Delta \)-ideal of Z, - (v)
if Z is 2-torsion-free (respectively, \({\mathrm{char}}\,{\mathbb {K}}\ne 2\)), then Z is reduced if and only if \(Z^A\) is reduced,
- (vi)
if Z is 2-torsion-free (respectively, \({\mathrm{char}}\,{\mathbb {K}} \ne 2\)) and I, J are commutating ideals of Z (i.e.,
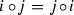 for \(i\in I\) and \(j\in J\)), then
for \(i\in I\) and \(j\in J\)), then 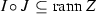 ,
, - (vii)
if K is an additive \(\Delta \)-closed subgroup of Z, then
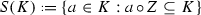 is a right \(\Delta \)-ideal of Z,
is a right \(\Delta \)-ideal of Z, - (viii)
if I, J are \(\Delta \)-ideals of Z, then
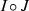 is a right \(\Delta \)-ideal of Z,
is a right \(\Delta \)-ideal of Z, - (ix)
if K is an associative ideal of Z, then
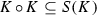 ,
, - (x)
if \(e=e^2\in Z^A\), then \(e=0\).
Proof
Let \(z,t\in Z\).
(i) Clearly  is a subgroup of the additive group \((Z,+)\) and
is a subgroup of the additive group \((Z,+)\) and  Hence
Hence  is a right ideal of Z.
is a right ideal of Z.
(ii) If \(x\in X\), \(u\in {\mathrm{rann}}\,X\), then  and so
and so  . Moreover,
. Moreover, 
(iii) Assume that \(i,j\in I\). Since  ,
,  and
and  , we deduce that
, we deduce that  . We also see that
. We also see that

and

(iv) If \(a\in \mathrm{lann}\, X\), \(i\in X\), then  .
.
(v) It follows from  .
.
(vi) Assume that \(i\in I\) and \(j\in J\). Then

and from this

On the other hand,

(vii) If \(u\in S(K)\), then

(viii) Straightforward.
(ix) If \(a,b\in K\), then  and the assertion holds.
and the assertion holds.
(x) Since  , we conclude that \(e=0\).\(\square \)
, we conclude that \(e=0\).\(\square \)
Lemma 5.3
If Z is a Zinbiel ring (respectively, algebra) and \(\varnothing \ne \Delta \subseteq {\mathrm{Der}}\,Z\), then the following properties hold:
- (i)
if K is an associative \(\Delta \)-ideal of Z, then
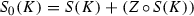 is a \(\Delta \)-ideal of Z,
is a \(\Delta \)-ideal of Z, - (ii)
if I, J are associative ideals of Z such that
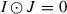 , then
, then 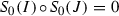 .
.
Proof
(i) By Lemma 5.2 (vii), (ix) and (iii), \(S_0(K)\) is a \(\Delta \)-ideal of A.
(ii) Let \(a\in S(I)\), \(b\in S(J)\) and \(z,t\in Z\). Then  and we have
and we have  . Since
. Since  ,
,

and

we conclude that  .\(\square \)
.\(\square \)
Corollary 5.4
Let Z be a Zinbiel ring (respectively, algebra) and \(\varnothing \ne \Delta \subseteq {\mathrm{Der}}\,Z\). If \(Z^A\) is \(\Delta \)-simple (respectively, \(\Delta \)-prime or \( \Delta \)-semiprime), then Z is the same.
Proof
If \(\Delta \subseteq {\mathrm{Der}}\,Z\), then  .
.
Simplicity. Since every \(\Delta \)-ideal of Z is a \( \Delta \)-ideal of  , the simplicity of \(Z^A\) implies that Z is simple.
, the simplicity of \(Z^A\) implies that Z is simple.
Primeness. Let \(Z^A\) be a \(\Delta \)-prime ring (respectively, algebra) and I, J be \(\Delta \)-ideals of Z such that  . Then I, J, and \(J\cap I\) are \(\Delta \)-ideals of \(Z^A\) and
. Then I, J, and \(J\cap I\) are \(\Delta \)-ideals of \(Z^A\) and

Since  , we conclude that
, we conclude that  . But then
. But then  and consequently \(I=0\) or \(J=0\).
and consequently \(I=0\) or \(J=0\).
Semiprimeness. By analogy as in the prime case.\(\square \)
Proof of Proposition 4.2
Let \(a\in Z\). By \( a^{\odot n}\) we denote the n-th power of a in the algebra \(Z^A\) (n is a positive integer). We have
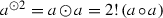 ,
,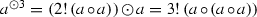 .
.
Now assume that

and compute

\(\square \)
6 Balinsky–Novikov properties
Lemma 6.1
([25, 26, 43, 48, Lemma 2.3] and [50, Proposition 2.4]) If A is an associative commutative algebra, \(\delta \in {\mathrm{Der}}\,A\), and \(\xi \in A\), then \(A^{\delta ,\xi }\) is a Balinsky–Novikov algebra.
Lemma 6.2
Let A be an associative commutative algebra, \(\delta \in {\mathrm{Der}}\,A\), and \(\xi \in A\). Then we have:
- (i)
\(d\in {\mathrm{Der}}\,A^{\delta ,\xi }\) if and only if
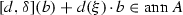 for all \(b\in A\),
for all \(b\in A\), - (ii)
if \(1\in A\), then \(d\in {\mathrm{Der}}\,A^{\delta ,\xi }\) if and only if
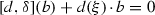 for all \(b\in A\),
for all \(b\in A\), - (iii)
\(d\in {\mathrm{Der}}\,A^{\delta ,0}\) if and only if
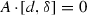 ,
, - (iv)
if \(1\in A\), then \(d\in {\mathrm{Der}}\,A^{\delta ,0}\) if and only if \( [d,\delta ]=0\).
Proof
(i) For any \(a,b\in A\) and \(d\in {\mathrm{Der}}\,A^{\delta ,\xi }\) we have

if and only if  .
.
(ii)–(iv) The rest follows from part (i).\(\square \)
Lemma 6.3
Let \(\delta \) be a surjective derivation of an associative commutative algebra A with 1. If I is a right ideal of a Balinsky–Novikov algebra \(A^{\delta ,\xi } \), then I is an ideal of A.
Proof
Indeed, if \(i\in I\) and \(a\in A\), then  and therefore
and therefore  . Since \(\delta \) is surjective, we have
. Since \(\delta \) is surjective, we have  and so
and so  .\(\square \)
.\(\square \)
It is easy to see that  for any idempotent \(e^2=e\in A\).
for any idempotent \(e^2=e\in A\).
Lemma 6.4
Let A be an associative commutative algebra, \(\delta \in {\mathrm{Der}}\,A\), and \(\xi \in A\). Then the following properties hold:
- (i)
[37, Lemma 3.1] if \({\mathrm{char}}\,{\mathbb {K}}\ne 2\) and U is an ideal of the Lie algebra \(A^{\delta ,L}\), then \([U,U]=0\) or U contains a non-zero \(\delta \)-ideal of A,
- (ii)
if I is a \(\delta \)-ideal of A, then I is an ideal of the Balinsky–Novikov algebra \(A^{\delta ,\xi }\),
- (iii)
if K is an additive subgroup of a Balinsky–Novikov algebra \(A^{\delta ,\xi }\) and \(\delta (K)\subseteq K\), then
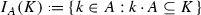 is a \(\delta \)-ideal of A,
is a \(\delta \)-ideal of A, - (iv)
if \(1\in A\) and B is an ideal of \(A^{\delta ,\xi }\), then
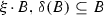 ,
, - (v)
if C is a left ideal of \(A^{\delta ,0}\), then \(\delta (C)\subseteq I_A(C)\),
- (vi)
if I is a \(\delta \)-ideal of A, then I is an ideal of \(A^{\delta ,L}\),
- (vii)
if e is an idempotent of A, then \(e\in {\mathrm{rann}}\,A^{\delta ,0} \),
- (viii)
the kernel
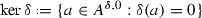 of \(\delta \) is a left ideal of \(A^{\delta ,0}\),
of \(\delta \) is a left ideal of \(A^{\delta ,0}\), - (ix)
if
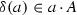 , then
, then 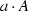 is an ideal of \( A^{\delta ,L}\),
is an ideal of \( A^{\delta ,L}\), - (x)
if B is an ideal of \(A^{\delta ,\xi }\), then B is an ideal of the Lie algebra \(A^{\delta ,L}\),
- (xi)
if S is an ideal of \(A^{\delta ,\xi }\), then
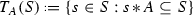 is an ideal of \(A^{\delta ,L}\) and \(T_A(S)\subseteq S\),
is an ideal of \(A^{\delta ,L}\) and \(T_A(S)\subseteq S\), - (xii)
if \(1\in A\) and I is an ideal \(A^{\delta ,L}\), then \(\delta (I)\subseteq I \) and
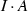 is a \(\delta \)-ideal of A,
is a \(\delta \)-ideal of A, - (xiii)
if W is an ideal of \(A^{\delta ,\xi }\), then
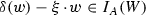 for any \(w\in W\),
for any \(w\in W\), - (xiv)
if \({\mathrm{char}}\,{\mathbb {K}}\ne 2\) and
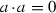 , then
, then 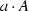 is a right ideal of \(A^{\delta ,\xi }\) such that
is a right ideal of \(A^{\delta ,\xi }\) such that 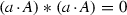 .
.
Proof
(i) For the proof see [37].
(ii) Indeed,  and
and  for any \(i\in I\) and \(a\in A\).
for any \(i\in I\) and \(a\in A\).
(iii) Assume that \(k\in I_A(K)\) and \(x\in A\). Then  , what implies that \(I_A(K)\) is an ideal of A. Since
, what implies that \(I_A(K)\) is an ideal of A. Since  and
and  , we conclude that
, we conclude that  . Hence \(\delta (I_A(K))\subseteq I_A(K)\).
. Hence \(\delta (I_A(K))\subseteq I_A(K)\).
(iv) It is easy to see that  and
and  for any \(b\in B\). Consequently,
for any \(b\in B\). Consequently,  .
.
(v) For any \(a\in A\) and \(c\in C\) we see that  , whence \(\delta (C)\subseteq I_A(C)\).
, whence \(\delta (C)\subseteq I_A(C)\).
(vi) If \(i\in I\) and \(a\in A\), then  , the claim follows.
, the claim follows.
(vii) Since \(\delta (e)=0\), we obtain  .
.
(viii) If \(u\in \ker \delta \) and \(a\in A\), then  . Hence
. Hence  .
.
(ix) For any \(t,b\in A\)

(x) Since  ,
,  , we deduce that \([B,A]\subseteq B\).
, we deduce that \([B,A]\subseteq B\).
(xi) Let \(a,x\in A\) and \(s\in T_A(S)\). Then

and therefore  .
.
(xii) For any \(i\in I\),

(xiii) By (x), W is an ideal of the Lie algebra \(A^{\delta ,L} \) and so  and
and  for any \(w\in W\) and \( a\in A\). Then
for any \(w\in W\) and \( a\in A\). Then  . Hence
. Hence  .
.
(xiv) We compute that  and
and

for any \(b,c\in A\).\(\square \)
If \(x\in A\), then

is called a left transformation operator of the Balinsky–Novikov algebra \(A^{\delta ,\xi }\).
Lemma 6.5
Let A be an associative commutative algebra, \(\delta \in {\mathrm{Der}}\,A \), and \(x,\xi \in A\). Then the following properties hold:
- (i)
if
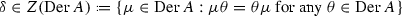 , then \({\mathrm{Der}}\,A\subseteq {\mathrm{Der}}\,A^{\delta ,0}\),
, then \({\mathrm{Der}}\,A\subseteq {\mathrm{Der}}\,A^{\delta ,0}\), - (ii)
\(r_x\in {\mathrm{Der}}\,A^{\delta ,0}\) if and only if
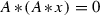 ,
, - (iii)
\(l_x\in {\mathrm{Der}}\,A^{\delta ,0}\) if and only if
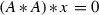 ,
, - (iv)
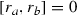 for any \(a,b\in A^{\delta ,\xi }\),
for any \(a,b\in A^{\delta ,\xi }\), - (v)
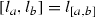 for any \(a,b\in A^{\delta ,\xi }\),
for any \(a,b\in A^{\delta ,\xi }\), - (vi)
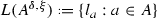 is a Lie algebra.
is a Lie algebra.
Proof
(i) If \(\delta \in {\mathrm{Der}}\,A\), then

for any \(a,b\in A^{\delta ,0}\). Therefore, \(d\in {\mathrm{Der}}\,A^{\delta ,0}\).
(ii) If \(r_x\in {\mathrm{Der}}\,A^{\delta ,0}\), then

and so  for any \( a,b\in A^{\delta ,0}\). This is equivalent to
for any \( a,b\in A^{\delta ,0}\). This is equivalent to  . Hence
. Hence  .
.
(iii) By the same argument as in (ii).
(iv)–(vi) Obvious.\(\square \)
Zhelyabin and Tikhov [51] asked: Is true that an associative commutative algebra with a derivation\(\delta \)is\(\delta \)-simple in the usual sense if and only if its corresponding Balinsky–Novikov algebra\((A,+,*)\)is simple?
with a derivation\(\delta \)is\(\delta \)-simple in the usual sense if and only if its corresponding Balinsky–Novikov algebra\((A,+,*)\)is simple?
Lemma 6.6
Let A be an associative commutative algebra, \(\delta \in {\mathrm{Der}}\,A\), and \(\xi \in A\). Then A is a \(\delta \)-simple algebra if and only if \(A^{\delta ,\xi }\) is a simple Balinsky–Novikov algebra.
Proof
For the proof see [48, Proposition 2.8].\(\square \)
Corollary 6.7
If A is a field, \(\delta \in {\mathrm{Der}}\,A\), and \(\xi \in A\), then \(A^{\delta ,\xi }\) is a simple Balinsky–Novikov algebra.
Further we shall need the following result.
Lemma 6.8
Let A be an associative commutative \(\delta \)-semiprime algebra with 1, \({\mathrm{char}}\,{\mathbb {K}}\ne 2\), and \(\delta \in {\mathrm{Der}}\,A\). If I is a \(\delta \)-ideal of A and \(\delta ^2(I)=0\), then \(\delta (I)=0\) and  .
.
Proof
If \(i\in I\), then

and therefore  . Then
. Then  and so
and so  . Moreover,
. Moreover,

\(\square \)
Lemma 6.9
Let A be an associative commutative algebra with 1, \(0\ne \delta \in {\mathrm{Der}}\,A\), and \(\xi \in A\). Then A is a \(\delta \)-prime algebra if and only if \(A^{\delta ,\xi }\) is a prime Balinsky–Novikov algebra.
Proof
\((\Rightarrow )\) Let I and J be ideals of \(A^{\delta ,\xi }\) such that  . This means that
. This means that  for all \(i\in I\) and \(j\in J\). By Lemma 6.4 (iv),
for all \(i\in I\) and \(j\in J\). By Lemma 6.4 (iv),  and
and  . Moreover, \(\mathrm{ann}\, I\) and
. Moreover, \(\mathrm{ann}\, I\) and  are \(\delta \)-ideals of A,
are \(\delta \)-ideals of A,  and
and

Assume that \(I\ne 0\). Then \(\mathrm{ann}\, I=0\) and so  for any \(j\in J\). Then
for any \(j\in J\). Then

for any \(k\in J\) and, as a consequence,  . Since
. Since  is a \(\delta \)-ideal of A, we conclude that
is a \(\delta \)-ideal of A, we conclude that  . Then \(\xi =0\) and, in view of (35),
. Then \(\xi =0\) and, in view of (35),
Since  , we obtain that
, we obtain that  by (35) and (36).
by (35) and (36).
If  , then
, then  , a contradiction. Hence
, a contradiction. Hence  . Then
. Then  and \(\delta (I)=0\) by Lemma 6.8. As a consequence,
and \(\delta (I)=0\) by Lemma 6.8. As a consequence,  . This means that
. This means that  , what forces that \(\delta (A)=0\), a contradiction.
, what forces that \(\delta (A)=0\), a contradiction.
\((\Leftarrow )\) Let \(A^{\delta ,\xi }\) be a \(\delta \)-prime Balinsky–Novikov algebra. Assume that X and Y are \(\delta \)-ideals of A such that  . By Lemma 6.4 (ii), X and Y are ideals of \(A^{\delta ,\xi }\) and
. By Lemma 6.4 (ii), X and Y are ideals of \(A^{\delta ,\xi }\) and  . Thus \(X=0\) or \(Y=0\).\(\square \)
. Thus \(X=0\) or \(Y=0\).\(\square \)
Lemma 6.10
Let A be an associative commutative algebra with 1, \(0\ne \delta \in {\mathrm{Der}}\,A\), and \(\xi \in A\). Then A is a \(\delta \)-semiprime algebra if and only if \(A^{\delta ,\xi }\) is a semiprime Balinsky–Novikov algebra.
Proof
By the same argument as in the proof of Lemma 6.9.\(\square \)
Lemma 6.11
[17] Let \((N,+,*)\) be a Balinsky–Novikov algebra. Then Z(N) and [N, N] are ideals of N and  .
.
Lemma 6.12
Let A be an associative commutative algebra with 1, \({\mathrm{char}}\,{\mathbb {K}}\ne 2\), \(0\ne \delta \in {\mathrm{Der}}\,A\), and \(\xi \in A\). If A is a \(\delta \)-prime algebra, then \(Z(A^{\delta ,\xi })=0\).
Proof
By Lemma 6.11,  . If
. If  , then
, then  for all \(a,b\in A\). Therefore,
for all \(a,b\in A\). Therefore,

This gives that  and so
and so  . Since
. Since  is a \(\delta \)-ideal and \(\delta (A)\ne 0\), we obtain that
is a \(\delta \)-ideal and \(\delta (A)\ne 0\), we obtain that  . Then
. Then  for any \(a,b\in A\) and
for any \(a,b\in A\) and  . This yields that
. This yields that  , a contradiction. Consequently,
, a contradiction. Consequently,  and thus \(Z(A^{\delta ,\xi })=0\).\(\square \)
and thus \(Z(A^{\delta ,\xi })=0\).\(\square \)
7 Lie properties
Lemma 7.1
Let A be an associative commutative algebra with 1, \(\xi \in A\), and \(\delta \in {\mathrm{Der}}\,A\). If \(\delta (A)\nsubseteq P\) for any minimal \(\delta \)-prime ideal P of A, then:
- (i)
every abelian ideal I of the Lie algebra \(A^{\delta ,L}\) is contained in the \(\delta \)-prime radical
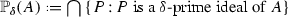 ,
, - (ii)
the Lie algebra \(A^{\delta ,L}\) is not solvable.
Proof
(i) Let I be a non-zero abelian ideal of the Lie algebra \(A^{\delta ,L}\). If \(I\nsubseteq {{\mathbb {P}}}_{\delta }(A)\), then there exists a minimal \( \delta \)-prime ideal of P of A such that \(I\nsubseteq P\). Obviously,
is a non-zero derivation of the quotient algebra A/P. Since A/P is a \(\Delta \)-prime algebra, \((A/P)^{\Delta ,\eta }\) is a prime Lie algebra, where \( \eta =\xi +P\). Hence \((I+P)/P\) is zero, a contradiction.
(ii) It follows from (i).\(\square \)
Lemma 7.2
[37, Theorem 3.3] Let A be an associative commutative algebra with 1 and \(0\ne \delta \in {\mathrm{Der}}\,A\). Then A is a \(\delta \)-simple algebra if and only if \(A^{\delta ,L}\) is a simple Lie algebra.
Proof
By the same argument as in the proof of Lemma 6.9.\(\square \)
Lemma 7.3
Let A be an associative commutative algebra with 1, \({\mathrm{char}}\,{\mathbb {K}}\ne 2\), and \(0\ne \delta \in {\mathrm{Der}}\,A\). If I is an abelian Lie ideal of a semiprime Balinsky–Novikov algebra \(A^{\delta ,\xi }\), then \(\delta (I)=0\). If, moreover, \(A^{\delta ,L}\) is prime, then \(I=0\).
Proof
(a) Let I be an ideal of \(A^{\delta ,L}\) such that \([I,I]=0 \). Then  for any \(u,v\in I\). If \(x\in A\) , then
for any \(u,v\in I\). If \(x\in A\) , then

This means that
because \(\mathrm{ann}\, I\) is a \(\delta \)-ideal of A. If \(y\in A\), then

Hence  . Then
. Then  . Since \(\mathrm{ann}\, \delta (I)\) is a \(\delta \)-ideal of A and \(\delta (I)\subseteq \mathrm{ann}\, \delta (I)\), we conclude that \(\delta (I)=0\).
. Since \(\mathrm{ann}\, \delta (I)\) is a \(\delta \)-ideal of A and \(\delta (I)\subseteq \mathrm{ann}\, \delta (I)\), we conclude that \(\delta (I)=0\).
(b) Now assume that \(A^{\delta ,\xi }\) is prime. In view of (37),  If \(I\ne 0\), then \(\delta ^2(A)=0\) and so \(\delta =0\) by Lemma 6.8, a contradiction.\(\square \)
If \(I\ne 0\), then \(\delta ^2(A)=0\) and so \(\delta =0\) by Lemma 6.8, a contradiction.\(\square \)
Lemma 7.4
Let A be an associative commutative algebra with 1, \({\mathrm{char}}\,{\mathbb {K}}\ne 2\), \(0\ne \delta \in {\mathrm{Der}}\,A\), and \(\xi \in A\). Then A is a \(\delta \)-prime algebra if and only if \(A^{\delta ,L}\) is a prime Lie algebra.
Proof
\((\Leftarrow )\) Suppose that B and C are \(\delta \)-ideals of A such that  . Then
. Then  and therefore
and therefore  by the \( \delta \)-primeness of A. Since B and C are ideals of \(A^{\delta ,L}\) by Lemma 6.4 (vi) and \([B,C]=0\), we deduce that \(B=0\) or \(C=0\).
by the \( \delta \)-primeness of A. Since B and C are ideals of \(A^{\delta ,L}\) by Lemma 6.4 (vi) and \([B,C]=0\), we deduce that \(B=0\) or \(C=0\).
\((\Rightarrow )\) By Lemma 6.9, \(A^{\delta ,\xi }\) is a prime Balinsky–Novikov algebra. Assume that I and J are non-zero ideals of \(A^{\delta ,L} \) such that \([I,J]=0\). Then I (respectively, J) is a Lie ideal of \(A^{\delta ,\xi }\). If \([I,I]=0\) (respectively, \([J,J]=0\)), then \(\delta (I)=0\) (respectively, \(\delta (J)=0\)) by Lemma 7.3 and so  (respectively,
(respectively,  ), what implies that \(I=0\) or \(J=0\), a contradiction. Therefore, \([I,I]\ne 0\), \([J,J]\ne 0\) and therefore I (respectively, J) contains a non-zero \(\delta \)-ideal \(I_0\) (respectively, \(J_0 \)) of A by Lemma 6.4 (i) such that \([I_0,J_0]=0\). Since \( [I_0\cap J_0,I_0\cap J_0]=0\) and \(I_0\cap J_0\) is an ideal of \(A^{\delta ,\xi }\) by Lemma 6.4 (ii), we obtain that \(\delta (I_0\cap J_0)=0\) by Lemma 7.3. Then
), what implies that \(I=0\) or \(J=0\), a contradiction. Therefore, \([I,I]\ne 0\), \([J,J]\ne 0\) and therefore I (respectively, J) contains a non-zero \(\delta \)-ideal \(I_0\) (respectively, \(J_0 \)) of A by Lemma 6.4 (i) such that \([I_0,J_0]=0\). Since \( [I_0\cap J_0,I_0\cap J_0]=0\) and \(I_0\cap J_0\) is an ideal of \(A^{\delta ,\xi }\) by Lemma 6.4 (ii), we obtain that \(\delta (I_0\cap J_0)=0\) by Lemma 7.3. Then  and, consequently,
and, consequently,  , which leads to a contradiction.\(\square \)
, which leads to a contradiction.\(\square \)
Lemma 7.5
Let A be an associative commutative algebra with 1, \({\mathrm{char}}\,{\mathbb {K}}\ne 2\), \(0\ne \delta \in {\mathrm{Der}}\,A\), and \(\xi \in A\). Then A is a \(\delta \)-semiprime algebra if and only if \(A^{\delta ,L}\) is a semiprime Lie algebra.
Proof
By the same argument as in the proof of Lemma 7.4.\(\square \)
Proof of Theorem 4.1
It follows from Lemmas 6.6, 6.9, 7.2, 7.4 and 7.5. \(\square \)
We specified some of interesting properties of an associative commutative algebra A and its \(\delta \)-associated algebra \(A^{\delta ,L}\), which earlier were investigated by Ribenboim [43], C.R. Jordan, D.A. Jordan [29, 30], and Nowicki [37]. Moreover, as follows from the results stated above, there exist deep and very interesting relationships between associative commutative algebras A, their \(\delta \)-associated Balinsky–Novikov algebras \(A^{\delta ,\xi }\) and \(\delta \)-associated Lie algebras \(A^{\delta ,L}\).
References
Abraham, R., Marsden, J.E.: Foundations of Mechanics, 2nd edn. Benjamin/Cummings, Reading (1978)
Agrachev, A.A.: The exponential representation of flows and the chronological calculus. Mat. Sb. (N.S.) 35(6), 727–785 (1979)
Agrachev, A.A., Gamkrelidze, R.V.: Chronological algebras and nonstationary vector fields. J. Soviet Math. 17(1), 1650–1675 (1981)
Arnold, V.I.: Mathematical Methods of Classical Mechanics. Graduate Texts in Mathematics, vol. 60. Springer, New York (1989)
Bai, C.: Introduction to pre-Lie algebras. Lectures at CIMPA Research School “Algebra, Combinatorics and Physics” at Valparaiso, Chile, during January 20–31, 2014 and at International Chair in Mathematical Physics and Applications, Berlin (2014). http://einspem.upm.edu.my/equals8/CSS/pre-Lie.pdf
Bai, C., Meng, D.: On the realization of transitive Novikov algebras. J. Phys. A 34(16), 3363–3372 (2001)
Bai, C., Meng, D.: The classification of Novikov algebras in low dimensions. J. Phys. A 34(8), 1581–1594 (2001)
Bai, C., Meng, D.: Addendum: the classification of Novikov algebras in low dimensions: invariant bilinear forms. J. Phys. A 34(39), 8193–8197 (2001)
Bai, C., Meng, D.: Transitive Novikov algebras on four-dimensional nilpotent Lie algebras. Internat. J. Theoret. Phys. 40(10), 1761–1768 (2001)
Balinsky, A.A., Balinsky, A.I.: On the algebraic structures connected with the linear Poisson brackets of hydrodynamics type. J. Phys. A 26(7), 361–364 (1993)
Balinsky, A.A., Burman, Yu.M.: Quadratic Poisson brackets compatible with an algebra structure. J. Phys. A 27(18), L693–L696 (1994)
Balinsky, A.A., Burman, Yu.M.: Quadratic Poisson brackets and Drinfeld theory for associative algebras. Lett. Math. Phys. 38(1), 63–75 (1996)
Balinsky, A.A., Novikov, S.P.: Poisson brackets of hydrodynamic type, Frobenius algebras and Lie algebras. Soviet Math. Dokl. 283(5), 1036–1039 (1985)
Belavin, A.A., Drinfel’d, V.G.: Solutions of the classical Yang–Baxter equation for simple Lie algebras. Funct. Anal. Appl. 16(3), 159–180 (1982)
Blackmore, D., Prykarpatsky, A.K., Samoylenko, V.H.: Nonlinear Dynamical Systems of Mathematical Physics. World Scientific, Hackensack (2011)
Błaszak, M.: Multi-Hamiltonian Theory of Dynamical Systems. Texts and Monographs in Physics. Springer, Berlin (1998)
Burde, D., Dekimpe, K., Vercammen, K.: Novikov algebras and Novikov structures on Lie algebras. Linear Algebra Appl. 429(1), 31–41 (2008)
Dokas, I.: Zinbiel algebras and commutative algebras with devided powers. Glasg. Math. J. 52(2), 303–313 (2010)
Dorfman, I.: Dirac Structures and Integrability of Nonlinear Evolution Equations. Non-linear Science: Theory and Applications. Wiley, Chichester (1993)
Dubrovin, B.A., Novikov, S.P.: Hamiltonian formalism of one-dimensional systems of hydrodynamic type and the Bogolyubov–Whitman averaging method. Soviet Math. Dokl. 27, 665–669 (1983)
Dubrovin, B.A., Novikov, S.P.: On Poisson brackets of hydrodynamic type. Soviet Math. Dokl. 30, 651–654 (1984)
Dzhumadil’daev, A.S.: Zinbiel algebras under \(q\)-commutator. J. Math. Sci. (N.Y.) 144(2), 3909–3925 (2007)
Dzhumadil’daev, A.S., Tulenbaev, K.M.: Nilpotency of Zinbiel algebras. J. Dyn. Control Syst. 11(2), 195–213 (2005)
Faddeev, L.D., Takhtadjan, L.A.: Hamiltonian Methods in the Theory of Solitons. Springer Series in Soviet Mathematics. Springer, Berlin (1987)
Filippov, V.T.: A class of simple nonassociative algebras. Math. Notes 45(1), 68–71 (1989)
Gelfand, I.M., Dorfman, I.Y.: Hamiltonian operators and algebraic structures associated with them. Funct. Anal. Appl. 13(4), 248–262 (1979)
Herstein, I.N.: Topics in Ring Theory. The University of Chicago Press, Chicago (1969)
Jacobson, N.A.: Lie Algebras. Tracts in Pure and Applied Mathematics, vol. 10. Interscience Publishers, New York (1962)
Jordan, C.R., Jordan, D.A.: Lie rings of derivations of associative rings. J. Lond. Math. Soc. 17(1), 33–41 (1978)
Jordan, C.R., Jordan, D.A.: The Lie structure of a commutative ring with derivation. J. Lond. Math. Soc. 18(1), 39–49 (1978)
Kawski, M., Sussmann, H.J.: Noncommutative power series and formal Lie-algebraic techniques in nonlinear control theory. In: Helmke, U., Prätzel-Wolters, D., Zerz, E. (eds.) Operators, Systems and Linear Algebra, pp. 111–128. Teubner, Stuttgart (1997)
Kim, H.: Complete left-invariant affine structures on nilpotent Lie groups. J. Differential Geom. 24(3), 373–394 (1986)
Loday, J.-L.: Cup-product for Leibniz cohomology and dual Leibniz algebras. Math. Scand. 77(2), 189–196 (1995)
Loday, J.-L., Frabetti, A., Chapoton, F., Goichot, F.: Dialgebras and Related Operads. Lecture Notes in Mathematics, vol. 1763. Springer, Berlin (2001)
Loday, J.-L., Pirashvili, T.: Universal enveloping algebras of Leibniz algebras and (co)homology. Math. Ann. 296(1), 139–158 (1993)
Mokhov, O.I.: Symplectic and Poisson Geometry on Loop Spaces of Smooth Manifolds and Integrable Equations. Computer Science Institute, Izhevsk (2004). (in Russian)
Nowicki, A.: The Lie structure of a commutative ring with a derivation. Arch. Math. (Basel) 45(4), 328–335 (1985)
Olver, P.J.: Applications of Lie Groups to Differential Equations. Graduate Texts in Mathematics, vol. 107, 2nd edn. Springer, New York (1993)
Omirov, B.A.: Classification of two-dimensional complex Zinbiel algebras. Uzbek. Mat. Zh. 2002(2), 55–59 (2002). (in Russian)
Osborn, J.M.: Novikov algebras. Nova J. Algebra Geom. 1(1), 1–13 (1992)
Prykarpatsky, Y.A., Artemovych, O.D., Pavlov, M.V., Prykarpatsky, A.K.: The differential-algebraic and bi-Hamiltonian integrability analysis of the Riemann type hierarchy revisited. J. Math. Phys. 53(10), 103521 (2012)
Ribenboim, P.: Algebraic theory higher-order derivations. Trans. R. Soc. Can. 7, 279–287 (1969)
Ribenboim, P.: Higher derivations of rings II. Rev. Roumaine Math. Pures Appl. 16(2), 245–272 (1971)
Rocha, E.M.: On computation of the logarithm of the Chen-Fliess series for nonlinear systems. In: Zinober, A.S.I., Owens, D.H. (eds.) Nonlinear and Adaptive Control. Lecture Notes in Control and Information Sciences, vol. 281, pp. 317–326. Springer, Berlin (2003)
Semenov-Tian-Shansky, M.A.: What is a classical \(r\)-matrix? Funct. Anal. Appl. 17(4), 259–272 (1983)
Sergyeyev, A.: A simple way of making a Hamiltonian systems into a bi-Hamiltonian one. Acta Appl. Math. 83(1–2), 183–197 (2004)
Strachan, I.A.B., Szablikowski, B.M.: Novikov algebras and a classification of multicomponent Camassa–Holm equations. Stud. Appl. Math. 133(1), 84–117 (2014)
Xu, X.: On simple Novikov algebras and their irreducible modules. J. Algebra 185(3), 905–934 (1996)
Xu, X.: Novikov–Poisson algebras. J. Algebra 190(2), 253–279 (1997)
Xu, X.: Classification of simple Novikov algebras and their irreducible modules of characteristic \(0\). J. Algebra 246(2), 673–707 (2001)
Zhelyabin, V.N., Tikhov, A.S.: Novikov–Poisson algebras and associative commutative derivation algebras. Algebra Logic 47(2), 107–117 (2007)
Acknowledgements
Authors cordially thank Professor Taras Banakh (Lviv National University), Maciej Błaszak (Poznań University), Professor Jan Cieśliński (Białystok University), and Professor Maxim Pavlov (Novosibirsk State University) for cooperation and useful discussions of the results obtained.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Artemovych, O.D., Blackmore, D. & Prykarpatski, A.K. Non-associative structures of commutative algebras related with quadratic Poisson brackets. European Journal of Mathematics 6, 208–231 (2020). https://doi.org/10.1007/s40879-020-00398-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-020-00398-w
Keywords
- Balinsky–Novikov algebra
- Lie algebra
- Leibniz algebra
- Zinbiel algebra
- Derivation
- Pre-Poisson brackets
- Lie–Poisson structure



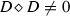 and any
and any 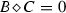 implies that
implies that 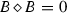 implies that
implies that 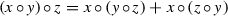 ,
, and
and 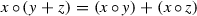
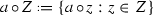 is a right ideal of Z,
is a right ideal of Z,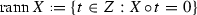 of X is an associative ideal of Z and
of X is an associative ideal of Z and 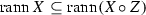 ,
, and
and 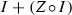 are
are 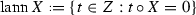 is a right
is a right 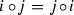 for
for 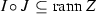 ,
,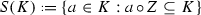 is a right
is a right 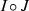 is a right
is a right 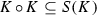 ,
, .
.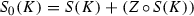 is a
is a 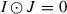 , then
, then 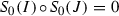 .
.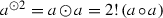 ,
,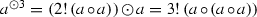 .
.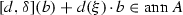 for all
for all 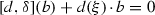 for all
for all 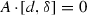 ,
,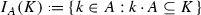 is a
is a 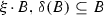 ,
,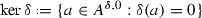 of
of 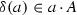 , then
, then 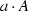 is an ideal of
is an ideal of 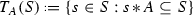 is an ideal of
is an ideal of 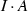 is a
is a 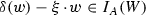 for any
for any 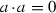 , then
, then 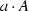 is a right ideal of
is a right ideal of 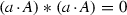 .
.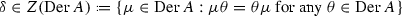 , then
, then 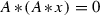 ,
,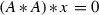 ,
,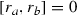 for any
for any 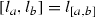 for any
for any 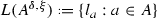 is a Lie algebra.
is a Lie algebra.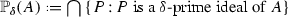 ,
,