Abstract
We show that the global (log) canonical threshold of d-sheeted covers of the M-dimensional projective space of index 1, where \(d\geqslant 4\), is equal to 1 for almost all families (except for a finite set). The varieties are assumed to have at most quadratic singularities, the rank of which is bounded from below, and to satisfy the regularity conditions. This implies birational rigidity of new large classes of Fano–Mori fibre spaces over a base, the dimension of which is bounded from above by a constant that depends (quadratically) on the dimension of the fibre only.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Statement of the main results
In [12] general d-sheeted covers of the complex projective space \({{\mathbb {P}}}={{\mathbb {P}}}^M\) which are Fano varieties of index 1 with at most quadratic singularities, the rank of which is bounded from below, were shown to be birationally superrigid. In this paper we prove that for almost all values of the discrete parameters defining these varieties a general multiple projective space of index 1 satisfies a much stronger property: its global canonical (and the more so, log canonical) threshold is equal to 1. Then [9] immediately implies the birational rigidity type results for fibre spaces, the fibres of which are multiple projective spaces, and new classes of Fano direct products [6]. Let us give precise statements.
Fix a pair of positive integers \((d,l)\in {{\mathbb {Z}}}^{\times 2}_+\) in the set described by the following table:

Set  . The symbol \({{\mathbb {P}}}\) stands for the complex projective space \({{\mathbb {P}}}^M\). Consider the weighted projective space
. The symbol \({{\mathbb {P}}}\) stands for the complex projective space \({{\mathbb {P}}}^M\). Consider the weighted projective space

with homogeneous coordinates \(x_0,\dots ,x_M\), \(\xi \), where \(x_i\) are of weight 1 and \(\xi \) is of weight l, and a quasi-homogeneous polynomial

of degree dl (that is, \(A_i(x_0,\dots ,x_M)\) is a homogeneous polynomial of degree il for \(i=1,\dots ,d\)). The space

parameterizes all such polynomials. If the hypersurface
has at most quadratic singularities of rank \(\geqslant 7\) (and we will consider hypersurfaces with stronger restrictions for the rank), then V is a factorial variety with terminal singularities, see [12], so that
where H is the class of a “hyperplane section”, that is, of the divisor \(V\cap \{\lambda =0\}\), where \(\lambda (x_0,\dots ,x_M)\) is an arbitrary linear form. Below for all the values of d, l under consideration we will define explicitly a positive integral-valued function \(\varepsilon (d,l)\), which behaves as \(M^2/2\) as the dimension M grows.
As in [12], we identify the polynomial  and the corresponding hypersurface \(\{F=0\}\), which makes it possible to write
and the corresponding hypersurface \(\{F=0\}\), which makes it possible to write  . The following theorem is the main result of the present paper.
. The following theorem is the main result of the present paper.
Theorem 1.1
There is a Zariski open subset  such that:
such that:
-
(i)
every hypersurface
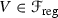 has at most quadratic singularities of rank \(\geqslant 8\) and for that reason is a factorial Fano variety of index 1 with terminal singularities,
has at most quadratic singularities of rank \(\geqslant 8\) and for that reason is a factorial Fano variety of index 1 with terminal singularities, -
(ii)
the inequality

holds,
-
(iii)
for every variety
 and every divisor \(D\sim nH\) the pair \(\bigl (V,\frac{1}{n}D\bigr )\) is canonical.
and every divisor \(D\sim nH\) the pair \(\bigl (V,\frac{1}{n}D\bigr )\) is canonical.
Now [9, Theorem 1.1] makes it possible to describe the birational geometry of Fano–Mori fibre spaces, the fibres of which are multiple projective spaces of index 1.
Let \({\overline{\eta }}:{{\mathbb {X}}}\rightarrow S\) be a locally trivial fibre space, the base of which is a non-singular projective rationally connected variety S of dimension
and the fibre is the weighted projective space \(\overline{{\mathbb {P}}}\). Consider an irreducible hypersurface \(W\subset {{\mathbb {X}}}\), such that for every point \(s\in S\) the intersection

is a multiple projective space of the type described above. Claim (ii) of Theorem 1.1 implies that we may assume that

for every point of the base \(s\in S\), if the linear system |W| is sufficiently mobile on \({{\mathbb {X}}}\), and the hypersurface W is sufficiently general in that linear system. Set
The variety W by claim (i) of Theorem 1.1 has at most quadratic singularities of rank \(\geqslant 8\), and for that reason is a factorial variety with terminal singularities. Therefore, \(\eta :W\rightarrow S\) is a Fano–Mori fibre space, the fibres of which are multiple projective spaces of index 1. Let  be an arbitrary rationally connected fibre space, that is, a morphism of projective algebraic varieties, where the base \(S'\) and the fibre of general position \((\eta ')^{-1}(s')\),
be an arbitrary rationally connected fibre space, that is, a morphism of projective algebraic varieties, where the base \(S'\) and the fibre of general position \((\eta ')^{-1}(s')\),  , are rationally connected, and moreover,
, are rationally connected, and moreover,  . Now [9, Theorem 1.1], combined with Theorem 1.1, immediately gives the following result.
. Now [9, Theorem 1.1], combined with Theorem 1.1, immediately gives the following result.
Theorem 1.2
Assume that the Fano–Mori fibre space \(\eta :W\rightarrow S\) satisfies the following condition: for every mobile family  of curves on the base S, sweeping out S, and a general curve
of curves on the base S, sweeping out S, and a general curve  the class of an algebraic cycle
the class of an algebraic cycle

is not effective, that is, it is not rationally equivalent to an effective cycle of dimension M. Then every birational map \(\chi :W\dashrightarrow W'\) onto the total space of the rationally connected fibre space  (if such maps exist) is fibre-wise, that is, there is a rational dominant map \(\zeta :S\dashrightarrow S'\), such that the following diagram commutes:
(if such maps exist) is fibre-wise, that is, there is a rational dominant map \(\zeta :S\dashrightarrow S'\), such that the following diagram commutes:

Corollary 1.3
In the assumptions of Theorem 1.2 on the variety W there are no structures of a rationally connected fibre space (and, the more so, of a Fano–Mori fibre space), the fibre of which is of dimension less than M. In particular, the variety W is non-rational and every birational self-map of the variety W commutes with the projection \(\eta \) and for that reason induces a birational self-map of the base S.
The condition for the cycles of dimension M, described in Theorem 1.2, is satisfied if the linear system |W| is sufficiently mobile on \({{\mathbb {X}}}\). Let us demonstrate it by an especially visual example, when  is the trivial fibre space over S. Let
is the trivial fibre space over S. Let  be the only singular point of the weighted projective space \(\overline{\mathbb {P}}\). Consider the projection “from the point \(o^*\)”
be the only singular point of the weighted projective space \(\overline{\mathbb {P}}\). Consider the projection “from the point \(o^*\)”

where  . Let \({\overline{H}}\) be the \(\pi _{{\mathbb {P}}}\)-pullback of the class of a hyperplane in \({{\mathbb {P}}}\) on \(\overline{{{\mathbb {P}}}}\). The pullback of the class \({\overline{H}}\) on
. Let \({\overline{H}}\) be the \(\pi _{{\mathbb {P}}}\)-pullback of the class of a hyperplane in \({{\mathbb {P}}}\) on \(\overline{{{\mathbb {P}}}}\). The pullback of the class \({\overline{H}}\) on  with respect to the projection onto the first factor we denote for simplicity by the same symbol \({\overline{H}}\). Now
with respect to the projection onto the first factor we denote for simplicity by the same symbol \({\overline{H}}\). Now

so that for some class \(R\in \mathop {\mathrm{Pic}}\, S\) the relation
holds and for that reason
This implies that the condition of Theorem 1.2 holds if for any mobile family of curves  , sweeping out S, and a general curve
, sweeping out S, and a general curve  , the inequality
, the inequality

holds. Therefore, the following claim is true.
Theorem 1.4
Assume that the class \(R+K_S\in \mathrm{Pic}\, S\) is pseudo-effective and for every point \(s\in S\) we have  . Then in the notations of Theorem 1.2 every birational map \(\chi :W \dashrightarrow W'\) is fibre-wise. In particular, every birational self-map \(\chi \in \mathrm{Bir}\, W\) induces a birational self-map of the base S.
. Then in the notations of Theorem 1.2 every birational map \(\chi :W \dashrightarrow W'\) is fibre-wise. In particular, every birational self-map \(\chi \in \mathrm{Bir}\, W\) induces a birational self-map of the base S.
Another standard application of Theorem 1.1 is given by the theorem on birational geometry of Fano direct products [6, Theorem 1]. Recall that the following statement is true.
Theorem 1.5
Assume that primitive Fano varieties \(V_1,\dots , V_N\) satisfy the following properties:
-
(i)
for every effective divisor
$$\begin{aligned} D_i\sim {}-nK_{V_i} \end{aligned}$$the pair \(\bigl (V_i,\frac{1}{n}D_i\bigr )\) is log canonical,
-
(ii)
for every mobile linear system
$$\begin{aligned} \Sigma _i\subset |{-}nK_{V_i}| \end{aligned}$$and a general divisor \(D_i\in \Sigma _i\) the pair \(\bigl (V_i,\frac{1}{n}D_i\bigr )\) is canonical.
Then on the direct product

there are no other structures of a rationally connected fibre space, apart from projections onto direct fibres  .
.
Property (ii) was shown in [12] for a wider class of multiple projective spaces than the one that is considered in this paper. Of course, Theorem 1.1 implies that conditions (i) and (ii) are satisfied for every variety  . Therefore, every variety considered in the present paper can be taken as a factor of the direct product in Theorem 1.5.
. Therefore, every variety considered in the present paper can be taken as a factor of the direct product in Theorem 1.5.
1.2 The regularity conditions
The open subset  is given by explicit local regularity conditions, which we will now describe. To begin with, let us introduce an auxiliary integral-valued parameter \(\rho \in \{1,2,3,4\}\), depending on (d, l). Its meaning, the number of reductions to a hyperplane section, used in the proof of Theorem 1.1, will become clear later. Set \(\rho =4\), if \(d=4\) and \(21\leqslant l\leqslant 25\) and \(\rho =1\), if \(d\geqslant 18\) and \(l\geqslant 2\). For the remaining possible pairs (d, l) the value \(\rho \geqslant 2\) is given by the following table:
is given by explicit local regularity conditions, which we will now describe. To begin with, let us introduce an auxiliary integral-valued parameter \(\rho \in \{1,2,3,4\}\), depending on (d, l). Its meaning, the number of reductions to a hyperplane section, used in the proof of Theorem 1.1, will become clear later. Set \(\rho =4\), if \(d=4\) and \(21\leqslant l\leqslant 25\) and \(\rho =1\), if \(d\geqslant 18\) and \(l\geqslant 2\). For the remaining possible pairs (d, l) the value \(\rho \geqslant 2\) is given by the following table:


If the pair (d, l) is not in the table, then \(\rho =1\) (for instance, for \(d=14\), \(l\geqslant 4\)).
One more table gives the function \(\varepsilon (d,l)\), bounding from below the codimension of the complement to the set  . Write this function as a function of the dimension
. Write this function as a function of the dimension  , for each of the possible values of the parameter \(\rho \) defined above.
, for each of the possible values of the parameter \(\rho \) defined above.

Now let us state the regularity conditions.
Let \(o\in V\) be some point. The coordinate system  can be chosen in such a way that
can be chosen in such a way that

(see [12, Section 1]). The corresponding affine coordinates are

Now in the affine chart \(\{x_0\ne 0\}={\mathbb {A}}^{M+1}_{z_1,\dots ,z_M,y}\) the hypersurface \(V\cap \{x_0\ne 0\}\) is given by the equation \(f=0\), where

with the (non-homogeneous) polynomial \(a_i(z_*)\) of degree \(\leqslant il\). Furthermore, the following fact is true [12]: for any homogeneous polynomial \(\gamma (x_0,\dots ,x_M)\) of degree l the equation \(\xi =\gamma (x_*)\) defines a hypersurface \(R_{\gamma }\subset \overline{{\mathbb {P}}}\) that does not contain the point  , and moreover the projection
, and moreover the projection
is an isomorphism. In this way, the hypersurface \(V\cap R_{\gamma }\) in \(R_{\gamma }\) identifies naturally with a hypersurface in \({{\mathbb {P}}}={{\mathbb {P}}}^M\), and its intersection with the affine chart \(\{x_0\ne 0\}\) identifies with a hypersurface in the affine space \({{\mathbb {A}}}^M_{z_1,\dots ,z_M}\). The regularity conditions, given below, are assumed to be satisfied for the hypersurface \(V_{\gamma }=V\cap R_{\gamma }\) for a general polynomial \(\gamma (x_*)\).
Assume that the point \(o\in V\) is non-singular, so that \(o\in V_{\gamma }\) is non-singular, too. Let \(P\subset {{\mathbb {A}}}^M\) be an arbitrary linear subspace of codimension \(\rho - 1\), that is, \(o\in P\), that is not contained in the tangent hyperplane \(T_oV_{\gamma }\). Let
be the affine equation of the hypersurface \(P\cap V_{\gamma }\), which is non-singular at the point o, decomposed into homogeneous components (with respect to an arbitrary system of linear coordinates on P).
-
(R1.1)
For any linear form
$$\begin{aligned} \lambda \not \in \langle q_1\rangle \end{aligned}$$the sequence of homogeneous polynomials
$$\begin{aligned} q_1|_{\{\lambda =0\}},\quad q_2|_{\{\lambda =0\}},\quad \dots ,\quad q_{M-\rho -2}|_{\{\lambda =0\}} \end{aligned}$$is regular in the local ring
 .
. -
(R1.2)
The linear span of any irreducible component of the closed set
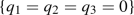
is the hyperplane \(\{q_1=0\}\).
-
(R1.3)
For any linear form \(\lambda \not \in \langle q_1\rangle \) the set
$$\begin{aligned} \overline{P\cap V_{\gamma }\cap \{q_1=q_2=0\}\cap \{\lambda =0\}} \end{aligned}$$is irreducible and reduced.
-
(R1.4)
If \(\rho \geqslant 2\), then the rank of the quadratic form
$$\begin{aligned} q_2|_{\{q_1=0\}} \end{aligned}$$is at least \(8+2(\rho -2)\).
We say that a non-singular point \(o\in V\) is regular, if for a general polynomial \(\gamma (x_*)\) and any subspace \(P\not \subset T_oV_{\gamma }\) conditions (R1.1–3) are satisfied.
Assume now that the point \(o\in V\) is singular, so that the hypersurface \(V_{\gamma }\) is also singular at that point.
-
(R2.1)
The point \(o\in V_{\gamma }\) is a quadratic singularity of rank \(\geqslant 2\rho +6\).
Let \(P\subset {{\mathbb {A}}}^M\) be an arbitrary linear subspace of codimension \(\rho +2\), that is, \(o\in P\), and
is the affine equation of the hypersurface \(P\cap V_{\gamma }\), decomposed into homogeneous components (in particular, \(q_2\) is a quadratic form of rank \(\geqslant 2\)).
-
(R2.2)
The sequence of homogeneous polynomials
$$\begin{aligned} q_2,\;\; q_3,\;\;,\dots ,\;\; q_{M-\rho -4} \end{aligned}$$is regular in the local ring
 .
.
We say that a singular point \(o\in V\) is regular, if for a general polynomial \(\gamma (x_*)\) and any subspace \(P\subset {{\mathbb {A}}}^M\) of codimension \(\rho +2\) conditions (R2.1–2) hold.
Finally, we say that the variety V is regular, if it is regular at every point \(o\in V\), singular or non-singular. Set

to be the Zariski open subset of regular hypersurfaces (that it is non-empty, follows from the estimate for the codimension of the complement). Obviously, every hypersurface  has at worst quadratic singularities of rank \(\geqslant 8\), so that claim (i) of Theorem 1.1 is true.
has at worst quadratic singularities of rank \(\geqslant 8\), so that claim (i) of Theorem 1.1 is true.
1.3 The structure of the paper and historical remarks
A proof of Theorem 1.1 (ii) is given in Sects. 2.2 and 2.3. A proof of Theorem 1.1 (iii) in Sect. 2.1 is reduced to two facts about hypersurfaces in the projective space \({{\mathbb {P}}}^N\), which are applied to the hypersurface \(V_{\gamma }\subset {{\mathbb {P}}}\), both in the singular and non-singular cases. Proofs of those two facts are given, respectively, in Sects. 3 and 4.
The equality of the global (log) canonical threshold to 1 is shown for many families of primitive Fano varieties, starting from the pioneer paper [6] (for a general variety in the family). For Fano complete intersections in the projective space the best progress in that direction (in the sense of covering the largest class of families) was made in [10]. The double covers were considered in [7]. Fano three-folds, singular and non-singular, were studied in the papers [2,3,4,5] and many others. However, the non-cyclic covers of index 1 in the arbitrary dimension were never studied up to now: the reason, as it was explained in [12], was that the technique of hypertangent divisors does not apply to these varieties in a straightforward way. As it turned out (see [12]), the technique of hypertangent divisors should be applied to a certain subvariety, which identifies naturally with a hypersurface (of general type) in the projective space. This approach is used in the present paper, too.
2 Proof of the main result
In Sect. 2.1 the proof Theorem 1.1 (iii) is reduced to two intermediate claims, the proofs of which are given in Sect. 3 and 4. In Sects. 2.2, 2.3, we show Theorem 1.1 (ii). First (Sect. 2.2) we give the estimates for the codimension of the sets of polynomials, violating each of the regularity conditions, after that (Sect. 2.3) we explain how to obtain these estimates.
2.1 Exclusion of maximal singularities
Fix the parameters d, l. Recall that the integer \(\rho \in \{1,2,3,4\}\) depends on d, l (see the table in Sect. 1.2). Fix a variety  . Assume that \(D\sim nH\) is an effective divisor on V such that the pair \(\bigl (V,\frac{1}{n}D\bigr )\) is not canonical. Our aim is to get a contradiction. This would prove claim (iii).
. Assume that \(D\sim nH\) is an effective divisor on V such that the pair \(\bigl (V,\frac{1}{n}D\bigr )\) is not canonical. Our aim is to get a contradiction. This would prove claim (iii).
If there is a non-canonical singularity of the pair \(\bigl (V,\frac{1}{n}D\bigr )\), the centre of which is of positive dimension, then the pair
where \(\Gamma =V_{\gamma }\) for some polynomial \(\gamma (x_*)\) of general position (see Sect. 1.2) and \(D_{\Gamma }=D|_{\Gamma }\), is again non-canonical. If the centres of all non-canonical singularities of the pair \(\bigl (V,\frac{1}{n}D\bigr )\) are points, let us take a polynomial \(\gamma (x_*)\) of general position such that the hypersurface \(\Gamma =V_{\gamma }\) contains one of them. In that case the pair \(\bigl (\Gamma ,\frac{1}{n}D_{\Gamma }\bigr )\) is even non-log canonical.
In any case we obtain a factorial hypersurface \(\Gamma \subset {{\mathbb {P}}} ={{\mathbb {P}}}^M\) of degree dl with at worst quadratic singularities of rank \(\geqslant 2\rho +6\geqslant 8\), and an effective divisor \(D_{\Gamma }\sim nH_{\Gamma }\) on it (where \(H_{\Gamma }\) is the class of a hyperplane section, so that \(\mathrm{Pic}\,\Gamma ={{\mathbb {Z}}}H_{\Gamma }\)), such that the pair \(\bigl (\Gamma ,\frac{1}{n}D_{\Gamma }\bigr )\) is non-canonical. Now we work only with that pair, forgetting about the original variety V (within the limits of the proof of claim (iii) of Theorem 1.1). Let

be the union of the centres of all non-canonical singularities of that pair.
Proposition 2.1
The closed set  is contained in the singular locus \(\mathrm{Sing}\,\Gamma \) of the hypersurface \(\Gamma \).
is contained in the singular locus \(\mathrm{Sing}\,\Gamma \) of the hypersurface \(\Gamma \).
The proof makes the contents of Sect. 3.
Therefore,

Let us define a sequence of rational numbers \(\alpha _k\), \(k\in {{\mathbb {Z}}}_+\), in the following way:
(We can simply write \(\alpha _k=2-{1}/{2^k}\), but for us it is important how \(\alpha _{k+1}\) and \(\alpha _k\) are related.) In order to exclude the maximal (non-canonical) singularities, we will need only the four values:

Let \(o\in \Gamma \) be a point of general position on the irreducible component of maximal dimension of the closed set  . Consider a general 5-dimensional subspace in \({{\mathbb {P}}}\), containing the point o. Let P be the section of the hypersurface \(\Gamma \) by that subspace. Obviously, \(P\subset {{\mathbb {P}}}^5\) is a hypersurface of degree dl with a unique singular point, a non-degenerate quadratic point o. Denoting \(D_{\Gamma |_P}\) by the symbol \(D_P\), we get \(D_P\sim nH_P\), where \(H_P\) is the class of a hyperplane section. By the inversion of adjunction, the point o is the centre of a non-log canonical singularity of the pair \(\bigl (P,\frac{1}{n}D_P\bigr )\), and moreover,
. Consider a general 5-dimensional subspace in \({{\mathbb {P}}}\), containing the point o. Let P be the section of the hypersurface \(\Gamma \) by that subspace. Obviously, \(P\subset {{\mathbb {P}}}^5\) is a hypersurface of degree dl with a unique singular point, a non-degenerate quadratic point o. Denoting \(D_{\Gamma |_P}\) by the symbol \(D_P\), we get \(D_P\sim nH_P\), where \(H_P\) is the class of a hyperplane section. By the inversion of adjunction, the point o is the centre of a non-log canonical singularity of the pair \(\bigl (P,\frac{1}{n}D_P\bigr )\), and moreover,

This implies that
and therefore
Proposition 2.2
There is a sequence of irreducible varieties \(\Gamma _i\), \(i=0,1,\dots ,\rho \), such that:
-
(i)
\(\Gamma _0=\Gamma \) and \(\Gamma _{i+1}\) is a hyperplane section of the hypersurface \(\Gamma _i\subset {{\mathbb {P}}}^{M-i}\), containing the point o,
-
(ii)
on the variety \(\Gamma _{\rho }\) there is a prime divisor
 , where \(H^*\) is the class of a hyperplane section of the hypersurface \(\Gamma _{\rho }\), satisfying the inequality
, where \(H^*\) is the class of a hyperplane section of the hypersurface \(\Gamma _{\rho }\), satisfying the inequality 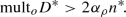
The proof makes the contents of Sect. 4.
Note that by condition (R2.1) all hypersurfaces \(\Gamma _1,\dots ,\Gamma _{\rho }\) are factorial, so that \(\mathrm{Pic}\,\Gamma _{\rho }={{\mathbb {Z}}}H^*\). Furthermore, \(\rho \geqslant 1\), so that
Now let us consider general hypertangent divisors \(D_2,\dots ,D_{M-\rho -2}\) on the hypersurface \(\Gamma _{\rho }\) (for the definition and construction of hypertangent divisors, see [8, Chapter 3]) and construct in the usual way a sequence of irreducible subvarieties \(Y_i\subset \Gamma _{\rho }\) of codimension \(i=1,2,\dots ,M-\rho -3\), such that \(Y_1=D^*\), the subvariety \(Y_2\) is an irreducible component of the effective cycle  with the maximal ratio of the multiplicity \(\mathrm{mult}_o\) to the degree \(\mathrm{deg}\), and for \(i=3,\dots ,M-\rho -3\) the subvariety \(Y_i\) is an irreducible component of the effective cycle
with the maximal ratio of the multiplicity \(\mathrm{mult}_o\) to the degree \(\mathrm{deg}\), and for \(i=3,\dots ,M-\rho -3\) the subvariety \(Y_i\) is an irreducible component of the effective cycle  with the maximal value of the ratio of the multiplicity \(\mathrm{mult}_o\) to the degree. That it is possible to go through with this construction, is ensured by condition (R2.2). Note that the first step of this construction is possible because the hypertangent divisor \(D_2\) is irreducible, \(D_2\sim 2H^*\) and the equality
with the maximal value of the ratio of the multiplicity \(\mathrm{mult}_o\) to the degree. That it is possible to go through with this construction, is ensured by condition (R2.2). Note that the first step of this construction is possible because the hypertangent divisor \(D_2\) is irreducible, \(D_2\sim 2H^*\) and the equality

holds, so that \(Y_1\ne D_2\). The hypertangent divisor \(D_3\) does not take part in the construction.
For the irreducible surface
we get the estimate

which is impossible (the last inequality checks directly for each of the possible values of \(\rho \) and the corresponding values of d, l). Thus we obtained a contradiction, which completes the proof of claim (iii) of Theorem 1.1.
2.2 Estimating the codimension of the set 
Let us prove claim (ii) of Theorem 1.1. Denote by the symbol  the closure of the set of hypersurfaces
the closure of the set of hypersurfaces  , violating condition (R i.j) at at least one point. Here
, violating condition (R i.j) at at least one point. Here
For these values of i.j we set, respectively,

We omit the symbols d, l in order to simplify the formulas, however \(\varepsilon _{i.j}=\varepsilon _{i.j}(d,l)\) are functions of these parameters. The following claim is true.
Proposition 2.3
The following inequalities hold:
-
(i)
\(\varepsilon _{1.1}\geqslant (M^2-(4\rho +5)M+(3\rho ^2+3\rho ))/2\),
-
(ii)
\(\varepsilon _{1.2}\geqslant (M^2-(4\rho +11)M+(3\rho ^2-15\rho +32))/2\),
-
(iii)
\(\varepsilon _{1.3}\geqslant (M^2-(4\rho +13)M+(3\rho ^2+11\rho +42))/2\),
-
(iv)
\(\varepsilon _{1.4}\geqslant (M^2-(4\rho +9)M+(4\rho ^2+14\rho +16))/2\),
-
(v)
\(\varepsilon _{2.1}\geqslant (M^2-(6\rho +7)M+(4\rho ^2+14\rho +12))/2\),
-
(vi)
\(\varepsilon _{2.2}\geqslant (M^2-(4\rho +1)M+(3\rho ^2-\rho ))/2\).
Proof
The regularity conditions must be satisfied for any point o, any linear subspace P of the required codimension, and any linear form \(\lambda \) (the polynomial \(\gamma (x_*\)) is assumed to be general and does not influence the estimating of the codimension of the sets  ). Therefore, the problem of getting a lower bound for the numbers \(\varepsilon _{i.j}\) reduces obviously to a similar problem for varieties
). Therefore, the problem of getting a lower bound for the numbers \(\varepsilon _{i.j}\) reduces obviously to a similar problem for varieties  violating condition (R i.j) at a fixed point o, for a fixed linear subspace and a fixed linear form \(\lambda \). The solution of the latter problem comes from the claims of Propositions 2.4 and 2.6, shown below. More precisely, the estimates for conditions (R1.4) and (R2.1) follow from Proposition 2.4 (i), for condition (R1.2) from Proposition 2.4 (ii), for condition (R1.3) from Proposition 2.4 (iii). The estimates for conditions (R1.1) and (R2.2) follow from Proposition 2.6. \(\square \)
violating condition (R i.j) at a fixed point o, for a fixed linear subspace and a fixed linear form \(\lambda \). The solution of the latter problem comes from the claims of Propositions 2.4 and 2.6, shown below. More precisely, the estimates for conditions (R1.4) and (R2.1) follow from Proposition 2.4 (i), for condition (R1.2) from Proposition 2.4 (ii), for condition (R1.3) from Proposition 2.4 (iii). The estimates for conditions (R1.1) and (R2.2) follow from Proposition 2.6. \(\square \)
Now, in order to prove claim (ii) of Theorem 1.1, it is sufficient to check that the function \(\varepsilon (d,l)\) is the minimum of the right-hand sides in inequalities (i)–(vi) of Proposition 2.3. This work is elementary and we do not give it here.
2.3 Quadratic forms and regular sequences
By the symbol  we denote the linear space of homogeneous polynomials of degree \(i\in {{\mathbb {Z}}}_+\) in N variables \(u_1,\dots ,u_N\). For \(i\leqslant j\) we write
we denote the linear space of homogeneous polynomials of degree \(i\in {{\mathbb {Z}}}_+\) in N variables \(u_1,\dots ,u_N\). For \(i\leqslant j\) we write

and  . The number of variables N is fixed, so we omit the symbol N and write
. The number of variables N is fixed, so we omit the symbol N and write  and so on. Let
and so on. Let

be the closed subset of quadratic forms of rank \(\leqslant r\). Let

be the closed subset of pairs \((w_2,w_3)\), such that the closed set \(\{w_2=w_3=0\}\subset {{\mathbb {P}}}^{N-1}\) has at least one degenerate component (that is, a component, the linear span of which is of dimension \(\leqslant N-2\)). Let \(Q\subset {\mathbb P}^{N-1}\) be a factorial quadric. For \(m\geqslant 4\) let

be the closed subset of polynomials \(w_m\), such that the divisor \(\{w_m|_Q=0\}\) on Q is reducible or non-reduced. The following claim is true.
Proposition 2.4
-
(i)
The following equality holds:

-
(ii)
The following inequality holds:

-
(iii)
The following inequality holds:

Proof
Claim (i) is well known. Let us show inequality (ii). Taking into account part (i), we may assume that the quadratic form \(w_2\) is of rank \(\geqslant 5\), so that the quadric \(\{w_2=0\}\) is factorial. If the closed set \(w_2=w_3=0\) has a degenerate component, then the divisor \(\{w_3|_{\{w_2=0\}}=0\}\) on the quadric \(\{w_2=0\}\) is either reducible, or non-reduced, so that in any case it is a sum of a hyperplane section and a section of the quadric \(\{w_2=0\}\) by some quadratic hypersurface. Calculating the dimensions of the corresponding linear systems, we get that for a fixed quadratic form \(w_2\) of rank \(\geqslant 5\) the closed set of polynomials  , such that the divisor \(\{w_3|_{\{w_2=0\}}=0\}\) is reducible or non-reduced, is of codimension
, such that the divisor \(\{w_3|_{\{w_2=0\}}=0\}\) is reducible or non-reduced, is of codimension
in  . It is easy to see that this expression is higher than the right-hand side of inequality (ii). This proves claim (ii).
. It is easy to see that this expression is higher than the right-hand side of inequality (ii). This proves claim (ii).
Let us show inequality (iii). Recall that the quadric  is assumed to be factorial (that is, the rank of the corresponding quadratic form is at least 5). Set
is assumed to be factorial (that is, the rank of the corresponding quadratic form is at least 5). Set  for \(m\geqslant 1\). It is easy to check that
for \(m\geqslant 1\). It is easy to check that
is a polynomial in m with positive coefficients. This implies that for \(0<s<t\leqslant m/2\) the inequality
holds, which can be re-written as
If the divisor \(\{w_m|_Q=0\}\) is not irreducible and reduced, then it is a sum of two effective divisors on Q, which are cut out on Q by hypersurfaces of degree \(1\leqslant a\leqslant m/2\) and \(m-a\). For that reason,

By what was said above, the right-hand side of that inequality is \(h_Q(1)+h_Q(m-1)\), so that

Elementary computations show that the right-hand side of the last equality is
which is certainly higher than

Remark 2.5
The estimates for \(\varepsilon _{1.2},\varepsilon _{1.4}\) and \(\varepsilon _{2.1}\), given in Proposition 2.3, are obtained from claims (i) and (ii) of Proposition 2.4 by elementary computations. It is slightly less obvious, how to obtain the estimate for \(\varepsilon _{1.3}\), starting from claim (iii) of Proposition 2.4, for that reason we will explain briefly, how to do it. Fixing the linear subspace P and the linear forms \(q_1\) and \(\lambda \), consider the quadric
The codimension of the set of quadratic forms, for which this quadric is of rank \(\leqslant 4\) and so not factorial, is given by Proposition 2.4 (i). It is from here that we get the estimate for \(\varepsilon _{1.3}\) in Proposition 2.3. It remains to show that the violation of condition (R1.3) under the assumption that the quadric (1) is factorial, gives at least the same (in fact, much higher) codimension. It is to the factorial quadric (1) that we apply estimate (iii) of Proposition 2.4. There is, however, a delicate point here. The hypersurface \(P\cap V_{\gamma }\) is given by a polynomial that has at the point o the linear part \(q_1\) and the quadratic part \(q_2\), which both vanish when restricted onto the quadric (1). The other homogeneous components \(q_3,\dots ,q_{dl}\) are arbitrary. In inequality (iii) of Proposition 2.4 the codimension of the “bad” set  is considered with respect to the whole space
is considered with respect to the whole space  , whereas in order to prove inequality (iii) of Proposition 2.3, we need the codimension with respect to the space of homogeneous polynomials of degree dl, the non-homogeneous presentation of which at the fixed point o has zero linear and quadratic components. However, this does not make any influence on the final result, because the codimension of the set
, whereas in order to prove inequality (iii) of Proposition 2.3, we need the codimension with respect to the space of homogeneous polynomials of degree dl, the non-homogeneous presentation of which at the fixed point o has zero linear and quadratic components. However, this does not make any influence on the final result, because the codimension of the set  in
in  is very high.
is very high.
Now let for \(2\leqslant k\leqslant N-2\),

be the set of non-regular tuples \((h_2,\dots ,h_k)\) of length \(k-1\leqslant N-3\), where  , that is, the system of equations
, that is, the system of equations
defines in  a closed subset of codimension \(\leqslant k-2\).
a closed subset of codimension \(\leqslant k-2\).
Proposition 2.6
The following equality holds:

Proof
See [8, Chapter 3, Section 1].\(\square \)
3 Exclusion of maximal singularities at smooth points
In this section we consider factorial hypersurfaces \(X\subset {{\mathbb {P}}}^N\), satisfying certain additional conditions. We show that the centre of every non-canonical singularity of the pair \(\bigl (X,\frac{1}{n} D_X\bigr )\), where \(D_X\sim nH_X\) is cut out on X by a hypersurface of degree \(n\geqslant 1\), is contained in the singular locus \(\mathrm{Sing} \,X\). In Sect. 3.1 we list the conditions that are satisfied by the hypersurface X, state the main result and exclude non-canonical singularities with the centre of a small (\(\leqslant 3\)) codimension on X. In Sects. 3.2 and 3.3, following (with minor modification) the arguments of [6, Subsection 2.1], we exclude non-canonical singularities of the pair \(\bigl (X,\frac{1}{n} D_X\bigr )\), the centre of which is not contained in \(\mathrm{Sing} \,X\). In Sect. 3.3 we use, for this purpose, the standard technique of hypertangent divisors. As a first application, we obtain a proof of Proposition 2.1.
3.1 Regular hypersurfaces
Let \(X\subset {{\mathbb {P}}}^N\), where \(N\geqslant 8\), be a hypersurface, satisfying the condition

In particular, X is factorial and \(\mathrm{Pic}\,X={\mathbb {Z}}H_X\), where \(H_X\) is the class of a hyperplane section. Let \(o\in X\) be a non-singular point and
a system of affine coordinates on  with the origin at the point o, and the hypersurface X in this coordinate system is given by the equation \(h=0\), where
with the origin at the point o, and the hypersurface X in this coordinate system is given by the equation \(h=0\), where
and the polynomials \(h_i\) are homogeneous of degree i. We assume that the inequality
holds.
Now let us state the regularity conditions for the hypersurface X at the point o.
-
(N1)
For any linear form
$$\begin{aligned} \lambda (z_*)\not \in \langle h_1\rangle \end{aligned}$$the sequence of homogeneous polynomials
$$\begin{aligned} h_1|_{\{\lambda =0\}},\quad h_2|_{\{\lambda =0\}},\quad ,\dots ,\quad h_{N-3}|_{\{\lambda =0\}} \end{aligned}$$is regular (in the local ring
 ).
). -
(N2)
The linear span of every irreducible component of the closed set
$$\begin{aligned} h_1=h_2=h_3=0 \end{aligned}$$is the hyperplane \(\{h_1=0\}\).
-
(N3)
For any linear form \(\lambda \not \in \langle h_1\rangle \) the set
$$\begin{aligned} \overline{X\cap \{h_1=h_2=0\}\cap \{\lambda =0\}} \end{aligned}$$is irreducible and reduced.
Proposition 3.1
Assume that the hypersurface X satisfies conditions (N1–3) at every non-singular point \(o\in X\). Then for every pair \(\bigl (X,\frac{1}{n}D_X\bigr )\), where \(D_X\sim nH_X\) is an effective divisor, the union of the centres of all non-canonical singularities  of that pair is contained in the closed set \(\mathrm{Sing}\, X\).
of that pair is contained in the closed set \(\mathrm{Sing}\, X\).
Proof
Assume the converse: for some effective divisor \(D_X\sim nH_X\),

Let Y be an irreducible component of the set  , which is not contained in \(\mathrm{Sing}\, X\), the dimension of which is maximal among all such components.
, which is not contained in \(\mathrm{Sing}\, X\), the dimension of which is maximal among all such components.
Lemma 3.2
The following inequality holds:

Proof
Assume the converse:  . Since Y is the centre of some non-canonical singularity of the pair \(\bigl (X,\frac{1}{n}D_X\bigr )\) and \(Y\not \subset \mathrm{Sing}\, X\), we get the inequality \(\mathrm{mult}_YD_X>n\). Since the codimension of the set \(\mathrm{Sing}\, X\) is at least 5, we can take a curve \(C\subset X\) such that
. Since Y is the centre of some non-canonical singularity of the pair \(\bigl (X,\frac{1}{n}D_X\bigr )\) and \(Y\not \subset \mathrm{Sing}\, X\), we get the inequality \(\mathrm{mult}_YD_X>n\). Since the codimension of the set \(\mathrm{Sing}\, X\) is at least 5, we can take a curve \(C\subset X\) such that

Obviously, \(\mathrm{mult}_C D_X>n\). Now repeating the arguments in the proof of [8, Chapter 2, Lemma 2.1] word for word, we get a contradiction which completes the proof. \(\blacksquare \)
3.2 Restriction onto a hyperplane section
Let \(o\in Y\) be a point of general position, \(o\not \in \mathrm{Sing}\,X\). Consider the section \(P\subset X\) by a general linear subspace of dimension 4, containing the point o. The hypersurface \(P\subset {{\mathbb {P}}}^4\) is non-singular, so that \(\mathrm{Pic}\, P={{\mathbb {Z}}}H_P\) by the Lefschetz theorem, where \(H_P\) is the class of a hyperplane section of the variety P. Set \(D_P=D_X|_P\), so that \(D_P\sim nH_P\). By inversion of adjunction, the pair \(\bigl (P,\frac{1}{n}D_P\bigr )\) is not log canonical; moreover, by construction,

Let \(\varphi _P:P^+\!\rightarrow P\) be the blow-up of the point o, \(E_P=\varphi ^{-1}_P(o)\cong {{\mathbb {P}}}^2\) the exceptional divisor, \(D^+_P\) the strict transform of the divisor \(D_P\) on \(P^+\).
Lemma 3.3
There is a line \(L\subset E_P\), satisfying the inequality
Proof
This follows from [6, Proposition 9]. \(\blacksquare \)
The blow-up \(\varphi _P\) can be viewed as the restriction onto the subvariety P of the blow-p \(\varphi _X:X^+\!\rightarrow X\) of the point o with the exceptional divisor \(E_X\cong {\mathbb {P}}^{N-2}\). Lemma 3.3 implies that there is a hyperplane \(\Theta \subset E_X\), satisfying the inequality
The rest of the proof of Proposition 3.1 repeats the proof of [6, 2.1, Theorem 2 (i)] almost word for word. For the convenience of the reader we briefly reproduce those arguments. By the symbol \(|H_X-\Theta |\) we denote the pencil of hyperplane sections R of the hypersurface X, such that \(R\ni o\) and \(R^+\cap E_X=\Theta \) (where \(R^+\!\subset X^+\) is the strict transform). Let \(R\in |H_X-\Theta |\) be a general element of the pencil. Set \(D_R=D_X|_R\).
Lemma 3.4
The following inequality holds:
Proof
This is [6, Lemma 3] (our claim follows directly from inequality (3) and the choice of the section R). \(\blacksquare \)
Consider the tangent hyperplane \(T_oR\subset {{\mathbb {P}}}^{N-1}\) to the hypersurface R at the point o. The intersection \(T_R=R\cap T_oR\) is a hyperplane section of R. Therefore, \(T_R\sim H_R\) is a prime divisor on R. By condition (N1) the equality \(\mathrm{mult}_oT_R=2\) holds. Therefore, if
where \(a\in {{\mathbb {Z}}}_+\) and the effective divisor  does not contain \(T_R\) as a component, then the inequality
does not contain \(T_R\) as a component, then the inequality
holds. In order not to make the notations too complicated, we assume that \(a=0\), that is, \(D_R\sim nH_R\) does not contain \(T_R\) as a component. Moreover, by the linearity of inequality (4) in \(D_R\), we may assume that \(D_R\) is a prime divisor.
3.3 Hypertangent divisors
Getting back to the coordinates \(z_1,\dots ,z_N\), write down
for \(i=1,\dots ,\mathrm{deg}\, X\) and consider the second hypertangent system

where \(s_0\in {{\mathbb {C}}}\) and \(s_1\) runs through the space of linear forms in \(z_*\). By condition (N3) the base set  is irreducible and reduced, and by condition (N1) it is of codimension 2 on R. Therefore, a general divisor
is irreducible and reduced, and by condition (N1) it is of codimension 2 on R. Therefore, a general divisor  does not contain the prime divisor \(D_R\) as a component, so that we get a well-defined effective cycle
does not contain the prime divisor \(D_R\) as a component, so that we get a well-defined effective cycle

of codimension 2 on R, satisfying the inequality

By the linearity of the equivalent inequality
in \(Y_2\) we may replace the cycle \(Y_2\) by its suitable irreducible component and assume \(Y_2\) to be an irreducible subvariety of codimension 2.
Lemma 3.5
The subvariety \(Y_2\) is not contained in the tangent divisor \(T_R\).
Proof
The base set of the hypertangent system  is
is

It is irreducible, reduced and therefore

By condition (N1) the equality
holds. Therefore, \(Y_2\ne S_R\). However, a certain polynomial
vanishes on \(Y_2\), where \(s_0\ne 0\), since the divisor  is chosen to be general. If we had
is chosen to be general. If we had
then we would have got \(h_{\leqslant 2}|_{Y_2}\equiv 0\). Since \(h_{\leqslant 2}=h_1+h_2\), this would have implied that \(h_2|_{Y_2}\equiv 0\) and  , which is not true. \(\blacksquare \)
, which is not true. \(\blacksquare \)
By the lemma that we have just shown, the effective cycle

of codimension 3 on R is well defined. It satisfies the inequality

The cycle \(Y_3\) can be assumed to be an irreducible subvariety of codimension 3 on R for the same reason as \(Y_2\).
Now applying the technique of hypertangent divisors in the usual way [8, Chapter 3], we intersect \(Y_3\) with general hypertangent divisors

using condition (N1), and obtain an irreducible curve \(C\subset R\), satisfying by (2) the inequality

which is impossible.
This completes the proof of Proposition 3.1. \(\square \)
Proof of Proposition 2.1
It is sufficient to check that the hypersurface \(\Gamma \) satisfies all the assumptions that were made about the hypersurface X. Indeed, \(\Gamma \) has at most quadratic singularities of rank \(\geqslant 8\), so that

That inequality (2) is true for \(\Gamma \), one checks by elementary computations. Condition (N1) follows from (R1.1), condition (N2) from (R1.2), condition (N3) from (R1.3). Therefore, we can apply Proposition 3.1. \(\square \)
4 Reduction to a hyperplane section
In this section we consider hypersurfaces \(X\subset {{\mathbb {P}}}^N\) with at most quadratic singularities, the rank of which is bounded from below, which also satisfy some additional conditions. For a non-canonical pair \(\bigl (X,\frac{1}{n} D_X\bigr )\), where \(D_X\sim nH_X\) does not contain hyperplane sections of the hypersurface X, we construct a special hyperplane section \(\Delta \), such that the pair \(\bigl (\Delta ,\frac{1}{n} D_{\Delta }\bigr )\), where \(D_{\Delta }=D_X|_{\Delta }\), is again non-canonical and, into the bargain, somewhat “better” than the original pair: the multiplicity of the divisor \(D_{\Delta }\) at some point \(o\in \Delta \) is higher than the multiplicity of the original divisor \(D_X\) at this point.
4.1 Hypersurfaces with singularities
Take \(N\geqslant 8\) and let \(X\subset {{\mathbb {P}}}^N\) be a hypersurface, satisfying the following conditions:
-
(S1)
every point \(o\in X\) is either non-singular, or a quadratic singularity of rank \(\geqslant 7\),
-
(S2)
for every effective divisor \(D\sim nH_X\), where \(H_X\in \mathrm{Pic}\, X\) is the class of a hyperplane section and \(n\geqslant 1\), the union
 of the centres of all non-log canonical singularities of the pair \(\bigl (X,\frac{1}{n}D_X\bigr )\) is contained in \(\mathrm{Sing}\, X\),
of the centres of all non-log canonical singularities of the pair \(\bigl (X,\frac{1}{n}D_X\bigr )\) is contained in \(\mathrm{Sing}\, X\), -
(S3)
for every effective divisor Y on the section of X by a linear subspace of codimension 1 or 2 in \({{\mathbb {P}}}^N\) and every point \(o\in Y\), singular on X, the following inequality holds:
 (5)
(5)
Condition (S1), Grothendieck’s theorem on parafactoriality [1], and the Lefschetz theorem imply that X is a factorial variety and \(\mathrm{Cl}\, X=\mathrm{Pic}\, X={{\mathbb {Z}}} H_X\), since  . As every hyperplane section of the hypersurface X is a hypersurface in \({{\mathbb {P}}}^{N-1}\), the singular locus of which has codimension at least 4, it is also factorial.
. As every hyperplane section of the hypersurface X is a hypersurface in \({{\mathbb {P}}}^{N-1}\), the singular locus of which has codimension at least 4, it is also factorial.
Assume, furthermore, that \(D_X\sim nH_X\) is an effective divisor such that we have  , and moreover, there is a point
, and moreover, there is a point  (see condition (S2)) which is a quadratic singularity of rank \(\geqslant 8\). Let
(see condition (S2)) which is a quadratic singularity of rank \(\geqslant 8\). Let

be its blow-up with the exceptional divisor \(E=\varphi ^{-1}(o)\), which by our assumption is a quadric of rank \(\geqslant 8\). For the strict transform \(D^+_X\subset X^+\) we can write
where by condition (S3) we have \(\alpha <2\), since \(\mathrm{mult}_oD_X<4n\).
Remark 4.1
As we will see below, under our assumptions the inequality \(\alpha >1\) holds. Since for every hyperplane section \(\Delta \ni o\) of the hypersurface X and its strict transform  we have
we have
the pair \((X,\Delta )\) is canonical, so that we may assume that the effective divisor \(D_X\) does not contain hyperplane sections of the hypersurface X as components (if there are such components, they can be removed with all assumptions being kept). For that reason, for any hyperplane section \(\Delta \ni o\) the effective cycle  of codimension 2 on X is well defined. We will understand this cycle as an effective divisor on the hypersurface \(\Delta \subset {{\mathbb {P}}}^{N-1}\) and denote it by the symbol \(D_{\Delta }\).
of codimension 2 on X is well defined. We will understand this cycle as an effective divisor on the hypersurface \(\Delta \subset {{\mathbb {P}}}^{N-1}\) and denote it by the symbol \(D_{\Delta }\).
Proposition 4.2
There is a hyperplane section \(\Delta \ni o\) of the hypersurface X such that

and \(D^+_{\Delta }\sim n(H_{\Delta }-\alpha _{\Delta }E_{\Delta })\), and, moreover, the following inequality holds:
(Here \(H_{\Delta }\) is the class of a hyperplane section of the hypersurface \(\Delta \subset {{\mathbb {P}}}^{N-1}\), and \(E_{\Delta }=\Delta ^+\cap E\) is the exceptional divisor of the blow-up  , where \(\Delta ^+\) is the strict transform of \(\Delta \) on \(X^+\) and \(D^+_{\Delta }\) is the strict transform of the divisor \(D_{\Delta }\) on \(\Delta ^+\).)
, where \(\Delta ^+\) is the strict transform of \(\Delta \) on \(X^+\) and \(D^+_{\Delta }\) is the strict transform of the divisor \(D_{\Delta }\) on \(\Delta ^+\).)
Proof
Obviously, \(D_{\Delta }\sim nH_{\Delta }\). We have

for every hyperplane section \(\Delta \), so that we only need to show the existence of the hyperplane section \(\Delta \) for which inequality (6) is satisfied. This fact is obtained by the arguments, repeating the proof of [9, Theorem 1.4, see Subsections 4.2, 4.3] almost word for word. We will go through the main steps of these arguments, dwelling on the necessary modifications. Whenever possible, we use the same notations as in [9, Subsections 4.2, 4.3].
4.2 Preliminary constructions
Consider the section P of the hypersurface X by a general 5-dimensional linear subspace, containing the point o. Obviously, \(P\subset {{\mathbb {P}}}^5\) is a factorial hypersurface, \(o\in P\) is an isolated quadratic singularity of the maximal rank. Let  be the strict transform of the hypersurface P, so that \(E_P=P^+\cap E\) is a non-singular 3-dimensional quadric. Set
be the strict transform of the hypersurface P, so that \(E_P=P^+\cap E\) is a non-singular 3-dimensional quadric. Set  . Obviously, by the inversion of adjunction the pair \((P,\frac{1}{n}D_P)\) has the point o as an isolated centre of a non-log canonical singularity. Since \(a(E_P)=2\) and \(D^+_P\sim nH_P-\alpha nE_P\) (where \(H_P\) is the class of a hyperplane section of the hypersurface \(P\subset {{\mathbb {P}}^5}\)), and moreover \(\alpha <2\), we conclude that the pair
. Obviously, by the inversion of adjunction the pair \((P,\frac{1}{n}D_P)\) has the point o as an isolated centre of a non-log canonical singularity. Since \(a(E_P)=2\) and \(D^+_P\sim nH_P-\alpha nE_P\) (where \(H_P\) is the class of a hyperplane section of the hypersurface \(P\subset {{\mathbb {P}}^5}\)), and moreover \(\alpha <2\), we conclude that the pair  is not log canonical and the union
is not log canonical and the union

of the centres of all non-log canonical singularities of that pair, intersecting the exceptional divisor \(E_P\), is a connected closed subset of the quadric \(E_P\). Let \(S_P\) be an irreducible component of maximal dimension of that set. Since \(S_P\) is the centre of certain non-log canonical singularity of the pair  , the inequality
, the inequality
holds. Furthermore,  (and if \(S_P\) is a point, then we have
(and if \(S_P\) is a point, then we have  by the connectedness of that set). Coming back to the original pair \(\bigl (X,\frac{1}{n}D_X\bigr )\), we see that the pair
by the connectedness of that set). Coming back to the original pair \(\bigl (X,\frac{1}{n}D_X\bigr )\), we see that the pair  has a non-log canonical singularity, the centre of which is an irreducible subvariety \(S\subset E\), such that \(S\cap E_P=S_P\); in particular,
has a non-log canonical singularity, the centre of which is an irreducible subvariety \(S\subset E\), such that \(S\cap E_P=S_P\); in particular,

and if the last codimension is equal to 3, then \(S\cap E_P\) is a point and for that reason \(S\subset E\) is a linear subspace of codimension 3. However, on a quadric of rank \(\geqslant 8\) there can be no linear subspaces of codimension 3, so that  .
.
Proposition 4.3
The case  is impossible.
is impossible.
Proof
Assume that this case takes place. Then \(S\subset E\) is a prime divisor, which is cut out on E by a hypersurface of degree \(d_S\geqslant 1\), that is, \(S\sim d_SH_E\), where \(H_E\) is the class of a hyperplane section of the quadric E. We have  , so that
, so that
and for that reason \(S\sim H_E\) is a hyperplane section of the quadric E. Let \(\Delta \in |H|\) be the uniquely determined hyperplane section of the hypersurface X, such that \(\Delta \ni o\) and  . For the effective divisor \(D_{\Delta }\) the inequality
. For the effective divisor \(D_{\Delta }\) the inequality

holds. Taking into account that  , we get a contradiction with condition (S3), which by assumption is satisfied for the hypersurface X. \(\blacksquare \)
, we get a contradiction with condition (S3), which by assumption is satisfied for the hypersurface X. \(\blacksquare \)
4.3 The case of codimension 2
We proved above that \(S\subset E\) is a subvariety of codimension 2. Following [11, Section 3], for distinct points \(p\ne q\) on the quadric E we denote by the symbol [p, q] the line joining these two points, provided that it is contained in E, and the empty set, otherwise, and set

(where the line above means the closure).
Lemma 4.4
One of the following two options takes place:
-
(a)
 is a hyperplane section of the quadric E, on which S is cut out by a hypersurface of degree \(d_S\geqslant 2\),
is a hyperplane section of the quadric E, on which S is cut out by a hypersurface of degree \(d_S\geqslant 2\), -
(b)
 is the section of the quadric E by a linear subspace of codimension 2.
is the section of the quadric E by a linear subspace of codimension 2.
Proof
The proof repeats the proof of [9, Lemma 4.1], and we do not give it here. (The key point in the arguments is that due to the inequality \(\alpha <2\) every line \(L=[p,q]\subset E\), joining some point \(p,q\in S\) and lying on E, is contained in \(D^+_X\), because \(\mathrm{mult}_SD^+_X>n\).) \(\blacksquare \)
Proposition 4.5
Option (b) does not take place.
Proof
Assume the converse: case (b) takes place. Let \(P\subset X\) be the section of the hypersurface X by the linear subspace of codimension 2 in \({{\mathbb {P}}}^N\), that is uniquely determined by the conditions \(P\ni o\) and \(P^+\cap E=S\).
The symbol \(|H-P|\) stands for the pencil of hyperplane sections of the hypersurface X, containing P. For a general divisor \(\Delta \in |H-P|\) we have the equality
Write down  , where \(a\in {{\mathbb {Z}}}_+\) and G is an effective divisor on \(\Delta \), not containing P as a component. Obviously, \(G\in |mH_{\Delta }|\), where \(m=n-a\) and \(H_{\Delta }\) is the class of a hyperplane section of \(\Delta \subset {{\mathbb {P}}}^{N-1}\). The symbols \(G^+\) and \(\Delta ^+\) stand for the strict transforms of G and \(\Delta \) on \(X^+\), respectively. Now,
, where \(a\in {{\mathbb {Z}}}_+\) and G is an effective divisor on \(\Delta \), not containing P as a component. Obviously, \(G\in |mH_{\Delta }|\), where \(m=n-a\) and \(H_{\Delta }\) is the class of a hyperplane section of \(\Delta \subset {{\mathbb {P}}}^{N-1}\). The symbols \(G^+\) and \(\Delta ^+\) stand for the strict transforms of G and \(\Delta \) on \(X^+\), respectively. Now,
where \(E_{\Delta }=\Delta ^+\cap E\) is a hyperplane section of the quadric E and, besides,
By construction, the effective cycle  of codimension 2 on \(\Delta \) is well defined. One can consider it as an effective divisor on the hypersurface \(P\subset {{\mathbb {P}}}^{N-2}\). The following inequality holds:
of codimension 2 on \(\Delta \) is well defined. One can consider it as an effective divisor on the hypersurface \(P\subset {{\mathbb {P}}}^{N-2}\). The following inequality holds:

Since  , we obtain a contradiction with condition (S3), which is satisfied for the hypersurface X. \(\blacksquare \)
, we obtain a contradiction with condition (S3), which is satisfied for the hypersurface X. \(\blacksquare \)
4.4 The hyperplane section \(\Delta \)
We have shown that case (a) takes place. Set  . This is a hyperplane section of the quadric E, where \(\Lambda \subset D^+_X\). Set
. This is a hyperplane section of the quadric E, where \(\Lambda \subset D^+_X\). Set
We know that \(\mu >n\) and \(\mu \leqslant \alpha n<2n\) (the second inequality holds, because for a general linear subspace \(\Pi \subset E\) of maximal dimension the divisor  on \(\Pi \) is a hypersurface of degree \(\alpha n\), containing every point of the set \(S\cap \Pi \) with multiplicity \(\geqslant \mu \)).
on \(\Pi \) is a hypersurface of degree \(\alpha n\), containing every point of the set \(S\cap \Pi \) with multiplicity \(\geqslant \mu \)).
Lemma 4.6
The following inequality holds:
Proof
This is [9, Lemma 4.2]. The claim of the lemma is a local fact and for that reason the proof given in [9, 4.3] does not require any modifications and works word for word. \(\blacksquare \)
Now let us consider the uniquely determined hyperplane section \(\Delta \) of the hypersurface \(X\subset {{\mathbb {P}}}^N\) such that \(\Delta \ni o\) and \(\Delta ^+\cap E=\Lambda \), where \(\Delta ^+\!\subset X^+\) is the strict transform of \(\Delta \). Write down

Obviously, \(\mathrm{mult}_o D_{\Delta }=2(\alpha n+a)\), so that
(recall that \(D^+_{\Delta }\sim n(H_{\Delta }-\alpha _{\Delta }E_{\Delta })\), where \(E_{\Delta }=\Lambda \)). Since the subvariety S is cut out on the quadric \(\Lambda \) by a hypersurface of degree \(d_S\geqslant 2\), we obtain the inequality

Since  , we get
, we get

Consider the blow-up \(\sigma _S:{\widetilde{\Delta }}\rightarrow \Delta ^+\) of the subvariety \(S\subset \Delta ^+\) of codimension 2 and denote its exceptional divisor \(\sigma _S^{-1}(S)\) by the symbol \(E_S\).
Proposition 4.7
For some irreducible divisor \(S_1\subset E_S\), such that the projection \(\sigma _S|_{S_1}\) is birational, the inequality
holds, where \({\widetilde{D}}_{\Delta }\) and \({\widetilde{\Lambda }}\) are the strict transforms, respectively, of \(D^+_{\Delta }\) and \(\Lambda \) on \({\widetilde{\Delta }}\).
Proof
This is a well-known fact, see [6, Proposition 9]. (Note that the subvariety S is, generally speaking, singular, however \(\Delta ^+\) is non-singular at the general point of S and \({\widetilde{\Delta }}\) is non-singular at the general point of \(S_1\).) \(\blacksquare \)
4.5 End of the proof
Set \(\mu _S=\mathop {\mathrm{mult}}_SD^+_{\Delta }\) and \(\beta =\mathrm{mult}_{S_1}{\widetilde{D}}_{\Delta }\). One of the two cases takes place:
-
the case of general position \(S_1\ne E_S\cap {\widetilde{\Lambda }}\), so that \(S_1\not \subset {\widetilde{\Lambda }}\),
-
the special case \(S_1=E_S\cap {\widetilde{\Lambda }}\).
Let us consider them separately. In the case of general position inequality (8) takes the form
since \(\mathrm{mult}_{S_1}{\widetilde{\Lambda }}=0\). Furthermore, \(\mu _S\geqslant \beta \), so that the more so
On the other hand, from inequality (7) we get \(2\mu _S\leqslant \alpha n+a\), which implies that
and for that reason

Inequality (6) in the case of general position is now proven.
Let us consider the special case. Here \(\mathrm{mult}_{S_1}{\widetilde{\Lambda }}=1\), so that inequality (8) takes the form
Besides, the effective cycle  , considered as an effective divisor on \(\Lambda \), is cut out on the quadric \(\Lambda \) by a hypersurface of degree \(\alpha n+a\), and contains the divisor \(S\sim d_SH_{\Lambda }\) (where \(H_{\Lambda }\) is the class of a hyperplane section of \(\Lambda \)) with multiplicity \(\geqslant \mu _S+\beta \), so that
, considered as an effective divisor on \(\Lambda \), is cut out on the quadric \(\Lambda \) by a hypersurface of degree \(\alpha n+a\), and contains the divisor \(S\sim d_SH_{\Lambda }\) (where \(H_{\Lambda }\) is the class of a hyperplane section of \(\Lambda \)) with multiplicity \(\geqslant \mu _S+\beta \), so that
whence we get \(\alpha n+5a>4n\) and for that reason

that is,  (since \(\alpha >1\)). This inequality is stronger than (6), which completes the proof in the special case.
(since \(\alpha >1\)). This inequality is stronger than (6), which completes the proof in the special case.
The proof of Proposition 4.2 is now complete. \(\square \)
Proof of Proposition 2.2
Let us check that the operation of reduction, described in Sect. 4.1, can be \(\rho \) times applied to the hypersurface \(\Gamma \subset {{\mathbb {P}}}^M\). Consider the hypersurface \(\Gamma _i\subset {{\mathbb {P}}}^{M-i}\), where \(i\in \{0,\dots ,\rho -1\}\). Let us show, in the first place, that \(\Gamma _i\) satisfies condition (S1). Let \(p\in \Gamma _i\) be an arbitrary singularity. If \(i=0\), then by condition (R2.1), the point p is a quadratic singularity of rank \(\geqslant 8\). If \(i\geqslant 1\), then there are two options: either \(p\in \Gamma \) is a non-singular point, or \(p\in \Gamma \) is a singularity (recall that \(\Gamma _i\) is a section of the hypersurface \(\Gamma \) by a linear subspace of codimension i in \({{\mathbb {P}}}^M\)). In the second case by condition (R2.1) the point p is a quadratic singularity of \(\Gamma \) of rank \(\geqslant 2\rho +6\geqslant 2i+8\), since \(\rho \geqslant i+1\). Since a hyperplane section of a quadric of rank \(r\geqslant 3\) is a quadric of rank \(\geqslant r-2\), we conclude that \(p\in \Gamma _i\) is a quadratic singularity of rank \(\geqslant 8\), so that condition (S1) is satisfied at that point (for the hypersurface \(\Gamma _i\)).
In the first case the point p is non-singular on \(\Gamma \), so that \(\Gamma _i\) is a section of \(\Gamma \) by a linear subspace of codimension i, which is contained in the tangent hyperplane  . By condition (R1.4) the point \(p\in \Gamma _i\) is a quadratic singularity of rank
. By condition (R1.4) the point \(p\in \Gamma _i\) is a quadratic singularity of rank

(one should take into account that the cutting subspace is of codimension \(i-1\) in  ). Therefore, condition (S1) is satisfied in any case.
). Therefore, condition (S1) is satisfied in any case.
Let us show that the hypersurface \(\Gamma _i\) satisfies condition (S2) as well. In order to do it, we must check that for \(\Gamma _i\) all assumptions of Sect. 3.1 are satisfied. By what was said above, the codimension of the set \(\mathop {\mathrm{Sing\,}}\Gamma _i\) with respect to \(\Gamma _i\) it at least 7 — this is higher than we need. Inequality (2) takes the form of the estimate
which is easy to check. Finally, conditions (N1), (N2) and (N3) follow from conditions (R1.1), (R1.2) and (R1.3), respectively. By Proposition 3.1 we conclude that the hypersurface \(\Gamma _i\) satisfies condition (S2).
Finally, let us consider condition (S3). Obviously, it is sufficient to check that inequality (5) holds for any prime divisor Y on the section of the hypersurface \(\Gamma _i\) by a linear subspace \(P^*\) of codimension 2 in \({{\mathbb {P}}}^{M-i}\). Assume the converse:

In some affine coordinates with the origin at the point o on the subspace  the equation of the hypersurface \(P^*\cap \Gamma _i\) has the form
the equation of the hypersurface \(P^*\cap \Gamma _i\) has the form
where by condition (R2.2) the sequence of homogeneous polynomials
is regular. Consider general hypertangent divisors
The first hypertangent divisor \(D^*_2\) is irreducible and satisfies the equality

so that \(D^*_2\ne Y\) and the effective cycle of the scheme-theoretic intersection  is well defined. It satisfies the inequality
is well defined. It satisfies the inequality

Let \(Y_2\) be an irreducible component of that cycle with the maximal value of the ratio \(\mathrm{mult}_o/\mathrm{deg}\). Intersecting \(Y_2\) with the divisors
in the usual way (see [8, Chapter 3] or Sect. 3.3 of the present paper), we construct a sequence of irreducible subvarieties
where  and the last subvariety \(Y^*_{M-\rho -6}\) (the dimension of which is \(\rho -i+3\geqslant 4\)) satisfies the inequality
and the last subvariety \(Y^*_{M-\rho -6}\) (the dimension of which is \(\rho -i+3\geqslant 4\)) satisfies the inequality

It is easy to check that the right-hand side of the last inequality for the values of d, l and \(\rho \) under consideration is higher than 1, which gives a contradiction with assumption (9) and proves that the hypersurface \(\Gamma _i\) satisfies condition (S3).
Note that all singular points of \(\Gamma _i\) are quadratic singularities of rank \(\geqslant 8\), so that the additional assumption about the point o made in Sect. 4.1 is satisfied.
Now applying Proposition 4.2, we complete the proof of Proposition 2.2.\(\square \)
References
Call, F., Lyubeznik, G.: A simple proof of Grothendieck’s theorem on the parafactoriality of local rings. In: Heinzer, W.J., Huneke, C.L., Sally, J.D. (eds.) Commutative Algebra: Syzygies, Multiplicities, and Birational Algebra. Contemporary Mathematics, vol. 159, pp. 15–18. American Mathematical Society, Providence (1994)
Cheltsov, I.A.: Log canonical thresholds of Fano threefold hypersurfaces. Izv. Math. 73(4), 727–795 (2009)
Cheltsov, I.: Fano varieties with many selfmaps. Adv. Math. 217(1), 97–124 (2008)
Cheltsov, I., Park, J., Won, J.: Log canonical thresholds of certain Fano hypersurfaces. Math. Z. 276(1–2), 51–79 (2014)
Cheltsov, I.A., Shramov, K.A.: Log canonical thresholds of smooth Fano threefolds. Russian Math. Surveys 63(5), 859–958 (2008)
Pukhlikov, A.V.: Birational geometry of Fano direct products. Izv. Math. 69(6), 1225–1255 (2005)
Pukhlikov, A.V.: Birational geometry of Fano double covers. Sb. Math. 199(8), 1225–1250 (2008)
Pukhlikov, A.: Birationally Rigid Varieties. Mathematical Surveys and Monographs, vol. 190. American Mathematical Society, Providence (2013)
Pukhlikov, A.V.: Birationally rigid Fano fibrations. II. Izv. Math. 79(4), 809–837 (2015)
Pukhlikov, A.V.: Canonical and log canonical thresholds of Fano complete intersections. Eur. J. Math. 4(1), 381–398 (2018)
Pukhlikov, A.V.: Birational geometry of singular Fano hypersurfaces of index two. Manuscripta Math. https://doi.org/10.1007/s00229-018-1075-3
Pukhlikov, A.V.: Birationally rigid finite covers of the projective space. Proc. Steklov Math. Inst. DOI:Mi tm4026. arXiv:1901.01086
Acknowledgements
The author is grateful to the colleagues in the Divisions of Algebraic Geometry and Algebra at Steklov Institute of Mathematics for the interest to his work, and to the colleagues algebraic geometers at the University of Liverpool for the general support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author thanks The Leverhulme Trust for the support of the present work (Research Project Grant RPG-2016-279).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pukhlikov, A.V. Canonical and log canonical thresholds of multiple projective spaces. European Journal of Mathematics 7, 135–162 (2021). https://doi.org/10.1007/s40879-019-00388-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-019-00388-7





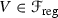 has at most quadratic singularities of rank
has at most quadratic singularities of rank 
 and every divisor
and every divisor  .
.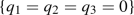
 .
. , where
, where 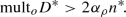




 ).
). of the centres of all non-log canonical singularities of the pair
of the centres of all non-log canonical singularities of the pair 
 is a hyperplane section of the quadric E, on which S is cut out by a hypersurface of degree
is a hyperplane section of the quadric E, on which S is cut out by a hypersurface of degree  is the section of the quadric E by a linear subspace of codimension 2.
is the section of the quadric E by a linear subspace of codimension 2.