Abstract
We prove that there are exactly two G-minimal surfaces which are G-birational to the quintic del Pezzo surface, where  . These surfaces are the quintic del Pezzo surface itself and the surface
. These surfaces are the quintic del Pezzo surface itself and the surface  .
.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of finite subgroups of the Cremona group is classical, but the first serious treatment has been done by Igor V. Dolgachev and Vasily A. Iskovskikh at the beginning of this century, starting with Iskovskikh’s paper [11]. In their seminal work [7] all finite subgroups of the Cremona group \(\mathrm{Cr}_2(\mathbb {C})\) are classified up to isomorphism. In the section “What is left” in [7] it is stated that not all conjugacy classes of \(\mathrm{Cr}_2(\mathbb {C})\) are known and that a finer description of the the conjugacy classes would be desirable.
Let us recall from [11] that two subgroups of the Cremona group given by the biregular actions of a finite group G on two rational surfaces are conjugate if there exists a G-birational map  . By general theory such a map can be factorised into elementary links [9]. In this paper we will contribute to the open questions from [7] by proving:
. By general theory such a map can be factorised into elementary links [9]. In this paper we will contribute to the open questions from [7] by proving:
Theorem 1.1
Let \(S_5\) be the smooth del Pezzo surface of degree 5, and let  be a subgroup of order 20 in
be a subgroup of order 20 in  . Then \(\mathrm{Pic}^{G_{20}}(S_5)=\mathbb {Z}\) and
. Then \(\mathrm{Pic}^{G_{20}}(S_5)=\mathbb {Z}\) and
-
1.
\(S_5\) is not \(G_{20}\)-birational to any conic bundle,
-
2.
there exists a unique G-minimal del Pezzo surface which is \(G_{20}\)-birational to \(S_5\), that is
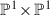 ,
, -
3.
the group of \(G_{20}\)-birational automorphisms is given by
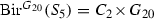 .
.
Here \(C_n\) is a cyclic group of order n. It should be noticed that there are no G-conic fibrations birational to \(S_5\).
In the notation of [1] we can say that \(S_5\) is \(G_{20}\)-solid.
Remark 1.2
In the proof of Theorem 1.1 we will also see that the only smooth del Pezzo surfaces G-birational to \(S_5\) are  and the Clebsch cubic surface. But the latter is not \(G_{20}\)-minimal, i.e., \(\mathrm{Pic}^{G_{20}}(\widetilde{S}) \ne \mathbb {Z}\). Indeed we will show in Remark 5.2, that its \(G_{20}\)-invariant Picard group is \(\mathbb {Z}^2\).
and the Clebsch cubic surface. But the latter is not \(G_{20}\)-minimal, i.e., \(\mathrm{Pic}^{G_{20}}(\widetilde{S}) \ne \mathbb {Z}\). Indeed we will show in Remark 5.2, that its \(G_{20}\)-invariant Picard group is \(\mathbb {Z}^2\).
Throughout this paper we assume all varieties to be complex and projective. For all notation in birational geometry, such as G-biregular, we use the conventions introduced in [7].
2 G-Sarkisov links
We will dedicate this section to the introduction of the notion of G-Sarkisov links where G is a finite group. For simplicity we will only consider the dimension 2 here. For a more detailed study see [5]. This language will allow us to state Theorem 1.1 in a more precise and technical way. We will firstly define a G-Mori fibre space.
Definition 2.1
A 2-dimensional G-Mori fibre space is
-
DP:
a smooth G-minimal del Pezzo surface S, i.e., \(\mathrm{Pic}^G(S)=\mathbb {Z}\);
-
CB:
a G-conic bundle, i.e., a G-equivariant morphism
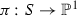 , where S is a smooth surface and the general fibre of \(\pi \) is
, where S is a smooth surface and the general fibre of \(\pi \) is 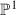 such that \(\mathrm{Pic}^G(S)=\mathbb {Z}^2\).
such that \(\mathrm{Pic}^G(S)=\mathbb {Z}^2\).
The main result about 2-dimensional G-Sarkisov link is the following:
Theorem 2.2
([5]) Let \(S,S'\) be 2-dimensional G-Mori fibre spaces and let \(\chi :S \dashrightarrow S'\) be a non-biregular G-birational map. Then \(\chi \) is a composition of elementary links known as G-Sarkisov links.
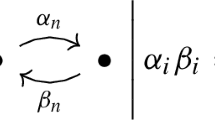
There are five different G-Sarkisov links of dimension 2 which are described below. The first type is given by

where S and \(S'\) are G-minimal del Pezzo surfaces and \(\alpha \) and \(\beta \) are blow-ups of G-orbits in S and \(S'\) respectively. The second type is given by

where S is a G-minimal del Pezzo surface, \(\alpha \) is a blow-up of a G-orbit and \(\beta \) is a G-conic bundle. The third type is given by

where \(S'\) is a G-minimal del Pezzo surface, \(\beta \) is a blow-up of a G-orbit and \(\alpha \) is a G-conic bundle. We shall notice that this is the inverse link of type (II). The fourth type is given by

where \(\alpha \) and \(\beta \) are G-conic bundles. Finally, the fifth type is given by

where S and \(S'\) are not G-minimal del Pezzo surfaces and \(\alpha \) and \(\beta \) are blow-ups of G-orbits in S and \(S'\) respectively. Additionally, \(\pi \) and \(\pi '\) are G-conic bundles and we call the whole link an elementary transformation of G-conic bundles (see [9]). This diagram commutes.
The notion of G-Sarkisov links is a good way to replace the technical result of the Noether–Fano inequality (see [6, 10]).
Remark 2.3
It follows from the definition of G-links that \(\widehat{S}\) is a del Pezzo surface if S is a del Pezzo surface. Thus in the links of type (I), (II), (III) and (IV), the surface \(\widehat{S}\) is a del Pezzo surface.
Using the notion of G-Sarkisov links we are able to restate Theorem 1.1.
Theorem 2.4
Let \(S_5\) be the smooth del Pezzo surface of degree 5, and let  be a subgroup of order 20 in
be a subgroup of order 20 in  . Then \(\mathrm{Pic}^{G_{20}}(S_5)=\mathbb {Z}\) and the following assertions hold:
. Then \(\mathrm{Pic}^{G_{20}}(S_5)=\mathbb {Z}\) and the following assertions hold:
-
1.
There exists a unique \(G_{20}\)-Sarkisov link that starts at \(S_5\). It is given by
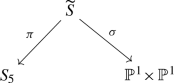 (1)
(1)where \(\pi \) is the blow-up of the unique \(G_{20}\)-orbit of length 2 in \(S_5\), \(\sigma \) is a blow-up of one of two \(G_{20}\) orbits of length 5 and \(\widetilde{S}\) is the Clebsch cubic surface.
-
2.
Let
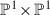 be equipped with the \(G_{20}\)-action coming from (1). Then the only \(G_{20}\)-Sarkisov links starting from
be equipped with the \(G_{20}\)-action coming from (1). Then the only \(G_{20}\)-Sarkisov links starting from 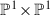 are the inverse of (1) and
are the inverse of (1) and 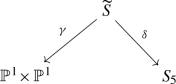 (2)
(2)where \(\gamma \) is the blow-up of another \(G_{20}\)-orbit of length 5, \(\widetilde{S}\) is the Clebsch cubic surface and \(\delta =\pi \) is the blow-up of the unique \(G_{20}\)-orbit of length 2 in \(S_5\).
Combining (1) and (2) yields a non-biregular \(G_{20}\)-birational map  .
.
These links were constructed and described numerically by Dolgachev and Iskovskikh in [7, Proposition 7.13] but for our purposes we reconstruct them here and will fill in the details for these links.
3 Motivation
In this section, we want to motivate Theorem 1.1. There are various different starting points to investigate conjugacy in the Cremona group. We decided to start our research on del Pezzo surfaces. Those surfaces have been introduced by Pasquale del Pezzo in the late 18th century and since then various ways of studying them have been encountered.
For our purposes we will understand a del Pezzo surface of degree d, denoted by \(S_d\), as the blow-up of  in \(9-d\) points in general position. To start our investigation of conjugacy classes of the Cremona group we need to introduce the notion of G-birational (super-) rigidity.
in \(9-d\) points in general position. To start our investigation of conjugacy classes of the Cremona group we need to introduce the notion of G-birational (super-) rigidity.
Definition 3.1
Let S be a smooth del Pezzo surface and  be a finite group such that \(\mathrm{Pic}^G(S)=\mathbb {Z}\). We say S is G-birationally rigid whenever
be a finite group such that \(\mathrm{Pic}^G(S)=\mathbb {Z}\). We say S is G-birationally rigid whenever
-
(a)
if S is G-birational to any G-minimal del Pezzo surface \(S'\), then \(S'\) is G-biregular to S, and
-
(b)
S is not G-birational to any G-conic bundle.
Condition (a) is equivalent to saying that for any birational G-map \(\chi :S \dashrightarrow S'\), where \(S'\) is a G-minimal del Pezzo surface, there exists a G-birational automorphism \(\theta :S \dashrightarrow S\) such that \(\chi {\circ } \theta \) is a G-isomorphism.
Definition 3.1 means, that the only G-Sarkisov links starting in S are of the form

where \(\alpha \) and \(\beta \) are blow-ups of G-orbits.
Definition 3.2
Let S be a smooth del Pezzo surface and  be a finite group such that \(\mathrm{Pic}^G(S)=\mathbb {Z}\). The surface S is G-birationally superrigid if it is G-birationally rigid and \(\text {Bir}^G(S)=\mathrm{Aut}^G(S)\).
be a finite group such that \(\mathrm{Pic}^G(S)=\mathbb {Z}\). The surface S is G-birationally superrigid if it is G-birationally rigid and \(\text {Bir}^G(S)=\mathrm{Aut}^G(S)\).
Definition 3.2 means that there are no G-Sarkisov links starting at S. With these definitions in hand we are able to state.
Theorem 3.3
([7]) Let S be a smooth del Pezzo surface of degree d, that is \(K_S^2=d\), and let  be such that \(\mathrm{Pic}^G(S)=\mathbb {Z}\). Then the following assertions hold:
be such that \(\mathrm{Pic}^G(S)=\mathbb {Z}\). Then the following assertions hold:
-
(a)
If S does not contain a G-orbit of length less then d, then S is G-birationally superrigid.
-
(b)
If S does not contain a G-orbit of length less then \(d-2\), then S is G-birationally rigid.
Sketched Proof Assume \(\widehat{S}\) is a smooth del Pezzo surface. Then by Remark 2.3, \(\alpha :S \rightarrow \widehat{S}\) is a blow-up of a G-orbit of length less then d, because \(K_{\widehat{S}}>0\). This proves (a).
If there is a G-orbit of length \(d-1\), the blow-up of this orbit is \(\widehat{S}=S_1\), the del Pezzo surface of degree 1, so we can use the Bertini involution there. Similarly, if there exists a G-orbit of length \(d-2\), the del Pezzo surface of degree 2, we can blow up this orbit to obtain \(\widehat{S}=S_2\), and we can use the Geiser involution. This proves (b). \(\square \)
From Theorem 3.3 we can immediately deduce the following corollary.
Corollary 3.4
([7]) Let S be a smooth del Pezzo surface of degree \(d <3\), and let  be a finite group such that \(\mathrm{Pic}^G(S)=\mathbb {Z}\). If S is of degree 1, then S is G-birationally superrigid. If S is of degree 2 or 3, then S is G-birationally rigid.
be a finite group such that \(\mathrm{Pic}^G(S)=\mathbb {Z}\). If S is of degree 1, then S is G-birationally superrigid. If S is of degree 2 or 3, then S is G-birationally rigid.
This result is known for quite some time and was implicitly proven by Segre in 1943 and Manin in 1962. For proofs of Theorem 3.3 and Corollary 3.4 see [7, Section 7.1]. The proof of Theorem 3.3 easily implies
Theorem 3.5
([7]) Let S be a smooth del Pezzo surface of degree 4, and let  be a finite group such that \(\mathrm{Pic}^G(S)=\mathbb {Z}\). Then
be a finite group such that \(\mathrm{Pic}^G(S)=\mathbb {Z}\). Then
-
1.
if there are no G-fixed points, then S is G-birational rigid,
-
2.
if there exists a G-fixed point, then there exists a G-Sarkisov link
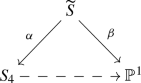
where \(\alpha \) is the blow-up of a G-orbit, \(\widetilde{S}\) is a smooth cubic surface and \(\beta \) is a conic bundle.
In this paper, we are mostly interested in G-birational rigid del Pezzo surfaces or those which are close to them. By close we mean that these are del Pezzo surfaces which are not G-birational to any conic bundle (in the language of [1] these are G-solid del Pezzo surfaces).
Following Corollary 3.4 and Theorem 3.5 we will investigate links starting from the smooth del Pezzo surface of degree 5, which we will call \(S_5\), in this paper. It is well known that

the symmetric group of five elements. A proof is provided in [4] . If we want \(S_5\) to be a G-minimal surface (i.e., \(\mathrm{Pic}^G(S_5)=\mathbb {Z}\)), we require G to be one of the following (see [7, Theorem 6.4]):
-
the symmetric group \(\mathfrak {S}_5\) of five elements of order 120;
-
the alternating group \(\mathfrak {A}_5\) of five elements of order 60;
-
the semidirect product
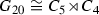 of order 20;
of order 20; -
the dihedral group \(D_{10}\) of order 10;
-
the cyclic group \(C_5\) of order 5.
For \(\mathfrak {S}_5\) and \(\mathfrak {A}_5\) the quintic del Pezzo surface is G-birationally superrigid (see [2]). For \(C_5\) there exists a G-birational map from \(S_5\) to  (see [3]) such that \(C_5\) has a fixed point there (see Lemma 4.1). The construction of this map can be generalised for \(D_{10}\) which is done in Corollary 4.2. Hence these groups are better addressed when studying the G-equivariant birational geometry of
(see [3]) such that \(C_5\) has a fixed point there (see Lemma 4.1). The construction of this map can be generalised for \(D_{10}\) which is done in Corollary 4.2. Hence these groups are better addressed when studying the G-equivariant birational geometry of  . This has been done in [12]. We shall also notice that \(S_5\) is not G-solid in this case.
. This has been done in [12]. We shall also notice that \(S_5\) is not G-solid in this case.
In this paper we will therefore focus on the group  as a subgroup of
as a subgroup of  , which is also known as the general affine group of degree 1 over the field with five elements, denoted by
, which is also known as the general affine group of degree 1 over the field with five elements, denoted by  .
.
4 The quintic del Pezzo surface
In the proof of Theorem 2.4 we will investigate the existence of \(G_{20}\)-equivariant birational maps between quintic del Pezzo surface, denoted by \(S_5\), and the surface  . First we need to understand the action of \(G_{20}\) on \(S_5\). To do this we use the following result from [3].
. First we need to understand the action of \(G_{20}\) on \(S_5\). To do this we use the following result from [3].
Lemma 4.1
([3]) There is a \(C_5\)-birational map \(\phi \) (i.e., a \(C_5\)-Sarkisov link) between \(S_5\) and  given by the \(C_5\)-commutative diagram
given by the \(C_5\)-commutative diagram

Here \(\alpha \) is the blow-up of a \(C_5\)-fixed point in \(S_5\), and \(\beta \) is the blow-up of five points in  which form a \(C_5\)-orbit. \(S_4\) is a quartic del Pezzo surface.
which form a \(C_5\)-orbit. \(S_4\) is a quartic del Pezzo surface.
Proof
For the proof we will start with  and invert the link (\(\blacktriangle \)). Consider \(C_5\) as a subgroup of
and invert the link (\(\blacktriangle \)). Consider \(C_5\) as a subgroup of  . There exists a \(C_5\)-equivariant Veronese embedding
. There exists a \(C_5\)-equivariant Veronese embedding  which defines a faithful action of \(C_5\) on
which defines a faithful action of \(C_5\) on  such that there exists a \(C_5\)-invariant conic
such that there exists a \(C_5\)-invariant conic  (that is the image of
(that is the image of  ). Thus we can blow up the \(C_5\)-orbit of length 5 on this conic to obtain the quartic del Pezzo surface, denoted by \(S_4\).
). Thus we can blow up the \(C_5\)-orbit of length 5 on this conic to obtain the quartic del Pezzo surface, denoted by \(S_4\).
If we contract the the proper transform of K there we get the unique quintic del Pezzo surface. Since  is unique up to conjugation the composition of the two described maps yields the desired link \(\phi \).
is unique up to conjugation the composition of the two described maps yields the desired link \(\phi \).
In more elementary terms, we may say that five points \(P_1,\ldots ,P_5\) in general position in \(\mathbb {P}^2\) always lie on a unique conic K. Then the group \(C_5\) fixes two points \(A_1\), \(A_2\) on a conic [4] (i.e., the line through these two points is \(C_5\)-invariant). Additionally, it fixes a point  which does not lie on the conic. The blow-up \(\alpha \) of \(P_1, \ldots , P_5\) does not affect B, neither does the contraction \(\beta \). Thus there is a point
which does not lie on the conic. The blow-up \(\alpha \) of \(P_1, \ldots , P_5\) does not affect B, neither does the contraction \(\beta \). Thus there is a point
which is fixed by \(C_5\). We know that \(\alpha ^{-1}(K)\) is a \(\beta \)-exceptional curve in \(S_4\). After the contraction \(\beta \), we have
which is another fixed point of \(C_5\) in \(S_5\). Thus we know that for  there exist two \(C_5\)-fixed points \(Q_1\) and \(Q_2\). We shall mention that all other orbits are of length 5. \(\square \)
there exist two \(C_5\)-fixed points \(Q_1\) and \(Q_2\). We shall mention that all other orbits are of length 5. \(\square \)
From the proof of Lemma 4.1 we can easily deduce.
Corollary 4.2
There is a \(D_{10}\)-birational map \(\phi \) (i.e., a \(D_{10}\)-Sarkisov link) between \(S_5\) and  corresponding to the \(D_{10}\)-commutative diagram (\(\blacktriangle \)).
corresponding to the \(D_{10}\)-commutative diagram (\(\blacktriangle \)).
Proof
In the same way as in the proof of Lemma 4.1 we can construct the inverse link of (\(\blacktriangle \)). Furthermore the action of  lifts to an action on
lifts to an action on  . Then we can use the same argument as before.
. Then we can use the same argument as before.
In the notation of the proof of Lemma 4.1 we may say that the action of \(D_{10}\) on  interchanges the points \(A_1\) and \(A_2\) but fixes the point B. Thus we can use the same link \(\phi \) as in Lemma 4.1 and by the same argument as above \(D_{10}\) fixes points \(Q_1\) and \(Q_2\) in \(S_5\). \(\square \)
interchanges the points \(A_1\) and \(A_2\) but fixes the point B. Thus we can use the same link \(\phi \) as in Lemma 4.1 and by the same argument as above \(D_{10}\) fixes points \(Q_1\) and \(Q_2\) in \(S_5\). \(\square \)
We are now in the position to investigate orbits of small length \(r < 5\) of the \(G_{20}\)-action on \(S_5\).
We want to proceed in a similar way as in [11] which means that we need to classify all G-orbits of length  . Then we will concentrate on those orbits of which the points are in general position, because this is a necessary condition for the existence of links starting from the surface \(S_5\).
. Then we will concentrate on those orbits of which the points are in general position, because this is a necessary condition for the existence of links starting from the surface \(S_5\).
Remark 4.3
We say that points of an orbit are in general position if the blow-up of \(S_5\) in this orbit is a del Pezzo surface again.
Lemma 4.4
There is a unique \(G_{20}\)-orbit of length \(r <5\) on \(S_5\). It is the orbit of length \(r=2\) consisting of the points \(Q_1\) and \(Q_2\).
Proof
Let us consider all possible lengths for orbits.
\(r=1\): Such an orbit does not exist. Assume it does. By Lemma 4.1 and Corollary 4.2, this point can only be \(Q_1\), because if all of \(G_{20}\) fixes it, the normal subgroups \(C_5\) and \(D_{10}\) fix it in particular. Hence the link (\(\blacktriangle \)) yields \(G_{20}\)-equivariant link from \(S_5\) to  . This means that \(G_{20}\) acts on
. This means that \(G_{20}\) acts on  and preserves the conic K. This implies that \(G_{20}\) acts faithfully on
and preserves the conic K. This implies that \(G_{20}\) acts faithfully on  , but this is clearly a contradiction. Hence no orbit of length \(r=1\) exists.
, but this is clearly a contradiction. Hence no orbit of length \(r=1\) exists.
\(r=2\): \(\{ Q_1,Q_2\}\) is such an orbit. We know that \(G_{20}\) has \(D_{10}\) as a normal subgroup. If we consider the action of \(D_{10}\) on \(S_5\), then Corollary 4.2 tells us that there is indeed a unique orbit of length 2 which is the orbit \(\{Q_1,Q_2 \}\).
\(r=3\): Such an orbit does not exist because \(3\not \mid 20 = |G_{20}|\), which is required by the orbit-stabilizer theorem.
\(r=4\): Such an orbit does not exist. If there were such an orbit the stabilizer would satisfy  but we know that \(C_5\) actually fixes the same points as \(D_{10}\) by Theorem 4.2 and hence the stabilizer would actually be \(D_{10}\) which cannot give an orbit of length 4. \(\square \)
but we know that \(C_5\) actually fixes the same points as \(D_{10}\) by Theorem 4.2 and hence the stabilizer would actually be \(D_{10}\) which cannot give an orbit of length 4. \(\square \)
Lemma 4.4 implies that the only possible \(G_{20}\)-Sarkisov link starting from \(S_5\) consists of a blow-up of the described orbit of length \(r=2\).
Lemma 4.5
The blow-up of \(Q_1\) and \(Q_2\) in \(S_5\) yields a smooth del Pezzo surface \(\widetilde{S}\).
Proof
We need to prove that \(-K_{\widetilde{S}}\) is ample. This is equivalent to saying that \(Q_1\) and \(Q_2\) neither lie on the \((-1)\)-curves nor in an exceptional conic in \(S_5\). We prove this by contradiction. For this we will consider different cases.
-
We first prove that there are no \((-1)\)-curves containing \(Q_1\) or \(Q_2\). Assume \(Q_1\) lies on one of the 10 exceptional curves in \(S_5\). Clearly \(Q_2\) needs to lie on such a curve as well. If they lie on two different exceptional curves these two are interchanged by the group action of \(G_{20}\). This contradicts the fact that \(\mathrm{Pic}^{G_{20}}(S_5)=\mathbb {Z}\).
Similarly, we may assume that \(Q_1\) lies on one of the intersections of two exceptional curves. Again this contradicts \(\mathrm{Pic}^{G_{20}}(S_5)=\mathbb {Z}\). So indeed \(Q_1\) and \(Q_2\) do not lie on the \((-1)\)-curves in \(S_5\) which proves that the blow-up of these two points yields another del Pezzo surface.
-
It remains to show that \(Q_1\) and \(Q_2\) are not contained in an exceptional conic \(S_5\). There are five classes of conic in \(S_5\) and each of them has self-intersection
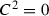 . Going through all these cases in detail one can show that \(Q_1\) and \(Q_2\) either lie on one line which we ruled out previously or they cannot lie on one conic. Due to heavy computational work we omit the different cases at this point. \(\square \)
. Going through all these cases in detail one can show that \(Q_1\) and \(Q_2\) either lie on one line which we ruled out previously or they cannot lie on one conic. Due to heavy computational work we omit the different cases at this point. \(\square \)
The resulting surface of this blow-up will have degree \(5-2=3\), so it is a cubic surface. The only smooth cubic surface with a \(G_{20}\)-action is the Clebsch cubic surface (this was proved in [8]) which we will investigate in the next section.
5 The Clebsch cubic surface
Theorem 2.4 states that the only G-Sarkisov links starting from the quintic del Pezzo surface \(S_5\) are of the form

From Lemma 4.4 we know that \(\pi \) is the blow-up of the unique \(G_{20}\)-orbit \(\{Q_1, Q_2\}\) of length 2. Hence \(\widetilde{S}\) is the Clebsch cubic surface, which is defined as follows:
Definition 5.1
The Clebsch cubic surface, denoted by \(\widetilde{S}\), is a cubic given by two defining equations in  :
:
Remark 5.2
In [7] it is shown that \(\mathrm{Pic}^{G_{20}}(\widetilde{S})\ne \mathbb {Z}\). The link (\(\blacklozenge \)) proves that in fact, \(\mathrm{Pic}^{G_{20}}(\widetilde{S})=\mathbb {Z}^2\).
Now it is well known that the automorphism group of the Clebsch cubic surface is \(\mathfrak {S}_5\). Thus the action of \(G_{20}\) can be described very explicitly by understanding \(G_{20}\) as a subgroup of \(\mathfrak {S}_5\) acting by permutation on the coordinates of this surface.
We know that all representations of \(G_{20}\) are conjugate to each other and thus we will use a generation by \(\sigma _{(12345)}\) and \(\sigma _{(2354)}\), where we use the notation introduced in [4]. Considering orbits of length 4 on \(\widetilde{S}\) we obtain
Lemma 5.3
There is a unique orbit of length 4 of the \(G_{20}\)-action on the Clebsch cubic surface given by the points

with \(\zeta \) being a primitive fifth root of unity.
Proof
An orbit of length 4 has the stabilizer \({\text {Stab}}_G = K \cong C_5\) which is isomorphic to the group generated by \(\sigma _{(12345)}\), which is the unique subgroup of \(G_{20}\) isomorphic to \(C_5\). It has exactly the fixed points as stated in Lemma 5.3, which are obtained by straightforward calculations. It is easy to verify that these four points lie indeed on \(\widetilde{S}\) and form an orbit of length 4. \(\square \)
The orbits of length 5 are a bit more sophisticated.
Lemma 5.4
There are three orbits of length 5 of the \(G_{20}\)-action on the Clebsch cubic surface given by:

Proof
An orbit of length 5 has the stabilizer  in \(G_{20}\). There are five subgroups of \(G_{20}\) which are isomorphic to \(C_4\). Let \(H \cong C_4\) be the subgroup generated by \(\sigma _{(2354)}\). Then H fixes four points in
in \(G_{20}\). There are five subgroups of \(G_{20}\) which are isomorphic to \(C_4\). Let \(H \cong C_4\) be the subgroup generated by \(\sigma _{(2354)}\). Then H fixes four points in  with
with  which are
which are

whereas the \(R_4\) does not lie on \(\widetilde{S}\) because the cubes of the coordinates do not sum to zero. Again it is easy to verify that the points \((R_1,\ldots ,R_4)\) are indeed fixed points. Acting by an element of order 5, we obtain fixed points corresponding to the action of \(\sigma _{(12345)}\) on the coordinates of \(R_i\). Thus we deduce, that there are three orbits of length 5 on \(\widetilde{S}\) as stated in Lemma 5.4. \(\square \)
We shall notice that \(R_2\) and \(R_3\) lie on the line \(x_1+x_4=x_2+x_3=0\). Generalising this we make the following important observation.
Corollary 5.5
The points  and
and  respectively lie on one of the 27 real lines on the Clebsch cubic surfaces. These five resulting lines in the link are:
respectively lie on one of the 27 real lines on the Clebsch cubic surfaces. These five resulting lines in the link are:
-
(i)
\(L_1:x_1+x_4=x_2+x_3=0\) through \(U_1\) and \(W_1\).
-
(ii)
\(L_2:x_0+x_2=x_3+x_4=0\) through \(U_2\) and \(W_2\).
-
(iii)
\(L_3:x_0+x_4=x_1+x_3=0\) through \(U_3\) and \(W_3\).
-
(iv)
\(L_4:x_0+x_1=x_2+x_4=0\) through \(U_4\) and \(W_4\).
-
(v)
\(L_5:x_0+x_3=x_1+x_2=0\) through \(U_5\) and \(W_5\).
It is easy to see that these five lines are disjoint.
Proof
This is an easy exercise of calculating the lines through each pair of points and comparing it with the lines on the Clebsch cubic, which are well known. \(\square \)
Lemmas 5.3 and 5.4 allow us to state the main result for this section.
Proposition 5.6
Let \(\widetilde{S}\) be the Clebsch cubic surface. Then the \(G_{20}\)-orbits of length \(r < 8\) on \(\widetilde{S}\) are:
-
(a)
The unique orbit
 described in Lemma 5.3 of length 4.
described in Lemma 5.3 of length 4. -
(b)
The three orbits
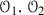 and
and 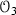 described in Lemma 5.4 of length 5.
described in Lemma 5.4 of length 5.
Proof
The orbit-stabilizer theorem tells us immediately that orbits of length \(r=6\) or \(r=7\) cannot exist. It remains to show that there are no orbits of length 1 or 2 on \(\widetilde{S}\). This follows directly from our description of the orbits but we include computational explanation, too. An orbit of length 1 would have the whole group \(G_{20}\) as its stabilizer. We see immediately that this is not possible because the subgroups K and H generated by \(\sigma _{(12345)}\) and \(\sigma _{(2354)}\) have completely different fixed points.
By a similar argument, there cannot be any orbits of length 2. These would have the subgroup \(F \cong D_{10}\) generated by \(\sigma _{(12345)}\) and \(\sigma _{(25)(34)}\) as its stabilizer. Again it is easy to verify that F has \(K\cong C_5\) as a subgroup. On the other hand F has the group generated isomorphic to \(C_2\) generated by \(\sigma _{(25)(34)}\) which is a subgroup of H as a subgroup.
But we have seen that H and K do not have any common fixed points. Hence F cannot have fixed points which means that there does not exist an orbit of length 2. \(\square \)
Remark 5.7
Proposition 5.6 supports the statement of Lemma 4.4. For the unique orbit  of length 4 each pair of points lies on one of 27 real lines on the Clebsch cubic. Hence after contracting two of them to obtain \(S_5\), we are left with an orbit of length 2.
of length 4 each pair of points lies on one of 27 real lines on the Clebsch cubic. Hence after contracting two of them to obtain \(S_5\), we are left with an orbit of length 2.
An orbit of length 4 in \(S_5\) would lift to a different orbit of length 4 in \(\widetilde{S}\), but for the given reason this cannot be  , which means that there do not exist orbits of length 4 in the quintic del Pezzo surface.
, which means that there do not exist orbits of length 4 in the quintic del Pezzo surface.
Given Corollary 5.5, we may consider the contraction of these five lines.
Proposition 5.8
The contraction of the five lines \(L_1,\ldots ,L_5\) described in Corollary 5.5 yields the surface  and this is the only other contraction that can be conducted apart from the inverse of the blow-up from \(S_5\).
and this is the only other contraction that can be conducted apart from the inverse of the blow-up from \(S_5\).
Proof
We know that \(\widetilde{S}\) is a del Pezzo surface, so \(-K_{\widetilde{S}}\) is ample. Remark 2.3 tells us that the resulting surface of the described contraction will be a del Pezzo surface of degree \(3+5=8\), so it can only be  or \(\mathbb {F}_1\), but \(\mathrm{Pic}^{G_{20}}(\mathbb {F}_1) \ne \mathbb {Z}\), which we require.
or \(\mathbb {F}_1\), but \(\mathrm{Pic}^{G_{20}}(\mathbb {F}_1) \ne \mathbb {Z}\), which we require.
In Remark 5.2 we have seen that \(\mathrm{Pic}^{G_{20}}(\widetilde{S})=\mathbb {Z}^2\). From this we conclude that there are two external rays in the Mori cone. We have shown that one consists of two lines and the other one of five. These are the only possible contraction of \(\widetilde{S}\). \(\square \)
Proposition 5.8 allows us to state the following lemma about the link (\(\blacklozenge \)) which we introduced at the beginning of this section.
Lemma 5.9
Considering the desired link (\(\blacklozenge \)) from \(S_5\) to  , we know
, we know
-
1.
\(\pi \) is the contraction of two disjoint lines \(E_1, E_2\) in the Clebsch cubic surface (respectively the blow-up of \(Q_1\) and \(Q_2\) in \(S_5\)).
-
2.
\(\sigma \) is the contraction of five disjoint lines \(F_1,\ldots ,F_5\) in the Clebsch cubic surface (respectively the blow-up of five points in
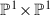 ).
). -
3.
The following equations hold for the exceptional divisors:
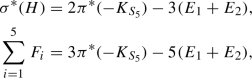
where \(-K_{S_5}\) is the anticanonical divisor of \(S_5\), \(E_1+E_2\) are the two \((-1)\)-curves of the blow-up of \(Q_1\) and \(Q_2\), H is a divisor of bidegree (1, 1) on
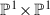 and
and 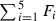 are the \((-1)\)-curves of the blow-up of five points in
are the \((-1)\)-curves of the blow-up of five points in 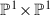 .
.
Lemma 5.9 implies that \(\pi (F_i)\) is a smooth twisted cubic curve in \(S_5\) and \(E_1\) and \(E_2\) are smooth twisted cubics of bidegree (2, 1) and (1, 2) respectively.
6 The surface 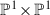
The \(G_{20}\)-action on  cannot be understood in a way which is as simple as in Sect. 4 or Sect. 5. For that reason, we will use our previous observations to analyse the \(G_{20}\)-orbits on
cannot be understood in a way which is as simple as in Sect. 4 or Sect. 5. For that reason, we will use our previous observations to analyse the \(G_{20}\)-orbits on  .
.
Lemma 6.1
There is a unique \(G_{20}\)-orbit  of length 4 in
of length 4 in  . The four points are given by the intersections \(F_{11} \cap F_{21}, F_{11} \cap F_{22}, F_{12} \cap F_{21}\) and \(F_{12} \cap F_{22}\) of the four rulings \(F_{11}, F_{12}, F_{21}\) and \(F_{22}\).
. The four points are given by the intersections \(F_{11} \cap F_{21}, F_{11} \cap F_{22}, F_{12} \cap F_{21}\) and \(F_{12} \cap F_{22}\) of the four rulings \(F_{11}, F_{12}, F_{21}\) and \(F_{22}\).
Proof
The orbit of length 4 described in Lemma 5.3 lies away from the lines of contraction, thus it has an embedding in  .
.
Generally, four points need eight different lines to describe them. A \(G_{20}\)-orbit of length 4 has the stabilizer \(C_5\). But we know that  acts on the rulings of
acts on the rulings of  which are copies of
which are copies of  . Hence the \(C_5\)-action cannot split over each of the four points (i.e., interchanging the two lines) but fixes the rulings.
. Hence the \(C_5\)-action cannot split over each of the four points (i.e., interchanging the two lines) but fixes the rulings.
For this reason, the four points on the \(G_{20}\)-orbit need to lie on the four intersections of four copies of  (i.e., the rulings of
(i.e., the rulings of  ), because otherwise it would not be an orbit of length 4. Hence all four points in this orbit lie on two rulings in
), because otherwise it would not be an orbit of length 4. Hence all four points in this orbit lie on two rulings in  . \(\square \)
. \(\square \)
Remark 6.2
We could prove Lemma 6.1 in a different way by considering the orbit of length 4 in the Clebsch cubic surface and considering their configuration there. We can show merely computationally that there exist four conics each passing through exactly one of the four points and not intersecting the \((-1)\)-curves. Considering the blow-up \(\sigma \) we obtain Lemma 6.1 for the four points on  .
.
As in Sect. 5 the orbits of length 5 are a bit more difficult.
Lemma 6.3
There are exactly two \(G_{20}\)-orbits  and
and  of length 5 in
of length 5 in  .
.
Proof
We will now identify  as a quadric
as a quadric  in \(\mathbb {P}^3\). We know that
in \(\mathbb {P}^3\). We know that  has a natural embedding (Segre) into \(\mathbb {P}^3\). Similar to the Clebsch cubic we can understand \(\mathbb {P}^3\) as a hyperplane in \(\mathbb {P}^4\) with
has a natural embedding (Segre) into \(\mathbb {P}^3\). Similar to the Clebsch cubic we can understand \(\mathbb {P}^3\) as a hyperplane in \(\mathbb {P}^4\) with  . Now let
. Now let  be the quadric given by
be the quadric given by

\(G_{20}\) acts on  by permutations of coordinates in a similar way as described in the previous section for the Clebsch cubic.
by permutations of coordinates in a similar way as described in the previous section for the Clebsch cubic.
We found the orbits of length 5 explicitly on \(\widetilde{S}\). Observe that the orbits  and
and  lie in
lie in  , whereas
, whereas  does not. Hence we may assume
does not. Hence we may assume  and
and  .
.
Additionally, we can check computationally that the points of each of the orbits lie in general position (i.e., no two on a line in  and no four on a plane). Hence we can indeed consider the blow-up of each of these orbits which will yield the Clebsch cubic surface and together with Lemma 5.9 shows that this blow-up is indeed the inverse link of the described contraction.
and no four on a plane). Hence we can indeed consider the blow-up of each of these orbits which will yield the Clebsch cubic surface and together with Lemma 5.9 shows that this blow-up is indeed the inverse link of the described contraction.
Furthermore, we see that the orbits  and
and  are essentially the same orbits, only permuted by complex conjugation. In fact these two orbits are interchanged by an automorphism of a quadric which is proven in Theorem 7.3. \(\square \)
are essentially the same orbits, only permuted by complex conjugation. In fact these two orbits are interchanged by an automorphism of a quadric which is proven in Theorem 7.3. \(\square \)
Now we can finally state the last proposition we need for the proof of Theorem 1.1.
Proposition 6.4
The only \(G_{20}\)-orbits of length \(r < 8\) on  are:
are:
-
(a)
The unique orbit
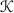 described in Lemma 6.1 of length 4.
described in Lemma 6.1 of length 4. -
(b)
The two orbits
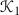 and
and 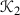 described in Lemma 6.3 of length 5 where the five points lie in general position.
described in Lemma 6.3 of length 5 where the five points lie in general position.
Proof
It remains to show that there are no other orbits than the ones described in Lemmas 6.1 and 6.3.
Orbits of length 6, 7 or 8 cannot exist by the orbit-stabilizer theorem as \(6,7,8 \not \mid 20=|G_{20}|\). Assume there is an orbit of length less than 4. Then an orbit of this length would also exist in the Clebsch cubic surface but Proposition 5.6 tells us, that they do not exist there. \(\square \)
7 Proof of Theorem 2.4
The link (1) in Theorem 2.4 is the only G-Sarkisov link starting from the quintic del Pezzo surface \(S_5\). From Lemma 4.4 we know that \(\pi \) is the blow-up of the unique \(G_{20}\)-orbit \(\{Q_1, Q_2\}\) of length 2.
Now Corollary 5.5 tells us that there are five disjoint lines on the Clebsch cubic which we can contract to obtain  and Proposition 6.4 says that we need to consider two different cases for birational maps starting from
and Proposition 6.4 says that we need to consider two different cases for birational maps starting from  .
.
Lemma 7.1
(orbit of length 4) Let  be the blow-up of the four points \(P_1,\ldots , P_4\) in the orbit
be the blow-up of the four points \(P_1,\ldots , P_4\) in the orbit  and let \(E_1,\ldots ,E_4\) be the corresponding exceptional curves. Then the proper transforms of the described rulings are \((-2)\)-curves. This means that the resulting surface \(\widehat{S}\) is not a del Pezzo surface.
and let \(E_1,\ldots ,E_4\) be the corresponding exceptional curves. Then the proper transforms of the described rulings are \((-2)\)-curves. This means that the resulting surface \(\widehat{S}\) is not a del Pezzo surface.
Proof
This follows immediately from Lemma 6.1. \(\square \)
Lemma 7.1 tells us that we cannot continue from \(\mathbb {P}^1 {\times } \mathbb {P}^1\) to obtain a G-Sarkisov link by blowing up the orbit  of length 4.
of length 4.
Lemma 7.2
Let  be a blow-up of the five points \(P_1,\ldots , P_5\) in the orbits
be a blow-up of the five points \(P_1,\ldots , P_5\) in the orbits  or
or  respectively. Then one of the following holds for \(\tau \):
respectively. Then one of the following holds for \(\tau \):
-
(a)
\(\tau \) is the same as the blow-up \(\sigma \) described in (\(\blacklozenge \)), so that
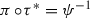 .
. -
(b)
\(\tau \) is the same as the blow-up \(\gamma \) described in diagram (2) of Theorem 2.4, so that
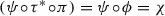 is a \(G_{20}\)-birational map \(S_5 \dashrightarrow S_5\).
is a \(G_{20}\)-birational map \(S_5 \dashrightarrow S_5\).
Proof
It is clear that we can obtain case (a) if we blow up the five points in  or
or  , i.e., \(\tau = \sigma \) in the link (\(\blacklozenge \)). We get back exactly the model of the Clebsch cubic we had before because the elements in
, i.e., \(\tau = \sigma \) in the link (\(\blacklozenge \)). We get back exactly the model of the Clebsch cubic we had before because the elements in  or
or  are the points we obtained by the contraction described in Lemma 5.9. For symmetric reasons, we may assume that these are the points in
are the points we obtained by the contraction described in Lemma 5.9. For symmetric reasons, we may assume that these are the points in  . Therefore
. Therefore  as described in (\(\blacklozenge \)).
as described in (\(\blacklozenge \)).
Proposition 6.4 tells us that the two orbits  and
and  are interchanged by an automorphism. Let us now consider the blow-up
are interchanged by an automorphism. Let us now consider the blow-up  of the orbit
of the orbit  , which is not the same blow-up as \(\sigma \). Then we may contract the two \((-1)\)-curves, \(E_1\) and \(E_2\), on the Clebsch cubic.
, which is not the same blow-up as \(\sigma \). Then we may contract the two \((-1)\)-curves, \(E_1\) and \(E_2\), on the Clebsch cubic.
This gives us back \(S_5\) because the smooth quintic del Pezzo surface is unique. This means that  is a birational map \(S_5 \dashrightarrow S_5\). We obtain that
is a birational map \(S_5 \dashrightarrow S_5\). We obtain that  as shown in (\(\clubsuit \)). This is a birational map \(S_5 \dashrightarrow S_5\) which is not biregular. \(\square \)
as shown in (\(\clubsuit \)). This is a birational map \(S_5 \dashrightarrow S_5\) which is not biregular. \(\square \)

Lemmas 7.1 and 7.2 tell us that there is no \(G_{20}\)-equivariant link starting from  , that leads to a different minimal surface than the quintic del Pezzo surface or
, that leads to a different minimal surface than the quintic del Pezzo surface or  itself. This together with Remark 5.2 finalises the proof of Theorem 2.4 and implies the first two parts of Theorem 1.1.
itself. This together with Remark 5.2 finalises the proof of Theorem 2.4 and implies the first two parts of Theorem 1.1.
In Theorem 2.4 we additionally stated that \(\mathrm{Bir}^{G_{20}}(S_5)\) is of order 40. In fact one can show that
Theorem 7.3
Let \(S_5\) be the smooth del Pezzo surface of degree 5, and let  be a subgroup of order 20 in
be a subgroup of order 20 in  . Then
. Then
where  .
.
Proof
We need to find the normalizer  . Obviously, it is enough to find \(G_{40} \cap H\), where H is the subgroup of
. Obviously, it is enough to find \(G_{40} \cap H\), where H is the subgroup of  which preserves rulings. Certainly, \(G_{40} \cap H\) lies inside the group \(\mathrm{Norm}_{H} (D_{10})\). The normalizer of \(D_{10}\) in
which preserves rulings. Certainly, \(G_{40} \cap H\) lies inside the group \(\mathrm{Norm}_{H} (D_{10})\). The normalizer of \(D_{10}\) in  is equal to \(D_{20}\) and generated by \(D_{10}\) and the involution
is equal to \(D_{20}\) and generated by \(D_{10}\) and the involution  . Thus \(G_{40}\cap H\) lies inside the group \(\langle D_{10}, a, b\rangle \), with
. Thus \(G_{40}\cap H\) lies inside the group \(\langle D_{10}, a, b\rangle \), with

One can easily check that only ab normalizes the group \(G_{20}\) and  . \(\square \)
. \(\square \)
This proof was communicated to me by Artem Avilov and I thank him for thus completing the proof of Theorem 1.1.
References
Ahmadinezhad, H., Okada, T.: Birationally rigid Pfaffian Fano 3-folds. Algebr. Geom. 5(2), 160–199 (2018)
Bannai, S., Tokunaga, H.: A note on embeddings of \(S_4\) and \(A_5\) into the two-dimensional Cremona group and versal Galois covers. Publ. Res. Inst. Math. Sci. 43(4), 1111–1123 (2007)
Beauville, A., Blanc, J.: On Cremona transformations of prime order. C. R. Math. Acad. Sci. Paris 339(4), 257–259 (2004)
Blanc, J.: Finite abelian subgroups of the Cremona group of the plane. C. R. Math. Acad. Sci. Paris 344(1), 21–26 (2007)
Corti, A.: Factoring birational maps of threefolds after Sarkisov. Appendix: surfaces over nonclosed fields. J. Algebraic Geom. 4(2), 223–254, 248–254 (1995)
Dolgachev, I.V.: Classical Algebraic Geometry. Cambridge University Press, Cambridge (2012)
Dolgachev, I.V., Iskovskikh, V.A.: Finite subgroups of the plane Cremona group. In: Tschinkel, Yu., Zarhin, Yu. (eds.) Algebra, Arithmetic, and Geometry, Vol. I. Progress in Mathematics, vol. 269, pp. 443–548. Birkhäuser, Boston (2009)
Hosoh, T.: Automorphism groups of cubic surfaces. J. Algebra 192(2), 651–677 (1997)
Iskovskikh, V.A.: Factorization of birational maps of rational surfaces from the viewpoint of Mori theory. Russian Math. Surv. 51(4), 585–652 (1996)
Iskovskikh, V.A.: On the Noether–Fano inequalities. In: Collino, A. (ed.) The Fano Conference, pp. 25–35. Università di Torino, Turin (2004)
Iskovskikh, V.A.: Two non-conjugate embeddings of \(S_3\times \mathbb{Z} _2\) into the Cremona group. II. In: Konno, K., Nguyen-Khac, V. (eds.) Algebraic Geometry in East Asia–Hanoi 2005. Advanced Studies in Pure Mathematics, vol. 50, pp. 251–267. Mathematical Society of Japan, Tokyo (2008)
Sakovics, D.: \(G\)-birational rigidity of the projective plane. Eur. J. Math. https://doi.org/10.1007/s40879-018-0261-x (2018). arXiv:1712.01587
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wolter, J. Equivariant birational geometry of quintic del Pezzo surface. European Journal of Mathematics 4, 1278–1292 (2018). https://doi.org/10.1007/s40879-018-0272-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0272-7



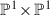 ,
,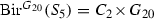 .
.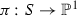 , where S is a smooth surface and the general fibre of
, where S is a smooth surface and the general fibre of 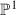 such that
such that 
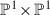 be equipped with the
be equipped with the 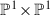 are the inverse of (
are the inverse of (

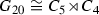 of order 20;
of order 20;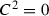 . Going through all these cases in detail one can show that
. Going through all these cases in detail one can show that  described in Lemma
described in Lemma 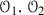 and
and 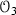 described in Lemma
described in Lemma 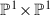 ).
).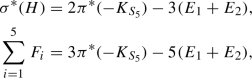
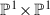 and
and  are the
are the  .
.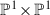
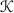 described in Lemma
described in Lemma 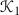 and
and 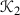 described in Lemma
described in Lemma 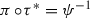 .
.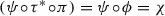 is a
is a