Abstract
We study the moduli space of triples \((C, L_1, L_2)\) consisting of quartic curves C and lines \(L_1\) and \(L_2\). Specifically, we construct and compactify the moduli space in two ways: via geometric invariant theory (GIT) and by using the period map of certain lattice polarized K3 surfaces. The GIT construction depends on two parameters \(t_1\) and \(t_2\) which correspond to the choice of a linearization. For \(t_1=t_2=1\) we describe the GIT moduli explicitly and relate it to the construction via K3 surfaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The construction of compact moduli spaces with geometric meanings is an important problem in algebraic geometry. In this article, we discuss the case of the moduli of K3 surfaces of degree 2 obtained as minimal resolutions of double covers of  branched at a quartic C and two lines \(L_1,L_2\), for which we give two constructions, one via Geometric Invariant Theory (GIT) for the plane curves \((C, L_1, L_2)\) depending on a choice of two parameters for each of the lines, and one via the period map of K3 surfaces. For a particular choice of parameters, we show that the constructions agree. Similar examples include [1, 2, 17, 18, 22, 23, 30]. Our interest on this example arose after the first two authors considered studying the variations of GIT quotients for a cubic surface and a hyperplane section [12]. The moduli of del Pezzo surfaces of degree 2 with two anti-canonical sections seems to be closely related to the moduli of K3 surfaces considered in this article, since del Pezzo surfaces of degree 2 with canonical singularities can be obtained as double-covers of
branched at a quartic C and two lines \(L_1,L_2\), for which we give two constructions, one via Geometric Invariant Theory (GIT) for the plane curves \((C, L_1, L_2)\) depending on a choice of two parameters for each of the lines, and one via the period map of K3 surfaces. For a particular choice of parameters, we show that the constructions agree. Similar examples include [1, 2, 17, 18, 22, 23, 30]. Our interest on this example arose after the first two authors considered studying the variations of GIT quotients for a cubic surface and a hyperplane section [12]. The moduli of del Pezzo surfaces of degree 2 with two anti-canonical sections seems to be closely related to the moduli of K3 surfaces considered in this article, since del Pezzo surfaces of degree 2 with canonical singularities can be obtained as double-covers of  branched at a (possibly singular) quartic curve. Also, a generic global Torelli for certain double covers of these K3 surfaces (namely, minimal resolutions of bi-double covers of
branched at a (possibly singular) quartic curve. Also, a generic global Torelli for certain double covers of these K3 surfaces (namely, minimal resolutions of bi-double covers of  along a quartic and four lines, cf. [14, Section 5.4.2]) can be derived using the results in this article and the methods in [28].
along a quartic and four lines, cf. [14, Section 5.4.2]) can be derived using the results in this article and the methods in [28].
Following the general theory of variations of GIT quotients developed by Dolgachev and Hu [9] and independently by Thaddeus [32], we construct GIT compactifications  for the moduli space of triples \((C, L_1, L_2)\) consisting of a smooth plane quartic curve C and two labeled lines \(L_1,L_2\) in Sect. 2. These compactifications depend on parameters \(t_1,t_2\) which are the ratio polarizations of the parameter spaces of quartic and linear homogeneous forms representing C and \(L_1,L_2\). We generalize the study in [13] of GIT quotients of pairs (X, H) formed by a hypersurface X of degree d in
for the moduli space of triples \((C, L_1, L_2)\) consisting of a smooth plane quartic curve C and two labeled lines \(L_1,L_2\) in Sect. 2. These compactifications depend on parameters \(t_1,t_2\) which are the ratio polarizations of the parameter spaces of quartic and linear homogeneous forms representing C and \(L_1,L_2\). We generalize the study in [13] of GIT quotients of pairs (X, H) formed by a hypersurface X of degree d in  and a hyperplane H to tuples \((X, H_1, \ldots , H_k)\) with several hyperplanes \(H_i\), considering the relation between the moduli spaces of tuples with labeled and unlabeled hyperplanes. We then apply the setting to the case at hand, namely plane quartic curves and two lines. One sees in Lemma 2.9 that the space where the set of stable points is not empty can be precisely described. Furthermore, given a particular tuple, we can bound the set of parameters for which it is semistable (cf. Lemma 2.11).
and a hyperplane H to tuples \((X, H_1, \ldots , H_k)\) with several hyperplanes \(H_i\), considering the relation between the moduli spaces of tuples with labeled and unlabeled hyperplanes. We then apply the setting to the case at hand, namely plane quartic curves and two lines. One sees in Lemma 2.9 that the space where the set of stable points is not empty can be precisely described. Furthermore, given a particular tuple, we can bound the set of parameters for which it is semistable (cf. Lemma 2.11).
Next we focus on the case when \(t_1=t_2=1\). The moduli space  can also be constructed via Hodge theory (cf. Sect. 3). The idea is to consider the K3 surface \(S_{(C, L_1, L_2)}\) obtained by taking the desingularization of the double cover \(\overline{S}_{(C,L_1,L_2)}\) of
can also be constructed via Hodge theory (cf. Sect. 3). The idea is to consider the K3 surface \(S_{(C, L_1, L_2)}\) obtained by taking the desingularization of the double cover \(\overline{S}_{(C,L_1,L_2)}\) of  branched along the sextic curve \(C+L_1+L_2\). Note that generically \(\overline{S}_{(C,L_1,L_2)}\) admits nine ordinary double points (coming from the intersection points \(C \cap L_1\), \(C \cap L_2\) and \(L_1 \cap L_2\)). It follows that the K3 surface \(S_{(C,L_1,L_2)}\) contains nine \((-2)\)-curves which form a certain configuration. Call the saturated sublattice generated by these curves
branched along the sextic curve \(C+L_1+L_2\). Note that generically \(\overline{S}_{(C,L_1,L_2)}\) admits nine ordinary double points (coming from the intersection points \(C \cap L_1\), \(C \cap L_2\) and \(L_1 \cap L_2\)). It follows that the K3 surface \(S_{(C,L_1,L_2)}\) contains nine \((-2)\)-curves which form a certain configuration. Call the saturated sublattice generated by these curves  . Then the K3 surface \(S_{(C,L_1,L_2)}\) is naturally M-polarized in the sense of Dolgachev [8]. Let
. Then the K3 surface \(S_{(C,L_1,L_2)}\) is naturally M-polarized in the sense of Dolgachev [8]. Let  be the locus where the sextic curves \(C+L_1+L_2\) have at worst simple singularities (also known as ADE singularities or Du Val singularities). By associating to the triples \((C,L_1,L_2)\) the periods of the M-polarized K3 surfaces \(S_{(C,L_1,L_2)}\) one obtains a period map
be the locus where the sextic curves \(C+L_1+L_2\) have at worst simple singularities (also known as ADE singularities or Du Val singularities). By associating to the triples \((C,L_1,L_2)\) the periods of the M-polarized K3 surfaces \(S_{(C,L_1,L_2)}\) one obtains a period map  from
from  to a certain period domain
to a certain period domain  . We shall prove that
. We shall prove that  is an isomorphism.
is an isomorphism.
Theorem 3.23
Consider the triples \((C, L_1, L_2)\) consisting of quartic curves C and lines \(L_1,L_2\) such that \(C + L_1 + L_2\) has at worst simple singularities. Let \(S_{(C,L_1,L_2)}\) be the K3 surface obtained by taking the minimal resolution of the double plane branched along \(C + L_1 +L_2\). The map sending \((C, L_1, L_2)\) to the periods of \(S_{(C,L_1,L_2)}\) extends to an isomorphism  .
.
The approach is analoguos to the one used by Laza [17]. Roughly speaking, we first consider the generic case where C is smooth and \(C+L_1+L_2\) has simple normal crossings. Then we compute the (generic) Picard lattice M and the transcendental lattice \(T = M_{\Lambda _{K3}}^{\perp }\) (see Proposition 3.13), determine the period domain  and choose a suitable arithmetic group \(\Gamma \) (cf. Sect. 3.3, N.B. \(\Gamma \) is not the standard arithmetic group \(O^*(T)\) used in [8] but an extension of \(O^*(T)\)). Finally we extend the construction to the non-generic case (using the methods and some results of [17]) and apply the global Torelli theorem and the surjectivity of the period map for K3 surfaces to prove the theorem (cf. Sects. 3.4 and 3.5).
and choose a suitable arithmetic group \(\Gamma \) (cf. Sect. 3.3, N.B. \(\Gamma \) is not the standard arithmetic group \(O^*(T)\) used in [8] but an extension of \(O^*(T)\)). Finally we extend the construction to the non-generic case (using the methods and some results of [17]) and apply the global Torelli theorem and the surjectivity of the period map for K3 surfaces to prove the theorem (cf. Sects. 3.4 and 3.5).
Note that the period domain  is a type IV Hermitian symmetric domain. The arithmetic quotients of
is a type IV Hermitian symmetric domain. The arithmetic quotients of  admit canonical compactifications called Baily–Borel compactifications. To compare the GIT compactification and the Baily–Borel compactification we consider a slightly different moduli space
admit canonical compactifications called Baily–Borel compactifications. To compare the GIT compactification and the Baily–Borel compactification we consider a slightly different moduli space  (constructed by taking a quotient of the GIT quotient
(constructed by taking a quotient of the GIT quotient  ) parameterizing triples \((C,L,L')\) consisting of quartic curves C and unlabeled lines \(L,L'\). In a similar manner, we construct a period map
) parameterizing triples \((C,L,L')\) consisting of quartic curves C and unlabeled lines \(L,L'\). In a similar manner, we construct a period map  and prove that
and prove that  is an isomorphism between the locus
is an isomorphism between the locus  where \(C+L+L'\) has at worst simple singularities and a certain locally symmetric domain
where \(C+L+L'\) has at worst simple singularities and a certain locally symmetric domain  (cf. Sect. 3.6). Moreover, we show in Corollary 2.16 that
(cf. Sect. 3.6). Moreover, we show in Corollary 2.16 that  is the union of three points
is the union of three points  and five rational curves
and five rational curves  ,
,  whose incidence structure is describe in Fig. 1. The quasi-projective variety
whose incidence structure is describe in Fig. 1. The quasi-projective variety  has codimension higher than 1 and hence the period map
has codimension higher than 1 and hence the period map  extends to the GIT compactification
extends to the GIT compactification  . Note also that
. Note also that  preserves the natural polarizations (the polarization of
preserves the natural polarizations (the polarization of  is induced by the polarization of the moduli of plane sextics and the polarization of
is induced by the polarization of the moduli of plane sextics and the polarization of  comes from the polarization of moduli of degree 2 K3 surfaces). A proof similar to [21, Theorem 7.6] shows that the extension of
comes from the polarization of moduli of degree 2 K3 surfaces). A proof similar to [21, Theorem 7.6] shows that the extension of  induces an isomorphism between the GIT quotient
induces an isomorphism between the GIT quotient  and the Baily–Borel compactification
and the Baily–Borel compactification  (see Sect. 3.7). Some computations and remarks on the Baily–Borel boundary components are also included in the paper (cf. Sect. 3.8).
(see Sect. 3.7). Some computations and remarks on the Baily–Borel boundary components are also included in the paper (cf. Sect. 3.8).
Theorem 3.24
The period map  extends to an isomorphism of projective varieties
extends to an isomorphism of projective varieties  denotes the Baily–Borel compactification of
denotes the Baily–Borel compactification of  .
.
We conclude by the following remarks. The moduli space of quartic triples\((C,L_1,L_2)\) is closely related to the moduli space of degree 5 pairs (cf. [17, Definition 2.1]) consisting of a quintic curve and a line (i.e. given a triple \((C, L_1, L_2)\) that we consider, compare it with the pairs  and
and  ). Motivated by studying deformations of \(N_{16}\) singularities, Laza [17] has constructed the moduli space of degree 5 pairs using both the GIT and Hodge theoretic approaches. His work is an important motivation for us and the prototype of what we do here. Also, the study of singularities and incidences lines on quartic curves is a classical topic (see for example the work of Edge [10, 11]) and a classifying space for such pairs may be related to our GIT compactification.
). Motivated by studying deformations of \(N_{16}\) singularities, Laza [17] has constructed the moduli space of degree 5 pairs using both the GIT and Hodge theoretic approaches. His work is an important motivation for us and the prototype of what we do here. Also, the study of singularities and incidences lines on quartic curves is a classical topic (see for example the work of Edge [10, 11]) and a classifying space for such pairs may be related to our GIT compactification.
2 Variations of GIT quotients
In [13] the first two authors introduced a computational framework to construct all GIT quotients of pairs (X, H) formed by a hypersurface X of degree d and a hyperplane H in  . They drew from the general theory of variations of GIT quotients developed by Dolgachev and Hu [9] and independently by Thaddeus [32]. The motivation was to construct compact moduli spaces of log pairs
. They drew from the general theory of variations of GIT quotients developed by Dolgachev and Hu [9] and independently by Thaddeus [32]. The motivation was to construct compact moduli spaces of log pairs  where X is Fano or Calabi–Yau. In this article we need to extend this setting to the case of tuples \((C,L_1,L_2)\) where C is a plane quartic curve and \(L_1,L_2\) are lines. However, extending our work in [13] to two hyperplanes entails the same difficulties as for an arbitrary number of hyperplanes, while the dimension does not play an important role in the setting. Therefore we will consider the most general setting of a hypersurface in projective space and k hyperplane sections.
where X is Fano or Calabi–Yau. In this article we need to extend this setting to the case of tuples \((C,L_1,L_2)\) where C is a plane quartic curve and \(L_1,L_2\) are lines. However, extending our work in [13] to two hyperplanes entails the same difficulties as for an arbitrary number of hyperplanes, while the dimension does not play an important role in the setting. Therefore we will consider the most general setting of a hypersurface in projective space and k hyperplane sections.
2.1 Variations of GIT quotients for n-dimensional hypersurfaces of degree d together with k (labeled) hyperplanes
Let  be the parameter scheme of tuples \((F_d,l_1,\ldots ,l_k)\), where \(F_d\) is a polynomial of degree d and \(l_1,\ldots , l_k\) are linear forms in variables \((x_0,\ldots , x_{n+1})\), modulo scalar multiplication. We have
be the parameter scheme of tuples \((F_d,l_1,\ldots ,l_k)\), where \(F_d\) is a polynomial of degree d and \(l_1,\ldots , l_k\) are linear forms in variables \((x_0,\ldots , x_{n+1})\), modulo scalar multiplication. We have

where \(N= {\left( {\begin{array}{c}n+1+d\\ d\end{array}}\right) }-1\) and natural projections  ,
,  for \(i=1,\ldots , k\). The natural action of
for \(i=1,\ldots , k\). The natural action of  in
in  extends to each of the factors in
extends to each of the factors in  and therefore to
and therefore to  itself. The set of G-linearizable line bundles
itself. The set of G-linearizable line bundles  is isomorphic to \(\mathbb {Z}^{n+1}\). Then a line bundle
is isomorphic to \(\mathbb {Z}^{n+1}\). Then a line bundle  is ample if and only if \(a>0\), \(b_i>0\) for \(i=1,\ldots , k\), where
is ample if and only if \(a>0\), \(b_i>0\) for \(i=1,\ldots , k\), where

The latter is a trivial generalization of [13, Lemma 2.1]. Hence, for  , the GIT quotient is defined as
, the GIT quotient is defined as

where \(t_i={b_i}/{a}\). Next, we explain why it is enough to consider the vector  instead of \((a;b_1,\ldots , b_k)\). Let us introduce some notation.
instead of \((a;b_1,\ldots , b_k)\). Let us introduce some notation.
Given a maximal torus  , we can choose projective coordinates
, we can choose projective coordinates  such that T is diagonal in G. Hence, any one-parameter subgroup
such that T is diagonal in G. Hence, any one-parameter subgroup  is a diagonal matrix with diagonal entries \(s^{r_i}\) where \(r_i\in \mathbb Z\) for all i and
is a diagonal matrix with diagonal entries \(s^{r_i}\) where \(r_i\in \mathbb Z\) for all i and  . We say that \(\lambda \) is normalized if \(r_0\geqslant \cdots \geqslant r_{n+1}\) and \(\lambda \) is not trivial. Any homogeneous polynomial g of degree d can be written as
. We say that \(\lambda \) is normalized if \(r_0\geqslant \cdots \geqslant r_{n+1}\) and \(\lambda \) is not trivial. Any homogeneous polynomial g of degree d can be written as  , where
, where  ,
,  ,
,  and
and  . The support of g is
. The support of g is  . We have a natural pairing
. We have a natural pairing  , which we use to introduce the Hilbert–Mumford function for homogeneous polynomials:
, which we use to introduce the Hilbert–Mumford function for homogeneous polynomials:

Define

which is piecewise linear on \(\lambda \) for fixed \((f,l_1,\ldots ,l_k)\). Since the Hilbert–Mumford function is functorial [25, Definition 2.2, cf. p. 49], we can generalise [13, Lemma 2.2] to show that a tuple \((f,l_1,\ldots ,l_k)\) is (semi-)stable with respect to a polarisation  if and only if
if and only if

is negative (respectively, non-positive) for any normalized non-trivial one-parameter subgroup \(\lambda \) of any maximal torus T of G. Hence the stability of a tuple is independent of the scaling of  and as such, we may define:
and as such, we may define:
Definition 2.1
Let \(\vec t\in (\mathbb Q_{\geqslant 0})^k\). The tuple \((f,l_1,\ldots ,l_k)\) is \(\vec t\)
-stable (respectively \(\vec t\)
-semistable) if  (respectively
(respectively  ) for all non-trivial normalized one-parameter subgroups \(\lambda \) of G. A tuple \((f,l_1,\ldots ,l_k)\) is \(\vec t\)
-unstable if it is not \(\vec t\)-semistable. A tuple \((f,l_1,\ldots ,l_k)\) is strictly
\(\vec t\)
-semistable if it is \(\vec t\)-semistable but not \(\vec t\)-stable.
) for all non-trivial normalized one-parameter subgroups \(\lambda \) of G. A tuple \((f,l_1,\ldots ,l_k)\) is \(\vec t\)
-unstable if it is not \(\vec t\)-semistable. A tuple \((f,l_1,\ldots ,l_k)\) is strictly
\(\vec t\)
-semistable if it is \(\vec t\)-semistable but not \(\vec t\)-stable.
Notice that the stability of a tuple \((f,l_1,\ldots ,l_k)\) is completely determined by the support of f and \(l_1,\ldots ,l_k\). Moreover, notice that the \(\vec t\)-stability of a tuple is invariant under the action of G. Hence, we may say that a tuple \((X,H_1,\ldots , H_k)\) formed by a hypersurface  and hyperplanes
and hyperplanes  is \(\vec t\)
-stable (respectively, \(\vec t\)
-semistable) if some (and hence any) tuple of homogeneous polynomials \((f,l_1,\ldots ,l_k)\) defining \((X,H_1,\ldots ,H_k)\) is \(\vec t\)
-stable (respectively, \(\vec t\)
-semistable). A tuple \((X,H_1,\ldots , H_k)\) is \(\vec t\)
-unstable if it is not \(\vec t\)-semistable.
is \(\vec t\)
-stable (respectively, \(\vec t\)
-semistable) if some (and hence any) tuple of homogeneous polynomials \((f,l_1,\ldots ,l_k)\) defining \((X,H_1,\ldots ,H_k)\) is \(\vec t\)
-stable (respectively, \(\vec t\)
-semistable). A tuple \((X,H_1,\ldots , H_k)\) is \(\vec t\)
-unstable if it is not \(\vec t\)-semistable.
In [13], for fixed torus T in G, we introduced the fundamental set \(S_{n,d}\) of one-parameter subgroups—a finite set—and we showed that if \(k=1\) it was sufficient to consider the one-parameter subgroups in \(S_{n,d}\) for each T to determine the \(\vec t\)-stability of any \((X,H_1)\). Let us recall the definition—slightly simplified from the original [13, Definition 3.1]—and extend the result to any k.
Definition 2.2
The fundamental set
\(S_{n,d}\)
of one-parameter subgroups
\(\lambda \in T\) consists of all elements  where
where

satisfying the following:
-
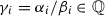 such that
such that  for all \(i=0,\ldots ,n+1\) and
for all \(i=0,\ldots ,n+1\) and 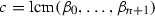 .
. -
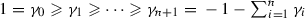 .
. -
\((\gamma _0,\ldots ,\gamma _{n+1})\) is the unique solution of a consistent linear system given by n equations chosen from the following set:

The set \(S_{n,d}\) is finite since there are a finite number of monomials of degree d in \(n+2\) variables. Observe that \(S_{n,d}\) is independent of the value of k. The following lemma is a straight forward generalization of [13, Lemma 3.2] which we include here for the convenience of the reader:
Lemma 2.3
A tuple \((X,H_1,\ldots ,H_k)\) given by equations \((f,l_1,\ldots ,l_k)\) is not \(\vec t\)-stable (respectively not \(\vec t\)-semistable) if and only if there is \(g \in G\) satisfying

Moreover  .
.
Proof
Let  be the non-\({\vec t}\)-stable loci of
be the non-\({\vec t}\)-stable loci of  with respect to a maximal torus T, and let
with respect to a maximal torus T, and let  be the non-\(\vec t\)-stable loci of
be the non-\(\vec t\)-stable loci of  .
.
By [7, p. 137],  . Let \((f,l_1,\ldots ,l_k)\) be the equations in some coordinate system—inducing a maximal torus \(T\subset G\)—of a non-\(\vec t\)-stable tuple \((X,H_1,\ldots , H_k)\). Then,
. Let \((f,l_1,\ldots ,l_k)\) be the equations in some coordinate system—inducing a maximal torus \(T\subset G\)—of a non-\(\vec t\)-stable tuple \((X,H_1,\ldots , H_k)\). Then,  for some \(\rho \in T'\) in a maximal torus \(T'\) which may be different from T. All the maximal tori are conjugate to each other in G, and by [7, Exercise 9.2 (i)], we have
for some \(\rho \in T'\) in a maximal torus \(T'\) which may be different from T. All the maximal tori are conjugate to each other in G, and by [7, Exercise 9.2 (i)], we have  for all \(g\in G\). Hence, there is
for all \(g\in G\). Hence, there is  such that
such that  is normalized and
is normalized and  satisfies
satisfies . Normalized one-parameter subgroups in the coordinate system induced by T are the intersection of \(\sum r_i=0\) and the convex hull of \(r_i-r_{i+1}\geqslant 0\), where \(i=0,\ldots , n\). The restriction of the \(n+1\) linearly independent inequalities in \(n+1\) variables to \(\sum r_i=0\) gives a closed convex polyhedral subset \(\Delta \) of dimension \(n+1\) (in fact, a simplex) in the \(\mathbb Q\)-lattice of characters of T—isomorphic to the lattice of monomials (in variables \(x_0,\ldots , x_{n+1}\)) tensored by \(\mathbb Q\), which in turn is isomorphic to \(\mathbb Q^{n+2}\).
. Normalized one-parameter subgroups in the coordinate system induced by T are the intersection of \(\sum r_i=0\) and the convex hull of \(r_i-r_{i+1}\geqslant 0\), where \(i=0,\ldots , n\). The restriction of the \(n+1\) linearly independent inequalities in \(n+1\) variables to \(\sum r_i=0\) gives a closed convex polyhedral subset \(\Delta \) of dimension \(n+1\) (in fact, a simplex) in the \(\mathbb Q\)-lattice of characters of T—isomorphic to the lattice of monomials (in variables \(x_0,\ldots , x_{n+1}\)) tensored by \(\mathbb Q\), which in turn is isomorphic to \(\mathbb Q^{n+2}\).
Given a fixed \((f,l_1,\ldots ,l_k)\), the function  is piecewise linear and its critical points—the points in \(\mathbb Q^{n+2}\) where
is piecewise linear and its critical points—the points in \(\mathbb Q^{n+2}\) where  fails to be linear—correspond to those monomials
fails to be linear—correspond to those monomials  such that
such that  , or equivalently, the points
, or equivalently, the points  such that
such that  for some
for some  . These points define a hyperplane in \(\mathbb Q^{n+2}\) and the intersection of this hyperplane with \(\Delta \) is a simplex
. These points define a hyperplane in \(\mathbb Q^{n+2}\) and the intersection of this hyperplane with \(\Delta \) is a simplex  of dimension n. As
of dimension n. As  is linear on the complement of
is linear on the complement of  , the minimum of
, the minimum of  is achieved on the boundary, i.e. either on \(\partial \Delta \) or on
is achieved on the boundary, i.e. either on \(\partial \Delta \) or on  (for some \(I,I'\)), all of which are convex polytopes of dimension n. By finite induction, we conclude that the minimum of
(for some \(I,I'\)), all of which are convex polytopes of dimension n. By finite induction, we conclude that the minimum of  is achieved at one of the vertices of \(\Delta \) or
is achieved at one of the vertices of \(\Delta \) or  , which correspond precisely, up to multiplication by a constant, to the finite set of one-parameter subgroups in \(S_{n,d}\). Indeed, observe that if
, which correspond precisely, up to multiplication by a constant, to the finite set of one-parameter subgroups in \(S_{n,d}\). Indeed, observe that if  is one such vertex, then
is one such vertex, then  for some
for some  where
where  and
and  . In addition, observe that we can find one such \(\delta \) so that
. In addition, observe that we can find one such \(\delta \) so that  , thus giving the equations determining the maximal facets of \(\Delta \), i.e. those where \(r_i=r_{i+1}\). The lemma follows from the observation that
, thus giving the equations determining the maximal facets of \(\Delta \), i.e. those where \(r_i=r_{i+1}\). The lemma follows from the observation that  .\(\square \)
.\(\square \)
Definition 2.4
The space of GIT stability conditions is

The space of GIT stability conditions is bounded, as it can be realized as a hyperplane section of  . Since
. Since  is a product of vector spaces (and hence a Mori dream space),
is a product of vector spaces (and hence a Mori dream space),  is also a rational polyhedron. It is possible to precisely describe it and we will do this later for
is also a rational polyhedron. It is possible to precisely describe it and we will do this later for  . Moreover, there is a finite number of non-isomorphic GIT compactifications
. Moreover, there is a finite number of non-isomorphic GIT compactifications  as
as  in varies. Therefore we have a natural division of
in varies. Therefore we have a natural division of  into a finite number of disjoint rational polyhedrons of dimension k called chambers and the intersection of any two-chambers is a (possibly empty) rational polyhedron of smaller dimension which we will call a wall [9, Theorem 0.2.3]. The quotient
into a finite number of disjoint rational polyhedrons of dimension k called chambers and the intersection of any two-chambers is a (possibly empty) rational polyhedron of smaller dimension which we will call a wall [9, Theorem 0.2.3]. The quotient  is constant as \(\vec t\) moves in the interior of a face or chamber. It is possible to find these walls explicitly by means of Lemma 2.3 (see [13, Theorem 1.1]) for given (n, d, k), since all walls of dimension \(k-1\) should be a subset of the finite set of equations
is constant as \(\vec t\) moves in the interior of a face or chamber. It is possible to find these walls explicitly by means of Lemma 2.3 (see [13, Theorem 1.1]) for given (n, d, k), since all walls of dimension \(k-1\) should be a subset of the finite set of equations

Another interesting feature is that the the \(\vec t\)-stability of tuples \((X,H_1,\ldots , H_k)\) is equivalent of the t-stability of reducible GIT hypersurfaces of higher degree. Indeed:
Lemma 2.5
Let  where
where  for all \(i=1,\ldots , k\). Let
for all \(i=1,\ldots , k\). Let  ,
,  such that
such that  and let
and let  . Let
. Let  . A tuple \((X,H_1,\ldots ,H_k)\) is \(\vec t\)-(semi)stable if and only if the tuple
. A tuple \((X,H_1,\ldots ,H_k)\) is \(\vec t\)-(semi)stable if and only if the tuple

is \(\vec {t'}\)-(semi)stable.
In particular, if \(t_1,\ldots , t_k\) are natural numbers, \((X,H_1,\ldots ,H_k)\) is \(\vec t\)-(semi)stable if and only if \(X+{t_1}H_1+\cdots +{t_k}H_{k}\) (semi)stable in the classical GIT sense.
Proof
Let \(\lambda \) be a normalized one-parameter subgroup, m be a positive integer and \(g=\sum g_Ix^I\) be a homogeneous polynomial. Let J be such that

Then, since \(\lambda \) is normalized,  .
.
Let \((f,l_1,\ldots ,l_k)\) be the equations of \((X,H_1,\ldots , H_k)\) under some system of coordinates and let \(\lambda \) be a normalized one-parameter subgroup. Using the above observation, the lemma follows from:

Corollary 2.6
Let  and
and  , \(j\leqslant k\). Then a tuple \((X,H_1,\ldots , H_k)\) is \(\vec t\)-semistable if and only if
, \(j\leqslant k\). Then a tuple \((X,H_1,\ldots , H_k)\) is \(\vec t\)-semistable if and only if  is \(\vec {t'}\)-semistable.
is \(\vec {t'}\)-semistable.
Lemma 2.7
(cf. [12, Corollary 1.2]) If the locus of stable points is not empty, and \(d \geqslant 3\), then

Proof
From [27, Theorem 2.1], any hypersurface  where f is a homogeneous polynomial of degree \(d\geqslant 3\) has
where f is a homogeneous polynomial of degree \(d\geqslant 3\) has  . Hence, for any tuple \(p=(X,H_1,\dots , H_K)\) such that X is smooth and \(X\cap H_i\) has simple normal crossings, its stabilizer
. Hence, for any tuple \(p=(X,H_1,\dots , H_K)\) such that X is smooth and \(X\cap H_i\) has simple normal crossings, its stabilizer  satisfies
satisfies

where the last equality follows from [27, Theorem 2.1]. The result follows from [7, Corollary 6.2]:

Now let us consider the case of the symmetric polarization of  . In order to do so, observe that the group \(S_k\) acts on
. In order to do so, observe that the group \(S_k\) acts on  by defining the action of \(h\in S_k\) as
by defining the action of \(h\in S_k\) as
Define  , which parametrizes classes of tuples \([(f,l_1,\ldots , l_k)]\) up to multiplication by a scalar and permutation of
, which parametrizes classes of tuples \([(f,l_1,\ldots , l_k)]\) up to multiplication by a scalar and permutation of  , i.e.
, i.e.  for \(g\in S_k\) and
for \(g\in S_k\) and  . Hence, we parameterize the same elements as in
. Hence, we parameterize the same elements as in  but we forget the ordering of the linear forms. In particular \(\mathscr {R}'_{n,d,k}\) parametrizes pairs \([(X,H_1,\ldots , H_k)]\) formed by a hypersurface
but we forget the ordering of the linear forms. In particular \(\mathscr {R}'_{n,d,k}\) parametrizes pairs \([(X,H_1,\ldots , H_k)]\) formed by a hypersurface  of degree d and k unordered hyperplanes. The quotient morphism
of degree d and k unordered hyperplanes. The quotient morphism  is G-equivariant. Let
is G-equivariant. Let  such that \(({b_1}/{a},\ldots ,{b_k}/{a})=(1,\ldots ,1)\) (i.e. we are considering \(\vec t\)-stability with respect to
such that \(({b_1}/{a},\ldots ,{b_k}/{a})=(1,\ldots ,1)\) (i.e. we are considering \(\vec t\)-stability with respect to  ). If the condition
). If the condition

holds, then a tuple \((f,l_1,\ldots , l_k)\) is \(t_1\)-(semi)stable if and only if  is stable with respect to
is stable with respect to  by [25, Theorem 1.1 and p. 48]. Hence, it is natural to define the GIT quotient
by [25, Theorem 1.1 and p. 48]. Hence, it is natural to define the GIT quotient

which is the GIT quotient of unordered tuples
\((X,H_1,\cdots , H_k)\)
with respect to the polarization
 . We have a commutative diagram
. We have a commutative diagram

We want to determine all the orbits represented in  from the orbits represented in
from the orbits represented in  via
via  .
.
Choose \(1\leqslant j_1< \cdots < j_l\leqslant k\) and define the G-equivariant morphism  given by
given by

By Lemma 2.5, we have a commutative diagram

Proposition 2.8
Let \(1\leqslant j_1< \cdots <j_l\leqslant k\) and suppose that (2) holds. An unordered tuple \([(X,H_1,\dots ,H_k)]\)—where X is a hypersurface of degree d in  and \(H_1,\ldots , H_k\) are k unordered hyperplanes—is (semi)stable with respect to
and \(H_1,\ldots , H_k\) are k unordered hyperplanes—is (semi)stable with respect to  if and only if
if and only if

—a pair represented by a tuple in  —is \(\vec {t_*}\)-(semi)stable. Moreover an orbit
—is \(\vec {t_*}\)-(semi)stable. Moreover an orbit  is closed if and only if and only if
is closed if and only if and only if  is closed. In addition, an orbit
is closed. In addition, an orbit  is closed if and only if
is closed if and only if  is closed.
is closed.
Proof
Since (2) holds, all the spaces in the above diagram are non-empty. As \(\pi \) is finite, the pair \([(X,H_1,\dots ,H_k)]\)—represented by the classes of tuples in  —is (semi)stable with respect to
—is (semi)stable with respect to  if and only if every \((X,H_1, \dots ,H_k)\) in the class \([(X,H_1,\cdots ,H_k)]\) is \(\vec t_*\)-(semi)stable, by [25, Theorem 1.1 and p. 48]. By Lemma 2.5, \((X,H_1, \dots ,H_k)\)—represented by tuples in
if and only if every \((X,H_1, \dots ,H_k)\) in the class \([(X,H_1,\cdots ,H_k)]\) is \(\vec t_*\)-(semi)stable, by [25, Theorem 1.1 and p. 48]. By Lemma 2.5, \((X,H_1, \dots ,H_k)\)—represented by tuples in  —is \( \vec t_*\)-(semi)stable if and only if
—is \( \vec t_*\)-(semi)stable if and only if  —represented by tuples in
—represented by tuples in  —is \(\vec t_{*}\)-(semi)stable (note that we use the notation \(\vec t_*\) for vectors with all entries equal 1, whether \(\vec t_*\) has k or \(k-l\) entries). The last statement regarding closed orbits follows from noting that finite morphisms are closed, and hence
—is \(\vec t_{*}\)-(semi)stable (note that we use the notation \(\vec t_*\) for vectors with all entries equal 1, whether \(\vec t_*\) has k or \(k-l\) entries). The last statement regarding closed orbits follows from noting that finite morphisms are closed, and hence  is closed.\(\square \)
is closed.\(\square \)
2.2 Symmetric GIT quotient of a quartic curve and two lines
We have seen how to construct GIT quotients  for
for  . In this section we apply our results to the case of quartic plane curves (\(d=4\)), but let us first show that our setting satisfies condition (2) for arbitrary degree. Hence, for the rest of the article, we assume that \(n=1\) and \(k=2\).
. In this section we apply our results to the case of quartic plane curves (\(d=4\)), but let us first show that our setting satisfies condition (2) for arbitrary degree. Hence, for the rest of the article, we assume that \(n=1\) and \(k=2\).
Lemma 2.9
The space of GIT stability conditions is

In particular, (2) holds.
Proof
Let  be a vector and \((C,L_1,L_2)\) be a \(\vec t\)-semistable tuple. By choosing an appropriate change of coordinates, we may assume
be a vector and \((C,L_1,L_2)\) be a \(\vec t\)-semistable tuple. By choosing an appropriate change of coordinates, we may assume

Let  . Then, as \(t_1\geqslant 0, t_2\geqslant 0\), we have
. Then, as \(t_1\geqslant 0, t_2\geqslant 0\), we have

Similarly, by taking a change of coordinates such that  ,
,  , we may show that
, we may show that  .
.
Recall that the space of GIT stability conditions is convex [9, 0.2.1]. Hence it is enough to show that all the vertices of the right hand side in (4) have a semistable tuple \((C, L_1,L_2)\) (and hence, they belong to  ). These vertices correspond to the points (0, 0), (d / 2, 0), (0, d / 2) and (d, d). By Corollary 2.6, a tuple \((C, L_1,L_2)\) is (d / 2, 0)-semistable if and only if \((C, L_1)\) is (d / 2)-semistable, but the space of GIT t-stability conditions for plane curves and one hyperplane is
). These vertices correspond to the points (0, 0), (d / 2, 0), (0, d / 2) and (d, d). By Corollary 2.6, a tuple \((C, L_1,L_2)\) is (d / 2, 0)-semistable if and only if \((C, L_1)\) is (d / 2)-semistable, but the space of GIT t-stability conditions for plane curves and one hyperplane is  [13, Theorem 1.1]. A mirrored argument applies for the stability point (0, d / 2).
[13, Theorem 1.1]. A mirrored argument applies for the stability point (0, d / 2).
Hence, we only need to exhibit a tuple \((C, L_1,L_2)\) which is (d, d)-semistable. Let  . By Lemma 2.5, such a pair is t-semistable if and only if the reducible curve \(C+dL_1+dL_2\) (defined by the equation \(x_0^dx_1^dx_2^d=0\)) of degree 3d is semistable in the usual GIT sense. The latter follows from the centroid criterion [13, Lemma 1.5].\(\square \)
. By Lemma 2.5, such a pair is t-semistable if and only if the reducible curve \(C+dL_1+dL_2\) (defined by the equation \(x_0^dx_1^dx_2^d=0\)) of degree 3d is semistable in the usual GIT sense. The latter follows from the centroid criterion [13, Lemma 1.5].\(\square \)
There are two natural problems regarding the subdivision of  into chambers and walls. One of them is to determine the walls and the solution is usually rather heavy computationally and geometrically speaking (see [12, 13] for the case \((n,d,k)=(2,3,1)\) and for a partial answer when \(k=1\) and (n, d) are arbitrary). Given a tuple \((X, H_1,\cdots , H_k)\) the second problem consists on determining for which chambers and walls this tuple is (semi)stable. This problem may be easier to solve, especially when the answer to the first problem is known. The problem is simpler when \(k=1\), as then
into chambers and walls. One of them is to determine the walls and the solution is usually rather heavy computationally and geometrically speaking (see [12, 13] for the case \((n,d,k)=(2,3,1)\) and for a partial answer when \(k=1\) and (n, d) are arbitrary). Given a tuple \((X, H_1,\cdots , H_k)\) the second problem consists on determining for which chambers and walls this tuple is (semi)stable. This problem may be easier to solve, especially when the answer to the first problem is known. The problem is simpler when \(k=1\), as then  is one-dimensional has a natural order. Nevertheless, we can give a partial answer when \(n=1\), \(k=2\) and d is arbitrary.
is one-dimensional has a natural order. Nevertheless, we can give a partial answer when \(n=1\), \(k=2\) and d is arbitrary.
Definition 2.10
Let  be the loci such that
be the loci such that  if and only \((C,L_1,L_2)\) is t-semistable.
if and only \((C,L_1,L_2)\) is t-semistable.
Lemma 2.11
Suppose that C is a plane curve of degree d whose only singular point \(p \in C\) is a linearly semi-quasihomogeneous singularity [17, Definition 2.21] with respect to the weights \(\vec w=(w_1,w_2)\), \(w_1 \geqslant w_2>0\). Suppose further that \(C+L_1+L_2\) have simple normal crossings in  . Let f be the localization of the equation of f at p and \(\vec w(f)\) be its weighted degree with respect to \(\vec w\).
. Let f be the localization of the equation of f at p and \(\vec w(f)\) be its weighted degree with respect to \(\vec w\).
-
(a)
Suppose that \(p\not \in L_1\cup L_2\). Then
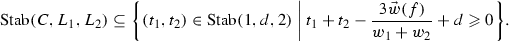
-
(b)
Suppose that \(p\not \in L_2\) and \(p\in L_1\cap C\). Then

Proof
We may choose a coordinate system such that  is the singular point of C. We consider the one-parameter subgroup \(\lambda = (2w_1-w_2, 2w_2-w_1,-w_1-w_2)\) which is normalized, as \(w_1 \geqslant w_2\).
is the singular point of C. We consider the one-parameter subgroup \(\lambda = (2w_1-w_2, 2w_2-w_1,-w_1-w_2)\) which is normalized, as \(w_1 \geqslant w_2\).
(a) The first statement is equivalent to show that if  and
and  then the triple is
then the triple is  -unstable.
-unstable.
Let \(l_1(x_0,x_1)+x_2\) and \(l_2(x_0,x_1)+x_2\) be the equations of the lines \(L_1\) and \(L_2\), respectively, where \(l_1,l_2\) are linear forms. We have

Therefore, \(\mu _{t_1,t_2}(C,L_1, L_2, \lambda ) >0\) and the triple is destabilized by \(\lambda \).
(b) The lines \(L_1\) and \(L_2\) have equation \(l_1(x_0,x_1)\) and \(l_2(x_0,x_1) +x_2\), respectively, where \(l_1,l_2\) are linear forms. If  , as \(w_1\geqslant w_2\), we have
, as \(w_1\geqslant w_2\), we have

For the rest of the paper we consider tuples \((C, L_1, L_2)\) formed by a plane quartic C and two lines  . The following result will come useful:
. The following result will come useful:
Lemma 2.12
(Shah [30, Section 2], cf. [19, Theorem 1.3]) Let Z be a plane sextic, and X the double cover of  branched along Z. Then X has semi-log canonical singularities if and only if Z is semistable and the closure of the orbit of Z does not contain the orbit of the triple conic. In particular, a sextic plane curve with simple singularities is stable.
branched along Z. Then X has semi-log canonical singularities if and only if Z is semistable and the closure of the orbit of Z does not contain the orbit of the triple conic. In particular, a sextic plane curve with simple singularities is stable.
Lemma 2.13
Let \(\vec t =(1,1)\) and \((C, L_1, L_2)\) be a tuple such that the sextic \(C+L_1+L_2\) is reduced. Then, \((C, L_1, L_2)\) is \(\vec t\)-(semi)stable if and only if the double cover X of  branched at \(C+L_1+L_2\) has at worst simple singularities (respectively simple elliptic or cuspidal singularities).
branched at \(C+L_1+L_2\) has at worst simple singularities (respectively simple elliptic or cuspidal singularities).
Proof
The sextic  (where f is a quartic curve and \(l_1, l_2\) are distinct linear forms not in the support of f) cannot degenerate to a triple conic and it is reduced by hypothesis. By Lemma 2.12, Z is a GIT-semistable sextic curve if and only if X has slc singularities. The surface X is normal, as Z is reduced [6, Proposition 0.1.1]. In particular
(where f is a quartic curve and \(l_1, l_2\) are distinct linear forms not in the support of f) cannot degenerate to a triple conic and it is reduced by hypothesis. By Lemma 2.12, Z is a GIT-semistable sextic curve if and only if X has slc singularities. The surface X is normal, as Z is reduced [6, Proposition 0.1.1]. In particular  has hypersurface log canonical singularities away from the singular point
has hypersurface log canonical singularities away from the singular point  , and by the classification of such singularities in [20, Table 1], they can only consist of either simple, simple elliptic or cuspidal singularities. If Z has only simple singularities then Z is GIT-stable by Lemma 2.12. Now suppose Z is GIT-stable and reduced. By [19, Theorem 1.3 and Remark 1.4] a GIT-semistable plane sextic curve has either simple singularities or it is in the open orbit of a sextic containing a double conic or a triple conic in its support, contradicting the fact that Z is reduced. Hence Z has only simple singularities. The proof follows from Lemma 2.5.\(\square \)
, and by the classification of such singularities in [20, Table 1], they can only consist of either simple, simple elliptic or cuspidal singularities. If Z has only simple singularities then Z is GIT-stable by Lemma 2.12. Now suppose Z is GIT-stable and reduced. By [19, Theorem 1.3 and Remark 1.4] a GIT-semistable plane sextic curve has either simple singularities or it is in the open orbit of a sextic containing a double conic or a triple conic in its support, contradicting the fact that Z is reduced. Hence Z has only simple singularities. The proof follows from Lemma 2.5.\(\square \)
Remark 2.14
Although, we will not discuss other polarizations. It is worth to notice that for \(\vec t=( \epsilon , \epsilon )\) the stability is very similar to the one of plane quartics. In particular, if C is a semistable quartic and \(L_1,L_2\) are lines in general position. Then, the triple \((C, L_1, L_2)\) is stable.
Let  and
and  be the set of \(\vec t\)-stable and \(\vec t\)-semistable tuples \((f,l_1,l_2)\), respectively. Let
be the set of \(\vec t\)-stable and \(\vec t\)-semistable tuples \((f,l_1,l_2)\), respectively. Let

Let \(\vec t=(1,1)\). By Lemma 2.12,  . Let
. Let  ,
,  and recall that
and recall that  . Then
. Then  . We are interested in describing the compactification of
. We are interested in describing the compactification of  by
by  . We use the notation in [19].
. We use the notation in [19].
Lemma 2.15
The quotient  is the compactification of
is the compactification of  by three points and six rational curves. The three points correspond to the closed orbit of tuples \((C,L_1,L_2)\) defined up to projective equivalence by the following tuples:
by three points and six rational curves. The three points correspond to the closed orbit of tuples \((C,L_1,L_2)\) defined up to projective equivalence by the following tuples:

The six rational curves correspond to the closed orbit of tuples \((C,L_1,L_2)\) defined up to projective equivalence by the following cases:

where \(a \ne 0,1, \infty \).
Proof
Let  , parametrising tuples \((g,l_1)\) up to multiplication by scalar where g is a quintic homogeneous polynomial and \(l_1\) is a linear form. As we have seen in Proposition 2.8, we have a morphism
, parametrising tuples \((g,l_1)\) up to multiplication by scalar where g is a quintic homogeneous polynomial and \(l_1\) is a linear form. As we have seen in Proposition 2.8, we have a morphism  defined by
defined by  , and an orbit O of
, and an orbit O of  is closed if and only if the orbit \(\phi _2(O)\) of
is closed if and only if the orbit \(\phi _2(O)\) of  is closed.
is closed.
Hence the points which compactify  into
into  corresponding to closed orbits of
corresponding to closed orbits of  are mapped via \(\phi _2\) onto points in
are mapped via \(\phi _2\) onto points in  corresponding to closed orbits in
corresponding to closed orbits in  . Hence we just need to identify closed orbits in
. Hence we just need to identify closed orbits in  . Our result is a straight forward identification of these orbits in the classification of
. Our result is a straight forward identification of these orbits in the classification of  in [17, Proposition 3.22] (Fig. 2).\(\square \)
in [17, Proposition 3.22] (Fig. 2).\(\square \)
Triples parametrized by  . The dotted and dashed lines represent the lines \(L_1\) and \(L_2\), respectively (see Lemma 2.15)
. The dotted and dashed lines represent the lines \(L_1\) and \(L_2\), respectively (see Lemma 2.15)
Lemma 2.15, together with Proposition 2.8 gives us the following compactification which will be of interest for the next section:
Corollary 2.16
Let  be the GIT compactification of a quartic plane curve and two unlabeled lines and let
be the GIT compactification of a quartic plane curve and two unlabeled lines and let  be the open loci parametrizing triples \((C,L,L')\) such that \(C+L+L'\) is reduced and has at worst simple singularities. Then,
be the open loci parametrizing triples \((C,L,L')\) such that \(C+L+L'\) is reduced and has at worst simple singularities. Then,  is the union of three points,
is the union of three points,  ,
,  , and five rational curves,
, and five rational curves,  ,
,  ,
,  ,
,  ,
,  , which are obtained as images—via the natural morphism
, which are obtained as images—via the natural morphism  —of points and rational curves described in Lemma 2.15, as follows:
—of points and rational curves described in Lemma 2.15, as follows:
-
the points
 are the images of the points
are the images of the points  , and
, and -
the rational curves
 ,
,  are the images of the rational curves
are the images of the rational curves  .
.
Moreover, the boundary components  and
and  in
in  are mapped onto the same boundary component
are mapped onto the same boundary component  in
in  .
.
3 Moduli of quartic plane curves and two lines via K3 surfaces
3.1 On K3 surfaces and lattices
By a lattice we mean a finite dimensional free \(\mathbb {Z}\)-module L together with a symmetric bilinear form \((-,-)\). The basic invariants of a lattice are its rank and signature. A lattice is even if \((x,x) \in 2\mathbb {Z}\) for every \(x \in L\). The direct sum  of two lattices \(L_1\) and \(L_2\) is always assumed to be orthogonal, which will be denoted by
of two lattices \(L_1\) and \(L_2\) is always assumed to be orthogonal, which will be denoted by  . For a lattice \(M \subset L\), \(M_L^{\perp }\) denotes the orthogonal complement of M in L. Given two lattices L and \(L'\) and a lattice embedding \(L \hookrightarrow L'\), we call it a primitive embedding if
. For a lattice \(M \subset L\), \(M_L^{\perp }\) denotes the orthogonal complement of M in L. Given two lattices L and \(L'\) and a lattice embedding \(L \hookrightarrow L'\), we call it a primitive embedding if  is torsion free.
is torsion free.
We shall use the following lattices: the (negative definite) root lattices \(A_n\) (\(n \geqslant 1\)), \(D_m\) (\(m \geqslant 4\)), \(E_r\) (\(r = 6,7,8\)) and the hyperbolic plane U. Given a lattice L, L(n) denotes the lattice with the same underlying \(\mathbb {Z}\)-module as L but with the bilinear form multiplied by n.
Notation 3.1
Given any even lattice L, we define:
-
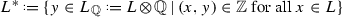 , the dual lattice;
, the dual lattice; -
 , the discriminant group endowed with the induced quadratic form
, the discriminant group endowed with the induced quadratic form 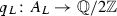 ;
; -
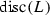 : the determinant of the Gram matrix (i.e. the intersection matrix) with respect to an arbitrary \(\mathbb {Z}\)-basis of L;
: the determinant of the Gram matrix (i.e. the intersection matrix) with respect to an arbitrary \(\mathbb {Z}\)-basis of L; -
O(L): the group of isometries of L;
-
\(O(q_L)\): the automorphisms of \(A_L\) that preserve the quadratic form \(q_L\);
-
\(O_{-}(L)\): the group of isometries of L of spinor norm 1 (see [29, Section 3.6]);
-
\(\widetilde{O}(L)\): the group of isometries of L that induce the identity on \(A_L\);
-
\(O^*(L) = O_{-}(L) \cap \widetilde{O}(L)\);
-
\(\Delta (L)\): the set of roots of L (\(\delta \in L\) is a root if
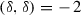 );
); -
W(L): the Weyl group, i.e. the group of isometries generated by reflections \(s_{\delta }\) in root \(\delta \), where
 .
.
For a surface X, the intersection form gives a natural lattice structure on the torsion-free part of \(H^2(X, \mathbb {Z})\) and on the Néron–Severi group  . For a K3 surface S, we have
. For a K3 surface S, we have  , and hence
, and hence  . Both \(H^2(S, \mathbb {Z})\) and
. Both \(H^2(S, \mathbb {Z})\) and  are torsion-free and the natural map
are torsion-free and the natural map  is a primitive embedding. Given any K3 surface S, \(H^2(S,\mathbb {Z})\) is isomorphic to
is a primitive embedding. Given any K3 surface S, \(H^2(S,\mathbb {Z})\) is isomorphic to  , the unique even unimodular lattice of signature (3, 19). We shall use \(O(S),\Delta (S),W(S)\), etc. to denote the corresponding objects of the lattice
, the unique even unimodular lattice of signature (3, 19). We shall use \(O(S),\Delta (S),W(S)\), etc. to denote the corresponding objects of the lattice  . We also denote by \(\Delta ^+(S)\) and \(V^+(S)\) the set of effective \((-2)\) divisor classes in
. We also denote by \(\Delta ^+(S)\) and \(V^+(S)\) the set of effective \((-2)\) divisor classes in  and the Kähler cone of S respectively.
and the Kähler cone of S respectively.
In our context, a polarization for a K3 surface is the class of a nef and big divisor H (and not the most restrictive notion of ample divisor, we follow the terminology in [17]) and \(H^2\) is its degree. More generally there is a notion of lattice polarization. We shall consider the period map for (lattice) polarized K3 surfaces and use the standard facts on K3 surfaces: the global Torelli theorem and the surjectivity of the period map. We also need the following theorem (see [24, p. 40] or [17, Theorem 4.8, Proposition 4.9]).
Theorem 3.2
Let H be a nef and big divisor on a K3 surface S. The linear system |H| has base points if and only if there exists a divisor D such that  and \(D^2=0\).
and \(D^2=0\).
3.2 The K3 surfaces associated to a generic triple
We first consider the K3 surfaces arising as a double cover of  branched at a smooth quartic curve C and two different lines \(L_1\) and \(L_2\) such that \(C+L_1+L_2\) has simple normal crossings. We shall show that these K3 surfaces are naturally polarized by a certain lattice.
branched at a smooth quartic curve C and two different lines \(L_1\) and \(L_2\) such that \(C+L_1+L_2\) has simple normal crossings. We shall show that these K3 surfaces are naturally polarized by a certain lattice.
Denote by \(\overline{S}_{(C,L_1,L_2)}\) the double cover of  branched along \(C+L_1+L_2\). Let \(S_{(C,L_1,L_2)}\) be the K3 surface obtained as the minimal resolution of the nine singular points of \(\overline{S}_{(C,L_1,L_2)}\). Let
branched along \(C+L_1+L_2\). Let \(S_{(C,L_1,L_2)}\) be the K3 surface obtained as the minimal resolution of the nine singular points of \(\overline{S}_{(C,L_1,L_2)}\). Let  be the natural morphism. Note that
be the natural morphism. Note that  also factors as the composition of the blow-up of
also factors as the composition of the blow-up of  at the singularities of \(C+L_1+L_2\) and the double cover of the blow-up branched along the strict transforms of C, \(L_1\) and \(L_2\) (see [4, Section III.7]).
at the singularities of \(C+L_1+L_2\) and the double cover of the blow-up branched along the strict transforms of C, \(L_1\) and \(L_2\) (see [4, Section III.7]).
Let  be the pullback of the class of a line in
be the pullback of the class of a line in  . The class h is a degree 2 polarization of \(S_{(C,L_1,L_2)}\). We assume that \(C \cap L_1 = \{p_1, p_2, p_3, p_4\}\),
. The class h is a degree 2 polarization of \(S_{(C,L_1,L_2)}\). We assume that \(C \cap L_1 = \{p_1, p_2, p_3, p_4\}\),  and
and  . Denote the classes of the exceptional divisors corresponding to \(p_i\), \(q_i\), and r by \(\alpha _i\), \(\beta _i\) and \(\gamma \) respectively (\(1 \leqslant i \leqslant 4\)). Let us also denote by \(l_1'\) (respectively \(l_2'\)) the class of the strict transform of \(L_1\) (respectively \(L_2\)). Note that the morphism
. Denote the classes of the exceptional divisors corresponding to \(p_i\), \(q_i\), and r by \(\alpha _i\), \(\beta _i\) and \(\gamma \) respectively (\(1 \leqslant i \leqslant 4\)). Let us also denote by \(l_1'\) (respectively \(l_2'\)) the class of the strict transform of \(L_1\) (respectively \(L_2\)). Note that the morphism  is given by the class
is given by the class

It is straightforward to check that  ,
,  ,
,  for \(1 \leqslant i,j \leqslant 4\). Clearly, we have
for \(1 \leqslant i,j \leqslant 4\). Clearly, we have  ,
,  , and
, and  for \(1 \leqslant i,j \leqslant 4\).
for \(1 \leqslant i,j \leqslant 4\).
Consider the sublattice of the Picard lattice of \(S_{(C,L_1,L_2)}\) generated by the curve classes \(\gamma ,l_1',\alpha _1, \ldots , \alpha _4,l_2',\beta _1, \ldots , \beta _4\). Let

It follows from (5) that  forms a \(\mathbb {Z}\)-basis of the sublattice. The Gram matrix with respect to this basis is computed as follows:
forms a \(\mathbb {Z}\)-basis of the sublattice. The Gram matrix with respect to this basis is computed as follows:
Notation 3.3
Let M be the abstract lattice of rank 10 spanned by an ordered basis

with the intersection form given by the above Gram matrix, which we will call \(G_M\). Notice that M is an even lattice. If \(S_{(C,L_1,L_2)}\) is a K3 surface obtained as above from a smooth quartic C and two lines \(L_1,L_2\) such that \(C+L_1+L_2\) has simple normal crossings, then there is a natural lattice embedding  as described before.
as described before.
We set \(h = \gamma + \xi \). Observe that \(\jmath (h)\) is linearly equivalent to the pullback of a line in  via \(\pi \) and therefore, it is a base point free polarization. In particular, we have \((h,h) = 2\), \((h,l_1') = (h, l_2') = 1\), and
via \(\pi \) and therefore, it is a base point free polarization. In particular, we have \((h,h) = 2\), \((h,l_1') = (h, l_2') = 1\), and  for
for  . We also let
. We also let  and
and  .
.
Let us compute the discriminant group \(A_M\) and the quadratic form  .
.
Lemma 3.4
The discriminant group  is isomorphic to \((\mathbb {Z}/2\mathbb {Z})^{\oplus 6}\).
is isomorphic to \((\mathbb {Z}/2\mathbb {Z})^{\oplus 6}\).
Proof
Let us denote by  (respectively
(respectively  ) the dual element of \(\alpha _i\in M\) (respectively
) the dual element of \(\alpha _i\in M\) (respectively  , for \(1 \leqslant i,j \leqslant 3\)). Recall that \(\alpha _i^*\) is defined to be the unique element of \(M^*\) such that \((\alpha _i^*, \alpha _i) = 1\) and the pairing of \(\alpha _i^*\) with any other element of the basis
, for \(1 \leqslant i,j \leqslant 3\)). Recall that \(\alpha _i^*\) is defined to be the unique element of \(M^*\) such that \((\alpha _i^*, \alpha _i) = 1\) and the pairing of \(\alpha _i^*\) with any other element of the basis  is 0. We define
is 0. We define  and \(\xi ^*\) in a similar way. The coefficients of the dual elements \(\gamma ^*\!, l_1'^*, \alpha _1^*, \alpha _2^*, \alpha _3^*, l_2'^*, \beta _1^*, \beta _2^*, \beta _3^*, \xi ^*\) (with respect to the basis
and \(\xi ^*\) in a similar way. The coefficients of the dual elements \(\gamma ^*\!, l_1'^*, \alpha _1^*, \alpha _2^*, \alpha _3^*, l_2'^*, \beta _1^*, \beta _2^*, \beta _3^*, \xi ^*\) (with respect to the basis  ) can be read from the rows or columns of the inverse matrix \(G_M^{-1}\) of the Gram matrix \(G_M\) of M:
) can be read from the rows or columns of the inverse matrix \(G_M^{-1}\) of the Gram matrix \(G_M\) of M:
For instance,  , where we identify each element of M with its image in \(M^*\). By abuse of notation, we also use
, where we identify each element of M with its image in \(M^*\). By abuse of notation, we also use  to denote the corresponding elements in
to denote the corresponding elements in  . Observe that \(l_1'^* = l_2'^* \equiv 0 \in A_M\). It is straightforward to verify that \(A_M\) can be generated by
. Observe that \(l_1'^* = l_2'^* \equiv 0 \in A_M\). It is straightforward to verify that \(A_M\) can be generated by  and hence \(A_M\) is isomorphic to \((\mathbb {Z}/2\mathbb {Z})^{ \oplus 6}\). Indeed, this follows from observing from the columns of \(G_M^{-1}\) that \(\alpha ^*_3=\gamma ^* + \alpha _1^*+\alpha _2^*\in A_M\) and \(\beta ^*_3=\gamma ^* + \beta _1^*+\beta _2^*\in A_M\).\(\square \)
and hence \(A_M\) is isomorphic to \((\mathbb {Z}/2\mathbb {Z})^{ \oplus 6}\). Indeed, this follows from observing from the columns of \(G_M^{-1}\) that \(\alpha ^*_3=\gamma ^* + \alpha _1^*+\alpha _2^*\in A_M\) and \(\beta ^*_3=\gamma ^* + \beta _1^*+\beta _2^*\in A_M\).\(\square \)
Remark 3.5
We derive a formula for the quadratic form \(q_M:A_M \rightarrow \mathbb {Q}/2\mathbb {Z}\):
Proposition 3.6
Let S be a K3 surface. If  is a lattice embedding such that \(\jmath (h)\) is a base point free polarization and
is a lattice embedding such that \(\jmath (h)\) is a base point free polarization and  , and
, and  (\(1 \leqslant i,j \leqslant 3\)) all represent irreducible curves, then \(\jmath \) is a primitive embedding.
(\(1 \leqslant i,j \leqslant 3\)) all represent irreducible curves, then \(\jmath \) is a primitive embedding.
Proof
Assume that \(\jmath \) is not primitive. Then the embedding \(\jmath \) must factor through the saturation  of M which is a non-trivial even overlattice of M:
of M which is a non-trivial even overlattice of M:  . By [26, Proposition 1.4.1], there is a bijection between even overlattices of M and isotropic subgroups of
. By [26, Proposition 1.4.1], there is a bijection between even overlattices of M and isotropic subgroups of  (which are generated by isotropic elements, i.e. \(v\in A_M\) such that \(q_M(v)=0\)). Using Lemma 3.4 and Remark 3.5, it is easy to classify the isotropic elements of \(A_M\). As
(which are generated by isotropic elements, i.e. \(v\in A_M\) such that \(q_M(v)=0\)). Using Lemma 3.4 and Remark 3.5, it is easy to classify the isotropic elements of \(A_M\). As  and
and  in \(A_M\), there are only three cases to consider. We drop the embedding \(\jmath \) in the rest of the proof.
in \(A_M\), there are only three cases to consider. We drop the embedding \(\jmath \) in the rest of the proof.
Case 1. The isotropic element is \(\gamma ^*\). From the columns of \(G_M^{-1}\) we see that \(\gamma ^* = \xi /2 \in A_M\). Hence, we have \(\xi = 2x\) for some  . But then
. But then  and
and  which would imply that h is not base point free by Theorem 3.2.
which would imply that h is not base point free by Theorem 3.2.
Case 2. The isotropic element is  where \(1 \leqslant i,j \leqslant 3\). Let us take \(\alpha _1^* + \beta _1^*\) for example. The other cases are similar. Note that
where \(1 \leqslant i,j \leqslant 3\). Let us take \(\alpha _1^* + \beta _1^*\) for example. The other cases are similar. Note that  in \(A_M\). We have \(\alpha _2 + \alpha _3 + \beta _2 + \beta _3 = 2y\) for some
in \(A_M\). We have \(\alpha _2 + \alpha _3 + \beta _2 + \beta _3 = 2y\) for some  . Because S is a K3 surface and
. Because S is a K3 surface and  , either y or \(-y\) is effective. Note that \(l_1'\), \(l_2'\), \(\alpha _i\) and
, either y or \(-y\) is effective. Note that \(l_1'\), \(l_2'\), \(\alpha _i\) and  (\(1 \leqslant i,j \leqslant 3\)) are irreducible curves (by the assumption), h is nef and
(\(1 \leqslant i,j \leqslant 3\)) are irreducible curves (by the assumption), h is nef and  . It follows that
. It follows that  is nef. Since
is nef. Since  , y is effective. Because \((y,\alpha _2) = (y, \alpha _3) = (y, \beta _2) = (y, \beta _3) = -1\), we know \(\alpha _2,\alpha _3,\beta _2\) and \(\beta _3\) are in the support of y. Write \(y = m\alpha _2 + n\alpha _3 + k \beta _2 + l \beta _3 + D = (\alpha _2 + \alpha _3 + \beta _2 + \beta _3)/2\) where D is an effective divisor,
, y is effective. Because \((y,\alpha _2) = (y, \alpha _3) = (y, \beta _2) = (y, \beta _3) = -1\), we know \(\alpha _2,\alpha _3,\beta _2\) and \(\beta _3\) are in the support of y. Write \(y = m\alpha _2 + n\alpha _3 + k \beta _2 + l \beta _3 + D = (\alpha _2 + \alpha _3 + \beta _2 + \beta _3)/2\) where D is an effective divisor,  and \(m,n,k,l \geqslant 1\). But then we have a contradiction
and \(m,n,k,l \geqslant 1\). But then we have a contradiction

Case 3. The isotropic element is  where \(1 \leqslant i,j \leqslant 3\). Take \(\alpha _1^* + \beta _1^* + \gamma ^*\) for example. Since \(\alpha _1^* + \beta _1^* + \gamma ^* = \alpha _2 /2+ \alpha _3/2 + \beta _2/2 + \beta _3/2 + \xi /2\) in \(A_M\), there exists an element z of
where \(1 \leqslant i,j \leqslant 3\). Take \(\alpha _1^* + \beta _1^* + \gamma ^*\) for example. Since \(\alpha _1^* + \beta _1^* + \gamma ^* = \alpha _2 /2+ \alpha _3/2 + \beta _2/2 + \beta _3/2 + \xi /2\) in \(A_M\), there exists an element z of  such that
such that  . Because S is a K3 surface,
. Because S is a K3 surface,  and \((z,h) = 1\), the class z represents an effective divisor. By the assumption \(l_1',l_2',\alpha _i\) and
and \((z,h) = 1\), the class z represents an effective divisor. By the assumption \(l_1',l_2',\alpha _i\) and  (\(1 \leqslant i,j \leqslant 3\)) represent irreducible curves. Note that
(\(1 \leqslant i,j \leqslant 3\)) represent irreducible curves. Note that  . Let us write \(z = m\alpha _2 + n\alpha _3 + k\beta _2 + l\beta _3 + D\), where D is effective,
. Let us write \(z = m\alpha _2 + n\alpha _3 + k\beta _2 + l\beta _3 + D\), where D is effective,  and \(m,n,k,l > 0\). Then we have
and \(m,n,k,l > 0\). Then we have

which implies that \((D, l_1') < 0\) and \((D, l_2') < 0\). Now we write
where \(D'\) is effective,  and \(m,n,k,l,s,t \geqslant 1\). But this is impossible: \(2\leqslant s+t \leqslant (z, h) = 1\). \(\square \)
and \(m,n,k,l,s,t \geqslant 1\). But this is impossible: \(2\leqslant s+t \leqslant (z, h) = 1\). \(\square \)
Corollary 3.7
Let C be a smooth plane quartic curve and \(L_1\), \(L_2\) two distinct lines such that \(C+L_1+L_2\) has simple normal crossings and let  be the lattice embedding given in Notation 3.3. Then \(\jmath \) is a primitive embedding.
be the lattice embedding given in Notation 3.3. Then \(\jmath \) is a primitive embedding.
The proof of Proposition 3.6 can easily be adapted to proof the following lemma.
Lemma 3.8
Let S be a K3 surface and  be a lattice embedding. If none of \(\jmath (\xi )\),
be a lattice embedding. If none of \(\jmath (\xi )\),  or
or  (\(1 \leqslant i, i'\!, j, j' \leqslant 3\)) is divisible by 2 in
(\(1 \leqslant i, i'\!, j, j' \leqslant 3\)) is divisible by 2 in  , then the embedding \(\jmath \) is primitive.
, then the embedding \(\jmath \) is primitive.
Proposition 3.9
Assume that S is a K3 surface such that  is isomorphic to the lattice M. Then S is the double cover of
is isomorphic to the lattice M. Then S is the double cover of  branched over a reducible curve \(C + L_1 + L_2\) where C is a smooth plane quartic, \(L_1, L_2\) are lines and \(C+L_1+L_2\) has simple normal crossings.
branched over a reducible curve \(C + L_1 + L_2\) where C is a smooth plane quartic, \(L_1, L_2\) are lines and \(C+L_1+L_2\) has simple normal crossings.
Proof
By assumption there exist  satisfying the numerical conditions in Notation 3.3. Without loss of generality, we assume that h is nef (this can be achieved by acting by \(\pm W(S)\)). Then \(l_1'\) and \(l_2'\) are both effective (as
satisfying the numerical conditions in Notation 3.3. Without loss of generality, we assume that h is nef (this can be achieved by acting by \(\pm W(S)\)). Then \(l_1'\) and \(l_2'\) are both effective (as  , \((h,l_i')=1\)). We further assume that
, \((h,l_i')=1\)). We further assume that  (\(1 \leqslant i,j \leqslant 4\)) and \(\gamma \) are effective (apply \(s_{\alpha _i}\) or
(\(1 \leqslant i,j \leqslant 4\)) and \(\gamma \) are effective (apply \(s_{\alpha _i}\) or  or \(s_{\gamma }\) if necessary).
or \(s_{\gamma }\) if necessary).
As h is nef and \((h,h)=2>0\), h is a polarization of degree 2. We will show that h is base point free by reductio ad absurdum. By Theorem 3.2, there exists a divisor D such that \((D, D) = 0\) and \((h, D) = 1\). Note that this is a numerical condition. Write D as a linear combination of \(\gamma , l_1', \alpha _1, \ldots , \alpha _3, l_2', \beta _1, \ldots , \beta _3\) and \(\xi \), with coefficients \(c_1,\ldots , c_{10}\). Let \(S_{(Q,L,L')}\) be the K3 surface associated to a smooth quartic curve Q and two lines \(L,L'\) such that \(Q+L+L'\) has simple normal crossings. Find the curve classes corresponding to \(\gamma , l_1', \alpha _1, \ldots , \alpha _3, l_2', \beta _1, \ldots , \beta _3,\xi \) (as what we did at the beginning of this subsection) and consider their linear combination \(D'\) with coefficients \(c_1,\ldots , c_{10}\), the same values as in the expression for D. Then, both D and \(D'\) satisfy the same numerical conditions in S (respectively \(S_{(Q,L,L')}\)) with respect to the divisor class \(h= \gamma + \xi \). Again, by Theorem 3.2 the pull-back h of  in \(S_{(Q,L,L')}\) has base points, which gives a contradiction. So the linear system of h defines a degree two map
in \(S_{(Q,L,L')}\) has base points, which gives a contradiction. So the linear system of h defines a degree two map  . Since S is a K3 surface of degree 2, the branching locus must be a sextic curve B.
. Since S is a K3 surface of degree 2, the branching locus must be a sextic curve B.
Consider  . Note that \((h'\!, h')>0\) and \((h'\!, h) > 0\). We can write any effective divisor as
. Note that \((h'\!, h')>0\) and \((h'\!, h) > 0\). We can write any effective divisor as

where \(a_i, b_i, c\in \mathbb Z\), where \(0\leqslant i\leqslant 4\). Let \(k_i= a_0/2-a_i\), \(l_i= b_0/2-b_i\) where \(1\leqslant i\leqslant 4\). It follows that

Let \(D\in \Delta (S)\) as in (6). Then  implies that
implies that

First note that when \(a_0+b_0=(D,h)=0\), then (8) gives that either  and
and  or \(c=0\), and all coefficients in
or \(c=0\), and all coefficients in  but one equal 0 and
but one equal 0 and  . In particular,
. In particular,  . If \(D\in \Delta ^+(S)\cap \langle h \rangle ^{\perp }_M\), then \((D,h)=a_0+b_0=0\) which in turn implies that
. If \(D\in \Delta ^+(S)\cap \langle h \rangle ^{\perp }_M\), then \((D,h)=a_0+b_0=0\) which in turn implies that  .
.
Now suppose that \(D\in \Delta ^+(S)\) and \((h,D)>0\). Then (7) implies that \(a_0+b_0>0\) and (8) gives \(c\geqslant 0\). Then, by the arithmetic-geometric mean inequality and (8), we get

where the latter inequality follows from observing that the first summand is positive and

Hence \((h'\!,D)>0\) for all \(D\in \Delta ^+(S)\). Moreover, if \(D \subset S\) is rational and \( D \not \in \Delta ^+(S)\), then \(\pi _*(D)\ne 0\) and  . Hence, by [15, Corollary 8.1.7], \(h'\) is ample.
. Hence, by [15, Corollary 8.1.7], \(h'\) is ample.
Because \((h'\!, l_1')=1\), the class \(l_1'\) is represented by an irreducible curve. Similarly, \(l_2',\alpha _i\) and  (\(1 \leqslant i,j \leqslant 3\)) all correspond to irreducible curves. It follows that the irreducible rational curves \(\alpha _1, \ldots , \alpha _4, \beta _1, \ldots , \beta _4\) are contracted by \(\pi \) to ordinary double points of the sextic B. Let \(L_1'\) (respectively \(L_2'\)) be the unique irreducible curve in S corresponding to the class \(l_1'\) (respectively \(l_2'\)) and set \(L_1 = \pi (L_1')\) (respectively \(L_2 = \pi (L_2')\)). Since
(\(1 \leqslant i,j \leqslant 3\)) all correspond to irreducible curves. It follows that the irreducible rational curves \(\alpha _1, \ldots , \alpha _4, \beta _1, \ldots , \beta _4\) are contracted by \(\pi \) to ordinary double points of the sextic B. Let \(L_1'\) (respectively \(L_2'\)) be the unique irreducible curve in S corresponding to the class \(l_1'\) (respectively \(l_2'\)) and set \(L_1 = \pi (L_1')\) (respectively \(L_2 = \pi (L_2')\)). Since  , the projection formula implies that \(L_1\) is a line. Moreover, the line \(L_1\) has to pass through four ordinary double points of the branched curve B since
, the projection formula implies that \(L_1\) is a line. Moreover, the line \(L_1\) has to pass through four ordinary double points of the branched curve B since  . Similarly, \(L_2\) is also a line passing through four different ordinary double points of B. (Note that both \(L_1\) and \(L_2\) pass through the singularity of B corresponding to \(\gamma \).) By Bezout’s theorem, the two lines \(L_1\) and \(L_2\) are both components of B (otherwise we have contradictions:
. Similarly, \(L_2\) is also a line passing through four different ordinary double points of B. (Note that both \(L_1\) and \(L_2\) pass through the singularity of B corresponding to \(\gamma \).) By Bezout’s theorem, the two lines \(L_1\) and \(L_2\) are both components of B (otherwise we have contradictions:  and analogously for \(L_2\)).\(\square \)
and analogously for \(L_2\)).\(\square \)
Corollary 3.10
For a sufficiently general triple \((C, L_1, L_2)\) (i.e. outside the union of a countable number of proper subvarieties of the moduli space), the Picard lattice  coincides with M via the embedding \(\jmath \).
coincides with M via the embedding \(\jmath \).
Proof
The argument in [16, Corollary 6.19] works here. Alternatively, let \(L_1\) and \(L_2\) be given by linear forms \(l_1\) and \(l_2\), respectively, and consider the elliptic fibration  defined by the function
defined by the function  . If \((C, L_1, L_2)\) is sufficiently general, then the pencil of lines generated by \(L_1\) and \(L_2\) only consists of lines intersecting C normally or lines tangent to C at a point. As a result, the elliptic fibration contains two reducible singular fibers of type \(I_0^*\) (i.e. with 5 components) and 12 singular fibers of type \(I_1\) (i.e. with one nodal component), where we follow Kodaira’s notation as in [4, Section V.7], [15, Section 11.1.3]. Note that the fibration admits a 2-section \(\gamma \). Consider the associated Jacobian fibration
. If \((C, L_1, L_2)\) is sufficiently general, then the pencil of lines generated by \(L_1\) and \(L_2\) only consists of lines intersecting C normally or lines tangent to C at a point. As a result, the elliptic fibration contains two reducible singular fibers of type \(I_0^*\) (i.e. with 5 components) and 12 singular fibers of type \(I_1\) (i.e. with one nodal component), where we follow Kodaira’s notation as in [4, Section V.7], [15, Section 11.1.3]. Note that the fibration admits a 2-section \(\gamma \). Consider the associated Jacobian fibration  (see for example [15, Section 11.4]). By the Shioda–Tate formula [15, Corollaries 11.3.4 and 11.4.7], the K3 surface \(S_{(C,L_1,L_2)}\) has Picard number 10 which equals the rank of M. Moreover, we have [15, Section 11, (4.5)]:
(see for example [15, Section 11.4]). By the Shioda–Tate formula [15, Corollaries 11.3.4 and 11.4.7], the K3 surface \(S_{(C,L_1,L_2)}\) has Picard number 10 which equals the rank of M. Moreover, we have [15, Section 11, (4.5)]:

It is easy to compute that the Gram matrix \(G_M\) has determinant \((-64)\). The proposition then follows from the following standard fact on lattices (which implies ):
):

As  and they have the same rank and discriminant, then
and they have the same rank and discriminant, then  .\(\square \)
.\(\square \)
Now let us consider the case when C has at worst simple singularities not contained in \(L_1+L_2\) and \(C+L_1+L_2\) has simple normal crossings away from the singularities of C. We still use \(S_{(C,L_1,L_2)}\) to denote the K3 surface obtained as a minimal resolution of the double cover of  along \(C+L_1+L_2\). The rank 10 lattice M is the same as in Notation 3.3.
along \(C+L_1+L_2\). The rank 10 lattice M is the same as in Notation 3.3.
Lemma 3.11
If C has at worst simple singularities not contained in \(L_1+L_2\) and \(C+L_1+L_2\) has simple normal crossings away from the singularities of C, then there exists a primitive embedding  such that \(\jmath (h)\) is a base point free degree two polarization.
such that \(\jmath (h)\) is a base point free degree two polarization.
Proof
Thanks to the transversal intersection, we define the embedding \(\jmath \) as in the generic case. In particular, the morphism  is defined by \(\jmath (h)\). The embedding \(\jmath \) is primitive by Proposition 3.6.\(\square \)
is defined by \(\jmath (h)\). The embedding \(\jmath \) is primitive by Proposition 3.6.\(\square \)
3.3 M-polarized K3 surfaces and the period map
In this subsection let us compute the (generic) Picard lattice M and the transcendental lattice T. Then we shall determine the period domain  and define a period map for generic triples \((C, L_1, L_2)\) via the periods of M-polarized K3 surfaces \(S_{(C, L_1, L_2)}\).
and define a period map for generic triples \((C, L_1, L_2)\) via the periods of M-polarized K3 surfaces \(S_{(C, L_1, L_2)}\).
Definition 3.12
Let M be the lattice defined in Notation 3.3. An M
-polarized
K3 surface is a pair \((S, \jmath )\) such that  is a primitive lattice embedding. The embedding \(\jmath \) is called the M
-polarization of S. We will simply say that S is an M
-polarized
K3 surface when no confusion about \(\jmath \) is likely.
is a primitive lattice embedding. The embedding \(\jmath \) is called the M
-polarization of S. We will simply say that S is an M
-polarized
K3 surface when no confusion about \(\jmath \) is likely.
We now determine the lattice M and show that it admits a unique primitive embedding into the K3 lattice \(\Lambda _{K3}\).
Proposition 3.13
Let M be the lattice defined in Notation 3.3. Then M is isomorphic to the lattice \(U(2) \perp A_1^{2} \perp D_6\) and admits a unique primitive embedding (up to isometry) \(M \hookrightarrow \Lambda _{K3}\) into the K3 lattice \(\Lambda _{K3}\). The orthogonal complement  with respect to the embedding is isometric to \(U \perp U(2) \perp A_1^{2} \perp D_6\).
with respect to the embedding is isometric to \(U \perp U(2) \perp A_1^{2} \perp D_6\).
Proof
By [26, Corollary 1.13.3] the lattice M is uniquely determined by its invariants which can be easily computed from the Gram matrix \(G_M\) (see also Lemma 3.4 and Remark 3.5).
-
M has rank 10 and signature (1, 9).
-
The Gram matrix \(G_M\) has determinant \((-64)\).
-
The discriminant group is
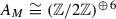 with quadratic form
with quadratic form 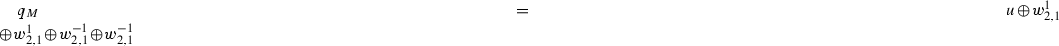 , where \(u,w_{2,1}^{1}\) and \(w_{2,1}^{-1}\) are the discriminant forms associated to \(U(2),E_7\) and \(A_1\) respectively (cf. [5, Section 1.5 and Appendix A] and references therein). Note that
, where \(u,w_{2,1}^{1}\) and \(w_{2,1}^{-1}\) are the discriminant forms associated to \(U(2),E_7\) and \(A_1\) respectively (cf. [5, Section 1.5 and Appendix A] and references therein). Note that 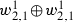 is isomorphic to the discriminant form of \(D_6\).
is isomorphic to the discriminant form of \(D_6\).
By [26, Theorem 1.14.4] the lattice M admits a unique primitive embedding into \(\Lambda _{K3}\). The claim on the orthogonal complement T follows from [26, Proposition 1.6.1].\(\square \)
Remark 3.14
Note that both M and T are even indefinite 2-elementary lattices (a lattice L is 2-elementary if  for some k). One could also invoke Nikulin’s classification [26, Theorem 3.6.2] of such lattices to prove the previous proposition. Moreover, M and T are orthogonal to each other in a unimodular lattice and hence
for some k). One could also invoke Nikulin’s classification [26, Theorem 3.6.2] of such lattices to prove the previous proposition. Moreover, M and T are orthogonal to each other in a unimodular lattice and hence  .
.
The moduli space of M-polarized K3 surfaces is a quotient  for a certain Hermitian symmetric domain
for a certain Hermitian symmetric domain  of type IV and some arithmetic group \(\Gamma \) (see [8]). Fix the (unique) embedding \(M \hookrightarrow \Lambda _{K3}\) and define
of type IV and some arithmetic group \(\Gamma \) (see [8]). Fix the (unique) embedding \(M \hookrightarrow \Lambda _{K3}\) and define

to be one of the two connected components. Note that  can also be identified with
can also be identified with

To specify the moduli of M-polarized K3 surfaces, one also needs to determine the arithmetic group \(\Gamma \). In the standard situation considered in [8] it is required that the M-polarization is pointwise fixed by the arithmetic group and one takes \(\Gamma \) to be \(O^*(T)\). In our geometric context the choice is different. Specifically, the permutations among \(\alpha _1, \ldots , \alpha _4\) and among \(\beta _1, \ldots , \beta _4\) are allowed. Observe that at the moment we view the lines \(L_1\) and \(L_2\) as labeled lines, distinguishing the tuples \((C, L_1, L_2)\) and \((C, L_2, L_1)\) and we do not consider the isometry of M induced by flipping the two lines.
Let L be an even lattice. Recall that any \(g \in O(L)\) naturally induces  by \(g^*\varphi :v \mapsto \varphi (g^{-1}v)\) (which further defines an automorphism of \(A_L\) preserving \(q_L\), therefore giving a natural homomorphism \(r_L:O(L)\rightarrow O(q_L)\)).
by \(g^*\varphi :v \mapsto \varphi (g^{-1}v)\) (which further defines an automorphism of \(A_L\) preserving \(q_L\), therefore giving a natural homomorphism \(r_L:O(L)\rightarrow O(q_L)\)).
Lemma 3.15
The homomorphisms \(r_M:O(M) \rightarrow O(q_M)\) and \(r_T:O(T) \rightarrow O(q_T)\) are both surjective.
Proof
The lemma follows from Lemma 3.4 and [26, Theorem 1.14.2].\(\square \)
In particular, we have \(O(M) \twoheadrightarrow O(q_M) \cong O(q_T) \twoheadleftarrow O(T)\). By [26, Theorem 1.6.1, Corollary 1.5.2], an automorphism \(g_M \in O(M)\) can be extended to an automorphism of \(\Lambda _{K3}\) if and only if  . In our case, any automorphism \(g_M \in O(M)\) can be extended to an element in \(O(\Lambda _{K3})\).
. In our case, any automorphism \(g_M \in O(M)\) can be extended to an element in \(O(\Lambda _{K3})\).
Lemma 3.16
Let \(g_M\) (respectively \(g_T\)) be an automorphism of M (respectively T). If \(r_M(g_M) = r_T(g_T)\), then \(g_M\) can be lifted to \(g \in O(\Lambda _{K3})\) with \(g|_T = g_T\). The same statement holds for \(g_T\).
Proof
The proof is similar to that for [15, Proposition 14.2.6]. Take any \(x = x_M + x_T \in \Lambda _{K3}\) with \(x_M \in M^*\) and  . View \(\Lambda _{K3}\) as an overlattice of
. View \(\Lambda _{K3}\) as an overlattice of  . The corresponding isotropic subgroup (cf. [26, Section 1.4]) of
. The corresponding isotropic subgroup (cf. [26, Section 1.4]) of  is
is  . Since \(x \in \Lambda _{K3}\), \(\overline{x}_M + \overline{x}_T\) is contained in
. Since \(x \in \Lambda _{K3}\), \(\overline{x}_M + \overline{x}_T\) is contained in  (where \(\overline{x}_M\) denotes the corresponding element of \(x_M\) in \(A_M\) and similarly for \(\overline{x}_T\)). Consider
(where \(\overline{x}_M\) denotes the corresponding element of \(x_M\) in \(A_M\) and similarly for \(\overline{x}_T\)). Consider  . Note that the image of \(g_M(x_M) + g_T(x_T)\) under the map
. Note that the image of \(g_M(x_M) + g_T(x_T)\) under the map  is \(r_M(g_M)(\overline{x}_M) + r_T(g_T)(\overline{x}_T)\). Recall that \(A_M\) and \(A_T\) are identified via the natural projections
is \(r_M(g_M)(\overline{x}_M) + r_T(g_T)(\overline{x}_T)\). Recall that \(A_M\) and \(A_T\) are identified via the natural projections  . Because \(r_M(g_M) = r_T(g_T)\), \(r_M(g_M)(\overline{x}_M) + r_T(g_T)(\overline{x}_T)\) is contained in
. Because \(r_M(g_M) = r_T(g_T)\), \(r_M(g_M)(\overline{x}_M) + r_T(g_T)(\overline{x}_T)\) is contained in  . In other words, we have \(g_M(x_M) + g_T(x_T) \in \Lambda _{K3}\).\(\square \)
. In other words, we have \(g_M(x_M) + g_T(x_T) \in \Lambda _{K3}\).\(\square \)
Let \(\Sigma _{\alpha } \subset O(M)\) (respectively  ) be the subgroup which permutes
) be the subgroup which permutes  (respectively the subgroup which permutes \(\{\beta _1, \ldots , \beta _4\}\)). We seek automorphisms of T which can be extended to automorphisms of \(\Lambda _{K3}\) whose restrictions to M belong to \(\Sigma _\alpha \) or \(\Sigma _\beta \). We observe that there is a natural inclusion
(respectively the subgroup which permutes \(\{\beta _1, \ldots , \beta _4\}\)). We seek automorphisms of T which can be extended to automorphisms of \(\Lambda _{K3}\) whose restrictions to M belong to \(\Sigma _\alpha \) or \(\Sigma _\beta \). We observe that there is a natural inclusion  .
.
Lemma 3.17
The composition  is injective.
is injective.
Proof
First let us describe the automorphisms of \(A_M\) induced by the transpositions in \(\Sigma _\alpha \) and \(\Sigma _{\beta }\). We consider \(\Sigma _\alpha \) and the case of \(\Sigma _\beta \) is analogous. The image of the transposition \((\alpha _i\alpha _i')\) (with \(1 \leqslant i \ne i' \leqslant 3\)) defines the element \(r_M((\alpha _i\alpha _i'))\) in \(O(q_M)\) given by \(\alpha _i^* \mapsto \alpha _{i'}^*\), \(\alpha _{i'}^* \mapsto \alpha _i^*\), leaving \(\gamma ^*\!,\alpha _{i''}^*\) ( ),
),  (\(1 \leqslant j \leqslant 3\)) and \(\xi ^*\) invariant.
(\(1 \leqslant j \leqslant 3\)) and \(\xi ^*\) invariant.
The automorphism of \(A_M\) induced by the transposition \((\alpha _1\alpha _4)\) between \(\alpha _1\) and \(\alpha _4\) is given by
and  (\(1 \leqslant j \leqslant 3\)) are invariant by this action. The case of transpositions \((\alpha _2\alpha _4)\) and \((\alpha _3\alpha _4)\) is analogous. As it is well-known, the transpositions generate \(\Sigma _\alpha \) and \(\Sigma _\beta \). It is easy to compute the image of
(\(1 \leqslant j \leqslant 3\)) are invariant by this action. The case of transpositions \((\alpha _2\alpha _4)\) and \((\alpha _3\alpha _4)\) is analogous. As it is well-known, the transpositions generate \(\Sigma _\alpha \) and \(\Sigma _\beta \). It is easy to compute the image of  in \(O(q_M)\) using the previous descriptions.
in \(O(q_M)\) using the previous descriptions.
Let \(g_\alpha \in \Sigma _\alpha \) and \(g_\beta \in \Sigma _\beta \). Now we describe how to univocally recover  from the induced action \(\overline{g}\) on \(A_M\). In particular, this will show that the composed map
from the induced action \(\overline{g}\) on \(A_M\). In particular, this will show that the composed map  is injective. Consider \(\overline{g}(\xi ^*)\). Because
is injective. Consider \(\overline{g}(\xi ^*)\). Because  , the induced action \(\overline{g}\) sends \(\xi ^*\) to an element \(v^*\) satisfying
, the induced action \(\overline{g}\) sends \(\xi ^*\) to an element \(v^*\) satisfying  . By Remark 3.5 such elements are \(\xi ^*\), \(\xi ^* + \alpha _i^*\),
. By Remark 3.5 such elements are \(\xi ^*\), \(\xi ^* + \alpha _i^*\),  and
and  (\(1 \leqslant i,j \leqslant 3\)).
(\(1 \leqslant i,j \leqslant 3\)).
-
If \(\overline{g}(\xi ^*) = \xi ^*\), then \(g_\alpha \) (respectively \(g_\beta \)) fixes \(\alpha _4\) (respectively \(\beta _4\)) by the description of the permutations above and \(g_\alpha \) (respectively \(g_\beta \)) can be recovered from the action of \(\overline{g}\) on the set
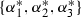 (respectively \(\{\beta _1^*, \beta _2^*, \beta _3^*\}\)).
(respectively \(\{\beta _1^*, \beta _2^*, \beta _3^*\}\)). -
If \(\overline{g}(\xi ^*) = \xi ^* + \alpha _i^*\) (\(1 \leqslant i \leqslant 3\)), then \(g_\alpha \) maps \(\alpha _4\) to \(\alpha _i\) and \(g_\beta \) fixes \(\beta _4\). Then \(g_\alpha \) (respectively \(g_\beta \)) is determined by the action of \(\overline{g}\) on the set
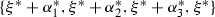 (respectively \(\{\beta _1^*, \beta _2^*, \beta _3^*\}\)).
(respectively \(\{\beta _1^*, \beta _2^*, \beta _3^*\}\)). -
If
 (\(1 \leqslant j \leqslant 3\)), then \(g_\beta \) maps \(\beta _4\) to
(\(1 \leqslant j \leqslant 3\)), then \(g_\beta \) maps \(\beta _4\) to  and \(g_\alpha \) fixes \(\alpha _4\). Then \(g_\alpha \) (respectively \(g_\beta \)) is determined by the action of \(\overline{g}\) on the set
and \(g_\alpha \) fixes \(\alpha _4\). Then \(g_\alpha \) (respectively \(g_\beta \)) is determined by the action of \(\overline{g}\) on the set 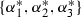 (respectively \(\{\xi ^*+ \beta _1^*, \xi ^*+\beta _2^*, \xi ^*+\beta _3^*, \xi ^*\}\)).
(respectively \(\{\xi ^*+ \beta _1^*, \xi ^*+\beta _2^*, \xi ^*+\beta _3^*, \xi ^*\}\)). -
If
 (\(1 \leqslant i,j \leqslant 3\)), then \(g_\alpha \) maps \(\alpha _4\) to \(\alpha _i\) and \(g_\beta \) maps \(\beta _4\) to
(\(1 \leqslant i,j \leqslant 3\)), then \(g_\alpha \) maps \(\alpha _4\) to \(\alpha _i\) and \(g_\beta \) maps \(\beta _4\) to  . Then \(g_\alpha \) (respectively \(g_\beta \)) can be recovered by the action of \(\overline{g}\) on the set
. Then \(g_\alpha \) (respectively \(g_\beta \)) can be recovered by the action of \(\overline{g}\) on the set 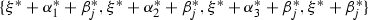 (respectively
(respectively 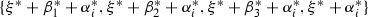 ). \(\square \)
). \(\square \)
By abuse of notation, we also use  to denote its image in \(O(q_T) \cong O(q_M)\). There exists a natural exact sequence \(1 \rightarrow \widetilde{O}(T) \rightarrow O(T) \xrightarrow {r_T} O(q_T) \rightarrow 1\) which also induces \(1 \rightarrow O^*(T) \rightarrow O_-(T) \rightarrow O(q_T) \rightarrow 1\). We define \(\Gamma \subset O_{-} (T)\subset O(T)\) as the following extension:
to denote its image in \(O(q_T) \cong O(q_M)\). There exists a natural exact sequence \(1 \rightarrow \widetilde{O}(T) \rightarrow O(T) \xrightarrow {r_T} O(q_T) \rightarrow 1\) which also induces \(1 \rightarrow O^*(T) \rightarrow O_-(T) \rightarrow O(q_T) \rightarrow 1\). We define \(\Gamma \subset O_{-} (T)\subset O(T)\) as the following extension:

By Lemmas 3.16 and 3.17, the group \(\Gamma \) fixes M but may permute the elements \(\alpha _1, \ldots , \alpha _4\) (respectively \(\beta _1, \ldots , \beta _4\)). Note that \(O^*(T)\) is a normal subgroup of \(\Gamma \) and  . Also, \(\Gamma \) and O(T) are commensurable and hence \(\Gamma \) is an arithmetic group. There is a natural action of \(\Gamma \) on
. Also, \(\Gamma \) and O(T) are commensurable and hence \(\Gamma \) is an arithmetic group. There is a natural action of \(\Gamma \) on  (see the description of
(see the description of  in (10)).
in (10)).
Recall that  is the moduli space of triples \((C, L_1, L_2)\) consisting of a quartic curve C and (labeled) lines \(L_1\), \(L_2\) such that \(C + L_1 + L_2\) has at worst simple singularities.
is the moduli space of triples \((C, L_1, L_2)\) consisting of a quartic curve C and (labeled) lines \(L_1\), \(L_2\) such that \(C + L_1 + L_2\) has at worst simple singularities.
Proposition 3.18
The period map  that associates to a (generic) triple \((C, L_1, L_2)\) the periods of the K3 surface \(S_{(C,L_1,L_2)}\) defines a birational map
that associates to a (generic) triple \((C, L_1, L_2)\) the periods of the K3 surface \(S_{(C,L_1,L_2)}\) defines a birational map  .
.
Proof
Let U be an open subset of  parameterizing triples \((C, L_1, L_2)\) with C smooth quartic curves and \(L_1,L_2\) two (labeled) lines such that \(C+L_1+L_2\) has simple normal crossings. Set \(\Sigma _4\) to be the permutation group of four elements and note that \(\Sigma _\alpha \cong \Sigma _\beta \cong \Sigma _4\). Let \(\widetilde{U}\) be the
parameterizing triples \((C, L_1, L_2)\) with C smooth quartic curves and \(L_1,L_2\) two (labeled) lines such that \(C+L_1+L_2\) has simple normal crossings. Set \(\Sigma _4\) to be the permutation group of four elements and note that \(\Sigma _\alpha \cong \Sigma _\beta \cong \Sigma _4\). Let \(\widetilde{U}\) be the  -cover of U that parametrizes quintuples \((C, L_1, L_2, \sigma _1,\sigma _2)\) where
-cover of U that parametrizes quintuples \((C, L_1, L_2, \sigma _1,\sigma _2)\) where  , \(k=1,2\), is a labeling of the intersection points of \(C \cap L_k\). Note that the monodromy group acts as the permutation group \(\Sigma _4\) on the four points of intersection \(C \cap L_k\). By Corollary 3.7, \(\sigma _1\) and \(\sigma _2\) determine an M-polarization \(\jmath \) of the K3 surface \(S_{(C, L_1, L_2)}\). Therefore there is a well-defined map
, \(k=1,2\), is a labeling of the intersection points of \(C \cap L_k\). Note that the monodromy group acts as the permutation group \(\Sigma _4\) on the four points of intersection \(C \cap L_k\). By Corollary 3.7, \(\sigma _1\) and \(\sigma _2\) determine an M-polarization \(\jmath \) of the K3 surface \(S_{(C, L_1, L_2)}\). Therefore there is a well-defined map

By the global Torelli theorem and the surjectivity of the period map for K3 surfaces (see also Proposition 3.9), the map  is a birational morphism. The group
is a birational morphism. The group  acts naturally on both \(\widetilde{U}\) and
acts naturally on both \(\widetilde{U}\) and  as \(\Gamma \) is an extension of
as \(\Gamma \) is an extension of  and \(O^*(T)\). Essentially, the actions are induced by the permutation of the labeling of the intersection points \(C \cap L_k\) (\(k=0,1\)). It follows that
and \(O^*(T)\). Essentially, the actions are induced by the permutation of the labeling of the intersection points \(C \cap L_k\) (\(k=0,1\)). It follows that  is
is  -equivariant and descends to the birational map
-equivariant and descends to the birational map  (see also Lemmas 3.16 and 3.17).\(\square \)
(see also Lemmas 3.16 and 3.17).\(\square \)
3.4 M-polarization for non-generic intersections
We will show in this section that the birational map  in Proposition 3.18 extends to a birational morphism
in Proposition 3.18 extends to a birational morphism  . To do this, we need to extend the construction of M-polarization
. To do this, we need to extend the construction of M-polarization  to the non-generic triples \((C, L_1, L_2)\) and show that the construction fits in families. The idea is to use the normalized lattice polarization (cf. [17, Definition 4.24]) for degree 5 pairs constructed in [17, Section 4.2.3]. A degree
d
pair (D, L) consists of a degree d plane curve D and a line
to the non-generic triples \((C, L_1, L_2)\) and show that the construction fits in families. The idea is to use the normalized lattice polarization (cf. [17, Definition 4.24]) for degree 5 pairs constructed in [17, Section 4.2.3]. A degree
d
pair (D, L) consists of a degree d plane curve D and a line  (see [17, Definition 2.1]). Given a triple \((C, L_1, L_2)\) of a quartic curve C and two different lines \(L_1\) and \(L_2\), one can construct a degree 5 pair in two ways: \((C+L_2, L_1)\) or \((C+L_1, L_2)\). We follow the notation of the previous subsections, especially Notation 3.3. We will determine the images of \(\gamma , l_1', \alpha _1, \ldots , \alpha _4\) (respectively \(\gamma , l_2', \beta _1, \ldots , \beta _4\)) using the degree 5 pair \((C+L_2, L_1)\) (respectively \((C+L_1, L_2)\)).
(see [17, Definition 2.1]). Given a triple \((C, L_1, L_2)\) of a quartic curve C and two different lines \(L_1\) and \(L_2\), one can construct a degree 5 pair in two ways: \((C+L_2, L_1)\) or \((C+L_1, L_2)\). We follow the notation of the previous subsections, especially Notation 3.3. We will determine the images of \(\gamma , l_1', \alpha _1, \ldots , \alpha _4\) (respectively \(\gamma , l_2', \beta _1, \ldots , \beta _4\)) using the degree 5 pair \((C+L_2, L_1)\) (respectively \((C+L_1, L_2)\)).
Let us briefly review the construction of normalized lattice polarization for degree 5 pairs. See [17, Section 4.2.3] for more details. Let (D, L) be a degree 5 pair such that  has at worst simple singularities. Let \(\overline{S}_{(D,L)}\) be the normal surface obtained as the double cover of
has at worst simple singularities. Let \(\overline{S}_{(D,L)}\) be the normal surface obtained as the double cover of  branched along B. Let \(S_{(D,L)}\) be the minimal resolution of \(\overline{S}_{(D,L)}\), called the K3 surface associated to (D, L). The surface \(S_{(D,L)}\) can also be obtained as the canonical resolution of \(\overline{S}_{(D,L)}\), see [4, Section III.7]. Namely, there exists a commutative diagram:
branched along B. Let \(S_{(D,L)}\) be the minimal resolution of \(\overline{S}_{(D,L)}\), called the K3 surface associated to (D, L). The surface \(S_{(D,L)}\) can also be obtained as the canonical resolution of \(\overline{S}_{(D,L)}\), see [4, Section III.7]. Namely, there exists a commutative diagram:

where \(S'\) is obtained by an inductive process. Start with  and \(B_{-1} = B = D+ L\). Simultaneously blow up all the singular points of B. Let
and \(B_{-1} = B = D+ L\). Simultaneously blow up all the singular points of B. Let  be the resulting surface and set \(B_0\) to be the strict transform of B together with the exceptional divisors of \(\epsilon _0\) reduced mod 2. Repeat the process for \(S_0\) and \(B_0\) until the resulting divisor \(B_N\) is smooth. Let \(S' = S_N\), \(B' = B_N\) and
be the resulting surface and set \(B_0\) to be the strict transform of B together with the exceptional divisors of \(\epsilon _0\) reduced mod 2. Repeat the process for \(S_0\) and \(B_0\) until the resulting divisor \(B_N\) is smooth. Let \(S' = S_N\), \(B' = B_N\) and  . Now take the double cover \(\pi ':S_{(D, L)} \rightarrow S'\) branched along the smooth locus \(B'\).
. Now take the double cover \(\pi ':S_{(D, L)} \rightarrow S'\) branched along the smooth locus \(B'\).
The construction of a normalized lattice polarization for degree 5 pairs is a modification of the process of canonical resolution. We may choose a labeling of the intersection points of D and L, which means a surjective map  satisfying
satisfying  for every \(p \in D \cap L\). As argued in [17, Proposition 4.25], L is blown up exactly 5 times in the desingularization process described above. The blown-up points can be chosen as the first five steps of the sequence of blow-ups:
for every \(p \in D \cap L\). As argued in [17, Proposition 4.25], L is blown up exactly 5 times in the desingularization process described above. The blown-up points can be chosen as the first five steps of the sequence of blow-ups:  , and the labeling determines the order of these first five blow-ups. Let \(\{p_k\}_{k=0}^4\) be the centers of these blow-ups and \(E_k\) be the exceptional divisors. Note that \(p_k \in S_{k-1}\) (the image of \(p_k\) under the contraction to
, and the labeling determines the order of these first five blow-ups. Let \(\{p_k\}_{k=0}^4\) be the centers of these blow-ups and \(E_k\) be the exceptional divisors. Note that \(p_k \in S_{k-1}\) (the image of \(p_k\) under the contraction to  is a point of intersection \(D \cap L\)) and \(E_k\) is a divisor on \(S_k\) for \(k = 0, \ldots , 4\). We define the following divisors:
is a point of intersection \(D \cap L\)) and \(E_k\) is a divisor on \(S_k\) for \(k = 0, \ldots , 4\). We define the following divisors:

for \(0 \leqslant k \leqslant 4\). The divisor \(D_k\) on \(S_{(D,L)}\) is Artin’s fundamental cycle (see for example [4, p. 76]) associated to the simple singularity of the curve \(B_{k-1}\) at the point \(p_k\).
The procedure described above produces five divisors: \(D_0, \ldots , D_4\). One can also consider the strict transform of L in \(S'\) and take its preimage in \(S_{(D,L)}\). This is a smooth rational curve on the K3 surface and we will denote its corresponding class by \(L'\). We summarize the properties of these 6 divisors \(L'\!, D_0, \ldots , D_4\) in the following result. Given families of curves (C, L), we can carry out a simultaneous resolution in families. As a result the construction above fits well in families, see [17, p. 2141].
Lemma 3.19
For a pair (D, L) and the surface \(S_{(D,L)}\) as described above the following statements hold:
-
(a)
the polarization class of \(S_{(D,L)}\) is
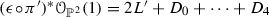 , and
, and -
(b)
their intersections are
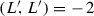 ,
, 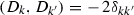 , \((L'\!, D_k) = 1\) for \(0 \leqslant k,k' \leqslant 4\).
, \((L'\!, D_k) = 1\) for \(0 \leqslant k,k' \leqslant 4\).
Proof
See the proof of [17, Proposition 4.25].\(\square \)
Let us consider triples \((C, L_1, L_2)\) consisting of a quartic curve C and lines \(L_1\), \(L_2\) such that \(C+L_1+L_2\) has worst simple singularities. Let \(\overline{S}_{(C,L_1,L_2)}\) be the double plane branched along \(C+L_1+L_2\) and \(S_{(C,L_1,L_2)}\) be the K3 surface obtained by taking the minimal resolution of \(\overline{S}_{(C,L_1,L_2)}\). Let  be the natural morphism. To define a lattice embedding
be the natural morphism. To define a lattice embedding  , one needs to specify the images of \(\gamma , l_1', \alpha _1, \ldots , \alpha _4, l_2', \beta _1, \ldots , \beta _4\) so that the intersection form is preserved. There is a compatibility condition induced by \(2l_1' + \alpha _1 + \ldots + \alpha _4 = 2l_2' + \beta _1 + \cdots + \beta _4\). Recall that \(h=\xi + \gamma = 2l_1' + \alpha _1 + \ldots + \alpha _4 +\gamma = 2l_2' + \beta _1 + \cdots + \beta _4 + \gamma \). We also require that \(\jmath (h)\) is the class of the base point free polarization
, one needs to specify the images of \(\gamma , l_1', \alpha _1, \ldots , \alpha _4, l_2', \beta _1, \ldots , \beta _4\) so that the intersection form is preserved. There is a compatibility condition induced by \(2l_1' + \alpha _1 + \ldots + \alpha _4 = 2l_2' + \beta _1 + \cdots + \beta _4\). Recall that \(h=\xi + \gamma = 2l_1' + \alpha _1 + \ldots + \alpha _4 +\gamma = 2l_2' + \beta _1 + \cdots + \beta _4 + \gamma \). We also require that \(\jmath (h)\) is the class of the base point free polarization  .
.
Given a triple \((C, L_1, L_2)\), one has two associated degree 5 pairs:  and
and  , which induce the same K3 surface \(S_{(D,L)}\), constructed as above. Let us fix two labelings
, which induce the same K3 surface \(S_{(D,L)}\), constructed as above. Let us fix two labelings  and
and  such that
such that  . Every degree 5 pair produces six divisors as described above. For the pair \((C+L_2, L_1)\) (respectively \((C+L_1, L_2)\)), we denote the 6 divisors by \(L_1', R_0, \ldots , R_4\) (respectively \(L_2', T_0, \ldots , T_4\)). Note that
. Every degree 5 pair produces six divisors as described above. For the pair \((C+L_2, L_1)\) (respectively \((C+L_1, L_2)\)), we denote the 6 divisors by \(L_1', R_0, \ldots , R_4\) (respectively \(L_2', T_0, \ldots , T_4\)). Note that  . We define
. We define  as follows:
as follows:
-
\(\jmath (\gamma ) = R_0 = T_0\) (by our choice of the labelings, both \(R_0\) and \(T_0\) are the fundamental cycle associated to the singularity of \(C+L_1+L_2\) at the point \(L_1 \cap L_2\));
-
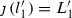 and
and  ;
; -
\(\jmath (\alpha _i) = R_i\) and
 for \(1 \leqslant i,j \leqslant 4\).
for \(1 \leqslant i,j \leqslant 4\).
After the first blow-up \(\epsilon _0\), the strict transforms of the two lines \(L_1\) and \(L_2\) are disjoint and hence, we have  for \(1 \leqslant i,j \leqslant 4\). Using Lemma 3.19, it is straightforward to verify that \(\jmath \) is a well-defined lattice embedding. The embedding \(\jmath \) also satisfies the following geometric properties and fits well in families (cf. [17, Section 4.2.3], especially the last paragraph on p. 2141).
for \(1 \leqslant i,j \leqslant 4\). Using Lemma 3.19, it is straightforward to verify that \(\jmath \) is a well-defined lattice embedding. The embedding \(\jmath \) also satisfies the following geometric properties and fits well in families (cf. [17, Section 4.2.3], especially the last paragraph on p. 2141).
-
\(\jmath (h)\) is the class of the base point free polarization
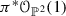 .
. -
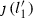 and
and 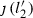 are the classes of irreducible rational curves.
are the classes of irreducible rational curves. -
\(\jmath (\gamma ), \jmath (\alpha _1), \ldots , \jmath (\alpha _4)\) (respectively \(\jmath (\gamma ), \jmath (\beta _1), \ldots , \jmath (\beta _4)\)) are classes of effective divisors which are contracted by \(\pi \) to the points of the intersection \(C \cap L_1\) (respectively \(C \cap L_2\)). In particular, \(\jmath (\gamma )\) is contracted to the point \(L_1 \cap L_2\).
To conclude that \(\jmath \) is an M-polarization we also need the following lemma.
Lemma 3.20
The lattice embedding  is primitive.
is primitive.
Proof
This follows from a case by case analysis. Specifically, we check the conditions of Lemma 3.8 as in the proof of Proposition 3.6.\(\square \)
Proposition 3.21
The birational map in Proposition 3.18 extends to a morphism  . Moreover, the map
. Moreover, the map  is injective.
is injective.
Proof
Given a triple \((C, L_1, L_2)\) consisting of a quartic curve C and lines \(L_1\), \(L_2\) such that \(C + L_1 + L_2\) has at worst simple singularities, we consider the M-polarized K3 surface \((S_{(C, L_1, L_2)}, \jmath )\) where \(S_{(C,L_1,L_2)}\) is the K3 surface obtained by taking the minimal resolution of the double plane branched along \(C + L_1 +L_2\) and \(\jmath \) is the lattice polarization constructed above. By [8], the M-polarized K3 surface \((S_{(C, L_1, L_2)}, \jmath )\) corresponds to a point in  . The polarization \(\jmath \) depends only on \((C, L_1, L_2)\), the ordering of \(C \cap L_1\) and the ordering of \(C \cap L_2\), and it is compatible with the action of
. The polarization \(\jmath \) depends only on \((C, L_1, L_2)\), the ordering of \(C \cap L_1\) and the ordering of \(C \cap L_2\), and it is compatible with the action of  . Consequently, we can associate to every triple \((C, L_1, L_2)\) a point in
. Consequently, we can associate to every triple \((C, L_1, L_2)\) a point in  . In other words, we have a well-defined morphism
. In other words, we have a well-defined morphism  extending the birational map in Proposition 3.18.
extending the birational map in Proposition 3.18.
Choose a point  (more precisely, \(\omega \) is a \(\Gamma \)-orbit) which corresponds to an M-polarization K3 surface \(S_{(C, L_1, L_2)}\). Lemma 3.16 allows us to extend an element of \(\Gamma \) to an isometry of the K3 lattice \(\Lambda _{K3}\). The global Torelli theorem for K3 surfaces implies that the period \(\omega \) determines the isomorphism class of the K3 surface \(S_{(C + L_1 + L_2)}\). By our construction the classes h, \(l_1'\) and \(l_2'\) are fixed by \(\Gamma \). It follows that the period point \(\omega \) uniquely expresses the K3 surface as a double cover of
(more precisely, \(\omega \) is a \(\Gamma \)-orbit) which corresponds to an M-polarization K3 surface \(S_{(C, L_1, L_2)}\). Lemma 3.16 allows us to extend an element of \(\Gamma \) to an isometry of the K3 lattice \(\Lambda _{K3}\). The global Torelli theorem for K3 surfaces implies that the period \(\omega \) determines the isomorphism class of the K3 surface \(S_{(C + L_1 + L_2)}\). By our construction the classes h, \(l_1'\) and \(l_2'\) are fixed by \(\Gamma \). It follows that the period point \(\omega \) uniquely expresses the K3 surface as a double cover of  and determines two line components of the branched locus. Now we conclude that \(\omega \) determines uniquely the triple \((C, L_1, L_2)\). \(\square \)
and determines two line components of the branched locus. Now we conclude that \(\omega \) determines uniquely the triple \((C, L_1, L_2)\). \(\square \)
3.5 Surjectivity of the period map
We will show in this section that the period map  is surjective. Given the general result of surjectivity of period maps for (lattice) polarized K3, one has to establish that any K3 surface carrying an M-polarization is of type \(S_{(C, L_1, L_2)}\).
is surjective. Given the general result of surjectivity of period maps for (lattice) polarized K3, one has to establish that any K3 surface carrying an M-polarization is of type \(S_{(C, L_1, L_2)}\).
Proposition 3.22
Let S be a K3 surface such that there exists a primitive embedding  . Then there exists a plane quartic curve C and two different lines
. Then there exists a plane quartic curve C and two different lines  such that \(S \cong S_{(C, L_1, L_2)}\) and \(C+L_1+L_2\) has at worst simple singularities.
such that \(S \cong S_{(C, L_1, L_2)}\) and \(C+L_1+L_2\) has at worst simple singularities.
Proof
We apply [17, Proposition 4.31] (see also [17, Lemmas 4.27, 4.28, 4.30]). The idea is to consider the primitive sublattices \(M_1\) and \(M_2\) of M generated by \(l_1', \gamma , \alpha _1, \ldots , \alpha _4\) and \(l_2', \gamma , \beta _1, \ldots , \beta _4\) respectively. Both of the sublattices have the following Gram matrix
Hence they are isomorphic to the lattice considered in [17, Notation 4.11] for degree 5 pairs. In particular, S is both \(M_1\)-polarized and \(M_2\)-polarized. Indeed, recall that

which coincides with Laza’s lattice (for both \(M_1\) and \(M_2\)). Using [17, Proposition 4.31], we find two degree 5 pairs \((D_1, L_1)\) and \((D_2, L_2)\) (where, a priori, \(D_1\) and \(D_2\) may be irreducible) such that \(D_1 + L_1 = D_2 + L_2\) has at worst simple singularities. The two morphisms  associated to each degree 5 pair are both defined by \(\jmath (h)\), and hence they are the same. Because \(L_1\) and \(L_2\) are both contained in the branch locus of the map
associated to each degree 5 pair are both defined by \(\jmath (h)\), and hence they are the same. Because \(L_1\) and \(L_2\) are both contained in the branch locus of the map  , \(D_1=L_2+C\) and \(D_2=L_1+C\), where C is a quartic plane curve such that \(C+L_1+L_2\) has at worst simple singularities. \(\square \)
, \(D_1=L_2+C\) and \(D_2=L_1+C\), where C is a quartic plane curve such that \(C+L_1+L_2\) has at worst simple singularities. \(\square \)
Theorem 3.23
Consider the triples \((C, L_1, L_2)\) consisting of a quartic curve C and lines \(L_1,L_2\) such that \(C + L_1 + L_2\) has at worst simple singularities. Let \(S_{(C,L_1,L_2)}\) be the K3 surface obtained by taking the minimal resolution of the double plane branched along \(C + L_1 +L_2\). The birational map sending \((C, L_1, L_2)\) to the periods of \(S_{(C,L_1,L_2)}\) in Proposition 3.18 extends to an isomorphism  .
.
Proof
It suffices to prove that  is surjective. Let
is surjective. Let  be a period point. By the surjectivity of the period map of lattice-polarized K3 surfaces (see [8, Theorem 3.1]) there exists an M-polarized K3 surface
be a period point. By the surjectivity of the period map of lattice-polarized K3 surfaces (see [8, Theorem 3.1]) there exists an M-polarized K3 surface  corresponding to \(\omega \). By Proposition 3.22, the K3 surface S is the double cover of
corresponding to \(\omega \). By Proposition 3.22, the K3 surface S is the double cover of  branched at a plane quartic curve C and two different lines \(L_1,L_2\). Moreover, let \(M_1\) and \(M_2\) be the primitive sublattices of M defined in the proof of Proposition 3.22. After choosing the Kähler cone \(V^+(S)\) and the set of effective \((-2)\) curves \(\Delta ^+(S)\) as in the proof of [17, Theorem 4.1], we may assume that the restrictions \(\jmath |_{M_1}\) and \(\jmath |_{M_2}\) of the polarization \(\jmath \) to the sublattices \(M_1\) and \(M_2\) are both normalized embeddings, as defined in [17, Definition 4.24]. The embeddings \(\jmath |_{M_1}\) and \(\jmath |_{M_2}\) are unique up to permutation of the classes \(\alpha _1,\ldots , \alpha _4\) (\(\beta _1,\ldots , \beta _4\), respectively) thanks to [17, Lemma 4.29]. It follows that the polarization \(\jmath \) is unique up to action of
branched at a plane quartic curve C and two different lines \(L_1,L_2\). Moreover, let \(M_1\) and \(M_2\) be the primitive sublattices of M defined in the proof of Proposition 3.22. After choosing the Kähler cone \(V^+(S)\) and the set of effective \((-2)\) curves \(\Delta ^+(S)\) as in the proof of [17, Theorem 4.1], we may assume that the restrictions \(\jmath |_{M_1}\) and \(\jmath |_{M_2}\) of the polarization \(\jmath \) to the sublattices \(M_1\) and \(M_2\) are both normalized embeddings, as defined in [17, Definition 4.24]. The embeddings \(\jmath |_{M_1}\) and \(\jmath |_{M_2}\) are unique up to permutation of the classes \(\alpha _1,\ldots , \alpha _4\) (\(\beta _1,\ldots , \beta _4\), respectively) thanks to [17, Lemma 4.29]. It follows that the polarization \(\jmath \) is unique up to action of  and coincides with our construction in Sect. 3.4. By Propositions 3.18 and 3.21, the period map
and coincides with our construction in Sect. 3.4. By Propositions 3.18 and 3.21, the period map  is a bijective birational morphism between normal varieties. As a result,
is a bijective birational morphism between normal varieties. As a result,  is an isomorphism, by Zariski’s Main Theorem.\(\square \)
is an isomorphism, by Zariski’s Main Theorem.\(\square \)
3.6 The period map for unlabeled triples
Consider the compact space  and
and  , consisting on the subset of triples \((C, L, L')\) formed by a quartic curve C and unlabeled lines \(L,L'\) such that the sextic curve \(C + L + L'\) is reduced and has at worst simple singularities, as constructed in Corollary 2.16. In this subsection we define the period map
, consisting on the subset of triples \((C, L, L')\) formed by a quartic curve C and unlabeled lines \(L,L'\) such that the sextic curve \(C + L + L'\) is reduced and has at worst simple singularities, as constructed in Corollary 2.16. In this subsection we define the period map  —for an appropriately chosen arithmetic group \(\Gamma '\)—and show that
—for an appropriately chosen arithmetic group \(\Gamma '\)—and show that  is an isomorphism. We use the same approach taken to define
is an isomorphism. We use the same approach taken to define  (Propositions 3.18 and 3.21) and to prove Theorem 3.23. The modification one needs to do is to choose a different arithmetic group \(\Gamma '\). We follow the same notation as in the previous subsections, especially regarding the description of the subgroup
(Propositions 3.18 and 3.21) and to prove Theorem 3.23. The modification one needs to do is to choose a different arithmetic group \(\Gamma '\). We follow the same notation as in the previous subsections, especially regarding the description of the subgroup  in Lemma 3.17. Consider the subgroup
in Lemma 3.17. Consider the subgroup  where the factor \(\mathbb {Z}/2\mathbb {Z}\) corresponds to the swap of \(\alpha _i\)’s and \(\beta _i\)’s for \(0 \leqslant i \leqslant 4\) (the induced action on \(A_M\) exchanges \(\alpha _i^*\) with \(\beta _i^*\) for \(1 \leqslant i \leqslant 3\) and fixes \(\gamma ^*\) and \(\xi ^*\)). As in the proof of Lemma 3.17, we can verify that the composition
where the factor \(\mathbb {Z}/2\mathbb {Z}\) corresponds to the swap of \(\alpha _i\)’s and \(\beta _i\)’s for \(0 \leqslant i \leqslant 4\) (the induced action on \(A_M\) exchanges \(\alpha _i^*\) with \(\beta _i^*\) for \(1 \leqslant i \leqslant 3\) and fixes \(\gamma ^*\) and \(\xi ^*\)). As in the proof of Lemma 3.17, we can verify that the composition  is injective. Now we define \(\Gamma '\) to be the following extension:
is injective. Now we define \(\Gamma '\) to be the following extension:

For  (such that \(C+L+L'\) is reduced and has at worst simple singularities) we consider the period of the K3 surface \(S_{(C,L,L')}\) which is the minimal resolution of the double cover of
(such that \(C+L+L'\) is reduced and has at worst simple singularities) we consider the period of the K3 surface \(S_{(C,L,L')}\) which is the minimal resolution of the double cover of  branched along \(C+L+L'\). Because \(S_{(C,L,L')}\) is polarized by the lattice M, the period corresponds to a point in
branched along \(C+L+L'\). Because \(S_{(C,L,L')}\) is polarized by the lattice M, the period corresponds to a point in  . The lattice polarization depends on the labeling of L and \(L'\), the ordering of \(C \cap L\) and the ordering of \(C \cap L'\), and thus is compatible with the action of
. The lattice polarization depends on the labeling of L and \(L'\), the ordering of \(C \cap L\) and the ordering of \(C \cap L'\), and thus is compatible with the action of  . Therefore we have a well-defined period map
. Therefore we have a well-defined period map  (see also Propositions 3.18 and 3.21). Moreover, the same argument in Proposition 3.21 and Theorem 3.23 allows us to prove that the period map
(see also Propositions 3.18 and 3.21). Moreover, the same argument in Proposition 3.21 and Theorem 3.23 allows us to prove that the period map  is an isomorphism.
is an isomorphism.
3.7 Comparison of the GIT and the Baily–Borel compactifications
Consider the moduli space  of triples \((C, L, L')\) formed by a quartic curve C and unlabeled lines L, \(L'\) such that the sextic curve \(C + L + L'\) has at worst simple singularities. We have constructed a period map
of triples \((C, L, L')\) formed by a quartic curve C and unlabeled lines L, \(L'\) such that the sextic curve \(C + L + L'\) has at worst simple singularities. We have constructed a period map  in Sect. 3.6 and have shown that it is an isomorphism. There are two natural ways to compactify
in Sect. 3.6 and have shown that it is an isomorphism. There are two natural ways to compactify  as the GIT quotient
as the GIT quotient  defined in (3) and described in Corollary 2.16, or as the Baily–Borel compactification [3]. We compare these two compactifications by applying some general results of Looijenga [21]. See also [17, Theorem 4.2].
defined in (3) and described in Corollary 2.16, or as the Baily–Borel compactification [3]. We compare these two compactifications by applying some general results of Looijenga [21]. See also [17, Theorem 4.2].
Theorem 3.24
The period map  extends to an isomorphism of projective varieties
extends to an isomorphism of projective varieties  where
where  denotes the Baily–Borel compactification of
denotes the Baily–Borel compactification of  .
.
Proof
We apply a general framework of comparing GIT compactifications to certain compactifications of the period domain developed by Looijenga. Specifically, by [21, Theorem 7.6] an isomorphism  (typically coming from a period map) between a geometric quotient
(typically coming from a period map) between a geometric quotient  and a complement of an arithmetic hyperplane arrangement
and a complement of an arithmetic hyperplane arrangement  in a type IV domain \(\Omega \) extends to an isomorphism
in a type IV domain \(\Omega \) extends to an isomorphism  between the GIT compactification
between the GIT compactification  and the Looijenga compactification \(\widetilde{\Omega /\Lambda }\) associated to
and the Looijenga compactification \(\widetilde{\Omega /\Lambda }\) associated to  if their polarizations agree and
if their polarizations agree and  . We have
. We have  . The hyperplane arrangement is empty and the associated Looijenga compactification is the Baily–Borel compactification
. The hyperplane arrangement is empty and the associated Looijenga compactification is the Baily–Borel compactification  . Moreover, by Corollary 2.16 and Lemma 2.7, we have
. Moreover, by Corollary 2.16 and Lemma 2.7, we have

and their polarizations agree by restriction of the isomorphic polarizations for the GIT of sextic curves and for the compact moduli of K3 surfaces of degree 2 (see [21, Section 8]). Hence, by [21, Theorem 7.6]  is an isomorphism for polarized varieties. \(\square \)
is an isomorphism for polarized varieties. \(\square \)
Question 3.25
Does the period map for labeled triples  (cf. Theorem 3.23) preserve the natural polarizations?
(cf. Theorem 3.23) preserve the natural polarizations?
A positive answer to this question would imply that the period map  can be extended to an isomorphism
can be extended to an isomorphism  . We strongly believe that the answer is yes (by pulling back the polarizations for sextic curves and degree 2 K3 surfaces via the double covers
. We strongly believe that the answer is yes (by pulling back the polarizations for sextic curves and degree 2 K3 surfaces via the double covers  and
and  ).
).
3.8 The Baily–Borel compactification
The locally symmetric space  admits a canonical minimal compactification, the Baily–Borel compactification
admits a canonical minimal compactification, the Baily–Borel compactification  (cf. [3]). The boundary components of
(cf. [3]). The boundary components of  are either 0-dimensional (Type III components) or 1-dimensional (Type II components), and they correspond to the primitive rank 1, respectively, rank 2 isotropic sublattices of T up to \(\Gamma '\)-equivalence. Following the approach of [17, 29, 31], we determine the number of the Type III boundary components of
are either 0-dimensional (Type III components) or 1-dimensional (Type II components), and they correspond to the primitive rank 1, respectively, rank 2 isotropic sublattices of T up to \(\Gamma '\)-equivalence. Following the approach of [17, 29, 31], we determine the number of the Type III boundary components of  and compute certain invariants for the Type II boundary components. Notice that by Theorem 3.24, the number of these boundary components and some of their invariants (such as the dimension) can be worked out from the boundary components of the GIT quotient
and compute certain invariants for the Type II boundary components. Notice that by Theorem 3.24, the number of these boundary components and some of their invariants (such as the dimension) can be worked out from the boundary components of the GIT quotient  described in Corollary 2.16.
described in Corollary 2.16.
We determine the 0-dimensional components of  using [29, Proposition 4.1.3]. The 0-dimensional boundary components are in one-to-one correspondence with the \(\Gamma '\)-orbits of primitive isotropic rank 1 sublattices of T. By Proposition 3.13 and [26, Theorem 3.6.2] we have
using [29, Proposition 4.1.3]. The 0-dimensional boundary components are in one-to-one correspondence with the \(\Gamma '\)-orbits of primitive isotropic rank 1 sublattices of T. By Proposition 3.13 and [26, Theorem 3.6.2] we have  . (In particular, T contains two hyperbolic planes.) Write
. (In particular, T contains two hyperbolic planes.) Write  (see Sect. 3.6). Note that for \(v \in T\) one can associate a vector
(see Sect. 3.6). Note that for \(v \in T\) one can associate a vector  defined by
defined by  \(\mathrm{mod}\,T\) (where
\(\mathrm{mod}\,T\) (where  is the divisor of v which is a positive integer such that
is the divisor of v which is a positive integer such that  ). If v is a primitive isotropic vector then \(\overline{v}\) is an isotropic element in \(A_T\). By [29, Proposition 4.1.3] the map \(\mathbb {Z}v \mapsto \overline{v}\) induces a bijection between the equivalence classes of primitive isotropic rank 1 sublattices of T and \(\Gamma ^*\)-orbits of isotropic elements of \(A_T\). Because T is the orthogonal complement of M in \(\Lambda _{K3}\), one has
). If v is a primitive isotropic vector then \(\overline{v}\) is an isotropic element in \(A_T\). By [29, Proposition 4.1.3] the map \(\mathbb {Z}v \mapsto \overline{v}\) induces a bijection between the equivalence classes of primitive isotropic rank 1 sublattices of T and \(\Gamma ^*\)-orbits of isotropic elements of \(A_T\). Because T is the orthogonal complement of M in \(\Lambda _{K3}\), one has  . We have computed the discriminant quadratic form \(q_M\) in Lemma 3.4. In particular, there are 20 isotropic elements in \(A_M \cong A_T\): \(0, \gamma ^*\),
. We have computed the discriminant quadratic form \(q_M\) in Lemma 3.4. In particular, there are 20 isotropic elements in \(A_M \cong A_T\): \(0, \gamma ^*\),  and
and  (\(1 \leqslant i,j \leqslant 3\)). The action of \(\Gamma ^*\) has been described in the proof of Lemma 3.17 and Sect. 3.6. It is easy to see that
(\(1 \leqslant i,j \leqslant 3\)). The action of \(\Gamma ^*\) has been described in the proof of Lemma 3.17 and Sect. 3.6. It is easy to see that  and
and  (\(1 \leqslant i,j \leqslant 3\)) form one \(\Gamma ^*\)-orbit. As a result, the Baily–Borel compactification
(\(1 \leqslant i,j \leqslant 3\)) form one \(\Gamma ^*\)-orbit. As a result, the Baily–Borel compactification  consists of three 0-dimensional boundary components.
consists of three 0-dimensional boundary components.
Remark 3.26
Similarly, one can show that  has three 0-dimensional boundary components (compare Lemma 2.15).
has three 0-dimensional boundary components (compare Lemma 2.15).
Remark 3.27
As discussed in [17, Section 4.4.1], one important invariant for the \(O_-(T)\)-equivalence class of isotropic sublattices E of T is the isomorphism classes of  (and we shall use it to label E). Let us compute the isomorphism classes of
(and we shall use it to label E). Let us compute the isomorphism classes of  (where \(\mathbb {Z}v\) is a primitive isotropic rank 1 sublattice of T). Observe that
(where \(\mathbb {Z}v\) is a primitive isotropic rank 1 sublattice of T). Observe that  . One could compute the Gram matrix of
. One could compute the Gram matrix of  explicitly. Alternatively, we consider
explicitly. Alternatively, we consider  (cf. [17, Section 4.4.1]) which is an isotropic subgroup of \(A_T \cong (\mathbb {Z}/2\mathbb {Z})^6\) and the discriminant group \(A_{v^{\perp }/\mathbb {Z}v} \cong H_v^{\perp }/H_v\). In our case, \(H_v\) equals either 0 or \(\mathbb {Z}/2\mathbb {Z}\). The lattice
(cf. [17, Section 4.4.1]) which is an isotropic subgroup of \(A_T \cong (\mathbb {Z}/2\mathbb {Z})^6\) and the discriminant group \(A_{v^{\perp }/\mathbb {Z}v} \cong H_v^{\perp }/H_v\). In our case, \(H_v\) equals either 0 or \(\mathbb {Z}/2\mathbb {Z}\). The lattice  is an even hyperbolic (N.B. the signature is (1, 9)) 2-elementary lattice. By a direct computation we get the following (see also [26, Theorem 3.6.2]).
is an even hyperbolic (N.B. the signature is (1, 9)) 2-elementary lattice. By a direct computation we get the following (see also [26, Theorem 3.6.2]).
-
If \(\overline{v}=0\), then
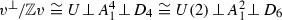 .
. -
If \(\overline{v}=\gamma ^*\), then
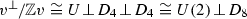 .
. -
If
 or
or  (\(1 \leqslant i,j \leqslant 3\)), then
(\(1 \leqslant i,j \leqslant 3\)), then  .
.
To determine the 1-dimensional components of  , one needs to compute the equivalence classes of primitive isotropic rank 2 sublattices of T. We use the algorithm for classifying isotropic vectors in hyperbolic lattices due to Vinberg [33]. Specifically, for each of the equivalence classes of primitive isotropic rank 1 sublattices \(\mathbb {Z}v\) of T we apply Vinberg’s algorithm to the hyperbolic lattice
, one needs to compute the equivalence classes of primitive isotropic rank 2 sublattices of T. We use the algorithm for classifying isotropic vectors in hyperbolic lattices due to Vinberg [33]. Specifically, for each of the equivalence classes of primitive isotropic rank 1 sublattices \(\mathbb {Z}v\) of T we apply Vinberg’s algorithm to the hyperbolic lattice  (with respect to the action by the stabilizer \(\Gamma '_v\) of v).
(with respect to the action by the stabilizer \(\Gamma '_v\) of v).
Now we briefly recall Vinberg’s algorithm [33] (see also [31, Section 4.3]). Let N be a hyperbolic lattice of signature (1, n). (In our case we take  .) The algorithm starts by fixing an element \(h \in N\) of positive square. Then one needs to inductively choose roots \(\delta _1, \delta _2, \ldots \) such that the distance function \({(h,\delta )^2}/{|(\delta ,\delta )|}\) is minimized. The algorithm stops with the choice of \(\delta _N\) if every connected parabolic subdiagram (i.e. the extended Dynkin diagram of a root system) of the Dynkin diagram \(\Sigma \) associated to the roots \(\delta _1, \delta _2, \ldots , \delta _N\) is a connected component of some parabolic subdiagram of rank \(n-1\). If the algorithm stops then the W(N)-orbits of the isotropic lines in N correspond to the parabolic subdiagrams of rank \(n-1\) of \(\Sigma \) (N.B. the isomorphism classes of
.) The algorithm starts by fixing an element \(h \in N\) of positive square. Then one needs to inductively choose roots \(\delta _1, \delta _2, \ldots \) such that the distance function \({(h,\delta )^2}/{|(\delta ,\delta )|}\) is minimized. The algorithm stops with the choice of \(\delta _N\) if every connected parabolic subdiagram (i.e. the extended Dynkin diagram of a root system) of the Dynkin diagram \(\Sigma \) associated to the roots \(\delta _1, \delta _2, \ldots , \delta _N\) is a connected component of some parabolic subdiagram of rank \(n-1\). If the algorithm stops then the W(N)-orbits of the isotropic lines in N correspond to the parabolic subdiagrams of rank \(n-1\) of \(\Sigma \) (N.B. the isomorphism classes of  , where E is an isotropic rank 2 sublattice of T containing v, are determined by the Dynkin diagrams of the parabolic subdiagrams). To determine the equivalence classes of the isotropic vectors by a larger group which contains the Weyl group W(N) as a subgroup of finite index, one should take certain symmetries of \(\Sigma \) into consideration.
, where E is an isotropic rank 2 sublattice of T containing v, are determined by the Dynkin diagrams of the parabolic subdiagrams). To determine the equivalence classes of the isotropic vectors by a larger group which contains the Weyl group W(N) as a subgroup of finite index, one should take certain symmetries of \(\Sigma \) into consideration.
In our case, a straightforward application of Vinberg’s algorithm allows us to compute the isomorphism classes of  .
.
-
If \(\overline{v}=0\), then
 has at least three equivalence classes of isotropic vectors which correspond to
has at least three equivalence classes of isotropic vectors which correspond to  ,
,  and
and  respectively.
respectively. -
If \(\overline{v}=\gamma ^*\), then
 has at least two equivalence classes of isotropic vectors which correspond to
has at least two equivalence classes of isotropic vectors which correspond to  and \(D_8\) respectively.
and \(D_8\) respectively. -
If
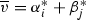 or
or 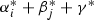 (\(1 \leqslant i,j \leqslant 3\)), then
(\(1 \leqslant i,j \leqslant 3\)), then 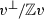 has at least three equivalence classes of isotropic vectors which correspond to
has at least three equivalence classes of isotropic vectors which correspond to 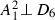 ,
,  and \(D_8\) respectively.
and \(D_8\) respectively.
By Theorem 3.24 and Corollary 2.16 we conclude that the Baily–Borel compactification  consists of five 1-dimensional boundary components labeled by
consists of five 1-dimensional boundary components labeled by  ,
,  ,
,  ,
,  and \(D_8\) respectively.
and \(D_8\) respectively.
Remark 3.28
Using the Clemens–Schmid exact sequence and the incidence relation of the GIT boundary components (see also [17, Theorem 4.32]), we match the GIT boundary of  in Corollary 2.16 with the Baily–Borel boundary of
in Corollary 2.16 with the Baily–Borel boundary of  .
.
GIT boundary | Baily–Borel boundary |
|---|---|
|
|
|
|
|
|
|
|
| \(D_8\) |
|
|
|
|
|
|
References
Allcock, D., Carlson, J.A., Toledo, D.: The complex hyperbolic geometry of the moduli space of cubic surfaces. J. Algebraic Geom. 11(4), 659–724 (2002)
Allcock, D., Carlson, J.A., Toledo, D.: The Moduli Space of Cubic Threefolds as a Ball Quotient. Memoirs of the American Mathematical Socierty, vol. 209, no. 985. American Mathematical Society, Providence (2011)
Baily Jr., W.L., Borel, A.: Compactification of arithmetic quotients of bounded symmetric domains. Ann. Math. 84, 442–528 (1966)
Barth, W.P., Hulek, K., Peters, C.A.M., Van de Ven, A.: Compact Complex Surfaces. 2nd edn. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A. Springer, Berlin (2004)
Belcastro, S.M.: Picard Lattices of Families of K3 Surfaces. PhD thesis, University of Michigan (1997)
Cossec, F.R., Dolgachev, I.V.: Enriques Surfaces. I. Progress in Mathematics, vol. 76. Birkhäuser, Boston (1989)
Dolgachev, I.: Lectures on Invariant Theory. London Mathematical Society Lecture Note Series, vol. 296. Cambridge University Press, Cambridge (2003)
Dolgachev, I.V.: Mirror symmetry for lattice polarized \(K3\) surfaces. J. Math. Sci. 81(3), 2599–2630 (1996)
Dolgachev, I.V., Hu, Y.: Variation of geometric invariant theory quotients. Inst. Hautes Études Sci. Publ. Math. 87, 5–56 (1998). With an appendix by Nicolas Ressayre
Edge, W.L.: A plane quartic curve with twelve undulations. Edinburgh Math. Notes 1945(35), 10–13 (1945)
Edge, W.L.: A plane quartic with eight undulations. Proc. Edinburgh Math. Soc. 8, 147–162 (1950)
Gallardo, P., Martinez-Garcia, J.: Moduli of cubic surfaces and their anticanonical divisors (2016). arXiv:1607.03697
Gallardo, P., Martinez-Garcia, J.: Variations of geometric invariant quotients for pairs, a computational approach. Proc. Amer. Math. Soc. 146(6), 2395–2408 (2018)
Garbagnati, A.: Smooth double covers of K3 surfaces (2016). arXiv:1605.03438 (to appear in Ann. Sc. Norm. Super. Pisa Cl. Sci.)
Huybrechts, D.: Lectures on K3 Surfaces. Cambridge Studies in Advanced Mathematics, vol. 158. Cambridge University Press, Cambridge (2016)
Laza, R.: Deformations of Singularities and Variations of GIT Quotients. PhD thesis, Columbia University (2006)
Laza, R.: Deformations of singularities and variation of GIT quotients. Trans. Amer. Math. Soc. 361(4), 2109–2161 (2009)
Laza, R.: The moduli space of cubic fourfolds via the period map. Ann. Math. 172(1), 673–711 (2010)
Laza, R.: The KSBA compactification for the moduli space of degree two \(K3\) pairs. J. Eur. Math. Soc. (JEMS) 18(2), 225–279 (2016)
Liu, W., Rollenske, S.: Two-dimensional semi-log-canonical hypersurfaces. Matematiche (Catania) 67(2), 185–202 (2012)
Looijenga, E.: Compactifications defined by arrangements. II. Locally symmetric varieties of type IV. Duke Math. J. 119(3), 527–588 (2003)
Looijenga, E.: The period map for cubic fourfolds. Invent. Math. 177(1), 213–233 (2009)
Looijenga, E., Swierstra, R.: The period map for cubic threefolds. Compositio Math. 143(4), 1037–1049 (2007)
Morrison, D.R.: The geometry of K3 surfaces (1988). http://web.math.ucsb.edu/~drm/manuscripts/cortona.pdf
Mumford, D., Fogarty, J., Kirwan, F.: Geometric Invariant Theory. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 34, 3rd edn. Springer, Berlin (1994)
Nikulin, V.V.: Integer symmetric bilinear forms and some of their geometric applications. Math. USSR-Izv. 14(1), 103–167 (1979)
Orlik, P., Solomon, L.: Singularities. II. Automorphisms of forms. Math. Ann. 231(3), 229–240 (1977/78)
Pearlstein, G., Zhang, Z.: A generic global Torelli theorem for certain Horikawa surfaces (2017). arXiv:1702.06204 (to appear in Algebraic Geom.)
Scattone, F.: On the Compactification of Moduli Spaces for Algebraic \(K3\) Surfaces. Memoirs of the American Mathematical Socierty, vol. 70, no. 374. American Mathematical Society, Providence (1987)
Shah, J.: A complete moduli space for \(K3\) surfaces of degree \(2\). Ann. Math. 112(3), 485–510 (1980)
Sterk, H.: Compactifications of the period space of Enriques surfaces. I. Math. Z. 207(1), 1–36 (1991)
Thaddeus, M.: Geometric invariant theory and flips. J. Amer. Math. Soc. 9(3), 691–723 (1996)
Vinberg, E.B.: Some arithmetical discrete groups in Lobačevskiĭ spaces. In: Baily Jr., W.L. (ed.) Discrete Subgroups of Lie Groups and Applications to Moduli. Tata Institute of Fundamental Research Studies in Mathematics, vol. 7, pp. 323–348. Oxford University Press, Bombay (1975)
Acknowledgements
We thank Radu Laza and Gregory Pearlstein for useful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
P. Gallardo is supported by the NSF Grant DMS-1344994 of the RTG in Algebra, Algebraic Geometry, and Number Theory, at the University of Georgia. J. Martinez-Garcia acknowledges support from the Max Planck Institute for Mathematics in Bonn and would like to thank the Simons Foundation for its support of his research under the Simons Collaboration on Special Holonomy in Geometry, Analysis and Physics (Grant # 488631, Johannes Nordström). This work was partially carried out at the Institute for Computational and Experimental Research in Mathematics (ICERM) during a visit by the authors as part of a Collaborate@ICERM project. The authors would like to thank ICERM for making this visit possible.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gallardo, P., Martinez-Garcia, J. & Zhang, Z. Compactifications of the moduli space of plane quartics and two lines. European Journal of Mathematics 4, 1000–1034 (2018). https://doi.org/10.1007/s40879-018-0248-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0248-7


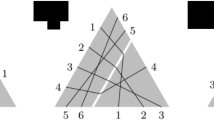
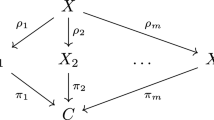

 in
in  . We denote
. We denote 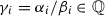 such that
such that  for all
for all 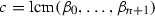 .
.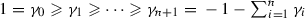 .
.
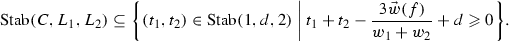


 are the images of the points
are the images of the points  , and
, and ,
,  are the images of the rational curves
are the images of the rational curves  .
.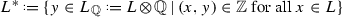 , the dual lattice;
, the dual lattice; , the discriminant group endowed with the induced quadratic form
, the discriminant group endowed with the induced quadratic form 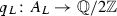 ;
;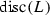 : the determinant of the Gram matrix (i.e. the intersection matrix) with respect to an arbitrary
: the determinant of the Gram matrix (i.e. the intersection matrix) with respect to an arbitrary 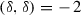 );
); .
.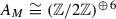 with quadratic form
with quadratic form 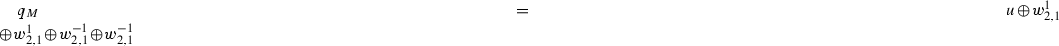 , where
, where 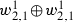 is isomorphic to the discriminant form of
is isomorphic to the discriminant form of 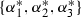 (respectively
(respectively 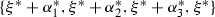 (respectively
(respectively  (
(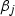 and
and  (respectively
(respectively  (
( . Then
. Then 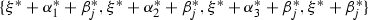 (respectively
(respectively 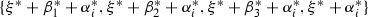 ).
). 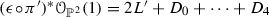 , and
, and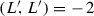 ,
, 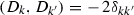 ,
, 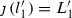 and
and  ;
; for
for  .
. and
and 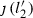 are the classes of irreducible rational curves.
are the classes of irreducible rational curves.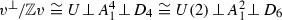 .
.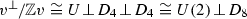 .
. or
or  (
( .
. has at least three equivalence classes of isotropic vectors which correspond to
has at least three equivalence classes of isotropic vectors which correspond to  ,
,  and
and  respectively.
respectively. has at least two equivalence classes of isotropic vectors which correspond to
has at least two equivalence classes of isotropic vectors which correspond to  and
and 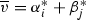 or
or 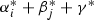 (
(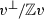 has at least three equivalence classes of isotropic vectors which correspond to
has at least three equivalence classes of isotropic vectors which correspond to 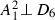 ,
, 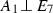 and
and 













