Abstract
This paper is about the family of smooth quartic surfaces  that are invariant under the Heisenberg group \(H_{2,2}\). For a very generic X, we show that the Picard number of X is 16 and determine its Picard lattice. It turns out that a very generic X contains 320 irreducible conics which generate the Picard group of X.
that are invariant under the Heisenberg group \(H_{2,2}\). For a very generic X, we show that the Picard number of X is 16 and determine its Picard lattice. It turns out that a very generic X contains 320 irreducible conics which generate the Picard group of X.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let A be an Abelian surface over \(\mathbb {C}\), that is a projective group variety of dimension 2. The subgroup  has order 16 and therefore
has order 16 and therefore  . The involution
. The involution  induces a
induces a  action on A and the quotient, which we denote by \(K_A\), is called the Kummer surface of A. If A admits a certain kind of line bundle (see Sect. 2.1) there is an induced map \(A \rightarrow \mathbb {P}^3\) which factors through an embedding \(K_A \rightarrow \mathbb {P}^3\) such that the image of the Kummer surface is a quartic with 16 nodes. Moreover, the natural action of \(A_2\) on \(K_A\) extends to a linear action on \(\mathbb {P}^3\). In one set of coordinates
action on A and the quotient, which we denote by \(K_A\), is called the Kummer surface of A. If A admits a certain kind of line bundle (see Sect. 2.1) there is an induced map \(A \rightarrow \mathbb {P}^3\) which factors through an embedding \(K_A \rightarrow \mathbb {P}^3\) such that the image of the Kummer surface is a quartic with 16 nodes. Moreover, the natural action of \(A_2\) on \(K_A\) extends to a linear action on \(\mathbb {P}^3\). In one set of coordinates  on \(\mathbb {P}^3\) this action is given by identifying \(A_2\) with the subgroup of
on \(\mathbb {P}^3\) this action is given by identifying \(A_2\) with the subgroup of  which is generated by the following four transformations:
which is generated by the following four transformations:

The subject of this paper is the family of all quartic surfaces in \(\mathbb {P}^{3}\) which are invariant under these transformations. We will refer to such surfaces as Heisenberg invariant quartics or just invariant quartics. This family of quartics appeared in the classical treatises [20, 24] and also in several later works [4, 28, 36]. The family is parameterized by  and the subfamily of Kummer surfaces described above constitutes a Zariski open dense subset of a hypersurface
and the subfamily of Kummer surfaces described above constitutes a Zariski open dense subset of a hypersurface  known as the Segre cubic. However, the general Heisenberg invariant quartic is smooth. Special smooth members of the family appear throughout the literature, for example the Fermat quartic \(x^4+y^4+z^4+w^4=0\) which is studied in [34] and the pencil \(x^4+y^4+z^4+w^4+\lambda xyzw=0\), which has been studied from the point of view of mirror symmetry [11] and the periodicity of the Clebsch contravariant [13]. In [4], Barth and Nieto study the locus of Heisenberg invariant quartics that contain a line and find a quintic threefold
known as the Segre cubic. However, the general Heisenberg invariant quartic is smooth. Special smooth members of the family appear throughout the literature, for example the Fermat quartic \(x^4+y^4+z^4+w^4=0\) which is studied in [34] and the pencil \(x^4+y^4+z^4+w^4+\lambda xyzw=0\), which has been studied from the point of view of mirror symmetry [11] and the periodicity of the Clebsch contravariant [13]. In [4], Barth and Nieto study the locus of Heisenberg invariant quartics that contain a line and find a quintic threefold  such that the general point corresponds to a desingularized Kummer surface of an Abelian surface with a (1, 3) polarization. Prior to that, these surfaces had been discovered by Traynard [35] and discussed by Godeaux [16] and Naruki [29]. The present paper was motivated by the following question: which Heisenberg invariant quartics contain a conic? It turns out that a general invariant quartic contains 320 smooth conics. The conics are found by a direct computation using the geometry of the family. Another result of this paper is that a very general member of the family of surfaces has Picard number 16. This is in accordance with the fact that certain moduli spaces of K3 surfaces whose Picard lattices contain (an isomorphic copy of) a fixed lattice M have dimension
such that the general point corresponds to a desingularized Kummer surface of an Abelian surface with a (1, 3) polarization. Prior to that, these surfaces had been discovered by Traynard [35] and discussed by Godeaux [16] and Naruki [29]. The present paper was motivated by the following question: which Heisenberg invariant quartics contain a conic? It turns out that a general invariant quartic contains 320 smooth conics. The conics are found by a direct computation using the geometry of the family. Another result of this paper is that a very general member of the family of surfaces has Picard number 16. This is in accordance with the fact that certain moduli spaces of K3 surfaces whose Picard lattices contain (an isomorphic copy of) a fixed lattice M have dimension  . The group action on the surfaces induces an action on the Picard group and we also show that, for a very general surface in the family, the sublattice of invariant divisor classes is generated by the class of the hyperplane section. In particular, any invariant curve on such a surface is a complete intersection. Next we determine the Picard lattice of a very general Heisenberg invariant quartic and show that it is generated by the 320 smooth conics. This is done by computing the configuration of the 320 conics as well as using some general facts on the existence of curves on Kummer surfaces.
. The group action on the surfaces induces an action on the Picard group and we also show that, for a very general surface in the family, the sublattice of invariant divisor classes is generated by the class of the hyperplane section. In particular, any invariant curve on such a surface is a complete intersection. Next we determine the Picard lattice of a very general Heisenberg invariant quartic and show that it is generated by the 320 smooth conics. This is done by computing the configuration of the 320 conics as well as using some general facts on the existence of curves on Kummer surfaces.
The paper is organized as follows. Sections 2 and 3 set the notation and review some results that we need for the sequel. In Sect. 4 we determine the Picard number of a very generic invariant quartic. Section 5 concerns the existence of the 320 conics. In Sects. 6 and 7 we study configurations of lines on Heisenberg invariant quartic surfaces and use the results to determine the configuration of the 320 smooth conics on a very general surface. In Sect. 8 we determine the Picard lattice of a very general surface in the family up to isomorphism and show that it is generated by the 320 smooth conics.
2 The family of invariant quartics
2.1 Kummer surfaces
We begin with an overview of Kummer surfaces, for proofs and notation see [8, 18, 20, 28]. Let A be an Abelian surface over \(\mathbb {C}\). The subgroup of 2-torsion points  has order 16 and hence
has order 16 and hence  . To an element \(a \in A\) we associate a translation map
. To an element \(a \in A\) we associate a translation map  . The involution
. The involution  induces a
induces a  action on A and the quotient
action on A and the quotient  is an algebraic surface called the Kummer surface of A. Let \(\pi :A\rightarrow K_A\) be the projection. The Kummer surface has 16 singular points, namely \(\pi (A_2)\), and the action of \(A_2\) on A by translations induces an action on \(K_A\). For an ample line bundle L on A we define the Heisenberg group
is an algebraic surface called the Kummer surface of A. Let \(\pi :A\rightarrow K_A\) be the projection. The Kummer surface has 16 singular points, namely \(\pi (A_2)\), and the action of \(A_2\) on A by translations induces an action on \(K_A\). For an ample line bundle L on A we define the Heisenberg group

and the set

If  and
and  then there is an induced isomorphism
then there is an induced isomorphism  . Using that
. Using that  we put a group structure on
we put a group structure on  by letting
by letting

These two groups are connected by an exact sequence,

where  . The kernel of the map
. The kernel of the map  is the group of automorphisms of L, which is the multiplicative group \(\mathbb {C}^{*}\) acting by multiplication by constants. We will consider the case where A has a principal polarization \(L'\), that is \(L'\) is an ample line bundle on A whose elementary divisors are both equal to 1. In addition we assume that \(L'\) is symmetric and irreducible. The former means that
is the group of automorphisms of L, which is the multiplicative group \(\mathbb {C}^{*}\) acting by multiplication by constants. We will consider the case where A has a principal polarization \(L'\), that is \(L'\) is an ample line bundle on A whose elementary divisors are both equal to 1. In addition we assume that \(L'\) is symmetric and irreducible. The former means that  where
where  , and the latter means that the polarized Abelian surface \((A,L')\) does not split as a product of elliptic curves. We say that the line bundle
, and the latter means that the polarized Abelian surface \((A,L')\) does not split as a product of elliptic curves. We say that the line bundle  is of type (2, 2). Then \(H(L)=A_2\),
is of type (2, 2). Then \(H(L)=A_2\),  and if D is a divisor on A that corresponds to L, then
and if D is a divisor on A that corresponds to L, then  . The group
. The group  has an action on the space of global sections of L: for
has an action on the space of global sections of L: for  and \(s \in \Gamma (A,L)\), \(\phi \) induces a section \(\phi (s)\) of \(t_x^*L\) and the translation \(t_{-x}^*\) induces a section \(t_{-x}^*(\phi (s))\) of \(L=t_{-x}^*(t_x^*L)\). Thus we put \(zs=t_{-x}^{*}(\phi (s))\). This makes \(\Gamma (A,L)\) into an irreducible
and \(s \in \Gamma (A,L)\), \(\phi \) induces a section \(\phi (s)\) of \(t_x^*L\) and the translation \(t_{-x}^*\) induces a section \(t_{-x}^*(\phi (s))\) of \(L=t_{-x}^*(t_x^*L)\). Thus we put \(zs=t_{-x}^{*}(\phi (s))\). This makes \(\Gamma (A,L)\) into an irreducible  module such that \(\mathbb {C}^{*}\) acts by rescaling. After choosing a basis of \(\Gamma (A,L)\), this gives a faithful linear action of \(H(L)=A_2\) on \(\mathbb {P}^{3}\). The rational map \(A\rightarrow \mathbb {P}^{3}\) induced by L is defined everywhere and factors through an embedding \(K_A \rightarrow \mathbb {P}^{3}\) and the image of the Kummer surface is a quartic with 16 nodes. This is the maximal number of nodes of a quartic surface in \(\mathbb {P}^{3}\) and any quartic in \(\mathbb {P}^{3}\) with 16 nodes is a Kummer surface. For each of the nodes p, there is a plane P which contains p and five other points in the orbit of p under H(L). Moreover, these six points lie on a non-degenerate conic C and the plane P touches the Kummer surface along C. We say that P is a trope. In total we have 16 tropes arising this way and together with the 16 nodes they form Kummer’s \(16_6\) configuration: each plane contains six points and there are six planes through each point. Now, the H(L) action on \(\mathbb {P}^{3}\) restricts to the given \(A_2\) action on \(K_A\) and the embedded Kummer surface is thus invariant under the linear action on the ambient space. The Stone–von-Neumann–Mumford theorem states that, up to isomorphism,
module such that \(\mathbb {C}^{*}\) acts by rescaling. After choosing a basis of \(\Gamma (A,L)\), this gives a faithful linear action of \(H(L)=A_2\) on \(\mathbb {P}^{3}\). The rational map \(A\rightarrow \mathbb {P}^{3}\) induced by L is defined everywhere and factors through an embedding \(K_A \rightarrow \mathbb {P}^{3}\) and the image of the Kummer surface is a quartic with 16 nodes. This is the maximal number of nodes of a quartic surface in \(\mathbb {P}^{3}\) and any quartic in \(\mathbb {P}^{3}\) with 16 nodes is a Kummer surface. For each of the nodes p, there is a plane P which contains p and five other points in the orbit of p under H(L). Moreover, these six points lie on a non-degenerate conic C and the plane P touches the Kummer surface along C. We say that P is a trope. In total we have 16 tropes arising this way and together with the 16 nodes they form Kummer’s \(16_6\) configuration: each plane contains six points and there are six planes through each point. Now, the H(L) action on \(\mathbb {P}^{3}\) restricts to the given \(A_2\) action on \(K_A\) and the embedded Kummer surface is thus invariant under the linear action on the ambient space. The Stone–von-Neumann–Mumford theorem states that, up to isomorphism,  has a unique irreducible representation such that \(\mathbb {C}^{*}\) acts by rescaling. Throughout the paper we will fix coordinates on \(\mathbb {P}^3\) and the particular action of H(L) given in the introduction. Fixing the action of H(L) merely reflects a choice of coordinates though, see for example [18, Lemma 1.52].
has a unique irreducible representation such that \(\mathbb {C}^{*}\) acts by rescaling. Throughout the paper we will fix coordinates on \(\mathbb {P}^3\) and the particular action of H(L) given in the introduction. Fixing the action of H(L) merely reflects a choice of coordinates though, see for example [18, Lemma 1.52].
2.2 The Heisenberg group
Let  be coordinates on \(\mathbb {C}^{4}\) and consider the following four elements of \(\mathrm{SL}_{4} (\mathbb {C})\):
be coordinates on \(\mathbb {C}^{4}\) and consider the following four elements of \(\mathrm{SL}_{4} (\mathbb {C})\):

Let \(H_{2,2}\) be the subgroup of \(\mathrm{SL}_{4} (\mathbb {C})\) generated by \(\sigma _1, \sigma _2, \tau _1\), and \(\tau _2\). This group is of order 32 and the center and commutator of \(H_{2,2}\) are both equal to  , where 1 denotes the identity matrix of size 4. Let
, where 1 denotes the identity matrix of size 4. Let

a group of order 16. Since every element of H has order 2, it follows that

In the sequel we will refer to H as the Heisenberg group.
We consider H as an \(\mathbb {F}_2\)-vector space  . It carries a symplectic form given by \(\langle g,h \rangle =0\) if \(g,h \in H_{2,2}\) commute and \(\langle g,h \rangle =1\) if they anticommute. For each element \(g \in H_{2,2}\), \(g \ne \pm \,1\), the fixed points of \(g \in H\) form two skew lines in \(\mathbb {P}^{3}\). These correspond to the eigenspaces of g in \(\mathbb {C}^{4}\), with eigenvalues \(\pm \,1\) or \(\pm \sqrt{-1}\). In total we have 30 such lines in \(\mathbb {P}^{3}\) which will be called the fix lines. If \(h \in H_{2,2}\) commutes with g, then h leaves the fix lines belonging to g invariant and, if h anticommutes with g, then it flips the fix lines of g. Two fix lines belonging to \(g,h \in H_{2,2}\), where
. It carries a symplectic form given by \(\langle g,h \rangle =0\) if \(g,h \in H_{2,2}\) commute and \(\langle g,h \rangle =1\) if they anticommute. For each element \(g \in H_{2,2}\), \(g \ne \pm \,1\), the fixed points of \(g \in H\) form two skew lines in \(\mathbb {P}^{3}\). These correspond to the eigenspaces of g in \(\mathbb {C}^{4}\), with eigenvalues \(\pm \,1\) or \(\pm \sqrt{-1}\). In total we have 30 such lines in \(\mathbb {P}^{3}\) which will be called the fix lines. If \(h \in H_{2,2}\) commutes with g, then h leaves the fix lines belonging to g invariant and, if h anticommutes with g, then it flips the fix lines of g. Two fix lines belonging to \(g,h \in H_{2,2}\), where  , intersect if and only if g and h commute.
, intersect if and only if g and h commute.
Let \(\mathfrak {S}_n\) denote the symmetric group on n letters and let N be the normalizer of \(H_{2,2}\) in \(\mathrm{SL}_{4} (\mathbb {C})\),

Let \(n \in N\). The reason for introducing N is that if a subset  is invariant under H and \(n \in N\), then nX is also invariant. In fact, for any \(g \in H_{2,2}\) there is an \(h \in H_{2,2}\) such that \(gn=nh\), and hence
is invariant under H and \(n \in N\), then nX is also invariant. In fact, for any \(g \in H_{2,2}\) there is an \(h \in H_{2,2}\) such that \(gn=nh\), and hence  . We now proceed to give a useful relation between N and \(\mathfrak {S}_6\). Since N acts on \(H_{2,2}\) by conjugation, and acts as the identity on the center
. We now proceed to give a useful relation between N and \(\mathfrak {S}_6\). Since N acts on \(H_{2,2}\) by conjugation, and acts as the identity on the center  , N acts on the vector space
, N acts on the vector space  . This action is linear and the transformations preserve the symplectic form. Thus we have a map
. This action is linear and the transformations preserve the symplectic form. Thus we have a map
The kernel obviously contains \(H_{2,2}\). In fact it contains the group  of order 64 which is generated by \(H_{2,2}\) and multiplication by
of order 64 which is generated by \(H_{2,2}\) and multiplication by  , where \(i=\sqrt{-1}\). By [10, Theorem 118], \(\mathrm{Sp}_{4} (\mathbb {F}_2) \cong \mathfrak {S}_6\) and we get a sequence
, where \(i=\sqrt{-1}\). By [10, Theorem 118], \(\mathrm{Sp}_{4} (\mathbb {F}_2) \cong \mathfrak {S}_6\) and we get a sequence

In [30] it is shown that this sequence is exact, and thus  .
.
2.3 The family of surfaces
Consider the following elements of  :
:

For \(\lambda =(A,B,C,D,E) \in \mathbb {C}^{5}\) define
Then  is the set of all homogeneous quartic polynomials in
is the set of all homogeneous quartic polynomials in  invariant under \(H_{2,2}\). Now let
invariant under \(H_{2,2}\). Now let  be the corresponding family of Heisenberg invariant quartic surfaces:
be the corresponding family of Heisenberg invariant quartic surfaces:

There is a linear embedding of  into
into  which better exposes the symmetry of the situation. The normalizer N of \(H_{2,2}\) in \(\mathrm{SL}_{4} (\mathbb {C})\) acts on the 5-dimensional vector space of \(H_{2,2}\)-invariant polynomials via the natural action on \(\mathbb {C}^4\). Following [4, 20, 30] we use six invariant quartic polynomials \(t_0,\dots ,t_5\), which satisfy the relation
which better exposes the symmetry of the situation. The normalizer N of \(H_{2,2}\) in \(\mathrm{SL}_{4} (\mathbb {C})\) acts on the 5-dimensional vector space of \(H_{2,2}\)-invariant polynomials via the natural action on \(\mathbb {C}^4\). Following [4, 20, 30] we use six invariant quartic polynomials \(t_0,\dots ,t_5\), which satisfy the relation  , to embed the parameter space in
, to embed the parameter space in  :
:
We use homogeneous coordinates  on
on  , expressing an invariant quartic polynomial as
, expressing an invariant quartic polynomial as  . The polynomials \(t_0,t_1,t_2,t_3,t_4,t_5\) generate the space of all \(H_{2,2}\) invariant quartic polynomials. The action of
. The polynomials \(t_0,t_1,t_2,t_3,t_4,t_5\) generate the space of all \(H_{2,2}\) invariant quartic polynomials. The action of  permutes these six elements up to a sign change and the group acts on
permutes these six elements up to a sign change and the group acts on  as the full permutation group. Let
as the full permutation group. Let  be the linear subspace of
be the linear subspace of  given by
given by

The parameter space  of
of  with coordinates (A, B, C, D, E) is identified with U via the relations
with coordinates (A, B, C, D, E) is identified with U via the relations

The transformation from U to the parameters (A, B, C, D, E) may be written as

The point is that \(\mathfrak {S}_6\) acts on U by permuting the coordinates, and on the level of the quartic surfaces the action is by means of projective transformations on \(\mathbb {P}^{3}\).
Let  be the projection. For a point \(u \in U\) we have a corresponding surface
be the projection. For a point \(u \in U\) we have a corresponding surface  . By Heisenberg invariant quartic surface (or simply invariant quartic), we shall understand a fiber
. By Heisenberg invariant quartic surface (or simply invariant quartic), we shall understand a fiber  for some \(u \in U\). In addition to these there are 15 pencils of quartic surfaces in \(\mathbb {P}^{3}\) which are invariant under H, but whose defining polynomials are not invariant under \(H_{2,2}\) (these will, however, not be considered).
for some \(u \in U\). In addition to these there are 15 pencils of quartic surfaces in \(\mathbb {P}^{3}\) which are invariant under H, but whose defining polynomials are not invariant under \(H_{2,2}\) (these will, however, not be considered).
2.4 The Segre cubic, the Igusa quartic and the Nieto quintic
In this section we introduce three hypersurfaces in  relevant for the study of Heisenberg invariant quartics. If a group G acts on a set A we use \(\mathrm{orb}_{G} (a)\) to denote the orbit of a point \(a \in A\).
relevant for the study of Heisenberg invariant quartics. If a group G acts on a set A we use \(\mathrm{orb}_{G} (a)\) to denote the orbit of a point \(a \in A\).
First consider the following sets of points, planes and 3-planes in the parameter space U:

These points, planes and 3-planes relate to a \(\mathfrak {S}_6\)-invariant cubic hypersurface  known as the Segre cubic. In
known as the Segre cubic. In  it is defined by the equations
it is defined by the equations

The Segre cubic has ten nodes, namely the \( \mathfrak {S}_6\)-orbit  . It also contains the 15 points of
. It also contains the 15 points of  , and the set of 3-planes
, and the set of 3-planes  is the set of tangent spaces to \(S_3\) at these points. For
is the set of tangent spaces to \(S_3\) at these points. For  the intersection between \(S_3\) and the tangent space \(T_t S_3\) is a union of three 2-planes. In total we have 15 such planes in \(S_3\), called the Segre planes. This is the set
the intersection between \(S_3\) and the tangent space \(T_t S_3\) is a union of three 2-planes. In total we have 15 such planes in \(S_3\), called the Segre planes. This is the set  . In [31], Nieto follows Jessop [24] in proving the following statement.
. In [31], Nieto follows Jessop [24] in proving the following statement.
Proposition 2.1
Let  . The surface
. The surface  is singular if and only if
is singular if and only if

In other words, the subset of U parameterizing the singular invariant quartics is the threefold

It is shown in [20, 24] that a general point on the Segre cubic corresponds to an invariant surface with exactly 16 nodes which constitute an orbit under the Heisenberg group. Such a surface acquires Kummer’s \(16_6\) configuration of nodes and tropes and is a Kummer surface associated to some Abelian surface.
Proposition 2.2
For generic \(u \in S_3\),  is a Kummer surface.
is a Kummer surface.
For \(u \in U\), we say that  is a quadric of multiplicity two, if its defining polynomial is a square of a degree two polynomial. By invariant tetrahedron we understand a Heisenberg invariant quartic surface which is a union of four planes. One checks by direct computation that there are exactly 10 quadrics of multiplicity 2 and 15 invariant tetrahedra in the family. These correspond to the 10 nodes
is a quadric of multiplicity two, if its defining polynomial is a square of a degree two polynomial. By invariant tetrahedron we understand a Heisenberg invariant quartic surface which is a union of four planes. One checks by direct computation that there are exactly 10 quadrics of multiplicity 2 and 15 invariant tetrahedra in the family. These correspond to the 10 nodes  of \(S_3\) and the 15 points
of \(S_3\) and the 15 points  . The quadrics of multiplicity two are called the fundamental quadrics. There is an explanation of the fundamental quadrics and invariant tetrahedra in terms of the symplectic structure on \(H \cong (\mathbb {F}_2)^4\). This vector space has 35 planes, each consisting of four points. If \(g,h \in H_{2,2}\) span a plane in H, then that plane will be called isotropic if g and h commute and non-isotropic if they anticommute. Of the 35 planes, 15 are isotropic and 20 are non-isotropic. For an isotropic plane
. The quadrics of multiplicity two are called the fundamental quadrics. There is an explanation of the fundamental quadrics and invariant tetrahedra in terms of the symplectic structure on \(H \cong (\mathbb {F}_2)^4\). This vector space has 35 planes, each consisting of four points. If \(g,h \in H_{2,2}\) span a plane in H, then that plane will be called isotropic if g and h commute and non-isotropic if they anticommute. Of the 35 planes, 15 are isotropic and 20 are non-isotropic. For an isotropic plane  , the three pairs of fix lines belonging to g, h and gh are the edges of an invariant tetrahedron. Similarly the non-isotropic planes explain the fundamental quadrics. A plane is isotropic if and only if it is equal to its orthogonal complement and therefore the non-isotropic planes form 10 pairs of orthogonal planes. For each such pair \(P_1,P_2\), the six fix lines belonging to elements of \(P_1\) are skew and likewise for \(P_2\). Moreover, the six fix lines belonging to elements of \(P_1\) intersect all the six fix lines belonging to elements of \(P_2\). All 12 lines lie on a fundamental quadric, with six lines in one ruling and six lines in the other.
, the three pairs of fix lines belonging to g, h and gh are the edges of an invariant tetrahedron. Similarly the non-isotropic planes explain the fundamental quadrics. A plane is isotropic if and only if it is equal to its orthogonal complement and therefore the non-isotropic planes form 10 pairs of orthogonal planes. For each such pair \(P_1,P_2\), the six fix lines belonging to elements of \(P_1\) are skew and likewise for \(P_2\). Moreover, the six fix lines belonging to elements of \(P_1\) intersect all the six fix lines belonging to elements of \(P_2\). All 12 lines lie on a fundamental quadric, with six lines in one ruling and six lines in the other.
The dual variety of \(S_3\) is a quartic hypersurface in  called the Igusa quartic, which we denote by \(I_4\). The singular locus of \(I_4\) consists of 15 lines. One way to view \(I_4\) is to look at the linear system of invariant quartics. Recall the basis
called the Igusa quartic, which we denote by \(I_4\). The singular locus of \(I_4\) consists of 15 lines. One way to view \(I_4\) is to look at the linear system of invariant quartics. Recall the basis  of this system introduced above. Because the system does not have a base point we have a morphism
of this system introduced above. Because the system does not have a base point we have a morphism

The image of \(\alpha \) is \(I_4\) [1]. For a hyperplane  we have a corresponding Heisenberg invariant quartic surface \(X_L=\alpha ^{-1}(L)\). In the following proposition we we will call a surface W a quotient by H of \(X_L\) if there is a morphism
we have a corresponding Heisenberg invariant quartic surface \(X_L=\alpha ^{-1}(L)\). In the following proposition we we will call a surface W a quotient by H of \(X_L\) if there is a morphism  whose fibers are exactly the orbits of H.
whose fibers are exactly the orbits of H.
Proposition 2.3
For any hyperplane  , \(L \cap I_4\) is a quotient of
, \(L \cap I_4\) is a quotient of  by the Heisenberg group with quotient map
by the Heisenberg group with quotient map  .
.
The major part of Proposition 2.3 follows from the discussion in [1, Chapter VII, p. 209]. More precisely it is shown there that if  is such that \(xyzw \ne 0\) then \(\alpha ^{-1}(\alpha (p))\) has at most 16 elements. Thus, if in addition we assume that p is not on any fix line (that is the orbit of p has 16 elements), we have that \(\alpha ^{-1}(\alpha (p))\) is exactly the orbit of p since clearly \(\alpha \) is constant on the orbits. It is straightforward to verify the remaining special cases where some coordinate of p is zero or p is on a fix line.
is such that \(xyzw \ne 0\) then \(\alpha ^{-1}(\alpha (p))\) has at most 16 elements. Thus, if in addition we assume that p is not on any fix line (that is the orbit of p has 16 elements), we have that \(\alpha ^{-1}(\alpha (p))\) is exactly the orbit of p since clearly \(\alpha \) is constant on the orbits. It is straightforward to verify the remaining special cases where some coordinate of p is zero or p is on a fix line.
A generic hyperplane  intersects \(I_4\) in a quartic surface with 15 singular points and 10 tropes. The singular points come from the intersections with the singular lines of \(I_4\). On the quotient \(X_L/H\), there are 15 singularities that come from points with nontrivial stabilizers in H. Namely, for any of the 15 non-identity elements of H, the two fix lines intersect \(X_L\) in an eight point orbit that maps to one singular point on \(X_L/H\) by the quotient map. Now, if L is a generic tangent space to \(I_4\), then
intersects \(I_4\) in a quartic surface with 15 singular points and 10 tropes. The singular points come from the intersections with the singular lines of \(I_4\). On the quotient \(X_L/H\), there are 15 singularities that come from points with nontrivial stabilizers in H. Namely, for any of the 15 non-identity elements of H, the two fix lines intersect \(X_L\) in an eight point orbit that maps to one singular point on \(X_L/H\) by the quotient map. Now, if L is a generic tangent space to \(I_4\), then  has an additional singularity at the point of tangency and
has an additional singularity at the point of tangency and  is a Kummer surface. In this way \(I_4\) is a compactification of a moduli space of principally polarized Abelian surfaces with a level-2 structure [15, 20].
is a Kummer surface. In this way \(I_4\) is a compactification of a moduli space of principally polarized Abelian surfaces with a level-2 structure [15, 20].
Let us now look at one more \( \mathfrak {S}_6\) invariant threefold in the parameter space  , the Nieto quintic \(N_5\). This is the Hessian variety to \(S_3\), that is the zeros of the determinant of the Hessian matrix of the polynomial defining \(S_3\). The singular locus of \(N_5\) consists of 20 lines together with the 10 nodes of \(S_3\). With our choice of coordinates, viewing
, the Nieto quintic \(N_5\). This is the Hessian variety to \(S_3\), that is the zeros of the determinant of the Hessian matrix of the polynomial defining \(S_3\). The singular locus of \(N_5\) consists of 20 lines together with the 10 nodes of \(S_3\). With our choice of coordinates, viewing  , \(N_5\) is defined by the equations
, \(N_5\) is defined by the equations

where  . The Nieto quintic and its connection to Heisenberg invariant quartics which contain lines is studied in [4] where the following is proved ([4, Sections 7 and 8]):
. The Nieto quintic and its connection to Heisenberg invariant quartics which contain lines is studied in [4] where the following is proved ([4, Sections 7 and 8]):
Proposition 2.4
The locus in U parameterizing Heisenberg invariant quartics which contain a line is equal to \(N_5\) together with the 10 tangent cones to the isolated singular points of \(N_5\) (the 10 nodes of \(S_3\)).
3 K3 surfaces, lattices and moduli
This section consists of background material on lattices, K3 surfaces, Picard groups and moduli spaces. In particular, we state some well-known results on moduli spaces of K3 surfaces and relations to Picard groups, references on this topic include [11, 12, 21,22,23, 33].
A lattice M is a finitely generated free Abelian group equipped with an integral symmetric bilinear form. An important invariant of M is the discriminant, denoted  , which is equal to the determinant of any matrix representing the bilinear form. We shall deal only with non-degenerate lattices, that is we assume that the discriminant is non-zero. If the discriminant is equal to \(\pm 1\), the lattice is called unimodular. If \(N \subseteq M\) is a sublattice of full rank, then
, which is equal to the determinant of any matrix representing the bilinear form. We shall deal only with non-degenerate lattices, that is we assume that the discriminant is non-zero. If the discriminant is equal to \(\pm 1\), the lattice is called unimodular. If \(N \subseteq M\) is a sublattice of full rank, then  , where
, where  is the index of N in M, see [3, I.2.1]. If \(N \subseteq M\) is a sublattice, we use the notation \(N^{\perp }\) for the orthogonal complement of N in M. A lattice is called even if the \(\mathbb {Z}\)-valued quadratic form associated to the bilinear form takes on even values only. There is an induced bilinear form on the real vector space
is the index of N in M, see [3, I.2.1]. If \(N \subseteq M\) is a sublattice, we use the notation \(N^{\perp }\) for the orthogonal complement of N in M. A lattice is called even if the \(\mathbb {Z}\)-valued quadratic form associated to the bilinear form takes on even values only. There is an induced bilinear form on the real vector space  which may be diagonalized in such a way that only \(\pm 1\) appear on the diagonal. The signature of a lattice M is a pair of numbers
which may be diagonalized in such a way that only \(\pm 1\) appear on the diagonal. The signature of a lattice M is a pair of numbers  , where a is the number of positive entries in such a diagonal matrix and b the number of negative entries. The sum of a and b is the rank of M. A sublattice N of a lattice M is called primitive if M / N is torsion free. An isomorphism of lattices is a group isomorphism that also respects the bilinear form.
, where a is the number of positive entries in such a diagonal matrix and b the number of negative entries. The sum of a and b is the rank of M. A sublattice N of a lattice M is called primitive if M / N is torsion free. An isomorphism of lattices is a group isomorphism that also respects the bilinear form.
For a scheme X, the Picard group is the group of isomorphism classes of line bundles on X, and is denoted  . If X is a smooth variety over an algebraically closed field, then
. If X is a smooth variety over an algebraically closed field, then  is isomorphic to the group of Weil divisors on X modulo linear equivalence. For a smooth complex projective variety X, let \(\mathrm{Pic}^0 (X)\) denote the subgroup of
is isomorphic to the group of Weil divisors on X modulo linear equivalence. For a smooth complex projective variety X, let \(\mathrm{Pic}^0 (X)\) denote the subgroup of  corresponding to divisors algebraically equivalent to 0 and define the Néron–Severi group by
corresponding to divisors algebraically equivalent to 0 and define the Néron–Severi group by  . The Néron–Severi group is a finitely generated Abelian group and its rank is called the Picard number of X. Now suppose that X is a complex projective K3 surface, which means that X is a smooth simply connected projective complex variety of dimension 2, whose canonical bundle is trivial. In this case \(\mathrm{Pic}^0 (X)=\{0\}\) and thus
. The Néron–Severi group is a finitely generated Abelian group and its rank is called the Picard number of X. Now suppose that X is a complex projective K3 surface, which means that X is a smooth simply connected projective complex variety of dimension 2, whose canonical bundle is trivial. In this case \(\mathrm{Pic}^0 (X)=\{0\}\) and thus  and
and  is free and finitely generated. It is well known that \(1 \leqslant \rho (X) \leqslant 20\), where
is free and finitely generated. It is well known that \(1 \leqslant \rho (X) \leqslant 20\), where  is the Picard number of X. The second cohomology group \(H^2(X,\mathbb {Z})\) is also free and of rank 22, and the cup product defines a bilinear form giving it the structure of a lattice. Abstractly, this lattice is isomorphic to the so-called K3 lattice
is the Picard number of X. The second cohomology group \(H^2(X,\mathbb {Z})\) is also free and of rank 22, and the cup product defines a bilinear form giving it the structure of a lattice. Abstractly, this lattice is isomorphic to the so-called K3 lattice

Here, U is the hyperbolic plane, a rank 2 lattice with bilinear form given by the matrix
and \(E_8\) is the lattice of rank 8 whose bilinear form is given by the Cartan matrix of the root system \(E_8\). The K3 lattice is even, unimodular and of signature (3, 19). The Picard group of X may be viewed as a non-degenerate sublattice of \(H^2(X,\mathbb {Z})\) with signature \((1,\rho {(X)}-1)\), where the bilinear form on  is the intersection product. Since the lattice L is even, so is
is the intersection product. Since the lattice L is even, so is  . The orthogonal complement of
. The orthogonal complement of  in \(H^2(X,\mathbb {Z})\) is called the transcendental lattice and is denoted by \(T_X\).
in \(H^2(X,\mathbb {Z})\) is called the transcendental lattice and is denoted by \(T_X\).
We now turn to a particular class of K3 surfaces, namely smooth quartic surfaces in \(\mathbb {P}^3\). A homogeneous quartic polynomial in four variables has 35 coefficients and therefore \(\mathbb {P}^{34}\) parameterizes quartic surfaces in \(\mathbb {P}^3\). Consider the open set \(O \subseteq \mathbb {P}^{34}\) that parameterizes smooth surfaces. The group \(\mathrm{PGL}_{4} (\mathbb {C})\) acts on O by means of isomorphisms of \(\mathbb {P}^3\) and we will use  to denote the GIT quotient with respect to this action, see [22, Chapter 5, Example 2.5]. Thus
to denote the GIT quotient with respect to this action, see [22, Chapter 5, Example 2.5]. Thus  is the (coarse) moduli space of smooth quartic surfaces in \(\mathbb {P}^3\) parameterizing such surfaces up to projective transformations. It is an irreducible quasi projective variety of dimension 19.
is the (coarse) moduli space of smooth quartic surfaces in \(\mathbb {P}^3\) parameterizing such surfaces up to projective transformations. It is an irreducible quasi projective variety of dimension 19.
A marking of a K3 surface X is an isomorphism of lattices \(L \cong H^2(X,\mathbb {Z})\). Below we will make use of the (fine) moduli space of marked polarized K3 surfaces of degree 4. This is a complex manifold which we will denote by  , see [22, Chapter 6, 3.4]. For
, see [22, Chapter 6, 3.4]. For  , let \(\rho (m)\) denote the Picard number of the surface corresponding to m and consider the higher Noether–Lefschetz loci,
, let \(\rho (m)\) denote the Picard number of the surface corresponding to m and consider the higher Noether–Lefschetz loci,

where k is an integer \(1\leqslant k \leqslant 20\). The Noether–Lefschetz locus \(\mathrm{NL}_{k}\) may be written as a countable union of analytic subvarieties of  of dimension \(20-k\), see [22, Chapter 17, 1.3].
of dimension \(20-k\), see [22, Chapter 17, 1.3].
Definition 3.1
We say that a condition holds for a very generic point, or very general point, of a variety Y if there is a countable union \(K=\bigcup _{i \in \mathbb {Z}} K_i\) of proper Zariski-closed subsets  , such that the condition holds for all points
, such that the condition holds for all points  .
.
Let \(O \subset \mathbb {P}^{34}\) be the subset parameterizing smooth quartic surfaces, let \(Z \subseteq O\) be a subvariety and  the corresponding family of surfaces. We use \(\rho _0(Z)\) to denote the minimal Picard number of any fiber in the family.
the corresponding family of surfaces. We use \(\rho _0(Z)\) to denote the minimal Picard number of any fiber in the family.
Lemma 3.2
If \(Z \subseteq O \subseteq \mathbb {P}^{34}\) is a subvariety of O such that  is generically finite to one, then
is generically finite to one, then  .
.
Proof
Let \(k = \rho _0(Z)\). For a general smooth point \(p \in Z\) there is an open analytic neighborhood \(V \subseteq O\) of p such that  is injective. By shrinking V we may assume that \(B=V\cap Z\) is smooth, connected and simply connected. The family of surfaces with base B may be marked by choosing a marking of some fiber, which yields a canonical marking of all fibers, see [22, Chapter 6, 2.2]. This gives a holomorphic map
is injective. By shrinking V we may assume that \(B=V\cap Z\) is smooth, connected and simply connected. The family of surfaces with base B may be marked by choosing a marking of some fiber, which yields a canonical marking of all fibers, see [22, Chapter 6, 2.2]. This gives a holomorphic map  which is also injective since if \(\phi (b)=\phi (b')\) then the fibers over b and \(b'\) are projectively equivalent. Since \(\phi (B) \subseteq \mathrm{NL}_{k}\) and \(\mathrm{NL}_{k}\) is a countable union of \((20-k)\)-dimensional analytic subvarieties of
which is also injective since if \(\phi (b)=\phi (b')\) then the fibers over b and \(b'\) are projectively equivalent. Since \(\phi (B) \subseteq \mathrm{NL}_{k}\) and \(\mathrm{NL}_{k}\) is a countable union of \((20-k)\)-dimensional analytic subvarieties of  ,
,  . \(\square \)
. \(\square \)
4 The Picard number
We will show that the Picard number of a very general Heisenberg invariant quartic is 16. A corollary to this is that any invariant divisor class is a multiple of the hyperplane section. We start with some generalities on symplectic group actions on K3 surfaces.
If a group G acts on a K3 surface X, then G acts on \(H^2(X,\mathbb {Z})\) and the action restricts to the sublattices  and \(T_X\). We will write this action \(g^{*}l\) for \(g \in G\) and \(l \in H^2(X,\mathbb {Z})\). Let
and \(T_X\). We will write this action \(g^{*}l\) for \(g \in G\) and \(l \in H^2(X,\mathbb {Z})\). Let

and  . Since the canonical bundle of a K3 surface X is trivial, X has a unique non-zero holomorphic 2-form \(\omega \), up to rescaling. Hence for
. Since the canonical bundle of a K3 surface X is trivial, X has a unique non-zero holomorphic 2-form \(\omega \), up to rescaling. Hence for  , \(f^* \omega =\lambda \omega \), where \(\lambda \in \mathbb {C}\). If \(\lambda =1\), then f is called symplectic. In the following proposition, the first claim is due to Nikulin [32] and the second claim is due to Mukai [27].
, \(f^* \omega =\lambda \omega \), where \(\lambda \in \mathbb {C}\). If \(\lambda =1\), then f is called symplectic. In the following proposition, the first claim is due to Nikulin [32] and the second claim is due to Mukai [27].
Proposition 4.1
Let G be a finite group of symplectic automorphisms of a K3 surface X and let  be the orthogonal complement of \(H^2(X,\mathbb {Z})^G\) in \(H^2(X,\mathbb {Z})\). For \(g \in G\), \(g \ne 1\), let f(g) be the number of fixed points of \(g \in G\) and put \(f(1)=24\). Then
be the orthogonal complement of \(H^2(X,\mathbb {Z})^G\) in \(H^2(X,\mathbb {Z})\). For \(g \in G\), \(g \ne 1\), let f(g) be the number of fixed points of \(g \in G\) and put \(f(1)=24\). Then
-
(a)
\(T_X \subseteq H^2(X,\mathbb {Z})^G\) and
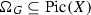 ,
, -
(b)
 .
.
The generic member of our family is a smooth quartic in \(\mathbb {P}^{3}\) and hence a K3 surface. Since the action of the Heisenberg group is induced by a representation \(H_{2,2} \rightarrow \mathrm{SL}_{4} (\mathbb {C})\) and the action of \(H_{2,2}\) preserves the defining polynomials of our surfaces, the action of H is symplectic by [27, Lemma 2.1].
Corollary 4.2
If \(X \subset \mathbb {P}^{3}\) is a generic Heisenberg invariant quartic, then
-
(a)
 ,
, -
(b)
\(16 \leqslant \rho (X)\).
Proof
Let \(g \in H\), \(g\ne 1\). The fixed points of g form two skew lines in \(\mathbb {P}^{3}\), and hence g has eight fixed points on X. By Proposition 4.1,  and
and  . Assume that
. Assume that  . The hyperplane class
. The hyperplane class  is invariant and thus there is an integer \(n>0\) such that \(nh \in T_X\). Since \(T_X\) is the orthogonal complement of
is invariant and thus there is an integer \(n>0\) such that \(nh \in T_X\). Since \(T_X\) is the orthogonal complement of  ,
,  , a contradiction. Hence
, a contradiction. Hence  . It follows that
. It follows that  , since
, since  . \(\square \)
. \(\square \)
For homogeneous  , let
, let  and consider the Hessian surface of X,
and consider the Hessian surface of X,

where  is the Hessian matrix of second derivatives of F. Let \(T \in \mathrm{GL}_{4} (\mathbb {C})\) and denote the induced automorphism of \(\mathbb {P}^{3}\) also by T. Let \(Y=T(X)\) and let \((T^{-1})^t\) denote the transpose of \(T^{-1}\). Note that for \(p \in \mathbb {C}^{4}\),
is the Hessian matrix of second derivatives of F. Let \(T \in \mathrm{GL}_{4} (\mathbb {C})\) and denote the induced automorphism of \(\mathbb {P}^{3}\) also by T. Let \(Y=T(X)\) and let \((T^{-1})^t\) denote the transpose of \(T^{-1}\). Note that for \(p \in \mathbb {C}^{4}\),

It follows that T takes the Hessian surface of X to the Hessian surface of Y, with preserved multiplicities of irreducible components. In particular, the Hessian surface of a Heisenberg invariant quartic is a Heisenberg invariant octic.
Example 4.3
Let \(u=(1,1,1,1,-\,2,-\,2) \in U\). We will look at linear transformations of the Fermat quartic  for the purpose of applying Lemma 3.2.
for the purpose of applying Lemma 3.2.
There are 15 surfaces in the family that are projectively equivalent to X corresponding to the \(\mathfrak {S}_6\)-orbit of \((1,1,1,1,-2,-2)\), and we shall see that there are no others. The Hessian surface of the Fermat quartic is the zeros of \(x^2y^2z^2w^2\), an invariant tetrahedron of double multiplicity. Note that the invariant tetrahedron defined by xyzw corresponds to the point \((0,0,0,0,1,-\,1) \in U\). Suppose that \(T \in \mathrm{GL}_{4} (\mathbb {C})\) takes X to some Heisenberg invariant quartic Y. By the discussion above, the Hessian surface of Y must be one of the 15 invariant tetrahedra, counted with multiplicity 2. These correspond to the \(\mathfrak {S}_6\)-orbit of \((0,0,0,0,1,-\,1)\). Let \(S \in \mathrm{SL}_{4} (\mathbb {C})\) be a transformation in the normalizer of \(H_{2,2}\) in \(\mathrm{SL}_{4} (\mathbb {C})\) which takes  to
to  . Then
. Then  induces an automorphism of
induces an automorphism of  and therefore corresponds to a permutation of the coordinates
and therefore corresponds to a permutation of the coordinates  possibly combined with a rescaling of the axes. Since S(T(X)) is an invariant quartic, \(S(T(X))=X\) and \(T(X)=S^{-1}(X)\). Therefore T(X) is in the \(\mathfrak {S}_6\)-orbit of \((1,1,1,1,-2,-2)\).
possibly combined with a rescaling of the axes. Since S(T(X)) is an invariant quartic, \(S(T(X))=X\) and \(T(X)=S^{-1}(X)\). Therefore T(X) is in the \(\mathfrak {S}_6\)-orbit of \((1,1,1,1,-2,-2)\).
Theorem 4.4
A very generic Heisenberg invariant quartic \(X \subset \mathbb {P}^{3}\) has Picard number 16.
Proof
By the second claim of Corollary 4.2, \(\rho (X) \geqslant 16\). Let \(Z \subset \mathbb {P}^{34}\) be the subset parameterizing smooth Heisenberg invariant quartics. The quotient map  is generically finite to one by upper-semi-continuity of the dimension of fibers and Example 4.3. By Lemma 7.1, \(\rho (X)=\rho _0(Z)\) and using Lemma 3.2 we get \(\rho (X) \leqslant 20-4=16\). \(\square \)
is generically finite to one by upper-semi-continuity of the dimension of fibers and Example 4.3. By Lemma 7.1, \(\rho (X)=\rho _0(Z)\) and using Lemma 3.2 we get \(\rho (X) \leqslant 20-4=16\). \(\square \)
Corollary 4.5
For very generic \(u \in U\) and  ,
,  , where
, where  is the class of the hyperplane section. In particular, every invariant curve on X is a complete intersection between X and another surface in \(\mathbb {P}^{3}\).
is the class of the hyperplane section. In particular, every invariant curve on X is a complete intersection between X and another surface in \(\mathbb {P}^{3}\).
Proof
Since  ,
,

Because  , and \(T_X\) is contained in the rank 7 lattice \(H^2(X,\mathbb {Z})^H\), it follows that
, and \(T_X\) is contained in the rank 7 lattice \(H^2(X,\mathbb {Z})^H\), it follows that  has rank at most 1. Clearly, the class h is invariant under H and thus
has rank at most 1. Clearly, the class h is invariant under H and thus  . Let D be a generator of
. Let D be a generator of  and let \(n \in \mathbb {Z}\) be such that \(h=nD\). Since
and let \(n \in \mathbb {Z}\) be such that \(h=nD\). Since  , and \(D^2\) is even since
, and \(D^2\) is even since  is an even lattice, it follows that \(n=\pm 1\). \(\square \)
is an even lattice, it follows that \(n=\pm 1\). \(\square \)
5 Conics on the invariant surfaces
Definition 5.1
Let X be a quartic surface in \(\mathbb {P}^{3}\). We say that a plane L in \(\mathbb {P}^{3}\) is a trope of X if \(X \cap L\) is an irreducible conic counted with multiplicity 2.
Lemma 5.2
A quartic surface \(X \subset \mathbb {P}^{3}\) which has a trope L is necessarily singular.
Proof
Let  be coordinates on \(\mathbb {P}^{3}\). Change coordinates so that
be coordinates on \(\mathbb {P}^{3}\). Change coordinates so that  . Then X is defined by
. Then X is defined by  , for some cubic polynomial F and quadratic polynomial G. Then the set
, for some cubic polynomial F and quadratic polynomial G. Then the set  is nonempty and inside the singular locus of X. \(\square \)
is nonempty and inside the singular locus of X. \(\square \)
Below we shall make use of the following fact: for generic \(u \in S_3\), the Kummer surface  is uniquely determined by any of its nodes as well as any of its tropes. To establish this, let
is uniquely determined by any of its nodes as well as any of its tropes. To establish this, let  be a Heisenberg invariant polynomial depending on the parameters \(\lambda =(A,B,C,D,E)\) as in (1). For a general \(p \in \mathbb {P}^{3}\) there is a unique \(u \in U\) such that
be a Heisenberg invariant polynomial depending on the parameters \(\lambda =(A,B,C,D,E)\) as in (1). For a general \(p \in \mathbb {P}^{3}\) there is a unique \(u \in U\) such that  is singular at p. To see this, it is enough to check that there is a point
is singular at p. To see this, it is enough to check that there is a point  such that the system of linear equations
such that the system of linear equations

has a unique solution  (this is true for example if \(p=(1,2,3,4)\)). In fact, there exists a unique invariant quartic singular at \(p \in \mathbb {P}^3\) exactly when p is not on a fix line [4]. Using \(\mathfrak {S}_6\)-invariance one checks that the set of \(u \in U\) such that
(this is true for example if \(p=(1,2,3,4)\)). In fact, there exists a unique invariant quartic singular at \(p \in \mathbb {P}^3\) exactly when p is not on a fix line [4]. Using \(\mathfrak {S}_6\)-invariance one checks that the set of \(u \in U\) such that  has a singular point that lies on some fix line is equal to the union of the 15 tangent spaces \(T_t S_3\) where
has a singular point that lies on some fix line is equal to the union of the 15 tangent spaces \(T_t S_3\) where  is an invariant tetrahedron. We conclude that a generic Heisenberg invariant Kummer surface is determined by any of its nodes. The corresponding statement for tropes is clear once we see that \(p \in \mathbb {P}^{3}\) is a node precisely when the plane
is an invariant tetrahedron. We conclude that a generic Heisenberg invariant Kummer surface is determined by any of its nodes. The corresponding statement for tropes is clear once we see that \(p \in \mathbb {P}^{3}\) is a node precisely when the plane  with the same coordinates as p is a trope. Let p be a node, and note that we may assume p to be a generic point in \(\mathbb {P}^3\). As in [20, Chapter I, Section 3], there are six points in the orbit of p that lie in \(p^{*}\). It follows that the six points are multiple points of the curve of intersection between \(p^{*}\) and
with the same coordinates as p is a trope. Let p be a node, and note that we may assume p to be a generic point in \(\mathbb {P}^3\). As in [20, Chapter I, Section 3], there are six points in the orbit of p that lie in \(p^{*}\). It follows that the six points are multiple points of the curve of intersection between \(p^{*}\) and  . This curve must then either contain a line as an irreducible component or be a conic of multiplicity two. The first case is excluded by Proposition 2.4. The set of 16 tropes is hence the orbit of \(p^{*}\).
. This curve must then either contain a line as an irreducible component or be a conic of multiplicity two. The first case is excluded by Proposition 2.4. The set of 16 tropes is hence the orbit of \(p^{*}\).
Theorem 5.3
A generic invariant quartic  contains at least 320 smooth conics.
contains at least 320 smooth conics.
Proof
Pick \(u \in U\) generic and let q be a node of the Segre cubic \(S_3\). The line through u and q intersects \(S_3\) in one additional point p, let  . Since u is generic, K(q) is a Kummer surface by Proposition 2.2, and thus has 16 tropes which form an orbit under H. Let T be a trope of K(q) and note that
. Since u is generic, K(q) is a Kummer surface by Proposition 2.2, and thus has 16 tropes which form an orbit under H. Let T be a trope of K(q) and note that  is a quadric of multiplicity two. The polynomial defining
is a quadric of multiplicity two. The polynomial defining  , in homogeneous coordinates on T, is a linear combination of squares, and thus reducible. The generic member of the family does not contain any line (Proposition 2.4), and since
, in homogeneous coordinates on T, is a linear combination of squares, and thus reducible. The generic member of the family does not contain any line (Proposition 2.4), and since  is smooth nor does it have a trope (Lemma 5.2). We conclude that
is smooth nor does it have a trope (Lemma 5.2). We conclude that  is a union of two smooth conics.
is a union of two smooth conics.
For two different nodes \(q_1\) and \(q_2\) of \(S_3\) the corresponding Kummer surfaces  and
and  are different, since we may assume that u is not on the line through \(q_1\) and \(q_2\). Since a generic Heisenberg invariant Kummer surface is determined by any of its tropes, all tropes of the Kummer surfaces K(q), for all of the 10 nodes q of \(S_3\), are different. Since two different planes cannot have a smooth conic in common, we conclude that there are at least
are different, since we may assume that u is not on the line through \(q_1\) and \(q_2\). Since a generic Heisenberg invariant Kummer surface is determined by any of its tropes, all tropes of the Kummer surfaces K(q), for all of the 10 nodes q of \(S_3\), are different. Since two different planes cannot have a smooth conic in common, we conclude that there are at least  smooth conics on
smooth conics on  . \(\square \)
. \(\square \)
For a general invariant quartic X, we will refer to the conics in Theorem 5.3 as the 320 conics on X. As we show in Proposition 7.2, these conics are the only conics on a very general surface in the family.
6 Invariant surfaces containing lines
The generic Heisenberg invariant quartic does not contain any line. The invariant surfaces that contain a line are parameterized by the Nieto quintic \(N_5\) and the 10 tangent cones to the isolated singularities of \(N_5\) [4]. In this section we will look at the configuration of lines on a Heisenberg invariant quartic that corresponds to a general point on \(N_5\). This will be used to compute the intersection matrix of the 320 smooth conics on a very generic invariant quartic. General references for this section are [2, 4, 6] and in particular the proof of Proposition 6.1 follows arguments made in [2] and [6].
Let \((p_{01},p_{02},p_{03},p_{12},p_{13},p_{23})\) be the Plücker coordinates on  . The Plücker embedding identifies the Grassmannian of lines in \(\mathbb {P}^3\) with the quadric in
. The Plücker embedding identifies the Grassmannian of lines in \(\mathbb {P}^3\) with the quadric in  defined by the Plücker relation
defined by the Plücker relation

We will use so-called Klein coordinates  , which are defined in terms of Plücker coordinates by
, which are defined in terms of Plücker coordinates by

where  . In Klein coordinates the Plücker relation reads
. In Klein coordinates the Plücker relation reads

and the condition that a line with coordinates  is coplanar with a line with coordinates \((y_0,\dots ,y_5)\) is
is coplanar with a line with coordinates \((y_0,\dots ,y_5)\) is

The Heisenberg group acts on the space of lines in \(\mathbb {P}^3\) and in Klein coordinates the action is given neatly by sign changes in accordance with the table

where \(\sigma _1,\sigma _2,\tau _1,\tau _2\) are the generators from Sect. 2.2.
In [4] it is shown that for a generic \(u \in N_5\),  contains exactly 32 lines. In the same paper it is proved that such a surface is a desingularized Kummer surface coming from an Abelian surface A with a (1, 3)-polarization. The Klein coordinates for any of the 32 lines satisfy the condition
contains exactly 32 lines. In the same paper it is proved that such a surface is a desingularized Kummer surface coming from an Abelian surface A with a (1, 3)-polarization. The Klein coordinates for any of the 32 lines satisfy the condition
by which we mean that

The 32 lines constitute two orbits under the Heisenberg group, each containing 16 lines. There is an involution relating the two orbits: if  are Klein coordinates for a line in one of the orbits, then
are Klein coordinates for a line in one of the orbits, then

are Klein coordinates for a line in the other orbit. The 16 lines in any of the two orbits are mutually disjoint, in fact one of the orbits is the union of the exceptional divisors coming from blowing up the singular Kummer surface in its 16 nodes. The configuration of lines is called a \(32_{10}\) since any line in one orbit intersects exactly 10 lines in the other orbit. There are thus exactly 160 reducible conics on the surface. If two lines, one from each orbit, are coplanar then their complement on the surface is an irreducible conic. In other words, the plane that contains the reducible conic intersects the surface in the union of two lines and an irreducible conic. This gives rise to 160 irreducible conics on  .
.
Proposition 6.1
For a very general \(u \in N_5\) there are no other irreducible conics on  except for the 160 complements to reducible conics.
except for the 160 complements to reducible conics.
Proof
Let  . The surface X is a desingularized Kummer surface of an Abelian surface A admitting a (1, 3)-polarization. In fact, there is an open subset of the moduli space of Abelian surfaces which admit a (1, 3)-polarization together with the choice of a level-2 structure which is naturally an unbranched double cover of the open subset of \(N_5\) parameterizing smooth surfaces [4]. Since \(u \in N_5\) is very general we may assume that A has Picard number 1 (see [8, Section 15.1]). Let \(e_1,\dots ,e_{16}\) denote the halfperiods of A, that is \(e_i\) is a 2-torsion point or the identity element. Let \(\widetilde{A}\) denote the blow-up of A in
. The surface X is a desingularized Kummer surface of an Abelian surface A admitting a (1, 3)-polarization. In fact, there is an open subset of the moduli space of Abelian surfaces which admit a (1, 3)-polarization together with the choice of a level-2 structure which is naturally an unbranched double cover of the open subset of \(N_5\) parameterizing smooth surfaces [4]. Since \(u \in N_5\) is very general we may assume that A has Picard number 1 (see [8, Section 15.1]). Let \(e_1,\dots ,e_{16}\) denote the halfperiods of A, that is \(e_i\) is a 2-torsion point or the identity element. Let \(\widetilde{A}\) denote the blow-up of A in  . We have morphisms
. We have morphisms
where \(\gamma \) is a double cover branched over the 16 lines \(L_1,\dots ,L_{16}\) in one of the orbits and \(\alpha \) is the blow-up map [4]. Let \(E_i = \alpha ^{-1}(e_i)\), \(i=1,\dots ,16\). Then  if \(i \ne j\), \(E_i^2=-1\) and up to reordering \(\gamma (E_i)=L_i\). Now, as is explained in [4], if M is the line bundle corresponding to the sheaf
if \(i \ne j\), \(E_i^2=-1\) and up to reordering \(\gamma (E_i)=L_i\). Now, as is explained in [4], if M is the line bundle corresponding to the sheaf  , then the line bundle
, then the line bundle  on \(\widetilde{A}\) descends to a line bundle on A which defines a polarization of type (2, 6). Further, there is a symmetric line bundle \(\theta \) on A of type (1, 3) such that
on \(\widetilde{A}\) descends to a line bundle on A which defines a polarization of type (2, 6). Further, there is a symmetric line bundle \(\theta \) on A of type (1, 3) such that  , see [4]. Let T denote the divisor class in the Néron–Severi group of A that corresponds to \(\theta \) and let \(H_X\) be the hyperplane class of X. Then we have that
, see [4]. Let T denote the divisor class in the Néron–Severi group of A that corresponds to \(\theta \) and let \(H_X\) be the hyperplane class of X. Then we have that  where \((d_1,d_2)=(1,3)\) [28]. Thus
where \((d_1,d_2)=(1,3)\) [28]. Thus  .
.
Now let \(C \subseteq X\) be an irreducible conic different from the complements of reducible conics. By the adjunction formula, we have that  . Let \(F=\alpha _*(\gamma ^*(C))\). Since
. Let \(F=\alpha _*(\gamma ^*(C))\). Since  is square free, T generates the Néron–Severi group of A and we may write \(F=dT\) for some integer d. Now let \({m_i=C \cdot L_i=\gamma ^*(C) \cdot E_i}\) for \(i=1,\dots ,16\). Then \({\alpha ^*(F)=\gamma ^*(C)+\sum _{i=1}^{16}m_iE_i}\). Thus \(6d^2=(dT)^2=F^2=\alpha ^*(F)^2=\bigl (\gamma ^*(C)+\sum _{i=1}^{16}m_iE_i\bigr )^2\), and therefore \(6d^2= \gamma ^*(C)^2+2\sum _{i=1}^{16}m_i\gamma ^*(C) \cdot E_i+\sum _{i=1}^{16}m_i^2E_i^2= 2C^2+2\sum _{i=1}^{16}m_i^2-\sum _{i=1}^{16}m_i^2\). In conclusion,
is square free, T generates the Néron–Severi group of A and we may write \(F=dT\) for some integer d. Now let \({m_i=C \cdot L_i=\gamma ^*(C) \cdot E_i}\) for \(i=1,\dots ,16\). Then \({\alpha ^*(F)=\gamma ^*(C)+\sum _{i=1}^{16}m_iE_i}\). Thus \(6d^2=(dT)^2=F^2=\alpha ^*(F)^2=\bigl (\gamma ^*(C)+\sum _{i=1}^{16}m_iE_i\bigr )^2\), and therefore \(6d^2= \gamma ^*(C)^2+2\sum _{i=1}^{16}m_i\gamma ^*(C) \cdot E_i+\sum _{i=1}^{16}m_i^2E_i^2= 2C^2+2\sum _{i=1}^{16}m_i^2-\sum _{i=1}^{16}m_i^2\). In conclusion,

Furthermore, \(12d=2T \cdot dT=2T \cdot F=\alpha ^*(2T)\cdot \alpha ^*(F)=\bigl (\gamma ^*(H_X)+\sum _{i=1}^{16}E_i\bigr )\cdot \bigl (\gamma ^*(C)+\sum _{i=1}^{16}m_iE_i\bigr )\), and hence \(12d=\gamma ^*(H_X)\cdot \gamma ^*(C)+\sum _{i=1}^{16}m_iE_i\cdot \gamma ^*(H_X)+\sum _{i=1}^{16}E_i \cdot \gamma ^*(C)+\sum _{i=1}^{16}m_iE_i^2\), which implies that

Since \(L_i\) and C are not coplanar,  or
or  for all i. It follows by (4) that \(d=1\). Note also that
for all i. It follows by (4) that \(d=1\). Note also that  for all i. But then (3) gives
for all i. But then (3) gives  and (4) gives
and (4) gives  , a contradiction. \(\square \)
, a contradiction. \(\square \)
Let \(u \in N_5\) be very generic and put  . As long as all the Klein coordinates
. As long as all the Klein coordinates  of a line l are non-zero, the matter of whether some Heisenberg translate of l intersects some Heisenberg translate of the image of l under the involution does not depend on l. From the description above of the action of the Heisenberg group on the Grassmannian of lines in \(\mathbb {P}^3\), the condition (2), and the involution relating the two sets of 16 lines on X, it is straightforward to compute the intersection matrix of the 160 reducible conics on X. Since the 160 irreducible conics on X are coplanar with reducible conics, the intersection matrix of all 320 conics on X is readily deducible from the intersection matrix of the 160 reducible conics. We will not do this in detail but we note in passing that if C and D are conics on X such that C and D belong to different orbits under the Heisenberg group H, then
of a line l are non-zero, the matter of whether some Heisenberg translate of l intersects some Heisenberg translate of the image of l under the involution does not depend on l. From the description above of the action of the Heisenberg group on the Grassmannian of lines in \(\mathbb {P}^3\), the condition (2), and the involution relating the two sets of 16 lines on X, it is straightforward to compute the intersection matrix of the 160 reducible conics on X. Since the 160 irreducible conics on X are coplanar with reducible conics, the intersection matrix of all 320 conics on X is readily deducible from the intersection matrix of the 160 reducible conics. We will not do this in detail but we note in passing that if C and D are conics on X such that C and D belong to different orbits under the Heisenberg group H, then
-
 for six different \(g \in H\), \(g\ne 1\),
for six different \(g \in H\), \(g\ne 1\), -
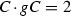 for nine different \(g \in H\), \(g\ne 1\),
for nine different \(g \in H\), \(g\ne 1\), -
 for four different \(g \in H\),
for four different \(g \in H\), -
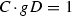 for eight different \(g \in H\),
for eight different \(g \in H\), -
 for four different \(g \in H\).
for four different \(g \in H\).
We will see in Sect. 7 that the intersection matrix of the conics on X is the same as the intersection matrix associated to the 320 smooth conics on a very generic Heisenberg invariant quartic.
Remark 6.2
For later purposes we will consider the intersections of a special set of 16 reducible conics on X. We need to put an order on the set of all reducible conics on X. We will order the elements of the Heisenberg group as follows. Let \(g \in H\), \(g=\sigma _1^i \sigma _2^j \tau _1^k \tau _2^l\) where \(0 \leqslant i,j,k,l \leqslant 1\) and \(\sigma _1,\sigma _2,\tau _1\) and \(\tau _2\) are the generators from Sect. 2.2. Then we order H by interpreting  as a number in binary form that marks the place of g. Let L be a line on X. The order on H puts an order on the orbit of L as well as the orbit of the image of L under the involution. This induces an order on the set of reducible conics by saying that if line number a in the orbit of L intersects line number b in the other orbit, and likewise for \(a'\) and \(b'\) with
as a number in binary form that marks the place of g. Let L be a line on X. The order on H puts an order on the orbit of L as well as the orbit of the image of L under the involution. This induces an order on the set of reducible conics by saying that if line number a in the orbit of L intersects line number b in the other orbit, and likewise for \(a'\) and \(b'\) with  , then the reducible conic indexed by
, then the reducible conic indexed by  is prior to the conic indexed by
is prior to the conic indexed by  if and only if \(a<a'\), or \(a=a'\) and \(b < b'\). With that order of rows and columns, let N denote the intersection matrix of the reducible conics on X. Let M be the submatrix of N given by picking out the following rows and columns:
if and only if \(a<a'\), or \(a=a'\) and \(b < b'\). With that order of rows and columns, let N denote the intersection matrix of the reducible conics on X. Let M be the submatrix of N given by picking out the following rows and columns:
This particular choice of conics has been made because, as we shall see in Sect. 8, it defines a sublattice with minimal discriminant (the conics were found using a computer aided search). Then

and  .
.
7 The intersection matrix of the 320 conics
In Sect. 6 we determined the configuration of conics (reducible or irreducible) on an invariant quartic  for very generic \(u \in N_5\). In this section we shall show that this configuration is the same as the configuration of the 320 irreducible conics on a very general invariant quartic. That is, the intersection matrices of the two collections of curves are the same up to reordering of the curves. The 320 smooth conics vary in a family of curves whose configuration we can compute in a special case, namely the case of a surface that contains lines.
for very generic \(u \in N_5\). In this section we shall show that this configuration is the same as the configuration of the 320 irreducible conics on a very general invariant quartic. That is, the intersection matrices of the two collections of curves are the same up to reordering of the curves. The 320 smooth conics vary in a family of curves whose configuration we can compute in a special case, namely the case of a surface that contains lines.
In the process we shall also show that there are no more conics on a very general Heisenberg invariant quartic than the 320 conics of Theorem 5.3.
Lemma 7.1
Let \(O \subset \mathbb {P}^{34}\) be the open subset parameterizing smooth quartic surfaces, let \(Z \subseteq O\) be a smooth subvariety and  the corresponding family of surfaces. For a very general point \(z \in Z\) and any
the corresponding family of surfaces. For a very general point \(z \in Z\) and any  there is an injection of lattices
there is an injection of lattices

which respects hyperplane classes.
Proof
The Néron–Severi group of the geometric generic fiber of  injects into
injects into  for any \(z \in Z\) (see [26, Proposition 3.6 (a)]). Moreover, for very general \(z \in Z\), that injection is an isomorphism (see [26, Proposition 3.6 (a) and Corollary 3.9]). This induces an injection
for any \(z \in Z\) (see [26, Proposition 3.6 (a)]). Moreover, for very general \(z \in Z\), that injection is an isomorphism (see [26, Proposition 3.6 (a) and Corollary 3.9]). This induces an injection  , for a very general \(z \in Z\) and any
, for a very general \(z \in Z\) and any  . This injection respects intersection numbers (see [22, Chapter 17, Proposition 2.10]). Also, the following diagram commutes:
. This injection respects intersection numbers (see [22, Chapter 17, Proposition 2.10]). Also, the following diagram commutes:

where \(r_1\) is the restriction map \(j^*\) with  the inclusion and similarly for \(r_2\) (this follows from the construction in [7, X, 7.8]). Consider the polarizations on
the inclusion and similarly for \(r_2\) (this follows from the construction in [7, X, 7.8]). Consider the polarizations on  and
and  that define the embeddings as quartic surfaces in \(\mathbb {P}^3\). For a hyperplane \(L \subset \mathbb {P}^3\), these polarizations both come from the divisor class
that define the embeddings as quartic surfaces in \(\mathbb {P}^3\). For a hyperplane \(L \subset \mathbb {P}^3\), these polarizations both come from the divisor class  on
on  via the restriction maps. Hence, i maps the hyperplane class of
via the restriction maps. Hence, i maps the hyperplane class of  to the hyperplane class of
to the hyperplane class of  . \(\square \)
. \(\square \)
Proposition 7.2
For very general points \(u \in U\) and  we have that
we have that
-
(a)
the quartic
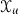 has exactly 320 conics and no lines,
has exactly 320 conics and no lines, -
(b)
the configuration of irreducible conics on
 is the same as the configuration of conics (reducible or irreducible) on
is the same as the configuration of conics (reducible or irreducible) on  .
.
Proof
Let \(u \in U\) and  be such that there are only 320 conics on
be such that there are only 320 conics on  , the surfaces
, the surfaces  and
and  are smooth,
are smooth,  contains the configuration of 320 smooth conics and there is an injection of lattices
contains the configuration of 320 smooth conics and there is an injection of lattices

which respects hyperplane classes. As we have seen, these conditions are satisfied for very general points \(u \in U\) and  , see Lemma 7.1 for the part about i. Let
, see Lemma 7.1 for the part about i. Let  be the class of a conic. Since
be the class of a conic. Since  , either i(C) or
, either i(C) or  is effective, see [3, Chapter VIII, Proposition 3.7 (i)]. But the degree of i(C) is equal to 2, and hence i(C) is effective. Since
is effective, see [3, Chapter VIII, Proposition 3.7 (i)]. But the degree of i(C) is equal to 2, and hence i(C) is effective. Since  , i(C) is represented either by an irreducible conic or a reducible conic. But there are only 320 conics on
, i(C) is represented either by an irreducible conic or a reducible conic. But there are only 320 conics on  , and it follows that there are no more conics on
, and it follows that there are no more conics on  either. Moreover, since i maps the classes of the 320 smooth conics on
either. Moreover, since i maps the classes of the 320 smooth conics on  onto the set of classes of conics on
onto the set of classes of conics on  , we have that the configurations of conics on the two surfaces coincide. \(\square \)
, we have that the configurations of conics on the two surfaces coincide. \(\square \)
8 The Picard group
In this section we determine the Picard group of a very general Heisenberg invariant quartic and show that it is generated by the 320 conics on the surface.
It has been known since over a hundred years that every curve C on a general enough Kummer surface Y in \(\mathbb {P}^3\) is such that C counted with multiplicity 2 is a complete intersection between Y and some other surface in \(\mathbb {P}^3\), see [20, Chapter XIII]. A modern treatment is given in [17, 18]. In particular, every curve on Y has even degree. To be more precise, if \(Y \subset \mathbb {P}^3\) is the Kummer surface of a principally polarized Abelian surface A with Picard number 1, which is true for a very general point of the moduli space of principally polarized Abelian surfaces, then every curve on Y has even degree (see [18, Theorem 4.32]). The Kummer surfaces that appear in the family  are Heisenberg invariant but this merely reflects a choice of coordinates on \(\mathbb {P}^3\) (see [18, Lemma 1.52]).
are Heisenberg invariant but this merely reflects a choice of coordinates on \(\mathbb {P}^3\) (see [18, Lemma 1.52]).
Lemma 8.1
For a very generic Heisenberg invariant quartic surface X, no curve on X has odd degree.
Proof
Let \(\text {Hilb}_{(d,g)}(\mathbb {P}^3)\) denote the Hilbert scheme of curves in \(\mathbb {P}^3\) with Hilbert polynomial \(P(x)=dx+(1-g)\). Recall that \(\text {Hilb}_{(d,g)}(\mathbb {P}^3)\) is projective, see [25, Chapter I, 1.4]. Let  be the universal family. Define an incidence \(I_{(d,g)}\) by
be the universal family. Define an incidence \(I_{(d,g)}\) by

and let  denote the projection. Now, since for odd d and any g, the parameter point of a general enough Heisenberg invariant Kummer surface is not in \(\pi (I_{(d,g)})\), we have that \(\pi (I_{(d,g)}) \ne U\) if d is odd. A surface whose parameter point is outside the countable union \(\bigcup _{k,g} \pi (I_{(2k+1,g)})\) has no curve of odd degree. \(\square \)
denote the projection. Now, since for odd d and any g, the parameter point of a general enough Heisenberg invariant Kummer surface is not in \(\pi (I_{(d,g)})\), we have that \(\pi (I_{(d,g)}) \ne U\) if d is odd. A surface whose parameter point is outside the countable union \(\bigcup _{k,g} \pi (I_{(2k+1,g)})\) has no curve of odd degree. \(\square \)
Finite Abelian groups with a symplectic action on some K3 surface have been classified by Nikulin [32]. In that paper, Theorem 4.7, it is shown that if G is finite Abelian and acts symplectically on a K3 surface X, then the induced action of G on \(H^2(X,\mathbb {Z})\) is independent of the surface, up to isomorphism of lattices. It follows that the lattices \(H^2(X,\mathbb {Z})^G\) and  are determined by G up to isomorphism. In [14] these lattices are worked out in each case of the classification and in the case of the Heisenberg group, \(\Omega _H\) turns out to be well known. It is isomorphic to
are determined by G up to isomorphism. In [14] these lattices are worked out in each case of the classification and in the case of the Heisenberg group, \(\Omega _H\) turns out to be well known. It is isomorphic to  , where \(\Lambda _{15}\) is the so-called laminated lattice of rank 15, see [9].
, where \(\Lambda _{15}\) is the so-called laminated lattice of rank 15, see [9].
Remark 8.2
The discriminant of \(\Lambda _{15}\) is \(2^9\) and \(\Lambda _{15}\) is positive definite, see [9] for a detailed treatment. In one basis, the bilinear form on \(\Lambda _{15}\) is given by
Theorem 8.3
Let X be a very generic Heisenberg invariant quartic and let  be the hyperplane class. Then
be the hyperplane class. Then
-
(a)
the sublattice
 has index 2,
has index 2, -
(b)
 .
.
Proof
We first show that the group  is cyclic. Since
is cyclic. Since  and \(H^2(X,\mathbb {Z})^H\) has rank 7,
and \(H^2(X,\mathbb {Z})^H\) has rank 7,  is a full rank sublattice. If
is a full rank sublattice. If  and \(lh=0\), then l kills
and \(lh=0\), then l kills  and therefore \(l \in \Omega _H\). Since
and therefore \(l \in \Omega _H\). Since  , it follows that \(\Omega _H\) is the orthogonal complement of
, it follows that \(\Omega _H\) is the orthogonal complement of  in
in  . Observe that \(\Omega _H\) is a primitive sublattice of
. Observe that \(\Omega _H\) is a primitive sublattice of  , that is if \(nl \in \Omega _H\) for some non-zero \(n \in \mathbb {Z}\) and some
, that is if \(nl \in \Omega _H\) for some non-zero \(n \in \mathbb {Z}\) and some  , then \(l \in \Omega _H\). In other words
, then \(l \in \Omega _H\). In other words  is torsion free. Because
is torsion free. Because  has rank 1, there is an element
has rank 1, there is an element  such that
such that  , as Abelian groups. The class of l in
, as Abelian groups. The class of l in  generates
generates  . Further, note that for
. Further, note that for  , \(v=nh+\omega \) with \(\omega \in \Omega _H\) and \(n \in \mathbb {Z}\), we have that
, \(v=nh+\omega \) with \(\omega \in \Omega _H\) and \(n \in \mathbb {Z}\), we have that  . If it were true that
. If it were true that  then the degree of any curve on X would be a multiple of 4, but this is not the case since X contains a conic. Now let
then the degree of any curve on X would be a multiple of 4, but this is not the case since X contains a conic. Now let  . It follows by Lemma 8.1 that Dh is even, say \(Dh=2m\). Then
. It follows by Lemma 8.1 that Dh is even, say \(Dh=2m\). Then  and hence \((2D-mh) \in \Omega _H\). Consequently,
and hence \((2D-mh) \in \Omega _H\). Consequently,  and thus
and thus  has index 2 in
has index 2 in  .
.
Since

and

we have that  . \(\square \)
. \(\square \)
Corollary 8.4
The Picard group of a very generic Heisenberg invariant quartic X is generated by the 320 conics.
Proof
By Proposition 7.2, some set of 16 conics on X correspond to the 16 conics of Remark 6.2. Let  be the sublattice generated by these 16 conics on X. Because
be the sublattice generated by these 16 conics on X. Because  , the index of P in
, the index of P in  is equal to 1, that is
is equal to 1, that is  . \(\square \)
. \(\square \)
The proof of the corollary shows that (in some basis) the lattice structure of the Picard group of a very generic Heisenberg invariant quartic is given by the matrix M in Remark 6.2.
References
Baker, H.F.: Principles of Geometry, vol. IV. Cambridge University Press, Cambridge (1925)
Barth, W., Bauer, Th.: Smooth quartic surfaces with 352 conics. Manuscripta Math. 85(3–4), 409–417 (1994)
Barth, W.P., Hulek, K., Peters, C.A.M., Van de Ven, A.: Compact Complex Surfaces, 2nd edn. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 4. Springer, Berlin (2004)
Barth, W., Nieto, I.: Abelian surfaces of type \((1,3)\) and quartic surfaces with 16 skew lines. J. Algebraic Geom. 3(2), 173–222 (1994)
Bates, D.J., Hauenstein, J.D., Sommese, A.J., Wampler, C.W.: Bertini: Software for Numerical Algebraic Geometry. http://www.nd.edu/~sommese/bertini
Bauer, Th.: Quartic surfaces with 16 skew conics. J. Reine Angew. Math. 464, 207–217 (1995)
Berthelot, P., Grothendieck, A., Illusie, L.: Théorie des intersections et théorème de Riemann–Roch. With the collaboration of D. Ferrand, J.-P. Jouanolou, O. Jussila, S. Kleiman, M. Raynaud and J.-P. Serre. Séminaire de Géométrie Algébrique du Bois Marie 1966–1967 (SGA 6). Lecture Notes in Mathematics, vol. 225. Springer, Berlin (1971)
Birkenhake, C., Lange, H.: Complex Abelian Varieties, 2nd edn. Grundlehren der Mathematischen Wissenschaften, vol. 302. Springer, Berlin (2004)
Conway, J.H., Sloane, N.J.A.: Sphere Packings, Lattices and Groups, 3rd edn. Grundlehren der mathematischen Wissenschaften, vol. 290. Springer, New York (1999)
Dickson, L.E.: Linear Groups: With an Exposition of the Galois Field Theory. B.G. Teubner, Leipzig (1901)
Dolgachev, I.V.: Mirror symmetry for lattice polarized \(K3\) surfaces. J. Math. Sci. 81(3), 2599–2630 (1996)
Dolgachev, I.V., Kondō, S.: Moduli of K3 surfaces and complex ball quotients. In: Holzapfel, R.-P., Uludağ, A.M., Yoshida, M. (eds.) Arithmetic and Geometry Around Hypergeometric Functions. Progress in Mathematics, vol. 260, pp. 43–100. Birkhäuser, Basel (2007)
Edge, W.L.: A type of periodicity of certain quartic surfaces. Proc. Edinburgh Math. Soc. 7(1), 73–80 (1942)
Garbagnati, A., Sarti, A.: Elliptic fibrations and symplectic automorphisms on \(K3\) surfaces. Comm. Algebra 37(10), 3601–3631 (2009)
van der Geer, G.: On the geometry of a Siegel modular threefold. Math. Ann. 260(3), 317–350 (1982)
Godeaux, L.: Sur la surface du quatrième ordre contenant trente-deux droites. Acad. R. Belg. Bull. Cl. Sci. 25, 539–552 (1939)
Gonzalez-Dorrego, M.R.: Curves on a Kummer surface in \({\mathbb{P}}^3\), I. Math. Nachr. 165, 133–158 (1994)
Gonzalez-Dorrego, M.R.: \((16,6)\) Configurations and Geometry of Kummer Surfaces in \({\mathbb{P}}^{3}\). Memoirs of the American Mathematical Society, vol. 107, no. 512. American Mathematical Society, Providence (1994)
Grayson, D., Stillman, M.: Macaulay2: a software system for research in algebraic geometry. http://www.math.uiuc.edu/Macaulay2
Hudson, R.W.H.T.: Kummer’s Quartic Surface. Cambridge University Press, Cambridge (1905)
Hunt, B.: The Geometry of Some Special Arithmetic Quotients. Lecture Notes in Mathematics, vol. 1637. Springer, Berlin (1996)
Huybrechts, D.: Lectures on K3 Surfaces. Cambridge Studies in Advanced Mathematics, vol. 158. Cambridge University Press, Cambridge (2016)
Iskovskikh, V.A., Shafarevich, I.R.: Algebraic surfaces. In: Shafarevich, I.R. (ed.) Algebraic Geometry II. Encyclopaedia of Mathematical Sciences, vol. 35, pp. 127–262. Springer, Berlin (1996)
Jessop, C.M.: A Treatise on the Line Complex. Cambridge University Press, Cambridge (1903)
Kollár, J.: Rational Curves on Algebraic Varieties. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, vol. 32. Springer, Berlin (1996)
Maulik, D., Poonen, B.: Néron–Severi groups under specialization. Duke Math. J. 161(11), 2167–2206 (2012)
Mukai, S.: Finite groups of automorphisms of K3 surfaces and the Mathieu group. Invent. Math. 94(1), 183–221 (1988)
Mumford, D.: On the equations defining abelian varieties I. Invent. Math. 1(4), 287–354 (1966)
Naruki, I.: On smooth quartic embedding of Kummer surfaces. Proc. Japan Acad. Ser. A Math. Sci. 67(7), 223–225 (1991)
Nieto, I.: The normalizer of the level \((2,2)\)-Heisenberg group. Manuscripta Math. 76(3–4), 257–267 (1992)
Nieto, I.: The singular \(H_{2,2}\)-invariant quartic surfaces in \(\mathbb{P}_3\). Geom. Dedicata 57(2), 157–170 (1995)
Nikulin, V.V.: Finite groups of automorphisms of Kählerian \(K_3\) surfaces. Tr. Mosk. Mat. Obs. 38, 75–137 (1979) (in Russian)
Pyatetskii-Shapiro, I.I., Shafarevich, I.R.: A Torelli theorem for algebraic surfaces of type \(K3\). Math. USSR-Izv. 5(3), 547–588 (1971)
Segre, B.: On the quartic surface \(x_1^4+x_2^4+x_3^4+x_4^4=0\). Proc. Cambridge Philos. Soc. 40, 121–145 (1944)
Traynard, M.E.: Sur les fonctions thêta de deux variables et les surfaces Hyperelliptiques. Ann. Sci. Éc. Norm. Supér. 24, 77–177 (1907)
Verra, A.: The fibre of the prym map in genus three. Math. Ann. 276(3), 433–448 (1987)
Acknowledgements
The author thanks Kristian Ranestad for guidance and inspiration, as well as making it possible for me spend two months during the spring of 2009 at the University of Oslo. Thanks to Igor Dolgachev for pointing out relevant references. During the course of this work, the software packages Bertini [5] and Macaulay 2 [19] were used for experimentation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Eklund, D. Curves on Heisenberg invariant quartic surfaces in projective 3-space. European Journal of Mathematics 4, 931–952 (2018). https://doi.org/10.1007/s40879-018-0216-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0216-2


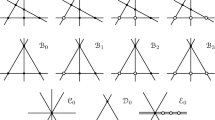

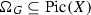 ,
, .
. ,
, for six different
for six different 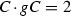 for nine different
for nine different  for four different
for four different 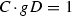 for eight different
for eight different  for four different
for four different 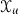 has exactly 320 conics and no lines,
has exactly 320 conics and no lines, is the same as the configuration of conics (reducible or irreducible) on
is the same as the configuration of conics (reducible or irreducible) on 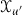 .
. has index 2,
has index 2, .
.