Abstract
The Schur index of the \((A_1, X_n)\)-Argyres–Douglas theory is conjecturally a character of a vertex operator algebra. Here such vertex algebras are found for the \(A_{\text {odd}}\) and \(D_{\text {even}}\)-type Argyres–Douglas theories. The vertex operator algebra corresponding to \(A_{2p-3}\)-Argyres–Douglas theory is the logarithmic  -algebra of Creutzig et al. (Lett Math Phys 104(5):553–583, 2014), while the one corresponding to \(D_{2p}\), denoted by
-algebra of Creutzig et al. (Lett Math Phys 104(5):553–583, 2014), while the one corresponding to \(D_{2p}\), denoted by  , is realized as a non-regular quantum Hamiltonian reduction of \(L_{k}(\mathfrak {sl}_{p+1})\) at level
, is realized as a non-regular quantum Hamiltonian reduction of \(L_{k}(\mathfrak {sl}_{p+1})\) at level  . For all n one observes that the quantum Hamiltonian reduction of the vertex operator algebra of \(D_n\)-Argyres–Douglas theory is the vertex operator algebra of \(A_{n-3}\)-Argyres–Douglas theory. As a corollary, one realizes the singlet and triplet algebras (the vertex algebras associated to the best understood logarithmic conformal field theories) as quantum Hamiltonian reductions as well. Finally, characters of certain modules of these vertex operator algebras and the modular properties of their meromorphic continuations are given.
. For all n one observes that the quantum Hamiltonian reduction of the vertex operator algebra of \(D_n\)-Argyres–Douglas theory is the vertex operator algebra of \(A_{n-3}\)-Argyres–Douglas theory. As a corollary, one realizes the singlet and triplet algebras (the vertex algebras associated to the best understood logarithmic conformal field theories) as quantum Hamiltonian reductions as well. Finally, characters of certain modules of these vertex operator algebras and the modular properties of their meromorphic continuations are given.
Similar content being viewed by others
Notes
We thank Tomoyuki Arakawa for pointing out that
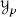 is similar to chiral Hecke algebras of \({\mathfrak {sl}}_2\).
is similar to chiral Hecke algebras of \({\mathfrak {sl}}_2\).
References
Adamović, D.: A construction of admissible \(A_1^{(1)}\)-modules of level \(-4/3\). J. Pure Appl. Algebra 196(2–3), 119–134 (2005)
Adamović, D.: A realization of certain modules for the \(N=4\) superconformal algebra and the affine Lie algebra \(A_2^{(1)}\). Transform. Groups 21(2), 299–327 (2016)
Adamović, D.: The vertex algebras \(R(p)\) and their logarithmic representations (in preparation)
Adamović, D., Kac, V.G., Möseneder Frajria, P., Papi, P., Perše, O.: Finite vs. infinite decompositions in conformal embeddings. Comm. Math. Phys. 348(2), 445–473 (2016)
Adamović, D., Kac, V.G., Möseneder Frajria, P., Papi, P., Perše, O.: Conformal embeddings of affine vertex algebras in minimal \(W\)-algebras I: structural results. J. Algebra (2017). doi:10.1016/j.jalgebra.2016.12.005
Adamović, D., Kac, V.G., Möseneder Frajria, P., Papi, P., Perše, O.: Conformal embeddings of affine vertex algebras in minimal \(W\)-algebras II: decompositions (2016) (Japan J. Math. submitted). arXiv:1604.00893
Adamović, D., Lin, X., Milas, A.: ADE subalgebras of the triplet vertex algebra \({\cal{W}}(p)\): \(A\)-series. Commun. Contemp. Math. 15(6), # 1350028 (2013)
Adamović, D., Milas, A.: Logarithmic intertwining operators and \({\cal{W}} (2, 2p-1)\)-algebras. J. Math. Phys. 48(7), # 073503 (2007)
Adamović, D., Milas, A.: On the triplet vertex algebra \({\cal{W}}(p)\). Adv. Math. 217(6), 2664–2699 (2008)
Adamović, D., Milas, A.: On \(W\)-algebras associated to \((2, p)\) minimal models and their representations. Int. Math. Res. Not. IMRN 2010(20), 3896–3934 (2010)
Alfes, C., Creutzig, T.: The mock modular data of a family of superalgebras. Proc. Amer. Math. Soc. 142(7), 2265–2280 (2014)
Arakawa, T.: Representation theory of \({\cal{W}}\)-algebras. Invent. Math. 169(2), 219–320 (2007)
Arakawa, T.: Introduction to \(W\)-algebras and their representation theory (2016). arXiv:1605.00138
Arakawa, T., Creutzig, T., Kawasetsu, K., Linshaw, A.R.: Orbifolds and cosets of minimal \({\cal{W}}\)-algebras. Comm. Math. Phys. (2017). doi:10.1007/s00220-017-2901-2
Arakawa, T., Molev, A.: Explicit generators in rectangular affine \({\cal{W}}\)-algebras of type \(A\). Lett. Math. Phys. 107(1), 47–59 (2017)
Argyres, P.C., Douglas, M.R.: New phenomena in \({\rm SU}(3)\) supersymmetric gauge theory. Nuclear Phys. B 448(1–2), 93–126 (1995)
Auger, J., Creutzig, T., Kanade, S., Rupert, M.: Work in progress
Beem, C., Lemos, M., Liendo, P., Peelaers, W., Rastelli, L., van Rees, B.C.: Infinite chiral symmetry in four dimensions. Comm. Math. Phys. 336(3), 1359–1433 (2015)
Beem, C., Peelaers, W., Rastelli, L., van Rees, B.S.: Chiral algebras of class \({\cal{S}}\). J. High Energy Phys. 2015(5), # 20 (2015)
Beem, C., Rastelli, L.: Higgs branches, vertex operator algebras and modular differential equations (in preparation)
Bringmann, K., Creutzig, T., Rolen, L.: Negative index Jacobi forms and quantum modular forms. Res. Math. Sci. 1, # 11 (2014)
Buican, M., Nishinaka, T.: On the superconformal index of Argyres–Douglas theories. J. Phys. A 49(1), # 015401 (2016)
Córdova, C., Gaiotto, D., Shao, S.-H.: Infrared computations of defect Schur indices. J. High Energy Phys. 2016(11), # 106 (2016)
Córdova, C., Gaiotto, D., Shao, S.-H.: Surface defect indices and chiral algebras (2017). arXiv:1704.01955
Córdova, C., Shao, S.-H.: Schur indices, BPS particles, and Argyres–Douglas theories. J. High Energy Phys. 2016(1), # 40 (2016)
Creutzig, T., Gaiotto, D.: Work in progress
Creutzig, T., Gannon, T.: Logarithmic conformal field theory, log-modular tensor categories and modular forms (2016). arXiv:1605.04630
Creutzig, T., Kanade, S., Linshaw, A.R.: Simple current extensions beyond semi-simplicity (2015). arXiv:1511.08754
Creutzig, T., Kanade, S., Linshaw, A.R., Ridout, D.: Schur–Weyl duality for Heisenberg cosets (2016). arXiv:1611.00305
Creutzig, T., Kanade, S., McRae, R.: Tensor categories for vertex operator superalgebra extensions (2017). arXiv:1705.05017
Creutzig, T., Linshaw, A.R.: Cosets of affine vertex algebras inside larger structures (2014). arXiv:1407.8512v3
Creutzig, T., Milas, A.: False theta functions and the Verlinde formula. Adv. Math. 262, 520–545 (2014)
Creutzig, T., Milas, A.: Higher rank partial and false theta functions and representation theory (2016) (Adv. Math. submitted). arXiv:1607.08563
Creutzig, T., Milas, A., Rupert, M.: Logarithmic link invariants of \(\overline{U}^H_{q}({\mathfrak{sl}}_2)\) and asymptotic dimensions of singlet vertex algebras (2016). arXiv:1605.05634
Creutzig, T., Ridout, D.: Modular data and Verlinde formulae for fractional level WZW models I. Nuclear Phys. B 865(1), 83–114 (2012)
Creutzig, T., Ridout, D.: Relating the archetypes of logarithmic conformal field theory. Nuclear Phys. B 872(3), 348–391 (2013)
Creutzig, T., Ridout, D.: Modular data and Verlinde formulae for fractional level WZW models II. Nuclear Phys. B 875(2), 423–458 (2013)
Creutzig, T., Ridout, D., Wood, S.: Coset constructions of logarithmic \((1, p)\) models. Lett. Math. Phys. 104(5), 553–583 (2014)
Feigin, B.L., Semikhatov, A.M.: \({\cal{W}}^{(2)}_n\) algebras. Nuclear Phys. B 698(3), 409–449 (2004)
Fredrickson, L., Pei, D., Yan, W., Ye, K.: Argyres–Douglas theories, chiral algebras and wild Hitchin characters (2017). arXiv:1701.08782
Frenkel, E., Ben-Zvi, D.: Vertex Algebras and Algebraic Curves. Mathematical Surveys and Monographs, vol. 88, 2nd edn. American Mathematical Society, Providence (2004)
Feigin, B.L., Tipunin, I.Y.: Logarithmic CFTs connected with simple Lie algebras (2010). arXiv:1002.5047
Gadde, A., Rastelli, L., Razamat, S.S., Yan, W.: Four dimensional superconformal index from \(q\)-deformed two dimensional Yang–Mills theory. Phys. Rev. Lett. 106, # 241602 (2011)
Gaiotto, D.: Twisted compactifications of \(3d\) \(N = 4\) theories and conformal blocks (2016). arXiv:1611.01528
Genra, N.: Screening operators for \({\cal{W}}\)-algebras. Selecta Math. (N.S.) (2017). doi:10.1007/s00029-017-0315-9
Gorelik, M., Kac, V.: On simplicity of vacuum modules. Adv. Math. 211(2), 621–677 (2007)
Kac, V.G., Kazhdan, D.A.: Structure of representations with highest weight of infinite-dimensional Lie algebras. Adv. Math. 34(1), 97–108 (1979)
Kac, V.G., Möseneder Frajria, P., Papi, P., Xu, F.: Conformal embeddings and simple current extensions. Int. Math. Res. Not. IMRN 2015(14), 5229–5288 (2015)
Kac, V.G., Wakimoto, M.: Modular invariant representations of infinite-dimensional Lie algebras and superalgebras. Proc. Nat. Acad. Sci. USA 85(14), 4956–4960 (1988)
Kac, V.G., Wakimoto, M.: Integrable highest weight modules over affine superalgebras and number theory. In: Brylinski, J.-L., Brylinski, R., Guillemin, V., Kac, V. (eds.) Lie Theory and Geometry. Progress in Mathematics, vol. 123, pp. 415–456. Birkhäuser, Boston (1994)
Kac, V.G., Wakimoto, M.: Integrable highest weight modules over affine superalgebras and Appell’s function. Comm. Math. Phys. 215(3), 631–682 (2001)
Kac, V.G., Wakimoto, M.: Quantum reduction and representation theory of superconformal algebras. Adv. Math. 185(2), 400–458 (2004)
Kac, V.G., Wakimoto, M.: A remark on boundary level admissible representations (2016). arXiv:1612.07423
Kumar, S.: Extension of the category \({\cal{O}}^g\) and a vanishing theorem for the Ext functor for Kac–Moody algebras. J. Algebra 108(2), 472–491 (1987)
Rastelli, L.: Infinite Chiral Symmetry in Four and Six Dimensions. Seminar at Harvard University (2014)
Ridout, D.: \(\widehat{\mathfrak{sl}}(2)_{-1/2}\): a case study. Nuclear Phys. B 814(3), 485–521 (2009)
Ridout, D.: \(\widehat{\mathfrak{sl}}(2)_{-1/2}\) and the triplet model. Nuclear Phys. B 835(3), 314–342 (2010)
Tachikawa, Y.: On some conjectures on VOAs (2013). http://member.ipmu.jp/yuji.tachikawa
Tsuchiya, A., Wood, S.: The tensor structure on the representation category of the \({\cal{W}}_{p}\) triplet algebra. J. Phys. A 46(44), # 445203 (2013)
Xie, D., Yan, W., Yau, S.-T.: Chiral algebra of Argyres–Douglas theory from M5 brane (2016). arXiv:1604.02155
Zwegers, S.P.: Mock Theta Functions. Ph.D. thesis, Utrecht University (2002)
Acknowledgements
Most of all, I am very grateful to Shu-Heng Shao for many discussions on this topic. I also would like to thank Tomoyuki Arakawa, Chris Beem, Leonardo Rastelli and Davide Gaiotto for explanations on the relation of vertex operator algebras and four-dimensional quantum field theory. I thank Dražen Adamović for his useful comments on the draft and discussion. Finally I very much appreciate discussions with Wenbin Yan and Ke Ye and sharing [40] with me.
Author information
Authors and Affiliations
Corresponding author
Additional information
The author is supported by NSERC RES0020460 and has benefitted from the workshop Exact Operator Algebras in Superconformal Field Theories on the topic at the Perimeter Institute.
Rights and permissions
About this article
Cite this article
Creutzig, T. W-algebras for Argyres–Douglas theories. European Journal of Mathematics 3, 659–690 (2017). https://doi.org/10.1007/s40879-017-0156-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0156-2



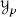 is similar to chiral Hecke algebras of
is similar to chiral Hecke algebras of