Abstract
The mixed scalar curvature of a foliated Riemannian manifold, i.e., an averaged mixed sectional curvature, has been considered by several geometers. We explore the Yamabe type problem: to prescribe the leafwise constant mixed scalar curvature for a foliation by a conformal change of the metric in normal directions only. For a harmonic foliation, we derive the leafwise elliptic equation and explore the corresponding nonlinear heat type equation on a closed manifold (leaf). Then we assume that a foliation is defined by an orientable fiber bundle, and use spectral parameters of certain Schrödinger operator to find solution, which is an attractor of the equation.
Similar content being viewed by others
1 Introduction
Geometrical problems of prescribing curvature-like invariants (e.g. the scalar curvature and the mean curvature) of manifolds and foliations are popular for a long time, see [6, 7, 19, 22]. There are many proofs of a positive answer to the Yamabe problem: given a closed Riemannian manifold (M, g) of \(\dim M\ge 3\), find a metric conformal to g with constant scalar curvature. The study of this geometrical problem was began by Yamabe in 1960 and completed by Trudinger, Aubin and Schoen in 1986, its solution is expressed in terms of the existence and multiplicity of solutions of a given elliptic PDE in the Riemannian manifold, see [2, 15]. Several authors developed an analog of the problem for CR-manifolds, see [10], and its generalization to contact (real or quaternionic) manifolds. The problem when metrics of constant scalar curvature can be produced on warped product manifolds has been studied in several articles, see [9].
Let (M, g) be endowed with a foliation \(\mathscr {F}\). Denote by \({\mathscr {D}}=T\mathscr {F}\), \(\dim {\mathscr {D}}=p\), the tangent distribution and  ,
,  , the orthogonal distribution (or the normal subbundle) of the tangent bundle TM. In [4], a tensor calculus adapted to the orthogonal splitting
, the orthogonal distribution (or the normal subbundle) of the tangent bundle TM. In [4], a tensor calculus adapted to the orthogonal splitting
is developed to study the geometry of both distributions and the ambient manifolds. We have \(g = g_\mathscr {F}+ g^\perp \), where  and
and  is the projection of TM onto \({\mathscr {D}}^\bot \). Obviously, biconformal metrics \(\widetilde{g} = v^{2} g_\mathscr {F}+ u^{2} g^\perp \), \(u,v>0\), preserve (1) and extend the class of conformal metrics (i.e., \(u=v\)). Biconformal metrics (e.g. doubly-twisted products, introduced by Ponge and Reckziegel in [13]) have many applications in differential geometry, relativity, quantum-gravity, etc., see [9]. The \({\mathscr {D}}^\bot \)- or \({\mathscr {D}}\)-conformal metrics correspond to \(v\equiv 1\) or \(u\equiv 1\), see [18–21].
is the projection of TM onto \({\mathscr {D}}^\bot \). Obviously, biconformal metrics \(\widetilde{g} = v^{2} g_\mathscr {F}+ u^{2} g^\perp \), \(u,v>0\), preserve (1) and extend the class of conformal metrics (i.e., \(u=v\)). Biconformal metrics (e.g. doubly-twisted products, introduced by Ponge and Reckziegel in [13]) have many applications in differential geometry, relativity, quantum-gravity, etc., see [9]. The \({\mathscr {D}}^\bot \)- or \({\mathscr {D}}\)-conformal metrics correspond to \(v\equiv 1\) or \(u\equiv 1\), see [18–21].
Using the natural representation of  on TM, Naveira [12] distinguished thirty-six classes of Riemannian almost-product manifolds \((M,g,{\mathscr {D}},{\mathscr {D}}^\bot )\); some of them are foliated, e.g., harmonic, totally geodesic, conformal, and Riemannian foliations. Following this line of research, several geometers completed the geometric interpretation and gave examples for each class of almost-product structures. The simple examples of harmonic foliations are geodesic ones (e.g., parallel circles or winding lines on a flat torus, and a Hopf field of great circles on the 3-sphere). Rummler characterized harmonic foliations by existence of an \(\mathscr {F}\)-closed differential p-form that is transverse to \(\mathscr {F}\). Sullivan’s topological tautness condition is equivalent to the existence of a metric on M making a foliation harmonic, see [6, 7].
on TM, Naveira [12] distinguished thirty-six classes of Riemannian almost-product manifolds \((M,g,{\mathscr {D}},{\mathscr {D}}^\bot )\); some of them are foliated, e.g., harmonic, totally geodesic, conformal, and Riemannian foliations. Following this line of research, several geometers completed the geometric interpretation and gave examples for each class of almost-product structures. The simple examples of harmonic foliations are geodesic ones (e.g., parallel circles or winding lines on a flat torus, and a Hopf field of great circles on the 3-sphere). Rummler characterized harmonic foliations by existence of an \(\mathscr {F}\)-closed differential p-form that is transverse to \(\mathscr {F}\). Sullivan’s topological tautness condition is equivalent to the existence of a metric on M making a foliation harmonic, see [6, 7].
The components of the curvature of a foliation can be tangential, transversal, and mixed. The tangential geometry of a foliation is infinitesimally modeled by the tangent distribution to the leaves, while the transversal geometry by the orthogonal distribution \({\mathscr {D}}^\bot \). Prescribing the sign of tangential scalar curvature has been studied for foliated spaces, for example, there is no foliation of positive leafwise scalar curvature on any torus, see [26]. The transversal scalar curvature is well studied for Riemannian foliations, e.g. the “transversal Yamabe problem”, see [25].
The mixed scalar curvature, \(\mathrm{S}_\mathrm{mix}\), for foliated (sub)manifolds has been considered by several geometers, see [3, 14, 24], but its constancy (so called “mixed Yamabe problem”) is less studied. In [20, 21], we prescribed the sign of \(\mathrm{S}_\mathrm{mix}\) using flows of \({\mathscr {D}}^\bot \)-conformal metrics. In this paper we explore the following Yamabe type problem: Given a harmonic foliation \(\mathscr {F}\) of a Riemannian manifold (M, g), find a \({\mathscr {D}}^\bot \) -conformal metric \(\widetilde{g}\) with leafwise constant mixed scalar curvature. For a general foliation, the topology of the leaf through a point can change dramatically with the point; this gives many difficulties in studying leafwise parabolic and elliptic equations. Therefore, in the paper (at least in the main results) we assume that
The proofs of the main results are based on Sect. 2.2 (with variation formulae for geometrical quantities under \({\mathscr {D}}^\bot \)-conformal change of a metric), Sect. 2.3 (with Proposition 2.11 and Corollary 2.12), Sect. 3 (about attractor of the nonlinear heat equation on a closed manifold and about solution of its stationary equation with parameter) and Sect. 4 (about smooth dependence of a solution on a transversal parameter).
A slight change in the proof allows us to extend the main results for the case when the prescribed mixed scalar curvature is not leafwise constant.
2 Main results
The main results of the paper are the following.
Theorem 2.1
Let \(\mathscr {F}\) be a harmonic and nowhere totally geodesic foliation of a closed Riemannian manifold (M, g) with condition (2). Then there exists a \({\mathscr {D}}^\bot \)-conformal metric \(\widetilde{g}\) with leafwise constant mixed scalar curvature.
If \({\mathscr {D}}^\bot \) is integrable than Corollary 2.12 is applicable. In particular case of codimension-one foliations, we have the following.
Corollary 2.2
Let \(\mathscr {F}\) be a codimension-one harmonic and nowhere totally geodesic foliation of a Riemannian manifold (M, g) with condition (2). Then there exists a \({\mathscr {D}}^\bot \)-conformal metric \(\widetilde{g}\) with leafwise constant Ricci curvature in the normal direction.
There are examples of foliations of codimension \({>}1\) with minimal, not totally geodesic leaves on (compact) Lie groups with left-invariant metrics, see [23]; further, the metric can be chosen to be bundle-like with respect to \(\mathscr {F}\). Such foliations have leafwise constant mixed scalar curvature.
Theorem 2.3
Let \(\mathscr {F}\), \(\dim \mathscr {F}>1\), be a totally geodesic foliation of a closed Riemannian manifold (M, g) with condition (2) and integrable normal distribution. Then there exists a \({\mathscr {D}}^\bot \)-conformal metric \(\widetilde{g}\) with leafwise constant mixed scalar curvature.
2.1 Preliminaries
Denote by \(R(X,Y)=\nabla _Y\nabla _X-\nabla _X\nabla _Y+\nabla _{[X,Y]}\) the curvature tensor of Levi-Civita connection. The sectional curvature  , where \(X\in T\mathscr {F}\), \(Y\in {\mathscr {D}}^\bot \) are unit vectors, is called mixed. It regulates (through the Jacobi equation) the deviation of leaves along the leaf geodesics. Foliations with constant mixed sectional curvature play an important role in differential geometry, but are far from being classified. Examples are k-nullity foliations on Riemannian manifolds which are totally geodesic, relative nullity foliations, which determine a ruled structure of submanifolds in space forms, foliations produced by the Reeb vector field on Sasakian manifolds, etc. Totally geodesic foliations on complete manifolds with \(K_\mathrm{mix}\equiv 0\) split. For a k-dimensional totally geodesic foliation with \(K_\mathrm{mix}\equiv 1\) on a closed manifold \(M^{n+k}\), we have the Ferus inequality \(k<\rho (n)\), where \(\rho (n)-1\) is the number of linear independent vector fields on a sphere \(S^{n-1}\), see [16].
, where \(X\in T\mathscr {F}\), \(Y\in {\mathscr {D}}^\bot \) are unit vectors, is called mixed. It regulates (through the Jacobi equation) the deviation of leaves along the leaf geodesics. Foliations with constant mixed sectional curvature play an important role in differential geometry, but are far from being classified. Examples are k-nullity foliations on Riemannian manifolds which are totally geodesic, relative nullity foliations, which determine a ruled structure of submanifolds in space forms, foliations produced by the Reeb vector field on Sasakian manifolds, etc. Totally geodesic foliations on complete manifolds with \(K_\mathrm{mix}\equiv 0\) split. For a k-dimensional totally geodesic foliation with \(K_\mathrm{mix}\equiv 1\) on a closed manifold \(M^{n+k}\), we have the Ferus inequality \(k<\rho (n)\), where \(\rho (n)-1\) is the number of linear independent vector fields on a sphere \(S^{n-1}\), see [16].
The mixed scalar curvature is an averaged mixed sectional curvature,
and is independent of the choice of a local orthonormal frame \(\{{\mathscr {E}}_j,{E}_a\}_{j\le n,a\le p}\) of TM adapted to \({\mathscr {D}}^\bot \) and \( T\mathscr {F}\), see [16, 17, 24]. If either \({\mathscr {D}}^\bot \) or \( T\mathscr {F}\) is one-dimensional and tangent to a unit vector field N, then \(\mathrm{S}_\mathrm{mix}\) is the Ricci curvature in the N-direction.
Let \({\mathfrak X}_M\) be the module over \(C^\infty (M)\) of all vector fields on M, and \({\mathfrak X}^\bot \) and \({\mathfrak X}^\top \) the modules of all vector fields on \({\mathscr {D}}^\bot \) and \( T\mathscr {F}\), respectively. The extrinsic geometry of a foliation is related to the second fundamental form of the leaves, \(h(X,Y) = (\nabla _X Y)^\perp \), where \(X,Y\in {\mathfrak X}^\top \), and its invariants (e.g., the mean curvature \(H=\mathrm{Tr}_g h\)). Special classes of foliations such as totally geodesic, \(h = 0\) (with the simplest extrinsic geometry); totally umbilical,  ; and harmonic, \(H=0\), have been studied by many geometers, see the survey in [16]. Let \(h^\bot \) be the second fundamental form of \({\mathscr {D}}^\bot \), \(H^\bot =\mathrm{Tr}_g h^\bot \) the mean curvature, and T the integrability tensor of \({\mathscr {D}}^\bot \). We have
; and harmonic, \(H=0\), have been studied by many geometers, see the survey in [16]. Let \(h^\bot \) be the second fundamental form of \({\mathscr {D}}^\bot \), \(H^\bot =\mathrm{Tr}_g h^\bot \) the mean curvature, and T the integrability tensor of \({\mathscr {D}}^\bot \). We have

The formula in [24], for foliations reads as

We calculate norms of tensors using local adapted basis as

Example 2.4
(constant mixed scalar curvature on doubly-twisted products) The doubly twisted product of Riemannian manifolds \((B,g_\mathscr {F})\) and \((F, g^\perp )\), is a manifold  with the metric \(g = v^2 g_\mathscr {F}+ u^2 g^\perp \), where
with the metric \(g = v^2 g_\mathscr {F}+ u^2 g^\perp \), where  are positive functions. The leaves
are positive functions. The leaves
 of a doubly-twisted product
of a doubly-twisted product  and the fibers
and the fibers
 are totally umbilical. We have
are totally umbilical. We have

By the above,  ,
,  , and
, and

Next we derive

where  is the leafwise Laplacian and \(\mathrm{\Delta }^\perp \) is the fiberwise Laplacian. Substituting in (4) with \(T=0\), we obtain the formula
is the leafwise Laplacian and \(\mathrm{\Delta }^\perp \) is the fiberwise Laplacian. Substituting in (4) with \(T=0\), we obtain the formula

Let B be a closed manifold. Given a positive function  , define a leafwise Schrödinger operator
, define a leafwise Schrödinger operator  , where \(\beta = p(\mathrm{\Delta }^\perp v)/nv\). For any compact leaf, the spectrum of \(\mathscr {H}\) is discrete, the least eigenvalue \(\lambda _0\) is isolated from other eigenvalues, and the eigenfunction \(e_0\) (called the ground state) can be chosen positive, see Sect. 3. Since \(\mathscr {H}(e_0)=\lambda _0 e_0\), a doubly-twisted product
, where \(\beta = p(\mathrm{\Delta }^\perp v)/nv\). For any compact leaf, the spectrum of \(\mathscr {H}\) is discrete, the least eigenvalue \(\lambda _0\) is isolated from other eigenvalues, and the eigenfunction \(e_0\) (called the ground state) can be chosen positive, see Sect. 3. Since \(\mathscr {H}(e_0)=\lambda _0 e_0\), a doubly-twisted product  has leafwise constant mixed scalar curvature equal to \(n\lambda _0\).
has leafwise constant mixed scalar curvature equal to \(n\lambda _0\).
We focus on the mixed Yamabe problem for harmonic foliations, which amounts to finding a positive solution of the leafwise elliptic equation, see Proposition 2.10,

where  , and a leafwise constant \(\widetilde{\mathrm{S}}_\mathrm{mix}\) corresponds to a \({\mathscr {D}}^\bot \)-conformal metric \(\widetilde{g}\). Proposition 2.6 allows us to reduce (5) to the case of
, and a leafwise constant \(\widetilde{\mathrm{S}}_\mathrm{mix}\) corresponds to a \({\mathscr {D}}^\bot \)-conformal metric \(\widetilde{g}\). Proposition 2.6 allows us to reduce (5) to the case of  . By Lemma 2.8, \({\mathscr {D}}^\bot \)-conformal changes of the metric preserve harmonic foliations. For non-harmonic foliations, (5) has additional first order terms.
. By Lemma 2.8, \({\mathscr {D}}^\bot \)-conformal changes of the metric preserve harmonic foliations. For non-harmonic foliations, (5) has additional first order terms.
Example 2.5
The global structure of totally geodesic foliations with integrable normal bundle (i.e., \({\mathscr {D}}^\bot \) is tangent to a foliation \(\mathscr {F}^\bot \)) has been studied in [5]: the universal cover \(\widetilde{M}\) is topologically a product  of universal covers of the leaves of both foliations, \(\mathscr {F}\) and \(\mathscr {F}^\bot \). Let \(\mathscr {F}\) be a totally geodesic foliation with integrable normal bundle of a closed Riemannian manifold (M, g) with conditions (2) and
of universal covers of the leaves of both foliations, \(\mathscr {F}\) and \(\mathscr {F}^\bot \). Let \(\mathscr {F}\) be a totally geodesic foliation with integrable normal bundle of a closed Riemannian manifold (M, g) with conditions (2) and  . Then \(\mathrm{\Psi }_1=\mathrm{\Psi }_2=0\), and (5) becomes the linear elliptic equation on F,
. Then \(\mathrm{\Psi }_1=\mathrm{\Psi }_2=0\), and (5) becomes the linear elliptic equation on F,

where  . Suppose that \(\mathrm{S}_\mathrm{mix}\ne \mathrm{const}\) and \(\mathrm{\Phi }=\mathrm{const}\). Then \({\mathscr {H}}(u_*)=\mathrm{\Phi } u_*\), where \(u_*=e_0\) and \(\mathrm{\Phi }=\lambda _0\) for the Schrödinger operator
. Suppose that \(\mathrm{S}_\mathrm{mix}\ne \mathrm{const}\) and \(\mathrm{\Phi }=\mathrm{const}\). Then \({\mathscr {H}}(u_*)=\mathrm{\Phi } u_*\), where \(u_*=e_0\) and \(\mathrm{\Phi }=\lambda _0\) for the Schrödinger operator  . Assuming \(\nabla ^\bot u_{|F}=0\), continue \(u_*\) smoothly on M. Thus, the mixed scalar curvature of the Riemannian manifold
. Assuming \(\nabla ^\bot u_{|F}=0\), continue \(u_*\) smoothly on M. Thus, the mixed scalar curvature of the Riemannian manifold  .
.
Proposition 2.6
Let \(\mathscr {F}\) be a foliation of a closed Riemannian manifold (M, g) with condition (2). Then there exists a smooth function \(u>0\) on M such that  for the metric \(\widetilde{g}=g_\mathscr {F}+ u^2 g^\perp \).
for the metric \(\widetilde{g}=g_\mathscr {F}+ u^2 g^\perp \).
Proof
Recall the equality for any \(X,Y\in {\mathfrak X}^\bot \) and \(U,V\in {\mathfrak X}^\top \), see [16],

where the co-nullity operator  is defined by
is defined by  , \(U\in {\mathfrak X}^\top \), \(X\in {\mathfrak X}_M\). Note that
, \(U\in {\mathfrak X}^\top \), \(X\in {\mathfrak X}_M\). Note that

Thus, tracing (6) over \(\mathscr {D}\) and taking the antisymmetric part, we obtain  , where the 2-form
, where the 2-form  is defined by
is defined by

Then we apply Lemma 2.7. \(\square \)
Lemma 2.7
([19, Theorem 1.1]) Let \(\mathscr {F}\) be a foliation of a closed Riemannian manifold (M, g) with condition (2), and  . Then the Cauchy problem
. Then the Cauchy problem

has a unique solution \(g_t\), \(t\ge 0\), that converges as \(t\rightarrow \infty \) to a metric with  .
.
2.2 \({\mathscr {D}}^\bot \)-conformal change of a metric
We shall find how various geometrical quantities are transformed under \({\mathscr {D}}^\bot \)-conformal change of a metric. The Weingarten operator \(A^\bot _U\) of \({\mathscr {D}}^\bot \) and the skew-symmetric operator \(T^\#_U\), where \(U\in {\mathfrak X}^\top \), are given by
Lemma 2.8
Given a foliation \(\mathscr {F}\) on \((M,g = g_\mathscr {F}+ g^\perp )\), and \(\phi \in C^1(M)\), define a new metric \(\widetilde{g}=g_\mathscr {F}+ e^{2\phi } g^\perp \). Then


Hence, \({\mathscr {D}}^\bot \)-conformal variations preserve total umbilicity, harmonicity, and total geodesy of \(\mathscr {F}\), and preserve total umbilicity of the normal distribution \({\mathscr {D}}^\bot \).
Proof
The Levi-Civita connection \(\nabla \) of a metric g is given by the known formula

\(X,Y,Z\in {\mathfrak X}_M\). Formula (7) follows from (10):

We deduce (8) using  . From \(\widetilde{T}=T\) and
. From \(\widetilde{T}=T\) and

formula (9) follows. By (10), for any \(X,Y\in {\mathfrak X}^\bot \) and \(U\in {\mathfrak X}^\top \) we have

From this, skew-symmetry of T and (3), we deduce (8). Then we get (9) using

Similarly, we prove (9):

The orthonormal bases of \({\mathscr {D}}^\bot \) in both metrics are related by \(\widetilde{\mathscr {E}}_j = e^{-\phi }{\mathscr {E}}_j\). To show this we calculate for any \(j\le n\),

By (8), we have

From this and the definition  , the equality (8) follows. \(\square \)
, the equality (8) follows. \(\square \)
Remark 2.9
By Lemma 2.8, for a leafwise constant \(\phi \) we obtain  and \(\widetilde{H}^\bot \! = H^\bot \). Hence, \({\mathscr {D}}^\bot \)-scalings of g preserve harmonicity and total geodesy of \({\mathscr {D}}^\bot \).
and \(\widetilde{H}^\bot \! = H^\bot \). Hence, \({\mathscr {D}}^\bot \)-scalings of g preserve harmonicity and total geodesy of \({\mathscr {D}}^\bot \).
Proposition 2.10
The mixed scalar curvature of a harmonic foliation \(\mathscr {F}\) under \({\mathscr {D}}^\bot \)-conformal change of a metric \(\widetilde{g} = g_\mathscr {F}+ u^{2}g^\perp \), where \(u>0\) is a smooth function, is transformed according to the formula

If, in particular, u is leafwise constant (i.e., \(\widetilde{g}\) is a \({\mathscr {D}}^\bot \)-scaling of g), then we have

Proof
By Lemma 2.8, we have

Indeed, the formulae for  and \(\Vert \widetilde{T}\Vert ^2_{\widetilde{g}}\) follow from
and \(\Vert \widetilde{T}\Vert ^2_{\widetilde{g}}\) follow from

Formula for  follows from
follows from  for \(U\in {\mathfrak X}^\top \) and
for \(U\in {\mathfrak X}^\top \) and

From

the formulae for  and \(\Vert \widetilde{H}^\bot \Vert ^2_{\widetilde{g}}\) follow. Then, using (12), \(\widetilde{\mathscr {E}}_i=e^{-\phi }{\mathscr {E}}_i\), and
and \(\Vert \widetilde{H}^\bot \Vert ^2_{\widetilde{g}}\) follow. Then, using (12), \(\widetilde{\mathscr {E}}_i=e^{-\phi }{\mathscr {E}}_i\), and

we obtain the formula

Substituting \(\phi =\log u\) and  ,
,  into (13) yields the required formula (11), which is equivalent to (5). \(\square \)
into (13) yields the required formula (11), which is equivalent to (5). \(\square \)
2.3 Proof of main results
Proposition 2.6 allows us to assume  . Then we associate with (5) the leafwise parabolic equation with a leafwise constant \(\widetilde{\mathrm{S}}_\mathrm{mix}\)
. Then we associate with (5) the leafwise parabolic equation with a leafwise constant \(\widetilde{\mathrm{S}}_\mathrm{mix}\)

We shall study asymptotic behavior of solutions to (14) with appropriate initial data using spectral parameters of a leafwise Schrödinger operator  . The least eigenvalue \(\lambda ^\top _0\) of \(\mathscr {H}^\top \) is simple and obeys the inequalities
. The least eigenvalue \(\lambda ^\top _0\) of \(\mathscr {H}^\top \) is simple and obeys the inequalities

its eigenfunction \(e_0\) (called the ground state) may be chosen positive, see Sect. 3. By (2) and results in Sect. 4, the leafwise constant \(\lambda ^\top _0\) and \(e_0\) are smooth on M.
Assume \(h\ne 0\), \(\mathrm{\Phi }<n\lambda _0^\top \) and consider the functions (compare with Sect. 3),

If the discriminant  , each of (15) has four real roots (two of them are positive). Their maximal (positive) roots
, each of (15) has four real roots (two of them are positive). Their maximal (positive) roots

obey the inequalities \(y^\top _- < y_3^\top < y^\top _+\), where \(y_3^\top \) is the maximal root of \((\phi ^\top _-)'(y)\),

see (26). For a positive function \(f\in C(F)\) define  .
.
Proposition 2.11
Let \(\mathscr {F}\) be a harmonic and nowhere totally geodesic foliation on a Riemannian manifold (M, g) with condition (2) and  . Then for any leafwise constant \(\mathrm{\Phi }\in C^\infty (M)\) obeying the inequalities (along any leaf F)
. Then for any leafwise constant \(\mathrm{\Phi }\in C^\infty (M)\) obeying the inequalities (along any leaf F)

there exists a unique \(u_*\) in the set  such that the mixed scalar curvature of \(\widetilde{g} = g_\mathscr {F}+ u_*^2 g^\perp \) is \(\mathrm{\Phi }\). Moreover, \(y^\top _-\le u_*/e_0\le y^\top _+\) and
such that the mixed scalar curvature of \(\widetilde{g} = g_\mathscr {F}+ u_*^2 g^\perp \) is \(\mathrm{\Phi }\). Moreover, \(y^\top _-\le u_*/e_0\le y^\top _+\) and  , where u solves (14) with \(\widetilde{\mathrm{S}}_\mathrm{mix}=\mathrm{\Phi }\), does not depend on the value
, where u solves (14) with \(\widetilde{\mathrm{S}}_\mathrm{mix}=\mathrm{\Phi }\), does not depend on the value  .
.
Proof
By Theorem 4.4, the leafwise constant \(\lambda _0^\top \) (the least eigenfunction of \(\mathscr {H}^\top \)) and its leafwise eigenvector \(e_0\) are smooth, i.e., they belong to \(C^\infty (M)\). If M is closed then there exist many functions \(\mathrm{\Phi }\) obeying (16), e.g.  for small enough \(\varepsilon >0\).
for small enough \(\varepsilon >0\).
By the conditions, any leaf \(F_0\) has an open neighborhood diffeomorphic to  and
and  . Since
. Since  are compact minimal submanifolds, their volume form
are compact minimal submanifolds, their volume form  does not depend on \(q\in {\mathbb R}^n\), see [16]. Thus, the vector bundles \(\{L_2(F_q)\}_{q\in {\mathbb R}^n}\) and \(\{H^k(F_q)\}_{q\in {\mathbb R}^n}\) coincide with the products
does not depend on \(q\in {\mathbb R}^n\), see [16]. Thus, the vector bundles \(\{L_2(F_q)\}_{q\in {\mathbb R}^n}\) and \(\{H^k(F_q)\}_{q\in {\mathbb R}^n}\) coincide with the products  and
and  . Let \(\mathrm{\Phi }\) obey (16) and let \(u_0>e_0, y^\top _3\) hold. We shall use the notation
. Let \(\mathrm{\Phi }\) obey (16) and let \(u_0>e_0, y^\top _3\) hold. We shall use the notation

Then (14) with \(\widetilde{\mathrm{S}}_\mathrm{mix}=\mathrm{\Phi }\) becomes (19), while (16) follows from

which becomes (24). Hence, the claim follows from Theorem 3.6. \(\square \)
Corollary 2.12
Let \(\mathscr {F}\) be a harmonic and nowhere totally geodesic foliation of a Riemannian manifold (M, g) with condition (2), integrable normal subbundle \({\mathscr {D}}^\bot \) and  . Then for any leafwise constant \(\mathrm{\Phi }\in C^\infty (M)\) such that \(\mathrm{\Phi }<n\lambda ^\top _0\) there exists a unique positive function \(u_*\in C^\infty (M)\) such that (along any leaf F)
. Then for any leafwise constant \(\mathrm{\Phi }\in C^\infty (M)\) such that \(\mathrm{\Phi }<n\lambda ^\top _0\) there exists a unique positive function \(u_*\in C^\infty (M)\) such that (along any leaf F)

and the mixed scalar curvature of the metric \(\widetilde{g} = g_\mathscr {F}+ u_*^2g^\perp \) is \(\mathrm{\Phi }\).
Proof
This is similar to the proof of Proposition 2.11. Since \(\mathrm{\Psi }_2\equiv 0\) and \(\lambda _0>0\), each of  and
and  has one positive root \(y_1^-=\sqrt{\mathrm{\Psi }_1^-/\lambda _0}\) and \(y_1^+=\sqrt{\mathrm{\Psi }_1^+/\lambda _0}\), see also Example 3.2 (c). \(\square \)
has one positive root \(y_1^-=\sqrt{\mathrm{\Psi }_1^-/\lambda _0}\) and \(y_1^+=\sqrt{\mathrm{\Psi }_1^+/\lambda _0}\), see also Example 3.2 (c). \(\square \)
Proof of Theorem 2.1 By Proposition 2.6, there exists a metric \(g_1\), \({\mathscr {D}}^\bot \)-conformal to g, for which  (the mean curvature of \({\mathscr {D}}^\bot \)). By Lemma 2.8, the equality \(H=0\) is preserved for \(g_1\). By Proposition 2.11, there exists a metric \(\widetilde{g}\), \({\mathscr {D}}^\bot \)-conformal to \(g_1\), for which \(\widetilde{\mathrm{S}}_\mathrm{mix}\) is leafwise constant; moreover, \(H=0\) holds. \(\square \)
(the mean curvature of \({\mathscr {D}}^\bot \)). By Lemma 2.8, the equality \(H=0\) is preserved for \(g_1\). By Proposition 2.11, there exists a metric \(\widetilde{g}\), \({\mathscr {D}}^\bot \)-conformal to \(g_1\), for which \(\widetilde{\mathrm{S}}_\mathrm{mix}\) is leafwise constant; moreover, \(H=0\) holds. \(\square \)
Proof of Theorem 2.3 By Corollary 2.12, there is a metric \(g_1\) that is \({\mathscr {D}}^\bot \)-conformal to g, for which  . By Lemma 2.8, \(h=0\) is preserved for \(g_1\). Since \(T=0\), equation (5) reads as the eigenproblem
. By Lemma 2.8, \(h=0\) is preserved for \(g_1\). Since \(T=0\), equation (5) reads as the eigenproblem  , where
, where  is a leafwise Schrödinger operator on \((M,g_1)\) with potential
is a leafwise Schrödinger operator on \((M,g_1)\) with potential  . Let \(e_0>0\) be the ground state of \(\mathscr {H}\) with the least eigenvalue \(\lambda ^\top _0\) (leafwise constant). Thus, the metric \(\widetilde{g} = g_\mathscr {F}+ e_0^2 g_1^\perp \) has \(\widetilde{\mathrm{S}}_\mathrm{mix}=n\lambda ^\top _0\); moreover, the equality \(h=0\) is preserved for \(\widetilde{g}\). \(\square \)
. Let \(e_0>0\) be the ground state of \(\mathscr {H}\) with the least eigenvalue \(\lambda ^\top _0\) (leafwise constant). Thus, the metric \(\widetilde{g} = g_\mathscr {F}+ e_0^2 g_1^\perp \) has \(\widetilde{\mathrm{S}}_\mathrm{mix}=n\lambda ^\top _0\); moreover, the equality \(h=0\) is preserved for \(\widetilde{g}\). \(\square \)
3 Results for the nonlinear heat equation
Let (F, g) be a smooth closed p-dimensional Riemannian manifold (e.g., a leaf of a compact foliation) with the Riemannian distance d(x, y). Functional spaces over F will be denoted without writing (F), e.g., \(L_2\) instead of \(L_2(F)\). Let \(H^k\) be the Hilbert space of Sobolev real functions of order k on F with the inner product  and the norm
and the norm  . In particular, \(H^0=L_2\) with the product
. In particular, \(H^0=L_2\) with the product  and the norm
and the norm  . Denote by
. Denote by  the norm in the Banach space \(C^k\) for \(1\le k<\infty \), and
the norm in the Banach space \(C^k\) for \(1\le k<\infty \), and  for \(k=0\). In local coordinates \((x_1,\ldots , x_p)\) on F, we have
for \(k=0\). In local coordinates \((x_1,\ldots , x_p)\) on F, we have  , where \(m\ge 0\) is the multi-index of order \(|m|=\sum _{i}m_i\) and \(d^m\) is the partial derivative (in fact, a finite atlas of F must be considered). For \(\alpha \in (0,1)\) and integer \(k\ge 0\) denote by \(C^{k,\alpha }\) the Banach space of such functions \(u\in C^k\), for which all partial derivatives of order k belong to Hölder class \(C^{0,\alpha }\). The norm in this space is defined as follows:
, where \(m\ge 0\) is the multi-index of order \(|m|=\sum _{i}m_i\) and \(d^m\) is the partial derivative (in fact, a finite atlas of F must be considered). For \(\alpha \in (0,1)\) and integer \(k\ge 0\) denote by \(C^{k,\alpha }\) the Banach space of such functions \(u\in C^k\), for which all partial derivatives of order k belong to Hölder class \(C^{0,\alpha }\). The norm in this space is defined as follows:

Proposition 3.1
(scalar maximum principle, see [8, Theorem 4.4]) Let \(X_t\) and \(g_t\) be smooth families of vector fields and metrics on a closed Riemannian manifold F, and  . Suppose that
. Suppose that  is a \(C^\infty \) solution to
is a \(C^\infty \) solution to

and let \(y:[0,T]\rightarrow {\mathbb R}\) solve the Cauchy problem for the ODEs: \(y' = f(y(t),t)\), \(y(0)=y_0\). If  , then
, then  for all \(t\in [0, T)\).
for all \(t\in [0, T)\).
3.1 The nonlinear heat equation
We are looking for stable solutions of the elliptic equation, see (5) with  ,
,

where \(\mathrm{\Psi }_1>0\), \(\mathrm{\Psi }_2\ge 0\) and \(\beta \) are smooth functions on F. To study (18), we shall look for attractors of the Cauchy problem for the nonlinear heat equation,

Let  be cylinder with the base F. By [2, Theorem 4.51], (19) has a unique smooth solution in \(\mathscr {C}_{t_0}\) for some \(t_0>0\). Let \(S_t\) be a map which relates to each initial value \(u_0\in C\) the value of this solution at \(t\in [0,t_0)\). Since the rhs of (19) does not depend explicitly on t, the family \(\{S_t\}\) has the semigroup property, and it is a semigroup (i.e., \(t_0=\infty \)) when (19) has a global solution for any \(u_0(x)\in C\).
be cylinder with the base F. By [2, Theorem 4.51], (19) has a unique smooth solution in \(\mathscr {C}_{t_0}\) for some \(t_0>0\). Let \(S_t\) be a map which relates to each initial value \(u_0\in C\) the value of this solution at \(t\in [0,t_0)\). Since the rhs of (19) does not depend explicitly on t, the family \(\{S_t\}\) has the semigroup property, and it is a semigroup (i.e., \(t_0=\infty \)) when (19) has a global solution for any \(u_0(x)\in C\).
Let \(\mathscr {H}=-\mathrm{\Delta } -\beta \) be a Schrödinger operator with domain in \(H^2\) and \(\sigma (\mathscr {H})\) the spectrum. One can add a real constant to \(\beta \) such that \(\mathscr {H}\) becomes invertible in \(L_2\) (e.g. \(\lambda _0>0\)) and \(\mathscr {H}^{-1}\) is bounded in \(L_2\).
Elliptic Regularity Theorem (see [2]) If \(0\notin \sigma (\mathscr {H})\), then for any integer \(k\ge 0\) we have \(\mathscr {H}^{-1}:H^k\rightarrow H^{k+2}\).
By the Elliptic Regularity Theorem with \(k=0\), we have \(\mathscr {H}^{-1}:L_2\rightarrow H^2\), and the embedding of \(H^2\) into \(L_2\) is continuous and compact, see [2]. Hence, the operator \(\mathscr {H}^{-1}:L_2\rightarrow L_2\) is compact. Thus, the spectrum \(\sigma (\mathscr {H})\) is discrete, i.e., consists of an infinite sequence of real eigenvalues \(\lambda _0\le \lambda _1\le \cdots \le \lambda _j\le \cdots \) with finite multiplicities, bounded from below and \(\lim _{j\rightarrow \infty }\lambda _j=\infty \). One may fix in \(L_2\) an orthonormal basis of eigenfunctions \(\{e_j\}\), i.e., \(\mathscr {H}(e_j)=\lambda _j e_j\). Since the eigenvalue \(\lambda _0\) is simple, its eigenfunction \(e_0(x)\) can be chosen positive, see [20, Proposition 3].
The following examples show us that (19) may have
-
(i)
stationary (i.e., t-independent) solutions on a closed manifold F;
-
(ii)
attractors (i.e., asymptotically stable stationary solutions) when \(\beta <0\).
Example 3.2
Let \(\beta \) and \(\mathrm{\Psi }_1>0\), \(\mathrm{\Psi }_2\ge 0\) be real constants. Then (19) is the Cauchy problem for the ODE
(a) Let \(\beta <0\) and \(\mathrm{\Psi }_2>0\). Positive stationary (i.e., constant) solutions of (20) are the roots of a biquadratic equation  . If
. If  , then we have two positive solutions
, then we have two positive solutions  and \(y_1>y_2\). The linearization of (20) at the point \(y_k\), \(k=1,2\), is \(v'=f'(y_k)v\), where
and \(y_1>y_2\). The linearization of (20) at the point \(y_k\), \(k=1,2\), is \(v'=f'(y_k)v\), where  . Hence, \(f'(y_1)<0\) and \(f'(y_2)>0\), and \(y_1\) is asymptotically stable, but \(y_2\) is unstable. If
. Hence, \(f'(y_1)<0\) and \(f'(y_2)>0\), and \(y_1\) is asymptotically stable, but \(y_2\) is unstable. If  , then (20) has one positive stationary solution, see Fig. 1(a), and has no stationary solutions if
, then (20) has one positive stationary solution, see Fig. 1(a), and has no stationary solutions if  .
.
Example 3.2: the nonlinear heat equation. (a) \(\beta y^4 +\mathrm{\Psi }_1 y^{2} -\mathrm{\Psi }_2\) with \(\beta <0\) and  : \(y_1\) stable, \(y_2\) unstable, (b) \(\mathrm{\Psi }_1>0\), \(\mathrm{\Psi }_2=0\) and \(\beta <0\)
: \(y_1\) stable, \(y_2\) unstable, (b) \(\mathrm{\Psi }_1>0\), \(\mathrm{\Psi }_2=0\) and \(\beta <0\)
(b) Let \(\beta >0\) and \(\mathrm{\Psi }_2>0\). Then the biquadratic equation  has one positive root
has one positive root  . We find
. We find

hence, \(y_1\) is unstable. One may also show that in the case \(\beta =0\), (20) has a unique positive stationary solution, which is unstable.
(c) Let \(\mathrm{\Psi }_2=0\) and \(\mathrm{\Psi }_1>0\). Then \(f(y)=\beta y+\mathrm{\Psi }_1 y^{-1}\). If \(\beta \ge 0\), then there are no positive stationary solutions. If \(\beta <0\), then f has one positive root \(y_1=({\mathrm{\Psi }_1/|\beta |})^{1/2}\). Since  , the solution \(y_1\) is an attractor.
, the solution \(y_1\) is an attractor.
Example 3.3
Let F be a circle \(S^1\) of length l. Then (19) is the Cauchy problem
The stationary equation with u(x) for (21) has the form
Rewrite (22) as the dynamical system
Periodic solutions of (22) correspond to solutions of (23) with the same period. System (23) is Hamiltonian, since \(\partial _u v=\partial _v f(u)\), its Hamiltonian  (the first integral) solves
(the first integral) solves  ,
,  . Then
. Then  . The trajectories of (23) belong to level lines of
. The trajectories of (23) belong to level lines of  . Consider the cases.
. Consider the cases.
(a) Assume \(\beta <0\). Then (23) has two fixed points: \((y_i,0)\), \(i=1,2\), with \(y_1>y_2\). To clear up the type of fixed points, we linearize (23) at \((y_i,0)\),

Since \(f'(y_1)<0\) and \(f'(y_2)>0\), the point \((y_1,0)\) is a “saddle” and \((y_2,0)\) is a “center”. The separatrix is  , i.e., see Fig. 2(a),
, i.e., see Fig. 2(a),

The separatrix divides the half-plane \(u>0\) into three simply connected areas. Then \((y_2,0)\) is a unique minimum point of \(\mathrm {H}\) in  . The phase portrait of (23) in D consists of the cycles surrounding the fixed point \((y_2,0)\), all correspond to non-constant solutions of (22) with various l. Other two areas do not contain cycles, since they have no fixed points.
. The phase portrait of (23) in D consists of the cycles surrounding the fixed point \((y_2,0)\), all correspond to non-constant solutions of (22) with various l. Other two areas do not contain cycles, since they have no fixed points.
Example 3.3. (a) \(\beta <0\), (b) \(\beta >0\)
(b) Assume \(\beta \ge 0\). Then (23) has one fixed point \((y_1,0)\) and \(f'(y_1)>0\). Hence, \((y_1,0)\) is a “center”. Since \((y_1,0)\) is a unique minimum of  in the semiplane \(u>0\), the phase portrait of (23) consists of the cycles surrounding the fixed point \((y_1,0)\), all correspond to non-constant solutions of (22) with various l, see Fig. 2(b).
in the semiplane \(u>0\), the phase portrait of (23) consists of the cycles surrounding the fixed point \((y_1,0)\), all correspond to non-constant solutions of (22) with various l, see Fig. 2(b).
For \(\mathrm{\Psi }_2=0\) and \(\mathrm{\Psi }_1>0\), the Hamiltonian of (23) is  . Solving
. Solving  with respect to v and substituting to (23), we get
with respect to v and substituting to (23), we get  . If \(\beta \ge 0\), then (23) has no cycles (since it has no fixed points); hence, (22) has no solutions. If \(\beta <0\), then the separatrix
. If \(\beta \ge 0\), then (23) has no cycles (since it has no fixed points); hence, (22) has no solutions. If \(\beta <0\), then the separatrix  , see Example 3.2 (c), is
, see Example 3.2 (c), is  , (23) has a unique fixed point \((u_*,0)\) which is a “saddle”. The separatrix divides the half-plane \(u>0\) into four simply connected areas with these lines, see Fig. 1(b). Since each of these areas has no fixed points of (23), the system has no cycles. Hence, \(u_*\) is a unique solution of (22).
, (23) has a unique fixed point \((u_*,0)\) which is a “saddle”. The separatrix divides the half-plane \(u>0\) into four simply connected areas with these lines, see Fig. 1(b). Since each of these areas has no fixed points of (23), the system has no cycles. Hence, \(u_*\) is a unique solution of (22).
(c) Consider (22) for \(\mathrm{\Psi }_1=0\), \(\mathrm{\Psi }_2>0\) and \(l=2\pi \). Set \(p=u'\) and represent \(p=p(u)\) as a function of u. Then \(u''={dp}/{du}\) and

After separation of variables and integration, we obtain

(in the first case \(C_1^2\ge 4\beta \mathrm{\Psi }_2\)). Hence, for \(\beta \le 0\), (22) has no positive solutions, while for \(\beta >0\) the solution is \(2\pi \)-periodic and positive only if
-
\(\beta \ne {n^2}/{4}\), \(n\in {\mathbb N}\), and
 ; a solution \(u_*=(\mathrm{\Psi }_2/\beta )^{1/4}\) is unique, or
; a solution \(u_*=(\mathrm{\Psi }_2/\beta )^{1/4}\) is unique, or -
\(\beta ={n^2}/{4}\), \(n\in {\mathbb N}\); the set of solutions forms a two-dimensional manifold

3.2 Attractor of the nonlinear heat equation
Denote by

Let \(\mathrm{\Psi }_2^+>0\) (the case of \(\mathrm{\Psi }_2^+=0\) is similar) and

Each of the two functions of variable \(y>0\),

has four real roots, two of which, \(y_2^+<y_1^+\) and \(y_2^-<y_1^-\), are positive. Since \(\phi _-(y)\le \phi _+(y)\) for \(y>0\), we also have \(y_1^- \le y_1^+\). Denote by

a unique positive root of \(\phi _-'(y)\). Clearly, \(y_3^-\in (y_2^-,y_1^-)\). Notice that \(\phi _-(y)>0\) for \(y\in (y_2^-,y_1^-)\) and \(\phi _-(y)<0\) for  ; moreover, \(\phi _-(y)\) increases in \((0,y_3^-)\) and decreases in \((y_3^-,\infty )\). The line \(z=-\lambda _0y\) is asymptotic for the graph of \(\phi _-(y)\) when \(y\rightarrow \infty \), and
; moreover, \(\phi _-(y)\) increases in \((0,y_3^-)\) and decreases in \((y_3^-,\infty )\). The line \(z=-\lambda _0y\) is asymptotic for the graph of \(\phi _-(y)\) when \(y\rightarrow \infty \), and  . Next, \(\phi _-'(y)\) decreases in \((0,y_4^-)\) and increases in \((y_4^-,\infty )\), where
. Next, \(\phi _-'(y)\) decreases in \((0,y_4^-)\) and increases in \((y_4^-,\infty )\), where  , and \(\lim _{y\rightarrow \infty }\phi _-'(y)=-\lambda _0\), see Fig. 3. Hence,
, and \(\lim _{y\rightarrow \infty }\phi _-'(y)=-\lambda _0\), see Fig. 3. Hence,

for \(\sigma \in (0,y_1^- -y_3^-)\). Similar properties have \(y_3^+, y_4^+\) and \(\mu ^+(\sigma )\) defined for \(\phi _+'(y)\).
Lemma 3.4
Let y(t) be a solution of the Cauchy problem
-
(i)
If \(y_0^- > y_2^-\) then \(\lim _{t\rightarrow \infty }y(t)=y_1^-\). Furthermore, if \(y_0^-\in (y_2^-,y_1^-)\) then y(t) is increasing and if \(y_0^->y_1^-\) then y(t) is decreasing.
-
(ii)
If \(y_0^-\ge y_1^- -\varepsilon \) for some \(\varepsilon \in (0,y_1^- -y_3^-)\) then
 (29)
(29)
Similar claims are valid for the Cauchy problem \(y'=\phi _+(y)\), \(y(0)=y_0^+>0\).
Proof
(i) Assume that \(y_0^-\in (y_2^-,y_1^-)\). Since \(\phi _-(y)\) is positive in \((y_2^-,y_1^-)\), y(t) is increasing. The graph of y(t) cannot intersect the graph of the stationary solution \(y_1^-\); hence, the solution y(t) exists and is continuous on the whole \([0,\infty )\), and it is bounded there. There exists \(\lim _{t\rightarrow \infty }y(t)\), which coincides with \(y_1^-\), since \(y_1^-\) is a unique solution of \(\phi (y)=0\) in \((y_2^-,\infty )\). The case \(y_0^- > y_1^-\) is treated similarly. Notice that if \(y_0^- \in (y_2^-, y_1^-)\) then y(t) is increasing, and if \(y_0^- > y_1^-\) then y(t) is decreasing.
(ii) For \(y_0^-\ge y_1^- -\varepsilon \), where \(\varepsilon \in (0, y_1^- - y_3^-)\), denote \(z(t)=y_1^- - y(t)\). We obtain from (28), using definition of \(\mu ^-(\varepsilon )\) and the fact that \(\phi _-(y_1^-)=0\),

This differential inequality implies (29). The case \(y_0^- > y_1^-\) is treated similarly. \(\square \)
Under assumption (24), define nonempty sets \({\mathscr {U}}_{2}^{\varepsilon ,\eta }\subset {\mathscr {U}}_{1}^{\varepsilon }\), closed in C, with \(\varepsilon \in (0,y_1^--y_3^-)\) and \(\eta >0\) by

Then, \(\mathscr {U}_{1}^{\varepsilon }\subset \mathscr {U}_{1}\), where  is open in C.
is open in C.
Proposition 3.5
Let (24) hold. Then the Cauchy problem (19) with \(u_0\in {\mathscr {U}}_{1}^{\varepsilon }\) for some \(\varepsilon \in (0,y_1^--y_3^-)\), admits a unique global solution. Furthermore, the sets \({\mathscr {U}}_{1}^{\varepsilon }\) and \({\mathscr {U}}_{2}^{\varepsilon ,\eta }\), \(\eta >0\), are invariant for the semigroup of operators corresponding to (19).
Proof
Let  , \(t\ge 0\), solve (19) with \(u_0\in \mathscr {U}_{1}^{\varepsilon }\) for some \(\varepsilon \in (0,y_1^--y_3^-)\). Substituting \(u=e_0 w\) and using
, \(t\ge 0\), solve (19) with \(u_0\in \mathscr {U}_{1}^{\varepsilon }\) for some \(\varepsilon \in (0,y_1^--y_3^-)\). Substituting \(u=e_0 w\) and using  , yields the Cauchy problem
, yields the Cauchy problem

for w(x, t), where

From (30) and (25) we obtain the differential inequalities

By Proposition 3.1, applied to the left inequality of (32), and Lemma 3.4, in the maximal domain \(D_M\) of the existence of the solution w(x, t) of (30), we obtain the inequality

which implies that w(x, t) cannot “blowdown” to zero. Since \(\phi _+(w)\le {\mathrm{\Psi }^+_1}{w^{-1}}\), from the right inequality of (32), applying Proposition 3.1, we obtain in \(D_M\)

where \(w_+(t)\) solves the Cauchy problem for the ODE

By the above, the solution u(x, t) of (19) exists for all \((x,t)\in {\mathscr {C}}_\infty \), and the set \({\mathscr {U}}_{1}^{\varepsilon }\) is invariant for the semigroup of operators  , \(t\ge 0\), in
, \(t\ge 0\), in  , corresponding to (19). Assuming \(u_0\in {\mathscr {U}}_{1}^{\varepsilon ,\eta }\) and applying again Proposition 3.1 and Lemma 3.4 to the right inequality of (32), we get
, corresponding to (19). Assuming \(u_0\in {\mathscr {U}}_{1}^{\varepsilon ,\eta }\) and applying again Proposition 3.1 and Lemma 3.4 to the right inequality of (32), we get

Thus,  , \(t>0\). Hence, also the set \({\mathscr {U}}_{2}^{\varepsilon ,\eta }\) is invariant for all \(\mathscr {S}_t\). \(\square \)
, \(t>0\). Hence, also the set \({\mathscr {U}}_{2}^{\varepsilon ,\eta }\) is invariant for all \(\mathscr {S}_t\). \(\square \)
Theorem 3.6
-
(i)
If (24) holds then (18) admits in \(\mathscr {U}_{1}\) a unique solution \(u_*\) (on F), which is smooth; moreover,
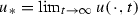 , where u solves (19) with \(u_0\in \mathscr {U}_{1}\), and \(y_1^-\le u_*/e_0\le y_1^+\). Furthermore, for any \(\varepsilon \in (0,y_1^- -y_3^-)\), the set \(\mathscr {U}_{1}^{\varepsilon }\) is attracted by (19) exponentially fast to the point \(u_*\) in C-norm:
, where u solves (19) with \(u_0\in \mathscr {U}_{1}\), and \(y_1^-\le u_*/e_0\le y_1^+\). Furthermore, for any \(\varepsilon \in (0,y_1^- -y_3^-)\), the set \(\mathscr {U}_{1}^{\varepsilon }\) is attracted by (19) exponentially fast to the point \(u_*\) in C-norm:  (33)
(33) -
(ii)
If \(\beta ,\mathrm{\Psi }_1,\mathrm{\Psi }_2\) are smooth functions on the product
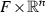 with a smooth leafwise metric
with a smooth leafwise metric  and (24) holds for any leaf
and (24) holds for any leaf 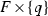 , \(q\in {\mathbb R}^n\), then the leafwise solution \(u_*\) of (18) is smooth on
, \(q\in {\mathbb R}^n\), then the leafwise solution \(u_*\) of (18) is smooth on  .
.
Proof
(i) By Proposition 3.5, the set \(\mathscr {U}_{1}^{\varepsilon }\) is invariant for the semigroup of operators  , \(t\ge 0\), corresponding to (19), i.e., \({\mathscr {S}}_t(\mathscr {U}_{1}^{\varepsilon })\subseteq \mathscr {U}_{1}^{\varepsilon }\) for \(t\ge 0\). Take \(u_i^0\in \mathscr {U}_{1}^{\varepsilon }\), \(i=1,2\), and denote by
, \(t\ge 0\), corresponding to (19), i.e., \({\mathscr {S}}_t(\mathscr {U}_{1}^{\varepsilon })\subseteq \mathscr {U}_{1}^{\varepsilon }\) for \(t\ge 0\). Take \(u_i^0\in \mathscr {U}_{1}^{\varepsilon }\), \(i=1,2\), and denote by

Using (30) and the equalities

with \(\overline{w}=w_2-w_1\), we obtain

We estimate the last term, using \(w_i\ge y_1^- -\varepsilon >y_3^-\), \(i=1,2\), (27) and (31),

Thus, the function \(v=(w_2-w_1)^2\) satisfies the differential inequality

By Proposition 3.1,  , where \(v_+(t)\) solves the Cauchy problem for the ODE:
, where \(v_+(t)\) solves the Cauchy problem for the ODE:

Thus,

i.e., the operators \(\mathscr {S}_t\), \(t\ge 0\), corresponding to (19) satisfy in \(\mathscr {U}_{1}^{\varepsilon }\) the Lipschitz condition with respect to C-norm with the Lipschitz constant \(\delta ^{-1}_{e_0} e^{-\mu ^-(\varepsilon )t}\).
By Proposition 3.5, for any \(t\ge 0\) the operator \({\mathscr {S}}_t\) for (19) maps the set \(\mathscr {U}_{1}^{\varepsilon }\), which is closed in C, into itself, and for \(t>(\ln \delta ^{-1}_{e_0})/\mu ^-(\varepsilon )\) it is a contraction there. Since all operators \({\mathscr {S}}_t\) commute one with another, they have a unique common fixed point \(u_*\) in \(\mathscr {U}_{1}^{\varepsilon }\). Since \(\varepsilon \in (0,y_1^- -y_3^-)\) is arbitrary, \(u_*\) is a unique common fixed point of all \({\mathscr {S}}_t\) in the set \(\mathscr {U}_{1}\). For any \(u_0\in \mathscr {U}_{1}^{\varepsilon }\) and \(t\ge 0\), (33) holds. Thus, \(u_*\in C\) is a generalized solution of (18). By the Elliptic Regularity Theorem, \(u_*\in C^\infty \) and it is a classical solution. By Proposition 3.5, \(\mathscr {U}^{\varepsilon ,\eta }_{2}\subset \mathscr {U}^{\varepsilon }_{1}\) is also \({\mathscr {S}}_t\)-invariant, hence \(u_*\in \mathscr {U}_{2}^{\varepsilon ,\eta }\). Since  and \(\eta >0\) are arbitrary, we get \(y_1^-\le u_*/e_0\le y_1^+\).
and \(\eta >0\) are arbitrary, we get \(y_1^-\le u_*/e_0\le y_1^+\).
Notice that if the functions \(\mathrm{\Psi }_1\) and \(\mathrm{\Psi }_2\) are constant then \(\phi _+=\phi _-\), see (25); in this case, \(u_*/e_0=y_1^+=y_1^-\) is constant, too.
(ii) Let \(e_0(x,q)>0\) be the normalized eigenfunction for the minimal eigenvalue \(\lambda _0(q)\) of the operator  . By Theorem 4.4, \(\lambda _0\in C^\infty ({\mathbb R}^n)\) and
. By Theorem 4.4, \(\lambda _0\in C^\infty ({\mathbb R}^n)\) and  , hence \(y_3^-\), defined by (26), smoothly depends on q. As we have proved in (i), for any \(q\in {\mathbb R}^n\) the stationary equation, see also (18),
, hence \(y_3^-\), defined by (26), smoothly depends on q. As we have proved in (i), for any \(q\in {\mathbb R}^n\) the stationary equation, see also (18),
with  has a unique solution \(u_*(x,q)\) in the open set
has a unique solution \(u_*(x,q)\) in the open set  .
.
Since \(y_3^-(q)\) and \(e_0(x,q)\) are continuous, for any \(k\in {\mathbb N}\) and \(\alpha \in (0,1)\), there exist open neighborhoods \(U_*\subseteq C^{k+2,\alpha }\) of \(u_*(x,0)\) and \(V_0\subset {\mathbb R}^n\) of 0 such that
We claim that all eigenvalues of the linear operator  , acting in \(L_2\) with the domain \(H^2\), are positive. To show this, observe that
, acting in \(L_2\) with the domain \(H^2\), are positive. To show this, observe that  . Let \(\widetilde{u}(x,t)\) be a solution of the Cauchy problem for the evolution equation
. Let \(\widetilde{u}(x,t)\) be a solution of the Cauchy problem for the evolution equation

Using the same arguments as in the proof of (i), we obtain that the function  obeys the differential inequality with
obeys the differential inequality with  :
:

By Proposition 3.1,  , where \(v_+(t)\) solves the Cauchy problem for the ODE
, where \(v_+(t)\) solves the Cauchy problem for the ODE

moreover, for any \(\widetilde{u}_0\in C\) the function \(\widetilde{u}(x,t)\) tends to 0 exponentially fast, as \(t\rightarrow \infty \). On the other hand, if \(\widetilde{\lambda }_\nu \) is any eigenvalue of \(\mathscr {H}_*\) and \(\widetilde{e}_\nu (x)>0\) the corresponding normalized eigenfunction then  solves (36) with \(\widetilde{u}_0(x)=\widetilde{e}_\nu (x)\). Thus, \(\widetilde{\lambda }_\nu >0\) that completes the proof of the claim.
solves (36) with \(\widetilde{u}_0(x)=\widetilde{e}_\nu (x)\). Thus, \(\widetilde{\lambda }_\nu >0\) that completes the proof of the claim.
Using Theorem 4.8, we conclude that for any integers \(k\ge 0\) and \(l\ge 1\) we can restrict the neighborhoods \(U_*\) of \(u_*(x,0)\) and \(V_0\) of 0 in such a way that for any \(q\in V_0\) there exists in \(U_*\) a unique solution \(\widetilde{u}(x,q)\) of (34) and the mapping  belongs to class \(C^l(V_0,U_*)\). In view of (35),
belongs to class \(C^l(V_0,U_*)\). In view of (35),  . \(\square \)
. \(\square \)
References
Akhiezer, N.I., Glazman, I.M.: Theory of Linear Operators in Hilbert Space. Dover, New York (1993)
Aubin, T.: Some Nonlinear Problems in Riemannian Geometry. Springer Monographs in Mathematics. Springer, Berlin (1998)
Bădiţoiu, G., Ianus, S., Pastore, A.M.: Spectral geometry of Riemannian Legendre foliations. Bull. Math. Sci. Math. Roumanie 56(104)(2), 135–150 (2013)
Bejancu, A., Farran, H.R.: Foliations and Geometric Structures. Mathematics and Its Applications, vol. 580. Springer, Dordrecht (2006)
Blumenthal, R.A., Hebda, J.J.: De Rham decomposition theorems for foliated manifolds. Ann. Inst. Fourier (Grenoble) 33(2), 183–198 (1983)
Candel, A., Conlon, L.: Foliations, I. Graduate Studies in Mathematics, vol. 23. American Mathematical Society, Providence (2000)
Candel, A., Conlon, L.: Foliations, II. Graduate Studies in Mathematics, vol. 60. American Mathematical Society, Providence (2003)
Chow, B., Knopf, D.: The Ricci Flow. Mathematical Surveys and Monographs, vol. 110. American Mathematical Society, Providence (2004)
Dobarro, F., Ünal, B.: About curvature, conformal metrics and warped products. J. Phys. A 40(46), 13907–13930 (2007)
Ho, P.T.: The long-time existence and convergence of the CR Yamabe flow. Commun. Contemp. Math. 14(2), 1250014 (2012)
Krein, S.G.: Linear Differential Equations in Banach Space. Translations of Mathematical Monographs, vol. 29. American Mathematical Society, Providence (1971)
Naveira, A.M.: A classification of Riemannian almost-product manifolds. Rend. Mat. Appl. (7) 3(3), 577–592 (1983)
Ponge, R., Reckziegel, H.: Twisted products in pseudo-Riemannian geometry. Geom. Dedicata 48(1), 15–25 (1993)
Popescu, P., Popescu, M.: On a class of singular vector subbundles. BSG Proc. 20, 79–88 (2013)
Ramírez-Ospina, H.F.: Multiplicity of constant scalar curvature metrics in \(T^k \times M\). Nonlinear Anal. 109, 103–112 (2014)
Rovenski, V.Y.: Foliations on Riemannian Manifolds and Submanifolds. Birkhäuser, Boston (1998)
Rovenski, V.Y.: On solutions to equations with partial Ricci curvature. J. Geom. Phys. 86, 370–382 (2014)
Rovenski, V., Walczak, P.: Topics in Extrinsic Geometry of Codimension-One Foliations. Springer Briefs in Mathematics. Springer, New York (2011)
Rovenski, V., Wolak, R.: Deforming metrics of foliations. Cent. Eur. J. Math. 11(6), 1039–1055 (2013)
Rovenski, V., Zelenko, L.: Prescribing the positive mixed scalar curvature of totally geodesic foliations. In: Walczak, P., et al. (eds.) Foliations 2012, pp. 163–203. World Scientific, Hackensack (2013)
Rovenski, V., Zelenko, L.: Prescribing the mixed scalar curvature of a foliation. In: Rovenski, V., Walczak, P. (eds.) Geometry and Its Applications. Springer Proceedings in Mathematics & Statistics, vol. 72, pp. 83–123. Springer, Cham (2014)
Schweitzer, P., Walczak, P.G.: Prescribing mean curvature vectors for foliations. Illinois J. Math. 48(1), 21–35 (2004)
Takagi, R., Yorozu, S.: Minimal foliations on Lie groups. Tohoku Math. J. 36(4), 541–554 (1984)
Walczak, P.G.: An integral formula for a Riemannian manifold with two orthogonal complementary distributions. Colloq. Math. 58(2), 243–252 (1990)
Wang, G., Zhang, Y.: A conformal integral invariant on Riemannian foliations. Proc. Amer. Math. Soc. 141(4), 1405–1414 (2013)
Zhang, W.: Dirac operators on foliations: the Lichnerowicz inequality (2012). arXiv:1204.2224
Author information
Authors and Affiliations
Corresponding author
Appendix: Elliptic equation with parameter
Appendix: Elliptic equation with parameter
Let  be the product with a compact leaf F, and
be the product with a compact leaf F, and  a leafwise Riemannian metric (i.e., on
a leafwise Riemannian metric (i.e., on  for \(q\in {\mathbb R}^n\)) such that the volume form of the leaves
for \(q\in {\mathbb R}^n\)) such that the volume form of the leaves  depends on \(x\in F\) only (e.g., the leaves are minimal submanifolds, see Sect. 2). This assumption simplifies arguments used in the proof of Lemma 4.2, etc. (we consider products
depends on \(x\in F\) only (e.g., the leaves are minimal submanifolds, see Sect. 2). This assumption simplifies arguments used in the proof of Lemma 4.2, etc. (we consider products  and
and  instead of infinite-dimensional vector bundles over \({\mathbb R}^n\)), on the other hand, it is sufficient for proof of the geometric results. The Laplacian in a local chart (U, x) on \((F,g_{|\mathscr {F}})\) is written as
instead of infinite-dimensional vector bundles over \({\mathbb R}^n\)), on the other hand, it is sufficient for proof of the geometric results. The Laplacian in a local chart (U, x) on \((F,g_{|\mathscr {F}})\) is written as  , see [2] with opposite sign. This defines a self-adjoint elliptic operator \(-\mathrm{\Delta }_q\), where \(q\in {\mathbb R}^n\) is a parameter and \(\mathrm{\Delta }_0=\mathrm{\Delta }\),
, see [2] with opposite sign. This defines a self-adjoint elliptic operator \(-\mathrm{\Delta }_q\), where \(q\in {\mathbb R}^n\) is a parameter and \(\mathrm{\Delta }_0=\mathrm{\Delta }\),

Here  are smooth functions in
are smooth functions in  . The Schrödinger operator
. The Schrödinger operator  acts (and is self-adjoint) in the Hilbert space \(L_2\) with the domain \(H^2\). Denote
acts (and is self-adjoint) in the Hilbert space \(L_2\) with the domain \(H^2\). Denote  and
and  for any \(q\in {\mathbb R}^n\).
for any \(q\in {\mathbb R}^n\).
1.1 The Schrödinger operator
If B and C are Banach spaces with norms  and
and  , denote by \(\mathfrak {B}^r(B,C)\) the Banach space of all bounded r-linear operators \(A:\prod _{i=1}^r B\rightarrow C\) with the norm
, denote by \(\mathfrak {B}^r(B,C)\) the Banach space of all bounded r-linear operators \(A:\prod _{i=1}^r B\rightarrow C\) with the norm

If \(r=1\), we shall write \(A:B\rightarrow C\) and \(\mathfrak {B}(B,C)\), and if \(B=C\) we shall write \(\mathfrak {B}^r(B)\) and \(\mathfrak {B}(B)\), respectively. If M is a k-regular manifold or an open neighborhood of the origin in a real Banach space, and N is a real Banach space, we denote by \(C^k(M,N)\), \(k\ge 1\), the Banach space of all \(C^k\)-regular functions \(f:M\rightarrow N\), for which the following norm is finite:

We shall use the simplified version of
Banach Closed Graph Theorem If a linear operator \(A:B\rightarrow C\) (of Banach spaces B and C) is bijective and bounded, then its inverse \(A^{-1}:C\rightarrow B\) is also bounded.
Lemma 4.1
Let \(\beta \in C^\infty \) and  . Then
. Then
-
(i)
\({\mathscr {H}}-\mu \) acts from \(H^2\) into \(L_2\), it is continuously invertible and the inverse operator \(({\mathscr {H}}-\mu )^{-1}:L_2\rightarrow L_2\) is compact;
-
(ii)
for any \(k\in {\mathbb N}\) the operator \({\mathscr {H}}_k-\mu \) acts from \(H^{k+2}\) into \(H^k\), it is continuously invertible and \(({\mathscr {H}}_k-\mu )^{-1}:H^k\rightarrow H^k\) is compact;
-
(iii)
for any integer \(k\ge 0\) the spectrum of \({\mathscr {H}}_k\), acting in \(H^k\) with the domain \(H^{k+2}\), is discrete, and it coincides with the spectrum \(\sigma ({\mathscr {H}})\);
-
(iv)
for any integer \(k\ge 0\) and \(\lambda \notin \sigma ({\mathscr {H}})\) we have
 (38)
(38) (39)
(39)
Proof
(i) Clearly, there exists \(C>0\) such that for any \(u\in H^2\) we have

Thus, \({\mathscr {H}}-\mu \in \mathfrak {B}(H^2,L_2)\). On the other hand, since \(\beta (x)+\mu <0\), the operator \({\mathscr {H}}-\mu \) is positive definite as acting in \(L_2\) with the domain \(H^2\); hence, it is continuously invertible, i.e., \(\mu \notin \sigma ({\mathscr {H}})\). Thus, \({\mathscr {H}}-\mu \) maps \(H^2\) injectively onto \(L_2\). By the Banach Closed Graph Theorem, \({\mathscr {H}}-\mu :H^2\rightarrow L_2\) has a bounded inverse. Compactness of the embedding \(H^2\hookrightarrow L_2\) yields compactness of \(({\mathscr {H}}-\mu )^{-1}:H^k\rightarrow H^k\).
(ii) For any \(u\in H^{k+2}\) a similar to (40) estimate holds with \(H^k\) and \(H^{k+2}\) instead of \(L_2\) and \(H^2\), respectively. Hence,  . By (i), \({\mathscr {H}}-\mu :H^2\rightarrow L_2\) is bijective, and by the Elliptic Regularity Theorem, \(({\mathscr {H}}-\mu )^{-1}(H^k)\subseteq H^{k+2}\) holds. Hence, \({\mathscr {H}}_k-\mu :H^{k+2}\rightarrow H^k\) is bijective, too. Thus, the Banach Closed Graph Theorem and the compactness of the embedding \(H^{k+2}\hookrightarrow H^k\) complete the proof of (ii).
. By (i), \({\mathscr {H}}-\mu :H^2\rightarrow L_2\) is bijective, and by the Elliptic Regularity Theorem, \(({\mathscr {H}}-\mu )^{-1}(H^k)\subseteq H^{k+2}\) holds. Hence, \({\mathscr {H}}_k-\mu :H^{k+2}\rightarrow H^k\) is bijective, too. Thus, the Banach Closed Graph Theorem and the compactness of the embedding \(H^{k+2}\hookrightarrow H^k\) complete the proof of (ii).
(iii) Since for any integer \(k\ge 0\) the operator \(({\mathscr {H}}_k-\mu )^{-1}:H^k\rightarrow H^k\) is compact, its spectrum consists of \(\nu =0\) and a countable number of non-zero eigenvalues \(\nu _n\) of finite multiplicity, which can accumulate only at \(\nu =0\). Hence, the spectrum of \({\mathscr {H}}_k\) on \(H_k\) (with domain in \(H^{k+2}\)) is discrete. Since \({\mathscr {H}}\) extends \({\mathscr {H}}_k\), each eigenfunction of \({\mathscr {H}}_k\) is an eigenfunction of \({\mathscr {H}}\); hence, \(\sigma ({\mathscr {H}}_k)\subseteq \sigma ({\mathscr {H}})\). To show the opposite inclusion, let e(x) be an eigenfunction of \({\mathscr {H}}\), related to \(\lambda \in \sigma ({\mathscr {H}})\) (hence, \(e\in H^2\)). The obvious equality \(e=(\lambda -\nu )^j({\mathscr {H}}-\mu )^{-j}e\) is valid for any \(j\in {\mathbb N}\). Applying (several times) the Elliptic Regularity Theorem, from \(e\in H^{2}\) we obtain that \(e\in H^{k+2}\).
(iv) Similarly to the proof of (ii), we obtain inclusion (38). Let us prove (39). By the well-known property of the resolvent, we have

Take an arbitrary \(\lambda _0\notin \sigma ({\mathscr {H}})\) and choose \(\delta >0\) such that the set  does not intersect \(\sigma ({\mathscr {H}})\). Using the resolvent identity, see [1],
does not intersect \(\sigma ({\mathscr {H}})\). Using the resolvent identity, see [1],

we have the following estimate for \(\lambda \in D_\delta \):

which implies the desired inclusion (39). \(\square \)
1.2 The ground state
We will show smooth dependence on q of the least eigenvalue \(\lambda (q)\) of \(\mathscr {H}_q\) and of the corresponding normalized eigenfunction \(e(x,q)>0\).
Lemma 4.2
If  then for any \(l\in {\mathbb N}\) and integer \(k\ge 0\) the mapping \(\mathfrak {D}:(u,q)\mapsto \mathscr {H}_q(u)\) is a \(C^l\)-morphism (of trivial vector bundles) from \(\mathbb {B}_{k+2}\) into \(\mathbb {B}_k\).
then for any \(l\in {\mathbb N}\) and integer \(k\ge 0\) the mapping \(\mathfrak {D}:(u,q)\mapsto \mathscr {H}_q(u)\) is a \(C^l\)-morphism (of trivial vector bundles) from \(\mathbb {B}_{k+2}\) into \(\mathbb {B}_k\).
Proof
Fix a finite atlas \(\{(U_a,x_a)\}_{1\le a\le A}\) on F, and let \(\{\rho _a(x)\}_{1\le a\le A}\) be a subordinated partition of unity. Taking \(u\in H^{k+2}\), \(q,s\in {\mathbb R}^n\) and using (37), we obtain

in a local chart, where

Hence,

holds for some \(C>0\) that does not depend on u. We conclude that  has the partial Gâteaux differential \(\partial _q\mathfrak {D}(u,q)\) at each point (u, q), and it is equal to
has the partial Gâteaux differential \(\partial _q\mathfrak {D}(u,q)\) at each point (u, q), and it is equal to  . Similarly, for any
. Similarly, for any  , \(i=1,2\), we obtain
, \(i=1,2\), we obtain

and conclude that the partial differential \(\partial _q\mathfrak {D}\) is continuous:

One may prove by induction that for any \(l\in {\mathbb N}\) the mapping  has at any point
has at any point  the partial differential of l-th order \(\partial _q^l \mathfrak {D}(u,q)\), and it has the form
the partial differential of l-th order \(\partial _q^l \mathfrak {D}(u,q)\), and it has the form

in a local chart, and  . Since \(\mathfrak {D}(u,q)\) and \(\partial _q^l\mathfrak {D}(u,q)\) are linear by u, this differential is continuous and \(\mathfrak {D}(u,q)\) has continuous differentials by q and u of any order. \(\square \)
. Since \(\mathfrak {D}(u,q)\) and \(\partial _q^l\mathfrak {D}(u,q)\) are linear by u, this differential is continuous and \(\mathfrak {D}(u,q)\) has continuous differentials by q and u of any order. \(\square \)
Lemma 4.3
Let K be a compact subset of  for some integer \(k\ge 0\). If
for some integer \(k\ge 0\). If  , then there is an open neighborhood \(W\subseteq {\mathbb R}^n\) of the origin such that
, then there is an open neighborhood \(W\subseteq {\mathbb R}^n\) of the origin such that

and the following inclusion holds for any \(l\in {\mathbb N}\):

Proof
The following obvious representation holds for \(\lambda \in K\):

where

Using Lemma 4.2, we get that for any integer \(l\ge 0\),

Taking into account Lemma 4.1 (iv), we have for any  ,
,

Hence, and in view of (45) with \(l=0\), there exists an open neighborhood \(W\subset {\mathbb R}^n\) of the origin such that

Thus, for any  the operator \(\mathrm{id\,}+L(q,\lambda )\in \mathfrak {B}(H^k)\) is continuously invertible and its inverse is expressed by the Neumann series
the operator \(\mathrm{id\,}+L(q,\lambda )\in \mathfrak {B}(H^k)\) is continuously invertible and its inverse is expressed by the Neumann series  converging in the \(\mathfrak {B}(H^k)\)-norm. In view of (43), we conclude that (41) is valid and for any
converging in the \(\mathfrak {B}(H^k)\)-norm. In view of (43), we conclude that (41) is valid and for any  we have
we have

Lemma 4.1 (iv) and (44)–(45) imply  for \(\lambda \in K\) and \(l\in {\mathbb Z}\), and using the resolvent identity, we obtain
for \(\lambda \in K\) and \(l\in {\mathbb Z}\), and using the resolvent identity, we obtain  for \(\lambda ,\mu \in K\). Hence,
for \(\lambda ,\mu \in K\). Hence,

This estimate implies

By [20, Lemma 7] and the arguments in the end of the proof of [20, Lemma 8], and in view of (46) and (48), we get  . Then (47) and Lemma 4.1 (iv) imply the desired inclusion (42). \(\square \)
. Then (47) and Lemma 4.1 (iv) imply the desired inclusion (42). \(\square \)
Theorem 4.4
Let \(\lambda (q)\) be the least eigenvalue of \(\mathscr {H}_q\), \(q\in {\mathbb R}^n\). If  then \(\lambda \in C^\infty ({\mathbb R}^n)\) and there exists a unique smooth section
then \(\lambda \in C^\infty ({\mathbb R}^n)\) and there exists a unique smooth section  such that
such that  is a positive eigenfunction of \(\mathscr {H}_q\) related to \(\lambda (q)\) with
is a positive eigenfunction of \(\mathscr {H}_q\) related to \(\lambda (q)\) with  .
.
Proof
Assume without loss of generality that \(\beta (x,q)<0\) (otherwise we can consider \(\mathscr {H}_q-\mu \) instead of \(\mathscr {H}_q\) with a suitable \(\mu >0\)). Since \(\lambda (q)\) is a simple eigenvalue of \(\mathscr {H}_q\) for any \(q\in {\mathbb R}^n\), there exists a unique positive eigenfunction  , related to it, such that
, related to it, such that  . Let \(\lambda _0\) be the least eigenvalue of the operator \(\mathscr {H}_{0}\) and \(e_0\) be the eigenfunction related to \(\lambda _0\) and satisfying conditions mentioned above. Let \(\mathrm{\Gamma }\) be a circle of small radius in the complex plane \({\mathbb C}\) not intersecting \(\sigma (\mathscr {H}_0)\) and surrounding only \(\lambda _0\). By Lemma 4.3 (with \(k=0\)), one may restrict on the open neighborhood Q of 0 in such a way that
. Let \(\lambda _0\) be the least eigenvalue of the operator \(\mathscr {H}_{0}\) and \(e_0\) be the eigenfunction related to \(\lambda _0\) and satisfying conditions mentioned above. Let \(\mathrm{\Gamma }\) be a circle of small radius in the complex plane \({\mathbb C}\) not intersecting \(\sigma (\mathscr {H}_0)\) and surrounding only \(\lambda _0\). By Lemma 4.3 (with \(k=0\)), one may restrict on the open neighborhood Q of 0 in such a way that  for any \(q\in Q\), and inclusion (42) is valid with \(K=\mathrm{\Gamma }\). Hence, in view of \(H^2\hookrightarrow L_2\), the Riesz projection
for any \(q\in Q\), and inclusion (42) is valid with \(K=\mathrm{\Gamma }\). Hence, in view of \(H^2\hookrightarrow L_2\), the Riesz projection

onto the invariant subspace of \(\mathscr {H}_q\) corresponding to the part of its spectrum lying inside of \(\mathrm{\Gamma }\) [11, Introduction, Section 4] has the property for any \(l\in {\mathbb N}\):

In particular, one may restrict Q in such a way that \(\Vert P(q)-P(0)\Vert _{\mathfrak {B}(L_2)}\le 1/2\) for any \(q\in Q\). Then, taking into account that P(q) are orthogonal projections (since \({\mathscr {H}}_q\) are self-adjoint), we have  , see [1, Chapter III, Section 34]. This means that for \(q\in Q\) the operator \(\mathscr {H}_q\) has inside of \(\mathrm{\Gamma }\) only one simple eigenvalue \(\widetilde{\lambda }(q)\), it is real because \(\mathscr {H}_q\) is self-adjoint,
, see [1, Chapter III, Section 34]. This means that for \(q\in Q\) the operator \(\mathscr {H}_q\) has inside of \(\mathrm{\Gamma }\) only one simple eigenvalue \(\widetilde{\lambda }(q)\), it is real because \(\mathscr {H}_q\) is self-adjoint,  is the eigenspace of \(\mathscr {H}_q\) related to \(\widetilde{\lambda }(q)\), and \(\widetilde{\lambda }(0)=\lambda _0\). Denote
is the eigenspace of \(\mathscr {H}_q\) related to \(\widetilde{\lambda }(q)\), and \(\widetilde{\lambda }(0)=\lambda _0\). Denote  . We have for any \(q\in Q\),
. We have for any \(q\in Q\),

Thus, \(\widetilde{e}(x,q)\) is an eigenvector of \(\mathscr {H}_q\) related to \(\widetilde{\lambda }(q)\) such that \(\widetilde{e}(x,0)=e_0(x)\). By (50),

for any \(l\in {\mathbb N}\). Then the equality  and Lemma 4.3 (with \(k=0\) and \(K=\{0\}\)) imply that \(\widetilde{\lambda }\in C^\infty (Q,{\mathbb R})\).
and Lemma 4.3 (with \(k=0\) and \(K=\{0\}\)) imply that \(\widetilde{\lambda }\in C^\infty (Q,{\mathbb R})\).
Take an arbitrary \(m\in {\mathbb N}\) and set \(j=[p/4+m/2]+1\). Since the equality  is valid, then in view of (51) and Lemma 4.3, we can restrict Q in such a way that
is valid, then in view of (51) and Lemma 4.3, we can restrict Q in such a way that  for any \(l\in {\mathbb N}\). On the other hand, by the Sobolev Embedding Theorem, \(H^{2j}\hookrightarrow C^m\), see [2]. Thus, for any \(m\in {\mathbb N}\) there is an open neighborhood Q of 0 such that
for any \(l\in {\mathbb N}\). On the other hand, by the Sobolev Embedding Theorem, \(H^{2j}\hookrightarrow C^m\), see [2]. Thus, for any \(m\in {\mathbb N}\) there is an open neighborhood Q of 0 such that  . In particular, since \(e_0>0\), we can restrict Q in such a way that
. In particular, since \(e_0>0\), we can restrict Q in such a way that  for any \(q\in Q\). Clearly, e(x, q) is an eigenfunction of \(\mathscr {H}_q\), related to the eigenvalue \(\widetilde{\lambda }_q\) and
for any \(q\in Q\). Clearly, e(x, q) is an eigenfunction of \(\mathscr {H}_q\), related to the eigenvalue \(\widetilde{\lambda }_q\) and  . It remains only to show that it is possible to restrict Q in such a way that \(\widetilde{\lambda }(q)\) is the least eigenvalue of \(\mathscr {H}_q\) for any \(q\in Q\), i.e., \(\widetilde{\lambda }(q)=\lambda (q)\). Indeed, otherwise there is a sequence \(q_\nu \in Q\) such that \(\lim _{\nu \rightarrow \infty }q_\nu =0\) and for any \(\nu \) there exists an eigenvalue \(\widetilde{\lambda }_\nu \) of \(\mathscr {H}_{q_\nu }\) obeying \(\widetilde{\lambda }_\nu <\widetilde{\lambda }(q_\nu )\). Since the operators \(\mathscr {H}_{q_\nu }\) are positive definite and for some \(\delta >0\) in the interval \((\lambda _0-\delta ,\lambda _0+\delta )\) there is only the eigenvalue \(\widetilde{\lambda }(q_\nu )\) of \(\mathscr {H}_{q_\nu }\), we get \(\widetilde{\lambda }_\nu \in [0,\lambda _0-\delta ]\) for any \(\nu \). Let \(\lambda _*\in [0,\lambda _0-\delta ]\) be a concentration point of the sequence \(\{\widetilde{\lambda }_\nu \}_{\nu \in {\mathbb N}}\). Choosing a subsequence, we can assume that \(\lim _{\nu \rightarrow \infty }\widetilde{\lambda }_\nu =\lambda _*\). Surrounding \(\lambda _*\) by a small enough circle \(\mathrm{\Gamma }\) such that \(\mathrm{\Gamma }\cap [\lambda _0,\infty )=\emptyset \), considering for each \(\nu \) the Riesz projection
. It remains only to show that it is possible to restrict Q in such a way that \(\widetilde{\lambda }(q)\) is the least eigenvalue of \(\mathscr {H}_q\) for any \(q\in Q\), i.e., \(\widetilde{\lambda }(q)=\lambda (q)\). Indeed, otherwise there is a sequence \(q_\nu \in Q\) such that \(\lim _{\nu \rightarrow \infty }q_\nu =0\) and for any \(\nu \) there exists an eigenvalue \(\widetilde{\lambda }_\nu \) of \(\mathscr {H}_{q_\nu }\) obeying \(\widetilde{\lambda }_\nu <\widetilde{\lambda }(q_\nu )\). Since the operators \(\mathscr {H}_{q_\nu }\) are positive definite and for some \(\delta >0\) in the interval \((\lambda _0-\delta ,\lambda _0+\delta )\) there is only the eigenvalue \(\widetilde{\lambda }(q_\nu )\) of \(\mathscr {H}_{q_\nu }\), we get \(\widetilde{\lambda }_\nu \in [0,\lambda _0-\delta ]\) for any \(\nu \). Let \(\lambda _*\in [0,\lambda _0-\delta ]\) be a concentration point of the sequence \(\{\widetilde{\lambda }_\nu \}_{\nu \in {\mathbb N}}\). Choosing a subsequence, we can assume that \(\lim _{\nu \rightarrow \infty }\widetilde{\lambda }_\nu =\lambda _*\). Surrounding \(\lambda _*\) by a small enough circle \(\mathrm{\Gamma }\) such that \(\mathrm{\Gamma }\cap [\lambda _0,\infty )=\emptyset \), considering for each \(\nu \) the Riesz projection  , defined by the rhs of (49) with \(q=q_\nu \) and using the above arguments, we get that
, defined by the rhs of (49) with \(q=q_\nu \) and using the above arguments, we get that  , where \(\widetilde{P}(0)\) is defined by the rhs of (49) with \(q=0\). Since \(q_\nu \) lies inside \(\mathrm{\Gamma }\) for a large enough \(\nu \), \(\dim \mathrm {Im} P(0)>0\). Hence, there is at least one eigenvalue of \(\mathscr {H}_{0}\) inside of \(\mathrm{\Gamma }\). But this is impossible, because \(\lambda _0\) is the least eigenvalue of \(\mathscr {H}_{0}\). \(\square \)
, where \(\widetilde{P}(0)\) is defined by the rhs of (49) with \(q=0\). Since \(q_\nu \) lies inside \(\mathrm{\Gamma }\) for a large enough \(\nu \), \(\dim \mathrm {Im} P(0)>0\). Hence, there is at least one eigenvalue of \(\mathscr {H}_{0}\) inside of \(\mathrm{\Gamma }\). But this is impossible, because \(\lambda _0\) is the least eigenvalue of \(\mathscr {H}_{0}\). \(\square \)
1.3 Solution of the stationary equation
Consider the compact domain in 

where \(u_-,u_+\in C^\infty \) and \(u_-\le u_+\). Define sets  for \(k>0\), where \(G\subset C\) is a bounded, closed and convex set given by
for \(k>0\), where \(G\subset C\) is a bounded, closed and convex set given by

Lemma 4.5
Let \(m,l\in {\mathbb N}\), \(\mathrm{\Pi }\) be an open domain in  of the form
of the form  , and
, and  be a continuous function. Then for any \(q\in {\mathbb R}^n\) the superposition operator \({\Theta }(v,q)(x)=\theta (v(x),x,q)\) maps the set
be a continuous function. Then for any \(q\in {\mathbb R}^n\) the superposition operator \({\Theta }(v,q)(x)=\theta (v(x),x,q)\) maps the set

into the set \(C(F,{\mathbb R}^l)\), and the inclusion  holds.
holds.
Proof
The first claim is obvious. Let us prove the second one. Suppose that \(v_0\in Y\). Consider the set \(\mathrm{\Gamma }(v_0)=\{(v_0(x),x)\}_{x\in F}\). Take a relatively compact open set \({Q}\subset {\mathbb R}^n\) such that \(0\in {Q}\). In order to construct a similar open neighborhood of the set \(\mathrm{\Gamma }(v_0)\), observe that it is compact in \(\mathrm{\Pi }\). Then there is a finite open covering \(\{U_j\}_{j=1}^k\) of \(\mathrm{\Gamma }(v_0)\) such that \(\overline{U_j}\subset \mathrm{\Pi }\), \(1\le j\le k\), and each of \(\overline{U_j}\) is compact. Consider the open set \(\mathrm{\Pi }'=\bigcup _{j=1}^k U_j\). Then \(\mathrm{\Gamma }(v_0)\subset \mathrm{\Pi }'\), \(\overline{\mathrm{\Pi }'}=\bigcup _{j=1}^k\overline{U_j}\subset \mathrm{\Pi }\) and the set \(\overline{\mathrm{\Pi }'}\) is compact. Consider the following open subset of \(C(F,{\mathbb R}^m)\):

It is clear that \(v_0\in Y'\). Since \(\theta (u,x,q)\) is uniformly continuous on the compact  , for any \(\varepsilon >0\) there is \(\delta >0\) such that \(|\theta (v_1,x,q)-\theta (v_2,x,0)|<\varepsilon \) for all \((v_1,x),(v_2,x)\in \overline{\mathrm{\Omega }'}\) and \(q\in \overline{{Q}'}\), where \(\Vert v_1-v_2\Vert <\delta \) and \(\Vert q\Vert <\delta \). Let us choose \(\sigma \in (0,\delta )\) such that \(B_\sigma (v_0)=\{v\in C(F,{\mathbb R}^m):\Vert v-v_0\Vert _{C(F,{\mathbb R}^m)}<\sigma \}\subset Y'\). If \(v\in B_\sigma (u_0)\) and \(\Vert q\Vert <\delta \) then \(\Vert {\Theta }(u,q)-{\Theta }(u_0,0)\Vert _{C(F,{\mathbb R}^l)}<\varepsilon \) holds. \(\square \)
, for any \(\varepsilon >0\) there is \(\delta >0\) such that \(|\theta (v_1,x,q)-\theta (v_2,x,0)|<\varepsilon \) for all \((v_1,x),(v_2,x)\in \overline{\mathrm{\Omega }'}\) and \(q\in \overline{{Q}'}\), where \(\Vert v_1-v_2\Vert <\delta \) and \(\Vert q\Vert <\delta \). Let us choose \(\sigma \in (0,\delta )\) such that \(B_\sigma (v_0)=\{v\in C(F,{\mathbb R}^m):\Vert v-v_0\Vert _{C(F,{\mathbb R}^m)}<\sigma \}\subset Y'\). If \(v\in B_\sigma (u_0)\) and \(\Vert q\Vert <\delta \) then \(\Vert {\Theta }(u,q)-{\Theta }(u_0,0)\Vert _{C(F,{\mathbb R}^l)}<\varepsilon \) holds. \(\square \)
Lemma 4.6
Let  . Then the superposition operator
. Then the superposition operator

obeys  for any integers \(k,l\ge 0\).
for any integers \(k,l\ge 0\).
Proof
This is divided into two steps.
Step 1. First, we shall reduce the operator (52), acting from \(G^k\) into \(C^k\) to a superposition operator, acting in spaces of continuous vector functions. Take  for some \(k\in {\mathbb N}\). Observe that differentials \(d^ju(x)\), \(1\le j\le k\), can be considered as functions defined on F with values in \({\mathbb R}^{n_j}\) (e.g., \(n_1=p\), \(n_2=p(p+1)/2\) and so on). We have the following:
for some \(k\in {\mathbb N}\). Observe that differentials \(d^ju(x)\), \(1\le j\le k\), can be considered as functions defined on F with values in \({\mathbb R}^{n_j}\) (e.g., \(n_1=p\), \(n_2=p(p+1)/2\) and so on). We have the following:

and so on. Hence,

where \(v(x)=(du(x),d^2u(x),\ldots ,d^ku(x),u(x))\) is the vector function on F, and the function  is smooth. Here
is smooth. Here  and \(N=1+\sum _{j=1}^kn_j\). It is enough to show that the superposition operator \(\mathrm{\Psi }(v,q)=\psi (v(x),x,q)\) obeys
and \(N=1+\sum _{j=1}^kn_j\). It is enough to show that the superposition operator \(\mathrm{\Psi }(v,q)=\psi (v(x),x,q)\) obeys

for any \(l\in {\mathbb N}\), where \(X=\{v\in C(F,{\mathbb R}^N):(v(x),x)\in \mathrm{\Omega }, x\in F\}\).
Step 2. In aim to prove (53), take \(v\in X\), \(q\in {\mathbb R}^n\), \(h\in C(F,{\mathbb R}^N)\) and \(\delta >0\) such that \(u+th\in X\) for any \(t\in [0,\delta ]\). We have the following representation for \(t\in [0,\delta ]\):

Hence,

Since for any fixed \(q\in {\mathbb R}^n\) the function  is uniformly continuous in
is uniformly continuous in  , the last estimate implies
, the last estimate implies

Hence, for any \(q\in {\mathbb R}^n\) the operator  has at any \(u\in X\) the Gâteaux partial differential \(\partial _v\mathrm{\Psi }(v,q)\) of the form
has at any \(u\in X\) the Gâteaux partial differential \(\partial _v\mathrm{\Psi }(v,q)\) of the form

We see that \(\partial _v\mathrm{\Psi }(v,q)\in \mathfrak {B}(C(F,{\mathbb R}^N))\) and

By Lemma 4.5 applied to the superposition operator,
the partial differential \(\partial _v\mathrm{\Psi }(v,q)\) is continuous in the sense that  . Hence, \(\partial _v\mathrm{\Psi }(v,q)\) is the Fréchet partial differential. Similarly, one may show that at any
. Hence, \(\partial _v\mathrm{\Psi }(v,q)\) is the Fréchet partial differential. Similarly, one may show that at any  there is the Gâteaux partial differential
there is the Gâteaux partial differential

where \(s\in {\mathbb R}^n\), and the limit is taken with respect to the \(C(F,{\mathbb R}^N)\)-norm. Furthermore, this differential is continuous: \(. \) Again, this fact implies that \(\partial _q\mathrm{\Psi }(v,q)\) is the Fréchet partial differential. Thus, we have proved that the superposition operator \(\mathrm{\Psi }(v,q)(x)=\psi (v(x),x,q)\) belongs to class  . Applying similar arguments to superposition operators
. Applying similar arguments to superposition operators
one may show that  . Further, we can prove by induction that (53) holds for any \(l\in {\mathbb N}\). \(\square \)
. Further, we can prove by induction that (53) holds for any \(l\in {\mathbb N}\). \(\square \)
Lemma 4.7
Let \(\mathrm{\Delta }_q\) be the elliptic operator in (37). Then for any \(l\in {\mathbb N}\) the mapping  belongs to class
belongs to class  .
.
Proof
Fix a finite atlas \(\{(U_a,x_a)\}_{1\le a\le A}\) of F. Taking \(u\in C^{k+2,\alpha }\), \(q\in {\mathbb R}^n\) and \(s\in {\mathbb R}^n\), we obtain in a local chart, see (37):

where  . In view of (17),
. In view of (17),

holds for some \(C_a>0\) that does not depend on u. Replacing \(C_a\) by \(C=\max _{1\le a\le A} C_a\), we find that  has the partial Gâteaux differential \(\partial _q\mathfrak {D}(u,q)\) at each point (u, q), and it is equal to \(\mathfrak {D}_1(u,q)\). Similarly to the proof of Lemma 4.2, we obtain that \(\mathfrak {D}\) has continuous mixed partial differentials by q and x (of any order) at any point
has the partial Gâteaux differential \(\partial _q\mathfrak {D}(u,q)\) at each point (u, q), and it is equal to \(\mathfrak {D}_1(u,q)\). Similarly to the proof of Lemma 4.2, we obtain that \(\mathfrak {D}\) has continuous mixed partial differentials by q and x (of any order) at any point  . \(\square \)
. \(\square \)
Theorem 4.8
Let  and
and  be a smooth solution of (34) with \(q=0\) such that \(\lambda =0\) is not an eigenvalue of the operator
be a smooth solution of (34) with \(q=0\) such that \(\lambda =0\) is not an eigenvalue of the operator  on \(L_2\) with domain in \(H^2\). Then for any integers \(k\ge 0\) and \(l\ge 1\) and \(\alpha \in (0,1)\) there are open neighborhoods \(U_*\subseteq C^{k+2,\alpha }\) of \(u_*\) and \(V_0\subseteq {\mathbb R}^n\) of \(\,0\) such that for any \(q\in V_0\) there exists in \(U_*\) a unique solution u(x, q) of (34), in particular, \(u_*(x)=u(x,0)\), such that the function
on \(L_2\) with domain in \(H^2\). Then for any integers \(k\ge 0\) and \(l\ge 1\) and \(\alpha \in (0,1)\) there are open neighborhoods \(U_*\subseteq C^{k+2,\alpha }\) of \(u_*\) and \(V_0\subseteq {\mathbb R}^n\) of \(\,0\) such that for any \(q\in V_0\) there exists in \(U_*\) a unique solution u(x, q) of (34), in particular, \(u_*(x)=u(x,0)\), such that the function  belongs to class
belongs to class  .
.
Proof
By Lemma 4.6, for any \(q\in {\mathbb R}^n\) and integers \(k,l\ge 0\) the operator (52) maps the set  and
and  . Since \(C^{k+2,\alpha }\) and \(C^{k+2}\) are continuously embedded into \(C^{k+2}\) and \(C^{k,\alpha }\), respectively, we get
. Since \(C^{k+2,\alpha }\) and \(C^{k+2}\) are continuously embedded into \(C^{k+2}\) and \(C^{k,\alpha }\), respectively, we get  , where
, where  . Consider operators
. Consider operators  , \(q\in {\mathbb R}^n\), defined on \(G_{k+2,\alpha }\). By Lemma 4.7,
, \(q\in {\mathbb R}^n\), defined on \(G_{k+2,\alpha }\). By Lemma 4.7,  Let \(\widetilde{\mathscr {H}}\) be \({\mathscr {H}}\) restricted on \(C^{k,\alpha }\) with the domain \(C^{k+2,\alpha }\). Set \(\beta =\partial _u f(u_*(x),x,0)\). By (17), there is \(C>0\) such that \(\Vert \mathrm{\Delta } u\Vert _{C^{k,\alpha }}\le C\Vert u\Vert _{C^{k+2,\alpha }}\) for any \(u\in C^{k+2,\alpha }\); hence,
Let \(\widetilde{\mathscr {H}}\) be \({\mathscr {H}}\) restricted on \(C^{k,\alpha }\) with the domain \(C^{k+2,\alpha }\). Set \(\beta =\partial _u f(u_*(x),x,0)\). By (17), there is \(C>0\) such that \(\Vert \mathrm{\Delta } u\Vert _{C^{k,\alpha }}\le C\Vert u\Vert _{C^{k+2,\alpha }}\) for any \(u\in C^{k+2,\alpha }\); hence,  . Let
. Let  . By [2, Theorem 4.18], \({\mathscr {H}}(u)-\mu u=f(x)\) has a unique solution \(u\in C^{k+2,\alpha }\) for any \(f\in C^{k,\alpha }\), i.e., \(\widetilde{\mathscr {H}}-\mu \) maps \(C^{k+2,\alpha }\) injectively onto \(C^{k,\alpha }\). As in the proof of Lemma 4.1 (i), using the Banach Closed Graph Theorem and compactness of the embedding \(C^{k+2,\alpha }\hookrightarrow C^{k,\alpha }\), we prove that \(\widetilde{\mathscr {H}}-\mu \) is continuously invertible and \((\widetilde{\mathscr {H}}-\mu )^{-1}:C^{k,\alpha }\rightarrow C^{k,\alpha }\) is compact.
. By [2, Theorem 4.18], \({\mathscr {H}}(u)-\mu u=f(x)\) has a unique solution \(u\in C^{k+2,\alpha }\) for any \(f\in C^{k,\alpha }\), i.e., \(\widetilde{\mathscr {H}}-\mu \) maps \(C^{k+2,\alpha }\) injectively onto \(C^{k,\alpha }\). As in the proof of Lemma 4.1 (i), using the Banach Closed Graph Theorem and compactness of the embedding \(C^{k+2,\alpha }\hookrightarrow C^{k,\alpha }\), we prove that \(\widetilde{\mathscr {H}}-\mu \) is continuously invertible and \((\widetilde{\mathscr {H}}-\mu )^{-1}:C^{k,\alpha }\rightarrow C^{k,\alpha }\) is compact.
By the above, the spectrum of \((\widetilde{\mathscr {H}}-\mu )^{-1}\) consists of the point \(\nu =0\) and a countable number of non-zero eigenvalues \(\nu _n\) of finite multiplicity, which can accumulate only at the point \(\nu =0\). Hence the spectrum of \(\widetilde{\mathscr {H}}\) is discrete. By Lemma 4.1 (i–iii), \(\sigma ({\mathscr {H}})\) is discrete and \(\mu \notin \sigma ({\mathscr {H}})\). By the same arguments as in the proof of Lemma 4.1 (iii), we find that the spectrum of \(\widetilde{\mathscr {H}}\) is discrete and coincides with \(\sigma ({\mathscr {H}})\).
Let \(\lambda \notin \sigma ({\mathscr {H}})\). Then \(\widetilde{\mathscr {H}}-\lambda \) maps injectively \(C^{k+2,\alpha }\) into \(C^{k,\alpha }\) and it is bounded. By the Elliptic Regularity Theorem, this operator is surjective. By the Banach Closed Graph Theorem, \(\widetilde{\mathscr {H}}-\lambda \) acts from \(C^{k+2,\alpha }\) into \(C^{k,\alpha }\) and it is continuously invertible. Since \(0\notin \sigma ({\mathscr {H}})\), the partial differential is continuously invertible

These facts and the Implicit Function Theorem, see [2], complete the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Rovenski, V., Zelenko, L. The mixed Yamabe problem for foliations. European Journal of Mathematics 1, 503–533 (2015). https://doi.org/10.1007/s40879-015-0061-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-015-0061-5
Keywords
- Foliation
- Riemannian metric
- Harmonic
- Mixed scalar curvature
- Conformal
- Leafwise Schrödinger operator
- Parabolic equation
- Attractor






 ; a solution
; a solution 


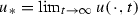 , where u solves (
, where u solves (
 with a smooth leafwise metric
with a smooth leafwise metric  and (
and ( ,
,  .
.
