Introduction

Instabilities at interfaces between two dissimilar materials such as the Kelvin–Helmholtz (KHI) , Rayleigh–Taylor (RTI), and Richtmyer–Meshkov (RMI) instabilities are important in a number of physical phenomena and man-made applications. While the KHI is driven by shearing of the interface, both RTI and RMI are controlled by normal loading of the interface. RTI is characterized by acceleration loading of the interface with the lighter material driven into the denser material, while RMI is characterized by a shock propagating across the interface with the materials in either orientation. In real applications, these instabilities often occur simultaneously, sequentially, or at different length scales, but in the laboratory efforts are usually made to isolate only one. Zhou [1, 2] has comprehensively reviewed RTI and RMI, while Brouillette [3] provides a review of RMI, focusing on fluids and gases. A thorough mathematical treatment of the KHI can be found in Friedlander and Lipton-Lifschitz [4], and its role in explosive welding is reviewed by Carpenter and Wittman [5]. Finally, Bakhrakh et al. [6] provides a review of work performed on these three instabilities in the former Soviet Union.

While these instabilities are of interest because of their importance to other phenomena and applications, they have also been exploited as a means to probe material behavior since their evolution is affected by properties such as viscosity, surface tension, and, of particular interest here, strength. Early work by Barnes et al. [7, 8] examined the evolution of RTI in solid samples driven by explosive products. Similar work has continued [9,10,11], and the approach has been extended to laser-drive configurations to reach higher pressures (c.f. Remington et al. [12]). The RMI has also been used as a means to “measure” material strength [13,14,15,16,17,18]. We use the term measure to denote the process of estimating strength from an RMI experiment through analytical expression or simulation calibrated to experimental measurements. Mikhailov [19] provides a nice overview of the use of instabilities to study material behavior in the former Soviet Union and Russia.

The paper is laid out as follows. “The Richtmyer–Meshkov Instability” section provides an overview of the RMI and reviews previous work on it. In “Analysis Methods” section, the details of the modeling approach are given, while “Simulation Results” section provides results from simulations exploring the sensitivities of the tamped RMI configuration. “Scaling” section presents results for a large ensemble of simulations that are used to study scaling relationships for tamped RMI. In “Relationship to Experiments” section, we discuss implications for experiments that are drawn from the simulations in “Simulation Results” and “Scaling” sections. Finally, conclusions are drawn and recommendations for future work are given in “Conclusions and Future Work” section.

The Richtmyer–Meshkov Instability

In this section, we first define the key terms of the RMI. We then review the previous theoretical, computational, and experimental work for the case where one side of the interface is vacuum. Finally, we examine previous work for systems with two materials that have density of the same order.

Configuration and Terminology

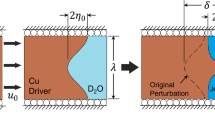
The configuration associated with the RMI is illustrated in Fig. 1. Two materials are in contact with one another. They are denoted 1 and 2 without regard to their properties. We will refer to material 1 as the driver and material 2 as the tamper. The interface between the two materials is assumed to have an imperfection idealized as a sine wave of wavelength \(\lambda\) and initial amplitude \(\eta _{o}\). The severity of the imperfection is described by the non-dimensional product of the amplitude and the wave number (k), which is given by

$$\begin{aligned} k\eta _{o} = \frac{2\pi \eta _{o}}{\lambda }. \end{aligned}$$
(1)

Larger values of \(k\eta _{o}\) promote greater instability. While some treatments of RMI, including the seminal work of Richtmyer [20] assume small perturbations of the interface (\(k\eta _{o} \ll 1\)), none of the cases considered herein satisfy that criterion. A shock of amplitude \(P_{1}\) (ignoring strength effects) propagates from the left at velocity \(U_{1}\) through material 1, bringing it to a mass velocity of \(u_{1}\). Eventually, it reaches the interface and distorts it. Because of the different impedances of the two materials, the material 2 is shocked to pressure \(P_{2}\) and velocity \(u_{2}\), and an unloading or reloading wave propagates back into material 1 taking it to the same pressure and velocity.

A key to the behavior of the interface is the Atwood number, a non-dimensional parameter describing the relative densities of the two materials

$$\begin{aligned} A = \frac{\rho _{2} - \rho _{1}}{\rho _{2} + \rho _{1}}. \end{aligned}$$
(2)

Thus, positive A indicates the shock propagates from a lower density material to a higher density one, while a negative value denotes the converse. As with \(k\eta _{o}\), increased magnitude of A promotes instability development. Note that if material 2 is vacuum, then \(A = -1\), an important case for RMI. If \(\rho _{2} = \rho _{1}\) then \(A = 0\) and there is no driving force for instability development.

Fig. 1
figure 1

Schematic of the initial configuration for an RMI experiment. The shock, shown in red, propagates through the driver, across the interface with the sinusoidal perturbation, and into the tamper (Color figure online)

Full size image

If \(A < 0\) and the factors promoting instability (e.g. \(k\eta _{o}\), \(\mid A\mid\)) are sufficient to outweigh those stabilizing the interface (e.g. viscosity, strength), then the imperfection inverts and material near \(x=0\) from 1 jets into 2. In the literature, such jets are generally referred to as “spikes”, while the regions of the sine wave 180 degrees out of phase are referred to as “bubbles”. This process is examined in more detail in “Baseline Case for \(A<0\)” section. For the case of \(A = -1\), the formation of spikes that ultimately separate leads to the formation of particles referred to as ejecta (c.f. Buttler et al. [21]), but our interest lies elsewhere.

If \(A > 0\), the shock initially causes the amplitude to decrease, but after its passage the amplitude typically increases. However, there is no inversion of the imperfection. Here, we focus on the other case, saving the \(A > 0\) case for future work.

Previous Theoretical and Modeling Work

A few treatments of RMI have been developed for materials with strength. They are generally extensions of solutions for fluids and utilize numerical simulations to provide insight or to calibrate constants. The notation and physical quantities in the formulae developed by the various authors can vary, and there is, at times, some ambiguity about the meaning of certain terms. Nevertheless, the results of these treatments are more alike than they are different.

Some of the first work reported on RMI in solids is that of Piriz et al. [13, 14]. They considered the case of \(A=+1\) and found that the late-time amplitude of the interface imperfection is given by

$$\begin{aligned} k(\eta _{\infty } - \eta _{o}) = 0.29 (k\eta _{o})^{2} \frac{\rho u_{2}^{2}}{Y}, \end{aligned}$$
(3)

where Y is the flow strength of the material. The constant factor was set at 0.29 through comparison to numerical simulations of the RMI configuration.

Dimonte et al. [15] performed simulations of the \(A\approx -1\) case, finding a result for the maximum spike amplitude (ignoring the leading constant term) of

$$\begin{aligned} kh_{sp}^{\infty } = 0.24 \frac{\rho _{1}(u_{sp}^{max})^{2}}{Y_{1}} \end{aligned}$$
(4)

where \(u_{sp}^{max}\) is the maximum spike velocity. For the cases examined, \(u_{sp}^{max}\) can be reasonably approximated as \(k\eta _{o}u_{1}\), so that their result is quite similar to that of Piriz et al. They also provide a limiting criterion for spike arrest: \(\rho _{1}(u_{sp}^{max})^{2}/Y_{1} < 10\pm 1\). If the inequality is not satisfied, then the spike does not arrest and instead breaks up, leading to ejecta.

Both [22] and [23] performed hydrocode simulations of the RMI for \(A=-1\) and found results similar to those of Piriz et al., albeit with slightly different constant prefactors.

Because they considered a range of A, the findings of [24] and [25] are discussed below in “The Case of \(\mid A\mid < 1\)” section.

Previous Experimental Work

While there have been many studies of RMI in liquids and gases (see [3] and references therein), only a small number have been performed with solids to measure strength. Strain rates in these experiments were of order \(10^{7}\) \(\hbox{s}^{-1}\), though strain rates and total strain varied across the regions of the sample. Most were performed into vacuum (\(A = -1\)), with only the work by Olles et al. [26] and Hudspeth et al. [27] involving a tamped configuration (\(A > -1\)); they are discussed in the next section.

Buttler et al. [28] examined jetting of tin and copper, using both proton radiography and laser Doppler interferometry to monitor the growth of the spikes. Although much of their attention was devoted to ejecta characteristics, they found that \(k\eta _{o}\) could be varied to achieve negligible grow of the spikes, spikes that formed and grew but arrested, or spikes that grew without arresting and eventually broke up. They extracted strength values for copper using a relations similar to that of Piriz et al. [13, 14] utilizing the arrested spike length. Although their analysis was based on the assumption of elastic-perfectly plastic behavior, they argued that this is inadequate.

Jensen et al. [16] tested cerium metal, utilizing both high-speed X-ray radiography and interferometry to monitor spike formation and growth. They used the expression of Dimonte et al. [15] to calculate the strength from the measured spike velocity. Measurements from radiography were found to lead to smaller uncertainties than those from interferometry. In their experiments, the cerium samples were cycled through a solid-solid phase transformation but returned to the ambient phase upon release. In a similar study, [29] performed magnetically-driven, cylindrically-convergent RMI experiments on tin using proton radiography. Manipulating the initial shock pressure caused the samples to release into solid, liquid, or mixed states, which affected the spike growth behavior.

Prime et al. studied jetting of copper [17] and tantalum [18] but utilized only interferometry as a diagnostic. They pointed out issues associated with damage and, as a result, adopted peak spike velocity as their metric for evaluating strength. This also permits useful data to be extracted from spikes that do not arrest. By comparison to hydrocode simulations, they were able to extract strengths, though they found that their simulations were also sensitive to both resolution and the artificial viscosity formulation used. In contrast to Buttler et al. [28], they argued that simple elastic–plastic constitutive models were sufficient for simulating the jetting process. Their goal in doing so was to obtain a value of strength for one specific set of conditions that would then be used in the calibration of a more sophisticated constitutive model.

The Case of \(\mid A\mid < 1\)

The studies discussed above all involve one component of the system being vacuum so that \(A = \pm 1\). This leads to the limitation that the results are obtained for zero pressure since most of the plastic deformation occurs after a release wave from the free surface has propagated back into the driver. Adding a tamper to back the driver as shown in Fig. 1 allows the driver to remain at a nonzero pressure. If \(A < 0\), then \(P_{1} > P_{2}\); the converse is true if \(A > 0\)

Though other values of A have been explored in the fluids literature, there are few such reports from the shock physics community. Benjamin and Fritz [30] studied the jetting of Wood’s metal tamped with water (\(A \approx -0.8\)). Wood’s metal is an alloy with a low melting point (70 \(^{\circ }\)C), so the passage of the shock melts it. Thus, this study did not address the issue of strength in a tamped configuration.

The most significant study of tamped RMI is the work reported by Bakhrakh et al. [6] and Mikhailov [19]. They performed explosively-driven RMI experiments with recovery for several metal pairs with values of A ranging from − 0.16 to + 0.22. In Bakhrakh et al. [6], an abrupt loss of stability is attributed to shock melting, but Mikhailov [19] revises that conclusion to indicate that stability is lost well before melting occurs or is lost during release.

A few recent studies [31,32,33] have utilized laser-driven loading for \(0<A<1\). Samples were recovered, and post mortem examination of the imperfection growth was correlated to strength. Both 2-D and 3-D configurations were studied. The length scales in these studies were significantly smaller than in the others discussed, and strain rates were of order \(10^7\,\hbox{s}^{-1}\).

Recently, synchrotron radiation has been utilized to diagnose RMI experiments driven by planar impact. Olles et al. [26] examined copper drivers tamped by deuterated water. Hudspeth et al. [27] utilized the same configuration, but their objective was to probe the strength behavior of the tamper material, a \(\hbox{SiO}_{{2}}\) powder. This was possible because the strength of the copper was independently established in the two studies. Through numerical simulations of the problem, they were able to estimate the strength of the material of interest by matching the spike growth behavior observed experimentally.

Of the theoretical treatments mentioned earlier, only Mikaelian [24] considered the case of arbitrary A. He found that the length of the arrested spikes is given by

$$\begin{aligned} k(\eta _{\infty } - \eta _{o}) = \frac{1}{3} A^{2} (k\eta _{o})^{2} \frac{\overline{\rho }u_{2}^{2}}{\overline{Y}}. \end{aligned}$$
(5)

Here \(\overline{\rho }\) and \(\overline{Y}\), the effective density and strength for the two-material configuration, are given by

$$\begin{aligned} \overline{\rho } = \rho _{1} + \rho _{2}. \end{aligned}$$
(6)

and

$$\begin{aligned} \overline{Y} = Y_{1} + Y_{2}. \end{aligned}$$
(7)

If \(A=-1\) the relationship differs from that of Piriz et al. only in the constant prefactor.

Chen et al. [25] considered the case where material 1 is an elastic–plastic solid and material 2 is a fluid. They arrived at a slightly different relationship for the spike length. Ignoring the elastic term, they find

$$\begin{aligned} k\eta _{max} = F(A) A^{2} (k\eta _{o})^{2} \frac{\rho _{s}u_{2}^{2}}{\overline{Y}}, \end{aligned}$$
(8)

where \(\rho _{s}\) is the density of the solid material and F(A) is given by

$$\begin{aligned} F(A) = \alpha (\beta \mid A\mid + \beta + 2)^{2}. \end{aligned}$$
(9)

The constants \(\alpha\) and \(\beta\) are found to have values of 0.0034 and 3.0374, respectively, through fitting to simulation results. For the case of \(A=-1\), this reduces to a value of 0.222, which is similar to values of 0.24 [15] and 0.22 [22] found previously.

The significantly more complicated cylindrically convergent RMI configuration was examined numerically by Lopez Ortega et al. [34] and Wu et al. [35]. The former performed continuum simulations, while the latter study utilized classical molecular dynamics. While only values of A close to -1 were examined in both studies, corresponding to a dense gas fill, it was shown that the value of A at the solid/gas interface could change dramatically due to the greater compressibility. For the case of \(A=-0.818\) initially, A actually became positive as the shock converged.

Analysis Methods

Simulations of the RMI configuration were conducted using the Sandia hydrocode CTH [36], which is well-suited to treating strong shocks and large deformations in fluids and solids. The simulations were, in general, conducted in the two-dimension (2-D) planar geometry shown in Fig. 1 under plane strain conditions. Because of the periodicity of the problem, rigid boundaries were prescribed at the boundaries at \(x=\pm \lambda /2\) with λ = 2 mm. A flyer plate of material 1 strikes the driver (also material 1) at a velocity V sending a shock wave into it and the tamper. The impactor and tamper are made large to ensure that the interface can evolve without being affected by the boundaries in the y direction. The evolution of the interface is monitored by tracking its position at \(x=0\) (\(y_{s}\)) and \(x=\lambda /2\) (\(y_{b}\)). We define the length of the spike as

$$\begin{aligned} \xi = y_{s}-y_{b}. \end{aligned}$$
(10)

At the beginning of the simulation, \(\xi _{o} = -2\eta _{o}\).

For simplicity, a Mie–Grüneisen [37] equation of state (EOS) with a quadratic \(U_{s}-u_{p}\) form is used for both the driver and the tamper. Parameters for the tantalum (Ta) used as the driver are shown in Table 1. The tamper material is a sodium metatungstate (\(\hbox{Na}_{6}\hbox{[H}_{2}\hbox{W}_{12}\hbox{O}_{40}]\)) solution [38], which is amongst the densest liquids not presenting significant health hazards. Since no EOS information is available for it, the EOS parameters are assumed to be those of water [39] except for the density, where a value of \(3.10\,\hbox{g/cm}^{3}\) is used.

Table 1 Material EOS model parameters used in simulations
Full size table

Strength behavior of the driver is modeled using an elastic-perfectly plastic (EPP) response with yield stress \(Y_{1}\) and Poisson’s ratio \(\nu _{1} = 0.385\). The tamper is generally treated hydrodynamically, though an EPP treatment with strength \(Y_{2}\) is used in some cases. A baseline resolution of 100 cells per wavelength is used; the effect of resolution is examined in “Simulation Resolution” section.

Simulation Results

In this section, we present results for simulations of RMI growth. We consider a specific example and then examine the effect of variations in the model parameters on the simulation results.

Baseline Case for \(A<0\)

In order to illustrate the tamped RMI, we consider a simulation of jetting of Ta into a high-density tamper fluid (\(\hbox{Na}_{{2}}\) \(\hbox{WO}_{{4}}\) solution) as an example. A thick Ta impactor traveling at 2 km/s strikes the Ta driver with an initial perturbation given by \(k\eta _{o} = 0.63\). The Ta driver is tamped by a high-density liquid with EOS properties given in “Analysis Methods” section. The resulting Atwood number is \(A = -0.69\). For simplicity, an elastic-perfectly plastic strength model with \(Y=0.75\) GPa is used for the Ta, and the tamper is treated hydrodynamically (i.e. no strength). Results that are qualitatively similar are obtained if a more physically-motivated strength model such as the PTW model [40] is used, though different empirical and semi-empirical models calibrated for Ta were found to give different values of the arrested spike length.

Images from a simulation of this configuration with an impact velocity of 2 km/s are shown in Fig. 2. Rows of Lagrangian tracers at increasing distance from the edge of the Ta driver are used to illustrate its deformation. By the second image at 0.5 μs after impact, the shock has traveled into the tamper, accelerating the trough of the sine wave in the Ta so that the interface is nearly flat. By the third image at 1.0 μs, the sine wave has inverted so that the Ta has jetted into the tamper. Because material has flowed inward to form the spike, the vertical tracer spacing decreases as the horizontal spacing increases. The two rightmost lines of tracers bulge outward significantly, but the center part of the other two bulge slightly to the left. In the fourth and fifth images at 1.5 and 2.0 μs, this pattern persists as the front region of the spike stretches only minimally. However, the material outside the spike continues to shear, leading to additional distortion of the tracer pattern.

Fig. 2
figure 2

Images of a simulation of Ta impactor (dark) impacting a Ta driver (light), which jets into a high-density liquid tamper (medium). Tracer particles are shown in the driver to illustrate the deformation patterns. Images are shown for the a initial state and at b 0.5 μs, c 1.0 μs, d 1.5 μs, and e 2.0 μs after impact

Full size image

The evolution of the spike amplitude for the simulation shown in Fig. 2 is shown in Fig. 3a. The spike amplitude grows with a gradually decreasing rate. The spike is seen to arrest with an amplitude of about 0.91 mm. The velocity histories for the spike and bubble are shown in Fig. 3b. Both initially experience a strong shock at nearly the same time. Following that, the velocity of the spike (bubble) increases (decrease) to a maximum (minimum) and gradually falls (increases), in most cases, to a value close to the initial shock amplitude.

Fig. 3
figure 3

Results from simulations with the strength varied: a spike amplitude evolution and b spike and bubble velocity histories

Full size image

The spike growth process illustrated in Fig. 2 is complex, involving large deformations and high strain rates at elevated pressures. Here, we examine that process and quantify the factors of strain, strain rate, and pressure. In the simulation, we distribute a 20 × 20 grid of Lagrangian tracers similar to the arrangement shown in Fig. 2 over the region within \(\lambda /2\) of the driver/tamper interface. The Lagrangian tracer points move with the material as it deforms, and we track the pressure and plastic strain rate at each of those points, recording those values at a fixed time interval of 5 ns. For each time step, we assume that the strain rate is constant so that the increment in plastic strain can be taken to be:

$$\begin{aligned} \varDelta \epsilon _{p} = \varDelta t \dot{\epsilon }_{p}. \end{aligned}$$
(11)

The total plastic strain can be found by summing the increments from Eq. 11 over time. Strains at individual points as high as 2.0 are found, though the strain levels generally decay away from the driver/tamper interface. For comparison, if the interface perturbation is not present, then the total plastic strain for a specific point from the initial shock and the release from the tamper is approximately 0.25, significantly less than for the regions deforming the most in the RMI configuration.

The strain rates associated with the initial shock in the driver are calculated to be over \(10^{7}\) \(\hbox{s}^{-1}\), but that value is not physically meaningful since it is largely determined by the resolution of the simulation and the artificial viscosity used to spread the shock front. The real strain rates are probably even higher, though how high is unclear because of the difficulties in resolving high-pressure shock rise times and a lack of data on tantalum. Crowhurst et al. [41] reported strain rates of order \(10^{10}\hbox{ s}^{-1}\) in aluminum shocked to around 40 GPa. In the planar case, a release wave will propagate from the driver/buffer interface, eventually unloading the driver and impactor to \(P_{2}\). Since the release wave forms a rarefaction fan as it propagates, the strain rate will decrease as the distance from the tamper interface increases. At 1 mm from the interface, this results in strain rates of the order of \(10^{6}\) \(\hbox{s}^{-1}\).

To quantify the states at which the plastic strain occurs in the RMI simulation, we bin the increments in plastic strain for all 400 tracer points (Eq. 11) according to the values of pressure and strain rate at which they occur and plot them in Fig. 4. Since we are using an elastic-perfectly plastic constitutive model and the tracers are equally spaced initially, the plastic strain value shown in the plot is proportional to the plastic work done in the region of interest. There are three main features seen in the plot. The large arc going from zero pressure to \(\sim\)75 GPa and reaching a strain rate of \(1.3 \times 10^{7}\) \(\hbox{s}^{-1}\) results from the arrival of the initial shock as discussed above. The second, smaller arch from \(\sim\)75 to \(\sim\)35 GPa at strain rates around \(10^{6}\) \(\hbox{s}^{-1}\) is from the release when the shock reaches the tamper. Both these features are found in simulations where the interface perturbation is not present. The third feature, the pronounced spike in accumulated plastic strain, is due to the growth of the spike in the RMI configuration. As seen in the inset, its peak is at approximately 24 GPa and a plastic strain rate of about \(10^{5}\) \(\hbox{s}^{-1}\). Clearly, the vast majority of the plastic deformation due to the RMI occurs at or near those conditions. Thus, even though a wide range pressures and strain rates occur in the RMI configuration, assigning a specific pressure and strain rate for the purposes of calibration of a strength model is not unreasonable. Further, this observation supports the use of an EPP strength model for simulations used to estimate an average strength, with that strength value then used to calibrate more complex strength models for those conditions. However, if the spikes exhibit significantly less growth than seen here, this approach would be less appropriate since the plastic strain due to the RMI configuration would be less dominate. While the pressure and strain rate are relatively constant, there is some temperature rise due to plastic work: peak temperatures of about 1400 K are estimated. Significant work hardening of the material would also complicate usage of RMI results to calibrate a constitutive model. If that model is then used for a problem where there is significantly different work hardening than the RMI because the overall strain level is much lower or higher, then some error will be introduced. Finally, we note that there is no significant accumulation of plastic strain at negative pressures, but there are regions that do develop them despite the tamper. The effect of damage in those regions will be examined in “The Role of Damage” section.

Fig. 4
figure 4

Accumulated plastic strain from the volume within \(\lambda /2\) of the driver/tamper interface plotted against the pressure and plastic strain rate at which it occurs. The inset shows a close-up view of the region of peak accumulated strain

Full size image

Sensitivity to Strength

In the following sections, we examine the sensitivity of spike growth to the simulation parameters. Since this paper focuses on the role of strength in tamped RMI, we examine that aspect first in Fig. 3. Results for spike amplitude from EPP simulations are shown in Fig. 3a. Strength values of \(Y_{1} \approx 0.75\) GPa and greater result in spike arrest, and for the highest values of \(Y_{1}\) the spike region barely inverts. Spike and bubble velocity histories for those same strength values are shown in Fig. 3b. The maximum value of the spike velocity decreases as Y increases, and the velocity decays more rapidly to the equilibrium value with increased Y as well.

In the tamped RMI configuration, both the driver and tamper can be fluid or have strength. Mikaelian [24] suggested that the sum of the strengths of the two materials is the relevant parameter. In Fig. 5 we show results for three ways of distributing the strength between the driver and tamper: \(Y_{1}= 0.75\) GPa and \(Y_{2}= 0\); \(Y_{1}= Y_{2}= 0.375\) GPa; and \(Y_{1}= 0\) and \(Y_{2}= 0.75\) GPa. To first order, constant values of the sum \(Y_{1}+Y_{2}\) do give similar results, but there are some differences. A fluid driver (\(Y_{1}= 0\)) gives the greatest spike growth, while the equal distribution of strength gives the least; the case of the fluid tamper (\(Y_{2}= 0\)) is intermediate. The insets show the shapes of the arrested spikes for the three cases. While the three are similar, the spike for the fluid driver case has a flat front, and that for the equal distribution case is more rounded overall. For cases of smaller spike growth, the effect of the strength distribution is less pronounced. We have not examined conditions where the spikes grow further or break up, but one would expect the effect of the strength distribution to be even greater.

Fig. 5
figure 5

Spike amplitude evolution for different distributions of strength between the driver and tamper. Insets illustrate the arrested spike shape at late time

Full size image

Role of A and \(k\eta _{o}\)

Varying the other two controlling parameters of the RMI, the wave parameter \(k\eta _{o}\) and the Atwood number A, will also affect the spike evolution. To investigate the effect of varying A, we increased and decreased \(\rho _{2}\) by 50%, which changes A by about 20%. This change in density causes \(P_{2}\) to change as well, as illustrated by the \(P-u\) diagram in Fig. 6a. Increasing the tamper density increases \(P_{2}\) to 31 GPa, while decreasing it gives 13 GPa. Note that one could maintain a constant value of \(P_{2}\) with the denser tamper by decreasing the impact velocity to 1.65 km/s. Such a change would result in a lower initial shock pressure, resulting in a lower temperature for the driver during the RMI growth phase. The mass velocity \(u_{2}\) could similarly be held constant by adjusting the impact velocity. Also shown in the figure for comparison are the Hugoniots for tin (Sn) and mercury (Hg), which have a low melting point and are a fluid, respectively. The spike evolution for increased and decreased \(\rho _{2}\) are shown in Fig. 6b with the results shown previously for \(A=-0.69\). For higher tamping (increased \(\rho _{2}\)), spike growth is suppressed, while the opposite occurs for lower tamping. In the latter case, the spike eventually fails and the tip separates.

Fig. 6
figure 6

Effects of varying the Atwood number A: a \(P-u\) diagram showing pressure states achieved and b spike amplitude evolution. Inset images show the spike configurations at late times

Full size image

Similar effects are seen as \(k\eta _{o}\) is varied as seen in Fig. 7. For lower values, spike growth is reduced, leading to spikes similar to that for the \(A=-0.56\) case. Increasing it leads to enhanced spike growth, with the \(k\eta _{o}=0.79\) case giving results similar to the \(A=-0.83\) case. For even higher values, the spike “mushrooms” as seen in the inset. Such mushrooming only occurs in RMI when there is tamping.

Fig. 7
figure 7

Spike amplitude evolution for variations in the wave parameter \(k\eta _{o}\). Inset image shows mushrooming of the spike at late times for \(k\eta _{o}=1.26\)

Full size image

EOS of Driver and Tamper

To investigate the sensitivity of the RMI to the EOSs of the driver and tamper, we independently varied the Mie–Grüneisen parameters \(c_{o}\) and s by 25% for each of the materials. The spike length is found to be somewhat sensitive to the EOS parameters for the driver: there is about a 10% change when \(c_{o}\) of the tantalum is varied by \(\pm 25\%\), and about a 3% change when \(s_{1}\) is varied. Varying the parameters of the tamper results in a change of 2% or less in the spike length. Some of the effect from varying the parameters can be explained through changes in the interface velocity \(u_{2}\), but there are other effects that play a role. In particular, we note that Mikaelian [42] suggests the use of an effective Atwood number accounting for compressibility. Nevertheless, the EOS parameters appear to play only a modest role in the RMI, so precise knowledge of the EOSs are not required. It should be mentioned that phase transformations such as those studied by Jensen et al. [16] and Freeman et al. [29] could have a much more pronounced effect than the variations considered here.

In addition to the changes in the EOSs considered above, we also consider a more dramatic change. Rather than utilizing a fluid as the tamper, one could use a powdered form of a metal with a relatively low melting point. For example, we consider tamping using a tin (Sn) powder with density 3.1 g/\(\hbox{cm}^{3}\), which corresponds to a porosity level of about 57%. This provides the same value of \(A=-0.69\) as that used previously. Using a simple \(P-\alpha\) model [43] to describe the removal of porosity in the tin powder, we find that \(P_{2} = 17\) GPa, somewhat lower than the 24 GPa for the baseline case. Given the 505 K melting temperature of tin under ambient pressure, we would expect porous tin to be completely melted or at least so hot as to have no significant strength under that shock loading. The simulation show that the spike amplitude increases only by about 2.5%, even though the Atwood number changes significantly so that its final value is \(A_{f}=-0.42\). Thus, it appears that even if the driver and tamper have very different compressibilities, the spike growth is controlled, at least to first order, by the initial value of A. Additional discussion of the use of metal powder tampers can be found in “Tamper Materials” section.

The Role of Damage

Prime et al. [17, 18] found that their experiments with \(A=-1\) were quite sensitive to damage that occurs in the sample due to the release from the free surface. While the tamped configuration does lead to release propagating into the driver, the pressure is maintained at \(P_{2}\), which reduces the role of damage. As shown previously (see Fig. 4), there is no appreciable plastic work done in the presence of negative pressure for the sodium metatungstate solution tamper. To examine the effect of damage, we utilized the simple Johnson-Cook fracture model [44] for the Ta driver. While the Johnson-Cook fracture model is relatively simplistic and may not be suitable for all cases that might be of interest, it does provide an easy way to evaluate the role of damage. For \(A=-1\), a significant effect on the jet length is found. If water is used as the tamper (\(A=-0.89\)), only about a 5% increase in spike length is found due to the addition of the damage model. We note that the result is relatively insensitive to the damage model parameters. For the sodium metatungstate tamping (\(A=-0.69\)), though, we find no significant effect on spike length due to the damage model. Examination of the damage fields indicate that for water tamping there is a relatively small region of slightly (\(D<0.1\), where D is the scalar damage parameter that varies from 0 in the undamaged state to 1 if fully damaged) damaged material near the bubble. For sodium metatungstate solution tamping, the damaged region is smaller and even less damaged (\(D<0.05\)). Based on these results it appears that even modest tamping, say \(A>-0.90\) minimizes the effect of damage on a ductile driver. However, a less ductile driver material or a material with a lower spall strength may still be susceptible to damage at that level of tamping. Thus, a more careful evaluation of damage is probably merited when studying a material at low levels of tamping.

Dimensionality

Most experimental and simulation work on RMI with solids has been performed in a 2-D configuration. While studies of RTI indicate that the instability grows more rapidly in 3-D [45], Bakhrakh et al. [6] report that under some conditions the strength of the material can cause 3-D instabilities to grow more rapidly. The same conclusion is reached for RMI in fluids by Chapman and Jacobs [46], but there does not appear to be a definitive study for RMI involving strong solids. Sternberger et al. performed 2-D and 3-D RMI experiments with tantalum [32] and copper [33]. Unfortunately, differences in wavelength between the two configurations made comparisons difficult. Here, we evaluate the effect of dimensionality using a slightly different approach.

In simulations, the 2-D configuration with many wavelengths can be treated as periodic by using rigid lateral boundaries, as has been done here. To avoid expensive three-dimension calculations, we consider an axisymmetric configuration, which we will refer to as 2-DA. As can be seen in Fig. 8a, \(\xi\) grows somewhat faster initially and reaches larger magnitudes for the 2-DA case. In fact, while all of the 2-D cases shown arrest, only one of the 2-DA cases does in the time shown.

Fig. 8
figure 8

Spike amplitude evolution for 2-D and 2-DA perturbations for varying wave parameters for the case considered previously (\(A=-0.69\), \(Y_{1}=0.75\) GPa) with a rigid boundaries at \(x=\lambda /2\) and b isolated conditions

Full size image

The 2-D configuration with periodic wavelengths can be treated with rigid boundaries at \(x=\pm \lambda /2\), which is computationally convenient. Treating the 2-DA simulations with a rigid boundary at \(r=\lambda /2\) does not correspond to a periodic condition, though it is reasonably close to a hexagonal arrangement of perturbations. In order to compare the 2-D and 2-DA configurations in another manner, we consider a single perturbation surrounded by a flat region of the driver: an isolated perturbation. For this case, we report the amplitude as \(\xi = y_{s} - y_{\infty }\) where \(y_{\infty }\) is the position of the driver far away from the perturbation. As seen in Fig. 8b, 2-DA perturbations again grow faster and more than 2-D ones. The two configurations are only slightly different for the 2-DA case, but in 2-D, perhaps somewhat surprisingly, periodic perturbations lead to larger spikes than does an isolated one.

Experimentally, Bolis et al. [47] used an axisymmetric configuration in RTI experiments. The axisymmetry of the problem allowed them to use multiple flash X-ray setups to track the spike evolution. The enhancement of spike formation seen in Fig. 8 suggests that an axisymmetric configuration could be useful to enhance spike formation when it is marginal. The ability to arrange separated axisymmetric perturbations on the plane of the driver could also be exploited to utilize radiography capabilities better.

Simulation Resolution

Previous studies [17], [32], [33], [34] found that calculations of RMI growth were sensitive to cell size, so this aspect was investigated by refining the cell size from the baseline case of \(\lambda /\varDelta x = 100\). The spike evolution as a function of cell size is shown in Fig. 9. Each reduction in cell size results in a slightly greater late-time arrested spike length \(\xi _{\infty }\). Fitting a power law relationship (see inset of figure) gives \(\xi _{\infty } \rightarrow 1.133\) mm as \(\varDelta x/\lambda \rightarrow 0\), an error of about 20% for the baseline resolution. Examination of behavior for a less severe initial perturbation (\(k\eta =0.31\), see Fig. 7) and a stronger one (\(k\eta =0.94\)) indicate that the relative errors are consistent across a reasonably wide range of conditions. Since our purpose here is to examine broad trends, issues of resolution are not of great concern. On the other hand, if one is trying to calibrate a strength model to RMI growth characteristics, then resolution effects should be accounted for.

We note that the power law exponent for mesh convergence for \(k\eta _{o}=0.63\) is 0.42, while that for \(k\eta _{o}=0.31\) is 0.75. Both of these are lower than the value of 0.97 reported by [32]. It is not clear if this large difference is due to the different configuration (\(A>0\) versus \(A<0\) here) they utilized or is associated with the computational approach used.

Fig. 9
figure 9

Spike amplitude evolution with cell size refinement. The inset shows the evolution of the spike amplitude and a power-law fit to the results and its limit value

Full size image

Scaling

Motivated by observations of the effect of the three different parameters A, \(k\eta _{o}\), and \(\overline{Y}\) as illustrated in Figs. 3, 6b,  and 7, here we explore scaling relationships between spike growth and the key non-dimensional parameters. The first two parameters are non-dimensional, and \(\overline{Y}\) is incorporated into the term \(1/{\tilde{Y}} = \overline{\rho }u_{2}^{2} / \overline{Y}\) (the tilde over-symbol denotes a non-dimensional parameter) following the approach of Mikaelian [24]. While different expressions for spike growth have been proposed as discussed in “The Richtmyer–Meshkov Instability” section, there has not been a comprehensive study of the role of the three non-dimensional parameters, especially in the non-linear regime. Scaling laws that might be found would be useful for designing experiments where different parameters can be varied simultaneously. In this section, we perform a large number of simulations by randomly sampling parameter values in order to establish an appropriate relationship for all three that is valid into the non-linear regime. First, we focus on the spike length for simulations where a stable arrested spike is formed without separation or mushrooming, which is probably the preferred case when radiography is used. Second, we consider spike and bubble velocities, both their peak values and the time for them to equilibrate, since those quantities could be measured using laser interferometry.

To generate a data set with which to examine scaling, we perform an ensemble of simulations by randomly sampling some parameter values while holding the remaining parameters constant. We fix \(\lambda = 2\) mm, and the driver is taken to have the EOS parameters of tantalum (see Table 1). The Mie–Grüneisen EOS parameters of the tamper except the density are fixed as those given in Table 1, and we assume it behaves as a fluid (\(Y_{2}=0\)). In each simulation of the ensemble, values of tamper density \(\rho _{2}\), strength of the driver \(Y_{1}\), perturbation parameter \(k\eta _{o}\), and impact velocity \(V_{imp}\) are chosen uniformly from the ranges given in Table 2. The range of \(\rho _{2}\) gives values of A from −0.89 to −0.36. A total of 2000 simulations were performed with the parameters uniformly sampled across the given ranges. The simulations were generally run for a simulation time of 5 μs. From each simulation, we extract values of the maximum spike velocity \(u_{sp}^{max}\) and \(\xi _{end}\), the spike amplitude at the end of the simulation. We also determine the value of \(u_{2}\) from a separate 1-D calculation.

Table 2 Ranges for simulation parameters used in ensemble calculations
Full size table

Spike Length

We first focus on the length of the spikes that form and arrest. This quantity can be readily measured with radiographic imaging, but it can, in principal, also be measured using laser velocimetry [16, 28]. This is more easily done for the \(A = -1\) case, but it has been attempted with water tamping [26], though the optical behavior of the shocked liquid can complicate analysis. We screen the ensemble for those realizations for which \(\dot{\xi }/u_{2} > 0.02\) at 5 μs in an attempt to ensure that only results for arrested spikes are considered. This criterion is not always reliable, so we utilize the visualization tool Slycat [48] to examine the results, particularly the outliers when plotted where \(\dot{\xi }/u_{2} < 0.02\) as well as those where \(0.02< \dot{\xi }/u_{2} < 0.10\). In some cases, it was necessary to run the simulations beyond 5 μs to conclusively determine if the case arrested. Given, the large number of simulations, it is possible that some of those deemed to have arrested actually still displayed mushrooming or separation, though spot-checking did not reveal any examples. If the spike arrests, then there is a well-defined value of \(\xi _{\infty } = \xi _{end}\), but if it separates or mushrooms then \(\xi _{\infty }\) is not defined.

The results for non-dimensional spike length \({\tilde{\xi }}_{\infty }\) = \(\pi (\xi _{\infty }+2\eta _{o})/\lambda\) from the ensemble of simulations are plotted against the non-dimensional parameters A, \(k\eta _{o}\), and \(1/{\tilde{Y}}\) in Fig. 10. Simulations in which the spike arrests are denoted by blue symbols, while red symbols show those cases that do not arrest. By inspection, the exponents associated with these parameters that collapse the ensemble best are 2, 2, and 1, respectively. The exponents associated with \(k\eta _{o}\) and \(1/{\tilde{Y}}\), are consistent with previous results [13, 15, 24, 25], and that associated with A is the same as that from Mikaelian [24] and similar to that of Chen et al. [25].

A linear fit to the data that passes through the origin has a slope of 0.18 but does not fit the data well. Restricting the fit to low values of spike amplitude would give a somewhat higher slope to the fit in line with previous results [13, 15, 24]. A power law form given by

$$\begin{aligned} \frac{\pi (\xi _{\infty }+2\eta _{o})}{\lambda } = 0.30 \left( A^{2} (k\eta _{o})^{2} \frac{\overline{\rho }u_{2}^2}{\overline{Y}}\right) ^{0.77} \end{aligned}$$
(12)

fits the data well. We note that a separate ensemble of simulations using copper drivers and a tamper with strength gave very similar values for the power law fit, as one would expect if the problem is indeed governed by the non-dimensional parameters used here.

Fig. 10
figure 10

Scaling of late-time spike amplitude for 2000 realizations of Ta tamped by a liquid in which A, \(k\eta\), and \(Y_{1}\) are randomly varied over the ranges given in the text. Larger blue symbols indicate that the spike arrested, while smaller red ones indicate that the spike did not arrest (Color figure online)

Full size image

The results that arrest become noticeably sparse for \({\tilde{\xi }}_{\infty } > 20\), and the longest spike found is \({\tilde{\xi }}_{\infty } = 29.2\). Of course, it is possible that sampling more from the current phase space or a larger one would result in an example that gives a greater \({\tilde{\xi }}_{\infty }\). We also note that the longest spikes generally arrest after necking has begun, suggesting that it would be very difficult to experimentally achieve values of \({\tilde{\xi }}_{\infty } > 20\) and be able to verify that they have arrested.

In the realizations that arrest, there is no significant correlation between \({\tilde{\xi }}_{\infty }\) and A, but the maximal \({\tilde{\xi }}_{\infty }\) achieved increases nearly linearly with \(k\eta _{o}\) as shown in Fig. 11a. Thus, the longest spikes all occur in realizations with relatively large \(k\eta _{o}\). The maximum value for \({\tilde{\xi }}_{\infty }\) initially increases approximately linearly with \(1/{\tilde{Y}}\). After that, the maximum value increases a bit more before gradually falling off for larger values of \(1/{\tilde{Y}}\). The largest value for which the spike is found to arrest is \(1/{\tilde{Y}} = 377\), but arresting spikes were found for the entire range of A and \(k\eta _{o}\) sampled.

Fig. 11
figure 11

Spike amplitudes for realizations in which it arrests (a) as a function of the wave parameter \(k\eta _{o}\) and b as a function of \(1/{\tilde{Y}}\)

Full size image

Spike and Bubble Velocities

While arrested spike length is an attractive experimental metric if high-speed radiography is available, velocimetry is much more available for routine use. Partly for this reason, Prime et al. [17, 18] utilized the maximum spike velocity \(u_{sp}^{max}\) as their experimental metric. The normalized maximum velocity from the ensemble of simulations is shown in Fig. 12 with the symbols again denoting whether the spike arrests or not. Of course, as pointed out by Prime et al. maximum spike velocity can be utilized even for cases where the spike does not arrest. The data for the arresting cases are collapsed reasonably well using a scaling different from that used in Fig. 10, namely exponents of 1.5, 1, and 0.2 on A, \(k\eta _{o}\), and \(1/{\tilde{Y}}\), respectively. Thus, the maximum velocity is relatively insensitive to the value of \(Y_{1}\) for cases that arrest, which is consistent to what was seen previously in Fig. 3. Those cases that arrest are represented reasonably well by the linear fit shown in the figure. In contrast, those that do not arrest are more scattered due to the multiple types of behavior they display (e.g. breaking up, mushrooming), and many deviate significantly from the scaling mentioned above. Some are intermingled with the cases that arrest, and those cases are found to separate. Somewhat surprisingly, the highest of the velocities for the non-arresting cases are only slightly higher than those for the arresting cases. The effect of simulation resolution on \(u_{sp}^{max}\) is small: only a 2.6% error is found between the value for \(\lambda/\varDelta x =100\) and the estimate for the converged value.

Fig. 12
figure 12

Scaling of maximum spike velocity for 2000 realizations of Ta tamped by a liquid in which A, \(k\eta\), and \(Y_{1}\) are randomly varied over the ranges given in the text. Larger blue symbols indicate that the spike arrested, while smaller red ones indicate that the spike did not arrest (Color figure online)

Full size image

Because certain case in “Spike Length” section took longer than the initial default run time to arrest, the time at which the spike arrests was examined further. For the simulations where the spike arrests, we extract the value of \(t_{cross}\), which is defined as the first time when \(u_{sp} = u_{bub}\). Referring back to the results in Fig. 3, \(t_{cross}\) is about 3.7 μs for the \(Y=0.75\) GPa case. In some cases, \(u_{sp}\) and \(u_{bub}\) can oscillate about a mean value (\(u_2\)) after \(t_{cross}\) due to wave reverberations. This typically occurs for cases where the spike growth arrests rapidly. It is found that at \(t_{cross}\) all the points along the driver/tamper interface are, to a good approximation, moving at the same velocity in the y direction. The normalized crossing time \({\tilde{t}}_{cross}\) from each of those simulations that arrest are shown in Fig. 13. The exponents associated with the parameters A, \(k\eta _{o}\), and \(1/{\tilde{Y}}\) that collapse the ensemble best are 1, 1, and 1. Thus, we find that the \({\tilde{t}}_{cross}\) is much more sensitive to \({\tilde{Y}}\) than \({\tilde{u}}_{sp}^{max}\) is. The effect of the simulation resolution on \(t_{cross}\) is comparable to that on spike length: an error of about 16% is estimated for a resolution of \(\lambda/\varDelta x =100\).

Fig. 13
figure 13

Scaling of the time when the spike and bubble velocities are equal for the realizations of the ensemble where the spike arrests. Symbols shown in purple are cases where the spike localizes (Color figure online)

Full size image

Scrutiny of the data in the region where they are more scattered reveals that many of the simulations are moderately to severely localized due to the spikes necking down near their base. Since cases that localize but still arrest are likely to be highly sensitive to the details of the simulation, we focus on the remainder. A power law fit to those results captures them well; the coefficients for that can be found in the figure. A linear fit to the data that fall below ten on the x-axis gives a slope of 0.11. The largest value of arrest time without significant necking is \({\tilde{t}}_{cross} \approx 14\). This case has \(A=-0.385\), \(k\eta _{o}=0.468\), and \(Y_{1}=0.132\) GPa. In fact, all of the simulations with relatively large values of \({\tilde{t}}_{cross}\) had low values of \(Y_{1}\), but there does not appear to be a strong correlation with A or \(k\eta _{o}\). We note that Piriz et al. [13] found a similar relationship for the time to achieve the maximum imperfection amplitude with linear dependence on \(k\eta _{o}\) and \(1/\overline{Y}\), and their constant (0.092) was quite close to the 0.11 value found here.

Relationship to Experiments

This examination of the tamped RMI configuration is intended to provide insight for future experimental studies. Tamped RMI experiments can be conducted on most materials, but if the experiment is intended to measure strength of either the driver or tamper then a few issues should be considered:

General Considerations

  • An Atwood number that is large in magnitude provides the greatest flexibility in designing the experiment through greater spike growth. Thus, one might want to utilize materials that have very high or very low density. On the other hand, a large value of \(\mid A\mid\) will lead to a large difference between \(P_{1}\) and \(P_{2}\) as seen in Fig. 6a. This might be undesirable if the goal is to study the strength behavior of the driver at \(P_{2}\) since there will be significant residual heating from the initial shock to \(P_{1}\). Also, a smaller value of \(\mid A\mid\) will reduce the role of damage in the behavior of the driver.

Driver Materials

  • The driver material in the RMI should be ductile or fluid. Though brittle materials can behave similarly in RMI configurations to ductile metals, the complicated physics of brittle failure and post-failure behavior would make the interpretation of the experiment difficult.

  • The strength of one of the two materials should, ideally, be zero (a fluid) or small and well-characterized. The use of a fluid is preferred, but there are constraints on that as discussed below. In lieu of a fluid, a soft metal that readily deforms can be used. Copper [26, 27] is a good choice since it is readily available and widely studied. Precious metals such as gold and platinum are attractive because of their high densities, ductility, and relatively low strength.

  • If one of the materials is very, or even moderately, strong, design of a tamped RMI experiment can be challenging. Referring back to Fig. 3b, one sees that the \(Y=2\) GPa case results in little spike growth beyond the inversion for those values of A and \(k\eta\). Thus, greater levels of strength will probably result in incomplete inversion unless the magnitude of the other parameters can be increased to compensate.

Tamper Materials

  • As mentioned above, in an RMI strength experiment it is desirable to have one of the materials be a strengthless fluid—typically this would be the tamper. Liquids also have the advantage that they will conform to perturbations such as those examined here. Water (1.0 g/\(\hbox{cm}^{3}\)) or deuterated (heavy) water are well characterized and have been used in recent studies [26, 27]. The densest fluid at ambient conditions is mercury (13.6 g/\(\hbox{cm}^{3}\)), though it presents numerous concerns for experimental work. Zinc chloride solution (1.88 g/\(\hbox{cm}^{3}\)) [49], bromine (3.1 g/\(\hbox{cm}^{3}\)), thallium formate and thallium malonate (Clerici solution—4.25 g/\(\hbox{cm}^{3}\)) [50] and liquid metal (gallium/indium/tin/zinc—6.5 g/\(\hbox{cm}^{3}\)) are others of intermediate density.

  • Metals with low melting points such as Wood’s metal [30] have been utilized in RMI experiments because their low melting points would cause them to melt under shock loading. In fact, because they can be formed or cast into stable shapes, they may be more suited to experiments than fluids. Through casting at very modest temperatures, they can also conform to perturbations in the driver.

  • Beyond liquids and low melting point solids, porous metals may be viable tamper materials. Most metal powders are likely to be around 50% of their crystalline density. If the material has a relatively low melting point and is soft, then the porous form will likely melt at least partially when shocked. Pure metals such as tin, copper, silver, and gold would have densities of 3.64, 4.47, 5.25, and 9.66 \(\mathrm{g}/\mathrm{cm}^{3}\) at 50% porosity. Utilizing an alloy (e.g. gold/silver) or varying the volume fraction by manipulating the particle morphology or particle size distribution would add additional flexibility to tailor the tamper. Powdered metals will also conform to perturbations in the driver surface if their particle size is sufficiently small (\(d \ll \lambda , \eta _{o}\)).

  • For tampers less dense than water, polymer foams or even aerogels would be suitable, though one would need to ensure that the foam pore size is small compared to the dimensions \(\eta _{o}\) and \(\lambda\). Such materials would likely experience large changes in density, changing A and, potentially, the overall behavior. There are also a number of liquids that are less dense than water such as butane (0.60 g/\(\hbox{cm}^{3}\)). Cryogenic liquids are also a possibility though they would necessarily entail cold initials temperatures in the driver material.

Instrumentation

  • The tamper material chosen has implications for the instrumentation that can be utilized. For example, synchrotron radiation such as that available at the Advanced Photon Source [16] has been used to image through water [26] and \(\hbox{SiO}_{{2}}\) powder [27], but it would not penetrate any reasonable thickness of mercury or Wood’s metal. On the other hand, proton radiography [15, 28, 29] has much greater penetrating capability and could be used with, in principle, almost any tamper material.

  • Water (or heavy water) and some solutions (e.g. zinc chloride [49]) are penetrable to light used in interferometers, though their use in this manner in tamped RMI experiments would likely require characterization of their optical characteristics. Velocity interferometry is more readily available than synchrotron X-rays or proton radiography, but it is likely better suited to measuring \(u_{s}^{max}\) or \(t_{cross}\) than arrested spike amplitude. The scaling laws shown in Figs. 12 and 13 for \(u_{s}^{max}\) or \(t_{cross}\) suggest that the latter quantity is more sensitive to Y. Also, because all points on the driver/tamper interface are moving at the same velocity at \(t_{cross}\), detailed knowledge of the optical properties of the tamper may be less critical. Though it remains to be seen if the quantity can be measured accurately in experiments, the velocity records reported in some studies [16,17,18, 28] for \(A=-1\) suggest that it may be possible.

  • Recovery and post mortem examination of samples has only been used in a few studies [6, 31,32,33], and only the studies by the LLNL group have attempted to be quantitative. Further, recovery in shock experiments is fraught with difficulties so there is often some question about the states a sample experienced. Despite these issues, recovery requires no special instrumentation and, in principal, provides complete freedom in the choice of materials used. Given these potential advantages, utilizing recovery of RMI samples merits additional study.

Conclusions and Future Work

In this study, we have examined the Richtmyer–Meshkov instability in a tamped configuration as a means to study the strength of materials under conditions of high strain rate and high pressure. This work extends previous studies utilizing RMI in the untamped configuration and provides useful information on designing such experiments. One important finding is that the tamped configuration significantly reduces the role of damage by avoiding the development of tensile pressures. A second finding is that the vast majority of plastic work in the jetting driver occurs over a relatively small range of pressures and strain rates. This means that it appropriate to think of a tamped RMI experiment as probing the strength for specific conditions, and calibration to that condition using a simulation with an elastic-perfectly plastic model will provide the appropriate strength value for those conditions. By careful selection of the experimental parameters, the tamped RMI configuration should make it possible to map out the strength of materials as a function of strain rate and pressure, similar to the mapping shown by Prime et al. [18] using multiple experimental platforms.

We have examined the sensitivity of RMI growth to the parameters such as the Atwood number A, the wave parameter \(k\eta _o\), the strength of the materials, and others. We performed an ensemble of simulations in which the parameters are varied over specific ranges. When the parameters are plotted in non-dimensional form, the cases in the ensemble where the spikes arrest collapse to a single curve. Somewhat different sensitivities to the input parameters were found when the arrested spike length and the maximum spike velocity were considered. Specifically, the spike length varies as \(Y^{-1}\), while the maximum spike velocity varies as \(Y^{-0.2}\) for cases that arrest. However, by utilizing non-arresting cases the maximum spick velocity can be made a more sensitive measure, and the ability to measure the quantity with velocimetry and to utilize cases where the jet does not arrest are attractive. An additional experimental quantity to measure, the time at which the spike and bubble velocities are equal, was suggested. This quantity can be measured using velocity interferometry, and it varies as \(Y^{-1}\). It remains to be seen, however, if this quantity can be measured accurately in experiments.

To fully realize the potential of tamped RMI experiments, there is a need for improved understanding of potential tamper materials. In most of the simulations shown in “Simulation Results” section, a sodium metatungstate solution is used. However, there are no known measurements of shock behavior for it, nor does any data exist for optical properties that might be needed in order for laser interferometry to be used with it. Other liquids or low-melting-point materials may also prove useful as tampers, especially if one can handle the hazards associated with them. When utilizing radiography, metal powders that melt under shock loading seem to provide much greater flexibility than the relatively few high-density fluids that are known.

The focus of this study of the tamped RMI configuration is its use in studying the strength of the driver material. However, if the behavior of the driver material is adequately known the configuration can be used to study the strength of the tamper material as has been reported by Hudspeth et al. [27] for \(\hbox{SiO}_2\) powder. Use of RMI in this manner merits further study to address outstanding questions. For example, the pressure and strain rate states experienced by the tamper (see Fig. 4) has not been investigated.

While we have extensively examined the case where \(A < 0\) (\(\rho _{1} > \rho _{2}\)), little attention has been given to the case where \(A > 0\). This configuration may have some advantages in probing material strength due to the lack of unloading in either the driver or tamper. However, this configuration makes it difficult or impossible to monitor the interface with optical velocimetry and, thus, probably requires the use of radiography or recovery.

Finally, we note that something similar to the Richtmyer–Meshkov instability involving a non-planar shock wave intersecting a planar interface can be realized through the use of a periodic “lens” as suggested by Bakhrakh et al. [6]. While this configuration will likely also require radiography or recovery, it offers additional flexibility in designing experiments. Further, this configuration could be used for samples for which it is impractical to make sinusoidal interfaces: e.g. very hard materials such as armor ceramics or high-strength steels. Such materials could be tested using flat samples. To date, though, this configuration appears not to have been used in a quantitative manner to “measure” material strength.